Abstract
We consider the problem of metastability for stochastic dynamics with exponentially small transition probabilities in the low temperature limit. We generalize previous model-independent results in several directions. First, we give an estimate of the mixing time of the dynamics in terms of the maximal stability level. Second, assuming the dynamics is reversible, we give an estimate of the associated spectral gap. Third, we give precise asymptotics for the expected transition time from any metastable state to the stable state using potential-theoretic techniques. We do this in a general reversible setting where two or more metastable states are allowed and some of them may even be degenerate. This generalizes previous results that hold for a series of only two metastable states. We then focus on a specific Probabilistic Cellular Automata (PCA) with configuration space \({\mathcal {X}}=\{-1,+1\}^\varLambda \) where \(\varLambda \subset {\mathbb {Z}}^2\) is a finite box with periodic boundary conditions. We apply our model-independent results to find sharp estimates for the expected transition time from any metastable state in \(\{\underline{-1}, {\underline{c}}^o,{\underline{c}}^e\}\) to the stable state \(\underline{+1}\). Here \({\underline{c}}^o,{\underline{c}}^e\) denote the odd and the even chessboard respectively. To do this, we identify rigorously the metastable states by giving explicit upper bounds on the stability level of every other configuration. We rely on these estimates to prove a recurrence property of the dynamics, which is a cornerstone of the pathwise approach to metastability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Metastability is a phenomenon that occurs when a physical system is close to a first order phase transition. Among classical examples are super-saturated vapors and ferromagnetic materials in a hysteresis loop [52]. The metastability phenomenon occurs only for some thermodynamical parameters when a system is trapped for a long time in a state different from the stable state. This is the so-called metastable state. While the system is trapped, it behaves as if it was in equilibrium, except that at a certain time it makes a sudden transition from the metastable state to the stable state. Metastability occurs in several physical situations and this has led to the formulation of numerous models for metastable behavior. However, in each case, three interesting issues are typically investigated. The first is the study of the transition time from any metastable state to any stable state. The fluctuations of the dynamics should facilitate the transition, but these are very unlikely, so the system is typically stuck in the metastable state for an exponentially long time. The second issue is the identification of certain configurations, the so-called critical configurations, that trigger the transition. The system fluctuates in a neighborhood of the metastable state until it visits the set of critical configurations during the last excursion. After this, the system relaxes to equilibrium. The third and last issue is the study of the typical paths that the system follows during the transition from the metastable state to the stable state, the so-called tube of typical trajectories. This issue is especially interesting from a physics point of view.
The goal of this paper is twofold. First, we prove some model-independent results. In particular we consider general dynamics with exponentially small transition probabilities and we give an estimate of the mixing time. Moreover, for a reversible dynamics, we estimate the spectral gap of the transition matrix in terms of the maximal stability level, and we compute the expected value of the transition time for a series of more than two (possibly degenerate) metastable states. Second, we focus on a specific Probabilistic Cellular Automata in a finite volume, at small and fixed magnetic field, in the limit of vanishing temperature and we prove sharp results describing the metastable behaviour of the system.
Let us now discuss the two goals in detail, starting with a comparison between our estimates for the mixing time and the spectral gap and the literature on the topic. Similar results on the estimate of the mixing time and the spectral gap have been proved for the model of simulated annealing in [14]. The authors use Sobolev inequalities to study the simulated annealing algorithm and they demonstrate that this approach gives detailed information about the rate at which the process is tending to its ground state. Thanks to this result, the mixing time is estimated for Metropolis dynamics in [46, Proposition 3.24]. We give a model-independent estimate of the mixing time for a dynamics (not necessarily Metropolis) with exponentially small transition probabilities, in a finite volume.
The analysis of the spectral gap between the zero eigenvalue and the next-smallest eigenvalue of the generator is very interesting for Markov processes, since it is useful to control convergence to equilibrium. In [10] the authors focus on the connection between metastability and spectral theory for the so-called generic Markov chains under the assumption of non-degeneracy. In particular, they use spectral information to derive sharp estimates on the transition times. We refer also to [7, Chapters 8 and 16], where the authors incorporate all the previous results about the study of metastability through spectral data. In particular, they show that the spectrum of the generator decomposes into a cluster of very small real eigenvalues that are separated by a gap from the rest of the spectrum. In order to study the PCA in Sect. 3.1, we need to extend their estimates of the spectral gap to the case of degenerate in energy metastable states and to a model with the Hamiltonian that depends on the asymptotic parameter \(\beta \). The states \(\sigma \) and \(\eta \) are degenerate metastable states if they have the same energy and the energy barrier between them is smaller then the energy barrier between a metastable state and the stable state (see Condition 2.1 for a precise formulation and see [7, Chapter 16.5 point 3] for a discussion). To suit our purposes, we express these estimates as functions of the virtual energy instead of the Hamiltonian function, see Eq. (2.4) for the specific definition and [14, 21]. Indeed, when the Hamiltonian function depends on some asymptotic parameter, it is convenient to compute the model-dependent quantities in terms of the virtual energy.
Regarding the expected transition time, in [25] the authors consider series of two metastable states with decreasing energy in the framework of reversible finite state space Markov chains with exponentially small transition probabilities. Under certain assumptions, not only they find the (exponential) order of magnitude of the transition time from the first metastable state to the stable state, they also give an addition rule to compute the prefactor. We generalize their results on the mean transition time and their addition rule to a setting with several degenerate metastable states, see Sect. 2.4 for details.
The second goal concerns a particular Probabilistic Cellular Automata (PCA). Cellular Automata (CA) are discrete-time dynamical systems on a spatially extended discrete space and are used in a wide range of applications, for example to model natural and social phenomena. Probabilistic Cellular Automata (PCA) are the stochastic version of Cellular Automata, where the updating rules are random, i.e., the configurations are chosen according to probability distributions determined by the neighborhood of each site. Mathematically, we consider PCA with parallel (synchronous) dynamics, i.e., systems of finite-states Markov chains whose distribution at time n depends only on the states in a neighboring set at time \(n-1\). PCA are characterized by a matrix of transition probabilities from any configuration \(\sigma \) to any other configuration \(\eta \) defined as a product of local transition probabilities as
where \(\varLambda \subset {\mathbb {Z}}^2\) is a finite box with periodic boundary conditions and \({\mathcal {X}}=\{-1,+1\}^{\varLambda }\) is the set of all configurations. Here we consider a specific PCA in the class introduced by Derrida [31], where the local transition probability is a certain function of the sum of neighboring spins \(S_{\sigma }(\cdot )\) (2.28) and the external magnetic field h
We obtain our PCA by summing only over the nearest neighbor sites, see (3.1) and Fig. 1. When the sum is carried out over a symmetric set, the resulting dynamics is reversible with respect to a suitable Gibbs-like measure \(\mu \) defined via a translation invariant multi-body potential, see (2.26). This measure depends on a parameter \(\beta \) which can be thought of as the inverse of the temperature of the system. For small values of the temperature, the PCA is likely to be found in the local minima of the Hamiltonian associated to \(\mu \). The metastable behavior of this model has been investigated on heuristic and numerical grounds in [6]. A key quantity in the study of metastability is the energy barrier from one of the metastable states to the stable state. This is the minimum, over all paths connecting the metastable to the stable state, of the maximal transition energy along each path, minus the energy of the starting configuration (see (2.6)–(2.7)). Intuitively, the energy barrier from \(\eta \) to \(\sigma \) is the energy that the system must overcome to reach \(\eta \) starting from \(\sigma \).
For our choice of parameters, our PCA has one stable state \(\underline{+1}\) and peculiarly three metastable states, which we identify rigorously as \(\{\underline{-1},{\underline{c}}^e, {\underline{c}}^o\}\). To prove this, we will construct for each configuration \(\sigma \notin \{\underline{-1},{\underline{c}}^e, {\underline{c}}^o, \underline{+1} \}\) a path starting from \(\sigma \) and ending in a lower energy state, such that the maximal energy, along the path, is lower than the energy barrier from \(\underline{-1}\) to \(\underline{+1}\). This leads to an explicit upper-bound \(V^*\) for the stability level of every configuration except \(\{\underline{-1},{\underline{c}}^e,{\underline{c}}^o,\underline{+1}\}\), in Lemma 3.1, which we will refer to as our main technical tool. We rely on this estimate to prove two recurrence properties. The first is that, starting from any configuration, the system reaches the set \(\{\underline{-1},{\underline{c}}^e, {\underline{c}}^o,\underline{+1}\}\) in a time smaller than \(e^{\beta V^*}\) with probability exponentially close to one. The second is that starting from any configuration the system reaches \(\underline{+1}\) in a time smaller than \(e^{\beta \varGamma ^{\text {PCA}}}\). To prove this, we combine our main tool with the computation of the energy barrier \(\varGamma ^{\text {PCA}}\) in [19] to prove the second recurrence property. We remark that \({\underline{c}}^e\) and \({\underline{c}}^o\) are two degenerate metastable states, since they have the same energy and the energy barrier between them is zero. Hence, we will use the shorthand \({\underline{c}}=\{{\underline{c}}^e,{\underline{c}}^o\}\).
In order to find sharp estimates of the transition time from \(\underline{-1}\) to \(\underline{+1}\) for the PCA model in Sect. 3.1, we extend the model-independent theorems given in [25], which hold for a series of two metastable states. Indeed, we are interested in analyzing energy landscapes characteried by a series of three or more metastable states, possibly degenerate. To do so, in Sect. 2.4, we generalize the three model-independent conditions upon which Theorems 2.3, 2.4, 2.6, 2.7, 2.8 hinge. The first condition for our PCA model is stated and proved in Theorem 3.1, while it was assumed to hold without proof in [24]. The second condition is the property that starting from \(\underline{-1}\) the system visits the chessboard \({\underline{c}}\) before reaching \(\underline{+1}\) with high probability, that is proved in [19]. The third condition is the computation of the constants \(k_1\) and \(k_2\) done in [24]. Having verified the three model-independent conditions for our PCA model, we apply Theorems 2.6, 2.7, 2.8 and we conclude the sharp estimate for the mean transition time in Theorem 3.2.
Regarding the model-dependent results, [19] focuses on the transition from the metastable states to the stable state. In particular, the authors describe the tube of typical trajectories and they also estimate the transition time. To do this, they analyze the geometrical conditions for the shrinking or the growing of a cluster. Furthermore, they characterize the local minima of the energy and the so-called traps for the PCA dynamics. Building on this, we construct a specific path from any cluster to the stable state that the system follows with probability tending to one. Our estimates of the stability levels in Lemma 3.1 are based on these characterizations.
The authors in [23] consider a reversible PCA model with self-interactions, that is a specific model which we use as second example in Sect. 2.3. In particular they prove the recurrence to the set \(\{\underline{-1},\underline{+1}\}\) and that \(\underline{-1}\) is the unique metastable state. They estimate the transition time in probability, in \(L^1\) and in law. Moreover, they characterize the critical droplet that is visited by the system with probability tending to one during its excursion from the metastable to the stable state. Furthermore, in [45] they prove sharp estimates for expected transition time by computing the prefactor explicitly.
State of the art. A first mathematical description of metastability [52] was inspired by Gibbsian Equilibrium Statistical Mechanics and was based on the computation of the expected values with respect to restricted equilibrium states. The first dynamical approach, known as pathwise approach, was initiated in [13] and developed in [49, 50, 55], see also [51]. This approach derives large deviation estimates of the first hitting time and of the tube of typical trajectories. It is based on the notions of cycles and cycle paths and it hinges on a detailed knowledge of the energy landscape. Independently, similar results based on a graphical definition of cycles were derived in [14, 15] and applied to reversible Metropolis dynamics and to simulated annealing in [16, 56]. The pathwise approach was further developed in [20, 21, 41] to disentangle the study of transition time from the one of typical trajectories. This method was applied in [1, 18, 26, 29, 37, 38, 40, 44, 47, 48, 51] for Metropolis dynamics and in [19, 22, 23] for parallel dynamics.
The potential-theoretical approach is based on the study of the hitting time through the use of the Dirichlet form and spectral properties of the transition matrix. One of the advantages of this method is that it provides an estimate of the expected value of the transition time including the prefactor, by exploiting a detailed knowledge of the critical configurations, see [7, 11]. This method was applied in [2, 8, 12, 25, 30] for Metropolis dynamics and in [45] for parallel dynamics.
Recently other approaches are described in [3, 4, 34] and in [5].
The more involved infinite volume limit, at low temperature or vanishing magnetic field, was studied for Metropolis dynamics via large deviation techniques in [17, 28, 42, 43, 53, 54] and via the potential-theoretical approach in [9, 33, 35, 36, 38].
Outline. The paper is organized as follows, in Sect. 2 we define a general setup and we present the main model-independent results with some applications to concrete models. In Sect. 3 we describe the reversible PCA model that we consider and we present the main model-dependent results. In Sect. 4 we carry out the proof of the model-independent results, and in Sect. 5 we carry out the proof of the model-dependent results. Finally in Appendix we prove theorems stated in Sect. 2.4.
2 Model-Independent Results
2.1 General Setup and Definitions
Let \({\mathcal {X}}\) be a finite set, which we refer to as state space, and let \(\varDelta :{\mathcal {X}} \times {\mathcal {X}} \longrightarrow {\mathbb {R}}^+ \cup \{ \infty \}\) be a function, which we call rate function. \(\varDelta \) is said to be irreducible if for every \(x,y \in {\mathcal {X}}\) there exist a path \(\omega =(\omega _1,...,\omega _n) \in {\mathcal {X}}^n\) with \(\omega _1=x\), \(\omega _n=y\) and \(\varDelta (\omega _i,\omega _{i+1}) < \infty \) for every \(1 \le i \le n-1\), where n is a positive integer. A family of time-homogeneous Markov chains \((X_n)_{n \in {\mathbb {N}}}\) on \({\mathcal {X}}\) with transition probabilities \({\mathcal {P}}_\beta \) indexed by a positive parameter \(\beta \) is said to have rare transitions with rate function \(\varDelta \) when
for any \(x,y \in {\mathcal {X}}\). Intuitively, \(\varDelta (x,y)= + \infty \) should be understood as the fact that, when \(\beta \) is large, there is no possible transition between states x and y. We also note that condition (2.1) is sometimes written more explicitly as [21, Eq. (2.2)]: for any \(\gamma >0\), there exists \(\beta _0>0\) such that
for any \(\beta >\beta _0\) and any \(x,y \in {\mathcal {X}}\), where the parameter \(\gamma \) is a function of \(\beta \) that vanishes for \(\beta \rightarrow \infty \). Because of this, we also refer to the function \(\varDelta (x,y)\) as the energy cost of the transition from x to y. Next, we define the Gibbs measure
where \(G: {\mathcal {X}} \longrightarrow {\mathbb {R}}\) is the so-called Hamiltonian function. Now, we are able to give the definition of the virtual energy
Definition (2.4) is well-posed, since for large \(\beta \), the Markov chain \((X_n)_{n}\) is irreducible and its invariant probability distribution \(\mu \) in (2.3) is such that for any \(x \in {\mathcal {X}}\) the limit \(\lim _{\beta \rightarrow \infty }-\frac{1}{\beta }\log \mu (x)\) exists and is a positive real number, see [14] and [21, Prop. 2.1].
We define the transition energy for a pair of configurations as the sum between the virtual energy of the first configuration and the energy cost of the transition between the two configurations.
where x, y are configurations in \({\mathcal {X}}\). Note that for Metropolis dynamics the transition energy between two configurations is given by the maximum of the energy of the two configurations.
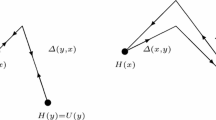
Let \(\omega =\{\omega _1,...,\omega _n\}\) be a finite sequence of configurations such that \({\mathcal {P}}_\beta (\omega _i,\omega _{i+1})>0\) for \(i=1,...,n-1\), \(\omega \) is a path of length \(|\omega |=n\) with starting configuration \(\omega _1\) and final configuration \(\omega _n\) (Fig. 2). We define the height along \(\omega \) either as \(\varPhi _\omega =H(\omega _1)\) if \(|\omega |= 1\), or if \(|\omega |>1\)
Let \(x,y\in {\mathcal {X}}\) be two configurations. The communication height between two configurations x, y is defined as
where \(\varTheta (x,y)\) the set of all the paths \(\omega \) starting from x and ending in y (Fig. 3). Similarly, we also define the communication height between two sets \(A, B \subset {\mathcal {X}}\) as
The first hitting time of \(A\subset {\mathcal {X}}\) starting from \(x \in {\mathcal {X}}\) is defined as
Whenever possible we shall drop from the notation the superscript denoting the starting point. For any \(x\in {\mathcal {X}}\), let \({\mathcal {I}}_x\) be the set of configurations with energy strictly lower than H(x), i.e.,
The stability level \(V_{x}\) of x is the energy barrier that, starting from x, must be overcome to reach the set \({\mathcal {I}}_x\), i.e.,
If \({\mathcal {I}}_x\) is empty, then we let \(V_x=\infty \). We denote by \({\mathcal {X}}^s\) the set of global minima of the energy, and we refer to these as ground states. The metastable states are those states that attain the maximal stability level \(\varGamma _m< \infty \), that is
Since the metastable states are defined in terms of their stability level, a crucial role in our proofs is played by the set of all configurations with stability level strictly greater than V, that is
We frame the problem of metastability as the identification of metastable states and the computation of transition times from the metastable states to the stable configurations. In summary, from the mathematical point of view, the metastability phenomenon for a given system is described in terms of \({\mathcal {X}}^s\), \(\varGamma _m\) and \({\mathcal {X}}^m\). Now we define formally the energy barrier \(\varGamma \) as
where \(y_m\in {\mathcal {X}}^m\) and \(y_s\in {\mathcal {X}}^s\). Note that \(\varGamma \) does not depend on the specific choice of \(y_m, y_s\). The energy barrier is the minimum energy necessary to trigger the nucleation. The energy \(\varGamma \) turns out to be equal to \(\varGamma _m\) under specific assumptions [20, Theorem 2.4].
2.2 Main Model-Independent Results
The following theorems give estimates of the mixing time and the spectral gap in the general setting.
Theorem 2.1
Let \((P_\beta (x,y))_{x,y\in {\mathcal {X}}}\) be the transition matrix of a Markov chain. Assume there exists at least a stable state s such that
Then, for any \(0<\epsilon <1\) we have
where \(t^{mix}_{\beta }:=\min \{n \ge 0 \, | \, \max _{x\in {\mathcal {X}}}||{\mathcal {P}}^n_\beta (x,\, \cdot \,)-\mu (\, \cdot \,)||_{TV}\le \epsilon \}\) and \(||\nu -\nu '||_{TV}=\frac{1}{2}\sum _{x\in {\mathcal {X}}}{|\nu (x)-\nu '(x)|}\) for every \(\nu ,\nu '\) probability distribution on \({\mathcal {X}}\).
We call weakly reversible dynamics with respect to \(H(\cdot )\) a dynamics for which the following equation is satisfied for any \(x,y \in {\mathcal {X}}\)
We note that this condition is satisfied for Metropolis dynamics in the first example of Sect. 2.3 and for the class of probabilistic cellular automata that we discuss in Sect. 3.1 and in the second example of 2.3.
We say that the Markov chain \((X_n)_n\) is reversible if it satisfies the detailed balance property
for any \(x,y \in {\mathcal {X}}\). This implies that the measure \(\mu \) is stationary, that is \(\sum _{x\in {\mathcal {X}}}\mu (x){\mathcal {P}}_\beta (x,y)=\mu (y)\). By taking the limit \(\beta \rightarrow \infty \) in (2.19), we get (2.18). In other words if the dynamics is reversible with respect to the Gibbs measure (2.3) that depends on \(G_\beta \), then it is also weakly reversible with respect to \(H(\cdot )\).
In the rest of Section we assume that the dynamics is reversible.
The Dirichlet form associated with reversible Markov chain is the functional
where \(f:{\mathcal {X}}\rightarrow {\mathbb {R}}\) is a function. Thus, given two not empty disjoint sets \(Y,Z\subset {\mathcal {X}}\) the capacity of the pair Y and Z defined as

Note that the capacity is a symmetric function of the sets Y and Z. It can be proven that the right hand side of (2.21) has a unique minimizer called equilibrium potential of the pair Y and Z. There is a nice interpretation of the equilibrium potential in terms of hitting times. For any \(x \in {\mathcal {X}}\), we denote by \({\mathbb {P}}_x(\cdot )\) and \({\mathbb {E}}_x[\cdot ]\) respectively the probability and the average along the trajectories of the process started at x. Then, it can be proven that the equilibrium potential of the pair Y and Z is equal to the function \(h_{Y,Z}\) defined as follows
where \(\tau _Y\) and \(\tau _Z\) are, respectively, the first hitting time to Y and Z for the chain started at x. It can be also proven that, for any \(Y\subset {\mathcal {X}}\) and \(z\in {\mathcal {X}}\setminus Y\),
see [7, Eq. (7.1.16)]. In the following we define the set of metastable states as in [10].
Definition 2.1
According to the potential-theoretic approach, a set \(M\subset {\mathcal {X}}\) is said to be metastable if
We observe that M is different from the set of metastable states defined in (2.13), in particular M includes the configurations in \({\mathcal {X}}^m \cup {\mathcal {X}}^s\) that satisfy the Eq. (2.24). In order to avoid confusion, we will denote the states that satisfy (2.24) as p.t.a.-metastable. The physical meaning of the above definition can be understood once one remarks that the quantity \(\mu _\beta (x)/\text {cap}_\beta (x,y)\), for any \(x,y\in {\mathcal {X}}\), is strictly related to the communication cost between the states x and y, see Proposition A.2 for details. Thus, condition (2.24) ensures that the communication cost between any state outside M and M itself is smaller than the communication cost between any two states in M.
Theorem 2.2
Let \((P_\beta (x,y))_{x,y\in {\mathcal {X}}}\) be a reversible transition matrix. Let \(\rho _{\beta }=1-a^{(2)}_{\beta }\) be the spectral gap, where \(a^{(2)}_\beta \) is the second eigenvalue of the transition matrix such \(1=a^{(1)}_\beta >a^{(2)}_\beta \ge ...\ge a^{(|{\mathcal {X}}|)}_\beta \ge -1\). Then there exist two constants \(0<c_1<c_2<\infty \) independent of \(\beta \) such that for every \(\beta >0\),
where \(\gamma _1,\gamma _2\) are functions of \(\beta \) that vanish for \(\beta \rightarrow \infty \).
2.3 Results for Some Concrete Models
In this section we show that several well-known models in statistical mechanics satisfy the assumption (2.16) of Theorem 2.1. In particular we are able to get precise asymptotics for the mixing time of these models, that are given in Corollaries 2.1 and 2.2.
Throughout this section we denote by \(\varLambda \) a finite subset of \({\mathbb {Z}}^2\), by \({\mathcal {X}}\) the configuration space and by s a stable state.
In the basic example of Metropolis dynamics, the assumption (2.16) and the result are proved in [46, Prop. 3.24]. Note that Kawasaki dynamics is a type of Metropolis dynamics, so it falls into this case.
Derrida’s PCA model for Spin Systems. For this model, the Hamiltonian function is given by
and the virtual energy is obtained by (2.4)
Here
where \(K(i-j) \ne 0\) for \(j \in U_i\) a neighborhood of i. Different choices of \(K(\cdot )\) and \(U_i\) yield different PCA. It can be shown that, if \(U_i\) is symmetric, then the Markov chain is reversible with respect to \(G_\beta (\cdot )\) and weakly reversible with respect to \(H(\cdot )\). The transition probabilities are given by
where, for \(i\in \varLambda \) and \(\sigma \in {\mathcal {X}}\), \(p_{i,\sigma }(\cdot )\) is the probability measure on \(\{-1,+1\}\) defined as
with \(a \in \{-1,+1\}\). We have
where we used the inequality \((1+x)^{\alpha } \le 1+\alpha x\) with \(\alpha \in (0,1)\). In this model the unique stable state is \(s=\underline{+1}\), so we conclude in the following way
where in the last equality we used that \(h \ge 0\) and \(|U_i|\) is the same for all \( i \in \varLambda \). By (2.32) and Theorem 2.1, we have the following Corollary.
Corollary 2.1
Let \(\varGamma ^{\text {DPCA}}_m\) be \(\varGamma _m\) for this model. Then, for any \(0<\epsilon <1\) we have
Irreversible PCA model. The Hamiltonian function of the following PCA model is given by
with \(k^u:=(i,j+1)\), \(k^r:=(i+1,j)\) for \(k=(i,j)\in \varLambda ^2_N\). The transition probabilities are given by
Note that the subset \({\mathcal {X}} \setminus {\mathcal {X}}^s\) is not empty since G is not constant. Observe that the dynamics is irreversible with with a unique stationary distribution [27, Proposition 2.1]. We compute
Take \(\overline{\tau }\in {\mathcal {X}}\) such that \( \displaystyle G(s,\overline{\tau })=\min _\tau G(s,\tau ) \). We get
The last term goes to zero since N is finite. Since in this model \(s=\underline{+1}\), we have
and (2.16) follows for this model. Using Theorem 2.1, we get the following Corollary.
Corollary 2.2
Let \(\varGamma ^{\text {IPCA}}_m\) be \(\varGamma _m\) for this model. Then, for any \(0<\epsilon <1\) we have
2.4 Series of Metastable States
In this Section we generalize the results in [25, Sects. 2.5, 2.6] to a degenerate context. Indeed, in [25] the authors analyze a setting with a series of two metastable states, while we prove similar results for a setting with a series of more than two metastable states possibly degenerate. We will use this generalization for PCA model in Sect. 3.1, that has three metastable states with one non-degenerate-in-energy metastable state and two degenerate metastable states.
Let Q be the set of pairs \((x,y)\in {\mathcal {X}} \times {\mathcal {X}}\) such that \({\mathcal {P}}_\beta (x,y)>0\) or, equivalently, \(\varDelta (x,y)< \infty \). The quadruple \(({\mathcal {X}},Q,H,\varDelta )\) is then a weakly reversible dynamics on the energy landscape \(({\mathcal {X}},H)\) [20].
Condition 2.1
We assume that the energy landscape \(({\mathcal {X}},Q,H,\varDelta )\) is such that there exist four or more states \(x_0\), \(x_1^1, x_1^2,..., x_1^n\) and \(x_2\) such that \({\mathcal {X}}^s=\{x_0\}\), \({\mathcal {X}}^m=\{x_1^1,...,x_1^n,x_2\}\), and \(H(x_2)>H(x_1^r)\), \(H(x_1^r)=H(x_1^q)\), \(\varPhi (x_1^r,x_1^q)-H(x_1^r)<\varGamma _m\) for every \(r,q=1,...,n\), with \(n \in {\mathbb {N}}\).
Recalling the definition of the set of ground states \({\mathcal {X}}^s\) and \({\mathcal {X}}^m\) in (2.13), we immediately have
Moreover, from the definition (2.11) of maximal stability level it follows that (see [20, Theorem 2.3]) the communication cost from \(x_2\) to \(x_0\) is equal to the communication cost from \(x_1^r\) to \(x_0\) for every \(r=1,...,n\), that is
Note that, since \(x_2\) is a metastable state, its stability level cannot be lower than \(\varGamma _m\). Then, recalling that \(H(x_2)>H(x_1^r)\) for every \(r=1,...,n\), one has that \(\varPhi (x_2,x_1^r)-H(x_2)\ge \varGamma _m\). On the other hand, (2.40) implies that there exists a path \(\omega \in \varTheta (x_2,x_1^r)\) such that \(\varPhi _\omega =H(x_2)+\varGamma _m\) and, hence, \(\varPhi (x_2,x_1^r)-H(x_2)\le \varGamma _m\) for every \(r=1,...,n\). The two bounds finally imply that
Note that the communication cost from \(x_0\) to \(x_2\) and that from \(x_1^r\) to \(x_2\) are larger than \(\varGamma _m\), i.e.,
Indeed, recalling the reversibility property (2.18), we have
where in the last two steps we have used (2.41) and Condition 2.1, which proves the second of the two Eq. (2.42). The first of them can be proved similarly. In the following we give a condition on the dynamical property of the system: starting from \(x_2\), with high probability the system visits \(x_1^r\) before \(x_0\) for every \(r=1,...,n\).
Condition 2.2
Condition 2.1 is satisfied and
We remark that the Condition 2.2 is in fact a condition on the equilibrium potential \(h_{x_0,x_1^r}\) evaluated at \(x_2\), for every \(r=1,...,n\).
One of important goals of this paper is to prove an additional rule for the mean hitting time of \(\underline{+1}\) starting at \(\underline{-1}\) using Theorem 2.8 for the expectation of the transition time \(\tau _{x_0}\) for the chain started at \(x_2\). Such an expectation, hence, will be of order \(\exp (\beta \varGamma _m)\) and the prefactor will be that given in (2.53).
We can thus formulate the further assumptions that we shall need in the sequel.
Condition 2.3
Condition 2.1 is satisfied and there exists two positive constants \(k_1,k_2<\infty \) and such that
where o(1) denotes a function tending to zero in the limit \(\beta \rightarrow \infty \).
Condition 2.4
Condition 2.1 is satisfied and there exists n positive constants \(c_1, c_2,..., c_n<\infty \) such that
where o(1) denotes a function tending to zero in the limit \(\beta \rightarrow \infty \).
The following theorems generalize respectively Theorem 1, 2, 3, and 4 in [25]. The novelty of these proofs consists in dealing with the degeneracy of the metastable states \(\{x_1^1,x_1^2,...,x_1^n\}\), that is not present in [25]. We prove them in Appendix.
Theorem 2.3
Assume Condition 2.1 is satisfied. Then for every \(r=1,...,n\) we have \(\{x_0,x_1^r,x_2\} \subset {\mathcal {X}}\) is a p.t.a.-metastable set.
Theorem 2.4
Assume Condition 2.1 is satisfied. Then
Let \(A,B \subset {\mathcal {X}}\) be two non-empty disjoint sets. Let \(\nu _{A,B}\) be the probability distribution on A given by
where \({ \text {cap}}_{\beta }(A,B)=\sum _{x \in A}\mu (x){\mathbb {P}}_x(\tau _B< \tau _A)\), see [7, Eqs. 7.1.38–7.1.39]. Moreover, recalling [7, Corollary 7.11], we have
and we are able to state the following theorem.
Theorem 2.5
Assume Condition 2.1 is satisfied. Then
Theorem 2.6
Assume Conditions 2.1 and 2.3 are satisfied. Then
Theorem 2.7
Assume Conditions 2.1 and 2.4 are satisfied. Then
The following theorem is one of our main results. It gives an estimate of the transition time from the metastable state with higher energy and the stable state, in a general reversible setting.
Theorem 2.8
Assume Conditions 2.1, 2.2, and 2.3 are satisfied. Then
We remark that Theorem 2.8 gives an addition formula for the mean hitting time of \(x_0\) starting at \(x_2\). Neglecting terms of order o(1), such a mean time can be written as the sum of the mean hitting time of the subset \(\{x_1^1,...,x_1^n,x_0\}\) starting at \(x_2\) and of the mean hitting time of \(x_0\) starting from any state in \(\{x_1^1,...,x_1^n\}\), see Eq. (A.18) and Condition 2.2 in the proof of the Theorem. It is very interesting to note that in this decomposition no role is played by the mean hitting time of \(\{x_1^1,...,x_1^n\}\) starting at \(x_2\).
3 Model-Dependent Results
3.1 The Model
We consider the PCA model for Spin Systems introduced by Derrida in [31], see also [19]. In the second example of Sect. 2.3, we considered a class of PCA which is reversible with respect to \(G_\beta (\cdot )\) and weakly reversible with respect to \(H(\cdot )\). From now on we restrict ourselves to a specific nearest-neighbor interaction, see Fig. 1. Consider the two-dimensional torus with L even \(\varLambda ^2_{L}:=\{0,...,L-1\}^{2}\), endowed with the Euclidean metric. To each site \(i\in \varLambda \) we associate a variable \(\sigma (i)\in \{-1,+1\}\). \(\varLambda ^2_{L}\) represents an interacting particles system characterized by their spin and we interpret \(\sigma (i)=+1\) (respectively \(\sigma (i)=-1\)) as indicating that the spin at site i is pointing upwards (respectively downwards). Let \({\mathcal {X}}:=\{-1,+1\}^{\varLambda }\) be the configuration space, let \(\beta :=\frac{1}{T} >0\) where T is thought of as the temperature. Let \(h\in (0,1)\) be a parameter representing the external ferromagnetic field. We do not consider the case \(h>1\), because in that case there is no metastable behavior. The dynamics of the system are modelled as a Markov chain \((\sigma _n)_{n \in {\mathbb {N}}}\) on \({\mathcal {X}}\) with transition matrix defined in (2.28), (2.29). In the rest of the paper, we will choose
Note that the transition probability \(p_{i,\sigma }(s)\) for the spin \(\sigma (i)\) given in (2.30) depends only on the values of the adjacent spins.
The system evolves in discrete time steps, where at each step, all the spins are updated simultaneously according to the probability distribution (2.30). Intuitively, the value of the spin is likely to align with the local effective field \(S_\sigma (i)+h\). Here \(S_\sigma (i)\) represents a ferromagnetic interaction among spins.
The Markov chain \(\sigma _n\) satisfies the detailed balance property (2.19), where \(G_{\beta }(\cdot )\) in (2.26) is the Hamiltonian function. Equivalently, the Markov chain is reversible with respect to the Gibbs measure (2.3) and this implies that the measure \(\mu \) is stationary. Finally, given \(\sigma ,\eta \) \(\in {\mathcal {X}}\), we define the energy cost of the transition from \(\sigma \) to \(\eta \) for our specific PCA, as
Note that \(\varDelta (\sigma ,\eta )\ge 0\) and, perhaps surprisingly, \(\varDelta (\sigma ,\eta )\) is not necessarily equal to \(\varDelta (\eta ,\sigma )\). We also note that condition (3.2) is sometimes written more explicitly as in (2.2). The last equality in (3.2) is obtained as follows,
Let us fix the notation of some important states as follows:
-
\(\underline{+1}\) is the configuration such that \(\underline{+1}(i)=+1\) for every \(i\in \varLambda \);
-
\(\underline{-1}\) is the configuration such that \(\underline{-1}(i)=-1\) for every \(i\in \varLambda \);
-
\({\underline{c}}^e\) and \({\underline{c}}^o\) are the configurations such that \({\underline{c}}^e(i)=(-1)^{i_1+i_2}\) and \({\underline{c}}^o(i)=(-1)^{i_1+i_2+1}\) for every \(i=(i_1,i_2)\in \varLambda \). These configuration are called chessboard configurations.
Next we define the virtual energy as the limit
We distinguish two cases.
-
Case \(h=0\). In this case \(H(\sigma )=-\sum _{i \in \varLambda }|S_{\sigma }(i)|\), so there exist four minima of H given by the configurations \(\underline{+1}, \underline{-1}\) and the chessboard configurations. The configurations +1, \(\underline{-1}\) and \({\underline{c}}\) are ground states and each site of them contributes \(-4\) to the total energy.
-
Case \(h >0\). In this case +1 is the unique ground state. The energy of this state is \((-h-(4+h)) |\varLambda |\), so each site contributes \(-h-(4+h)\) to the total energy.
From now on we assume \(h>0\), fixed and small. Under periodic boundary conditions, the energy of these configurations is, respectively
-
\(H(\underline{+1}) =-L^2(4 + 2h)\),
-
\(H(\underline{-1}) =-L^2(4-2h)\),
-
\(H({\underline{c}}^e)=H({\underline{c}}^0) =-4L^2\).
Since \(H({\underline{c}}^e)=H({\underline{c}}^o)\) and \(\varDelta ({\underline{c}}^e,{\underline{c}}^o)=\varDelta ({\underline{c}}^o,{\underline{c}}^e)=0\), from now on we will indicate either element of the set \(\{{\underline{c}}^e, \, {\underline{c}}^o\}\) as \({\underline{c}}\), this is an example of stable pair (see Definition 5.1). Therefore, \(H(\underline{-1})> H({\underline{c}})> H(\underline{+1})\) for \(0< h < 1\). Our first goal is to show that \(\{\underline{-1},{\underline{c}}\}\) is the set of metastable states and \(\underline{+1}\) is the global minimum (or ground state).
3.2 Main Model-Dependent Results
In the setup introduced in [41], the minimal description of the metastability phenomenon is given in terms of \({\mathcal {X}}^s\), \({\mathcal {X}}^m\) and \(\varGamma _m\), so we concentrate our attention on these. In particular we determine the metastable and stable stases and we show that the maximal stability level \(\varGamma _m\) is equal to the energy barrier \(\varGamma ^{\text {PCA}}\), defined as [19, (3.29)]
where \(\lambda \) is the critical length computed in [19, (3.24)] and defined as
where \([\cdot ]\) is the integer part. Assuming that the system is prepared in the state \(\sigma _0=\underline{-1}\), with probability tending to one as \(\beta \rightarrow \infty \) the system visits the chessboard \({\underline{c}}\) before relaxing to the stable state \(\underline{+1}\). Moreover, by [19, Theorem 3.11, Theorem 3.13] along the tube of paths from \(\underline{-1}\) to \({\underline{c}}\) the system visits a certain set of configurations called critical droplets from \(\underline{-1}\) to \({\underline{c}}\). The critical droplets are all those configurations that have a single chessboard droplet of a specific size in a sea of minuses. Instead, along the tube of paths from \({\underline{c}}\) to \(\underline{+1}\) the system visits a certain set of configurations, also called critical droplets from \({\underline{c}}\) to \(\underline{+1}\), but in this case these are all those configurations that have a single plus droplet of a specific size in a chessboard. The droplet size, in both cases, is the so-called critical length \(\lambda \). We then say that a rectangle is supercritical (resp. subcritical) if the side of the rectangle is greater than \(\lambda \) (resp. smaller than \(\lambda \)). Formally, the chessboard droplet is a supercritical rectangle with a one-by-one protuberance attached to one of the two longest sides and with the spin plus in this protuberance. Note that starting from different initial configurations yields different kinds of droplets.
We are finally ready to present our model-dependent results. In Lemma 3.1 we show that all states different from \({\underline{+1},\underline{-1},{\underline{c}}}\) have a strictly lower stability level than \(\varGamma ^{\text {PCA}}\). Using this lemma and [19, Lemmas 3.4, 4.1], we show that \(\varGamma ^{\text {PCA}}=\varGamma _m\), allowing us to conclude in Theorem 3.1 that the only metastable states are indeed \(\underline{-1}\) and \({\underline{c}}\).
Lemma 3.1
(Estimate of stability levels) For every \(\eta \in {\mathcal {X}}\setminus \{\underline{-1},{\underline{c}},\underline{+1}\},\) there exists \(V^*\) such that \(V_\eta \le V^*<\varGamma ^{\text {PCA}}\).
Theorem 3.1
(Identification of metastable states) For the reversible PCA model (3.1) we have \(\varGamma _m=\varGamma ^{\text {PCA}}\) and thus \({\mathcal {X}}^m=\{\underline{-1},{\underline{c}}\}\).
Theorem 3.2 below implies that the system visits a metastable state or a ground state in a time shorter than \(e^{\beta V^*+\epsilon }\) and visits a stable state in a time shorter than \(e^{\beta \varGamma _m+\epsilon }\), uniformly in the starting state for any \(\epsilon >0\). We say that a function \(\beta \mapsto f(\beta )\) is super exponentially small (SES) if
Theorem 3.2
(Recurrence property) For any \(\epsilon >0\), the functions
are SES.
Equation (3.7) in the next theorem already appeared in [24, Theorem 3.1], however the proof there was incomplete. Thanks to the previous theorems we are able to prove it rigorously here. The second part of the next theorem is an application of Theorem 2.1 to the reversible PCA model by Derrida.
Theorem 3.3
For \(\beta \) large enough, we have
where \(k_1=k_2=8\lambda |\varLambda |\). Moreover for any \(0<\epsilon <1\) we have
and there exist two constants \(0<c_1<c_2<\infty \) independent of \(\beta \) such that for every \(\beta >0\)
where \(\gamma _1,\gamma _2\) are functions of \(\beta \) that vanish for \(\beta \rightarrow \infty \), and \(\rho _{\beta }\) is the spectral gap.
The first term \(\frac{1}{k_1}e^{\beta \varGamma ^{\text {PCA}}}\) represents the contribution of the mean hitting time \({\mathbb {E}}_{\underline{-1}}[\tau _{{\underline{c}}}\mathbf{1 }_{\{\tau _{{\underline{c}}}< \tau _{\underline{+1}}\}}]\) while the second term \(\frac{1}{k_2}e^{\beta \varGamma ^{\text {PCA}}}\) represents the contribution of \({\mathbb {E}}_{{\underline{c}}}[\tau _{\underline{+1}}]\).
4 Proof of Model-Independent Results
Before we prove Theorem 2.1, let us recall some important definitions.
Definition 4.1
(Cycle, [21, Def. 2.3], [14, Def. 4.2]) Let \((X_n)_n\) be a Markov chain. A nonempty set \(C \subset {\mathcal {X}}\) is a cycle if it is either a singleton or for any \(x,y \in C\), such that \(x\ne y\),
In other words, a nonempty set \(C \subset {\mathcal {X}}\) is a cycle if it is either a singleton or if for any \(x \in C\), the probability for the process starting from x to leave C without first visiting all the other elements of C is exponentially small. We denote by \({\mathcal {C}}({\mathcal {X}})\) the set of cycles of \({\mathcal {X}}\).
Definition 4.2
(Energy Cycle, [21, (2.17)], [21, Def. 3.5]) A nonempty set \(A \subset {\mathcal {X}}\) is an energy-cycle if and only if it is either a singleton or it verifies the relation
Definition 4.3
Given a cycle \(C \subset {\mathcal {X}}\), we denote by \({\mathcal {F}}(C)\) the set of the minima of the energy in C, namely
The proposition [21, Prop. 3.10] establishes the equivalence between cycle and energy-cycle and allows us to use the equivalence between the approach in [15, 16, 39] and the path-wise approaches [19, 21, 41, 46, 49,50,51] that uses the energy-cycle. Next we define the collection of maximal cycles.
Definition 4.4
([46, Def. 20], [21, Def. 2.4]) Given a nonempty subset \(A \subset {\mathcal {X}}\), we denote by \({\mathcal {M}}(A)\) the collection of maximal cycles that partitions A, that is
Moreover, we extend to the general setting the definition of the maximal depth given in [46, Def. 21] for the setting of Metropolis dynamics.
Definition 4.5
The maximal depth \(\tilde{\varGamma }(A)\) of a nonempty subset \(A \subset {\mathcal {X}}\) is the maximal depth of a cycle contained in A, that is
Trivially \(\tilde{\varGamma }(C):=\varGamma (C)\) if \(C \in {\mathcal {C}}({\mathcal {X}})\).
Proof of Theorem 2.1
We prove (2.17) by generalizing [46, Prop. 3.24]. To do this, we show that \(\tilde{\varGamma }({\mathcal {X}} \setminus \{s\})\) is equal to \(\varGamma _m\). Recall definition (2.12)
Since \(\varPhi (x,{\mathcal {I}}_x)\le \varPhi (x,s)\), we have that \(\varGamma _m\le \tilde{\varGamma }({\mathcal {X}}\setminus \{s\})\). To prove the reverse inequality \(\varGamma _m\ge \tilde{\varGamma }({\mathcal {X}}\setminus \{s\})\), we consider \(R_D(x)\), the union of \(\{x \}\) and of the points in \({\mathcal {X}}\) which can be reached by means of paths starting from x with height smaller than the height that is necessary to escape from \(D \subset {\mathcal {X}}\) starting from x [21, (3.58)]. We consider
We partition \({\mathcal {X}}\) into the set of local minima \({\mathcal {X}}_0\) (i.e., \({\mathcal {X}}_V\) with \(V=0\)) and its complement, as \({\mathcal {X}}={\mathcal {X}}_0 \cup ({\mathcal {X}} \setminus {\mathcal {X}}_0)\), so that \({\mathcal {X}} \setminus \{s\}=( {\mathcal {X}}_0 \cup ({\mathcal {X}} \setminus {\mathcal {X}}_0)) \setminus \{s\}=({\mathcal {X}}_0 \setminus \{s\}) \cup ({\mathcal {X}} \setminus {\mathcal {X}}_0)\). Then,
Let us analyze the two terms on the right separately.
-
If \(x\in {\mathcal {X}}_0 \setminus \{s\}\), then \(R_{{\mathcal {X}}\setminus \{s\}}(x)=\{y \in {\mathcal {X}} \,\, | \,\, \varPhi (x,y)< \varPhi (x,s)\}\) is a non-trivial cycle. Using [21, Prop. 3.17],
-
(i)
If \(x\in {\mathcal {F}}(R_{{\mathcal {X}}\setminus \{s\}}(x))\), then \(\varGamma (R_{{\mathcal {X}} \setminus \{s\}}(x)) \le V_x\), by [21, Prop. 3.17 (3)].
-
(ii)
Suppose that \(x\not \in {\mathcal {F}}(R_{{\mathcal {X}}\setminus \{s\}}(x))\). Consider \(\tilde{x}=\text {argmin}_{x\in R_{{\mathcal {X}}\setminus \{s\}}(x)}H(x)\), then \({\tilde{x}} \in {\mathcal {F}}(R_{{\mathcal {X}}\setminus \{s\}}(x))\) and by [21, Prop. 3.17 (2), (3)] we have \(V_x <\varGamma (R_{{\mathcal {X}} \setminus \{s\}}(x))=\varGamma (R_{{\mathcal {X}} \setminus \{s\}}(\tilde{x})) = V_{\tilde{x}}\). So
$$\begin{aligned} \max _{y \in R_{{\mathcal {X}}\setminus \{s\}}(x)}V_y=V_{{\tilde{x}}}=\varGamma (R_{{\mathcal {X}}\setminus \{s\}}(x)). \end{aligned}$$(4.8)
From this follows that
$$\begin{aligned} \max _{x \in {\mathcal {X}}_0 \setminus \{s\}}\varGamma (R_{{\mathcal {X}} \setminus \{s\}}(x)) = \max _{x \in {\mathcal {X}}_0 \setminus \{s\}}\max _{y\in R_{{\mathcal {X}} \setminus \{s\}}(x)} V_y \le \varGamma _m. \end{aligned}$$(4.9) -
(i)
-
If \(x\in {\mathcal {X}}\setminus {\mathcal {X}}_0\), we proceed as follows
-
(I)
If \(\varPhi (x,s)=H(x)\), then \(R_{{\mathcal {X}} \setminus \{s\}}(x)=\{x\}\) because \(\{y \in {\mathcal {X}} \,\, | \,\, \varPhi (x,y)<H(x)\}\) is empty. Indeed, \(\varPhi (x,y)\) is always greater than or equal to H(x). So, \(\varGamma (R_{{\mathcal {X}} \setminus \{s\}}(x))=\varGamma (\{x\})=0\).
-
(II)
If \(\varPhi (x,s)>H(x)\), we choose \(\tilde{x}=\text {argmin}_{x\in R_{{\mathcal {X}}\setminus \{s\}}(x)}H(x)\), so \(\tilde{x} \in {\mathcal {X}}_0 \setminus \{s\}\) and \(\varPhi (x,s)=\varPhi (\tilde{x}, s)\). Then \(\{y \in {\mathcal {X}} \,\, | \,\, \varPhi (x,y)< \varPhi (x,s)\} \subseteq R_{{\mathcal {X}} \setminus \{s\}}(\tilde{x})\) and we refer to the previous case \(x \in {\mathcal {X}}_0\), since \({\tilde{x}} \in {\mathcal {X}}_0 \setminus \{s \}\).
-
(I)
This concludes the proof that \(\varGamma _m\ge {\tilde{\varGamma }} ({\mathcal {X}}\setminus \{s\})\) and hence that \(\varGamma _m= {\tilde{\varGamma }} ({\mathcal {X}}\setminus \{s\})\). \(\square \)
The key step in [46, Prop. 3.24] was to show that \(H_2 = H_3\), \(H_2\) is defined as [14, Theorem 5.1]
The critical depth \(H_3\) is defined as [14, Theorem 5.1]
where \(F=\{(x,x)| \, x \in {\mathcal {X}}\}\), \(\widetilde{\varGamma }({\mathcal {X}} \times {\mathcal {X}} \setminus F)=\max _{C \in {\mathcal {M}}({\mathcal {X}} \times {\mathcal {X}} \setminus F)}\varGamma (C)\) and \({\mathcal {M}}({\mathcal {X}} \times {\mathcal {X}}\setminus F)=\{C \in {\mathcal {C}}({\mathcal {X}}) \,\,| \,\, C\) maximal cycle by inclusion under the constraint \(C \subseteq {\mathcal {X}} \times {\mathcal {X}}\}\). Through the equivalence of two definitions of cycles, given by [21, Prop. 3.10], the critical depth \(H_2\) is equal to \(\tilde{\varGamma }({\mathcal {X}} \setminus \{s\})\). This quantity is well defined because its value is independent of the choice of s [14, Theorem 5.1]. Now we consider two independent Markov chains, \(X_t\) and \(Y_t\), on the same energy landscape and with the same inverse temperature \(\beta \). We define the two dimensional Markov chain \(\{(X_t,Y_t)\}\) on \({\mathcal {X}} \times {\mathcal {X}}\) with transition probabilities \({\mathcal {P}}_{\beta }^{\otimes 2}\) given by
[14, Theorem 5.1] states that \(H_2 \le H_3\) and if the null-cost directed graph \(G=(E,{\mathcal {X}}^s)\) with \(E=\{(s,s') \in {\mathcal {X}}^s \times {\mathcal {X}}^s \, | \, \lim _{\beta \rightarrow \infty }- \frac{1}{\beta }\log {\mathcal {P}}_{\beta }(s,s')=0\}\) has an aperiodic component, then \(H_2=H_3\). The assumption (2.16) concludes the proof.
Proof of Theorem 2.2
Before proving the bounds (2.25)
we recall the Definition 2.20 and we define the generator of a Markov process. \(\square \)
Definition 4.6
For any function \(f: {\mathcal {X}} \longrightarrow {\mathbb {R}}\), \({\mathbb {L}}_\beta f\) is the function defined as
The result (2.25) is an immediate consequence of the next two lemmas and it is obtained by generalizing [39, Theorem 2.1, Lemmas 2.3, 2.7].
Lemma 4.1
There exists a constant \(C \le \infty \) such that for all \(\beta \ge 0\),
where \(\gamma \) is a function of \(\beta \) that vanishes for \(\beta \rightarrow \infty \).
Proof
We first observe that by assumption \(\varGamma _m>0\). Without loss of generality, we may assume that \(x_0 \in {\mathcal {X}}^m, y_0 \in {\mathcal {X}}^s\) and \(H(y_0)=0\). Therefore \(\varGamma _m=\varPhi (x_0,y_0)-H(x_0)\) since \({\mathcal {X}}\) is finite. We write the spectral gap \(\rho _\beta \) as
where \(\text {Var}_\beta (f):=\sum _{x \in {\mathcal {X}}} f^2(x)\mu (x)-(\sum _{x \in {\mathcal {X}}} f(x)\mu (x))^2\), and \(L^2\) is the space of functions with finite second moment under the measure \(\mu \). We will find a function F and a constant \(C<\infty \), such that
Let \(x_0 \in {\mathcal {X}}\) and \(y_0 \in {\mathcal {I}}_{x_0}\) be two points for which \(\varPhi (x_0,y_0)-H(x_0)=\varGamma _m\) and let us consider the set \({\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)=\{y_0\} \cup \{x \in {\mathcal {X}} \,\, | \,\, \varPhi (y_0,x)< \varPhi (y_0,x_0)\}\). Note that \(x_0 \not \in {\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)\) and \(y_0 \in {\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)\). Moreover if \(x \in {\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)\) and \(y \not \in {\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)\), then
In this figure we draw an example energy-landscape, compatible with the assumptions on \(x_0,y_0\) and x. We also draw four \(y_i \not \in {\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)\), \(i=1,2,3,4\), for which (4.17) is valid
(See Fig. 4) For any \(x \in {\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)\) and \(y \not \in {\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)\), by reversibility we have
where, to obtain the inequality, the first term is estimated by (2.1) and [21, Eq. (2.2)], i.e.,
The second term in (4.18) is estimated by (2.4) and (2.3), that is
where \({\tilde{\gamma }}_1, {\tilde{\gamma }}_2\) and \(\gamma ^*_1={\tilde{\gamma }}_1+{\tilde{\gamma }}_2\) are functions of \(\beta \) that vanish for \(\beta \rightarrow \infty \). Then using (4.17) we get
Let \(F(x)=\mathbb {1}_{{\mathcal {R}}_{{\mathcal {X}} \setminus \{x_0\}}(y_0)}(x)\), then
On the other hand,
where the last inequality is obtained by (4.20), and by our assumption \(H(y_0)=0\). We conclude that
where C is a constant and \(\gamma =\gamma ^*_1+2{\tilde{\gamma }}_2\).
Lemma 4.2
There exists a constant \(C>0\), such that for all \(\beta \ge 0\),
where \(\gamma \) is a function of \(\beta \) that vanishes for \(\beta \rightarrow \infty \).
Proof
It will be enough to find a constant \(c>0\) such that for every \(\beta \ge 0\) and every \(f\in L^2(\mu )\),
We consider \(x, y \in {\mathcal {X}}\) and \(\omega \in \varTheta (x,y)\) with length \(|\omega |=n(x,y)\) and define
For \(z \in {\mathcal {X}},w \in {\mathcal {I}}_z\), we define the function \({\mathbb {F}}_{(z,w)}: \varTheta (x,y) \longrightarrow \{0,1\}\) as
Then,
where in the last equality we use that \(\omega \in \varTheta (x,y)\) with \(|\omega |=n(x,y)\) and we wrote \(f(y)-f(x)\) as a telescopic sum. Using (4.26) and (4.27), we get the following inequalities
We estimate \(\mu (x)\mu (y)\) as in (4.20),
Then we have
Moreover
5 Proof of Model-Dependent Results
In Sect. 5.1 we prove the main model-dependent results except for Lemma 3.1, which we postpone to Sect. 5.2.
5.1 Proof of Theorems 3.1, 3.2, 3.3
Note that our PCA verifies [20, Definition 2.1]. In order to prove Theorem 3.1 we will lean on [20, Theorem 2.4]. Roughly speaking, if we have an ansatz for the set of metastable configurations and one for the communication height, and we show that these verify two conditions, then [20, Theorem 2.4] guarantees that the anzatzes are correct.
Proof of Theorem 3.1 (Identification of metastablestates)
In [19] the authors computed the value of \(\varGamma \) to be \(\varGamma ^{\text {PCA}}=-2h\lambda ^2+2\lambda (4+h)-2h\). There, it was also proven that
By [19, Lemmas 3.4, 4.1] we have that \(\varPhi (-{\underline{1}},{\underline{c}})=\varGamma ^{\text {PCA}}+H(-{\underline{1}})\), that is \(\varGamma ^{\text {PCA}}+H(-{\underline{1}})\) is the minmax between \(-{\underline{1}}\) and \({\underline{c}}\). The first assumption of [20, Theorem 2.4] is satisfied for \(A=\{\underline{-1},{\underline{c}}\}\) and \(a=\varGamma ^{\text {PCA}}\) thanks to [19, Theorem 3.11, Lemmas 3.4, 4.1], hence
Moreover, the second assumption of [20, Theorem 2.4] is satisfied because by Lemma 3.1 either \({\mathcal {X}}\setminus (\{\underline{-1},{\underline{c}}\} \cup {\mathcal {X}}^s)=\emptyset \) or
Finally, by applying [20, Theorem 2.4], we conclude that \(\varGamma _m=\varGamma ^{\text {PCA}}\) and \({\mathcal {X}}^m=\{\underline{-1}, {\underline{c}}\}\). \(\square \)
Proof of Theorem 3.2 (Recurrence property)
In Lemma 3.1 we compute \(V^*=2(2-h)\). Recall the definition of \({\mathcal {X}}_V\) in (2.14) and apply [21, Prop. 2.8] with \(a=V^*\), \({\mathcal {X}}_{V^*}=\{\underline{-1},{\underline{c}}, \underline{+1}\}\). We get
With a similar reasoning with \(a=\varGamma _m\), \({\mathcal {X}}_{\varGamma _m}={\mathcal {X}}^s\), we get
\(\square \)
Proof of Theorem 3.3
In [24] the proof of [24, Theorem 3.1] was only sketched in Section 4. Recall Theorem 2.8, then Condition 2.1 is satisfied thanks to our Theorem 3.1, Condition 2.2 is satisfied thanks to [24, Lemmas 3.3, 3.4] and Condition 2.3 is satisfied thanks to [24, Lemma 3.5]. Thus, applying Theorem 2.8 concludes the rigorous proof of (3.7). In the second example of Sect. 2.3 we verify the assumptions of Theorems 2.1 and 2.2 for general reversible PCA model in order to get (3.8) and (3.9). \(\square \)
5.2 Proof of Main Lemma 3.1
Definition 5.1
We call stable configurations those configurations \(\sigma \in {\mathcal {X}}\) such that \(p(\sigma ,\sigma )\rightarrow 1\) in the limit \(\beta \rightarrow \infty \). Equivalently, \(\sigma \in {\mathcal {X}}\) is a stable configuration if and only if \(p(\sigma ,\eta )\rightarrow 0\) in the limit \(\beta \rightarrow \infty \) for all \(\eta \in {\mathcal {X}}\setminus \{ \sigma \}\).
For any \(\sigma \in {\mathcal {X}}\) there exists a unique configuration \(\eta \in {\mathcal {X}}\) such that the transition \(\sigma \rightarrow \eta \) happens with high probability as \(\beta \rightarrow \infty \), that is \(p(\sigma , \eta ) \overset{\beta \rightarrow \infty }{\longrightarrow } 1\). So let \(\eta \) and \(\sigma \) be two configurations in \({\mathcal {X}}\) such that \(\eta =T\sigma \), where
is the map such that for each \(x\in \varLambda \)
Definition 5.2
Let \(\sigma , \eta \in {\mathcal {X}}\) be two different configurations. We say that \(\sigma \) and \(\eta \) form a stable pair if and only if \(\eta = T \sigma \) and \(T \eta =\sigma \). Moreover, we say that \(\sigma \in {\mathcal {X}}\) is a trap if either \(\sigma \) is a stable configuration or the pair \((\sigma ,T\sigma )\) is a stable pair. We denote by \({\mathcal {T}} \subset {\mathcal {X}}\) the collection of all traps.
We define two further maps, that will be useful later on. For any given \(j\in \varLambda \), \(T_j^{F}(\sigma )=T(\sigma )\) except in the site j, where \(T_j^{F}(\sigma )=\sigma (j)\). Formally,
For any given \(j\in \varLambda \), \(T_j^{C}(\sigma )=T(\sigma )\) except in the site j, where \(T_j^{C}(\sigma )=-\sigma (j)\). Formally,
The two maps are similar to \(T(\sigma )\), the only difference being that \(T_j^{F}(\sigma )\) fixes the value of the spin in j and \(T_j^{C}(\sigma )\) changes the value of the spin in j.
We say that \(x,y \in \varLambda \) are nearest neighbors if and only if the lattice distance d between x, y is one, i.e., \(d(x,y)=1\). We indicate by \(R_{l,m} \subseteq \varLambda \) the rectangle with sides l and m, \(2 \le l \le m\) and we call non-interacting rectangles two rectangles \(R_{l,m}\) and \(R_{l',m'}\) such that any of the following conditions hold:
-
\(d(R_{l,m},R_{l',m'})\ge 3\), if \(\sigma _{R_{l,m}}={\underline{c}}^o_{R_{l,m}}\) and \(\sigma _{R_{l',m'}}={\underline{c}}^o_{R_{l',m'}}\);
-
\(d(R_{l,m},R_{l',m'})\ge 3\), if \(\sigma _{R_{l,m}}={\underline{c}}^e_{R_{l,m}}\) and \(\sigma _{R_{l',m'}}={\underline{c}}^e_{R_{l',m'}}\);
-
\(d(R_{l,m},R_{l',m'})\ge 3\), if \(\sigma _{R_{l,m}}=\underline{+1}_{R_{l,m}}\) and \(\sigma _{R_{l',m'}}=\underline{+1}_{R_{l',m'}}\);
-
\(d(R_{l,m},R_{l',m'})=1\), if \(\sigma _{R_{l,m}}={\underline{c}}^o_{R_{l,m}}\) and \(\sigma _{R_{l',m'}}={\underline{c}}^e_{R_{l',m'}}\);
-
\(d(R_{l,m},R_{l',m'})=1\), if \(\sigma _{R_{l,m}}={\underline{c}}_{R_{l,m}}\), \(\sigma _{R_{l',m'}}=\underline{+1}_{R_{l',m'}}\) and the sides on the interface are of the same length.
Whenever two rectangles are not non-interacting, we call them interacting.
Proof of Lemma 3.1
We begin by giving a rough sketch of the proof. Without loss of generality, we consider only configurations in \({\mathcal {U}}:={\mathcal {X}}_0\setminus \{\underline{-1},{\underline{c}},\underline{+1}\}\), since the configurations in \({\mathcal {X}} \setminus {\mathcal {X}}_0\) have stability level zero. Indeed, if \(\sigma \in {\mathcal {X}} \setminus {\mathcal {X}}_0\), we construct the path \(\overline{\omega }=(\sigma , T(\sigma ))\), so that \(T(\sigma ) \in {\mathcal {I}}_\sigma \) and \(V_\sigma =0\), where \(\mathcal {I_{\sigma }}\) was defined in (2.10). We will partition \({\mathcal {X}}_0\setminus \{\underline{-1},{\underline{c}},\underline{+1}\}\) into several subsets A, B, D, E and for each of these we will construct a path \({\overline{\omega }} \in \varTheta (\sigma ,\mathcal {I_{\sigma }} \cap {\mathcal {X}}_0)\). Denote with \(\sigma _{\varLambda '}\) a configuration \(\sigma \in \varLambda ' \subseteq \varLambda \). We will find an explicit upper-bound \(V^*_{\sigma }\) on the transition energy along \(\overline{\omega }\) as
We define
and since
from (5.9) and (5.10) follows that, for any \(\sigma \in {\mathcal {X}}_0 \setminus \{\underline{-1}, {\underline{c}}, \underline{+1}\}\),
This means that all configurations in \({\mathcal {X}}_0\setminus \{\underline{-1},{\underline{c}},\underline{+1}\}\) have a lower stability level than \(\varGamma ^{\text {PCA}}\). We now proceed with the detailed proof. We partition the set \({\mathcal {X}}_0\setminus \{\underline{-1},{\underline{c}},\underline{+1}\}\) into four subset as \({\mathcal {X}}_0\setminus \{\underline{-1},{\underline{c}},\underline{+1}\}=A \cup B \cup D \cup E\) [19, Prop. 3.3]. For each set A, B, D, E, we first describe it in words and then give its formal definition. \(\square \)
We define the set A to be the set of configurations consisting of a single rectangle containing either \({\underline{c}}\) or \(\underline{+1}\), and surrounded by either \(\underline{-1}\) or \({\underline{c}}\), see Fig. 5. More precisely, \(A=A_1 \cup A_2 \cup A_3 \cup A_4 \cup A_5 \cup A_6\), where:
-
\(A_1\) (respectively \(A_2\)) is the collection of configurations such that \(\exists ! \, R_{l,m} \subset \varLambda \) with \(l<\lambda \) (respectively \(l \ge \lambda \)), \(\sigma _{R_{l,m}}={\underline{c}}_{R_{l,m}}\) and \(\sigma _{\varLambda \setminus R_{l,m}}=\underline{-1}_{\varLambda \setminus R_{l,m}}\);
-
\(A_3\) (respectively \(A_4\)) is the collection of configurations such that \(\exists ! \, R_{l,m}\subset \varLambda \) with \(l<\lambda \) (respectively \(l \ge \lambda \)), \(\sigma _{R_{l,m}}=\underline{+1}_{R_{l,m}}\) and \(\sigma _{\varLambda \setminus R_{l,m}}={\underline{c}}_{\varLambda \setminus R_{l,m}}\);
-
\(A_5\) (respectively \(A_6\)) is the collection of configurations such that \(\exists ! \, R_{l,m}\subset \varLambda \) with \(l<\lambda \) (respectively \(l \ge \lambda \)), \(\sigma _{R_{l,m}}=\underline{+1}_{R_{l,m}}\) and \(\sigma _{\varLambda \setminus R_{l,m}}=\underline{-1}_{\varLambda \setminus R_{l,m}}\).
Configurations in the set B consist of a single chessboard rectangle which may contain an island of \(\underline{+1}\), surrounded by \(\underline{-1}\), see Fig. 6. More precisely, \(B=B_1 \cup B_2 \cup B_3\), where:
-
\(B_1\) is the collection of configurations such that \(\exists ! \, R_{l,m}\) with \(\sigma _{R_{l,m}}=\underline{+1}_{R_{l,m}}\) and \(\exists ! \, R_{l',m'} \supsetneq R_{l,m}\) with \(l'<\lambda \), \(\sigma _{R_{l',m'} \setminus R_{l,m}}={\underline{c}}_{R_{l',m'} \setminus R_{l,m}}, \,\,\, \sigma _{\varLambda \setminus R_{l',m'}}=\underline{-1}_{\varLambda \setminus R_{l',m'}}\);
-
\(B_2\) is the collection of configurations such that \(\exists ! \, R_{l,m}\) with \(l \ge \lambda \), \(\sigma _{R_{l,m}}=\underline{+1}_{R_{l,m}}\) and \(\exists ! \, R_{l',m'} \supsetneq R_{l,m}\) such that \(\sigma _{R_{l',m'} \setminus R_{l,m}}={\underline{c}}_{R_{l',m'} \setminus R_{l,m}}, \,\,\, \sigma _{\varLambda \setminus R_{l'-,m'}}=\underline{-1}_{\varLambda \setminus R_{l',m'}}\);
-
\(B_3\) is the collection of configurations such that \(\exists ! \, R_{l,m}\) with \(l < \lambda \), \(\sigma _{R_{l,m}}=\underline{+1}_{R_{l,m}}\) and \(\exists ! \, R_{l',m'} \supsetneq R_{l,m}\) with \(l' \ge \lambda \) such that \(\sigma _{R_{l',m'} \setminus R_{l,m}}={\underline{c}}_{R_{l',m'} \setminus R_{l,m}}, \,\,\, \sigma _{\varLambda \setminus R_{l',m'}}=\underline{-1}_{\varLambda \setminus R_{l',m'}}\).
The set D contains all configurations with more than one rectangle, see Fig. 7. More precisely, \(D=D_1 \cup D_2 \cup D_3 \cup D_4 \cup D_5\), where:
-
\(D_1\) is the collection of configurations such that there exist subcritical non-interacting rectangles \({\mathcal {R}}:=(R_{l,m})_{l,m}\) such that \(\sigma _{\varLambda \setminus {\mathcal {R}}}=\underline{-1}_{\varLambda \setminus {\mathcal {R}}}\) and any rectangle of chessboard may contain one or more non-interacting rectangles of pluses;
-
\(D_2\) is the collection of configurations such that there exist rectangles \({\mathcal {R}}:=(R_{l,m})_{l,m}\) where at least one of them is supercritical and such that \(\sigma _{\varLambda \setminus {\mathcal {R}}}=\underline{-1}_{\varLambda \setminus {\mathcal {R}}}\). Moreover, any rectangle of chessboard may contain one or more non-interacting rectangles of pluses;
-
\(D_3\) is the collection of configurations consisting of interacting rectangles \({\mathcal {R}}:=(R_{l,m})_{l,m}\) with \(l<\lambda \) and such that any rectangle of chessboard may contain one or more non-interacting rectangles of pluses;
-
\(D_4\) is the collection of configurations consisting of non-interacting rectangles \({\mathcal {R}}:=(R_{l,m})_{l,m}\) with \(l<\lambda \) such that \(\sigma _{R_{l,m}}=\underline{+1}_{R_{l,m}}\) and \(\sigma _{\varLambda \setminus {\mathcal {R}}}={\underline{c}}_{\varLambda \setminus {\mathcal {R}}}\);
-
\(D_5\) is the collection of configurations consisting of rectangles \({\mathcal {R}}:=(R_{l,m})_{l,m}\) where at least one has \(l\ge \lambda \) and such that \(\sigma _{R_{l,m}}=\underline{+1}_{R_{l,m}}\) and \(\sigma _{\varLambda \setminus {\mathcal {R}}}={\underline{c}}_{\varLambda \setminus {\mathcal {R}}}\);
The set E contains all possible strips, that is, rectangles winding around the torus, see Fig. 8. More precisely, \(E=E_1 \cup E_2 \cup E_3 \cup E_4 \cup E_5 \cup E_6 \cup E_7\), where:
-
\(E_1\) (respectively \(E_3\)) is the collection of configurations containing strips of \({\underline{c}}\) (respectively \(\underline{+1}\)) of width one surrounded by \(\underline{-1}\), and possibly rectangles of \(\underline{+1}\) and \({\underline{c}}\);
-
\(E_2\) is the collection of configurations containing strips of \(\underline{+1}\) of width one surrounded by \({\underline{c}}\), and possibly rectangles of \(\underline{+1}\);
-
\(E_4\) is the collection of configurations containing pairs of adjacent strips of \({\underline{c}}\) and \(\underline{-1}\). For at least one of these pairs, both strips have width greater than one. Furthermore, there may be rectangles of \({\underline{c}}\) and \(\underline{+1}\) surrounded by \(\underline{-1}\), and rectangles of \(\underline{+1}\) surrounded by \({\underline{c}}\);
-
\(E_5\) (respectively \(E_6\)) is the collection of configurations containing pairs of adjacent strips of \({\underline{c}}\) and \(\underline{+1}\) (respectively \(\underline{+1}\) and \(\underline{-1}\)). For at least one of these pairs, both strips have width greater than one. Furthermore, there may be rectangles of \(\underline{+1}\) surrounded by \({\underline{c}}\) (respectively rectangles of \({\underline{c}}\) and \(\underline{+1}\) surrounded by \(\underline{-1}\));
-
\(E_7\) is the collection of configurations containing strips of \({\underline{c}}\), \(\underline{-1}\) and \(\underline{+1}\) with at least one width greater than one, and possibly rectangles of \({\underline{c}}\) and \(\underline{+1}\) in \(\underline{-1}\), and possibly rectangles of \(\underline{+1}\) in \({\underline{c}}\);
We begin by considering the set A. Consider first the set \(A_1\).
Case \(A_1\). For any configuration \(\sigma \in A_1\) we construct a path that begins in \(\sigma \) and ends in a configuration in \(A_1 \cup \{\underline{-1}\}\) with lower energy than \(\sigma \), i.e., \(\overline{\omega }\in \varTheta (\sigma ,\mathcal {I_{\sigma }} \cap (A_1 \cup \{\underline{-1}\}))\). We now fix \(\sigma \equiv \omega _1\in A_1\) and we begin by defining \(\omega _2\). If there is a minus corner in \(\sigma _{R_{l,m}}\) , say in \(j_1\), then \(\sigma (j_1)\) is kept fixed and all other spins in the rectangle switch sign, i.e., \(\omega _2:=T^{F}_{j_1}(\omega _1)\). On the other hand, if there is no minus corner in \(\sigma _{R_{l,m}}\), then we call the next configuration in the path \(\omega _1'\) and we define it as \(\omega _1':=T(\omega _1)\), i.e., all the spins in the rectangle switch sign. After this step, \(\omega _1'\) has a minus corner, so we can proceed as above and define \(\omega _2:=T^{F}_{j_1}(\omega _1')\). Note that in \(\omega _2\) there are two minus corners in the rectangle that are nearest neighbors of \(j_1\). For the next step, keep fixed the minus corner that is contained in a side of length l, say in \(j_2\), and define \(\omega _3:=T^{F}_{j_2}(\omega _2)\). By iterating this procedure \(l-2\) times, a full slice of the droplet is erased and we obtain the configuration \(\eta \equiv \omega _l\) such that \(\eta _{R_{l,m-1}}={\underline{c}}\) and \(\eta _{\varLambda \setminus R_{l,m-1}}=\underline{-1}\). In order to determine where the maximum of the transition energy is attained, we rewrite for \(k=1, \ldots , l-1\)
with the convention that a sum over an empty set is equal to zero. From the reversibility property of the dynamics follows that
and since \(\varDelta (\omega _{k+1},\omega _k)=0\) for \(k=1,\ldots ,l-2\), for the path \(\overline{\omega }\),
It can be shown that \(H(\omega _{m+1})-H(\omega _m)=2h>0\) for \(m=1,\ldots ,l-2\) and \(\varDelta (\omega _{l-1},\omega _l)=2h\) [19, Tab. 1], so the maximum is attained in the pair of configurations \((\omega _{l-1}, \omega _l)\). Hence,
Since \(V^*_{\sigma }\) depends only on the length l, we find \(V^*_{A_1}=\max _{\sigma \in A_1} V^*_{\sigma }\) by taking the maximum over l. Since \(l<\lambda \), we have
Finally, let us check that \(\omega _l \in \mathcal {I_{\sigma }} \cap (A_1 \cup \{\underline{-1}\})\). Using (5.14), (5.16) and [19, Tab. 1], we get
The rectangle \(R_{l,m}\) is subcritical if and only if \(l<2/h\), and so
which concludes the proof for \(A_1\).
Case \(A_2\). For any configuration \(\sigma \in A_2\) we construct a path that begins in \(\sigma \) and ends in a configuration in \(A_2 \cup \{{\underline{c}}\}\) with lower energy than \(\sigma \), i.e., \(\overline{\omega }\in \varTheta (\sigma ,\mathcal {I_{\sigma }} \cap (A_2 \cup \{{\underline{c}}\}))\). We now fix \(\sigma \equiv \omega _1\in A_2\) and we begin by defining \(\omega _2\). We call \(j\in R_{l,m}\) a site in one of the sides of length l and such that \(\sigma (j)=+1\). Furthermore, we call \(j_1 \in \varLambda \setminus R_{l,m}\) the nearest neighbor of j such that (necessarily) \(\sigma (j_1)=-1\) and we define \(\omega _2:=T^{C}_{j_1}(\omega _1)\), i.e., \(\sigma (j_1)\) switches sign and the signs of all other sites in \(\sigma _{\varLambda \setminus R_{l,m}}\) remain fixed. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until a new slice is filled with chessboard. We obtain the configuration \(\eta \) such that \(\eta _{R_{l,m+1}}={\underline{c}}\) and \(\eta _{\varLambda \setminus R_{l,m+1}}=\underline{-1}\). Note that at the first step of the dynamics either one or two nearest neighbors of \(j_1\) in the external side of the rectangle switch sign when T is applied. Analogously, at each subsequent application of T, either one of two further sites in the external side of the rectangle switch sign. Therefore, the maximum number of iterations of the map T is \(l-1\). In order to determine where the maximum of the transition energy is attained, we rewrite the energy difference as in (5.13). Using (5.14) and since \(\varDelta (\omega _k,\omega _{k+1})=0\) for \(k=2,\ldots ,l-1\), for the path \(\overline{\omega }\),
It can be shown that \(H(\omega _{m+1})-H(\omega _m)=-\varDelta (\omega _{m+1},\omega _m)=-2h<0\) for \(m=2,\ldots ,l\) [19, Tab. 1], so the maximum is attained in the pair of configurations in \((\omega _1, \omega _2)\), hence
Since \(V^*_{\sigma }\) is the same for all configurations in \(A_2\), \(V^*_{A_2}=\max _{\sigma \in A_2} V^*_{\sigma }=2(2-h)\). Finally, let us check that \(\omega _l \in \mathcal {I_{\sigma }} \cap (A_2 \cup \{{\underline{c}}\})\). Using (5.14), (5.21) and [19, Tab. 1], we get
The rectangle \(R_{l,m}\) is supercritical if and only if \(l>2/h\), and so
which concludes the proof for \(A_2\).
Case \(A_3\). For any configuration \(\sigma \in A_3\) we construct a path that begins in \(\sigma \) and ends in a configuration in \(A_3 \cup \{{\underline{c}}\}\) with lower energy than \(\sigma \), i.e., \(\overline{\omega } \in \varTheta (\sigma ,\mathcal {I_{\sigma }} \cap (A_3 \cup \{{\underline{c}}\}))\). We now fix \(\sigma \equiv \omega _1\in A_3\) and we begin by defining \(\omega _2\). If in \(\sigma _{R_{l,m}}\) there is a plus corner surrounded by two minuses, say in \(j_1\), then \(\sigma (j_1)\) switches sign and the signs of all other spins in the rectangle remain fixed, i.e., \(\omega _2:=T^{C}_{j_1}(\omega _1)\). On the other hand, if in \(\sigma _{R_{l,m}}\) there are no plus corners surrounded by minuses, then we call the next configuration in the path \(\omega _1'\) and we define it as \(\omega _1':=T(\omega _1)\), i.e., all the spins in \(\sigma _{\varLambda \setminus R_{l,m}}\) switch sign. After this step, \(\omega _1'\) has a plus corner surrounded by two minuses, so we can proceed as above and define \(\omega _2:=T^{C}_{j_1}(\omega _1')\). Note that in \(\omega _2\) there are two plus corners in the rectangle that are nearest neighbors of \(j_1\). For the next step, the plus corner, say in \(j_2\), that is contained in a side of length l, switches sign, i.e., \(\omega _3:=T^{C}_{j_2}(\omega _2)\). By iterating this step \(l-2\) times, a full slice of the droplet is erased and we obtain the configuration \(\eta \equiv \omega _l\) such that \(\eta _{R_{l,m-1}}=\underline{+1}\) and \(\eta _{\varLambda \setminus R_{l,m-1}}={\underline{c}}\). In order to determine where the maximum of the transition energy is attained, we rewrite the energy difference as in (5.13). Using (5.14), we obtain the same result as in (5.15). Hence,
Since \(V^*_{\sigma }\) depends only on the length l, we find \(V^*_{A_3}=\max _{\sigma \in A_3} V^*_{\sigma }\) by taking the maximum over l. Since \(l<\lambda \), we have
Finally, let us check that \(\omega _l \in \mathcal {I_{\sigma }} \cap (A_3 \cup \{{\underline{c}}\})\). Using (5.14), (5.24) and [19, Tab. 1], we get
The rectangle \(R_{l,m}\) is subcritical if and only if \(l<2/h\), and so
which concludes the proof for \(A_3\).
Case \(A_4\). For any configuration \(\sigma \in A_4\) we construct a path that begins in \(\sigma \) and ends in a configuration in \(A_4 \cup \{\underline{+1}\}\) with lower energy than \(\sigma \), i.e., \(\overline{\omega } \in \varTheta (\sigma ,\mathcal {I_{\sigma }} \cap (A_4 \cup \{\underline{+1}\}))\). We now fix \(\sigma \equiv \omega _1\in A_4\) and we begin by defining \(\omega _2\). Pick any site \(j \in R_{l,m}\) in one of the sides of length l, such that its nearest neighbor \(j_1\in \varLambda \setminus R_{l,m}\) is such that \(\sigma (j_1)=+1\). We define \(\omega _2:=T^{F}_{j_1}(\omega _1)\), i.e., \(\sigma (j_1)\) is kept fixed and all the spins in \(\sigma _{\varLambda \setminus R_{l,m}}\) switch sign. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until a new slice is filled with \(+1\). We obtain the configuration \(\eta \) such that \(\eta _{R_{l,m+1}}=\underline{+1}\) and \(\eta _{\varLambda \setminus R_{l,m+1}}={\underline{c}}\). Note that at the first step of the dynamics either one or two nearest neighbors of \(j_1\) in the external side of the rectangle switch sign when T is applied. Analogously, at each subsequent application of T, either one of two further sites in the external side of the rectangle switch sign. Therefore, the maximum number of iterations of the map T is \(l-1\). In order to determine where the maximum of the transition energy is attained, we rewrite the energy difference as in (5.13). Using (5.14), we obtain the same result as in (5.20). Hence,
Since \(V^*_{\sigma }\) is the same for all configurations in \(A_4\), \(V^*_{A_4}=\max _{\sigma \in A_4} V^*_{\sigma }=2(2-h)\). Finally, let us check that \(\omega _l \in \mathcal {I_{\sigma }} \cap (A_4 \cup \{\underline{+1}\})\). Using (5.14), (5.28) and [19, Tab. 1], we get
The rectangle \(R_{l,m}\) is supercritical if and only if \(l>2/h\), and so
which concludes the proof for \(A_4\).
Case \(A_5\). For any configuration \(\sigma \in A_5\) we construct a path that begins in \(\sigma \) and ends in a configuration in \(D_1\) with lower energy than \(\sigma \), i.e., \(\overline{\omega }\in \varTheta (\sigma ,\mathcal {I_{\sigma }} \cap D_1)\). We now fix \(\sigma \equiv \omega _1\in A_5\) and we begin by defining \(\omega _2\). We call \(j_1\) a corner in \(R_{l,m}\) such that (necessarily) \(\sigma (j_1)=+1\) and we define \(\omega _2:=T^{C}_{j_1}(\omega _1)\), i.e., \(\sigma (j_1)\) switches sign and the signs of all other spins in the rectangle remain fixed. Note that in \(\omega _2\) there are two plus corners in the rectangle that are nearest neighbors of \(j_1\). For the next step, the plus corner, say in \(j_1\), that is contained in a side of length l switches sign, i.e., \(\omega _3:=T^{C}_{j_2}(\omega _2)\). After this, the spin of the nearest neighbor of \(j_2\) along the same side of \(R_{l,m}\) and different from \(j_1\), say in \(j_3\), switches spin, i.e., \(\omega _4:=T^{C}_{j_3}(\omega _3)\). By iterating this step \(l-3\) times, a full slice of the droplet is erased and we obtain the configuration \(\omega _l \equiv \eta \) such that \(\eta _{R_{l,m-1}}=\underline{+1}\), \(\eta _{R_{l,1}}={\underline{c}}\), \(\eta _{\varLambda \setminus R_{l,m}}=\underline{-1}\). The configuration \(\eta \) is a configuration in \(D_1\). In order to determine where the maximum of the transition energy is attained, we rewrite the energy difference as in (5.13). Using (5.14), we obtain the same result (5.15). Hence,
Since \(V^*_{\sigma }\) depends only on the length l, we find \(V^*_{A_5}=\max _{\sigma \in A_5} V^*_{\sigma }\) by taking the maximum over l. Since \(l<\lambda \), we have
Finally, let us check that \(\omega _l \in \mathcal {I_{\sigma }} \cap D_1\). Using (5.14), (5.31) and [19, Tab. 1], we get
The rectangle \(R_{l,m}\) is subcritical if and only if \(l<2/h\), and so
which concludes the proof for \(A_5\).
Case \(A_6\). For any configuration \(\sigma \in A_6\) we construct a path that begins in \(\sigma \) and ends in a configuration in \(D_3\) with lower energy than \(\sigma \), i.e., \(\overline{\omega }\in \varTheta (\sigma ,\mathcal {I_{\sigma }} \cap D_3)\). We now fix \(\sigma \equiv \omega _1\in A_6\) and we begin by defining \(\omega _2\). We call \(j \in R_{l,m}\) a site in a side of \(R_{l,m}\), and note that (necessarily) \(\sigma (j)=+1\). Without loss of generality, we choose a side of length l. Furthermore, we call \(j_1\in \varLambda \setminus R_{l,m}\) the nearest neighbor of j contained in the external side with length l such that (necessarily) \(\sigma (j_1)=-1\). We define \(\omega _2:=T^{C}_{j_1}(\omega _1)\), i.e., \(\sigma (j_1)\) switches sign and the signs of all other spins in \(\sigma _{\varLambda \setminus R_{l,m}}\) remain fixed. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T(\omega _2)\) and so on until a new slice is filled with \({\underline{c}}\), so we obtain the configuration \(\eta \) such that \(\eta _{R_{l,m}}=\underline{+1}\), \(\eta _{R_{l,1}}={\underline{c}}\) and \(\eta _{\varLambda \setminus R_{l,m+1}}=\underline{-1}\). Note that at the first step of the dynamics either one or two nearest neighbors of \(j_1\) in the external side of the rectangle switch sign when T is applied. Analogously, at each subsequent application of T, either one of two further sites in the external side of the rectangle switch sign. Therefore, the maximum number of iterations of the map T is \(l-1\). The configuration \(\eta \) is a configuration in \(D_2\). In order to determine where the maximum of the transition energy is attained, we rewrite the energy difference as in (5.13). Using (5.14), we obtain the same result as in (5.20). Hence,
Since \(V^*_{\sigma }\) is the same for all configurations in \(A_6\), \(V^*_{A_6}=\max _{\sigma \in A_6} V^*_{\sigma }=2(2-h)\). Finally, let us check that \(\omega _l \in \mathcal {I_{\sigma }} \cap D_3\). Using (5.14), (5.35) and [19, Tab. 1], we get
The rectangle \(R_{l,m}\) is supercritical if and only if \(l>2/h\), and so
which concludes the proof for \(A_6\). In conclusion,
Next we consider the set B.
Case \(B_1\). For every configuration in \(B_1\), both rectangles are subcritical. Following a path that changes a slice of \(\underline{+1}\) into a slice of \({\underline{c}}\), analogously as was done for \(A_3\), we get a configuration in \({\mathcal {I}}_\sigma \cap (B_1 \cup A_1)\). We have
Case \(B_2\). For every configuration in \(B_2\), both rectangles are supercritical. Following a path that adds a slice of \({\underline{c}}\), analogously as was done for \(A_2\), we get a configuration in \({\mathcal {I}}_\sigma \cap (B_2 \cup A_4)\). We have
Case \(B_3\). For every configuration in \(B_3\), the external rectangle is supercritical and the internal rectangle is subcritical. Following a path that adds a slice of \({\underline{c}}\), analogously as was done for \(A_2\), we get a configuration in \({\mathcal {I}}_\sigma \cap (B_3 \cup A_3)\). We have
We conclude that
Next we consider the set D.
Case \(D_1\). For every configuration \(\sigma \) in \(D_1\), all rectangles are subcritical and non-interacting. If \(\sigma \) contains at least one rectangle of \(\underline{+1}\) surrounded by \({\underline{c}}\), we take our path to be the path that cuts a slice of \(\underline{+1}\), analogously as was done for \(A_3\). We get a configuration in \({\mathcal {I}}_\sigma \cap D_1\). Otherwise, if \(\sigma \) contains at least one rectangle of \(\underline{+1}\) surrounded by \(\underline{-1}\), we take our path to be the path that changes a slice of \(\underline{+1}\) into a slice of \({\underline{c}}\), analogously as was done for \(A_5\). We get a configuration in \({\mathcal {I}}_\sigma \cap D_3\). Finally, we consider all remaining configurations, namely chessboard rectangles in a sea of minus. We take our path to be the path that cuts a slice of \({\underline{c}}\), analogous to the one described in \(A_1\). We get a configuration in \({\mathcal {I}}_\sigma \cap (D_1 \cup A_1)\). So, we have
Case \(D_2\). For every configuration \(\sigma \) in \(D_2\), there exists at least one supercritical rectangle. If this is a chessboard rectangle, then we take the path that makes the rectangle grow a slice of \({\underline{c}}\), analogously as was done for \(A_2\). We get a configuration in \({\mathcal {I}}_\sigma \cap (A_3 \cup A_4 \cup D_2 \cup D_4 \cup D_5 \cup E_4 \cup \{{\underline{c}}\})\). Otherwise, if this supercritical rectangle contains \(\underline{+1}\), we take the path that makes the rectangle grow a slice of \({\underline{c}}\), analogously as was done for \(A_6\). We get a configuration in \({\mathcal {I}}_\sigma \cap (D_2 \cup D_4 \cup D_5)\). So, we have
Case \(D_3\). For every configuration \(\sigma \) in \(D_3\), all rectangles are subcritical and non-interacting. If \(\sigma \) contains at least one rectangle of \(\underline{+1}\) surrounded by \({\underline{c}}\), we take our path to be the path that cuts a slice of \(\underline{+1}\), analogously as was done for \(A_3\). We get a configuration in \({\mathcal {I}}_\sigma \cap D_3\). Otherwise, if \(\sigma \) contains at least one rectangle of \(\underline{+1}\) at lattice distance one from a rectangle of \({\underline{c}}\), we take the path that changes a slice of \(\underline{+1}\) into a slice of \({\underline{c}}\) along the interface between the two rectangles, analogously as was done for \(A_3\). We get a configuration in \({\mathcal {I}}_\sigma \cap (A_1 \cup D_1 \cup D_3)\). In the remaining cases, \(\sigma \) contains at least two rectangles of different chessboard parity at lattice distance one. We take our path to be a path that changes a slice of \({\underline{c}}\), analogously as was done for \(A_1\). We get a configuration in \({\mathcal {I}}_\sigma \cap (A_1 \cup D_1 \cup D_3)\). So, we have
Case \(D_4\). For every configuration \(\sigma \) in \(D_4\), all rectangles of \(\underline{+1}\) surrounded by \({\underline{c}}\) are subcritical and non-interacting. We take our path to be a path that cuts a slice of \(\underline{+1}\), analogously as was done for \(A_3\). We get a configuration in \({\mathcal {I}}_\sigma \cap (D_4 \cup A_3)\). So, we have
Case \(D_5\). For every configuration \(\sigma \) in \(D_5\), there exists at least a supercritical rectangle of \(\underline{+1}\) surrounded \({\underline{c}}\). We consider this rectangle and we take the path that makes the rectangle grow a slice of \(\underline{+1}\), analogously as was done for \(A_4\). We get a configuration in \({\mathcal {I}}_\sigma \cap (D_5 \cup A_4 \cup E_5)\). So, we have
In conclusion,
The last set E is composed of strips.
Case \(E_1\). A configuration \(\sigma \equiv \omega _1\) in \(E_1\) has at least a strip of \({\underline{c}}\) of width one. Pick a site j in the strip such that \(\sigma (j)=-1\) and define \(\omega _2=T_j^F(\omega _1)\), i.e., \(\sigma (j)\) is kept fixed. The energy difference is \(H(\omega _2)-H(\omega _1)=2h\) [19, Tab.1]. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until we obtain a configuration in \({\mathcal {I}}_\sigma \cap (E_1 \cup D_1 \cup D_2 \cup D_3 \cup A_1 \cup A_2 \cup A_5 \cup A_6 \cup B \cup \{\underline{-1}\})\). So, we have
Case \(E_2\). A configuration \(\sigma \equiv \omega _1\) in \(E_2\) contains at least a strip of \(\underline{+1}\) of width one. Let \(\sigma (j)\) be a plus in the strip surrounded by one or two minuses. We define \(\omega _2=T_j^C(\omega _1)\), i.e., \(\sigma (j)\) switches sign. The maximum energy difference is \(H(\omega _2)-H(\omega _1)=2(2-h)\) [19, Tab.1]. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until we obtain a configuration in \({\mathcal {I}}_{\sigma } \cap (E_2 \cup E_7 \cup \{{\underline{c}}\})\). So, we have
Case \(E_3\). A configuration \(\sigma \equiv \omega _1\) in \(E_3\) has at least a strip of \(\underline{+1}\) of width one. If in \(\sigma \) there is a strip of \(\underline{+1}\) surrounded by two chessboards with the same parity, then pick a plus \(\sigma (j)\) in the strip and define \(\omega _2=T_j^C(\omega _1)\), i.e., \(\sigma (j)\) switches sign. The energy difference is \(H(\omega _2)-H(\omega _1)=2h\) [19, Tab.1]. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until we obtain a configuration in \({\mathcal {I}}_\sigma \cap (E_1 \cup E_7)\). Instead, if in \(\sigma \) there is a strip of \(\underline{+1}\) surrounded by two chessboards with different parity, then pick a plus \(\sigma (j)\) in a chessboard at lattice distance one from the strip and define \(\omega _2=T_j^F(\omega _1)\), i.e., \(\sigma (j)\) is kept fixed. The energy difference is \(H(\omega _2)-H(\omega _1)=2(2-h)\) [19, Tab.1]. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until we obtain a configuration in \({\mathcal {I}}_\sigma \cap E_5\). So, we have
Case \(E_4\). We consider a configuration \(\sigma \equiv \omega _1\) in \(E_4\) and pick a plus on the interface between \({\underline{c}}\) and \(\underline{-1}\), and call j the site of this plus. We call \(j_1\) the nearest neighbor of j in \(\underline{-1}\) and we define \(\omega _2=T_{j_1}^C(\omega _1)\), i.e., \(\sigma (j_1)\) switches sign. The energy difference is \(H(\omega _2)-H(\omega _1)=2(2-h)\) [19, Tab.1]. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until we obtain a configuration in \({\mathcal {I}}_\sigma \cap (E_4 \cup D_4 \cup D_5 \cup E_7 \cup \{{\underline{c}}\})\). So, we have
Case \(E_5\). We consider a configuration \(\sigma \equiv \omega _1\) in \(E_5\) and pick a plus in \({\underline{c}}\) on the interface between \({\underline{c}}\) and \(\underline{+1}\), and call j the site of this plus. We define \(\omega _2=T_{j}^F(\omega _1)\), i.e., \(\sigma (j)\) is kept fixed. The energy difference is \(H(\omega _2)-H(\omega _1)=2(2-h)\) [19, Tab.1]. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until we obtain a configuration in \({\mathcal {I}}_\sigma \cap (E_5 \cup \{\underline{+1}\})\). So, we have
Case \(E_6\). We consider a configuration \(\sigma \equiv \omega _1\) in \(E_6\) and pick a minus on the interface between \(\underline{-1}\) and \(\underline{+1}\), and call j the site of this minus. We define \(\omega _2=T_{j}^C(\omega _1)\), i.e., \(\sigma (j)\) switches sign. The energy difference is \(H(\omega _2)-H(\omega _1)=2(2-h)\) [19, Tab.1]. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until we obtain a configuration in \({\mathcal {I}}_\sigma \cap E_7\). So, we have
Case \(E_7\). If the configuration \(\sigma \equiv \omega _1\) in \(E_7\) contains a strip of \(\underline{-1}\) adjacent to a strip of \(\underline{+1}\) and both have width greater then one, then we pick a minus one on the interface between \(\underline{-1}\) and \(\underline{+1}\) and we take a path analogously as was done for \(E_6\). We get a configuration in \({\mathcal {I}}_\sigma \cap (E_7 \cup E_5)\). Otherwise, \(E_7\) contains a strip of \({\underline{c}}\) adjacent to a strip of \(\underline{-1}\), both with width greater then one. Then, we pick a plus one, say in j, in the strip of \({\underline{c}}\). We call \(j_1\) the nearest neighbor of j in \(\underline{-1}\) and we define \(\omega _2=T_{j_1}^C(\omega _1)\), i.e., \(\sigma (j_1)\) switches sign. The energy difference is \(H(\omega _2)-H(\omega _1)=2(2-h)\) [19, Tab.1]. We define \(\omega _3:=T(\omega _2)\), \(\omega _4:=T(\omega _3)=T^2(\omega _2)\) and so on until we obtain a configuration in \({\mathcal {I}}_\sigma \cap (E_7 \cup E_5)\). So, we have
Then
To conclude the proof, we compare the value of \(V^*=\max \{V^*_A,V^*_B,V^*_D,V^*_E\}=2(2-h)\) and \(\varGamma ^{\text {PCA}}\), and we get
References
Arous, G.B., Cerf, R.: Metastability of the three dimensional Ising model on a torus at very low temperatures. Electron. J. Probab. 1, 59 (1996)
Bashiri, K.: A note on the metastability in three modifications of the standard Ising model. arXiv preprint arXiv:1705.07012 (2017)
Beltran, J., Landim, C.: Tunneling and metastability of continuous time Markov chains. J. Stat. Phys. 140(6), 1065–1114 (2010)
Beltrán, J., Landim, C.: Tunneling and metastability of continuous time Markov chains ii, the nonreversible case. J. Stat. Phys. 149(4), 598–618 (2012)
Bianchi, A., Gaudilliere, A.: Metastable states, quasi-stationary distributions and soft measures. Stoch. Process. Appl. 126(6), 1622–1680 (2016)
Bigelis, S., Cirillo, E.N.M., Lebowitz, J.L., Speer, E.R.: Critical droplets in metastable states of Probabilistic Cellular Automata. Phys. Rev. E 59(4), 3935 (1999)
Bovier, A., Den Hollander, F.: Metastability: A Potential-Theoretic Approach, vol. 351. Springer, New York (2016)
Bovier, A., Den Hollander, F., Nardi, F.R.: Sharp asymptotics for Kawasaki dynamics on a finite box with open boundary. Probab. Theory Relat. fields 135(2), 265–310 (2006)
Bovier, A., Den Hollander, F., Spitoni, C., et al.: Homogeneous nucleation for Glauber and Kawasaki dynamics in large volumes at low temperatures. Ann. Probab. 38(2), 661–713 (2010)
Bovier, A., Eckhoff, M., Gayrard, V., Klein, M.: Metastability and low lying spectra in reversible Markov chains. Commun. Math. Phys. 228(2), 219–255 (2002)
Bovier, A., Eckhoff, M., Gayrard, V., Klein, M.: Metastability in reversible diffusion processes I. Sharp asymptotics for capacities and exit times. J. Eur. Math. Soc. 7, 69–99 (2004)
Bovier, A., Manzo, F.: Metastability in Glauber dynamics in the low-temperature limit: beyond exponential asymptotics. J. Stat. Phys. 107(3–4), 757–779 (2002)
Cassandro, M., Galves, A., Olivieri, E., Vares, M.E.: Metastable behavior of stochastic dynamics: a pathwise approach. J. Stat. Phys. 35(5–6), 603–634 (1984)
Catoni, O.: Simulated annealing algorithms and Markov chains with rare transitions. In: Séminaire de probabilités XXXIII, pp. 69–119. Springer (1999)
Catoni, O., Cerf, R.: The exit path of a Markov chain with rare transitions. ESAIM 1, 95–144 (1997)
Catoni, O., Trouvé, A.: Parallel annealing by multiple trials: a mathematical study. Simul. Ann. 9, 129–143 (1992)
Cerf, R., Manzo, F.: Nucleation and growth for the Ising model in \( d \) dimensions at very low temperatures. Ann. Probab. 41(6), 3697–3785 (2013)
Cirillo, E.N.M., Lebowitz, J.L.: Metastability in the two-dimensional Ising model with free boundary conditions. J. Stat. Phys. 90(1–2), 211–226 (1998)
Cirillo, E.N.M., Nardi, F.R.: Metastability for a stochastic dynamics with a parallel heat bath updating rule. J. Stat. Phys. 110(1–2), 183–217 (2003)
Cirillo, E.N.M., Nardi, F.R.: Relaxation height in energy landscapes: an application to multiple metastable states. J. Stat. Phys. 150(6), 1080–1114 (2013)
Cirillo, E.N.M., Nardi, F.R., Sohier, J.: Metastability for general dynamics with rare transitions: escape time and critical configurations. J. Stat. Phys. 161(2), 365–403 (2015)
Cirillo, E.N.M., Nardi, F.R., Spitoni, C.: Competitive nucleation in reversible Probabilistic Cellular Automata. Phys. Rev. E 78(4), 040601 (2008)
Cirillo, E.N.M., Nardi, F.R., Spitoni, C.: Metastability for reversible Probabilistic Cellular Automata with self-interaction. J. Stat. Phys. 132(3), 431–471 (2008)
Cirillo, E.N.M., Nardi, F.R., Spitoni, C.: Sum of exit times in series of metastable states in Probabilistic Cellular Automata. In: International Workshop on Cellular Automata and Discrete Complex Systems, pp. 105–119. Springer (2016)
Cirillo, E.N.M., Nardi, F.R., Spitoni, C.: Sum of exit times in a series of two metastable states. Eur. Phys. J. Spec. Top. 226(10), 2421–2438 (2017)
Cirillo, E.N.M., Olivieri, E.: Metastability and nucleation for the Blume–Capel model. Different mechanisms of transition. J. Stat. Phys. 73(3–4), 473–554 (1996)
Dai Pra, P., Scoppola, B., Scoppola, E.: Fast mixing for the low temperature 2d Ising model through irreversible parallel dynamics. J. Stat. Phys. 159(1), 1–20 (2015)
Dehghanpour, P., Schonmann, R.H.: Metropolis dynamics relaxation via nucleation and growth. Commun. Math. Phys. 188(1), 89–119 (1997)
Den Hollander, F., Nardi, F.R., Olivieri, E., Scoppola, E.: Droplet growth for three-dimensional Kawasaki dynamics. Probab. Theory Relat. Fields 125(2), 153–194 (2003)
Den Hollander, F., Nardi, F.R., Troiani, A.: Metastability for low-temperature Kawasaki dynamics with two types of particles. Electron. J. Probab. 17, 1–26 (2012)
Derrida, B.: Dynamical phase transitions in spin models and automata. Technical Report, CEA Centre d’Etudes Nucleaires de Saclay (1989)
Gaudillière, A.: Condenser physics applied to Markov chains. Lecture Notes for the 12th Brazilian School of Probability (2009)
Gaudillière, A., Den Hollander, F., Nardi, F.R., Olivieri, E., Scoppola, E.: Ideal gas approximation for a two-dimensional rarefied gas under Kawasaki dynamics. Stoch. Process. Appl. 119(3), 737–774 (2009)
Gaudilliere, A., Landim, C.: A Dirichlet principle for non reversible Markov chains and some recurrence theorems. Probab. Theory Relate. Fields 158, 55–89 (2014)
Gaudillière, A., Milanesi, P., Vares, M.E.: Asymptotic exponential law for the transition time to equilibrium of the metastable kinetic Ising model with vanishing magnetic field. J. Stat. Phys. 179, 1–46 (2020)
Gaudilliere, A., Nardi, F.R.: An upper bound for front propagation velocities inside moving populations. Braz. J. Probab. Stat. 24(2), 256–278 (2010)
Gaudilliere, A., Olivieri, E., Scoppola, E.: Nucleation pattern at low temperature for local Kawasaki dynamics in two dimensions. Markov Process. Relat. Fields 11, 553–628 (2005)
Hollander, F.D., Olivieri, E., Scoppola, E.: Metastability and nucleation for conservative dynamics. J. Math. Phys. 41(3), 1424–1498 (2000)
Holley, R., Stroock, D.: Simulated annealing via Sobolev inequalities. Commun. Math. Phys. 115(4), 553–569 (1988)
Koteckỳ, R., Olivieri, E.: Shapes of growing droplets-a model of escape from a metastable phase. J. Stat. Phys. 75(3–4), 409–506 (1994)
Manzo, F., Nardi, F.R., Olivieri, E., Scoppola, E.: On the essential features of metastability: tunnelling time and critical configurations. J. Stat. Phys. 115(1–2), 591–642 (2004)
Manzo, F., Olivieri, E.: Relaxation patterns for competing metastable states: a nucleation and growth model. Markov Proc. Relat. Fields 4, 549–570 (1998)
Manzo, F., Olivieri, E.: Dynamical Blume–Capel model: competing metastable states at infinite volume. J. Stat. Phys. 104(5–6), 1029–1090 (2001)
Nardi, F.R., Olivieri, E.: Low temperature stochastic dynamics for an Ising model with alternating field. Markov Proc. Relat. Fields 2, 117–166 (1996)
Nardi, F.R., Spitoni, C.: Sharp asymptotics for stochastic dynamics with parallel updating rule. J. Stat. Phys. 146(4), 701–718 (2012)
Nardi, F.R., Zocca, A., Borst, S.C.: Hitting time asymptotics for hard-core interactions on grids. J. Stat. Phys. 162(2), 522–576 (2016)
Neves, E.J., Schonmann, R.H.: Critical droplets and metastability for a Glauber dynamics at very low temperatures. Commun. Math. Phys. 137(2), 209–230 (1991)
Neves, E.J., Schonmann, R.H.: Behavior of droplets for a class of Glauber dynamics at very low temperature. Probab. Theory Relat. Fields 91(3–4), 331–354 (1992)
Olivieri, E., Scoppola, E.: Markov chains with exponentially small transition probabilities: first exit problem from a general domain I. The reversible case. J. Stat. Phys. 79(3–4), 613–647 (1995)
Olivieri, E., Scoppola, E.: Markov chains with exponentially small transition probabilities: first exit problem from a general domain. II. The general case. J. Stat. Phys. 84(5–6), 987–1041 (1996)
Olivieri, E., Vares, M.E.: Large Deviations and Metastability, vol. 100. Cambridge University Press, Cambridge (2005)
Penrose, O., Lebowitz, J.L.: Rigorous treatment of metastable states in the Van der Waals-Maxwell theory. J. Stat. Phys. 3(2), 211–236 (1971)
Schonmann, R.H.: Slow droplet-driven relaxation of stochastic Ising models in the vicinity of the phase coexistence region. Commun. Math. Phys. 161(1), 1–49 (1994)
Schonmann, R.H., Shlosman, S.B.: Wulff droplets and the metastable relaxation of kinetic Ising models. Commun. Math. Phys. 194(2), 389–462 (1998)
Scoppola, E.: Metastability for Markov chains: a general procedure based on renormalization group ideas. In: Probability and Phase Transition, pp. 303–322. Springer (1994)
Trouvé, A.: Rough large deviation estimates for the optimal convergence speed exponent of generalized simulated annealing algorithms. Ann. Probab. Stat. 32(3), 299–348 (1996)
Acknowledgements
The research of Francesca R. Nardi was partially supported by the NWO Gravitation Grant 024.002.003—NETWORKS and by the PRIN Grant 20155PAWZB “Large Scale Random Structures”.
Funding
Open access funding provided by Università degli Studi di Firenze within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by Alessandro Giuliani.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In this section we prove theorems given in Sect. 2.4.
Proof of Theorem 2.3
Recall the equivalence relation above Theorem 3.6 in [20] for \(x,y \in {\mathcal {X}}\)
The configurations \(x_1^1,...,x_1^n\) are in the same equivalence class. Thus, the theorem follows immediately by Condition 2.1, (2.41), and [20, Theorem 3.6]. \(\square \)
Before given the proof of Theorem 2.4, we state two useful lemmas. In the first of the two lemmas we collect two bounds on the energy cost to go from any state \(x\ne x_1^r\) to \(x_1^r\) or to \(x_0\), for \(r=1,...,n\). The second lemma is similar.
Lemma A.1
Assume Condition 2.1 is satisfied. For any \(x\in {\mathcal {X}}\) and \(x\ne x_1^r\), for every \(r=1,...,n\). If \(H(x)\le H(x_1^r)\), we have that
Proof
Let us prove the first inequality. By Theorem 2.3 in [20] we have that \(\varPhi (x,x_0)\le \varGamma _m+H(x)\). If by contradiction \(\varPhi (x,x_0)=\varGamma _m+H(x)\) then, by the same Theorem 2.3 in [20], \(x\in {\mathcal {X}}^m\) which is in contradiction with Condition 2.1. Next we turn to the proof of the second inequality and we distinguish two cases. If \(H(x)<H(x_1^r)\), then we have that \(x\in {\mathcal {I}}_{x_1^r}\). By (2.19) and by (2.11), we get
that proves the inequality. If \(H(x)=H(x_1^r)\), then let us define the set
We will show that \(x\not \in {\mathcal {C}}\). Since \(H(x)= H(x_1^r)\), the identity \({\mathcal {I}}_{x}={\mathcal {I}}_{x_1^r}\) follows. Furthermore, since \(x_1^r\in {\mathcal {X}}^m\), we have \({\mathcal {C}}\cap {\mathcal {I}}_{x_1^r}=\emptyset \); hence, \({\mathcal {C}}\cap {\mathcal {I}}_{x}=\emptyset \) as well. Moreover, if \(x\in {\mathcal {C}}\) then \(V_x=\varPhi (x,{\mathcal {I}}_x)-H(x)\ge H(x_1^r)+\varGamma _m-H(x)=\varGamma _m\). By (2.19), x would be a metastable state, in contradiction with Condition 2.1. Hence, since \(x\not \in {\mathcal {C}}\), we have that
This proves the inequality for every \(r=1,...,n\). \(\square \)
Lemma A.2
Assume Condition 2.1 is satisfied. For any \(x\in {\mathcal {X}}\) and \(x\notin \{x_2,x_1^1,...,x_1^n,x_0\}\). If \(H(x)\le H(x_2)\), then
Proof
Let us prove the first inequality. By Theorem 2.3 in [20] we have \(\varPhi (x,\{x_1^1,...,x_1^n,x_0\}) \le \varPhi (x,x_0)\le \varGamma _m+H(x)\). We proceed by contradiction and assume that \(\varPhi (x,x_0)=\varGamma _m+H(x)\). By [20, Theorem 2.3], \(x\in {\mathcal {X}}^m\) which is in contradiction with Condition 2.1. Next we turn to the proof of the second inequality we distinguish two cases. If \(H(x)<H(x_2)\), then we have that \(x\in {\mathcal {I}}_{x_2}\). By (2.19) of metastable state and by (2.11), we get
This proves the inequality. If \(H(x)=H(x_2)\), then let us define the set
We will show that \(x\not \in {\mathcal {C}}\). Since \(H(x)= H(x_2)\), the identity \({\mathcal {I}}_{x}={\mathcal {I}}_{x_2}\) follows. Furthermore, since \(x_2\in X_{ \text {m}}\), we have \({\mathcal {C}}\cap {\mathcal {I}}_{x_2}=\emptyset \); hence, \({\mathcal {C}}\cap {\mathcal {I}}_{x}=\emptyset \) as well. Moreover, if \(x\in {\mathcal {C}}\) then \(V_x=\varPhi (x,{\mathcal {I}}_x)-H(x)\ge H(x_2)+\varGamma _m-H(x)=\varGamma \). By (2.19), x would be a metastable state, in contradiction with Condition 2.1. Hence, since \(x\not \in {\mathcal {C}}\), we have that
This proves the inequality. \(\square \)
Proof of Theorem 2.4
We begin by proving Eq. (2.46).
The proof is based on Lemmas A.1 and A.2. In the proof we only use the representation of the expected mean time in terms of the Green function [11, Corollary 3.3], see also [32, Eq. (4.29)]. Indeed, recalling (2.23) above, we rewrite the expected value in terms of the capacity as
Since \(h_{x_2,\{x_1^1,...,x_1^n,x_0\}}(x_2)=1\), we get the following lower bound:
In order to give an upper bound, we first use the boundary conditions in (2.22) to rewrite (A.4) as follows:
Next we bound \(\mu _{\beta }(x)\) as \(\mu _\beta (x) \le \mu _\beta (x_2)\exp (-\beta \delta )\) for some positive \(\delta =\min _x \{H(x) -H(x_2)\}\) and for any \(x\in {\mathcal {X}}\) such that \(H(x)>H(x_2)\). We get
Next we upper bound the equilibrium potential \(h_{x_2,\{x_1^1,...,x_1^n,x_0\}}(x)\) by applying Proposition A.1 with \(x=x\), \(Y=\{x_2\}\), \(Z=\{x_1^1,...,x_1^n, x_0\}\), as
Furthermore, if \(H(x)\le H(x_2)\) and \(x \notin {\mathcal {X}}^m \cup {\mathcal {X}}^s\), then
where \(C_1,\delta _1\) are suitable positive constants. In the first inequality we used Proposition A.2, in the second we used Lemmas A.1 and A.2. By using (A.6) we get
which implies
where we have used that the configuration space is finite. Equation (2.46) finally follows by (A.5) and (A.7).
Next we prove Eq. (2.47). Recalling (2.23) above, we rewrite the expected value in terms of the capacity as
Considering the contribution of every \(x_1^r\) in the sum and observing that \(h_{x_1^r,x_0}(x_1^r)=1\) and \(h_{x_1^r,x_0}(x_1^q) \simeq 1\) for every \(q=1,...,n\) , we get the following lower bound:
where the last equality follows from the definition of Gibbs-measure and \(H(x_1^r)=H(x_1^q)\) for every \(q=1,...,n\). In order to give an upper bound, we first use the boundary conditions in (2.22) to rewrite (A.8) as follows:
Next we bound \(\mu _{\beta }(x)\) as \(\mu _\beta (x) \le \mu _\beta (x_1^r)\exp (-\beta \delta )\) for some positive \(\delta =\min _x \{H(x) -H(x_1^r)\}\) and for any \(x\in {\mathcal {X}}\) such that \(H(x)>H(x_1^r)\). Recalling that \(h_{x_1^r,x_0}(x_1^r)=1\), \(h_{x_1^r,x_0}(x_1^q)=1+o(1)\) for every \(q=1,...,n\) with \(q \ne r\), we get
Next we upper bound the equilibrium potential \(h_{x_1^r,x_0}(x)\) by applying Proposition A.1 with \(x=x\), \(Z=\{x_0\}\) and \(Y=\{x_1^r\}\) for every \(i=1,...,n\)
Furthermore, if \(H(x)\le H(x_1^r)\) and \(x \ne x_1^q\) for every \(q=1,...,n\), then
where \(C_3,\delta _3\) are suitable positive constants. In the first inequality we used Proposition A.2, in the second we used Lemmas A.1 and A.2. By using (A.10) we get
which implies
where we have used that the configuration space is finite and \(H(x_1^r)=H(x_1^q)\) for every \(q=1,...,n\).
Proof of Theorem 2.5
We prove Eq. (2.49).
Recalling (2.23) above, we rewrite the expected value in terms of the capacity as
Considering the contribution of \(x_1^r\) for every \(r=1,...,n\) in the sum and observing that \(h_{\{x_1^1,...,x_1^n\},x_0}(x_1^q)=1\) for every \(q=1,...,n\), we get the following lower bound:
where the last equality follows from the definition of Gibbs-measure and \(H(x_1^r)=H(x_1^q)\) for every \(r,q =1,...,n\). In order to give an upper bound, we first use the boundary conditions in (2.22) to rewrite (A.12) as follows:
Next we bound \(\mu _{\beta }(x)\) as \(\mu _\beta (x) \le \mu _\beta (x_1^r)\exp (-\beta \delta )\) for some positive \(\delta =\min _x \{H(x) -H(x_1^r)\}\) and for any \(x\in {\mathcal {X}}\) such that \(H(x)>H(x_1^r)\). We get
Next we upper bound the equilibrium potential \(h_{\{x_1^1,...,x_1^n\},x_0}(x)\) by applying Proposition A.1 with \(x=x\), \(Y=\{x_1^1,...,x_1^n\}\) and \(Z=\{x_0\}\)
Furthermore, if \(H(x)\le H(x_1^r)\) and \(x \notin \{x_1^1,...,x_1^n,x_0\}\), then
where \(C_2,\delta _2\) are suitable positive constants. In the first inequality we used Proposition A.2, in the second we used Lemmas A.1 and A.2. By using (A.15) we get
which implies
where we have used that the configuration space is finite. Equation (2.49) finally follows recalling \(n\mu _\beta (x_1^r)=\mu _\beta (\{x_1^1,...x_1^n\})\) and by (A.13) and (A.16). \(\square \)
Proof of Theorem 2.6 and Theorem 2.7
The two theorems follow immediately by exploiting Condition 2.3 and applying Theorem 2.4. \(\square \)
The proof of Theorem 2.8 is based on the following lemma.
Lemma A.3
Given three or more states \(y,w^1,...,w^n,z\in {\mathcal {X}}\) pairwise mutually different, we have that the following holds
Proof
First of all we note that
We now rewrite the first term as follows
where we have used the fact that \(\tau _{\{w^1,...,w^n\}}=\min \{\tau _{w^1},...,\tau _{w^n}\}\) is a stopping time, that \({\mathbf {1}}_{\{\tau _{\{w^1,...,w^n\}}\}}\) is measurable with respect to the pre-\(\tau _{\{w^1,...,w^n\}}\)–\(\sigma \)–algebra \({\mathcal {F}}_{\tau _{\{w^1,...,w^n\}}}\) and the strong Markov property which gives \({\mathbb {E}}_y[\tau _z|{\mathcal {F}}_{\tau _{\{w^1,...,w^n\}}}]=\tau _{\{w^1,...,w^n\}}+ {\mathbb {E}}_{\{w^1,...,w^n\}}[\tau _z]\) on the event \(\{\tau _{\{w^1,...,w^n\}}\le \tau _z\}\). Since \( (\tau _{\{w^1,...,w^n\}}{\mathbf {1}}_{\{ \tau _{\{w^1,...,w^n\}}<\tau _z \}}+\tau _z{\mathbf {1}}_{\{ \tau _{\{w^1,...,w^n\}}\ge \tau _z \}})=\tau _{\{w^1,...,w^n,z\}}\), (A.17) follows. \(\square \)
Proof of Theorem 2.8
By (A.17) we have that
By Theorem 2.6 and Condition 2.2 it follows that
which concludes the proof. \(\square \)
Proposition A.1
Consider the Markov chain defined in Sect. 2.1. We have that
for any \(Y=\{y^1,...,y^t\}\subset {\mathcal {X}}\) for \(t \in {\mathbb {N}}\), \(Z=\{z^1,...,z^{t'}\}\subset {\mathcal {X}}\) for \(t' \in {\mathbb {N}}\), \(Y \cap Z=\emptyset \), \(x\in {\mathcal {X}} \setminus \{Y \cup Z\}\).
Proof
Given \(Y,Z \subset {\mathcal {X}}\) such that \(Y \cap Z=\emptyset \) and \(x\in {\mathcal {X}} \setminus \{Y \cup Z\}\), a renewal argument and the strong Markov property yield
Therefore
Recalling (2.23), we can rewrite the ratio in terms of ratio of capacities:
Hence, we get Eq. (A.19).
Proposition A.2
[8, Lemma 3.1.1] Consider the Markov chain defined in Sect. 2.1. For every not empty disjoint sets \(Y,Z\subset X\) there exist constants \(0<C_1<C_2<\infty \) such that
for all \(\beta \) large enough.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bet, G., Jacquier, V. & Nardi, F.R. Effect of Energy Degeneracy on the Transition Time for a Series of Metastable States. J Stat Phys 184, 8 (2021). https://doi.org/10.1007/s10955-021-02788-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10955-021-02788-0
Keywords
- Stochastic dynamics
- Probabilistic cellular automata
- Metastability
- Potential theory
- Low temperature dynamics
- Mixing times