Strong and Weak Optimizations in Classical and Quantum Models of Stochastic Processes

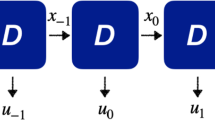
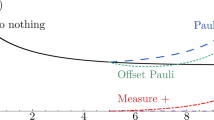
Abstract

Among the predictive hidden Markov models that describe a given stochastic process, the $\epsilon \text{-machine }$ is strongly minimal in that it minimizes every Rényi-based memory measure. Quantum models can be smaller still. In contrast with the $\epsilon \text{-machine }$ ’s unique role in the classical setting, however, among the class of processes described by pure-state hidden quantum Markov models, there are those for which there does not exist any strongly minimal model. Quantum memory optimization then depends on which memory measure best matches a given problem’s circumstance.

Appendix: Weak Minimality of \(\mathbf {D}_3\)

Here, we prove that $\mathfrak {D}_3$ is the unique 2D representation of the 3-state MBW process. We show this by considering the entire class of 2D models and applying the completeness constraint.

We note that a pure-state quantum model of the 3-state MBW process must have three states $\left| \eta _A\right\rangle$, $\left| \eta _B\right\rangle$, and $\left| \eta _C\right\rangle$, along with three dual states $\left\langle \epsilon _A\right|$, $\left\langle \epsilon _B\right|$, and $\left\langle \epsilon _C\right|$ such that:

$$\begin{aligned} \left\langle \epsilon _A|\eta _A\right\rangle&= e^{i\phi _{AA}}\sqrt{\frac{2}{3}} ,\\ \left\langle \epsilon _A|\eta _B\right\rangle&= e^{i\phi _{AB}}\frac{1}{\sqrt{6}} ,~\text {and}\\ \left\langle \epsilon _A|\eta _C\right\rangle&= e^{i\phi _{AC}}\frac{1}{\sqrt{6}} ,\\ \left\langle \epsilon _B|\eta _A\right\rangle&= e^{i\phi _{BA}}\frac{1}{\sqrt{6}} ,\\ \left\langle \epsilon _B|\eta _B\right\rangle&= e^{i\phi _{BB}}\sqrt{\frac{2}{3}} ,~\text {and}\\ \left\langle \epsilon _B|\eta _C\right\rangle&= e^{i\phi _{BC}}\frac{1}{\sqrt{6}}, \end{aligned}$$

and

$$\begin{aligned} \left\langle \epsilon _C|\eta _A\right\rangle&= e^{i\phi _{CA}}\frac{1}{\sqrt{6}},\\ \left\langle \epsilon _C|\eta _B\right\rangle&= e^{i\phi _{CB}}\frac{1}{\sqrt{6}},\\ \left\langle \epsilon _C|\eta _C\right\rangle&= e^{i\phi _{CC}}\sqrt{\frac{2}{3}}. \end{aligned}$$

We list the available geometric symmetries that leave the final stationary state unchanged:

• 1. Phase transformation on each state, $\left| \eta _x\right\rangle \mapsto e^{i\phi _x}\left| \eta _x\right\rangle$;

• 2. Phase transformation on each dual state, $\left| \epsilon _x\right\rangle \mapsto e^{i\phi _x}\left| \epsilon _x\right\rangle$; and

• 3. Unitary transformation $\left| \eta _x\right\rangle \mapsto U\left| \eta _x\right\rangle$ and $\left\langle \epsilon _x\right| \mapsto \left\langle \epsilon _x\right| U^\dagger$.

From these symmetries we can fix gauge in the following ways:

• 1. Set $\left\langle 0|\eta _x\right\rangle$ to be real and positive for all x.

• 2. Set $\phi _{AA}=\phi _{BB}=\phi _{CC}=0$.

• 3. Set $\left\langle 0|\eta _A\right\rangle =0$ and set $\left\langle 1|\eta _B\right\rangle$ to be real and positive.

These gauge fixings allow us to write:

$$\begin{aligned} \left| \eta _A\right\rangle&= \left| 0\right\rangle , \\ \left| \eta _B\right\rangle&= \alpha _B \left| 0\right\rangle +\beta _B\left| 1\right\rangle , ~\text {and}\\ \left| \eta _C\right\rangle&= \alpha _C \left| 0\right\rangle +e^{i\theta }\beta _C\left| 1\right\rangle , \end{aligned}$$

for $\alpha _B,\alpha _C\ge 0$, $\beta _B=\sqrt{1-\alpha _B^2}$ and $\beta _C=\sqrt{1-\alpha _C^2}$ and a phase $\theta$.

That these states are embedded in a 2D Hilbert space means there must exist some linear consistency conditions. For some triple of numbers $\mathbf {c}=(c_A, c_B, c_C)$ we can write:

$$\begin{aligned} c_A\left| \eta _A\right\rangle +c_B\left| \eta _B\right\rangle +c_C\left| \eta _C\right\rangle = 0 . \end{aligned}$$

Up to a constant, this triplet has the form:

$$\begin{aligned} (c_A, c_B, c_C) = \left( e^{i\theta }\alpha _B\frac{\beta _C}{\beta {B}}-\alpha _C,\,-e^{i\theta }\frac{\beta _C}{\beta {B}},\,1\right) . \end{aligned}$$

Consistency requires that this relationship between vectors is preserved by the Kraus operator dynamic. Consider the matrix $\mathbf {A}:=(A_{xy}) = \left( \left\langle \epsilon _x|\eta _y\right\rangle \right)$. The vector $\mathbf {c}$ must be a null vector of $\mathbf {A}$; i.e. $\sum _y A_{xy}c_y=0$. This first requires that $A_{xy}$ be degenerate. One way to enforce this is to check that the characteristic polynomial $\det (\mathbf {A}-\lambda \mathbf {I}_3)$ has an overall factor of $\lambda$. For simplicity, we compute the characteristic polynomial of $\mathbf {A}\sqrt{6}$:

$$\begin{aligned} \det (\sqrt{6}\mathbf {A}-\lambda \mathbf {I}_3) =&\quad \left( 2-\lambda \right) ^3 + \left( e^{i(\phi _{AB}+\phi _{BC}+\phi _{CA})}+e^{i(\phi _{BA}+\phi _{CB}+\phi _{AC})}\right) \\&\quad \quad - (2-\lambda )\left( e^{i(\phi _{AB}+\phi _{BA})}+e^{i(\phi _{AC}+\phi _{CA})}+e^{i(\phi _{BC}+\phi _{CB})}\right) . \end{aligned}$$

To have an overall factor of $\lambda$, we need:

$$\begin{aligned} 0&= 8 + \left( e^{i(\phi _{AB}+\phi _{BC}+\phi _{CA})}+e^{i(\phi _{BA}+\phi _{CB}+\phi _{AC})}\right) \\&\quad \quad -2\left( e^{i(\phi _{AB}+\phi _{BA})}+e^{i(\phi _{AC}+\phi _{CA})}+e^{i(\phi _{BC}+\phi _{CB})}\right) . \end{aligned}$$

Typically, there will be several ways to choose phases to cancel out vectors, but in this case since the sum of the magnitudes of the complex terms is 8, the only way to cancel is at the extreme point where $\phi _{AB}=-\,\phi _{BA}=\phi _1$, $\phi _{BC}=-\,\phi _{CB}=\phi _2$, and $\phi _{CA}=-\,\phi _{AC}=\phi _3$ and:

$$\begin{aligned} \phi _{1}+\phi _2+\phi _3=\pi . \end{aligned}$$

To recapitulate the results so far, $\mathbf {A}$ has the form:

$$\begin{aligned} \mathbf {A} = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} 2 &{} e^{i\phi _1} &{} -e^{i(\phi _1+\phi _2)}\\ e^{-i\phi _1} &{} 2 &{} e^{i\phi _2}\\ -e^{-i(\phi _1+\phi _2)} &{} e^{-i\phi _2} &{} 2 \end{array}\right) . \end{aligned}$$

We now need to enforce that $\sum _y A_{xy}c_y=0$. We have the three equations:

$$\begin{aligned} 2c_A+e^{i\phi _1}c_B -e^{i(\phi _1+\phi _2)}c_C&= 0 , \\ 2c_B+e^{-i\phi _1}c_A +e^{i\phi _2}c_C&= 0 , ~\text {and}\\ 2c_C+e^{-i\phi _2}c_B -e^{-i(\phi _1+\phi _2)}c_A&= 0 . \end{aligned}$$

It can be checked that these are solved by:

$$\begin{aligned} c_A&= e^{i(\phi _1+\phi _2)}c_C ~\text {and} \\ c_B&= - \,e^{i\phi _2}c_C . \end{aligned}$$

Taking our formulation of the $\mathbf {c}$ vector, we immediately have $\beta _B=\beta _C=\beta$ (implying $\alpha _B=\alpha _C=\alpha$), $\phi _2 = \theta$, and:

$$\begin{aligned} e^{-i\phi _3}&= \alpha (1-e^{i\theta }) \\&=-\,2i\alpha \sin (\theta )e^{i\theta /2} \\&=\alpha \sin (\theta )e^{i(\theta -\pi )/2}. \end{aligned}$$

This means:

$$\begin{aligned} \alpha&= \frac{1}{2} \left| \csc \left( \frac{\theta }{2}\right) \right| ~\text {and}\\ \phi _3&= \frac{-\,\theta +\mathrm {sgn}(\theta )\pi }{2} , \end{aligned}$$

where we take $-\pi \le \theta \le \pi$ and $\mathrm {sgn}(\theta )$ is the sign of $\theta$.

Note, however, that for $-\frac{\pi }{3}< \theta < \frac{\pi }{3}$, we have $|\csc (\theta )|> 1$, so these values are unphysical.

We see that all parameters in our possible states $\left| \eta _x\right\rangle$, as well as all the possible transition phases, are dependent on the single parameter $\theta$. To construct the dual basis, we start with the new forms of the states:

$$\begin{aligned} \left| \eta _A\right\rangle&= \left| 0\right\rangle , \\ \left| \eta _B\right\rangle&= \alpha \left| 0\right\rangle + \beta \left| 1\right\rangle , ~\text {and}\\ \left| \eta _C\right\rangle&= \alpha \left| 0\right\rangle + e^{i\theta }\beta \left| 1\right\rangle . \end{aligned}$$

We note directly that we must have:

$$\begin{aligned} \left\langle \epsilon _A|0\right\rangle&= \sqrt{\frac{2}{3}}, \\ \left\langle \epsilon _B|0\right\rangle&= \frac{1}{\sqrt{6}}e^{-i\phi _1}, ~\text {and}\\ \left\langle \epsilon _C|0\right\rangle&= \frac{1}{\sqrt{6}}e^{i\phi _3}, \end{aligned}$$

from how the dual states contract with $\left| \eta _A\right\rangle$. These can be used with the contractions with $\left| \eta _B\right\rangle$ to get:

$$\begin{aligned} \left\langle \epsilon _A|1\right\rangle&= \frac{1}{\beta }\sqrt{\frac{2}{3}}\left( \frac{1}{2}e^{i\phi _1}-\alpha \right) ,\\ \left\langle \epsilon _B|1\right\rangle&= \frac{1}{\beta }\sqrt{\frac{2}{3}}\left( 1-\frac{1}{2}\alpha e^{-i\phi _1}\right) , ~\text {and}\\ \left\langle \epsilon _C|1\right\rangle&= \frac{1}{2\beta }\sqrt{\frac{2}{3}}\left( e^{-i\phi _2}-\alpha e^{i\phi _3}\right) . \end{aligned}$$

It is quickly checked that these coefficients are consistent with the action on on $\left| \eta _C\right\rangle$ by making liberal use of $e^{-i\phi _3} =\alpha (1-e^{i\theta })$.

Recall that with the correct dual states, the Kraus operators take the form:

$$\begin{aligned} K_A&= \left| \eta _A \right\rangle \left\langle \epsilon _A\right| , \\ K_B&= \left| \eta _B \right\rangle \left\langle \epsilon _B\right| , ~\text {and}\\ K_C&= \left| \eta _C \right\rangle \left\langle \epsilon _C\right| . \end{aligned}$$

Completeness requires:

$$\begin{aligned} \left| \epsilon _A \right\rangle \left\langle \epsilon _A\right| + \left| \epsilon _B \right\rangle \left\langle \epsilon _B\right| + \left| \epsilon _C \right\rangle \left\langle \epsilon _C\right| = I . \end{aligned}$$

Define the vectors $u_x = \left\langle \epsilon _x | 0\right\rangle$ and $v_x = \left\langle \epsilon _x | 1\right\rangle$. One can check that the above relationship implies $\sum _x u_x^*u_x = \sum _x v_x^*v_x = 1$ and $\sum _x u_x v^*_x = 0$. However, for our model, it is straightforward (though a bit tedious) to check that:

$$\begin{aligned} \sum _x u_x^*u_x&= \frac{2}{3}+\frac{1}{6}+\frac{1}{6} = 1 ~\text {and}\\ \sum _x v_x^*v_x&= \frac{1}{\beta ^2}\left( 1+\alpha ^2-\alpha \cos \phi _1\right) . \end{aligned}$$

Using the definitions of $\alpha$, $\beta$, and $\phi _1$, the second equation can be simplified to:

$$\begin{aligned} \sum _x v_x^*v_x = \frac{2+\csc ^2\frac{\theta }{2}}{4-\csc ^2\frac{\theta }{2}} . \end{aligned}$$

This is unity only when $\csc ^2\frac{\theta }{2}=1$, which requires that $\theta = \pi$. This is, indeed, the model $\mathfrak {D}_3$ that we have already seen.

This establishes that the only two-dimensional pure-state quantum model which reproduces the 3-state MBW process is the one with a nonminimal statistical memory $S(\rho _\pi )$. This means there cannot exist a quantum representation of the 3-state MBW process that majorizes all other representations of the same. For, if it existed, it must be a two-dimensional model and also minimize $S(\rho _\pi )$.