Discrete Velocity Models for Mixtures Without Nonphysical Collision Invariants

Abstract

An important aspect of constructing discrete velocity models (DVMs) for the Boltzmann equation is to obtain the right number of collision invariants. It is a well-known fact that DVMs can also have extra collision invariants, so called spurious collision invariants, in plus to the physical ones. A DVM with only physical collision invariants, and so without spurious ones, is called normal. For binary mixtures also the concept of supernormal DVMs was introduced, meaning that in addition to the DVM being normal, the restriction of the DVM to any single species also is normal. Here we introduce generalizations of this concept to DVMs for multicomponent mixtures. We also present some general algorithms for constructing such models and give some concrete examples of such constructions. One of our main results is that for any given number of species, and any given rational mass ratios we can construct a supernormal DVM. The DVMs are constructed in such a way that for half-space problems, as the Milne and Kramers problems, but also nonlinear ones, we obtain similar structures as for the classical discrete Boltzmann equation for one species, and therefore we can apply obtained results for the classical Boltzmann equation.

1 Introduction

The Boltzmann equation is a fundamental equation in kinetic theory [17, 18]. It is a well-known fact that discrete velocity models (DVMs) can approximate the Boltzmann equation up to any order [12, 23, 26], and that these discrete approximations can be used for numerical methods [25] (and references therein). One important aspect in the construction of DVMs is to not have any extra collision invariants, in addition to the physical ones [24]. In contrast to the continuous case, DVMs can have non-physical or spurious collision invariants in addition to the physical ones; mass, momentum, and energy. DVMs without spurious collision invariants are called normal. Their construction is a classical problem that has been studied for single species as well as binary mixtures [11, 13, 14, 19–21, 28–30].

It was for a while conjectured that all normal DVMs could be obtained from some minimal models by so called one-extensions [10, 11, 13, 28]. A one-extension is obtained by, having already three velocities (out of four) from a possible collision in a normal DVM, adding the fourth velocity and so obtaining a new normal DVM, with one more velocity. However, it was found in [13, 31], that this is not the case. Still, the method of one-extensions is an effective way of creating new normal DVMs out of already existing ones, as well as for single species as for binary mixtures and other extensions.

For a DVM for a binary mixture to be normal, the two restrictions of the DVM to the single species, don’t need to be normal. Therefore the concept of supernormal DVMs for binary mixtures was introduced for normal DVMs, such that the two restrictions of the DVM to the single species also are normal. We generalize this concept to DVMs for mixtures of several species. We introduce a new concept of semi-supernormal DVMs for multicomponent mixtures for normal DVMs, with the property that the restrictions of the DVM to the single species also are normal. The concept of supernormal DVMs for multicomponent mixtures is kept for normal DVMs, with the property that not only the restrictions of the DVM to the single species are also normal, but, moreover, such that the restrictions to any collection of species also are normal. We present algorithms for constructing such DVMs. Actually, to check whether a DVM for a multicomponent mixture is supernormal or not, we just have to consider the restrictions to all possible binary mixtures and check whether they are supernormal or not. We also prove that for any finite number of species and any combinations of rational mass ratios there is a supernormal DVM. Our constructed DVMs can always be extended to larger DVMs by the method of one-extensions. It is also always possible to 2ex2tend them to DVMs that are symmetric with respect to the axes in this way.

The construction of the DVMs is such that for half-space problems [3], as the Milne and Kramers problems [2], but also nonlinear ones [27], one obtain similar structures as for the classical discrete Boltzmann equation for one species. We present the half-space problems and applicable existence results to our case, without any proofs, since they can be found elsewhere [5, 6, 9]. The results obtained in [6] can also be generalized by similar methods. To our knowledge no similar results exist in the continuous case for multicomponent mixtures, except for binary mixtures; for the linearized problem see [1], and for the nonlinear case, with equal masses, see [4].

The remaining part of the paper is organized as follows.

We review DVMs for single species and the concept of normal DVMs in Sect. 2, and DVMs for binary mixtures and the concept of normal and supernormal DVMs in Sect. 3. Our main results are presented in Sect. 4, where the concept of supernormal DVMs is generalized to mixtures of several species, algorithms of their construction are presented, and explicit constructions are made. In particular, it is proved that for any finite number of species and any combinations of rational mass ratios there is a supernormal DVM. In Sect. 5 we state the problems and applicable results for linearized (Sect. 5.1) and nonlinear (Sect. 5.2) half-space problems.

2 Normal Discrete Velocity Models

The general discrete velocity model (DVM), or the discrete Boltzmann equation, (see [16, 24] and references therein) reads

$$\begin{aligned} \frac{\partial f_{i}}{\partial t}+\mathbf {\xi }_{i}\cdot \nabla _{\mathbf {x} }f_{i}=Q_{i}\left( f,f\right) ,\quad i=1,...,n\text {,} \end{aligned}$$

(1)

where $\mathrm {V}=\left\{ \mathbf {\xi }_{1},...,\mathbf {\xi }_{n}\right\} \subset \mathbb {R}^{d}$ is a finite set of velocities, $f_{i}=f_{i}\left( \mathbf {x},t\right) =f\left( \mathbf {x},t,\mathbf {\xi }_{i}\right)$ for $i=1,...,n$, and $f=f\left( \mathbf {x},t,\mathbf {\xi }\right)$ represents the microscopic density of particles with velocity $\mathbf {\xi }$ at time $t\in \mathbb {R}_{+}$ and position $\mathbf {x}\in \mathbb {R}^{d}$.

For a function $g=g(\mathbf {\xi })$ (possibly depending on more variables than $\mathbf {\xi }$), we identify g with its restrictions to the points $\mathbf {\xi }\in \mathrm {V}$, i.e.

$$\begin{aligned} g=\left( g_{1},...,g_{n}\right) ,\text { with }g_{i}=g\left( \mathbf {\xi } _{i}\right) \text { for }i=1,...,n\text {.} \end{aligned}$$

Then $f=\left( f_{1},...,f_{n}\right)$ in Eq. (1).

The collision operators $Q_{i}\left( f,f\right)$ in (1) are given by

$$\begin{aligned} Q_{i}\left( f,f\right) =\sum \limits _{j,k,l=1}^{n}\varGamma _{ij}^{kl}\left( f_{k}f_{l}-f_{i}f_{j}\right) \text { for }i=1,...,n\text {,} \end{aligned}$$

(2)

where it is assumed that the collision coefficients $\varGamma _{ij}^{kl}$, $1\le i,j,k,l\le n$, satisfy the relations

$$\begin{aligned} \varGamma _{ij}^{kl}=\varGamma _{ji}^{kl}=\varGamma _{kl}^{ij}\ge 0\text {,} \end{aligned}$$

(3)

with equality unless the conservation laws (conservation of momentum and kinetic energy)

$$\begin{aligned} \mathbf {\xi }_{i}+\mathbf {\xi }_{j}=\mathbf {\xi }_{k}+\mathbf {\xi }_{l}\text { and }\left| \mathbf {\xi }_{i}\right| ^{2}+\left| \mathbf {\xi } _{j}\right| ^{2}=\left| \mathbf {\xi }_{k}\right| ^{2}+\left| \mathbf {\xi }_{l}\right| ^{2} \end{aligned}$$

(4)

are satisfied. A collision is obtained by the exchange of velocities

$$\begin{aligned} \left\{ \mathbf {\xi }_{i},\mathbf {\xi }_{j}\right\} \leftrightarrows \left\{ \mathbf {\xi }_{k},\mathbf {\xi }_{l}\right\} \text {,} \end{aligned}$$

(5)

and can occur if and only if $\varGamma _{ij}^{kl}\ne 0$. Geometrically, the collision obtained by (5) is represented by a rectangle (see Fig. 1) in $\mathbb {R}^{d}$ with corners in $\left\{ \mathbf {\xi }_{i},\mathbf {\xi }_{j},\mathbf {\xi }_{k},\mathbf {\xi } _{l}\right\}$, where $\mathbf {\xi }_{i}$ and  $\mathbf {\xi }_{j}$ (and therefore, also $\mathbf {\xi }_{k}$ and $\mathbf {\xi }_{l}$) are diagonal corners.

Fig. 1

Elastic collision

A function $\phi =\phi \left( \mathbf {\xi }\right)$ is a collision invariant, if and only if

$$\begin{aligned} \phi _{i}+\phi _{j}=\phi _{k}+\phi _{l}\text {,} \end{aligned}$$

(6)

for all indices such that $\varGamma _{ij}^{kl}\ne 0$, or, equivalently, if and only if

$$\begin{aligned} \left\langle \phi ,Q\left( f,f\right) \right\rangle =0\text {,} \end{aligned}$$

(7)

for all non-negative functions f. We have the trivial collision invariants (also called the physical collision invariants) $\phi _{0}=1$, $\phi _{1}=\xi ^{1},...,\phi _{d}=\xi ^{d}$, $\phi _{d+1}=\left| \mathbf {\xi } \right| ^{2}$ (including all linear combinations of these). Here and below, we denote by $\left\langle \cdot ,\cdot \right\rangle$ the Euclidean scalar product on $\mathbb {R}^{n}$.

In the continuous case the only collision invariants are the physical ones. However, it is well known that for DVMs there can also be so called spurious collision invariants. DVMs without spurious collision invariants, i.e. with only physical collision invariants of the form

$$\begin{aligned} \phi =a+\mathbf {b\cdot \xi }+c\left| \mathbf {\xi }\right| ^{2} \end{aligned}$$

(8)

for some constant $a,c\in \mathbb {R}$ and $\mathbf {b}\in \mathbb {R}^{d}$ (methods of their construction are described in e.g. [11, 13]), are called normal, if the collision invariants $1,\xi ^{1},...,\xi ^{d},\left| \mathbf {\xi }\right| ^{2}$ are linearly independent. A DVM such that $1,\xi ^{1},...,\xi ^{d},\left| \mathbf {\xi }\right| ^{2}$ are linearly dependent is called degenerate, and non-degenerate if $1,\xi ^{1},...,\xi ^{d},\left| \mathbf {\xi }\right| ^{2}$ are linearly independent. Typical examples of degenerate DVMs are the Broadwell models [15].

A Maxwellian distribution (or just a Maxwellian) is a function $M=M(\mathbf { \xi })$, such that

$$\begin{aligned} Q(M,M)=0\text { and }M\ge 0\text {,} \end{aligned}$$

and is for normal DVMs of the form

$$\begin{aligned} M=e^{\phi }=Ke^{\mathbf {b\cdot \xi }+c\left| \mathbf {\xi }\right| ^{2}},\text { with }K=e^{a}>0\text {, } \end{aligned}$$

(9)

where $\phi$ is given in Eq. (8).

3 Supernormal DVMs for Binary Mixtures

The general DVM, or the discrete Boltzmann equation, for a binary mixture of the species A and B reads

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial f_{i}^{A}}{\partial t} +\mathbf {\xi }_{i}^{A}\cdot \nabla _{\mathbf {x}}f_{i}^{A}=Q_{i}^{AA}(f^{A},f^{A})+Q_{i}^{BA}(f^{B},f^{A}) \text {, }\quad i=1,...,n_{A} \\ \dfrac{\partial f_{j}^{B}}{\partial t}+\mathbf {\xi }_{j}^{B}\cdot \nabla _{ \mathbf {x}}f_{j}^{B}=Q_{j}^{AB}(f^{A},f^{B})+Q_{j}^{BB}(f^{B},f^{B})\text {, }\quad j=1,...,n_{B} \end{array} \right. , \end{aligned}$$

(10)

where $\mathrm {V}^{\alpha }=\left\{ \mathbf {\xi }_{1}^{\alpha },...,\mathbf { \xi }_{n_{\alpha }}^{\alpha }\right\} \subset \mathbb {R}^{d}$, with $\alpha \in \left\{ A,B\right\}$, are finite sets of velocities, $f_{i}^{\alpha }=f_{i}^{\alpha }(\mathbf {x},t)=f^{\alpha }(\mathbf {x},t,\mathbf {\xi } _{i}^{\alpha })$ for $i=1,...,n_{\alpha }$, and $f^{\alpha }=f^{\alpha }\left( \mathbf {x},t,\mathbf {\xi }\right)$ represents the microscopic density of particles (of species $\alpha$) with velocity $\mathbf {\xi }$ at time $t\in \mathbb {R}_{+}$ and position $\mathbf {x}\in \mathbb {R}^{d}$. We denote by $m_{\alpha }$ the mass of a molecule of species $\alpha$. Here and below, $\alpha ,\beta \in \left\{ A,B\right\}$.

For a function $g^{\alpha }=g^{\alpha }(\mathbf {\xi })$ (possibly depending on more variables than $\mathbf {\xi }$), we identify $g^{\alpha }$ with its restrictions to the points $\mathbf {\xi }\in \mathrm {V}_{\alpha }$, i.e.

$$\begin{aligned} g^{\alpha }=(g_{1}^{\alpha },...,g_{n^{\alpha }}^{\alpha }),\text { with } g_{i}^{\alpha }=g^{\alpha }\left( \mathbf {\xi }_{i}^{\alpha }\right) \text {.} \end{aligned}$$

Then $f^{\alpha }=(f_{1}^{\alpha },...,f_{n^{\alpha }}^{\alpha })$ in Eq. (10).

The collision operators $Q_{i}^{\beta \alpha }(f^{\beta },f^{\alpha })$ in (10) are given by

$$\begin{aligned} Q_{i}^{\beta \alpha }(f^{\beta },f^{\alpha })=\sum \limits _{k=1}^{n_{\alpha }}\sum \limits _{j,l=1}^{n_{\beta }}\varGamma _{ij}^{kl}\left( \beta ,\alpha \right) (f_{k}^{\alpha }f_{l}^{\beta }-f_{i}^{\alpha }f_{j}^{\beta })\text { for }i=1,...,n_{\alpha }\text {,} \end{aligned}$$

where it is assumed that the collision coefficients $\varGamma _{ij}^{kl}\left( \beta ,\alpha \right)$, with $1\le i,k\le n_{\alpha }$ and $1\le j,l\le n_{\beta }$, satisfy the relations

$$\begin{aligned} \varGamma _{ij}^{kl}\left( \alpha ,\alpha \right) =\varGamma _{ji}^{kl}\left( \alpha ,\alpha \right) \text { and }\varGamma _{ij}^{kl}(\alpha ,\beta )=\varGamma _{kl}^{ij}(\alpha ,\beta )=\varGamma _{ji}^{lk}(\beta ,\alpha )\ge 0\text {,} \end{aligned}$$

with equality unless the conservation laws (conservation of momentum and kinetic energy)

$$\begin{aligned} m_{\alpha }\mathbf {\xi }_{i}^{\alpha }+m_{\beta }\mathbf {\xi }_{j}^{\beta }=m_{\alpha }\mathbf {\xi }_{k}^{\alpha }+m_{\beta }\mathbf {\xi }_{l}^{\beta } \text { and }m_{\alpha }\left| \mathbf {\xi }_{i}^{\alpha }\right| ^{2}+m_{\beta }\left| \mathbf {\xi }_{j}^{\beta }\right| ^{2}=m_{\alpha }\left| \mathbf {\xi }_{k}^{\alpha }\right| ^{2}+m_{\beta }\left| \mathbf {\xi }_{l}^{\beta }\right| ^{2} \end{aligned}$$

are satisfied. A collision is obtained by the exchange of velocities

$$\begin{aligned} \left\{ \mathbf {\xi }_{i}^{\alpha },\mathbf {\xi }_{j}^{\beta }\right\} \leftrightarrows \left\{ \mathbf {\xi }_{k}^{\alpha },\mathbf {\xi } _{l}^{\beta }\right\} \text {,} \end{aligned}$$

(11)

and can occur if and only if $\varGamma _{ij}^{kl}(\alpha ,\beta )\ne 0$. Geometrically, the collision obtained by (11) is represented by an isosceles trapezoid, see Fig. 2 for $\alpha \ne \beta$, (in particular, a rectangle, cf. Fig. 1 for single species, if $\alpha =\beta$) in $\mathbb {R}^{d}$, with the corners in $\left\{ \mathbf {\xi }_{i}^{\alpha },\mathbf {\xi }_{j}^{\beta },\mathbf { \xi }_{k}^{\alpha },\mathbf {\xi }_{l}^{\beta }\right\}$, where $\mathbf {\xi }_{i}^{\alpha }$ and $\mathbf {\xi }_{j}^{\beta }$ (and therefore, also $\mathbf {\xi }_{k}^{\alpha }$ and $\mathbf {\xi }_{l}^{\beta }$) are diagonal corners, and

$$\begin{aligned} m_{\alpha }\left| \mathbf {\xi }_{i}^{\alpha }-\mathbf {\xi }_{k}^{\alpha }\right| =m_{\beta }\left| \mathbf {\xi }_{j}^{\beta }-\mathbf {\xi } _{l}^{\beta }\right| . \end{aligned}$$

Fig. 2

Mixed elastic collision

A function $\phi =\left( \phi ^{A},\phi ^{B}\right)$, with $\phi ^{\alpha }=\phi ^{\alpha }(\mathbf {\xi })$, is a collision invariant, if and only if

$$\begin{aligned} \phi _{i}^{\alpha }+\phi _{j}^{\beta }=\phi _{k}^{\alpha }+\phi _{l}^{\beta } \text {,} \end{aligned}$$

for all indices such that $\varGamma _{ij}^{kl}(\alpha ,\beta )\ne 0$. Normal DVMs, i.e. non-degenerate DVMs without spurious collision invariants, or equivalently, non-degenerate DVMs only with the physical collision invariants (which are trivial by our assumptions on the collision coefficients)

$$\begin{aligned} \phi =\left( \phi ^{A},\phi ^{B}\right) \text {, with }\phi ^{\alpha }=\phi ^{\alpha }(\mathbf {\xi })=a_{\alpha }+m_{\alpha }\mathbf {b\cdot \xi } +cm_{\alpha }\left| \mathbf {\xi }\right| ^{2}, \end{aligned}$$

(12)

for some constant $a_{A},a_{B},c\in \mathbb {R}$ and $\mathbf {b}\in \mathbb {R} ^{d}$, have exactly $d+3$ linearly independent collision invariants. Methods of their construction can be found in e.g. [11, 13]. If in addition to the DVM being normal, the DVMs $\mathrm {V}^{A}$ and $\mathrm {V} ^{B}$ are normal, respectively, then the DVM is said to be supernormal [13].

The Maxwellians are

$$\begin{aligned} M=e^{\phi }\text {, i.e. }M=\left( M^{A},M^{B}\right) \text {, with }M^{\alpha }=e^{\phi ^{\alpha }}\text {,} \end{aligned}$$

where (for normal models) $\phi$ is given by Eq. (12).

4 DVMs for Mixtures

In this section we will generalize the concept of supernormal DVMs to the case of multicomponent mixtures. We begin by introducing a different approach for considering the discrete Boltzmann equation for mixtures.

Assume that we have s different species, labelled with $\alpha _{1},...,\alpha _{s}$, with the masses $m_{\alpha _{1}},...,m_{\alpha _{s}}$ . For each species $\alpha _{i}$ we fix a set of velocity vectors $V^{\alpha _{i}}=\left\{ \mathbf {\xi }_{1}^{\alpha _{i}},...,\mathbf {\xi }_{n_{\alpha _{i}}}^{\alpha _{i}}\right\} \subset \mathbb {R}^{d}$ and assign the label $\alpha _{i}$ to each velocity vector in $V^{\alpha _{i}}$. We obtain a set of $n=n_{\alpha _{1}}+...+n_{\alpha _{s}}$ pairs (each pair being composed of a velocity vector and a label).

$$\begin{aligned} \mathcal {P}= & {} \left\{ \left( \mathbf {\xi }_{1}^{\alpha _{1}},\alpha _{1}\right) ,...,\left( \mathbf {\xi }_{n_{\alpha _{1}}}^{\alpha _{1}},\alpha _{1}\right) ,...,\left( \mathbf {\xi }_{1}^{\alpha _{s}},\alpha _{s}\right) ,...,\left( \mathbf {\xi }_{n_{\alpha _{s}}}^{\alpha _{s}},\alpha _{s}\right) \right\} \nonumber \\= & {} \{\left( \mathbf {v}_{1},\alpha (1)\right) ,...,\left( \mathbf {v} _{n},\alpha (n)\right) \}\text {, with }n=n_{\alpha _{1}}+...+n_{\alpha _{s}} \text {.} \end{aligned}$$

(13)

Obviously, the same velocity can be repeated many times, but only for different species.

We consider the system (1)–(2) with the collision coefficients

$$\begin{aligned} \varGamma _{ij}^{kl}=\varGamma _{ji}^{kl}=\varGamma _{kl}^{ij}\ge 0 \end{aligned}$$

(14)

with equality unless we have conservation of mass for each species, momentum, and kinetic energy

$$\begin{aligned} \left\{ \alpha (i),\alpha (j)\right\}&= \,\left\{ \alpha (k),\alpha (l)\right\} \text {,} \nonumber \\ m_{\alpha (i)}\mathbf {v}_{i}+m_{\alpha (j)}\mathbf {v}_{j}&= \,m_{\alpha (k)} \mathbf {v}_{k}+m_{\alpha (l)}\mathbf {v}_{l}\text {, and } \nonumber \\ m_{\alpha (i)}\left| \mathbf {v}_{i}\right| ^{2}+m_{\alpha (j)}\left| \mathbf {v}_{j}\right| ^{2}&=\, m_{\alpha (j)}\left| \mathbf {v}_{k}\right| ^{2}+m_{\alpha (l)}\left| \mathbf {v} _{l}\right| ^{2}. \end{aligned}$$

(15)

A collision is obtained by the exchange of velocities

$$\begin{aligned} \left\{ \left( \mathbf {v}_{i},\alpha (i)\right) ,\left( \mathbf {v} _{j},\alpha (j)\right) \right\} \leftrightarrows \left\{ \left( \mathbf {v} _{k},\alpha (k)\right) ,\left( \mathbf {v}_{l},\alpha (l)\right) \right\} \text {,} \end{aligned}$$

(16)

and can occur if and only if $\varGamma _{ij}^{kl}\ne 0$. Geometrically, the collision obtained by (16) is, as in the case of binary mixtures, represented by an isosceles trapezoid, cf. Fig. (a rectangle if $\alpha (i)=\alpha (j)$ or more generally if and only if $m_{\alpha (i)}=m_{\alpha (j)}$) in $\mathbb {R}^{d}$, with the corners in $\left\{ \mathbf {v}_{i},\mathbf {v}_{j},\mathbf {v}_{k},\mathbf {v}_{l}\right\}$ , where $\mathbf {v}_{i}$ and $\mathbf {v}_{j}$ (and therefore, also $\mathbf {v}_{k}$ and $\mathbf {v}_{l}$) are diagonal corners, and

$$\begin{aligned} m_{\alpha (i)}\left| \mathbf {v}_{i}-\mathbf {v}_{k}\right| =m_{\alpha (j)}\left| \mathbf {v}_{j}-\mathbf {v}_{l}\right| , \end{aligned}$$

(17)

if $\alpha (i)=\alpha (k)$, and with k and l interchanged in (17), otherwise.

A function $\phi =\phi (\mathbf {v})$, is a collision invariant, if and only if

$$\begin{aligned} \phi _{i}+\phi _{j}=\phi _{k}+\phi _{l}\text {,} \end{aligned}$$

for all indices such that $\varGamma _{ij}^{kl}\ne 0$. The collision invariants include, and for normal models are restricted to

$$\begin{aligned} \phi =\left( \phi _{1},...,\phi _{n}\right) \text {, with }\phi _{i}=a_{\alpha (i)}+m_{\alpha (i)}\mathbf {b\cdot v}_{i}+cm_{\alpha (i)}\left| \mathbf {v}_{i}\right| ^{2} \end{aligned}$$

(18)

for some constant $a_{\alpha _{1}},...,a_{\alpha _{s}},c\in \mathbb {R}$ and $\mathbf {b}\in \mathbb {R}^{d}$. For normal models we will have exactly $s+d+1$ linearly independent collision invariants. We will below address how to construct special types of such normal models.

The Maxwellians are

$$\begin{aligned} M=e^{\phi }\text {, i.e. }M=\left( M_{1},...,M_{n}\right) \text {, with } M_{i}=e^{\phi _{i}}\text {,} \end{aligned}$$

(19)

where (for normal models) $\phi$ is given by Eq. (18).

4.1 Supernormal DVMs for Mixtures

The notion of supernormal models was introduced for binary mixtures by Bobylev and Vinerean in [13] (see Sect. 3), and denotes a normal discrete velocity model, which is normal also considering the sets of velocities for the different species separately.

Here we extend the concept of supernormal DVMs for binary mixtures to include also the cases of several species.

Definition 1

A DVM $\left\{ \mathrm {V}^{\alpha _{1}},\ldots ,\mathrm {V}^{\alpha _{s}}\right\}$ for a mixture of s species is called normal if the DVM is non-degenerate and has exactly $s+d+1$ linearly independent collision invariants.

Definition 2

A DVM $\left\{ \mathrm {V}^{\alpha _{1}},\ldots ,\mathrm {V}^{\alpha _{s}}\right\}$ for a mixture of s species is called semi-supernormal if the DVM is normal as a mixture and the restriction to each velocity set $\mathrm {V}^{\alpha _{i}}$, $1\le i\le s$, is a normal DVM.

Definition 3

A DVM $\left\{ \mathrm {V}^{\alpha _{1}},\ldots ,\mathrm {V}^{\alpha _{s}}\right\}$ for a mixture of s species is called supernormal if the restriction to each collection

$$\begin{aligned} \left\{ \mathrm {V}_{1},\ldots ,\mathrm {V}_{r}\right\} \subseteq \left\{ \mathrm {V}^{\alpha _{1}},\ldots ,\mathrm {V}^{\alpha _{s}}\right\} \text {, } 1\le r\le s, \end{aligned}$$

of velocity sets is a normal DVM for a mixture of r species.

Theorem 1

A DVM for a mixture of s species with the velocity sets $\mathrm {V}^{\alpha _{i}}$, $1\le i\le s$, is semi-supernormal if, for each $2\le j\le s$ there exists $1\le i<j\le s$, such that the restriction to the pair $\left\{ \mathrm {V}^{\alpha _{i}},\mathrm {V}^{\alpha _{j}}\right\}$ of velocity sets is a supernormal DVM for a binary mixture.

Proof

The restriction to each velocity set $\mathrm {V}^{\alpha _{i}}=\left\{ \mathbf {\xi }_{1}^{\alpha _{i}},...,\mathbf {\xi }_{n_{\alpha _{i}}}^{\alpha _{i}}\right\}$, $1\le i\le s$, is normal. Hence, the collision invariants will be of the form $\phi =\left( \phi ^{\alpha _{1}},...,\phi ^{\alpha _{s}}\right)$, where $\phi _{j}^{\alpha _{i}}=a_{\alpha _{i}}+m_{\alpha _{i}}\mathbf {b}^{\alpha _{i}}\cdot \mathbf {\xi }_{j}^{\alpha _{i}}+c_{\alpha _{i}}m_{\alpha _{i}}\left| \mathbf {\xi }_{j}^{\alpha _{i}}\right| ^{2}$ for $1\le j\le n_{\alpha _{i}}$ and $1\le i\le s$.

We denote $\mathbf {b}^{\alpha _{1}}\mathbf {=b}$ and $c_{\alpha _{1}}=c$ and apply mathematical induction. Assume that $\mathbf {b}^{\alpha _{j-1}}\mathbf { =b}^{\alpha _{j-2}}\mathbf {=...=b}^{\alpha _{1}}\mathbf {=b}$ and $c_{\alpha _{j-1}}=c_{\alpha _{j-2}}=...=c_{\alpha _{1}}=c$ for some $2\le j\le s$. Then there exists $1\le i\le j-1$, such that the restriction to the pair $\left\{ \mathrm {V}^{\alpha _{i}},\mathrm {V}^{\alpha _{j}}\right\}$ of velocity sets is normal and therefore $\mathbf {b}^{\alpha _{j}}\mathbf {=b} ^{\alpha _{i}}\mathbf {=b}$ and $c_{\alpha _{j}}=c_{\alpha _{i}}=c$. Hence, the collision invariants will be of the form $\phi =\left( \phi ^{\alpha _{1}},...,\phi ^{\alpha _{s}}\right)$, where $\phi _{j}^{\alpha _{i}}=a_{\alpha _{i}}+m_{\alpha _{i}}\mathbf {b\cdot \xi }_{j}^{\alpha _{i}}+cm_{\alpha _{i}}\left| \mathbf {\xi }_{j}^{\alpha _{i}}\right| ^{2}$ for $1\le j\le n_{\alpha _{i}}$ and $1\le i\le s$. $\square$

Theorem 2

A DVM $\left\{ \mathrm {V}^{\alpha _{1}},\ldots ,\mathrm {V}^{\alpha _{s}}\right\}$ for a mixture of s species is supernormal if and only if the restriction to each pair $\left\{ \mathrm {V}^{\alpha _{i}},\mathrm {V} ^{\alpha _{j}}\right\}$, $1\le i<j\le s$, of velocity sets is a supernormal DVM for a binary mixture.

Proof

The theorem follows directly from the definition of supernormal DVMs and Theorem 1.$\square$

We will below use the concept of ”linearly independent” collisions. Intuitively, a set of collisions is linearly dependent if one of them can be obtained by a combination of (some of) the other collisions (including corresponding reverse collisions), and correspondingly linearly independent if this is not the case. More formally, each collision can be represented by an $n-$dimensional vector with 0, $-1$, and 1 as the only coordinates, see e.g. [13] , in the way that collision (11) is represented by a vector

$$\begin{aligned} (0,...,0,\underset{i}{\underbrace{1}},0,...,0,\underset{j}{\underbrace{1}} ,0,...,0,\underset{k}{\underbrace{-1}},0,...,0,\underset{l}{\underbrace{-1}} ,0,...,0)\in \mathbb {Z}^{n}. \end{aligned}$$

We then say that a set of collisions is linearly independent if and only if the set of the corresponding vectors is linearly independent.

Algorithm for construction of semi-supernormal DVMs for mixtures

• (1) Choose a set of velocities $\mathrm {V}^{\alpha _{1}}$ such that it corresponds to a normal DVM for single species. This set should be chosen in such a way, that we can obtain normal models for any mass ratio we intend to consider. If this is not the case, we might need to extend the set later.

• (2) Iteration step. For $i=2,\ldots ,s:$ Choose a normal set of velocities $\mathrm {V}^{\alpha _{i}}$ such that, it together with one of $\mathrm {V}^{\alpha _{1}},\ldots ,\mathrm {V} ^{\alpha _{i-1}}$ corresponds to a supernormal DVM for binary mixtures.

For an example of how this can be done, see subsection 4.2 below.

Remark 1

If we don’t allow any collisions between the two species, we will have $2d+4$ linearly independent collision invariants, but we would like to have $d+3$ linearly independent collision invariants. Hence, cf. [13] , we need to have $d+1$ linearly independent (also with respect to the collisions inside the two species) collisions between the two species.

Algorithm for construction of supernormal DVMs for mixtures

• (1) Choose a set of velocities $\mathrm {V}^{\alpha _{1}}$ such that it corresponds to a normal DVM for single species. The comment of Step 1) in the construction of semi-supernormal DVMs above is still applicable here.

• (2) Iteration step. For $i=2,\ldots ,s:$ Choose a normal set of velocities $\mathrm {V}^{\alpha _{i}}$ such that, together with each of $\mathrm {V}^{\alpha _{1}},\ldots ,\mathrm {V} ^{\alpha _{i-1}}$ it corresponds to a supernormal DVM for binary mixtures. Also here, Remark 1 is applicable, in all cases, and examples can be found in Sect. 4.2 below.

4.2 Construction of a Family of Supernormal DVMs for Mixtures

We start with a normal DVM $\mathrm {V}$, which contains the normal DVM with the 6 velocities

$$\begin{aligned} \left\{ (\pm 1,\pm 1),(3,\pm 1)\right\} \end{aligned}$$

for $d=2$ or the normal DVM with the 10 velocities

$$\begin{aligned} \left\{ (\pm 1,\pm 1,\pm 1),(3,\pm 1,1)\right\} \end{aligned}$$

for $d=3$.

Extensions to larger normal models (of any finite size) can be obtained by the so-called one-extension method [10, 11, 13, 28]. A one-extension is obtained by, having three velocities from a possible collision, but not the fourth, in the velocity set, add the fourth velocity from the collision to the velocity set and obtain a new linearly independent (with respect to previously existing collisions) collision. The geometrical interpretation of a one-extension (in a set of velocities for a single species), having three corners of a rectangle, but not the fourth, in the velocity set, add the fourth corner to the velocity set. In particular, our starting models can be extended to normal DVMs symmetric to the axes by the one-extension method. The smallest symmetric normal extensions of our starting models are the 12-velocity DVM

$$\begin{aligned} \left\{ (\pm 1,\pm 1),(\pm 3,\pm 1),(\pm 1,\pm 3)\right\} \end{aligned}$$

for $d=2$ and the 32-velocity DVM

$$\begin{aligned} \left\{ (\pm 1,\pm 1,\pm 1),(\pm 3,\pm 1,\pm 1),(\pm 1,\pm 3,\pm 1),(\pm 1,\pm 1,\pm 3)\right\} \end{aligned}$$

for $d=3$. All models, constructed below, can be extended to DVMs symmetric to the axes (still having the desired properties) by the one-extension method.

We let

$$\begin{aligned} \mathrm {V}^{\alpha _{i}}=\frac{h}{m_{\alpha _{i}}}\mathrm {V}\text {, }\quad i=1,...,s\text {,} \end{aligned}$$

(20)

for some positive number $h>0$. Our starting models are normal DVMs, which easily can be checked by methods in [13]. Note that the starting models only allow mass ratio 1.

However, for example, the 36-velocity model in $d=2$ with components in $\{\pm 1,\pm 3,\pm 5\}$ can be used for $\mathrm {V}$ to obtain a supernormal DVM for binary mixtures with mass ratios including

$$\begin{aligned} \left\{ 2,3,4,5,\dfrac{3}{2},\dfrac{4}{3},\dfrac{5}{2},\dfrac{5}{3},\dfrac{5 }{4}\right\} \text {,} \end{aligned}$$

and the 216-velocity model in $d=3$ with components in $\{\pm 1,\pm 3,\pm 5\}$ can be used for $\mathrm {V}$ to obtain a supernormal DVM for binary mixtures with mass ratios including

$$\begin{aligned} \left\{ 2,3,4,5,6,7,8,9,\dfrac{3}{2},\dfrac{4}{3},\dfrac{5}{2},\dfrac{5}{3}, \dfrac{5}{4},\dfrac{6}{5},\dfrac{7}{2},\dfrac{7}{3},\dfrac{7}{4},\dfrac{7}{5} ,\dfrac{7}{6},\dfrac{8}{3},\dfrac{8}{5},\dfrac{8}{7},\dfrac{9}{2},\dfrac{9}{4 },\dfrac{9}{5},\dfrac{9}{7},\dfrac{9}{8}\right\} \end{aligned}$$

Hence, for $d=2$, if we choose masses from the set $\{m,2m,\ldots ,5m\}$, the DVM, obtained by using the 36-velocity model as $\mathrm {V}$, will be supernormal. Furthermore, in this case we can, for example, let $s=5$ and $m_{i}=i\cdot m$ for $i=1,\ldots ,5$ to obtain a supernormal DVM by using the 36-velocity model as $\mathrm {V}$. Moreover, for $d=3$, if we choose masses from the set $\{m,2m,\ldots ,5m,6m,7m,8m,9m\}$, the DVM, obtained by using the 216-velocity model as $\mathrm {V}$, will be supernormal. In this case we can, for example, let $s=9$ and $m_{i}=i\cdot m$ for $i=1,\ldots ,9$ to obtain a supernormal DVM by using the 216-velocity model as $\mathrm {V}$.

More generally, we can use different sets $\mathrm {V}$ (as long as they contain the necessary velocities) for different species. Below, we will consider some more general cases.

Lemma 1

Let $d=2$ or $d=3$. For any given positive integer $m=\dfrac{m_{A}}{m_{B}}$, there is a supernormal DVM for a binary mixture with mass ratio m.

Proof

For $d=2$, let $\mathrm {V}$ be a normal DVM, such that

$$\begin{aligned} \left\{ (\pm 1,\pm 1),(3,\pm 1),(m-2,1),(m+2,1)\right\} \subseteq \mathrm {V} \end{aligned}$$

if m is odd, and

$$\begin{aligned} \left\{ (\pm 1,\pm 1),(3,\pm 1),(m-3,1),(m+1,3)\right\} \subseteq \mathrm {V} \end{aligned}$$

if m is even. Such normal DVMs can be obtained from the normal DVM $\left\{ (\pm 1,\pm 1),(3,\pm 1)\right\}$ by one-extensions. Furthermore, let

$$\begin{aligned} \mathrm {V}^{A}=\frac{h}{m_{A}}\mathrm {V}\text { and }\mathrm {V}^{B}=\frac{h}{ m_{B}}\mathrm {V}\text {.} \end{aligned}$$

Without any collisions between the different species we will, since the DVMs are normal, have the collision invariants

$$\begin{aligned} \phi =\left( \phi ^{A},\phi ^{B}\right) \text {, where }\phi _{j}^{\alpha }=a_{\alpha }+m_{\alpha }\mathbf {b}^{\alpha }\cdot \mathbf {\xi }_{j}^{\alpha }+c_{\alpha }m_{\alpha }\left| \mathbf {\xi }_{j}^{\alpha }\right| ^{2}\text { for }1\le j\le n_{\alpha }\text {,} \end{aligned}$$

(21)

with $a_{\alpha },c_{\alpha }\in \mathbb {R}$, $\mathbf {b}^{\alpha }=(b_{1}^{\alpha },b_{2}^{\alpha })\in \mathbb {R}^{2}$, and $\alpha \in \left\{ A,B\right\}$. The collisions obtained by (below, we omit the indices A and B for the velocities, since they are implicit by the masses appearing)

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(1,1),\frac{h}{m_{B}}(-1,1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(-1,1),\frac{h}{m_{B}}(1,1)\right\} \text {,} \end{aligned}$$

(22)

and

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(1,1),\frac{h}{m_{B}}(1,-1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(1,-1),\frac{h}{m_{B}}(1,1)\right\} \end{aligned}$$

(23)

will imply that $b_{1}^{A}=b_{1}^{B}$ and $b_{2}^{A}=b_{2}^{B}$, respectively. Furthermore, the collisions obtained by

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(m+2,1),\frac{h}{m_{B}}(-1,1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(m-2,1),\frac{h}{m_{B}}(3,1)\right\} \text {,} \end{aligned}$$

if m is odd, and

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(m+1,3),\frac{h}{m_{B}}(-1,-1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(m-3,1),\frac{h}{m_{B}}(3,1)\right\} \end{aligned}$$

(24)

if m is even, will imply that $c_{A}=c_{B}$. It follows that the collision invariants will be on the form

$$\begin{aligned} \phi =\left( \phi ^{A},\phi ^{B}\right) \text {, where }\phi _{j}^{\alpha }=a_{\alpha }+m_{\alpha }\mathbf {b}\cdot \mathbf {\xi }_{j}^{\alpha }+cm_{\alpha }\left| \mathbf {\xi }_{j}^{\alpha }\right| ^{2}\text { for }1\le j\le n_{\alpha }\text {,} \end{aligned}$$

(25)

with $a_{\alpha },c\in \mathbb {R}$, $\mathbf {b}\in \mathbb {R}^{2}$, and $\alpha \in \left\{ A,B\right\}$.

For $d=3$, let V be a normal DVM, such that

$$\begin{aligned} \left\{ (\pm 1,\pm 1,\pm 1),(3,\pm 1,1),(m-2,1,1),(m+2,1,1)\right\} \subseteq \mathrm {V} \end{aligned}$$

if m is odd, and

$$\begin{aligned} \left\{ (\pm 1,\pm 1,\pm 1),(3,\pm 1,1),(m-3,1,1),(m+1,3,1)\right\} \subseteq \mathrm {V} \end{aligned}$$

if m is even. Such normal DVMs can be obtained from the normal DVM $\left\{ (\pm 1,\pm 1,\pm 1),(3,\pm 1,1)\right\}$ by one-extensions. Furthermore, let

$$\begin{aligned} \mathrm {V}^{A}=\frac{h}{m_{A}}\mathrm {V}\text { and }\mathrm {V}^{B}=\frac{h}{ m_{B}}\mathrm {V}\text {.} \end{aligned}$$

Without any collisions between the different species we will, since the DVMs are normal, have the collision invariants

$$\begin{aligned} \phi =\left( \phi ^{A},\phi ^{B}\right) \text {, where }\phi _{j}^{\alpha }=a_{\alpha }+m_{\alpha }\mathbf {b}^{\alpha }\cdot \mathbf {\xi }_{j}^{\alpha }+c_{\alpha }m_{\alpha }\left| \mathbf {\xi }_{j}^{\alpha }\right| ^{2}\text { for }1\le j\le n_{\alpha }\text {,} \end{aligned}$$

(26)

with $a_{\alpha },c_{\alpha }\in \mathbb {R}$, $\mathbf {b}^{\alpha }=(b_{1}^{\alpha },b_{2}^{\alpha },b_{3}^{\alpha })\in \mathbb {R}^{3}$, and $\alpha \in \left\{ A,B\right\}$. The collisions obtained by

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(1,1,1),\frac{h}{m_{B}}(-1,1,1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(-1,1,1),\frac{h}{m_{B}} (1,1,1)\right\} \text {,} \end{aligned}$$

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(1,1,1),\frac{h}{m_{B}}(1,-1,1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(1,-1,1),\frac{h}{m_{B}} (1,1,1)\right\} \text {,} \end{aligned}$$

and

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(1,1,1),\frac{h}{m_{B}}(1,1,-1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(1,1,-1),\frac{h}{m_{B}} (1,1,1)\right\} \end{aligned}$$

will imply that $b_{1}^{A}=b_{1}^{B}$, $b_{2}^{A}=b_{2}^{B}$, and $b_{3}^{A}=b_{3}^{B}$, respectively. Furthermore, the collisions obtained by

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(m+2,1,1),\frac{h}{m_{B}}(-1,1,1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(m-2,1,1),\frac{h}{m_{B}} (3,1,1)\right\} \text {,} \end{aligned}$$

if m is odd, and

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(m+1,3,1),\frac{h}{m_{B}}(-1,-1,1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(m-3,1,1),\frac{h}{m_{B}} (3,1,1)\right\} \text {,} \end{aligned}$$

if m is even, will imply that $c_{A}=c_{B}$. It follows that the collision invariants will be on the form (25) (with $\mathbf {b} \in \mathbb {R}^{3}$). $\square$

Example 1

Assume that $d=2$, $s=2$, and the mass ratio $m=2$, and let

$$\begin{aligned} \mathrm {V=}\left\{ (\pm 1,\pm 1),(3,\pm 1),(1,3),(3,3)\right\} , \end{aligned}$$

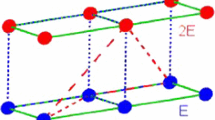
which is a normal DVM, in Eq. (20). Then the collisions (22)–(23) are represented by the blue/dashed ( - - - - - ) isosceles trapezoids in Fig. 3, and the red/broken $\left( { - - - } \right)$ isosceles trapezoids represents the collision (24).

Example 2

We now consider the case $d=2$ and $s=3$, with masses m, 2m, and 4m. If we let $\mathrm {V}$ be as in Example 1 in Eq. (20), then we obtain a semi-supernormal DVM (see Fig. 4). On the other hand, if we let

$$\begin{aligned} \mathrm {V=}\left\{ (\pm 1,\pm 1),(3,\pm 1),(1,3),(3,3),(5,1),(5,3)\right\} , \end{aligned}$$

(27)

in Eq. (20), then we obtain a supernormal DVM (see Fig. 5). Instead of using the same $\mathrm {V}$ for all species, we can use different sets for different species. The DVM in Fig. is still supernormal, even if we only used the set (27) for the heavy species, while we used the set from Example 1 for the ”middle” species, and the set

$$\begin{aligned} \mathrm {V=}\left\{ (\pm 1,\pm 1),(3,\pm 1)\right\} , \end{aligned}$$

for the ”light” species.

In fact in Fig. 4 still the collisions (22)–(23) are represented by the blue/dashed ( - - - - - ) isosceles trapezoids and the collision (24) (for mass ratios 2) by the red/broken $\left( { - - - } \right)$ isosceles trapezoids. However, the collision (24) is missing for mass ratio 4 (and there is no other to replace it either), and so the DVM fails to be supernormal. However, in Figs. 5 and 6 the collision (24) for mass ratio 4 is represented by the brown/chain

isosceles trapezoid, and hence the DVMs are supernormal.

Fig. 3

16-velocity supernormal model for binary mixture with mass ratio 2

Fig. 4

24-velocity semi-supernormal model for mixture of three species with mass ratios 2, 2, 4

Fig. 5

30-velocity supernormal model for mixture of three species with mass ratios 2, 2, 4

Fig. 6

24-velocity supernormal model for mixture of three species with mass ratios 2, 2, 4

Theorem 3

Let $d=2$ or $d=3$. For any given positive rational number $m= \dfrac{m_{A}}{m_{B}}$ there is a supernormal DVM for a binary mixture with mass ratio m.

Proof

Assume that $m=\dfrac{m_{A}}{m_{B}}=\dfrac{p}{q}$, with $p,q\in \mathbb {Z}$ and $\mathrm {SGD}(p,q)=1$.

For $d=2$, let $\mathrm {V}$ be a normal DVM, such that

$$\begin{aligned} \left\{ (\pm 1,\pm 1),(3,\pm 1),(p-2,1),(p+2,1),(q-2,1),(q+2,1)\right\} \subseteq \mathrm {V} \end{aligned}$$

if p and q are odd,

$$\begin{aligned} \left\{ (\pm 1,\pm 1),(3,\pm 1),(p-3,1),(p+1,3),(q-2,-1),(q+2,1)\right\} \subseteq \mathrm {V} \end{aligned}$$

if p is even and q is odd (or with p and q interchanged, if p is odd and q is even), and

$$\begin{aligned} \left\{ (\pm 1,\pm 1),(3,\pm 1),(p-3,1),(p+1,3),(q-3,1),(q+1,3)\right\} \subseteq \mathrm {V} \end{aligned}$$

if p and q are even. Such normal DVMs can be obtained from the normal DVM $\left\{ (\pm 1,\pm 1),(3,\pm 1)\right\}$ by one-extensions. Furthermore, let

$$\begin{aligned} \mathrm {V}^{A}=\frac{h}{m_{A}}\mathrm {V}\text { and }\mathrm {V}^{B}=\frac{h}{ m_{B}}\mathrm {V}\text {.} \end{aligned}$$

Without any collisions between the different species we will, since the DVMs are normal, have the collision invariants (21). Similarly as in the proof of Lemma 1, $\mathbf {b}^{A}=\mathbf {b}^{B}$ . Furthermore, the collisions obtained by

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(p+2,1),\frac{h}{m_{B}}(q-2,1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(p-2,1),\frac{h}{m_{B}}(q+2,1)\right\} \text {,} \end{aligned}$$

if p and q are odd,

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(p+1,3),\frac{h}{m_{B}}(q-2,-1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(p-3,1),\frac{h}{m_{B}}(q+2,1)\right\} \text {,} \end{aligned}$$

if p is even and q is odd (or with p and q interchanged, if p is odd and q is even), and

$$\begin{aligned} \left\{ \frac{h}{m_{A}}(p+1,3),\frac{h}{m_{B}}(q-3,1)\right\} \leftrightarrows \left\{ \frac{h}{m_{A}}(p-3,1),\frac{h}{m_{B}}(q+1,3)\right\} \text {,} \end{aligned}$$

if p and q are even, will imply that $c_{A}=c_{B}$.

For $d=3$, let instead $\mathrm {V}$ be a normal DVM, such that

$$\begin{aligned} \left\{ (\pm 1,\pm 1,\pm 1),(3,\pm 1,1),(p-2,1,1),(p+2,1,1),(q-2,1,1),(q+2,1,1)\right\} \subseteq \mathrm {V} \end{aligned}$$

if p and q are odd,

$$\begin{aligned} \left\{ (\pm 1,\pm 1,\pm 1),(3,\pm 1,1),(p-3,1,1),(p+1,3,1),(q-2,-1,1),(q+2,1,1)\right\} \subseteq \mathrm {V} \end{aligned}$$

if p is even and q is odd (or with p and q interchanged, if p is odd and q is even), and

$$\begin{aligned}&\left\{ (\pm 1,\pm 1,\pm 1),(3,\pm 1,1),(p-3,1,1),(p+1,3,1),(q-3,1,1),(q+1,3,1)\right\} \subseteq \mathrm {V} \end{aligned}$$

if p and q are even. Similar extensions of the case $d=2$ as in the proof of Lemma 1 imply that $\mathbf {b}^{A}=\mathbf {b}^{B}$ and $c_{A}=c_{B}$ in Eq. (26). $\square$

Note that the sets of velocities used in the proofs of Lemma 1 and Theorem 2, in no way are unique. Furthermore, there can also be sets of velocities that do not contain the velocities assumed in the proof, but still are supernormal for the given mass ratio. We have just proven that there exist such sets of velocities for any rational mass ratio.

Theorem 4

Let $d=2$ or $d=3$. For any given number s of species with given rational masses $m^{\alpha _{1}},...,m^{\alpha _{s}}$ there is a supernormal DVM for the mixture.

Proof

This is an immediate consequence of Theorem 2 and Theorem 3. Just take the velocity set to be large enough to include any possible mass ratio $m_{ij}=\dfrac{m^{\alpha _{i}}}{m^{\alpha _{j}}}$. $\square$

In this study we are considering the problem of constructing DVMs for mixtures with the right number of collision invariants. Another important issue is the one of approximating the full Boltzmann equation for mixtures by DVMs. One possible way to address this problem is provided in [10]. In [10] the same velocity set is used for different species. This is not the case in the DVMs constructed above. However, if desirable, it is possible to find ”large” normal (and symmetric) DVMs that contains the velocity sets for all of the species and hence, can be used as a common velocity set for all species. For meaningful simulations in the case of a mixture we need to have “enough” many collisions between each two species. We have been satisfied by finding $d+1$ collisions between each two species. However, one important aspect is that we have demanded these collisions to be linearly independent (also with respect to the collisions inside the two species) in the way that none of them can be obtained by combining the others (including corresponding reverse collisions), also in combination with the collisions inside the two species. These $d+1$ collisions are certainly not the only ones between the two species. However, all collisions between the two species can be obtained by combining (one or more of) those $d+1$ linearly independent collisions (including corresponding reverse collisions) with the collisions inside the two species. For example: in the simplified cases when $V=\left\{ (\pm 1,\pm 1)\right\}$ for $d=2$ or $V=\left\{ (\pm 1,\pm 1,\pm 1)\right\}$ for $d=3$ in Eq. (20), we will have two and three linearly independent collisions between two species, respectively, while the total number of possible collisions between two species are 10 and 52 (counting a collision and the reverse collision as the same collision), respectively.

Remark 2

Lemma 1, Theorem 2, and Theorem 3 can in an obvious way also be proved to be valid for any $d\ge 4$.

Remark 3

We can combine the approach in this section with one for polyatomic molecules (with a finite number of internal energies), which can be obtained in a similar way, to obtain models for mixtures with internal energies. It is then also possible to add bimolecular reactive collisions [8] and by that extend to models for bimolecular chemical reactions.

5 Boundary Layers for Mixtures

The approach for considering the discrete Boltzmann equation for mixtures in Sect. 4, cf. Eqs. (13)–(15), results in that the system (1)–(2) has a similar structure for mixtures as for single species. One general difference (not mentioning the numerical differences in concrete cases) is that the number of collision invariants (for normal models) are increased from $d+2$ for single species to $d+s+1$ for mixtures of s components. However, apart of this the general structure will be the same. We will below present some results for half-space problems that now can be extended to the case of multicomponent mixtures from the case of single species [5, 6, 9] (see also [7] for the case of binary mixtures).

The planar stationary system for the discrete Boltzmann equation reads

$$\begin{aligned} v_{i}^{1}\frac{dF_{i}}{dx}=Q_{i}\left( F,F\right) \text {, }x\in \mathbb {R} _{+},\text { }i=1,...,n\text {, } \end{aligned}$$

or

$$\begin{aligned} B\dfrac{dF}{dx}=Q\left( F,F\right) \text {, }x\in \mathbb {R}_{+}\text {, }B= \mathrm {diag}(v_{1}^{1},...,v_{n}^{1}), \end{aligned}$$

(28)

where $\mathbf {v}_{i}=\left( v_{i}^{1},...,v_{i}^{d}\right) ,$ $i=1,...,n$, and we assume that

$$\begin{aligned} v_{i}^{1}\ne 0\text {, for }i=1,...,n\text {.} \end{aligned}$$

Given a Maxwellian M (19) we denote

$$\begin{aligned} F=M+M^{1/2}f\text {,} \end{aligned}$$

(29)

in Eq. (28), and obtain

$$\begin{aligned} B\dfrac{df}{dx}+Lf=S(f,f)\text {,} \end{aligned}$$

(30)

where L is the linearized collision operator ($n\times n$ matrix) and S is the quadratic part. The linearized operator L still has a similar structure for mixtures as in the case of single species, since it is obtained in a similar way. Therefore by using similar methods as in the case of single species, see for example [5, 9], one can prove that the matrix L is symmetric and semi-positive, and that the null-space N(L) of L is given by

$$\begin{aligned} N(L)=\left\{ M^{1/2}\phi ~\left| ~\phi \text { is a collision invariant} \right. \right\} \text {.} \end{aligned}$$

(31)

Furthermore, S belongs to the orthogonal complement of N(L), i.e.

$$\begin{aligned} S\left( f,f\right) \in N(L)^{\perp } \end{aligned}$$

(32)

and

$$\begin{aligned} \left| S\left( g,g\right) -S\left( h,h\right) \right| \le \widetilde{K}(\left| g\right| +\left| h\right| )\left| g-h\right| \end{aligned}$$

(33)

for some positive constant $\widetilde{K}>0$.

We denote by $n^{\pm }$, where $n^{+}+n^{-}=n$, and $m^{\pm }$, with $m^{+}+m^{-}=q$, the numbers of positive and negative eigenvalues (counted with multiplicity) of the matrices B and $B^{-1}L$ respectively, and by $m^{0}$ the number of zero eigenvalues of $B^{-1}L$. Moreover, we denote by $k^{+}$, $k^{-}$, and l the numbers of positive, negative, and zero eigenvalues of the $p\times p$ matrix K, with entries

$$\begin{aligned} k_{ij}=\left\langle y_{i},y_{j}\right\rangle _{B}=\left\langle y_{i},By_{j}\right\rangle \text {,} \end{aligned}$$

such that $\left\{ y_{1},...,y_{p}\right\}$ is a basis of the null-space of L, i.e.

$$\begin{aligned} N(L)=\mathrm{span}\left( y_{1},...,y_{p}\right) \text {.} \end{aligned}$$

The numbers $k^{+}$, $k^{-}$, and l are independent of the choice of basis $\left\{ y_{1},...,y_{p}\right\}$. By [9] (see also [5]) there is a basis

$$\begin{aligned} \left\{ u_{1},...,u_{q},y_{1},...,y_{k},z_{1},...,z_{l},w_{1},...,w_{l}\right\} \end{aligned}$$

(34)

of $\mathbb {R}^{n}$, such that

$$\begin{aligned} y_{i},z_{r}\in N(L),\text { }B^{-1}Lw_{r}=z_{r}\text { and }B^{-1}Lu_{\alpha }=\lambda _{\alpha }u_{\alpha }, \end{aligned}$$

(35)

and

$$\begin{aligned} \left\langle u_{\alpha },u_{\beta }\right\rangle _{B}=\lambda _{\alpha }\delta _{\alpha \beta }\text {, with }\lambda _{1},...,\lambda _{m^{+}}>0 \text { and }\lambda _{m^{+}+1},...,\lambda _{q}<0\text {,} \nonumber \\ \left\langle y_{i},y_{j}\right\rangle _{B}=\gamma _{i}\delta _{ij}\text {, with }\gamma _{1},...,\gamma _{k^{+}}>0\text { and }\gamma _{k^{+}+1},...,\gamma _{k}<0, \nonumber \\ \left\langle u_{\alpha },z_{r}\right\rangle _{B}=\left\langle u_{\alpha },w_{r}\right\rangle _{B}=\left\langle u_{\alpha },y_{i}\right\rangle _{B}=\left\langle w_{r},y_{i}\right\rangle _{B}=\left\langle z_{r},y_{i}\right\rangle _{B}=0, \nonumber \\ \left\langle w_{r},w_{s}\right\rangle _{B}=\left\langle z_{r},z_{s}\right\rangle _{B}=0\text { and }\left\langle w_{r},z_{s}\right\rangle _{B}=\delta _{rs}. \end{aligned}$$

(36)

Here $\left\{ u_{1},...,u_{m^{+}}\right\}$ are eigenvectors corresponding to positive eigenvalues, $\left\{ u_{m^{-}},...,u_{q}\right\}$ are eigenvectors corresponding to negative eigenvalues, $\left\{ y_{1},...,y_{k},z_{1},...,z_{l}\right\}$ is a basis for the eigenspace corresponding to the eigenvalue zero, and $\left\{ w_{1},...,w_{l}\right\}$ are generalized eigenvectors corresponding to the eigenvalue zero.

If the Maxwellian in Eq. (29) is non-drifting in the x -direction (i.e. with $b_{1}=0$, where $b_{1}$ is the first component of $\mathbf {b}$ in Eq. (9) or Eq. (19) for single species and mixtures respectively), then $l=d$ for single species and $l=d+s-1$ for a mixture of s components, the DVM is normal and symmetric with respect to the axes. In addition there are (for normal DVMs symmetric with respect to the axes) typically two other values of $b_{1}$ for which l is non-zero (cf. [22] for the continuous case of single species). These numbers will differ for single species and mixtures cf. [5–7], but the general structure will remain the same.

We can (without loss of generality) assume that

$$\begin{aligned} B=\left( \begin{array}{ll} B_{+} &{} 0 \\ 0 &{} -B_{-} \end{array} \right) , \end{aligned}$$

(37)

where

$$\begin{aligned} B_{+}&=\mathrm {diag}\left( v_{1}^{1},...,v_{n^{+}}^{1}\right) \text { and } B_{-}=-\mathrm {diag}\left( v_{n^{+}+1}^{1},...,v_{n}^{1}\right) \text {, with } \\&\quad v_{1}^{1},...,v_{n^{+}}^{1}>0\text { and }v_{n^{+}+1}^{1},...,v_{n}^{1}<0 \text {.} \end{aligned}$$

We also define the projections $R_{+}:\mathbb {R}^{n}\rightarrow \mathbb {R} ^{n^{+}}$ and $R_{-}:\mathbb {R}^{n}\rightarrow \mathbb {R}^{n^{-}}$, by

$$\begin{aligned} R_{+}s=s^{+}=\left( s_{1},...,s_{n^{+}}\right) \text { and } R_{-}s=s^{-}=\left( s_{n^{+}+1},...,s_{n}\right) \end{aligned}$$

for $s=\left( s_{1},...,s_{n}\right)$.

Remark 4

The results below can be extended in a natural way (cf. [5, 6]), to yield also for singular matrices B, if

$$\begin{aligned} N(L)\cap N(B)=\left\{ 0\right\} \text {.} \end{aligned}$$

Remark 5

For the discrete Nordheim–Boltzmann (or Uehling–Uhlenbeck) equation the collision operator (2) in Eq. (1) is replaced with

$$\begin{aligned} Q_{i}^{\varepsilon }\left( F\right) =\sum \limits _{j,k,l=1}^{N}\varGamma _{ij}^{kl}(F_{k}F_{l}\left( 1+\varepsilon F_{i}\right) \left( 1+\varepsilon F_{j}\right) -F_{i}F_{j}\left( 1+\varepsilon F_{k}\right) \left( 1+\varepsilon F_{l}\right) )\text {,} \end{aligned}$$

where it is assumed that the collision coefficients $\varGamma _{ij}^{kl}$ satisfy the relations

$$\begin{aligned} \varGamma _{ij}^{kl}=\varGamma _{ji}^{kl}=\varGamma _{kl}^{ij}\ge 0\text {,} \end{aligned}$$

with equality unless the conservation laws (4), respectively, are satisfied. Here $\varepsilon =0$ corresponds to the classical discrete Boltzmann equation, and we have $\varepsilon =1$ for bosons and $\varepsilon =-1$ for fermions.

Then the singular points are

$$\begin{aligned} P=\frac{M}{1-\varepsilon M}\text {,} \end{aligned}$$

where M is a Maxwellian, but the collision invariants are unchanged for normal DVMs. Hence, the ideas and the DVMs constructed in Sect. 3 can be used also for these cases.

However, we need to replace Eq. (29) by

$$\begin{aligned} f=P+\sqrt{R}F\text {, with }R=P(1+\varepsilon P)\text {,} \end{aligned}$$

to obtain corresponding properties for the operators L and S, and replace Eq. (33) by

$$\begin{aligned} \left| S\left( g\right) -S\left( h\right) \right| \le \widetilde{K} (1+\left| g\right| +\left| h\right| )(\left| g\right| +\left| h\right| )\left| g-h\right| \end{aligned}$$

for some positive constant $\widetilde{K}>0$.

5.1 Linearized Problem

We consider the inhomogeneous (or homogeneous if $g=0$) linearized problem

$$\begin{aligned} B\frac{df}{dx}+Lf=g\text {,} \end{aligned}$$

(38)

where $g=g(x)\in L^{1}(\mathbb {R}_{+},\mathbb {R}^{n})$, with one of the boundary conditions

• (O) the solution tends to zero at infinity, i.e.

  $$\begin{aligned} f(x)\rightarrow 0\text { as }x\rightarrow \infty ; \end{aligned}$$

• (P) the solution is bounded, i.e.

  $$\begin{aligned} \left| f(x)\right| <\infty \text { for all }x\in \mathbb {R}_{+}\text {; } \end{aligned}$$

• (Q) the solution can be slowly increasing at infinity, i.e.

  $$\begin{aligned} \left| f(x)\right| \,e^{-\varepsilon x}\rightarrow 0\text { as } x\rightarrow \infty \text {, for all }\varepsilon >0\text {.} \end{aligned}$$

In case of boundary condition (O) we additionally assume that

$$\begin{aligned} g(x)\in N(L)^{\perp }\text { for all }x\in \mathbb {R}_{+}. \end{aligned}$$

(39)

Remark 6

Boundary condition (O) corresponds to the case when we have made the linearization (29) around a Maxwellian M, such that $F\rightarrow M$ as $x\rightarrow \infty$. Boundary conditions (P) and (Q) are the boundary conditions in the Milne and Kramers problem respectively.

At $x=0$ we assume the boundary condition

$$\begin{aligned} f^{+}(0)=Cf^{-}(0)+h_{0}\text {,} \end{aligned}$$

(40)

where C is a given $n^{+}\times n^{-}$ matrix and $h_{0}\in \mathbb {R} ^{n^{+}}$ (cf. [5, 6]).

Theorem 5

[5]

• (i) Let

  $$\begin{aligned} U_{+}=\mathrm {span}\left( u_{1},...,u_{m^{+}}\right) =\mathrm {span}\left\{ \left. u\,\right| \,B^{-1}Lu=\lambda u\text { for some }\lambda >0\right\} . \end{aligned}$$

  Assume that condition (39) is fulfilled, that

  $$\begin{aligned} \dim \left( R_{+}-CR_{-}\right) U_{+}=m^{+}\text {,} \end{aligned}$$

  and that

  $$\begin{aligned} h_{0},\left( R_{+}-CR_{-}\right) e^{xB^{-1}L}B^{-1}g(x)\in \left( R_{+}-CR_{-}\right) U_{+}\text { for all }x\in \mathbb {R}_{+}\text {.} \end{aligned}$$

  Then the system (38) with boundary conditions (O) and (40) has a unique solution.

• (ii) Assume that

  $$\begin{aligned} \lim _{x\rightarrow \infty }x\int \limits _{x}^{\infty }\left\langle g\left( \sigma \right) ,z_{j}\right\rangle \,d\sigma =0\text { for }j=1,...,l\text {,} \end{aligned}$$

  and that

  $$\begin{aligned} \dim \left( R_{+}-CR_{-}\right) X_{+}=n^{+}\text {,} \end{aligned}$$

  (41)

  with $X_{+}=\mathrm {span}\left( u_{1},...,u_{m^{+}},y_{1},...,y_{k^{+}},z_{1},...,z_{l}\right)$. Then the system (38) with boundary conditions (P) and (40) has a unique solution with the asymptotic flow

  $$\begin{aligned} f_{A}=\sum \limits _{i=1}^{k}\mu _{i}^{\infty }y_{i}+\sum \limits _{j=1}^{l}\eta _{j}^{\infty }z_{j}\text {,} \end{aligned}$$

  if the $k^{-}$ parameters $\mu _{k^{+}+1}^{\infty },...,\mu _{k}^{\infty }$ are prescribed.

• (iii) Assume that condition (41) or the condition

  $$\begin{aligned} \dim \left( R_{+}-CR_{-}\right) \widetilde{X}_{+}=n^{+}\text {,} \end{aligned}$$

  with $\widetilde{X}_{+}=\mathrm {span}\left( u_{1},...,u_{m^{+}},y_{1},...,y_{k^{+}},z_{1}+w_{1},...,z_{l}+w_{l}\right)$ is fulfilled. Then the system (38) with boundary conditions (Q) and (40) has a unique solution with the asymptotic flow

  $$\begin{aligned} f_{A}(x)=\sum \limits _{i=1}^{k}\mu _{i}^{\infty }y_{i}+\sum \limits _{j=1}^{l}\left( \left( \eta _{j}^{\infty }-x\alpha _{j}^{\infty }\right) z_{j}+\alpha _{j}^{\infty }w_{j}\right) \text {,} \end{aligned}$$

  if the $k^{-}+l$ parameters $\mu _{k^{+}+1}^{\infty },...,\mu _{k}^{\infty }$ and $\alpha _{1}^{\infty },...,\alpha _{l}^{\infty }$ are prescribed.

5.2 Non-linear Problem

We now consider the non-linear system

$$\begin{aligned} \left\{ \begin{array}{l} B\frac{df}{dx}+Lf=S(f,f) \\ f^{+}(0)=Cf^{-}(0)+h_{0} \\ f(x)\rightarrow 0\text { as }x\rightarrow \infty \text {,} \end{array} \right. \end{aligned}$$

(42)

where C is a given $n^{+}\times n^{-}$ matrix, $h_{0}\in \mathbb {R}^{n^{+}}$, and the non-linear part fulfills

$$\begin{aligned} S\left( f,f\right) \in N(L)^{\perp } \end{aligned}$$

and

$$\begin{aligned} \left| S\left( g,g\right) -S\left( h,h\right) \right| \le \widetilde{K}G(\left| g\right| ,\left| h\right| )\left| g-h\right| \end{aligned}$$

(43)

for some positive constant $\widetilde{K}>0$ and differentiable function $G: \mathbb {R}_{+}\times \mathbb {R}_{+}\rightarrow \mathbb {R}_{+}$ with positive partial derivatives and $G(0,0)=0$. Assumption (43) is a generalization of the corresponding assumption (33), used in [6]. Assumption (33) is enough for the discrete Boltzmann equation for mixtures. However, we need the generalization (43), if we want to be able to consider for example the Nordheim-Boltzmann equation (see Remark 5).

The boundary condition $f(x)\rightarrow 0$ as $x\rightarrow \infty$ corresponds to the case when we have made the transformation (29) for a Maxwellian $M=M_{\infty }$, such that $F\rightarrow M_{\infty }$ as $x\rightarrow \infty$.

We assume that

$$\begin{aligned} \dim \left( R_{+}-CR_{-}\right) \widehat{X}_{+}=n^{+}\text {, } \end{aligned}$$

(44)

with $\widehat{X}_{+}=\mathrm {span}\left( u_{1},...,u_{m^{+}},y_{1},...,y_{k^{+}},w_{1},....,w_{l}\right)$.

If $C=0$, then condition (44) is fulfilled. In particular,

$$\begin{aligned} \left\{ u_{1}^{+},...,u_{m^{+}}^{+},y_{1}^{+},...,y_{k^{+}}^{+},w_{1}^{+},...,w_{l}^{+}\right\} \end{aligned}$$

is a basis of $\mathbb {R}^{n^{+}}$.

The following result on boundary layers gives the number of conditions that must be posed on the given data $h_{0}$ to obtain a well-posed problem. Theorem 6 below can be proved by similar arguments as the corresponding Theorem in [6].

Theorem 6

Let condition (44) be fulfilled and suppose that $\left\langle h_{0},h_{0}\right\rangle _{B_{+}}$ is sufficiently small. Then with $k^{+}+l$ conditions on $h_{0}$, the system (42) has an (at least locally) unique solution.