1 Introduction

The analysis concerning the growth and the motion of polygonal interfaces by the crystalline curvature has become a popular subject of research in recent years. It has attracted much attention largely due to the celebrated works by Angenent and Gurtin [2] and Taylor [20, 21], who explored the dynamics of interface between the two-face and stated the evolution law, now known as the crystalline motion or as the evolution by crystalline curvature. This law is established for a special class of piecewise linear closed curves, called admissible, for which the motion is described by a system of ordinary differential equations (ODEs). Since the evolution by crystalline curvature is defined for a special class of nonsmooth curves, it naturally extends ordinary curvature for smooth curves both in the sense of the normal velocity formulation and in terms of variational structures. We refer to the notable monograph by Gurtin [9] and also to the papers by Almgren and Wang [1], Górka [6–8], Rybka [15–19] and Dudziński and Górka [4], for comprehensive reviews on the research relating to these kinds of evolutions.

In our paper, we are concerned with the motion of spiral-shaped polygonal curves described in terms referring to the crystalline curvature. We assume that the discussed polygonal curves spiral out to infinity and have one end fixed at the origin. We use a suitable system of ODEs to model the crystalline motion of spirals. Our principal objective is to prove the local existence and uniqueness of the solution to this system.

There are two major reasons for which it is worth to deal with the issue of spiral-shaped polygonal curves. Firstly, the spiral patterns are frequently detected in practice—in particular, they are commonly observed in real crystal growth as well as in a variety of biological and chemical systems. The spiral waves observed in the Belousov–Zhabotinsky reaction are most likely the best-known examples of such the presence and much attention has been focused on both numerical and analytical modeling of this phenomena. We mention in this context the articles by Belmonte et al. [3], Jahnke and Winfree [12], Luengviriya et al. [13], Mikhailov et al. [14], and the references therein. Secondly, understanding the spiral shapes by constructing appropriate models seems interesting from the purely mathematical point of view.

To our knowledge, not much work regarding the mathematical investigations on spirals in crystals has been done so far. Among the rare, but undoubtedly valuable, papers devoted to this topic, we cite the works by Taylor [20] and Imai et al. [10, 11]. The last two of the mentioned publications encouraged us to undertake some research relating to this field.

The system of equations (4), (5) in Imai et al. [10], governing the motion of the crystalline curvature on each of the line segments of the spiral-shaped polygonal curve, is the starting point of our considerations. However, our assumption varies from the conditions imposed in Imai et al. [10]. Also, the techniques involved in our proof of the local existence and uniqueness of the solution to the proposed system differ from those implemented by the mentioned authors.

The remainder of the paper is structured as follows. In Sect. 2, we introduce the subject of our research, the necessary terminology and notations as well as, we comment on the imposed assumptions. In Sect. 3, we formulate and prove our main result. Section 4 concludes and summarizes our study.

2 Preliminaries and Notations

In this part of the paper, the problem setting together with the essential terminology and notations are presented.

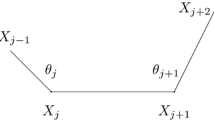
Assume that the spiral-shaped polygonal curve \(S(t)\) is given for any \(t\) from some interval \(\left[ 0,T\right) \). Without loss of generality, we suppose that \(S(t)\) spirals out anticlockwise. We denote by \(L_{i}(t)\), \(i = 0,1,2,\ldots \), the line segments of the curve \(S(t)\), numbered from the origin and by \(l_{i}(t)\), \(i=0,1,2,\ldots \), the corresponding lengths of \(L_{i}(t)\). Moreover, it is assumed that the origin maintains fixed during the evolution and that, for \(i\in \left\{ 0,1,2,\ldots \right\} \): \(1^{0}\) the unit normals \(\nu _{i}\) to the segments \(L_{i}(t)\) have the outward orientation and are independent of \(t\), \(2^{0}\) the set of possible orientations of \(\nu _{i+1}\) is finite and \(\nu _{i+1}\) is attained by turning \(\nu _{i}\) left.

The studied problem may be graphically presented as shown in Fig. 1 below.

Fig. 1
figure 1

Spiral-shaped polygonal curve

Full size image

With reference to the imposed conditions, we obtain—due to the relations in (4), (5) from Imai et al. [10]—the following system of infinitely dimensional ordinary differential equations (ODEs) for \(i\in \mathbb {N}\)

$$\begin{aligned} \left\{ \begin{array}{c} \frac{d}{dt}z_{i}(t)=\dfrac{\left( \cot \theta _{i}+\cot \theta _{i+1}\right) -1/\sin \theta _{i}-1/\sin \theta _{i+1}}{-z_{i}\left( t\right) \left( \cot \theta _{i}+\cot \theta _{i+1}\right) +\frac{z_{i-1}\left( t\right) }{\sin \theta _{i}}+\frac{z_{i+1}\left( t\right) }{\sin \theta _{i+1}}}, \\ z_{i}\left( 0\right) =a_{i}, \end{array} \right. \end{aligned}$$
(1)

where \(z_{0}\left( t\right) =0\) for any \(t\in \left[ 0,T\right) \) and, for the given \(i\), \(z_{i}\left( t\right) \) denotes the distance from the origin to the line containing \(L_{i}(t)\) and \(\theta _{i}\) stands for the angle between \(\nu _{i-1}\) and \(\nu _{i}\); we also assume that \(z_{i}\in C^{1}\left( \left[ 0,T\right) \right) \) for all \(i\). It is worth to underline that the system in (1) is the reduced version of the general model describing the dynamics of evolving phase boundaries, which is given in the form of the following equation

$$\begin{aligned} b\left( \nu \right) V=\left( f\left( \nu \right) +f^{\prime \prime }\left( \nu \right) \right) K-F, \end{aligned}$$

where \(\nu \), \(V\), \(K\) denote, respectively: the angle to the interface normal, the normal velocity, the curvature of the interface, and where: \(F\left( \nu \right) \) denotes the difference in bulk energy between the two phases, \(f\left( \nu \right) \) is the interfacial energy, \(b\left( \nu \right) \) stands for the appropriate positive kinetic coefficient. By putting \(b\equiv 1\) and \(F\equiv 0\) as well as assuming that \(f\) is piecewise a unity and using the fact that the crystalline curvature \(K_{i}\left( t\right) \) is the derivative of the distance \(z_{i}\left( t\right) \), we get

$$\begin{aligned} \frac{d}{dt}z_{i}(t)=K_{i}\left( t\right) =g\big ( \theta _{i-1},\theta _{i},\theta _{i+1},z_{i-1}\left( t\right) ,z_{i}\left( t\right) ,z_{i+1}\left( t\right) \big ) ,\quad i\in \mathbb {N}, \end{aligned}$$

where \(g\) is the function on the right-hand side of the basic system of equations in (1).

Clearly, the system in (1)—describing the dynamics of the spiral-shaped polygonal curves in terms involving the crystalline curvatures \(K_{i}\left( t\right) =\dfrac{d}{dt}z_{i}(t)\)—may be rewritten as follows

$$\begin{aligned} \left\{ \begin{array}{c} \frac{d}{dt}z_{i}(t)=\dfrac{\sin \left( \theta _{i}+\theta _{i+1}\right) -\sin \theta _{i}-\sin \theta _{i+1}}{z_{i+1}\left( t\right) \sin \theta _{i}-z_{i}\left( t\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +z_{i-1}\left( t\right) \sin \theta _{i+1}}, \\ z_{i}\left( 0\right) =a_{i}, \quad i\in \mathbb {N}. \end{array} \right. \end{aligned}$$
(2)

Before proceeding further, we replace the assumptions (A1)–(A3) in [10] by the condition

$$\begin{aligned} \underset{i\in \mathbb {N}}{\inf }\big \vert a_{i+1}\sin \theta _{i}-a_{i}\sin \big ( \theta _{i}+\theta _{i+1}\big ) +a_{i-1}\sin \theta _{i+1}\big \vert >0. {\hbox {(Assu)}} \end{aligned}$$

Our goal is to show that, providing the assumption in (Assu) holds, the system in (2) is uniquely solvable.

Although the system (2), introduced in [10], is the starting point of our investigations, our assumption differs from the conditions imposed in [10]. In our research, we skipped the assumptions (A1)–(A3) from [10] in favour of the condition (Assu), which does not overlap with the constraints in (A1)–(A3). Also, the methods employed in our proof vary from the approach implemented by the mentioned authors; in particular, our proof is shorter, more direct and concise as compared with the corresponding proof from the cited work. We treat the system (2) as ODE in the Banach space \(\ell _{\infty }\).

In the subsequent section, we formulate and prove Theorem 1, which is our principal assertion.

3 Main Result

Let us recall the standard notation. By \(C^{1}\left( \left[ 0,T\right) \right) \), we denote the space of continuous and differentiable functions on the interval \(\left[ 0,T\right) \), endowed with the norm

$$\begin{aligned} \Vert f \Vert _{C^1([0,T))}= \underset{t\in \left[ 0,T\right) }{\sup }\left| f \left( t\right) \right| + \underset{t\in \left[ 0,T\right) }{\sup }\left| f' \left( t\right) \right| . \end{aligned}$$

Moreover, by \(C\left( \left[ 0,T\right) ;\ell _{\infty }\right) \), we denote the space of continuous functions with values in the Banach space \(\ell _{\infty }\). This space is endowed with the following norm

$$\begin{aligned} \left\| f\right\| _{C\big ( \left[ 0,T\right) ;\ell _{\infty }\big ) }=\underset{i\in \mathbb {N},\text { }t\in \left[ 0,T\right) }{\sup } \left| f_{i}\left( t\right) \right| . \end{aligned}$$

Our purpose is to prove the following claim.

Theorem 1

Under the assumption (Assu), there exists a unique local solution \(z=\left( z_{i}\right) _{i=1}^{\infty }\) to the system (2) in the class of functions satisfying:

$$\begin{aligned}&z_{i}\in C^{1}\big ( \left[ 0,T\right) \big ) ,\text { for any }i\in \mathbb { N}, \\&z-a\in C \big ( \left[ 0,T\right) ;\ell _{\infty }\big ) , \end{aligned}$$

and

$$\begin{aligned} \underset{i\in \mathbb {N},\text { }t\in \left[ 0,T\right) }{\inf }\left| z_{i+1}\left( t\right) \sin \theta _{i}-z_{i}\left( t\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +z_{i-1}\left( t\right) \sin \theta _{i+1}\right| >0. \end{aligned}$$

Proof

The proof is divided into the two parts, denoted by (a), (b). In part (a), we show the local existence of the solution to the proposed system, while in part (b), we prove the corresponding uniqueness.

  1. (a)

    The proof of existence. Let, for the considered functions \(z_{i}\) and the initial values \(a_{i}=z_{i}\left( 0\right) , \) \(w_{i}\left( t\right) :=z_{i}\left( t\right) -a_{i}\), \(i=1,2,\ldots \) Then, the system in (2) may be rewritten as

    $$\begin{aligned} \left\{ \begin{array}{c} \frac{d}{dt}w_{i}(t)=\dfrac{\sin \left( \theta _{i}+\theta _{i+1}\right) -\sin \theta _{i}-\sin \theta _{i+1}}{w_{i+1}\left( t\right) \sin \theta _{i}-w_{i}\left( t\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +w_{i-1}\left( t\right) \sin \theta _{i+1}+C_{i}}, \\ w_{i}\left( 0\right) = 0 \end{array} \right. \end{aligned}$$

    where

    $$\begin{aligned} C_{i}:=a_{i+1}\sin \theta _{i}-a_{i}\sin \big (\theta _{i}+\theta _{i+1}\big )+a_{i-1}\sin \theta _{i+1}. \end{aligned}$$

    It follows from (Assu) that

    $$\begin{aligned} \inf _{i \in \mathbb {N}}\big \vert a_{i+1}\sin \theta _{i}-a_{i}\sin \big (\theta _{i}+\theta _{i+1}\big )+a_{i-1}\sin \theta _{i+1}\big \vert =\eta >0. \end{aligned}$$

    We denote by \(X_{\eta }^{T}\) the set of the form

    $$\begin{aligned} X_{\eta }^{T}:=\Big \{ w\in C\left( \left[ 0,T\right) ;\ell _{\infty }\right) \text {:} \quad \left\| w\right\| _{C\left( \left[ 0,T\right) ;\ell _{\infty }\right) }\le \frac{\eta }{6}\Big \} . \end{aligned}$$

    In addition, we define the map \(\mathcal {F}\): \(X_{\eta }^{T}\rightarrow C\left( \left[ 0,T\right) ;\ell _{\infty }\right) \) in the following manner

    $$\begin{aligned} \left( \mathcal {F}\left( w\right) \right) _{i}\left( t\right) = \int _{0}^{t} \frac{\sin \left( \theta _{i}+\theta _{i+1}\right) -\sin \theta _{i}-\sin \theta _{i+1}}{w_{i+1}\left( s\right) \sin \theta _{i}-w_{i}\left( s\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +w_{i-1}\left( s\right) \sin \theta _{i+1}+C_{i}}ds,\\ \end{aligned}$$

    \(i=1,2,\ldots \), where the constants \(C_{i}\) are the same as at the beginning of the current proof. The proof of existence is twofold. In the first step, we will show that

    $$\begin{aligned} \mathcal {F} : X_{\eta }^{T}\rightarrow X_{\eta }^{T}, \end{aligned}$$

    for sufficiently small \(T\). Indeed, as \(w\in X_{\eta }^{T}\), we have, for any \(i\), \(s\),

    $$\begin{aligned} \left| {w_{i+1}\left( s\right) \sin \theta _{i}-w_{i}\left( s\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +w_{i-1}\left( s\right) \sin \theta _{i+1}}\right| \le \frac{\eta }{6}+\frac{\eta }{6}+\frac{\eta }{6}=\frac{\eta }{2}. \end{aligned}$$

    This and the assumption (Assu) imply, for any \(i\), \(s\),

    $$\begin{aligned}&\big \vert {w_{i+1}\left( s\right) \sin \theta _{i}-w_{i}\left( s\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +w_{i-1}\left( s\right) \sin \theta _{i+1}+C_{i}}\big \vert \\&\quad \ge \big \vert {\left| w_{i+1}\left( s\right) \sin \theta _{i}-w_{i}\left( s\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +w_{i-1}\left( s\right) \sin \theta _{i+1}\right| -\left| {C_{i}}\right| }\big \vert \\&\quad =\left| {C_{i}}\right| -\big \vert {w_{i+1}\left( s\right) \sin \theta _{i}-w_{i}\left( s\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +w_{i-1}\left( s\right) \sin \theta _{i+1}}\big \vert \ge \eta -\frac{\eta }{2}. \end{aligned}$$

    Since in addition,

    $$\begin{aligned} \left| {B_{i}}\right| \le 3, \quad \mathrm{where}\,\,B_{i}:=\sin \left( \theta _{i}+\theta _{i+1}\right) -\sin \theta _{i}-\sin \theta _{i+1}, \end{aligned}$$

    we get

    $$\begin{aligned} \left| \left( \mathcal {F}\left( w\right) \right) _{i}\right| \le \int _{0}^{T}\frac{3}{\left( \eta -\frac{\eta }{2}\right) }ds=\frac{6}{\eta }T. \end{aligned}$$

    Thus, we obtain that \(\mathcal {F}\): \(X_{\eta }^{T}\rightarrow X_{\eta }^{T}\), if \(T\le \left( \eta /6\right) ^{2}\). In the second step, we will prove that \(\mathcal {F}\) is a contraction mapping on \(X_{\eta }^{T}\), provided \(T\) is sufficiently small. Namely, observe that, for any \(u,v\in X_{\eta }^{T}\),

    $$\begin{aligned} \left| \left( \mathcal {F}\left( u\right) -\mathcal {F}\left( v\right) \right) _{i}\left( t\right) \right| \ \le \int _{0}^{T}\frac{\left| {B_{i}}\right| \left| {C^{\left( u\right) }_{i}\left( s\right) -C^{\left( v\right) }_{i}\left( s\right) }\right| }{\left| {C^{\left( u\right) }_{i}\left( s\right) +C_{i}}\right| \left| {C^{\left( v\right) }_{i}\left( s\right) +C_{i}}\right| }ds, \end{aligned}$$

    where the constants \(B_{i}\), \(C_{i}\) are defined earlier, and:

    $$\begin{aligned} C^{\left( u\right) }_{i}\left( s\right) :=u_{i+1}\left( s\right) \sin \theta _{i}-u_{i}\left( s\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +u_{i-1}\left( s\right) \sin \theta _{i+1}, \end{aligned}$$
    $$\begin{aligned} C^{\left( v\right) }_{i}\left( s\right) :=v_{i+1}\left( s\right) \sin \theta _{i}-v_{i}\left( s\right) \sin \left( \theta _{i}+\theta _{i+1}\right) +v_{i-1}\left( s\right) \sin \theta _{i+1}. \end{aligned}$$

    It is easily seen that, for any \(u,v\in X_{\eta }^{T}\) and all \(i\), \(s\),

    $$\begin{aligned} \left| {C^{\left( u\right) }_{i}\left( s\right) -C^{\left( v\right) }_{i}\left( s\right) }\right| \le 3\left\| u-v\right\| _{C\left( \left[ 0,T\right) ;\ell _{\infty }\right) }. \end{aligned}$$

    Furthermore, it follows from the previous derivations that

    $$\begin{aligned} \left| {C^{\left( u\right) }_{i}\left( s\right) +C_{i}}\right| \ge \eta -\frac{\eta }{2}\,\,\mathrm{and}\,\,\left| {C^{\left( v\right) }_{i}\left( s\right) +C_{i}}\right| \ge \eta -\frac{\eta }{2}. \end{aligned}$$

    Thus, we obtain

    $$\begin{aligned} \begin{aligned} \left| \left( \mathcal {F}\left( u\right) -\mathcal {F}\left( v\right) \right) _{i}\left( t\right) \right| \ \le \int _{0}^{T}\frac{9\left\| u-v\right\| _{C\left( \left[ 0,T\right) ;\ell _{\infty }\right) }}{\left( \eta -\frac{\eta }{2}\right) \left( \eta - \frac{\eta }{2}\right) }ds. \end{aligned} \end{aligned}$$

    Therefore, for any \(i\in \left\{ 1,2,\ldots \right\} ,\)

    $$\begin{aligned} \left| \left( \mathcal {F}\left( u\right) -\mathcal {F}\left( v\right) \right) _{i}\left( t\right) \right| \le \frac{36}{\eta ^{2}}T\left\| u-v\right\| _{C\left( \left[ 0,T\right) ;\ell _{\infty }\right) }. \end{aligned}$$

    Hence, by taking the supremum over \(i\in \left\{ 1,2,\ldots \right\} \) and \(t\in \left[ 0,T\right) \), we have

    $$\begin{aligned} \left\| \mathcal {F}\left( u\right) -\mathcal {F}\left( v\right) \right\| _{C\left( \left[ 0,T\right) ;\ell _{\infty }\right) }\le \frac{36}{\eta ^{2}}T\left\| u-v\right\| _{C\left( \left[ 0,T\right) ;\ell _{\infty }\right) }. \end{aligned}$$

    This indicates that \(\mathcal {F}\) is a contraction mapping, if \(T<\eta ^{2}/36 \). Thus, by virtue of the Banach Fixed-Point Theorem, \(\mathcal {F}\) admits a unique fixed-point in \(X_{\eta }^{T}\), which is the solution to the system in (2). This proves the existence of the solution to our system. Thus, it remains to establish that this solution is unique.

  2. (b)

    The proof of uniqueness. Assume that, there exist two different solutions, say \(z\), \(\tilde{z}\), to the system in (2). Then,

    $$\begin{aligned} \left( z-\tilde{z}\right) _{i}\left( t\right) =\int _{0}^{t}\left( \frac{B_{i}}{C^{\left( z\right) }_{i}\left( s\right) } - \frac{B_{i}}{C^{\left( \tilde{z}\right) }_{i}\left( s\right) }\right) ds= \int _{0}^{t}\frac{B_{i}\left( C^{\left( \tilde{z}\right) }_{i}\left( s\right) -C^{\left( z\right) }_{i}\left( s\right) \right) }{\left( C^{\left( z\right) }_{i}\left( s\right) C^{\left( \tilde{z}\right) }_{i}\left( s\right) \right) }ds, \end{aligned}$$

    where \(B_{i}\), \(C^{\left( z\right) }_{i}\), \(C^{\left( \tilde{z}\right) }_{i}\) are defined earlier. Clearly, we have, for any \(i \in \mathbb {N}\), \(s \in \left[ 0,T\right) \),

    $$\begin{aligned} \vert {C^{\left( \tilde{z}\right) }_{i}\left( s\right) -C^{\left( z\right) }_{i}\left( s\right) }\vert \le 3 \left\| z\left( s\right) -\tilde{z}\left( s\right) \right\| _{l_{\infty }}. \end{aligned}$$

    Moreover, we have:

    $$\begin{aligned} \vert C^{\left( z\right) }_{i}\left( s\right) \vert&\ge \underset{i,s}{\inf }\!\big \vert z_{i+1}\left( s\right) \sin \theta _{i}\!-\! z_{i}\left( s\right) \!\left( \sin \theta _{i}\!+\!\sin \theta _{i+1}\right) \!+\!z_{i-1}\left( s\right) \sin \theta _{i+1}\big \vert =:D_{1}\left( z\right) >0,\\ \vert C^{\left( \tilde{z}\right) }_{i}\left( s\right) \vert&\ge \underset{i,s}{\inf }\big \vert \tilde{z}_{i+1}\left( s\right) \sin \theta _{i}\!-\! \tilde{z}_{i}\!\left( s\right) \left( \sin \theta _{i}\!+\!\sin \theta _{i+1}\right) \!+\!\tilde{z}_{i-1}\left( s\right) \sin \theta _{i+1}\big \vert \!=:D_{2}\left( \tilde{z}\right) >0, \end{aligned}$$

    where \(D_{1}\left( z\right) \), \(D_{2}\left( \tilde{z}\right) \) stand for some constants, depending on \(z\), \(\tilde{z}\), respectively. Consequently, we may write that, for any \(i \in \mathbb {N}\), \(t\in \left[ 0,T\right) \),

    $$\begin{aligned} \big ( z-\tilde{z}\big ) _{i}\left( t\right) \le \frac{9}{\left( D_{1}\left( z\right) D_{2}\left( \tilde{z}\right) \right) } \int _{0}^{t}\left\| z\left( s\right) -\tilde{z}\left( s\right) \right\| _{l_{\infty }}ds. \end{aligned}$$

    Hence, by passing to the supremum over \(i \in \mathbb {N}\), we get

    $$\begin{aligned} \left\| z\left( t\right) -\tilde{z}\left( t\right) \right\| _{\ell _{\infty }}\le \frac{9}{\left( D_{1}\left( z\right) D_{2}\left( \tilde{z}\right) \right) } \int _{0}^{t}\left\| z\left( s\right) -\tilde{z}\left( s\right) \right\| _{l_{\infty }}ds, \end{aligned}$$

    for all \(t\in \left[ 0,T\right) \). Thus, due to the Bellman–Gronwall inequality, we obtain, for any \(t\in \left[ 0,T\right) \),

    $$\begin{aligned} \left\| z\left( t\right) -\tilde{z}\left( t\right) \right\| _{\ell _{\infty }}=0. \end{aligned}$$

    Therefore, \(z=\tilde{z}\), which proves the desired uniqueness and simultaneously, completes the entire proof of our assertion. \(\square \)

4 Conclusions

We have proved the local existence and uniqueness of the solution to the system of ordinary differential equations describing the dynamics of spiral-shaped polygonal interfaces with regard to the crystalline curvature. Similar investigations have been conducted by Imai et al. in [10], but the assumptions proposed in our claim do not overlap with the conditions used by the mentioned authors and additionally, our theorem has been proved in the more straightforward manner than the corresponding result stated in [10]. Furthermore, the techniques and tools implemented in the proof of our assertion differ from the approach employed by Imai et al.

It is worth mentioning that the existence of the global in time solution to the system governing the crystalline growth and motion of the spiral-shaped curves is not to be expected, since in this case the segments of the curve may be bonded together and the blow-up may take place.