Can Diffusions Propagate?

Abstract

The diffusion of relativistic particle in a fluid at equilibrium is investigated through an analytical and numerical study of the Relativistic Ornstein-Uhlenbeck process (ROUP). Contrary to expectations, the ROUP exhibits short-time propagation in physical space and only displays typical diffuse behavior at asymptotic times. The short-time propagation is understood through an analytical computation and the density profile is fitted at all times by a simple Ansatz. A generalization of Fick’s law is finally obtained, in which the diffusion coefficient is replaced by a time-dependent metric. These results connect relativistic diffusion with gravitational horizons and geometrical flows.

Appendix

Consider an arbitrary problem of finite speed transport and model it by a Langevin-type stochastic process. Restricting the discussion to 1D situations and using the same notations are in the core of the article, we write this process as:

(31)

(32)

where F is a friction or dissipative term and σ is a noise coefficient. Since we are modeling finite speed transport, we suppose that the initial condition and the process itself restricts v to a finite interval, say I=(−c,+c), where c is an arbitrary constant. A simple one-to-one map of this interval onto ℝ is of course:

$$ \begin{array}{rll} p: I & \rightarrow&\mathbb{R} \cr\noalign{\vspace{3pt}} v & \rightarrow& p(v) = \gamma(v) \, v \end{array} $$

(33)

with $\gamma(v) = (1 - \frac{v^{2}}{c^{2}})^{-1/2}$. Note that v→±c corresponds to p→±∞. The first equation of the process transcribes into

(34)

with Γ(p)=(1+p ²/c ²)^1/2.

Consider now as initial condition x=0 and a certain probability law in p, which we denote by F ^∗(p)dp. To make the discussion simpler, suppose also that F ^∗ isotropic, and write F ^∗(p)=exp(−Φ(Γ(p))). Reasoning as in Sect. 3.2 leads to the following approximate expression for the short-time density of the process in 1D space:

(35)

The first and second partial derivatives of n with respect to x read:

(36)

and

(37)

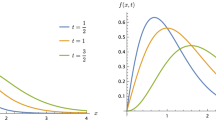
At early times, the density n thus admits an extremum at x=0 i.e. for γ=1. The second derivative of the density at x=0 is non-negative provided Φ′(1)≤3 and x=0 is then a local minimum of n. Suppose for example that Φ(γ)=a+q ² γ. The initial momentum distribution is then a Jüttner distribution of temperature k _B θ _i =mc ²/q ² and Φ′(1)=q ². In this case, the origin x=0 is a minimum for n at early times provided q ²≤3 or, equivalently, $k_{B} \theta_{i} \geq mc^{2}/\sqrt{3}$ i.e. for large enough initial temperatures. For initial temperatures smaller than $mc^{2}/\sqrt{3}$, x=0 is a maximum for n. For these temperatures, the initial expectation or mean value ${\bar{\gamma}}$ of the Lorentz factor does not exceed ∼1.2; the initial conditions for which x=0 is a maximum of n are thus at most weakly relativistic.

Suppose now Φ is a strictly increasing function of γ and that the equation γ  Φ′(γ)=3 has a single solution γ ^∗. This is so for Φ(γ)=a+q ² γ, in which case γ ^∗=3/q ². At each time t, the value γ ^∗ corresponds to $x/ct = \pm\, x^{*}/ct = \pm\sqrt{ 1 - 1/\gamma^{*2}}$. The second derivative of the density n at these points has the same sign as D ^∗=−3γ ^∗−γ ^∗3 Φ″(γ ^∗). A sufficient (but not necessary) condition for D ^∗ to be positive is that Φ be convex in γ. Thus, for any convex function Φ, the short-time density profile exhibits two peaks which travel at velocity $c \sqrt{ 1 - 1/\gamma^{*2}}$. For Φ(γ)=a+q ² γ, a direct computation shows that the quotient n(t,±x ^∗)/n(t,0) is always greater or equal to unity and only reaches unity for $q = \sqrt{3}$. Thus, for this choice of Φ, the peaks are always higher than the extremum at x=0, even when this extremum is a local maximum. The short-time transport is then always mainly propagative.