1 Introduction

In this paper, we explore the construction of schedules for clients who are serviced on a periodic basis, where clients receive identical service durations but at different intervals. An immediate practical problem motivates our research, namely local transmission of data in Wireless Mesh Networks (WMN) which is of increasingly importance for communication worldwide (Akyildiz et al. 2005). In wireless networks, data are transmitted in packets, and this feature can be exploited to extract considerable energy saving of a factor of 5 to 10 through efficient algorithms for packet scheduling (Quintas and Friderikos 2012). Wireless Mesh Networks represent a technology that economically increases the geographical area within which mobile clients may access broadband communication.

Mesh routers facilitate multi-hop wireless transmission to relay data over extended distances without the cost, delay and disruption of installing cabled access points. The routers also act as local access points for devices or clients (e.g. for WiFi access). The routers typically have a fixed location and can be mounted on buildings, street lamps, etc. It is the provision of local access (i.e. devices connecting to the access point) that is of relevance in this paper. Local access is governed by a star topology with all devices connecting to the local access point. Bandwidth must be scheduled so that at any point in time, an access point is servicing at most one client. In this scenario, perfect periodic scheduling provides numerous benefits associated with predictability of activity time. A schedule is perfect periodic when each client is itself serviced regularly at a fixed interval, known as its periodicity. The duration and periodicity of service for each client is given. In classic machine scheduling context, processing of a job is synonymous with servicing of a client, and processing time with duration. We will use these two paradigms interchangeably throughout. The predictability allows the total power consumption of the network to be minimised and the interference from competing simultaneous transmissions to be reduced or even eliminated.

Several studies have been undertaken on perfect periodic scheduling problems. The problem of finding a feasible perfect periodic schedule has been proved by Bar-Noy et al. (2002a) to be NP-hard in general. However, there are some special cases for which simple closed form expressions offer a polynomial time solution method. For three products with three distinct periodicities, Glass (1992) derives a simple test for existence of a feasible schedule, and a method of constructing feasible schedules if one exists. In addition, Glass (1994) and Glass et al. (1994) study the feasibility problem in the context of the Economic Lot Scheduling Problem where several products with different durations are produced periodically so as to minimise holding and set up costs. For two (three) products with two (three) distinct periodicities, they develop a simple necessary and sufficient condition for the feasibility test and construction of a feasible schedule. For three products with three distinct periodicities, she derive a simple test for existence of a feasible schedule, and a method of constructing feasible schedules if one exists (Glass 1992).

Due to the difficulty of finding a feasible perfect periodic schedule for any given periodicities, called as request periodicity, heuristics are therefore used to allocated close values, called as allocated periodicity, using specific criteria. Brakerski et al. (2006) study perfect periodic scheduling for multiple servers, with the objective is to minimise the maximum ratio of the allocated periodicity and requested periodicity. They develop some approximation algorithms for the problem. Patil and Garg (2006) propose an adaptive algorithm, called Adapmin. They find a worst case performance bound on the quality of schedules produced by Adaptmin and compare Adapmin to the algorithm of Brakerski et al.. Chen and Huang (2008) propose an efficient algorithm of requested periodicities with high density and large variance.

For perfect periodic scheduling with identical processing times, Bar-Noy et al. (2004) consider two objective measures of maximum and weighted average ratios between the allocated periodicity and requested periodicity. They present a few efficient heuristic algorithms using a methodology, called tree scheduling, based on an hierarchical round-robin approach, where the hierarchy is a form of tree. Bar-Noy et al. (2002b) develop tree-based approximation algorithms for perfect periodic scheduling with the objective of minimising weighted average ratios between the allocated periodicity and requested periodicity. Brakerski et al. (2003) study the question of dispatching in a perfect periodic schedule, namely how to find the next item to schedule, assuming that the schedule is already given somehow.

All of the above approaches to finding a perfect periodic schedule are limited in the range of schedules which they consider. For example, tree scheduling algorithms (Bar-Noy et al. 2002b; Brakerski et al. 2003) restrict their solution space to a set of periodicities with a non-trivial greatest common divisor. Moreover, Brakerski et al. (2006), Patil and Garg (2006), and Chen and Huang (2008) constrain solutions to those for which the ratio between any pair of two allocated periodicities is a power of 2. Thus, further improvements in heuristics depend upon being able to establish perfect periodic schedules with a wider range of periodicities. Additional motivation for developing our understanding of perfect period scheduling, arises in the context of wireless mesh networks where the response time variability in transmissions, known as jitter, is an important issue. Jitter relates to quality of reception and is measured by total response time variation as well as the ”bottleneck metric,” of maximum deviation from an ideal interval, identified by Steiner and Yeomans (1993). Corominas et al. (2007) provide effective heuristics for measures which prove to be optimal for the case of two tasks. However, they avoid attempts to find solutions with no interval variation, which are perfectly periodic, because of ”the serious practical disadvantage \(\ldots \) that there may not be a feasible solution.”

The aim of this paper is to address the issue of feasibility for perfect periodic scheduling problem on a single resource. We restrict our attention to problems with identical task durations and at most three distinct periodicities in total. Observe that the focus on tasks with identical durations is generally no limitation in the packet scheduling environment of wireless networks. Current practice is to use a common cycle time to co-ordinate packet scheduling (Quintas and Friderikos 2012). Thus, any methodology which facilitates variety in periodicities infers enhanced flexibility and thus potential additional energy savings for network operators. In the context of a wireless network with homogeneous link bandwidth, transmission time for a data packet is uniform throughout the network, and time may thus be divided into unit slots accordingly for scheduling purposes. Our dual contributions are to provide a test of feasibility and a method for constructing a feasible schedule (when one exists).

This article contributes to a broader programme of research into energy efficient scheduling for WMNs using time slot models. A complementary algorithm for coordinating given periodic schedules at mesh nodes with data transmission through the routing tree of the access network is provided by Allen et al. (2012a), and demonstrated on simple networks. Then, for routing trees with a binary structure, Kim and Glass (2012) develop a perfect periodic scheduling methodology for efficiently transmitting data through the access network, while providing the local clients at a mesh node with a common scheduling cycle. For a general routing tree, Allen et al. (2012b) introduce an integer programming formulation to describe an optimised schedule with time slots, and a fast heuristic approximation which produces near-optimal solutions. They additionally explore the potential for increasing throughput in a wireless mesh network by varying transmission rates at individual links, taking account of signal interference.

The remainder of the paper is structured as follows. The problem itself is formulated in purely mathematical terms in the next section. Our results rely only upon classic properties in modulo arithmetic, which are included for completeness. We then analyse the case of two distinct periodicities in Sect. 3. We establish a closed form test for the existence of a perfect periodic schedule, and in doing so indicate the structure of a feasible solution. Section 4 provides similar results for the case of three periodicities. Various cases are analysed, resulting in a test for feasibility which runs in \(O(n^4)\) time, where \(n\) is the total number of clients, in the last subsection. The construction of a feasible solution itself, where one exists, is presented explicitly in Sect. 6. A few concluding remarks are then offered in Sect. 7. For convenience, the remainder of the paper is framed in the telecommunications context of “service” to “clients,” and not in the alternative machine scheduling terminology of “processing” of “jobs.”

2 Problem formulation and background results

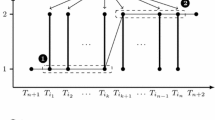
In order to understand the difficulty of devising perfectly period schedules consider the following small examples with only two clients. First suppose that each client requests a periodicity of 2. In this case, their requests can be accommodated by scheduling one client in the odd numbered time slots and the other in even numbered time slots, although there would be no residual capacity for any other client. If, however, one of the clients reduces their demand by a half to periodicity 3, then there would appear to be residual capacity, but in fact the problem becomes impossible to solve rather than easier, as illustrated in Fig. 1. By contract, there is no difficulty in scheduling two clients with longer periodicities of 6 and 9 time slots without overlap, as illustrated in Fig. 2. It is thus the relationship between the periodicities, and not simply their total effective capacity requirement, which determines whether a feasible schedule can be constructed.

Fig. 1
figure 1

The only possible, infeasible, schedule for two clients with periodicities 2 and 3, respectively

Full size image
Fig. 2
figure 2

A feasible schedule for two clients with periodicities 6 and 9, respectively

Full size image

The problem of finding a Perfect Periodic Schedule with unit service (or processing) times is generally formulated as follows. We use \(R(a, b)\) to denote the remainder function of two positive integers, \(a\) and \(b\), that is, \(R(a, b) = a- b\left\lfloor a/b\right\rfloor \).

Given a set of clients with associated service periodicity \(q_i \in \mathbb{N }\) for \(i=1, \dots , n\), find time slot \(\tau _{i}\) for which the following time slots are distinct:

$$\begin{aligned} \tau _{i}^{(k)} = R(\tau _{i}, q_i) + (k-1)q_i,\; k \in \mathbb{N } \end{aligned}$$

for \(1 \le i\le n\).

However, as we consider a restricted number of periodicities, it is more efficient for us to employ High Multiplicity encoding Brauner et al. (2005).

PPS1: Given a set of \(n_i\) clients with associated service periodicity \(q_i\) for \(i=1, \ldots , m\) (with \(n_i, q_i \in \mathbb{N }\)), find time slot \(\tau _{ij}\) for which the following time slots are distinct:

$$\begin{aligned} \tau _{ij}^{(k)} = R(\tau _{ij}, q_i) + (k-1)q_i,\; k \in \mathbb{N } \end{aligned}$$

for \(0\le j\le n_i-1\) and \(1\le i \le m\).

The above high multiplicity formulation has input data: \(m, q_1, \dots , q_m, n_1, \dots , n_m\) which may be encoded in\(O(m \log q_{\max })\) steps, where \(q_{\max } = \max _{1\le i\le m}q_i\) (since instances are restricted to having \(n_i < q_i\) to avoid obvious infeasibility). A drawback of this super-efficient encoding is that it does not afford a polynomial time solution algorithm since describing a solution, \(\tau _{ij}\), takes more than polynomial time in the input variables. Thus, PPS cannot belong to P nor NP under high multiplicity encoding. However, the problem in terms of the standard encoding, with input variables \(n, q_1, \dots , q_n\) , is known to be NP-hard from Bar-Noy et al. (2002a) as mentioned above. It is therefore sensible to evaluate the computational complexity of a solution procedure in terms of the standard encoding.

In the PPS1 scenario, any feasible schedule is periodic and the length of the period, \(T\), is the least common multiple of \(q_i\) for all \(i=1, \dots , m\), \(lcm(q_1, \dots , q_m)\). Service to a client with periodicity \(q_i\) is repeated \(lcm(q_1, \dots , q_m)/q_i\) times within the overall period \(T\), for each \(i\). It is sufficient, therefore, to find a feasible schedule over \(T=lcm(q_1, \dots , q_m)\) time slots instead of over the infinite horizon. Many results relating to PPS1 are based on classic properties of congruences from Number Theory. Let \(gcd(a, b)\) denote the greatest common divisor of integers \(a\) and \(b\).

Chinese Remainder Theorem

Let \(a_1\) and \(a_2\) be positive integers, and \(b_1\) and \(b_2\) be any integers. Then, the simultaneous congruences \(t \equiv {b_1}\; \text{ mod }\; {a_1}\; \text{ and }\; t \equiv b_2\; \text{ mod }\; a_2\) have a solution if and only if \(gcd(a_1, a_2)\) divides \(b_1 - b_2\).

The following result follows directly from the Chinese Remainder Theorem as observed by Bar-Noy et al. (2002a, Lemma 12).

Lemma 1

A solution is feasible if and only if \(\tau _{ij} \not \equiv \tau _{i^{\prime }j^{\prime }} \; \text{ mod }\; gcd(q_i, q_{i^{\prime }})\) for \(i \ne i^{\prime }\) or \(j \ne j^{\prime }\).

By Lemma 1, there is no feasible schedule for any set of periodicities \(q_1, \dots , q_m\) which contains a pair of periodicities, \(q_i\) and \(q_{i^{\prime }}\) which are coprime, i.e. \(gcd(q_i, q_{i^{\prime }})=1\). Congruence results have a direct relationship to the theory of linear Diophantine equations (eg. \(a_1x + a_2y =b\)). In this equation form, the following result was used as long ago as 1st century AD (eg. by Indian mathematician Brahmagupta, around AD 628) Jones and Jones (1998).

Lemma 2

$$\begin{aligned} a_1x \equiv b\; \text{ mod }\, a_2 \end{aligned}$$

has a solution if and only if \(gcd(a_1, a_2)\) divides \(b\).

3 Two distinct periodicities

In this section, we study the case when there are two distinct periodicities. A test of existence of a feasible schedule is provided in Theorem 1 and a schedule construction in its proof. Throughout this section, we use a partition \({\varvec{\Lambda }}\) of time slots \(\{0, \dots , lcm(q_1, q_2)-1\}\) into sets \(\Lambda _l = \{t \; | \;t \equiv l\; \text{ mod }\; gcd(q_1, q_2), 0\le t \le lcm(q_1, q_2)-1\}\) for \(l=0, \dots , gcd(q_1, q_2)-1\). We refer to the time slot \(l+p\cdot gcd(q_1, q_2)\) in \(\Lambda _l\) as position \(p\) in \(\Lambda _l\).

Note that \(|\Lambda _l| = lcm(q_1, q_2)/gcd(q_1, q_2)\) for \(l=0, \dots , gcd(q_1, q_2)-1\), and a client with the periodicity of \(q_i\) is repeated \(lcm(q_1, q_2)/q_i\) time in \(T = lcm(q_1, q_2)\), from which the following observation follows.

Lemma 3

Up to \(q_i/gcd(q_1, q_2)\) clients with the periodicity of \(q_i\) for \(i=1, 2\) may be serviced in a single \({\varvec{\Lambda }}\)-set, and a client is serviced in just one \({\varvec{\Lambda }}\)-set.

Proof

Observe that the difference between any two consecutive time slots in each \({\varvec{\Lambda }}\)-set is \(gcd(q_1, q_2)\). Since \(gcd(q_1, q_2)\) divides both \(q_1\) and \(q_2\), each client has to be serviced in only one of \({\varvec{\Lambda }}\)-sets. Moreover, the services for a client with the periodicity of \(q_i\) occur in every \(q_i / gcd(q_1, q_2)\) time slots in a single \({\varvec{\Lambda }}\)-set. Thus, up to \(q_i/gcd(q_1, q_2)\) clients with the periodicity of \(q_i\) can be serviced in a single \({\varvec{\Lambda }}\)-set. \(\square \)

Lemma 4

Any two clients whose periodicities differ cannot be scheduled in the same \({\varvec{\Lambda }}-\)set.

Proof

Clients \(j\) and \(j^{\prime }\) with periodicities \(q_1\) and \(q_2\), respectively, can be scheduled only if \(\tau _{1j} \not \equiv \tau _{2j^{\prime }} \; \text{ mod }\; gcd(q_1, q_2)\) by Lemma 1, and hence any two clients with different periodicities cannot be scheduled in the same \({\varvec{\Lambda }}\)-set. \(\square \)

Theorem 1

An instance with two distinct periodicities, \(q_1\) and \(q_2\) with \(n_1\) and \(n_2\) clients, respectively, is perfect periodically schedulable if and only if

$$\begin{aligned} \left\lceil \frac{n_1}{q_1/gcd(q_1, q_2)}\right\rceil \!+\! \left\lceil \frac{n_2}{q_2/gcd(q_1, q_2)}\right\rceil&\!\le \!&gcd(q_1, q_2).\nonumber \\ \end{aligned}$$
(1)

Proof

\((\Rightarrow )\) From Lemma 3, the number of \({\varvec{\Lambda }}\)-sets required for scheduling \(n_i\) clients with the periodicity of \(q_i\) is \(\left\lceil n_i/ (q_i/gcd(q_1, q_2))\right\rceil \) for \(i=1,2\). Thus, by Lemma 4, the instance is schedulable only if

$$\begin{aligned} \left\lceil \frac{n_1}{q_1/gcd(q_1, q_2)}\right\rceil + \left\lceil \frac{n_2}{q_2/gcd(q_1, q_2)}\right\rceil \le gcd(q_1, q_2). \end{aligned}$$

\((\Leftarrow )\) We now construct a feasible solution for an instance satisfying the condition (1). We determine the first time slot in which client \(j\) with the periodicity of \(q_i\) is serviced, \(\tau _{ij}\), as follows. Let

$$\begin{aligned} \tau _{1j}&= \left\lfloor \frac{j}{q_1/gcd(q_1, q_2)} \right\rfloor \nonumber \\&+R\left( j, \frac{q_1}{gcd(q_1, q_2)}\right) gcd(q_1, q_2) \end{aligned}$$
(2)

for \(j=0, \dots , n_1-1\), and

$$\begin{aligned} \tau _{2j}&= \left\lceil \frac{n_1}{q_1/gcd(q_1, q_2)}\right\rceil + \left\lfloor \frac{j}{q_2/gcd(q_1, q_2)} \right\rfloor \nonumber \\&+ R\left( j, \frac{q_2}{gcd(q_1, q_2)}\right) gcd(q_1, q_2) \end{aligned}$$
(3)

for \(j=0, \dots , n_2-1\).

We now show that the time slots allocated by (2) and (3) provide a feasible solution. From Lemma 1, it is sufficient to prove that \(\tau _{ij} \not \equiv \tau _{i^{\prime }j^{\prime }} \; \text{ mod }\; gcd(q_i, q_{i^{\prime }}) \) for \(i \ne i^{\prime }\) or \(j \ne j^{\prime }\). Take the case when \(i=1\), \(i^{\prime }=2\), \(0 \le j_1 \le n_1 -1\) and \(0 \le j_2 \le n_2 -1\), and consider \(\tau _{1j_1}\), \(\tau _{2j_2}\) modulo \(gcd(q_1, q_2)\). From (2) and (3),

$$\begin{aligned} 0&\le \left\lfloor \frac{j_1}{q_1/gcd(q_1, q_2)} \right\rfloor < \left\lceil \frac{n_1}{q_1/gcd(q_1, q_2)} \right\rceil \\&\le \left\lceil \frac{n_1}{q_1/gcd(q_1, q_2)} \right\rceil +\left\lfloor \frac{j_2}{q_2/gcd(q_1, q_2)} \right\rfloor \end{aligned}$$

and

$$\begin{aligned} 0&< \left\lfloor \frac{j_2}{q_2/gcd(q_1, q_2)} \right\rfloor \le \left\lfloor \frac{n_2-1}{q_2/gcd(q_1, q_2)} \right\rfloor \\&\le \left\lceil \frac{n_2}{q_2/gcd(q_1, q_2)} \right\rceil - 1. \end{aligned}$$

Thus,

$$\begin{aligned} 0&\le \left\lfloor \frac{j_1}{q_1/gcd(q_1, q_2)} \right\rfloor \\&< \left\lceil \frac{n_1}{q_1/gcd(q_1, q_2)} \right\rceil +\left\lfloor \frac{j_2}{q_2/gcd(q_1, q_2)} \right\rfloor \\&< \left\lceil \frac{n_1}{q_1/gcd(q_1, q_2)} \right\rceil + \left\lceil \frac{n_2}{q_2/gcd(q_1, q_2)} \right\rceil -1 \\&\le gcd(q_1, q_2)-1 \end{aligned}$$

since (1) holds. Thus, \(\tau _{1j_1} \not \equiv \tau _{2j_2} \; \text{ mod }\; gcd(q_1, q_{2})\) as claimed.

It remains to show that \(\tau _{ij} \equiv \tau _{ij^{\prime }} \; \text{ mod }\; q_i\) implies that \(j=j^{\prime }\) for \(i=1,2\). Consider the case with \(i=1\). Observe that

$$\begin{aligned} 0&\le R\left( j, \frac{q_1}{gcd(q_1, q_2)}\right) \le \frac{q_1}{gcd(q_1, q_2)} - 1,\; \text{ and }\\ 0&\le \left\lfloor \frac{j}{q_1/gcd(q_1, q_2)} \right\rfloor < gcd(q_1, q_2) \end{aligned}$$

from above. Thus,

$$\begin{aligned} 0&\le \tau _{1j}\\&= \left\lfloor \frac{j}{q_1/gcd(q_1, q_2)} \right\rfloor + R\left( j, \frac{q_1}{gcd(q_1, q_2)}\right) gcd(q_1, q_2) \\&< gcd(q_1, q_2) + \left( \frac{q_1}{gcd(q_1, q_2)} - 1\right) gcd(q_1, q_2)\\&\le q_1 \end{aligned}$$

for each \(j=0, \dots , n_1-1\), showing that distinct \(\tau _{ij}\) values cannot be congruent modulo \(q_1\). A similar argument holds for the case with \(i=2\), completing the proof. \(\square \)

In the feasible solution described above, the clients with the periodicity of \(q_1\) are scheduled in \(\Lambda _l\) for \(l=0, \dots , \) \(\left\lceil n_1/(q_1/gcd(q_1, q_2))\right\rceil -1\), and the clients with periodicity of \(q_2\) in \(\Lambda _l\) for \(l=\left\lceil n_1/(q_1/gcd(q_1, q_2))\right\rceil , \dots ,\) \(\left\lceil n_1/(q_1/gcd(q_1, q_2))\right\rceil +\left\lceil n_2/(q_2/gcd(q_1, q_2))\right\rceil -1\). The following example illustrates the construction of a perfect periodic schedule described in Theorem 1.

Example 1

Consider the case of two periodicities \(q_1=6\) and \(q_2=9\) with \(n_1=3\) and \(n_2=2\), respectively. This instance satisfies criterion (1) for the schedulability, since

$$\begin{aligned}&\left\lceil \frac{n_1}{q_1/gcd(q_1, q_2)}\right\rceil + \left\lceil \frac{n_2}{q_2/gcd(q_1, q_2)}\right\rceil \\&\quad \quad = \left\lceil \frac{3}{2} \right\rceil + \left\lceil \frac{2}{3}\right\rceil = 3 \le 3 = gcd(q_1, q_2). \end{aligned}$$

Following the construction of the above proof, we calculate the first time slots in which each client is serviced using (2) and (3) as follows:

$$\begin{aligned} \tau _{10}&= \left\lfloor 0/2 \right\rfloor +R(0,2)3\;=\;0\\ \tau _{11}&= \left\lfloor 1/2 \right\rfloor +R(1,2)3\;=\;3\\ \tau _{12}&= \left\lfloor 2/2 \right\rfloor +R(2,2)3\;=\;1\\ \tau _{20}&= \left\lceil 3/2 \right\rceil + \left\lfloor 0/3 \right\rfloor +R(0,3)3\;=\;2\\ \tau _{21}&= \left\lceil 3/2 \right\rceil + \left\lfloor 1/3 \right\rfloor +R(1,3)3\;=\;5. \end{aligned}$$

Therefore, the first client with the periodicity of \(q_1\) is serviced in the set of time slots \(\{0, 6, 12\}\), and the second and third in the set of time slots \(\{3, 9, 15\}\) and in the set of time slots \(\{1, 7, 13\}\), respectively. Similarly, the first client with the periodicity of \(q_2\) is serviced in the set of time slots \(\{2, 11\}\), and second client with the periodicity of \(q_2\) in the set of time slots \(\{5, 14\}\). A single complete period of length (\(T=18\)) of feasible schedule is depicted in Fig. 3a and its partition into \({\varvec{\Lambda }}\)-sets in Fig. 3b.

Fig. 3
figure 3

A solution for Example 1 a schedule in [0, \(T-1\)], b partition of schedule into \({\varvec{\Lambda }}\)-set

Full size image

4 Theoretical results for three distinct periodicities

In this section, we study the existence of a feasible solution where there are three distinct periodicities, \(q_1,\;q_2\) and \(q_3\). It is convenient to identify the factors of the periodicities, \(q_1\), \(q_2\) and \(q_3\). Let \(g = gcd(q_1, q_2, q_3),\;g_{12} = gcd(q_1, q_2)/g,\;g_{23} \!=\! gcd(q_2, q_3)/g,\;g_{31} \!=\! gcd(q_3, q_1)/g\), \(g_{10} = q_1/(gg_{12}g_{31}),\;g_{20} = q_2/(gg_{23}g_{12})\), and \(g_{30} = q_3/(gg_{31}g_{23})\). Thus, the periodicities are presented as \(q_1 = gg_{10}g_{12}g_{31}\), \(q_2 = gg_{20}g_{12}g_{23}\) and \(q_3 = gg_{30}g_{23}g_{31}\). Observe that integers in sets \(\{g_{10}, g_{20}, g_{30}\}\), \(\{g_{12}, g_{23}, g_{31}\}\), \(\{g_{10}, g_{23}\}\), \(\{g_{20}, g_{31}\}\) and \(\{g_{30}, g_{12}\}\) are coprime within each set but not necessarily coprime to \(g\) nor between sets. We first show that any instance can be reduced to one in which \(g_{i0} = 1\) for \(i=1, 2, 3\) in Sect. 4.1. Then, we consider the case when \(g_{i0} =1\) for \(i=1, 2, 3\) and \(gcd(q_1, q_2, q_3) =1\) in Sect. 4.2, and we later extend the results to general periodicities in Sects. 4.3 and 5.

4.1 Problem reduction

The following theorem shows how an instance can be reduced to an instance with \(g_{i0} = 1\) by letting \(n_i^{\prime } = \lceil n_i /g_{i0} \rceil \) and \(q_i^{\prime } = q_i /g_{i0}\) for \(i = 1, 2, 3\). The proof relies on a congruence relationship given in Lemma 5 below.

Theorem 2

An instance with \(n_1\), \(n_2\), \(n_3\) clients with the periodicity of \(q_1\), \(q_2\), \(q_3\), respectively, is feasible if and only if there is a feasible perfect periodic schedule for \(\left\lceil n_i/g_{i0} \right\rceil \) clients with a periodicity of \(q_i/g_{i0}\) for \(i=1, 2, 3\).

Proof

(\(\Rightarrow \)) Take a feasible schedule. If a client with the periodicity of \(q_2\) or \(q_3\) is serviced in a time slot \(t\), then it is also serviced in time slots \(t+ hT/g_{10}\), for \(h=0, \dots , g_{10}-1\), since both \(q_2\) and \(q_3\) divide \(T/g_{10}\). Hence, the subschedule consisting of clients with the periodicity of \(q_2\) or \(q_3\) has periodicity \(T/g_{10}\) and is repeated \(g_{10}\) times within the overall period \(T\) of the three periodicities. Now by Lemma 5, a client, say \(j\), with the periodicity of \(q_1\) occupies time slots \(\tau _{1j} + hq_1/g_{10}\) for \(h=0, \dots , \left( T/q_1\right) -1\) within the period \(T^{\prime } = \{0, \dots , T/g_{10}-1\}\). Moreover, no client with the periodicity of \(q_2\) or \(q_3\) can be serviced in these time slots. Thus, up to \(g_{10}\) clients with the periodicity of \(q_1\) can be scheduled in these time slots, i.e. \(\{t \; | \;t \equiv \tau _{1j}+ hq_1/g_{10}\, \text{ mod }\, T/g_{10}, 0 \le h \le T/q_1-1\}\). From this perspective, feasibility depends upon \(\left\lceil n_1/g_{10} \right\rceil \), but not on \(n_1\) itself. Therefore, repeating this argument for \(i=1, 2, 3\), any instance can be reduced to an instance with \(g_{i0} = 1\) by letting \(n_i^{\prime } = \lceil n_i /g_{i0} \rceil \) and \(q_i^{\prime } = q_i /g_{i0}\) for \(i = 1, \dots , 3\).

(\(\Leftarrow \)) Given a feasible schedule for the reduced problem, i.e. \(\tau ^{\prime }_{ij}\) for \(i=1, 2, 3\), \(j=0, \dots , \lceil n_i /g_{i0} \rceil - 1,\) set initial time slots for clients in the original problem as follows:

$$\begin{aligned} \tau _{ij} = \tau ^{\prime }_{i \lfloor j/g_{i0}\rfloor } + R(j, g_{i0})(q_i/g_{i0}) \end{aligned}$$
(4)

for \(i=1, 2, 3\), \(j=0, \dots , n_{i}-1\). We now show that the schedule implied by (4) provides a feasible solution.

From Lemma 1, it is sufficient to prove that \(\tau _{ij} \not \equiv \tau _{i^{\prime }j^{\prime }} \; \text{ mod }\; gcd(q_i, q_{i^{\prime }}) \) for \(i \ne i^{\prime }\) or \(j \ne j^{\prime }\). Suppose otherwise. Then there are non-identical pairs \(i\), \(j\) and \(i^{\prime }\), \(j^{\prime }\) for which \(\tau _{ij} \equiv \tau _{i^{\prime }j^{\prime }} \; \text{ mod }\; gcd(q_i, q_{i^{\prime }})\). However, if \(i=i^{\prime }\), then

$$\begin{aligned} \tau ^{\prime }_{ij} - \tau ^{\prime }_{ij^{\prime }} \equiv \left( R\left( j^{\prime }, g_{i0}\right) - R\left( j, g_{i0}\right) \right) \left( q_i/g_{i0} \right) \; \text{ mod }\; q_i \end{aligned}$$

implying that \(\tau ^{\prime }_{ij} \equiv \tau ^{\prime }_{ij^{\prime }} \; \text{ mod }\; q_i\), and hence that \(j = j^{\prime }\), by Lemma 1 and feasible of schedule \(i\). On the other hand, if \(i \ne i^{\prime }\), \(i=1\) and \(i^{\prime }=2\) say, then

$$\begin{aligned}\tau ^{\prime }_{1 \left\lfloor j/q_{10} \right\rfloor }-\tau ^{\prime }_{2 \left\lfloor j^{\prime }/q_{20} \right\rfloor }&\equiv R\left( j^{\prime }, g_{20}\right) g_{12}g_{23} \\&- R\left( j, g_{10}\right) g_{12}g_{13} \; \text{ mod }\; q_{12} \end{aligned}$$

implying that \(\tau ^{\prime }_{1 \left\lfloor j/q_{10} \right\rfloor } \equiv \tau ^{\prime }_{2 \left\lfloor j/q_{20} \right\rfloor } \; \text{ mod }\; gcd(q^{\prime }_1, g^{\prime }_2)\) since \(gcd(q^{\prime }_1, g^{\prime }_2)=gcd(q_1, g_2)=g_{12}\). This provides the required contradiction, from Lemma 1 and feasibility of \(i\). \(\square \)

Lemma 5

The following sets are congruent modulo \(T/g_{i0}\)

$$\begin{aligned} \{kq_i \; | \;k\!\!=\!\!0, \!\dots \!, T/q_i\!-\!1\}\,\text{ and }\, \{k^{\prime }q_i/g_{i0} \; | \;k^{\prime }\!=\!0, \!\dots \!, T/q_i\!\!-\!\!1\} \end{aligned}$$

for \(i=1, 2, 3\).

Proof

Consider the expression \(kq_1 \equiv k^{\prime }q_1/g_{10}\, \text{ mod } \, T/g_{10}\). Since \(g_{12}g_{31}\) divides \(q_1\), \(q_1/g_{10}\) and \(T/g_{10}\), this is equivalent to \(kq_1/(g_{12}g_{31}) \equiv k^{\prime }q_1/(g_{10}g_{12}g_{31})\, \text{ mod }\,\) \( T/(g_{10}g_{12}g_{31})\), that is, \(kg_{10} \equiv k^{\prime }\, \text{ mod }\, g_{20}g_{30}g_{23}\) for \(0 \le k, k^{\prime } \le g_{20}g_{30}g_{23}-1\). Thus, it is sufficient to show that \(\Gamma = \{t \; | \;t \equiv kg_{10}\, \text{ mod }\, g_{20}g_{30}g_{23},\; 0 \le k \le g_{20}g_{30}g_{23} - 1\} = \{0, 1, \dots , g_{20}g_{30}g_{23} - 1\}\). Suppose otherwise, then \(|\Gamma | < g_{20}g_{30}g_{23}\), and there must exist \(k\) and \(k^{\prime }\), \(k \ne k^{\prime }\), such that \(g_{10}k \equiv g_{10}k^{\prime }\, \text{ mod }\, g_{20}g_{30}g_{23}\) where \(0 \le k, k^{\prime } \le g_{20}g_{30}g_{23}-1\). Then, \(g_{10}k - g_{10}k^{\prime }= g_{10}(k-k^{\prime }) \equiv 0 \, \text{ mod }\, g_{20}g_{30}g_{23}\). Since \(g_{10}\) and \(g_{20}g_{30}g_{23}\) are coprime, this implies that \(k-k^{\prime } \equiv 0 \, \text{ mod }\, g_{20}g_{30}g_{23}\), which cannot hold for the given choice of \(k\) and \(k^{\prime }\), giving the required contradiction. A similar argument can be applied for \(i=2,3\). \(\square \)

4.2 Special case of \(gcd(q_1, q_2, q_3)=1\), for the reduced problem

While the analysis in this section focuses of \(q_3\), the choice is purely arbitrary. We assume that \(g=1\) and \(g_{i0} = 1\) for \(i = 1, 2, 3\), and thus \(T=lcm(q_1, q_2, q_3)=g_{12}g_{23}g_{31}\). Take a partition \({\varvec{\Delta }}\) of time slots \(\{0, 1, \dots , T-1\}\) into sets \(\Delta _l = \{t \; | \;t \equiv l\; \text{ mod }\; g_{12}, 0\le t \le T-1\}\) for \(l=0, \dots , g_{12}-1\). We refer to the time slot \(l+pg_{12}\) in \(\Delta _l\) as position \(p\) in \(\Delta _l\). Observe that \(|\Delta _l| = T/g_{12} = g_{23}g_{31}\) for \(l=0, \dots , g_{12}-1\).

Lemma 6

Each client with the periodicity of \(q_1\) or \(q_2\) receives all its service slots in the same \({\varvec{\Delta }}\)-set. Moreover, no \({\varvec{\Delta }}\)-set accommodates both a client with the periodicity of \(q_1\) and a client with the periodicity of \(q_2\).

Proof

Observe that \(g_{12}\) is the difference between any two consecutive time slots in each \({\varvec{\Delta }}\)-set. Since \(g_{12}\) divides both \(q_1\) and \(q_2\), each client with the periodicity of \(q_1\) or \(q_2\) has to be serviced in a single \({\varvec{\Delta }}\)-set. Moreover, clients \(j\) and \(j^{\prime }\) with the periodicities of \(q_1\) and \(q_2\), respectively, are simultaneously scheduled if and only if \(\tau _{1j} \not \equiv \tau _{2j^{\prime }} \text{ mod } g_{12}\) by Lemma 1, and hence any two clients with the periodicities of \(q_1\) and \(q_2\) cannot be scheduled in the same \({\varvec{\Delta }}\)-set. \(\square \)

The partition \({\varvec{\Delta }}\) of time slots thus enable us to view the schedule of service to clients with the periodicities of \(q_1\) and \(q_2\) independently. We now consider the interplay with clients with the periodicity of \(q_3\). Observe that there is an integer \(\bar{q_3}\), \(1 \le \bar{q_3} \le g_{12}-1\) for which \(q_3\bar{q_3} \equiv 1\, \text{ mod }\, g_{12}\), from Lemma 2 since \(gcd(q_3, g_{12})=1\). Let \(p_{3j}^{[l]}\) denote the first position in \(\Delta _l\) of service to client \(j\) with the periodicity of \(q_3\) corresponding to time slot \(l + p_{3j}^{[l]}g_{12}\).

Lemma 7

In a feasible schedule for any instance with three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\), with \(g=1\) and \(g_{i0}=1\) for \(i=1, 2, 3\), any client \(j\) with the periodicity of \(q_3\) is serviced exactly once in each set \(\Delta _l\) for \(l=0, \dots , g_{12}-1\). Moreover, then its position in \(\Delta _l\) is given by

$$\begin{aligned} p_{3j}^{[l]} = R(\tau _{3j}/g_{12}+ l(q_3\bar{q_3}-1)/g_{12}, q_3) \end{aligned}$$

where \(\bar{q_3}\) is the integer, \(1 \le \bar{q_3} \le g_{12}-1\), for which \(q_3\bar{q_3} \equiv 1\, \text{ mod }\, g_{12}\), and \(\tau _{3j} \equiv 0 \, \text{ mod }\,g_{12}\).

Proof

We first show that any client with the periodicity of \(q_3\) is serviced exactly once in each \({\varvec{\Delta }}\)-set. To that end, it is sufficient to show that \(\Gamma =\{\tau _{3j} + q_3k\, \text{ mod }\, g_{12} \; | \;k=0, 1, \dots , g_{12}-1\}=\{0, 1, \dots , g_{12}-1\}\). Suppose otherwise, then \(|\Gamma | < g_{12}\), and there must exist \(k\) and \(k^{\prime }\), \(k \ne k^{\prime }\), \(0 \le k, k^{\prime } \le g_{12}-1\) such that \(\tau _{3j}+q_3k \equiv \tau _{3j}+q_3k^{\prime }\, \text{ mod }\, g_{12}\). Thus, \(q_3(k-k^{\prime }) \equiv 0 \, \text{ mod }\, g_{12}\). Since \(q_3\) and \(g_{12}\) are coprime, this implies that \(k-k^{\prime } \equiv 0 \, \text{ mod }\, g_{12}\), which contradicts the given choice of \(k\) and \(k^{\prime }\) by \(|k - k^{\prime }| < g_{12}\).

Since service is cyclic and \(\{\tau _{3j}^{(k)} \; | \;k=0, \ldots , g_{12}-1\}\) covers all elements in set \(\{\Delta _{l} \; | \;l=0, \ldots , g_{12}-1\}\), we may assume without loss of generality that \(\tau _{3j} \equiv 0 \, \text{ mod }\, g_{12}\), and so \(\tau _{3j} \in \Delta _{0}\). Thus, \(\tau _{3j}^{(k)} = \tau _{3j} + kq_3 \equiv l \, \text{ mod }\, g_{12}\) for \(k \equiv l\bar{q_3} \, \text{ mod }\, g_{12}\). Then, the position of service to client \(j\) with the periodicity of \(q_3\) in set \(\Delta _{l}\) is

$$\begin{aligned} p_{3j}^{[l]}&= R((\tau _{3j}^{(k)} - l)/g_{12}, q_3)\\&= R((\tau _{3j} + lq_3\bar{q_3} - l)/g_{12}, q_3)\\&= R(\tau _{3j}/g_{12}+ l(q_3\bar{q_3}-1)/g_{12}, q_3) \end{aligned}$$

for \(j=0, \ldots , n_3\) and \(l=0, \ldots , g_{12}-1\). \(\square \)

By Lemma 7, we assume without loss of generality that \(\tau _{3j} \in \Delta _{0}\), and hence the position of subsequent services to a client \(j\) with the periodicity of \(q_3\) within a set \(\Delta _l\) depends only on \(l\) and not on \(k\). We therefore introduce the concept of relative position within a \(\Delta _l\) set as

$$\begin{aligned} \widehat{p} = p - l(q_3\bar{q_3}-1)/g_{12} \end{aligned}$$

taken modulo \(q_3\), where the original position \(p\) within the set corresponds to time slot \(l + pg_{12}\). Thus, we can rearrange time slots in each set \(\Delta _{l}\), so that any client with the periodicity of \(q_3\) appears to be serviced in the same relative position in all \(\Delta _{l}\)’s by putting time slot \(R(lq_3\bar{q_3}, T)\) in the first position of set \(\Delta _{l}\). Figure 4 depicts the procedure when \(q_1 =12\), \(q_2 =20\) and \(q_3 =15\) i.e. \(g_{12}=4\), \(g_{23}=5\) and \(g_{31}=3\), and \(n_3 =4\).

Fig. 4
figure 4

Rearranging time slots in each \(\Delta _l\) with respect to \(q_3\)

Full size image

Corollary 1

Each client with the periodicity of \(q_3\) occupies the same single relative position in each of the \({\varvec{\Delta }}\)-sets, i.e.

$$\begin{aligned} \widehat{p}_{3j}^{[l]} = R( \tau _{3j}/g_{12}, q_3)\, \text{ for }\, l=0, \dots , g_{12}-1. \end{aligned}$$

For any feasible schedule, a relative position \(\widehat{p}\) is referred to as free if no client with the periodicity of \(q_1\) or \(q_2\) is serviced in the \(p\)th relative position of any of the \({\varvec{\Delta }}\)-sets. Hence, in a feasible schedule, the number of free relative positions is at least as great as \(n_3\) because a client with the periodicity of \(q_3\) is serviced in a particular relative position of each of the \({\varvec{\Delta }}\)-sets by Corollary 1. In order to establish the precise condition for accommodating \(n_3\) clients with the periodicity of \(q_3\) in Theorem 3, we now examine the interplay between (relative) positions occupied by clients with the periodicities of \(q_1\) or \(q_2\).

Lemma 8

In a feasible schedule for any instance with three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\), with \(g=1\) and \(g_{i0}=1\) for \(i=1, 2, 3\), for any pair of clients, one with the periodicity of \(q_1\) and the other with the periodicity of \(q_2\), there exist precisely one position in which both clients are serviced.

Proof

Take a client \(j_1\) with the periodicity of \(q_1\) and a client \(j_2\) with the periodicity of \(q_2\). If there is no position which serves both clients, then both clients can be serviced in same set, which contradicts to the results of Lemma 1.

If there is more than one position within \(T\) which serves the two given clients, then there exist integers \(k_1\), \(k^{\prime }_1\), \(k_2\) and \(k^{\prime }_2\) such that \(\tau _{1j_{1}}^{(k_1)} - l_1 = \tau _{2j_{2}}^{(k_2)} - l_2\) and \(\tau _{1j_{1}}^{(k^{\prime }_1)} - l_1 = \tau _{2j_{2}}^{(k^{\prime }_2)} - l_2\) where \(0 \le k_1, k^{\prime }_1 \le g_{23}\), \(0 \le k_2, k^{\prime }_2 \le g_{31}\), \(k_1 \ne k^{\prime }_1\), \(k_2 \ne k^{\prime }_2\). Thus, \(\tau _{1j_{1}}^{(k_1)} - \tau _{2j_{2}}^{(k_2)} = l_1 - l_2 = \tau _{1j_{1}}^{(k^{\prime }_1)} - \tau _{2j_{2}}^{(k^{\prime }_2)}\), and hence \(k_1q_1 - k_2q_2 = k^{\prime }_1q_1 - k^{\prime }_2q_2\), and therefore \((k_1 - k^{\prime }_1)q_1=(k_2 - k^{\prime }_2)q_2\). Since \(g_{12} > 0\) and \(g_{23}\) is coprime to \(g_{31}\), \(g_{23}\) divides \(|k_1 - k^{\prime }_1|\) and \(g_{31}\) divides \(|k_2 - k^{\prime }_2|\), this implies, for the given range of the \(k\) variables, that \(k_1 = k_1^{\prime }\) and \(k_2 = k_2^{\prime }\) completing the proof. \(\square \)

Corollary 2

Consider an instance of the PPS problem with three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\), with \(g=1\) and \(g_{i0}=1\) for \(i=1, 2, 3\). Suppose that \(\alpha \) clients with the periodicity of \(q_1\) are serviced in a single \({\varvec{\Delta }}\)-set and \(\beta \) clients with the periodicity of \(q_2\) in another \({\varvec{\Delta }}\)-set. Then, there exist precisely \(\alpha \beta \) positions which serve both a client with the periodicities \(q_1\) and a client with the periodicity of \(q_2\).

Proof

From the result of Lemma 8, any pairs of clients with the periodicities of \(q_1\) and \(q_2\) has precisely one position in which both clients are serviced. There are \(\alpha \beta \) different pairs of clients, one with the periodicity of \(q_1\) and the other with the periodicity of \(q_2\). Thus, there are \(\alpha \beta \) positions in which both clients with the periodicities \(q_1\) and \(q_2\) are serviced. \(\square \)

Theorem 3

Consider an instance with clients of each of three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\), with \(g =1\) and \(g_{i0}=1\) for \(i=1, 2, 3\). The instance is schedulable if and only if there exists an integer \(x\), \(1 \le x \le g_{12}-1\) such that

$$\begin{aligned} \left\lceil \frac{n_1}{x}\right\rceil&\le g_{31} -1, \end{aligned}$$
(5)
$$\begin{aligned} \left\lceil \frac{n_2}{g_{12} - x}\right\rceil&\le g_{23} -1,\end{aligned}$$
(6)
$$\begin{aligned} n_3&\le \left( g_{31}- \left\lceil \frac{n_1}{x}\right\rceil \right) \left( g_{23}- \left\lceil \frac{n_2}{g_{12}-x}\right\rceil \right) . \end{aligned}$$
(7)

Proof

\((\Rightarrow )\) Take a feasible solution. Let \(x_i\) denote the number of sets of \({\varvec{\Delta }}\) serving clients with the periodicity of \(q_i\), respectively, for \(i=1, 2\). Let \(\alpha \) and \(\beta \) denote the maximum number of clients with the periodicity of \(q_1\) and \(q_2\), respectively, serviced in a single set in \({\varvec{\Delta }}\). Thus, \(\alpha \ge \left\lceil n_1/x_1\right\rceil \) and \(\beta \ge \left\lceil n_2/x_2 \right\rceil \). Note that \(|\Delta _l| = g_{23}g_{31}\) and that a client with the periodicity of \(q_1\) and \(q_2\) occurs exactly \(g_{23}\) and \(g_{31}\) times, respectively, in a single set in \({\varvec{\Delta }}\). Hence, from the result of Corollary 2, the maximum number of free relative positions in \(\Delta _l\) is

$$\begin{aligned}&g_{23}g_{31} - \left( g_{23}\alpha + g_{31}\beta -\alpha \beta \right) \\&\quad = \left( g_{31}- \alpha \right) \left( g_{23} - \beta \right) \\&\quad \le \left( g_{31}- \left\lceil \frac{n_1}{x_1}\right\rceil \right) \left( g_{23} - \left\lceil \frac{n_2}{x_2}\right\rceil \right) . \end{aligned}$$

Now \(x_2 \le g_{12} \!-\!x_1\) ensures that \(\left\lceil n_2/x_2 \right\rceil \ge \left\lceil n_2/(g_{12}\!-\!x_1) \right\rceil \). Since each \({\varvec{\Delta }}\)-set has at least \(n_3\) time slots to accommodate the \(n_3\) clients with the periodicity of \(q_3\), inequality (7) is satisfied by setting \(x=x_1\). Moreover, since a client with the periodicity of \(q_3\) is serviced once in each \({\varvec{\Delta }}\)-set by Lemma 7, the maximum number of clients with the periodicity of \(q_1\) (or \(q_2\)) in a \({\varvec{\Delta }}\)-set, \(\alpha \) (or \(\beta \)), is at most \(g_{31}-1\) (or \(g_{23}-1\)), implying conditions (5) and (6).

\((\Leftarrow )\) Now suppose that there exists an integer \(x\), \(1 \le x \le g_{12}-1\), satisfying the inequalities, (5), (6) and (7). Let \(\alpha = \left\lceil n_1/x \right\rceil \) and \(\beta = \left\lceil n_2/(g_{12}-x) \right\rceil \). We construct a feasible solution as follows. We schedule the first time slots of the clients with the periodicity of \(q_1\) at

$$\begin{aligned} \tau _{1j}&= R(q_3\bar{q_3}\left\lfloor j/\alpha \right\rfloor + R(j, \alpha )g_{12},\; q_1) \\&= \left\lfloor \frac{j}{\alpha } \right\rfloor + \left( \frac{q_3\bar{q_3} - 1 }{g_{12}}\left\lfloor \frac{j}{\alpha } \right\rfloor + R(j, \alpha ) \right) g_{12}\, {\text{ mod }}\, q_1,\nonumber \end{aligned}$$
(8)

for \(j=0, \ldots , n_1-1\). Observe that client \(j\) with the periodicity of \(q_1\) is in position \(l(q_3\bar{q_3}-1)/g_{12} + R(j, \alpha )\) of set \(\Delta _l\), for \(l=\left\lfloor j / \alpha \right\rfloor \). Thus, there are \(\alpha \) clients with the periodicity of \(q_1\) in each set \(\Delta _l\) for \(l=0, \ldots , x-2\), and the remainder, i.e. \(n_1 - \alpha (x-1)\) clients, in \(\Delta _{x-1}\). The first time slots of the clients with the periodicity of \(q_2\) is placed in time slots

$$\begin{aligned} \tau _{2j} = R(q_3\bar{q_3}\left( x + \left\lfloor j/\beta \right\rfloor \right) + R(j, \beta )g_{12}, \; q_2), \end{aligned}$$
(9)

for \(j=0, \dots , n_2-1\). Client \(j\) with the periodicity of \(q_2\) is therefore in position \(l(q_3\bar{q_3}-1)/g_{12} + R(j, \beta )\) of set \(\Delta _l\), for \(l=x + \left\lfloor j / \beta \right\rfloor \). Thus, there are \(\beta \) clients with the periodicity of \(q_2\) in each set \(\Delta _l\) for \(l=x, \dots , g_{12}-2\), and the remainder, i.e. \(n_2 - \beta (g_{12}-x-1)\), clients in \(\Delta _{g_{12}-1}\).

Then each client with the periodicity of \(q_1\) in \(\Delta _{0}\) occupies \(g_{23} = T/q_1\) positions, and the each client with the periodicity of \(q_2\) in \(\Delta _{x}\) occupies \(g_{31} = T/q_2\) positions. Moreover, the above construction ensures that all clients with the periodicity of \(q_1\) are scheduled in the same relative positions within a set as those in set \(\Delta _{0}\), and all clients with the periodicity of \(q_2\) are in the relative positions used in set \(\Delta _{x}\). It thus follows from Corollary 2 that \(g_{23}\alpha + g_{31}\beta - \alpha \beta \) relative positions are occupied by clients with the periodicities of \(q_1\) and \(q_2\). The remaining \(g_{23}g_{31}- (g_{23}\alpha + g_{31}\beta - \alpha \beta )=(g_{31} -\alpha )(g_{23}-\beta )\) relative positions remain for clients with the periodicity of \(q_3\). From (7), there are at least \(n_3\) such free relative positions and the clients with the periodicity of \(q_3\) may therefore be scheduled as follows. Schedule the first time slot of the client \(j\) with the periodicity of \(q_3\) at

$$\begin{aligned} \tau _{3j} = R(\widehat{p}_{j}g_{12}, q_3) \end{aligned}$$

for \(j=0, \dots , n_3-1\), where \(\widehat{p}_j\) denote \((j+1)\)th free relative position in \(\Delta _{0}\). \(\square \)

Observe that the conditions for feasibility given in Theorem 3 are asymmetric in the three periodicities, which at first sight seems odd. However, the conditions are in fact symmetric in the periodicities as proved in Appendix 1. The following Lemma studies the computational complexity of finding an integer \(x\) referred to in Theorem 3.

Lemma 9

For an instance with three distinct periodicities with \(g =1\) and \(g_{i0}=1\) for \(i=1, 2, 3\), there is a test for feasibility whose computational complexity is \(O(n)\).

Proof

From the result of Theorem 3, the feasibility test can be done in \(O(g_{12})\) steps by examining each integer \(x\), \(1 \le x \le g_{12}-1\) and testing inequality (7). If \(g_{12} \le 2\max \{n_1, n_2\}\), then there are \(O(n)\) operations as claimed since \(\max \{n_1, n_2\} \le n\). On the other hand, if \(g_{12} > 2\max \{n_1, n_2\}\), then set \(x= \max \{n_1, n_2\}\). Then, the inequality (7) reduces to \(n_3 \le \left( g_{31}- 1\right) \left( g_{23}- 1\right) \). As a result, the complexity of feasibility test is \(O(n)\). \(\square \)

The following example illustrates the construction of a perfect periodic schedule described in Theorem 3.

Example 2

Consider the case of three periodicities \(q_1=12\), \(q_2=20\) and \(q_3=15\) (ie. \(g_{12} = 4\), \(g_{23} = 5\) and \(g_{31} = 3\)) with \(n_1=6\), \(n_2=1\) and \(n_3=4\), respectively. This instance is schedulable since taking \(x=3\) satisfies \(x \le 3 = g_{12}-1\) and conditions (5)–(7) of Theorem 3. The construction of the above proof then results in the feasible schedule presented in Fig. 5.

Fig. 5
figure 5

A solution for Example 2 a schedule in [0, \(T-1\)], b partition of schedule into \({\varvec{\Delta }}\)-set

Full size image

4.3 Case of \(gcd(q_1,q_2,q_3) \ge 2\), for the reduced problem

In this section, we consider the more general case of three distinct periodicities when \(g=gcd(q_1, q_2, q_3) \ge 1\), while maintaining the restriction that \(g_{i0} =1\) for \(i=1, 2, 3\). Our focus is that of describing the feasible solution space, which forms the theoretical basis of the test for feasibility presented in Sect. 5 and the algorithm for constructing a feasible solution in Sect. 6.

Throughout this section, we use a partition, \({\varvec{\Lambda }}\), of time slots \(\{0, 1, \dots ,\) \( T-1\}\) into sets \(\Lambda _l = \{t \; | \;t \equiv l\, \text{ mod }\, g, 0\le t \le T-1\}\) for \(l=0, \dots , g-1\). We denote the number of sets serving clients with just one periodicity of \(q_i\) by \(\lambda _i\), the number serving two separate periodicities, \(i\) and \(i^{\prime }\), by \(\lambda _{ii^{\prime }}\), for \(i \ne i^{\prime }\) and \(i, i^{\prime } \in \{1, 2, 3\}\) and the number serving all three periodicities by \(\lambda _{123}\). The number of clients with the periodicity of \(q_1\) in set \(\lambda _{1}\), \(\lambda _{12}\), \(\lambda _{31}\), \(\lambda _{123}\) are denoted by \(n_{10}\), \(n_{12}\), \(n_{13}\), \(\mu _1\), respectively, and similar notation is used for the other periodicities. Observe that \(n_1 = n_{10} + n_{12} + n_{13} + \mu _1\), \(n_2 = n_{20} + n_{21} + n_{23} + \mu _2\) and \(n_3 = n_{30} + n_{31} + n_{32} + \mu _3\), and denote the distribution of clients to sets in \({\varvec{\Lambda }}\) by \(\underline{n}=(n_{10}, n_{20}, n_{30}, n_{12}, n_{21}, n_{23}, n_{32}, n_{31}, n_{13}, \mu _1, \mu _2, \mu _3 )\).

We now analyse the relationship between the number of the sets of each type, the \(\lambda s\), and the number of clients of each periodicity distributed to these sets, in Lemmas 10–12. We will then return to the issue of testing for the existence of a feasible solution in Theorem 4.

Lemma 10

A feasible PPS instance with three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\), and \(g_{i0} = 1\) for \(i=1, 2, 3\) has a solution in which \(\lambda _{12}\), \(\lambda _{23}\) and \(\lambda _{31}\) are each at most one.

Proof

Take an instance for which any such feasible schedule has at least one of \(\lambda _{12}\), \(\lambda _{23}\) and \(\lambda _{31}\) greater than 1. Take a solution with smallest possible \(\max (\lambda _{12}, \lambda _{23},\) \(\lambda _{31})= \lambda _{12}\) say. Let \(\Lambda \) and \(\Lambda ^{\prime }\) denote two of the sets serving clients with the periodicities of \(q_1\) and \(q_2\).

Suppose that \(n_1\) and \(n_2\) clients with the periodicity of \(q_1\) and \(q_2\), respectively, are serviced together in \(\Lambda _l\), and that \(n^{\prime }_1\) and \(n^{\prime }_2\) clients with the periodicity of \(q_1\) and \(q_2\), respectively, are serviced together in \(\Lambda _{l^{\prime }}\). The schedule with the set \(\Lambda _l\) (or \(\Lambda _{l^{\prime }}\)) may be viewed as a single schedule for the clients \(n_1\) and \(n_2\) (or \(n^{\prime }_1\) and \(n^{\prime }_2\)) alone with the periodicity of \(q_1^{\prime } = q_1/g\) and \(q_2^{\prime } =q_2/g\), respectively. Thus, \(gcd(q_1^{\prime }, q_2^{\prime })=g_{12}\), and by Theorem 1,

$$\begin{aligned} \left\lceil \frac{n_1}{q_1/gg_{12}}\right\rceil + \left\lceil \frac{n_2}{q_2/gg_{12}}\right\rceil&\le g_{12} \;\; \text{ and }\\ \left\lceil \frac{n^{\prime }_1}{q_1/gg_{12}}\right\rceil + \left\lceil \frac{n^{\prime }_2}{q_2/gg_{12}}\right\rceil&\le g_{12}. \end{aligned}$$

If \(\left\lceil n_2/(q_2/gg_{12})\right\rceil \ge \left\lceil n^{\prime }_1/(q_1/gg_{12})\right\rceil \), then let \(\widetilde{n}_2 = \min \{q_2/gg_{12}\left\lceil n^{\prime }_1/(q_1/gg_{12})\right\rceil ,\; n_2\}\), and thus

$$\begin{aligned} \left\lceil \frac{n_1+n^{\prime }_1}{q_1/gg_{12}}\right\rceil + \left\lceil \frac{n_2-\widetilde{n}_2}{q_2/gg_{12}}\right\rceil&\le g_{12} \;\; \text{ and }\\ \left\lceil \frac{\widetilde{n}_2+n^{\prime }_2}{q_2/gg_{12}}\right\rceil \le \left\lceil \frac{\widetilde{n}_2}{q_2/gg_{12}}\right\rceil + \left\lceil \frac{n^{\prime }_2}{q_2/gg_{12}}\right\rceil&\le g_{12}. \end{aligned}$$

Hence, exchanging \(\widetilde{n}_2\) clients of the \(n_2\) clients with the periodicity of \(q_2\) in \(\Lambda _l\) with all \(n^{\prime }_1\) clients with the periodicity of \(q_1\) in \(\Lambda _{l^{\prime }}\) results in time slots in a set \(\Lambda _{l^{\prime }}\) serving only clients with the periodicity of \(q_2\) and \(\Lambda _{12}\) has been reduced by 1. If \(\left\lceil n_2/(q_2/gg_{12})\right\rceil < \left\lceil n^{\prime }_1/(q_1/gg_{12})\right\rceil \), then the same argument applies with clients in \(\Lambda _l\) exchanged with clients in \(\Lambda _{l^{\prime }}\), providing the required contradiction. \(\square \)

A similar result holds for \(\lambda _{123}\), as captured in Lemma 11 below, but its proof is more lengthy and therefore relegated to Appendix 2.

Lemma 11

A feasible PPS instance with three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\), and \(g_{i0} = 1\) for \(i=1, 2, 3\) has a solution in which \(\lambda _{123} \le 1\).

Lemma 12

A feasible PPS instance with three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\), and \(g_{i0} = 1\) for \(i=1, 2, 3\) has a solution in which \(\lambda _{12}\), \(\lambda _{23}\), \(\lambda _{31}\) and \(\lambda _{123}\) are each at most one.

Proof

The result follows by taking a feasible solution which satisfies Lemma 11, i.e. with \(\lambda _{123} \le 1\), and applying the exchange described in the proof of Lemma 10. Since no new \({\varvec{\Lambda }}\)-set with three periodicities is created by the exchange, \(\lambda _{123}\) is not increased, and the resultant solution satisfies Lemma 12. \(\square \)

Theorem 4

For an instance with three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\), and \(g_{i0} = 1\) for \(i=1, 2, 3\) which has a feasible solution, there exist an (non-negative) integer vector \(\underline{n}=(n_{10}, n_{20}, n_{30}, n_{12}, n_{21},\) \(n_{23}, n_{32}, n_{31}, n_{13}, \mu _1, \mu _2, \mu _3)\), and non-negative integers, \(\lambda _{1}\), \(\lambda _{2}\), \(\lambda _{3}\), \(\lambda _{12}\), \(\lambda _{23}\), \(\lambda _{31}\) and \(\lambda _{123}\) for which

$$\begin{aligned} \sum _{i^{\prime }=0, i^{\prime } \ne i}^{3}n_{ii^{\prime }} + \mu _i&= n_i \;\; \text{ for } \, i=1, 2, 3 \end{aligned}$$
(10)
$$\begin{aligned} \lambda _{1} + \lambda _{2} + \lambda _{3} + \lambda _{12} + \lambda _{23} + \lambda _{31} + \lambda _{123}&\le g \end{aligned}$$
(11)
$$\begin{aligned} \left\lceil \frac{n_{i0}}{q_i/g}\right\rceil&= \lambda _i \quad \text{ for } i=1, 2, 3 \end{aligned}$$
(12)
$$\begin{aligned} \lambda _{12}, \lambda _{23}, \lambda _{31}&\le 1 \end{aligned}$$
(13)
$$\begin{aligned} \left\lceil \frac{n_{12}}{q_1/(gg_{12})} \right\rceil + \left\lceil \frac{n_{21}}{q_2/(gg_{12})} \right\rceil&\le g_{12}\lambda _{12} \end{aligned}$$
(14)
$$\begin{aligned} \left\lceil \frac{n_{23}}{q_2/(gg_{23})} \right\rceil + \left\lceil \frac{n_{32}}{q_3/(gg_{23})} \right\rceil&\le g_{23}\lambda _{23} \end{aligned}$$
(15)
$$\begin{aligned} \left\lceil \frac{n_{31}}{q_3/(gg_{31})} \right\rceil + \left\lceil \frac{n_{13}}{q_1/(gg_{31})} \right\rceil&\le g_{31}\lambda _{31} \end{aligned}$$
(16)

and

$$\begin{aligned} \lambda _{123}&\le 1 \end{aligned}$$
(17)
$$\begin{aligned} (1 - \lambda _{123})(\mu _1 + \mu _2 + \mu _3)&= 0 \end{aligned}$$
(18)
$$\begin{aligned} \left\lceil \frac{\mu _1}{x}\right\rceil&\le g_{31} - 1 \end{aligned}$$
(19)
$$\begin{aligned} \left\lceil \frac{\mu _2}{g_{12}-x}\right\rceil&\le g_{23} - 1 \end{aligned}$$
(20)
$$\begin{aligned} \left( g_{31} - \left\lceil \frac{\mu _1}{x}\right\rceil \right) \left( g_{23} - \left\lceil \frac{\mu _2}{g_{12}-x}\right\rceil \right)&\ge \mu _3 \end{aligned}$$
(21)

for some integer \(x\), \(1 \le x \le g_{12} - 1\).

Proof

Consider a feasible schedule for an instance of PPS problem with three distinct periodicities, with the notation of \({\varvec{\Lambda }}\)-sets and number of clients, \(n_{ii^{\prime }}\), as defined at the beginning of this section. For the solution to be feasible, the total number of \({\varvec{\Lambda }}\)-sets required can be no more than \(g\), as captured by (11). We consider each type of \({\varvec{\Lambda }}\)-set in turn: those with clients of one, two and then three different periodicities. Without loss of generality, we may assume from Lemma 12 that there is no more than one \({\varvec{\Lambda }}\)-set for clients with each possible combination of two or three periodicities within the set, implying (13) and (17).

The \({\varvec{\Lambda }}\)-sets with just clients of a single periodicity, \(q_i\) say, can each service up to \(q_i/g\) clients by Lemma 3. The number of sets required to schedule the clients associated with \(n_{i0}\), \(\lambda _{i0}\), is therefore \(\left\lceil n_{i0}/(q_i/g)\right\rceil \) as given by (12) for \(i=1, 2, 3\).

Consider \({\varvec{\Lambda }}\)-sets with clients of two different periodicities. If \(\lambda _{12}=0\), then (14) holds for \(n_{12}=n_{21}=0\). Otherwise, \(\lambda _{12}=1\), and \(n_{12}\) and \(n_{21}\) clients with the periodicity of \(q_1\) and \(q_2\), respectively, are serviced together in a single \({\varvec{\Lambda }}\)-set. From the result of Theorem 1 applied for periodicities of \(q_1/g\) and \(q_2/g\),

$$\begin{aligned}\left\lceil \frac{n_{12}}{q_1/(gg_{12})} \right\rceil + \left\lceil \frac{n_{21}}{q_2/(gg_{12})} \right\rceil \le g_{12}\lambda _{12}\end{aligned}$$

as given by (14). Similar expressions hold for the other two pairs of periodicities, and are given by (15) and (16), respectively.

Finally, consider a \({\varvec{\Lambda }}\)-set with clients of three different periodicities. If \(\lambda _{123} =0\), then there is no set with clients of each of the three periodicities, \(\mu _i =0\) for \(i=1, 2, 3\), and inequalities (18), (19), (20) and (21) hold for \(x=1\). Otherwise, \(\lambda _{123} =1\), (18) holds, and the \(\mu _1\), \(\mu _2\) and \(\mu _3\) clients with the periodicity of \(q_1\), \(q_2\) and \(q_3\), respectively, are serviced in a single \({\varvec{\Lambda }}\)-set. From Theorem 3 applied for periodicities of \(q_i^{\prime }=q_i/g\) for \(i=1, 2, 3\), the inequalities (19), (20) and (21) hold for some integer \(x\), \(1 \le x \le g_{12} - 1\), completing the proof. \(\square \)

5 Feasibility test for three distinct periodicities

In this section, we develop a polynomial test for feasibility, based upon the results of Theorems 3 and 4. The feasibility test systematically searches for a vector \(\underline{n}\) to satisfy constraints (10)–(21) of Theorem 4. In doing so, it reveals information about a feasible solution, where one exists. However, it is convenient to reserve the lengthy construction of the feasible solution itself for a separate algorithm presented in the next section. The feasibility test, FeasTest, is developed in two parts. We first present a subprocedure, RedFeas, for finding an integer vector \(\underline{n}\) with \(\mu _1 = \mu _2 = \mu _3=0\), for reduced instances. Then, we extend this algorithm to cover the general case, where \(g_{i0}\) and \(\mu _{i0}\) for \(i=1, 2, 3\) may take non-zero values.

figure a

Observe that the computational complexity of Algorithm RedFeas is determined by the number of iterations of Step 2, which is itself bounded by \(n\) because \(n_1 \le n\) and \(q_1/(gg_{12}) = g_{31} \ge 1\). Therefore, the overall complexity of Algorithm RedFeas is \(O(n)\). We now verify that RedFeas is indeed a feasibility test.

Lemma 13

Consider an instance with \(g_{i0} =1\) for \(i=1, 2, 3\), for which there exists a feasible solution with \(\lambda _{123}=0\). Then, Algorithm RedFeas returns an integer vector \(\underline{n}\) with \(\mu _1 = \mu _2 = \mu _3 = 0\) corresponding to a feasible solution.

Proof

Observe that Algorithm RedFeas produces a solution of a particular form. It considers all possible values for \(n_{12}\) which satisfies (22). Then, all other values are determined iteratively as follows: \(n_{ii^{\prime }}\) for \(i, i^{\prime } = 1, 2, 3, i \ne i^{\prime }\) in Step 2.1–2.3 as in (23)–(27) below, followed by \(n_{10}\), \(n_{20}\), \(n_{30}\) in Step 2.4 as in (28)–(30). Therefore, Algorithm RedFeas tests for all solutions of this form.

$$\begin{aligned} n_{12}&= n_1 \text{ or } \delta q_1/gg_{12} \text{ for } \text{ some } \delta \in \{0, 1, \dots , g_{12}-1\} \end{aligned}$$
(22)
$$\begin{aligned} n_{21}&= \left\{ {\begin{array}{*{20}l} 0 \quad \text{ if } \quad n_{12} = 0\\ \min \{ n_2, \;q_2/g - q_2/(gg_{12}) \left\lceil {n_{12}/(q_1/gg_{12})} \right\rceil \}\quad \text{ otherwise } \quad \\ \end{array}} \right. \end{aligned}$$
(23)
$$\begin{aligned} n_{23}&= \left\{ {\begin{array}{*{20}l} 0 \quad \text{ if } \quad R(n_2 -n_{21}, q_2/gg_{23}) > (g_{23}-1)q_2/(gg_{23})\\ R(n_2 -n_{21}, q_2/gg_{23}) \quad \text{ otherwise } \quad \\ \end{array}} \right. \end{aligned}$$
(24)
$$\begin{aligned} n_{32}&= \left\{ {\begin{array}{*{20}l} 0 \quad \text{ if } \quad n_{23} = 0\\ \min \{ n_3, \;q_3/g - q_3/(gg_{23}) \left\lceil { n_{23} /(q_2/gg_{23}) } \right\rceil \} \quad \text{ otherwise } \quad \\ \end{array}} \right. \end{aligned}$$
(25)
$$\begin{aligned} n_{31}&= \left\{ {\begin{array}{*{20}l} 0 \quad \text{ if } \quad R(n_3 -n_{32}, q_3/gg_{31}) > (g_{31}-1)q_3/(gg_{31}) \text{ or } \\ n_1 = n_{12} \quad R(n_3 - n_{32}, q_3/gg_{31}) \quad \text{ otherwise } \quad \\ \end{array}} \right. \end{aligned}$$
(26)
$$\begin{aligned} n_{13}&= \left\{ {\begin{array}{*{20}l} 0 \quad \text{ if } \quad n_{31} = 0\\ \min \{ n_1 \!-\! n_{12}, \;q_1/g \!-\! q_1/(gg_{31})\\ \left\lceil {n_{31}/(q_3/gg_{31})} \right\rceil \}\quad \text{ otherwise } \quad \\ \end{array}} \right. \end{aligned}$$
(27)
$$\begin{aligned} n_{10}&= n_1 - n_{12} - n_{13}\end{aligned}$$
(28)
$$\begin{aligned} n_{20}&= n_2 - n_{21} - n_{23}\end{aligned}$$
(29)
$$\begin{aligned} n_{30}&= n_3 - n_{31} - n_{32} \end{aligned}$$
(30)

Now take a feasible solution \(\underline{n}^{\prime }=(n^{\prime }_{10}, n^{\prime }_{20}, n^{\prime }_{30}, n^{\prime }_{12}, n^{\prime }_{21}, n^{\prime }_{23}, n^{\prime }_{32}, n^{\prime }_{31}, n^{\prime }_{13}, 0, 0, 0)\) with \(\lambda _{123}=0\), for which without loss of generality, \(\lambda _{12} \le 1\), \(\lambda _{23}\le 1\) and \(\lambda _{31}\le 1\) by Lemma 12, and \(\lambda _{23}\) is as small as possible and for this minimum \(\lambda _{23}\) value, \(\lambda _{31}\) is as small as possible. We now show that this feasible solution with \(\lambda _{123}=0\) can be modified to one which satisfies (22)–(30).

We first modify \(n^{\prime }_{12}\) and \(n^{\prime }_{21}\), if required. If \(\lambda _{12} =0\), then \(n^{\prime }_{12}\) and \(n^{\prime }_{21}\) remain unchanged at 0 (i.e. we set \(n_{12} = n_{21}=0\)). Otherwise, \(\lambda _{12} =1\) (and \(n^{\prime }_{12} \ge 1\) and \(n^{\prime }_{21} \ge 1\)). By (14) of Theorem 4, we may increase \(n^{\prime }_{12}\) up to \(n_{12} = \min \{n_1, (q_1/gg_{12})\lceil n_{12}/(q_1/gg_{12})\rceil \}\) and \(n^{\prime }_{21}\) to \(n_{21} = \min \{n_2,\; q_2/g - q_2/(gg_{12})\left\lceil n_{12}/(q_1/(gg_{12})) \right\rceil \}\), respectively, without increasing \(\lambda \). Observe that \(n_{12}\) and \(n_{21}\) satisfies (22) and (23), respectively.

We now modify \(n^{\prime }_{23}\) and \(n^{\prime }_{20}\), having determined \(n_{21}\). Suppose that \(\lambda _{23} =0\) (and \(n^{\prime }_{23}=0\)). If \(R(n_2 - n_{21}, q_2/g) > (g_{23}-1)q_2/(gg_{23})\) (and \(\lambda _{23} = 0\)), then \(n^{\prime }_{23}\) is left unchanged at \(0\) and \(n^{\prime }_{20}\) modified to \(n_{20} = n_2 -n_{21}\), satisfying (29) without increasing \(\lambda _2\) (since \(n_{21} \ge n^{\prime }_{21}\)). If on the other hand \(R(n_2 - n_{21}, q_2/g) \le (g_{23}-1)q_2/(gg_{23})\), then we modify \(n^{\prime }_{23}\) to \(n_{23} = R(n_2 - n_{21}, q_2/g)\) and \(n^{\prime }_{20}\) to \(n_{20} = n_2 - n_{21} - n_{23}\) preserving (29), which results in \(\lambda _{23} = 1 \) and \(\lambda _{2}\) is decreased by one, leaving \(\lambda \) unchanged. Thus, (24) is satisfied for the modified solution in the case when \(\lambda _{23} =0\), for the original solution. Now suppose that \(\lambda _{23} =1\) (and \(n^{\prime }_{23} \ge 1\)). Then, by hypothesis, there is no feasible solution for given \(\lambda _{12}\) value, with \(\lambda _{23}=0\). The \(\lambda _{2}\) value is unaffected by increasing \(n^{\prime }_{20}\), if necessary, to \(n_{20} = q_2/g\lceil n^{\prime }_{20}/(q_2/g) \rceil \) from (12) of Theorem 4. Thus, \(n^{\prime }_{23}\) may be decreased to \(n_{23} = n_2 - n_{21} - n_{20} = R(n_2 - n_{21}, q_2/g) > 0\) satisfying (24) and reserving (29), without increasing \(\lambda \).

We now modify \(n^{\prime }_{32}\). Recall that \(n_{23} =0\) only in the case when \(n^{\prime }_{23} = 0\) (and \(n^{\prime }_{32} =0\)) and we then leave \(n^{\prime }_{32}\) unmodified, i.e. we set \(n_{32} = 0\), without increasing \(\lambda \). Now suppose that \(n_{23} \ge 1\). By (15) of Theorem 4, we modify \(n^{\prime }_{32}\) to \(n_{32} = \min \{ n_3, \;q_3/g - q_3/(gg_{23}) \left\lceil { n_{23} /(q_2/gg_{23}) } \right\rceil \}\) without increasing \(\lambda \). Thus, \(n_{32}\) satisfies (25).

We now modify \(n^{\prime }_{31}\) and \(n^{\prime }_{30}\) given \(n_{32}\) to satisfy (26) and then (30), respectively. The validity of the modification follows by the same argument as used above for \(n^{\prime }_{23}\) and \(n^{\prime }_{20}\), but for the permitted indices, since \(\lambda _{31}\) (as well as \(\lambda _{23}\)) is selected by as small as possible.

Finally, we modify \(n^{\prime }_{13}\) and \(n^{\prime }_{10}\). In the case that \(n_{31} =0\), \(n^{\prime }_{31} = 0\) and \(n^{\prime }_{13} =0\) in the original feasible solution, and we set \(n_{13} = 0\) and \(n_{10} = n_1 - n_{12} - n_{13}\) without increasing \(\lambda \). Now suppose that \(n_{31} \ge 1\). By (16) of Theorem 4, we may modify \(n^{\prime }_{13}\) to \(n_{13} = \min \{n_1 - n_{12}, \;q_1/g - q_1/(gg_{31}) \left\lceil {n_{31} /(q_3/gg_{31}) } \right\rceil \}\) and \(n^{\prime }_{10}\) to \(n_{10} = n_1 - n_{12} - n_{13}\) without increasing \(\lambda \). Thus, \(n_{13}\) and \(n_{10}\) satisfies (27) and (28), respectively. \(\square \)

We now develop an algorithm allowing a \({\varvec{\Lambda }}\)-set with three periodicities. By Lemma 11, it is sufficient to explore all combinations of constructing at most one \({\varvec{\Lambda }}-\)set with three periodicities. We now give a formal description of the algorithm.

Observe that \(\mu _1\), \(\mu _2\) and \(\mu _3\) are each bounded by \(n\). By Lemma 9, finding an integer \(x\) in Step 4 can be done in \(O(n)\). Therefore, the overall complexity of FeasTest is \(O(n^4)\).

Lemma 14

Consider an instance for which there exists a feasible solution. Then, Algorithm FeasTest returns an integer vector \(\underline{n}\), for which \(\lambda _{12}\), \(\lambda _{23}\), \(\lambda _{31}\) and \(\lambda _{123}\) are each at most one for the corresponding reduced problem.

Proof

Taking a feasible solution for any given instance. By Theorem 2, there is a corresponding feasible solution to the reduced problem instance, \(\underline{n}\) say. We make another instance by letting \(\widetilde{n}_i = n_i -\mu _i\) for \(i=1, 2, 3\). Then, since there exists a feasible solution for the original (reduced) instance, there must be a feasible solution with \(\lambda _{123}=0\) for the new (reduced) instance. By Lemma 13, a feasible solution with \(\lambda _{12} \le 1\), \(\lambda _{23} \le 1\) and \(\lambda _{31} \le 1\) for the new (reduced) instance will be identified by Algorithm RedFeas. Since Algorithm FeasTest explores all combination of \(\mu _i\) for \(i=1, 2, 3\), it will find an integer vector \(\underline{n}\) corresponding to a feasible solution for the given (reduced) instance if one exists, and hence, equivalently, to the original instance by Theorem 2. \(\square \)

figure b

6 Construction of a feasible schedule for three distinct periodicities

In this section, we develop a construction for a feasible perfect periodic schedule with three distinct periodicities, when one exists. We build upon the feasibility tests of the last section, using the structure of the solution which it provides in the form of the \(\underline{n}\) vector. The construction of a feasible schedule in algorithm 3PPS-Sched follows that indicated in the proof of Theorem 2. It builds upon a feasible solution to the reduced instance produced by subroutine RedSched. We now outline the algorithmic construction, 3PPS-Sched and RedSched, of a feasible solution. The validity and computational complexity of the algorithm(s) are then considered in Theorems 5 and 6. An illustrative example is offered at the end of this section.

We now develop an algorithm for constructing a feasible schedule from the composition of \({\varvec{\Lambda }}\)-sets provided by integer vector \(\underline{n}\) from Algorithm FeasTest, for the reduced problem. The construction, for \({\varvec{\Lambda }}\)-sets with two and three different periodicities, is based upon the proofs of Theorems 1 and 3.

figure c

Theorem 5

An instance with three distinct periodicities, \(q_1\), \(q_2\) and \(q_3\) with \(g_{i0} =1\) for \(i=1, 2, 3\) is schedulable if and only if Algorithm RedSched returns a feasible schedule.

Proof

Algorithm RedSched returns a set of first service time slots \(\tau _{ij}\) for \(i=1, 2, 3\), \(j=0, \dots , n_i-1\), based upon the integer vector \(\underline{n}\) returned by Algorithm FeasTest. Now by Lemma 14, \(\underline{n}\) associates clients with \({\varvec{\Lambda }}\)-sets (\(n_{i0}\) of periodicity \(q_i\) with \(\lambda _{i}\) sets, \(n_{ii^{\prime }}\) and \(n_{i^{\prime }i}\) with \(\lambda _{ii^{\prime }}\) sets and \(\mu _1\), \(\mu _2\), \(\mu _3\) with \(\lambda _{123}\) sets, for \(i, i^{\prime }= 1, 2, 3\), \(i \ne i^{\prime }\)), and \(\lambda _{12}\), \(\lambda _{23}\), \(\lambda _{31}\) and \(\lambda _{123}\) are each no greater than one. We shall show that algorithm RedSched constructs a solution based upon this prescribed division of \({\varvec{\Lambda }}\)-sets. The index \(l\) keeps track of the \({\varvec{\Lambda }}\)-set(s) under consideration at each step of the algorithm. To see this, observe that \(l\) is initialized to \(0\) and incremented in the last statement of each step. The increment in step 3 is \(\left\lceil n_{i0}/(q_i/g) \right\rceil \) which is indeed \(\lambda _{i}\) for \(i=1, 2, 3\). Each of steps 4–7 is skipped if the corresponding \({\varvec{\Lambda }}\)-set is empty, since \(\lambda _{1}=0\) when \(n_{12} + n_{21} =0\), etc and \(\lambda _{123}=0\) when \(\mu _1 + \mu _2 + \mu _3 =0\). Moreover, when any of steps 4–7 is implemented, \(l\) is increased by 1, in accordance with Lemma 14. It remains only to show that the construction within each \({\varvec{\Lambda }}\)-set is feasible.

Observe that in Step 3 of Algorithm RedSched, the first \(q_i/g\) positions are used for the first service of clients with the periodicity of \(q_i\) in a \({\varvec{\Lambda }}\)-set. Thus, no service to these clients is overlapped by Lemma 3.

Now, the time slots within a \(\Lambda _l\)-set are of the form \(l+gp\) where \(p\) is the position within the set. Consider the \({\varvec{\Lambda }}\)-set, \(\Lambda ^{\prime }\) say, which contains the clients with the periodicities of both \(q_1\) and \(q_2\), when \(\lambda _{12}=1\). The interval between consecutive positions in \(\Lambda ^{\prime }\) of service to a client with the periodicity of \(q_1\) (or \(q_2\)) is \(q_1/g=g_{12}g_{31}\) (or \(q_2/g = g_{12}g_{23}\)). Thus, the positions given to \(\tau _{1j}\) and \(\tau _{2j}\) in Step 4 are precisely those prescribed by (2) and (3) in the proof of Theorem 1. The validity of Step 5 and 6 for \(\lambda _{23}\) and \(\lambda _{31}\), respectively, follows by analogy.

Now consider the case when \(\lambda _{123}=1\) (and \(\mu _1 + \mu _2+ \mu _3 >0\)). The construction of \(x\), \(\alpha \), \(\beta \) and \(\bar{f}\) in Step 7.1 accords with that in Sect. 4.2 for the reduced problem with periodicities \(q_i/g\) for \(i=1, 2, 3\). Time slot \(t\) in the reduced problem corresponds to time slot in \(\Lambda _l\) in the original problem with value of \(l +gt\). Thus, the allocation of the first time slot to clients with the periodicity of \(q_1\) and \(q_2\) described in Step 7.2 corresponds to (8) and (9) in the proof of Theorem 3. The above allocation is designed to leave as many sets of relative free positions available for clients with the periodicity of \(q_3\) as possible, as described in Theorem 3. The set of occupied relative positions is given by \(P_1\) and \(P_2\) in Step 7.3 for the periodicity of \(q_1\) and \(q_2\), and the allocation of the clients with the periodicity of \(q_3\) to the free relative positions performed in Step 7.4. \(\square \)

figure d
figure e

Theorem 6

Algorithm 3PPS-Sched constructs a feasible perfect periodic schedule for an instance with three distinct periodicities in \(O\left( \max \{n^4,\; q_{\max }\}\right) \) time if one exists, where \(n=\sum _{i=1}^{3}n_{i}\) and \(q_{\max }=\max _{i}q_i/g_{i0}\).

Proof

Take an instance of PPS which has a feasible solution. Then by Theorem 2, the corresponding reduced instance is as constructed in Step 2 of Algorithm 3PPS-Sched, and is itself feasible by Theorem 5. Moreover, the corresponding schedule for the original instance given in Step 3, is as constructed in (4) of the proof of Theorem 2 and is therefore feasible.

Observe that Step 1 of Algorithm RedSched can be done in \(O(n^4)\). Step 7 of Algorithm RedSched can be done in \(O(q_{\max })\) because Steps 7.1 and 7.4 are bounded by \(O(g_{12})\) and \(O(g_{23}g_{31})\), respectively. All other steps of Algorithm RedSched can be done in \(O(n)\). Therefore, the overall computational complexity of Algorithm 3PPS-Sched is \(O\left( \max \{n^4,\; q_{\max }\}\right) \). \(\square \)

The following example illustrates the construction of Algorithm 3PPS-Sched.

Example 3

Consider the case of three periodicities \(q_1=48\), \(q_2=80\) and \(q_3=60\) (ie. \(g=4,\;g_{12}=4,\;g_{23}=5,\;g_{31}=3\), and \(g_{i0} =1\) for \(i=1, 2, 3\)) with \(n_1=14\), \(n_2=5\) and \(n_3=36\), respectively. For this instance, Algorithm FeasTest gives rise to values \(\lambda _1 = \lambda _2 =\lambda _{12} =0\) and \(\lambda _{3} = \lambda _{23} = \lambda _{31} = \lambda _{123} =1\) and returns an integer vector \(\underline{n} \!=\! (n_{10}, n_{20}, n_{30}, n_{12}, n_{21}, n_{23}, n_{32}, n_{31}, n_{13}, \mu _1, \mu _2, \mu _3) = (0, 0, 15, 0, 0, 4, 12, 5, 8, 6, 1, 4)\). Algorithm 3PPS-Sched then produces a feasible schedule as depicted in Fig. 6. The underlying structure of the \({\varvec{\Lambda }}\)-sets is given by Algorithm RedSched in shown in Fig. 7.

Fig. 6
figure 6

A feasible schedule for Example 3

Full size image
Fig. 7
figure 7

The structure of each \({\varvec{\Lambda }}\)-set in the feasible schedule for Example 3, as a \({\varvec{\Delta }}\)-partition

Full size image

7 Conclusions

This paper examines the perfect periodic scheduling problem with unit service time. We have extended the range of perfect periodic scheduling problem which are amenable to polynomial time algorithms from one periodicity to three distinct periodicities. The extent of such special cases is likely to be limited since the existence of perfect periodic schedule problem for the general case is NP-hard. The only models commonly used in the literature are based upon a single common periodicity: either the single periodicity itself, its powers (eg. power of 2), or based upon repeated divisibility (depicted as a tree structure).

We have presented an algorithm for testing for the existence of a feasible schedule for any combination of clients with up to three distinct periodicities, which runs in \(O(n^4)\). In addition, we have provided the construction of a feasible schedule where one exists. We have thus extended the range of feasible perfect periodic schedules available for operating Wireless Mesh Networks beyond those with a common factor.

The next obvious step is to embed these algorithms within heuristics for meeting the requests of mobile telecommunication clients, according to different service level quality measures, see Bar-Noy et al. (2004), Brakerski and Patt-Shamir (2006). There is potential for accommodating a wide range of combinations of periodicities, by incorporating multiples of the three basic periodicities in particular power of 2. The addition of a fourth distinct periodicity might be investigated. However, it is unlikely to be an attractive option due to the large number of idle time slots imposed in the schedule. Future research will evaluate the advantage of the wider solution spaces made accessible through the current article. In particular, efficient methodologies will be sought for combining perfect periodic schedules for local clients at mesh nodes, with approaches to data transmission through a routing tree, such as Allen et al. (2012a, b), as is applicable for Internet access through Wireless Mesh Networks.