1 Introduction

The processes of blasting and ore extraction in underground mines significantly disturb the local stress field in the surrounding rock mass, forming stress accumulation zones, which results in brittle fracturing of the rock mass (induced seismicity). Although the seismic events in the mines are small compared to natural seismicity, they can pose hazard to the mining infrastructure, operations, and safety of the workers. To reduce the risk of injuries, some areas of the mines can be temporarily closed in case of increased seismicity or higher probability of larger seismic events. The duration of aftershock sequences in the mines together with the short-term probability forecasting of strong aftershocks are among the seismicity features considered for temporary closure of mine areas. In such cases, the question about the re-entry rules arises.

Different approaches to develop guidelines and subsequently re-entry protocols for mines have been in development in recent years, some of which are based on correlation between mining production and seismicity (Vallejos and McKinnon 2011). Other studies (Malek and Leslie 2006) investigate the relation between seismic risk and some seismicity parameters like seismic work, spatial clustering, and strain rate (see definitions in Vallejos 2010). Considering the essential influence of strong event magnitude on seismic risk in mines, Vallejos and Estay (2018) investigated the correlations between mining seismic parameters and the magnitude of the main event. Mendecki et al. (2019) tested the concept that induced seismicity prior to relatively large mining tremor can be inferred from the cumulative Benioff strain release as power law time-to-failure before the strong event. Nordström et al. (2020) examined the behavior of several short-term hazard indicators for Kiirunavaara Mine such as Seismic Activity Rate, Cumulative Seismic Moment, Energy Index, etc. prior to an impending strong seismic event.

The single most important parameter that is monitored for re-entry purposes is the seismicity rate (number of events per unit time). Studying changes in seismic activity in the mines and relating these changes to increased seismic risk are the main focus of many scientific studies. Some investigations explore the change-point of linear trends of seismicity rate (Kubacki et al. 2014). Other authors try to approach the seismic risk problem by examining blast-related mining sequences and the correlation between production and mining seismicity (Woodward and Wesseloo 2015; Woodward et al. 2017; Dineva and Boskovic 2017).

Similar to the natural earthquakes, some of the stronger mining-induced seismic events are followed by a temporary rise of seismicity rate (aftershocks). In mines, the aftershock rate gradually decays to background levels within hours to days. Although the magnitudes of the aftershocks are not large and the extent of aftershock area in the mine is relatively small, the rock mass in the vicinity of the main shock, which was already damaged or with decreased competence, can be damaged further by the aftershocks. Observations showed that single events or aftershocks with magnitude as low as 0.5 can cause rock damage in Kiirunavaara Mine.

The decision for re-entry after closure is commonly based on the requirement for some monitored parameters to return to a previously defined background/normal level for a given time window. If the monitored parameter exceeds a pre-set threshold during that time window, the re-entry clock is reset and the restriction continues. Re-entry rules for temporary closure and re-opening after large seismic events in mines were discussed in Vallejos and Estay (2018), Vallejos and McKinnon (2008), and Tierney and Morkel (2017). The probabilistic forecasting of natural seismicity is based on stochastic modeling of the aftershock sequence (Marzocchi and Lombardi 2009; Jordan et al. 2011; Marzocchi et al. 2012; Gospodinov et al. 2015) and the same can apply to mining seismicity. These models are statistical fits of empirical functions to common patterns of aftershock sequences and regardless of whether they explain the underlying physics of the problem the patterns, which they fit, are valuable for re-entry protocol applications.

When considering stochastic modeling of aftershock rate decay, the simplest and most widely applied model is the modified Omori formula (MOF; Utsu 1961) which is applicable both, for natural and mining-induced earthquakes. In this model, the main event controls the entire aftershock sequence. First, McGarr and Green (1978) applied it successfully to describe the duration and number of aftershocks after two mine tremors. Later Spottiswoode (2000) established that post-blast seismicity (blast aftershocks) were in agreement with the MOF for eleven sequences in four different mines. Vallejos and McKinnon (2009) and Vallejos (2010) statistically demonstrated that the MOF model could be adequately used to describe the event decay rate of mining-induced aftershock sequences. The authors examined the application of several criteria, based on MOF, for preliminary estimate of the time, which may be considered appropriate to re-enter the mine area, among them (1) when a preset level in the MOF cumulative density function is reached; (2) when MOF rate decays to a previously defined rate level; and (3) when MOF curve reaches its maximum curvature.

MOF, however, is not applicable for aftershock sequences, which include secondary excitations after strong aftershocks. For such more complex cases, Vallejos (2010) applied the Epidemic-Type Aftershock Sequence (ETAS) model, developed by Ogata (1988) and Ogata and Zhuang (2006), to model aftershock temporal evolution in mines. This model is based on a point process in which every event can produce its offspring of events and the model can be considered as an extension of a single modified Omori’s formula. In his study, Vallejos (2010) set all ETAS model parameters as a-priori calculated site specific averages.

Reasenberg and Jones (1994) combined the MOF and Gutenberg and Richter (1944) scaling relations in a stochastic parametric model, which provides the possibility to assess the occurrence probability of either significant aftershocks or an event stronger than the main shock during time intervals following the main event. Vallejos (2010) used the Reasenberg and Jones model for mining seismicity to estimate occurrence probabilities of aftershocks of one magnitude unit weaker than the main shock for subsequent time intervals.

The ETAS model was used by Marzocchi and Lombardi (2009) and Marzocchi et al. (2012) to perform true real-time prospective forecasts of natural seismicity rate for L’Aquila and Emilia earthquake sequences, respectively, with their model being calibrated on data before the main shock occurrence.

MOF and ETAS are based on two end assumptions, the first considering one trigger event (the main), and the second, assuming all aftershocks to be capable of inducing secondary events. In that way, these two models do not consider cases in which not all but only some stronger aftershocks control the rate decay process. This gap was covered by a model, offered by Gospodinov and Rotondi (2006) which presumes that only aftershocks above a certain magnitude level can trigger new events. The authors applied the model for natural seismicity to model aftershock activity after two sequences in Italy and Bulgaria. The model was named Restricted Epidemic-Type Aftershock Sequence (RETAS) model due to its similarity to ETAS. Gospodinov et al. (2015) applied it also to examine the temporal evolution of the occurrence probability of strong aftershocks in the 2014 Kefalonia aftershock sequence in Greece.

In the present study, we address two problems, one related to statistical modeling of the aftershocks of seismic events in underground mines and the second one considering a possible approach to reduce seismic risk by optimizing the guidelines for developing re-entry protocols and applying this approach for the induced seismicity in Kiirunavaara Mine (Sweden). We resolve the first problem by performing RETAS model analysis sequentially on data samples covering cumulative periods of time from the first 2 h and increasing them by 2 h until the end of the 72-h sequence. At the end of each period, Monte Carlo model simulation of the best RETAS version is executed to allow the estimation of strong aftershock (M ≥ 0.5) occurrence probability for the upcoming 2-h period. We consider the second problem by reasoning how the use of the temporal evolution of these probabilities can be applied as input for decision-making to suspend and restart the mining operations.

2 Induced seismicity in Kiirunavaara Mine

Kiirunavaara (Kiruna) iron ore mine, owned by LKAB (Sweden), is one of the world’s largest underground mines. Mining started in 1898 as an open pit mine. In mid-1950, the mine started a transition to underground mining using the sublevel caving method. The mine was declared seismically active in 2008.

The mine experiences on average 5000 seismic events per day with magnitudes up to 2.4 according to the in-mine seismic system but on May 18, 2020 a seismic event with Mw 4.2 occurred in the mine (Dineva et al., 2022). There are ~ 300 larger events (M > 1.5) recorded since 2008. The number of events with magnitude > 2 increased in the past 5 years. The Swedish National Seismic Network records the largest of these events. Induced seismicity in the mine is related to re-distribution of the local stresses around the production levels and is concentrated around the current production levels and below them (Dineva and Boskovic, 2017), but there is also a large number of seismic events that is related to the caving of the hanging wall.

The seismic events are recorded automatically by the underground in-mine seismic system, delivered by IMS (Institute of Mine Seismology, www.imseismology.org). The number of the sensors (geophones with natural frequencies of 4.5, 14, and a few of 30 Hz) in the underground seismic system changed with time and the increasing production depth. By the end of 2020, the mine had the largest underground seismic system in the world with 256 operational geophones. All parameters of the seismic events are calculated routinely by IMS after semiautomatic picking of the P- and S-arrival times. The configuration of the underground seismic system allows to estimate the accuracy of the hypocenters with average error ~ 23 m (du Toit 2015). Dynamic source parameters are calculated following a procedure similar to the one described by Nordström et al. (2017) but using systematically data only for the 18–20 sensors closest to the event hypocenter. For events of concern, data from more sensors are used.

3 Data

Many of the larger events (M > 1.5) in the Kiirunavaara Mine are followed by aftershocks, which continue usually for hours but sometimes for days. The aftershocks occur in an area in the order of hundreds of meters around the main shock. A special study on the spatial distribution of the aftershocks and their relation to the Coulomb stress changes caused by the main shock was conducted for two events in the mine (Kozlowska et al. 2021).

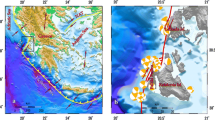
One of the aftershock series studied by Kozlowska et al. (2021) was chosen also for testing the methodology developed in the current study. The main event occurred on August 13, 2016, in one of the most seismically active blocks of the mine (Block #34). The main shock local magnitude calculated from the underground system was estimated to be 1.85. The estimation of the moment magnitude from the regional broadband seismic stations showed a much larger magnitude (M2.8). The underestimation of the magnitude was related to the limited frequency band of the sensors of the underground seismic system. For consistency of the current study, all magnitudes that are used are local magnitudes estimated by the underground seismic system. The already modeled Coulomb stress changes showed an aftershock area ~ 200 m around the main shock. A sphere with this radius, centered on the main shock, was used to select the events in the current study (Fig. 1).

Fig. 1
figure 1

Spatial distribution of the seismic events 200 m around the main shock during 72 h: a) 3D view facing NW with Levels 1022 and 1165 (blue lines); b) horizontal projection (level 1022). The red star shows a production blast ~ 38 h after the main event. Thin inclined blue lines in a) are the ore passes. The color and the size of the individual events correspond to the magnitude (see the legend). The main shock (yellow sphere) is at the center of the aftershock volume. The plots are made by mXrap software (Harris and Wesseloo 2015)

Full size image

During the chosen period of time of 72 h, there were 408 events recorded with magnitudes from − 2.6 to 0.8. Only the events in the footwall were selected for the study. The first aftershock occurred within a few seconds after the main event. In total, there were 7 larger events with M > 0 up to 40 h after the main event (Fig. 2) at distances up to ~ 160 m. Within the 72-h period, there was one production blast in the 200-m sphere (see Figs. 1 and 2) ~ 38 h after the main event at distance ~ 50 m.

Fig. 2
figure 2

Time distribution (hours after the main event/trigger) of the hourly and cumulative number of seismic events within 200 m for 72 h after the main shock on August 13, 2016. The color and the size of the individual events along the cumulative plot correspond to the magnitude (see Fig. 1). The star at time 38 h represents a production blast within the sphere. The plot is made by mXrap software (Harris and Wesseloo 2015)

Full size image

4 Considerations and approach for developing of re-entry protocol for Kiirunavaara Mine (methodology)

Taking into account the vast variety of methods and approaches already used to model mining seismicity and to tackle re-entry problems, we decided to follow several benchmarks in our investigation. It seems reasonable that when dealing with problems related to stopping and resuming mining activities, it is adequate to use seismic parameters that are continuous over time. Variations in the values of these parameters below and above certain preselected levels could control the closure and re-entry in the mines. In our current investigation, we decided to consider the occurrence probability of large events in a mining seismic sequence, which could increase seismic risk and necessitate mine area closure, as such a parameter.

For modeling the temporal decay of the chosen aftershock sequence in Kiirunavaara Mine, we selected to apply the Restricted Epidemic-Type Aftershock Sequence (RETAS) model, developed by Gospodinov and Rotondi (2006) for natural seismicity based on the assumption that not all events in the sequence, but only aftershocks with magnitudes larger or equal to a chosen triggering magnitude threshold can induce secondary aftershocks. In fact, RETAS comprises a set of model versions, depending on the chosen magnitude threshold. It has the advantage of including MOF and ETAS as its end versions and also considers all intermediate versions by verifying all possible triggering magnitudes values. In addition to model a single aftershock sequence, RETAS has been applied to depict general seismicity for several regions in Greece and proven to work well for some of them (Gospodinov et al. 2007). This motivated our choice of RETAS to analyze the selected sequence, although modeling of general seismicity remains beyond the scope of this study and is a subject of further investigations.

RETAS has also successfully been used to perform pseudo-prospective probability forecasts of strong aftershock occurrence in a seismic sequence in Greece for 30 subsequent days (Gospodinov et al. 2015). Here we apply the same approach to estimate the probability evolution of large events in a chosen sequence in Kiirunavaara Mine. Our purpose is not the elaboration of a precise re-entry protocol, but (1) addressing statistically how well the RETAS model can describe the aftershock decay rate of mining-induced seismicity and (2) adjusting the methodology for estimating the occurrence probability of larger seismic events in mines. The applicability of the results for use in the frame of re-entry guidelines elaboration was carefully examined after this.

One of the first statistical models used to describe and analyze mining seismicity and to develop re-entry protocols is the modified Omori formula/model (Utsu 1961). This model is useful for examining a particular aftershock sequence. It sets the decaying frequency of aftershocks per unit time, which is described to follow a negative power law

$$n\left(t\right)=\frac{K}{{\left(t+c\right)}^{p}}$$
(1)

where t is the time elapsed from the time of the main shock, K is a constant that depends on the total number of aftershocks in the sequence, p is a coefficient of attenuation, and c is a temporal shift. The frequency n(t) in Eq. (1) is identified with the intensity function of a point process.

For more complex aftershock sequences, Ogata (1988) introduced the idea of self-similarity into the MOF by extending the capacity of generating secondary events to every aftershock of a sequence. He called the model an Epidemic-Type Aftershock Sequence (ETAS) model, and its resultant rate density of aftershocks is given by

$$\lambda (t|{H}_{t})=\mu +\sum_{{t}_{i}<t}\frac{{K}_{0}{e}^{\alpha ({M}_{i}-{M}_{0})}}{\text{}{(\text{}t-{t}_{i}+c)}^{\text{}p}}$$
(2)

In this equation, μ is the background rate of seismic activity, ti is the occurrence time of the ith event, p is a coefficient of attenuation, and c is a constant. In this case, the history Ht consists of the times ti and magnitudes Mi of all the events which occurred before time t and the summation is taken over every ith aftershock with a magnitude stronger than the cutoff Mi ≥ M0, i.e., over all events in the sample.

The “triggered” seismicity in Eq. (2) is represented by a superposition of the modified Omori functions shifted in time. The coefficient α in formula (2) measures the magnitude efficiency of a shock in generating its aftershock activity and K0 measures the productivity of the aftershock activity during a short period right after the main shock (Utsu 1970).

As mentioned previously, MOF and ETAS fail to consider sequences in which aftershocks are being triggered not by one event (the main shock) or by all events in the sequence, but only by some “trigger” shocks. Models to cover similar cases can be grouped according to a subset of such shocks, which may include randomly distributed events (Vere-Jones and Davies 1966) or previously identified (Ogata 2001).

For the RETAS model, developed by Gospodinov and Rotondi (2006), primary events, as in Ogata (2001), are those of magnitude greater than or equal to a threshold magnitude Mth; however, contrary to Ogata (2001), the dependence of conditional intensity on magnitude is like the one in ETAS; hence, the function of the conditional intensity of this model is

$$\lambda (t|{H}_{t})=\mu +\sum_{\begin{array}{c}\text{\hspace{0.17em}}\text{\hspace{0.17em}}\text{\hspace{0.05em}}\text{\hspace{0.17em}}\text{\hspace{0.17em}}{t}_{i}<t\\ {M}_{i}\ge {M}_{th}\end{array}}\frac{{K}_{0}{e}^{\alpha ({M}_{i}-{M}_{0})}}{\text{\hspace{0.05em}}{(\text{\hspace{0.05em}}t-{t}_{i}+c)}^{\text{\hspace{0.05em}}p}}$$
(3)

Here the summation occurs for all aftershocks with magnitude bigger than or equal to \({M}_{th}\), which occurred before time t. As can be seen, the model described by Eq. (3) is quite similar to the ETAS model, with the restriction \({M}_{i}\ge {M}_{th}\). For this reason and for reasons of clarity, the authors named the model a Restricted Epidemic-Type Aftershock Sequence (RETAS) model. A specific feature of the RETAS model represented by Eq. (3) is that it implies a possible interaction between aftershocks in a set, which allows each of them of magnitude \({M}_{i}\ge {M}_{th}\) to cause further shocks of subsequent generations. Events smaller than \({M}_{th}\), however, are excluded from the triggering process and are only considered as “offsprings.”

By putting different values for the triggering magnitude \({M}_{th}\) in the range \({M}_{0}\le {M}_{th}\le {M}_{m}\), where \({M}_{m}\) is the main event magnitude, a number of RETAS model versions can be verified. Gospodinov and Rotondi (2006) have also elaborated a Fortran program to calculate the best-fit RETAS model parameters by maximizing the log-likelihood function

$$\mathrm{log}\,L(\theta )=\sum_{i=1}^{N}\mathrm{log}\,{\lambda }_{\theta }(\text{}{t}_{i}\,|\,{H}_{{t}_{i}})-{\int }_{0}^{T}{\lambda }_{\theta }(t|\,{H}_{t})dt$$
(4)

where \(\left[0,T\right]\) is the time period under study, during which \(N\) earthquakes occur at times \({t}_{i}\left(i=1,\dots ,N\right)\) with a low magnitude cutoff \({M}_{0}\). The best version for certain data is identified by the smallest value of the Akaike information criterion (AIC) for each version

$$AIC=-2\mathrm{maxlog}L+2k$$
(5)

where \(k\) is the number of parameters used in the model and L is the likelihood function of the process (Akaike 1974). It has to be pointed out that for the marginal values of the triggering magnitude level \({M}_{th}={M}_{m}\) and \({M}_{th}={M}_{0}\) the RETAS model coincides with the MOF or the ETAS model, respectively. In that way by applying RETAS, we also verify these two models together with all intermediate cases. These advantages motivated us to apply RETAS in the present study. After identifying the best RETAS version for our data, we may apply the Reasenberg and Jones model (1994) as it allows to evaluate the occurrence probability evolution of a strong event in the sequence. According to this model, if the temporal distribution is presented by MOF, the process intensity of magnitude M or larger is given by

$$\uplambda \left(\mathrm{t},\mathrm{M}\right)={10}^{\mathrm{a}+\mathrm{b}\left({\mathrm{M}}_{\mathrm{m}}-\mathrm{M}\right)}{\left(\mathrm{t}+\mathrm{c}\right)}^{-\mathrm{p}}$$
(6)

Here t is the time since the occurrence of the main shock with magnitude Mm. For a non-stationary Poisson process, the probability P for at least one aftershock of magnitude between M1 and M2, occurring in the period (T1, T2) after the main shock, is given by:

$$P({M}_{1},{M}_{2};{T}_{1},{T}_{2})=1-\mathrm{exp}\left[-\underset{{M}_{1}}{\overset{{M}_{2}}{\int }}\underset{{T}_{1}}{\overset{{T}_{2}}{\int }}\lambda \left(t,\text{\hspace{0.17em}}M\right)dM dt\right]$$
(7)

By merging Eqs. (6) and (7), this probability can be calculated analytically. As for the present study, we applied RETAS and not MOF only. There was only one sample in which the data followed the MOF formula as the best-fit model and we ran Eqs. (6) and (7) to calculate the occurrence probability. As for the other data samples, for which the best-fit model was another version of RETAS, different from MOF, instead of an analytical solution the number of events in Eq. (7) for the period (T1, T2) has been determined by a Monte Carlo simulation of RETAS for that period. Random simulations of RETAS have already been performed for natural seismicity analysis (Gospodinov and Rotondi 2006; Gospodinov et al. 2007). Papadimitriou et al. (2013), Karakostas et al. (2014), and Gospodinov et al. (2015) also apply model simulation after RETAS, which allowed the successful estimation of the occurrence probabilities of strong aftershocks in several seismic sequences in Greece.

The simulation procedure for event times was first described by Gospodinov and Rotondi (2006) where they followed the thinning method (Ogata 1999). As for the size of each event, they have assumed that magnitude and occurrence time are independent and the magnitude follows an exponential distribution with a parameter \(\beta =b{log}_{e}10\), where b is the parameter of the Gutenberg-Richter formula (1944). We executed the same procedure in our present analysis.

5 Results from the RETAS model analysis and occurrence probability forecasting of strong aftershocks

Following the main purpose of this paper which is to validate to what extent the occurrence probability of a strong aftershock in a sequence can be used to develop a re-entry protocol, we must be able to estimate this probability. That means that in some way we have to simulate a nearly real-time prospective analysis.

To test this idea, calculations of strong event occurrence probability were performed for subsequent periods in the magnitude range M = 0.5–1.85. The lower limit M=0.5 of the magnitude here was chosen, which is the lowest magnitude that caused damage in the mine. Following our purpose to analyze prospective forecasting, we performed calculations based on data up to the beginning of the forecast period.

Seismicity rate and hence the number of aftershocks that will occur in a future forecast period depends on both all events that occurred before the beginning of this period and aftershocks that would occur during the period. We do not have prior information about these recent events and therefore they were simulated using the selected model. In our study, we chose the forecast period to be 2 h. The main idea in our analysis was to follow a situation in which the occurrence probability of strong aftershocks is predicted prospectively over the forecast period of time. To this end, several basic steps have been followed. The entire catalog of the aftershock sequence was divided into subsequent sub-catalogs, each of which started from the beginning of the sequence and lasted 2 h longer than the previous one. The number of events N = 39 in the shortest first two-hour period is sufficient to correctly identify the best-fit RETAS version for that period. Each sub-catalog was initially analyzed by ZMAP (Wiemer 2001) to define its recurrence law parameters, mainly the b-value from the Gutenberg-Richter law and the magnitude of completeness, which is needed for the model simulation. Then, by applying the RETAS model, the best-fit model version was identified for each sample. After that, a Monte Carlo simulation of the selected model was performed for the forecasted period of 2 h after the end time of each sub-catalog. The simulation is done at the beginning of the following 2-h period and it allows us to make an occurrence probability forecast of strong aftershocks for that period (see Eq. (7)). By executing the above steps for all samples, we got the evolution of the occurrence probability for the subsequent 2-h periods, which cover the duration of the whole aftershock series.

We started our analysis by applying the RETAS model to the data for the entire examined period of 72 h (3 days). First, the Gutenberg-Richter relation was obtained for all 408 events with magnitudes from − 2.6 to 0.8 and the graph is revealed on Fig. 3. The identified completeness magnitude was M0 =  − 1.7 but it varied over time for the other sub-samples. To be sure that the data we explore contain all events that occurred and considering the fact that usually the magnitude of completeness is higher at the sequence onset, we decided to set this value to M0 =  − 1.4 for the 72-h data. For simplicity in the analysis, we later used the same magnitude of completeness for all samples. All events weaker than M0 for each corresponding sample were excluded and the rest were analyzed through the RETAS model (the background rate was assumed to be zero for all samples).

Fig. 3
figure 3

Gutenberg–Richter graph for the selected main shock-aftershock series (200 m around the main shock within 72 h after it). The colored isolines correspond to the probability envelopes contour (see the legend). The plot is made by mXrap software (Harris and Wesseloo 2015)

Full size image

From the magnitude distribution on Fig. 3, it turns out that the b-value (slope of the Gutenberg-Richter graph) is 0.99 ± 0.06. A number of N = 139 aftershocks have magnitudes larger or equal to M0 for the total data and they were processed through RETAS. The minimum AIC value was obtained for triggering magnitude Mth = M0 (see Fig. 4a) that is the best-fit RETAS version coincides with ETAS.

Fig. 4
figure 4

a) AIC values (Eq. (5)) vs triggering magnitude. The minimum AIC value is for Mth = M0 that is the best-fit model is ETAS; b) real (circles) and model cumulative number (thick blue line by Eq. (10) for the total data sample. Real data values are fitted well by the identified model staying within the model error bounds (dashed lines) except for the first hour of the sequence.

Full size image

We provide a picture of the aftershock sequence temporal evolution by comparing the cumulative number of events with the predicted rate, calculated after the best-fit RETAS version (see Fig. 4b). The expected cumulative number of events \(\Lambda \left(S,t\right)\) in a certain period (S, t), as calculated by the model, can be obtained by Eq. (8):

$$\Lambda \left(S,t\right)=\underset{S}{\overset{t}{\int }}\lambda \left(v\right)dv$$
(8)

We can use Eq. (3) to calculate the error bounds and hence the significance of deviations of real to model cumulative numbers. We have to point out that we assume μ = 0 for the aftershock sequence. As each term in the summation in Eq. (3) represents a MOF process, then the total process depicted by this equation is a superposition of non-stationary Poisson processes. The resulting process is a non-stationary Poisson process itself and for such processes both the common mean and the variance are calculated by Eq. (10) for S = 0 (Karlin and Taylor 1984). In this way, the latter equation provides a tool to estimate the standard deviation of the expected cumulative number by which we defined the error bounds. A similar approach was followed to define the error bounds when assessing the difference between the simulated and the real data for the two-hour periods.

On Fig. 4b, we exhibit the real (circles) and model (thick blue line) cumulative numbers for the entire data, calculated after the best-fit model. There real values stay within the error bounds except for the first hour of the sequence. There they slightly surpass the model curve, which can be interpreted as an indication of more intense clustering of strong shocks at the beginning of the sequence than expected if random.

There are several events with magnitudes greater than M = 0.0 at about 1.5–1.6 days after the main event (dashed ellipse on Fig. 4) which most probably are related to the production blast that took place at that time.

Applying the defined steps to all data samples from two hours to 72 h, we first recognized the best-fit RETAS version for each of them (see Table 1 and the electronic supplement). Plots of AIC vs. the triggering magnitude Mth for the obtained different RETAS model versions for all 36 data samples were presented as an electronic supplement (the minimum AIC value there recognizes the best RETAS version).

Table 1 Results from the RETAS analysis performed for the data samples at the end of each 2-h period (b-value is from the G-R law and p-value is from Eq. (5), respectively). The last column presents the estimated 2-h probabilities for aftershock occurrence
Full size table

All b-values of the G-R law for different samples were also estimated by the ZMAP software (Wiemer 2001) as they are important considering the magnitude distribution of the events from each sample and hence the occurrence probability calculation (Eq. (7); see Table 1).

The identified triggering magnitudes Mth vs. time were plotted in Fig. 5. The observed Mth variability for the data samples (see also Table 1) reveals a complete change of the rate decay pattern, hence the clustering pattern, during the sequence evolution. The best-fit model for the first 2-h period is MOF; then, the model changes to RETAS for the next several data samples with Mth ∈ [− 0.7, − 1.18] and after the 20th hour of the sequence the best-fit model shifts to ETAS and remains so until the end of the aftershock sequence.

Fig. 5
figure 5

Change of the triggering magnitude Mth, hence the aftershock clustering pattern with time for different data samples

Full size image

In fact, the obtained diverse best-fit models for different data samples show the advantage of using a model like RETAS compared to ETAS and MOF models, as the one to offer a set of possible versions, adequate to each specific data.

One of the key purposes of this paper is to verify the applicability of RETAS to model the temporal evolution of a mining seismicity sequence allowing the calculation of strong event occurrence probability in it. Based on the chosen RETAS version for each data sample, we simulated the best-fit model for the next 2-h period after the sample. The simulation was done within a certain magnitude range, the lower limit being equal to the determined M0 and the upper limit equal to the main event magnitude.

To forecast the aftershock rate for the 2 h after the time to which the corresponding data sample was prepared, we had to consider all events in the sample, which were stronger than or equal to the magnitude threshold Mth and the ones that would occur during the next 2 h. The latter events were obtained by Monte Carlo simulation of the selected best-fit model. For each forecast 1000 different synthetic 2-h catalogs were simulated by following the thinning method (Ogata 1999). The seismic rate was estimated by taking the average value. Considering the fact that for this process the mean and the variance coincide, we calculated the standard deviation and used it to form the error bounds. The estimated average was then inserted to Eq. (7), and by integrating in the magnitude range (M0.5–M1.85), we calculated the occurrence probability of at least one event in this range.

On Fig. 6, we displayed the estimated 2-h occurrence probabilities of M0.5–M1.85 aftershocks in the examined mining sequence, estimated on the basis of the identified best-fit model (thick red line). Real activity (circles) for each 2 h, turned into probability, was plotted, too. The latter was calculated by placing the actual number of occurred aftershocks for a given forecast period in Eq. (7) and the corresponding probability is obtained after the period is over.

Fig. 6
figure 6

Evolution of aftershock occurrence probability (M0.5–M1.85). Thick red line shows the estimated probability for each two hours following the simulated best-fit model. Dashed lines reflect the estimated probability following the MOF formula as follows: (1) with estimated parameters for the first two hours only (lower green dashed line); (2) with estimated parameters for the subsequent data samples (upper blue dashed line). Red circles display the calculated probability on the basis of the real number of occurred events for each 2 h

Full size image

There we have also exhibited the calculated occurrence probabilities, based not on the identified best-fit RETAS version for each sample, but only on MOF. We considered two cases—MOF models on data only for the first 2 h (lower dashed line on Fig. 6) and on the subsequent data sets (upper dashed line on Fig. 6). For the first case, the MOF model fails to fit well real data. For the second case, the model (in fact a set of subsequent MOF models) is nearer to real values, but still cannot capture the secondary activation in the 1.5–2-day period of the sequence while the RETAS model versions cover this rate increase quite well. During this period of time at about the 38th hour, there was a production blast.

The secondary probability increase on Fig. 7, forecasted by RETAS and starting at about 1.6 days after the main shock, is quite probably related to the production blast which could be the cause of several strong aftershocks, taking place at that period (see Fig. 4).

Fig. 7
figure 7

Evolution of aftershock occurrence probability (M0.5–M1.85). Thick blue line shows the estimated probability for each 2 h following the simulated best-fit model. Lower and upper dashed lines reflect the calculated error bounds considering that for Poisson processes the mean and the variance are equal

Full size image

In fact all the analysis that we performed up to now was aiming at validating the applicability of the RETAS model to represent the temporal progress of a mining-induced aftershock sequence and to estimate the occurrence probability progress of strong aftershocks in the sequence.

We now face the key question of how to use the results obtained to develop guidelines for re-entry protocols development for the mines. Let focus on Fig. 7 where we display the estimated occurrence probability of strong aftershocks (M0.5–M1.85) in the sequence together with the error bounds.

Let us imagine that in some way we have determined a limit value of the estimated probability of a strong aftershock (in Fig. 7, we have chosen quite arbitrarily this value to be 0.1), over which there is a good reason to cease activity in the mine (or in part of it) and to evacuate workers. Then, the approach we have examined so far allows, at a given moment, based on the seismicity that has already occurred and the possible simulated one for the forecast period, to determine the occurrence probability and to decide whether the calculated probability exceeds the limit. In our case that was done for each 2 h, this period can easily be changed. We consider as an advantage of the RETAS model approach that the identified “alarm” period in Fig. 7 (1.5–2 days from the beginning) is a period with really increased seismic activity. The approach we use depends on a number of external parameters (“alarm” probability, magnitude range of events whose probability is being estimated, magnitude of completeness, forecasting period, etc.) that we will discuss in the next section.

6 Discussion and outlook

As shown in the previous sections, the probability evolution of strong aftershocks in time may be used to assess seismic hazard and decide when to close and re-open specific mine areas. This probability depends on different aspects, the applied stochastic model being one of the most important ones. The MOF model is the easiest to be used for this purpose because the history of the process includes only the main event occurrence time and combining Eq. (6) and Eq. (7) directly allows to calculate the needed occurrence probability without any necessity to simulate the model. MOF, however, is only applicable to the so-called simple aftershock sequences which are few among all series that occur and not relevant to model overall mining seismicity.

ETAS is an alternative of MOF for complex aftershock sequences and can be used for occurrence probability calculation by its simulation for the forecasted period but it is only one marginal version of RETAS and is less appropriate for cases when the clustering pattern changes during the sequence progress. As it is revealed in Fig. 5 and Table 1, being a set of different versions, the RETAS model provides a possibility to follow changes in the clustering type. Following Fig. 5, one can find that for the first two hours of the sequence the best-fit model is the MOF one. Our explanation of this result is that the clustering pattern in time during this period was mainly controlled by the stress changes due to the coseismic slip of the first main event. Then, the clustering type changes and starts following the RETAS model (for the next data samples up to the time period of 20 h), which reveals that the randomness in clustering increased. After that, clustering in the sequence becomes even more random the data temporal evolution being modeled best by ETAS. In these cases, the AIC plots start to change more slowly because much less events occur in the following 2-h periods. We want to emphasize that it is the application of the RETAS model that has enabled the possibility to capture the clustering pattern variation of the sequence (Figs. 5 and 6 and Table 1). Generalizing our results on the stochastic modeling part of the occurrence probability estimation, we conclude that RETAS is applicable to identify the model version, which is best fitting a certain mining-induced aftershock sequence and in that way to provide adequate grounds for subsequent probability calculations of strong events occurrence in a sequence. As a model RETAS is relatively good to forecast seismicity rate and thus the occurrence probability evolution (see Fig. 7), but is not principally adept for predicting the occurrence of a certain large event (see also Marzocchi and Lombardi 2009).

The occurrence probability depends also on other parameters as the magnitude of completeness M0 and the upper and lower magnitude limits for the model simulation. The choice of the lower limit is rather a technical problem, related to the network detectability and here is set to be equal to the completeness magnitude, M0. As M0 varies over time, in our analysis, we chose its value to be M0 =  − 1.4 for all data samples for the sake of simplicity. The upper magnitude, needed for the simulation, is a matter of choice, which in our study is equal to the main event magnitude but its selection could also be set based on the seismicity history of the examined mine area and the information about the geomechanical settings of the examined volume.

As we already mentioned, past seismicity has been used for operational purposes (forecasting) for natural seismicity. Jordan et al. (2011) generalized different aspects of operational earthquake forecasting, also based on continuous probability calculations as in our study. What makes a difference in our approach is the application of the RETAS model, which increases the number of model versions (keeping MOF and ETAS as end cases).

In our investigation, we chose 2-h forecasting periods of the occurrence probability. On the one hand, the forecast period should be short due to the fast dynamics of the processes and the need for a corresponding reaction of the operational staff who decides to restrict/allow the access to certain areas in the mine. On the other hand, this period should be long enough to suit the actual situation in the mine where certain time is needed to perform suspension or re-entry operations.

When analyzing the 2-h occurrence probability, we have to bear in mind that it was calculated after the addition rule in probability theory, which means that this is the total probability for the next 2 h. In fact, the forecast is for a probability of at least one event in the considered magnitude range for the entire period of the following 2 h, which means that for a shorter period this probability would be different. We may tune our algorithm and software on a different probability forecasting period (e.g., 4 h) and perform model simulation after each new event that occurred to follow the probability evolution in more details.

This is the first time RETAS model was used to analyze and forecast mining seismicity. The outlook for its further utilization concerning seismicity rate modeling and its application for re-entry protocol elaboration addresses several issues which must be considered.

The choice of an appropriate value of the limit occurrence probability over which it would be reasonable to temporarily suspend the activity in the mine or part of it is beyond the scope of the present study. However, this value is crucial when discussing the possible mine closure rules; therefore, it deserves a special attention. In our study, we have arbitrarily chosen this value to be 0.1. The choice of the limit probability will most probably be empirically based on the level of the background seismicity. Additional case studies are required to define the probability parameter and also to establish some similarities and variations between the series and more practical rules for using in real time.

There is one more issue related to the use of mining-induced seismicity as a basis for occurrence probability estimation and from there to re-opening protocol development. For natural seismicity, RETAS is based on the assumption that seismicity rate at a certain time during an aftershock sequence is controlled by the main event and other aftershocks that have occurred previously hence the latter influence occurrence probabilities of future seismic events. Aftershock process history, including event magnitudes and times (see Eq. (3)) seems enough to fit well crustal seismicity on which we have full data about magnitudes. However, the seismicity in mines is more complex. Seismicity rate within an aftershock sequence could be affected not only by the main event and previously occurred aftershocks but also by changes with time due to mining activities and most importantly blasts. While our present search revealed that RETAS is applicable to model both a single aftershock sequence and eventually overall seismicity, we cannot successfully use it for the latter case unless we find a way to include the post-blasts seismicity in the whole seismicity-induced process.

Stochastic modeling and probabilistic forecasting of continuous seismicity in mines, which can be used as a basis for re-entry protocol considerations, is a challenging task and it necessitates the application of RETAS not only on aftershocks but also to model general seismicity. The model could be applied on data, covering time periods much longer than an aftershock sequence. Such an objective requires the consideration also of the spatial distribution of events, which makes the development of a spatial extension of the RETAS model a requisite and practical purpose.