SWprocess: a workflow for developing robust estimates of surface wave dispersion uncertainty

Abstract

Non-invasive surface wave methods are increasingly being used as the primary technique for estimating a site’s small-strain shear wave velocity (Vs). Yet, in comparison to invasive methods, non-invasive surface wave methods suffer from highly variable standards of practice, with each company/group/analyst estimating surface wave dispersion data, quantifying its uncertainty (or ignoring it in many cases), and performing inversions to obtain Vs profiles in their own unique manner. In response, this work presents a well-documented, production-tested, and easy-to-adopt workflow for developing estimates of experimental surface wave dispersion data with robust measures of uncertainty. This is a key step required for propagating dispersion uncertainty forward into the estimates of Vs derived from inversion. The paper focuses on the two most common applications of surface wave testing: the first, where only active-source testing has been performed, and the second, where both active-source and passive-wavefield testing has been performed. In both cases, clear guidance is provided on the steps to transform experimentally acquired waveforms into estimates of the site’s surface wave dispersion data and quantify its uncertainty. In particular, changes to surface wave data acquisition and processing are shown to affect the resulting experimental dispersion data, thereby highlighting their importance when quantifying uncertainty. In addition, this work is accompanied by an open-source Python package, swprocess, and associated Jupyter workflows to enable the reader to easily adopt the recommendations presented herein. It is hoped that these recommendations will lead to further discussions about developing standards of practice for surface wave data acquisition, processing, and inversion.

1 Introduction

Non-invasive surface wave methods are increasingly being used as the primary technique for estimating a site’s small-strain shear wave velocity (Vs) for engineering projects. Non-invasive techniques are being selected due their speed and ease of acquisition and ability to be deployed in areas and geologies adversarial to traditional invasive techniques. The most common non-invasive surface wave techniques include spectral analysis of surface waves (SASW) (Stokoe et al. 1994), multi-channel analysis of surface waves (MASW) (Park et al. 1999), refraction microtremor (ReMi) (Louie 2001), and microtremor array measurements (MAM) (Aki 1957; Capon 1969; Lacoss et al. 1969). While this paper will focus on the application of MASW and MAM methods for developing a workflow to quantify experimental dispersion data uncertainty, the principles discussed herein can easily be extended to any other surface wave methods used to generate dispersion data.

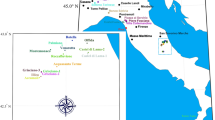
MASW (Park et al. 1999) is an active-source surface wave testing technique that utilizes a linear array of sensors and a surface wave generating source operated by the experimenters. MASW arrays typically contain between 12 and 96 sensors set at a constant spacing between 0.5 and 5 m. A schematic plan view of a typical MASW array is shown at the center of several larger, circular MAM arrays in Fig. 1a, with the linear MASW array shown in greater detail in Fig. 1b. The sensors used for MASW are most commonly single component geophones (velocity transducers) with a resonant frequency of approximately 5 Hz. A MASW array may be used to record waveforms with strong Rayleigh- or Love-wave content. To generate waves with strong Rayleigh-wave content, a vertical source impact is most commonly used. To measure waveforms with strong Rayleigh-wave content, the array should consist of either vertically oriented geophones or horizontal geophones oriented in the radial (in-line) direction. To generate waves with strong Love-wave content, a horizontal source impact is made on a shear-plank coupled to the ground surface in the cross-line direction. To measure waveforms with strong Love-wave content, the array should consist of horizontal geophones oriented in the transverse (cross-line) direction. The source, regardless of type (Rayleigh or Love), is operated on a line collinear with the array’s sensors to ensure the measurement of true, rather than apparent, surface wave velocities. Although it may be common for some to use only a single source location per array, the authors, for reasons discussed later, strongly recommend using multiple source locations. Ideally, the source would be operated on both sides of the array, as clearly shown in Fig. 1b, but if this is not possible it should at least be operated in multiple locations on one side of the array in order to mitigate nearfield effects and help quantify dispersion uncertainty. The acquisition stage of MASW concludes with the recording of waveforms (one per sensor) for each source impact. An example of a set of MASW time-domain records is shown in Fig. 2a. For a more in depth discussion of the acquisition of waveforms for MASW, the reader is referred to the Guidelines for the Good Practice of Surface Wave Analysis (Foti et al. 2018).

Fig. 1

source and passive-wavefield surface wave testing layout. The layout includes a linear multi-channel analysis of surface waves (MASW) array with several source locations off either end and three concentric circular microtremor array measurement (MAM) arrays of increasing size. Note that b is a zoomed-in view of the center of a and serves to highlight the MASW array and smallest MAM array

Plan view of a combined active-

Fig. 2

source and/or passive-wavefield surface wave time-domain records, as shown in a and c, respectively. The workflow uses existing processing methods to transform these time-domain records into raw estimates of the site’s experimental surface wave dispersion data, as shown in b and d. The workflow requires and facilitates the repetition of this process as a means to combine raw dispersion data that accounts for aleatory variability (e.g., arrays of different sizes and/or locations across the site) and epistemic uncertainty (e.g., different source locations, time windows, and processing methods), as shown in e. The workflow concludes with the manual removal of low-quality/outlier dispersion data using interactive trimming, followed by the calculation of dispersion statistics, as shown in f

An overview of the proposed workflow for developing estimates of a site’s experimental surface wave dispersion data with robust measures of uncertainty. The workflow begins after the acquisition of active-

MAM (Aki 1957; Capon 1969; Lacoss et al. 1969) is a passive-wavefield surface wave testing technique which uses multiple sensors deployed in a two-dimensional array (circular, triangular, or L-shaped) to record the propagation of ambient surface waves. Sensors are most commonly three-component broadband seismometers capable of recording frequencies between approximately 0.05 (20-s period) and 100 Hz; however, other sensors with more limited frequency bandwidth may also be used. Arrays may be composed of any number of sensors; however, they most commonly contain between 4 and 15 stations. An example MAM array which is composed of eight stations set out in a circular pattern (one at the center and seven around the circumference) is shown in Fig. 1b. To compensate for a limited number of stations, and in order to capture surface waves over a broad range of frequencies/wavelengths, it is common to deploy multiple MAM arrays of varying size consecutively (refer to Fig. 1a). Arrays typically have maximum interstation distances between 30 and 1 km, depending on the desired depth of profiling and spatial constraints at the site, although larger and smaller arrays are possible. Arrays are typically left to record ambient wavefields for between 30 min and several hours, with the largest arrays, which are used for recording the lowest frequencies/longest wavelengths, demanding the longest recording times. The acquisition stage of MAM data concludes with the recording of ambient noise records. At a minimum, the vertical component at each station is processed as a means to extract passive-wavefield Rayleigh wave dispersion data. However, recent innovations in passive-wavefield processing have made it possible to extract both Rayleigh and Love wave dispersion data using three-component processing methods (e.g., Wathelet et al. 2018). An example set of passive-wavefield records showing only the vertical components of eight broadband stations during MAM testing is shown in Fig. 2c. Note that we choose to show only the vertical component for simplicity. For additional detailed information about the acquisition of MAM data, the reader is again referred to the Guidelines for the Good Practice of Surface Wave Analysis (Foti et al. 2018).

Following acquisition, active-source and passive-wavefield recordings need to be transformed into experimental dispersion data. Some example sets of MASW and MAM dispersion data are shown in Fig. 2b and d, respectively. Dispersion, in this context, refers to a property of surface waves where their phase velocities are frequency (or, equivalently, wavelength) dependent. Meaning, surface waves of different frequencies/wavelengths travel at different phase velocities. Importantly, the site-specific dispersion trends exhibited by surface waves are related to the subsurface materials through which they travel, thereby allowing information about a site’s subsurface material properties to be inferred from measurements of a site’s surface wave dispersion. An intuitive, albeit overly simplified, approach to understanding surface wave dispersion begins with the approximate relationship between wavelength (λ) and the depth through which a surface wave propagates. In general, the depth of material which most significantly affects the surface wave’s phase velocity is expressed as $\lambda /df$, where $\lambda$ is the wavelength of interest and $df$ is the depth factor, which is typically 2 or 3 (Foti et al. 2018). Therefore, surface waves with shorter wavelengths (higher frequencies) sample the near-surface materials, whereas longer wavelengths (lower frequencies) will sample both the near-surface materials (although to a lesser extent than shorter wavelengths) and the materials at greater depths. With each wavelength (or frequency) of the surface wave sampling different materials, the wave’s phase velocity can be thought of as a complex average of the subsurface material properties over the depths probed by the given wavelength. As the remainder of this work addresses how to transform experimental wavefields into measurements of a site’s surface wave dispersion, including robust estimates of uncertainty, we will end this brief introduction to dispersion data here. However, it is important to point out that after dispersion data are obtained from the processing stage, there is one final stage of surface wave testing, called inversion, that is required to turn the dispersion data into estimates of the site’s 1D subsurface material properties, with particular interest in obtaining the Vs profile. The inverse problem involved in obtaining realistic layered earth models from surface wave dispersion data is inherently ill-posed, non-linear, and mix-determined, without a unique solution (Cox and Teague 2016). As such, the results obtained from inversion are highly dependent on the quality of the dispersion data and its associated uncertainties. The inversion process must be conducted rigorously to propagate dispersion uncertainties forward into the resulting Vs profiles, as realistic estimates of Vs uncertainty are often required for subsequent engineering analyses (e.g., seismic site response). For a detailed discussion of surface wave inversion and the need to appropriately account for dispersion uncertainty, the reader is referred to two recent publications by the authors on this topic (Vantassel and Cox 2021a, b). Inversion will not be discussed further herein.

As discussed by Griffiths et al. (2016) and Teague and Cox (2016), the uncertainty inherent in experimental surface wave dispersion data is the result of both aleatory and epistemic uncertainties. Unfortunately, these sources of uncertainty are impossible to decouple in surface wave dispersion data and, therefore, must be handled simultaneously. While a full discussion of these uncertainty categories is beyond the scope of this paper, we briefly note that aleatory uncertainty refers to the inherent randomness of the property being measured, whereas epistemic uncertainty refers to uncertainty stemming from a lack of knowledge. When using these terms in reference to site characterization, aleatory uncertainty, commonly referred to as aleatory variability, is generally used in reference to the spatial variability of material properties across a site, whereas epistemic uncertainty is generally used in reference to the many judgment-based decisions made during data acquisition and processing. Aleatory uncertainty in surface wave measurements is due to the use of arrays that span relatively large areas and, therefore, spatially average (both vertically and horizontally) the materials within their extents. This is particularly true when larger and larger arrays are used in order to profile deeper and deeper. As such, the degree of aleatory uncertainty incorporated in the dispersion data will largely be controlled by choices made during data acquisition (e.g., the size of arrays used and/or the use of multiple arrays spread across a site to purposely investigate spatial variability), but aleatory variability is inherent in the dispersion data and cannot be removed or quantified separately from epistemic uncertainty. Epistemic uncertainty in surface wave measurements is due to the many choices made during data acquisition (e.g., source types and locations, receiver spacings) and dispersion processing (e.g., number of time records stacked, waveform filtering and/or muting, wavefield transformation method). This paper will focus primarily on establishing procedures that can be used to account for various sources of epistemic uncertainty in surface wave processing, as epistemic uncertainty in experimental dispersion data should be considered regardless of how data acquisition was performed. The authors strongly encourage the reader to think critically about how their approach to data acquisition can be designed/improved to best account for these two important categories of uncertainty.

Figure 2 presents a broad overview of the proposed workflow for developing estimates of a site’s surface wave dispersion data with robust measures of uncertainty. This overview is presented to give a very high-level view of topics we intend to discuss in more depth later in the paper. Figure 2a shows the time-domain records from a single source recorded by the vertical components of 24 receivers on an active-source MASW array, while Fig. 2c shows ambient noise recordings from the vertical components of an eight-station MAM array. These time-domain wavefield measurements, the entire time record in the active case and only a single portion/window of the time records in the passive case, are processed to produce observations of the site’s surface wave dispersion data, as shown in Fig. 2b and d, for the MASW and MAM data, respectively. In order to quantify dispersion data uncertainty, the processing is repeated using various time-domain records from MASW and/or MAM, including potentially using various processing techniques (e.g., different wavefield transformations), to ultimately produce many distinct observations of the site’s surface wave dispersion data, as shown in Fig. 2e, where the MASW and MAM dispersion data have been combined in preparation for calculating dispersion statistics. As some of the time-domain recordings and/or processing techniques will not produce good estimates of the site’s dispersion data, for example, active-source records with significant offline noise, or ambient noise records without coherent surface wave energy, low-quality estimates need to be removed prior to calculating dispersion statistics so as to not bias the resulting surface wave dispersion data. The removal of low-quality dispersion data through a manual, interactive trimming process is subjective and non-trivial in many cases (e.g., when contributions from several modes must be segregated), and care must be taken by the analyst not to remove data that represents realistic uncertainty. The surface wave dispersion data after interactive trimming is shown in Fig. 2f. The trimmed dispersion data can then be used to quantify the site’s surface wave dispersion uncertainty, as shown with the error bars representing the mean ($\mu$) and $\pm$ one standard deviation ($\sigma$) (i.e., the 68% CI) dispersion data, which is consistent with experimental dispersion data being normally distributed (Lai et al. 2005). The details required to perform each step of this process are discussed below.

This paper presents a workflow for transforming active-source and passive-wavefield time-domain surface wave records into estimates of a site’s surface wave dispersion data with robust measures of uncertainty. In order to help users more easily implement this workflow, we have developed an open-source Python package called swprocess (Vantassel 2021) that incorporates all of the data processing and statistical calculations discussed herein. However, the principles of this workflow are software agnostic and can be applied without the use of swprocess if desired. The paper begins with a discussion of the factors to be considered during active-source processing in order to develop the best possible estimates of surface wave dispersion data. Following this discussion, active-source data from a real site are processed and summarized into a statistical representation of dispersion data accounting for aleatory and epistemic uncertainty. Next, the paper discusses the parameters of importance for passive-wavefield processing to produce quality estimates of surface wave dispersion data. The paper concludes with an example from another real site where both active-source and passive-wavefield data were acquired, processed, and combined into broadband statistical representations of both Rayleigh and Love dispersion data accounting for aleatory and epistemic uncertainty. Throughout the paper, a variety of experimental datasets, acquired by the authors over the past 5 years, have been used to illustrate key points. We hope that the use of multiple, unique datasets gives the reader clear examples of the issues discussed and an appreciation for the variety and complexity of dispersion data encountered in practice.

2 Active-source processing

2.1 Signal preprocessing

We begin our discussion with active-source MASW processing. The purpose of MASW processing is to transform active-source time-domain records from the time-offset (t-x) domain to the frequency-phase velocity (f-v) domain to allow for the identification of frequency-velocity pairs with high wave power, which correspond to the site’s surface wave dispersion data. Before discussing the details of the wavefield transformation process, it is important to first discuss the impact of preprocessing the time-domain records on the resulting dispersion image (i.e., wave power as a function of frequency and velocity). As stated previously, MASW data acquisition concludes and processing begins with time-domain records saved from each source impact (Park et al. 1999). As multiple source impacts at each source location are recommended to increase the signal-to-noise ratio (SNR), there is a question as to how those individual records should be handled. Common alternatives include the following: (1) processing each time-domain record individually without stacking as a means to estimate uncertainty, (2) processing each time-domain record individually and stacking the resulting dispersion images in the f-v domain prior to estimating dispersion uncertainty, and (3) stacking each record in the time domain and then transforming the stacked record into the f-v domain prior to estimating uncertainty. As shown below, the choice of which alternative to use will affect the dispersion estimates and their associated uncertainty bounds, so it is important to know which alternative(s) are superior. In addition, another common geophysical preprocessing technique which can be combined with any of the three alternatives just described is time-domain muting. Time-domain muting involves the user manually identifying the predominantly surface wave-portion of the record and setting the remainder of the record to zero. Time-domain muting can be an effective approach to enhancing the SNR of the portion of the signal one is most interested in. However, it involves significant user interaction and a potentially subjective assessment of the acquired wavefield. In summary, the four preprocessing techniques which we will consider using examples below include the following: no stacking, no stacking with time-domain muting, frequency-domain stacking, and time-domain stacking. While we do not consider the muting of records prior to frequency-domain stacking or after time-domain stacking, we note that such processing combinations are possible, although quite uncommon.

The four preprocessing techniques discussed above are first compared at a site with significant background noise (i.e., a “noisy” site). A waterfall plot illustrating one set of experimental MASW waveforms (24 vertical receivers spaced at 2-m intervals) acquired at this noisy site with a vertical sledgehammer source located 20 m off of the end of the array is shown in Fig. 3a. Clear surface wave arrivals are visible on all receivers until a distance of approximately 20 m from the first receiver, where the background noise exceeds the signal and masks the surface wave arrival. The dispersion image resulting from the wavefield transform of the unstacked record is shown in Fig. 4a. The transformation used in this case is the frequency-domain beamformer (FDBF) with cylindrical-wave steering vector and square-root-distance weighting (Zywicki 1999; Zywicki and Rix 2005). More details about the FDBF and other common wavefield transformation methods are discussed at length later in the paper. The coloring of each dispersion image indicates the calculated wavefield power normalized relative to the maximum at each processing frequency; cool colors indicate low wave power and warm colors indicate high wave power. The white circles in Fig. 4a indicate the peak power at each frequency where a clear, presumably Rayleigh wave fundamental mode (R0) trend exists in the dispersion image. These peak power points represent the dispersion data extracted from the unstacked, noisy MASW time records from Fig. 3a. Figure 4b shows the dispersion image obtained from the same wavefield transformation applied to the unstacked time-domain records after muting. The location of the muting window is shown in Fig. 3a using two diagonal dotted lines. For purposes of direct comparison, the peak power points obtained from Fig. 4a (i.e., noisy records with no muting or stacking) are shown on Fig. 4b (and all other panels of Fig. 4) to provide a common point of reference. It is obvious that muting the noisy waveforms allowed for better resolution of the high-frequency (f > 50 Hz) dispersion data, although a clear trend is still not present. Figure 4c presents the dispersion image obtained from the same wavefield transformation applied to the noisy records without muting, but following stacking of ten dispersion images, one from each of the ten distinct source impacts used at this location, in the wavefield transform domain. While the R0 dispersion trend in Fig. 4c is clearer than that in Fig. 4a, stacking in the wavefield transformation domain does not clear up the dispersion image at f > 50 Hz when muting is not utilized. Finally, Fig. 4d presents the dispersion image obtained from applying the same FDBF wavefield transformation to a set of records with a higher SNR that were obtained from stacking the same ten sets of records in the time domain that were obtained from ten distinct source impacts. For reference, the stacked time-domain records are shown in Fig. 3b. We observe from Fig. 3b that the time-domain stacked records are much clearer than their unstacked counterparts, with the surface wave arrival being clearly visible on all sensors. Furthermore, when the wavefield transformation is applied to this set of stacked records, some additional R0 data at f > 50 Hz is now visible, as well as a clearly resolved 1st higher Rayleigh wave mode (R1). Interestingly, the high power points around approximately 15 Hz, which are visible in all of the panels of Fig. 4, are significantly mitigated through time-domain stacking. While purely conjecture, this may indicate that uncorrelated offline noise with significant energy near 15 Hz was propagating obliquely to the MASW array, yielding high apparent phase velocities. This example highlights the importance of stacking multiple shot records in the time domain to achieve the highest quality dispersion data prior to estimating dispersion statistics.

Fig. 3

source impact located 20 m off of the end of the array, b shows the time-domain stacked seismic records from ten source impacts at the same source location. Diagonal dotted lines in a show the selected boundaries for time-domain muting

Seismic records acquired using a 24-channel MASW array with 2-m spacing at a site with significant background noise (i.e., a “noisy” site). a shows the seismic records from a single

Fig. 4

Comparison of the dispersion images obtained from MASW seismic records when using four common preprocessing techniques at a site with significant background noise (i.e., a “noisy” site). The four techniques are as follows: a no stacking, b no stacking with time-domain muting, c stacking in the wavefield-transform domain (e.g., f-v domain), and d stacking in the time domain. All four panels use the frequency-domain beamformer (FDBF) with cylindrical-wave steering vector and square-root-distance weighting as their transformation method. The coloring of each dispersion image indicates the calculated wavefield power normalized relative to the maximum at each processing frequency; cool colors indicate low wave power and warm colors indicate high wave power. The white circular symbols shown in all panels indicate the approximate locations of maximum wave power (i.e., the fundamental mode experimental dispersion data) as selected from a and used as a basis for comparison between the preprocessing techniques. Where distinguishable, the apparent fundamental (R0) and first-higher (R1) Rayleigh wave modes are indicated in each panel

Figures 5 and 6 present results in an identical format to that described previously with respect to Figs. 3 and 4, except now at a different site with minimal background noise (i.e., a “quiet” site). A waterfall plot illustrating one set of experimental MASW waveforms (24 vertical receivers spaced at 2-m intervals) acquired at a quiet site with a vertical sledgehammer source located 10 m off of the end of the array is shown in Fig. 5a. The difference in waveform signal quality is apparent when comparing Fig. 3a from the noisy site with Fig. 5a from the quiet site. The signal is in fact so clear at the quiet site that the five time-domain stacked records in Fig. 5b are almost indistinguishable from the unstacked records in Fig. 5a. The effects of using different preprocessing techniques on the MASW dispersion data are compared in Fig. 6 after application of the FDBF wavefield transformation. Note that because the data was acquired at two different sites, the dispersion data in Figs. 4 and 6 are not directly comparable; however, several observations can be made in regards to the effectiveness of the signal preprocessing techniques discussed. First, the preprocessing techniques are shown to have a more significant effect on the dispersion images for the noisy site than the quiet site, as evidenced by the panels of Fig. 6 appearing more similar to one another than those in Fig. 4. Second, the preprocessing techniques considered herein primarily affect the frequency bandwidth of the acquired dispersion data and otherwise result in fairly consistent, although not identical, estimates of surface wave phase velocity. This is evidenced by observing that the white circular symbols obtained from the peak power points of the dispersion images obtained with no stacking (i.e., Figs. 4a and 6a) tend to fall along the peak power trends in the dispersion images obtained with various forms of muting and stacking. Third, and finally, the no stacking approach tends to produce the narrowest frequency bandwidth of the four techniques, whereas stacking in the time domain tends to produce the broadest frequency bandwidth, with the time-domain-muting approach and frequency-domain stacking approach residing somewhere in between. In Fig. 6, muting and/or stacking enables resolving frequencies down to 5 Hz (albeit with some scatter/uncertainty), a notable improvement over the lower-bound frequency of 12 Hz from the no stacking approach. While not illustrated herein, time-domain stacking performed in conjunction with muting can also be quite effective at obtaining high-quality dispersion data prior to calculating dispersion statistics.

Fig. 5

source impact located 10 m off the end of the array, whereas b shows the time-domain stacked seismic records from five source impacts at the same source location. Diagonal dotted lines in a show the selected boundaries for time-domain muting

Seismic records acquired using a 24-channel MASW array with 2-m spacing at a site with minimal background noise (i.e., a “quiet” site). a shows the seismic records from a single

Fig. 6

Comparison of the dispersion images obtained from MASW seismic records when using four common preprocessing techniques at a site with minimal background noise (i.e., a “quiet” site). The four techniques are as follows: a no stacking, b no stacking with time-domain muting, c stacking in the wavefield-transform domain (e.g., f-v domain), and d stacking in the time domain. All four panels use the frequency-domain beamformer (FDBF) with cylindrical-wave steering vector and square-root-distance weighting as their transformation method. The coloring of each dispersion image indicates the calculated wavefield power normalized relative to the maximum at each processing frequency; cool colors indicate low wave power and warm colors indicate high wave power. The white circles shown in all panels indicate the approximate locations of maximum power (i.e., the fundamental mode experimental dispersion data) as selected from a and used as a basis for comparison between the preprocessing techniques. The apparent fundamental Rayleigh wave mode (R0) is indicated in each panel

For the set of noisy MASW records discussed in regards to Figs. 3 and 4, the benefits of stacking records from multiple source impacts in the time domain are obvious. For the set of quiet MASW records discussed in regards to Figs. 5 and 6, the benefits of stacking records in the time domain are less obvious, but still important and result in better quality dispersion data. Reasonable attempts should be made to obtain the best dispersion data possible prior to calculating dispersion statistics. Dispersion data obtained from noisy records will contribute to a perceived increase in uncertainty, when in some cases this uncertainty can easily be reduced using simple and common-sense methods, such as time-domain stacking, that have been used to increase SNR in geophysical data processing for decades. Hence, we strongly recommend stacking MASW records in the time domain from at least three to five distinct source impacts to obtain the best possible dispersion data from each source location prior to estimating dispersion uncertainty. This approach will be used throughout the remainder of this work wherever MASW data are presented. However, as some users may wish to use one of the other approaches presented herein, the accompanying Python package swprocess (Vantassel 2021) includes options for no-stacking, frequency-domain stacking, and time-domain stacking, as well as the ability to combine these preprocessing techniques with time-domain muting. As some users may wish to define their own custom preprocessing workflows, all preprocessing workflows have been implemented in swprocess using the registry design pattern to enable new workflows to be defined dynamically without requiring the user to directly manipulate the swprocess source code. If not using swprocess, stacked time-domain records can be saved by most standard seismographs and commercial software packages often include options for muting and/or frequency-domain stacking.

2.2 Wavefield transformations

Following preprocessing, the seismic wavefield is transformed from the t-x domain to the f-v domain. Many authors have proposed different wavefield transformations for active-source surface wave data; however, to limit the scope of this section, we discuss and compare four of the most popular. First, is the FDBF with a plane-wave steering vector and no amplitude weighting (Zywicki 1999). This approach can be shown to be equivalent to the classical and more commonly used frequency-wavenumber (FK) transform (Gabriels et al. 1987; Nolet and Panza 1976). Using the FDBF approach to calculate the FK transform rather than the classical 2D Fourier transform approach has three key benefits: (1) it allows for the handling of non-uniformly spaced arrays, (2) the transformation can be done directly from the t-x domain to the f-v domain, removing the intermediate computation of the frequency-wavenumber (f-k) domain, and (3) it easily accommodates the calculation of dispersion power above the aliasing wavenumber. Second, is the transform proposed by McMechan and Yedlin (1981), which in this work we will refer to as the slant-stack transform. We understand that using this name may be a bit confusing to some, given that a slant stack (Thorson and Claerbout 1985) is already a standard transformation used in geophysical signal processing. However, as the alternate names for this transformation, such as the $\omega -p$ or $p-f$ transform (Louie 2001; McMechan and Yedlin 1981), are quite general and could be used to describe any of the transformations discussed in this section, we prefer using the more specific name of slant-stack transform. Third, is the phase-shift transform (Park et al. 1998), which is by far one of the most widely used wavefield transformations due to its implementation in a number of commercial software packages. Note that just as with the FK transform, the phase-shift transform can be produced through frequency-domain beamforming by using the plane-wave steering vector and inverse-amplitude weighting (Foti et al. 2015), although it has not been implemented this way in swprocess. Fourth, and finally, is the FDBF with a cylindrical-wave steering vector and square-root-distance weighting (Zywicki 1999; Zywicki and Rix 2005). Importantly, this final approach is the most consistent with surface wave propagation theory, as it avoids the assumption of a plane wavefield and instead models the cylindrical spreading of surface waves and their corresponding decay in amplitude according to the square-root of offset.

The four wavefield transformations discussed above are compared for a time-domain stacked MASW seismic record in Fig. 7. The five individual records composing the stacked MASW seismic record were acquired on 24 vertical receivers spaced at 2-m intervals from a source located 1 m off of the end of the array. While, in general, we do not recommend using source locations this close to the array for surface wave testing, for reasons discussed at length later in the paper, we do so here to show a clear example of how different the wavefield transformations can be for the same seismic record. The coloring of each dispersion image indicates the calculated wavefield power normalized relative to the maximum at each processing frequency; cool colors indicate low wave power and warm colors indicate high wave power. To facilitate a more direct comparison between the dispersion images in each panel, the peak power points for the apparent R0 and R1 modes obtained from the dispersion image in Fig. 7a (i.e., the classical FK approach, or FDBF with plane-wave steering vector and no amplitude weighting) are shown with white circles and white diamonds, respectively, on the dispersion images in all four panels. A quick comparison of the four panels reveals reasonably consistent estimates of the site’s R0 and R1 dispersion data across the four transformations, but not identical results. As such, the choice of wavefield transformation is a clear source of epistemic uncertainty in dispersion data. For example, the FK and slant-stack transforms shown in Fig. 7a and b, respectively, more clearly resolve the R0 mode between 35 and 75 Hz than the phase-shift and FDBF with cylindrical-wave steering and square-root-distance weighting shown in Fig. 7c and d, respectively. However, the transformations used for Fig. 7c and d more clearly resolve the R1 mode between 40 and 75 Hz. Furthermore, there are some differences between the low-frequency (< 25 Hz) dispersion data obtained from the various transformations, which can be seen best by comparing the dispersion images in Fig. 7a and d. This single example serves to highlight that while various wavefield transforms may be quite similar, and some can even be shown to be mathematically equivalent (Foti et al. 2015), they do not always produce identical results in practice due to a number of factors, including their differing sensitivity to body waves and background seismic noise. Furthermore, it is obvious that by combining the results from several methods a clearer estimate of the site’s R0 and R1 dispersion data can be obtained. Therefore, the authors strongly recommend that multiple transformations be considered, especially when the surface wave data are complex, to ensure a rigorous interrogation of the active-source experimental data and to account for epistemic uncertainty in the wavefield transform process. While, to our knowledge, no commercial software package allows users to choose between various wavefield transformation methods, all of the transformations discussed in this section have been implemented in the accompanying Python package swprocess (Vantassel 2021). In addition, to allow users to implement their own preferred transformations in swprocess, all of the included wavefield transforms utilize the registry design pattern to enable new transforms to be developed and used without requiring the user to directly manipulate the swprocess source code.

Fig. 7

Comparison of four different wavefield transformation methods commonly used to obtain experimental dispersion data from MASW seismic records. The transformations have been applied to the same time-domain stacked seismic records. They include the following: a the frequency-domain beamformer (FDBF) method with a plane-wave steering vector and no amplitude weighting, which is mathematically equivalent to the classic frequency-wavenumber (FK) transform, b the slant-stack transform, c the phase-shift transform, and d the FDBF with a cylindrical-wave steering vector and square-root-distance weighting. The coloring of each dispersion image indicates the calculated wavefield power normalized relative to the maximum at each processing frequency; cool colors indicate low wave power and warm colors indicate high wave power. The white circles and diamonds correspond to the apparent fundamental (R0) and first-higher (R1) Rayleigh wave modes, respectively, as selected from a and used as a basis for comparison between processing methods

2.3 Multi-component data

While MASW is typically performed using the vertical components of a wavefield with strong Rayleigh-wave content, it may also be performed using the horizontal in-line (i.e., radial) component of a wavefield with strong Rayleigh-wave content or the horizontal cross-line (i.e., transverse) component of a wavefield with strong Love-wave content. To demonstrate examples of how this multi-component data can be useful, and to encourage the reader to consider acquisition of this additional information whenever possible, we present comparisons between Rayleigh wave dispersion images obtained from vertical and horizontal radial components in Fig. 8 and between Rayleigh wave and Love wave dispersion images in Fig. 9. The calculations for Figs. 8 and 9 were made with the FDBF transform with a cylindrical-wave steering vector and square-root-distance weighting. Figure 8 compares the surface wave dispersion images resulting from processing the vertical (Fig. 8a) and horizontal radial (Fig. 8b) components of a predominantly Rayleigh wavefield generated from a vertical source impact located 15 m away from two adjacent 24-geophone linear arrays (separate, but co-located vertical and horizontal-inline arrays) with 2-m receiver intervals. The seismic records were the result of time-domain stacking five distinct source impacts at the same aforementioned source location. The white circles and diamonds presented in both panels represent the peak power points for the R0 and R1 modes, respectively, as determined from the dispersion image in Fig. 8a obtained from the vertical components. Using these symbols as a common point of reference between images, we observe that for this example the vertical and radial wavefields show good agreement where they overlap, but that by utilizing both the vertical and radial wavefields a more complete description of the site’s R0 and R1 modes can be resolved. In particular, the higher frequency dispersion data of both the R0 and R1 modes are resolved significantly better using the horizontal radial components. While not commonly utilized at the present time, the authors expect that incorporating Rayleigh dispersion data from both the vertical and horizontal radial components will become more common in the future, and that the use of both components will aid in determining more robust measurements of a site’s dispersion data and associated uncertainty.

Fig. 8

source impact located 15 m away from the array. The coloring of each dispersion image indicates the calculated wavefield power normalized relative to the maximum at each processing frequency; cool colors indicate low wave power and warm colors indicate high wave power. The white circles and diamonds in both panels indicate the approximate location of the fundamental (R0) and first-higher (R1) Rayleigh wave modes, respectively, selected from the vertical components in a and used as a basis for comparison between components

Surface wave dispersion images resulting from the FDBF transform with a cylindrical-wave steering vector and square-root-distance weighting applied to the following: a the vertical components and b the horizontal radial/in-line components of MASW seismic records obtained simultaneously from the same vertical

Fig. 9

source impact producing strong Rayleigh-wave content and b the horizontal transverse/cross-line components of MASW seismic records obtained from a horizontal source impact on a shear plank producing strong Love-wave content. Both sets of seismic records were obtained from the same source location located 10 m away from the array using vertical and horizontal geophones, respectively, located adjacent to one another. The coloring of each dispersion image indicates the calculated wavefield power normalized relative to the maximum at each processing frequency; cool colors indicate low wave power and warm colors indicate high wave power

Surface wave dispersion images resulting from FDBF transform with a cylindrical-wave steering vector and square-root-distance weighting applied to the following: a the vertical components of MASW seismic records obtained from a vertical

Figure 9 compares the surface wave dispersion images resulting from processing the predominantly Rayleigh wavefield (i.e., vertical components from a vertical source impact; Fig. 9a) and the predominantly Love wavefield (i.e., horizontal cross-line components from a horizontal source impact; Fig. 9b) collected at a new example site. In both cases, a linear array of 24, 4.5-Hz geophones with a constant receiver interval of 2 m was used to record the wavefields generated by sledgehammer blows located 10 m away from the array. Five source impacts for both the vertical and horizontal shots were stacked in the time domain to produce the seismic records used for MASW processing. A visual comparison of Fig. 9a and b illustrates the significant difference in the clarity of the Rayleigh and Love dispersion data acquired at this site. The Rayleigh wave data are both strongly bandlimited, with discontinuous peak power trends extending only between 15 and 50 Hz, and difficult to interpret, as it is unclear whether or not the small peak power trend around 35 Hz and 200 m/s is a processing anomaly or perhaps a tiny piece of the site’s R0 mode. If the piece identified as “R0?” is determined to be a processing anomaly, the higher velocity trend might be interpreted to be R0 instead of R1, which would lead to a very different and much stiffer interpretation of the site, making such a determination incredibly important but extremely difficult given the poor quality Rayleigh dispersion data. In contrast, the Love wave dispersion data are broadband, extending from 10 to 65 Hz, and clear in their interpretation as the site’s fundamental Love wave mode (L0). The Love wave data in these circumstances can be used in conjunction with, or in lieu of, the questionable Rayleigh wave data to robustly characterize the site. In both of the cases presented in Figs. 8 and 9, the use of complementary, multi-component data are shown to be extremely beneficial, especially for challenging sites. This complementary information can mitigate or eliminate significant uncertainty in the ultimate statistical representation and mode interpretation of the site’s dispersion data. Therefore, the authors strongly recommend the acquisition of complementary, multi-component data whenever time and resources permit.

2.4 Array layout and source offset

In addition to the other factors previously discussed, the selected array layout and source offset can have a significant impact on the measured dispersion data (Dikmen et al. 2010; Foti et al. 2018; Park et al. 1999). Important considerations include the length of the array, sensor spacing, source type, and source offset. As the number of sensors is typically fixed by the quantity of equipment available, the length of the array (L) is directly controlled by the sensor spacing. Shorter arrays with smaller sensor spacing will permit the acquisition of shorter wavelengths (higher frequencies) and, therefore, better resolution of the near-surface with less spatial averaging across the array, whereas longer arrays with larger sensor spacing will permit the acquisition of longer wavelengths (lower frequencies) but with lower near-surface resolution and more spatial averaging across the array. Therefore, array lengths must be selected to compromise between the desired depth of characterization, the level of near-surface resolution, and the desired degree of spatial averaging. The minimum and maximum depths of characterization are typically quantified by two guiding wavelength limits that are based on the array dimensions and the source offset (Foti et al. 2018; Park et al. 1999; Yoon and Rix 2009). The first is the minimum-wavelength (high-frequency) array limit (${\lambda }_{a,min}$) that governs near-surface resolution (i.e., the thickness of the thinnest resolvable layer) and is controlled by the potential for spatial aliasing of short wavelengths (i.e., insufficient sampling in space). It can be shown ${\lambda }_{a,min}=2x$, where $x$ is the sensor spacing. Meaning, at least two samples (i.e., sensors) are required per wavelength for effective sampling in space, which the reader will note is analogous to the Shannon-Nyquist theorem for sampling in time. However, unlike with sampling in time, it is unlikely that for typical sensor spacings and MASW sources very short wavelengths ($\lambda \ll {\lambda }_{a,min}$) will be present in the wavefield to be aliased by the MASW array. Therefore, some analysts choose to relax the spatial aliasing criteria slightly if the dispersion data appears reliable at short wavelengths/high frequencies following transformation (Foti et al. 2018). The second guiding wavelength is the maximum-wavelength (low-frequency) limit (${\lambda }_{a,max}$) that governs the maximum depth of profiling and has been the topic of some disagreement in the literature. Some have argued that an MASW array can generally not be used to accurately resolve dispersion data at wavelengths greater than its length (${\lambda }_{a,max}=L)$ (Foti et al. 2018), whereas others have noted that an MASW array can be used to resolve dispersion data at wavelengths up to three times its length (${\lambda }_{a,max}=3L$) (Park 2005).

When determining ${\lambda }_{a,max}$ it is also important to consider the source location in addition to the length of the array (Yoon and Rix 2009). The source location is commonly specified as a source offset, which is the distance from the source to the array’s closest sensor. The source offset must be selected with two specific criteria in mind: (1) the source should be sufficiently distant from the array to avoid “near-field effects” caused by the contamination of body waves and the general development of the surface wave’s cylindrical wave front and (2) the source should be sufficiently close to the array to avoid “far-field effects” caused by the attenuation of the seismic wavefield, particularly high frequencies, through material and radiation damping. Unfortunately, unlike the array’s layout, which can generally be selected in advance and used from site to site, in the experience of the authors a single optimal source offset capable of mitigating both near-field and far-field effects is rather difficult/impossible to determine a priori. In response, we adopt the multi-source-offset technique proposed by Cox and Wood (2011). The multi-source-offset technique involves utilizing multiple source offsets, preferably off of both sides of the array when feasible, to allow for the identification and mitigation of both near-field and far-field effects. The multi-source-offset technique also plays a key role in the quantification of epistemic and, to some extent, aleatory uncertainty in dispersion data. An example of this technique applied to a real dataset is shown in Fig. 10. Figure 10a, b, and c show the Rayleigh dispersion images obtained from the vertical components of wavefields generated when the vertical impact source was located at 5 m, 10 m, and 20 m from the first geophone on the “near” side of the 46-m long array (24 geophones with constant 2-m spacing). Figure 10e, f, and g show the dispersion images obtained when the source was located at 5 m, 10 m, and 20 m from the last geophone on the “far” side of the array. Figure 10d compares the dispersion peak power points selected from these six dispersion images. The MASW seismic records for this example were preprocessed using time-domain stacking of five distinct source impacts. All dispersion images were generated using the FDBF transform with a cylindrical-wave steering vector and square-root-distance weighting. At frequencies above ~ 10 Hz, Fig. 10d reveals consistency between the six sets of experimental dispersion data. However, the results are certainly not identical, indicating that the choice of source offset is a clear source of dispersion uncertainty that should be quantified. At frequencies below ~ 10 Hz, Fig. 10d clearly shows large discrepancies between the dispersion data obtained from the close and distant source offsets, with close offsets of 5 m and 10 m drifting to low phase velocities regardless of which side of the array the source was operated on. This divergence between the close and distant source offsets, with the closer offsets being biased to lower phase velocities, is a classic symptom of near-field effects. Meaning, if surface waves are recorded too close to their point of origin, their phase velocities are often underestimated. In general, it is often assumed that surface waves need to propagate at least ½ a wavelength before being sampled to avoid recording low-frequency waves contaminated by near-field effects. Several researchers (Li and Rosenblad 2011; Yoon and Rix 2009) have proposed recommendations for limiting ${\lambda }_{a,max}$ to avoid/mitigate near-field effects in dispersion data determined from MASW testing. It would be wise for the reader to familiarize themselves with those recommendations to avoid trusting low-frequency/long-wavelength dispersion data obtained from arrays that are too short or sources that are too close to the array. However, near-field effects are also known to be site specific, and the guidelines for limiting ${\lambda }_{a,max}$ as a means to mitigate near-field effects may be either too restrictive or too lenient on a site-by-site basis. As such, the authors have found it more practical to always acquire multiple source offsets in order to visually identify dispersion data that may be contaminated by near-field effects, like the ones observed for the 5 m and 10 m source offsets in Fig. 10d. A discussion regarding the use of interactive trimming to remove dispersion data contaminated by near-field effects prior to calculating dispersion statistics is presented below.

Fig. 10

source offset locations for a single 46-m long MASW array using the FDBF transform with a cylindrical-wave steering vector and square-root-distance weighting. a, b, and c show dispersion data from near-side source offsets of 5 m, 10 m, and 20 m, respectively, whereas e, f, and g show dispersion data from equivalent far-side source offsets. The source offset locations relative to the array’s first (i.e., near) or last (i.e., far) geophone are shown in the upper right of each panel. The coloring of each dispersion image indicates the calculated wavefield power normalized relative to the maximum at each processing frequency; cool colors indicate low wave power and warm colors indicate high wave power. d compares the peak power dispersion data selected from the six dispersion images

Rayleigh wave dispersion data obtained from different

In summary, the array layout and source offset play a significant role in determining the minimum and maximum wavelengths, ${\lambda }_{a,min}$ and ${\lambda }_{a,max}$, respectively, that can be reliably extracted from MASW dispersion images. Unfortunately, there is no final, definitive answer to be presented here that can be used in all cases to set ${\lambda }_{a,min}$ and ${\lambda }_{a,max}$. Rather, the analyst is encouraged to be cautious about using high-frequency/short-wavelength data at wavelengths less than two times the sensor spacing (i.e., ${\lambda }_{a,min}=2x$). This guideline can often be relaxed if a clear, coherent trend in dispersion data are observed at high frequencies. The choice of ${\lambda }_{a,max}$, however, is much more critical to performing high-quality site characterization. If ${\lambda }_{a,max}$ is too restrictive, good quality low-frequency/long-wavelength data will be discarded and the maximum depth of profiling will be limited unnecessarily. If ${\lambda }_{a,max}$ is too large, low-quality dispersion data will be accepted, often resulting in significantly underestimating the site’s stiffness at depth (Garofalo et al. 2016). Therefore, it is wise to be careful about extracting dispersion data at wavelengths that are greater than the array length (Foti et al. 2018), or greater than the distance between the source and the center of the array (Li and Rosenblad 2011; Yoon and Rix 2009). As the absolute determination of ${\lambda }_{a,max}$ is site specific, we recommend using dispersion data obtained from multiple source offsets (e.g., 5 m, 10 m, 20 m, and possibly larger offsets) to identify near-field effects and quantify dispersion data uncertainty.

3 Quantifying dispersion uncertainty: active-source MASW

This section presents an overview of the process for quantifying dispersion uncertainty when only active-source MASW data are available. For the sake of brevity, we will reuse the same data as was presented in Fig. 10, which was obtained from a 24-sensor MASW array with a 2-m spacing using six source locations (three locations off either side of the array at distances of 5 m, 10 m, and 20 m). Before discussing the quantification of uncertainty, we reiterate that in order for the resulting dispersion uncertainty to be meaningful it should account for all reasonable/important sources of epistemic and aleatory uncertainty, which for this example we consider to primarily include the source location and wavefield transformation method. While we do not do so here for the sake of simplicity, the analyst may wish to consider additional aleatory uncertainty, beyond that already accounted for by the spatial extents of the single surface wave array and multiple source offsets used, by deploying multiple arrays across the site. The choice of whether to do this or not depends on the purpose of the testing and is left to the discretion of the analyst.

The dispersion data obtained from processing time-domain stacked MASW records from six distinct source offset locations using four different wavefield transformations for the example site originally discussed in regards to Fig. 10 are presented in Fig. 11a. For reference, we have plotted two different ${\lambda }_{a,max}$ values (1L and 2L) in all panels of Fig. 11 to guide subsequent data processing, although we again note that we will primarily mitigate near-field effects based on multiple source offsets rather than on a wavelength determined exclusively by the array’s geometry. As expected, Fig. 11a reveals notable near-field effects below approximately 8 Hz, with reasonably consistent dispersion data being resolved across all source offsets and all transformation methods between approximately 9 and 40 Hz. At higher frequencies, we observe two potential higher modes; however, as they are rather bandlimited and only apparent when considering the dispersion data obtained from the 20 m source offset on the far side of the array (refer to Figs. 10d and 11a), we will not consider them further in this example.

Fig. 11

Progression of surface wave dispersion post-processing to calculate robust estimates of dispersion uncertainty from MASW dispersion data. The progression includes the following: a the raw dispersion data obtained from a single array considering multiple source offsets (5, 10, and 20 m) off of both ends of the array (near and far offsets) and multiple wavefield transformation methods (FK, SS, PS, and FDBF), b the trimmed dispersion data where obvious outliers have been removed and the apparent fundamental mode has been isolated, and (c) and (d) the trimmed dispersion data shown in terms of frequency and wavelength, respectively, with dispersion statistics. Note that the vertical error bars indicate the mean ($\mu$) $\pm$ one standard deviation ($\sigma$) range of the dispersion statistics. Two common maximum wavelength limits (${\lambda }_{a,max}$) for MASW based on the array length (L) are shown in all four panels for reference

Figure 11b shows the raw dispersion data from Fig. 11a after interactive trimming. Interactive trimming by the analyst involves identifying a continuous mode segment of interest, in this case the apparent R0 mode, and isolating it by trimming/removing dispersion data that are as follows: (1) clearly contaminated by near-field effects, (2) associated with other modes, and (3) judged to be significant outliers relative to the identified dispersive trend. This is a subjective process that must be performed with care to avoid removing data that represents realistic uncertainty. Not all data processing can be automated, and this is one step we have found that requires the manual interaction of an appropriately trained analyst. The authors note that the ability to perform interactive trimming has been provided through swprocess (Vantassel 2021) and its accompanying Jupyter workflows. The interactive-trimming process allows the user to remove low-quality data points by clicking on a plot of the raw dispersion data to define rectangular regions (or even individual data points) for removal. If necessary, the interactive-trimming process can be repeated in stages until the desired continuous mode segment is isolated and all undesirable data points have been removed by the analyst. Importantly, the goal is not to obtain as clean of a dispersive trend as possible. Rather, the goal is to remove data points that are obvious outliers and leave all other dispersion data as a means to quantify realistic uncertainty. The reader is warned that if the interactive-trimming process is not performed properly, the site’s dispersion data can become biased and its uncertainty significantly underestimated. This will then result in biased Vs profiles which will be perceived to have greater accuracy and lower variability than in reality. The compounding effects of bias and improperly reduced uncertainty in the resulting Vs profiles must be considered as consequences of improper interactive trimming and/or complete disregard of dispersion uncertainty. Unfortunately, most commercial software packages used for surface wave processing do not provide analysts with the ability to perform interactive trimming or to directly calculate dispersion statistics. At the conclusion of interactive trimming, the dispersion data contributing to the mode segment of interest can be saved for future reference using swprocess into the platform and language agnostic, text-based JSON format for future use. While not illustrated in this example, interactive trimming can and should be repeated several times on the raw dispersion data to extract and save data segments contributing to other surface wave modes, if present. Figure 11b shows the experimental dispersion data after the conclusion of interactive trimming to isolate the R0 mode. Note that one might argue that additional data below 10 Hz should be trimmed due to significant scatter and potential contamination by near-field effects. We leave this data to show the impact of choices that must be made by the analyst during processing. However, the penalty associated with trying to resolve lower frequency/longer wavelength data is increased dispersion uncertainty, which will result in more variable Vs profiles during the inversion stage (not illustrated herein).

After interactive trimming, the statistical representation of each continuous mode segment is calculated. The statistical representation of the R0 mode under consideration in the present example is shown in terms of frequency and wavelength in Fig. 11c and d, respectively. The statistical calculations for MASW dispersion data require a three-step process. First, the dispersion data obtained from each combination of array, source offset, and wavefield transformation are treated as an independent observation of the site’s true dispersive trend. Therefore, for the present example with one array, six source offsets, and four wavefield transformations, we have 24 independent observations. Second, as this dispersion data may not have been processed at the same frequencies as those wanted for determining statistics, and in fact is almost certainly too dense in terms of frequency sampling to use during the subsequent inversion stage, it must be interpolated (i.e., resampled) along each independent observation to create a consistently sampled matrix of dispersion data observations. The dispersion data observation matrix has one dimension representing the number of observations (24 in this case) and the other dimension equal to the desired number of statistical data points (12 in the case of the data presented in Fig. 11c and d). The number of statistical data points is determined by the analyst depending on the bandwidth of the data and consideration that the statistics should be numerous enough to smoothly follow the dispersive trend, yet coarse enough so as not to significantly slow down the numerical calculations in the subsequent inversion phase. For limited bandwidth data like that presented in Fig. 11, 10–15 statistical points are generally sufficient. However, for dispersion data spanning a larger bandwidth (e.g., combined active-source and passive-wavefield data, as discussed below), a minimum of 20–30 points are generally required (Vantassel and Cox 2021a). Importantly, this resampling has been implemented in swprocess, such that it can be performed with any desired number of points using either linear or logarithmic sampling in any domain (e.g., frequency-velocity, frequency-slowness, wavelength-velocity) of the analysts choosing. For this example, we present results resampled in the log-wavelength-velocity domain, following the recommendations of Vantassel and Cox (2021a). Note that we prefer to resample rather than bin the experimental dispersion data, as proposed by others previously (e.g., Cox and Wood 2011), for three specific reasons. First, binning is affected by the underlying sampling of the raw data, whereas resampling is not. Second, binning mixes measurements from adjacent observations, whereas resampling does not. Third, resampling is consistent with the fact that theoretical dispersion curves computed during inversion are, in general, smooth and continuous. Once the data has been resampled into the observation matrix, the final step of the process is to calculate the data’s statistical representation. In some circumstances, the analyst may wish to apply unique statistical weights to the different dispersion observations according to their perceived quality and/or importance. For example, an analyst may wish to weight the results of the FDBF transform with cylindrical-wave steering and square-root-distance weighting higher than those from the slant-stack transform, as the former is theoretically superior to the later and, therefore, should, at least in theory, produce superior results. For simplicity, we have chosen not to apply unique statistical weights for this example and instead treat all observations as equally probable. Whether or not unique statistical weighting is applied, calculating the data’s statistical representation involves, at a minimum, calculating the mean and sample standard deviation of the dispersion data’s phase velocity at each statistical point/frequency. We assume that the dispersion data’s phase velocity at each statistical point can be represented as a normal distribution based on work by others (Lai et al. 2005), although strictly speaking the outlined approach is general enough to support any suspected statistical distribution (e.g., lognormal). In addition to the mean and sample standard deviation, the correlation coefficients between statistical points can also be calculated to allow for the development of uncertainty-consistent Vs profiles following the procedures proposed by Vantassel and Cox (2021b). Of course, the calculation of correlation coefficients is only possible if the observation matrix is completely filled with data, which many not always be the case. Therefore, assumptions must be made about the behavior of the data and/or correlations. Work on this topic is ongoing and expected to be published in the near future, as such, it is unfortunately not possible to present those findings herein. In Fig. 11c and d, we present error bars illustrating the mean ($\mu$) and $\pm$ one standard deviation ($\sigma$) range for the apparent fundamental mode dispersion data’s phase velocity in terms of frequency and wavelength, respectively. It is clear that the uncertainty bounds increase with decreasing frequency. This is quite common, as lower frequency active-source data generally has lower SNR and inherently captures greater spatial variability due to the associated longer wavelengths. Several blind studies have shown that it is common for dispersion data to have coefficients of variation (COV) on the order of 5 to 10%, with COVs increasing at low frequencies (e.g., Cox et al. 2014; Garofalo et al. 2016). The analyst can decide what level of uncertainty (e.g., ± one, two, or three standard deviations) to carry forward into the inversion stage. In the past, we have often used ± one standard deviation. However, our new inversion approach for developing Vs profiles that are consistent with measured dispersion uncertainty requires the full statistical distribution at each frequency/wavelength.

4 Passive-wavefield processing

4.1 Processing methods

As with active-source data processing, a variety of passive-wavefield processing methods are available for extracting surface wave dispersion data from ambient vibrations. As others have worked diligently to implement and provide open-source tools for passive-wavefield processing, we have not attempted to re-implement such techniques in swprocess. Instead, we have focused on providing tools for post-processing the results from one of the most popular open-source software suites available for ambient vibration processing, Geopsy (Wathelet et al. 2020). In particular, we have focused on being able to post-process the results from classic beamforming (i.e., classic frequency-wavenumber transform) (Lacoss et al. 1969), high-resolution beamforming (i.e., high-resolution frequency-wavenumber transform) (Capon 1969), and, the recently proposed, Rayleigh three-component beamforming (RTBF) (Wathelet et al. 2018). As these techniques have already been evaluated by Wathelet et al. (2018), we will not repeat any such evaluations here and instead focus on the utilization of the RTBF method, which the authors believe, based on their experience, to be superior to the other methods for extracting experimental dispersion data. Nonetheless, just as with the active-source processing methods, it is wise to consider multiple passive-wavefield processing methods as a means to enhance data quality and/or quantify epistemic uncertainty. As we have already discussed how to incorporate the effects of multiple processing techniques in the calculation of dispersion uncertainty in regard to active-source processing, for brevity, we will not do so again here for passive-wavefield processing. We will, instead, use the RTBF method to elucidate the most relevant parameters of passive-wavefield processing for estimating dispersion uncertainty.

4.2 Number of cycles, blocks, and block sets

The first important decision for ambient noise processing is selecting how the longer, continuous time-domain records will be divided into smaller windows/block sets to develop estimates of the site’s surface wave dispersion data and uncertainty. With the implementation of the RTBF, Wathelet et al. (2018) also implemented block averaging to amplify coherent wave energy when calculating the cross-spectral matrix. In practice, block averaging involves first breaking the noise record into a number of non-overlapping blocks and then averaging those blocks in the frequency-domain to develop block sets for use in the beamformer calculations. The length of each block is typically selected by ensuring some minimum number of periods at each processing frequency. Wathelet et al. (2018) recommended using block lengths which were frequency-dependent and contained 100 periods per frequency. For example, a 100-period frequency-dependent block would be 100-s long at a processing frequency of 1 Hz and only 25-s long at a processing frequency of 4 Hz. However, to facilitate calculation of dispersion statistics, and ultimately allow each block set to be treated as an independent observation (discussed later), the authors prefer the use of fixed-length time blocks where the length of each block is selected to contain at least 30 periods at the lowest processing frequency. For example, processing between 1 and 4 Hz would require a fixed-length time block of at least 30 s to ensure at least 30 cycles at 1 Hz and would provide 120 cycles at 4 Hz. Once the time records have been divided into blocks, they must then be grouped into block sets. For grouping blocks into block sets, we echo the recommendations of Wathelet et al. (2018) that 4 N blocks should be used to create each block set, where N is the number of sensors deployed in the MAM array. The one potential shortfall of using 4 N blocks per block set is the amount of recording time required to produce a sufficient number of non-overlapping block sets (preferably more than 30) for estimating dispersion statistics. To illustrate this, consider again the case of processing between 1 and 4 Hz using a 30-s fixed-length time block. If the MAM array consisted of 10 sensors, this would mandate a block set 20 min in length and an overall recording time of 10 h to achieve 30 samples for calculating dispersion statistics. This may or may not be feasible for any given study. If long recording times are not possible, we follow Wathelet et al. (2018) in relaxing the requirements that block sets should not overlap in order to determine a statistically significant number of samples using whatever time is available for acquisition in the field. If long time records are available, little to no overlap may be required (preferred) to obtain at least 30 block sets. If shorter time records are available, more overlap may be required to obtain at least 30 block sets, depending on the lowest frequency sought in the dispersion processing. We recommend using no less than 30 to 60 min of passive-wavefield data for MAM arrays with smaller apertures (30–50 m) and no less than 120 min of passive-wavefield data for MAM arrays with larger apertures (200–500 m). Please note that these recommended recording times may need to be extended if the testing environment contains a limited number of ambient noise sources or contains many near-field sources that may interfere with the ambient noise measurements. As mentioned previously, each block set is then processed using the RTBF method to produce estimates of the site’s phase velocity at each processing frequency. These estimates can then be used to calculate a statistical representation of the site’s dispersion data, similar to the process described previously with regard to active-source data, although with a few additional complications, as discussed in the following sections.

4.3 Effects of considering multiple peaks

Once the analyst decides how to divide the time records into blocks and block sets, they must then decide how many peaks per block set should be exported by the selected processing method. While it may seem intuitive to only select the peak with the single highest beam power, there are two primary benefits to selecting multiple peaks from each block set at each processing frequency. These benefits include the following: (1) the increased potential to identify multiple surface wave modes and (2) the reduced potential that the selected peak power points will occur at a spurious phase velocity. To view these benefits more concretely, compare the dispersion data shown in Fig. 12a and b, which were obtained from RTBF processing of three-component broadband seismometers from two nested MAM arrays, aptly named MAM 1 and MAM 2. MAM 1 was composed of 15, 3-component broadband seismometers organized into two concentric circles. The inner circle was composed of seven stations and had a diameter of 50 m; the outer circle was also composed of seven stations but had a diameter of 150 m. The 15th sensor was placed at the center of two circles. MAM 1 was left to record for approximately 1.5 h. MAM 2 was composed of 16, 3-component broadband seismometers organized into two non-concentric circles. The smaller circle was composed of eight stations (seven along the perimeter and one at the center) and had a diameter of 300 m. The larger circle was also composed of eight stations (seven along the perimeter and one at the center) and had a diameter of 1000 m. MAM 2 was left to record overnight for approximately 14 h. Figure 12a shows the untrimmed/raw experimental dispersion data where only the point with the single maximum power was selected from each block set (i.e., N_MAXIMA = 1). Figure 12b, in contrast, shows the results of the same processing as in Fig. 12a, except that the five highest maximum power points were selected from each block set (i.e., N_MAXIMA = 5). By selecting multiple peaks, we obtain a nearly continuous R0 mode and a much more complete R1 mode. Of course, one minor disadvantage of using multiple peaks is the significant number of additional outliers in Fig. 12b compared to those in Fig. 12a, which must be addressed later during interactive trimming. One of the most concerning differences between the dispersion data in Fig. 12a and b is the missing data in the vicinity of 0.84 Hz when only one maxima is used (refer to Fig. 12a). To investigate the root cause of the missing data, we present a slice in the f-k_x-k_y space at 0.84 Hz in Fig. 12c from one of the block sets from MAM 2. We indicate the three highest-power peaks identified by the RTBF method with an “x” and number them in descending order according to their beam power. For reference, Fig. 12c also includes two rings of constant phase velocity: one at 5000 m/s, which resides in close proximity to peaks 1 and 2 and is an unreasonably high surface wave phase velocity even for bedrock, and the other at 1500 m/s, which resides in close proximity to peak 3 and is a reasonable phase velocity for bedrock. Viewing the first two peaks and their unrealistically high phase velocities, it is clear that the implementation of the RTBF processing in Geopsy automatically suppresses peaks with unrealistic velocities (greater than approximately 3500 m/s) and chooses instead to omit the likely invalid values from the .max file rather than returning them and risking their potential misuse. This results in a gap in the dispersion data when only a single peak is extracted, then discarded, as occurs in Fig. 12a at 0.84 Hz. When multiple peaks are picked, it is clear from Fig. 12c that peak 3 has a phase velocity that is consistent with the R0 trend observed at neighboring frequencies. This results in dispersion data being present in the vicinity of 0.84 Hz when multiple peaks are picked (refer to Fig. 12b). Therefore, we strongly recommend that multiple peaks be considered when processing passive surface wave dispersion data to ensure the best possible resolution of surface wave modes and mitigation of spurious velocity peaks. The authors have found N_MAXIMA = 5 to work well as a compromise between the size of the resulting .max file exported by Geopsy and the computational cost of loading and manipulating a potentially large number of peaks for the eventual determination of dispersion statistics. However, the decision of an acceptable value is ultimately left with the analyst and should be selected carefully and in consultation with the f-k_x-k_y slices viewable through the Geopsy graphical-user interface.

Fig. 12

source software Geopsy. a shows the raw experimental dispersion data obtained from two nested MAM arrays (i.e., MAM 1 and MAM 2) where only the peak with the highest beam power at each frequency was exported (i.e., N_MAXIMA = 1). b shows the raw experimental dispersion data from the same two MAM arrays processed using the same settings, except the peaks with the five highest beam powers at each frequency were exported (i.e., N_MAXIMA = 5). The vertical black line in a and b indicates the location of a slice in the f-k_x-k_y domain shown in c. The data in c was obtained from processing a single block set from MAM 2. The locations of three peaks identified by the RTBF are numbered in descending order according to their beam power. Two rings of constant phase velocity, one at 5000 m/s, near peaks 1 and 2, and the other at 1500 m/s, near peak 3, are also shown

Effect of considering multiple peaks during passive-wavefield surface wave data processing using the Rayleigh three-component beamforming (RTBF) method from the open-

5 Quantifying dispersion uncertainty: combined active-source and passive-wavefield

This final section presents a step-by-step procedure that can be used to combine active-source and passive-wavefield measurements to obtain a broadband statistical representation of the site’s experimental surface wave dispersion data. As with the active-source example presented previously, we will present a dataset acquired at a real site. Importantly, we note that the data from this real site is unique from all data presented previously. To begin, we first discuss the layout of the field experiment, in particular the sizes and locations of the linear MASW array and the three circular MAM arrays deployed at the site. For reference, the geometry and relative locations of these arrays are the same as that shown in Fig. 1. The MASW array consisted of 24 sensors at a constant 2-m spacing with source offsets at 5 m, 10 m, and 20 m off of both ends of the array. Active-source Rayleigh wave records were obtained at the MASW location using vertical 4.5-Hz geophones and vertical sledgehammer impacts. Active-source Love wave records were obtained at the MASW location using horizontal 4.5-Hz geophones oriented in the cross-line direction and horizontal sledgehammer impacts on a cross-line-oriented shear plank. Geophones were coupled to the ground surface using a 7.6-cm stainless steel spike. Five source impacts were recorded at each source location and saved individually for subsequent time-domain stacking. The three MAM arrays deployed at the site were concentric circles, each composed of eight broadband seismometers (seven along the circumference and one at the center), with diameters of 50 m, 300 m, and 1000 m. These diameters were selected such that the theoretical resolution limits for each array resided close to one another to encourage overlap in the acquired experimental dispersion data. The calculation of a two-dimensional array’s resolution limits, typically presented in terms of wavenumber as k_min/2 and k_max, is more complex than those for active-source processing and therefore will not be discussed here. Instead, the reader is referred to the work of Wathelet et al. (2008) on this topic for a full discussion. For consistency with active-source processing, we typically prefer to discuss these array resolution limits in terms of wavelengths rather than wavenumbers. The minimum and maximum array resolution limits in terms of wavelength for a two-dimensional array are ${\lambda }_{a,max}=2\pi /({k}_{min}/2)=4\pi /{k}_{min}$ and ${\lambda }_{a,min}=2\pi /{k}_{max}$, respectively.

The Rayleigh and Love active-source records for each source location were stacked in the time-domain and then transformed to the frequency-phase velocity domain using the four active-source MASW wavefield transformations discussed previously as a means to account for epistemic uncertainty. All active-source processing was performed using swprocess (Vantassel 2021). The raw Rayleigh and Love experimental dispersion data from MASW testing are shown in Figs. 13a and 14a, respectively. The raw Rayleigh wave dispersion data in Fig. 13a includes a presumed R0 mode extending from approximately 10 to 30 Hz and an easily distinguishable higher mode (presumably R1) extending from approximately 10 to 100 Hz. The raw Love wave dispersion data in Fig. 14a reveals an exceptionally broadband, presumably L0 mode extending from approximately 5 to 100 Hz. In addition, the raw Love wave dispersion data also shows what may be evidence of several incoherent higher modes between 50 and 100 Hz; however, after carefully reviewing the experimental dispersion images from MASW processing, the results were too inconsistent between offsets to isolate a coherent trend. Therefore, this group of potential higher-mode Love wave dispersion points will be removed during interactive trimming.

Fig. 13

Progression of surface wave dispersion post-processing to calculate robust estimates of Rayleigh wave dispersion uncertainty from combined MASW and MAM surface wave testing. The progression includes the following: a the raw dispersion data obtained from multiple arrays using multiple processing methods, b the trimmed dispersion data where obvious outliers have been removed and various potential modes have been isolated, and c and d the trimmed dispersion data shown in terms of frequency and wavelength, respectively, with duplicate peaks removed to facilitate the calculation of dispersion statistics. The vertical error bars in c and d indicate the mean ($\mu$) $\pm$ one standard deviation ($\sigma$) range of the dispersion statistics. The minimum and maximum wavelength resolution limits for each surface wave array are shown in all four panels for reference

Fig. 14

Progression of surface wave dispersion post-processing to calculate robust estimates of Love wave dispersion uncertainty from combined MASW and MAM surface wave testing. The progression includes the following: a the raw dispersion data obtained from multiple arrays using multiple processing methods, b the trimmed dispersion data where obvious outliers have been removed, and c and d the trimmed dispersion data shown in terms of frequency and wavelength, respectively, with duplicate peaks removed to facilitate the calculation of dispersion statistics. The vertical error bars in c and d indicate the mean ($\mu$) $\pm$ one standard deviation ($\sigma$) range of the dispersion statistics. The minimum and maximum wavelength resolution limits for each surface wave array are shown in all four panels for reference

The ambient vibration data acquired from the three MAM arrays was processed using the RTBF method in Geopsy. A 70-min recording from MAM 1 and 130-min recording from MAM 2 were processed from 1 to 30 Hz using 30-s fixed-length blocks. A 13-h recording from MAM 3 was processed from 0.5 to 3 Hz using 60-s fixed-length blocks. Block sets for all three arrays included 32 blocks [i.e., (4 blocks/sensor) * (8 sensors) = 32 blocks], which were allowed to overlap up to 4 N-1 blocks, where again N is the number of sensors composing the array, to ensure a statistically significant number of block sets (i.e., 30 for this example). For reasons discussed previously, up to five peaks were selected from each block set after RTBF processing (i.e., N_MAXIMA = 5) and exported in Geopsy’s .max format. The raw Rayleigh and Love dispersion data obtained from the RTBF processing from the three arrays is shown in Figs. 13a and 14a, respectively. The raw Rayleigh wave data, while containing a notable amount of scatter, particularly in the vicinity of each array’s minimum array resolution limit (i.e.,${\lambda }_{a,min}$), shows a reasonably clear fundamental mode trend that overlaps well across MAM arrays and lines up well with the MASW data at approximately 12 Hz. In addition, a second trend from MAM 1, that is apparent between 10 and 30 Hz, is consistent with the higher-mode data measured from the MASW array. The bulk of the remaining dispersion data points from MAM processing are outliers obtained from picking multiple peaks and/or from windows with incoherent phase at certain frequencies. These data will need to be trimmed out prior to calculating dispersion statistics. The raw Love wave data in Fig. 14a similarly shows a significant amount of scatter around the minimum array resolution limits of each array (i.e.,${\lambda }_{a,min}$); however, it also shows a clear fundamental mode trend which overlaps with the active MASW data at approximately 20 Hz and extends down to 0.6 Hz. One point of note with regard to the Love wave data is the bias toward higher phase velocities that is observed for the MAM 2 data in the vicinity of 1 Hz, which is close to its maximum array resolution limit (i.e.,${\lambda }_{a,max}$). This potential for beamforming-type processing to over-estimate phase velocities at low frequencies near their maximum array resolution limit is well-known and has been discussed widely in the literature (e.g., Asten and Hayashi 2018; Bettig et al. 2001; Wathelet et al. 2008). The practical approach to avoid biasing experimental dispersion data toward higher velocities when using beamforming techniques is to always remove experimental dispersion data at frequencies below the array’s maximum resolution limit (i.e.,${\lambda }_{a,max}$), unless a larger array is available to corroborate the measured phase velocities. This is done during interactive trimming.

In a process similar to that previously discussed in regard to active-source data, interactive trimming is performed to isolate each continuous mode segment visible in the Rayleigh and Love dispersion data. Again, the reader will note that this interactive-trimming process is accomplished using swprocess and the accompanying Jupyter workflows released in conjunction with this paper. The mode isolation process is identical to that previously discussed, with the results from each array being examined individually, paying special attention to remove points which are members of other mode segments, clear outliers, or beyond the array’s resolution limits prior to processing all of the dispersion data collectively in order to obtain statistics. Just as before, the interactive-trimming process can be repeated several times if needed until finally the desired continuous mode segment is isolated according to the analyst’s best judgment. Again, we emphasize that the purpose of interactive trimming is not to create the clearest dispersive trend possible, but rather to allow the removal of points which are clear outliers that would contaminate the dispersion statistics. Once a mode segment is isolated, it is saved for future reference into the platform and language agnostic, text-based JSON format for future use in calculating dispersion statistics. The entire process is then repeated until all of the continuous mode segments of interest have been isolated and saved in the JSON format. Figures 13b and 14b show the raw experimental dispersion data after the conclusion of the interactive-trimming process for the Rayleigh and Love wave data, respectively. As this process can be challenging for complex datasets, we again strongly encourage analyst to perform dispersion trimming carefully and in close consultation with the raw processing results (e.g., f-k_x-k_y slices for passive-wavefield data and dispersion images for active-source data) and any other complementary site information.

After isolating each continuous mode segment of interest, the statistical representation of each mode segment is calculated. The statistical calculations are similar to those described previously, except with one additional step. This additional step is to remove any remaining duplicate peaks from the trimmed MAM dispersion data, such that only the peak with the single maximum beam power is kept for the statistical calculation. Recall that the purpose of including multiple peaks in the MAM processing was to avoid spurious phase velocity estimates and to clearly identify all available modes, and since we have accomplished both of these objectives, we must now remove any duplicate peaks to avoid potentially biasing the statistics to a few time blocks which contain multiple similar phase velocity peaks. For example, the dispersion data in Figs. 13c and 14c looks very similar to that from Figs. 13b and 14b; however, on close inspection, one can observe some frequencies where fewer data points are present due to removing all but the highest-power peak for any given MAM array and block set. Once the duplicate peaks have been removed, the statistical calculations can proceed as usual, wherein dispersion data obtained from each active-source array, source offset, and wavefield transformation method, and each passive-wavefield array, block set, and wavefield transformation can be treated as independent observations. These observations are then resampled to form the observation matrix. As with the active case, the observation matrix has one dimension representing the number of observations and the other dimension equal to the desired number of statistical data points. It is important to note that the number of observations for each mode segment may be different. For example, the observation matrix for R0 (see Fig. 13c and d) contains 114 observations, 90 from MAM (3 arrays * 30 block sets * 1 transformation) and 24 from MASW (1 array * 6 offsets * 4 transformations), whereas R1 contains 54 observations, 30 from MAM (1 array * 30 block sets * 1 transformation) and 24 from MASW (1 array * 6 offsets * 4 transformations). The number of statistical data points, as with the active case, is set by the analyst depending on the bandwidth of the data. Since L0 (Fig. 14c and d) is the most broadband, it utilizes the greatest number of points (21), whereas R1 (Fig. 13c and d) is the most bandlimited, it utilizes the fewest number of points (8). Following the development of the observation matrix, just as in the previous active-source example, custom statistical weights may be applied, although we do not do so herein for simplicity. The observation matrix and the custom statistical weights (if any) are then used to calculate the dispersion statistics. Again, while we assume a normal distribution for each statistical point, any suspected distribution may be used if desired. In Fig. 13c and d, we present error bars illustrating the mean ($\mu$) and $\pm$ one standard deviation ($\sigma$) range for the apparent R0 and R1 dispersion data in terms of frequency and wavelength, respectively. In Fig. 14c and d, we present error bars illustrating the $\mu$ $\pm$ $\sigma$ range for the apparent L0 dispersion data in terms of frequency and wavelength, respectively.

While not illustrated herein, the statistical representations of the Rayleigh and Love wave dispersion data can be simultaneously targeted and jointly inverted using the Dinver module (Wathelet et al. 2004) of Geopsy (Wathelet et al. 2020). Guidance on how to do this, including how to develop Vs profiles that are consistent with measured dispersion uncertainty, may be found in Vantassel and Cox (2021a, b). An important point to note about the development of uncertainty-consistent Vs profiles following the procedure of Vantassel and Cox (2021b) is that it requires the calculation of correlation coefficients between statistical points. Of course, the calculation of correlation coefficients is only possible if the observation matrix is completely filled with data, which is not possible when combining data from various arrays spanning different bandwidths. Therefore, assumptions must be made about the behavior of the data and/or the underlying correlation structure. Work on this topic is ongoing and expected to be published in the near future, as such, it is unfortunately not possible to present those findings herein. Despite this limitation, the workflow presented in this paper represents an important step forward toward a standardized procedure, complete with open-source tools, for rigorously transforming surface wave field measurements into dispersion data that account for all reasonable sources of epistemic and aleatory uncertainty. Once the dispersion data has been represented statistically, it can be inverted as a means to propagate the uncertainty forward into suites of Vs profiles that can be used to rationally account for uncertainty in subsequent engineering design.

6 Conclusions

This paper presents a workflow for transforming experimental surface wave measurements into estimates of surface wave dispersion data with robust measures of uncertainty. The paper opens with a discussion of the importance of acquiring and processing experimental surface wave measurements in a manner that will allow one to account for all reasonable sources of epistemic and aleatory uncertainty. These include, for active-source measurements, the use of multiple arrays, source offsets, and wavefield transformations, and for passive-wavefield measurements the use of multiple arrays, block sets, and wavefield transformations. The paper details how these active-source and passive-wavefield measurements can be processed using open-source software and provides specific recommendations in regards to the processing settings that have the greatest impact on the dispersion statistics. To illustrate how the dispersion peak power points from surface wave processing are ultimately used to calculate a robust statistical representation of the experimental dispersion data, two common applications of surface wave testing are presented using real experimental datasets. The first, demonstrates the case where only active-source data are available, and, the second, where both active-source and passive-wavefield data are available. In both cases, clear guidance is provided on the steps required, which include the following: identifying and isolating continuous mode segments using interactive trimming, structuring the trimmed data into independent observations, resampling those observations at discrete statistical points, applying custom statistical weights (if desired), and, finally, calculating robust statistical representations of the experimental dispersion data. The guidance provided for developing robust estimates of dispersion uncertainty forms a critical step required for developing suites of Vs profiles, through inversion, that are consistent with the uncertainty in the experimental data. To enable the reader to easily adopt the recommendations presented herein, this work is accompanied by an open-source Python package, swprocess, and associated Jupyter workflows (Vantassel 2021). The authors hope that the publication of this work will lead to further discussions about the possibility of developing standards of practice for surface wave data acquisition, processing, and inversion.