Moho depth analysis of the eastern Pannonian Basin and the Southern Carpathians from receiver functions

Abstract

Receiver function analysis is performed for the easternmost part of the Pannonian Basin and across the Southern Carpathians, a geologically and geodynamically complex region featuring microplates, mountain belts, and locally deep sedimentary basins. We exploited seismological data of 56 stations including temporary broadband stations of the South Carpathian Project (SCP) and two permanent stations in Hungary. We calculated P-to-S receiver functions to determine the variation of Moho depth across the basin and the mountains along a NW–SE-oriented swath about 600 km long and 200 km wide. We applied threefold quality control on the raw and the processed data. The Moho depth was determined by two independent approaches, common conversion point migration and H-K grid search method. The determined Moho depths show shallow values between the AlCaPa and the Tisza-Dacia blocks, with typical depths between 22 and 28 km, and the shallowest depths in the area of eastern Pannonian Basin. We could estimate the Moho depth beneath one station in the Mid-Hungarian Zone, between the AlCaPa and the Tisza-Dacia blocks. The crust was thicker under the Apuseni Mountains (28–32 km), and in the investigated region, the Moho was deepest beneath the Southern Carpathians (33–43 km). We observed a southeastward crustal thickness increase, and we presented an interpolated Moho map over the area of study.

Introduction

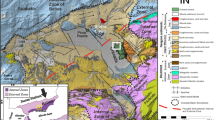
Our study area is the transition zone between the Carpathian Mountains and the Pannonian Basin in Central Europe (Fig. 1). Several studies describe the evolution and tectonic structure of this transition zone (Horváth et al. 2006; Kovács et al. 2007; Schmid et al. 2008). The Tethys Ocean had closed in the Jurassic (Handy et al. 2010), which triggered the development of subduction zones and collisional belts between the Adriatic microplate and the European continent in the Cretaceous (Horváth et al. 2006). In the next phase formed the Pannonian Basin, a geologically complex extensional back-arc basin (Horváth et al. 2006). The development history of the basin features several processes. In the early Miocene, lithospheric extension resulted in basin thinning because the extension velocity was larger than the sediment fill rate (Csontos et al. 1992). During this time, north-eastward movement of the Adria block and collision with Europe occurred. This has resulted in the formation of the AlCaPa and Tisza-Dacia terrains (Horváth et al. 2006). The rotation of the AlCaPa block was counterclockwise, and the rotation was clockwise for the Tisza-Dacia block. In the next phase, the two blocks underwent SW–NE-oriented extension, but were still separated by the Mid-Hungarian Zone (MHZ), located between these two blocks and being the continuation of the Periadriatic Line (Csontos and Nagymarosy 1998; Tari et al. 1999). This zone is defined between the Balaton Fault and the Mid-Hungarian Fault. In the next phase, in the middle Miocene, the thickness of sediments in the Pannonian Basin reached 6–7 km, as during this time, the sediment fill rate exceeded the extension velocity (Lenkey 1999). In the end of the Miocene, the area of the Basin is generally characterized by compressional stress fields and left-lateral movements (Fodor 2010). Furthermore, the transformation of stress field from the extension to the compression continued in the Pliocene age and this is still ongoing today. As for the neotectonic phase of the basin, GPS measurements indicate that with respect to the Eurasian Plate, the Adriatic microplate moves 4 mm/year in northeast direction (Bada et al. 2007). This movement has an impact on the AlCaPa structural elements. The eastern part of the block moves 0.3 mm/year, and the western part of the block moves 1.3 mm/year, while other parts of the block are relatively stable.

Fig. 1

The map shows the investigated area, the seismic stations used in this study, and the main tectonic features (black lines). The green triangles represent stations on hard rock and the brown triangles show stations on sediments. This distinction is important as sediments affect the receiver function waveforms. BUD and PSZ are the two permanent stations in Hungary used in this study. Two Romanian permanent stations (BMR: 3H07 and HUMR: 3F15) appear renamed for the SCP project. SCP1 to SCP6 mark the locations of migrated cross-sections. Abbreviations: AM, Apuseni Mountains; AP, AlCaPa block; BF, Balaton Fault; DI, Dinarides; EA, Eastern Alps; EC, Eastern Carpathians; MHF, Mid-Hungarian Fault; MHZ, Mid-Hungarian Zone; SC, Southern Carpathians; TD, Tisza-Dacia block; TP, Transylvanian Plateau; VB, Vienna Basin; WC, Western Carpathians

In the Pannonian Basin, the Moho discontinuity is generally at shallow depth, between 21 and 32 km (Horváth et al. 2015). The shallowest area is the Pannonian Basin, due to the lithosphere extension (Horváth et al. 2006). The structure of lithosphere is more complicated and the crust-mantle boundary is located deeper in the South Carpathians because of Adriatic convergence (Kovács et al. 2012).

Previous instrumental seismology studies in the investigated region usually used 2D, controlled-source seismic reflection, and refraction profiles, such as the CELEBRATION 2000 (Guterch et al. 2003), ALP 2002 (Brückl et al. 2007), and the SUDETES (Grad et al. 2008). The first passive array experiment, the Carpathian Basin Project (CBP), took place between 2007 and 2009 and studied the western part of the Pannonian Basin (Dando et al. 2011; Hetényi et al. 2015). In the western part of the Pannonian Basin, the crust-mantle interface beneath the MHZ was not identified by receiver function analysis probably because the velocity contrast at the crust-mantle boundary is not significant due to low vertical gradient of the velocity with depth (Hetényi et al. 2015).

The South Carpathian Project (SCP) deployed 54 temporary broadband seismographs between 2009 and 2011 in the eastern part of the basin and across the Southern Carpathians (Fig. 1). The SCP data were utilized for body wave tomography (Ren et al. 2012) and ambient noise tomography (Ren et al. 2013). The body wave tomography determined P wave velocity model of the upper mantle beneath the Carpathian-Pannonian region, while the ambient noise study determined an S wave velocity model for the crust, thus leaving a gap on the Moho depth beneath the region. So far, no receiver function studies have been published for the SCP region and the results from permanent station data remain scarce (e.g. Hetényi and Bus 2007). Furthermore, the region is sparsely covered by actual Moho depth measurements; therefore, the published maps on the depth of crust-mantle boundary (Grad et al. 2009; Horváth et al. 2015) lack data points and rely on falling back to background crustal thickness models in their interpolations.

We fill this data gap by carrying out P-to-S receiver function analysis for all SCP stations as well as for permanent stations (BUD, PSZ) in the area (Fig. 1). We focus on determining the depth of the Moho from receiver function analysis. The basis of receiver function analysis is that near vertically arriving teleseismic P waves are converted to S waves and other multiples at sharp velocity discontinuities such as the Moho below the receiver. By deconvolving the vertical component from the radial and transversal components of the waveform, we obtain the receiver function, which approximates the Green’s function, the Earth response beneath the station. This carries information about the velocity structure and the depth of the major discontinuities below the receiver. Hence, receiver function analysis is one of the primary tools for determining depth of Moho. The good station coverage provided by the SCP allows us to present the depth of the Moho in unprecedented details. We determine the Moho depth with two independent methods and present six migrated profiles for the study area.

Data and methodology

We used teleseismic earthquakes of magnitude larger than 5.5 from the USGS catalogue (https://earthquake.usgs.gov/earthquakes/search/), located between 28° and 95° epicentral distance from each seismological station. The dataset consists of data recorded between 2009 and 2011 at the 54 broadband seismological stations of the SCP array, and at the two permanent stations from between 2004 and August 2017. The SCP stations were deployed along four approximately NW–SE-oriented profiles in the Pannonian Basin and across the Southern Carpathians, with some stations located outside the profiles, and the two Hungarian permanent stations were along these lines (Fig. 1). The SCP temporary network provided broadband, three-component data, and the sensors at the stations consisted of 17 CMG-40T, 13 CMG-3T, and 24 CMG-6TD seismometers (Ren et al. 2012). The period range of CMG-40T was between 30 s and 50 Hz, the CMG-3 T was between 120 s and 50 Hz, and the CMG-6TD was between 30 s and 100 Hz. The data of the SCP project stations are freely available at the IRIS web site. The SCP network does not have a DOI, but can be identified on the FDSN website (http://www.fdsn.org/networks/detail/YD_2009/). Further waveforms were provided by the Hungarian National Seismological Network (doi: https://doi.org/10.14470/UH028726) and from the two renamed permanent Romanian stations Baia Mare (BMR, here 3H07) and Humele (HUMR, here 3F15) (doi: https://doi.org/10.1007/978-3-319-14,328-6_9). Figure 2 shows the 687 teleseismic events used for the SCP array stations and the 2887 events used for the two permanent stations.

Fig. 2

Epicentre maps of the 2887 and 687 teleseismic earthquakes used for receiver function calculation at permanent Hungarian stations (a) and SCP stations (b), respectively. The two inner circles show the epicentral distance limits at 28° and 95°

We downloaded altogether 76,734 three-component seismograms for the SCP array and 15,528 seismograms for the Hungarian permanent stations. We deleted the seismograms with gaps and where not all three components were available. Then we applied the first quality control (QC1) for the filtered three-component waveforms. In this step, we removed the mean and the trend in the waveforms, filtered them with a Butterworth band-pass filter between 0.1 and 1 Hz, and used a taper to eliminate the aliasing at the ends of the signal. The QC1 was an STA/LTA detector (Trnkoczy 2012). We used a 900-s time window, 300 s before and 600 s after the predicted first-arriving P wave. The length of the STA and LTA windows were 10 s and 50 s, respectively. Waveforms are rejected either if no detection was made, or if the STA/LTA value was smaller than 3.5. This reduced the dataset to 38,712 waveforms in the SCP array stations and 8415 at the two permanent stations for receiver function analysis.

Most of the investigated area (27 stations) is covered by thick sediments; therefore, background noise is relatively high, and ghost converted-phases appear for most events (Hetényi et al. 2015). Waveform ringing was also observed in data due to multiple reverberations of waves between the surface and the bottom of the basin. In the second quality control step (QC2), we measured various signal-to-noise ratio (SNR) norms (Hetényi et al. 2015, 2018a). Here we used the same filtered waveforms as for QC1, but we applied a shorter (120 s) time window (30 s before and 90 s after the first-arriving P). Waveforms were rejected if the two SNR values were below the respective thresholds. The first SNR value was the peak amplitude to background amplitude, with a minimum value of 3. The second was the peak amplitude to the background root mean square (rms), with a minimum value of 5. After the second QC step, we rotated the accepted ZNE seismograms into the ZRT coordinate system according to station-to-event azimuth (back-azimuth). The radial component was deconvolved from the vertical component using the iterative time-domain approach (Ligorría and Ammon 1999) with 150 iterations to calculate the receiver functions. The obtained series of spikes were then convolved with a Gaussian of width corresponding to the highest frequency of the signal to obtain the final radial receiver functions.

Finally, we applied the third quality control step (QC3) for the calculated radial receiver functions (Hetényi et al. 2015, 2018a): the maximum amplitude peak should be in the range − 0.5 to 2 s of the theoretical P arrival, and its amplitude must be positive but less than 0.8. After QC3, the high-quality dataset contains 2644 traces in the SCP array stations and 1510 traces at the two permanent stations. Figure 3 shows the evolution of the number of accepted waveforms in the SCP stations sorted by SCP lines.

Fig. 3

Statistics on the number traces at SCP stations during quality control (QC). The blue column represents the number of downloaded waveforms; the brown and red columns show the number of accepted waveforms after QC1 and QC2-3. See text for the description of these QC steps. The brown colour of the station names represents the hard rock stations and the green shows the sedimentary stations. About 35% of the receiver functions have passed all the quality control steps compared with the QC1 waveforms

We used the accepted receiver functions to determine the Moho depth below the stations, using two different methods.

First, we determined the Moho depth using the H-K grid search method (Zhu and Kanamori 2000) where H represents the Moho depth and K stands for the average crustal Vp/Vs ratio. Depending on the geologic settings, we set different crustal Vp velocities from published articles (Grad et al. 2006; Tasarova et al. 2009; Janik et al. 2009) for each station individually; these values range between 5.8 and 6.5 km/s. We defined the Vp/Vs ratio search range between 1.5 and 2.0. For the range of the Moho depth, we used 20 and 40 km in the basin areas and 20 and 45 km in the mountains, following Horváth et al. (2015). The Vp/Vs and Moho depth intervals represent physically meaningful limits for the investigated area. The weights of Ps (W1), PpPs (W2), and PpSs+PsPs (W3) phases were fine-tuned for each station. We experimented with two frequently used weighting methods. First, we gave a large weight to the direct conversion (W1) and smaller ones to the multiples (W2, W3), but in this case, the result is dominated by the higher-amplitude Ps phase for the Moho depth determination (Licciardi et al. 2014). Second, we assigned the same weight for each phase (e.g., Lombardi et al. 2008), but in this case, noisy multiples (W2 and W3) can result in poorly determined Moho and Vp/Vs values. Hence, in order to take into account the dominating multiples and reduce the impact of the noisy multiples, we assigned weights manually for each station. In all cases, W1 was always larger than W2 and W3. However, at stations over thick sedimentary cover, in some cases, we could not identify the multiples, and these were discarded from the analysis. Furthermore, we cannot identify regularity between the weights and the type of the stations, but usually we used larger W1 weight for stations on sediments than those on outcrops. We listed the weights for each station in the electronic supplement.

Second, we imaged the Moho depth with the common conversion point migration (Zhu 2000) using the local, one-dimensional velocity model by Gráczer and Wéber (2012), with a modified Moho depth to 45 km to allow the P-to-S conversions being mapped to the right depth with crustal velocity. The selected velocity model has a thin (3 km) top layer of slower P velocity (5.3 km/s), but this still appears to be too fast compared with velocity models of the upper crust from refraction profiles. Yet this model is clearly better for this region than the three global one-dimensional velocity models we tested, namely iasp91 (Kennett and Engdahl 1991), ak135 (Kennett et al. 1995), and CRUST1.0 (Laske et al. 2013). The iasp91 and ak135 models are acceptable beneath the Carpathians, but seem to be too fast for the eastern Pannonian Basin. The CRUST1.0 gave similar results as Gráczer and Wéber (2012), but we opted to choose a single local 1D velocity model of the region. Still, as nearly half (27 of 56) of the stations were located on top of thick sediments, we applied a depth correction at these stations for receiver function analysis. To this end, we used the pre-Cenozoic basement map in Hungary (Haas et al. 2010) and pre-Neogene basement depth values between Hungary and Carpathians (Royden and Horváth 1988). For the foreland of the South Carpathians, we used a pre-Miocene basement map (Matenco et al. 2003). The local Vp value for the sediments is taken from Grad et al. (2006) and Środa et al. (2006), and their Vp/Vs ratio was 2. We defined 6 cross-sections (Fig. 1) and we performed pre-stack migration (1 km horizontal and 0.5 km vertical resolution of the bin size), with results presented in raw format and interpreted profile.

Results and interpretation

Quality control

Figure 4 demonstrates the importance of quality control when calculating receiver functions. It shows receiver functions sorted by back-azimuth and stacks at the 4F07 hard rock station and the 6D04 sediment station before and after QC2-3. The amplitude of multiples becomes larger and the noise is significantly reduced after QC2-3. Furthermore, the time lags on the sedimentary station receiver functions (6D04 station) become more apparent. This is attributable due to the low velocity and young, unconsolidated sediment layer. We show the receiver function stacks before and after QC2-3 for all stations in the electronic supplement.

Fig. 4

Receiver function sorted by back-azimuth and stack of the receiver functions before (left) and after (right) QC2-3 at 4F07 (top) and 6D04 (bottom) stations. Numbers on the right of each back-azimuth bins are the number of included individual receiver function traces

We can check the quality of the receiver functions on the back-azimuth-dependent stacks. The back-azimuthal bin stacking of the receiver functions minimizes noise and increases coherent signal intensity. Furthermore, we can investigate local dip and anisotropy beneath the seismological stations. Figure 5 shows further four stations with more than 60 receiver functions and reasonable back-azimuthal coverage, stacked in 20°-wide back-azimuthal bins with 5° overlap. The radial receiver functions present the P peaks between 0 and 2 s. The P-to-S conversion of the crust-mantle boundary appears between 2.5 and 4 s at hard rock stations (Fig. 5a–d), while at the station above sediments, it can be observed 1–1.5 s later (Fig. 5c). We are able to clearly detect the PpPs phase in the two permanent stations, owing to the much larger amount of receiver functions (Fig. 5a and b). The sedimentary stations are noisier and the peaks of the multiples are more difficult to detect. The energy on the tangential components most likely stems from anisotropy and dipping boundaries of the first-order discontinuities beneath the seismic stations (Savage 1998). However, we do not have enough high-quality receiver functions at most stations from the SCP project to resolve confidently anisotropy and layer dip in this study. We present radial and tangential receiver functions at all stations in the electronic supplement.

Fig. 5

Radial and tangential receiver functions sorted by back-azimuth at stations PSZ (a), BUD (b), 6C03 (c), and 3C11 (d). Numbers to the right of the radial receiver functions are the number of the traces in each stack. The P, Ps, and PpPs lines identify the respective peaks

H-K analysis

We performed the H-K grid search method on the accepted receiver functions. The Moho depth varies between 22 and 43 km in the investigated area. The shallower values are found in the eastern Pannonian Basin beneath the Tisza-Dacia block, where these values are around 22 and 27 km (Fig. 6b). The crust-mantle boundary beneath the AlCaPa block is somewhat deeper, at around 27–30 km. Similar values are found at the northwest edge of the Carpathians, as well as at the transition zone between Pannonian Basin and Southern Carpathians (Fig. 6a). We found deeper values beneath the Apuseni Mountains (35 km) and the Southern Carpathians (Fig. 6c). The crust-mantle boundary is between 31 and 43 km in the Carpathians (31–43 km) (Fig. 6a). Overall, along the SCP profiles, the Moho depth gradually increases from NW to SE. The uncertainty of the Moho depth determination at the 86% confidence level is about ± 1.1 km on average from the H-K analysis, shown in Fig. 6 as the area in red. Similarly, the uncertainty in the initial Vp velocity is about ± 1.2 km. The stations on sediments (e.g., Fig. 6b) have noisier receiver functions than those on hard rock (e.g., Fig. 6a). We list the H-K analysis parameters and results for all stations in the electronic supplement. As the H-K method is based on post-stack analysis and an a priori crustal Vp value, we further our analysis with a pre-stack approach employing a 2D velocity model.

Fig. 6

Results of the H-K grid search method (Zhu and Kanamori 2000) at stations 3C11 (a), 6D04 (b), and 4F09 (c). The three stations represent different geologies. Station 3C11 is located in the Southern Carpathians, 6D04 station is in the eastern Pannonian Basin, and station 4F09 is located in the Apuseni Mountains. The left panel shows fit (sum of amplitudes) at various Moho depths and average crustal Vp/Vs values at the corresponding arrival times (right) of the Ps, PpPs, and PpSs+PsPs phase weighted respectively with W1, W2, and W3. The Ps, PpPs, and PpSs+PsPs lines show the location of each peak. The extent of the red area (86% of the peak) around the maximum (star) is a proxy for the uncertainty

Migration

We performed common conversion point migration to image the Moho depth beneath the SCP array profiles independently from the H-K analysis. This approach has proven to provide more realistic results, thanks to pre-stack migration with adapted velocity models. We defined four profiles through the AlCaPa and Tisza-Dacia blocks and across the MHZ, and two roughly perpendicular profiles through stations with names ending in “07” and “11” (Fig. 1). Figures 7 and 8 show the topography above the profiles (top), the raw (second), and the interpreted (third) migration profile results. The interpolated Moho depth results from the migration (dashed green lines) are compared with the result from H-K analysis (in orange).

Fig. 7

a Migrated P-to-S receiver function cross-sections for SCP1 line. The top panel shows the topography above each profile and the location of seismic stations projected to the SCP line, the middle panel presents the raw migration result, and the bottom panel shows the interpreted results. The green triangles represent stations on hard rock and the brown triangles show stations on sediments. The migrated sections are corrected by the elevation and refer to the sea level. The dotted green lines represent the Moho depth from migration methods. The green circles represent the interpolation points that were used to produce the Moho map. The orange circles show the depth of Moho beneath each station from H-K grid search method. The dotted orange lines show the interpolated depth of Moho from the H-K method. The abbreviations of structural elements are the same as in Fig. 1. b Migrated P-to-S receiver function cross-sections for SCP2 line. Panels and features are described in a. c Migrated P-to-S receiver function cross-sections for SCP3 line. Panels and features are described in a. d Migrated P-to-S receiver function cross-sections for SCP4 line. Panels and features are described in a

Fig. 8

Migrated P-to-S receiver function cross-sections for lines SCP5 (a) and SCP6 (b). Panels and features are described in Fig. 7a

The first profile, SCP1, was 560 km long with 11 stations (Fig. 7a). Most stations show clear Moho depth values. An important finding is beneath station 6C03 in the MHZ, where the Moho is clearly detected at 27–28 km. The MHZ is an intriguing target, as the Moho was not clear here in the western Pannonian Basin (Hetényi et al. 2015). However, the H-K analysis pointed to a 22-km deep crust-mantle boundary. The difference is due to the sedimentary layer (1.9 km) and the choice of the constant Vp velocity in the H-K method. The Moho appears deeper at the edge of the Tisza block and in the Southern Carpathians than in the AlCaPa block.

The SCP2 profile was 570 km long and used 14 stations (Fig. 7b). In the migrated image, some stations show no clear Moho beneath the AlCaPa and Tisza blocks, and some stations reveal a shallow crust-mantle boundary between 22 and 26 km depth. These stations are situated on thick sediments (5–6 km); therefore, the receiver functions are very noisy. This profile shows clear Moho conversion beneath the Southern Carpathians, at depths between 34 and 43 km; the deepest value is beneath the highest altitude mountains. At station 6D11, which is located in the high-Carpathians, the Moho depth mirrors the topography. The average 1000–1500 m topography can be isostatically compensated by a 7–12-km thick crustal root, which fits our depth observations.

The SCP3 profile used 14 stations and was 530 km long (Fig. 7c). This profile shows clear Moho beneath AlCaPa and Tisza blocks. The depth of Moho shows consistent deepening from AlCaPa to the Southern Carpathians. The root of the mountains is not as pronounced in this profile because the topography increases more gradually towards the Southern Carpathians.

The SCP4 profile, with 14 stations over 590 km, is shown in Fig. 7d. We can identify clear Moho signal beneath most stations. The situation is similar to profile SCP3, as the Apuseni Mountains represent a somewhat elevated topography and deepened Moho (28–33 km) before reaching the Carpathians (33–37 km). The Moho depth beneath the AlCaPa and Tisza blocks is very similar to those at the SCP1-3 profiles.

Figure 8 shows the two migration profiles along “07” and “11” stations, perpendicular to profiles SCP1-4. The SCP5 profile is shown in Fig. 8a. This was 350 km long with 6 stations. The depth of Moho increases from the Tisza block to the Transylvanian Plateau. The Transylvanian Plateau presents 28–31 km Moho depth. We do not detect drastic changes of Moho depth from west to east, as the SCP5 profile does not cross the Carpathians towards the east. The SCP6 profile was 380 km long and used 6 stations (Fig. 8b). This profile shows deeper Moho beneath the Carpathians (34 and 43 km), with a clear image of the mountain root.

Discussion

We applied two independent methods, the H-K grid search and the migration of receiver functions to obtain the depth of the crust-mantle boundary. We obtained consistent and very similar results with both methods, the differences being inherent in the various assumptions of the methods (Fig. 9a). We successfully applied the H-K grid search method on 42 out of 56 stations, and these results exhibit very good correlation with the migrated profiles. In most cases, we were able to detect a clear crust-mantle boundary beneath the seismological stations. The differences between the H-K results and the migration profiles are found mostly beneath the AlCaPa and Tisza blocks and attributed to thick sedimentary layers. We can identify similar differences in the southeast foreland of the South Carpathians, where the thickness of sediments reaches 2–3 km. Ultimately, we rely on the migrated profiles for the interpretation as the approach allows better spatial reconstruction of converters at depth. Furthermore, the pre-stack depth migration and the better-suited velocity model employed during migration yield a higher quality image. The H-K method stacks all RFs for each station prior to vertical 1D migration, which is based on an assumed constant Vp of the crust for each station. In other words, CCP creates a set of 2D images, while H-K is a set of 1D information.

Fig. 9

a Interpolated Moho map from the common conversion point migration method. Black circles represent the Moho depth points on the migrated profiles that served as the basis for the interpolation. Triangles show the depth of Moho beneath each station obtained from the H-K grid search method. The one-dimensional H-K results confirm the validity of the two-dimensional CCP migration results. b Moho map by Grad et al. (2009), with our research area contoured with a black rectangle. The abbreviations of structural elements are the same as in Fig. 1

One of our important results is that we successfully imaged a clear Moho beneath the MHZ from migration. Although this is the only Moho depth observation beneath the MHZ in this study, it is important as it shows that the velocity gradient across the crust-mantle interface can be sharp, as opposed to findings in the western Pannonian Basin, where the lack of Moho signal was interpreted as a broad vertical velocity gradient with depth (Hetényi et al. 2015). Therefore, the nature of the vertical velocity gradient across the Moho can vary along the MHZ.

We aim for a common interpretation for the six cross-sections to equilibrate the variable signal quality and success in mapping the Moho along the individual migrated profiles. We therefore picked the Moho depth on all profiles where they were identifiable with high confidence, and interpolated these Moho depth values to a Moho depth map over an area of 600 by 200 km as shown in Fig. 9a. Within the uncertainty of the depth determination, the Moho depths are similar beneath the AlCaPa and Tisza blocks, which confirms that they thinned to the same thickness during their geological part (Hetényi et al. 2015). Compared with the thin Moho (22–28 km) beneath eastern Pannonian Basin, the Apuseni Mountains have thicker crust (28–32 km), while the thickest crust is found beneath the Southern Carpathians (33–43 km). The SCP2 and SCP6 profiles show the root of the Southern Carpathians Mountain. Figure 9a shows that the general increase in Moho depth from the Pannonian Basin through the Transylvanian Plateau to the Southern Carpathians is clearly mapped.

Finally, we compare this map with the latest published local Moho map of the Pannonian Basin (Horváth et al. 2015) as well as the European Moho map (Grad et al. 2009) derived from seismic refraction profile data, body and surface wave tomography, and receiver function analysis. Figure 9b shows the Moho map by Grad et al. (2009) and the outline of our study region. Note that the scale of the maps is quite different as our map covers only a small fraction of the two other maps. On the other hand, we have much higher density of data points where the other maps lack dense data coverage and rely on interpolation or fall back to the initial background models. For instance, we obtained receiver functions from four stations in the Apuseni Mountains, where the Grad et al. (2009) map had no data at all. For the eastern part of Pannonian Basin, we obtain a similar depth of Moho (22–27 km) to that of in Horváth et al. (2015), but somewhat thinner crust (26–31 km) than in Grad et al. (2009). Horváth et al. (2015) show somewhat thinner crust (22–25 km) beneath Tisza-Dacia than the AlCaPa (25–27 km). Our map shows similar values beneath the two structural elements, and we cannot identify a decrease in Moho depth from AlCaPa to Tisza-Dacia. The Moho depth values are in good agreement in all three maps for the Southern Carpathians (35–43 km), the thinner values being located at edges of the mountains. We have achieved higher resolution over the roots of the Carpathian mountains, which allowed to resolve deeper Moho depths there (42–43 km) than in Grad et al. (2009).

Conclusions

We performed receiver function analysis in the eastern part of the Pannonian Basin and the Southern Carpathians region, including strict quality control procedures. We determined the Moho depth with two independent approaches: the H-K grid search method and the common conversion point migration method. Owing to the thick, young, and unconsolidated sediments, the H-K analysis failed to provide accurate results for the Moho depth beneath several stations of the eastern Pannonian Basin. However, with the common conversion point migration, we were able to account for the sedimentary cover, and to resolve the Moho beneath this area in most cases. The Moho depth results from the two methods agree well under the Carpathians. Based on topography and the imaged crustal root, it appears that the Southern Carpathians are in—or close to—isostatic equilibrium. At our only station in the Mid-Hungarian Zone, we observed a Moho, which points to a real discontinuity, unlike in the western Pannonian Basin where a broader vertical velocity gradient was interpreted.

We observed thin crust at the AlCaPa and Tisza blocks, which supports the tectonic view that the area went through an extension phase, proposed for the early Miocene according to the geological record. We observed gradual crustal thickening from the AlCaPa to the Southern Carpathians. Future studies will focus on larger areas in and around the Pannonian Basin, especially the western part of the Pannonian Basin exploiting the data from the AlpArray experiment (Gráczer et al. 2018; Hetényi et al. 2018b).