1 Introduction

Core–shell nanostructures have attracted intensive attention because of their promoted combination of electronic and optical properties [1]. This class of nanomaterials is used in many practical applications such as catalysis, impact modifiers, surface coating, sensors, and drug delivery systems [2]. Different types of core–shell nanostructures can be possibly combined; the selection of the core and the shell materials is strongly dependent on the requesting application [3]. Inorganic/organic is a highly functional type of core–shell nanostructures especially with spinel ferrites [4].

Core–shell spinel ferrites are composite particles in nanoscale dimensions consisting of at least two different materials; in principle, one could be the core (as a spinel ferrite particle) coated by the other (as a polymeric surfactant) [5]. Significant properties of the different materials can be combined in just one modified nanoparticle which has multi-modality functions [6].

Spinel ferrites are widely used in numerous areas of modern applications due to their distinctive features such as information storage devices, microwave devices, electronic industries, high-frequency devices, and drug delivery [7]. Various interesting properties like scale dimensions, high surface/volume ratio, and electrical and optical properties depend on the preparation technique. Nanoferrites with spinel structure can be synthesized by a variety of methods such as co-precipitation, conventional solid-state reaction, sol–gel, and auto-combustion. Among all preparation methods, the auto-combustion method is the most effective, lowest in cost, and the simplest [8].

The protective coating of spinel ferrites by polymer prevents the corrosion of iron and agglomeration of nanoparticles [9]. In recent decades, coating by natural polymers like protein is very quite common compared to synthesized polymers [10]. Although the biocompatibility of natural polymers in biomedical applications, they are water-soluble and also have poor mechanical strength [11]. This difficulty can be resolved by coating nano-CaFe2O4 with synthesized polymers which are of better mechanical strength such as polyvinyl alcohol (PVA), polyvinyl pyrrolidone (PVP) [12], and polyethylene glycol (PEG) [13]. The selection of synthesized polymer depends on the required physical properties for specific applications [14].

One interesting synthesized polymer is polyethylene glycol (PEG); polyethylene glycol results from the chemical interaction between ethylene oxide and water with the general linear structure HOــ [CH2ــ CH2 ــ O]nــ H where n is the average repeating number [9]. PEG has attracted great interest because of its physical and biomedical properties such as the ability to highly crystallize, non-toxic, and non-antigenic [15].

Ateia et al. [16,17,18] studied the characterization and the physical properties of CaFe2O4 before and after doping with different rare earth ion concentrations. As previously proved in their work, the optimum concentration of rare earth ions was found to be as shown in the present work [8, 16].

The main target of the present investigation is to create core–shell nanostructures with improved physical properties. Consequently, we proposed a synthesis strategy that involves two issues. The first one is synthesized CaFe1.925Gd0.025Sm0.05O4 NPs by a modified citrate technique to be a core part of the core–shell structure. The second issue is to keep the CaFe1.925Gd0.025Sm0.05O4 NPs from agglomeration by coating long-chain PEG on the surface, so that they do not lose their distinctive physical properties that depend on the existence of NPs at a specified nanoscale. Their characterizations were investigated by XRD, HRTEM, FTIR, EDAX, and XPS.

2 Experimental

2.1 Preparation of CaFe1.925Gd0.025Sm0.05O4 Nanoparticles

To achieve a relative nanoparticle size distribution of rare-earth-doped calcium ferrite samples, CaFe1.925Gd0.025Sm0.05O4 nanoparticles (RCFNPs) were prepared by using the citrate combustion method [17]. In this method, the stoichiometric quantities of calcium nitrate Ca (NO3)2.4H2O, ferric nitrate Fe (NO3)3.9H2O, gadolinium nitrate Gd (NO3)3.6H2O, and samarium nitrate Sm (NO3)3.6H2O are well mixed and dissolved in 20 ml of double-distilled water with citric acid as a chelating agent. The solution is continuously stirred well with a magnetic stirrer until a homogenous solution is obtained. The solution is, then, stirred vigorously and heated at 90 °C for 1 h till the solution turned into gel. This is followed by continuous heat at 200 °C until the gel is burned out and the sample transformed into gray ash. Then, the gray ash is collected and ground into fine powder. The powder is then calcined at 900 °C for 4 h in a furnace.

The specific concentration values of rare earth elements are chosen according to Saeid and Ateia [8]. If the preparation process is occurred by doping rare earth ions R3+ with a concentration of more than 3.75% in the B site of spinel ferrites instead of Fe3+, the secondary phases of the rare earth ions will be appeared [8].

2.2 Synthesis of CaFe1.925Gd0.025Sm0.05O4/PEG Core/Shell Nanoparticles

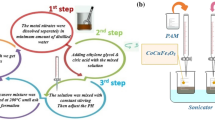
A pure grade of PEG (molecular weight 40,000 g/mol) was imported from Loba Chemie Pvt. Ltd., India. This polymer was chosen to encapsulate RCFNPs in a core/shell design, with the magnetic ferrite serving as the core, being capped with the polymeric surfactant shell. As shown in Fig. 1, the ultrasonication preparation method is used to obtain RCFNPs and PEG cores and shells. In the present study, 0.7 g of the RCFNPs was added to 30 ml of distilled water in a beaker as an aqueous solution. In another beaker, 0.3 g of PEG was dissolved in 30 ml of distilled water. The two entire solutions were sonicated thoroughly for about 4 h. Afterwards, the polymeric solution was added to the corresponding suspended ferrite solution, and the mixtures were then sonicated for 4 h. The mixtures were dried at 60 °C for 24 h to form the core–shell structure with a PEG surfactant polymer capping the core nanoparticles of RCFNP [18] of RCFNP core [18].

Fig. 1
figure 1

A schematic diagram of the ultrasonication preparation method

Full size image

2.3 Characterization Technique

The DIANO Corporation X-ray diffractometer (XRD) with target Cu-K (= 1.5424) identifies the nanocrystal structure and size; the Scherrer equation is used to estimate the average crystallite size. The morphology of the elements was studied by the SEM technique using a Quanta 250 EG (Emission Gun) attached to an EDX (energy dispersive X-rays) analysis unit at an accelerating voltage of 30 kV and Gun 1n resolution. The chemical states of all elements were observed by X-ray photoelectron spectroscopy (XPS), the Thermo Fisher Scientific K-Alpha system (USA), and monochromatic small spot X-ray Al K-alpha radiation using CASAXPS software. The crystallographic structure was characterized by the electron microscope system (HRTEM; model JEM-100S JEOL). The molecular signature of the samples was confirmed by a Fourier transform infrared spectrophotometer (FTIR; model IRAffinity-1S). The magnetic parameters were measured by recording M-H hysteresis loops using a vibrating sample magnetometer (VSM); LDJ model 9600. The electrical parameters were carried out on the LCR model HIOKI 3532–50 in the frequency range of 0.1 to 5 MHz with increasing temperatures up to 700 K. The optical properties were probed using a UV–VIS NIR spectrophotometer; model Shimadzu UV-3101PC.

3 Results and Discussion

3.1 Structural and Microscopic Studies

The X-ray diffraction pattern of RCFNPs, PEG, and coated samples of RCFNPs/PEG are recorded in the 2θ range of 20°–80° with a step size of 0.04° as illustrated in Fig. 2. The XRD patterns of RCFNPs (Fig. 2a) and RCFNPs/PEG (Fig. 2c) clarify that the peak broadness is a characteristic of nanoparticles and indexed to the orthorhombic unit cell of the crystal lattice. Notably, all peaks match the CaFe2O4 standard spectrum (ICDD 00–008-0100), which has been assigned to the typical crystallographic planes of high-purity calcium ferrite [19].

Fig. 2
figure 2

XRD pattern of for the samples (a) RCFNPs, (b) PEG, and (c) RCFNPs/PEG

Full size image

The XRD pattern of PEG in Fig. 2b shows two distinct peaks of its crystalline nature at 19.3° and 23.6°, representing the highly crystalline phase [20]. Figure 2c shows the XRD pattern of PEG-coated RCFNPs, two peaks at 19.3° and 23.6°, and characteristic of PEG have been observed, confirming the existence of PEG. All other peaks are attributed to the orthorhombic structure of RCFNPs.

The average crystallite size (d) of the synthesized NPs can be estimated from the broadening of the XRD peaks, and it is computed using the Scherrer equation as mentioned in the previous work [21]. The d for RCFNPs and RCFNPs/PEG is calculated as 18 and 20 nm, respectively. However, it is known that the Debye–Scherrer method is exaggerating the value of average crystallite size because the broadening in XRD lines comes not just from the nanocrystalline size but from the lattice strain (ε) as well. The d in addition to the ε can also be estimated using the G. K. Williamson and W. H. Hall (W–H) plot method as mentioned in the previous work [8]. The estimated data is shown in Fig. 3 and tabulated in Table 1.

Fig. 3
figure 3

The Williamson–Hall plot for RCFNPs/PEG

Full size image
Table 1 Average crystalline size (d), microstrain (ε), experimental lattice parameters (a, b, and c), theoretical density (Dx), and tolerance factor (T) for the prepared samples
Full size table

The X-ray diffraction pattern reveals that the d of RCFO orthoferrite NPs slightly changes after coating with PEG. This is due to the interaction of RCFNPs with long-chain polymers (PEG); consequently, the crystal growth will be extended.

The experimental lattice parameters a, b, and c are calculated on the basis of an orthorhombic unit cell and tabulated in Table 1. The lattice parameters of RCFNPs/PEG show no large changes compared to RCFNPs before coating. The theoretical density (Dx) is calculated for RCFNPs and RCFNPs/PEG [32]. The Dx of RCFO/PEG is higher compared to the uncoated samples. This can be explained on the basis of the effect of coating on the lattice shrinkage, which is the main issue for the observed reduction.

The tolerance factor, T, for the investigated samples is calculated from the following equation [22]

$$T=\frac{{R}_{A}+{R}_{O}}{\surd 2({R}_{B}+{R}_{O})}$$
(1)

where RO is the ionic radius of the oxygen ion and RA and RB are the ionic radii of the ions in A and B sites, respectively. The tolerance factors displayed in Table 1 are larger than unity. Thus, a small distortion occurs in the unit cell, leading to a lower symmetry structure.

As shown in Fig. 4, standard EDX analysis is performed to determine the elemental composition of the RCFNPs/PEG core–shell. The EDX spectrum (installed in SEM) of the sample clarifies the existence of Ca, Fe, Gd, Sm, C, and O. In addition, the index table in the figure represents the values of weight and atomic percentages, as expected and justified by EDX analysis.

Fig. 4
figure 4

SEM micrographs and EDX analysis of RCFNPs/PEG

Full size image

XPS spectroscopy is used to identify the changes in the elemental surface composition of coated nanopowder. The broad scanning of the XPS spectra in Fig. 5a clearly shows the presence of photoemissions peaks Ca 3p, Fe 2p, Gd 4d, Sm 3d, C 1 s, and O 1 s. Additionally, it also indicates the valence states of the elements for each of the two samples [23]. The increase in the C 1S and O 1S intensity for the RCFNPs/PEG sample is observed for the coated sample, which is attributed to the increase in carbon and oxygen content in the sample after coating, while the remarkable peak of C 1 s for the RCFNPs sample is related to the attaching of nanopowders to an organic adhesive tape of carbon within measurement [24].

Fig. 5
figure 5

a–g XPS analyses for the RCFNPs and RCFNPs/PEG samples

Full size image

The XPS spectra of Ca 2P for RCFNPs and RCFNPs/PEG samples are shown in Fig. 5b. The split of the calcium 2P peak into two components, 2P1/2 and 2P3/2, is caused by the spin–orbit coupling, while the invisibility of the satellite peak of RCFNPs/PEG is caused by the variation of the plasmon energy loss after coating [25]. Peaks of 2P3/2 at 346 eV and 2P1/2 at 350 eV are attributed to the orthorhombic Ca lattice and the surface-bound Ca non-lattice, respectively [38].

The doublet spectra of Fe atoms in Fig. 5c correspond to the spin–orbit coupling between 3d electrons in valence states and core electrons in 2P orbitals of Fe ions, respectively. The spin–orbit interaction of the valence states Fe 2P1/2 at binding energy 724 eV and Fe 2P3/2 states at 710 eV in the samples is attributed to the two splitting peaks of Fe ions. The two divided peaks inside the Fe 2P3/2 peak reveal the existence of Fe3+ ions which are centered at 713 eV and Fe2+ ions at 710 eV [26]. Similarly, the two peaks inside the Fe 2P1/2 refer to Fe3+ and Fe2+ ions located at 724 eV and 727 eV, respectively. At binding energies of 719 eV and 716 eV, respectively, satellite peaks of Fe 2P1/2 for Fe3+ and Fe2+ ions existed [40].

As shown in Fig. 5d, the spectral deconvolution of the XPS peak for C 1 s contains four components of various carbon species that exist in RCFNPs/PEG; the adventitious carbon accumulated on the sample surface at 285.68 eV which is attributed to airborne molecular contamination occurred in organic/inorganic compound, the single-bonded carbon in C–C at 286.58 eV, the single-bonded carbon in C–O–C at 286.98 eV, and the double-bonded carbon in O-C = O at 288.78 eV; the last three carbon species are originated from PEG [27]. The obtained data confirms that the PEG layer is successfully coated on the RCFNP sample [28].

The XPS spectrum of Gd 4d in Fig. 5e consists of two peaks that are associated with Gd 4d3/2 and Gd 4d5/2 oxidation states [29, 30]. The Gd 4d3/2 peak is centered at 152 eV for the two samples, while the Gd 4d5/2 peak is centered at 140 eV and 145 eV for RCFNPs and RCFNPs/PEG, respectively. Furthermore, the XPS spectra in Fig. 5f clearly show two sets of peaks at 1107 eV and 1182 eV, which are known as Sm 3d3/2 and Sm 3d5/2 [36].

As shown in Fig. 5g, the oxygen 1 s spectrum for RCFNPs demonstrates double peaks at 531 eV and 529 eV. The O 1 s peak at higher binding energy may be raised from the released oxygen vacancies resulting from the oxygen interaction in the crystal lattice [26]. The coating of PEG is responsible for the sharp decrease in the oxygen 1S peak for RCFNPs and PEG at lower binding energies (529 eV). The coating may reduce the number of individual oxygen ions that can be trapped within the grain boundaries during the ionization process [31].

The presence of various types of oxygen states at the surface can be indicated from the individual sub-peaks observed in XPS spectra for the prepared samples [32]. The observed sub-peaks correspond to the oxygen vacancies, the O2− in the crystal lattice (OLatt.), and the chemically adsorbed oxygen (OAds.) at the surface of the samples.

The HRTEM micrographs of the RCFNPs/PEG core/shell nanostructure are illustrated in Fig. 6a–e. The images reveal a well-designed hexagonal core/shell structure. Generally, uniform size distributions of RCFNPs in roughly hexagonal shapes and well-defined boundaries are integrated into polymeric shells with an average particle size that depends on the atomic weight of both samples [8].

Fig. 6
figure 6

a–f HRTEM micrographs for the prepared samples

Full size image

The NPs depending on the preparation conditions may have a polycrystalline or single-crystalline structure. The particle of solid matter is made up of several crystallites, and hence the particle size may be larger than the crystallite size except for single-crystal NPs, in which crystallite size and particle size are identical [33]. The combination of different crystallites (diffracting domains) to construct one particle can be shown in Fig. 6c. The particle size distribution of the samples is shown in Fig. 6f. The average particle size of RCFNPs decreases from 42 to 37 nm after coating. The hexagonal shell thickness of PEG is found in the range of 1 to 6 nm. It is noticed that the grains of the core have a homogeneous distribution with a relatively lower agglomeration. The coating with PEG prevents the agglomeration of the magnetic NPs.

The polycrystalline nature and high crystallinity of the CFRO/PEG are ratified by the selected area electron diffraction (SAED) pattern (inset of Fig. 6e). The bright rings indicate numerous diffraction planes in the single unit cell.

We performed FTIR analysis on the synthesized NPs to confirm the PEG capping on the surface of RCFNPs. Figure 7 shows the FTIR spectra of synthesized RCFNPs/PEG NPs.

Fig. 7
figure 7

FTIR spectra for the sample RCFNPs/PEG

Full size image

In a core region, the lower band around 463 cm−1 corresponds to the bending mode, which is indicative of any changes in the bond angle of Fe–O-Fe. The bands at 579 cm−1 and 702 cm−1 are attributed to the deformation of FeO6 (B sites) and the asymmetric stretching vibrations of Fe–O-Fe bonds. The band at 849 cm−1 is assigned to the strong Fe–O stretching vibration mode, which involves the internal motion of a change in Fe–O bond length [34].

In shell regions, the broad stretch at 3410 cm−1 is due to O–H stretching, while 1643 cm−1 is due to O–H bending vibrations [35]. The sharp C-H symmetrical stretch (-CH2 stretching) exists at two wave numbers 2878 cm−1 and 1265 cm−1 as well as the bending C-H stretch at two wave numbers: 1458 cm−1 and 1342 cm−1 (-CH2 and -CH3). Finally, a sharp ether C–O–C stretch at 1103 cm−1 in PEG-coated RCFNPs clearly confirms the presence of PEG on the prepared samples [9].

3.2 Magnetic Properties

The magnetization behavior in addition to the magnetic parameters can be accurately explored by measuring the M-H hysteresis loop for the prepared RCFNPs and RCFNPs/PEG as illustrated in Fig. 8. M-H hysteresis curves confirm the antiferromagnetic character of the studied samples. The existence of Sm3+ instead of Fe3+ in the magnetic structure increases the superexchange interactions (SE) due to the presence of Sm3+-O-Sm3+ in addition to Fe3+-O-Fe3+ interactions. The peculiarities of magnetocrystalline anisotropy as well as the mutual interactions between 3d and 4f electrons may be additional factors causing the magnetic properties of the samples under investigation [22, 36].

Fig. 8
figure 8

M-H hysteresis loops of RCFNPs and RCFNPs/PEG

Full size image

The antiferromagnetic alignment is caused by the coupling of unpaired electrons of Fe3+ and Sm3+ ions via the p orbitals of O2− ions, which is proportional to the degree of covalent bonding between the cations (Sm3+ and Fe3+) and O2− ions [37].

According to the crystal field theory, the iron atoms in FeO6 have an octahedral coordination and the 3d orbitals are split into two sets of orbitals t2g (\({3d}_{xy}, {3d}_{xz}, {3d}_{yz}\)) and eg (\({3d}_{{x}^{2}-{y}^{2}}\), \({3d}_{{z}^{2}}\)). Thus, each eg orbital contains one unpaired electron. The unpaired 3d electrons of Fe3+ ions (spin up) in the \({3d}_{{x}^{2}-{y}^{2}}\) orbital. Otherwise, an \({3d}_{{z}^{2}}\) orbital can only have covalent interaction with an electron that has opposing spins (spin down) in an oxygen ion’s filled p orbital, as shown in Fig. 9.

Fig. 9
figure 9

The arrangement of the unpaired 3d electrons of Fe3+ ions

Full size image

This arrangement leads to an antiferromagnetic alignment of the unpaired d electrons on the Fe3+ ions in addition to the unpaired 4f electrons on the sm3+ ions [38]. The magnetic moments of the samples align spontaneously in the presence of the external magnetic field but are not completely antiparallel to each other. Consequently, a small canting angle exists between the magnetic moments of the nearest cations as a result of the Dzyaloshinskii and Moriya (DM) antisymmetric interaction [22].

Generally, the mixed-valence of Fe3+ and Fe2+ ions as observed in the XPS spectrum as well as the existence of Sm3+ ions exhibit three types of ordering; magnetic, charge, and orbital ordering. As previously mentioned [31], some of the simplest magnetic orderings for cations in the B site represent four basic antiferromagnetic orderings (A, C, G, and E type).

From Table 2, the reduction of the magnetic parameters such as saturation magnetization (Ms), remnant magnetization (Mr), and coercivity (Hc) is detected. The reaction between RCFNPs as a core and a non-magnetic surface layer of PEG as a shell leads to the magnetic size being less than the physical size [9]. Additionally, the prepared composites of RCFNPs/PEG exhibit various surface effects such as spin canting and spin pinning. The disordered surface spins can be considered another cause of the reduction of the magnetic parameters [39]. The decrease in coercivity (Hc) after coating can be attributed to a decrease in the alignment direction of magnetic dipoles as well as the coupling of the spins of Sm3+ and Fe3+‏ ions in multidomain regions [40, 41]. The squareness ratio (Mr/Ms) is a significant parameter, and it can be calculated to determine the dimensional homogeneity of the particles. The squareness ratio (Mr/Ms) for the loops of RCFNPs and RCFNPs/PEG are 0.0786 and 0.0575, respectively. Their values are smaller than 0.5, indicating the formation of multi-domains in the magnetic structure [42].

Table 2 The magnetic parameters for the RCFNPs, and RCFNPs/PEG samples
Full size table

The switching-field distribution (SFD) is a significant magnetic parameter for ultra-high-density magnetic recording, like media design, optimal bias current, and storage materials. The SFD value measures the energy barrier distribution as a function of particle coercivity, and it can be calculated by the following equation [43].

$$SFD= \Delta H/{H}_{C}$$
(2)

HC is the coercivity and ΔH is the full width at the half maximum of the dM/dH curve, as shown in Fig. 10a, b. The dM/dH curve shows a doublet peak which corresponds to the competitiveness between two magnetic phases, strong dipole–dipole interaction and exchange coupling [44].

Fig. 10
figure 10

a, b Field dependence of dM/dH of the RCFNPs and RCFNPs/PEG samples

Full size image

SFD describes the steepness of the magnetic hysteresis loop for magnetic recording material. The smaller values of SFD and higher coercivity of the prepared samples (as shown in Table 2) are most appropriate for ultra-high-density recording performance. It is clear from the table that the coating with PEG has the advantage of reducing the SFD value because the particles of different shapes and sizes will be reversed by different values of magnetic field strengths.

3.3 Electrical Properties

Figure 11a, b illustrate the variation of the dielectric constant (ε′) for the RCFNPs and RCFNPs/PEG samples with the absolute temperature as a function of frequency in the range from 100 kHz to 5 MHz. The exchange interaction of electrons leads to a local displacement of the electrons in the field direction, which determines the direction and type of polarization [45]. The behavior of the dielectric constant with temperature and frequency for the prepared samples can be discussed on the basis of both the interfacial polarization and Maxwell–Wagner effects, respectively.

Fig. 11
figure 11

a, b Relation between dielectric constant (ε′) and absolute temperature (T) as a function of the applied frequency of a CFNPs and b CFNPs/PEG

Full size image

The ε′ is nearly constant as the temperature rises to around 500 K. This constancy in ε′ at low temperatures is due to dipole localization [46], which is typical of semiconductor (S. C.) NPs [8, 47, 48]. The rapid increase of ε′ for T > 500 is due to the interfacial polarization [49].

Figure 11 depicts the expected behavior of most nanoferrites, in which the dielectric decreases with increasing frequency due to dielectric relaxation. This behavior can be described on the basis of the Maxwell–Wagner polarization model [50], in agreement with Koop’s phenomenological theorem of ferrites [51]. The higher values of \({\varepsilon }^{\prime}\) at low frequencies (LF) are the result of the electron exchange between the ion pairs following the frequency of the applied electric field (AEF) causing the alignment of dipoles in the direction of AEF. The effective combination of both interfacial and dipolar polarization is also the cause of high values of \({\varepsilon }^{\prime}\) at LF [52].

At higher frequencies, the frequency of electron exchange cannot match the changes in AEF, as the rotation speed of the dipole at high frequency is insufficient to follow the field variation [53].

As a result, the dipole redistribution process is halted, resulting in random dipolar orientation and a decrease in \({\varepsilon }^{\prime}\). This is what causes the \({\varepsilon }^{\prime}\) at higher frequencies to become mostly frequency independent [54].

Figure 12a, b depict the relationship between AC conductivity (ln σ) and the reciprocal of absolute temperature (1000/T) for the samples RCFNPs and RCFNPs/PEG as a function of frequency in the 100 kHz to 5 MHz range. The samples are S. C., and the data follow the well-known Arrhenius equation [46]. This equation implies that electrical conductivity increases with the absolute temperature T. From the figure, it is observed that within the investigated temperature range, the samples show two different slope regions. This demonstrates that there are two conduction mechanisms implied in the samples depending on the temperature.

Fig. 12
figure 12

a, b Correlation between ln(σ) and reciprocal of absolute temperature as a function of applied frequency of a RCFNPs and b RCFNPs/PEG

Full size image

The increase in thermal activity drift mobility of charge carriers, which is temperature-dependent and characterized by high activation energy [55], is one of two factors that increase conductivity in the high-temperature region (region II). The second factor is the hopping mechanism of conduction with variable hopping lengths [56]. The hopping conduction in the samples is ascribed to electron hopping between Fe3+ and Fe2+ ions, giving an n-type charge carrier [57]. As cations are very densely packed in an orthorhombic structure compared to the spinel structure, the distance between consecutive Fe ions is too small, leading to effective electron exchange (EX) [56].

The activation energies (AE) of the samples are estimated by the Arrhenius equation and tabulated in Table 3. It is obvious that, for the two prepared samples, the AE at high temperature (EII) is greater than that at low temperature (E1). This means that more energy is required in the paramagnetic region to free the confined charges, resulting in EX between ion pairs and thus a contribution to the ion conduction process. The reported data shows that the AE is smaller for the RCFNPs/PEG sample. In other words, the σ of the pure sample RCFNPS is significantly increased with the addition of the PEG weight percentage (see Table 3). This indicates that PEG has a more effective conducting mechanism in RCFONPs/PEG composites. According to Ebrahim et al. [58], the AC conductivity curves would jump if the composite contained more than 20% weight of the polymer (PANI).

Table 3 The activation energies (E1 at low temperature and EII at high temperature) for the samples
Full size table

Figure 13a, b illustrate the temperature dependence of ln ac σ versus ln ω. It is obvious to demonstrate the general property of semiconductors, which is that it is frequency-dependent and increases linearly with the frequency of the applied field [59]. As the frequency is increased, the net pumping force pushes the charge carriers to hop between the different conduction states and hence increases the hopping rate of charge carriers between Fe2+ and Fe3+, leading to improving the conduction process [60, 61].

Fig. 13
figure 13

a, b Correlation between ln(σ) and ln(ω) at selected temperatures

Full size image

3.4 Optical Properties

The optical properties of the RCFNPS and RCFNPs/PEG pellets are probed using a UV–VIS NIR diffuse reflectance spectrometer (DRS) which is based on how much light is reflected by the outer and internal surfaces of the samples [62]. Figure 14a–c show the recorded reflectance spectra (RS) of RCFNPs and RCFNPs/PEG samples in the wavelength range of 200–2500 nm at room temperature. It is clear that the RS of RCFNPs/PEG has a lower value of reflectance at a wavelength in the visible and IR regions of the electromagnetic spectra.

Fig. 14
figure 14

a UV–Vis NIR diffuse reflectance spectra for the RCFNPs and RCFNPs/PEG samples, (hν*F(R∞))2 versus (hν) for b RCFNPs and c RCFNPs/PEG samples

Full size image

The reflection peaks of the RCFNPs/PEG are slightly shifted to a longer wavelength; this can be attributed to energy confinement produced from surface plasmon-excitation interaction as a result of the formation of the RCFNPs–PEG core–shell [63].

There is a noticeable reduction in reflectance due to the PEG coating on RCFNPs. The obtained data shows that the coating plays an important role in enhancing the reflection by up to 50%. The high reduction in reflectance is due to the fact that the electrons of the coated PEG at the outer surface can absorb the electromagnetic energy of the incident light and travel to higher levels of energy to occupy most of the vacant positions in the energy bands. Consequently, part of the incident light is absorbed by the 4f and 3d electrons of RCFNPs and cannot be reflected. Furthermore, the high molecular weight of PEG influences the reflection. The reflectance values decrease with increasing molecular weight, and the lowest reflectance value for RCFNPs/PEG appears in the IR region [64].

The optical band gap energy Eg of the samples can be easily estimated from reflectance measurements [65] by extrapolating the straight-line plot of (hν*F(R))2 versus hν shown in Fig. 14b, c. As mentioned in the previous work [66], the Kubelka–Munk function F(R) is given in terms of the eg. The obtained values of optical band gap energy are equal to 1.956 eV and 1.679 eV for RCFNPs and PEG-capped RCFNPs respectively.

4 Conclusion

The core/shell design is formed as a result of coating the rare-earth-doped calcium ferrite with PEG. The XRD pattern reveals the characteristics of coated PEG in addition to the formation of a single-phase orthorhombic structure in the magnetic core. The presence of PEG is confirmed based on the characteristic bands of PEG revealed in FTIR spectra. Magnetic hysteresis curves confirm the antiferromagnetic character of the samples, and small values of SFD are most appropriate for ultra-high-density recording performance. The electrical conductivity of the pure sample RCFNPS is significantly increased with the addition of the PEG weight percentage. The coating by PEG enhances the optical property by reducing the reflection by up to 50%.