Tuning Crystal Field Potential by Orbital Dilution in Strongly Correlated d⁴ Oxides

Abstract

We investigate the interplay between Coulomb-driven orbital order and octahedral distortions in strongly correlated Mott insulators due to orbital dilution, i.e., doping by metal ions without an orbital degree of freedom. In particular, we focus on layered transition metal oxides and study the effective spin–orbital exchange due to d³ substitution at d⁴ sites. The structure of the d³ − d⁴ spin–orbital coupling between the impurity and the host in the presence of octahedral rotations favors a distinct type of orbital polarization pointing towards the impurity and outside the impurity–host plane. This yields an effective lattice potential that generally competes with that associated with flat octahedra and, in turn, can drive an inversion of the crystal field interaction.

1 Introduction

Transition metal oxides (TMOs) are fascinating materials where several quantum degrees of freedom (i.e., spin, orbital, charge, lattice) are intertwined, and require to be treated on equal footing both from a fundamental point of view as well as for developing and enhancing applications in the areas of oxide electronics [1]. The competition of different types of ordered states is ubiquitous in strongly correlated TMOs, mainly arising from the complex nature of the spin–charge–orbital couplings where frustrated Coulomb-driven exchange competes with the kinetic energy of charge carriers.

A crucial step for accessing the emergent phenomena of correlated TMOs with spin–orbital–charge-coupled degrees of freedom is the understanding of the undoped regime [2], where the low-energy physics and spin–orbital order are dictated by effective spin–orbital superexchange [3,4,5,6,7,8,9,10,11,12,13,14]. In undoped 3d Mott insulators, for instance, large local Coulomb interactions localize electrons and the coupling between transition metal ions is controlled by a low-energy spin–orbital superexchange introduced first by Kugel and Khomskii [4]. When multi-orbital degrees of freedom are included, the enhanced quantum fluctuations for S = 1/2 compounds can result in destroying the long-range order [5]. On the other hand, spin–orbital entanglement in superexchange models may lead to exotic novel types of magnetic order [15], or stabilize topological order in the ground state and in excited states [16].

Long-range order in both spin and orbital sector develops in perovskite lattices when spin fluctuations are weaker for spin S larger than 1/2. The fate of spin–orbital order is, however, strongly tied to the character of the orbital degrees of freedom that emerges when electrons localize, and on the eventual influence of the atomic spin–orbit coupling. Taking the example of d⁴ ions, for large Hund’s exchange, high-spin S = 2 states emerge at Mn ions in LaMnO₃ [6, 17,18,19], and the corresponding A-type antiferromagnetic (A-AF) spin order follows the Goodenough–Kanamori rules [20]. On the other hand, when Hund’s exchange is weaker compared with t_2g–e_g splitting, e_g orbitals are empty and intermediate S = 1 spin states form at d⁴ ions. An example of such a t_2g system is Ca₂RuO₄ with spin–orbital superexchange described in Section 2. Here, the orbital degree of freedom is set by a doubly occupied orbital configuration called doublon [21,22,23] (see Fig. 1b–d), where we introduce the following notation to identify which orbital of the t_2g sector is doubly occupied [7],

$$ \left|a\right\rangle\equiv\left|yz\right\rangle, \quad \left|b\right\rangle\equiv\left|xz\right\rangle, \quad \left|c\right\rangle\equiv\left|xy\right\rangle. $$

(1)

Without distortions, only two out of three t_2g orbitals are active along each bond 〈ij〉∥ γ and contribute to the intersite kinetic energy, while the third orbital is inactive as the hopping via oxygen is forbidden by symmetry. The inactive t_2g orbital along a given cubic axis γ ∈{a, b, c} is in the basis (1) uniquely labeled as |γ〉.

Doping Mott insulators typically refer to the addition of charge carriers that leads to melting of the localized spin-orbital order [24, 25] and the formation of metallic states often accompanied by unconventional superconductivity, to novel patterns (stripes, nematic, etcetera [26]) of self-organized electronic states [27,28,29] or to the suppression of orbital order by the orbital rotation induced by charge defects [30]. In contrast, substitutional doping of transition metal elements can avoid the breakdown of the Mott insulating state and allows novel directions for tuning the degree of intertwining of the spin–orbital correlations. As an experimental motivation, we mention the anomalous magnetic reconstruction that realizes 3d³ substitution in a 4d⁴ host, or Mn doping in Sr₃Ru₂O₇ [31].

The potential to modify the valence of the transition metal elements without destroying the insulating state also allows to achieve non-standard regimes of competition between lattice and spin–orbital degrees of freedom. Indeed, specific for the present study is the physical case of the Mott-insulating Ca₂RuO₄ whose substitution of Ru with Mn [32], Cr [33], Fe [32], or Ir [34] atoms, apart from driving a modification of the spin–orbital order, leads to the observation of negative thermal expansion effects, i.e., the increase of the unit cell volume by thermal cooling. These examples suggest that the negative thermal expansion outcomes are strongly linked to the electronic correlations developing in the doped Mott phase.

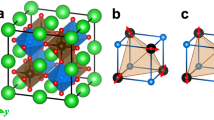
The doping path, indeed, makes possible the design of spin–orbital defects that in turn are expected to cause significant deviations from the standard exchange as related to the Goodenough–Kanamori rules [23, 35,36,37]. For instance, focusing on a TMO with t_2g orbital degrees of freedom, one can achieve orbital dilution by doping with orbitally inactive transition metal magnetic ions [23]. Such doping of t_2g sector can be realized by replacing a d⁴ Ru ion with low S = 1 spin and effective L = 1 angular momentum with a d³ ion corresponding with a local increase of spin to $S=\frac {3}{2}$ and removal of the orbital degree of freedom (see Fig. 1a and e). Alternative substitutional doping by d² ions employs both the orbital and charge degrees of freedom and is called charge dilution [36, 37].

Fig. 1

Artist’s view of the orbital doping when ad⁴ Ru ion with spin S = 1 and three t_2g orbitals split by the crystal field, with L = 1 angular momentum, e is substituted by the d³ Cr ion without orbital degree of freedom (L = 0) and spin S = 3/2 due to Hund’s exchange. Spins are shown by red arrows and doubly occupied t_2g orbitals (doublons) are indicated by blue arrows. Depending on the octahedral distortion, the doublon occupies b|c〉 orbital for a flat octahedron, or c, d one of two degenerate doublet {|a〉, |b〉} orbitals for an elongated octahedron

Focusing on d³ substitution in d⁴ systems, the impurity–host spin–orbital exchange is strongly dependent on the orbital that is doubly occupied in the t_2g sector. Indeed, the impurity can act as an orbital vacancy for weak host–impurity coupling or favor an orbital polaronic configuration with the doublon sitting in the active orbitals along the 3d − 4d bond [23]. For an (a, b) plane, the orbital selection of the doublon configuration couples in a different way to the octahedral distortions corresponding to flat or elongated modes (see Fig. 1b–d). Thus, we explore the interrelation between the orbital order developing around the impurity and the character of the compatible octahedral distortions. We find that the rotation of the octahedra is able to pin uniquely the type of orbital order around the impurity (see Fig. 2). This result indicates a strong bias in the induced octahedral distortions. The main outcomes of the present investigation include (i) the determination of the effective d³ − d⁴ superexchange in the presence of octahedral rotations, (ii) establishing orbital order around the impurity, and (iii) providing a discussion on the way the orbital order is linked to the flat or elongated distortions of the octahedra in the host.

Fig. 2

Artist’s view of the evolution of orbital order from a the undoped (a, b) plane of d⁴ ions in centers of rotated octahedra (arrows) forming a two-sublattice pattern, b the plane with a d³ ion in the center, and c undistorted (elongated) octahedra at (around) the impurity, respectively, shown by gray (orange) color. The undoped state (a) has a uniform ferro-orbital (FO) order with the doublon occupying the |c〉 orbital. Panel d shows the possible orbital configurations (1) of the doublon at an undoped d⁴ site (see Fig. 1). Finally, the violet circles stand for oxygen sites in the (a, b) plane

2 Spin–Orbital Superexchange in the Host

First we consider the effective spin–orbital superexchange in the host taking the limit of strong local Coulomb interactions U₂ at Ru ions in 4d⁴ local configurations, i.e., charge excitations ${d^{4}_{i}}{d^{4}_{j}}\rightarrow {d^{5}_{i}}{d^{3}_{j}}$, along each bond 〈ij〉 generate effective superexchange [21,22,23],

$$ {\mathcal{H}}_{d^{4}-d^{4}}=J_{\text{host}}\sum\limits_{\langle ij\rangle\parallel\gamma} \left\{{\mathcal{J}}_{ij}^{(\gamma)}\left( \vec{S}_{i}\cdot\vec{S}_{j}+1\right) +{\mathcal{K}}_{ij}^{(\gamma)}\right\}. $$

(2)

Here superexchange ∝ J_host involves spin operators for S = 1 spins and includes on the orbital operators, ${\mathcal {J}}_{ij}^{(\gamma )}$ and ${\mathcal {K}}_{ij}^{(\gamma )}$, which depend on the orbital doublet active along the bond direction γ (〈ij〉∥ γ). The superexchange (2) may be obtained from that for vanadium perovskites with V d² ions [38,39,40] by electron-hole transformation, where an empty site (holon) transforms into a doublon for d⁴ ions. The form of $\{{\mathcal {J}}_{ij}^{(\gamma )},{\mathcal {K}}_{ij}^{(\gamma )}\}$ was given in [38,39,40,41]; J_host depends on the hopping t and on Coulomb U₂ and Hund’s exchange ${J_{2}^{H}}$ host parameters, and $\eta _{\text {host}}\equiv {J_{2}^{H}}/U_{2}$. An additional aspect which we neglect here is that spin–orbital entangled variables that drive magnetism in ruthenates are influenced by electron–lattice coupling, for instance via pseudo-Jahn–Teller effect [42], which focuses on the distortions which split the t_2g orbitals.

We consider here a 2D square lattice with transition metal ions connected via oxygen ions as in an (a, b) RuO₂ plane, see Fig. 2, of Ca₂RuO₄. In this case, |a〉 (|b〉) orbitals are active along the b (a) axis, while |c〉 orbitals are active along both a and b axes. Finite crystal field (CF) favors doublons in |c〉 orbitals (see Fig. 2a). Below, we investigate the effect of orbital dilution shown in Fig. 2b.

For the host sites, we assume AF spin order replacing spin–spin interactions by the correlation function $\langle \textbf {S}_{i}\textbf {S}_{j}\rangle \simeq -5/4$ (here we neglect spin quantum fluctuations) and add the anisotropic spin–orbit coupling term in a form of

$$ {\mathcal{H}}_{so}=\lambda\sum\limits_{i}(-1)^{i}h_{z}{L_{i}^{z}}, $$

where h_z is the local staggered magnetic moment assumed to be along z axis and the orbital ${L_{i}^{z}}$ operator has a standard form of ${L_{i}^{z}}=(ia_{i}^{\dagger }b_{i}+H.c.)$. Altogether, the total host Hamiltonian reads, ${{\mathcal{H}}}_{\text {host}}={{\mathcal{H}}}_{d^{4}-d^{4}}+{{\mathcal{H}}}_{so}$.

3 Hybrid Bond: Orbital Dilution

In this section, we present the results of the derivation of effective 3d³ − 4d⁴ spin–orbital superexchange as due to the coupling between orbitals of 3d and 4d ions through the oxygen 2p orbitals which build up the p − d hybridization $\propto V_{pd\pi }^{2}$. For our purposes, it is sufficient to analyze a pair of atoms forming a bond 〈ij〉, as the effective interactions are generated by charge excitations, ${d^{n}_{i}}{d^{m}_{j}}\rightarrow d^{(n+1)}_{i} d^{(m-1)}_{j}$ along a single bond [8]. In contrast to the reference d⁴ host where both atoms on the bond 〈ij〉 are equivalent, a d³ − d⁴ hybrid bond has explicitly different ionic configurations. The degenerate Hubbard Hamiltonian H(i, j) [43] includes in general the standard local Coulomb interaction H_int(i) and the effective d − d kinetic term, H_t(i, j); for a representative 3d–2p–4d bond after projecting out the oxygen degrees of freedom,

$$ H(i,j)=H_{t}(i,j)+H_{\text{int}}(i)+H_{\text{int}}(j) . $$

(3)

The case without octahedral rotation was investigated in [23]. Here we present the superexchange Hamiltonian for a bond 〈12〉 along the a axis between the d³ impurity at site i = 1 and a host d⁴ ion at site j = 2, in presence of octahedral rotation by angle ϕ,

$$ \begin{array}{@{}rcl@{}} {\mathcal{H}}_{d^{3}-d^{4}}^{(a)}(\phi) &=& J_{\text{imp}}\left( \textbf{S}_{1}\cdot\textbf{S}_{2}\right) \\ &&\times\left\{\alpha_{1}+\alpha_{2}\left( a_{2}^{\dagger}b_{2}^{}+b_{2}^{\dagger}a_{2}^{}\right) +\alpha_{3}a_{2}^{\dagger}a_{2}+\alpha_{4}b_{2}^{\dagger}b_{2}^{}\right\} \\ &&+\left\{\beta_{1}+\beta_{2}\left( a_{2}^{\dagger}b_{2}^{}+b_{2}^{\dagger}a_{2}^{}\right) +\beta_{3}a_{2}^{\dagger}a_{2}^{}+\beta_{4}b_{2}^{\dagger}b_{2}^{}\right\}.\\ \end{array} $$

(4)

Here the coefficients {α_i} and {β_i} are given by the Slater–Koster rules [44], with the property that {α₂,α₄} and {β₂,β₄} vanish for ϕ = 0, so they are generated by the rotation. At ϕ = 0, the Hamiltonian tends to project out the inactive orbital a along the bond 〈ij〉∥ a axis. With angle ϕ≠ 0, also the c orbital is disfavored so that only the b orbital is the preferred one. In this way, we obtain polarization of the orbitals {a, b} towards the impurity—the orbital polarizer mechanism (see Fig. 2).

The exact form of the coefficients {α_i} and {β_i} as function of rotation angle ϕ reads as

$$ \begin{array}{@{}rcl@{}} \alpha_{1}&=&-\frac{2}{9}\gamma+\frac{1}{6}q_{5}+\frac{4\gamma+3}{18}q_{3}, \\ \alpha_{2}&=&-\sin(2\phi)\left( -\frac{1}{9}-\frac{1}{12}q_{5}+\frac{1}{36}q_{3}\right), \\ \alpha_{3}&=&\left( \sin^{2}\phi-\gamma\right)\left( -\frac{2}{9}-\frac{1}{6}q_{5}+\frac{1}{18}q_{3}\right), \\ \alpha_{4}&=&\left( \cos^{2}\phi-\gamma\right)\left( -\frac{2}{9}-\frac{1}{6}q_{5}+\frac{1}{18}q_{3}\right), \end{array} $$

(5)

and

$$ \begin{array}{@{}rcl@{}} \beta_{1}&=&-\frac23\gamma-\frac14 q_{5}-\frac{4\gamma+3}{12}q_{3}, \\ \beta_{2}&=&-\sin(2\phi)\left( -\frac13 +\frac18 q_{5}-\frac{1}{24}q_{3}\right),\\ \beta_{3}&=&\left( \sin^{2}\phi-\gamma\right)\left( -\frac{2}{3}+\frac{1}{4}q_{5}-\frac{1}{12}q_{3}\right), \\ \beta_{4}&=&\left( \cos^{2}\phi-\gamma\right)\left( -\frac{2}{3}+\frac{1}{4}q_{5}-\frac{1}{12}q_{3}\right), \end{array} $$

(6)

with dimensionless parameters,

$$ q_{i}=\frac{1}{i\eta_{\text{imp}}+1} ,\quad \gamma=\left( \frac{t_{c,c}^{(a)}}{{\tilde V}_{pd\pi}^{2}}\right)^{2},\quad \eta_{\text{imp}}=\frac{{J_{1}^{H}}}{\varDelta}. $$

(7)

The d³ − d⁴ superexchange (4) is given by

$$ J_{\text{imp}} =\frac{4\tilde{V}_{pd\pi}^{4}}{\varDelta}, \varDelta=I_{e}+3(U_{1}+U_{2})-4\left( {J_{1}^{H}}-{J_{2}^{H}}\right), $$

(8)

and is determined by the effective hopping between two neighboring sites in a two-step process $\propto V_{pd\pi }^{2}$, involving a charge-transfer excitation energy Δ_CT along the d–p–dπ-bond. We introduce for convenience the energy, $\tilde {V}_{pd\pi }^{2}\equiv V_{pd\pi }^{2}/\varDelta _{\text {CT}}$; Coulomb and Hund’s exchange parameters are $\{U_{1},{J_{1}^{H}}\}$. The hopping amplitudes are given by the Slater–Koster rules [44],

$$ \begin{array}{@{}rcl@{}} t_{c,c}^{(a)}&=&-{\tilde V}_{pd\pi}^{2}\cos^{3}(2\phi) \\ &&+\frac{1}{8}\left\{ {\tilde V}_{pd\sigma} \left( 3{\tilde V}_{pd\sigma} - 4\sqrt{3}{\tilde V}_{pd\pi} \right) \sin(2\phi)\sin(4\phi)\right\} , \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} t_{a,a}^{(a)} & = & \quad \tilde{V}_{pd\pi}^{2}\sin^{2}\phi, \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} t_{b,b}^{(a)} & = & -\tilde{V}_{pd\pi}^{2}\cos^{2}\phi, \end{array} $$

(11)

$$ \begin{array}{@{}rcl@{}} t_{a,b}^{(a)} & = & -\tilde{V}_{pd\pi}^{2}\sin\phi\cos\phi.\end{array} $$

(12)

Here, we take a realistic assumption, ${\tilde V}_{pd\sigma }=2{\tilde V}_{pd\pi }$. To obtain the superexchange (4) for a b bond, we transform the coefficients as follows:

$$ \alpha_{1}\to \alpha_{1}, \quad \alpha_{2}\to -\alpha_{2}, \quad \alpha_{3}\to \alpha_{4}, \quad \alpha_{4}\to \alpha_{3}, $$

(13)

and analogous for the {β_i} ones.

4 Results: Crystal Field Modification

For the exact diagonalization, we use a periodic cluster of 10 sites with one impurity at site i = 10 (see Fig. 3). Since we want to focus on the effect of the impurity, we take it in the strong coupling regime, J_imp ≫ J_host. We neglect the quantum spin fluctuations and thus the size of the Hilbert space becomes computationally accessible. We consider a collinear AF state described by Ising variables, i.e., we assume the Néel AF spin order. The orbital order in the host is ferro-orbital (FO), with |c〉 doublons (see Fig. 2a). The impurity disturbs the orbitals at its neighbors and generates the effective change of the CF due to correlations at the host sites i ∈Ω. As a result, for small ${\varDelta _{i}^{c}}$, the doublons occupy directional orbitals pointing towards the impurity, similar to the orbital polarons in manganites [45,46,47].

Fig. 3

Schematic view of a 10-site periodic cluster (magenta boarder line) used for calculation of the crystal field at the nearest neighbors of d³ impurity (i ∈Ω, i = 1,3,7,9), with impurity at i = 10 and $S=\frac 32$. Orbital degrees of freedom remain undisturbed at next nearest neighbors (i = 2,4,6,8) and the only third nearest neighbor i = 5 in the cluster. Two-sublattice AF Néel spin order is indicated by green and red sites

To estimate the strength of this inverted CF, we put a finite CF ${\varDelta _{i}^{c}}$ at nearest neighbor sites of the impurity and find that for large enough ${\varDelta _{i}^{c}}$ the doublon orbital changes from |a〉 or |b〉 to |c〉, i.e., to the one along the bond (see Fig. 2b). The change of orbital occupation at sites around the impurity at ${\varDelta _{i}^{c}}\simeq 0.12J_{\text {host}}$ is shown in Fig. 4. Remarkably, the bonds along the a and b axes are equivalent and we observe a change of doublons from directional (${\varDelta _{i}^{c}}\le 0.12J_{\text {host}}$) to planar (${\varDelta _{i}^{c}}> 0.12J_{\text {host}}$) orbitals. The inversion of CF occurs at the same value of ${\varDelta _{i}^{c}}$ for the bonds along the a axis (i = 1,9) and along the b axis (i = 3,7) (see Fig. 4).

Fig. 4

Occupation of the c orbital at site i of the cluster shown in Fig. 3 as a measure of orbital order for ϕ = 0.25. The average doublon occupancy $\langle {n_{i}^{c}}\rangle$ changes at site i being a nearest neighbor (NN) of the impurity. For the increasing value of the CF splitting at NNs of impurity Δ^c, the doublon moves from a directional orbital, a or b, pointing towards the impurity to an in-plane |c〉 orbital (see insets) and the FO order is restored ($\langle \frac 12-{n_{i}^{c}}\rangle =\mp \frac 12$ stands for site i unoccupied/occupied by the c doublon). Energy parameters (all in units of J_host): λ = 0.1, J_imp = 8.0; other parameters: η_host = 0.05, η_imp = 0.2, $\langle \vec {S}_{i}\cdot \vec {S}_{10}\rangle =$-2.0 with i ∈Ω

An abrupt change of the doublon orbital is modified to a smooth crossover at finite temperature T (see Fig. 5). Thermal fluctuations generate a rather broad range of CF splitting ${\varDelta _{1}^{c}}$, where $\left \langle \frac 12-{n_{1}^{c}}\right \rangle \simeq 0$ and this quantity changes sign close to the value ${\varDelta _{1}^{c}}\simeq 0.14J_{\text {host}}$ found before at T = 0 (see Fig. 4). Interestingly, we find that the strength of the effective CF potential induced by exchange interaction is weakly dependent on temperature, so that such electronically driven orbital splitting is remarkably robust against thermal fluctuations.

Fig. 5

Evolution of the c orbital occupation at the host site i = 1 (green), neighboring with impurity (see Fig. 3), as function of CF ${\varDelta _{1}^{c}}$ and temperature T (in units of J_host ≡ 1). The average doublon occupancy $\langle {n_{1}^{c}}\rangle$ changes with increasing ${\varDelta _{1}^{c}}$ or T. The plane (dark red) sets the zero value for the c orbital polarization and separates the regions of a/b doublon ($\langle {n_{1}^{c}}\rangle =0$) and c doublon ($\langle {n_{1}^{c}}\rangle >0$). Parameters as in Fig. 4

5 Discussion and Conclusions

We have shown that orbital doping in the presence of octahedral rotations around the c axis tends to favor a distinct type of orbital order, with orbital polarization that is preferentially directional and distributed both towards the impurity and out-of-plane (i.e., with either xz or yz orbital symmetry). Remarkably, as already demonstrated in the tetragonal symmetric octahedra [23], the pinning of the orbital order can occur for both an antiferromagnetic and ferromagnetic exchange between host and dopants. Its manifestation depends either on the amplitude of Hund’s exchange coupling or on the relative strength of the host–host to host–impurity exchange interactions. This means that the local orbital order is a generic sign of the d³ dopant in a distorted host with octahedral rotations and is robust to spin fluctuations.

Another relevant and striking consequence of the specific orbital order induced locally by the d³ dopant is that the orbital pattern around the impurity is uniquely compatible with an elongated octahedral configuration (see Fig. 2). Hence, the impurity–host exchange yields an effective crystal field potential that is akin to that obtained when the lattice favors longer out-of-plane transition metal–oxygen bonds than the in-plane ones. On this basis, there are two possible emergent physical scenarios that can occur: (i) If the lattice potentially stabilizes an octahedral configuration that is flat, then, the host–impurity exchange tends to compete with it and, depending on their relative strength, can even end up reversing the sign of the crystal field interaction. This is the case we demonstrate in this paper. Such occurrence clearly implies that the optimal local deformation exhibits an effective enhanced volume of the unit cell due to the bond expansion of the octahedra along the c axis that, in turn, can play a relevant role in setting non-standard negative thermal expansion effects once orbital order is achieved at low temperature. (ii) On the contrary, for a host configuration with elongated octahedra, the effective host–impurity exchange can enhance the distortions around the impurity thus increasing the stiffness of the lattice. In the present paper, the analysis has been motivated by the study of d³ dopants in d⁴ Mott-insulating host with flat octahedra and antiferromagnetic order as it occurs in Mn-doped Ca₂RuO₄ compound [32]. Hence, we speculate that the outcome of the induced elongated octahedra by Coulomb-driven orbital exchange may be relevant for the anomalous volume expansion occurring below the onset temperatures of magnetic and orbital order [32].

It is interesting to point out that similar competing effects between electron correlations and lattice distortions do not occur in transition metal oxides with e_g orbital degrees of freedom, whereas the Jahn–Teller distortions are typically cooperating with the orbital exchange of electronic origin [6, 45, 48, 49]. The local lattice distortions associated with the variation of the orbital order at the metal-insulator transition have been detected by EXAFS and XANES in manganites [50] and recently in PbTiO₃-based perovskites systems [51]. Therefore, we expect that further experiments will provide interesting information in this field.

We also underline that the temperature dependence of the Coulomb-driven effective crystal field (Fig. 5) allows one to have an anomalous thermal behavior when considering the thermal expansion effects. Indeed, since the obtained results show that the amplitude of the effective exchange-driven crystal field potential is reduced by the increase of the temperature, then, one can achieve a regime of anomalous volume expansion only in a given window of temperature. This is, for instance, the case of Cr-doped Ca₂RuO₄ [33] where the negative thermal effects manifest predominantly in a range of temperature below the magnetic transition.

Finally, we point out that the proposed reconstruction of the orbital order around the dopant can be accessed by experimental probes based on X-ray spectroscopy which is element sensitive and has been successfully demonstrated to unveil the character of the ordered ground state and the corresponding spin–orbital excitations in such transition metal oxides [52, 53].