1 Spin-Orbital Physics

Spin-orbital physics was initiated by Kugel and Khomskii [1] who realized that orbital operators contribute to superexchange in Mott insulators in a similar way as spins, so both degrees of freedom contribute jointly to spin-orbital superexchange [2]. While the spin part has SU(2) symmetry, the orbital part has remarkable orbital fluctuations [3] and a much lower cubic symmetry in the perovskite systems where it is intrinsically frustrated [4]. This frustration is frequently released by spin order which coexists with orbital order following the Goodenough-Kanamori rules [5], and phases arise with alternating orbital (AO) order along ferromagnetic (FM) bonds coexisting with ferro-orbital (FO) order along antiferromagnetic (AF) bonds. Well known examples are spin-orbital orders in LaMnO 3 [6], LaVO 3 [7], and Ca 2RuO 4 [8] where spin-orbit coupling plays a role [9]—the latter two examples (V, Ru) involve t 2g orbitals. Indeed, a rather unique example of a spin-orbital system are perovskite vanadates, where a challenging competition between two types of spin-orbital order was observed [10]. But a different scenario is also possible—frustrated spin-orbital interactions may lead to the collapse of long-range order, as for instance in LiNiO 2 [11]. Another possibility is a spin-orbital liquid emerging from frustration [12, 13].

Doping of Mott insulators leads to several remarkable phenomena. Recently, short-range charge density wave called stripe phase was reported in doped cuprates [14]. When coupled to spins, it arises as self-organization of charge and spin degrees of freedom [15]. It has been suggested that the critical charge, orbital, and spin fluctuations near the quantum critical point provide the pairing interaction [16] and the spectral properties of stripe phases may be seen as a signature of their stability [17]. In manganites hole doping generates orbital polarons that emerge in an AF system by double-exchange mechanism [18], responsible for a change from AF insulator to FM metal with e g orbital liquid [19].

As in doped cuprates, the holes doped in e g orbitals are mobile in LaMnO 3, or in Kugel-Khomskii system [20], as well as in t 2g stripe phases with orbital polarons [21]. More complex phenomena are found in doped vanadates where a t 2g hole may hop only in two cubic directions [22], and robust C-type AF (C-AF) coexists with G-type AO (G-AO) order [23]. Doping generates finite spectral weight within the Mott-Hubbard gap already at low x≃0.02 Ca doping in Y 1−x Ca x VO 3 [24], while at higher doping the system remains insulating and develops a kinetic gap [25].

The purpose of this paper is to consider the consequences of immobile holes in a ruthenate due to transition metal ions with a lower valence which are substituted for Ru (d 4) ions. As an experimental motivation, we mention that (i) dilute Cr doping for Ru reduces the temperature of the orthorhombic distortion and induces FM order in Ca 2Ru 1−x Cr x O 4 (with 0<x<0.13) [26] and (ii) Mn-substituted single crystals of Sr 3Ru 2−x Mn x O 7 reveal an unusual E-type AF structure at x=0.16 [27]. Therefore, we consider (i) orbital dilution by 3d 3 (Mn 4+, Cr 3+) impurities in (Ca,Sr) 2RuO 4 [28] and (ii) charge dilution due to 3d 2 doping which generates hole-doublon interactions. These findings motivate the theoretical search for the consequences of both orbital and charge dilution. We show that spin-orbital order may even be globally changed and dictated by defects in case of orbital dilution with x=1/4 [29]. Note that in contrast to orbital dilution in cuprates [20] where holes remove both spin and orbital degree of freedom, the present doping (i) removes the orbital doublon but increases spin from S=1 to S=3/2, while in (ii) spins S=1 stay unchanged but a doublon is replaced by a hole in an orbital (holon).

2 Orbital Dilution

The spin-orbital model for Ca 2RuO 4 Mott insulator is equivalent by an electron-hole transformation to that introduced some 15 years ago for vanadates [30]. Thus, we consider an interplay between S=1 spins and the t 2g orbital doublet T=1/2 for a doublon active along a given cubic axis. For instance, the doublon involves {y z,z x} active orbitals along the c axis, while xy orbitals are filled by one electron each. The model is isomorphic to the vanadate d 2 model [7], with doublons transforming into empty orbitals (occupied by two holes). We label t 2g orbitals by index γ when a given orbital is inactive along a cubic axis γ∈{a,b,c}:

$$ \left|a\right\rangle\equiv\left|yz\right\rangle, \hskip .5cm \left|b\right\rangle\equiv\left|xz\right\rangle, \hskip .5cm \left|c\right\rangle\equiv\left|xy\right\rangle. $$
(1)

We consider a two-dimensional (2D) RuO 2 ab plane in Ca 2RuO 4 (SrRuO 3), with Ru ions connected via 2p π oxygen orbitals. For this plane |a〉 (|b〉), orbitals are active along the b (a) axis, while |c〉 orbitals are active along both a and b planar axes. The superexchange for the host bonds 〈i j〉 along the γ∈{a,b} axis [8],

$$ \mathcal{H}_{d^{4}-d^{4}}=J_{\text{host}}{\sum}_{\langle ij\rangle\parallel\gamma} \left\{J_{ij}^{(\gamma)}(\mathbf{S}_{i}\!\cdot\!\mathbf{S}_{j}+1)J_{ij} +K_{ij}^{(\gamma)}\right\}, $$
(2)

is \(\propto J_{\text {host}}\) and stabilizes C-AF phase for the realistic parameters of Ca 2RuO 4, see Fig. 1a. The above generic form [4] follows from charge excitations, \(4{d^{4}_{i}}4{d^{4}_{j}}\Rightarrow 4{d^{5}_{i}}4{d^{3}_{j}}\)—the interactions depend on the intraorbital Coulomb U 2 element and Hund’s exchange J 2 in the host. The orbital operators, \(J_{ij}^{(\gamma )}\) and \(K_{ij}^{(\gamma )}\), are defined by active t 2g orbital along the axis γ [8]. For a bond 〈i j〉∥γ, it may be rewritten in the orbital-only form by taking average over spin degrees of freedom, i.e.,

$$ \mathcal{H}_{d^{4}-d^{4}}^{\langle ij\rangle\parallel\gamma}= \left\{A_{\gamma}^{}{T_{i}^{z}}{T_{j}^{z}}+ \frac12 C_{\gamma}^{}\left( T_{i}^{+}T_{j}^{-}+T_{i}^{-}T_{j}^{+}\right)\right\}^{(\gamma)}, $$
(3)

with orbital operators \((T_{i}^{\alpha })^{(\gamma )}\) defined by the axis γ and with coefficients A γ and C γ depending on spin average 〈S i ⋅ S j 〉 on a bond 〈i j〉.

Fig. 1
figure 1

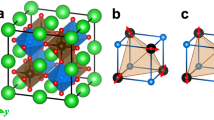
Top—Doping by transition metal ions in a spin-orbital system with C-AF and G-AO {a,c} order found in Mott insulators with d 2 (vanadates) or d 4 (ruthenates) ionic configuration: a orbital dilution with a orbital removed by the d 3 impurity with S=3/2 spin and b charge dilution with gray orbital indicating an orbital hole at the d 2 impurity with S=1 spin. Host S=1 spins interacting by J host are shown by red/black arrows and doublons in t 2g orbitals (a and c) are shown by green symbols. Here, doping occurs at a doublon site and spins are coupled by J imp along hybrid (red) bonds. Bottom left—c phase diagram for a single d 3 impurity replacing a doublon in c orbital in the C-AF host [28]; dashed boxes indicate change in the orbital order around the impurity by the orbital flip \(a\rightarrow b\). Bottom right—Orbital fluctuations promoted on d 2- d 4 hybrid bonds with: d AF and e FM spin correlations. In the latter case (e), the terms \(\propto J_{2}\) couple doublons at two orbitals in excited states (doublon and hole in ovals), and one obtains orbital flips \(\propto T_{i}^{-}T_{j}^{+}\) together with Ising terms \(\propto {T_{i}^{z}}{T_{j}^{z}}\), while double excitations \(\propto T_{i}^{+}T_{j}^{+}\) occur on AF bonds d even in the absence of Hund’s exchange (at J 2=0) and are amplified by finite {J 1,J 2}. Splittings between degenerate t 2g orbitals serve only as guides for the eye

Full size image

For the d 3- d 4, hybrid bonds charge \(3{d^{3}_{i}}4{d^{4}_{j}}\Rightarrow 3{d^{4}_{i}}4{d^{3}_{j}}\) excitations with the lowest energy do not generate an extra doublon but simply move it from 4d to 3d ion. We use the convention that i=1 stands for the impurity site and i=2 for its host neighboring ion. The energy involved in the charge excitation is,

$$ {\Delta}=I_{e}+3(U_{1}-U_{2})-4(J_{1}-J_{2})\,. $$
(4)

where U i and J i are the respective Coulomb and Hund’s elements. In addition, it depends on the ionic energy I e , i.e., the mismatch between the energy levels of the two atoms. For Mn or Cr impurities in ruthenates Δ>0 and plays a role of charge-transfer energy. The energy Δ (4) defines two parameters which characterize the interactions along the hybrid d 3- d 4 bonds [28]:

$$ J_{\text{imp}}=\frac{t^{2}}{4{\Delta}}, \hskip 1.2cm \eta_{\text{imp}} =\frac{J_{1}}{\Delta}. $$
(5)

The spin-orbital interaction on hybrid bond has the generic form similar to (2), but the orbital operators are now defined only by the host site, and the spin operators are for S=1 on host and S=3/2 on impurity ion. A more transparent form of the impurity-host bond couples the impurity spin S i with the neighboring host spin S j —it can be written as follows [28],

$$ \mathcal{H}_{d^{3}-d^{4}}^{\langle ij\rangle\parallel\gamma}\simeq \left\{J_{S}(D_{j}^{(\gamma)})(\mathbf{S}_{i}\!\cdot\!\mathbf{S}_{j}) + E_{D}^{\gamma} D_{j}^{(\gamma)}\right\}. $$
(6)

Here, the spin exchange couplings \(J_{S}(D_{j}^{(\gamma )})\) depend on doublon projection operator \(D_{j}^{(\gamma )}\) at host site j, and the doublon energy \(E_{D}^{\gamma }\) depends on Hund’s exchange η imp (5). It can be shown [28] that the latter is the dominant energy scale, so for a single d 3- d 4 bond the doublon avoids the inactive (γ) orbital and spins couple with \(J_{S}(D_{j}^{(\gamma )}=0)\) which can be either AF if η imp<0.43, or FM if η imp>0.43. The sign change at \(\eta _{\text {imp}}^{c}\simeq 0.43\) marks a quantum phase transition from AF to FM spin correlations, see Fig. 1c. Similar to the 2D Kugel-Khomskii model [31], this sign change leads here to rather exotic phases with nearly frustrated spins for several doping levels x∈[1/9,1/5] [28]. A single d 3 impurity at site i modifies the spin-orbital order at its nearest neighbors (NNs) \(j\in \mathcal {N}(i)\), while second NNs are little affected and thus they typically follow the C-AF/G-AO order in the host. In particular, the impurity spin reorients within the orbital polaron at \(\eta _{\text {imp}}^{c}\) which marks a transition from AF to FM regime.

Both for a single impurity and at low x≤1/8 doping, the d 3- d 4 bonds influence strongly spin-orbital order [28]. For a higher periodic doping x=1/4 when half of the superexchange bonds are d 3- d 4 hybrid bonds, the overall spin-orbital order is dictated by them [29]. One finds that only every second undoped vertical line ∥b is FM, as in the C-AF host phase, and host spins are inverted on any other vertical line and the doublon flips from orbital a to b. Such a modification of the orbital order stabilizes the FM interactions for c-a doublon pairs on the horizontal bonds by double-exchange, in analogy to a doped t 2g system [21]. In the phase diagram at x=1/4 doping [29], one finds a broad region of parameters where impurity spins are also frustrated. Frustration is released by quantum fluctuations which stabilize impurity spin orientation opposite to that expected in the host. At sufficiently large η imp (5), FM spin order takes over and G-AO order is then the same as in the undoped host. Thus, the most interesting novel spin-orbital phases are indeed found at the crossover from AF to FM interactions along hybrid bonds.

3 Charge Dilution

Doping a spin-orbital \(t_{2g}^{4}\) system by \(t_{2g}^{2}\) ions is even more challenging, see Fig. 1b. In this case, the impurity itself has another orbital degree of freedom, a hole (holon) in place of a doublon. A particular feature of d 2 ions is that they promote orbital fluctuations in case when c orbital (xy) is filled by one electron at all sites, and the other two {a,b} ({y z,z x}) fluctuate along the c axis, see (1). This supports FM spin order even in the absence of Hund’s exchange [30]. It is thus challenging to consider such ions within a ruthenate where similar orbital fluctuations are also expected.

The generic form of spin-orbital superexchange (2) applies as well to the hybrid d 2- d 4 bonds where charge \(3{d^{2}_{i}}4{d^{4}_{j}}\Rightarrow 3{d^{3}_{i}}4{d^{3}_{j}}\) excitations may generate an extra doublon in intermediate states at a 3d ion for AF bonds (not shown), or instead they create a high-spin state along FM bonds, see Fig. 1d. As a result, the spin-orbital interactions are here quite complex and include several terms, so we do not reproduce them here. They are controlled again by the charge-transfer energy and the same effective parameters as for orbital dilution, see (5). Again, the spin exchange depends on whether the doublon at the host ion is in the active or inactive orbital on the considered d 2- d 4 bond. It also depends on the configuration at the impurity site, i.e., whether the holon is in an active or inactive orbital.

The derivation of spin-orbital superexchange for the hybrid d 2- d 4 bonds demonstrates a remarkable difference to the orbital dilution on d 3- d 4 bonds discussed above. Consider first the AF spin bond shown in Fig. 1d. Charge excitations, \(3{d^{2}_{i}}4{d^{4}_{j}}\Rightarrow 3{d^{3}_{i}}4{d^{3}_{j}}\), create, inter alia, two high-spin configurations which generate novel orbital quantum fluctuations, \(\propto T_{i}^{+}T_{j}^{+}\), which go beyond those found in the host [30]. In addition, a doublon may be created at the 3d impurity ion and such configurations have to be combined with others to obtain eigenstates at both sites at finite {J 1,J 2}. As a result, the fluctuations \(\propto T_{i}^{+}T_{j}^{+}\) are amplified. They are accompanied by Ising orbital exchange terms and the usual fluctuations \(\propto T_{i}^{+}T_{j}^{-}\) activated by finite Hund’s exchange (not shown). For a FM spin configuration, the doublon gets a partner empty orbital at the host site and again, orbital quantum fluctuations \(\propto T_{i}^{-}T_{j}^{+}\) arise at finite J 2, see Fig. 1e.

Altogether, after averaging spin correlations, the purely orbital superexchange is,

$$\begin{array}{@{}rcl@{}} \mathcal{H}^{\langle ij\rangle\parallel\gamma}_{d^{2}-d^{4}}&=& \left\{A_{\gamma}^{\prime}{T_{i}^{z}}{T_{j}^{z}}+ \frac12 C_{\gamma}^{\prime}\left( T_{i}^{+}T_{j}^{-}+T_{i}^{-}T_{j}^{+}\right)\right. \\ &&+\left.\frac12 B_{\gamma}^{\prime}\left( T_{i}^{+}T_{j}^{+}+T_{i}^{-}T_{j}^{-}\right) \right\}^{(\gamma)}, \end{array} $$
(7)

with orbital operators \((T_{i}^{\alpha })^{(\gamma )}\) defined by the bond direction and the coefficients \(A_{\gamma }^{\prime }\), \(B_{\gamma }^{\prime }\), and \(C_{\gamma }^{\prime }\). As these parameters for the present hybrid bond are similar to those in the host (3), we use below,

$$ A_{\gamma}^{\prime}=A_{\gamma}, \quad B_{\gamma}^{\prime}\equiv B^{\prime}, \quad C_{\gamma}^{\prime}=C_{\gamma}, $$
(8)

i.e., we characterize the orbital superexchange on the hybrid bonds by the parameter \(B^{\prime }\) which stands for double excitations in Fig. 1d. Due to such terms, the orbital quantum number \(\mathcal {T}^{z}\) is not conserved.

A more complete analysis of charge dilution and the resulting phase diagrams will be presented elsewhere. Here, we focus on the consequences of orbital fluctuations \(\propto B^{\prime }\), both in C-AF and Néel AF spin configurations in the ab plane, see Fig. 2. Quantum fluctuations in the spin subsystem are small for S=1 spins and we neglect them. For realistic Hund’s exchange in the host and at the holon ion, one expects C-AF order. Its orbital pattern at \(B^{\prime }=0\) has equal orbital densities in a and c orbitals, see left column in Fig. 2. Indeed, this configuration guarantees maximal doublon fluctuations along the b axis where the order is FM, as in the vanadium perovskites with holon fluctuations involving a and b orbitals along the c axis [30]. Increasing orbital fluctuations gradually destroy this optimal state and favor AO order along vertical FM columns, with enhanced a or c holon density at every other site. For small \(B^{\prime }=1/2\), the \(T_{i}^{+}T_{j}^{+}\) term is active only along b-bonds and consequently there is no admixture of b orbitals in the ground state. At larger \(B^{\prime }=1\), we see the appearance of the b orbital polarization at the impurity site and two neighboring host sites along a-axis which goes together with a severe change of the global orbital order. At \(B^{\prime }=2\), a new state appears with almost complete separation into horizontal chains of a (c) orbitals and a small admixture of b orbital density. Holon site has a similar orbital density distribution, with somewhat enhanced b character. We suggest that the orbital fluctuations of alternating a and c orbitals along the vertical bonds replace here double exchange to stabilize FM spin order, while such fluctuations for the same orbitals along the horizontal bonds support AF spin order.

Fig. 2
figure 2

Orbital patterns obtained at x=1/8 charge dilution (with periodic cluster of N=8 sites) in two AF phases in an ab plane: left—C-AF phase with FM vertical (∥b) lines, and right—Néel AF phase (shown by arrows for \(B^{\prime }=0\)). Orbital fluctuations on the bonds around the impurity at site i=8 are \(\propto B^{\prime }\) (7) and increase from top to bottom. Bottom right—color convention for an orbital occupied by a doublon at host sites and a hole at impurity site (red circles), as well as the cluster of N=8 sites (dotted square) with the periodic boundary conditions on outer (red) bonds

Full size image

Actually, FO order in the ab plane supports AF Néel state following the Goodenough-Kanamori rules [5], see the right column in Fig. 2. This state is more robust and almost unchanged by double excitations \(\propto T_{i}^{+}T_{j}^{+}\) with a realistic \(B^{\prime }=1\), and only at a high value of \(B^{\prime }=10\), one finds increased a or b orbital densities following the checkerboard pattern around the impurity. This effect seems to be purely local because already the second neighbors of the impurity in the host are unaffected even for such a large value of \(B^{\prime }\). Unlike in C-AF spin order, we see that the defects in the orbital configurations are strongly localized or screened by the host. This screening has an interesting geometrical mechanism: if we look around the impurity, we see that the up and down neighbors get an admixture of the a orbitals from the \(\propto T_{i}^{+}T_{j}^{+}\) terms induced by the impurity. These a-orbital defects cannot however delocalize in the a direction (along two such bonds). The defects can only move up to the site number 7 in the cluster (see bottom right of Fig. 2). On the other hand, the horizontal neighbors of the impurity are in analogical situation with b-orbital defects which for the same reason can only go to the same site number 7. Finally, at this site, one expects a destructive interference of the a-orbital defects going from the top and bottom bonds and the b-orbital defects going from the left and right ones as it exhibits only the initial c-orbital polarization. It is thus possible that for a different distribution of impurities, we would observe a much weaker localization of the defects.

4 Discussion and Summary

Orbital (charge) dilution plays a role in several Mott insulators with spin-orbital order doped by transition metal ions with either d 3 or d 2 electron configuration. We have shown that the orbital order around such impurities changes in general, so even in the dilute limit one may expect observable effects such as islands of reversed spins or doublon fluctuations. We argue that the general trends reported here are generic and a meaningful insights into phase diagrams of systems with orbital dilution may be gained by investigating classical phase diagrams as quantum fluctuations are small [28]. Double exchange leads to local or global changes of spin-orbital order, similar to orbital polarons [18] or dimensional crossover with a change from G-AF to C-AF order in electron doped manganites [32]. Doping may also generate novel spin-orbital-charge modulated patterns reported recently for t 2g systems [33].

Summarizing, this study highlights the role played by orbital or charge dilution by transition metal ions in cubic spin-orbital systems and provides new insights necessary for theoretical understanding of (Mn,Cr)-doped layered ruthenates and related systems. Previous studies [28] have shown that d 3 impurities change radically spin-orbital order, and we expect an even stronger impact of d 2 impurities on spin-orbital order in the d 4 host—the changes may be strongly centered around the impurity sites, as shown in the FO case, or completely smeared out by the host’s fluctuations, as in the C-AF case. The theoretical studies of this doping are under way. It is challenging to investigate the consequences of enhanced orbital fluctuations in experimental systems.