Introduction

Radiotherapy is a cornerstone of modern oncology, and is frequently given in conjunction with chemical treatments to improve efficacy [1, 2]. Radiosensitizers are a class of chemical agents designed to enhance the radiation effect, e.g. by interfering with the cell’s repair of radiation-induced DNA damage [3]. During preclinical development of novel compounds, including radiosensitizers, a central question is how to select the most promising compounds from a large number of candidates [4,5,6]. Proper assessment of radiation and radiosensitizer combinations requires studies of efficacy as well as toxicology and adverse effects [7]. All compounds and doses cannot be tested in vivo—for reasons of time, resources, and ethics [8]. Experimental studies must therefore be supported by cheaper alternatives such as computer modeling and simulations [9, 10].

Numerous quantitative models have been developed to describe the effects of radiotherapy on tumors, with or without chemical intervention [11,12,13,14]. These models range from the simple, yet ubiquitous, linear-quadratic model of radiobiology [15], to complex systems pharmacology models that include particular pathways and processes (such as the cell cycle) that are relevant to the given treatment [16, 17]. In radiation oncology, models of Tumor Control Probability (TCP)—defined by whether a given radiation dose controls or eradicates an irradiated tumor—are commonly employed alongside Normal Tissue Complication Probability (NTCP) models that quantify toxicology and adverse risks [18,19,20].

Models have also been developed to describe the effects of radiotherapy on tumor volume over time. Watanabe et al. [21] proposed a radiation model with gradual cell death in response to single-dose treatment, and used it to describe tumor growth over time in rat rhabdomyosarcoma and in patients with metastatic brain tumors. More recently, Husband et al. developed and evaluated radiation models that describe tumor growth and survival in patient-derived xenograft mice for diffuse intrinsic pontine glioma [22].

In two earlier papers, we developed models that describe tumor growth in xenograft mice receiving radiotherapy and neoadjuvant radiosensitizing treatment [23, 24]. We also introduced the Tumor Static Exposure (TSE) concept—a model-based prediction of all combinations of radiation doses and radiosensitizer concentrations that result in tumor regression. However, these models only consider a single radiosensitzing compound and can therefore not fully illustrate the utility of the TSE concept in aiding the drug selection process.

In this paper, we use TSE to compare and rank three different combinations of radiation and radiosensitizing agents. One of our earlier models is used with data from a xenograft study involving radiotherapy administered alone or together with either of the radiosensitizers. The compounds are ranked by weighing efficacy (measured using TSE) against toxicity. Two different toxicological models are considered: a simple, linear model; and a more complex NTCP model adjusted to account for radiosensitizing treatment [25]. We also introduce the concept of Tumor Shrinkage Exposures, which can be used if tumor stasis is insufficient and tumor shrinkage with a particular rate is desired.

Methods

Experimental data are first described. Then, a previously-developed tumor model used to describe radiation and radiosensitizer combination therapies is summarized. Thereafter, a method for comparing and ranking radiation and radiosensitizer combinations, based on TSE, is presented. The method optimizes a given cost function, used to describe, e.g., toxicity and other adverse effects, along the TSE curve. Finally, computational aspects of the nonlinear mixed-effects modeling approach are provided.

Experimental data

Pharmacodynamic data were generated in FaDu xenograft mouse models treated with radiation either alone or together with one of three early-discovery radiosensitizing compounds, henceforth referred to as compounds A1, A2, and A3. A total of 54 female mice were divided into six treatment groups with nine mice in each group: (A) vehicle control, (B) monotherapy with radiation (2 Gy per dose), (C) combination therapy with radiation (2 Gy per dose) and compound A1 (100 mg/kg per dose), (D) combination therapy with radiation (2 Gy per dose) and compound A2 (25 mg/kg per dose), (E) combination therapy with radiation (2 Gy per dose) and compound A2 (100 mg/kg per dose), and (F) combination therapy with radiation (2 Gy per dose) and compound A3 (20 mg/kg per dose). Doses were given once per day Mon–Fri for 6 weeks.

Exposure data were generated in FaDu xenograft models for the compounds A1, A2, and A3. Single doses of the compounds A1, A2, and A3 were given orally to 16 animals divided into four treatment groups with four mice in each group: compound A1 (100 mg/kg), compound A2 (25 mg/kg), compound A2 (100 mg/kg) and compound A3 (20 mg/kg) Drug concentration in plasma was measured after 1, 2, and 6 h.

Experiments were approved in accordance with German animal welfare regulations by the Regierungspräsidium Darmstadt, Hessen, Germany (protocol registration numbers DA 4/Anz. 397 and DA 4/Anz. 398).

Tumor model for radiation and radiosensitizer combination treatment

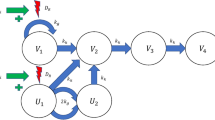
We use a previously-developed radiation model (Fig. 1) to describe tumor growth following treatment with radiation and radiosensitizing agents [23]. The model consists of a main compartment V1 representing proliferating cancer cells, three damage compartments V2, V3, and V4, that all dying cells traverse, and two radiation compartments U1, and U2, that allow irradiated cells up to one more cell division before dying. Irradiated cells are instantaneously transferred from V1 to U1. The fraction of proliferating cells that is transferred is based on the well-established linear-quadratic formula from radiobiology [14, 15]. Moreover, the presence of a radiosensitizing agent is accounted for via an increase in the number of lethally irradiated cells depending on the plasma concentration of the radiosensitizer at the time of irradiation. A high plasma concentration leads to a greater transfer of cells from V1 to U1. The model also incorporates natural cell death, meaning that some cells traverse the damage compartments even for untreated tumors.

Fig. 1
figure 1

Tumor model used to describe combination therapy with ionizing radiation (IR) and radiosensitizer compounds. Cancer cells in compartment V1 proliferate with rate kg and are eliminated with rate kk. Dying cells are transferred through three damage compartments V2, V3 and V4. Lethally irradiated cells are moved to a radiation-damage compartment U1 where they are allowed up to one more cell division, before dying. The compartment U2 represents irradiated cells after one cell division that can no longer divide

Full size image

The tumor model is described by the following differential equations

$$\begin{array}{*{20}l} {\frac{{dV_{1} }}{dt}} \hfill & { = k_{g} V_{1} - k_{k} V_{1} } \hfill \\ {\frac{{dV_{2} }}{dt}} \hfill & { = k_{k} V_{1} + k_{k} U_{1} + k_{k} U_{2} - k_{k} V_{2} } \hfill \\ {\frac{{dV_{3} }}{dt}} \hfill & { = k_{k} V_{2} - k_{k} V_{3} } \hfill \\ {\frac{{dV_{4} }}{dt}} \hfill & { = k_{k} V_{3} - k_{k} V_{4} } \hfill \\ {\frac{{dU_{1} }}{dt}} \hfill & { = - k_{g} U_{1} - k_{k} U_{1} } \hfill \\ {\frac{{dU_{2} }}{dt}} \hfill & { = 2k_{g} U_{1} - k_{k} U_{2} } \hfill \\ \end{array}$$
(1)

where kg is the growth rate of proliferating cancer cells, and kk the kill rate of cancer cells which is assumed to be the same for all compartments. The use of growth rate kg and the presence of the factor two in the transfer from U1 to U2 describes that cell division occurs between these states and therefore twice as many cells enter U2 than leave U1.

Radiation treatment is implemented as sudden transfer between compartments V1 and U1, corresponding to an instantaneous transfer of cells with the fraction given by (1-SF (DIR,Ci)). Here, SF (DIR,Cj) is the surviving fraction of proliferating cancer cells given a radiation dose DIR and concurrent drug plasma concentration Cj of compound Aj. Mathematically this can be described by the two equations

$$\begin{array}{*{20}l} {V_{1} \left( {t_{i}^{ + } } \right)} \hfill & { = V_{1} \left( {t_{i}^{ - } } \right) - \left( {1 - SF\left( {D_{IR} \left( {t_{i} } \right),C_{j} \left( {t_{i} } \right)} \right)} \right)V_{1} \left( {t_{i}^{ - } } \right),} \hfill \\ {U_{1} \left( {t_{i}^{ + } } \right)} \hfill & { = U_{1} \left( {t_{i}^{ - } } \right) + \left( {1 - SF\left( {D_{IR} \left( {t_{i} } \right),C_{j} \left( {t_{i} } \right)} \right)} \right)V_{1} \left( {t_{i}^{ - } } \right),} \hfill \\ \end{array}$$
(2)

where ti denotes the times of irradiation, and \({t}_{i}^{-}\) and \({t}_{i}^{+}\) can be interpreted as times just before and after irradiation. Note that radiation dose is given in terms of Gray (Gy), which is absorbed dose measured in joules per kilogram, i.e., the radiation dose is normalized with respect to animal weight and hence plays the role of exposure to radiation. The surviving fraction is given by

$$SF\left( {D_{IR} ,C_{j} } \right) = \exp \left[ { - \left( {1 + a_{j} C_{j} } \right)\left( {\alpha D_{IR} + \beta D_{IR}^{2} } \right)} \right]$$
(3)

where α and β are the linear and quadratic coefficients associated with radiation DNA damage, and aj is the pharmacodynamic parameter associated with the radiosensitizing capabilities of compound Aj. The initial conditions for the system are given by

$$V_{i} \left( 0 \right) = V^{0} \left( {\frac{{k_{k} }}{{k_{g} }}} \right)^{i - 1} ,\,U_{i} \left( 0 \right) = 0,$$
(4)

where V0 is the initial volume of the main compartment. With these initial conditions, untreated tumors grow exponentially with net growth rate kg − kk [26]. The total tumor volume, Vtotal, is obtained as the sum of all compartments

$$V_{{{\text{total}}}} = V_{1} + V_{2} + V_{3} + V_{4} + U_{1} + U_{2}$$
(5)

Comparing combinations of radiation and radiosensitizers

In the case study, the goal is to select one of three radiosensitizing agents for further experimental study. We propose a model-based approach that evaluates combinations based on how easily tumor regression is achieved, relative to toxicological or other adverse effects. The model described in the previous section is calibrated to data and then used to derive TSE curves for each radiosensitizing agent. Cost functions are introduced to describe toxicology and other potential costs associated with treatment, and an optimization problem is formulated to minimize the cost subject to the constraint that the tumor does not grow, i.e., that the exposure is on or above the TSE curve.

The Tumor Static Concentration (TSC) and TSE concepts have been introduced and used in several earlier papers [26,27,28,29]. The TSC curve corresponding to a particular combination therapy consists of all pairs (C1, C2) of plasma concentrations for which a maintained exposure leads to tumor stasis. In particular, maintaining exposure levels above the TSC curve leads to tumor regression. The TSE concept is a generalization of TSC that allows for treatments for which concentrations are unknown or not applicable, such as radiotherapy. The TSE curve for the model given in Eqs. 1 and 2 has previously been derived (see [23]). The curve consists of combinations of daily radiation doses and average radiosensitizer concentrations such that the tumor is kept in approximate stasis.

In the Results section, the calibrated tumor model is used to generate TSE curves for combination therapy with radiation and each of three radiosensitizers, which we denote A1, A2, and A3. We propose the following procedure for comparing and ranking combinations, while accounting for toxicity and other adverse effects.

For each treatment combination, introduce an associated cost function Ψ (E1, E2), where E1 and E2 refer to general exposure metrics. In our case study E1 = DIR is radiation dose, and E2 = Cj is the concurrent plasma concentration of radiosensitizer Ai. Alternatively, nondimensional exposures could be defined by E1 = DIR/Dref and E2 = Cj/Cref,j, where Dref and Cref,j are reference exposures. The cost function is a way to measure the toxicity of the combination, although other kinds of costs could also be included. Ψ is an increasing function, reflecting that a larger value corresponds to higher cost/toxicity.

In the simplest case, Ψ is linear function and is given by

$$\Psi \left( {E_{1} ,E_{2} } \right) = pE_{1} + qE_{2} ,$$
(6)

where p/q is the relative toxicity of the two compounds, assumed to be constant. Equation 6 assumes that toxicity increases linearly with exposure and is additive. Exposure pairs of equal costs, i.e., the level curves Ψ (E1, E2) = constant, are in this case lines with slope − p/q, with E1 and E2 are on the horizontal and vertical axes, respectively. An example of a TSE curve and a level set of the cost function is shown in Fig. 2.

Fig. 2
figure 2

TSE curve for two compounds with exposures E1 and E2 (blue). Exposure pairs above the curve give rise to tumor shrinkage, whereas exposure pairs below the curve result in tumor growth. A level set where the cost Ψ is constant is shown in black, dashed, with the corresponding Ψ* (color figure online)

Full size image

As an example of a more intricate cost function, we utilize the established framework around NTCP [18, 19]. Such models are commonly used to describe the probability of adverse events following radiation treatment [30,31,32]. A widely used model for NTCP is the Lyman–Kutcher–Burman (LKB) model which defines the NTCP as

$$NTCP\left( t \right) = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^{t} {e^{{{{ - x^{2} } \mathord{\left/ {\vphantom {{ - x^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}}} dx,}$$
(7)

where the variable t is defined by

$$t = \frac{{D_{eff} - TD_{50} }}{{mTD_{50} }},$$
(8)

and where Deff is the effective dose, which accounts for non-uniform dose distribution, TD50 is the dose associated with 50% complication risk, and m is a slope parameter for the sigmoidal curve [25, 33]. From these equations we can see that a larger value of Deff corresponds to a larger value for t, which in turns means a greater risk of complications.

The key question when defining a cost function for radiation and radiosensitizer combinations is how to introduce radiosensitizing treatment into the NTCP model. Since TD50 is a typical measure of radiation sensitivity, we propose to let the radiosensitizer modulate this parameter and thereby increase the risk of complications. Assuming an exponential sigmoidal modulation function gives a new definition of t,

$$t = \frac{{D_{eff} - TD_{50} I\left( C \right)}}{{mTD_{50} I\left( C \right)}}$$
(9)

where I(C) is an exponential inhibitory function with parameter ks [34]:

$$I\left( C \right) = \exp \left( { - k_{s} C} \right).$$
(10)

We can thus use the NTCP model as a cost function with exposures E1 = Deff = D (total radiation dose) and E2 = C, where C is the radiosensitizer concentration at the time of irradiation. Note that NTCP depends on the exposures E1 and E2 only through the variable t. Therefore, exposure combinations with equal complication risk have the same value for t. Thus, solving for Deff in Eq. 9 gives the expression for equal cost

$$D_{eff} = \left( {1 + mt} \right)TD_{50} \exp \left( { - k_{s} C} \right).$$
(11)

Equation 10 describes a sigmoidal relationship between exposure pairs (Deff, C) with equal cost.

Equipped with a cost function, we search along the TSE curve for the exposure pair with the lowest cost. Repeating this procedure for each combination gives a sequence of lowest costs, each corresponding to a different combination therapy. These values can then be used to compare and rank combination therapies.

The procedure for comparing and ranking combinations is summarized below:

  1. (1)

    Choose a suitable tumor model given available data and calibrate the model to obtain parameter estimates

  2. (2)

    Compute the TSE curves and insert the estimated parameter values

  3. (3)

    Choose an appropriate cost function Ψ for each combination and find the minimum cost Ψ* along the TSE curve

  4. (4)

    Repeat Steps 1–3 for each drug combination

  5. (5)

    Compare Ψ* across combination therapies and choose the combination with the lowest cost

Tumor shrinkage exposures

TSE curves are based on the requirement of tumor stasis. This is valuable since the curve divides the exposure plane into regions of tumor growth and tumor shrinkage. However, in practice, tumor shrinkage may not be enough and one can therefore look at tumor shrinkage with different rates. This leads to a generalization of TSE called tumor shrinkage exposure (TSEρ) where ρ is the relative change in volume for a given time unit, \(\rho = \frac{{V\left( {t_{1} } \right) - V\left( {t_{2} } \right)}}{{V\left( {t_{1} } \right)}}\), where t2 > t1 are two time point, and t2 − t1 is the chosen time unit. In particular, TSE0 is the regular TSE curve, and TSE0.5 requires that the tumor shrinks by 50% of its size every for every unit of time that elapses. TSEρ is derived analogously to TSE, with the difference that the growth rate is set to a constant different from zero. The concept of TSEρ curves is illustrated for the case study in the Results section.

Computational methods

The tumor model was calibrated to xenograft data using a nonlinear mixed-effects approach based on the first-order conditional estimation (FOCE) method in a computational framework developed at the Fraunhofer-Chalmers Research Centre for Industrial Mathematics (Gothenburg, Sweden) and implemented in Mathematica (Wolfram Research) [35]. Exposure data for compounds A1, A2, and A3 were described using one-compartment pharmacokinetic models. Model evaluation was based on goodness-of-fit, empirical Bayes estimates, and residual analysis.

Lognormal distributed between-subject variability was added to the initial volume of the main compartment V0 and the growth rate kg. Residual errors were assumed to be proportional to tumor volume with zero mean and variance \({\sigma }_{V}^{2}\). As done previously, the ratio between α and β was set to 10 [23, 36].

Results

First, the results of fitting the tumor model to the experimental data are presented. Then, TSE curves corresponding to combination therapy with radiation and each of the three radiosensitizers A1, A2, and A3, are computed. Finally, the procedure for comparing and ranking combinations is illustrated for two toxicological settings.

Tumor model for radiation and radiosensitizer combination treatment

Exposure profiles for each of the three radiosensitizers A1, A2, and A3 were described by standard one-compartment pharmacokinetic models, with parameter estimates given in Table 1. Simulated PK profiles used to drive the pharmacodynamic tumor model are shown in Fig. 3. The exposure of compound A1 (green) was approximately ten times lower than the exposures of compounds A2 (blue) and A3 (purple).

Table 1 Parameter estimates for the one-compartment pharmacokinetic models describing exposure to the compounds A1, A2, and A3 in terms of plasma concentration
Full size table
Fig. 3
figure 3

Simulated PK profiles for compounds A1, A2, and A3 with corresponding plasma concentrations C1, C2, and C3. Doses of 100 mg/kg (compounds A1 and A2) or 20 mg/kg (compound A3) were given 5 days a week for 6 weeks

Full size image

The tumor model adequately described observed data from each of the six treatment groups. Examples of individual fits for each treatment group are shown in Fig. 4. In the vehicle group, tumor growth was approximately exponential during the observed time period. Tumors treated with radiation monotherapy reached approximate stasis during treatment and in some cases showed signs of regression. Tumors treated with radiation and compound A1 combination therapy exhibited significant regression and in most cases the tumors were eradicated. Tumors treated with radiation and compound A2 showed significant regression with the lower dose (25 mg/kg) and in most cases tumor eradication with the higher dose (100 mg/kg). Lastly, tumors treated with radiation and compound A3 also exhibited tumor eradication in most instances. Visual predictive checks for the tumor model can be found in Supplemental Information S1.

Fig. 4
figure 4

Examples of individual fits for each of the six treatment groups: vehicle (black), radiation monotherapy with 2 Gy per dose (red), combination therapy with radiation and A1 at 100 mg/kg per dose (green), combination therapy with radiation and A2 at 25 mg/kg or 100 mg/kg per dose (blue), and combination therapy with radiation and A3 at 20 mg/kg per dose (purple) (color figure online)

Full size image

The parameter estimates from fitting the tumor model simultaneously to all treatment groups are given in Table 2. The net growth rate \(k_{g} - k_{k} = 0.16/{\text{day}}\) corresponds to an average doubling time of 4.3 days for the vehicle group. System and radiation parameters were estimated with good precision, whereas drug parameters were estimated with lower but still acceptable precision (RSE < 40%).

Table 2 Parameter estimates for the tumor model describing the effects of radiation and radiosensitizer combination therapy
Full size table

TSE curves for radiation and radiosensitizer combinations

Following the same principles as in [23] the following expression for the TSEρ curves was derived

$$D_{IR} = \frac{{ - \left( {\alpha + a_{j} \alpha C_{j} } \right) + \sqrt {\left( {\alpha + a_{j} \alpha C_{j} } \right)^{2} + 4\left( {\beta + a_{j} \beta C_{j} } \right)\left( {k_{g} T - k_{k} T + \log \left( {1 - \rho } \right)} \right)} }}{{2\left( {\beta + a_{j} \beta C_{j} } \right)}}$$
(12)

where DIR is the radiation dose given every T days, and Cj is the plasma concentration of Aj at the instance of irradiation. The details can be found in Supplemental Information S2.

The TSE curves for the three combination therapies involving radiation and one of the radiosensitizing agents A1, A2, and A3, were computed by inserting the parameter estimates from Table 2 into Eq. 12, using T = 1 day to indicate daily dosing. The resulting TSE curves are shown in Fig. 5.

Fig. 5
figure 5

TSE curves for combinations of radiation and radiosensitizers A1 (left), A2 (middle) and A3 (right) obtained by inserting the parameter estimates from Table 2 into Eq. 12. TSE curves are shown in blue. Regions above and below the curves correspond to combination pairs that result in tumor shrinkage, or tumor growth, respectively. The dashed reference lines indicate the daily radiation dose required for tumor shrinkage during monotherapy

Full size image

The TSE value for radiation monotherapy was estimated to 1.3 Gy, meaning that for the median individual a daily dose of 1.3 Gy would be sufficient for approximate tumor stasis. Since the compounds A1, A2, and A3, have no monotherapy effect, they have no TSE values. Instead, the TSE curves asymptotically approach the concentration axis as the plasma concentrations of the compounds approach infinity. The TSE curve for combinations of radiation and compound A1 (left) exhibits the largest curvature. Indeed, that TSE curve associated with A1 lies strictly below the TSE curve for the other two combination therapies.

Comparing combinations of radiation and radiosensitizers

The procedure outlined in the Methods section is applied to compare and rank the three combination therapies for two toxicological models. Using the first model, we consider two scenarios: one based on the assumption that all radiosensitizers are equally toxic, and one where the toxicity of compound A1 is increased tenfold. The cost functions are given by

$$\Psi \left( {D_{IR} ,C_{j} } \right) = pD_{IR} + q_{j} C_{j}$$
(13)

where DIR is the radiation dose with toxicity coefficient p, and Cj is the plasma concentrations of compound Aj with toxicity coefficient qj. First, assuming that all test compounds are equally toxic means that q1 = q2 = q3. The costs associated with each combination pair (DIR, Cj) on the corresponding TSE curve are illustrated in Fig. 6 (left). The parameter \(s\) indicates the location along the TSE curve with s = 0 corresponding to radiation monotherapy, and s = 1 corresponding to monotherapy with the radiosensitizer. Note that, for the particular tumor model in this case study, the radiosensitizers have no monotherapy effect, which means that s = 1 corresponds to an infinitely large exposure of the radiosensitizer and therefore also an infinite cost/toxicity. The parametrization has been performed such that s = 0.5 corresponds to Cj = 25 μg/mL. This is an arbitrary scaling of the parametrization that does not affect the optimization problem and is performed only to make the figures easier to interpret. This amounts to the parametrization given in Eq. 14 below

$$\Psi \left( s \right) = pD_{IR} \left( {\frac{25s}{{1 - s}}} \right) + q_{j} \frac{25s}{{1 - s}}$$
(14)

with DIR (Cj) given as in Eq. 12.

Fig. 6
figure 6

Hypothetical costs Ψ for different combinations along the TSE curves in Fig. 5 for combination therapy with radiation and radiosensitizers A1 (green), A2 (blue), and A3 (purple). The left plot assumes that all three compounds are equally toxic, whereas in the right plot the toxicity of A1 (green) has been increased by a factor ten. The parameter \(\mathrm{s}\) represents the position on the TSE curve with s = 0 corresponding to radiation monotherapy and s = 1 monotherapy with compound Aj (color figure online)

Full size image

The cost coefficients were set to p = 100/Gy and qj = 1 mL/μg. Figure 6 (left) shows that combination therapy with A1 has the lowest cost (for s ≈ 0.5\()\). We then consider the second scenario, where the toxicity of A1 has been increased by a factor ten, q1 = 10 mL/μg, which is illustrated in Fig. 6 (right). A1 is no longer the best treatment option, since A2 and A3 both have lowers costs (occurring at s ≈ 0.6).

Figure 7 shows the results using the more complex NTCP model as cost function. For this model, we use values of TD50 = 50 Gy and m = 0.5 to describe radiation treatment and set the radiation parameter ks to 0.02 mL/μg/day for all three radiosensitizers. Similar to the case with a linear cost function, A1, which is the most efficacious, has the lowest cost. Compared with the linear case, the value of the radiosensitizer parameter ks for A1 would need to be decreased approximately tenfold for another radiosensitizer to become the most promising candidate. The parametrization of the cost function along the TSE curve, with parameter s going from s = 0 (radiotherapy) to s = 1 (radiosensitizer monotherapy) is given in Eq. 15.

$$\Psi \left( s \right) = NTCP\left( {\frac{{D_{IR} \left( {\frac{25s}{{1 - s}}} \right) - TD_{50} I\left( {\frac{25s}{{1 - s}}} \right)}}{{TD_{50} I\left( {\frac{25s}{{1 - s}}} \right)}}} \right)$$
(15)

where DIR is given by Eq. 12, I is given by Eq. 10, and NTCP is given by Eq. 9.

Fig. 7
figure 7

Hypothetical costs Ψ using the NTCP model (Eq. 15) for radiation and radiosensitizer combinations, A1 (green), A2 (blue), and A3 (purple), along the TSE curves in Fig. 5. The left plot assumes equal toxicity, whereas the right plot assumes a tenfold increase for radiosensitizer A1 (color figure online)

Full size image

Tumor shrinkage exposures

Figures 5 and 6 are used to minimize the cost of combination therapy with the respect to the TSE curve, i.e., while making sure the tumor is not growing. As pointed out in the Methods section, it is also possible to require that the tumors shrink at a specified rate, by introducing the TSEρ curves. TSEρ curves are illustrated in Fig. 8 for combinations of radiation and compound A2, assuming a linear cost function as in Fig. 6. The three TSEρ curves (blue) consists of exposure pairs (DIR, Cj) that keep the tumor in stasis, shrink the tumor to half its size, and shrink the tumor to one eighth of its size, respectively.

Fig. 8
figure 8

Examples of TSE curves for combinations of radiation and compound A2. TSE1, TSE2, and TSE8 corresponding to shrinkage rates that keep the tumor in stasis, reduce the tumor to half its size, and reduce the number of proliferating tumor cells to one eighth of its size with each daily dose, respectively

Full size image

For each TSEρ curve, it is possible to minimize the costs of combination therapy following the same procedure as described earlier. Thus, for a given combination, consider how the minimum cost, Ψmin, varies depending on how quickly the tumor is required to shrink, i.e., ρ. Figure 9 depicts this scenario for combinations of radiation and the three radiosensitizers as a function of the parameter \({1 \mathord{\left/ {\vphantom {1 {1 - \rho }}} \right. \kern-\nulldelimiterspace} {1 - \rho }}\) under the assumption that all compounds are equally toxic. Note that combination therapy with A1 (green) always has the lowest cost.

Fig. 9
figure 9

Minimal costs ψ* as a function of relative shrinkage rate ρ for combinations of radiation and A1 (green), A2 (blue), and A3 (purple). Here \(\frac{1}{1 - \rho } = {{V_{1} \left( {t_{1} } \right)} \mathord{\left/ {\vphantom {{V_{1} \left( {t_{1} } \right)} {V_{1} \left( {t_{2} } \right)}}} \right. \kern-\nulldelimiterspace} {V_{1} \left( {t_{2} } \right)}}\) is a more natural parameter such that the minimal cost is an increasing function of the parameter. The figure shows that, for any value of ρ, the compound A1 has the lowest cost, since the curves never intersect

Full size image

Discussion

Recent decades have seen a growing focus on combination therapies as a way to combat resistances and to obtain synergistic effects [37, 38]. Our analysis of radiotherapy and radiosensitizer combinations in this paper is focused on the latter, while also addressing toxicity and side-effects. As with any model-based analysis, good predictions and results are contingent not only on data [39], but also on sound modeling methodology [40, 41]. Details on this topic, particularly in the context of oncology, can be found e.g. in several papers by Mould et al. [42,43,44]. The remainder of this discussion considers, in order: the mathematical tumor model, the resulting TSE curves and concepts, and, finally, our proposed optimization and ranking procedure for radiation and radiosensitizer combinations.

Tumor model for radiation and radiosensitizer combinations

The model used in this paper in based on an earlier model (see [23]), with two minor differences. As in [24] an exponential growth function was favored over logistic growth, since it proved sufficient to describe vehicle data and no plateaus in tumor volumes were observed. Secondly, we assumed no monotherapy effect for the radiosensitizers, which is expected to be negligible given that the compounds interact with the repair mechanisms of DNA damage induced by irradiation.

The growth and kill rates were estimated to similar values to those in [23, 24], and the net growth rate kg − kk of 0.15/day, corresponds to a doubling time of 4–5 days, which is similar to other models [21, 23, 26, 27, 45]. The estimated α and β values of 0.11/Gy and 0.0011/Gy2 are in line with reported ranges of 0.02 − 0.2 for α and 0.001 − 0.6 for β [46]. Model parameters were estimated with reasonable precision, although the radiosensitizer parameters ai had somewhat lower precision (RSE% ≈ 35), which is partially explained by the fact that each ai is only informed by one or two treatment groups, whereas other model parameters are informed by all data.

Like many tumor models used preclinically, our model contains a sequence of damage compartments [26, 27, 29, 45], and can be viewed as a combination of these models with the linear-quadratic model in radiobiology [15], or compartment radiation models that implement the linear-quadratic model with delay [21, 22]. Compared with systems pharmacology models for radiation and chemical combinations, e.g., Checkley et al. [17], Kosinsky et al. [16], our model is simpler and, although less mechanistic, can be calibrated to standard xenograft data.

TSE curves for radiation and radiosensitizer combinations

TSC and TSE have been developed and applied in a series of papers [23, 26, 27, 29]. They are tailored specifically to cancer treatments (single-agents or combinations), and are connected to qualitative behavior (tumor growth or shrinkage) of the disease as well as synergy, unlike general models such as the isobologram [47, 48] and the half-maximal effect curve [49] which focus only on synergy. In radiation oncology, TCP models are used to assess probabilities of tumor eradication, recurrence, or emergence of metastases [20, 50], which is similar to TSE in that it also aims to control or destroy cancer cells.

In our analysis, greatest synergy occurred with radiosensitizer A1, which can also be seen from the curvatures of the TSE curves (Fig. 5). This happens because although observed tumor growth was similar across combinations, exposure levels were approximately ten times lower for compounds A1 (see Fig. 3). However, proper assessment requires consideration not only of efficacy, but joint consideration of efficacy and toxicity.

Comparing combinations of radiation and radiosensitizers

In our case study involving radiation and three radiosensitizing agents, Fig. 6 (left) shows that radiosensitizer A1 is the superior radiosensitizer given that all compounds are equally toxic, which holds for either cost function. Moreover, Fig. 6 (right) shows that the toxicity of A1 would have to be increased tenfold over A2 and A3 for another radiosensitizer to become preferable. This result held true for both cost functions. However, since the NTCP model is nonlinear and contains multiple sigmoidal functions, these results depend on the chosen parameter values.

Our proposed method evaluates combinations of radiation and radiosensitizers by the ability to induce tumor regression relative to toxicity. Two toxicity functions, or cost functions are considered: one linear, and one based on NTCP. The former approach was also considered in [29] to find an optimal combination for two anticancer compounds. A similar analysis can be found in [51] where phase one clinical data were used to construct a toxicity function with linear terms as well as a quadratic term to penalize combination treatment.

In radiotherapy, TCP and NTCP models are often combined to optimize treatment [52, 53]. In our analysis, the tumor model together with TSE appear instead of a TCP model, which we consider in conjunction with the commonly used Lyman NTCP model [25]. Here, we note similar results using a linear model and an NTCP model (see Figs. 6, 7) although the sigmoidal nature of the NTCP model produced somewhat flatter cost around the minima, which implies that good therapeutic response is less sensitive to perturbations and is therefore easier to achieve. Alternative NTCP models also exist (see e.g., [54,55,56,57]) although most tend to be static (as opposed to dynamic, or temporal) and empirically founded.

Dynamic models of toxicity have also been developed. In [58] Krzyzanski et al. proposed a model of thrombocytopenia following combined chemotherapy and radiation treatment. Scenarios when the tumor model as well as the toxicity model are both dynamic can be approached using optimal control theory [59, 60]. The approach to selecting and ranking combinations presented in this paper could also be used in combination with other optimization approaches such as those that design treatment protocols to yield the most amount of information about the compounds [61, 62].

Conclusions and perspectives

We have demonstrated how a model-based approach, using TSE, can be used to compare and rank radiation and radiosensitizer combinations. The analysis weighs efficacy (tumor regression) against side-effects (toxicity) in order to provide a fair comparison and ranking of the different combinations.

While the chosen criteria for comparing combination therapies are natural, they are not the only reasonable choice. An alternative choice could be to compare the rate of tumor regression for each combination at a specified maximum tolerable exposure, i.e., exchanging the roles that efficacy and toxicity play in the optimization problem.

Our analysis is focused on radiotherapy combined with radiosensitizing treatment. A similar approach using TSE and cost functions could also be considered for chemical combinations. However, the underlying pharmacokinetic, pharmacodynamic, and toxicity modeling would have to account for potential drug interactions.