On the Solution Existence for Collocation Discretizations of Time-Fractional Subdiffusion Equations

Abstract

Time-fractional parabolic equations with a Caputo time derivative of order $\alpha \in (0,1)$ are discretized in time using continuous collocation methods. For such discretizations, we give sufficient conditions for existence and uniqueness of their solutions. Two approaches are explored: the Lax–Milgram Theorem and the eigenfunction expansion. The resulting sufficient conditions, which involve certain $m\times m$ matrices (where m is the order of the collocation scheme), are verified both analytically, for all $m\ge 1$ and all sets of collocation points, and computationally, for all $m\le 20$. The semilinear case is also addressed.

1 Introduction

We are interested in continuous collocation discretizations in time for time-fractional parabolic problems, of order $\alpha \in (0,1)$, of the form

$$\begin{aligned} \partial _t^{\alpha }u+\mathcal {L}u=f(x,t)\qquad \text{ for }\;\;(x,t)\in \Omega \times (0,T], \end{aligned}$$

(1)

also known as time-fractional subdiffusion equations. This equation is posed in a bounded Lipschitz domain $\Omega \subset \mathbb {R}^d$ (where $d\in \{1,2,3\}$), subject to an initial condition $u(\cdot ,0)=u_0$ in $\Omega$, and the boundary condition $u=0$ on $\partial \Omega$ for $t>0$.

The spatial operator $\mathcal {L}$ is a linear second-order elliptic operator:

$$\begin{aligned} \mathcal {L}u:= \sum _{k=1}^d \Bigl \{-\partial _{x_k}\!(a_k(x)\,\partial _{x_k}\!u) + b_k(x)\, \partial _{x_k}\!u \Bigr \}+c(x)\, u, \end{aligned}$$

(2)

with sufficiently smooth coefficients $\{a_k\}$, $\{b_k\}$ and c in $C(\bar{\Omega })$, for which we assume that $a_k>0$ in $\bar{\Omega }$, and also either $c\ge 0$ or $c-\frac{1}{2}\sum _{k=1}^d\partial _{x_k}\!b_k\ge 0$.

We also use $\partial _t^\alpha$, the Caputo fractional derivative in time [3], defined for $t>0$, by

$$\begin{aligned} \partial _t^{\alpha } u:= \frac{1}{\Gamma (1-\alpha )} \int _{0}^t(t-s)^{-\alpha }\, \partial _s {u}(\cdot , s)\, ds, \end{aligned}$$

(3)

where $\Gamma (\cdot )$ is the Gamma function, and $\partial _t$ denotes the classical first-order partial derivative in t.

In two recent publications [5, 6], we considered high-order continuous collocation discretizations for solving (1) in the context of a-posteriori error estimation and reliable adaptive time stepping algorithms. It should be noted that despite a substantial literature on the a-priori error bounds for problem of type (1), both on uniform and graded temporal meshes—see, e.g., [9, 10, 12, 14, 16, 19] and references therein— the a-priori error analysis of the collocation methods appears very problematic. By contrast, in combination with the adaptive time stepping algorithm (based on the theory in [13]), high-order collocation discretizations (of order up to as high as 8), were shown to yield reliable computed solutions and attain optimal convergence rates in the presence of solution singularities.

Note also that the a-posteriori error analysis in [13], as well as in related papers [5, 6, 15], is carried out under the assumption that there exists a computed solution, the accuracy of which is being estimated (as well as there exists a solution of the original problem); in other words, it was assumed that the discrete problem was well-posed at each time level. While this assumption is immediately satisfied by the L1 method (as well as by a few L2 methods, which may be viewed as generalizations of multistep methods for ordinary differential equations), the well-posedness of high-order collocation schemes appears to be an open problem, to which we devote this article.

Consider a continuous collocation method of order $m\ge 1$ for (1) (see, e.g., [2]), associated with an arbitrary temporal grid $0=t_0<t_1<\dots <t_M=T$. We require our computed solution U to be continuous in time on [0, T], a polynomial of degree m in time on each $[t_{k-1},t_k]$, and satisfy

$$\begin{aligned} (\partial _t^\alpha +\mathcal {L})\,U(x, t^\ell _k)=f(x, t_k^\ell )\qquad \text{ for }\;\; x\in \Omega ,\;\; \ell \in \{1,\ldots , m\},\;\;k=1\ldots , M, \end{aligned}$$

(4)

subject to the initial condition $U^0:=u_0$, and the boundary condition $U=0$ on $\partial \Omega$. Here a subgrid of collocation points $\{t_k^\ell \}_{\ell \in \{0,\dots ,m\}}$ is used on each time interval $[t_{k-1},t_k]$ with $t_k^\ell :=t_{k-1}+\theta _\ell \cdot (t_k-t_{k-1})$, and $0=\theta _0<\dots <\theta _m\le 1$.

Strictly speaking, (4) gives a semi-discretization of problem (1) in time, while applying any standard finite difference or finite element spatial discretization to (4) will yield a so-called full discretization. The latter can typically be described by a version of (4), with $\Omega$, $\mathcal {L}$, and f respectively replaced by the corresponding set $\Omega _h$ of interior mesh nodes, the corresponding discrete operator $\mathcal {L}_h$, and the appropriate discrete right-hand side $f_h$.

For $m=1$ the above collocation method is identical with the L1 method. In fact, then (4) involves one elliptic equation at each time level $t_k$, with the elliptic operator $\mathcal {L}+ \tau _k^{-\alpha }/\Gamma (2-\alpha )$, where $\tau _k:=t_k-t_{k-1}$ (or the corresponding discrete spatial operator $\mathcal {L}_h+\tau _k^{-\alpha }/\Gamma (2-\alpha )$). Hence, using a standard argument (see, e.g., [11, Lemma 2.1(i)]) one concludes that $c(\cdot )+\tau _k^{-\alpha }/\Gamma (2-\alpha )\ge 0$ in $\Omega$, $\forall \,k\ge 1$, is sufficient for existence and uniqueness of a solution U of (4).

Once $m\ge 2$, one needs to solve a system of m coupled elliptic equations at each time level (or a spatial discretization of such a system), so the well-posedness of such systems is less clear. By contrast, one can easily ensure the well-posedness in the case of a time-fractional ordinary differential equation (i.e. if $\mathcal {L}u$ in (1) is replaced by c(t)u) by simply choosing the time steps sufficiently small (see section 2.1). This approach is, however, not applicable to subdiffusion equations (as discussed Remark 4), since the eigenvalues of second-order elliptic operators are typically unbounded. Hence, in this paper we shall explore alternative approaches to establishing the well-posedness of (4).

The paper is organised as follows. We start our analysis by deriving, in section 2, a matrix representation of the collocation scheme (4). Next, in section 3, sufficient conditions for the well-posedness of (4) are obtained by means of the Lax–Milgram Theorem, with a detailed application for $m=2$. Furthermore, alternative sufficient conditions for the well-posedness of (4) are formulated in section 4 in terms of an eigenvalue test for a certain $m\times m$ matrix. This test is then used in section 4.1 to prove the existence of collocation solutions for all $m\ge 1$ and all sets of collocation points $\{\theta _\ell \}_{\ell =1}^m$; see our main result, Theorem 14. This test can also be applied computationally, as illustrated in section 4.2 for all $m \le 20$. Finally, in section 5, we present extensions to the semilinear case.

Notation. We use the standard spaces $L_2(\Omega )$ and $H^1_0(\Omega )$, the latter denoting the space of functions in the Sobolev space $W_2^1(\Omega )$ vanishing on $\partial \Omega$, as well as its dual space $H^{-1}(\Omega )$. The notation of type $(L_2(\Omega ))^m$ is used for the space of vector-valued functions $\Omega \rightarrow \mathbb {R}^m$ with all vector components in $L_2(\Omega )$, and the norm induced by $\Vert \cdot \Vert _{L_2(\Omega )}$ combined with any fixed norm in $\mathbb {R}^m$.

2 Matrix Representation of the Collocation Scheme (4)

As we are interested only in the existence and uniqueness of a solution of the collocation scheme (4), it suffices to consider only the first time interval $(0,t_1)$, i.e. $k=1$ in (4), and with a homogeneous initial condition. Furthermore, setting $\tau :=\tau _1$, we shall rescale the latter problem to the time interval (0, 1). Hence, we are ultimately interested in the well-posedness of the problem

$$\begin{aligned} (\partial _t^\alpha +\tau ^\alpha \mathcal {L})\,U(x, \theta _\ell )=F(x, \theta _\ell )\qquad \text{ for }\;\; x\in \Omega ,\;\; \ell \in \{1,\ldots , m\}, \end{aligned}$$

(5)

where U is a polynomial of degree m in time for $t\in [0,1]$ such that $U(\cdot , 0)=0$ and $U=0$ on $\partial \Omega$.

To relate (4) on any time interval $(t_{k-1},t_k)$ to (5), set $\theta :=(t-t_{k-1})/\tau _k\in (0,1)$ (so $t=t_k^\ell =t_{k-1}+\theta _\ell \cdot \tau _k$ corresponds to $\theta =\theta _\ell$) and $\hat{U}(\cdot ,\theta ):=U(\cdot ,t)-U(\cdot ,t_{k-1})$. Then a calculation shows that $\mathcal {L}U(\cdot ,t)=\mathcal {L}\hat{U}(\cdot ,\theta )-\mathcal {L}U(\cdot ,t_{k-1})$ and $\partial _t^\alpha U(\cdot ,t)=\tau _k^{-\alpha }\,\partial _\theta ^\alpha \hat{U}(\cdot ,\theta )+F_0(\cdot , t)$, where $F_0(\cdot , t):=\{\Gamma (1-\alpha )\}^{-1}\int _0^{t_{k-1}}(t-s)^{-\alpha }\partial _s U(\cdot ,s)\,ds$. Now, (4) on $(t_{k-1},t_k)$ is equivalent to

$$\begin{aligned} \partial _\theta ^\alpha \hat{U}(\cdot ,\theta _\ell )+\tau _k^{\alpha }\,\mathcal {L}\hat{U}(\cdot ,\theta _\ell )=F(\cdot ,\theta _\ell ), \;\;\text{ where }\; F(\cdot ,\theta ):=\tau _k^{\alpha }[f(\cdot , t)+\mathcal {L}U(t_{k-1})-F_0(\cdot , t)]. \end{aligned}$$

Finally, with a slight abuse of notation, replacing $\hat{U}$ in the above by a $U(\cdot ,t)$, and also using the notation $\tau :=\tau _k$ for the current time step to further simplify the presentation, one gets (5).

Furthermore, without loss of generality, our analysis will be presented only for the case $\theta _m=1$.

Remark 1

(Case $\theta _m<1$) All our findings for the case $0=\theta _0<\dots <\theta _m=1$ immediately apply to the general case $0=\theta _0<\dots <\theta _m\le 1$. Indeed, if $\theta _m<1$, it suffices to rescale (5) from the interval $(0,\theta _m)$ to (0, 1), using $\hat{U}(\cdot , t):=U(\cdot , t/\theta _m)$ and $\hat{F}(\cdot , t):=\theta _m^\alpha F(\cdot , t/\theta _m)$. Then $\partial _t^\alpha U(\cdot , t)=\theta _m^{-\alpha }\partial _t^\alpha \hat{U}(\cdot , t)$, so (5) becomes

$$\begin{aligned} (\partial _t^\alpha +\hat{\tau }^\alpha \mathcal {L})\,\hat{U}(x, \hat{\theta }_\ell )= F(x, \hat{\theta }_\ell ),\quad \text{ where }\;\; \hat{\tau }:=\theta _m\tau _k\;\;\text{ and }\;\; \{\hat{\theta }_\ell :=\theta _\ell /\theta _m\}_{\ell =1,\ldots , m}. \end{aligned}$$

The above is clearly a problem of type (5) with $0=\hat{\theta }_0<\dots <\hat{\theta }_m=1$.

A solution U of (5) is a polynomial in time, equal to 0 at $t=0$, so it can be represented using the basis $\{t^j\}_{j=1}^m$ as

$$\begin{aligned} U(x,t)=\sum _{j=1}^m v_j(x)\,t^j = \Bigl (t,\,t^2,\,\cdots ,\,t^m\Bigr )\begin{pmatrix}v_1(x)\\ v_2(x)\\ \vdots \;\;\\ v_m(x) \end{pmatrix}=:T(t)\, \vec {V}(x). \end{aligned}$$

(6)

Here we used the standard linear algebra multiplication, and, for convenience, we highlight column vectors in such evaluations with an arrow (as in $\vec {V}$). Other column vectors of interest are $\vec {\theta }:=\big (\theta _1,\theta _2,\cdots ,\theta _m\big )^{\!\!\top }$, and also $\vec {U}(x):=U(x,\vec {\theta })$ and $\vec {F}(x):=F(x,\vec {\theta })$ (where a function is understood to be applied to a vector argument elementwise). Thus, $\vec {U}$ can be represented using the Vandermonde-type matrix W as follows:

$$\begin{aligned} W:=\begin{pmatrix}T(\theta _1)\\ T(\theta _2)\\ \vdots \;\;\;\\ T(\theta _m) \end{pmatrix}= \begin{pmatrix}\theta _1 &{} \theta _1^2 &{} \cdots &{}\theta _1^m\\ \theta _2 &{} \theta _2^2 &{} \cdots &{}\theta _2^m\\ \vdots \ {} &{}\vdots \ {} &{}&{} \vdots \ \\ \theta _m &{} \theta _m^2 &{}\cdots &{} \theta _m^m \end{pmatrix} \; \Rightarrow \; \vec {U}(x)=U(x,\vec {\theta }) =W \vec {V}(x). \end{aligned}$$

(7)

Additionally, we shall employ two diagonal matrices

$$\begin{aligned} D_1=\textrm{diag}(\theta _1^{-\alpha },\cdots ,\theta _m^{-\alpha }), \;\; D_2:=\textrm{diag}(c_1,\cdots ,c_m),\;\; c_j=\frac{\Gamma (j+1)}{\Gamma (j+1-\alpha )}. \end{aligned}$$

(8)

Note that the coefficients of $D_2$ appear in $\partial _t^\alpha t^j=c_j\, t^{j-\alpha }$. Note also that, in view of $0<\theta _1<\ldots <\theta _m$, the Vandermonde-type matrix W has a positive determinant $\det (W)=\bigl (\prod _{j=1}^m \theta _j\bigr )\prod _{1\le i<j\le m}(\theta _j-\theta _i)>0$, so it is invertible.

With the above notations, (5) is equivalent to

$$\begin{aligned} \partial _t^\alpha U(x, \vec {\theta })+\tau ^\alpha \mathcal {L}U(x, \vec {\theta })=\vec {F}(x), \;\;\text{ where }\;\; \mathcal {L}U(x, \vec {\theta })=\mathcal {L}\vec {U}(x)=\mathcal {L}W \vec {V}(x), \end{aligned}$$

(9)

and where we still need to evaluate $\partial _t^\alpha U(x,\vec {\theta })$. For the latter, one has

$$\begin{aligned} \partial _t^\alpha U(x,t) =\sum _{j=1}^m v_j(x)\,\partial _t^\alpha t^j =\sum _{j=1}^m c_j\, t^{j-\alpha }\,v_j(x) = t^{-\alpha }\,T(t)\,D_2\,\vec {V}(x), \end{aligned}$$

so

$$\begin{aligned} \partial _t^\alpha U(x, \vec {\theta })=D_1WD_2\,\vec {V}(x). \end{aligned}$$

Substituting this in (9), we arrive at the following result.

Lemma 2

With the notations (6), (7), (8), the collocation scheme (5) is equivalent to

$$\begin{aligned} \bigl (D_1 WD_2+\tau ^\alpha \mathcal {L}W\bigr )\,\vec {V}(x) = \vec {F}(x). \end{aligned}$$

(10)

Remark 3

(Case $\mathcal {L}=\mathcal {L}(t)$) The matrix representation (10) is valid only if the spatial operator $\mathcal {L}$ is independent of t. If $\mathcal {L}=\mathcal {L}(t)$, then $\mathcal {L}$ in (10) should be replaced by the diagonal matrix $\textrm{diag}(\mathcal {L}(\theta _1),\mathcal {L}(\theta _2),\cdots ,\mathcal {L}(\theta _m))$.

2.1 Well-posedness for the Case $\mathcal {L}=c(t)$ Without Spatial Derivatives

In the case of a time-fractional ordinary differential equation of type (4) with $\mathcal {L}$ replaced by c(t), one needs to investigate the well-posedness of a version of (5) with $\mathcal {L}$ replaced by $\hat{c}(\theta _{\ell })$, where $\hat{c}(t):=c((t-t_{k-1})/\tau _k)$. Now, in view of Remark 3, the matrix representation (10) reduces to

$$\begin{aligned} \bigl (D_1 WD_2+\tau ^\alpha D_c W\bigr )\,\vec {V} = \vec {F}, \qquad D_c:=\textrm{diag}(\hat{c}(\theta _1),\cdots ,\hat{c}(\theta _m)), \end{aligned}$$

(11)

where $\vec {V}$ and $\vec {F}$ are x-independent, as well as the corresponding solution $U=U(t)$ of (5). Recall also that here the Vandermonde-type matrix W has a positive determinant and is invertible, as well as the diagonal matrices $D_1$ and $D_2$. Hence, the matrix equation (11) will have a unique solution if and only if the matrix $I+\tau ^\alpha (D_1 WD_2)^{-1}D_c W$ is invertible. A well-known sufficient condition for this is

$$\begin{aligned} \tau ^\alpha \Vert (D_1 WD_2)^{-1}D_c W\Vert <1, \end{aligned}$$

(12)

where $\Vert \cdot \Vert$ denotes any matrix norm.

Thus, for any bounded c(t), any $m\ge 1$, and any set of collocation points $\{\theta _\ell \}_{\ell =1}^m$, one can choose a sufficiently small $\tau$ to guarantee the well-posedness of (11).

Remark 4

Importantly, the above argument is not applicable to the collocation scheme (5) with an elliptic operator $\mathcal {L}$. For example, the simplest one-dimensional Laplace operator $\mathcal {L}=-\partial _x^2$ in the domain $\Omega =(0,1)$ has the set of eigenvalules $\{\lambda _n=(\pi n)^2\}_{n=1}^\infty$ and the corresponding basis of orthonormal eigenfunctions. Hence, an application of the eigenfunction expansion to the solution vector $\vec V(x)$ immediately implies that a version of (5) with $\mathcal {L}$ replaced by $\lambda _n$ needs to be well-posed $\forall \, n\ge 1$. Clearly, in this case one cannot satisfy a sufficient condition of type (12), which would take the form

$$\begin{aligned} \tau ^\alpha \,\lambda _n\,\Vert (D_1 WD_2)^{-1} W\Vert <1 \qquad \forall n\ge 1, \end{aligned}$$

(13)

in view of $\lambda _n\rightarrow \infty$ as $n\rightarrow \infty$. Hence, in this paper we explore alternative approaches to establishing the well-posedness of (5).

More generally, the eigenvalues of self-adjoint elliptic operators $\mathcal {L}$ with variable coefficients in $\Omega \subset \mathbb {R}^d$ (where $d\in \{1,2,3\}$) are also real and exhibit a similar behaviour $\lambda _n\rightarrow \infty$ as $n\rightarrow \infty$ [4, section 6.5.1], so the sufficient condition (13) simply cannot be satisfied in this case.

The situation somewhat improves once (5) is discretized in space, as then the operator $\mathcal {L}$ is replaced by a finite-dimensional discrete operator $\mathcal {L}_h$, the eigenvalues of which are bounded, so (13) can now be imposed, albeit it may be very restrictive. For example, for the standard finite difference discretization $\mathcal {L}_h$ of $\mathcal {L}=-\partial _x^2$ in the domain $\Omega =(0,1)$, it is well-known that $\max _{n}\lambda _n\approx 4\cdot DOF^{2}$, where DOF is the number of degrees of freedom in space. Furthermore, the maximal $\lambda _n$ may simply be unavailable for spatial discretizations of variable-coefficient elliptic operators in complex domains on possibly strongly non-uniform spatial meshes with local mesh refinements.

3 Well-posedness by Means of the Lax–Milgram Theorem

Let $D_0=\textrm{diag}(d_1,\cdots , d_m)$ be an arbitrary diagonal matrix with strictly positive diagonal elements. Note that a left multiplication of (10) by $W^{\top }D_0$ (where both W and $D_0$ are invertible) produces an equivalent system. Taking the inner product $\langle \cdot ,\cdot \rangle$ of the latter with an arbitrary $\vec V^*\in (H^1_0(\Omega ))^m$, in the sense of the $(L_2(\Omega ))^m$ space, yields a variational formulation of (10): Find $\vec V \in {(H^1_0(\Omega ))^m}$ such that

$$\begin{aligned} \mathcal {A}(\vec V, \vec V^*)= \langle W^{\top }D_0 D_1 WD_2\,\vec {V}, \vec V^* \rangle +\tau ^\alpha \langle W^{\top }D_0 \mathcal {L}W\vec V,\vec V^* \rangle = \langle W^{\top }D_0\vec {F},\vec {V}^*\rangle \nonumber \\ \end{aligned}$$

(14)

$\forall \, \vec V^*\in {(H^1_0(\Omega ))^m}$. The well-posedness of this problem can be established using the Lax–Milgram Theorem as follows.

Theorem 5

Suppose that the bilinear form $a(v,w):=\langle \mathcal {L}v, w\rangle$ on the space $H^1_0(\Omega )$ is bounded and coercive. Additionally, suppose that there exists a diagonal matrix D with strictly positive diagonal elements such that the symmetric matrix $W^{\top }D WD_2+(W^{\top }D WD_2)^{\top }$ is positive-semidefinite. Then the bilinear form $\mathcal {A}(\cdot , \cdot )$ on the space $(H^1_0(\Omega ))^m$ is also bounded and coercive for $D_0:=D D_1^{-1}$. If, additionally, $\vec F\in (H^{-1}(\Omega ))^m$, then there exists a unique solution to problem (14). Equivalently, if $\{F(\cdot , \theta _\ell )\}_{\ell =1}^m\in (H^{-1}(\Omega ))^m$, then (5) has a unique solution $\{U(\cdot , \theta _\ell )\}_{\ell =1}^m$ in $(H^1_0(\Omega ))^m$.

Proof

The boundedness and coercivity of $\mathcal {A}(\cdot , \cdot )$ follow from the boundedness and coercivity of $a(\cdot ,\cdot )$. In particular, for the coercivity, note that

$$\begin{aligned} \mathcal {A}(\vec V, \vec V)= \langle W^{\top }D_0 D_1 WD_2\,\vec {V}, \vec V \rangle +\tau ^\alpha \langle D_0 \mathcal {L}W\vec V, W\vec V \rangle . \end{aligned}$$

(15)

For the final term here, recalling that $\vec U=W\vec V$, one gets

$$\begin{aligned} \langle D_0 \mathcal {L}W\vec V, W\vec V \rangle =\langle D_0 \mathcal {L}\vec U, \vec U \rangle =\sum _{\ell =1}^m d_{\ell }\,a(U_\ell ,U_\ell ), \end{aligned}$$

where $\{d_\ell \}$ are strictly positive, so this term is coercive. Here we also used the equivalence of the norms of $\vec V$ and $\vec U=W\vec V$ in $(H^1_0(\Omega ))^m$ (as the matrix W is invertible).

Thus, for the coercivity of $\mathcal {A}(\cdot , \cdot )$, it remains to note that the quadratic form generated by the matrix $W^{\top }D_0 D_1 WD_2=W^{\top }D WD_2$ is positive-semidefinite, as the same quadratic form is also generated by the symmetric positive-semidefinite matrix $\frac{1}{2}[W^{\top }D WD_2+(W^{\top }D WD_2)^{\top }]$.

Finally, the existence and uniqueness of a solution to (14), or, equivalently, to (5), immediately follow by the Lax–Milgram Theorem (see, e.g., [1, section 2.7]). $\square$

Remark 6

(Case $\mathcal {L}=\mathcal {L}(t)$) Theorem 5 remains valid for a time-dependent $\mathcal {L}=\mathcal {L}(t)$ as long as $a(\cdot , \cdot )$ is coercive $\forall \,t>0$. The proof applies to this more general case with minimal changes, in view of Remark 3.

Remark 7

(Coercivity of $a(v,w):=\langle \mathcal {L}v, w\rangle$) One can easily check that for the coercivity of the bilinear form $a(v,w):=\langle \mathcal {L}v, w\rangle$ it suffices that the coefficients of $\mathcal {L}$ in (2) satisfy $a_k>0$ and $c-\frac{1}{2}\sum _{k=1}^d\partial _{x_k}\!b_k\ge 0$ in $\bar{\Omega }$.

Corollary 8

(Quadratic collocation scheme) If $m=2$, with the collocation points $\{\theta _1, 1\}$, for any $\theta _1\le \theta ^*:=1-\frac{1}{2}\alpha$, there exists a diagonal matrix D required by Theorem 5. Hence, under the other conditions of this theorem, there exists a unique solution to (5) in $(H^1_0(\Omega ))^2$.

Proof

Recall that for $m=2$, one has $0<\theta _1<\theta _2=1$. Let $D:=\textrm{diag}(1,p)$ with some $p>0$. Without loss of generality, we shall replace $D_2$, defined in (8), by its normalized version $\hat{D}_2:=D_2/c_1=\textrm{diag}(1,C)$, where

$$\begin{aligned} C:=\frac{c_2}{c_1}=\frac{\Gamma (3)}{\Gamma (3-\alpha )}\frac{\Gamma (2-\alpha )}{\Gamma (2)} =\frac{2}{2-\alpha }\in (1,2). \end{aligned}$$

(16)

Next, using the definition of W in (7), and setting $\theta :=\theta _1$ to simplify the presentation, one gets

$$\begin{aligned} W^{\top }D W\hat{D}_2 = \begin{pmatrix}\theta \,\, &{}1\,\,\\ \theta ^2 &{} 1^2 \end{pmatrix} \cdot \begin{pmatrix}1&{}0\\ 0&{}p \end{pmatrix} \cdot \begin{pmatrix}\theta &{} \theta ^2\\ 1 &{} 1^2 \end{pmatrix} \cdot \begin{pmatrix}1&{}0\\ 0&{}C \end{pmatrix} = \begin{pmatrix}\theta ^2+p &{} \ C(\theta ^3+p)\\ \theta ^3+p &{} C(\theta ^4+p) \end{pmatrix}. \end{aligned}$$

For the symmetric matrix $W^{\top }D W\hat{D}_2+(W^{\top }D W\hat{D}_2)^\top$ to be positive-semidefinite, by the Sylvester’s criterion, we need its derterminant to be non-negative (while its diagonal elements are clearly positive). Thus we need to check that, for some $p>0$,

$$\begin{aligned} \det \begin{pmatrix}2(\theta ^2+p) &{} \ (1+C)(\theta ^3+p)\\ (1+C)(\theta ^3+p) &{} 2C(\theta ^4+p) \end{pmatrix}\ge 0. \end{aligned}$$

This is equivalent to

$$\begin{aligned} (1+C)^2\, (\theta ^3+p)^2\le 4C\,(\theta ^2+p)\,(\theta ^4+p). \end{aligned}$$

Dividing the above by $4C\, \theta ^6$, and using the notation $P:=p/\theta ^{3}$ and $\psi (s):=s+s^{-1}-2=\frac{(s-1)^2}{s}$, yields

$$\begin{aligned} \bigl [1+{\textstyle \frac{1}{4}}\psi (C)\bigr ]\, (1+P)^2\le (\theta ^{-1}+P)\,(\theta +P), \end{aligned}$$

where we also used the observation that $\frac{(1+C)^2}{4C}=1+\frac{(C-1)^2}{4C}=1+\frac{1}{4}\psi (C)$. Next, a calculation yields $(\theta ^{-1}+P)\,(\theta +P)=(1+P)^2 +P\psi (\theta )$, so one gets

$$\begin{aligned} (1+P)^2+{\textstyle \frac{1}{4}}\psi (C)\,(1+P)^2 \le (1+P)^2 +P\psi (\theta ), \end{aligned}$$

or

$$\begin{aligned} (1+P)^2\le 4P\,\frac{\psi (\theta )}{\psi (C)}. \end{aligned}$$

Setting $\kappa :={\psi (\theta )}/{\psi (C)}$, the above is equivalent to $(P-1)^2\le 4(\kappa -1)P$. For any positive P to satisfy this condition, it is necessary and sufficient that $\kappa \ge 1$ (in which case, one may choose $P=1$, which corresponds to $p=\theta ^3$) Thus for the existence of a diagonal matrix D required by Theorem 5, we need to impose ${\psi (\theta )}\ge {\psi (C)}$. Finally, note that $C> 1$, while $\psi (\theta )=\psi (\theta ^{-1})$ and $\theta ^{-1}>1$. As $\psi (s)$ is increasing for $s>1$, we impose $\theta ^{-1}\ge C$, or $\theta _1=\theta \le \theta ^*=\frac{2-\alpha }{2}=1-\frac{1}{2}\alpha$. $\square$

Remark 9

(Case $\theta _2<1$) In view of Remark 1, Corollary 8 applies to the case $m=2$, with the collocation points $0=\theta _0<\theta _1<\theta _2\le 1$ under the condition $\theta _1\le \theta _2\left( 1-\frac{1}{2}\alpha \right)$.

Corollary 10

(Galerkin finite element discretization) The existence and uniqueness results of Theorem 5 and Corollary 8 remain valid for a version of (14) with $(H^1_0(\Omega ))^m$ replaced by $(S_h)^m$, where $S_h$ is a finite-dimensional subspace of $H^1_0(\Omega )$. Equivalently, they apply to the corresponding spatial discretization of (5).

For higher-order collocation schemes with $m\ge 3$, the construction of a suitable matrix D (as described in the proof of Corollary 8) requires $m-1$ positive parameters, so such constructions are unclear for general $\alpha \in (0,1)$ and $\{\theta _\ell \}_{\ell =1}^m$. In this case, D may still be constructed for particular values of $\alpha$ and $\{\theta _\ell \}$ of interest (then semi-computational techniques, such as employed in section 4.2, may be useful). Furthermore, in the next section 4, we shall describe alternative approaches to establishing the well-posedness of (5), which can be easily applied for any m of interest.

4 Well-posedness by Means of an Eigenvalue Test

Throughout this section, we shall assume that the time-independent operator $\mathcal {L}$ has a set of real positive eigenvalues $0<\lambda _1\le \lambda _2\le \lambda _3\le \ldots$ and a corresponding basis of orthonormal eigenfunctions $\{\psi _n(x)\}_{n=1}^\infty$. This assumption is immediately satisfied if $\mathcal {L}$ in (2) is self-adjoint (i.e. $b_k=0$ for $k=1 {,}\ldots ,d$) and $c\ge 0$; see, e.g., [4, section 6.5.1] for further details. (Even if $\mathcal {L}$ is non-self-adjoint, the problem can sometimes, as, e.g., for $\mathcal {L}= -\sum _{k=1}^d \bigl \{\partial ^2_{x_k} + (\partial _{x_k}\! B(x))\, \partial _{x_k} \bigr \}+c(x)$ [4, problem 8.6.2], be reduced to the self-adjoint case.)

The above assumption essentially allows us to employ the method of separation of variables. Thus, the well-posedness of problem (10) can be investigated using an eigenfunction expansion of its solution $\vec {V}(x)$.

Recall (10) and rewrite it using $\vec U=W\vec V$ as

$$\begin{aligned} \bigl (D_1 WD_2W^{-1}+\tau ^\alpha \mathcal {L}\bigr )\,\vec {U}(x) = \vec {F}(x). \end{aligned}$$

(17)

Next, using the eigenfunction expansions $\vec {U}(x)=\sum _{ {n}=1}^\infty \vec {U}_n\, \psi _n(x)$ and $\vec {F}(x)=\sum _{n=1}^\infty \vec {F}_n \psi _n(x)$, one reduces the above to the following matrix equations for vectors $\vec {U}_n$ $\forall \,n\ge 1$:

$$\begin{aligned} \bigl (D_1 WD_2W^{-1}+\tau ^\alpha \lambda _n {I} \bigr )\,\vec {U}_n = \vec {F}_n. \end{aligned}$$

(18)

For each n, we get an $m\times m$ matrix equation, the well-posedness of which is addressed by the following elementary lemma.

Lemma 11

Set $M:=D_1 WD_2W^{-1}$ and $R(\lambda ;M):=(M+\lambda {I})^{-1}$. Then

$$\begin{aligned} 0<\Vert R(\lambda ;M)\Vert \le C_M\;\;\;\forall \lambda \ge 0\quad \text{ and }\quad \lim _{\lambda \rightarrow \infty }\bigl \{\lambda \,\Vert R(\lambda ;M)\Vert \bigr \}=1, \end{aligned}$$

(19)

with some positive constant $C_M=C_M(\alpha , m, \{\theta _\ell \})$ (where $\Vert \cdot \Vert$ denotes the matrix norm induced by any vector norm in $\mathbb {R}^m$), if and only if M has no real negative eigenvalues.

Proof

The final assertion in (19) is obvious, in view of $R(\lambda \,;M)=\lambda ^{-1}(\lambda ^{-1}M+I)^{-1}\rightarrow \lambda ^{-1}I$ as $\lambda \rightarrow \infty$. Next, if M has a real negative eigenvalue $-\lambda ^*$, then $M+\lambda ^* {I}$ is a singular matrix, so $R(\lambda ^*;M)$ is not defined, so (19) is not true. If M has no real negative eigenvalues, then $R(\lambda ;M)$ is defined $\forall \,\lambda >0$. It is also defined for $\lambda =0$, as $M=D_1 WD_2W^{-1}$ is invertible (as discussed in section 2). Furthermore, $R(\lambda ;M)\,\vec v=0$ if and only if $\vec v=0$, so $\Vert R(\lambda \,;M)\Vert >0$ $\forall \, \lambda \ge 0$. As $\Vert R(\lambda \,;M)\Vert$ is a continuous positive function of $\lambda$ on $[0,\infty )$, which decays as $\lambda \rightarrow \infty$, it has to be bounded by some positive constant $C_M$. $\square$

As problem (17) (or, equivalently, (5)) is reduced to the set of problems (18), the above lemma immediately yields sufficient conditions for the well-posedness as long as $\vec {F}(x)$ allows an eigenfunction expansion, in which case there exists $\vec U(x)$ (the regularity of which follows from (19)). Thus, we get the following result.

Theorem 12

Suppose that the operator $\mathcal {L}$ has a set of real positive eigenvalues and a corresponding basis of orthonormal eigenfunctions, and $\vec {F}(x)$ is sufficiently smooth. If, additionally, the matrix $M=D_1 WD_2W^{-1}$ has no real negative eigenvalues, then there exists a unique solution to problem (17), or, equivalently, to problem (5).

Remark 13

(Full discretizations) The existence and uniqueness result of Theorem 12, as well as its important corollary presented as Theorem 14 below, remains valid for any spatial discretization of (17), or, equivalently, of problem (5), as long as the corresponding discrete operator $\mathcal {L}_h$ (which replaces $\mathcal {L}$ in (5) and, hence, (17)) has a set of real positive eigenvalues and a corresponding basis of orthonormal eigenvectors.

This includes standard Galerkin finite element discretizations in space. Indeed, as shown, e.g., in [18, chapter 6] (by representing the eigenvalues via the Rayleigh quotient), not only all eigenvalues $\{\lambda _n^h\}$ of the corresponding discrete operator $\mathcal {L}_h$ are real positive, but they also satisfy $\lambda _n^h\ge \lambda _n\ge \lambda _1>0$. The existence of an eigenvector basis follows from $\mathcal {L}_h$ being self-adjoint, i.e. being associated with a symmetric real-valued matrix.

Similarly, finite difference discretizations of spatial self-adjoint operators (such as discussed in [10, section 4]) typically satisfy the discrete maximum principle (which immediately excludes real negative and zero eigenvalues), and are associated with symmetric real-valued matrices (which mimics $\mathcal {L}$ being self-adjoint). Hence, all discrete eigenvalues are real positive, and there is a corresponding basis of eigenvectors. So Theorem 12 is applicable to such full discretizations as well.

To apply the above theorem, one needs to check whether the matrix $M=D_1 WD_2W^{-1}$ has no real negative eigenvalues. Clearly, M is a fixed matrix of a relatively small size $m\times m$; however, it depends on m, $\alpha$, and the set of collocation points $\{\theta _\ell \}$. Below we shall investigate the spectrum of M, first, analytically, and then using a semi-computational approach. Note also that in practical computations, the spectrum of M may be easily checked computationally for any fixed m, $\alpha$, and $\{\theta _\ell \}$ of interest.

4.1 An Analytical Approach

To ensure that $M=D_1 WD_2W^{-1}$ has no real negative eigenvalues, one does not necessarily need to evaluate the eigenvalues of this matrix. Instead, the coefficients of the characteristic polynomial may be used. In particular, for a characteristic polynomial of the form $\sum _{j=0}^m (-\lambda )^j a_j$ to have no real negative roots, it suffices to check that $a_j>0$ $\forall \,j=0 {,}\ldots ,m$. (We also note the stronger, and more intricate, Routh-Hurwitz stability criterion [7, Vol. 2, Sec. 6], which gives necessary and sufficient conditions for all roots of a given polynomial to have positive real parts.)

The above observation leads us to the main result of the paper on the existence and uniqueness of collocation solutions for any $\alpha \in (0,1)$, any $m\ge 1$, and any set of collocation points $\{\theta _\ell \}_{\ell =1}^m$.

Theorem 14

For any $m\ge 1$, no eigenvalue of the matrix $M=D_1 WD_2W^{-1}$ is real negative. Hence, Theorem 12 applies for any $\alpha \in (0,1)$ and any set of collocation points $0<\theta _1<\theta _2< \dots < \theta _m {\le 1}$.

Proof

Recalling the definitions of W, $D_1$, and $D_2$ from (7) and (8), let

$$\begin{aligned} M_\alpha :=D_1W D_2&=\begin{pmatrix}[c] c_1 \theta _1^{1-\alpha } &{} c_2 \theta _1^{2-\alpha } &{} \cdots &{} c_m \theta _1^{m-\alpha }\\ c_1 \theta _2^{1-\alpha } &{} c_2 \theta _2^{1-\alpha }&{} \cdots &{} c_m \theta _2^{m-\alpha }\\ \vdots &{} \vdots &{} &{} \vdots \\ c_1 \theta _m^{1-\alpha } &{} c_2 \theta _m^{1-\alpha }&{} \cdots &{} c_m \theta _m^{m-\alpha } \end{pmatrix},&W = \begin{pmatrix}\theta _1 &{} \theta _1^2 &{} \cdots &{}\theta _1^m\\ \theta _2 &{} \theta _2^2 &{} \cdots &{}\theta _2^m\\ \vdots \ {} &{}\vdots \ {} &{}&{} \vdots \ \\ \theta _m &{} \theta _m^2 &{}\cdots &{} \theta _m^m \end{pmatrix}. \end{aligned}$$

The eigenvalues of the matrix $M=D_1 WD_2W^{-1}$ are the roots of the characteristic polynomial of the form

$$\begin{aligned} \det (M_\alpha -\lambda W)=:\sum _{j=0}^m (-\lambda )^j a_j, \end{aligned}$$

(20)

while to show that no eigenvalue of the matrix $M=D_1 WD_2W^{-1}$ is real negative, it suffices to check that $a_j>0$ $\forall \,j=0 {,}\ldots ,m$.

Note that the coefficients $\{a_j\}$ in (20) can be represented via determinants of certain $m\times m$ matrices, denoted $M_\mathcal {I}$, where $\mathcal I$ is a subset of $\{1,\ldots ,m\}$, constructed column by column, using the corresponding kth column $M_\alpha ^k$ of $M_\alpha$ if $k\not \in \mathcal I$, or the kth column $W^k$ of W if $k\in \mathcal I$:

$$\begin{aligned} M_\mathcal {I}^{k}:= {\left\{ \begin{array}{ll} M_\alpha ^k &{} \text{ if }\;\;k\not \in \mathcal {I}\\ W^k &{}\text{ if }\;\; k\in \mathcal I \end{array}\right. } \qquad \text{ for } \text{ any }\;\; \mathcal {I}\subseteq \{1,\ldots , m\},\quad k=1,\ldots , m. \end{aligned}$$

For example, for $a_0$ and $a_m$ we immediately have:

$$\begin{aligned} a_m = \det W = \det M_{\{1,\ldots ,m\}} \quad \text {and}\quad a_0 = \det M_\alpha = \det M_{\emptyset }. \end{aligned}$$

For the other coefficients, note that if the kth column $A^k$ of some matrix A allows a representation $A^k=B^k-\lambda C^k$ for some column vectors $B^k$ and $C^k$, then

$$\begin{aligned}&\det \Bigl (A^1 \cdots A^{k-1}A^kA^{k+1}\cdots A^m\Bigr )\\ {}&\quad \qquad {}= \det \Bigl (A^1 \cdots A^{k-1}B^kA^{k+1}\cdots A^m\Bigr )-\lambda \, \det \Bigl (A^1 \cdots A^{k-1}C^kA^{k+1}\cdots A^m\Bigr ), \end{aligned}$$

which is easily checked using the kth column expansion. Using this property for all columns in $M_\alpha -\lambda W$, one gets

$$\begin{aligned} \det (M_\alpha -\lambda W)= \sum _{j=0}^m (-\lambda )^{j}\,\Bigl \{\sum _{\#\mathcal {I}=j}\! \det M_\mathcal {I}\Bigr \}, \end{aligned}$$

(21)

where $\#\mathcal {I}$ denotes the number of elements in any index subset $\mathcal {I}\subseteq \{1,\ldots , m\}$. (For $m=2, 3$, this is elaborated in Remark 15 below.)

Hence, to show that all coefficients $\{a_j\}$ in (20) are positive, and, thus, to complete the proof, it remains to check that $\det M_\mathcal {I}>0$ for any index subset $\mathcal {I}$. For the latter, recalling the columns $M_\alpha$ and W, and the construction of $M_\mathcal {I}$, one concludes that

$$\begin{aligned} \det M_\mathcal {I} = \Bigl (\prod _{k\not \in \mathcal {I}} c_k \Bigr )\, \det \begin{pmatrix}\theta _1^{\beta _1} &{} \theta _1^{\beta _2} &{} \cdots &{}\theta _1^{\beta _m}\\ \theta _2^{\beta _1} &{} \theta _2^{\beta _2} &{} \cdots &{}\theta _2^{\beta _m}\\ \vdots \ {} &{}\vdots \ {} &{}&{} \vdots \ \\ \theta _m^{\beta _1} &{} \theta _m^{\beta _2} &{}\cdots &{} \theta _m^{\beta _m} \end{pmatrix}, \qquad \beta _k:= {\left\{ \begin{array}{ll} k-\alpha &{} \text{ if }\;\;k\not \in \mathcal {I},\\ k &{}\text{ if }\;\; k\in \mathcal I. \end{array}\right. } \end{aligned}$$

(22)

Recall that, by (8), all $c_k>0$, so the positivity of $\det M_\mathcal {I}$ is equivalent to the positivity of the above determinant involving $0<\beta _1<\beta _2<\dots <\beta _m$ and $0<\theta _1<\theta _2<\dots <\theta _m$. This is, in fact, the determinant of a so-called generalised Vandermonde matrix [8], the positivity of which is established in [17, 20]. The desired assertion that $\det M_{\mathcal I}>0$ follows, which completes the proof. $\square$

Remark 15

(Characteristic polynomial (20) for $m=2,3$) To illustrate the representation of type (21) in the above proof, note that for $m=2$ it simplifies to

$$\begin{aligned} \det (M_\alpha -\lambda W)&= \lambda ^2\begin{vmatrix}\theta _1&\theta _1^2\\ \theta _2&\theta _2^2 \end{vmatrix} -\lambda \left( \begin{vmatrix}\theta _1&c_2\theta _1^{2-\alpha }\\ \theta _2&c_2\theta _2^{2-\alpha } \end{vmatrix} +\begin{vmatrix}c_1\theta _1^{1-\alpha }&\theta _1^2\\ c_1\theta _2^{1-\alpha }&\theta _2^2 \end{vmatrix}\right) +\begin{vmatrix}c_1\theta _1^{1-\alpha }&c_2\theta _1^{2-\alpha }\\ c_1\theta _2^{1-\alpha }&c_2\theta _2^{2-\alpha } \end{vmatrix}\\&=\lambda ^2\,\Bigl [\theta _1\theta _2(\theta _2-\theta _1)\Bigr ]\\&\quad -\lambda \Bigl [c_2\,\theta _1\theta _2(\theta _2^{1-\alpha }-\theta _1^{1-\alpha }) +c_1(\theta _1\theta _2)^{1-\alpha }(\theta _2^{1+\alpha }-\theta _1^{1+\alpha })\Bigr ]\\&\quad +\Bigl [c_1c_2(\theta _1\theta _2)^{1-\alpha }(\theta _2-\theta _1)\Bigr ], \end{aligned}$$

so we immediately see the coefficients (in square brackets) are positive for any $\alpha \in (0,1)$ and $0<\theta _1<\theta _2$.

For $m=3$, the cubic polynomial $\det (M_\alpha -\lambda W)$ in (20) reads as $(-\lambda )^3a_3+(-\lambda )^2a_2+(-\lambda )a_1+a_0$, where

$$\begin{aligned} a_3=&\begin{vmatrix}\theta _1&\theta _1^2&\theta _1^3\\ \theta _2&\theta _2^2&\theta _2^3\\ \theta _3&\theta _3^2&\theta _3^3 \end{vmatrix}, \qquad \quad a_0= \begin{vmatrix}c_1\theta _1^{1-\alpha }&c_2\theta _1^{2-\alpha }&c_3\theta _1^{3-\alpha }\\ c_1\theta _2^{1-\alpha }&c_2\theta _2^{2-\alpha }&c_3\theta _2^{3-\alpha }\\ c_1\theta _3^{1-\alpha }&c_2\theta _3^{2-\alpha }&c_3\theta _3^{3-\alpha } \end{vmatrix}, \\ a_2=&\begin{vmatrix}c_1\theta _1^{1-\alpha }&\theta _1^2&\theta _1^3\\ c_1\theta _2^{1-\alpha }&\theta _2^2&\theta _2^3\\ c_1\theta _3^{1-\alpha }&\theta _3^2&\theta _3^3 \end{vmatrix} +\begin{vmatrix}\theta _1&c_2\theta _1^{2-\alpha }&\theta _1^3\\ \theta _2&c_2\theta _2^{2-\alpha }&\theta _2^3\\ \theta _3&c_2\theta _3^{2-\alpha }&\theta _3^3 \end{vmatrix} +\begin{vmatrix}\theta _1&\theta _1^2&c_3\theta _1^{3-\alpha }\\ \theta _2&\theta _2^2&c_3\theta _2^{3-\alpha }\\ \theta _3&\theta _3^2&c_3\theta _3^{3-\alpha } \end{vmatrix}, \\ a_1=&\begin{vmatrix}\theta _1&c_2\theta _1^{2-\alpha }&c_3\theta _1^{3-\alpha }\\ \theta _2&c_2\theta _2^{2-\alpha }&c_3\theta _2^{3-\alpha }\\ \theta _3&c_2\theta _3^{2-\alpha }&c_3\theta _3^{3-\alpha } \end{vmatrix} +\begin{vmatrix}c_1\theta _1^{1-\alpha }&\theta _1^2&c_3\theta _1^{3-\alpha }\\ c_1\theta _2^{1-\alpha }&\theta _2^2&c_3\theta _2^{3-\alpha }\\ c_1\theta _3^{1-\alpha }&\theta _3^2&c_3\theta _3^{3-\alpha } \end{vmatrix} +\begin{vmatrix}c_1\theta _1^{1-\alpha }&c_2\theta _1^{2-\alpha }&\theta _1^3\\ c_1\theta _2^{1-\alpha }&c_2\theta _2^{2-\alpha }&\theta _2^3\\ c_1\theta _3^{1-\alpha }&c_2\theta _3^{2-\alpha }&\theta _3^3 \end{vmatrix}. \end{aligned}$$

After removing common positive factors in all columns and rows, and setting $\theta _3=1$ (for $\theta _3<1$ see Remark 1), all eight above determinants reduce to the following general determinant, where $\beta _2\in \{1-\alpha ,1,1+ \alpha \}$, $\beta _3\in \{2-\alpha ,2,2+\alpha \}$, and so $0<\beta _2<\beta _3$:

$$\begin{aligned} \begin{vmatrix} 1&\,\theta _1^{\beta _2}&\,\theta _1^{\beta _3}\\ 1&\theta _2^{\beta _2}&\theta _2^{\beta _3}\\ 1&1&1 \end{vmatrix} = \begin{vmatrix} 1&\ \theta _1^{\beta _2}-1&\ \theta _1^{\beta _3}-1\\ 1&\theta _2^{\beta _2}-1&\theta _2^{\beta _3}-1\\ 1&0&0 \end{vmatrix} = (1-\theta _1^{\beta _2})(1-\theta _2^{\beta _2}) \left( \frac{1-\theta _2^{\beta _3}}{1-\theta _2^{\beta _2}}-\frac{1-\theta _1^{\beta _3}}{1-\theta _1^{\beta _2}} \right) . \end{aligned}$$

Although the positivity of the above determinant follows from [17, 20], one can show this directly by checking that the function $g(s):=\frac{1-s^{\beta }}{1-s}$, where $\beta :=\beta _3/\beta _2>1$, is increasing $\forall \,s\in (0,1)$. Note that $g'(s)>0$ is equivalent to $\beta s^{\beta -1}(1-s)<1-s^\beta$, or $\hat{g}(s):=\beta s^{\beta -1}-(\beta -1)s^\beta <1$. The latter property follows from $\hat{g}(1)=1$ combined with $\hat{g}'(s):=\beta (\beta -1) s^{\beta -2}(1-s)>0$ for $s\in (0,1)$.

Remark 16

(Case $\alpha =1$) Setting $\alpha =1$ in (1) and throughout our evaluations, the discretization (17) becomes the collocation method for the classical parabolic differential equation

$$\begin{aligned} \partial _t u +\mathcal {L}u = f(x,t). \end{aligned}$$

Note that in this case (8) yields $c_j=\frac{\Gamma (j+1)}{\Gamma (j+1-\alpha )}=j$, while (21) and (22) remain unchanged. However, now we only have $\beta _1\le \beta _2\le \dots \le \beta _m$, and if there is one pair of equal powers, the corresponding determinant $\det M_\mathcal {I}$ is zero. Nevertheless, the sum $\sum _{\#{\mathcal I}=j}\! \det M_\mathcal {I}$ in (21) for each $j=1,\ldots , m$ includes exactly one positive determinant, which corresponds to $\mathcal {I}=\{m-j+1, \ldots , m\}$ (understood as $\mathcal {I}=\emptyset$ if $j=0$). Hence, each such sum is positive, so $a_j>0$ $\forall \, j=0,\ldots ,m$, so Theorem 14 remains valid for the classical parabolic case $\alpha =1$ with any $m\ge 1$ and any set of collocation points $0<\theta _1<\theta _2< \dots < \theta _m {\le 1}$.

4.2 A Semi-computational Approach

In addition to Theorem 14, which guarantees that the $m\times m$ matrix $M=D_1 WD_2W^{-1}$ from Theorem 12 has no real negative eigenvalues (and, hence, existence and uniqueness of collocation solutions for any $m\ge 1$ and any set of collocation points $\{ \theta _\ell \}$), it may be of interest to have more precise information about the eigenvalues of this matrix (in terms of where they lie on the complex plain). In most practical situations, one is interested in a particular distribution of the collocations points (such as equidistant points), in which case all eigenvalues of M for all $\alpha \in (0,1)$ are easily computable, as we now describe.

Given the order m of the collocation method and a particular distribution of the collocations points, the computation of approximate eigenvalues for the entire range $\alpha \in (0,1)$ can be easily performed using designated commands typically available in high-level programming languages (such as the command eig in Matlab). Here we provide a Matlab script, see Script 1, that computes, for any $\alpha$ and m, all eigenvalues of $M=D_1 WD_2W^{-1}$. Recall that Theorem 12 requires that this matrix has no real negative eigenvalues. Thus, such a code allows one to immediately check the applicability of the well-posedness result of Theorem 12 for any fixed m and collocation point set $\{\theta _\ell \}$ of interest (the latter is denoted by t in Script 1).

Fig. 1

Eigenvalues for collocation methods using Chebyshev points $m\in \{2,3,5,8\}$ (left to right) and real parts (top), imaginary parts (bottom)

Fig. 2

Eigenvalues for collocation methods using equidistant points and $m\in \{2,3,5,8\}$ (left to right) and real parts (top), imaginary parts (bottom)

Fig. 3

Eigenvalues for collocation methods using Lobatto points and $m\in \{2,3,5,8\}$ (left to right) and real parts (top), imaginary parts (bottom)

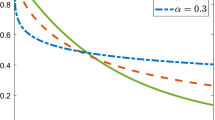
In Figs. 1, 2, 3 we plot the eigenvalues for $m\in \{2,3,5,8\}$ with, respectively, Chebyshev, equidistant, and Lobatto distributions of collocation points.

In addition to the presented graphs, we have numerically investigated the eigenvalues for $m\le 20$ and can report the following observations.

• None of the eigenvalues is a real negative number whether Chebyshev, Lobatto, or equidistant collocation point sets are used for $m\le 20$.

• If either Chebyshev or Lobatto collocation point sets are used for $m\le 20$, not only there are no real negative eigenvalues, but the real parts of all eigenvalues are positive.

• For equidistant collocation points we observe some eigenvalues with negative real parts for some m; see, e.g., the case $m=8$ in Fig. 2.

• For odd m one observes exactly one positive eigenvalue, all others are complex-conjugate pairs, while for even m we only have complex-conjugate pairs.

Overall, the above observations confirm the well-posedness of the considered collocation scheme for three popular distributions of collocation points for all $m\le 20$.

5 Semilinear Case

Consider a semilinear version of (1) of the form

$$\begin{aligned} \partial _t^{\alpha }u+\mathcal {L}u=f(x,t,u)\qquad \text{ where }\;\; |\partial _uf(\cdot ,\cdot ,\cdot )|\le \mu \;\;\text{ in }\;\Omega \times (0,T]\times \mathbb {R}, \end{aligned}$$

(23)

for some positive constant $\mu$. Without loss of generality, we shall assume that $c(x)=0$ in the definition (2) of $\mathcal {L}$ (as the term c(x)u can now be included in the semilinear term f(x, t, u)).

For the above semilinear equation, the collocation method of type (4) reads as

$$\begin{aligned} (\partial _t^\alpha +\mathcal {L})\,U(x, t^\ell _k)=f(x, t_k^\ell , U(x, t^\ell _k))\quad \text{ for }\;\; x\in \Omega ,\;\; \ell \in \{1,\ldots , m\},\;\;k\ge 1. \end{aligned}$$

(24)

Assuming that the above system has a solution, a standard linearization yields

$$\begin{aligned} f(x, t_k^\ell , U(x, t^\ell _k))=f(x, t_k^\ell , 0)+c(x,t^\ell _k)\,U(x, t^\ell _k), \end{aligned}$$

where $|c(x,t^\ell _k)|\le \mu$, so (24) shows even more resemblance with (4):

$$\begin{aligned} (\partial _t^\alpha +\mathcal {L}-c(x,t^\ell _k))\,U(x, t^\ell _k)=f(x, t_k^\ell , 0). \end{aligned}$$

Hence, recalling Lemma 2 and Remark 3, we arrive at the following version of (10) for $\vec V=\vec V(x)=W^{-1}\vec U(x)$:

$$\begin{aligned} \bigl (D_1 WD_2+\tau ^\alpha \mathcal {L}W\bigr )\,\vec {V} = \vec {\mathcal {F}}\vec U, \qquad \;\; \vec U = W \vec {V}, \end{aligned}$$

(25)

with $\vec {\mathcal {F}}\vec U=\vec {F}+\tau ^\alpha D_c \vec {U}$, where $\vec {F}=\vec {F}(x)$ remains as in (10) except for it is now defined using $f(\cdot ,\cdot , 0)$ in place of $f(\cdot ,\cdot )$, while

$$\begin{aligned} D_c:=\textrm{diag}(\hat{c}(x,\theta _1),\cdots ,\hat{c}(x,\theta _m)), \qquad \hat{c}(\cdot , t):=c(\cdot ,(t-t_{k-1})/\tau _k). \end{aligned}$$

The similarity stops here, as we cannot assume the positivity of $\hat{c}$, and instead rely on $|\hat{c}|\le \mu$ (not to mention that $D_c$ also depends on $\vec U$).

Note also that $\vec {\mathcal {F}}$ satisfies $\vec {\mathcal {F}}\vec U-\vec {\mathcal {F}}\vec U^*=\tau ^\alpha D_c^*(\vec U-\vec U^*)$ $\forall \, \vec U,\,\vec U^*\in (L_2(\Omega ))^m$, where $D_c^*$ is an $m\times m$ diagonal matrix, all elements of which satisfy $|\hat{c}^*_j(x)|\le \mu$.

Hence, a version of Theorem 5 remains applicable under the stronger condition that the matrix $W^{\top }D WD_2+(W^{\top }D WD_2)^{\top }$ is positive-definite (rather that positive-semidefinite), and the additional condition $\mu \tau ^\alpha <C_\mathcal {A}$, where the constant $C_\mathcal {A}$ is related to the coercivity of the first term in (15). (Note also that now in Corollary 8 (for $m=2$) we need to impose the strict inequality $\theta _1<\theta ^*=1-\frac{1}{2}\alpha$.)

To be more precise, $\tau$ is assumed sufficiently small to ensure that $\tau ^\alpha \mu \langle D_0 W\vec V, W\vec V \rangle$ is strictly dominated by the first term in (15). Thus, for some $\epsilon >0$ one has $\mathcal {A}(\vec V, \vec V)\ge (1+\epsilon )\,\tau ^\alpha \mu \langle D_0 \vec U, \vec U \rangle$. Then one can show that the operator $(D_1 WD_2W^{-1}+\tau ^\alpha \mathcal {L})^{-1}\vec {\mathcal {F}}$ is a strict contraction on $(L_2(\Omega ))^m$ (in the norm induced by the $m\times m$ matrix $D_0$), so Banach’s fixed point theorem [4, section 9.2.1] yields existence and uniqueness of a solution $\vec U$ (for the regularity of which one can use the original Theorem 5).

For the applicability of Theorem 12, rewrite (25) as $(M+\tau ^\alpha \mathcal {L})\vec U=\vec {\mathcal {F}}\vec U$, where $M=D_1 WD_2W^{-1}$. Now, in view of (19), $\tau ^\alpha \mu C_M<1$ guarantees that the operator $(M+\tau ^\alpha \mathcal {L})^{-1}\vec {\mathcal {F}}=R(\tau ^\alpha \mathcal {L};M)\vec {\mathcal {F}}$ is a strict contraction on $(L_2(\Omega ))^m$, so Banach’s fixed point theorem [4, section 9.2.1] again yields existence and uniqueness of a solution $\vec U$ in this case.

6 Conclusion

We have considered continuous collocation discretizations in time for time-fractional parabolic equations with a Caputo time derivative of order $\alpha \in (0,1)$. For such discretizations, sufficient conditions for existence and uniqueness of their solutions are obtained using two approaches: the Lax–Milgram Theorem and the eigenfunction expansion; see Theorems 5 and 12. The resulting sufficient conditions, which involve certain $m\times m$ matrices, are verified both analytically, for all $m\ge 1$ and all sets of collocation points (see Theorem 14), and computationally, for three popular distributions of collocation points and all $m\le 20$. Furthermore, the above results are extended to the semilinear case.