An $\alpha$-Robust and Second-Order Accurate Scheme for a Subdiffusion Equation

Abstract

We investigate a second-order accurate time-stepping scheme for solving a time-fractional diffusion equation with a Caputo derivative of order $\alpha \in (0,1)$. The basic idea of our scheme is based on local integration followed by linear interpolation. It reduces to the standard Crank–Nicolson scheme in the classical diffusion case, that is, as $\alpha \rightarrow 1$. Using a novel approach, we show that the proposed scheme is $\alpha$-robust and second-order accurate in the $L^2(L^2)$-norm, assuming a suitable time-graded mesh. For completeness, we use the Galerkin finite element method for the spatial discretization and discuss the error analysis under reasonable regularity assumptions on the given data. Some numerical results are presented at the end.

1 Introduction

We shall approximate the solution of the time-fractional diffusion equation

$$\begin{aligned} \partial _t^{\alpha } u({\varvec{x}},t)+\mathcal {A} u({\varvec{x}},t)=f({\varvec{x}},t) \quad \text {for }({\varvec{x}},t)\in \Omega \times (0,T], \end{aligned}$$

(1.1)

subject to homogeneous Dirichlet boundary conditions, that is, $u({\varvec{x}},t)= 0$ on $\partial \Omega \times (0,T]$, with $u({\varvec{x}},0)=u_0({\varvec{x}})$ at the initial time level $t=0.$ The spatial domain $\Omega \subset {\mathbb {R}}^d$ (with $d=1$, 2, 3) is a convex polyhedron, $0<\alpha <1$, the time fractional Caputo derivative

$$\begin{aligned}\partial _t^{\alpha } v(t):=\mathcal {I}^{1-\alpha }v'(t) =\int _0^t\omega _{1-\alpha }(t-s)v'(s)\,ds,\quad \textrm{with}\quad \omega _{1-\alpha }(t):=\frac{t^{-\alpha }}{\Gamma (1-\alpha )},\end{aligned}$$

where $v'=\partial v/\partial t$ and $\Gamma$ denotes the gamma function. We use the notation $\mathcal {I}v(t)$ for the standard time integral of v from 0 to t. In (1.1), $\mathcal {A}$ is an elliptic operator in the spatial variables, defined by ${\mathcal A}w({\varvec{x}})=-\nabla \cdot (\kappa ({\varvec{x}})\nabla w)({\varvec{x}})$. The diffusivity $\kappa \in L^\infty (\Omega )$ satisfies $0< \kappa _{\min } \le \kappa$ on $\Omega ,$ for some constant $\kappa _{\min }$. For the error analysis, we also require that $\kappa \in W^{1,\infty }(\Omega )$.

The presence of the nonlocal time fractional (Caputo) derivative in (1.1) and the fact that the solution u suffers from a weak singularity near $t=0$ have a direct impact on the accuracy, and consequently the convergence rates, of numerical methods. To overcome this difficulty, different approaches have been applied including corrections, graded meshes, and convolution quadrature [6, 9, 15, 24, 29, 30]. Indeed, the numerical solutions for model problems of the form (1.1), including a priori and a posteriori error analyses and fast algorithms, were studied by various authors over the past fifteen years using multiple approaches [1, 3, 5, 8, 10, 11, 13, 14, 18], see also [27, 31,32,33, 35, 36]. For more references and details, see the recent monograph by Jin and Zhou [12].

In this work, we investigate rigorously the error from approximating the solution of the initial-boundary value problem (1.1) using a uniform second-order accurate time-stepping method. The latter is defined via a local time-integration of problem (1.1) on each subinterval of the time mesh combined with continuous piecewise linear interpolation. The proposed scheme is identical to the piecewise-linear case of a discontinuous Petrov–Galerkin method proposed in [21]. Therein, with $\tau$ being the maximum time mesh step size, a suboptimal convergence rate of order $O(\tau ^{(3-\alpha )/2})$ was proved. A time-graded mesh (2.1) was employed to compensate for the singular behaviour of the continuous solution at $t=0$. In the limiting case as $\alpha \rightarrow 1$, the problem (1.1) reduces to the classical diffusion equation, and the considered numerical scheme reduces to the classical Crank–Nicolson method. In this case, $O(\tau ^{(3-\alpha )/2})$ reduces to $O(\tau )$ which is far from the optimal $O(\tau ^2)$ rate achieved in practice.

By using an innovative approach that relies on interesting implicit polynomial interpolations and duality arguments, we show $O(\tau ^2)$ convergence, whilst at the same time relaxing the imposed regularity assumptions from the earlier analysis [21]. This convergence rate is $\alpha$-robust in the sense that the constant in the error bound remains bounded as $\alpha \rightarrow 1$. Implementation wise, although the proposed scheme is uniformly second-order accurate, the computational cost is comparable to the well-known backward Euler or L1 [16, 24, 28] methods, which are not even first-order accurate.

For completeness, we discretize the problem (1.1) over the spatial domain $\Omega$ using the standard Galerkin finite element method (FEM), thereby defining a fully discrete approximation to u. An additional error of order $O(h^2)$ is anticipated under certain regularity assumptions on the continuous solution, where h is the maximum spatial finite element mesh size. This is proved via a concise approach that relies on the discrete version of the earlier error analysis. To make this feasible, the solution of the semidiscrete Galerkin finite element solution of problem (1.1) plays the role of the comparison function.

Outline of the paper. In the next section, we define our time-stepping scheme, introduce some notations and technical lemmas, and summarize the convergence results in Theorem 1. The required regularity properties are also highlighted. Section 3 proves some error bounds for the implicit piecewise-linear interpolant ${\widehat{u}}$ defined in (2.6). Section 4 is devoted to showing the second-order of accuracy of the proposed time-stepping scheme via a duality argument. In Sect. 5, we discretize in space via the Galerkin finite element method and discuss the convergence of the fully discrete solution. To support our theoretical findings, we present some numerical results in Sect. 6. Finally, a short technical appendix derives an $\alpha$-robust interpolation estimate.

2 Time-Stepping Scheme

This section is devoted to discretizing the model problem (1.1) over the time interval [0, T] through a second-order accurate method, and stating our main convergence results. We begin by introducing some notations that will be used throughout the paper.

For $\ell \ge 0,$ the norm on $H^\ell (\Omega )$ is denoted by $\Vert \cdot \Vert _\ell$. The Sobolev spaces $H^\ell (\Omega )$ and $H^1_0(\Omega )$ are defined as usual, and the norm $\Vert \cdot \Vert _{\dot{H}^r(\Omega )}$ in the (fractional-order) Sobolev space $\dot{H}^r(\Omega )$ is defined in the usual way via the Dirichlet eigenfunctions of the self-adjoint elliptic operator $\mathcal {A}$ on $\Omega$. The inner product in $L^2(\Omega )$ is denoted by $\langle \cdot ,\cdot \rangle$, and the associated norm by $\Vert \cdot \Vert$. The generic constant C remains bounded for $0<\alpha \le 1,$ and is independent of the time mesh and the finite element mesh, but may depend on $\Omega$, T, and other quantities, including $\kappa$, $u_0$ and f.

Define the time mesh $0=t_0<t_1<t_2<\cdots <t_N=T$ by

$$\begin{aligned} t_n=(n\,\tau )^\gamma ,\quad \text {with }\tau =T^{1/\gamma }/N\hbox { and } \gamma \ge 1, \quad \text {for }0\le n\le N, \end{aligned}$$

(2.1)

and let $\tau _n = t_n-t_{n-1}$. Such a time-graded mesh has the properties [19]

$$\begin{aligned} t_n\le 2^\gamma t_{n-1} \quad \text {and}\quad \gamma \tau t_{n-1}^{1-1/\gamma }\le \tau _n\le \gamma \tau t_n^{1-1/\gamma }, \quad \text {for }n\ge 2. \end{aligned}$$

(2.2)

Integrating problem (1.1) over  $I_n:=(t_{n-1},t_n)$ and then dividing by $\tau _n$ yields

$$\begin{aligned} \frac{1}{\tau _n}\int _{I_n} \partial _t^\alpha u\,dt +\mathcal {A}\bar{u}_n={\bar{f}}_n,\quad \textrm{for}~~1\le n\le N, \end{aligned}$$

(2.3)

where ${\bar{f}}_n=\tau _n^{-1}\int _{I_n}f(t)\,dt$ denotes the average value of a function f over the time interval $I_n$, and similarly, $\bar{u}_n$ is defined. Motivated by (2.3), for $t\in I_n$ and for $1\le n\le N,$ our semidiscrete approximate solution $U(t)\approx u(t)$ is defined by requiring that

$$\begin{aligned}U(t)=\frac{t_n-t}{\tau _n} U^{n-1}+\frac{t-t_{n-1}}{\tau _n} U^n,\quad U^n:=U(t_n),\end{aligned}$$

with

$$\begin{aligned} \frac{1}{\tau _n}\int _{I_n}\partial _t^\alpha U\,dt +\mathcal {A} U^{n-1/2}={\bar{f}}_n,\quad \textrm{with}~~U^0=U(0)=u_0, \end{aligned}$$

(2.4)

where $U^{n-1/2}={\bar{U}}_n =\tfrac{1}{2}( U^n+ U^{n-1}).$ If $\alpha \rightarrow 1$, then $\partial _t^\alpha u\rightarrow u'$ and $\partial _t^\alpha U\rightarrow U'$, implying that our scheme reduces to the Crank–Nicolson scheme for the classical diffusion equation.

Our convergence analysis relies on decomposing the error as

$$\begin{aligned} \eta =u- U=\psi -\theta \quad \text {with}\quad \psi =u-{\widehat{u}} \quad \text {and}\quad \theta = U-{\widehat{u}}, \end{aligned}$$

(2.5)

where ${\widehat{u}}$ is a continuous piecewise-linear function in time satisfying

$$\begin{aligned} \int _{I_n}{\widehat{u}}(t) \,dt=\int _{I_n} u(t)\,dt \quad \text {for } 1\le n\le N,\quad \text {with }{\widehat{u}}(0)={\widehat{u}}^0=u_0. \end{aligned}$$

(2.6)

Alternatively, ${\widehat{u}}$ can be defined via $\mathcal {I}{\widehat{u}}(t_n)=\mathcal {I}u(t_n)$ for $1\le n\le N$, with ${\widehat{u}}(0)=u_0$, and we say that ${\widehat{u}}$ interpolates u implicitly. The decomposition (2.5) of the error $\eta$ follows a well-known pattern, but the novel choice of the piecewise linear function ${\widehat{u}}$ makes possible our improved error analysis under reasonable regularity assumptions. The continuous average of u equals both the continuous and the discrete average of ${\widehat{u}}$ on each time subinterval $I_n$. For comparison, let $u_I$ denote the usual continuous piecewise-linear interpolant to u, that is,

$$\begin{aligned} u_I(t)=\frac{t_n-t}{\tau _n} u(t_{n-1})+\frac{t-t_{n-1}}{\tau _n} u(t_n) \quad \text {for }t\in I_n, \end{aligned}$$

(2.7)

and observe that $u_I$ and u have the same discrete average $\tfrac{1}{2}(u(t_n)+u(t_{n-1}))$ on each $I_n$, but their continuous averages will differ unless u is linear on $I_n$.

Subtracting (2.4) from (2.3) and using (2.6), we obtain

$$\begin{aligned}\int _{I_n}\partial _t^\alpha (\psi -\theta )\,dt -\int _{I_n}\mathcal {A}\theta \,dt=0.\end{aligned}$$

Taking the $L^2(\Omega )$-inner product with a test function $\varphi \in H^1_0(\Omega )$, and applying the divergence theorem, it follows that

$$\begin{aligned} \int _{I_n} \langle \mathcal {I}^{1-\alpha } \theta ',\varphi \rangle \,dt +\int _{I_n}\langle \kappa \nabla \theta ,\nabla \varphi \rangle \,dt =\int _{I_n}\langle \mathcal {I}^{1-\alpha } \psi ',\varphi \rangle \,dt. \end{aligned}$$

(2.8)

Choosing $\varphi =\theta '$ and summing over n yields

$$\begin{aligned}\mathcal {I}(\langle \mathcal {I}^{1-\alpha }\theta ',\theta ' \rangle )(t_n) +\mathcal {I}(\langle \kappa \nabla \theta ,\nabla \theta ' \rangle )(t_n) =\mathcal {I}(\langle \mathcal {I}^{1-\alpha } \psi ',\theta ' \rangle )(t_n).\end{aligned}$$

Since $\mathcal {I}(\langle \kappa \nabla \theta ,\nabla \theta ' \rangle )(t_n) =\tfrac{1}{2}(\Vert \sqrt{\kappa }\nabla \theta (t_n)\Vert ^2-\Vert \sqrt{\kappa }\nabla \theta (0)\Vert ^2)=\tfrac{1}{2}\Vert \sqrt{\kappa }\nabla \theta (t_n)\Vert ^2$,

$$\begin{aligned} \mathcal {I}(\langle \mathcal {I}^{1-\alpha }\theta ',\theta ' \rangle )(t_n)\le \mathcal {I}(\langle \mathcal {I}^{1-\alpha } \psi ',\theta ' \rangle )(t_n). \end{aligned}$$

(2.9)

To proceed in our analysis, we make use of the following technical lemma. For the proof, we refer to Mustapha and Schötzau [22, Lemma 3.1 (iii)].

Lemma 1

For $0<\alpha \le 1$ and $\epsilon >0$,

$$\begin{aligned} \mathcal {I}(\langle \mathcal {I}^{1-\alpha }v,w \rangle )(t)&\le \frac{1}{\alpha }\Big ( \mathcal {I}(\langle \mathcal {I}^{1-\alpha }v,v \rangle )(t)\Big )^{1/2} \Big (\mathcal {I}(\langle \mathcal {I}^{1-\alpha }w,w \rangle )(t)\Big )^{1/2}\\&\le \epsilon \mathcal {I}(\langle \mathcal {I}^{1-\alpha }v,v \rangle )(t) +\frac{1}{4\epsilon \alpha ^2}\mathcal {I}(\langle \mathcal {I}^{1-\alpha }w,w \rangle )(t). \end{aligned}$$

For later use, by expanding $\langle \mathcal {I}^{1-\alpha }(v+w),v+w) \rangle$ then applying Lemma 1 with $\epsilon =1/(2\alpha )$ we deduce the inequality in the next lemma.

Lemma 2

For $0<\alpha \le 1$,

$$\begin{aligned}\mathcal {I}(\langle \mathcal {I}^{1-\alpha }(v+w),v+w \rangle )(t) \le (1+\alpha ^{-1})\Big (\mathcal {I}(\langle \mathcal {I}^{1-\alpha }v,v \rangle )(t) +\mathcal {I}(\langle \mathcal {I}^{1-\alpha }w,w \rangle )(t)\Big ).\end{aligned}$$

We now apply Lemma 1 to the right-hand side of (2.9) with $\epsilon =1/(2\alpha ^2)$. Multiplying through by 2, and then cancelling the similar terms, leads to the estimate below that will be used later in our convergence analysis.

$$\begin{aligned} \mathcal {I}(\langle \mathcal {I}^{1-\alpha } \theta ',\theta ' \rangle )(t_n) \le \frac{1}{\alpha ^2}\mathcal {I}(\langle \mathcal {I}^{1-\alpha }\psi ',\psi ' \rangle )(t_n), \end{aligned}$$

(2.10)

Under reasonable regularity assumptions, a novel error analysis involving implicit interpolations and a duality argument leads to the convergence results in the next theorem. With $J=(0,T)$, an optimal $O(\tau ^2)$-rate of convergence is achieved in the $L^2(J; L^2(\Omega ))$-norm. Our numerical results illustrate this in the stronger $L^\infty (J; L^2(\Omega ))$-norm. Moreover, our numerical results suggest that the condition on the graded mesh exponent can be further relaxed. More precisely, instead of $\gamma >\max \{2/\sigma , (3-\alpha )/(2\sigma -\alpha )\}$ it suffices to impose $\gamma > 2/\sigma$.

The developed error analysis requires the following regularity property [11, Theorems 2.1 and 2.2], [26, Theorems 1 and 2], and: for some $\sigma >0$,

$$\begin{aligned} t\Vert u'(t)\Vert +t^2\Vert u''(t)\Vert +t^3\Vert u'''(t)\Vert \le C t^\sigma \quad \text {for } t>0. \end{aligned}$$

(2.11)

For example, if $f\equiv 0$ and $u_0\in \dot{H}^r(\Omega )$ with $1\le r\le 2$, then (2.11) holds true for $\sigma =r\alpha /2$.

For a given time interval Q, let

$$\begin{aligned}\Vert w\Vert _Q=\sup _{t\in Q}\Vert w(t)\Vert \quad \textrm{and}\quad \Vert w\Vert _{L^2(Q)}=\bigg (\int _Q\Vert w(t)\Vert ^2\,dt\bigg )^{1/2}\end{aligned}$$

denote the norms in $L^\infty \bigl (Q;L^2(\Omega )\bigr )$ and $L^2\bigl (Q;L^2(\Omega )\bigr )$, respectively.

Theorem 1

Let u and U be the solutions of (1.1) and (2.4), respectively. If the graded time mesh exponent $\gamma >\max \{2/\sigma , (3-\alpha )/(2\sigma -\alpha )\}$ and if the regularity assumption (2.11) holds true with $\sigma >\alpha /2$, then we have

$$\begin{aligned}\Vert u- U\Vert _{L^2(J)}\le C\alpha ^{-2}\tau ^2,\quad \textrm{for}\quad 0<\alpha <1.\end{aligned}$$

Proof

The desired estimate follows from Lemma 6 and Theorem 2 below. $\square$

3 Errors from Implicit Interpolations

In preparation for our convergence analysis, we now study the error from approximating u by ${\widehat{u}}$, and proceed to estimate $\Vert \psi \Vert$ and $\mathcal {I}(\langle \mathcal {I}^{1-\alpha } \psi ',\psi ' \rangle )$. These estimates assume that the regularity property (2.11) holds. For ease of reference, we here introduce the parameter $\delta =\sigma -\frac{2}{\gamma }$ which will subsequently appear repeatedly. We start this section with the following representation of the implicit interpolation error in the approximation $u\approx {\widehat{u}}$ at $t=t_n$.

Lemma 3

For $1\le n\le N$, $\psi ^n=\sum _{j=1}^n(-1)^{n+j+1}\Delta _j$ where

$$\begin{aligned}\Delta _j=\frac{2}{\tau _j}\int _{I_j}(u-u_I)\,dt =-\frac{1}{\tau _j}\int _{I_j}(t_j-t)(t-t_{j-1})u''(t)\,dt.\end{aligned}$$

Proof

Since $\int _{I_n}u_I\,dt=\tfrac{1}{2}\tau _n(u^n+u^{n-1})$, we find using (2.6) that

$$\begin{aligned}\psi ^n=-\psi ^{n-1}-\frac{2}{\tau _n}\int _{I_n}(u-u_I)\,dt.\end{aligned}$$

The formula for $\psi ^n$ then follows by induction on n, after noting that $\psi ^0=0$. Recalling the Peano kernel for the trapezoidal rule, we see that

$$\begin{aligned}\int _{I_j}(u-u_I)(t)\,dt=-\frac{1}{2}\int _{I_j}(t_j-t)(t-t_{j-1})u''(t)\,dt,\end{aligned}$$

implying the second expression for $\Delta _j$. $\square$

Lemma 4

For $1\le n\le N$,

$$\begin{aligned}\Vert \psi ^n\Vert \le \int _{I_1}t\Vert u''(t)\Vert \,dt+\frac{1}{12}\biggl (\tau _2^2\Vert u''(t_1)\Vert +2\tau _n^2\Vert u''(t_n)\Vert +3\sum _{j=2}^n\tau _j^2\int _{I_j}\Vert u'''\Vert \,dt \biggr )\end{aligned}$$

and $\Vert \psi (t)\Vert \le \Vert u(t)-u_I(t)\Vert +\max \bigl (\Vert \psi ^n\Vert , \Vert \psi ^{n-1}\Vert \bigr )$ for $t\in I_n$.

Proof

For $t \in I_j$, we have the identity

$$\begin{aligned}-u''(t)=\frac{1}{2}\int _t^{t_j}u'''(s)\,ds-\frac{1}{2}\int _{t_{j-1}}^tu'''(s)\,ds- (u''(t_j)+u''(t_{j-1}))/2.\end{aligned}$$

Multiply both sides by $(t_j-t)(t-t_{j-1})$ and integrate to obtain

$$\begin{aligned}\Delta _j=-\frac{\tau _j^2}{12}[u''(t_j)+u''(t_{j-1})]+R_j,\end{aligned}$$

where

$$\begin{aligned}R_j=\frac{1}{2\tau _j}\int _{I_j}(t_j-t)(t-t_{j-1})\biggl ( \int _t^{t_j}u'''(s)\,ds-\int _{t_{j-1}}^tu'''(s)\,ds\biggr )\,dt.\end{aligned}$$

Thus, by Lemma 3,

$$\begin{aligned}(-1)^n\psi ^n=\Delta _1+\frac{1}{12}\sum _{j=2}^n(-1)^j\tau _j^2 [u''(t_j)+u''(t_{j-1})]-\sum _{j=2}^n(-1)^jR_j.\end{aligned}$$

Shifting the summation index, so

$$\begin{aligned}\sum _{j=2}^n(-1)^j\tau _j^2u''(t_{j-1}) =\tau _2^2u''(t_1) -\sum _{j=2}^{n-1}(-1)^j\tau _{j+1}^2u''(t_j).\end{aligned}$$

Since $\Delta _1=-\tau _1^{-1}\int _{I_1}(t_1-s)su''(s)\,ds$ and since $\Vert R_j\Vert \le \frac{\tau _j^2}{6}\int _{I_j}\Vert u'''(t)\Vert \,dt,$

$$\begin{aligned} \Vert \psi ^n\Vert&\le \int _{I_1}t\Vert u''(t)\Vert \,dt+\frac{1}{12}\biggl ( \tau _2^2\Vert u''(t_1)\Vert +\tau _n^2\Vert u''(t_n)\Vert \\&\qquad {}+\sum _{j=2}^{n-1}(\tau _{j+1}^2-\tau _j^2)\Vert u''(t_j)\Vert +2\sum _{j=2}^n\tau _j^2\int _{I_j}\Vert u'''(t)\Vert \,dt\biggr ). \end{aligned}$$

Using

$$\begin{aligned} \sum _{j=2}^{n-1}\tau _{j+1}^2\Vert u''(t_j)\Vert =\sum _{j=3}^n\tau _j^2\Vert u''(t_{j-1})\Vert \le \sum _{j=3}^n\tau _j^2\Big (\Vert u''(t_j)\Vert +\int _{I_j}\Vert u'''(t)\Vert \,dt\Big ),\end{aligned}$$

and the bound for $\Vert \psi ^n\Vert$ follows after canceling the common terms.

The interpolant $\psi _I$, defined as in (2.7), satisfies $\psi _I=u_I-{\widehat{u}}$, leading to the representation

$$\begin{aligned} \psi =u-{\widehat{u}}=\psi _I+u-u_I, \end{aligned}$$

(3.1)

which implies the desired bound for $\Vert \psi (t)\Vert$ (as stated in the statement of this lemma) because $\Vert \psi _I(t)\Vert \le \max \bigl (\Vert \psi ^n\Vert , \Vert \psi ^{n-1}\Vert \bigr )$ for $t\in I_n$. $\square$

Corollary 1

Under the regularity assumption in (2.11) and for a time mesh of the form (2.1) with grading parameter $\gamma \ge 1$ we have, for $n\ge 1$,

$$\begin{aligned}\Vert \psi ^n\Vert \le \Vert \psi \Vert _{I_n}\le C\times {\left\{ \begin{array}{ll} \tau ^2\log (t_n/t_1),&{}\text {if }\gamma =2/\sigma ,\\ \tau ^{\min (\gamma \sigma ,2)}t_n^{\max (0,\delta )}, &{}\text {if } \gamma \ne 2/\sigma . \end{array}\right. }\end{aligned}$$

Proof

First we show that for $\gamma \ge 1,$

$$\begin{aligned} \Vert u-u_I\Vert _{I_n}\le C \tau ^{\min (\gamma \sigma ,2)}t_n^{\max (0,\delta )}. \end{aligned}$$

(3.2)

Since the interpolation error $u-u_I$ vanishes if u is a polynomial of degree 1, by computing the Peano kernel one finds that for $t\in I_n$,

$$\begin{aligned} u(t)-u_I(t)=-\frac{t_n-t}{\tau _n}\int _{t_{n-1}}^t(s-t_{n-1})u''(s)\,ds -\frac{t-t_{n-1}}{\tau _n}\int _t^{t_n}(t_n-s)u''(s)\,ds. \end{aligned}$$

(3.3)

The right-side is bounded by

$$\begin{aligned}\int _{t_{n-1}}^t(s-t_{n-1})\Vert u''(s)\Vert \,ds +\int _t^{t_n}(t-t_{n-1})\Vert u''(s)\Vert \,ds \le \int _{I_n}(s-t_{n-1})\Vert u''(s)\Vert \,ds\end{aligned}$$

and so, by using the time mesh properties in (2.2), we get

$$\begin{aligned}\Vert u-u_I\Vert _{I_n}\le C \tau _n t_n^{-1} \int _{I_n} t\Vert u''(t)\Vert \,dt \le C \tau _n t_n^{-1} \int _{I_n}t^{\sigma -1}\,dt\le C\tau _n^2t_n^{\sigma -2},~~n\ge 1.\end{aligned}$$

Since $\tau _n \le C \tau t_n^{1-1/\gamma }$, the proof of (3.2) is completed after noting that

$$\begin{aligned} \tau _n^2t_n^{\sigma -2}\le C\tau ^2t_n^\delta \le C\tau ^2\max (t_n^\delta ,t_1^\delta ) \le C\tau ^{\min (\gamma \sigma ,2)}t_n^{\max (0,\delta )}. \end{aligned}$$

(3.4)

Turning to the estimate for $\psi ^n$, Lemma 4 and (2.11) imply that

$$\begin{aligned} \Vert \psi ^n\Vert \le C\int _{I_1} t^{\sigma -1}\,dt +C\tau _2^2 t_1^{\sigma -2}+ C\tau _n^2 t_n^{\sigma -2}+ C\sum _{j=2}^n \tau _j^2\int _{I_j}t^{\sigma -3}\,dt,\end{aligned}$$

for $1\le n\le N.$ Since $t_1=\tau ^\gamma$ and $\tau _2\le 2^\gamma \tau ^\gamma ,$ $\int _{I_1}t^{\sigma -1}\,dt+\tau _2^2t_1^{\sigma -2}\le C\tau ^{\gamma \sigma },$ and we again bound $\tau _n^2t_n^{\sigma -2}$ using (3.4). For the sum over j,

$$\begin{aligned}\sum _{j=2}^n\tau _j^2\int _{I_j}t^{\sigma -3}\,dt \le C\sum _{j=2}^n\tau ^2t_j^{2-2/\gamma }\int _{I_j}t^{\sigma -3}\,dt \le C\tau ^2\int _{t_1}^{t_n}t^{\delta -1}\,dt,\end{aligned}$$

and the estimate for $\Vert \psi ^n\Vert$ follows. $\square$

The next target is to estimate $\mathcal {I}(\langle \mathcal {I}^{1-\alpha } \psi ',\psi ' \rangle )(t_n)$. Preceding this, we need to bound $\Vert \psi '\Vert$ in the next lemma.

Lemma 5

We have $\Vert \psi '(t)\Vert \le t^{\sigma -1}$ for $t\in I_1$. Moreover, $\Vert \psi '(t)\Vert \le C\tau ^2\tau _n^{-1}t_n^\delta$ for $t\in I_n$ with $n\ge 2,$ and for $\delta >0$.

Proof

Differentiating (3.1) and (3.3), we see for $t\in I_n$ that

$$\begin{aligned} \psi '(t)=\frac{1}{\tau _n}\int _{t_{n-1}}^t(s-t_{n-1})u''(s)\,ds -\frac{1}{\tau _n}\int _t^{t_n}(t_n-s)u''(s)\,ds+\tau _n^{-1}(\psi ^n-\psi ^{n-1}). \end{aligned}$$

Thus, if $t\in I_1$ then, by (2.11), Corollary 1, and the fact that $\psi ^0=0,$

$$\begin{aligned}\Vert \psi '(t)\Vert \le C\tau ^{-1}\int _0^ts^{\sigma -1}\,ds+C\tau _1^{-1}\int _t^{t_1}(t_1-s)s^{\sigma -2}\,ds +C\tau _1^{\sigma -1}\le Ct^{\sigma -1}.\end{aligned}$$

If $\delta >0$, $n\ge 2$ and $t\in I_n$ then, recalling (3.4) and using again (2.11),

$$\begin{aligned} \tau _n\Vert \psi '(t)\Vert \le C\tau _n\int _{I_n}t^{\sigma -2}\,dt+C \tau ^2t_n^\delta \le C\tau _n^2t_n^{\sigma -2}+C \tau ^2t_n^\delta \le C\tau ^2t_n^\delta ,\end{aligned}$$

showing that $\Vert \psi '(t)\Vert \le C\tau ^2\tau _n^{-1}t_n^\delta$. $\square$

Lemma 6

Assume $\sigma >\alpha /2$. Then $\big |\mathcal {I}(\langle \mathcal {I}^{1-\alpha } \psi ',\psi ' \rangle )(t_n)\big | \le C\tau ^{3-\alpha }$ for $n\ge 1$, provided that $\gamma >\max \{2/\sigma , (3-\alpha )/(2\sigma -\alpha )\}$.

Proof

For $n=1$, the Cauchy–Schwarz inequality, Lemma 5, and the assumption $\sigma >\alpha /2$ give

$$\begin{aligned} \Big |\mathcal {I}(\langle \mathcal {I}^{1-\alpha } \psi ',\psi ' \rangle )(t_1)\Big | \le C\int _0^{t_1} t^{\sigma -1}\int _0^t(t-s)^{-\alpha } s^{\sigma -1}\,ds\,dt \le C\tau _1^{2\sigma -\alpha }. \end{aligned}$$

(3.5)

To deal with the case $n\ge 2$, we make the splitting $\mathcal {I}^{1-\alpha }\psi '=T_1+T_2$ where

$$\begin{aligned}T_1(t)=\int _0^{t_{j-1}}\omega _{1-\alpha }(t-s)\psi '(s)\,ds \quad \text {and}\quad T_2(t)=\int _{t_{j-1}}^t\omega _{1-\alpha }(t-s)\psi '(s)\,ds\end{aligned}$$

for $t\in I_j$ and $j\ge 2$. Using Lemma 5 and (2.2), we observe that

$$\begin{aligned}\Vert T_2(t)\Vert \le C\int _{t_{j-1}}^t\omega _{1-\alpha }(t-s)\,\frac{\tau ^2s^\delta }{\tau _j}\,ds \le C\frac{\tau ^2t^\delta }{\tau _j}\omega _{2-\alpha }(t-t_{j-1}) \le C\tau ^2t^\delta \tau _j^{-\alpha }.\end{aligned}$$

For estimating $T_1(t)$, integrate by parts recalling $\psi ^0=0$,

$$\begin{aligned}T_1(t)=\omega _{1-\alpha }(t-t_{j-1})\psi ^{j-1} +\int _0^{t_{j-1}}\omega _{-\alpha }(t-s) \psi (s)\,ds,\end{aligned}$$

where $\omega _{-\alpha }(t)=\omega _{1-\alpha }'(t)=-\alpha t^{-\alpha -1}/\Gamma (1-\alpha )$. We apply Corollary 1 to conclude that $\Vert T_1(t)\Vert$ is bounded by

$$\begin{aligned} C\tau ^2 t_{j-1}^{\delta }\biggl (\omega _{1-\alpha }(t-t_{j-1}) -\int _0^{t_{j-1}}\omega _{-\alpha }(t-s)\,ds\biggr ) \le C\tau ^2 t_j^{\delta }\omega _{1-\alpha }(t-t_{j-1}). \end{aligned}$$

Lemma 5 and above estimates for $\Vert T_1\Vert$ and $\Vert T_2\Vert$ yield

$$\begin{aligned} \Vert \psi '\Vert _{I_j}\int _{I_j}\bigl (\Vert T_1\Vert +\Vert T_2\Vert \bigr )\,dt \le C(\tau ^2t_j^{\delta }\tau _j^{-1})\tau ^2t_j^\delta (\tau _j^{1-\alpha }) \le C\tau ^4t_j^{2\delta }\tau _j^{-\alpha },~~\textrm{for}~~j\ge 2.\end{aligned}$$

By using this and (3.5), and noting that $\gamma (2\sigma -\alpha )>3-\alpha$, we reach

$$\begin{aligned}&\Big |\mathcal {I}(\langle \mathcal {I}^{1-\alpha }\psi ',\psi ' \rangle )(t_n)\Big | \le \biggl |\int _0^{t_1}\langle \mathcal {I}^{1-\alpha }\psi ',\psi ' \rangle \,dt\biggr | +\biggl |\int _{t_1}^{t_n}\langle \mathcal {I}^{1-\alpha }\psi ',\psi ' \rangle \,dt\biggr |\\&\quad \le C\tau ^{3-\alpha }+\sum _{j=2}^n \Vert \psi '\Vert _{I_j}\int _{I_j}\bigl (\Vert T_1\Vert +\Vert T_2\Vert \bigr )\,dt\le C\tau ^{3-\alpha }+C\sum _{j=2}^n\tau ^4t_j^{2\delta }\tau _j^{-\alpha }, \end{aligned}$$

for $j\ge 2.$ By (2.2), if $j\ge 2$ then $\tau ^{1+\alpha }\le C\tau _j^{1+\alpha }t_j^{-(1+\alpha )(1-1/\gamma )}$ so

$$\begin{aligned}\tau ^{1+\alpha }\sum _{j=2}^nt_j^{2\delta }\tau _j^{-\alpha } \le C\sum _{j=2}^nt_j^{2\delta -(1+\alpha )(1-1/\gamma )}\tau _j \le C\int _{t_1}^{t_n}t^{2\sigma -\alpha -(3-\alpha )/\gamma -1}\,dt \le C,\end{aligned}$$

and therefore the desired bound holds. $\square$

4 Errors from the Time Discretizations

This section is devoted to estimating the error $\eta =u- U$ from the time discretization in the norm of $L^2(J;L^2(\Omega ))$. To achieve an optimal convergence rate, we employ a duality argument in addition to the usage of the time graded meshes. By reversing the order of integration, we find that

$$\begin{aligned} \mathcal {I}(\langle \mathcal {I}^\alpha v,w \rangle )(T)=\mathcal {I}(\langle v,\mathcal {J}_{T}^{\alpha }w \rangle )(T) \quad \text {where}\quad (\mathcal {J}_{T}^{\alpha }w)(t)=\int _t^T\omega _\alpha (s-t)w(s)\,ds. \end{aligned}$$

Using $\mathcal {I}(\langle \partial _t^\alpha v,w \rangle )(T) =\mathcal {I}(\langle v',\mathcal {J}_{T}^{1-\alpha }w \rangle )(T)$ and integrating by parts yield

$$\begin{aligned} \mathcal {I}(\langle \partial _t^\alpha v,w \rangle )(T) =-\langle v(0),(\mathcal {J}_{T}^{1-\alpha }w)(0) \rangle -\mathcal {I}(\langle v,(\mathcal {J}_{T}^{1-\alpha }w)' \rangle )(T), \end{aligned}$$

(4.1)

and since $\partial _t^\alpha v =\mathcal {I}^{1-\alpha }v'=(\mathcal {I}^{1-\alpha }v)'-v(0)\omega _{1-\alpha }$,

$$\begin{aligned} \mathcal {I}(\langle (\mathcal {I}^{1-\alpha }v)',w \rangle )(T) =-\mathcal {I}(\langle v,(\mathcal {J}_{T}^{1-\alpha }w)' \rangle )(T). \end{aligned}$$

(4.2)

We remark that Zhang et al. [34, Equation (89)] have recently exploited this dual operator $w\mapsto -(\mathcal {J}_{T}^{1-\alpha }w)'$ in the error analysis of a discontinuous Galerkin scheme for (1.1).

Suppose that $\varphi$ satisfies the final-value problem

$$\begin{aligned} \begin{aligned} -(\mathcal {J}_{T}^{1-\alpha }\varphi )'+\mathcal {A}\varphi =\eta \quad \text{ on }~~\Omega \times (0,T), \quad \text{ with } \varphi ({\varvec{x}},T)=0, \end{aligned} \end{aligned}$$

(4.3)

subject to homogeneous Dirichlet boundary conditions, that is, $\varphi ({\varvec{x}},t)= 0$ on $\partial \Omega \times (0,T)$. Let $y(t)=\varphi (0)+\int _0^t\varphi (s)\,ds$ so that y solves the initial-value problem

$$\begin{aligned} y'=\varphi \quad \text {for }0<t<T,\quad \text {with } y(0)=\varphi (0), \end{aligned}$$

(4.4)

and with $y_I$ denotes the continuous piecewise-linear function that interpolates y at the time levels $t_j$, put

$$\begin{aligned} Y=y-y_I. \end{aligned}$$

(4.5)

Lemma 7

With the notation above, $\Vert \eta \Vert ^2_{L^2(J)}\le \mathcal {I}( \langle Y',\mathcal {I}^{1-\alpha }\eta '+\mathcal {A}\eta \rangle )(T).$

Proof

Using (4.1), (4.3), $\eta (0)=0$ and (4.4),

$$\begin{aligned} \Vert \eta \Vert ^2_{L^2(J)} =\mathcal {I}(\langle -(\mathcal {J}_{T}^{1-\alpha }\varphi )'+\mathcal {A}\varphi ,\eta \rangle )(T) =\mathcal {I}(\langle y',\mathcal {I}^{1-\alpha }\eta '+\mathcal {A}\eta \rangle )(T). \end{aligned}$$

At the same time, (2.3) and (2.4) imply that

$$\begin{aligned}\frac{1}{\tau _n}\int _{I_n}\bigl ( \partial _t^\alpha \eta +\mathcal {A}\eta \bigr )\,dt=0 \quad \text {so}\quad \int _{I_n}\langle y_I',\partial _t^\alpha \eta +\mathcal {A}\eta \rangle \,dt=0,\end{aligned}$$

because $y_I'$ is constant on $I_n$. Since $Y'=y'-y_I'$, the inequality follows at once. $\square$

We will show below in Theorem 3 that the interpolation error Y satisfies

$$\begin{aligned} \mathcal {I}(\langle Y',\mathcal {I}^{1-\alpha }Y' \rangle )(T) +\mathcal {I}(\langle \mathcal {A}Y, \mathcal {I}^{\alpha }\mathcal {A}Y' \rangle )(T) \le C\tau ^{1+\alpha }\Vert \eta \Vert ^2_{L^2(J)}. \end{aligned}$$

(4.6)

Assuming this fact for now, we can derive an estimate for $\eta$ in terms of $\psi '$. We use the following notations: for a given time-dependent function g, 

$$\begin{aligned} F(g)=\bigl (\mathcal {I}(\langle \mathcal {I}^\alpha g',g \rangle )(T)\bigr )^{1/2}\quad \textrm{and}\quad G(g)=\bigl (\mathcal {I}(\langle \mathcal {I}^{1-\alpha }g',g' \rangle )(T)\bigr )^{1/2}. \end{aligned}$$

Theorem 2

We have $\alpha ^2\Vert \eta \Vert ^2_{L^2(J)} \le C\,\tau ^{\alpha +1} \mathcal {I}(\langle \mathcal {I}^{1-\alpha } \psi ',\psi ' \rangle )(T).$

Proof

It suffices to estimate the right-hand side of the inequality in Lemma 7. By Lemma 1,

$$\begin{aligned}\alpha \mathcal {I}(\langle Y',\mathcal {I}^{1-\alpha }\psi ' \rangle )(T) \le G(Y)G(\psi )~~\textrm{and}~~ \alpha \mathcal {I}(\langle Y',\mathcal {I}^{1-\alpha }\theta ' \rangle )(T) \le G(Y)G(\theta ).\end{aligned}$$

After using (2.10) and $\eta '=\psi '-\theta '$, we conclude that

$$\begin{aligned} \alpha ^2\mathcal {I}(\langle Y',\mathcal {I}^{1-\alpha }\eta ' \rangle )(T)\le 2 G(Y)G(\psi ). \end{aligned}$$

(4.7)

Since $Y(t_j)=0$ for $0\le j\le N$, integrating by parts, using $\mathcal {A}Y=\mathcal {I}\mathcal {A}Y'=\mathcal {I}^{1-\alpha }(\mathcal {I}^\alpha \mathcal {A}Y')$, and applying Lemma 1,

$$\begin{aligned} \alpha \mathcal {I}(\langle Y',\mathcal {A}\theta \rangle )(T)&=-\alpha \mathcal {I}(\langle \theta ',\mathcal {I}^{1-\alpha }(\mathcal {I}^\alpha \mathcal {A}Y') \rangle )(T) \le G(\theta )F(\mathcal {A}Y). \end{aligned}$$

The same estimate holds with $\theta$ replaced by $\psi$, so because $\eta =\psi -\theta$, and using (2.10) again,

$$\begin{aligned} \alpha ^2 \mathcal {I}(\langle Y',\mathcal {A}\eta \rangle )(T) \le 2F({\mathcal A}Y)G(\psi ). \end{aligned}$$

(4.8)

Adding (4.7) and (4.8), we see $\alpha ^2\Vert \eta \Vert ^2_{L^2(J)}\le 2G(\psi )(G(Y)+F(\mathcal {A}Y))$ by Lemma 7. Squaring both sides, we have

$$\begin{aligned}\alpha ^4\Vert \eta \Vert ^4_{L^2(J)}\le 4(G(\psi ))^2(G(Y)+F(\mathcal {A}Y))^2 \le 8 (G(\psi ))^2((G(Y))^2+(F(\mathcal {A}Y))^2).\end{aligned}$$

Since $(G(Y))^2+(F(\mathcal {A}Y))^2$ is just the left-hand side of (4.6), the desired inequality followed after cancelling the common factor $\Vert \eta \Vert ^2_{L^2(J)}$. $\square$

It remains to prove (4.6). We start by showing preliminary bounds for $\big |\mathcal {I}(\langle Y',\mathcal {I}^{1-\alpha }Y' \rangle )(T)\big |$ and $\big |\mathcal {I}(\langle \mathcal {A}Y,\mathcal {I}^{1-\alpha }\mathcal {A}Y' \rangle )(T)\big |$ in the next two lemmas. The regularity properties outlined in (2.11) are sufficient to ensure that the assumptions imposed on y in these lemmas hold true.

Lemma 8

Assume that $y,y' \in L^2(J;L^2(\Omega )),$ then for $0<\alpha <1,$ we have

$$\begin{aligned}\Big |\mathcal {I}(\langle Y', \mathcal {I}^{1-\alpha }Y' \rangle )(T)\Big | \le C(1-\alpha )\sum _{j=1}^{N-2}\tau _j^{-\alpha } \Vert Y\Vert _{I_j}^2 +C\tau ^{1-\alpha }\Vert Y'\Vert ^2_{L^2(J)}.\end{aligned}$$

Proof

For $t\in I_j$ with $j\ge 2$, we write $\mathcal {I}^{1-\alpha } Y'(t)=S_1(t)+S_2(t)$ where

$$\begin{aligned}S_1(t)=\int _{t_{j-2}}^t \omega _{1-\alpha }(t-s)Y'(s)\,ds ~\text {and}~ S_2(t)=\int _0^{t_{j-2}}\omega _{1-\alpha }(t-s)Y'(s)\,ds.\end{aligned}$$

Applying the Cauchy–Schwarz inequality, integrating, changing the order of integration, and integrating again, yields

$$\begin{aligned} \begin{aligned}&\Vert S_1\Vert ^2_{L^2(I_j)}\le \int _{I_j} \biggl (\int _{t_{j-2}}^t \omega _{1-\alpha }(t-s)\,ds\biggr ) \biggl (\int _{t_{j-2}}^t \omega _{1-\alpha }(t-s)\Vert Y'(s)\Vert ^2\,ds\biggr )\,dt\\ {}&\quad \le C(\tau _j+\tau _{j-1})^{1-\alpha }\biggl (\int _{I_j}\int _s^{t_j} +\int _{I_{j-1}}\int _{I_j}\biggr )\omega _{1-\alpha }(t-s)\,dt\,\Vert Y'(s)\Vert ^2\,ds\\ {}&\quad \le C(\tau _j+\tau _{j-1})^{2(1-\alpha )} \int _{t_{j-2}}^{t_j}\Vert Y'(s)\Vert ^2\,ds \le C\tau _j^{2(1-\alpha )}\int _{t_{j-2}}^{t_j}\Vert Y'(s)\Vert ^2\,ds. \end{aligned} \end{aligned}$$

For $t \in I_1$, let $S_1(t)=\int _0^t\omega _{1-\alpha }(t-s)Y'(s)\,ds$ and $S_2(t)=0$. Following the steps above, we find that $\Vert S_1\Vert ^2_{L^2(I_1)} \le C\tau _1^{2(1-\alpha )}\Vert Y'\Vert ^2_{L^2(I_1)}$. Thus,

$$\begin{aligned} \Vert S_1\Vert ^2_{L^2(J)} \le C\tau ^{2(1-\alpha )}\Vert Y'\Vert ^2_{L^2(J)}, \end{aligned}$$

and consequently

$$\begin{aligned} \mathcal {I}(|\langle Y', S_1 \rangle |)(T) \le \Vert Y'\Vert _{L^2(J)}\Vert S_1\Vert _{L^2(J)} \le C\tau ^{1-\alpha }\Vert Y'\Vert ^2_{L^2(J)}. \end{aligned}$$

(4.9)

Turning to the second term $S_2$, we integrate by parts (noting that $Y^{j-2}=0=Y^0$) and obtain

$$\begin{aligned}\Vert S_2(t)\Vert =\biggl \Vert \int _0^{t_{j-2}}\omega _{-\alpha }(t-s)Y(s)\,ds\biggr \Vert \le \sum _{i=1}^{j-2}\Vert Y\Vert _{I_i}\int _{I_i}|\omega _{-\alpha }(t-s)|\,ds.\end{aligned}$$

Since $|\omega _{-\alpha }(t-s)|\le |\omega _{-\alpha }(t_{j-1}-s)|$ for $t\in I_j$,

$$\begin{aligned}\int _{I_j}|\langle Y',S_2 \rangle |\,dt \le \sum _{i=1}^{j-2}\int _{I_j}\Vert Y'(t)\Vert \Vert Y\Vert _{I_i}\,dt\int _{I_i} |\omega _{-\alpha }(t_{j-1}-s)|\,ds,\end{aligned}$$

with

$$\begin{aligned}\int _{I_j}\Vert Y'(t)\Vert \Vert Y\Vert _{I_i}\,dt \le \frac{1}{2}\biggl (\Vert Y\Vert _{I_i}^2+\tau _j\Vert Y'\Vert ^2_{L^2(I_j)}\biggr ),\end{aligned}$$

and, remembering that $\omega _{-\alpha }(t)=-\alpha \,t^{-1}\omega _{1-\alpha }(t)$,

$$\begin{aligned}\int _{I_i}|\omega _{-\alpha }(t_{j-1}-s)|\,ds =\omega _{1-\alpha }(t_{j-1}-t_i)-\omega _{1-\alpha }(t_{j-1}-t_{i-1}).\end{aligned}$$

Since $t_j-t_i\ge t_{j-1}-t_{i-1}$, $\omega _{1-\alpha }(t_{j-1}-t_{i-1}) \ge \omega _{1-\alpha }(t_j-t_i)$, and thus,

$$\begin{aligned}{} & {} \int _{I_j}|\langle Y',S_2 \rangle |\,dt\le \frac{1}{2}\sum _{i=1}^{j-2}\Vert Y\Vert _i^2 [\omega _{1-\alpha }(t_{j-1}-t_i)-\omega _{1-\alpha }(t_j-t_i)]\\{} & {} \quad +\frac{\tau _j}{2}\Vert Y'\Vert ^2_{L^2(I_j)} \int _0^{t_{j-2}}|\omega _{-\alpha }(t_{j-1}-s)|\,ds, \end{aligned}$$

and in the second term, noting that $1/\Gamma (1-\alpha )=(1-\alpha )/\Gamma (2-\alpha )$,

$$\begin{aligned}\int _0^{t_{j-2}}|\omega _{-\alpha }(t_{j-1}-s)|\,ds =\omega _{1-\alpha }(t_{j-1}-t_{j-2})-\omega _{1-\alpha }(t_j) \le C(1-\alpha )\tau _{j-1}^{-\alpha }.\end{aligned}$$

By interchanging the order of the double sum,

$$\begin{aligned}&\mathcal {I}(|\langle Y',S_2 \rangle |)(T) =\sum _{j=2}^N\int _{I_j}|\langle Y',S_2 \rangle |\,dt\le C(1-\alpha )\\&\qquad \times \Big (\sum _{i=1}^{N-2}\Vert Y\Vert _{I_i}^2\sum _{j=i+2}^N [(t_{j-1}-t_i)^{-\alpha }-(t_{j}-t_{i})^{-\alpha }] +\Bigl ( \max _{2\le j\le N}\tau _j\tau _{j-1}^{-\alpha }\Bigr )\Vert Y'\Vert ^2_{L^2(J)}\Big )\\&\quad \le C(1-\alpha )\biggl (\sum _{i=1}^{N-2}\tau _{i+1}^{-\alpha }\Vert Y\Vert _{I_i}^2 +\tau ^{1-\alpha }\Vert Y'\Vert ^2_{L^2(J)}\biggr ), \end{aligned}$$

which, combined with (4.9), yields the desired estimate. $\square$

Lemma 9

Assume that $\mathcal {A} y \in L^\infty (J;L^2(\Omega ))$ and $\mathcal {A} y' \in L^1(J;L^2(\Omega ))$. Then for $0<\alpha <1,$

$$\begin{aligned}\Big |\mathcal {I}(\langle \mathcal {A}Y,\mathcal {I}^{\alpha }\mathcal {A}Y' \rangle )(T)\Big | \le C\sum _{j=1}^N\tau _j^\alpha \biggr [ \biggl (\int _{I_j}\Vert \mathcal {A}Y'\Vert \,dt\biggr )^2 +\Vert \mathcal {A}Y\Vert _{I_j}^2\biggr ].\end{aligned}$$

Proof

Integrating by parts,

$$\begin{aligned} \mathcal {I}(\langle \mathcal {A}Y,\mathcal {I}^{\alpha }\mathcal {A}Y' \rangle )(T) =-\int _0^T\langle \mathcal {A}Y',S_3 \rangle \,dt -\int _0^T\langle \mathcal {A}Y',S_4 \rangle \,dt, \end{aligned}$$

(4.10)

where we used the splitting $\mathcal {I}^{\alpha }\mathcal {A}Y=S_3+S_4$ with

$$\begin{aligned}S_3(t)=\int _{t_{j-1}}^t\omega _\alpha (t-s)\mathcal {A}Y(s)\,ds ~~\text {and}~~ S_4(t)=\int _0^{t_{j-1}}\omega _\alpha (t-s)\mathcal {A}Y(s)\,ds\end{aligned}$$

for $t\in I_j$. Since $\Vert S_3(t)\Vert \le \Vert \mathcal {A}Y\Vert _{I_j}\int _{t_{j-1}}^t\omega _\alpha (t-s)\,ds \le C\tau _j^\alpha \Vert \mathcal {A}Y\Vert _{I_j}$,

$$\begin{aligned} \biggl |\int _0^T\langle \mathcal {A}Y',S_3 \rangle \,dt\biggr | \le C\sum _{j=1}^N\tau _j^\alpha \Vert \mathcal {A}Y\Vert _{I_j} \int _{I_j}\Vert \mathcal {A}Y'(t)\Vert \,dt. \end{aligned}$$

(4.11)

For the estimate involving $S_4$, we reverse the order of integration and then integrate by parts, to obtain

$$\begin{aligned} \int _{I_j}\langle \mathcal {A}Y',S_4 \rangle \,dt&=-\int _0^{t_{j-1}}\Big \langle \mathcal {A}Y(s), \int _{I_j}\omega _{\alpha -1}(t-s)\mathcal {A}Y(t)\,dt \Big \rangle \,ds, \end{aligned}$$

and thus, applying the Cauchy–Schwarz inequality and using $\Vert \mathcal {A}Y\Vert _{I_i}\Vert \mathcal {A}Y\Vert _{I_j}\le \Vert \mathcal {A}Y\Vert _{I_i}^2+\Vert \mathcal {A}Y\Vert _{I_j}^2,$ we get

$$\begin{aligned}{} & {} \biggl |\int _0^T\langle \mathcal {A}Y',S_4 \rangle \,dt\biggr | \le \sum _{j=1}^N\sum _{i=1}^{j-1} \bigl (\Vert {\mathcal A}Y\Vert _{I_i}^2+\Vert \mathcal {A}Y\Vert _{I_j}^2\bigr ) \int _{I_i}\int _{I_j}|\omega _{\alpha -1}(t-s)|\,dt\,ds\\{} & {} \quad =\sum _{i=1}^{N-1}\Vert \mathcal {A}Y\Vert _{I_i}^2 \int _{I_i}\int _{t_i}^{t_n}|\omega _{\alpha -1}(t-s)|\,dt\,ds\\{} & {} \qquad +\sum _{j=1}^N \Vert \mathcal {A}Y\Vert _{I_j}^2 \int _{I_j}\int _0^{t_{j-1}}|\omega _{\alpha -1}(t-s)|\,ds\,dt\\{} & {} \quad \le \sum _{i=1}^{N-1}\Vert \mathcal {A}Y\Vert _{I_i}^2 \int _{I_i}\omega _{\alpha }(t_i-s)\,ds +\sum _{j=1}^N \Vert {\mathcal A}Y\Vert _{I_j}^2 \int _{I_j}\omega _{\alpha }(t-t_{j-1})\,dt\\{} & {} \quad \le C\sum _{j=1}^N\tau _j^\alpha \Vert \mathcal {A}Y\Vert _{I_j}^2. \end{aligned}$$

The proof is concluded by inserting this and (4.11) into the splitting (4.10). $\square$

By using the achieved estimates in the previous two lemmas, we are now able in the next theorem to provide the missing part in the proof of Theorem 2.

Theorem 3

The inequality (4.6) is satisfied by the function Y defined via (4.3)–(4.5).

Proof

Recall that $Y=y-y_I$ where $y_I$ is the piecewise linear polynomial that interpolates y at the time nodes, and $y'=\varphi$. Thus, if $t\in I_j$ then

$$\begin{aligned} Y(t)=y(t)-y_I(t)=\frac{t_j-t}{\tau _j}\int _{t_{j-1}}^t\varphi (s)\,ds -\frac{t-t_{j-1}}{\tau _j}\int _t^{t_j}\varphi (s)\,ds \end{aligned}$$

(4.12)

so $\Vert Y(t)\Vert \le \int _{I_j}\Vert \varphi \Vert \,ds$. Similarly, replacing u with y in (3.3), we have $\Vert Y(t)\Vert \le \tau _j\int _{I_j}\Vert \varphi '\Vert \,ds$, and therefore

$$\begin{aligned} \Vert Y\Vert _{I_j}^2\le \tau _j\Vert \varphi \Vert ^2_{L^2(I_j)} \quad \text {and}\quad \Vert Y\Vert _{I_j}^2\le \tau _j^3\Vert \varphi '\Vert ^2_{L^2(I_j)}. \end{aligned}$$

(4.13)

Consider the linear operator B defined by $(B\varphi )(t)=\tau _j^{-\alpha /2}\Vert Y\Vert _{I_j}$ for $t\in I_j$ and $1\le j\le N$. The estimates (4.13) give

$$\begin{aligned}\Vert B\varphi \Vert ^2_{L^2(J)}\le C\tau ^{1-\alpha }\Vert \varphi \Vert ^2_{L^2(J)} \quad \text {and}\quad \Vert B\varphi \Vert ^2_{L^2(J)}\le C\tau ^{3-\alpha }\Vert \varphi '\Vert ^2_{L^2(J)},\end{aligned}$$

and, since $\varphi (T)=0$ and $(\tau ^{1-\alpha })^{1-\alpha }(\tau ^{3-\alpha })^\alpha =\tau ^{1+\alpha }$, we may apply Corollary 2 from the Appendix to deduce that

$$\begin{aligned} \sum _{j=1}^N\tau _j^{-\alpha }\Vert Y\Vert _{I_j}^2 =\Vert B\varphi \Vert ^2_{L^2(J)} \le C\tau ^{1+\alpha }\Vert (\mathcal {J}_{T}^{1-\alpha }\varphi )'\Vert ^2_{L^2(J)}. \end{aligned}$$

(4.14)

Furthermore, by differentiating (4.12) and (3.3),

$$\begin{aligned}Y'(t)=\varphi (t)-\frac{1}{\tau _j}\int _{I_j}\varphi (s)\,ds =\frac{1}{\tau _j}\int _{t_{j-1}}^t(s-t_{j-1})\varphi '(s)\,ds -\frac{1}{\tau _j}\int _t^{t_j}(t_j-s)\varphi '(s)\,ds\end{aligned}$$

for $t\in I_j$, so

$$\begin{aligned}\Vert Y' (t)\Vert \le \Vert \varphi (t)\Vert +\frac{1}{\tau _j}\int _{I_j}\Vert \varphi (s)\Vert \,ds \quad \text {and}\quad \Vert Y'(t)\Vert \le \int _{I_j}\Vert \varphi '(s)\Vert \,ds,\end{aligned}$$

implying that

$$\begin{aligned} \Vert Y'\Vert ^2_{L^2(I_j)}\le 4\Vert \varphi \Vert ^2_{L^2(I_j)} \quad \text {and}\quad \Vert Y'\Vert ^2_{L^2(I_j)}\le \tau _j^2\Vert \varphi '\Vert ^2_{L^2(I_j)}. \end{aligned}$$

(4.15)

After summing over j and once again applying Corollary 2, we arrive at

$$\begin{aligned} \Vert Y'\Vert ^2_{L^2(J)} \le C\tau ^{2\alpha }\Vert (\mathcal {J}_{T}^{1-\alpha }\varphi )'\Vert ^2_{L^2(J)}. \end{aligned}$$

(4.16)

Now take the inner product of (4.3) with $-(\mathcal {J}_{T}^{1-\alpha }\varphi )'$ in $L_2(\Omega )$, and then integrate in time to obtain

$$\begin{aligned} \begin{aligned}\Vert (\mathcal {J}_{T}^{1-\alpha }\varphi )'\Vert ^2_{L^2(J)} -\mathcal {I}(\langle \mathcal {A}\varphi ,(\mathcal {J}_{T}^{1-\alpha }\varphi )' \rangle )(T)&=-\mathcal {I}(\langle \eta ,(\mathcal {J}_{T}^{1-\alpha }\varphi )' \rangle )(T)\\ {}&\le \frac{1}{2}\Vert \eta \Vert ^2_{L^2(J)} +\frac{1}{2}\Vert (\mathcal {J}_{T}^{1-\alpha }\varphi )'\Vert ^2_{L^2(J)}. \end{aligned} \end{aligned}$$

By (4.2),

$$\begin{aligned} -\mathcal {I}(\langle \mathcal {A}\varphi ,(\mathcal {J}_{T}^{1-\alpha }\varphi )' \rangle )(T) =\mathcal {I}(\langle (\mathcal {I}^{1-\alpha }\mathcal {A}^{1/2}\varphi )', \mathcal {A}^{1/2}\varphi \rangle )(T)\ge 0 \end{aligned}$$

(4.17)

and therefore

$$\begin{aligned} \Vert (\mathcal {J}_{T}^{1-\alpha }\varphi )'\Vert ^2_{L^2(J)}\le \Vert \eta \Vert ^2_{L^2(J)}. \end{aligned}$$

Combining this with (4.14), (4.16), we conclude that

$$\begin{aligned}\sum _{j=1}^N\tau _j^{-\alpha }\Vert Y\Vert _{I_j}^2 \le C\tau ^{1+\alpha }\Vert \eta \Vert ^2_{L^2(J)} \quad \text {and}\quad \Vert Y'\Vert ^2_{L^2(J)}\le C\tau ^{2\alpha }\Vert \eta \Vert ^2_{L^2(J)}\end{aligned}$$

and so, applying Lemma 8,

$$\begin{aligned} \mathcal {I}(\langle Y',\mathcal {I}^{1-\alpha }Y' \rangle )(T) \le C\tau ^{1+\alpha }\Vert \eta \Vert ^2_{L^2(J)}. \end{aligned}$$

(4.18)

By taking the inner product of (4.3) with $\mathcal {A}\varphi$ and proceeding as above, we deduce that

$$\begin{aligned} \Vert \mathcal {A}\varphi \Vert ^2_{L^2(J)}\le \Vert \eta \Vert ^2_{L^2(J)}. \end{aligned}$$

(4.19)

Repeating the arguments leading to the first estimate in (4.15) but with $Y'$ replaced by $\mathcal {A}Y'$, we see that $\Vert \mathcal {A}Y'\Vert ^2_{L^2(J)}\le \Vert \mathcal {A}\varphi \Vert ^2_{L^2(J)}$ and so

$$\begin{aligned}\sum _{j=1}^N\tau _j^\alpha \biggl (\int _{I_j}\Vert \mathcal {A}Y'\Vert \,dt\biggr )^2 \le \sum _{j=1}^N\tau _j^{1+\alpha }\Vert \mathcal {A}Y'\Vert ^2_{L^2(I_j)} \le C\tau ^{1+\alpha }\Vert \mathcal {A}\varphi \Vert ^2_{L^2(J)}.\end{aligned}$$

Likewise, $\Vert \mathcal {A}Y\Vert _{I_j}^2 \le \tau _j\Vert \mathcal {A}\varphi \Vert ^2_{L^2(I_j)}$ by the arguments leading to (4.12), so

$$\begin{aligned}\sum _{j=1}^N\tau _j^\alpha \Vert \mathcal {A}Y\Vert _{I_j}^2 \le \sum _{j=1}^N\tau _j^{1+\alpha }\Vert \mathcal {A}\varphi \Vert ^2_{L^2(I_j)} \le C\tau ^{1+\alpha }\Vert \mathcal {A}\varphi \Vert ^2_{L^2(J)}.\end{aligned}$$

Hence, by Lemma 9 and (4.19),

$$\begin{aligned} \mathcal {I}(\langle \mathcal {A}Y,\mathcal {I}^\alpha \mathcal {A}Y' \rangle )(T) \le C\tau ^{1+\alpha }\Vert \eta \Vert ^2_{L^2(J)}. \end{aligned}$$

(4.20)

Together, (4.18) and (4.20) imply the desired estimate (4.6). $\square$

5 A Fully Discrete Scheme and Error Analysis

In this section, we discretize the time-stepping scheme (2.4) in space using the continuous piecewise-linear Galerkin FEM and hence define a fully-discrete method. Thus, we introduce a family of regular (conforming) triangulations $\mathcal {T}_h$ of the domain $\overline{\Omega }$ indexed by $h=\max _{K\in \mathcal {T}_h}(h_K)$, where $h_{K}$ denotes the diameter of the element K. Let $V_h$ denote the space of continuous, piecewise-linear functions with respect to $\mathcal {T}_h$ that vanish on $\partial \Omega$. Let $\mathcal {W}(V_h)\subset \mathcal {C}([0,T];V_h)$ denote the space of linear polynomials on ${\overline{I}}_n$ for $1\le n\le N$, with coefficients in $V_h$. Motivated by the weak formulation of (2.4), our fully-discrete solution $U_h\in \mathcal {W}(V_h)$ is defined by requiring

$$\begin{aligned} \Big \langle \int _{I_n}\partial _t^\alpha U_h\,dt,v_h \Big \rangle +\tau _n\langle \kappa \nabla U_h^{n-1/2},\nabla v_h \rangle =\tau _n\langle {\bar{f}}_n,v_h \rangle \quad \text {for all }v_h\in V_h, \end{aligned}$$

(5.1)

and for $1\le n\le N$, where $U_h^n:= U_h(t_n)$ and $U_h^{n-1/2}=\tfrac{1}{2}( U_h^n+ U_h^{n-1})$. For the discrete initial data, we choose $U_h^0=R_h u_0\in V_h$, where $R_h:H^1_0(\Omega ) \mapsto V_h$ is the Ritz projection defined by $\langle \kappa \nabla (R_h w-w),\nabla v_h \rangle = 0$ for all $v_h\in V_h$.

In the next theorem, we prove that the numerical solution defined by (5.1) is second-order accurate in both time and space, provided that the time mesh exponent $\gamma$ is chosen appropriately. In comparison, under heavier regularity assumptions and stronger graded meshes, convergence of order $h^2+\tau ^{(3-\alpha )/2}$ was proved by Mustapha et al. [21]. Furthermore, the proof therein is more technical and lengthy. Use of the piecewise-linear polynomial function ${\widehat{u}}$, see (2.6), and a duality argument allowed us to improve the convergence rate, simplify the proof and also relax the regularity assumptions. In addition to the regularity assumption in (2.11), for $t>0,$ we impose

$$\begin{aligned} \Vert u'(t)\Vert _2+t\Vert u''(t)\Vert _2\le C\,t^{\upsilon -1},\quad \text {for some }\upsilon >0. \end{aligned}$$

(5.2)

Theorem 4

Let u be the solution of (1.1) and let $U_h^n$ be the approximate solution defined by (5.1). Assume that the regularity assumptions in (2.11) and (5.2) are satisfied for $\sigma ,\upsilon >\alpha /2$, and choose the mesh grading exponent $\gamma >\max \{2/\sigma ,1/\upsilon , (3-\alpha )/(2\sigma -\alpha )\}$. Then, $\Vert u- U_h\Vert _{L^2(J)}\le C(\tau ^2+h^2).$

Proof

Decompose the error as $u- U_h= (u- u_h)+(u_h- U_h)$, where $u_h$ is the Galerkin finite element solution of (1.1) defined by

$$\begin{aligned} \langle \partial _t^\alpha u_h,v_h \rangle +\langle \kappa \nabla u_h,\nabla v_h \rangle =\langle f,v_h \rangle \quad \text {for all }v_h\in V_h, \end{aligned}$$

(5.3)

for each fixed $t >0,$ with $u_h(0)= U_h^0=R_hu_0.$ From this, the weak formulation of (1.1), and the orthogonality property of the Ritz projection, we have

$$\begin{aligned} \langle \partial _t^\alpha (u_h-R_h u),v_h \rangle +\langle \kappa \nabla (u_h-R_hu),\nabla v_h \rangle =\langle \partial _t^\alpha (u-R_h u),v_h \rangle \quad \text {for }v_h\in V_h. \end{aligned}$$

Choose $v_h= (u_h-R_hu)'$, integrate over (0, t) and apply Lemma 1 to the right-hand side with $\epsilon =1/(4\alpha ^2)$. After canceling the common terms,

$$\begin{aligned}4\alpha ^2\Vert \sqrt{\kappa } \nabla (u_h-R_h u)(t)\Vert ^2 \le \mathcal {I}( \langle \partial _t^\alpha e_h,e_h' \rangle )(t),~~\textrm{with}~~ e_h=u-R_h u. \end{aligned}$$

The error bound for the Ritz projection and the regularity assumption in (5.2) yield $\Vert e_h'(t)\Vert \le Ch^2\Vert u'(t)\Vert _2\le Ch^2 t^{\upsilon -1}$. Hence, $\Vert \partial _t^\alpha e_h(t)\Vert \le Ch^2 t^{\upsilon -\alpha }$ and consequently, $\mathcal {I}( \langle \partial _t^\alpha e_h,e_h' \rangle )(t)\le Ch^4$ for $\upsilon >\alpha /2$. Inserting this estimate in the above equation, we obtain $\Vert \nabla (u_h-R_h u)(t)\Vert \le C h^2$ for $\upsilon >\alpha /2$, and thus, by applying the Poincaré and triangle inequalities, we get $\Vert u(t)- u_h(t)\Vert \le Ch^2.$

The remaining target now is to estimate $U_h- u_h.$ By analogy with our earlier splitting (2.5), we let

$$\begin{aligned}\eta _h= u_h- U_h,\quad \psi _h=u-R_h{\widehat{u}}\quad \textrm{and}\quad \theta _h= U_h-R_h {\widehat{u}}.\end{aligned}$$

From (5.1) and (5.3), and with $\chi _h=u_h-R_h{\widehat{u}},$ we have

$$\begin{aligned}\int _{I_n}[\langle \partial _t^\alpha \theta _h(t),v_h \rangle +\langle \kappa \nabla \theta _h(t),\nabla v_h \rangle ]\,dt =\int _{I_n}[\langle \partial _t^\alpha \chi _h(t),v_h \rangle +\langle \kappa \nabla \chi _h(t),\nabla v_h \rangle ]\,dt,\end{aligned}$$

for $v_h\in V_h$. Using the orthogonality property of the Ritz projection and the definition of ${\widehat{u}}$, in addition to (5.3),

$$\begin{aligned}\int _{I_n}\langle \kappa \nabla \chi _h(t),\nabla v_h \rangle \,dt =\int _{I_n}\langle \kappa \nabla ( u_h- u)(t),\nabla v_h \rangle \,dt=\int _{I_n}\langle \partial _t^\alpha (u- u_h)(t),v_h \rangle \,dt,\end{aligned}$$

and hence

$$\begin{aligned}\int _{I_n}[\langle \partial _t^\alpha \theta _h(t),v_h \rangle +\langle \kappa \nabla \theta _h(t),\nabla v_h \rangle ]\,dt =\int _{I_n}\langle \partial _t^\alpha \psi _h(t),v_h \rangle \,dt, \quad \text {for }v_h\in V_h.\end{aligned}$$

By repeating the steps from (2.8) to (2.10), we deduce that

$$\begin{aligned} \alpha ^2\mathcal {I}(\langle \partial _t^\alpha \theta _h,\theta _h' \rangle )(T) \le \mathcal {I}(\langle \partial _t^\alpha \psi _h,\psi _h' \rangle )(T). \end{aligned}$$

(5.4)

Applying Lemma 2 with $v={\widehat{e}}_h':=(\widehat{u}-R_h{\widehat{u}})'$ and $w=\psi '$ so that $\psi _h'=v+w$,

$$\begin{aligned}\mathcal {I}(\langle \partial _t^\alpha \psi _h,\psi _h' \rangle )(T) \le (1+\alpha ^{-1})\Big ( \mathcal {I}(\langle \partial _t^\alpha {\widehat{e}}_h, {\widehat{e}}_h' \rangle )(T) +\mathcal {I}(\langle \partial _t^\alpha \psi ,\psi ' \rangle )(T)\Big ).\end{aligned}$$

For $t\in I_j$, since ${\widehat{u}}'(t)=\tau _j^{-1}({\widehat{u}}^j-{\widehat{u}}^{j-1}),$ the Ritz projection error bound gives

$$\begin{aligned}\Vert {\widehat{e}}_h'(t)\Vert \le Ch^2\Vert {\widehat{u}}'(t)\Vert _2 \le Ch^2\tau _j^{-1}\Vert \psi ^j-\psi ^{j-1}\Vert _2 + Ch^2\tau _j^{-1}\int _{I_j}\Vert u'(s)\Vert _2\,ds.\end{aligned}$$

From Lemma 3, (5.2) and the time mesh property (2.2), we have

$$\begin{aligned}{} & {} \Vert \psi ^j-\psi ^{j-1}\Vert _2\le \Vert \psi ^j\Vert _2+\Vert \psi ^{j-1}\Vert _2\le 2\sum _{i=1}^j \int _{I_j}(t-t_{j-1})\Vert u''(t)\Vert _2\,dt \\{} & {} \quad \le C\tau _1^\upsilon + C\tau \int _{t_1}^{t_j} t^{\upsilon -1/\gamma -1}\,dt \le C\tau _1^\upsilon + C\tau t_j^{\upsilon -1/\gamma }\le C\tau t_j^{\upsilon -1/\gamma } \le C\tau _j t_j^{\upsilon -1}, \end{aligned}$$

for $\gamma >1/\upsilon$ with $j\ge 1.$ Combining the above two estimates, we conclude that $\Vert {\widehat{e}}_h'(t)\Vert \le Ch^2 t_j^{\upsilon -1}\le Ch^2 t^{\upsilon -1}$ for $t \in I_j$. This leads to $\Vert {\widehat{e}}_h'(t)\Vert \le Ch^2\omega _\upsilon (t)$ and $\Vert \partial _t^\alpha {\widehat{e}}_h(t)\Vert \le Ch^2\omega _{1-\alpha +\upsilon }(t).$ Thence,

$$\begin{aligned} \mathcal {I}(\langle \partial _t^\alpha {\widehat{e}}_h, {\widehat{e}}_h ' \rangle )(T) \le Ch^4\int _0^T\omega _{1-\alpha +\upsilon }\,\omega _\upsilon \,dt \le Ch^4\int _0^T t^{2\upsilon -\alpha -1}\,dt\le Ch^4, \end{aligned}$$

for $\upsilon >\alpha /2$, so by Lemma 6,

$$\begin{aligned} \mathcal {I}(\langle \partial _t^\alpha \psi _h,\psi _h' \rangle )(T) \le C\Big (h^4+\mathcal {I}(\langle \partial _t^\alpha \psi ,\psi ' \rangle )(T) \Big ) \le C(h^4+\tau ^{3-\alpha }). \end{aligned}$$

(5.5)

Adapting (4.3), suppose that $\varphi _h(t) \in V_h$ satisfies the discrete final-value problem

$$\begin{aligned} -(\mathcal {J}_{T}^{1-\alpha }\varphi _h)'(t)+\mathcal {A}_h \varphi _h(t) =\eta _h(t) \quad \text {for }0<t<T, \quad \text {with } \varphi _h(T)=0, \end{aligned}$$

(5.6)

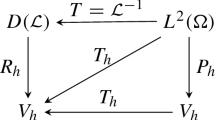
where the discrete elliptic operator $\mathcal {A}_h:V_h \rightarrow V_h$ is defined by $\langle \mathcal {A}_h v_h, q_h \rangle =\langle \kappa \nabla v_h,\nabla q_h \rangle$ for all $v_h,q_h \in V_h$. We now repeat the step in the error analysis of Sect. 4, with $\eta _h,$ $\theta _h$, $\psi _h$ and $\mathcal {A}_h$ playing the roles of $\eta ,$ $\theta$ $\psi$ and $\mathcal {A}$, respectively, and using (5.1) and (5.4) instead of (2.4) and (2.10), and (5.5) instead of Lemma 6. We notice for $\gamma > \max \{2/\sigma ,1/\upsilon , (3-\alpha )/(2\sigma -\alpha )\}$ and for $\sigma ,\upsilon > \alpha /2,$ that

$$\begin{aligned} \Vert u_h- U_h\Vert _{L^2(J)}^2 \le C\tau ^{1+\alpha }(h^4+\tau ^{3-\alpha }). \end{aligned}$$

The proof of this theorem is completed. $\square$

6 Numerical Results

In this section, we illustrate numerically the theoretical finding in Theorem 1. An $O(h^2)$ convergence of the finite element solution was confirmed for various choices of the given data [9, 11, 23]. In time, some numerical convergence results (piecewise linear discontinuous Petrov–Galerkin method) were also delivered [21]. However, we illustrate the errors and convergence rates in the stronger $L^\infty (J;L^2(\Omega ))$-norm on more realistic examples. We choose $\kappa =1$, $\Omega =(0,1)$ and a uniform spatial grid $\mathcal {T}_h$. In both examples, we choose h so that the error from the time discretization dominates.

Example 1

We choose $u_0(x)=x(1-x)$ and $f\equiv 0$. Thus, by separating variables, the continuous solution has a series representation in terms of the Mittag–Leffler function $E_\alpha$,

$$\begin{aligned} u(x,t)=8\sum _{m=0}^\infty \lambda _m^{-3}E_{\alpha }(-\lambda _m^2 t^{\alpha }) \sin (\lambda _m x),\quad \text {where } \lambda _m=(2m+1)\pi . \end{aligned}$$

Since $u_0\in \dot{H}^{2.5^-}(\Omega )$, the regularity estimate (2.11) is satisfied for $\sigma =\alpha$. Thus, we expect from Theorem 1 that $e_\tau :=\Vert u- U_h\Vert _{L^2(J)}\le C\tau ^2$ provided that the mesh exponent $\gamma > \max \{2/\alpha ,(3-\alpha )/\alpha \}=(3-\alpha )/\alpha$. The numerical results in Table 1 indicate order $\tau ^2$ convergence in the stronger $L^\infty (J;L^2(\Omega ))$-norm for $\gamma > 2/\alpha$. Rates of order $\tau ^{\sigma \gamma }$ for $1\le \gamma \le 2/\sigma =2/\alpha$ are observed. Thence, our imposed assumption on $\gamma$ is not sharp.

To measure the $L^\infty (J;L^2(\Omega ))$ error $E_\tau :=\max _{0\le t\le T}\Vert u-U_h\Vert$, we approximated $E_\tau$ by $\max _{1\le j\le N}\max _{1\le i\le 3} \Vert u(t_{i,j})- U_h(t_{i,j})\Vert$ where $t_{i,j}:=t_{j-1}+i\tau _j/3$. In our calculations, the $L^2(\Omega )$ norm, $\Vert \cdot \Vert ,$ is approximated using the two-point composite Gauss quadrature rule.

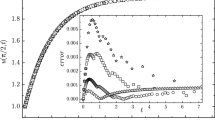
In all tables and figures, we evaluated the series solution by truncating the infinite series after 60 terms. The empirical convergence rate CR is calculated by halving $\tau$, that is, $\text {CR}=\log _2(E_{\tau }/E_{\tau /2})$. Figure 1 plots the nodal errors $\Vert U^n_h-u(t_n)\Vert$ against $t_n\in [0,1]$ for different values of N in the cases $\gamma =1$ and $\gamma =4$. The practical benefit of the mesh grading is evident.

Table 1 Errors and empirical convergence rates for Example 1 with $\alpha =0.5$, using different choices of the time mesh-grading exponent $\gamma$

Fig. 1

Errors for Example 1 as functions of t for different choices of N when $\alpha =0.5$, taking $\gamma =1$ in the left figure and $\gamma =4$ in the right figure

Example 2

We again take $f\equiv 0$ but now choose less regular initial data, namely, the hat function on the unit interval, $u_0(x)=1-2|x-\tfrac{1}{2}|$. So,

$$\begin{aligned} u(x,t)=4\sum _{m=0}^\infty (-1)^m\lambda _m^{-2}E_\alpha (-\lambda _m^2t^{\alpha }) \sin (\lambda _mx). \end{aligned}$$

Since $u_0 \in \dot{H}^{1.5^-}(\Omega )$, the regularity property (2.11) is satisfied for $\sigma =\tfrac{3}{4}\alpha$. As in Example 1, the numerical results in Table 2 exhibit convergence of order $\tau ^{\sigma \gamma }$ for $1\le \gamma \le 2/\sigma$ in the stronger $\Vert \cdot \Vert _J$-norm. For a graphical illustration of the impact of the graded mesh on the pointwise error, we fixed $N=80$ in Fig. 2 and plotted the error at the time nodal points for different choices of $\gamma$.

Table 2 Errors and empirical convergence rates for Example 2 using different values of N and different choices of the time mesh exponent $\gamma ,$ with $\alpha =0.7$

Fig. 2

Error at $t_n$ for $1\le n\le N$ in Example 2, for a fixed $N=80$ and different choices of the mesh exponent $\gamma$ with $\alpha =0.7$

Appendix: An \(\alpha \)-Robust Interpolation Estimate

The purpose of this appendix is to prove Corollary 2, which was used in the proof of Theorem 3. Suppose that Y is a complex Hilbert space with inner product $(\cdot ,\cdot )_Y$ and norm $\Vert \cdot \Vert _Y$. Put

$$\begin{aligned} \begin{aligned} X_0=L_2((0,T);Y)\quad \text{ and }\quad X_1=\{\,u\in X_0:u'\in X_0 \text{ and } u(0)=0\,\}, \end{aligned} \end{aligned}$$

(7.1)

equipped with the inner products

$$\begin{aligned} (u,v)_{X_0}=\int _0^T\bigl (u(t),v(t)\bigr )_Y\,dt \quad \text {and}\quad (u,v)_{X_1}=\int _0^T\bigl (u'(t),v'(t)\bigr )_Y\,dt. \end{aligned}$$

We define an unbounded operator $D_0$ on $X_0$ with domain $X_1$, by setting $D_0u=u'$ on the interval (0, T). Let $\Re z$ denote the real part of a complex number z. Since $\Re \bigl (u(t),D_0u(t)\bigr )_Y=\tfrac{1}{2}(d/dt)\Vert u(t)\Vert _Y^2$, we have $\Re (u,D_0u)_{X_0}=\tfrac{1}{2}\Vert u(T)\Vert _Y^2\ge 0$ for all $u\in X_1$. In addition, one easily verifies that

$$\begin{aligned} (\lambda +D_0)^{-1}u(t)=\int _0^te^{-\lambda (t-s)}u(s)\,ds \quad \text {for }0\le t\le T\hbox { and }\lambda \in \mathbb {C}, \end{aligned}$$

(7.2)

so $D_0$ is m-accretive [17, p. 9], and therefore a positive operator [17, pp. 1, 11] with $\sup _{\lambda >0}\Vert \lambda (\lambda +D_0)^{-1}\Vert _{X_0\rightarrow X_0}=1$, where $\Vert \cdot \Vert _{X_0\rightarrow X_0}$ denotes the operator norm induced by the norm of $X_0$.

Assume that $0<\Re \beta <1$. The operator $D_0^{-\beta }$ is defined via the integral [2, Equation (1.3)]

$$\begin{aligned} D_0^{-\beta }u=\frac{\sin \pi \beta }{\pi }\int _0^\infty \lambda ^{-\beta } (\lambda +D_0)^{-1}u\,d\lambda \quad \text {for }u\in X_0. \end{aligned}$$

A short calculation using (7.2) shows [2, Theorem 2.2] that $D_0^{-\beta }u=\mathcal {I}^\beta u$. One may then define [2, Equation 1.4], [17, Equation (3.1)]

$$\begin{aligned} D_0^\beta u=D_0^{\beta -1}D_0u=\frac{\sin \pi \beta }{\pi }\int _0^\infty \lambda ^{\beta -1}(\lambda +D_0)^{-1}D_0u\,d\lambda \quad \text {for } u\in X_1. \end{aligned}$$

The operator $D_0^\beta$ coincides with $\mathcal {I}^{1-\beta }u'=(\mathcal {I}^{1-\beta }u)'$, or in other words, with both the Caputo and Riemann–Liouville fractional derivatives of order $\beta$.

For $0\le \alpha \le 1$, let $X_\alpha$ denote the complex interpolation space [4, Chap. 4] arising from $X_0$ and $X_1$. The next result is known [17, Theorem 11.6.1], but we sketch the proof in order to verify that the constant does not depend on $\alpha$.

Theorem 5

Let $0<\alpha <1$. For the spaces (7.1) and any complex Hilbert space Z, if the linear operator B satisfies $\Vert Bu\Vert _Z\le M_j\Vert u\Vert _{X_j}$ for $u\in X_j$ and $j\in \{0,1\}$, then $\Vert Bu\Vert _Z\le e^{1+(\pi /4)^2}M_0^{1-\alpha }M_1^\alpha \Vert D_0^\alpha u\Vert _{X_0}$ for $D_0^\alpha u\in X_0.$

Proof

If we set $Z_0=Z_1=Z$, then $Z_\alpha =Z$ with equal norms [4, Theorem 4.2.1], so $\Vert Bu\Vert _Z\le M_0^{1-\alpha }M_1^\alpha \Vert u\Vert _{X_\alpha },$ and our task is to estimate the interpolation norm $\Vert u\Vert _{X_\alpha }$ in terms of the fractional derivative $D_0^\alpha u$. Define the closed strip $S=\{\,z\in \mathbb {C}:0\le \Re z\le 1\,\}$ in the complex plane, and let $\mathcal {F}$ denote the space of functions $f:S\rightarrow X_0+X_1$ that are bounded and continuous on S, analytic in the interior of S, and such that f(iy) and $f(1+iy)$ tend to zero as $|y|\rightarrow \infty$. It can be shown [4, Lemma 4.1.1] that $\mathcal {F}$ is a Banach space with respect to the norm

$$\begin{aligned}\Vert f\Vert _{\mathcal {F}}=\max \Bigl (\sup _{y\in \mathbb {R}}\Vert f(iy)\Vert _{X_0}, \sup _{y\in \mathbb {R}}\Vert f(1+iy)\Vert _{X_1}\Bigr ).\end{aligned}$$

The space $X_\alpha$ then consists of those $u\in X_0+X_1$ such that $u=f(\alpha )$ for some $f\in \mathcal {F}$, with the interpolation norm defined by

$$\begin{aligned}\Vert u\Vert _{X_\alpha }=\inf \{\,\Vert f\Vert _{\mathcal {F}}: u=f(\alpha )\text { and }f\in \mathcal {F}\,\}.\end{aligned}$$

If we define $f(z)=e^{(z-\alpha )^2}D_0^{\alpha -z}u$, then $f(\alpha )=u$ with

$$\begin{aligned}\Vert f(iy)\Vert _{X_0}=e^{\alpha ^2-y^2}\Vert D_0^{-iy}D_0^\alpha u\Vert _{X_0}\end{aligned}$$

and

$$\begin{aligned}\Vert f(1+iy)\Vert _{X_1}=e^{(1-\alpha )^2-y^2}\Vert D_0(D_0^{\alpha -1-iy}u)\Vert _{X_0}=e^{(1-\alpha )^2-y^2}\Vert D_0^{-iy}D_0^\alpha u\Vert _{X_0}.\end{aligned}$$

If $\Re \zeta \ge 0$ then $|\zeta ^{iy}|\le e^{\pi |y|/2}$ for $y\in \mathbb {R}$. Therefore, because $D_0$ is m-accretive, $\Vert D_0^{iy}u\Vert _{X_0}\le e^{\pi |y|/2}\Vert u\Vert _{X_0}$ for $u\in X_0$ ( [25, Example 2], [7, Theorem 7.1.7]). Thus

$$\begin{aligned}\Vert u\Vert _{X_\alpha }\le \Vert f\Vert _{\mathcal {F}} \le \max \Bigl (\sup _{y\in \mathbb {R}}e^{\alpha ^2-y^2+\pi |y|/2}, \sup _{y\in \mathbb {R}}e^{(1-\alpha )^2-y^2+\pi |y|/2}\Bigr ) \Vert D_0^\alpha u\Vert _{X_0},\end{aligned}$$

and since $-y^2+\tfrac{1}{2}\pi |y| =(\tfrac{1}{4}\pi )^2-(|y|-\tfrac{1}{4}\pi )^2\le (\tfrac{1}{4}\pi )^2,$ the proof is completed. $\square$

The interpolation estimate used in the proof of Theorem 3 now follows by repeating the preceding arguments with $D_0$ and $X_1$ replaced by their time-reversed equivalents

$$\begin{aligned}D_T u(t)=-u'(t)\quad \text {and}\quad X_{T,1}=\{\,u\in X_0:u'\in X_0\text { and }u(T)=0\,\}.\end{aligned}$$

In fact, $\Re (u,D_T u)_{X_0}=\tfrac{1}{2}\Vert u(0)\Vert _Y^2\ge 0$ for all $u\in X_{T,1}$, and

$$\begin{aligned}(\lambda +D_T)^{-1}u(t)=\int _t^Te^{-\lambda (s-t)}u(s)\,ds \quad \text {for }0\le t\le T\text { and }\lambda \in \mathbb {C},\end{aligned}$$

so $D_T$ is m-accretive, and we find that if $0<\Re \beta <1$ then $D_T^{-\beta }u=\mathcal {J}_{T}^{\beta }u$ for $u\in X_0$, with

$$\begin{aligned}D_T^\beta u=D_TD_T^{\beta -1}u=(\mathcal {J}_{T}^{1-\beta }u)' \quad \text {for }u\in X_{T,1}.\end{aligned}$$

Corollary 2

In the statement of Theorem 5, we may replace $D_0$ and $X_1$ with $D_T$ and $X_{T,1}$, respectively.