Analysis of an Energy-Dissipating Finite Volume Scheme on Admissible Mesh for the Aggregation-Diffusion Equations

Abstract

We develop the numerical analysis of an energy-dissipating finite volume scheme on admissible meshes for the non-local, nonlinear aggregation-diffusion equations. Crucially, this scheme keeps the dissipation property unconditionally of an associated fully discrete energy, and preserves the mass and positivity conservation of the density. We establish the well-posedness, stability and error analysis of the method. Several numerical examples are presented to verify the theoretical results.

Proof of (64)

• (1) (Proof of the estimate (64) for $E_{321}(\theta ^n)$) In view of $\tau _{ij} = \frac{| e^*_{ij} |}{ |\overrightarrow{p_i p_j}| }$, we see that $\frac{\rho ^n_i + \rho ^n_j}{2} \tau _{ij} \big (H'(\rho ^n_j) - H'(\rho ^n_i) \big ) = \int _{e^*_{ij}} \frac{\rho ^n_i + \rho ^n_j}{2} \frac{H'(\rho ^n_j) - H'(\rho ^n_i)}{|\overrightarrow{p_i p_j}|} ~ds$. Now $E_{321}(\theta ^n)$ becomes

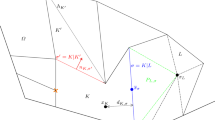
  $$\begin{aligned} E_{321}(\theta ^n)= & {} \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big )\\{} & {} \bigg (\int _{e^*_{ij}} \Big (\rho ^n_h \nabla H'(\rho ^n_h) \cdot \varvec{n}_{ij} - \frac{\rho ^n_i + \rho ^n_j}{2} \frac{H'(\rho ^n_j) - H'(\rho ^n_i)}{|\overrightarrow{p_i p_j}|} \Big ) ~ds \bigg ) \\= & {} \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \bigg (\int _{e^*_{ij}} \nabla H'(\rho ^n_h) \cdot \varvec{n}_{ij} \Big (\rho ^n_h - \frac{\rho ^n_i + \rho ^n_j}{2} \Big ) ~ds \bigg )\\{} & {} + \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \\{} & {} \bigg (\int _{e^*_{ij}} \frac{\rho ^n_i + \rho ^n_j}{2} \Big (\nabla H'(\rho ^n_h) \cdot \varvec{n}_{ij} - \frac{H'(\rho ^n_j) - H'(\rho ^n_i)}{|\overrightarrow{p_i p_j}|} \Big ) ~ds \bigg ) \\=: & {} E_{3211}(\theta ^n) + E_{3212}(\theta ^n). \end{aligned}$$

  We set $p^* = \frac{p_i + p_j}{2}$ (see Fig. 1(b)) and rewrite $E_{3211}(\theta ^n)$ as

  $$\begin{aligned} E_{3211}(\theta ^n)= & {} \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij} } \Big (H''(\rho ^n_h) \nabla \rho ^n_h \cdot \varvec{n}_{ij} \\{} & {} - H''(\rho ^n_h(p^*)) \nabla \rho ^n_h(p^*) \cdot \varvec{n}_{ij} \Big ) \Big (\rho ^n_h - \frac{\rho ^n_i + \rho ^n_j}{2} \Big )~ds \\{} & {} + \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij}} H''(\rho ^n_h(p^*)) \nabla \rho ^n_h(p^*) \cdot \varvec{n}_{ij} \Big (\rho ^n_h - \frac{\rho ^n_i + \rho ^n_j}{2} \Big )~ds. \end{aligned}$$

  Since $\rho ^n_h$ is a piecewise linear function, we have $\nabla \rho ^n_h \cdot \varvec{n}_{ij} = \nabla \rho ^n_h(p^*) \cdot \varvec{n}_{ij}$ on $e^*_{ij}$. Application of (28) enables us to write the first term of $E_{3211}(\theta ^n)$ as

  $$\begin{aligned} \begin{aligned}&\bigg | \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \big ( \nabla \rho ^n_h \cdot \varvec{n}_{ij} \big ) \int _{e^*_{ij}} \Big (H''(\rho ^n_h) - H''(\rho ^n_h(p^*)) \Big ) \Big (\rho ^n_h - \frac{\rho ^n_i + \rho ^n_j}{2} \Big )~ds \bigg | \\&\quad \le C \sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2(T_i \cup T_j)} \Vert \nabla \rho ^n_h \Vert _{L^{\infty }(T^*_i \cup T^*_j) } L h^{\frac{3}{2}} \Vert \rho ^n_h \Vert _{W^{1, 4}(T_i \cup T_j)} h^{\frac{1}{2}} \Vert \nabla \rho ^n_h \Vert _{L^{4}(T_i \cup T_j)} \\&\quad \le C h \Vert \nabla \theta ^n \Vert _{L^2} \Vert \nabla \rho ^n_h \Vert _{L^2} \Vert \rho ^n_h \Vert _{W^{1, 4}}^2 \le C h \Vert \nabla \theta ^n \Vert _{L^2}, \end{aligned} \end{aligned}$$

  (67)

  where the first inequality use the Lipschitz continuity of $H''$ (see (25b)) and (50). The second one applies (51) and the Hölder inequality. $\Vert \nabla \rho ^n_h \Vert _{L^2} \le C$ and the assumption $\Vert \rho ^n_h \Vert _{W^{1, 4}} \le C$ lead to the last inequality. Furthermore, on account of (28), (51), (50), and the assumption $H \in C^2({\mathbb {R}}^+)$ and $\Vert \rho ^n_h \Vert _{W^{1,4}} \le C$, the second term of $E_{3211}(\theta ^n)$ is calculated as follows

  $$\begin{aligned} \begin{aligned}&\bigg | \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \big (H''(\rho ^n_h(p^*)) \nabla \rho ^n_h(p^*) \cdot \varvec{n}_{ij} \big ) \int _{e^*_{ij}} \Big (\rho ^n_h - \frac{\rho ^n_i + \rho ^n_j}{2} \Big )~ds \bigg | \\&\quad \le C \sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2(T_i \cup T_j)} \Vert H''(\rho ^n_h) \Vert _{L^{\infty }(T^*_i \cup T^*_j)} \Vert \nabla \rho ^n_h \Vert _{L^{\infty }(T^*_i \cup T^*_j)} h^{\frac{3}{2}} \Vert \rho ^n_h \Vert _{W^{1,4}(T_i \cup T_j)} \\&\quad \le C h \Vert H''(\rho ^n_h) \Vert _{L^{\infty }} \Vert \rho ^n_h \Vert _{W^{1,4}}^2 \Vert \nabla \theta ^n \Vert _{L^2} \le C h \Vert \nabla \theta ^n \Vert _{L^2}. \end{aligned} \end{aligned}$$

  (68)

  Combining (67) and (68), we assert that

  $$\begin{aligned} | E_{3211}(\theta ^n) | \le C h \Vert \nabla \theta ^n \Vert _{L^2}. \end{aligned}$$

  (69)

  We proceed to analyze $E_{3212}(\theta ^n)$. We define two points $\tilde{p}$ (on $e^*_{ij}$) and $\bar{p}$ (on $| \overrightarrow{p_i p_j} |$) (see Fig. 1(b)) satisfying

  $$\begin{aligned} \begin{aligned}&\int _{e^*_{ij} } \nabla H'(\rho ^n_h) \cdot \varvec{n}_{ij} ~ds = |e^*_{ij}| \nabla H'(\rho ^n_h(\tilde{p})) \cdot \varvec{n}_{ij} = |e^*_{ij}| H''(\rho ^n_h(\tilde{p})) \nabla \rho ^n_h(\tilde{p}) \cdot \varvec{n}_{ij}, \\&\int _{e^*_{ij}} \frac{H'(\rho ^n_j) - H'(\rho ^n_i)}{|\overrightarrow{p_i p_j}|} ~ds = |e^*_{ij}| \nabla H'(\rho ^n_h(\bar{p})) \cdot \varvec{n}_{ij} = |e^*_{ij}| H''(\rho ^n_h(\bar{p})) \nabla \rho ^n_h(\bar{p}) \cdot \varvec{n}_{ij}, \end{aligned} \end{aligned}$$

  (70)

  and we see that $\nabla \rho ^n_h(\tilde{p}) \cdot \varvec{n}_{ij} = \nabla \rho ^n_h(\bar{p}) \cdot \varvec{n}_{ij}$ because $\rho ^n_h$ is a piecewise linear function. Then, substituting (70) into $E_{3212}(\theta ^n)$, we see that

  $$\begin{aligned} \begin{aligned} | E_{3212}(\theta ^n) |&= \bigg | \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \frac{\rho ^n_i + \rho ^n_j}{2} |e^*_{ij}| \\&\quad \bigg ( H''(\rho ^n_h(\tilde{p})) \nabla \rho ^n_h(\tilde{p}) \cdot \varvec{n}_{ij} - H''(\rho ^n_h(\bar{p})) \nabla \rho ^n_h(\bar{p}) \cdot \varvec{n}_{ij} \bigg ) \bigg | \\&= \bigg | \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \frac{\rho ^n_i + \rho ^n_j}{2} |e^*_{ij}|\\&\quad \nabla \rho ^n_h(\tilde{p}) \cdot \varvec{n}_{ij} \big (H''(\rho ^n_h(\tilde{p})) - H''(\rho ^n_h(\bar{p})) \big ) \bigg | \\&\le C h \sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2(T_i \cup T_j)} \Vert \rho ^n_h \Vert _{L^{\infty }(T^*_i \cup T^*_j)} \Vert \nabla \rho ^n_h \Vert _{L^{\infty }(T^*_i \cup T^*_j)} L h^{\frac{1}{2}} \Vert \nabla \rho ^n_h \Vert _{L^4(T_i \cup T_j)}\\&\le C h \Vert \nabla \theta ^n \Vert _{L^2} \Vert \rho ^n_h \Vert _{L^{\infty }} \Vert \nabla \rho ^n_h \Vert _{L^4}^2 \le C h \Vert \nabla \theta ^n \Vert _{L^2}, \end{aligned} \end{aligned}$$

  (71)

  where we used the assumptions $\Vert \nabla \rho ^n_h \Vert _{L^4} \le C$ and $\Vert \rho ^n_h \Vert _{L^{\infty }} \le C$, (28), the Hölder inequality, and the fact that $|e^*_{ij}| \simeq h$. Therefore, (69) and (71) give the estimate of $E_{321}(\theta ^n)$. $\square$

• (2) (Proof of the estimate (64) for $E_{322}(\theta ^n)$) The argument is similar to the estimate of $E_{321}(\theta ^n)$. We recall that $\frac{\rho ^n_i + \rho ^n_j}{2} \tau _{ij} (V_j - V_i) = \int _{e^*_{ij}} \frac{\rho ^n_i + \rho ^n_j}{2} \frac{V_j - V_i}{ |\overrightarrow{p_i p_j}|} ~ds$, and rewrite $E_{322}(\theta ^n)$ as

  $$\begin{aligned} \begin{aligned} E_{322}(\theta ^n)&= \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij}} \Big (\rho ^n_h \nabla V \cdot \varvec{n}_{ij} - \frac{\rho ^n_i + \rho ^n_j}{2} \frac{V_j - V_i}{ |\overrightarrow{p_i p_j}|} \Big ) ~ds \\&= \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \Big [ \int _{e^*_{ij} } \nabla V \cdot \varvec{n}_{ij} \big (\rho ^n_h - \frac{\rho ^n_i + \rho ^n_j}{2} \big ) ~ds \\&\quad + \int _{e^*_{ij} } \frac{\rho ^n_i + \rho ^n_j}{2} \big (\nabla V \cdot \varvec{n}_{ij} - \frac{V_j - V_i}{ |\overrightarrow{p_i p_j}|} \big ) ~ds \Big ]\\&=: E_{3221}(\theta ^n) + E_{3222}(\theta ^n). \end{aligned} \end{aligned}$$

  By (50), the Hölder inequality and $\Vert \rho ^n_h \Vert _{H^1} \le C$, it is obvious that

  $$\begin{aligned} | E_{3221}(\theta ^n) | \le C \sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2(T_i \cup T_j)} \Vert \nabla V \Vert _{L^{\infty }(T^*_i \cup T^*_j)} h \Vert \rho ^n_h \Vert _{H^1(T_i \cup T_j)} \le C h \Vert \nabla \theta ^n \Vert _{L^2}. \end{aligned}$$

  There exist two points $\tilde{p}$ (on $e^*_{ij}$) and $\bar{p}$ (on $| \overrightarrow{p_i p_j} |$) (see Fig. 1(b)), such that

  $$\begin{aligned} \int _{e^*_{ij} } \nabla V \cdot \varvec{n}_{ij} ~ds = |e^*_{ij}| \nabla V(\tilde{p}) \cdot \varvec{n}_{ij}, \qquad \int _{e^*_{ij} } \frac{V_j - V_i}{|\overrightarrow{p_i p_j}|} ~ds = |e^*_{ij}| \nabla V(\bar{p}) \cdot \varvec{n}_{ij}. \qquad \end{aligned}$$

  (72)

  By assumption (25c), $\Vert \rho ^n_h \Vert _{L^2} \le C$, and the fact that $| \tilde{p} - \bar{p} | \le Ch$, we have

  $$\begin{aligned} \begin{aligned} |E_{3222}(\theta ^n)|&= \bigg | \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \frac{\rho ^n_i + \rho ^n_j}{2} |e^*_{ij}| \big (\nabla V(\tilde{p}) - \nabla V(\bar{p}) \big ) \cdot \varvec{n}_{ij} \bigg | \\&\le C \sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2(T_i \cup T_j)} h \Big | \frac{\rho ^n_i + \rho ^n_j}{2} \Big | L | \tilde{p} - \bar{p} | \\&\le C h \Big (\sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2(T_i)}^2 \Big )^{\frac{1}{2}} \Big (\sum _{e^*_{ij} \in {\mathscr {E}}^*} h^2 \Big |\frac{\rho ^n_i + \rho ^n_j}{2}^2 \Big | \Big )^{\frac{1}{2}} \\&\le C h \Vert \nabla \theta ^n \Vert _{L^2} \Vert \rho ^n_h \Vert _{L^2} \le C h \Vert \nabla \theta ^n \Vert _{L^2}. \end{aligned} \end{aligned}$$

  According to the above estimates, we see that

  $$\begin{aligned} |E_{322}(\theta ^n)| \le C h \Vert \nabla \theta ^n \Vert _{L^2}. \end{aligned}$$

  (73)

  $\square$

• 3) (Proof of the estimate (64) for $E_{322}(\theta ^n)$) Our next objective is to evaluate $E_{323}(\theta ^n)$. We begin by recalling the definition of discrete convolution (9) and convolution $\nabla (W * \rho ^*_h) = \int _{\varOmega } \nabla W(x - x_2) \rho ^*_h(x_2) ~dx_2$. Substituting it into $E_{323}(\theta ^n)$, we find that

  $$\begin{aligned} \begin{aligned} E_{323}(\theta ^n)&= \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \bigg [\int _{e^*_{ij}} \bigg ( \rho ^n_h \Big (\int _{\varOmega } \nabla W(x - x_2) \\&\quad \rho ^*_h(x_2) ~dx_2 \Big ) \cdot \varvec{n}_{ij} - \Big ( \frac{\rho ^n_i + \rho ^n_j}{2} \sum _{l = 1}^{N_p} \frac{W_{j - l} - W_{i - l}}{| \overrightarrow{p_i p_j} |} \rho ^*_l | T^*_l | \Big ) \bigg )~ds \bigg ] \\&= \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij} } \Big ( \int _{\varOmega } \nabla W(x - x_2) \rho ^*_h(x_2) ~dx_2 \Big ) \cdot \varvec{n}_{ij} \\&\quad \big (\rho ^n_h - \frac{\rho ^n_i + \rho ^n_j}{2} \Big )~ds + \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij} } \frac{\rho ^n_i + \rho ^n_j}{2} \bigg (\Big ( \int _{\varOmega } \nabla W(x - x_2) \\&\quad \rho ^*_h(x_2) ~dx_2 \Big ) \cdot \varvec{n}_{ij} - \sum _{l = 1}^{N_p} \frac{W_{j - l} - W_{i - l}}{| \overrightarrow{p_i p_j} |} \rho ^*_l | T^*_l | \bigg )~ds \\&\quad =: E_{3231}(\theta ^n) + E_{3232}(\theta ^n). \end{aligned} \end{aligned}$$

  By (50) and $\Vert \rho ^n_h \Vert _{H^1} \le C$, the estimate of $E_{3231}(\theta ^n)$ is straightforward

  $$\begin{aligned} \begin{aligned} |E_{3231}(\theta ^n)| \le C \Vert \nabla W \Vert _{L^{\infty }} \Vert \rho ^*_h \Vert _{L^{\infty }} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2({T_i \cup T_j})} h \Vert \rho ^n_h \Vert _{H^1({T_i \cup T_j})} \le C h \Vert \nabla \theta ^n \Vert _{L^2}. \end{aligned} \end{aligned}$$

  We split $E_{3232}(\theta ^n)$ into two parts

  $$\begin{aligned} E_{3232}(\theta ^n)= & {} \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij}} \Bigg ( \frac{\rho ^n_i + \rho ^n_j}{2} \sum _{l = 1}^{N_p} \int _{T^*_l} \bigg ( \Big ( \nabla W(x - x_2) \\{} & {} \rho ^*_h(x_2) ~dx_2 \Big ) \cdot \varvec{n}_{ij} - \frac{W_{j - l} - W_{i - l}}{| \overrightarrow{p_i p_j} |} \rho ^*_l \bigg ) ~dx_2 \Bigg )~ds \\= & {} \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij}} \Bigg ( \frac{\rho ^n_i + \rho ^n_j}{2} \sum _{l = 1}^{N_p} \int _{T^*_l} \rho ^*_h(x_2) \Big ( \nabla W(x - x_2) \cdot \varvec{n}_{ij} \\{} & {} - \frac{W_{j - l} - W_{i - l}}{| \overrightarrow{p_i p_j} |} \Big ) ~dx_2 \Bigg ) ~ds + \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij}} \Bigg ( \frac{\rho ^n_i + \rho ^n_j}{2} \\{} & {} \sum _{l = 1}^{N_p} \int _{T^*_l} \frac{W_{j - l} - W_{i - l}}{| \overrightarrow{p_i p_j} |} \Big (\rho ^*_h(x_2) - \rho ^*_l \Big ) ~dx_2 \Bigg )~ds. \end{aligned}$$

  We note that $\frac{W_{j - l} - W_{i - l}}{| \overrightarrow{p_i p_j} |} = \frac{W(x_j - x_l) - W(x_i - x_l)}{| \overrightarrow{p_i p_j} |} = \frac{1}{| \overrightarrow{p_i p_j} |} \int _{ \overrightarrow{p_i p_j} } \nabla W(x - x_l) \cdot \varvec{n}_{ij} ~ds$. Moreover, due to the Lipshitz continuity of $\nabla W$ ( i.e., (24d)), we see that $\big | \nabla W (x - x_2) - \nabla W (x - x_l) \big | \le L |x_2 - x_l| \le C h$. Then, by (28), (51), $\Vert \rho ^i_n \Vert _{L^{\infty }} \le C$, $\Vert \rho ^i_h \Vert _{H^{1}} \le C ~ (\forall i = 0, 1, \cdots , n)$, and under the assumption (H1), we rewrite $E_{3232}(\theta ^n)$ and calculate as

  $$\begin{aligned} \begin{aligned} | E_{3232}(\theta ^n) |&= \Bigg | \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \int _{e^*_{ij}} \Bigg ( \frac{\rho ^n_i + \rho ^n_j}{2} \sum _{l = 1}^{N_p} \int _{T^*_l} \rho ^*_h(x_2) \\&\quad \bigg (\frac{1}{| \overrightarrow{p_i p_j} |} \int _{ \overrightarrow{p_i p_j} } \Big ( \nabla W(x - x_2) \\&\quad - \nabla W(x - x_l) \Big ) \cdot \varvec{n}_{ij} ~ds \bigg ) ~dx_2 \Bigg ) ~ds + \frac{1}{2} \sum _{e^*_{ij} \in {\mathscr {E}}^*} \big (\theta ^n(p_i) - \theta ^n(p_j) \big ) \\&\quad \int _{e^*_{ij}} \Bigg ( \frac{\rho ^n_i + \rho ^n_j}{2} \sum _{l = 1}^{N_p} \int _{T^*_l} \frac{W_{j - l} - W_{i - l}}{| \overrightarrow{p_i p_j} |} \Big (\rho ^*_h(x_2) - \rho ^*_l \Big ) ~dx_2 \Bigg )~ds \Bigg | \\&\le C \sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2(T_i \cup T_j)} | e^*_{ij} | \Vert \rho ^n_h \Vert _{L^{\infty }(T^*_i \cup T^*_j)} \sum _{l = 1}^{N_p} | T^*_l | \Vert \rho ^*_h \Vert _{L^{\infty }(T^*_l)} L h \\&\quad + C \sum _{e^*_{ij} \in {\mathscr {E}}^*} \Vert \nabla \theta ^n \Vert _{L^2(T_i \cup T_j)} | e^*_{ij} | \Vert \rho ^n_h \Vert _{L^{\infty }(T^*_i \cup T^*_j)} \sum _{l = 1}^{N_p} | T^*_l | h \Vert \nabla W \Vert _{L^{\infty }(T_i \cup T_j)}\\&\quad \frac{1}{| \overrightarrow{p_i p_j} |} \Vert \nabla \rho ^*_h \Vert _{L^2(T_i \cup T_j)} \\&\le C h \Vert \nabla \theta ^n \Vert _{L^2} \Vert \rho ^n_h \Vert _{L^{2}} \Vert \rho ^*_h \Vert _{L^{\infty }} + C h \Vert \nabla \theta ^n \Vert _{L^2} \Vert \rho ^n_h \Vert _{L^{\infty }} \Vert \nabla W \Vert _{L^{\infty }} \Vert \nabla \rho ^*_h \Vert _{L^2} \\&\le C h \Vert \nabla \theta ^n \Vert _{L^2}, \end{aligned} \end{aligned}$$

  where we use $| e^*_{ij} | \simeq h$, $| \overrightarrow{p_i p_j} | \simeq h$, and $\sum _{l = 1}^{N_p} | T^*_l | = | \varOmega | \le C$. Hence, we conclude (64). $\square$