Active Flux Methods for Hyperbolic Systems Using the Method of Bicharacteristics

Abstract

The Active Flux method is a third order accurate finite volume method for hyperbolic conservation laws, which is based on the use of point values as well as cell average values of the conserved quantities. The resulting method is fully discrete and has a compact stencil in space and time. An important component of Active Flux methods is the evolution formula for the update of the point values. A previously proposed exact evolution formula for acoustics is reviewed and used to construct an Active Flux method for the two-dimensional Maxwell’s equation. Furthermore, the method of bicharacteristics is discussed as a methodology for the derivation of truly multidimensional approximative evolution operators that can be used for the evolution of point values in Active Flux methods. We study accuracy and stability of the resulting methods for acoustics and compare with the Active Flux method that uses the exact evolution operator. Finally, we used the method of bicharacteristics to derive Cartesian grid Active Flux methods for the linearised and nonlinear Euler equations. Numerous test computations illustrate the performance of these new Active Flux methods.

1 Introduction

The Active Flux method is an evolving finite volume method for hyperbolic conservation laws that was previously introduced by Eymann and Roe [10,11,12] and Roe et al. [14, 27, 29]. Much earlier, in 1977, van Leer [33] already proposed a third order accurate method for the one-dimensional advection equation which is equivalent with the Active Flux method. In its original form the method is third order accurate, but higher order versions of the Active Flux method have recently also been proposed, see [2, 30] for details. Classical finite volume methods, which only use cell average values of the conserved quantities as degrees of freedom, increase the stencil in order to achieve high order accuracy in space. Higher order accuracy in time can either be obtained by using the Lax–Wendroff procedure or by using a method of lines approach, which further increases the stencil. In contrast, the Active Flux method enriches the stencil by adding point values as degrees of freedom. This leads to fully discrete methods with a compact stencil in space and time. While the enrichment is similar to discontinuous Galerkin methods, the evolution of the point values in Active Flux methods is computed differently. It uses truly multi-dimensional evolution formulas directly derived from the partial differential equations.

The point value degrees of freedom are located along the grid cell boundary. Together with the cell average values they are used to compute a globally continuous, piecewise quadratic reconstruction. The evolution of the cell average values is computed using a finite volume approach. A quadrature rule, typically Simpson’s rule, is used to approximate the fluxes over a grid cell interface. This requires values of the flux function at all nodes of the quadrature formula, i.e. not only at the previous time level but also at the new and an intermediate time level. Thus, the update of point values plays a crucial role in the definition of Active Flux methods. For scalar conservation laws characteristics can be used to compute the evolution of the point values, see, e.g., [7, 12]. One-dimensional nonlinear systems were studied in [4]. For the acoustic equations, i.e. the standard example of a linear hyperbolic system, exact evolution formulas are available, which can be evaluated for the Active Flux reconstruction and which have been used to construct truly multi-dimensional Active Flux methods. Details can be found in [5, 12, 14]. The solution of the acoustic equations is also an important substep in an operator splitting approach for the Euler equations, see for example [12, 13].

In the present paper we will use the method of bicharacteristics in order to derive truly multidimensional evolution formulas for the update of the point values in Active Flux methods. Bicharacteristics-based multi-dimensional evolution operators for hyperbolic conservation laws were extensively studied, e.g., in [21,22,23, 25, 26]. This approach will in particular allow us to derive new unsplit Active Flux methods for the linearised Euler equations. We will also compare the new approach with previously proposed Active Flux methods for the acoustic equations and show that the accuracy is comparable. Furthermore, we will extend this approach to the nonlinear Euler equations by using local linearisations around each point value degree of freedom. Our method for the Euler equations updates cell average values of the conserved quantities using a finite volume approach and point values of primitive variables using the method of bicharacteristics.

It has been argued, see [28, 30], that explicit, fully-discrete methods with compact stencil lead to more accurate approximations on coarser grids than classical high order accurate methods with larger stencils. Furthermore, they have better stability properties. This makes Active Flux methods an interesting candidate for the simulation of complex flow problems modeled by the Euler or Navier–Stokes equations.

This paper is organised as follows. In Sect. 2 we briefly review the Active Flux method for one and two-dimensional Cartesian grids. In Sect. 3 we propose an Active Flux method for Maxwell’s equations by exploring the relation to acoustics. In Sect. 4 we present the method of bicharacteristics. This allows us to derive new Active Flux methods for the acoustic equations and to study their accuracy and stability in Sect. 5. In Sect. 6 we consider Active Flux methods for the linearised Euler equations using the method of bicharacteristics. Finally, in Sect. 7 we present our new Active Flux method for the two-dimensional Euler equations. While we restrict our considerations to Cartesian grid versions of the Active Flux method, the method of bicharacteristics could also be used for the update of point values on unstructured grids.

2 The Active Flux Method for Hyperbolic Problems

Now we will briefly describe the basic components of the Active Flux method for the simple situation of a one-dimensional scalar conservation law $\partial _t q (x,t) + \partial _x f(q(x,t)) = 0,$ where $q: {\mathbb {R}} \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}$ is the conserved quantity and $f:{\mathbb {R}} \rightarrow {\mathbb {R}}$ is a flux function. We use the notation

$$\begin{aligned} Q_i^n \approx \frac{1}{\Delta x} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} q(x,t_n) \textrm{d}x, \quad Q_{i \pm \frac{1}{2}}^n \approx q\left( x_{i \pm \frac{1}{2}},t_n\right) \end{aligned}$$

for the cell average and the point values of the conserved quantities. In order to describe a time step of the method, we assume that $Q_i^n$ and $Q_{i \pm \frac{1}{2}}^n$ are at least third order accurate approximations. The cell average at the new time level is computed using the finite volume approach

$$\begin{aligned} Q_i^{n+1} = Q_i^n - \frac{\Delta t}{\Delta x} \left( F_{i+\frac{1}{2}} - F_{i-\frac{1}{2}} \right) , \end{aligned}$$

where Simpson’s quadrature rule is used to compute the numerical fluxes, i.e.

$$\begin{aligned} F_{i \pm \frac{1}{2}}:= \frac{1}{6} \left( f\left( Q_{i \pm \frac{1}{2}}^n\right) + 4 f\left( Q_{i \pm \frac{1}{2}}^{n+\frac{1}{2}}\right) + f\left( Q_{i \pm \frac{1}{2}}^{n+1}\right) \right) \approx \frac{1}{\Delta t} \int _{t_n}^{t_{n+1}} f\left( q\left( x_{i \pm \frac{1}{2}},t\right) \right) \textrm{d}t. \end{aligned}$$

The crucial step is the computation of the point values $Q_{i \pm \frac{1}{2}}^{n+\frac{1}{2}}$ and $Q_{i \pm \frac{1}{2}}^{n+1}$ at the grid cell interfaces. In the simplest case of scalar advection, i.e. for $f(q) = a q$, $a \in {\mathbb {R}}$, the exact evolution formula is well known and suggests an update of the form

$$\begin{aligned}{} & {} Q_{i \pm \frac{1}{2}}^{n+\frac{1}{2}} \approx q\left( x_{i \pm \frac{1}{2}},t_{n+\frac{1}{2}}\right) = q\left( x_{i \pm \frac{1}{2}}-a\frac{\Delta t}{2},t_n\right) , \nonumber \\{} & {} Q_{i \pm \frac{1}{2}}^{n+1} \approx q\left( x_{i \pm \frac{1}{2}},t_{n+1}\right) = q\left( x_{i \pm \frac{1}{2}}-a \Delta t,t_n\right) . \end{aligned}$$

To use this evolution formula the unknown solution $q(\cdot ,t_n)$ needs to be approximated by a reconstruction $q^{rec}(\cdot ,t_n)$. In the Active Flux method the reconstructed function is continuous and piecewise quadratic. In grid cell i the uniquely defined reconstruction interpolates the two point values $Q_{i-\frac{1}{2}}^{n}$ and $Q_{i+\frac{1}{2}}^n$ and preserves the cell average value $Q_i^n$. Figure 1 shows a schematic description of the one-dimensional Active Flux method for the advection equation. More details can be found in [12].

Fig. 1

Schematic description of the Active Flux method for the one-dimensional advection equation. In order to use Simpson’s rule we need to compute point values $Q_{i+\frac{1}{2}}^{n+\frac{1}{2}}$ and $Q_{i+\frac{1}{2}}^{n+1}$ of the conserved quantity. These values are obtained by tracing back the characteristics (marked as red curves)

Two-dimensional Active Flux methods on triangular grids were first presented in [12]. Cartesian grid Active Flux methods were proposed in [5, 17]. In both cases the two-dimensional version of Simpson’s rule is used to compute the numerical fluxes. For each grid cell the point values and the cell average value at the old time level are used to compute a quadratic reconstruction. Since the point values are located along the grid cell boundaries, as indicated in Fig. 2, this reconstruction is globally continuous.

A crucial step is again the update of the point values. For advection it is straight forward to use the exact evolution formula. This has for example been done in [12, 17]. Appropriate evolution formulas for the one- and two-dimensional Burgers’ equation were given in [8]. Advective transport in spatially and temporally varying velocity fields was considered in [7] and one-dimensional nonlinear systems were studied in [4]. For the two-dimensional linear acoustic equations, Eymann and Roe [12] originally used an evolution formula that is exact for initial values with constant vorticity (i.e., for irrotational flows). In this case the solution of the acoustic equations can be obtained by solving wave equations for pressure and velocity. For the acoustic equations with general initial values, exact evolution formulas have been derived by Fan and Roe [14] as well as by Barsukow et al. [5]

Fig. 2

Degrees of freedom of the two-dimensional Cartesian grid Active Flux method

In Calhoun et al. [7], a two-dimensional Cartesian grid Active Flux method with adaptive mesh refinement and sub-cycling was presented. The local stencil in space and time and the choice of the degrees of freedom allow a very efficient implementation on adaptively refined grids.

2.1 Previously Used Evolution Formulas for Acoustics

The two-dimensional acoustic equations are given by

$$\begin{aligned} \begin{aligned}&\partial _t p + c \nabla \cdot \textbf{u} = 0 \\&\partial _t \textbf{u} + c \nabla p = 0, \end{aligned} \end{aligned}$$

(1)

where $\textbf{u}:{\mathbb {R}}^2 \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}^2$ is the velocity, $p:{\mathbb {R}}^2 \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}$ is the pressure and $c\in {\mathbb {R}}^+$ is the speed of sound. The evolution formula for the point values of p and ${\textbf{u}}$ used by Eymann and Roe [12] is based on the observation that (1) can be rewritten as

$$\begin{aligned} \begin{aligned} \partial _{tt} p - c^2 \Delta p&= 0 \\ \partial _{tt} \textbf{u} - c^2 \Delta \textbf{u}&= c^2 \nabla \times \textbf{w}, \end{aligned} \end{aligned}$$

(2)

where $\textbf{w} = \nabla \times \textbf{u}$ is the vorticity and $\Delta$ the Laplacian operator. Thus, in a flow with constant vorticity (i.e. irrotational flow) pressure and velocity satisfy a wave equation. Moreover, it can easily be verified that the vorticity is stationary, i.e. $\partial _t \left( \nabla \times \textbf{u} \right) = 0$. Using an exact representation for the solution of the wave equation $\partial _{tt} \phi = c^2 \Delta \phi$ in the form

$$\begin{aligned} \phi (\textbf{x},t) = t M_{c t} \{ \partial _t \phi (\textbf{x},0) \} + \partial _t \left( t M_{c t} \{\phi (\textbf{x},0) \} \right) , \end{aligned}$$

(3)

that can be found, e.g., in Courant and Hilbert [9], Eymann and Roe [12] derived the evolution formulas

$$\begin{aligned} \begin{aligned} p(\textbf{x},t)&= M_R \{ p (\textbf{x},0)\} + R \left( \partial _R M_R \{ p (\textbf{x},0)\} - M_R \{ \nabla \cdot \textbf{u} (\textbf{x}, 0) \} \right) \\ \textbf{u}(\textbf{x},t)&= M_R \{ \textbf{u}(\textbf{x},0) \} + R \left( \partial _R M_R \{ \textbf{u} (\textbf{x},0) \} - M_R \{ \nabla p (\textbf{x},0) \} \right) , \end{aligned} \end{aligned}$$

(4)

where $R = c \cdot t$ and $M_R\{ f\}$ is the spherical mean. In the two-dimensional case, i.e. ${\textbf{x}}=(x,y)$, the spherical mean of a scalar function f over a disc with radius R can be computed via

$$\begin{aligned} M_R \{ f( \textbf{x} ) \}:= \frac{1}{2 \pi R} \int _0^{2\pi } \int _0^R f(x + r \cos (\theta ), y+r \sin (\theta ) ) \frac{r}{\sqrt{R^2 - r^2}} \, \textrm{d}r \, \textrm{d}\theta . \end{aligned}$$

For vector valued quantities the spherical mean is computed component wise. Details on how these formulas can be evaluated for the Active Flux reconstruction on triangular grids, can be found in the Appendix of [12].

In [14], Fan and Roe derived an exact evolution formula for general initial values based on the observation, see [13] for details, that (3) can be expressed in the form

$$\begin{aligned} \phi (\textbf{x},t) = \phi (\textbf{x},0) + t M_{c t} \{ \partial _t \phi (\textbf{x},0)\} + \int _0^{c t} t M_{c t} \{ \Delta \phi (\textbf{x},0) \} \textrm{d}t. \end{aligned}$$

(5)

The application of (5) to the acoustic equations (1) leads to an evolution formula of the form

$$\begin{aligned} \begin{aligned} p(\textbf{x},t)&= p( \textbf{x},0 ) - c t M_{ct} \{ \nabla \cdot \textbf{u} (\textbf{x},0) \}+ \int _0^{ct} t M_{ct} \{ \Delta p(\textbf{x},0) \} \textrm{d}t \\ \textbf{u} (\textbf{x},t)&= \textbf{u}(\textbf{x},0) - ct M_{ct} \{ \nabla p (\textbf{x},0)) \} + \int _0^{ct} t M_{ct} \{ \Delta \textbf{u} (\textbf{x},0)\} \textrm{d}t. \end{aligned} \end{aligned}$$

(6)

Using Helmholtz decomposition, Fan and Roe argued that this is indeed an exact evolution formula for the acoustic equations. The pressure and the curl free component of the velocity satisfy a wave equation and thus (6). The divergence free component is constant in time and therefore correctly contained in the term $\textbf{u}(\textbf{x},0)$.

From (6) it can be seen that changes in pressure are driven by the divergence of the velocity, rather than by velocity gradients, as implied by using dimensional splitting and one-dimensional Riemann solvers. This has been pointed out as a strong argument for using Active Flux methods, see for example [30].

While the derivation of Fan and Roe assumed sufficiently smooth data such that all derivatives can be computed in the classical sense, Barsukow [3] showed that the evolution formula is also valid more generally if interpreted in the distributional sense. Furthermore, a transformation can be used such that (6) is expressed using derivatives in radial direction r. The resulting formulas, which can be found in [5], have the form

$$\begin{aligned} \begin{aligned} p(\textbf{x},t)&= \partial _r \left( r M_r \{p(\textbf{x},0) \} \right) |_{r=c t} - \frac{1}{c t} \partial _r \left( r^2 M_r \{ \textbf{n} \cdot {\textbf{u}}(\textbf{x},0) \} \right) |_{r=c t} \\ {\textbf{u}}(\textbf{x},t)&= {\textbf{u}}(\textbf{x},0) - \frac{1}{c t} \partial _r \left( r^2 M_r \{ {\textbf{n}} p(\textbf{x},0) \} \right) |_{r = ct}\\&\quad + \int _0^{c t} \frac{1}{r} \partial _r \left( \frac{1}{r} \partial _r \left( r^3 M_r \{ (\textbf{n} \cdot \textbf{u}(\textbf{x},0) ) \textbf{n} \right) - r M_r \{ \textbf{u}(\textbf{x},0) \} \right) \, \textrm{d}r. \end{aligned} \end{aligned}$$

(7)

If applied to the Active Flux reconstruction, differentiation across grid cell interfaces is avoided and all terms can be evaluated in the classical sense. Moreover, Barsukow et al. [5] showed that on regular Cartesian grids the resulting Active Flux method preserves all steady states.

Fig. 3

Illustration of the update of point values for the acoustic equations on a Cartesian mesh

Each time step of the explicit Active Flux method is restricted so that the circle around the edge midpoint over which the integration takes place remains inside the two adjacent grid cells, as indicated in Fig. 3. This leads to a time step restriction of the form

$$\begin{aligned} \max \left( \frac{c \Delta t}{\Delta x}, \frac{c \Delta t}{\Delta y} \right) \le \frac{1}{2}. \end{aligned}$$

In [8] we showed that this necessary condition is sufficient for linear stability.

3 Maxwell’s Equations

In this section we derive an Active Flux method for Maxwell’s equations which makes use of the acoustic solver.

Let ${\textbf{E}}\!=\!(E_1(x,y,t), E_2(x,y,t), E_3(x,y,t))^T$, ${\textbf{H}}\!=\!(H_1(x,y,t),H_2(x,y,t),H_3(x,y,t))^T$ be the electric respectively magnetic field and let ${\textbf{D}}=\epsilon {\textbf{E}}$, ${\textbf{B}}=\mu {\textbf{H}}$ be the electric respectively magnetic field density, where $\epsilon$ is the permittivity and $\mu$ is the permeability. The source free Maxwell equations are

$$\begin{aligned} \begin{aligned} \partial _t {\textbf{B}}&+\nabla \times {\textbf{E}}&=0,\\ - \,\partial _t {\textbf{D}}&+\nabla \times {\textbf{H}}&=0. \end{aligned} \end{aligned}$$

(8)

The electric and magnetic fields satisfy the constraints $\nabla \cdot {\textbf{E}} = 0$ and $\nabla \cdot {\textbf{B}} = 0$ if this condition is satisfied initially. Since ${\textbf{E}}={\textbf{E}}(x,y,t)$, we have

$$\begin{aligned} \nabla \times {\textbf{E}}=\frac{\partial E_3}{\partial y}{\hat{x}}-\frac{\partial E_3}{\partial x}{\hat{y}}+\left( \frac{\partial E_2}{\partial x}-\frac{\partial E_1}{\partial y}\right) {\hat{z}}, \end{aligned}$$

(9)

the same holds for ${\textbf{H}}={\textbf{H}}(x,y,t)$, hence (8) is equivalent to

$$\begin{aligned}{} & {} \partial _t E_3-\frac{1}{\epsilon }(\partial _x H_2-\partial _y H_1)=0 \nonumber \\{} & {} \partial _t H_1+\frac{1}{\mu } \partial _y E_3=0 \nonumber \\{} & {} \partial _t H_2-\frac{1}{\mu } \partial _x E_3=0 \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \partial _t H_3+\frac{1}{\mu }(\partial _x E_2-\partial _y E_1)=0 \nonumber \\{} & {} \partial _t E_1-\frac{1}{\epsilon } \partial _y H_3=0 \nonumber \\{} & {} \partial _t E_2+\frac{1}{\epsilon } \partial _x H_3=0 \end{aligned}$$

(11)

This means, we can solve (8) by solving the two sets of Eqs. (10) and (11). Furthermore let $c=\frac{1}{\sqrt{\epsilon \mu }}$ and define

$$\begin{aligned} \begin{aligned} \phi&:=\frac{E_3}{\sqrt{\mu }}, \quad u:=-\,\frac{H_2}{\sqrt{\epsilon }}, \quad v:=\frac{H_1}{\sqrt{\epsilon }} \\ \text {and } {\widetilde{\phi }}&:=\frac{H_3}{\sqrt{\epsilon }}, \quad {\widetilde{u}}:=\frac{E_2}{\sqrt{\mu }}, \quad {\widetilde{v}}:=-\frac{E_1}{\sqrt{\mu }}. \end{aligned} \end{aligned}$$

(12)

Then by these transformations, (10) and (11) are equivalent to

$$\begin{aligned}{} & {} \partial _t \phi +c(\partial _x u+\partial _y v)=0 \nonumber \\{} & {} \partial _t u+c \partial _x \phi =0 \nonumber \\{} & {} \partial _t v+c \partial _y \phi =0 \end{aligned}$$

(13)

$$\begin{aligned}{} & {} \partial _t {\widetilde{\phi }}+c(\partial _x {\widetilde{u}}+\partial _y {\widetilde{v}})=0 \nonumber \\{} & {} \partial _t {\widetilde{u}}+c \partial _x {\widetilde{\phi }}=0 \nonumber \\{} & {} \partial _t {\widetilde{v}}+c \partial _y {\widetilde{\phi }}=0. \end{aligned}$$

(14)

We obtain the following result.

Theorem 3.1

An Active Flux method for the source free two-dimensional Maxwell equations (8) is obtained by solving two sets of two-dimensional acoustic equations. By using the exact acoustic solver (7), the resulting method is third order accurate and the numerical solutions satisfy the constraints $\nabla \cdot {\textbf{E}} = 0$, $\nabla \cdot {\textbf{B}} = 0$.

Proof

The above derivation reveals that one can solve Maxell’s equations (8) by solving the two sets of acoustic equations (13) and (14). Third order accuracy follows from third order accuracy of the Active Flux method for acoustics.

For the divergence of the electric field we obtain

$$\begin{aligned} \begin{aligned} \nabla \cdot {\textbf{E}}&= \partial _x E_1 + \partial _y E_2 \\&= -\,\sqrt{\mu } \partial _x {\tilde{v}} + \sqrt{\mu } \partial _y {\tilde{u}} \\&= \sqrt{\mu } \left( \partial _y {\tilde{u}} - \partial _x {\tilde{v}} \right) . \end{aligned} \end{aligned}$$

Analogously, the divergence of the magnetic field can be expressed in the form

$$\begin{aligned} \begin{aligned} \nabla \cdot {\textbf{B}}&= \partial _x B_1 + \partial _y B_2 \\&= \partial _x \mu H_1 + \partial _y \mu H_2 \\&= \partial _x \mu \sqrt{\epsilon } v - \partial _y \mu \sqrt{\epsilon } u\\&= -\, \sqrt{\epsilon } \mu \left( \partial _y u - \partial _x v \right) . \end{aligned} \end{aligned}$$

An acoustic solver, which exactly preserves the curl of the velocity field leads to an approximation of Maxwell’s equation which satisfies the divergence constraints $\nabla \cdot {\textbf{E}} = 0$ and $\nabla \cdot {\textbf{B}} = 0$. Barsukow et al. [5] showed that Cartesian grid Active Flux methods for the acoustic equations with exact evolution operators preserve all steady states. $\square$

3.1 Convergence Study

For our convergence study we consider a solution of the form described in [15, Chapter 20, Equation (20.25)] but with three components of E and H instead of two.

Example 3.2

We consider numerical solutions of (8) with initial values of the form

$$\begin{aligned} \begin{aligned} E_1(x,y,0)&=\alpha _1(y)+\alpha _2(y) \\ E_2(x,y,0)&=\gamma _1(x)+\gamma _2(x)\\ E_3(x,y,0)&=\beta _1(y)+\beta _2(y)+\delta _1(x)+\delta _2(x)\\ H_1(x,y,0)&= \frac{1}{\mu c}\left( -\beta _1(y)+\beta _2(y)\right) \\ H_2(x,y,0)&= \frac{1}{\mu c}\left( -\delta _1(x)+\delta _2(x)\right) \\ H_3(x,y,0)&=\frac{1}{\mu c}\left( -\alpha _1(y)+\alpha _2(y)\right) +\frac{1}{\mu c}\left( -\gamma _1(x)+\gamma _2(x)\right) , \end{aligned} \end{aligned}$$

(15)

with $\alpha _i, \beta _i, \gamma _i, \delta _i: {\mathbb {R}} \rightarrow {\mathbb {R}}$. The exact solution is then given by

$$\begin{aligned} \begin{aligned} E_1(x,y,t)&=\alpha _1(y+ct)+\alpha _2(y-ct) \\ E_2(x,y,t)&=\gamma _1(x-ct)+\gamma _2(x+ct)\\ E_3(x,y,t)&=\beta _1(y+ct)+\beta _2(y-ct)+\delta _1(x-ct)+\delta _2(x+ct)\\ H_1(x,y,t)&= \frac{1}{\mu c}\left( -\beta _1(y+ct)+\beta _2(y-ct)\right) \\ H_2(x,y,t)&= \frac{1}{\mu c}\left( -\delta _1(x-ct)+\delta _2(x+ct)\right) \\ H_3(x,y,t)&= \frac{1}{\mu c}\left( -\alpha _1(y+ct)+\alpha _2(y-ct)\right) +\frac{1}{\mu c}\left( -\gamma _1(x-ct)+\gamma _2(x+ct)\right) . \end{aligned} \end{aligned}$$

(16)

We set every initial wave to be $\exp (-\,40x^2)$ respectively $\exp (-\,40y^2)$ and impose periodic boundary conditions.

The results of a convergency study using the exact acoustic solver (7) are shown in Table 1, where we compare solutions with $64^2$, $128^2$ and $256^2$ grid cells at an early time $t = 0.1$, using time steps which satisfy CFL $=\,0.457$.

Table 1 Error measured in the $L_1$-norm and EOC for Example 3.2 using the exact update formula (7) with CFL $=\,0.457$ at time $t=0.1$

4 The Method of Bicharacteristics for Linear Hyperbolic Systems

Since exact evolution operators are only available for selected linear hyperbolic systems, we will review an approximative approach for obtaining truly multi-dimensional evolution formulas for the update of point values.

We consider a multi-dimensional linear hyperbolic system of the form

$$\begin{aligned} \partial _t \textbf{q}(\textbf{x},t) + \sum _{k=1}^d A_k \partial _{x_k} \textbf{q} (\textbf{x},t) = 0, \end{aligned}$$

(17)

with $\textbf{q}:{\mathbb {R}}^d \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}^m$, $A_k \in {\mathbb {R}}^{m \times m}$ for $k=1, \ldots , d$, where $d=2,3$ denotes the spatial dimension. Let us denote by $S^{d-1}$ the unit sphere embedded in ${\mathbb {R}}^d$. Hyperbolicity implies that for the linear combination $A(\textbf{n}):= \sum _{k=1}^d n_k A_k$, $\textbf{n} \in S^{d-1}$ of the coefficient matrices in direction $\textbf{n}$, there exists a corresponding matrix $R(\textbf{n})$, whose columns are the linearly independent right eigenvectors of $A(\textbf{n})$. If we apply the similarity transformation to the individual matrices $A_1, \ldots , A_d$, they will in general not be diagonalised individually. We define $B_k:= B_k({\textbf{n}}) = R(\textbf{n})^{-1} A_k R(\textbf{n})$, $k=1,\ldots ,d$ and decompose each matrix $B_k$ into its diagonal part and the remaining part, i.e. $B_k = \Lambda _k + B_k'$ with $\Lambda _k:= \Lambda _k({\textbf{n}}) = \text{ diag }(B_k)$ and $B_k':= B_k'({\textbf{n}}) = B_k - \Lambda _k$.

Multiplication of (17) from the left with $R^{-1}$ provides the quasidiagonalised system in characteristic variables ${\textbf{w}}:={\textbf{w}}({\textbf{x}},{\textbf{n}},t) = R^{-1}({\textbf{n}}){\textbf{q}}({\textbf{x}},t)$, i.e.

$$\begin{aligned} \partial _t \textbf{w} + \sum _{k=1}^d \Lambda _k \partial _{x_k} \textbf{w} = -\sum _{k=1}^d B_k' \partial _{x_k} \textbf{w} =: \textbf{S}. \end{aligned}$$

(18)

Let $\lambda _\ell ^k$ for $k=1, \ldots , d$ and $\ell = 1, \ldots , m$ denote the eigenvalues of $\Lambda _k$. Equation (18) can be integrated component-wise along the bicharacteristics

$$\begin{aligned} \frac{\textrm{d}\textbf{x}_\ell (t,\textbf{n})}{\textrm{d}t} = \left( \lambda _{\ell }^1({\textbf{n}}),\ldots ,\lambda _{\ell }^d({\textbf{n}}) \right) ^T \quad \text{ for } \ell =1, \ldots , m \end{aligned}$$

from its footpoint $Q_\ell (\textbf{n}) = (x_1-\lambda _{\ell }^1 \Delta t, \ldots ,x_d - \lambda _{\ell }^d \Delta t,t)$ to the point $P=(x_1,\ldots ,x_d,t+\Delta t)$ at the new time level.

For each equation we obtain

$$\begin{aligned} w_\ell (P,\textbf{n}) = w_\ell (Q_\ell (\textbf{n}),\textbf{n}) + \int _{t_n}^{t_{n+1}} S_\ell (\textbf{x}_\ell (t,\textbf{n}),t,\textbf{n}) dt, \quad \ell =1,\ldots ,m. \end{aligned}$$

(19)

The solution ${\textbf{q}}(P)$ is obtained by integrating $R(\textbf{n}) {\textbf{w}}(P,\textbf{n})$ over all possible directions $\textbf{n} \in S^{d-1}$. This can be expressed in the form

$$\begin{aligned} \textbf{q}(P) = \frac{1}{|S^{d-1}|} \int _{S^{d-1}} \sum _{\ell =1}^m w_\ell (Q_\ell (\textbf{n}),\textbf{n}) \textbf{r}_\ell (\textbf{n}) \, d\textbf{n} + \frac{1}{|S^{d-1}|} \int _t^{t+\Delta t} \int _{S^{d-1}}R(\textbf{n}) \textbf{S}({\tilde{t}},\textbf{n}) d\textbf{n} d{\tilde{t}}.\nonumber \\ \end{aligned}$$

(20)

4.1 Linear Acoustics

Applying the procedure presented above, we obtain for the two-dimensional acoustic equations the following exact representation of the solution,

$$\begin{aligned} \begin{aligned} p(P)&= \frac{1}{2\pi } \int _0^{2\pi } \left( p(Q_1(\theta )) - u(Q_1(\theta )) \cos (\theta ) - v(Q_1(\theta ))\sin (\theta )\right) \, \textrm{d}\theta \\&\quad - \frac{1}{2\pi } \int _t^{t+\Delta t} \int _0^{2\pi } S({\tilde{t}},\theta )\, \textrm{d}\theta \textrm{d}{\tilde{t}}\\ u(P)&= \frac{1}{2 \pi } \int _0^{2\pi } \left( -p(Q_1(\theta )) \cos (\theta ) + u(Q_1(\theta )) \cos ^2 (\theta ) + v(Q_1(\theta )) \sin (\theta ) \cos (\theta ) \right) \, \textrm{d}\theta \\&\quad + \frac{1}{2} u(Q_2) + \frac{1}{2\pi } \int _t^{t+\Delta t} \int _0^{2\pi }S({\tilde{t}},\theta ) \cos (\theta ) \, \textrm{d}\theta \textrm{d}{\tilde{t}} \\&\quad -\frac{1}{2} c \int _t^{t+\Delta t} p_x({\tilde{Q}}_2({\tilde{t}})) \textrm{d}{\tilde{t}} \\ v(P)&= \frac{1}{2\pi } \int _0^{2\pi } \left( -p(Q_1(\theta )) \sin (\theta ) + u(Q_1(\theta )) \sin (\theta ) \cos (\theta ) + v(Q_1(\theta )) \sin ^2 (\theta ) \right) \, \textrm{d}\theta \\&\quad + \frac{1}{2} v(Q_2) + \frac{1}{2\pi } \int _t^{t+\Delta t} \int _0^{2\pi } S({\tilde{t}},\theta ) \sin (\theta ) \, \textrm{d}\theta \textrm{d}{\tilde{t}} \\&\quad - \frac{1}{2} c \int _{t}^{t+\Delta t} p_y({\tilde{Q}}_2({\tilde{t}})) \textrm{d}{\tilde{t}}, \end{aligned} \end{aligned}$$

(21)

where

$$\begin{aligned} S({\tilde{t}},\theta ) =c \left( u_x({\tilde{x}},{\tilde{y}},{\tilde{t}}) \sin ^2 (\theta ) - (u_y({\tilde{x}},{\tilde{y}},{\tilde{t}}) + v_x({\tilde{x}},{\tilde{y}},{\tilde{t}})) \sin (\theta ) \cos (\theta ) + v_y({\tilde{x}},{\tilde{y}},{\tilde{t}}) \cos ^2 (\theta ) \right) \end{aligned}$$

with

$$\begin{aligned} ({\tilde{x}},{\tilde{y}}) = (x + c(t+\Delta t -{\tilde{t}}) \cos (\theta ), y + c(t+\Delta t-{\tilde{t}}) \sin (\theta )), \quad {\tilde{t}} \in [t,t+\Delta t], \end{aligned}$$

$Q_1(\theta ) = (x+c\Delta t \cos (\theta ),y+c\Delta t \sin (\theta ),t), \, Q_2 = (x,y,t)$ and ${\tilde{Q}}_2 = (x,y,{\tilde{t}})$ for ${\tilde{t}} \in [t,t+\Delta t]$. Note that due to symmetry terms depending on $Q_3 (\theta ) = (x-c\Delta t \cos (\theta ), y-c\Delta t \sin (\theta ),t)$ have been expressed using $Q_1(\theta )$. Details of the derivation can be found in [21].

By integrating the second equation of (1) from $P':= {\tilde{Q}}_2(x,y,t)=Q_2$ to $P:={\tilde{Q}}_2(x,y,t+\Delta t)$, we obtain

$$\begin{aligned} u(P) = u(P') - c \int _t^{t+\Delta t} p_x(x,y,{\tilde{t}}) \textrm{d}{\tilde{t}}. \end{aligned}$$

Thus, the second and fourth term on the right hand side of the second equation of (21) can be eliminated and we obtain the alternative exact evolution formula

$$\begin{aligned} \begin{aligned} u(P)&= \frac{1}{\pi } \int _0^{2\pi } \left( -p(Q_1(\theta )) \cos (\theta ) + u(Q_1(\theta )) \cos ^2 (\theta ) + v(Q_1(\theta )) \sin (\theta ) \cos (\theta ) \right) \, \textrm{d}\theta \\&\quad + \frac{1}{\pi } \int _t^{t+\Delta t} \int _0^{2\pi } S({\tilde{t}},\theta ) \cos (\theta ) \, \textrm{d}\theta \textrm{d}{\tilde{t}}. \end{aligned} \end{aligned}$$

(22)

Analogously, the evolution equation for v can be expressed in the form

$$\begin{aligned} \begin{aligned} v(P)&= \frac{1}{\pi } \int _0^{2\pi } \left( -p(Q_1(\theta )) \sin (\theta ) + u(Q_1(\theta )) \sin (\theta ) \cos (\theta ) + v(Q_1(\theta )) \sin ^2 (\theta ) \right) \, \textrm{d}\theta \\&\quad + \frac{1}{\pi } \int _t^{t+\Delta t} \int _0^{2\pi } S({\tilde{t}},\theta ) \sin (\theta ) \, \textrm{d}\theta \textrm{d}{\tilde{t}}. \end{aligned} \end{aligned}$$

(23)

Furthermore, it can be shown, compare with [21], that

$$\begin{aligned} \frac{1}{2\pi } \int _t^{t+\Delta t} \int _0^{2\pi } S({\tilde{t}}, \theta ) \, \textrm{d}\theta \textrm{d}{\tilde{t}} = \frac{c}{2} \int _0^{\Delta t} \langle \nabla \cdot (u,v) \rangle _{c(\Delta t-\tau )} \, \textrm{d}\tau , \end{aligned}$$

where $\langle \cdot \rangle _R$ represents an average over the disk of radius R. As pointed out earlier, this shows that the time evolution of p depends on the divergence of the velocity field.

Here, the time integrals are computed numerically. In order to obtain third order accurate Active Flux methods, the point values need to be computed with third order accuracy. This is possible by using the trapezoidal rule. We obtain

$$\begin{aligned} \begin{aligned}&\frac{1}{2\pi } \int _t^{t+\Delta t} \int _0^{2\pi } S({\tilde{t}},\theta ) \, \textrm{d}\theta \textrm{d}{\tilde{t}} \\&\quad = \frac{1}{2} \Delta t \left( \frac{1}{2\pi } \int _0^{2\pi } S(t+\Delta t,\theta ) \, \textrm{d}\theta + \frac{1}{2\pi } \int _0^{2\pi } S(t,\theta ) \, \textrm{d}\theta \right) + {{{\mathcal {O}}}}(\Delta t^3)\\&\quad = \frac{1}{2} \Delta t \left( \frac{1}{2} c (u_x(P)+v_y(P)) + \frac{1}{2\pi } \int _0^{2\pi } S(t,\theta ) \, \textrm{d}\theta \right) + \mathcal{O}(\Delta t^3). \end{aligned} \end{aligned}$$

(24)

The unknown quantities $u_x(P)+v_y(P)$ can be eliminated by integrating the first equation of (1) from $P' = (x,y,t)$ to $P=(x,y,t+\Delta t)$ but now using also the trapezoidal rule. This approach was introduced by Butler [6]. We obtain

$$\begin{aligned} p(P) - p(P') = -\, c \frac{\Delta t}{2} \left( u_x(P) + v_y(P) + u_x(P') + v_y(P') \right) + {{{\mathcal {O}}}}(\Delta t^3). \end{aligned}$$

(25)

Using (24) and (25) in the first equation of (21) provides an explicit representation of $p(P)=p(x,y,t+\Delta t)$ using only data at time t. It has the form

$$\begin{aligned} \begin{aligned} p(P)&= \frac{1}{\pi } \int _0^{2\pi } \left( p(Q_1(\theta )) -u(Q_1(\theta ))\cos (\theta ) -v(Q_1(\theta )) \sin (\theta ) \right) \, \textrm{d}\theta - p(P')\\&\qquad + c \frac{\Delta t}{2} (u_x(P') + v_y(P')) - \frac{\Delta t}{2\pi } \int _0^{2\pi } S(t,\theta ) \, \textrm{d}\theta + {{{\mathcal {O}}}}(\Delta t^3). \end{aligned} \end{aligned}$$

(26)

Similarly, the evolution of u and v can be expressed in the form

$$\begin{aligned} \begin{aligned} u(P)&= \frac{1}{\pi } \int _0^{2\pi } \left( - p(Q_1(\theta )) \cos (\theta ) + u(Q_1(\theta )) \cos ^2 (\theta ) + v(Q_1(\theta )) \sin (\theta ) \cos (\theta ) \right) \, \textrm{d}\theta \\&\quad + \frac{\Delta t}{2\pi } \int _0^{2\pi } S(t,\theta ) \cos (\theta ) \, \textrm{d}\theta + {{{\mathcal {O}}}}(\Delta t^3)\\ v(P)&= \frac{1}{\pi } \int _0^{2\pi } \left( -p(Q_1(\theta )) \sin (\theta ) + u(Q_1(\theta )) \sin (\theta ) \cos (\theta ) + v(Q_1(\theta ) \sin ^2 (\theta ) \right) \, \textrm{d}\theta \\&\quad + \frac{\Delta t}{2\pi } \int _0^{2\pi } S(t,\theta ) \sin (\theta ) \, \textrm{d}\theta + {{{\mathcal {O}}}}(\Delta t^3). \end{aligned} \end{aligned}$$

(27)

The computations can be simplified by introducing further third order accurate approximations in the evolution formulas. These approximations are justified by Lemma 2.1 from [21], which is cited here for completeness.

Lemma 4.1

(see [21]) Consider $2\pi$-periodic, continuously differentiable functions $w: {\mathbb {R}} \times {\mathbb {R}} \rightarrow {\mathbb {R}}$ and $p: {\mathbb {R}} \rightarrow {\mathbb {R}}$. For the integration around a circle of radius R, with a general point $Q(\theta ) = (R \cos (\theta ), R \sin (\theta ))$, the following relation holds

$$\begin{aligned} \int _0^{2\pi } p'(\theta ) w(Q(\theta )) d\theta = R \int _0^{2\pi } p(\theta ) \left( w_x(Q(\theta )) \sin (\theta ) - w_y(Q(\theta )) \cos (\theta ) \right) \textrm{d}\theta . \end{aligned}$$

Now we observe

$$\begin{aligned} \begin{aligned} \frac{\Delta t}{2\pi } \int _0^{2\pi } S(t,\theta ) \, \textrm{d}\theta&= \frac{c \Delta t}{2\pi } \int _0^{2\pi } \sin (\theta ) \left[ u_x(Q_1(\theta )) \sin (\theta ) - u_y(Q_1(\theta )) \cos (\theta ) \right] \textrm{d}\theta \\&\quad - \frac{c \Delta t}{2\pi } \int _0^{2\pi } \cos (\theta ) \left[ v_x(Q_1(\theta )) \sin (\theta ) - v_y(Q_1(\theta )) \cos (\theta ) \right] \textrm{d}\theta \\&= \frac{c \Delta t}{2\pi } \frac{1}{c \Delta t} \int _0^{2\pi } \left[ \cos (\theta ) u(Q_1(\theta )) + \sin (\theta ) v(Q_1(\theta )) \right] \textrm{d}\theta \\&= \frac{1}{2 \pi } \frac{1}{c \Delta t} \int _{D_{c \Delta t}} \nabla \cdot (u,v)\, \textrm{d}x \textrm{d}y \\&= \frac{1}{2 \pi c \Delta t} \left[ \pi c^2 \Delta t^2 \left( u_x(P')+v_y(P') + {{{\mathcal {O}}}}(\Delta t^2)\right) \right] \\&= \frac{c \Delta t}{2} \left( u_x(P') + v_y(P') \right) + \mathcal{O}(\Delta t^3). \end{aligned} \end{aligned}$$

Here we have used Lemma 4.1 to get the third line, the divergence theorem to get the fourth line and the midpoint rule to get the fifth line. Thus, in the approximation of the pressure the two terms in the second line of (26) cancel up to a third order term and can therefore be ignored. A similar approximation can be used for the velocity components to obtain the third order accurate approximations, the so-called EG2 approximate evolution operator,

$$\begin{aligned} \begin{aligned} p(P)&\approx \frac{1}{\pi } \int _0^{2\pi } \left( p(Q_1(\theta )) - u(Q_1(\theta )) \cos (\theta ) - v(Q_1(\theta )) \sin (\theta ) \right) \textrm{d}\theta - p(P') \\ u(P)&\approx \frac{1}{\pi } \int _0^{2\pi } \left( -p(Q_1(\theta )) \cos (\theta ) + u(Q_1(\theta )) \left( 2 \cos ^2(\theta ) - \frac{1}{2} \right) + 2 v(Q_1(\theta )) \sin (\theta )\cos (\theta ) \right) \textrm{d}\theta \\ v(P)&\approx \frac{1}{\pi } \int _0^{2\pi } \left( -p(Q_1(\theta )) \sin (\theta ) + 2 u(Q_1(\theta )) \sin (\theta ) \cos (\theta ) + v(Q_1(\theta )) \left( 2 \sin ^2 (\theta ) - \frac{1}{2}\right) \right) \textrm{d}\theta . \end{aligned}\nonumber \\ \end{aligned}$$

(28)

For the Active Flux reconstruction on Cartesian grids, Eq. (28) can be evaluated exactly. In Fig. 4 we show an illustration of the EG2 update of the point values used in the Active Flux scheme. The approximative evolution operator (28) integrates over a circle while the exact evolution operator (21) also includes the integration over the mantle of the bicharacteristic cone from t to $t+\Delta t$. Note that in (21) the approximation of the mantle integral is included by means of additional terms that are integrated over the base circle at time t. By using the exact evolution operator in the form proposed by Barsukow et al., i.e. (7), integration takes place over a disk at time t.

Fig. 4

Illustration of the update of point values for the acoustic equations on a Cartesian mesh using the EG2 operator

Theorem 4.1

We consider an Active Flux method for the two-dimensional acoustic equations which updates the point values via (28). For sufficiently smooth initial values the method is third order accurate in space and time.

Proof

By construction, the formulas (28) are third order accurate in time. Furthermore, for sufficiently smooth data the Active Flux reconstruction is third order accurate in space. The integrals in (28) can be evaluated exactly for the Active Flux reconstruction and therefore all point values are computed with third order accuracy. Consequently, the nodes of Simpson’s rule, used for the flux computation, are third order accurate in space and time and thus the cell average values are computed with third order accuracy. $\square$

Remark 4.2

Instead of using the trapezoidal rule, the double integrals could be approximated with the rectangle rule. Two different second order accurate evolution formulas were derived in [21], the so-called EG1 and EG3 formulas, see Eqs. (2.17)–(2.19) and (4.13)–(4.15) of [21].

In the context of Active Flux methods we found that both of these update formulas led to unstable approximations. If used in a finite volume method with piecewise constant reconstruction, Lukáčová-Medvid’ová et al. [21] found that one of the second order accurate update formulas, namely EG3, outperformed all other methods and in particular also the third order accurate EG2 approach used here.

Another second order accurate evolution formula for acoustics, the so-called EG4 operator, was presented in [25]. When used to update the point values in an Active Flux method, we observed stability for time steps satisfying $\text{ CFL } \le 0.154$ and second order accuracy.

Physically relevant systems of hyperbolic balance laws consist of two important differential operators: the convection operator and the operator modelling acoustic or gravity waves. These operators arise in many different systems, such as the Euler equations of gas dynamics, shallow water equations or the equations of magnetohydrodynamics. The steps used in the derivation of the approximative evolution operator for acoustics, which were reviewed in this section, can thus be mimicked in the derivation of evolution operators for other systems. This has been done for the linearised Euler equations in [23] and for the shallow water MHD equations in [19].

5 Stability and Accuracy Studies for the Acoustic Equations

5.1 Linear Stability Analysis

In order to perform a linear stability analysis of the Active Flux method with different evolution operators for the update of the point values, we consider discretisations on a quadratic domain with double periodic boundary conditions. The domain is discretised using $m \times m$ grid cells. We write the linear method in the form $Q^{n+1} = A Q^n$, where $Q \in {\mathbb {R}}^{12\,m^2}$ consists of all degrees of freedom at the current time level n and the matrix $A \in {\mathbb {R}}^{12m^2 \times 12m^2}$ represents the update of the two-dimensional numerical method during one time step. Recall that we have three unknowns p, u and v and four degrees of freedom per grid cell.

We say that a method is Lax–Richtmyer stable if and only if $\Vert A^n\Vert$ is bounded independently of n. It can be shown, see [32] for details, that stability is equivalent to the condition $|\lambda | \le 1$ for all eigenvalues $\lambda$ of A and if $|\lambda |=1$, then the geometric and algebraic multiplicity need to match. We explore the stability of the different evolution operators by computing the eigenvalues of the matrices A for a fixed grid using a method from the Python NumPy package. The results are shown in Table 2.

Table 2 Spectral radius of A using the four different EG evolution operators computed on a grid with resolution 16

Our numerical simulation and the linear stability analysis indicate that the Active Flux methods based on the EG1 and EG3 approximate operators are unstable. When we use the EG2 approximate evolution operator the eigenvalues are within the unit circle as long as the condition $\text{ CFL } \le 0.279$ is satisfied and for the EG4 approximate evolution operator this is the case as long as $\text{ CFL } \le 0.154$.

Thus, among the previously known approximate evolution operators constructed by means of the bicharacteristics, the EG2 operator is the best candidate when used in an Active Flux method. We will now compare the resulting Active Flux method with the other previously used methods described in Sect. 2.1. In Fig. 5 we show the eigenvalues of the different matrices using $\text{ CFL } = 0.279$. Figure 6 shows n versus $||A^n||$, $n=1,\ldots ,100$ for the three different methods using again $\text{ CFL }=0.279$. In all cases $||A^n||$ is bounded, indicating that the algebraic and geometric multiplicity of the eigenvalues of A with absolute value 1 do match.

Fig. 5

Location of the eigenvalues of the matrix A describing different versions of the Active Flux method for linear acoustics. (Left) using the method (4), which is exact for irrotational flows, (middle) using the method (7), which is exact for general data and (right) using (28), i.e. the third order accurate approximation derived from the method of bicharacteristics

Fig. 6

$\Vert A^n \Vert$ versus n for the different versions of the Active Flux method. (Left) using the method (4), which is exact for irrotational flows, (middle) using the method (7), which is exact for general data and (right) using (28), the third order accurate approximation derived from the method of bicharacteristics

Furthermore, the Active Flux method with the evolution formula that is exact for irrotational flows, compare with (4), as well as the method which uses the exact evolution that is exact for general data, compare with (7), are both stable for time steps satisfying $\text{ CFL } \le 0.5$. For the exact evolution formula this was first shown in [8].

5.2 Convergence Studies for Acoustics

Now we propose a new test case for studying the accuracy of methods for the acoustic equations. It is motivated by a test case from [21]. While the previous test case considered time- and space-periodic solutions with smooth irrotational initial values, we here propose a test problem with non-irrotational initial data.

Example 5.1

On the domain $[-1,1] \times [-1,1]$ we solve the acoustic equations with initial values

$$\begin{aligned} \begin{aligned} p(x,y,0)&= 0\\ u(x,y,0)&= -\,\frac{1}{c} \left( \sin (2 \pi x) + \sin (2 \pi y) \right) \\ v(x,y,0)&= \frac{1}{c} \left( \sin (2 \pi x) + \sin (2 \pi y) \right) . \end{aligned} \end{aligned}$$

(29)

The speed of sound is set to $c=1$ and periodic boundary conditions are imposed. It can easily be verified that the exact solution has the form

$$\begin{aligned} \begin{aligned} p(x,y,t)&= \frac{1}{c} \left( \cos (2 \pi x) - \cos (2 \pi y) \right) \sin (2 \pi c t)\\ u(x,y,t)&= -\,\frac{1}{c} \left( \sin (2 \pi x)\cos (2 \pi c t) + \sin (2 \pi y) \right) \\ v(x,y,t)&=\frac{1}{c} \left( \sin (2 \pi x) + \sin (2 \pi y) \cos (2 \pi c t) \right) . \end{aligned} \end{aligned}$$

(30)

Fig. 7

Solution of Example 5.1 at times $t=0, 0.25, 0.5, 0.75$: p (top), u (middle) and v (bottom)

The solution structure for Example 5.1 is depicted in Fig. 7. We compute the error at time $t=0.1$ measured in the $L_1$-norm and the experimental order of convergence (EOC) comparing grids with resolutions 64, 128 and 256. For the results shown in Table 3, the third order accurate approximative evolution operator (28), which was derived using the method of bicharacteristics, was used. In Table 4 we show results using the evolution operator (4), which is exact for irrotational flows as well as the operator (7), which is exact for general data, to update the point values in the Active Flux method.

Table 3 Error and EOC for the acoustic equations with initial data described in Example 5.1 measured in the $L_1$-norm using the EG2 evolution operator (28) with $CFL=0.267$ at time $t=0.1$

Table 4 Error and EOC for the acoustic equations with initial data described in Example 5.1 measured in the $L_1$-norm using the evolution operator (4), which is exact for initial data with constant vorticity (top) and using the exact evolution operator (7) (bottom) at time $t=0.1$ with CFL $=\,0.457$

For all three methods we have used time steps close to the stability limit, since this typically leads to the most accurate results. All three methods provide third order accurate approximations of the pressure. By using the approach of Eymann and Roe, which is only exact for irrotational flows, the approximation of the velocity field is less accurate. The experimentally observed order of convergence is reduced to two.

While the exact evolution operator provides accurate results, the experimental order of convergence in the velocity components is slightly reduced. Note that such an effect was also mentioned in a recent paper by Samani and Roe [30]. We have observed that for this time-periodic solution the loss in convergence rate is only seen for certain times. This is documented in Table 5. For the other two methods the observed order of convergence did not change with time. In particular, the Active Flux method with the EG2 approximative evolution operator leads to third order accurate approximations in all three components.

Table 5 Error and EOC for the acoustic equations with initial data (29) measured in the $L_1$-norm using the exact evolution operator (7) with $CFL=0.457$ on grids with resolutions 64 and 128

5.3 The Stationary Vortex

The approximation of a stationary vortex as proposed by Barsukow et al. [5] will now be used to illustrate the ability of different versions of the Active Flux method to preserve stationary states.

Example 5.2

We approximate solutions of the two-dimensional acoustic equations with initial values of the form

$$\begin{aligned} p(r,0) = 0, \quad {\textbf{u}}(r,0) = {\textbf{n}} \left\{ \begin{array}{lll} 5 r &{}: &{} 0 \le r \le 0.2 \\ 2-5 r &{}: &{} 0.2 < r \le 0.4 \\ 0 &{}: &{} r > 0.4,\end{array}\right. \end{aligned}$$

with $r = \sqrt{x^2 + y^2}$, ${\textbf{n}} = (-\,\sin (\theta ),\cos (\theta ))^T$, $\theta \in [0,2\pi )$ and ${\textbf{u}} = (u,v)^T$. The computational domain is $[-\,0.75,0.75] \times [-\,0.75,0.75]$, double periodic boundary conditions are imposed.

Barsukow et al. [5] showed that the third order accurate Cartesian grid Active Flux method with exact evolution operator, c.f. (7), is stationary preserving, i.e. it exactly preserves a discrete representation of all stationary states. In order to test how well other Active Flux methods approximate the steady state, we compute the solution at time $t=100$ on a grid with $128 \times 128$ grid cells. In Fig. 8 we show scatter plots of $|{\textbf{u}}|$ versus r. Since the flow is not irrotational, the evolution operator proposed by Eymann and Roe (4) is not exact and the numerical approximation (left plot) deviates from the exact solution structure shown as a solid line. The EG2 operator (28) also does not exactly preserve the steady state but leads to a more accurate approximation (middle). Numerical results obtained with the exact evolution operator (7) (right plot) confirm the exact preservation of the discrete representation of the steady state. In Figs. 9 and 10 we show scatter plots of the vorticity, i.e. of $v_x - u_y$ at three different times, obtained with the new Active Flux method that uses the EG2 evolution operator. These computations were carried out on a grid with $64 \times 64$ as well as $128 \times 128$ grid cells. For each grid cell the vorticity was computed using a centered finite difference approximation, which agrees with the analytical vorticity of the Active Flux reconstruction evaluated at the center of the grid cell. Although vorticity is not exactly preserved by the Active Flux method with EG2 evolution operator, this quantity is approximated quite well for a long time even on these relatively coarse grids.

Fig. 8

Approximations of the vortex at time $t=100$ using Active Flux methods with evolution operators (left) exact for irrotational flows, (middle) EG2, (right) exact for general flows

Fig. 9

Scatter plots of vorticity for Example 5.2 for the Active Flux approximations with EG2 evolution operator on a grid with $64 \times 64$ grid cells, (left) at time $t=10$, (middle) $t=50$, (right) $t=100$. The solid line represents the exact vorticity as a function of r

Fig. 10

Same as Fig. 9 but for a grid with $128 \times 128$ cells

5.4 Discontinuous Solutions

Next we consider an example with discontinuous initial values which was also studied in [21].

Example 5.3

We consider the two-dimensional acoustic equations with initial values

$$\begin{aligned} \begin{aligned} u_0(x,y)&=v_0(x,y)= {\left\{ \begin{array}{ll} \frac{1}{\sqrt{2}}&{}: |y|<|x| \\ -\frac{1}{\sqrt{2}}&{}: |y|\ge |x| \end{array}\right. }\\ p_0(x,y)&=1. \end{aligned} \end{aligned}$$

The speed of sound is set to $c=1$ and the computational domain is $[-1,1]\times [-1,1]$. We use zero-order extrapolation at the boundaries which takes the wave propagation in diagonal direction into account, e.g., ghost cells at the left boundary ${\mathcal {C}}_{0,j}$ are filled with cells ${\mathcal {C}}_{1,j-1}$ if they are not close to the bottom left corner, otherwise they are filled with cells ${\mathcal {C}}_{1,j+1}$.

Fig. 11

Solutions of the acoustic equations with initial values as described in Example 5.3 at time $t=0.5$ using Active Flux methods with evolution operators (left) exact for irrotational flows, (middle) EG2, (right) exact for general flows on a grid with $256 \times 256$ grid cells; (top) p, (middle) u, (bottom) v

Fig. 12

Same as Fig. 11 but at time $t=1$

In Figs. 11 and 12 we show the solution structure obtained with the Active Flux method on a grid with $256 \times 256$ grid cells using again the three different evolution operators for the update of the point values. The solution consists of a stationary contact at $x=y$ and an expanding acoustic wave starting from the main diagonal. The solution structure agrees with those observed in [21] but the discontinuities are represented much sharper with the Active Flux method. The radial symmetry in pressure is approximated well. Small differences can be observed in the velocity components along the diagonal, where the pressure is continuous but the velocity components are discontinuous. The Active Flux method with exact evolution operator appears to produce a slightly sharper discontinuity. All computations were performed without any limiting.

Our numerical results for smooth solutions of the acoustic equations confirm that the EG2 evolution operator leads to third order accurate results when used in a Cartesian grid Active Flux method. Furthermore, the method leads to accurate approximations of solutions with discontinuities. The discontinuities are represented much sharper than in the first and second order accurate methods considered by Lukáčová-Medvid’ová et al. [21]. The stationary vortex problem is not preserved exactly by the new Active Flux method but the Active Flux method with EG2 evolution operator still performs well and outperforms the method from [12]. Since the EG2 evolution operator was derived from a general theory, the approach can also be used for other linear hyperbolic systems in particular in situations, where no exact evolution operator is available.

6 Linearised Euler Equations

The linearised Euler equations with frozen coefficients $\rho '$, $u'$, $v'$ and $p'$ are given by

$$\begin{aligned} {\varvec{U}}_t+{\varvec{A}}_1 {\varvec{U}}_x+{\varvec{A}}_2 {\varvec{U}}_y=0, \end{aligned}$$

(31)

where ${\varvec{U}}= \left( \rho , u, v, p\right) ^T$ and

$$\begin{aligned} {\varvec{A_1}}=\begin{pmatrix} u' &{} \rho '&{}0&{}0 \\ 0 &{} u'&{}0&{}\frac{1}{\rho '}\\ 0 &{} 0&{}u'&{}0\\ 0 &{} \rho 'c'^2&{}0&{}u' \end{pmatrix},\ {\varvec{A_2}}=\begin{pmatrix} v' &{} 0&{}\rho '&{}0 \\ 0 &{} v'&{}0&{}0\\ 0 &{} 0&{}v'&{}\frac{1}{\rho '}\\ 0 &{} 0&{}\rho 'c'^2&{}v' \end{pmatrix}. \end{aligned}$$

(32)

Here ${\varvec{u}}=(u,v):{\mathbb {R}}^2 \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}^2$ is the velocity vector, $p:{\mathbb {R}}^2 \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}$ is the pressure, $\rho :{\mathbb {R}}^2 \times {\mathbb {R}}^+ \rightarrow {\mathbb {R}}$ is the density and $c'=\sqrt{\gamma \frac{p'}{\rho '}}$ is the local speed of sound with isotropic exponent $\gamma =1.4$. Similarly to the acoustic equations one can obtain an approximative evolution operator (EG2) using the theory of bicharacteristics. The update of point values has the form (compare with [24]):

$$\begin{aligned} \begin{aligned} \rho (P)&=\rho ({P'})-2\frac{p({P'})}{c'^2}+ \frac{1}{\pi }\int _{0}^{2\pi }\frac{p(Q(\theta ))}{c'^2}-\frac{\rho '}{c'}u(Q(\theta )) \cos (\theta )\\&\quad -\frac{\rho '}{c'}v(Q(\theta )) \sin (\theta ) \ \textrm{d}\theta + {{{\mathcal {O}}}}(\Delta t^3)\\ u(P)&=\frac{1}{\pi }\int _{0}^{2\pi } -\frac{p(Q(\theta ))}{\rho 'c'}\cos (\theta )+u(Q(\theta )) \left( 2\cos ^2(\theta )-\frac{1}{2}\right) \\&\quad +2v(Q(\theta )) \sin (\theta )\cos (\theta ) \, \textrm{d}\theta + {{{\mathcal {O}}}}(\Delta t^3)\\ v(P)&=\frac{1}{\pi }\int _{0}^{2\pi } -\frac{p(Q(\theta ))}{\rho 'c'}\sin (\theta )+2u(Q(\theta )) \sin (\theta ) \cos (\theta )\\&\quad +v(Q(\theta )) \left( 2\sin ^2(\theta )-\frac{1}{2}\right) \, \textrm{d}\theta + {{{\mathcal {O}}}}(\Delta t^3)\\ p(P)&=-p({P'})+\frac{1}{\pi }\int _{0}^{2\pi } p(Q(\theta ))-\rho 'c'u(Q(\theta )) \cos (\theta ) -\rho 'c'v(Q(\theta )) \sin (\theta ) \, \textrm{d}\theta \\&\quad + {{{\mathcal {O}}}}(\Delta t^3), \end{aligned} \end{aligned}$$

(33)

where $P=(x,y,t_{n+1})$ is a point at which we want to compute the solution, $P'=\left( x-u'\Delta t, y-v'\Delta t,t_n \right)$ and $Q(\theta )=\left( x-(u'-c'\cos (\theta ))\Delta t, y-(v'-c'\sin (\theta ))\Delta t, t_n\right)$. Figure 13 illustrates the update of an edge and a corner point value.

Fig. 13

Update of a corner point value using evolution operator (33)

The approximative evolution operator integrates over a circle with radius $c' \Delta t$. For the linearised Euler equations these circles are centered around the point $(x-u'\Delta t, y-v'\Delta t)$. We want to restrict the time step such that these circles lie in the neighbouring grid cells of the considered point value degree of freedom. For the evolution of a point value at the midpoint of a vertical grid cell interface five different constellations, as indicated in Fig. 14 (top), might arise for $u', v' \ge 0$. For the update of a corner point value the different situations for $u', v' \ge 0$ are shown in the bottom row of Fig. 14. Analogously for all the other point value degrees of freedom and other values of $u'$ and $v'$.

Fig. 14

Illustration of the update of point values for the linearised Euler equations on Cartesian grids using the EG2 operator

In all of our test computations for the linearised Euler equations we observed that the time step restriction for stability is the same as for linear acoustics, i.e. CFL$\le 0.279$, where the Courant number now has the form

$$\begin{aligned} \text{ CFL }:= \max \left( |u'| + c', |v'| + c' \right) \frac{\Delta t}{h}, \quad h=\Delta x = \Delta y. \end{aligned}$$

Due to this stability condition, only the constellations indicated in the first and the third picture of the top row of Fig. 14 will arise for the update of the edge centered point values of a vertical grid cell interface when $u',v' \ge 0$. For the update of a corner point value all configurations shown in the bottom row of the figure might arise.

In our implementation, the approximative evolution operator was implemented using exact integration of the Active Flux reconstruction over the circle segments.

Remark 6.1

The update of p, u and v in the linearised Euler equations is described by a linear superposition of advection and acoustics. This observation could be used to derive exact evolution formulas similar to those presented in Sect. 2.1. However, the evaluation of exact evolution operators on the circular discs arising for the linearised Euler equations would be more difficult. In particular, it would require to compute derivatives of the reconstructed functions across grid cell interfaces. The evaluation of the approximate EG2 evolution operator is for the linearised Euler equations more sophisticated than for acoustics but much simpler than the evaluation of an exact evolution operator. It requires the integration along a circle that intersects with the underlying Cartesian grid. Our accuracy studies for acoustics showed that the accuracy obtained with the approximative EG2 operator is comparable with the accuracy obtained by the exact evolution operator.

6.1 Convergence Study for Linearised Euler

We start with a test case where a density profile is simply advected with constant speed, such that a convergence study can easily be performed by comparing a sequence of numerical solutions with the exact solution.

Example 6.2

We consider numerical solutions of (31), (32) with initial values of the form

$$\begin{aligned} \begin{aligned} \rho (x,y,0)&= \frac{5}{2} \exp \left( -\,40 \left( (x-x_a)^2 + (y-y_a)^2\right) \right) + \frac{1}{10} \\ u(x,y,0)&= v(x,y,0) = p(x,y,0) = 1 \end{aligned} \end{aligned}$$

on the domain $[-1,1] \times [-1,1]$ with double-periodic boundary conditions. Two sets of parameter values in the linearised Euler equations have been considered, namely $\rho '=1$, $u'=v'=0.5$ and $c'=1$ as well as $\rho '=1$, $u'=v'=1$ and $c'=1$. These two cases correspond to supersonic flow and subsonic flow. In the description of the initial values we used $x_a = y_a = -\,0.31$.

Table 6 shows the error in density measured in the $L_1$-norm as well as the EOC at time $t=4$ and $t=2$, respectively, i.e. after one full rotation, using time steps which satisfy $\text{ CFL } = 0.275$ on grids with $32^2$, $64^2$, $128^2$ and $256^2$ grid cells. We observe the expected third order convergence rate of the method. Note that p, u and v remain constant up to machine precision.

Table 6 Error in the $L_1$-norm and EOC after one rotation for the density advection problem described in Example 6.2

In our next example we consider a test problem with a more interesting smooth solution structure.

Example 6.3

We consider the linearised Euler equations (31), (32) with initial values of the form

$$\begin{aligned} \begin{aligned} \rho (x,y,0)&= 2.5\exp (-\,40((x-x_a)^2+(y-y_a)^2))+0.5\exp (-\,40((x-x_b)^2+(y-y_b)^2))\\ u(x,y,0)&=0.05\exp (-\,40((x-x_b)^2+(y-y_b)^2)) \\ v(x,y,0)&=-\,0.05\exp (-\,40((x-x_b)^2+(y-y_b)^2)) \\ p(x,y,0)&= 2.5\exp (-\,40((x-x_a)^2+(y-y_a)^2)) \end{aligned} \end{aligned}$$

(34)

with $x_a=y_a=-0.31$, $x_b=y_b=0.39$, $u'=v'=0.5\sin (\pi /4)$ and $\rho '=c'=1$ on the domain $[-1,1] \times [-1,1]$.

Fig. 15

Solution structure of $\rho$ for Example 6.3 at times $t = 0, \, 0.332, \, 0.664$ along the diagonal from the lower left to the upper right corner using the EG2 evolution operator with CFL $=0.267$. The black line shows the solution obtained on a grid with $512 \times 512$ grid cells, the red dots show the solution obtained on a grid with $64 \times 64$ cells

The solution structure of $\rho$ along the diagonal from the lower left to the upper right corner at times $t = 0, \, 0.332, \, 0.664$ is shown in Fig. 15. In Fig. 16 we show numerical results using the Active Flux method with adaptive mesh refinement that was recently presented in [7].

Fig. 16

Solution structure of $\rho$ for Example 6.3 using the EG2 evolution operator with $\hbox {CFL}=0.267$

To perform a numerical convergence study we compute the error at time $t=0.166$ measured in the $L_1$-norm and the EOC comparing equidistant grids with resolutions $64\times 64$, $128\times 128$ and $256\times 256$ to a reference solution with resolution $1024\times 1024$ using CFL $=0.275$. The results are shown in Table 7 and confirm third order accuracy and high accuracy even on coarse grids.

Table 7 Error at time $t=0.166$ measured in $L_1$-norm and EOC for Example 6.3 using the evolution operator (33)

6.2 Stationary and Moving Vortex

We now consider the approximation of vortex structures for the linearised Euler equations. The first test problem is a stationary vortex analogously to Example 5.2 but now approximated using the Active Flux method for the linearised Euler equations. The second test problem is a moving vortex.

Example 6.4

We consider (31), (32) with $\rho ' = 1, u'=v'=0, c'=1$ on the domain $[-\,0.75,0.75] \times [-\,0.75,0.75]$ with double periodic boundary conditions. Initial values for p, u and v are the same as in Example 5.2. In addition, the density is initially set to $\rho (r,0)= 0$. The exact solution coincides with the initial values for all times.

Fig. 17

Scatter plots of $|{\textbf{u}}|$ for the stationary vortex, described in Example 6.4, at time $t=1$ (left) and $t=100$ (middle) as well as for the moving vortex problem, described in Example 6.5, at time $t=1$ (right). All computations use $128 \times 128$ grid cells

In Fig. 17 we show scatter plots of $|{\textbf{u}}|$ at times $t=1$ (left plot) and $t=100$ (middle) computed on a grids with $128 \times 128$ grid cells. The result at time $t=100$ compares well with the result for acoustics shown in Sect. 5.3.

In contrast to the acoustic equations, the linearised Euler equations allow to also approximate a moving vortex structure. Such a problem is considered in the next test problem.

Example 6.5

We consider (31), (32) with $\rho ' = 1, u'=v'=1.5, c'=1$ on the domain $[-\,0.75,0.75] \times [-\,0.75,0.75]$ with double periodic boundary conditions. The initial values are the same as in Example 6.4. At all times $t=n$, $n \in {\mathbb {N}}$, the exact solution coincides with the initial values.

In Fig. 18 we show the solution structure of $|{\textbf{u}}|$ for the moving vortex problem at different times. In Fig. 17 (right) we show a scatter plot at time $t=1$ which can be compared with Fig. 17 (left) to see the influence of the transport on the accuracy of the vortex structure.

Fig. 18

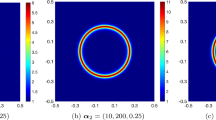
Solution structure of $|{\textbf{u}}|$ for the moving vortex problem, described in Example 6.5, combuted on a grid with $128 \times 128$ grid cells at times $t=0.25, 5, 0.75, 1$

6.3 Discontinuous Solutions

Next we consider a test problem with discontinuous solution structure in analogy to Example 5.3.

Example 6.6

We consider numerical solutions of (31), (32) with $\rho '=1, u'=v'=0, c'=1$ on the domain $[-1,1]\times [-1,1]$. The initial values for p, u, v agree with those of Example 5.3. The initial values for density are set to $\rho (x,y,0) = 1$. Our numerical boundary treatment takes the solution structure into account as described in Example 5.3.

Fig. 19

Numerical results for Example 6.6: $\rho , u, v, p$ (top to bottom) at times $t=0.5$ (left) and $t=1$ (middle) using a grid with $256 \times 256$ grid cells. The right column shows the solution at time $t=1$ using a grid with $128 \times 128$ cells

In Fig. 19 (left) and (middle), we show numerical solutions of Example 6.6 at times $t=0.5$ and $t=1$, computed on a grid with $256 \times 256$ grid cells, using time steps which satisfy $\text{ CFL }<0.275$. We observe a sharp approximation of discontinuities and a spherical solution structure in analogy to the results for acoustics shown in Figs. 11 and 12. In addition (right) we also show the solution structure computed on a coarser grid with $128 \times 128$ grid cells which again illustrates the ability of the Active Flux method to provide accurate approximations even on relatively coarse grids.

7 Euler Equations

Now we use the approximative evolution operator for the linearised Euler equations to construct an Active Flux method for the two-dimensional Euler equations, i.e. for the nonlinear system

$$\begin{aligned} \partial _t {\textbf{q}} + \partial _x f({\textbf{q}}) + \partial _y g({\textbf{q}}) = {\textbf{0}}, \end{aligned}$$

(35)

with ${\textbf{q}} = (\rho , \rho u, \rho v, E)^T$,

$$\begin{aligned} f({\textbf{q}}) = \left( \begin{array}{c} \rho u \\ \rho u^2 + p \\ \rho u v \\ u(E+p) \end{array}\right) , \quad g({\textbf{q}}) = \left( \begin{array}{c} \rho v \\ \rho u v \\ \rho v^2 + p\\ v(E+p)\end{array}\right) \end{aligned}$$

(36)

and the ideal gas equation of state

$$\begin{aligned} E = \frac{p}{\gamma -1} + \frac{1}{2} \rho (u^2 + v^2). \end{aligned}$$

(37)

Our Active Flux method for the Euler equations uses the conservative form (35) for the update of the cell average values of the conserved variables and local linearisations of the form (31), (32), to compute the evolution of the point values of the primitive variables using the method of bicharacteristics. This is in analogy to the lower order finite volume methods proposed by Lukáčová-Medvid’ová et al. [23]. In [1], Abgrall proposed a method for the one-dimensional Euler equations which also combines the evolution of conservative and primitive variables. It is a semi-discrete method and the use of a higher order accurate ode solver increases the stencil. Our method instead is fully discrete and thus uses a local stencil in space and time.

In our description of the method we denote with Q approximations of the conservative variables $(\rho , \rho u, \rho v, E)^T$ and with U approximations of the primitive variables $(\rho , u, v, p)^T$. The conservative variables are updated using a finite volume approach

$$\begin{aligned} Q_{ij}^{n+1} = Q_{ij}^n - \frac{\Delta t}{\Delta x} \left( F_{i+\frac{1}{2},j} -F_{i-\frac{1}{2},j} \right) - \frac{\Delta t}{\Delta y} \left( G_{i,j+\frac{1}{2}} - G_{i,j-\frac{1}{2}}\right) , \end{aligned}$$

where the numerical fluxes are calculated using Simpson’s rule. The horizontal flux, for example, is computed using

$$\begin{aligned} \begin{aligned} F_{i+\frac{1}{2},j}&= \frac{1}{36} \left( f\left( U_{i+\frac{1}{2},j-\frac{1}{2}}^n\right) + 4 f\left( U_{i+\frac{1}{2},j}^n\right) + f\left( U_{i+\frac{1}{2},j+\frac{1}{2}}^n\right) \right. \\&\left. \quad +\, 4 f\left( U_{i+\frac{1}{2},j-\frac{1}{2}}^{n+\frac{1}{2}}\right) + 16 f\left( U_{i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) + 4 f\left( U_{i+\frac{1}{2},j+\frac{1}{2}}^{n+\frac{1}{2}}\right) \right. \\&\left. \quad +\, f\left( U_{i+\frac{1}{2},j-\frac{1}{2}}^{n+1}\right) + 4 f\left( U_{i+\frac{1}{2},j}^{n+1}\right) + f\left( U_{i+\frac{1}{2},j+\frac{1}{2}}^{n+1}\right) \right) . \end{aligned} \end{aligned}$$

(38)

To compute these numerical fluxes, we use point values of $\rho$, u, v and p along the grid cell boundary at times $t_n$, $t_{n+\frac{1}{2}}$ and $t_{n+1}$. We assume that the point values of the primitive and conservative variables at time $t_n$ are known. Point values of $\rho$, u, v and p at the intermediate and the new time level are computed using the approximative evolution formula for the linearised Euler equations (33). Using these point values we then compute

$$\begin{aligned} f\left( U_{i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) = \left( \begin{array}{c} \rho _{i+\frac{1}{2},j}^{n+\frac{1}{2}}\\ \rho _{i+\frac{1}{2},j}^{n+\frac{1}{2}} u_{i+\frac{1}{2},j}^{n+\frac{1}{2}} \\[0.2cm] \rho _{i+\frac{1}{2},j}^{n+\frac{1}{2}} v_{i+\frac{1}{2},j}^{n+\frac{1}{2}} \\ \frac{1}{\gamma -1} p_{i+\frac{1}{2},j}^{n+\frac{1}{2}} + \frac{1}{2} \rho _{i+\frac{1}{2},j}^{n+\frac{1}{2}} \left( \left( u_{i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) ^2 +\left( v_{i+\frac{1}{2},j}^{n+\frac{1}{2}}\right) ^2\right) \end{array} \right) \end{aligned}$$

and analogously all the other terms on the right hand side of (38).

A piecewise quadratic reconstruction in primitive variables is required in order to evaluate (33) for the linearised Euler equations with third order accuracy. The Active Flux reconstruction for two-dimensional Cartesian grids, which is described in [5, 17], requires point values along the grid cell boundary as well as cell average values for each grid cell. While it is trivial to compute point values of the primitive variables U from point values of the conservative variables Q and vice versa, this is not the case for cell average values, since products of averages are not equal to averages of products.

To get third order accurate approximations of the cell averages in primitive variables, we first compute an Active Flux reconstruction in conservative variables. This reconstruction uses the cell averages $Q_{ij}^n$ of the conserved quantities, computed by the finite volume approach, and point values of the conserved quantities along the grid cell boundary that are easily obtained from point values in primitive variables. Point values for E can be computed via the equation of state (37). The reconstruction in conservative variables can be evaluated at the center of the grid cell, i.e. at $(x_i,y_j)$, leading to third order accurate approximations of point values in conservative variables $q^{rec}(x_i,y_j)$. From these point values in conservative variables we can compute point values of the primitive variables at the center of the grid cell. Finally, we use these point values at the center of the grid cell together with the point values along the grid cell boundary to compute cell average values by using Simpson’s rule. These cell average values of the primitive variables finally allow us to compute the third order accurate Active Flux reconstructions in primitive variables.

For the nonlinear Euler equations the linearisation (31), (32) is performed locally for each point value. An important aspect which arises in the nonlinear case is the choice of the state around which the linearisation should be performed. Previous results for the two-dimensional Burgers’ equation [4, 8] indicate that the linearisation should be performed around the solution we wish to approximate. This can be realised iteratively as described in Algorithm 1. The derivation and analysis of third order accurate Active Flux methods for the one-dimensional Euler equations presented by Barsukow [4] show that characteristics for nonlinear systems are in general curved lines and that the evolution operator needs to take the curvature of characteristics into account in order to obtain third order accurate Active Flux methods. In our current Active Flux method for the two-dimensional Euler equations we use the characteristic cone from the linear problem and ignore the influence of nonlinear effects on the geometry of the characteristic cones. The currently used update of the point values located at $(x_{i+\frac{1}{2}},y_j)$ is described in Algorithm 1.

Algorithm 1

Update of point values in the Active Flux method for the Euler equations

Example 7.1

We consider approximations of the Euler equations with initial values as described in Example 6.2. The exact solution again agrees with the initial values propagated with constant speed. Numerical simulations are performed on the domain $[-1,1] \times [-1,1]$ with periodicity imposed in both directions.

Table 8 shows results of a numerical convergence study for Example 7.1. For this simple problem the nonlinearity of the equations does not lead to geometric changes of the characteristic cones and we observe the expected third order convergence rate by using the described method with only one iteration, i.e. $L=0$, for the computation of the point values.

Table 8 Error of density measured in the $L_1$-norm and EOC after one rotation for Example 7.1

While we use a completely different method than in the case of the linearised Euler equations, the accuracy obtained for the nonlinear Euler equations compares well with the accuracy observed in Table 6 for the linearised Euler equations.

Example 7.2

The Gresho problem [16, 20] is a stationary rotating vortex problem. The velocity field agrees with those of Example 5.2. The pressure is prescribed in such a way that the centrifugal force is balanced by the pressure gradient:

$$\begin{aligned} p(r) = \left\{ \begin{array}{lcl} 5 + \frac{25}{2} r^2 &{}: &{} 0 \le r< 0.2 \\ 9 - 4 \ln 0.2 + \frac{25}{2}r^2 - 20 r + 4\ln r &{}: &{} 0.2 \le r < 0.4\\ 3 + 4 \ln 2 &{}: &{} r\ge 0.4.\end{array}\right. \end{aligned}$$

(39)

The density is set to one, the computational domain is $[-\,0.75,0.75] \times [-\,0.75,0.75]$ and periodic boundary conditions have been used.

In Figs. 20 and 21 we show numerical results obtained by running the Active Flux method for the Euler equations on a grid with $64 \times 64$ cells until time $t=3$ using time steps which satisfy $\text{ CFL } \le 0.275$. The density does not stay constant. Instead we observe values between 0.999275 and 1.001377. The circular geometry in p and $|{\textbf{u}}|$ is well preserved.

Fig. 20

Solution structure of the Gresho problem computed at time $t=3$ on a grid with $64 \times 64$ grid cells, (left) density, (middle) pressure, (right) angular velocity

Fig. 21

Scatter plot of the numerical solution at time $t=3$ for the Gresho problem computed on a grid with $64 \times 64$ cells, (left) pressure, (middle) angular velocity and (right) vorticity

Our next test problem considers a smooth moving vortex problem, which will also be used for a numerical convergence study.

Example 7.3

We consider a smooth traveling vortex for the Euler equations as introduced in [18]. A rotating vortex is initially located at (0.5, 0.5) and propagates with constant speed $(u_c,v_c)$. The initial values have the form

$$\begin{aligned} \begin{aligned} \rho (x,y,t)&= \left\{ \begin{array}{lcl} \rho _c + \frac{1}{2} (1-r^2)^6 &{}: &{} r<1\\ \rho _c &{}: &{} \text{ otherwise } \end{array}\right. \\ u(x,y,z)&= \left\{ \begin{array}{lcl} u_c -1024 \sin (\theta ) (1-r)^6 r^6 &{}: &{} r<1\\ u_c &{}: &{} \text{ otherwise } \end{array}\right. \\ v(x,y,t)&= \left\{ \begin{array}{lcl} v_c + 1024 \cos (\theta ) (1-r)^6 r^6 &{}: &{} r<1\\ v_c &{}: &{} \text{ otherwise } \end{array}\right. \\ p (x,y,t)&= \left\{ \begin{array}{lcl} p_c + (p(r) - p(1)) &{}: &{} r<1 \\ p_c &{}: &{} \text{ otherwise }. \end{array} \right. \end{aligned} \end{aligned}$$

Here r is the scaled distance from the initial center of the vortex, i.e.

$$\begin{aligned} r = \sqrt{(x-0.5)^2 + (y-0.5)^2} / R, \end{aligned}$$

where R is the radius of the vortex. The function p(r) is described in [18] as a polynomial of degree 36. One of the coefficients however is incorrect and should be $\left( -\frac{269}{15} r^{30}\right)$ instead of $\left( -\frac{259}{15} r^{30}\right)$. In our computation we use $R = 0.4$, $\rho _c = 0.5$, $u_c = v_c = 1$ and $p_c = 0.1$. We simulate the vortex on the domain $[0,1] \times [0,1]$ using periodic boundary conditions. At time $t=1$ the exact solution agrees with the initial values.

In Table 9 we show results of a numerical convergence study. The computation was performed using time steps which satisfy $\text{ CFL } \le 0.275$. The error was measured by comparing the numerical solution of the current grid with the solution on the next finer mesh. We show the results for a computation with one and two iterations, i.e. using $L=0$ and $L=1$ in Algorithm 1. As previously observed for scalar problems, the iterative process improves the accuracy. Since our method does not take changes of the characteristic cone due to the nonlinearity into account, we can not expect full third order. However, the experimentally observed order of convergence is still close to three if two iterations are used for the update of the point values. Figures 22 and 23 show the solution structure of the smooth moving vortex problem. At time $t=10$, shown in the right column of Fig. 22, perturbations of the spherical geometry are clearly visable. This can also be seen in the scatter plot of $|{\textbf{u}}|$ (Fig. 23 (middle)). If the same computation is performed on a grid with $128 \times 128$ cells, the spherical solution structure is preserved much better as can be seen in Fig. 23 (right).

Table 9 Error in the $L_1$-norm and EOC for the density at time $t=1$ with 1 and 2 iterations for the smooth vortex problem described in Example 7.3

Fig. 22

Solution structure of Example 7.3 at time $t=0$ (left column), $t=1$ (middle column) and $t=10$ (right column) computed on a grid with $64 \times 64$ grid cells; (top) $\rho$, (middle) p, (bottom) $|{\textbf{u}}|$

Fig. 23

Scatter plot of $|{\textbf{u}}|$ versus r for Example 7.3, (left) $t=1$, $64 \times 64$ grid, (middle) $t=10$, $64 \times 64$ grid, (right) $t=10$, $128 \times 128$ grid

Example 7.4

We consider a classical two-dimensional Riemann problem for the Euler equations, as described in [31], consisting of two forward moving shocks and two stationary contact discontinuities. On the interval $[0,1] \times [0,1]$ the initial values have the form

$$\begin{aligned} (\rho , u, v, p) = \left\{ \begin{array}{lcl} (0.5313,0,0,0.4) &{}: &{} x>0.5, y>0.5 \\ (1,0.7276,0,1) &{}: &{} x<0.5, y>0.5\\ (0.8,0,0,1) &{}: &{} x<0.5, y<0.5\\ (1,0,0.7276,1) &{}: &{} x>0.5, y<0.5. \end{array}\right. \end{aligned}$$

In Fig. 24 we show results for the density at different times. In the first row we used a grid with $128 \times 128$ grid cells, in the second row with $512 \times 512$ cells. The solution structure is well resolved even on the relatively coarse mesh.

Fig. 24

Contour plots of density at different times for the two-dimensional Riemann problem described in Example 7.4. We use the new Active Flux method for the Euler equations on grids with $128 \times 128$ grid cells (top) and $512 \times 512$ grid cells (bottom)

Note that all simulations shown in this paper were performed without the use of limiters.

8 Conclusions

We have derived and analysed new third order accurate Active Flux methods for two-dimensional linear and nonlinear hyperbolic systems. For the update of the point values we used truly multidimensional approximate evolution formulas, which have been derived using the method of bicharacteristics. For the acoustic equations we compared the resulting Active Flux method with previously proposed Active Flux methods using exact evolution formulas. The accuracy compares well but the newly proposed Active Flux methods have a reduced stability. However, the method of bicharacteristics is a general approach that can be used to derive evolution formulas for other linear hyperbolic systems. With this approach we obtained the first unsplit Active Flux method for the linearised Euler equations. Using a local linearisation for each point value degree of freedom, we furthermore obtained a new Active Flux method for the two-dimensional nonlinear Euler equations. The performance of the new Active Flux methods for linear and nonlinear hyperbolic systems is illustrated for a number of test problems.

In addition we proposed a third order accurate Active Flux method for Maxwell’s equation that explores the relation between Maxwell’s equations and acoustics.

All Active Flux methods presented in this paper are fully discrete, use a continuous piecewise quadratic reconstruction, a truly multi-dimensional evolution operator and a compact stencil in space and time. We implemented the new Active Flux methods in ForestClaw using patches of Cartesian grids that also allow adaptive mesh refinement and sub-cycling as described in [7].

Details on the Implementation

Exemplarily we describe for the acoustic equation the update of the pressure corner value of some cell using the EG2 evolution formula. We have

$$\begin{aligned} \begin{aligned} p(P)&=\frac{1}{\pi }\int _{0}^{2\pi }p(Q(\theta ))-u(Q(\theta )) \cos (\theta )-v(Q(\theta ))\sin (\theta ) \ \textrm{d}\theta -p(P') \\&=\frac{1}{\pi }\int _{0}^{\frac{\pi }{2}}p_{0,0}(Q_{0,0}(\theta ))-u_{0,0}(Q_{0,0}(\theta )) \cos (\theta )-v_{0,0}(Q_{0,0}(\theta ))\sin (\theta )\ \textrm{d}\theta \\&\quad +\frac{1}{\pi }\int _{\frac{\pi }{2}}^{\pi }p_{-1,0} (Q_{-1,0}(\theta ))-u_{-1,0}(Q_{-1,0}(\theta )) \cos (\theta )-v_{-1,0}(Q_{-1,0}(\theta ))\sin (\theta ) \ \textrm{d}\theta \\&\quad +\frac{1}{\pi }\int _{\pi }^{\frac{3\pi }{2}}p_{-1,-1} (Q_{-1,-1}(\theta ))-u_{-1,-1}(Q_{-1,-1}(\theta ))\cos (\theta )\\&\quad -v_{-1,-1}(Q_{-1,-1}(\theta ))\sin (\theta )\ \textrm{d}\theta \\&\quad + \frac{1}{\pi }\int _{\frac{3\pi }{2}}^{2\pi }p_{0,-1} (Q_{0,-1}(\theta ))-u_{0,-1}(Q_{0,-1}(\theta ))\cos (\theta )\\&\quad -v_{0,-1}(Q_{0,-1}(\theta ))\sin (\theta ) \ \textrm{d}\theta -p(P'), \end{aligned} \end{aligned}$$

(40)

where $p_{s,t}, u_{s,t}$ and $v_{s,t}$ are the reconstructions in cells with index (s, t) relative to our cell and

$$\begin{aligned} \begin{aligned} Q_{0,0}(\theta )&:=\left( -1+2\frac{ c\Delta t }{\Delta x}\cos (\theta ), -1+2\frac{ c\Delta t }{\Delta y}\sin (\theta )\right) \\ Q_{-1,0}(\theta )&:=\left( 1+2\frac{ c\Delta t }{\Delta x} \cos (\theta ),-1+2\frac{ c\Delta t }{\Delta y}\sin (\theta )\right) \\ Q_{-1,-1}(\theta )&:=\left( 1+2\frac{ c\Delta t }{\Delta x} \cos (\theta ),1+2\frac{ c\Delta t }{\Delta y}\sin (\theta )\right) \\ Q_{0,-1}(\theta )&:=\left( -1+2\frac{ c\Delta t }{\Delta x}\cos (\theta ), 1+2\frac{ c\Delta t }{\Delta y}\sin (\theta )\right) , \end{aligned} \end{aligned}$$

(41)

since every cell is mapped to the reference cell $[-1,1] \times [-1,1]$. The reconstruction in each cell is quadratic in x and y. On a Cartesian grid, the occurring integrals can be written as, e.g.,

$$\begin{aligned} \begin{aligned}&\frac{1}{\pi }\int _{0}^{\frac{\pi }{2}}p_{0,0}(Q_{0,0}(\theta ))-u_{0,0}(Q_{0,0}(\theta )) \cos (\theta )-v_{0,0}(Q_{0,0}(\theta ))\sin (\theta ) \ \textrm{d}\theta \\&\quad = \frac{1}{\pi }\int _{0}^{\frac{\pi }{2}} \sum _{n,m=0}^2 p^{n,m} \sin ^n(\theta )\cos ^m(\theta ) \left( \frac{c\Delta t}{\Delta x}\right) ^{n+m}\\&\qquad -\sum _{n,m=0}^2 u^{n,m} \sin ^n(\theta )\cos ^{m+1}(\theta )\left( \frac{c\Delta t}{\Delta x}\right) ^{n+m}\\&\qquad -\sum _{n,m=0}^2 v^{n,m} \sin ^{n+1}(\theta )\cos ^m(\theta )\left( \frac{c\Delta t}{\Delta x}\right) ^{n+m}\ \textrm{d}\theta \\&\quad = \sum _{n,m=0}^2 \left( {\tilde{p}}^{n,m} + {\tilde{u}}^{n,m} + {\tilde{v}}^{n,m}\right) \left( \frac{c\Delta t}{\Delta x}\right) ^{n+m}, \end{aligned} \end{aligned}$$

(42)

where $p^{n,m},{\tilde{p}}^{n,m},u^{n,m},{\tilde{u}}^{n,m},v^{n,m},{\tilde{v}}^{n,m}$ are linear combinations of the eight point values and the cell averaged value of our cell. Doing the same for the other three integrals lying in the cells with indices $(-1,0)$, $(-1,-1)$, $(0,-1)$ and extracting the coefficients gives the corresponding entries in the update matrix A, which now only depends on the CFL number. Similarly one gets the coefficients for the update of a face point value, where the integration takes place in only two cells. The update of the cell averaged value depends on all point values on the boundary of our cell at the current time but also at the intermediate and the next time step, giving the domain of dependency illustrated in Fig. 25.

Fig. 25

Domain of dependency for the update of a corner (left), a face (middle) and a cell averaged value (right)

To organise A, the degrees of freedom (DoFs) of our cells are ordered as

$$\begin{aligned} {\mathcal {C}} = \left[ p_{-\frac{1}{2},0},u_{-\frac{1}{2},0},v_{-\frac{1}{2},0}, p_{-\frac{1}{2},-\frac{1}{2}},u_{-\frac{1}{2},-\frac{1}{2}}, v_{-\frac{1}{2},-\frac{1}{2}},p_{0,-\frac{1}{2}}, u_{0,-\frac{1}{2}},v_{0,-\frac{1}{2}},p_{0,0},u_{0,0},v_{0,0} \right] \nonumber \\ \end{aligned}$$

(43)

and all cells concatenated row by row give the vector of all DoFs

$$\begin{aligned} Q^n=\left[ {\mathcal {C}}_{1,1},{\mathcal {C}}_{2,1}, \ldots ,{\mathcal {C}}_{m,1},{\mathcal {C}}_{1,2},{\mathcal {C}}_{2,2}, \ldots ,{\mathcal {C}}_{m-1,m},{\mathcal {C}}_{m,m}\right] . \end{aligned}$$

(44)

Since only four DoFs are associated with each cell, the update of our cell depends on the DoFs of 16 cells whose coefficients are stored in matrices $Z_{s,t} \in {\mathbb {R}}^{12 \times 12}, s,t=-\,1,0,1,2$, where (s, t) indicates the index relative to our cell. We define $P_m(\delta )\in {\mathbb {R}}^{m \times m}$ as the identity matrix shifted by $\delta$ columns to the right, then A is given by

$$\begin{aligned} A=\sum _{s,t=-\,1}^2 P_m(s) \otimes P_m(t) \otimes Z_{s,t}. \end{aligned}$$

(45)

A more detailed description of how A is organised can be found in [8].