Energy-Stable Global Radial Basis Function Methods on Summation-By-Parts Form

Abstract

Radial basis function methods are powerful tools in numerical analysis and have demonstrated good properties in many different simulations. However, for time-dependent partial differential equations, only a few stability results are known. In particular, if boundary conditions are included, stability issues frequently occur. The question we address in this paper is how provable stability for RBF methods can be obtained. We develop a stability theory for global radial basis function methods using the general framework of summation-by-parts operators often used in the Finite Difference and Finite Element communities. Although we address their practical construction, we restrict the discussion to basic numerical simulations and focus on providing a proof of concept.

1 Introduction

We investigate energy stability of global radial basis function (RBF) methods for time-dependent partial differential equations (PDEs). Unlike finite differences (FD) or finite element (FE) methods, RBF schemes are mesh-free, making them very flexible with respect to the geometry of the computational domain since the only used geometrical property is the pairwise distance between two centers. Further, they are suitable for problems with scattered data like in climate [12, 34] or stock market [6, 41] simulations. Finally, for smooth solutions, one can reach spectral convergence [11, 13]. In addition, they have recently become increasingly popular for solving time-dependent problems in quantum mechanics, fluid dynamics, etc. [7, 29, 30, 52]. One distinguishes between global RBF methods (Kansa’s methods) [31] and local RBF methods, such as the RBF generated finite difference (RBF-FD) [50] and RBF partition of unity (RBF-PUM) [55] method. However, there are some nuances regarding the computational efficiency to take into account. For instance, a naive approach results in a large dense differentiation matrix. Furthermore, care must be taken regarding the conditioning of the differentiation and associated Vandermonde matrices. There exists several strategies to combat these issues, including stable bases, compactly supported RBFs [3, 54], domain decomposition [9, 58], and local variants of RBF methods [12, 55]. Also see the monograph [14] and references therein. Even though the efficiency and good performance of RBF methods have been demonstrated for various problems, only a few stability results are known for advection-dominated problems. For example, an eigenvalue analysis was performed for a linear advection equation in [42], and it was found that RBF discretizations often produce eigenvalues with positive real part, lending to an exponential increase of the $L_2$ norm when boundary conditions were introduced. To illustrate this, consider the following example (also found in [21, Section 6.1]):

$$\begin{aligned} \partial _t u+ \partial _x u=0, \qquad u(x,0)= \textrm{e}^{-20x^2} \end{aligned}$$

(1)

with $x \in [-1,1]$, $t>0$, and where periodic boundary conditions are applied. In this example, a bump travels to the right, leaving the domain and re-entering at the left boundary.

Fig. 1

Gaussian kernel with $N=20$ points (equidistant points) after ten periods

In Figure 1, we plot the numerical solution and its energy up to $t=10$ using a global RBF method with a Gaussian kernel and $N=20$ points. An increase in the bump’s size and energy can be seen. For longer times, the computation breaks down. The discrete setting does not reflect the continuous one with zero energy growth and demonstrates the stability problem. To overcome those, it was shown in [21] that a weak formulation as used in classical FE methods could result in a stable method, whereas in [24] weakly imposed boundary conditions together with properly constructed boundary operators were used. Recently, $L_2$ estimates were also obtained using an oversampling technique [53], assuming that a sufficient amount of evaluation points are used. All these efforts use special techniques, and the question we address in this paper is how to stabilize RBF methods in a general way.

Classical summation-by-parts (SBP) operators were introduced during the 1970s in the context of FD schemes. They allow for a systematic development of energy-stable semi-discretizations of well-posed initial-boundary-value problems (IBVPs) [8, 49]. The SBP property is a discrete analog to integration by parts, and proofs from the continuous setting carry over directly to the discrete framework [38] if proper boundary procedures are added [49]. Based initially on polynomial approximations, the SBP theory has recently been extended to general function spaces developing so-called FSBP operators in [25]. Here, we investigate stability of global RBF methods through the lens of the FSBP theory. We demonstrate that many existing RBF discretizations do not satisfy the FSBP property, which explains the instability of these methods. Based on these findings, we show how RBF discretizations can be modified to obtain an SBP property. This then allows for a systematic development of energy-stable RBF methods. We provide some specific examples, including the most frequently used RBFs. Furthermore, we connect to some recent stability results from [53], where oversampling was used, to the FSBP property. For simplicity, we focus on the univariate setting for developing an SBP theory in the context of global RBF methods. That said, RBF methods and SBP operators can easily be extended to the multivariate setting, as demonstrated in our numerical tests. The focus of the present paper is to provide a proof of concept and use the FSBP theory to develop provable energy-stable global RBF methods. We restrict most of the discussion to the one-dimensional setting to avoid some technical difficulties that might otherwise distract the reader from the core concept. That said, future work will address the multi-dimensional case among other things, also including local RBF methods, accuracy, and efficient implementations.

The rest of this work is organized as follows. In Section 2, we provide some preliminaries on energy-stability of IBVPs and global RBF methods. Next, the concept of FSBP operators is shortly revisited in Section 3. We adapt the FSBP theory to RBF function spaces in Section 4. Here, it is also demonstrated that many existing RBF methods do not satisfy the SBP property and how to construct RBF operators in SBP form (RBFSBP). In Section 5, we give some concrete examples of RBFSBP operators resulting in energy-stable methods. Finally, we provide numerical tests in Section 6 and concluding thoughts in Section 7.

2 Preliminaries

We now provide a few preliminaries on IBVPs and RBF methods.

2.1 Well-posedness and Energy Stability

Following [28, 38, 49], we consider

$$\begin{aligned} \begin{aligned} \partial _t u&= {\mathcal {L}}(x,t,\partial _x) u+ {\mathcal {{\hat{F}}}(x,t)}, \quad{} & {} x_L< x < x_R, \ t > 0,\\ u(x,0)&= f(x), \quad{} & {} x_L \le x \le x_R, \\ {\mathcal {B}}_0(t,\partial _x) u(x_L,t)&= g_{x_L}(t), \quad{} & {} t \ge 0, \\ {\mathcal {B}}_1(t,\partial _x) u(x_R,t)&= g_{x_R}(t), \quad{} & {} t \ge 0, \end{aligned} \end{aligned}$$

(2)

where u is the solution and ${\mathcal {L}}$ is a differential operator with smooth coefficients. Further, $B_0$ and $B_1$ are operators defining the boundary conditions, ${\mathcal {{\hat{F}}}}$ is a forcing function, f is the initial data, and $g_{x_L}, g_{x_R}$ denote the boundary data. Examples of (2) include the advection equation

$$\begin{aligned} \partial _t u(x,t) + a \partial _x u(x,t)=0 \end{aligned}$$

(3)

with constant $a \in {\mathbb {R}}$, the diffusion equation

$$\begin{aligned} \partial _t u(x,t) = \partial _{x} \left( \kappa \partial _x u(x,t) \right) \end{aligned}$$

(4)

with $\kappa \in {\mathbb {R}}$ depending on x, t, as well as combinations of (3) and (4). Let us now formalize what we mean by the IBVP (2) being well-posed.

Definition 1

The IBVP (2) with ${\mathcal {{\hat{F}}}}=0$ and $g_{x_L}=g_{x_R}=0$ is well-posed, if for every $f\in C^{\infty }$ that vanishes in a neighborhood of $x=x_L,x_R$, (2) has a unique smooth solution u that satisfies

$$\begin{aligned} \left| \left| u(\cdot ,t)\right| \right| _{L_2} \le C \textrm{e}^{\alpha _C t}\left| \left| f\right| \right| _{L_2}, \end{aligned}$$

(5)

where $C, \alpha _c$ are constants independent of f. Moreover, the IBVP (2) is strongly well-posed, if it is well-posed and

$$\begin{aligned} \left| \left| u(\cdot ,t)\right| \right| ^2_{L_2} \le C(t) \left( \left| \left| f\right| \right| ^2_{L_2}+ \int _{0}^{t} \left( \left| \left| {\mathcal {{\hat{F}}}}(\cdot , \tau ) \right| \right| ^2_{L_2} +|g_{x_L}(\tau )|^2+|g_{x_R}(\tau )|^2 \right) d \tau \right) , \end{aligned}$$

(6)

holds, where the function C(t) is bounded for finite t and independent of ${\mathcal {{\hat{F}}}}, g_{x_L}, g_{x_R}$, and f.

Switching to the discrete framework, our numerical approximation $u^h$ of (2) should be constructed in such a way that similar estimates to (5) and (6) are obtained. We denote our grid quantity (a measure of the grid size) by h. In the context of RBF methods, h denotes the maximum distance between two neighboring points. We henceforth denote by $\Vert \cdot \Vert _h$ a discrete version of the $L_2$-norm and $\left| \left| \cdot \right| \right| _b$ represents a discrete boundary norm. Then, we define stability of the numerical solution as follows.

Definition 2

Let ${\mathcal {{\hat{F}}}}=0$, $g_{x_L}=g_{x_R}=0$, and $f^h$ be an adequate projection¹ of the initial data f which vanishes at the boundaries. The approximation $u^h$ is stable if

$$\begin{aligned} {\left| \left| u^h(t)\right| \right| _h \le C \textrm{e}^{\alpha _d t}\left| \left| f^h\right| \right| _h} \end{aligned}$$

(7)

holds for all sufficiently small h, where C and $\alpha _d$ are constants independent of $f^h$. The approximated solution $u^h$ is called strongly energy stable if it is stable and

$$\begin{aligned} \left| \left| u^h(t)\right| \right| ^2_h \le C(t) \left( \left| \left| f^h\right| \right| ^2_h+ \max \limits _{\tau \in [0,t]} \left| \left| {\mathcal {{\hat{F}}}}( \tau ) \right| \right| _h^2 +\max \limits _{\tau \in [0,t]} \left| \left| g_{x_L}(\tau )\right| \right| ^2_b+\max \limits _{\tau \in [0,t]} \left| \left| g_{x_R}(\tau )\right| \right| ^2_b \right) \nonumber \\ \end{aligned}$$

(8)

holds for all sufficiently small h. The function C(t) is bounded for finite t and independent of ${\mathcal {{\hat{F}}}}, g_{x_L}, g_{x_R}$, and $f^h$.

2.2 Discretization

To discretize the IBVP (2), we apply the method of lines. The space discretization is done using a global RBF method resulting in a system of ordinary differential equations (ODEs):

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} {\textbf{u}} = {\text {L}}({\textbf{u}}). \end{aligned}$$

(9)

Here, ${\textbf{u}}$ denotes the vector of coefficients and ${\text {L}}$ represents the spatial operator. We used the explicit strong stability preserving (SSP) Runge–Kutta (RK) method of third-order with three stages (SSPRK(3,3)) [47] for all subsequent numerical tests.

2.2.1 Radial Basis Function Interpolation

RBFs are powerful tools for interpolation and approximation [10, 14, 56]. In the context of the present work, we are especially interested in RBF interpolants. Let $u: {\mathbb {R}}\supset \Omega \rightarrow {\mathbb {R}}$ be a scalar valued function and $X_K = \{x_1,\dots ,x_K\}$ a set of interpolation points, referred to as centers. The RBF interpolant of u is

$$\begin{aligned} u^h(x) = \sum _{k=1}^K \alpha _k \varphi ( |x - x_k| ) + \sum _{l=1}^m \beta _k p_l(x). \end{aligned}$$

(10)

Here, $\varphi : {\mathbb {R}}_0^+ \rightarrow {\mathbb {R}}$ is the RBF (also called kernel) and $\{p_l\}_{l=1}^m$ is a basis for the space of polynomials up to degree $m-1$, denoted by ${\mathbb {P}}_{m-1}$. In our numerical section, we use mostly $m=1$ meaning that we include constants in our approximation space. Furthermore, the RBF interpolant (10) is uniquely determined by the conditions

$$\begin{aligned} u^h(x_k)&= u(x_k), \quad{} & {} k=1,\dots ,K, \end{aligned}$$

(11)

$$\begin{aligned} \sum _{k=1}^K \alpha _k p_l(x_k)&= 0 , \quad{} & {} l=1,\dots ,m. \end{aligned}$$

(12)

Note that (11) and (12) can be reformulated as a linear system for the coefficient vectors $\varvec{\alpha } = [\alpha _1,\dots ,\alpha _K]^T$ and $\varvec{\beta } = [\beta _1,\dots ,\beta _m]^T$:

$$\begin{aligned} \begin{bmatrix} \Phi &{} \textrm{P} \\ \textrm{P} ^T &{} 0 \end{bmatrix} \begin{bmatrix} \varvec{\alpha } \\ \varvec{\beta } \end{bmatrix} = \begin{bmatrix} {\textbf{u}} \\ {\textbf{0}} \end{bmatrix}, \end{aligned}$$

(13)

where ${\textbf{u}} = [u(x_1),\dots ,u(x_K)]^T$ and

$$\begin{aligned} \Phi = \begin{bmatrix} \varphi ( | x_1 - x_1 | ) &{} \dots &{} \varphi ( | x_1 - x_K | ) \\ \vdots &{} &{} \vdots \\ \varphi ( | x_K - x_1 | ) &{} \dots &{} \varphi ( | x_K - x_K | ) \end{bmatrix}, \ \textrm{P} = \begin{bmatrix} p_1(x_1) &{} \dots &{} p_m(x_1) \\ \vdots &{} &{} \vdots \\ p_1(x_K) &{} \dots &{} p_m(x_K) \end{bmatrix}. \end{aligned}$$

(14)

Incorporating polynomial terms of degree up to $m-1$ in the RBF interpolant (10) is important for several reasons:

• (i) The RBF interpolant (10) becomes exact for polynomials of degree up to $m-1$, i. e., $u^h = u$ for $u \in {\mathbb {P}}_{m-1}$.

• (ii) For some (conditionally positive) kernels $\varphi$, the RBF interpolant (10) only exists uniquely when polynomials up to a certain degree are incorporated.

In addition, we will show that (i) is needed for the RBF method to be conservative [21, 25]. The property (ii) is explained in more detail in (1) as well as in [10, Chapter 7] and [18, Chapter 3.1]. For simplicity and clarity, we will focus on the choices of RBFs listed in Table 1. More types of RBFs and their properties can be found in the monographs [10, 14, 56].

Table 1 Some frequently used RBFs

Note that the set of all RBF interpolants (10) forms a K-dimensional linear space, denoted by ${\mathcal {R}}_{m}(X_K)$. This space is spanned by the cardinal functions

$$\begin{aligned} c_i(x) = \sum _{k=1}^K \alpha _k^{(i)} \varphi ( |x - x_k| ) + \sum _{l=1}^m \beta ^{(i)}_l p_l(x), \quad i=1,\dots ,K, \end{aligned}$$

(15)

which are uniquely determined by the cardinal property

$$\begin{aligned} c_i(x_k) = \delta _{ik} := {\left\{ \begin{array}{ll} 1 &{} \text {if } i=k, \\ 0 &{} \text {otherwise}, \end{array}\right. } \quad i,k=1,\dots ,K, \end{aligned}$$

(16)

and condition (12). They also provide us with the following (nodal) representation of the RBF interpolant:

$$\begin{aligned} u^h(x) = \sum _{k=1}^K u(x_k) c_k(x). \end{aligned}$$

(17)

2.2.2 Radial Basis Function Methods

We outline the standard global RBF method for the IBVP (2). The domain $\Omega$ on which we solve (2) is discretized using two point sets:

• The nodal point set (centers) $X_K=\{x_1, \cdots , x_K \}$ used for constructing the cardinal basis functions (15).

• The grid (evaluation) point set $Y_N=\{y_1, \cdots , y_N \}$ for describing the IBVP (2), where $N\ge K$.

By selecting $Y_N=X_K$, we get a collocation method, and with $N>K$, a method using oversampling. The numerical solution ${\textbf{u}}$ is defined by the values of $u^h$ at $Y_N$ and the operator $L({\textbf{u}})$ by using the spatial derivative of the RBF interpolant $u^h$, also at $Y_N$. The RBF discretization can be summarized in the following three steps:

• 1. Determine the RBF interpolant $u^h\in {\mathcal {R}}_{m}(X_K)$.

• 2. Define $L({\textbf{u}})$ in the semidiscrete equation by inserting (17) into the continuous spatial operator. This yields

  $$\begin{aligned} {\text {L}}({\textbf{u}})=&\left( {\mathcal {L}}(y_n,t, \partial _x) u^h(t,y_n)+ {\mathcal {{\hat{F}}}}(t,y_n) \right) _{n=1}^N. \end{aligned}$$

  (18)

• 3. Use a classical time integration scheme to evolve (9).

Global RBF methods come with several free parameters. These include the center and evaluation points $X_K$ and $Y_N$, the kernel $\varphi$, the degree $m-1$ of the polynomial term included in the RBF interpolant (10). The kernel $\varphi$ might come with additional free parameters such as the shape parameter $\varepsilon$. Finally, we note that also the basis $c_k$ of the RBF approximation space ${\mathcal {R}}_{m}(X_K)$, that one uses for numerically computing the RBF approximation $u^h$ and its derivatives, can influence how well-conditioned the RBF method is in practice. Discussions of appropriate choices for these parameters are filling whole books [10, 14, 15, 56] and are avoided here. In this work, we have a different point in mind and focus on the basic stability conditions of RBF methods.

3 Summation-by-parts Operators on General Function Spaces

SBP operators were developed to mimic the behavior of integration by parts in the continuous setting and provide a systematic way to build energy-stable semi-discrete approximations. First, constructed for an underlying polynomial approximation in space, the theory was recently extended to general function spaces in [22, 25]. For completeness, we shortly review the extended framework of FSBP operators and repeat their basic properties. We consider the FSBP concept on the interval $[x_L, x_R]$ where the boundary points are included in the evaluation points $Y_N$. Using this framework, we give the following definition originally found in [25]:

Definition 3

(FSBP operators) Let ${\mathcal {F}} \subset C^1([x_L,x_R])$ be a finite-dimensional function space. An operator $D = P^{-1} Q$ is an ${\mathcal {F}}$-based SBP (FSBP) operator if

• (i) $D f({\textbf{x}}) =f'({\textbf{x}})$ for all $f \in {\mathcal {F}}$,

• (ii) P is a symmetric positive definite matrix, and

• (iii) $Q + Q^T = B = {{\,\textrm{diag}\,}}(-1,0,\dots ,0,1)$.

Here, $f({\textbf{y}}) = [f(y_1), \dots , f(y_N)]^T$ and $f'({\textbf{y}}) = [f'(y_1),\dots , f'(y_N)]^T$ respectively denote the vector of the function values of f and its derivative $f'$ at the evaluation points $y_1,\dots ,y_N$.

Further, D denotes the differentiation matrix and P is a matrix defining a discrete norm. In order to produce an energy estimate, we use that P is positive definite and symmetric such that it induces a norm. In this manuscript and in [25], we focus for stability reasons on diagonal norm FSBP operators [17, 35, 43]. The matrix Q is nearly skew-symmetric and can be seen as the stiffness matrix in context of FE. With these operators, integration-by-parts is mimicked discretely as:

$$\begin{aligned} \begin{aligned}{} & {} f({\textbf{x}})^T PD g({\textbf{x}})+ \left( D f({\textbf{x}}) \right) ^T P g({\textbf{x}})&= f({\textbf{x}})^T B g({\textbf{x}}) \\ \Longleftrightarrow{} & {} \int _{x_L}^{x_R} f(x)\cdot g'(x) d x + \int _{x_L}^{x_R} f'(x)\cdot g(x) d x&=[f(x)g(x)]_{x=x_L}^{x=x_R} \end{aligned} \end{aligned}$$

(19)

for all $f,g \in {\mathcal {F}}$.

3.1 Properties of FSBP Operators

In [25], the authors proved that the FSBP-SAT semi-discretization of the linear advection equation yields an energy stable semi-discretization. The so-called SAT term imposes the boundary condition weakly. Moreover, the underlying function space ${\mathcal {F}}$ should contain constants in order to ensure conservations.

In context of RBF methods, constants have to be included in the RBF interpolants (10), also for the reasons discussed above.

We will extend the previous investigation to the linear advection-diffusion equation.

$$\begin{aligned} \begin{aligned} \partial _t u + a \partial _x u&= \partial _x (\kappa \partial _x u), \quad x \in (x_L,x_R), \ t>0,\\ u(x,0)&= f(x),\\ au(x_L,t)-\kappa \partial _x u(x_L,t)&=g_{x_L}(t),\\ \kappa \partial _x u(x_R,t)&=g_{x_R}(t), \end{aligned} \end{aligned}$$

(20)

where $a>0$ is a constant and $\kappa >0$ can depend on x and t. The problem (20) is strongly well-posed, as can be seen by the energy rate

$$\begin{aligned} \begin{aligned} \left| \left| u\right| \right| _t^2+ 2 \left| \left| u_x\right| \right| ^2_{\kappa }=&a^{-1} \bigg ( g_{x_L}^2-\left( au(x_L,t)-g_{x_L}\right) ^2 - \left( au(x_R,t)-g_{x_R}^2 \right) ^2+g_{x_R}^2 \bigg ) \end{aligned} \end{aligned}$$

(21)

with $\left| \left| u_x\right| \right| ^2_{\kappa }= \int _{x_L}^{x_R} (\partial _x u)^2 \kappa \textrm{d} x.$ To translate this estimate to the discrete setting, we discretize (20). The most straightforward FSBP-SAT discretization reads

$$\begin{aligned} {\textbf{u}}_t +a D {\textbf{u}} = D( {\mathcal {K}} D {\textbf{u}} )+ P^{-1} {\mathbb {S}} \end{aligned}$$

(22)

with ${\mathcal {K}}= {{\,\textrm{diag}\,}}(\mathbf {\kappa })$ and

$$\begin{aligned} \begin{aligned} {\mathbb {S}}&:= [{\mathbb {S}}_0,0,\dots ,{\mathbb {S}}_1]^T, \\ {\mathbb {S}}_0&:= { \sigma _0 (a u_0}- ( {\mathcal {K}} D {\textbf{u}})_0-g_{x_L}),\\ {\mathbb {S}}_1&:= { \sigma _1 } ( ( {\mathcal {K}}D {\textbf{u}})_N-g_{x_R}). \end{aligned} \end{aligned}$$

(23)

We can prove the following result using Definition 3 where we additionally assume that ${\mathcal {K}}D{\textbf{u}} \subset {\mathcal {F}}$. Note that ${\mathcal {K}}D{\textbf{u}} \subset {\mathcal {F}}$ is always satisfied when ${\mathcal {F}}$ is invariant under differentiation (${\mathcal {F}} ' \subset {\mathcal {F}} )$ and $\kappa$ does not depend on x.

Theorem 1

The scheme (22) is strongly stable with $\sigma _0=-1$ and ${\sigma _1=-1}$.

Proof

We use the energy method together with the FSBP property. Multiplying (22) with ${\textbf{u}}^T P$ from the left, we get

$$\begin{aligned} {\textbf{u}}^T P{\textbf{u}}_t +a {\textbf{u}}^T P D {\textbf{u}} = {\textbf{u}}^T P D( {\mathcal {K}} D {\textbf{u}} )+ {\textbf{u}}^T {\mathbb {S}}. \end{aligned}$$

(24)

The FSBP property $P D + D^T P = B$ implies ${\textbf{u}}^T P D {\textbf{u}} = {\textbf{u}}^T B {\textbf{u}} - {\textbf{u}}^T D^T P {\textbf{u}}$. Substituting this into (24) yields

$$\begin{aligned} {\textbf{u}}^T P{\textbf{u}}_t + a {\textbf{u}}^T B {\textbf{u}} - a {\textbf{u}}^T D^T P {\textbf{u}} = {\textbf{u}}^T P D( {\mathcal {K}} D {\textbf{u}} )+ {\textbf{u}}^T {\mathbb {S}}. \end{aligned}$$

(25)

Observe that ${\textbf{u}}^T D^T P {\textbf{u}} = \left( {\textbf{u}}^T D^T P {\textbf{u}} \right) ^T = {\textbf{u}}^T P D {\textbf{u}}$ since this is a scalar term. Hence, adding (24) and (25), we get

$$\begin{aligned} 2 {\textbf{u}}^T P{\textbf{u}}_t + a {\textbf{u}}^T B {\textbf{u}} = 2 {\textbf{u}}^T P D( {\mathcal {K}} D {\textbf{u}} ) + 2 {\textbf{u}}^T {\mathbb {S}}. \end{aligned}$$

(26)

Furthermore, the FSBP property also implies ${\textbf{u}}^T P D( {\mathcal {K}} D {\textbf{u}} ) = {\textbf{u}}^T B {\mathcal {K}} D {\textbf{u}} - ( D {\textbf{u}} )^T P {\mathcal {K}} ( D {\textbf{u}} )$. This transforms (26) into

$$\begin{aligned} 2 {\textbf{u}}^T P{\textbf{u}}_t + 2 ( D {\textbf{u}} )^T P {\mathcal {K}} ( D {\textbf{u}} ) = - a {\textbf{u}}^T B {\textbf{u}} + 2 {\textbf{u}}^T B {\mathcal {K}} D {\textbf{u}} + 2 {\textbf{u}}^T {\mathbb {S}}. \end{aligned}$$

(27)

Using $\Vert {\textbf{u}} \Vert ^2_t = 2 {\textbf{u}}^T P{\textbf{u}}_t$ and $\left| \left| D{\textbf{u}}\right| \right| ^2_{ {\mathcal {K}}} = (D{\textbf{u}})^T P {\mathcal {K}}D{\textbf{u}}$, we get

$$\begin{aligned} \Vert {\textbf{u}} \Vert ^2_t + 2 \left| \left| D{\textbf{u}}\right| \right| ^2_{ {\mathcal {K}}} = - a {\textbf{u}}^T B {\textbf{u}} + 2 {\textbf{u}}^T B {\mathcal {K}} D {\textbf{u}} + 2 {\textbf{u}}^T {\mathbb {S}}. \end{aligned}$$

(28)

Finally, substituting (23) for the SAT term yields

$$\begin{aligned} \begin{aligned} \Vert {\textbf{u}} \Vert ^2_t + 2 \left| \left| D{\textbf{u}}\right| \right| ^2_{ {\mathcal {K}}} =&au_0^2-au_N^2 -2 u_0 ( {\mathcal {K}} Du)_0+2u_N( {\mathcal {K}} Du)_N -2au_0^2\\&+2 u_0 ( {\mathcal {K}} Du)_0 +2u_0g_{x_L} -2u_N ( {\mathcal {K}} Du)_N +2u_Ng_{x_R} \end{aligned} \end{aligned}$$

(29)

resulting in

$$\begin{aligned} \begin{aligned} \Vert {\textbf{u}} \Vert ^2_t + 2 \left| \left| D{\textbf{u}}\right| \right| ^2_{ {\mathcal {K}}} =- au_0^2-au_N^2 +2u_0g_{x_L} +2u_Ng_{x_R}. \end{aligned} \end{aligned}$$

(30)

By elementary transformation, we obtain

$$\begin{aligned} \begin{aligned} \left| \left| {\textbf{u}}\right| \right| _t^2 +2 \left| \left| D{\textbf{u}}\right| \right| ^2_{ {\mathcal {K}}} = a^{-1} \left( g_{x_L}^2-(au_0-g_{x_L})^2 -(au_N-g_{x_R})^2+g_{x_R}^2 \right) , \end{aligned} \end{aligned}$$

(31)

which is a discrete analog of the continuous estimate (21). Note that P and ${\mathcal {K}}$ have to be diagonal to ensure that we obtain our energy estimate. $\square$

Clearly, the FSBP operators automatically reproduce the results from the continuous setting, similar to the classical SBP operators based on polynomial approximations [49]. Note that no details are assumed on the specific function space, grid or the underlying methods. The only factors of importance is that the FSBP property is fulfilled and that well posed boundary condition are used.

Remark 1

(Second-derivative FSBP operators) In our analysis, we utilize the first-order derivative matrix twice to obtain a representation for the second derivative. Additionally, we assume $KD{\textbf{u}} \in {\mathcal {F}}$. This ensures that the first term on the right-hand side of (22) provides a discrete representation of the second-derivative operator within the function space. Notably, this assumption is not a requisite for stability, only for accuracy. For an in-depth examination of second derivative FSBP operators, we refer to our recent publication [23].

4 SBP operators for RBFs

First, we adapt the FSBP theory in Section 2.2 to the RBF framework. Next, we investigate classical RBF methods concerning the FSBP property, and demonstrate that standard global RBF schemes does not fulfill this property. Finally, we describe how RBFSBP operators can be constructed that lead to stability.

4.1 RBF-based SBP operators

The function space ${\mathcal {F}} \subset C^1$ for RBF methods is defined by the description in Subsection 2.2. Consider a set of K points, $X_K =\{x_1, \cdots , x_K \} \subset [x_L, x_R]$. The set of all RBF interpolants (10) forms a K-dimensional approximation space, which we denote by ${\mathcal {R}}_{m}(X_K)$. Let $\{c_k\}_{k=1}^K$ be a basis in ${\mathcal {R}}_{m}(X_K)$. Further, we have the grid points $Y_N =\{y_1, \cdots , y_N \} \subset [x_L, x_R]$ which include the boundaries. They are used to define the RBFSBP operators.

Definition 4

RBF (Summation-by-Parts Operators) An operator $D = P^{-1} Q \in {\mathbb {R}}^{N \times N}$ is an RBFSBP operator on the grid points $Y_N$ if

• (i) $D c_k({\textbf{x}}) = c_k'({\textbf{x}})$ for $k=1,2,\dots ,K$ and $c_k \in {\mathcal {R}}_{m}(X_K)$,

• (ii) $P \in {\mathbb {R}}^{N\times N}$ is a symmetric positive definite matrix, and

• (iii) $Q + Q^T = B$.

In the classical RBF discretizations, the exactness of the derivatives of the cardinal functions is the only condition which is imposed. However, to construct energy stable RBF methods, the existence of an adequate norm is as important as the condition on the derivative matrix. Hence it is often necessary to use a higher number of grid points than centers to ensure the existence of a positive quadrature formula to guarantee the conditions in Definition 4.

The norm matrix P in Definition 4 has only been assumed to be symmetric positive definite. However, as mentioned above for the remainder of this work, we restrict ourselves to diagonal norm matrices $P={{\,\textrm{diag}\,}}(\omega _1, \cdots ,\omega _N)$ where $\omega _i$ is the associated quadrature weight because Diagonal-norm operators are

• i) required for certain splitting techniques [17, 37, 40], and variable coefficients, see for example (31).

• ii) better suited to conserve nonquadratic quantities for nonlinear stability [32],

• iii) easier to extend to, for instance, curvilinear coordinates [5, 43, 48].

Remark 2

In Definition 4, we have two sets of points, the interpolation points $X_K$ and the grid points $Y_N$. The derivative matrix is constructed with respect to the exactness of the cardinal functions $c_k$ related to the interpolation points $X_K$. However, all operators are constructed with respect to the grid points $Y_N$, i.e. $D,P,Q \in {\mathbb {R}}^{N\times N}$. This is in particular essential when ensuring the existence of suitable norm matrix P. This means that the size of the SBP operator is determined by the quadrature formula. So, the number of grid points and their positioning highly effects the size of the operators and so the efficiency of the underlying method itself. In the future, this will be investigated in more detail.

4.2 Existing Collocation RBF Methods and the FSBP Property

In this part, we shortly investigate if classical collocation RBF methods fulfill the FSBP property for their underlying function space. In the classical collocation RBF approach, the centers intersect with the grid points, i.e. $X_K=Y_N$. It was shown in [25] that a diagonal-norm ${\mathcal {F}}$-exact SBP operator exists on the grid $Y_N = \{y_1, \cdots , y_N\}$ if and only if a positive and $({\mathcal {F}}{\mathcal {F}})'$-exact quadrature formula exists on the same grid (the same requirement as for classical SBP operators). The differentiation matrix $D \in {\mathbb {R}}^{N \times N}$ of a collocation RBF method can thus only satisfy the FSBP property if there exists a positive and $({\mathcal {R}}_{m}(Y_N) {\mathcal {R}}_{m}(Y_N))'$-exact quadrature formula on the grid $Y_N$. The weights ${\textbf{w}} \in {\mathbb {R}}^N$ of such a quadrature formula would have to satisfy

$$\begin{aligned} G {\textbf{w}} = {\textbf{m}}, \quad {\textbf{w}} > 0, \end{aligned}$$

(32)

with the coefficient matrix G and vector of moments ${\textbf{m}}$ given by

$$\begin{aligned} G = \begin{bmatrix} g_1(y_1) &{} \dots &{} g_1(y_N) \\ \vdots &{} &{} \vdots \\ g_L(y_1) &{} \dots &{} g_L(y_N) \end{bmatrix}, \quad {\textbf{m}} = \begin{bmatrix} \int _a^b g_1(y) \, \textrm{d}y\\ \vdots \\ \int _a^b g_L(y) \, \textrm{d}y \end{bmatrix}, \end{aligned}$$

(33)

In (33), $\{g_l\}_{l=1}^L$ is a basis of the function space $({\mathcal {R}}_{m}(Y_N) {\mathcal {R}}_{m}(Y_N))'$. In many cases, the dimension L of $({\mathcal {R}}_{m}(Y_N) {\mathcal {R}}_{m}(Y_N))'$ is larger than the dimension N of ${\mathcal {R}}_{m}(Y_N)$. In this case, $L > N$ and the linear system in (32) is overdetermined and has no solution. This is demonstrated in Table 2, which reports on the residual and smallest element of the least squares solution (solution with minimal $\ell ^2$-error) of (32) for different cases. In all of our considered tests, the residuals were always larger than zero indicating that the the classical RBF operators investigated are not in SBP form. Similar results are obtained for non-diagonal norm matrices P, which is outlined in Appendix.

Table 2 Residual $\Vert G{\textbf{w}}-{\textbf{m}} \Vert _2$ and smallest elements $\min {\textbf{w}}$ for the cubic PHS-RBF on equidistant, Halton, and random points, N is the number of points and $m-1$ is the polynomial degree

Remark 3

(Least Squares RBF Methods) It was observed in [51, 53] that using least squares RBF methods instead of collocation RBF methods leads to improved stability. The above discussion sheds some new light on this observation: The differentiation matrix D of the method can satisfy the FSBP property if and only if there exists a positive and $({\mathcal {R}}_{m}(X_K) {\mathcal {R}}_{m}(X_K))'$-exact quadrature formula on the grid $Y_N$. If N is sufficiently large, the linear system (32) becomes underdetermined ($N>L$) and will eventually admit a positive solution ${\textbf{w}}$, see [20]. For a least-squares RBF method, the centers $X_K$ and grid points $Y_N$ differ, with $N > K$. Indeed, one possible positive and exact solution is given by least squares quadratures, which we will subsequently use to construct RBF methods satisfying the SBP property. The (quasi-)Monte Carlo formula, used as part of the stability analysis in [53], gives a positive but inexact quadrature formula and therefore does not yield an exact SBP property.

4.3 Existence and Construction of RBFSBP Operators

Translating the main result from [25], we need quadrature formulas to ensure the exact integration of $({\mathcal {R}}_{m}(X_K) {\mathcal {R}}_{m}(X_K))'$. For RBF spaces, we use least-squares formulas, which can be used on almost arbitrary sets of grid points $Y_N$ and to any degree of exactness. The least squares ansatz always leads to a positive and $({\mathcal {R}}_{m}(X_K) {\mathcal {R}}_{m}(X_K))'$-exact quadrature formula as long a sufficiently large number of data points $Y_N$ is used.

Remark 4

Existing results on positivity and exactness of least squares quadrature formulas usually assume that the function space contains constants [19, 20]. Translating this to our setting, we need this property to be fulfilled for $({\mathcal {R}}_{m}(X_K) {\mathcal {R}}_{m}(X_K))'$. Therefore, ${\mathcal {R}}_{m}(X_K)$ should contain constants and linear functions. However, this assumption is primarily made for technical reasons and can be relaxed. Indeed, even when ${\mathcal {R}}_{m}(X_K)$ only contained constants, we were still able to construct positive and $({\mathcal {R}}_{m}(X_K) {\mathcal {R}}_{m}(X_K))'$-exact least squares quadrature formulas in all our examples. Future work will provide a theoretical justification for this.

Due to the least-square ansatz, we may always assume that we have a positive and $({\mathcal {R}}_{m}(X_K) {\mathcal {R}}_{m}(X_K))'$-exact quadrature formula. With that ensured, we summarize the algorithm to construct a diagonal norm RBFSBP operators in the following steps:

• 1. Build P by setting the quadrature weights on the diagonal.

• 2. Split Q into its known symmetric $\frac{1}{2}B$ and unknown anti-symmetric part $Q_A$.

• 3. Calculate $Q_A$ by using

  $$\begin{aligned} Q_AC =P C_x -\frac{1}{2} BC \text { with }C = [c_1({\textbf{y}}), \dots , c_K({\textbf{y}})] = \begin{bmatrix} c_1(y_1) &{} \dots &{}c_K(y_1) \\ \vdots &{} &{} \vdots \\ c_1(y_N) &{} \dots &{} c_K(y_N) \end{bmatrix} \end{aligned}$$

  and $C_x = [c_1'({\textbf{y}}), \dots , c_K'({\textbf{y}})]$ is defined analogous to C where $\{c_1,...,c_K\}$ is a basis of the K-dimensional function space.

• 4. Use $Q_A$ in $Q= Q_A+\frac{1}{2} B$ to calculate Q.

• 5. $D=P^{-1}Q$ gives the RBFSBP operator.

In the RBF context, one can always use cardinal functions as the basis. However, for simplicity reason is can be wise to use another basis representation, derived from the cardinal functions.

5 Examples of RBFSBP operators

Next, we construct RBFSBP operators for a few frequently used kernels². We consider a set of K points, ${X_K = \{x_1,\dots ,x_K\} \subset [x_L,x_R]}$, and assume that these include the boundaries $x_L$ and $x_R$. Henceforth, we will consider the kernels listed in Table 1 and augment them with constants. The set of all RBF interpolants including constants (10) forms a K-dimensional approximation space, which we denote by ${\mathcal {R}}_{1}(X_K)$. Recall that $m=1$ imply constants, but no higher-order polynomials, are included in the RBF approximation space. This space is spanned by the cardinal functions $c_k \in {\mathcal {R}}_{1}(X_K)$ which are uniquely determined by (16). The matching constraint is then simply $\sum _{k=1}^K \alpha _k = 0.$ That is,

$$\begin{aligned} {\mathcal {R}}_{1}(X_K) = \textrm{span}\{ \, c_k \mid k=1,\dots ,K \, \} \end{aligned}$$

(34)

with the approximation space ${\mathcal {R}}_{1}(X_K)$ having dimension K.

The product space ${\mathcal {R}}_{1}(X_K){\mathcal {R}}_{1}(X_K)$ and its derivative space $({\mathcal {R}}_{1}(X_K){\mathcal {R}}_{m}(X_K))'$ are respectively given by

$$\begin{aligned} {\mathcal {R}}_{1}(X_K){\mathcal {R}}_{1}(X_K)&= \textrm{span}\{ \, c_k c_l \mid k,l=1,\dots ,K \, \}, \end{aligned}$$

(35)

$$\begin{aligned} ({\mathcal {R}}_{1}(X_K){\mathcal {R}}_{1}(X_K))'&= \textrm{span}\{ \, c_k' c_l + c_k c_l' \mid k,l=1,\dots ,K \, \}. \end{aligned}$$

(36)

Note that the right-hand sides of (35) and (36) both use $K^2$ elements to span the product space ${\mathcal {R}}_{1}(X_K){\mathcal {R}}_{1}(X_K)$ and its derivative space $({\mathcal {R}}_{1}(X_K){\mathcal {R}}_{1}(X_K))'$. However, these elements are not linearly independent and the dimensions of ${\mathcal {R}}_{1}(X_K){\mathcal {R}}_{1}(X_K)$ and $({\mathcal {R}}_{1}(X_K){\mathcal {R}}_{1}(X_K))'$ are smaller than $K^2$. Indeed, we can observe that $c_k c_l = c_l c_k$ and the dimension of (35) is therefore bounded from above by

$$\begin{aligned} \textrm{dim} \,{\mathcal {R}}_{1}(X_K){\mathcal {R}}_{1}(X_K) \le \frac{K(K+1)}{2}. \end{aligned}$$

(37)

Subsequently, for ease of presentation, we round all reported numbers to the second decimal place.

5.1 RBFSBP Operators using Polyharmonic Splines

In the first test, we work with cubic polyharmonic splines, $\varphi (r) = r^3$. On $[x_L,x_R] = [0,1]$ and for the centers $X_3 = \{0,1/2,1\}$, the three-dimensional cubic RBF approximation space (34) is given by ${\mathcal {R}}_{1}(X_3) = \textrm{span}\{ \, c_1, c_2, c_3 \, \} = \textrm{span}\{ \, b_1, b_2, b_3 \, \}$ with cardinal functions

$$\begin{aligned} \begin{aligned} c_1(x)&= \frac{1}{2} |x|^3 - 2 | x - 1/2 |^3 + \frac{3}{2} |x-1|^3 - \frac{1}{4}, \\ c_2(x)&= -2 |x|^3 + 4 | x - 1/2 |^3 - 2 |x-1|^3 + \frac{3}{2}, \\ c_3(x)&= \frac{3}{2} |x|^3 - 2 | x - 1/2 |^3 + \frac{1}{2} |x-1|^3 - \frac{1}{4} \end{aligned} \end{aligned}$$

(38)

and alternative basis functions³

$$\begin{aligned} b_1(x) = 1, \quad b_2(x) = x^3 - |x-1/2|^3, \quad b_3(x) = x^3 + (x-1)^3. \end{aligned}$$

We make the transformation to the basis representation $\textrm{span}\{b_1,b_2, b_3\}$ to simplify the determination of $({\mathcal {R}}_{1}(X_3){\mathcal {R}}_{1}(X_3))'$. In this alternative basis representation, the product space ${\mathcal {R}}_{1}(X_3){\mathcal {R}}_{1}(X_3)$ and its derivative space $({\mathcal {R}}_{1}(X_3){\mathcal {R}}_{1}(X_3))'$ are respectively given by

$$\begin{aligned} \begin{aligned} {\mathcal {R}}_{1}(X_3){\mathcal {R}}_{1}(X_3)&= \textrm{span}\{ \, 1, b_2, b_3, b_2^2, b_3^2, b_2 b_3 \, \} \\ ({\mathcal {R}}_{1}(X_3){\mathcal {R}}_{1}(X_3))'&= \textrm{span}\{ \, b_2', b_3', b_2' b_2, b_3' b_3, b_2' b_3 + b_2 b_3' \, \}. \end{aligned} \end{aligned}$$

(39)

Next, we have to find an $({\mathcal {R}}_{1}(X_3){\mathcal {R}}_{1}(X_3))'$-exact quadrature formula with positive weights. For the chosen $N=4$ equidistant grid points, the least-squares quadrature formula has positive weights and is $({\mathcal {R}}_{1}(X_3){\mathcal {R}}_{1}(X_3))'$-exact. The points and weights are ${\textbf{x}} = \left[ 0, \frac{1}{3}, \frac{2}{3}, 1 \right] ^T$ and $P = {{\,\textrm{diag}\,}}\left( \frac{16}{129}, \frac{81}{215}, \frac{81}{215}, \frac{16}{129}\right)$. The corresponding matrices Q and D of the RBFSBP operator $D = P^{-1} Q$ obtained from the construction procedure described before are

$$\begin{aligned} Q \approx \left( \begin{array}{cccc} -\frac{1}{2} &{} \frac{59}{100} &{} -\frac{3}{20} &{} \frac{3}{50}\\ -\frac{59}{100} &{} 0 &{} \frac{37}{50} &{} -\frac{3}{20}\\ \frac{3}{20} &{} -\frac{37}{50} &{} 0 &{} \frac{59}{100}\\ -\frac{3}{50} &{} \frac{3}{20} &{} -\frac{59}{100} &{} \frac{1}{2} \end{array}\right) , \quad D \approx \left( \begin{array}{cccc} -\frac{403}{100} &{} \frac{473}{100} &{} -\frac{121}{100} &{} \frac{51}{100}\\ -\frac{39}{25} &{} 0 &{} \frac{49}{25} &{} -\frac{2}{5}\\ \frac{2}{5} &{} -\frac{49}{25} &{} 0 &{} \frac{39}{25}\\ -\frac{51}{100} &{} \frac{121}{100} &{} -\frac{473}{100} &{} \frac{403}{100} \end{array}\right) . \end{aligned}$$

(40)

This example was presented with less details in [25].

5.2 RBFSBP Operators using Gaussian Kernels

Next, we consider the Gaussian kernel $\varphi (r) = \exp (-r^2)$ on $[x_L,x_R] = [0,1]$ for the centers $X_3 = \{0,1/2,1\}$. The three-dimensional Gaussian RBF approximation space (34) is given by ${\mathcal {R}}_{1}(X_3) = \textrm{span}\{ \, c_1, c_2, c_3 \, \}$ with cardinal functions

$$\begin{aligned} \begin{aligned} c_1(x)&= 2.7698 \exp (-x^2) -3.9576 \exp (-(x-0.5)^2) + 1.1878 \exp (-(x-1)^2) +0.8754\\ c_2(x)&= -3.9576 \exp (-x^2) +7.9153 \exp (-(x-0.5)^2) -3.9576\exp (-(x-1)^2) -0.7509 \\ c_3(x)&=1.1878 \exp (-x^2) -3.9576\exp (-(x-0.5)^2) + 2.7698 \exp (-(x-1)^2)+0.87543 \end{aligned}\nonumber \\ \end{aligned}$$

(41)

Again for $N=4$ equidistant grid points in the least square quadrature formula, we obtain exactness and positive weights. They are ${\textbf{x}} = \left[ 0, \frac{1}{3}, \frac{2}{3}, 1 \right] ^T$ and $P = {{\,\textrm{diag}\,}}\left( 0.15, 0.36, 0.36,0.15 \right)$. The corresponding matrices Q and D of the RBFSBP operator $D = P^{-1} Q$ obtained from the construction procedure described before are

$$\begin{aligned} Q \approx \left( \begin{array}{cccc} -\frac{1}{2} &{} \frac{3}{5} &{} -\frac{3}{100} &{} -\frac{7}{100}\\ -\frac{3}{5} &{} 0 &{} \frac{16}{25} &{} -\frac{3}{100}\\ \frac{3}{100} &{} -\frac{16}{25} &{} 0 &{} \frac{3}{5}\\ \frac{7}{100} &{} \frac{3}{100} &{} -\frac{3}{5} &{} \frac{1}{2} \end{array}\right) , \quad D \approx \left( \begin{array}{cccc} -\frac{33}{10} &{} \frac{397}{100} &{} -\frac{23}{100} &{} -\frac{9}{20}\\ -\frac{42}{25} &{} 0 &{} \frac{89}{50} &{} -\frac{1}{10}\\ \frac{1}{10} &{} -\frac{89}{50} &{} 0 &{} \frac{42}{25}\\ \frac{9}{20} &{} \frac{23}{100} &{} -\frac{397}{100} &{} \frac{33}{10} \end{array}\right) . \end{aligned}$$

(42)

To include an example with non-equidistant points for the centers, we also build matrices and FSBP operators with Halton points $X_3$ for this case. A bit surprising, we need twice as many points than on an equidistant grid to get a positive exact quadrature formula. We obtain an exact quadrature using the nodes and weights ${\textbf{x}} = \left[ i/7, \right] ^T,$ with $i=0,\cdots ,7,$ and $P = {{\,\textrm{diag}\,}}\left( 0.04, 0.12, 0.19, 0.13, 0. 04, 0.10, 0.30, 0.08 \right)$. The corresponding matrices Q and D are ${\mathbb {R}}^{8 \times 8}$ and are given by

$$\begin{aligned} Q \approx \left( \begin{array}{cccccccc} -\frac{1}{2} &{} \frac{33}{100} &{} \frac{29}{100} &{} \frac{7}{100} &{} -\frac{7}{100} &{} -\frac{2}{25} &{} -\frac{19}{100} &{} \frac{3}{20}\\ -\frac{33}{100} &{} 0 &{} \frac{11}{100} &{} \frac{1}{10} &{} \frac{7}{100} &{} \frac{2}{25} &{} \frac{3}{50} &{} -\frac{1}{10}\\ -\frac{29}{100} &{} -\frac{11}{100} &{} 0 &{} \frac{9}{100} &{} \frac{1}{10} &{} \frac{13}{100} &{} \frac{11}{50} &{} -\frac{13}{100}\\ -\frac{7}{100} &{} -\frac{1}{10} &{} -\frac{9}{100} &{} 0 &{} \frac{3}{100} &{} \frac{3}{50} &{} \frac{23}{100} &{} -\frac{3}{50}\\ \frac{7}{100} &{} -\frac{7}{100} &{} -\frac{1}{10} &{} -\frac{3}{100} &{} 0 &{} \frac{1}{100} &{} \frac{4}{25} &{} -\frac{1}{20}\\ \frac{2}{25} &{} -\frac{2}{25} &{} -\frac{13}{100} &{} -\frac{3}{50} &{} -\frac{1}{100} &{} 0 &{} \frac{1}{10} &{} \frac{1}{10}\\ \frac{19}{100} &{} -\frac{3}{50} &{} -\frac{11}{50} &{} -\frac{23}{100} &{} -\frac{4}{25} &{} -\frac{1}{10} &{} 0 &{} \frac{59}{100}\\ -\frac{3}{20} &{} \frac{1}{10} &{} \frac{13}{100} &{} \frac{3}{50} &{} \frac{1}{20} &{} -\frac{1}{10} &{} -\frac{59}{100} &{} \frac{1}{2} \end{array}\right) , \\ D \approx \left( \begin{array}{cccccccc} -\frac{304}{25} &{} \frac{811}{100} &{} \frac{177}{25} &{} \frac{41}{25} &{} -\frac{7}{4} &{} -\frac{197}{100} &{} -\frac{451}{100} &{} \frac{71}{20}\\ -\frac{137}{50} &{} 0 &{} \frac{91}{100} &{} \frac{17}{20} &{} \frac{29}{50} &{} \frac{33}{50} &{} \frac{53}{100} &{} -\frac{79}{100}\\ -\frac{157}{100} &{} -\frac{59}{100} &{} 0 &{} \frac{23}{50} &{} \frac{14}{25} &{} \frac{69}{100} &{} \frac{29}{25} &{} -\frac{71}{100}\\ -\frac{27}{50} &{} -\frac{83}{100} &{} -\frac{69}{100} &{} 0 &{} \frac{21}{100} &{} \frac{12}{25} &{} \frac{46}{25} &{} -\frac{47}{100}\\ \frac{167}{100} &{} -\frac{33}{20} &{} -\frac{239}{100} &{} -\frac{31}{50} &{} 0 &{} \frac{29}{100} &{} \frac{191}{50} &{} -\frac{113}{100}\\ \frac{81}{100} &{} -\frac{81}{100} &{} -\frac{32}{25} &{} -\frac{3}{5} &{} -\frac{3}{25} &{} 0 &{} \frac{99}{100} &{} \frac{101}{100}\\ \frac{31}{50} &{} -\frac{11}{50} &{} -\frac{73}{100} &{} -\frac{77}{100} &{} -\frac{11}{20} &{} -\frac{33}{100} &{} 0 &{} \frac{99}{50}\\ -\frac{87}{50} &{} \frac{23}{20} &{} \frac{157}{100} &{} \frac{7}{10} &{} \frac{29}{50} &{} -\frac{6}{5} &{} -\frac{351}{50} &{} \frac{597}{100} \end{array}\right) \end{aligned}$$

5.3 RBFSBP Operators using Multiquadric Kernels

As the last example, we consider the RBFSBP operators using multiquadric kernels $\varphi (r) = \sqrt{1+r^2}$ on $[x_L,x_R] = [0,0.5]$ and centers $X_3 = \{0,1/4,1/2\}$. The $({\mathcal {R}}_{1}(X_3){\mathcal {R}}_{1}(X_3))'$-exact least square ansatz yields the points ${\textbf{x}} = \left[ 0, \frac{1}{6}, \frac{1}{3}, \frac{1}{2}\right] ^T$ and norm matrix $P = {{\,\textrm{diag}\,}}\left( 0.07, 0.18, 0.18,0.07 \right) .$ With this norm matrix, we obtain finally

$$\begin{aligned} Q \approx \left( \begin{array}{cccc} -\frac{1}{2} &{} \frac{57}{100} &{} -\frac{1}{50} &{} -\frac{1}{20}\\ -\frac{57}{100} &{} 0 &{} \frac{59}{100} &{} -\frac{1}{50}\\ \frac{1}{50} &{} -\frac{59}{100} &{} 0 &{} \frac{57}{100}\\ \frac{1}{20} &{} \frac{1}{50} &{} -\frac{57}{100} &{} \frac{1}{2} \end{array}\right) \quad D \approx \left( \begin{array}{cccc} -\frac{767}{100} &{} \frac{219}{25} &{} -\frac{29}{100} &{} -\frac{79}{100}\\ -\frac{309}{100} &{} 0 &{} \frac{319}{100} &{} -\frac{1}{10}\\ \frac{1}{10} &{} -\frac{319}{100} &{} 0 &{} \frac{309}{100}\\ \frac{79}{100} &{} \frac{29}{100} &{} -\frac{219}{25} &{} \frac{767}{100} \end{array}\right) \end{aligned}$$

(43)

6 Numerical Results

For all numerical tests presented in this work, we used an explicit SSP-RK methods. The step size $\Delta t$ was chosen to be sufficiently small not to influence the accuracy. To guarantee stability, we applied weakly enforced boundary conditions using Simultanuous Approximation Terms (SATs), as is usually done in the SBP community [1, 2, 39], and for RBFs in [24]. To avoid ill-conditioned matrix calculations inside the construction and application, we use a multi-block structure in some of our tests. In each block, a global RBF method is used and the blocks are coupled using SAT terms as in [4, 26]. While this is beyond the scope of this work, future work will address other techniques to overcome ill-conditioned matrices, including tailored point distributions, kernels, shape parameters, alternative bases, and efficient implementations. Additionally, most of the results can be calculated as well with classical SBP-FD operators and we get analogues results. We stress that this section provide a proof of concept and we focus on global RBF methods and their stability properties, not on efficiency and real application tests.

Fig. 2

Cubic kernels with approximation spaces $K=15/30$ on equidistant points after 1 period

Most numerical simulations are performed using polyharmonic splines to avoid a discussion about the shape parameter, which highly effects the accuracy and stability properties of the RBF approach [14, 30]. In future work, we will investigate the connection between the selection of the shape parameter and the construction of RBFSBP operators.

6.1 Advection with Periodic Boundary Conditions

In the first test, we consider the linear advection

$$\begin{aligned} \partial _t u + a \partial _x u = 0, \quad x \in (x_L,x_R), \ t>0, \end{aligned}$$

(44)

with $a=1$ and periodic BCs. The initial condition is $u(x,0) =\textrm{e}^{-20x^2}$ from the introducing example (1) and the domain is $[-1,1]$. We are in the same setting as shown in Figure 1. We compare a classical collocation RBF method with our new RBFSBP methods, focus on cubic splines and consider the final time to be $T=2$. In Figure 2a and Figure 2c, the solutions are plotted using collocation RBF method and the RBFSBP approach. In Figure 2a, we select $K=15$ for both approximations and $N=29$ evaluation points for the RBFSBP operator. The collocation RBF method dampens the Gaussian bump significantly while the RBFSBP method do better. The decrease can also be seen in the energy profile 2b where the collocation approach loses more. To obtain a comparable result between the collocation and RBFSBP methods, we double the number of interpolation points K in our second simulation for the collocation RBF method, cf. Figure 2c and Figure 2d. The RBFSBP method still performs better and demonstrates the advantage of the RBFSBP approach.

Next, we focus only on RBFSBP methods and demonstrate the high accuracy of the approach by increasing the degrees of freedom. In Figure 3, we plot the result and the energy using Gaussian ($\epsilon =1$) and cubic kernels. We use $K=5$ and $I=20$ blocks. We obtain an highly accurate solution and the energy remains constant.

Fig. 3

Gaussian and Cubic kernels with approximation space $K=5$ and $I=20$ blocks on equidistant points after 10 periods

6.2 Advection with Inflow Boundary Conditions

In the following test from [24], we consider the advection equation (44) with $a=1$ in the domain [0, 1]. The BC and IC are

$$\begin{aligned} g(t)=u_{\textrm{init}}(0.5-t), \quad u_{\textrm{init}}(x) = {\left\{ \begin{array}{ll} \textrm{e}^{8} \textrm{e}^{ \frac{-8}{1-(4x-1)^2} }&{} \text {if } 0< x < 0.5, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(45)

We have a smooth IC and an inflow BC at the left boundary $x=0$. We apply cubic splines with constants as basis functions and the discretization

$$\begin{aligned} {\textbf{u}}_t +a D {\textbf{u}} = P^{-1} {\mathbb {S}}. \end{aligned}$$

(46)

with the simultaneous approximate terms (SAT) ${\mathbb {S}} := [{\mathbb {S}}_0,0,\dots ,0]^T, \quad {\mathbb {S}}_0 := - (u_0-g).$ In Figures 4a - 4b, we show the solutions at time t = 0.5 with $K=5$ and $I=15, 20$ elements using equidistant point and randomly disturbed equidistant points. The numerical solutions using disturbed points in Figure 4a has wiggles but these are reduced by increasing the number of blocks, see Figure 4b. Note that the wiggles are more pronounced if the point selection is not distributed symmetrically around the midpoints, e.g. for the Halton points in Figures 4c - 4d. Next, we focus on the error behavior. As mentioned before, the RBF methods can reach spectral accuracy for smooth solutions. In Figure 5, the error behavior for $K=3-7$ basis functions using 20 blocks is plotted in a logarithmic scale. Spectral accuracy is indicated by the (almost) constant slope.

Remark 5

(Accuracy) For different point selections, we obtain similar convergence rates, e.g. same slopes, but the error can be different. This can be seen in the numerical results using Halton points which are not as accurate as the ones using equidistant points, cf. Figure 4.

Fig. 4

Cubic kernel with approximation space $K=5$ on equidistant, and Halton points

Fig. 5

Error plots using cubic kernels with approximation space $K=4-7$ on equidistant points with $I=20$ blocks. For $K=5$, the errors correspond to the solutions printed in the red dotted line on the right side of Figure 4

6.3 Advection-Diffusion

Next, the boundary layer problem from [59] is considered

$$\begin{aligned} \partial _t u + \partial _x u = \kappa \partial _{xx}^2 u, \quad 0 \le x \le 0.5, \ t>0. \end{aligned}$$

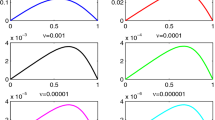
The initial condition is $u(x,0)=2x$ and the boundary conditions are $u(0,t)=0$ and $u(0.5,t)=1$. The exact steady state solution is $u(x)= \frac{\exp \left( \frac{x}{\kappa } \right) -1}{\exp \left( \frac{1}{2\kappa } \right) -1}.$ Cubic splines and Gaussian kernels with shape parameter 1 are used together with constants. We expect to obtain better results using Gaussian kernels due to structure of the steady state solution. In Figure 6, we show the solutions for different times using $K=5$ elements on equidistant grid points with diffusion parameters $\kappa =0.2$ and $\kappa =0.1$.

Fig. 6

Gaussian and Cubic kernels with approximation space $K=5$ and $I=1$ block on equidistant points at $T=2$.

Some overshoots can be seen in the more steep case for $\kappa =0.1$. This behavior can be circumvented by using more degrees of freedom and multi-blocks which are avoided in this case.

6.4 2D Linear Advection

We conclude our examples with a 2D case and consider the linear advection equation:

$$\begin{aligned} \partial _t u(x,y,t) + a \partial _x u(x,y,t) +b \partial _y u(x,y,t)=0 \end{aligned}$$

(47)

with constants $a,b \in {\mathbb {R}}$.

6.4.1 Periodic Boundary Conditions

In our first test, $a=b=1$ are used in (47). The initial condition is $u(x,y,0)= \textrm{e}^{-20\left( (x-0.5)^2+(y-0.5)^2 \right) }$ for $(x,y) \in [0,1]^2$ and periodic boundary conditions, i. e., $u(0,y,t)=u(1,y,t)$ and $u(x,0,t)=u(x,1,t)$, are considered. The coupling at the boundary was again done via SAT terms. We use cubic kernels ($K=13$) equipped with constants in each direction. Figure 7b illustrates the numerical solution at time $T=1$. The bump has once left the domain at the right upper corner and entered again in the left lower corner. It reaches its initial position at $T=1$. No visible differences between the numerical solution at $T=1$ and the initial condition can be seen. In Figure 7d the energy is reported over time. We notice a slight decrease of energy when the bump is leaving the domain (at $t=0.5$) due to weakly enforced slightly dissipative SBP-SAT coupling.

Fig. 7

Cubic kernels with approximation space $K=13$ on equidistant points

6.4.2 Dirichlet-Inflow Conditions

In the last simulation, we consider (47) with $a=0.5$, $b=1$, initial condition $u(x,y,0)= \textrm{e}^{-20\left( (x-0.25)^2+(y-0.25)^2 \right) }$ for $(x,y) \in [0,1]^2$ and zero inflow $u(0,y,t)=0$, and $u(x,0,t)=0$. We again use cubic kernels ($K=13$) equipped with constants. The boundary conditions are enforced weakly via SAT terms. The initial condition lies in the left corner, cf. Figure 7a. In Figure 8b, the numerical solution is shown. The bump moves in y direction with speed one and in x-direction with speed 0.5. Figure 8c shows a slight decrease of the energy over time due the bump leaving the domain.

Fig. 8

Cubic kernels with approximation space $K=13$ on equidistant points

6.5 Conditioning of the RBFSBP operators

A significant challenge associated with global RBF methods is that a direct approach leads to a large and dense differentiation matrix. Furthermore, the conditioning of the differentiation matrix, the corresponding norm matrix and the associated Vandermonde matrix, can become problematic, in particular they can become highly ill-conditioned resulting in stability issues of the scheme. To address these issues, extensive efforts have been made to analyze the conditioning of RBF methods and to improve the schemes. To give a concrete example: the selection of basis functions alongside their associated shape parameters and point distributions can substantially impact the efficiency of the methods. As noted in [44], a close relationship exists between the flatness of RBFs (using small shape parameter) and the resulting ill-conditioning of the matrix in equation (13). This directly affects the accuracy of the RBF interpolant, a concept referred to as the uncertainity or trade-off principle of direct RBF methods. For potential solutions, as well as applications and comprehensive discussions on this matter, we direct readers to references such as [16, 33, 36, 45, 46, 57].

In this paper we focus on other issues but provide a concrete example of the conditioning numbers in the differentiation matrices, the norm matrices and the Vandermonde matrices in the collocation approach. We consider cubic splines utilizing equidistant points, similar to the setup in Subsection 6.1. The numerical values for these condition numbers are presented in Table 3. Notably, an increase in the condition numbers can be recognized, particularly the norm matrix increases as the number of evaluation points N.

Table 3 Examples of condition numbers using cubic splines

Table 3 is provided to give a first impression of the condition numbers in classical RBF methods. We avoid further investigation using a collocation approach and instead point to the aforementioned literature concerning this situation, cf. [10, 15, 16, 33, 45, 46, 56] and the references therein. We focus on assessing the efficiency and conditioning of our RBFSBP operators. Note that the differentiation matrices within the (function-space) SBP framework are not regular, while the norm matrix remains exact within the finite function space. Therefore, focussing on the condition number of D and P does not provide us with any information about the performance of our algorithm since if these matrices exist, the schemes are energy stable as demonstrated in Section 3. The challenging aspect within our RBFSBP framework lies in constructing an appropriate norm matrix P corresponding to the derivative matrix D. As underscored in Remark 2, the matrices dimensions are determined by the availability of a suitable norm matrix. In our construction procedure, we apply a least square method to build P, as elaborated in Section 4.3. This involves iteratively solving the linear systems presented in equation (32), progressively increasing the number of evaluation points with each iteration. This iterative procedure continues until a suitable norm matrix P corresponding to the derivative matrix D is found ensuring the FSBP property.

Throughout all our computations up to this point, the evaluation points Y in our approach have been consistently selected using equidistant points. The matrix G is a Vandermonde like matrix. It is well-known that in classical polynomial interpolation formulating the Vandermonde matrix with respect to the wrong basis, e.g. monomials, this matrix gets highly ill-conditioned for increasing N. We see a similar behavior for most of our matrices $G \in {\mathbb {R}}^{L\times N}$, also for small K.

In the subsequent analysis, we provide an initial study of the overall performance of our algorithm focussing on these three properties: the condition number of $G^TG$, the number of points required for constructing the matrix P, and the norm of matrix D. We use cubic splines on equidistant points for the center points X.

Table 4 offers a first impression of the conditioning of our methods, revealing that in this simulation, the numerical values remain modest within the computations, e.g. all three values remain small. This finding intersects with the observations made in our previous numerical simulations, where no issues were encountered.

Table 4 Condition numbers of $G^TG$, N and K using cubic splines on equidistant points

In Table 5, we present comparable results while now employing Halton points as the center points X. Note that even with small values of K,  the condition number of $G^TG$ becomes high. A noteworthy observation is that increasing the dimension K doesn’t necessarily lead to an automatic increase in the required number of evaluation points N. Note that our evaluation procedure remains confined to equidistant points, signifying that we employ an equidistant point distribution for the evaluation points Y as opposed to using Halton points or any optimization procedure for the point distribution. While potential enhancements could stem from adopting diverse point selections for Y,  these considerations will be deferred to future investigations.

Table 5 Condition numbers of $G^TG$, N and K using cubic splines on Halton points

As mentioned before the shape parameter effects highly the conditioning numbers of the corresponding RBF methods. For flat RBF methods meaning small $\epsilon$, the matrices becoming ill-conditioned. Also in this case, we see a similar behavior for the RBFSBP operators. In Table 6, we give the numbers using $\epsilon =1$ in a Gaussian kernel. We recognize that the condition number of $G^TG$ is high and stress that even if we could derive G, our construction procedure of the RBFSBP methods from Subsection 4.3 would be problematic. The reason being that, we have to solve a linear system to obtain $Q_A$ where also the corresponding Vandermonde matrix is ill-conditioned. By increasing the shape parameter to 5, we get better result as reported in Table 7. In this example, we do not run into the ill-conditioning problem and we can increase the dimension of K.

Table 6 Condition numbers of $G^TG$, N and K using Gaussian RBF with $\epsilon =1$

Table 7 Condition numbers of $G^TG$, N and K using Gaussian RBF with $\epsilon =5$

7 Concluding Thoughts

RBF methods are a popular tool for numerical PDEs. However, despite their success for problems with sufficient inherent dissipation, stability issues are often observed for advection-dominated problems. In this work, we used the FSBP theory combined with a weak enforcement of BCs to develop provable energy-stable RBF methods. We found that one can construct RBFSBP operators by using oversampling to obtain suitable positive quadrature formulas. Existing RBF methods do not satisfy such an RBFSBP property, either because they are based on collocation or because an inappropriate quadrature is used. This is demonstrated for simple test cases and the one-dimensional setting. Our findings imply that the FSBP theory provides a building block for systematically developing stable RBF methods, filling a critical gap in the RBF theory.

In future work, it would be interesting to analyze the ill-condition property of the matrices with respect to the shape parameter using well-known techniques from the RBF community and to study the connection between the classical RBF and the RBFSBP framework. Additionally, it would be interesting to improve the quadrature procedure in the construction and optimize the point selection of the evaluation points Y to avoid the ill-conditioning of G. Also, instead of working with the basis representation of the cardinal functions, one may change the basis to avoid ill-conditioning of the Vandermonde matrices. However, these points are left for future work. Our investigation is a first consideration of the condition properties of the RBFSBP approach. Additionally, future work will address the extension to local RBF methods and multiple dimensions on complex domains.

Appendix

1.1 Necessity of Polynomials in RBFs

For completeness, we shortly explain why the RBF interpolant (10) exists uniquely when the kernel $\varphi$ is conditionally positive definite of order m and polynomials of degree up to $m-1$ are incorporated. To this end, recall that $\varphi$ is conditionally positive definite of order m when

$$\begin{aligned} \varvec{\alpha }^T \Phi \varvec{\alpha } > 0 \end{aligned}$$

(48)

for all $\varvec{\alpha } \in {\mathbb {R}}^K\setminus \{{\textbf{0}}\}$ that satisfy (12), where $\Phi$ is given by (14). Further, (12) is equivalent to $P^T \varvec{\alpha } = {\textbf{0}}$. Next note that the RBF interpolant (10) exists uniquely if and only if the linear system (13) has a unique solution for every ${\textbf{u}}$, which is equivalent to the corresponding homogeneous linear system

$$\begin{aligned} \Phi \varvec{\alpha } + P \varvec{\beta }&= {\textbf{0}}, \end{aligned}$$

(49)

$$\begin{aligned} P^T \varvec{\alpha }&= {\textbf{0}}, \end{aligned}$$

(50)

admitting only the trivial solution, $\varvec{\alpha } = {\textbf{0}}$ and $\varvec{\beta } = {\textbf{0}}$. To show that this is the case, we multiply both sides of (49) by $\varvec{\alpha }^T$ from the left, which yields

$$\begin{aligned} \varvec{\alpha }^T \Phi \varvec{\alpha } = {\textbf{0}}, \end{aligned}$$

(51)

since $\varvec{\alpha }^T P = {\textbf{0}}^T$ due to (50). Further, for conditionally positive definite $\varphi$, (51) implies $\varvec{\alpha } = {\textbf{0}}$. Substituting $\varvec{\alpha } = {\textbf{0}}$ into (49) yields $P \varvec{\beta } = {\textbf{0}}$, which means that the polynomial

$$\begin{aligned} p(x) = \sum _{l=1}^m \beta _l p_l(x) \end{aligned}$$

(52)

has zeros $x_1,\dots ,x_K$. Finally, for $m \le K$, this can only be the case if $\varvec{\beta } = {\textbf{0}}$.

1.2 RBFSBP property with Non-diagonal Norm Matrix

In Section 4.2, we demonstrated that there exist no diagonal P such that the RBFSBP properties are fulfilled in general. In the general definition (4), P must only be symmetric positiv definite and not necessarily diagonal. Therefore, some non-diagonal norm matrix might exists fulfilling the RBFSBP property. Here, we demonstrate that this is not the case. To investigate this, we set $X_K=Y_N$. The differentiation operators ${D \in {\mathbb {R}}^{N \times N}}$ of classic global RBF methods are usually constructed to be exact for the elements of the finite dimensional function space ${\mathcal {R}}_{m}(Y_N)$. Unfortunately, neither the norm matrix P nor the matrix Q are explicitly part of RBF methods, which only come with an RBF-exact differentiation operator ${D \in {\mathbb {R}}^{N \times N}}$ for the cardinal functions. That said, we will now demonstrate that in many cases existing collocation RBF methods cannot satisfy the RBFSBP property since certain conditions are violated.

To this end, let ${D \in {\mathbb {R}}^{N \times N}}$ be the RBF-differentiation operator. We assume that there exist a positive definite and symmetric norm matrix $P \in {\mathbb {R}}^{N \times N}$ and a matrix $Q \in {\mathbb {R}}^{N \times N}$ such that (see (4))

$$\begin{aligned} D = P^{-1} Q, \quad Q + Q^T = B. \end{aligned}$$

(53)

The two conditions in (53) can be combined to

$$\begin{aligned} PD + (PD)^T - B = 0. \end{aligned}$$

(54)

Next, we assume that the RBF interpolant include polynomials of most degree $m-1 \ge 0$. In this case, ${\mathcal {R}}_{1}(Y_N)$ contains constants and P must be associated with a ${\mathcal {R}}_{1}(Y_N)$-exact quadrature formula. Since D is ${\mathcal {R}}_{1}(Y_N)$-exact, this can be reformulated as

$$\begin{aligned} \int _{x_L}^{x_R} 1 \partial _x f d x= f|_{x_L}^{x_R} \Longleftrightarrow {\textbf{1}}^T P D {\textbf{f}} = f|_{x_L}^{x_R} \quad \forall f \in {\mathcal {R}}_{1}(Y_N) \end{aligned}$$

(55)

Since D and ${\textbf{f}}$ are formulated with respect to the same basis $\textrm{span}\{c_k\}$. The entries of D are given by $D_{jk} =c_k'(x_j)$ with collocation points $x_j$. Hence, (55) is used for every basis element $\textrm{span} \{ c_i\}$, e.g. for $c_1$:

$$\begin{aligned} c_1|_{x_L}^{x_R}=c_1(x_R)-c_1(x_L)=\int _{x_L}^{x_R} 1 \partial _x c_1 d x= \sum _{j=1}^N w_j c'_1(x_j)={\textbf{1}}^T P \mathbf {c_1'}. \end{aligned}$$

(56)

Since $\mathbf {c_i'}$ are the columns of the derivative matrix. We can collect every basis element using (56) resulting in

$$\begin{aligned} {\textbf{1}}^T P D = {\textbf{m}}. \end{aligned}$$

(57)

with ${\textbf{m}} = [ c_1|_{x_L}^{x_R}, \dots , c_N|_{x_L}^{x_R} ]$. We shall now summarize the above discussion: Let $m-1 \ge 0$ and ${b(P):= \Vert PD + (PD)^T - B \Vert _2}$. Moreover, for given D let us consider the following optimization problem:

$$\begin{aligned} \min _{P} \left\{ \, b(P) \ \text { s.t. } \ P = P^T, \ P > 0, \ {\textbf{1}}^T P D = {\textbf{m}} \, \right\} \end{aligned}$$

(58)

If the differentiation operator D of a classic global RBF method satisfies the FSBP property, then minimizers $P^*$ of the optimization problem (58) satisfy $b(P^*) = 0$. There exist a suitable quadrature formula to determine P through the minimization problem (58). It should be stressed that $b(P) = 0$ is necessary for the given D to satisfy the SBP property, but not sufficient. This follows directly from [25, Lemma 4.3] containing the fact that the derivatives of the basis functions are integrated exactly.

Table 8 Residual $\Vert PD + (PD)^T - B \Vert _2$ for the determined norm matrix P in the case of equidistant, Halton, and random grid points

In our implementation we solved (58) using Matlab’s CVX [27]. The results for different numbers and types of grid points ${\textbf{x}}$ as well as kernels $\varphi$ and polynomial degrees $m-1$ can be found in Table 8. Our numerical findings indicate that in all cases classic global RBF methods do not satisfy the RBFSBP property. This can be noted from the residual $b(P) = \Vert PD + (DP)^T - B \Vert _2$ corresponding to the minimizer P of (58) to be distinctly different from zero (machine precision in our implementation is around $10^{-16}$). This result is not suprising and in accordance with the observations made in the literature [21, 53].