1 Introduction

In the field of Computational Fluid Dynamics (CFD) there has been a significant effort to develop numerical algorithms for solving the RANS equations in conjunction with turbulence models. This effort has continued with the objective to extend the viability of CFD to perform a complete design of complex aircraft configurations. Thus, the convergence and reliability of a solver must be verified. Extensive data assessments of solution accuracy are clearly required. Prominent examples of these data assessments are the numerous Drag Prediction (see for example [1,2,3,4]) and High Lift Prediction Workshops (see for example [5,6,7]), which are carried out regularly.

Assertions about uncertainties and errors from computed numerical data are clearly a requirement to use data obtained by numerical simulations in the aerodynamic certification processes. When designing new aircraft using numerical data, this data must be proven to be reliable. Using past AIAA workshops as a guide, different CFD computer codes typically yield a wide spread in results, even when ostensibly solving the same equations. Reasons for the wide spread are difficult to determine. Considering the fact that all participants assume that they solve the same equations with a consistent and convergent method, differences in the results must disappear as the degrees of freedom increase. For some codes and some test cases this behavior can actually be observed. However, for simulations at the border of the flight envelope or if two-equation turbulence models are used, there are often significant deviations in the results shown at the workshops. Even statistical analyses are carried out to quantify the uncertainties [2,3,4]. Since convergence histories are rarely shown for these applications, this suggests that convergence may not be achieved; and hence, the results may be severely modified by numerical errors.

Significant improvements have been achieved in the last several years for the Spalart-Allmaras (SA) turbulence model [8, 9]. The improved solvability of the single transport equation of the model using the SA negative form is a major factor for the subtantial increase in using this turbulence model. Considering the results of the AIAA Drag Prediction and High-Lift workshops of the last few years, there are more computer codes appearing using this model that can also converge several orders of magnitude. In some cases, even fully converged solutions (i.e., solutions in which the residuals are reduced to near machine zero) are achieved. Perhaps, this is at least part of the reason for the focus on introducing correction terms (e.g., streamline curvature and rotation effects) in the SA model [10, 11]. Such correction terms can provide improvement in representation of the flow physics.

During roughly the same time period as for the SA model, a number of improvements were also made for two-equation turbulence models of the \(k\)-\(\omega \) type (i.e., Wilcox model and Menter SST model). Also, there was some effort to improve the solver for the RANS and two-equation models. There is a need for improvements in the convergence behavior and reliability. Thus, solving the RANS equations with such models is frequently avoided due to high difficulty in achieving reliable convergence. Typically, to converge the RANS equations in combination with \(k\)-\(\omega \) type models is a much more difficult task compared to a one-equation model.

Such two-equation turbulence models have been successfully applied to airfoil flows with small to moderate separation (e.g., see Menter [12], Swanson [13]). However, the difficulty of simulating a broad range of separated flows, including onset and extent of separation, still remains with this class of two-equation models, as well as other eddy viscosity models. Due to the demands on the data required for a certification process together with the observations from the workshops, it is clear that there is still a great need for the development of solution methods for the RANS equations, in particular for two- equation turbulence models.

From the perspective of the authors of this paper, to design such a numerical method providing both sufficiently accurate data together with a quantifiable bound on the error, the following four points are a minimum standard one has to consider:

  1. (a)

    The full differential or integral formulation of the equations together with the turbulence modelling equations is given.

  2. (b)

    Its exact implementation is documented.

  3. (c)

    A solution algorithm that is able to compute for a given number of degrees of freedom a solution free of numerical integration errors.

  4. (d)

    The solution algorithm works for systematic mesh refinement, that is, one can obtain mesh converged results.

As soon as one of these criteria is not satisfied, certain doubts about the assertions made from approximate solutions computed with the considered numerical method arise.

From the four criteria mentioned above, obviously the first two criteria are the simplest to satisfy. Straightforwardly, one simply has to write down the actual implementation of the equations. Nothing should be hidden such as cut-off values for certain variables. This fact is mentioned here explicitly, though often not mentioned, because a significant number of implementations use certain strategies to cut-off or to restrict several of the variables. As examples we refer to the technical documentations [14, 15]. A final solution is then generally not examined with respect to activity of such limiting processes. To assess the impact corresponding to such limitings, there must be transparency of the solutions. Since often authors do not discuss or do not even mention these intrusions into the equations, only conjectures about the reasons for discrepancies between the approximate solution and experimental data can be made. One conjecture of relevance is that c) mentioned above is not independent of b).

The reason for this, which is possibly the major issue in constructing a reliable algorithm to approximately solve the RANS equations and the two transport equations of \(k\)-\(\omega \) type turbulence models, is to ensure positivity of the turbulence kinetic energy k and the energy dissipation rate \(\omega \). Perhaps, the most relevant publications dealing with this topic are [16,17,18,19]. They apply an implicit algorithm to solve the RANS equations and the two equations of a \(k\)-\(\omega \) model in a loosely coupled manner. The advantage of this approach is that only the Jacobian matrix for the turbulence equations is manipulated such that it is an M-matrix for each time step. Hence, starting with a positive k and \(\omega \), all successive values of these two dependent variables remain positive throughout the iteration process. Another idea to ensure positivity of k and \(\omega \) uses variable subtitution (logarithmic form), which was suggested by Ilinca et al. [20]. A number of other finite element methods (FEMs), not only Continuous Petrov-Galerkin methods but also Discontinuous Galerkin (DG) methods, also employ this approach (e.g., [21,22,23]). In some FEMs realizability conditions are also imposed [21, 22]. As a consequence, it is not obvious if the transformed boundary-value problem is still equivalent to the original one. As discussed in [24], there are possible effects due to smoothness of the solution as well as the modified boundary condition that may have an impact on the resulting boundary-value problem. In this article, we suggest a rather simple algorithm to deal with this positivity issue.

Given the wide range of applications for which solutions to the RANS equations are required, it is desirable that a computer code should meet the following requirements:

  • It works for a large variety of parameters defining the boundary-value problem to solve, such as

    • a variety of geometries,

    • a large number of inflow conditions, which includes a range from very low Mach number to hypersonic flows,

    • a broad range of Reynolds numbers,

    • a large number of different boundary conditions;

  • It works for a broad range of parameters determining the actual solution method, such as

    • variation in CFL number,

    • inner linear solution methods,

    • linear and nonlinear multigrid as well as cycling strategies;

  • It always converges to a steady-state solution, if a steady state solution exists;

  • It does not show significant loss in convergence rates with systematic mesh refinement studies, for example, an increase in the number of degrees of freedom are considered.

From the point of view of the authors, at this time, the design of a solution method for the RANS equations satisfying all these conditions is an open problem. It can be assumed that various interventions (using cutoff values or restriction of variables) into several solution methods have been incorporated to be in a position to compute steady-state solutions, at least for a small number of problems with a specific choice of parameters.

Considering this background, the primary objective of this paper is to propose a numerical algorithm that efficiently solves the RANS equations in combination with two-equation models of the \(k\)-\(\omega \) type on structured and unstructured meshes. Numerical examples demonstrate that the number of nonlinear iterations is comparable to state-of-the art methods for one-equation models. In this regard, we refer to [25,26,27,28,29,30,31], where a similar number of nonlinear iterations is required using similar methods for the one-equation model of Spalart and Allmaras. We illustrate that a relibale behavior of the solution algorithm, that is without oscillations or a deterioration in the final convergence rate is not only possible for basic 2-D test cases but also for 3-D transonic test cases at the design point and for a 3-D high lift configuration. Beyond the pure heuristics and test cases, an analysis is performed in particular for the two-equation turbulence model, which reveals some of the special characteristics of these models and what one needs to consider in order to implement them successfully.

In Sects. 2 and 3 of the paper, the integral form of the RANS equations and the turbulence modeling equations, respectively, are defined. This includes the boundary conditions necessary for a well defined boundary-value problem. Section 4 considers the components of the numerical algorithm, which are the focus of the paper. Then, in Sect. 5, analysis of properties, including linear stability, of the solution algorithm is considered. Both two-dimensional (2-D) and three-dimensional (3-D) examples of applications of the numerical solution algorithm are shown and discussed in Sect. 6. Concluding remarks of the paper are made in Sect. 7.

2 Governing Equations of Fluid Flow

To describe flow behavior we consider for the domain \(G\subset \mathbb {R}^m\), \(m=2,3,\) i.e., an open and connected set, and an interval \([0,T )\subset \mathbb {R}\), \(T>0\), the conservative form of the RANS equations is expressed in integral form by

$$\begin{aligned} 0= & {} \frac{d}{dt}V_{G}\left( W\right) \left( t\right) \nonumber \\{} & {} \quad + R_{\partial G}\left( W\right) \left( t\right) ,\qquad t\in \left[ 0,T\right) , \end{aligned}$$
(1a)

where the integral operators \(V_{G}\) and \(R_{\partial G}\) are given by

$$\begin{aligned} V_{G}\left( W\right) \left( t\right):= & {} \int _{G}W\left( x,t\right) dx \end{aligned}$$
(1b)
$$\begin{aligned} R_{c,\partial G} \left( W\right) \left( t\right):= & {} \int _{\partial G}\left<f_c\left( W\left( y,t\right) \right) ,n(y)\right>ds(y),\end{aligned}$$
(1c)
$$\begin{aligned} R_{v,\partial G} \left( W\right) \left( t\right):= & {} \int _{\partial G}\left<f_v\left( W\left( y,t\right) \right) ,n(y)\right>ds(y),\end{aligned}$$
(1d)
$$\begin{aligned} R_{\partial G}:= & {} R_{c,\partial G} - R_{v,\partial G}, \end{aligned}$$
(1e)

and \(W: G\times [0,T)\rightarrow \mathbb {R}^{m+2}\),

$$\begin{aligned}{} & {} W\left( x,t\right) :=\left( \rho (x,t),\rho (x, t)u\right. \nonumber \\{} & {} \quad \left. (x,t),\rho (x, t)E(x,t) \right) ^T, \end{aligned}$$
(2)

denotes the vector field of conserved variables and n is the unit outward normal on \(\partial G\). The terms \(f_c\) and \(f_v\) describe the convective and viscous contributions

$$\begin{aligned}{} & {} f_c\left( W\right) := \left( \begin{array}{c} \rho u\\ \rho u_1u + pe_1\\ \vdots \\ \rho u_mu + pe_m\\ \rho Hu \end{array} \right) , \\{} & {} \quad f_v\left( W\right) := \left( \begin{array}{c} 0\\ \tau _{1}\left( W\right) \\ \vdots \\ \tau _{m}\left( W\right) \\ \theta \left( W\right) \end{array} \right) , \qquad m = 2,3. \end{aligned}$$

Here \(e_i\) is the ith unit vector. The quantities \(\rho \), \(u=\left( u_1,\ldots ,u_m\right) ^T\), \(E\) and

$$\begin{aligned} H:=E+p/\rho \end{aligned}$$
(3)

are the density, the velocity, the specific total energy, and the enthalpy of the fluid. The equation of state

$$\begin{aligned} p = (\gamma - 1)\rho \left( E - \frac{\Vert u\Vert _2^2}{2}\right) \end{aligned}$$
(4)

defines the pressure \(p\), and \(\gamma \) is the gas dependent ratio of specific heats, which is 1.4 for air. Assuming that an effective viscosity \(\mu _\textrm{eff}:= \mu _\textrm{eff}\left( W\right) = \mu _\textrm{eff}\left( W\left( x,t\right) \right) \) is given and using Stoke’s hypothesis, the bulk viscosity vanishes and the second coefficient of viscosity \(\lambda = -2/3\mu _\textrm{eff}\). Then, the viscous stress tensor is given by

$$\begin{aligned} \tau \left( W\right) := \mu _\textrm{eff}\mathcal {S} + \lambda \hspace{0.1cm}\textrm{div}(u)\mathrm Id= 2\mu _\textrm{eff}\overline{\mathcal {S}},\qquad \overline{\mathcal {S}}:= \mathcal {S} - \frac{1}{3}\hspace{0.1cm}\textrm{div}( u)\mathrm Id, \end{aligned}$$
(5)

and \(\mathcal {S}\) denotes the mean strain-rate tensor, which is given by the symmetric part of the total derivative of flow velocity vector u,

$$\begin{aligned}{} & {} \mathcal {S}:= \frac{1}{2}\left( \frac{du}{dx} + \left( \frac{du}{dx}\right) ^T\right) ,\qquad \text{ i.e., }\nonumber \\{} & {} \mathcal {S}_{ij} = \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) . \end{aligned}$$
(6)

Throughout the paper \(\mathrm Id(x) = x\) denotes the identity operator. The viscous flux term for the energy equation is given by

$$\begin{aligned} \theta \left( W\right):= & {} \tau \left( W\right) u + q\left( W\right) , \end{aligned}$$
(7a)
$$\begin{aligned} q\left( W\right):= & {} \kappa _\textrm{eff}\;\text{ grad } T. \end{aligned}$$
(7b)

The effective viscosity \(\mu _\textrm{eff}\) and effective conductivity \(\kappa _\textrm{eff}\) are computed by

$$\begin{aligned} \mu _\textrm{eff}:= \mu _l + \mu _t,\qquad \kappa _\textrm{eff}:= \kappa _l + \kappa _t, \end{aligned}$$
(8)

and the laminar viscosity is given by Sutherland’s law

$$\begin{aligned} \mu _l\left( W\right):= & {} \mu _{l,\infty }\left( \frac{T}{T_{\infty }}\right) ^{3/2} \frac{T_{\infty }+\bar{T}}{T+\bar{T}},\qquad \mu _{l,\infty }:=\frac{\rho _{\infty }u_{\infty }L}{Re}, \end{aligned}$$
(9)
$$\begin{aligned} \kappa _l\left( W\right):= & {} \frac{c_p\mu _l\left( W\right) }{Pr_l} \qquad \text{ and }\qquad \nonumber \\ c_p:= & {} \Re \frac{\gamma }{\gamma -1}, \end{aligned}$$
(10)

whereby \(T_{\infty } > 0\), \(\rho _{\infty } > 0\) and \(u_{\infty } > 0\) denote some constant reference temperature, density and velocity, \(L>0\) is some constant reference length scale, \(Re>0\) is the corresponding Reynolds number, \(\bar{T}:=110.4^{\circ }\text{ K }\) is Sutherland’s constant, \(\Re \) is the universal gas constant and the laminar Prandtl number is given by \(Pr_l:=0.72\).

In this article, we restrict consideration to linear, two equation turbulence models, represented by differential or integral equations stated in Sect. 3. The solutions of these equations reveal additional quantities in the considered fluid. These occurring variables extend the degrees of freedom given by the conservative variables \(W\) by a further unknown function

$$\begin{aligned} W_{t}: G\times [0,T)\rightarrow \mathbb {R}^2. \end{aligned}$$

The additional variables are used to determine the eddy viscosity,

$$\begin{aligned}{} & {} \mu _t = \mu _t\left( W_{t}\left( x,t\right) , W\left( x,t\right) \right) \\{} & {} \quad \ge 0\quad \text{ for } \text{ all }\quad \left( x,t\right) \in G\times \left[ 0,T\right) , \end{aligned}$$

required for (8). Given the eddy viscosity \(\mu _t\) the turbulent thermal conductivity is described by the algebraic relation

$$\begin{aligned} \kappa _t:= c_p\frac{\mu _t}{Pr_t},\qquad Pr_t:=0.9. \end{aligned}$$
(11)

The dependent variables of the turbulence models are the turbulence kinetic energy per unit mass k and the dissipation rate \(\omega \) of the turbulence kinetic energy. Before we state the two transport equations for k and \(\omega \), we define \(t=\left( t_{ij}\right) _{1\le i, j\le m}\) and the Reynolds stress tensor \(\tau ^\textrm{RS} = \left( \tau ^\textrm{RS}_{ij}\right) _{1\le i, j\le m}\), using the strain-rate tensors \(\mathcal {S}\) and \(\overline{\mathcal {S}}\), given in (6) and (5), and the mean molecular stress tensor, \(t=\left( t_{ij}\right) _{1\le i, j\le m}\). Then,

$$\begin{aligned}{} & {} t = 2\mu _\textrm{eff}\overline{\mathcal {S}},\qquad \rho \tau ^\textrm{RS} \nonumber \\{} & {} \quad = 2\mu _t \overline{\mathcal {S}} - \frac{2}{3}\rho k \mathrm Id. \end{aligned}$$
(12)

Additionally, we define the mean rotation tensor \(\Omega \), which is the skew-symmetric part of the total derivative of flow velocity u,

$$\begin{aligned}{} & {} \Omega := \frac{1}{2}\left( \frac{du}{dx} - \left( \frac{du}{dx}\right) ^T\right) , \qquad \text{ i.e. }\quad \Omega _{ij} \nonumber \\{} & {} \quad = \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} - \frac{\partial u_j}{\partial x_i}\right) . \end{aligned}$$
(13)

3 Two-Equation Turbulence Models of \(k\)-\(\omega \) Type

The principal elements of the \(k\)-\(\omega \) type turbulence models being considered are described in this section. The emphasis is on the 1988 and 2006 Wilcox models and the 2003 Menter Shear Stress Transport (SST) model. Presentation and extensive discussion of these models is given in references [32,33,34] and [12, 35,36,37]. An additional resource providing information on these and other turbulence models is NASA’s Turbulence Modeling Resource (TMR) website [38]. Important details of these models, such as parameters and closure coefficients, can be found in the TMR or in the original publications.

3.1 Wilcox \(k\)-\(\omega \) Model

In this article we consider \(k\)-\(\omega \) models of the form

$$\begin{aligned} \frac{\partial \left( \rho k\right) }{\partial t} + \hspace{0.1cm}\textrm{div}\left( \rho k u\right)= & {} \hspace{0.1cm}\textrm{div}\left( \left( \mu _l + \sigma _{k}\mu _t\right) \text{ grad } k\right) + \rho Q_{k,(k,\omega )}, \end{aligned}$$
(14a)
$$\begin{aligned} \frac{\partial \left( \rho \omega \right) }{\partial t} + \hspace{0.1cm}\textrm{div}\left( \rho \omega u\right)= & {} \hspace{0.1cm}\textrm{div}\left( \left( \mu _l + \sigma _{\omega }\mu _t\right) \text{ grad } \omega \right) + \rho Q_{\omega ,(k,\omega )}. \end{aligned}$$
(14b)

The presented and used 1988 and 2006 models of Wilcox are named as ”Wilcox1988” and ”Wilcox2006” on NASA’s (TMR) website [38]. The eddy viscosity in these models is computed by

$$\begin{aligned} \mu _t = \mu _t(W,k,\omega ) = \rho k / z\left( W,k,\omega \right) \end{aligned}$$
(15)

with a given function z. For example, in the 1988 and 2006 models of Wilcox, we have

$$\begin{aligned} z\left( W,k,\omega \right)= & {} \omega ,\qquad \text{(1988 } \text{ model) }, \end{aligned}$$
(16)
$$\begin{aligned} z\left( W,k,\omega \right)= & {} \max \left\{ \omega ,C_\textrm{lim}\sqrt{\frac{2\Omega : \Omega }{\beta ^*}}\right\} ,\qquad \text{(2006 } \text{ model). } \end{aligned}$$
(17)

The symbol  :  denotes a double dot tensor product. The source terms for the k and \(\omega \) equations include production (Pr) and destruction (De) terms. A cross-diffusion term (Di) is also included in the source term of the \(\omega \) equation for the 2006 Wilcox model (\(\Psi = 1\)), the 1988 model does not have such a term (\(\Psi = 0\)),

$$\begin{aligned}{} & {} Q_{k,(k,\omega )}:= \tilde{Pr}_{k,(k,\omega )} - De_{k,(k,\omega )},\quad Q_{\omega ,(k,\omega )} \nonumber \\{} & {} \quad := Pr_{\omega ,(k,\omega )} - De_{\omega ,(k,\omega )} + \Psi Di_{\omega ,(k,\omega )}, \end{aligned}$$
(18)

where

$$\begin{aligned} Pr_{k,(k,\omega )}:= & {} \tau ^\textrm{RS}:\frac{du}{dx},\qquad De_{k,(k,\omega )}:= \beta ^*k\omega \end{aligned}$$
(19a)
$$\begin{aligned} Pr_{\omega ,(k,\omega )}:= & {} \alpha \frac{\omega }{k}\tau ^\textrm{RS}:\frac{du}{dx},\qquad De_{\omega ,(k,\omega )}:= \beta \omega ^2. \end{aligned}$$
(19b)
$$\begin{aligned} Di_{\omega ,(k,\omega )}:= & {} \sigma _{d}\frac{1}{\omega }\left<\text{ grad } k,\text{ grad } \omega \right>. \end{aligned}$$
(19c)

In the 1988 Wilcox model, the production term of the k equation is generally limited according to

$$\begin{aligned} \tilde{Pr}_{k,(k,\omega )}:= & {} \min \left\{ Pr_{k,(k,\omega )}, 20 De_{k,(k,\omega )}\right\} , \end{aligned}$$
(20)

so as to prevent very large \(P_k\) during the initial phases of a calculation. An example to demonstrate the impact and influence of (20) on possible solutions was demonstrated in [24, Section 7]. This change is not included in the 2006 Wilcox model due to the introduction of a stress limiter. This stress limiter can have a significant effect on a shock location. The effect of varying the stress limiter on the shock location for the RAE 2822 airfoil (Case 10) is shown in Swanson and Rossow [39].

3.2 Menter \(k\)-\(\omega \) Model (SST Model)

The presented and used model of Menter is named as ”SST-2003” on NASA’s (TMR) website [38] with the only difference that (20) is used, that is the 20 was not replaced by 10. In the 2003 Menter SST model the constants \(\sigma _k\) and \(\sigma _{\omega }\) in the two transport equations (14a) and (14b) are replaced with blending functions \(\Phi _k\) and \(\Phi _{\omega }\). These blending functions depend on the values \(\sigma _k\) and \(\sigma _{\omega }\) in the \(k\)-\(\omega \) and \(k\)-\(\varepsilon \) models. The source terms are also changed due to blending functions for the \(k\)-\(\omega \) and \(k\)-\(\varepsilon \) models. The eddy viscosity is determined from (15) with \(z\left( W,k,\omega \right) \) given by

$$\begin{aligned}{} & {} z\left( W,k,\omega \right) = \frac{1}{\min \left\{ \frac{1}{\omega },\frac{a_1}{F_2\sqrt{2S: S}} \right\} } \nonumber \\{} & {} \quad = \max \left\{ \omega ,\frac{F_2\sqrt{2S: S}}{a_1}\right\} . \end{aligned}$$
(21)

Here, \(F_2\) is a blending function defined by

$$\begin{aligned} F_2:= \tanh \left( \left( \max \left\{ \Gamma _1,2\Gamma _3\right\} \right) ^2\right) \end{aligned}$$
(22)

where

$$\begin{aligned}{} & {} \Gamma _1:= \frac{C_{\Gamma _1}\nu _l}{d^2\omega },\qquad \nonumber \\{} & {} \Gamma _3 := \frac{\sqrt{ k}}{\beta ^* \omega d},\quad \beta ^*:=0.09, \end{aligned}$$
(23)

and d is the distance to the closest no-slip wall, and \(\nu _l\) is the kinematic viscosity. According to [12], the constants are \(a_1= 0.31\) and \(C_{\Gamma _1} = 500\). The source terms, having the same components as in (18), are given by

$$\begin{aligned}{} & {} Q_{k,\textrm{SST }} = \tilde{Pr}_{k,\textrm{SST }} - De_{k,\textrm{SST }},\qquad \nonumber \\{} & {} Q_{\omega ,\textrm{SST }} = Pr_{\omega ,\textrm{SST }} - De_{\omega ,\textrm{SST }} + Di_{\omega ,\textrm{SST }}, \end{aligned}$$
(24)

where

$$\begin{aligned} Pr_{k,\textrm{SST }}:= & {} \tau ^\textrm{RS}:\frac{du}{dx},\qquad De_{k,\textrm{SST }}:= \beta ^*k\omega , \end{aligned}$$
(25a)
$$\begin{aligned} Pr_{\omega ,\textrm{SST }}:= & {} \Phi _{\gamma }\frac{1}{\nu _t} \tau ^\textrm{RS}:\frac{du}{dx},\qquad De_{\omega ,\textrm{SST }}:= \Phi _{\beta }\omega ^2, \end{aligned}$$
(25b)
$$\begin{aligned} Di_{\omega ,\textrm{SST }}:= & {} 2\left( 1 - F_1\right) \sigma _{\omega _2}\frac{1}{\omega }\left<\text{ grad } k,\text{ grad } \omega \right>. \end{aligned}$$
(25c)

The blending of the SST model is controlled by a function \(\Phi = \Phi \left( x; \varepsilon _1,\varepsilon _2\right) \). This function is designed to detect the edge of the boundary layer, such that the SST model behaves inside the boundary layer like a \(k\)-\(\omega \) model and outside like a \(k\)-\(\varepsilon \) model, exploiting the convex combination \(\Phi : [0,1]\rightarrow [\varepsilon _1, \varepsilon _2]\),

$$\begin{aligned} \Phi \left( F_1;\varepsilon _1,\varepsilon _2\right):= & {} F_1\varepsilon _1 + \left( 1-F_1\right) \varepsilon _2. \end{aligned}$$
(26)

3.3 Simplifications of \(k\)-\(\omega \) Models

Although these models are formulated in their compressible form (14), their actual implementation and usage is often based on their incompressible version. In fact, this occurs even when they are used with respect to compressible flow. Then, one assumes

$$\begin{aligned} \hspace{0.1cm}\textrm{div}\left( u\right)= & {} 0, \end{aligned}$$
(27)

yielding for the equation of mass conservation \(0 = \frac{\partial \rho }{\partial t} + \left<\text{ grad } \rho , u\right>\), and hence

$$\begin{aligned} \frac{\partial \left( \rho k\right) }{\partial t} + \hspace{0.1cm}\textrm{div}\left( \rho k u\right)= & {} \rho \left( \frac{\partial k}{\partial t} + \hspace{0.1cm}\textrm{div}\left( ku\right) \right) , \end{aligned}$$
(28)
$$\begin{aligned} \frac{\partial \left( \rho \omega \right) }{\partial t} + \hspace{0.1cm}\textrm{div}\left( \rho \omega u\right)= & {} \rho \left( \frac{\partial \omega }{\partial t} + \hspace{0.1cm}\textrm{div}\left( \omega u\right) \right) . \end{aligned}$$
(29)

Inserting (28) and (29) into (14) gives

$$\begin{aligned} \frac{\partial k}{\partial t} + \hspace{0.1cm}\textrm{div}\left( k u\right)= & {} \frac{1}{\rho }\hspace{0.1cm}\textrm{div}\left( \left( \mu _l + \sigma _{k}\mu _t\right) \text{ grad } k\right) + Q_{k,(k,\omega )}, \end{aligned}$$
(30a)
$$\begin{aligned} \frac{\partial \omega }{\partial t} + \hspace{0.1cm}\textrm{div}\left( \omega u\right)= & {} \frac{1}{\rho }\hspace{0.1cm}\textrm{div}\left( \left( \mu _l + \sigma _{\omega }\mu _t\right) \text{ grad } \omega \right) + Q_{\omega ,(k,\omega )}, \end{aligned}$$
(30b)

and the independent variables \(W_t=(\rho k,\rho \omega )\) are replaced by \(W_t=(k,\omega )\). To be consistent using assumption (27) we have

$$\begin{aligned} \rho \tau = 2\mu _t\overline{\mathcal {S}}. \end{aligned}$$
(31)

In a second step, assumption (27) can be integrated into (31). This yields \(\overline{\mathcal {S}} = \mathcal {S}\) and finally

$$\begin{aligned} \rho \tau = 2\mu _t\mathcal {S}. \end{aligned}$$
(32)

Remark

Often, it is not indicated if the assumption (27) is included into the formulation of the turbulence model, that is, if (31) or (32) is used for the formulation of the production terms. For the implementation considered here we chose (31).

3.4 Integral Form of \(k\)-\(\omega \) Models

When integrating the diffusive terms in (30) over a control volume, they cannot be rewritten as a surface integral because of division with density \(\rho \). Hence, a further approximation is introduced,

$$\begin{aligned} \frac{1}{\rho }\hspace{0.1cm}\textrm{div}\left( \left( \mu _l + \sigma _{k}\mu _t\right) \text{ grad } k\right)\approx & {} \hspace{0.1cm}\textrm{div}\left( \left( \nu _l + \sigma _{k}\nu _t\right) \text{ grad } k\right) , \end{aligned}$$
(33a)
$$\begin{aligned} \frac{1}{\rho }\hspace{0.1cm}\textrm{div}\left( \left( \mu _l + \sigma _{\omega }\mu _t\right) \text{ grad } \omega \right)\approx & {} \hspace{0.1cm}\textrm{div}\left( \left( \nu _l + \sigma _{\omega }\nu _t\right) \text{ grad } \omega \right) . \end{aligned}$$
(33b)

Integration of (30) using the approximation of (33) gives the integral equation

$$\begin{aligned}{} & {} V_{G}\left( Q_{(k,\omega )}\left( W_t,W\right) \right) \left( t\right) \nonumber \\{} & {} \quad = \frac{d}{dt}V_{G}\left( W_t\right) \left( t\right) \nonumber \\{} & {} \qquad + R_{\partial G,(k,\omega )}\left( W_t,W\right) \left( t\right) , \end{aligned}$$
(34)

where the integral operators are \(R_{\partial G,(k,\omega )}:= R_{c,\partial G,(k,\omega )} - R_{v,\partial G,(k,\omega )}\), and

$$\begin{aligned}{} & {} R_{c,\partial G,(k,\omega )} \left( W_t,W\right) \left( t\right) \\{} & {} \quad := \int _{\partial G}\left<f_{c,(k,\omega )}\left( W_t\left( y,t\right) ,W\left( y,t\right) \right) ,n(y)\right>ds(y),\\{} & {} R_{v,\partial G,(k,\omega )} \left( W_t,W\right) \left( t\right) \\{} & {} \quad := \int _{\partial G}\left<f_{v,(k,\omega )}\left( W_t\left( y,t\right) ,W\left( y,t\right) \right) ,n(y)\right>ds(y). \end{aligned}$$

Here the convective \(f_{c,(k,\omega )}\) and viscous \(f_{v,(k,\omega )}\) contributions as well as the source terms \(Q_{(k,\omega )}\) are summarized by

$$\begin{aligned} f_{c,(k,\omega )}\left( W_t,W\right):= & {} \left( \begin{array}{c} k u\\ \omega u \end{array} \right) , \end{aligned}$$
(35a)
$$\begin{aligned} f_{v,(k,\omega )}\left( W_t,W\right):= & {} \left( \begin{array}{c} \left( \nu _{l} + \sigma _{k} \nu _t \right) \text{ grad } k\\ \left( \nu _{l} + \sigma _{\omega }\nu _t \right) \text{ grad } w \end{array} \right) , \end{aligned}$$
(35b)
$$\begin{aligned} Q_{(k,\omega )}\left( W_t,W\right):= & {} \left( \begin{array}{c} Pr_{k,(k,\omega )} - De_{k,(k,\omega )}\\ Pr_{\omega ,(k,\omega )} - De_{\omega ,(k,\omega )} + Di_{\omega , (k,\omega )} \end{array} \right) . \end{aligned}$$
(35c)

3.5 Nondimensionalization

For a numerical implementation a suited scaling and nondimensionalization is often crucial. Due to the no-slip wall boundary condition  (see [24]) for \(\omega \),

$$\begin{aligned} \lim _{h\rightarrow 0+}\omega \left( x - hn(x)\right) h^2 = \frac{6\nu _l}{\beta },\qquad x\in \partial D_{\mathrm{no-slip}}, \end{aligned}$$
(36)

typically the values for \(\omega \) related to k and the other conservative variables (2) may differ in orders of magnitude. For this reason, a scaling of \(\omega \) is introduced.

Throughout this subsection, we denote dimensional variables using the sign \(\hat{}\), for example dimensional density is denote by \(\hat{\rho }\). To nondimensionalize \(\hat{k}\) and \(\hat{\omega }\) we choose as reference values

$$\begin{aligned} k_\textrm{ref} = u_\textrm{ref}^2\qquad \text{ and }\qquad \omega _\textrm{ref} = \frac{u_\textrm{ref}}{L_\textrm{ref}}. \end{aligned}$$
(37)

Then the nondimensional variables are given by

$$\begin{aligned}{} & {} k = \frac{\hat{k}}{u_\textrm{ref}^2}\qquad \text{ and }\qquad \nonumber \\{} & {} \omega = \frac{\hat{\omega }}{\omega _{sc}\omega _\textrm{ref}},\qquad \nonumber \\{} & {} \omega _{sc} = \frac{Re}{\sqrt{\gamma }{M}_{\infty }L}, \end{aligned}$$
(38)

where \(\omega _{sc}\) denotes the additional scaling for \(\omega \). Such scaling may be motivated by the following argumentation. Boundary condition (36) is realized by

$$\begin{aligned}{} & {} \omega _\mathrm{no-slip}\left( p_{i,\textrm{bdry}}\right) \nonumber \\{} & {} \quad = \frac{60\nu _l\left( W(p_{i,\textrm{bdry}})\right) }{\beta \left\| {p}_{i,\textrm{bdry}}-{p}_{i,n}\right\| ^2_2},\nonumber \\{} & {} \quad p_{i,bdry}\in \partial D_{\mathrm{no-slip}}, \end{aligned}$$
(39)

where \(p_{i,bdry}\) denotes the point on the no-slip wall and \(p_{i,n}\) the closest, next discrete point in direction \(-n\left( p_{i,bdry}\right) \). Obviously, with respect to possible mesh refinements the distance to the closest wall satisfies

$$\begin{aligned} d_{h,i} \approx \left\| {p}_{i,\textrm{bdry}}-{p}_{h,i,n}\right\| _2\rightarrow 0,\qquad h\rightarrow 0, \end{aligned}$$

and hence possibly numerical instabilities emerge due to a significant increase in the boundary values \(\omega _\mathrm{no-slip}\). The above choice of \(\omega _{sc}\) serves a some normalization such that the largest values for \(\omega \) are in a range of the other variables. Naturally, a choice of \(\omega _{sc} = 1\) or any other reasonable choice is also possible.

To obtain an equivalent system of equations, this scaling parameter needs to be correctly incorporated in all terms and equations. For a detailed study we refer to [40, 41], here we just report the results. For example, to obtain the scaled, nondimensional version of the eddy viscosity (15) together with (21) for the SST model we have

$$\begin{aligned} \mu _t = \frac{1}{\omega _{sc}}\rho k\min \left\{ \frac{1}{\omega }, \frac{\omega _{sc}a_1}{F_2\sqrt{2\Omega : \Omega } } \right\} . \end{aligned}$$

Then, introducing (37) into (35a), (35b) and (35c), we compute

$$\begin{aligned} f_{c,(k,\omega )}\left( \hat{W}_t,\hat{W}\right)= & {} u_\textrm{ref}\left( \begin{array}{cc} k_\textrm{ref} &{} 0 \\ 0 &{} \omega _\textrm{ref}\omega _{sc} \end{array} \right) f_{c,(k,\omega )}\left( W_t,W\right) , \end{aligned}$$
(40)
$$\begin{aligned} f_{v,(k,\omega )}\left( \hat{W}_t,\hat{W}\right)= & {} u_\textrm{ref} \left( \begin{array}{cc} \frac{k_\textrm{ref}}{\omega _{sc}} &{} 0 \\ 0 &{} \omega _\textrm{ref} \end{array} \right) \tilde{f}_{v,(k,\omega )}\left( W_t,W\right) , \end{aligned}$$
(41)

where

$$\begin{aligned} \tilde{f}_{v,(k,\omega )}\left( W_t,W\right) := \left( \begin{array}{c} \left( \Gamma (T) + \sigma _k\nu _t \right) \text{ grad } k\\ \left( \Gamma (T) + \sigma _{\omega }\nu _t\right) \text{ grad } \omega \end{array} \right) ,\qquad \Gamma (T) = T^{3/2}\left( \frac{1+C_\textrm{suth}}{T+C_\textrm{suth}}\right) , \end{aligned}$$

and \(C_\textrm{suth}\) denotes Sutherland’s constant. For the source terms (35c) we obtain

$$\begin{aligned} Pr_{k,(k,\omega )}\left( \hat{W}_t,\hat{W}\right)= & {} \frac{u_\textrm{ref}^3}{L_\textrm{ref}\omega _{sc}}Pr_{k,(k,\omega )}\left( W_t,W\right) ,\hspace{1cm} \end{aligned}$$
(42a)
$$\begin{aligned} De_{k,(k,\omega )}\left( \hat{W}_t,\hat{W}\right)= & {} \frac{u_\textrm{ref}^3\omega _{sc}}{L_\textrm{ref}}De_{k,(k,\omega )}\left( W_t,W\right) , \end{aligned}$$
(42b)
$$\begin{aligned} Pr_{\omega ,(k,\omega )}\left( \hat{W}_t,\hat{W}\right)= & {} = \frac{u_\textrm{ref}^2}{L_\textrm{ref}^2}Pr_{\omega ,(k,\omega )}\left( W_t,W\right) , \end{aligned}$$
(42c)
$$\begin{aligned} De_{\omega ,(k,\omega )}\left( \hat{W}_t,\hat{W}\right)= & {} \frac{u_\textrm{ref}^2\omega _{sc}^2}{L_\textrm{ref}^2}De_{\omega ,(k,\omega )}\left( W_t,W\right) , \end{aligned}$$
(42d)
$$\begin{aligned} Di_{\omega ,(k,\omega )}\left( \hat{W}_t,\hat{W}\right)= & {} \frac{u_\textrm{ref}^2}{L_\textrm{ref}^2}Di_{\omega ,(k,\omega )}\left( W_t,W\right) . \end{aligned}$$
(42e)

Introducing the mapping \(g: D \rightarrow \hat{D}\), \(x \mapsto L_\textrm{ref}x\), which maps the computational domain D to its physical domain \(\hat{D}\), and application of substitution formulae

$$\begin{aligned} \int _{\hat{D}}v(x)dx= & {} L_\textrm{ref}^m\int _D v(g(y))dy, \end{aligned}$$
(43a)
$$\begin{aligned} \int _{\partial \hat{D}}\left<v(y),n(y)\right>ds(y)= & {} L_\textrm{ref}^{m-1}\int _{\partial D}\left<v(g(y)),n(y)\right>ds(y). \end{aligned}$$
(43b)

integral equation (34) turns into using (40), (41) and (42a)– (42e),

$$\begin{aligned}{} & {} \left( \begin{array}{c} \frac{L_\textrm{ref}^2u_\textrm{ref}^3}{\omega _{sc}}\int _DPr_{k,(k,\omega )}dy - L_\textrm{ref}^2u_\textrm{ref}^3\omega _{sc}\int _DDe_{k,(k,\omega )} dy\\ L_\textrm{ref}u_\textrm{ref}^2\int _D Pr_{\omega ,(k,\omega )}dy - L_\textrm{ref}u_\textrm{ref}^2\omega _{sc}^2\int _DDe_{\omega ,(k,\omega )} dy + L_\textrm{ref}u_\textrm{ref}^2\int _DDi_{\omega ,(k,\omega )} dy \end{array} \right) \\{} & {} \quad = \left( \begin{array}{cc} L_\textrm{ref}^2u_\textrm{ref}^3 &{} 0\\ 0 &{} \omega _{sc}L_\textrm{ref}u_\textrm{ref}^2 \end{array} \right) \left\{ \frac{d}{dt}V_D(W_t)(t) + R_{c,\partial G,(k,\omega )} \left( W_t,W\right) \left( t\right) \right\} \\{} & {} \qquad - \left( \begin{array}{cc} \frac{1}{\omega _{sc}}L_\textrm{ref}^2u_\textrm{ref}^3 &{} 0 \\ 0 &{} L_\textrm{ref}u_\textrm{ref}^2 \end{array} \right) \int _{\partial D}\left<\tilde{f}_{v,(k,\omega )}\left( W_t,W\right) ,n\right>ds(y). \end{aligned}$$

Multiplication of the whole system with the diagonal matrix \(\text{ diag } \left( \frac{1}{L_\textrm{ref}^2u_\textrm{ref}^3}, \frac{1}{\omega _{sc}}\frac{1}{L_\textrm{ref}u_\textrm{ref}^2} \right) \) gives the mathematically equivalent system of equations

$$\begin{aligned}{} & {} \left( \begin{array}{c} \omega _{sc}^{-1}\int _DPr_{k,(k,\omega )}dy - \omega _{sc}\int _DDe_{k,(k,\omega )} dy\nonumber \\ \omega _{sc}^{-1}\int _D Pr_{\omega ,(k,\omega )}dy - \omega _{sc}\int _DDe_{\omega ,(k,\omega )} dy + \omega _{sc}^{-1}\int _DDi_{\omega ,(k,\omega )} dy \end{array} \right) \nonumber \\{} & {} = \frac{d}{dt}V_D(W_t)(t) + R_{c,\partial G,(k,\omega )} \left( W_t,W\right) \left( t\right) \nonumber \\{} & {} \qquad - \left( \begin{array}{cc} \omega _{sc}^{-1} &{} 0 \\ 0 &{} \omega _{sc}^{-1} \end{array} \right) \int _{\partial D}\left<\tilde{f}_{v,(k,\omega )}\left( W_t,W\right) ,n\right>ds(y). \end{aligned}$$
(44)

The system of equations (44) is the actual system of equations which is implemented and solved. For a closed formulation of the complete boundary-value problem we refer to [24].

4 Solution Algorithm

4.1 Multigrid and Implicit Smoother

The discretization strategy followed is based on a finite-volume formulation. The inviscid terms are discretized using a central difference scheme with an added matrix-valued artificial viscosity [29]. A first-order upwind scheme is applied to the convective part of the turbulent flow equations. Gradients required for the viscous terms and for the source terms are computed using a Green-Gauss formulation (see [42]). For a detailed description of the discretization strategy and boundary conditions applied, we refer to [29, 30, 40]. To clarify that we deal now with the discretized equations we use bold letters from now on.

The discretization of the mean flow equations (1) together with the turbulent flow equations (34) yields the system of ordinary differential equations

$$\begin{aligned} \frac{d}{dt} \left( \begin{array}{c} \textbf{W}(t)\\ \textbf{W}_t(t) \end{array} \right) = \left( \begin{array}{c} -\textbf{M}^{-1}_\textrm{mean}\textbf{R}_\textrm{mean}\left( \textbf{W}(t), \textbf{W}_t(t)\right) \\ -\textbf{M}^{-1}_\textrm{turb}\textbf{R}_\textrm{turb}\left( \textbf{W}(t), \textbf{W}_t(t)\right) \end{array} \right) , \end{aligned}$$
(45)

where

$$\begin{aligned} \textbf{M}_\textrm{mean}:= & {} \text{ diag }\left( \text{ diag }\left( \text{ vol }\left( \Omega _i\right) \right) \right) \in \mathbb {R}^{5N_\textrm{elem}\times 5N_\textrm{elem}}\\ \textbf{M}_\textrm{turb}:= & {} \text{ diag }\left( \text{ diag }\left( \text{ vol }(\Omega _i)\right) \right) \in \mathbb {R}^{2\cdot N_\textrm{elem} \times 2\cdot N_\textrm{elem}} \end{aligned}$$

denote the mass matrix for mean and turbulent flow equations. To approximately solve (45) we assume that the mean flow equations depend only on \(\textbf{W}\), and \(\textbf{W}_t\) acts only as a parameter here, whereas the turbulent flow equations depend only on \(\textbf{W}_t\), and \(\textbf{W}\) acts as a parameter. Hence, we rewrite system (45) as

$$\begin{aligned} \frac{d}{dt}\textbf{W}(t)= & {} -\textbf{M}^{-1}_\textrm{mean}\textbf{R}_\textrm{mean}\left( \textbf{W}(t); \textbf{W}_t(t)\right) \end{aligned}$$
(46a)
$$\begin{aligned} \frac{d}{dt}\textbf{W}_t(t)= & {} -\textbf{M}^{-1}_\textrm{turb}\textbf{R}_\textrm{turb}\left( \textbf{W}_t(t); \textbf{W}(t)\right) . \end{aligned}$$
(46b)

Equations (46a) and (46b) are then solved in a loosely coupled manner (see loosely and fully coupled methods [43]).

To approximate a steady-state solution, we apply a nonlinear multigrid method (see [44]), which is called the Full Approximation Scheme (FAS), to the mean flow equation (46a). The turbulent flow equation (46b) is solved in a single grid mode, only. A multistage diagonally implicit Runge–Kutta method is used as smoother (see [40])

$$\begin{aligned} \textbf{W}^{(0)}:= & {} \textbf{W}^{n}\nonumber \\ \textbf{W}^{(j)}= & {} \textbf{W}^{(0)}- \alpha _{j+1,j} \textbf{P}_{j}\left( \textbf{W}^{(j-1)}\right) ^{-1} \textbf{R}\left( \textbf{W}^{(j-1)}\right) ,\; j = 1,\ldots ,s \end{aligned}$$
(47)
$$\begin{aligned} \textbf{W}^{n+1}= & {} \textbf{W}^{(s)},\nonumber \\ \textbf{P}_j\left( \textbf{W}^{(j-1)}\right):= & {} \left( \Delta T\right) ^{-1}\textbf{M} + \frac{d\textbf{R}}{d\textbf{W}}\left[ \textbf{W}^{(j-1)}\right] ,\, \Delta T:=\text{ diag } \left( \text{ diag }\left( \Delta t_i\right) \right) , \end{aligned}$$
(48)

where we have negelected the subindices mean and turb, and \(\Delta t_i\) denotes the local time step. To apply (47), the linear equation

$$\begin{aligned} \textbf{Prec}_j^{-1}\textbf{P}_j\textbf{x} = \alpha _{j+1,j}\textbf{Prec}_j^{-1}\textbf{R}(\textbf{W}^{(j-1)}). \end{aligned}$$
(49)

needs to be solved. Here, \(\textbf{Prec}_j\) denotes some preconditioner, which is the major ingredient of the algorithm. To find an approximation of (49), we apply a (left) preconditioned GMRES method (see for example [45]) with initial guess \(\textbf{x}^{(0)} = 0\):

  • Solve (approximately) \(\textbf{Prec}_j\textbf{r}_0 = \alpha _{j+1,j}\textbf{R}\left( \textbf{W}^{(j-1)}\right) \)

  • Compute \(\beta := \Vert \textbf{r}_0\Vert _2, \textbf{v}_1:=\frac{1}{\beta }\textbf{r}_0\)

  • for \(k=1,\ldots ,m\)

    • Solve (approximately) \(\textbf{Prec}_j\textbf{w} = \textbf{P}_j\textbf{v}_k\)

    • for \(i=1,\ldots k\)

      \(*\):

      \(h_{i,k}:= \left<\textbf{w},\textbf{v}_i\right>\)

      \(*\):

      \(\textbf{w}:= \textbf{w} - h_{i,k}\textbf{v}_i\)

    • \(h_{k+1,k} = \Vert \textbf{w}\Vert _2, \textbf{v}_{k+1} = \frac{1}{h_{k+1,k}}\textbf{w}\)

  • \(\textbf{V} = \left( \textbf{v}_1,\ldots ,\textbf{v}_m\right) , H_m = \left( h_{i,k}\right) _{1\le i\le k+1, 1\le k \le m}\)

  • Solve \(\textbf{y}_m:=\text{ argmin}_{\textbf{y}} \Vert \beta e_1 - H_m\textbf{y}\Vert _2\) by Given’s-rotations

  • \(\textbf{x}^{(m)}:= \textbf{x}^{(0)} + \textbf{V}_m\textbf{y}_m\)

In the GMRES method, the matrix–vector multiplication of the operator given in (49) applied to a vector is approximated by a finite-difference of the residual operator,

$$\begin{aligned} \frac{d\textbf{R}}{d\textbf{W}}\left( \textbf{W}\right) \textbf{h} \approx \frac{1}{2\epsilon }\left( \textbf{R}\left( \textbf{W} + \epsilon \textbf{h} \right) - \textbf{R}\left( \textbf{W}- \epsilon \textbf{h}\right) \right) . \end{aligned}$$

The choice of a suitable \(\epsilon >0\) is not trivial, as cancellation and approximation errors need to be balanced. A possible method can be found in [42, Chapter 6.2.5].

4.2 Construction of Preconditioner

The preconditioner has two contributions:

  1. (a)

    the linear operator \(\textbf{Prec}_j\) itself,

  2. (b)

    an iterative solution method for approximately solving the linear systems

    $$\begin{aligned} \textbf{Prec}_j\textbf{w} = \textbf{P}_j\textbf{v}_k. \end{aligned}$$
    (50)

For the construction of the linear operators we follow the approach presented in [29, 40]:

$$\begin{aligned} \textbf{Prec}_{j,\mathrm mean}:= & {} \left( \Delta T\right) ^{-1}\textbf{M}_\textrm{mean} + \varepsilon \alpha _{jj}\frac{d\tilde{\textbf{R}}^\textrm{comp}_\textrm{mean}}{d\textbf{W}}, \end{aligned}$$
(51)
$$\begin{aligned} \textbf{Prec}_{j,\mathrm turb}:= & {} \left( \Delta T\right) ^{-1}\textbf{M}_\textrm{turb} + \varepsilon \alpha _{jj}\frac{d\tilde{\textbf{R}}^{\textrm{comp}, \left( k,\omega \right) }_\textrm{turb}}{d\textbf{W}_t}. \end{aligned}$$
(52)

Here, \({d\tilde{\textbf{R}}^\textrm{comp}_\textrm{prec}}/{d\textbf{W}}\) is a linearization of a residual based on a compact discretization scheme. For details of \(\textbf{Prec}_{j,\mathrm mean}\) we refer to [29, 40]. To obtain \(\frac{d\tilde{\textbf{R}}^{\textrm{comp}, \left( k,\omega \right) }_\textrm{turb}}{d\textbf{W}_t}\) the upwind scheme is exactly differentiated. For the derivative of the viscous terms a thin shear layer assumption is assumed for the gradients. The source terms are also exactly differentiated, also the diffusion source terms which typically give entries to the off-diagonal entries of the matrix. But, to realize the preconditioner, the derivatives of the source terms to construct \(\textbf{Prec}_{j,\mathrm turb}\) do not include the destruction terms

$$\begin{aligned} \frac{\partial De_{k,(k,\omega )}}{\partial k_i}\qquad \text{ and }\qquad \frac{\partial De_{\omega ,(k,\omega )}}{\partial \omega _i}. \end{aligned}$$
(53)

The necessity for this modification is discussed in Sect. 5.1. Additionally, the viscosity \(\nu _t\) is also exactly differentiated and the arising terms are completely included. For the Wilcox 1988 model the approach is described in detail in [40, Chapter 4].

4.3 Solving Linear Systems and Truncation Criteria

To realize the preconditioned GMRES method approximately solving (49), we need to define appropriate truncation criteria. To this end, we distinguish two principal implementations of (47):

  1. (M1)

    When the number of GMRES steps is 0 and only the preconditioning step is evaluated,

  2. (M2)

    When the number of GMRES steps is \(> 0\).

To approximately solve (49) for the mean flow equations we follow both strategies M1 and M2:

  • When choosing M1, we apply either at most 250 symmetric Gauss–Seidel sweeps or iterate until

    $$\begin{aligned} \frac{\Vert \textbf{Prec}_j\textbf{r}_0 - \alpha _{j+1,j}\textbf{R}\left( \textbf{W}^{(j-1)}\right) \Vert _2}{\Vert \alpha _{j+1,j}\textbf{R}\left( \textbf{W}^{(j-1)}\right) \Vert _2} < 10^{-2}. \end{aligned}$$

  • When choosing M2, we truncate the GMRES iteration either after at most 20 steps or if

    $$\begin{aligned} \frac{\Vert \textbf{P}_j\textbf{x}^{(m)} - \alpha _{j+1,j} \textbf{R}(\textbf{W}^{(j-1)})\Vert _2}{\Vert \alpha _{j+1,j} \textbf{R}(\textbf{W}^{(j-1)})\Vert _2} < 10^{-2}. \end{aligned}$$

    For approximately solving the linear systems (50), we apply five symmetric Gauss–Seidel sweeps.

4.4 Choice of Time Step

To compute the local time steps \(\Delta t_i\) in (48) for both the mean flow equations and for the turbulence modeling equations, we use an approximation to the spectral radius of the diagonal blocks of \(\frac{d\textbf{R}}{d\textbf{W}}\), that is,

$$\begin{aligned} \Delta t_i:= & {} \text{ CFL }\cdot \text{ vol }\left( D_i\right) \left[ \sum _{j\in \mathcal {N}(i)} \textrm{svol}(e_{ij})\left( \rho \left( \frac{\partial \mathcal {H}^{1st,\textrm{Roe}}}{\partial W_i}\right) \right. \right. \\{} & {} \left. \left. + C_v\rho \left( \frac{\partial \left<f_v\left( W_i, W_j\right) , n_{e_{ij}}\right>}{\partial W_{i}}\right) ^{\textrm{TSL}, \mu =\textrm{const}}\right) \right] ^{-1},\qquad C_{v}:= 8. \end{aligned}$$

The \(\text{ CFL }\) number is chosen according to

$$\begin{aligned} \text{ CFL }= & {} \min \left\{ \text{ CFL}_\textrm{init}\cdot f(n), \text{ CFL}_\textrm{max}\right\} , \end{aligned}$$
(54a)
$$\begin{aligned} f(n)= & {} \left\{ \begin{array}{cc} 1, &{} n < 10,\\ \alpha ^{n-10}, &{} n \ge 10, \end{array} \right. \qquad \alpha > 1. \end{aligned}$$
(54b)

Typical values are \(\text{ CFL}_\textrm{init} = 3\) and \(\text{ CFL}_\textrm{max} = 1000\). For more details we refer to [29, 40, 46].

4.5 Positivity of k and \(\omega \)

To deal with the problem of positivity of k and \(\omega \) we simply introduced a damping of the updates. For example, Algorithm (47) gives for the variables \(k_i\) and \(\omega _i\), \(i=1,\ldots ,N_{elem}\), the updates

$$\begin{aligned} k_i^{(j)}= & {} k_i^{(0)} - \Delta k_i, \end{aligned}$$
(55a)
$$\begin{aligned} \omega _i^{(j)}= & {} \omega _i^{(0)} - \Delta \omega _i, \end{aligned}$$
(55b)

where \((\Delta k_i,\Delta \omega _i)\) denotes the symbol for ith entry of the solution vector that one obtains by evaluating

$$\begin{aligned} \alpha _{j+1,j}\textbf{P}_j^{-1}\textbf{R}\left( \textbf{W}^{(j-1)}\right) . \end{aligned}$$

Direct application of (55) often yields negative values, in particular for k. Most often this is observed for high-lift test cases, but for almost all test cases negative values show up for k and \(\omega \) at least during the starting phase of the iteration. Therefore, we replaced the update (55) by an application of Algorithm 1.

Algorithm 1
figure a

Update for \(k\)-\(\omega \) model

Full size image

Algorithm 1 represents a kind of damped Newton method introducing a further effect of regularization. Expressed in formulae, Algorithm 1 realizes the following condition:

$$\begin{aligned} s_{n,i}^{(k)}= & {} \min _{n\in \mathbb {N}_0}\left\{ \frac{1}{2^n}\right\} \quad \text{ such } \text{ that }\quad k_i^{(j)}> 0,\\ s_{n,i}^{(\omega )}= & {} \min _{n\in \mathbb {N}_0}\left\{ \frac{1}{2^n}\right\} \quad \text{ such } \text{ that }\quad \omega _i^{(j)} > 0. \end{aligned}$$

A side effect of this approach is the fact that the updates may become arbitrarily small, yielding an overall convergence corruption. However, so far, for none of the considered test cases has a stall of convergence been observed. Compared with many others methods tried to ensure positivity of k and \(\omega \), Algorithm 1 was found to be superior with the present implementation. The simplicity of Algorithm 1 is another argument for its use. Nevertheless, Algorithm 1 cannot guarantee convergence. Hence, future work may require focus on other mechanisms to ensure positivity of k and \(\omega \) without reformulating the \(k\)-\(\omega \) model itself. On the other hand, the damping of updates

$$\begin{aligned} k_i^\textrm{new}= & {} k_i^{(0)} - s_n\Delta k_i\\ \omega _i^\textrm{new}= & {} \omega _i^{(0)} - s_n\Delta \omega _i \end{aligned}$$

is not a severe restriction and is justified in the following sense. Using in general (47) to compute the updates, we have

$$\begin{aligned}{} & {} (\Delta k_i, \Delta \omega _i) = \alpha _{j+1,j}\left[ \left( \left( \Delta t\right) ^{-1}\textbf{M} \right. \right. \\{} & {} \quad \left. \left. + \alpha _{jj}\frac{d\textbf{R}}{d\textbf{W}}\left( \textbf{W}^{(j-1)}\right) \right) ^{-1,\textrm{app}}\textbf{R}(\textbf{W}^{(j-1)})\right] _i. \end{aligned}$$

A necessary criterion for convergence is \(\Vert \textbf{R}(\textbf{W}^{(j-1)}\Vert \rightarrow 0\), that is in particular

$$\begin{aligned} \left( \textbf{R}(\textbf{W}^{(j-1)}\right) _i\rightarrow 0. \end{aligned}$$

If the solution of the turbulence modeling equations converges, then at some iterate the updates \(\Delta k_i\) and \(\Delta \omega _i\) are so small that additional damping is not necessary, and at the same time, positivity of k and \(\omega \) is ensured. In this sense, Algorithm 1 is not a severe restriction.

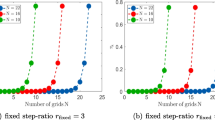
To illustrate the mode of operation of Algorithm 1, a plot of the number of k limitations and \(\omega \) limitations is given in Figs. 1 and 2 for the Wilcox model of 1988 and for the SST model, respectively. To approximate a solution, we performed for each multigrid cycle on the mean flow equations 20 subiterations on the turbulence modeling equations. The number of multigrid cycles is plotted on the upper x-axis, the total number of subiterations on the lower x-axis. From Fig. 1 (left) we can observe that not only the total number of limitations for k goes to zero, but also within each subiteration the number of limitations is significantly reduced. For the Wilcox model of 1988, no limitation of the  \(\omega \) variable is required, which is clearly seen in Fig. 1 (right).

Fig. 1
figure 1

Number of limitations for the 1988 Wilcox \(k\)-\(\omega \) model

Full size image
Fig. 2
figure 2

Number of limitations for the Menter SST model

Full size image

For the considered example, the number of limitations required for the SST-model is significantly smaller. Moreover, Fig. 2 (right) shows that for the SST-model also limitations for \(\omega \) are performed. As expected from considerations above, at some level in convergence the number of limitations for both the k and \(\omega \) variables is 0. This means, that discrete, positive solutions for k and \(\omega \) are obtained. This confirms numerically that the suggested limitation given by Algorithm 1 yields discrete solutions satisfying positivity for k and \(\omega \) if convergence of the equations is observed. However, as long as one of the functions for k or \(\omega \) is locally negative, the algorithm cannot converge.

5 Considerations for the \(k\)-\(\omega \) Model

In this section, at least for some of the heuristics and arguments previously given, we are going to present both an analysis for the linear and nonlinear parts of the solution algorithm.

5.1 Analysis of Linear Part

In Sect. 4.1 it is stated that the derivatives of the destruction terms (53) are neglected for the construction of the preconditioner. To illustrate this necessity, we use that the splitting method

$$\begin{aligned} x_{m+1} = Mx_m + Nb \end{aligned}$$

converges if and only if \(\rho (M) < 1\) (see e.g. [47]). For the Jacobi and Gauss–Seidel method the iteration matrix M is given by

$$\begin{aligned} M_\textrm{Jac} = D^{-1}\left( D - A\right) \qquad \text{ and }\qquad M_\textrm{GS} = -\left( D+L\right) ^{-1}R. \end{aligned}$$

Using Arnoldi’s method, as in the inner part of the GMRES method [29, 31], we can aproximate the spectrum of these operators for the preconditioner (52), including and neglecting (53). Figures 3 and 4 show the approximated eigenvalue distributions at the beginning and end of a nonlinear iteration, respectively. For each Figure, (53) is included on the left and excluded on the right. In particular, at the beginning of the iteration an inclusion of (53) changes the spectrum of the iteration matrices such that convergence of both the Gauss–Seidel and the Jacobi methods is not possible, whereas exclusion of (53) gives a converging method. For the final state the situation improves, but as one can observe in Fig. 4 (left), there are still a few approximate eigenvalues outside the range of stability. Hence, for the overall nonlinear iteration process it is necessary and beneficial to neglect (53). Moreover, when comparing the spectra of the Jacobi and the Gauss–Seidel methods, we observe a more equally distributed one for the latter one.

Fig. 3
figure 3

Eigenvalue distribution of Jacobi and Gauss–Seidel method in the beginning of nonlinear iteration

Full size image
Fig. 4
figure 4

Eigenvalue distribution of Jacobi and Gauss–Seidel method for the final nonlinear iteration

Full size image

5.2 Analysis of Nonlinear Part

To understand if we can expect convergence of the solution for the turbulence modeling equations for the outer nonlinear iteration, at least in a small neighborhood of a solution \(\left( \textbf{W}^{\dagger },\textbf{W}_t^{\dagger }\right) \), for example,

$$\begin{aligned} \textbf{R}_\textrm{turb}\left( \textbf{W}_t^{\dagger }, \textbf{W}^{\dagger }\right) = 0. \end{aligned}$$

We assume a small perturbation, that is, \(\left\| \textbf{W}_t\right\| <\epsilon \) of \(\textbf{W}_t^{\dagger }\). Using a Taylor series expansion and neglecting terms of higher order, we approximate

$$\begin{aligned} \frac{d \textbf{W}(t)}{dt}= & {} \frac{d \left( \textbf{W}^{\dagger } + \textbf{W}(t) \right) }{dt} = -\textbf{M}^{-1}\textbf{R}\left( \textbf{W}^{\dagger } + \textbf{W} \right) \\\approx & {} -\textbf{M}^{-1}\left( \textbf{R}\left( \textbf{W}^{\dagger }\right) + \frac{d\textbf{R}}{d\textbf{W}}\left( \textbf{W}^{\dagger }\right) \textbf{W}\right) \\= & {} -\textbf{M}^{-1}\textbf{A} \textbf{W}(t),\qquad \textbf{A}:=\frac{d\textbf{R}}{d\textbf{W}}\left( \textbf{W}^{\dagger }\right) . \end{aligned}$$
Fig. 5
figure 5

Range of stability for multistage schemes and approximate spectrum for two equation \(k\)-\(\omega \) model of CASE 9

Full size image

Then, the update of the multistage Runge–Kutta scheme (47) can be expressed by a polynomial expression,

$$\begin{aligned} \textbf{W}^{n+1}= & {} q_s\left( \textbf{Prec}^{-1, \mathrm app} \textbf{A}\right) \textbf{W}^{n},\nonumber \\ q_s(z)= & {} 1 + \sum _{j=1}^s(-1)^{j}z^j\Pi _{i=s - j + 1}^s{\alpha _{i+1,i}}. \end{aligned}$$
(56)

Thus, the multistage Runge–Kutta scheme (47) is stable, that is, it defines a contracting operator in a linear sense for all \(z\in \mathbb {C}\), if \(|q_s(z)| < 1\).

To compute approximations to the eigenvalues of \(\textbf{P}^{-1, \mathrm app}\textbf{A}\), we again exploit the GMRES method and its connection to the Arnoldi process (see [29, 31]). As a test case, we consider Case 9 from the experiments of Cook, McDonald and Firmin [48] and a \(320\times 64\) C-type mesh. This mesh is a member of a family of meshes used later in Sect. 6 on Numerical Examples. To transform the spectrum we restrict ourselves to the one-stage scheme with coefficients \(\alpha _{21} = 1.0\), the three-stage scheme with coefficients \(\alpha _{21}=0.15\), \(\alpha _{32}=0.4\), \(\alpha _{43}=1\) and the five-stage scheme with coefficients \(\alpha _{21}=0.0695\), \(\alpha _{32}=0.1602\), \(\alpha _{43}=0.2898\), \(\alpha _{54}=0.5060\) and \(\alpha _{65}=1.0\) (see [25]). Figure 5 shows the range of stability of these multistage schemes together with the approximate spectrum. For this test case and for both the three-stage and the five-stage schemes, we can expect a stable method, whereas the one stage scheme is expected to diverge.

6 Numerical Examples

To demonstrate the applicability of the suggested algorithms, we consider some standard 2-D and challenging 3-D test cases, which have been computed frequently in the literature. The 2-D cases are transonic flows over an airfoil. The 3-D cases include relatively low-speed flow over a wing-body geometry at a high angle of attack and transonic flow over a wing-body configuration. For the 2-D cases, we consider both the Wilcox and SST \(k\)-\(\omega \) models. The SST model is used in the 3-D computations. The density residual is evaluated by

$$\begin{aligned} \text{ Density } \text{ residual }(n):= & {} \sqrt{\sum _{j=1}^{N_{elem}}\frac{\left( \textbf{R}_{j, \mathrm mean, \rho }\left( \textbf{W}^\mathrm{T_n}\right) \right) ^2}{(\text{ vol }(\Omega _j))^2}}/ \sqrt{\sum _{j=1}^{N_{elem}} \frac{\left( \textbf{R}_{j, \mathrm mean, \rho }\left( \textbf{W}_{\infty }\right) \right) ^2}{(\text{ vol }(\Omega _j))^2}}, \end{aligned}$$

for \(k\)-\(\omega \) model we evaluate both corresponding residuals

$$\begin{aligned} k-\text{ residual }(n):= & {} \sqrt{\sum _{j=1}^{N_{elem}}\frac{\left( \textbf{R}_{j,\textrm{turb},k}\left( k^\mathrm{T_n},\omega ^\mathrm{T_n}\right) \right) ^2}{(\text{ vol }(\Omega _j))^2}} / \sqrt{\sum _{j=1}^{N_{elem}} \frac{\left( \textbf{R}_{j,\textrm{turb},k}\left( k_{\infty },\omega _{\infty }\right) \right) ^2}{(\text{ vol }(\Omega _j))^2}},\\ \omega -\text{ residual }(n):= & {} \sqrt{\sum _{j=1}^{N_{elem}}\frac{\left( \textbf{R}_{j,\textrm{turb},\omega }\left( k^\mathrm{T_n},\omega ^\mathrm{T_n}\right) \right) ^2}{(\text{ vol }(\Omega _j))^2}} / \sqrt{\sum _{j=1}^{N_{elem}} \frac{\left( \textbf{R}_{j,\textrm{turb},\omega }\left( k_{\infty },\omega _{\infty }\right) \right) ^2}{(\text{ vol }(\Omega _j))^2}}. \end{aligned}$$

To satisfy near machine zero, a computation is truncated, and the result is accepted as soon as \(\text{ density } \text{ residual }(n) < 10^{-14}\). The computations on unstructured grids were performed in parallel using MPI and either the \(\mathrm {C^2}{A^2}{S^2}{E^2}\) or CARA cluster of DLR.

6.1 RAE 2822 Airfoil

The first examples considered correspond to the RAE 2822 airfoil. These examples have been chosen because they are frequently considered when attempting to validate turbulence models. There are two cases, Case 9 and Case 10, for transonic flow over the RAE 2822 airfoil [48]. The flow conditions for these cases are given in Table 1. In Case 9 there is a fairly strong shock wave occurring on the upper surface of the airfoil, whereas in Case 10 there is a sufficiently strong shock on the upper surface to cause significant separation of the flow behind the shock.

We perform the computations on a sequence of C-type structured meshes described in Table 2. The meshes have a C-type topology. The finest mesh consists of 1280 cells around the airfoil (1024 cells on the airfoil) and 256 cells in normal direction. The normal mesh spacing at the surface of the finest mesh is approximately \(3 \times 10^{-6}\), and the maximum surface cell aspect ratio is about 560.

Table 1 Flow Conditions for RAE 2822 airfoil
Full size table
Table 2 Mesh data for RAE 2822 airfoil
Full size table
Table 3 Case 9: Computed lift and drag coefficients with 1988 \(k\)-\(\omega \) model
Full size table
Table 4 Case 9: Computed lift and drag coefficients with SST model
Full size table
Table 5 Case 10: Computed lift and drag coefficients with 1988 \(k\)-\(\omega \) model
Full size table
Table 6 Case 10: Computed lift and drag coefficients with SST model
Full size table

The initial numerical calculations for the two RAE 2822 cases were performed with the complete solution algorithm of this paper, which includes agglomerative multigrid and GMRES, in the framework of an unstructured grid computer code. Tables 3, 4, 5, 6 include the predicted lift and total drag coefficients, including the pressure and skin-friction contributions. In Figs. 6, 7, 8 and 9, convergence histories using the 1988 version of the Wilcox \(k\)-\(\omega \) and the 2003 Menter SST turbulence models are presented. The final plots, which are included in Fig. 10, show the computed surface pressure distributions for the two RAE cases compared with the experimental data of Cook, McDonald and Firman [48].

Fig. 6
figure 6

Convergence histories of solution computed for turbulent flow over RAE 2822 airfoil (Case 9). The effects of turbulence are represented with the Wilcox k-\(\omega \) model (1988). A family of grids is considered: \(320 \times 64\), \(640 \times 128\), and \(1280 \times 256\) cells. a Mean flow equations, b k-\(\omega \) equations. (unstructured grid code)

Full size image
Fig. 7
figure 7

Convergence histories of solution computed for turbulent flow over RAE 2822 airfoil (Case 10). The effects of turbulence are represented with the Wilcox k-\(\omega \) model (1988). A family of grids is considered: \(320 \times 64\), \(640 \times 128\), and \(1280 \times 256\) cells. a Mean flow equations, b k-\(\omega \) equations. (unstructured grid code)

Full size image
Fig. 8
figure 8

Convergence histories of solution computed for turbulent flow over RAE 2822 airfoil (Case 9). The effects of turbulence are represented with the Menter SST model (2003). A family of grids is considered: \(320 \times 64\), \(640 \times 128\), and \(1280 \times 256\) cells. a mean flow equations, b k-\(\omega \) equations. (unstructured grid code)

Full size image
Fig. 9
figure 9

Convergence histories of solution computed for turbulent flow over RAE 2822 airfoil (Case 10). The effects of turbulence are represented with the Menter SST model (2003). A family of grids is considered: \(320 \times 64\), \(640 \times 128\), and \(1280 \times 256\) cells. a Mean flow equations, b k-\(\omega \) equations (unstructured grid code)

Full size image
Fig. 10
figure 10

\(C_p-\)distribution for Case 9 and Case 10 and comparison with experimental data

Full size image
Fig. 11
figure 11

Convergence histories of solution computed for turbulent flow over RAE 2822 airfoil (Case 9). The effects of turbulence are represented with the Wilcox k-\(\omega \) model (2006). A family of grids is considered: \(320 \times 64\), \(640 \times 128\), and \(1280 \times 256\) cells. a Mean flow equations, b k-\(\omega \) equations. (structured grid code)

Full size image
Fig. 12
figure 12

Convergence histories of solution computed for turbulent flow over RAE 2822 airfoil (Case 10). The effects of turbulence are represented with the Wilcox k-\(\omega \) model (2006). A family of grids is considered: \(320 \times 64\), \(640 \times 128\), and \(1280 \times 256\) cells. a Mean flow equations, b k-\(\omega \) equations. (structured grid code)

Full size image
Fig. 13
figure 13

Convergence histories of solution computed for turbulent flow over RAE 2822 airfoil (Case 9). The effects of turbulence are represented with the Menter SST model (2003). A family of grids is considered: \(320 \times 64\), \(640 \times 128\), and \(1280 \times 256\) cells. a mean flow equations, b k-\(\omega \) equations. (structured grid code)

Full size image

In the second set of results for Cases 9 and 10, the numerical computations were performed using the core of the solution algorithm described previously in the framework of a structured grid computer code. Results are for both the 2006 version of the Wilcox \(k\)-\(\omega \) and the 2003 Menter SST turbulence models. The convergence history results from these calculations are displayed in Figs. 11, 12, 13, 14. As shown in these figures, the residuals for both the RANS equations and the transport equations of the turbulence models indicate a consistent, reliable linear convergence rate and solutions are attained in only 125 to 150 multigrid cycles. Additional discussion of applications of the structured grid code are given in [13].

6.2 Transonic Turbulent Flow over a Common Research Model

The next test case is the first of the two 3-D flow computations in this paper. This first case is turbulent flow over the Common Research Model (CRM). It was considered at the fifth AIAA Drag Prediction Workshop. The meshes provided by the workshop are block-structured. A sequence of hybrid meshes was generated from the pure hexahedral meshes. Table 7 provides information about the grids used in the computations. The relevant physical conditions for this case are also given. The computed lift and drag coefficients as well as computational times for both mesh sequences are given in Table 8. There is a detailed description of the meshes given in [49]. The computations were performed on DLR’s \(\text{ C}^2\text{ A}^2\text{ S}^2E\) cluster. For the L4, L3, L2, and L1 meshes, we used 192, 72, 48 and 24 domains, resp. This corresponds to about 92000 , 71000,  46000 and 28000 mesh points per domain.

  • Geometry: Wing-body configuration, fifth AIAA Drag Prediction Workshop

  • Reynolds number: \(Re = 5.0\cdot 10^6\)

  • Inflow Mach number: \(M_{\infty } = 0.85\)

  • Angle of attack 2.15°

It should be pointed out that it is difficult to find reports in the literature in which systematic mesh refinement studies together with two-equation turbulence models (e.g., the SST-model) are shown for 3-D turbulent flows and the solution algorithm shows a consistent and reliable convergence behavior. In this paper the objective is not to perform extensive mesh refinement studies and attempt to evaluate accuracy, but rather to demonstrate that the algorithm presented is effective in reducing residuals well below the truncation error of the numerical algorithm.

Figure 15 shows the convergence histories for the sequence of meshes for the considered test case. Application of the algorithm presented in Sect. 4 made it possible to reach similar consistent convergence behavior for both the hexahedral and hybrid sequence of meshes and the stoppig criterion was met in only a few hundred multigrid cycles. In Fig. 16, the surface \(C_p\) distribution for the Common Research Model using hybrid and hexahedral meshes is displayed.

Fig. 14
figure 14

Convergence histories of solution computed for turbulent flow over RAE 2822 airfoil (Case 10). The effects of turbulence are represented with the Menter SST model (2003). A family of grids is considered: \(320 \times 64\), \(640 \times 128\), and \(1280 \times 256\) cells. a Mean flow equations, b k-\(\omega \) equations. (structured grid code)

Full size image
Table 7 Mesh data for DPW5 CRM
Full size table
Table 8 lift and drag coefficient for CRM and SST model and computational times
Full size table
Fig. 15
figure 15

Convergence histories for DPW5 CRM and SST-model

Full size image
Fig. 16
figure 16

Surface \(C_p\) distribution for DPW5 CRM and SST-model on L4 hybrid and hexahedral mesh

Full size image

6.3 NASA TRAP Wing

As a final example, to investigate the behavior of the proposed solution algorithm towards the incompressible limit, we examine the NASA Trap Wing considered at the first AIAA High-Lift prediction workshop [5]. For this test case, the importance of an adequate low-speed preconditioner for the governing flow equations must be emphasized, as there are low-speed regions as well as regions in which the flow is significantly accelerated. The low-speed preconditioner applied in this algorithm has a numerical dissipation that is a function of the local Mach number (see [50] for details).

For the numerical computations, we used two meshes. The meshes were generated using VGrid and are marked as UH6 in Table 2 of [5]. Characteristics of these meshes are given in Table 9. Figure 17 provides a sense of the gridpoint distribution on the wing-body surface and symmetry plane for Grid 2. In addition, this figure shows the eddy viscosity contours corresponding to this grid on the symmetry plane.

Table 9 NASA TRAP Wing: Mesh data
Full size table
Fig. 17
figure 17

Left: Grid of NASA Trap Wing; Right: Computed eddy viscosity in the symmetry plane with the SST model

Full size image
Fig. 18
figure 18

Convergence histories of mean flow and turbulent flow equations for the NASA Trap Wing and the SST  model

Full size image

The flow conditions for this 3-D example are given by

  • Geometry: NASA TRAP Wing

  • Reynolds number: \(Re = 4.3\cdot 10^6\)

  • Inflow Mach number: \(M_{\infty } = 0.2\)

  • Angle of attack 28°

The high angle of attack (\(\alpha \)) is an especially important flow condition, due to the numerical challenge that it represents in achieving a fully converged solution, as evident in the literature. In addition, high \(\alpha \) aerodynamics can introduce numerous complexities into the flow field, including recirculation, vortical flow regions and various strong viscous types ofinteractions. Convergence histories for these computations with the SST model are displayed in Fig. 18. As in the results for the previous examples, these histories also exhibit near machine zero convergence.

7 Concluding Remarks

In this paper an effective numerical algorithm for solving the RANS equations and the two transport equations of \(k\)-\(\omega \) type turbulence models has been presented. The integral form of the RANS and k-\(\omega \) equations along with the corresponding boundary conditions for a well defined boundary-value problem have been presented and described. Details of the k-\(\omega \) type two-equation models, which include all elements exactly as implemented, have been given.

It is important to emphasize that the two-equation models considered in the paper have been implemented according to the original papers of Wilcox [32, 34] and Menter [37]. Consequently, there are no additional limiters on the dependent variables, which are often used in the application of the models and not discussed. Furthermore, there are no realizability conditions being imposed, as seen in some finite-element methods (e.g., [21, 22]), which use a logarithmic variable substitution. While one can certainly argue that changing the turbulence model for the purpose of what one can call numerical compatibility is appropriate, from the viewpoint of this paper, this should only be acceptable if the integrity of the model is not compromised.

To demonstrate the effectiveness and capability of the numerical solution algorithm, several examples of aerodynamic applications have been presented. Both 2-D and 3-D flows have been considered with varying degrees of difficulties due to the complexity of the turbulent flows being considered. In all cases, the convergence histories have been shown. The computed lift and drag coefficients have also been given.

An analysis of the numerical algorithm is addressed, which reflects some of the properties and stability of the solution algorithm. An approximate eigenspectrum of the preconditioner for the inner part of the GMRES method has been determined using Arnoldi’s method. The impact of the destruction terms, which are part of the source terms of a two-equation turbulence model, using Jacobi and Gauss–Seidel methods has been presented. Neglecting these terms in the Jacobian of the implicit preconditioner is necessary, in general, and highly beneficial. The distribution of the eigenvalues of the amplification matrix has been obtained for two-stage, three-stage and five-stage Runge–Kutta schemes with the implicit preconditioner. The advantage of the present technique with respect to local mode analysis [51] is that the stability is determined for a specific problem being solved.

As a final remark, in Sects. 3.3 and 3.4 the incompressible version of the considered models was introduced and finally implemeneted. When comparing with results from other codes using the original compressible version of the models for subsonic and transonic flow cases, no major differences between the results were observed. However, at the outset there seem to be no obvious obstacles to apply the methods proposed in this article also directly to the compressible version of the models. Future work will address how the methods proposed here can be directly applied to these compressible versions.