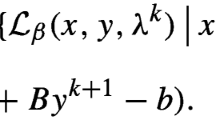Abstract
In this paper we consider from two different aspects the proximal alternating direction method of multipliers (ADMM) in Hilbert spaces. We first consider the application of the proximal ADMM to solve well-posed linearly constrained two-block separable convex minimization problems in Hilbert spaces and obtain new and improved non-ergodic convergence rate results, including linear and sublinear rates under certain regularity conditions. We next consider the proximal ADMM as a regularization method for solving linear ill-posed inverse problems in Hilbert spaces. When the data is corrupted by additive noise, we establish, under a benchmark source condition, a convergence rate result in terms of the noise level when the number of iterations is properly chosen.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The alternating direction method of multipliers (ADMM) was introduced and developed in the 1970 s by Glowinski and Marrocco [16] and Gabay and Mercier [15] for the numerical solutions of partial differential equations. Due to its decomposability and superior flexibility, ADMM and its variants have gained renewed interest in recent years and have been widely used for solving large-scale optimization problems that arise in signal/image processing, statistics, machine learning, inverse problems and other fields, see [5, 17, 21]. Because of their popularity, many works have been devoted to the analysis of ADMM and its variants, see [5, 8, 10, 14, 19, 26, 33] for instance. In this paper we will devote to deriving convergence rates of ADMM in two aspects: its applications to solve well-posed convex optimization problems and its use to solve linear ill-posed inverse problems as a regularization method.
In the first part of this paper we consider ADMM for solving linearly constrained two-block separable convex minimization problems. Let \(\mathcal X\), \(\mathcal Y\) and \(\mathcal Z\) be real Hilbert spaces with possibly infinite dimensions. We consider the convex minimization problem of the form
where \(c \in \mathcal Z\), \(A: \mathcal X\rightarrow \mathcal Z\) and \(B: \mathcal Y\rightarrow \mathcal Z\) are bounded linear operators, and \(f: \mathcal X\rightarrow (-\infty , \infty ]\) and \(g: \mathcal Y\rightarrow (-\infty , \infty ]\) are proper, lower semi-continuous, convex functions. The classical ADMM solves (1.1) approximately by constructing an iterative sequence via alternatively minimizing the augmented Lagrangian function
with respect to the primal variables x and y and then updating the dual variable \(\lambda \); more precisely, starting from an initial guess \(y^0\in \mathcal Y\) and \(\lambda ^0\in \mathcal Z\), an iterative sequence \(\{(x^k, y^k, \lambda ^k)\}\) is defined by
where \(\rho >0\) is a given penalty parameter. The implementation of (1.2) requires to determine \(x^{k+1}\) and \(y^{k+1}\) by solving two convex minimization problems during each iteration. Although f and g may have special structures so that their proximal mappings are easy to be determined, solving the minimization problems in (1.2) in general is highly nontrivial due to the appearance of the terms \(\Vert A x\Vert ^2 \) and \(\Vert B y\Vert ^2\). In order to avoid this implementation issue, one may consider to add certain proximal terms to the x-subproblem and y-subproblem in (1.2) to remove the terms \(\Vert A x\Vert ^2\) and \(\Vert B y\Vert ^2\). For any bounded linear positive semi-definite self-adjoint operator D on a real Hilbert space \(\mathcal H\), we will use the notation
By taking two bounded linear positive semi-definite self-adjoint operators \(P: \mathcal X\rightarrow \mathcal X\) and \(Q: \mathcal Y\rightarrow \mathcal Y\), we may add the terms \(\frac{1}{2} \Vert x-x^k\Vert _P^2\) and \(\frac{1}{2} \Vert y-y^k\Vert _Q^2\) to the x- and y-subproblems in (1.2) respectively to obtain the following proximal alternating direction method of multipliers ([4, 9, 19, 20, 22, 33])
The advantage of (1.3) over (1.2) is that, with wise choices of P and Q, it is possible to remove the terms \(\Vert A x\Vert ^2\) and \(\Vert B y\Vert ^2\) and thus make the determination of \(x^{k+1}\) and \(y^{k+1}\) much easier.
In recent years, various convergence rate results have been established for ADMM and its variants in either ergodic or non-ergodic sense. In [19, 25] the ergodic convergence rate
has been derived in terms of the objective error and the constraint error, where \(H_*\) denotes the minimum value of (1.1), k denotes the number of iterations, and
denote the ergodic iterates of \(\{x^k\}\) and \(\{y^k\}\) respectively; see also [4, Theorem 15.4]. A criticism on ergodic result is that it may fail to capture the feature of the sought solution of the underlying problem because ergodic iterate has the tendency to average out the expected property and thus destroy the feature of the solution. This is in particular undesired in sparsity optimization and low-rank learning. In contrast, the non-ergodic iterate tends to share structural properties with the solution of the underlying problem. Therefore, the use of non-ergodic iterates becomes more favorable in practice. In [20] a non-ergodic convergence rate has been derived for the proximal ADMM (1.3) with \(Q=0\) and the result reads as
By exploiting the connection with the Douglas-Rachford splitting algorithm, the non-ergodic convergence rate
in terms of the objective error and the constraint error has been established in [8] for the ADMM (1.2) and an example has been provided to demonstrate that the estimates in (1.6) are sharp. However, the derivation of (1.6) in [8] relies on some unnatural technical conditions involving the convex conjugate of f and g, see Remark 2.1. Note that the estimate (1.5) implies the second estimate in (1.6), however it does not imply directly the first estimate in (1.6). In Sect. 2 we will show, by a simpler argument, that similar estimate as in (1.5) can be established for the proximal ADMM (1.3) with arbitrary positive semi-definite Q. Based on this result and some additional properties of the method, we will further show that the non-ergodic rate (1.6) holds for the proximal ADMM (1.3) with arbitrary positive semi-definite P and Q. Our result does not require any technical conditions as assumed in [8].
In order to obtain faster convergence rates for the proximal ADMM (1.3), certain regularity conditions should be imposed. In finite dimensional situation, a number of linear convergence results have been established. In [9] some linear convergence results of the proximal ADMM have been provided under a number of scenarios involving the strong convexity of f and/or g, the Lipschitz continuity of \(\nabla f\) and/or \(\nabla g\), together with further full row/column rank assumptions on A and/or B. Under a bounded metric subregularity condition, in particular under the assumption that both f and g are convex piecewise linear-quadratic functions, a global linear convergence rate has been established in [32] for the proximal ADMM (1.3) with
where \(A^*\) and \(B^*\) denotes the adjoints of A and B respectively; the condition (1.7) plays an essential role in the convergence analysis in [32]. We will derive faster convergence rates for the proximal ADMM (1.3) in the general Hilbert space setting. To this end, we need first to consider the weak convergence of \(\{(x^k, y^k, \lambda ^k)\}\) and demonstrate that every weak cluster point of this sequence is a KKT point of (1.1). This may not be an issue in finite dimensions. However, this is nontrivial in infinite dimensional spaces because extra care is required to dealing with weak convergence. In [6] the weak convergence of the proximal ADMM (1.3) has been considered by transforming the method into a proximal point method and the result there requires restrictive conditions, see [6, Lemma 3.4 and Theorem 3.1]. These restrictive conditions have been weakened later in [31] by using machinery from the maximal monotone operator theory. We will explore the structure of the proximal ADMM and show by an elementary argument that every weak cluster point of \(\{(x^k, y^k, \lambda ^k)\}\) is indeed a KKT point of (1.1) without any additional conditions. We will then consider the linear convergence of the proximal ADMM under a bounded metric subregularity condition and obtain the linear convergence for any positive semi-definite P and Q; in particular, we obtain the linear convergence of \(|H(x^k, y^k) - H_*|\) and \(\Vert A x^k + B y^k - c\Vert \). We also consider deriving convergence rates under a bounded Hölder metric subregularity condition which is weaker than the bounded metric subregularity. This weaker condition holds if both f and g are semi-algebraic functions and thus a wider range of applications can be covered. We show that, under a bounded Hölder metric subregularity condition, among other things the convergence rates in (1.6) can be improved to
for some number \(\beta >1/2\); the value of \(\beta \) depends on the properties of f and g. To further weaken the bounded (Hölder) metric subregularity assumption, we introduce an iteration based error bound condition which is an extension of the one in [27] to the general proximal ADMM (1.3). It is interesting to observe that this error bound condition holds under any one of the scenarios proposed in [9]. Hence, we provide a unified analysis for deriving convergence rates under the bounded (Hölder) metric subregularity or the scenarios in [9]. Furthermore, we extend the scenarios in [9] to the general Hilbert space setting and demonstrate that some conditions can be weakened and the convergence result can be strengthened; see Theorem 2.11.
In the second part of this paper, we consider using ADMM as a regularization method to solve linear ill-posed inverse problems in Hilbert spaces. Linear inverse problems have a wide range of applications, including medical imaging, geophysics, astronomy, signal processing, and more [12, 18, 28]. We consider linear inverse problems of the form
where \(A: \mathcal X\rightarrow \mathcal H\) is a compact linear operator between two Hilbert spaces \(\mathcal X\) and \(\mathcal H\), \(\mathcal C\) is a closed convex set in \(\mathcal X\), and \(b \in \text{ Ran }(A)\), the range of A. In order to find a solution of (1.8) with desired properties, a priori available information on the sought solution should be incorporated into the problem. Assume that, under a suitable linear transform L from \(\mathcal X\) to another Hilbert spaces \(\mathcal Y\) with domain \(\text{ dom }(L)\), the feature of the sought solution can be captured by a proper convex penalty function \(f: \mathcal Y\rightarrow (-\infty , \infty ]\). One may consider instead of (1.8) the constrained optimization problem
A challenging issue related to the numerical resolution of (1.9) is its ill-posedness in the sense that the solution of (1.9) does not depend continuously on the data and thus a small perturbation on data can lead to a large deviation on solutions. In practical applications, the exact data b is usually unavailable, instead only a noisy data \(b^\delta \) is at hand with
for some small noise level \(\delta >0\). To overcome ill-posedness, regularization methods should be introduced to produce reasonable approximate solutions; one may refer to [7, 12, 23, 29] for various regularization methods.
The common use of ADMM to solve (1.9) with noisy data \(b^\delta \) first considers the variational regularization
then uses the splitting technique to rewrite (1.10) into the form (1.1), and finally applies the ADMM procedure to produce approximate solutions. The parameter \(\alpha >0\) is the so-called regularization parameter which should be adjusted carefully to achieve reasonable good performance; consequently one has to run ADMM to solve (1.10) for many different values of \(\alpha \), which can be time consuming.
In [21, 22] the ADMM has been considered to solve (1.9) directly to reduce the computational load. Note that (1.9) can be written as
where \(\iota _{\mathcal C}\) denotes the indicator function of \(\mathcal C\). With the noisy data \(b^\delta \) we introduce the augmented Lagrangian function
where \(\rho _1\), \(\rho _2\) and \(\rho _3\) are preassigned positive numbers. The proximal ADMM proposed in [22] for solving (1.9) then takes the form
where Q is a bounded linear positive semi-definite self-adjoint operator. The method (1.11) is not a 3-block ADMM. Note that the variables y and x are not coupled in \({\mathscr {L}}_{\rho _1, \rho _2, \rho _3}(z, y, x, \lambda , \mu , \nu )\). Thus, \(y^{k+1}\) and \(x^{k+1}\) can be updated simultaneously, i.e.
This demonstrates that (1.11) is a 2-block proximal ADMM.
It should be highlighted that all well-established convergence results on proximal ADMM for well-posed optimization problems are not applicable to (1.11) directly. Note that (1.11) uses the noisy data \(b^\delta \). If the convergence theory for well-posed optimization problems could be applicable, one would obtain a solution of the perturbed problem
of (1.9). Because A is compact, it is very likely that \(b^\delta \not \in \text{ Ran }(A^*)\) and thus (1.12) makes no sense as the feasible set is empty. Even if \(b^\delta \in \text{ Ran }(A^*)\) and (1.12) has a solution, this solution could be far away from the solution of (1.9) because of the ill-posedness.
Therefore, if (1.11) is used to solve (1.9), better result can not be expected even if larger number of iterations are performed. In contrast, like all other iterative regularization methods, when (1.11) is used to solve (1.9), it shows the semi-convergence property, i.e., the iterate becomes close to the sought solution at the beginning; however, after a critical number of iterations, the iterate leaves the sought solution far away as the iteration proceeds. Thus, properly terminating the iteration is important to produce acceptable approximate solutions. One may hope to determine a stopping index \(k_\delta \), depending on \(\delta \) and/or \(b^\delta \), such that \(\Vert x^{k_\delta }-x^\dag \Vert \) is as small as possible and \(\Vert x^{k_\delta }-x^\dag \Vert \rightarrow 0\) as \(\delta \rightarrow 0\), where \(x^\dag \) denotes the solution of (1.9). This has been done in our previous work [21, 22] in which early stopping rules have been proposed for the method (1.11) to render it into a regularization method and numerical results have been reported to demonstrate the nice performance. However, the work in [21, 22] does not provide convergence rates, i.e. the estimate on \(\Vert x^{k_\delta } - x^\dag \Vert \) in terms of \(\delta \). Deriving convergence rates for iterative regularization methods involving general convex regularization terms is a challenging question and only a limited number of results are available. In order to derive a convergence rate of a regularization method for ill-posed problems, certain source condition should be imposed on the sought solution. In Sect. 3, under a benchmark source condition on the sought solution, we will provide a partial answer to this question by establishing a convergence rate result for (1.11) if the iteration is terminated by an a priori stopping rule.
We conclude this section with some notation and terminology. Let \(\mathcal V\) be a real Hilbert spaces. We use \(\langle \cdot , \cdot \rangle \) and \(\Vert \cdot \Vert \) to denote its inner product and the induced norm. We also use “\(\rightarrow \)" and “\(\rightharpoonup \)" to denote the strong convergence and weak convergence respectively. For a function \(\varphi : \mathcal V\rightarrow (-\infty , \infty ]\) its domain is defined as \(\text{ dom }(\varphi ):= \{x\in \mathcal V: \varphi (x) <\infty \}\). If \(\text{ dom }(\varphi )\ne \emptyset \), \(\varphi \) is called proper. For a proper convex function \(\varphi : \mathcal V\rightarrow (-\infty , \infty ]\), its modulus of convexity, denoted by \(\sigma _\varphi \), is defined to be the largest number c such that
for all \(x, y \in \text{ dom }(\varphi )\) and \(0\le t\le 1\). We always have \(\sigma _\varphi \ge 0\). If \(\sigma _\varphi >0\), \(\varphi \) is called strongly convex. For a proper convex function \(\varphi : \mathcal V\rightarrow (-\infty , \infty ]\), we use \(\partial \varphi \) to denote its subdifferential, i.e.
Let \(\text{ dom }(\partial \varphi ):=\{x\in \mathcal V: \partial \varphi (x) \ne \emptyset \}\). It is easy to see that
for all \(y\in \mathcal V\), \(x\in \text{ dom }(\partial \varphi )\) and \(\xi \in \partial \varphi (x)\) which in particular implies the monotonicity of \(\partial \varphi \), i.e.
for all \(x, y \in \text{ dom }(\partial \varphi )\), \(\xi \in \partial \varphi (x)\) and \(\eta \in \partial \varphi (y)\).
2 Proximal ADMM for Convex Optimization Problems
In this section we will consider the proximal ADMM (1.3) for solving the linearly constrained convex minimization problem (1.1). For the convergence analysis, we will make the following standard assumptions.
Assumption 1
\(\mathcal X\), \(\mathcal Y\) and \(\mathcal Z\) are real Hilbert spaces, \(A: \mathcal X\rightarrow \mathcal Z\) and \(B: \mathcal Y\rightarrow \mathcal Z\) are bounded linear operators, \(P: \mathcal X\rightarrow \mathcal X\) and \(Q: \mathcal Y\rightarrow \mathcal Y\) are bounded linear positive semi-definite self-adjoint operators, and \(f: \mathcal X\rightarrow (-\infty , \infty ]\) and \(g: \mathcal Y\rightarrow (-\infty , \infty ]\) are proper, lower semi-continuous, convex functions.
Assumption 2
The problem (1.1) has a Karush-Kuhn-Tucker (KKT) point, i.e. there exists \((\bar{x}, \bar{y}, \bar{\lambda }) \in \mathcal X\times \mathcal Y\times \mathcal Z\) such that
It should be mentioned that, to guarantee the proximal ADMM (1.3) to be well-defined, certain additional conditions need to be imposed to ensure that the x- and y-subproblems do have minimizers. Since the well-definedness can be easily seen in concrete applications, to make the presentation more succinct we will not state these conditions explicitly.
By the convexity of f and g, it is easy to see that, for any KKT point \((\bar{x}, \bar{y}, \bar{\lambda })\) of (1.1), there hold
Adding these two equations and using \(A \bar{x}+ B\bar{y}-c =0\), it follows that
This in particular implies that \((\bar{x}, \bar{y})\) is a solution of (1.1) and thus \(H_*:= H(\bar{x}, \bar{y})\) is the minimum value of (1.1).
Based on Assumptions 1 and 2 we will analyze the proximal ADMM (1.3). For ease of exposition, we set \(\widehat{Q}:= \rho B^* B + Q\) and define
which is a bounded linear positive semi-definite self-adjoint operator on \(\mathcal X\times \mathcal Y\times \mathcal Z\). Then, for any \(u:=(x, y,\lambda ) \in \mathcal X\times \mathcal Y\times \mathcal Z\) we have
For the sequence \(\{u^k:=(x^k, y^k, \lambda ^k)\}\) defined by the proximal ADMM (1.3), we use the notation
We start from the first order optimality conditions on \(x^{k+1}\) and \(y^{k+1}\) which by definition can be stated as
By using \(\lambda ^{k+1}=\lambda ^k + \rho (A x^{k+1} + B y^{k+1} -c)\) we may rewrite (2.2) as
which will be frequently used in the following analysis. We first prove the following important result which is inspired by [19, Lemma 3.1] and [4, Theorem 15.4].
Proposition 2.1
Let Assumption 1 hold. Then for the proximal ADMM (1.3) there holds
for all \(u:= (x, y, \lambda ) \in \mathcal X\times \mathcal Y\times \mathcal Z\), where \(\sigma _f\) and \(\sigma _g\) denote the modulus of convexity of f and g respectively.
Proof
Let \(\tilde{\lambda }^{k+1}:= \lambda ^{k+1} - \rho B \Delta y^{k+1}\). By using (2.3) and the convexity of f and g we have for any \((x, y, \lambda ) \in \mathcal X\times \mathcal Y\times \mathcal Z\) that
Since \(\rho (A x^{k+1} + B y^{k+1} - c) = \Delta \lambda ^{k+1}\) we then obtain
By using the polarization identity and the definition of G, it follows that
Using the definition of \(\tilde{\lambda }^{k+1}\) gives
Therefore
Since \(\rho \Vert B \Delta y^{k+1}\Vert ^2 - \Vert \Delta y^{k+1}\Vert _{\widehat{Q}}^2 = - \Vert \Delta y^{k+1}\Vert _Q^2\), we thus complete the proof. \(\square \)
Corollary 2.2
Let Assumptions 1 and 2 hold and let \(\bar{u}:=(\bar{x}, \bar{y}, \bar{\lambda })\) be any KKT point of (1.1). Then for the proximal ADMM (1.3) there holds
for all \(k\ge 0\). Moreover, the sequence \(\{\Vert u^k-\bar{u}\Vert _G^2\}\) is monotonically decreasing.
Proof
By taking \(u = \bar{u}\) in Proposition 2.1 and using \(A \bar{x} + B \bar{y} - c =0\) we immediately obtain (2.4). According to (2.1) we have
Thus, from (2.4) we can obtain
which implies the monotonicity of the sequence \(\{\Vert u^k - \bar{u}\Vert _G^2\}\). \(\square \)
We next show that \(\Vert \Delta u^k\Vert _G^2 = o(1/k)\) as \(k\rightarrow \infty \). This result for the proximal ADMM (1.3) with \(Q =0\) has been established in [20] based on a variational inequality approach. We will establish this result for the proximal ADMM (1.3) with general bounded linear positive semi-definite self-adjoint operators P and Q by a simpler argument.
Lemma 2.3
Let Assumption 1 hold. For the proximal ADMM (1.3), the sequence \(\{\Vert \Delta u^k\Vert _G^2\}\) is monotonically decreasing.
Proof
By using (2.3) and the monotonicity of \(\partial f\) and \(\partial g\), we can obtain
Note that
We therefore have
By the polarization identity we then have
With the help of the definition of G, we obtain
which completes the proof. \(\square \)
Lemma 2.4
Let Assumptions 1 and 2 hold and let \(\bar{u}:=(\bar{x}, \bar{y}, \bar{\lambda })\) be any KKT point of (1.1). For the proximal ADMM (1.3) there holds
for all \(k \ge 1\).
Proof
We will use (2.3) together with \(-A^* \bar{\lambda }\in \partial f(\bar{x})\) and \(-B^* \bar{\lambda }\in \partial g(\bar{y})\). By using the monotonicity of \(\partial f\) and \(\partial g\) we have
By virtue of \(\rho (A x^{k+1} + B y^{k+1} - c\rangle = \Delta \lambda ^{k+1}\) we further have
By using the second equation in (2.3) and the monotonicity of \(\partial g\) we have
which shows that
Therefore
By using the polarization identity we then obtain
Recalling the definition of G we then complete the proof. \(\square \)
Proposition 2.5
Let Assumptions 1 and 2 hold. Then for the proximal ADMM (1.3) there holds \(\Vert \Delta u^k\Vert _G^2 = o(1/k)\) as \(k\rightarrow \infty \).
Proof
Let \(\bar{u}\) be a KKT point of (1.1). From Lemma 2.4 it follows that
for all \(k \ge 1\). By Lemma 2.3, \(\{\Vert \Delta u^{j+1}\Vert _G^2\}\) is monotonically decreasing. Thus
where [k/2] denotes the largest integer \(\le k/2\). Since (2.6) shows that
the right hand side of (2.7) must converge to 0 as \(k\rightarrow \infty \). Thus \((k+1) \Vert \Delta u^{k+1}\Vert _G^2 =o(1)\) and hence \(\Vert \Delta u^{k}\Vert _G^2 =o(1/k)\) as \(k\rightarrow \infty \). \(\square \)
As a byproduct of Proposition 2.5 and Corollary 2.2, we can prove the following non-ergodic convergence rate result for the proximal ADMM (1.3) in terms of the objective error and the constraint error.
Theorem 2.6
Let Assumptions 1 and 2 hold. Consider the proximal ADMM (1.3) for solving (1.1). Then
as \(k \rightarrow \infty \).
Proof
Since
we may use Proposition 2.5 to obtain the estimate \(\Vert A x^{k}+B y^{k} -c\Vert = o (1/\sqrt{k})\) as \(k\rightarrow \infty \).
In the following we will focus on deriving the estimate of \(|H(x^k, y^k) - H_*|\). Let \(\bar{u}:= (\bar{x}, \bar{y}, \bar{\lambda })\) be a KKT point of (1.1). By using (2.4) we have
By virtue of the monotonicity of \(\{\Vert u^k-\bar{u}\Vert _G^2\}\) given in Corollary 2.2 we then obtain
On the other hand, by using (2.1) we have
Therefore
Now we can use Proposition 2.5 to conclude the proof. \(\square \)
Remark 2.1
By exploiting the connection between the Douglas-Rachford splitting algorithm and the classical ADMM (1.2), the non-ergodic convergence rate (2.8) has been established in [8] for the classical ADMM (1.2) under the conditions that
and
where \(d_f (\lambda ):= f^*(A^* \lambda )\) and \(d_g(\lambda ):= g^*(B^*\lambda )-\langle \lambda , c\rangle \) with \(f^*\) and \(g^*\) denoting the convex conjugates of f and g respectively. The conditions (2.12) and (2.13) seems strong and unnatural because they are posed on the convex conjugates \(f^*\) and \(g^*\) instead of f and g themselves. In Theorem 2.6 we establish the non-ergodic convergence rate (2.8) for the proximal ADMM (1.3) with any positive semi-definite P and Q without requiring the conditions (2.12) and (2.13) and therefore our result extends and improves the one in [8].
Next we will consider establishing faster convergence rates under suitable regularity conditions. As a basis, we first prove the following result which tells that any weak cluster point of \(\{u^k\}\) is a KKT point of (1.1). This result can be easily established for ADMM in finite-dimensional spaces, however it is nontrivial for the proximal ADMM (1.3) in infinite-dimensional Hilbert spaces due to the required treatment of weak convergence; Proposition 2.1 plays a crucial role in our proof.
Theorem 2.7
Let Assumptions 1 and 2 hold. Consider the sequence \(\{u^k:=(x^k, y^k, \lambda ^k)\}\) generated by the proximal ADMM (1.3). Assume \(\{u^k\}\) is bounded and let \(u^\dag :=(x^\dag , y^\dag , \lambda ^\dag )\) be a weak cluster point of \(\{u^k\}\). Then \(u^\dag \) is a KKT point of (1.1). Moreover, for any weak cluster point \(u^*\) of \(\{u^k\}\) there holds \( \Vert u^*-u^\dag \Vert _G =0.\)
Proof
We first show that \(u^\dag \) is a KKT point of (1.1). According to Propositon 2.5 we have \(\Vert \Delta u^k\Vert _G^2 \rightarrow 0\) which means
as \(k\rightarrow \infty \). According to Theorem 2.6 we also have
Since \(u^\dag \) is a weak cluster point of the sequence \(\{u^k\}\), there exists a subsequence \(\{u^{k_j}:= (x^{k_j}, y^{k_j},\lambda ^{k_j})\}\) of \(\{u^k\}\) such that \(u^{k_j} \rightharpoonup u^\dag \) as \(j \rightarrow \infty \). By using the first equation in (2.15) we immediately obtain
By using Proposition 2.1 with \(k = k_j -1\) we have for any \(u:= (x, y, \lambda ) \in \mathcal X\times \mathcal Y\times \mathcal Z\) that
According to Corollary 2.2, \(\{\Vert u^k\Vert _G\}\) is bounded. Thus we may use Proposition 2.5 to conclude
as \(j \rightarrow \infty \). Therefore, by taking \(j \rightarrow \infty \) in (2.17) and using (2.14), (2.15) and \(\lambda ^{k_j} \rightharpoonup \lambda ^\dag \) we can obtain
for all \((x, y) \in \mathcal X\times \mathcal Y\). Since f and g are convex and lower semi-continuous, they are also weakly lower semi-continuous (see [11, Chapter 1, Corollary 2.2]). Thus, by using \(x^{k_j} \rightharpoonup x^\dag \) and \(y^{k_j} \rightharpoonup y^\dag \) we obtain
Since \((x^\dag , y^\dag )\) satisfies (2.16), we also have \(H(x^\dag , y^\dag ) \ge H_*\). Therefore \(H(x^\dag , y^\dag ) = H_*\) and then it follows from (2.18) and (2.16) that
for all \((x, y) \in \mathcal X\times \mathcal Y\). Using the definition of H we can immediately see that \(-A^* \lambda ^\dag \in \partial f(x^\dag )\) and \(-B^* \lambda ^\dag \in \partial g(y^\dag )\). Therefore \(u^\dag \) is a KKT point of (1.1).
Let \(u^*\) be another weak cluster point of \(\{u^k\}\). Then there exists a subsequence \(\{u^{l_j}\}\) of \(\{u^k\}\) such that \(u^{l_j} \rightharpoonup u^*\) as \(j \rightarrow \infty \). Noting the identity
Since both \(u^*\) and \(u^\dag \) are KKT points of (1.1) as shown above, it follows from Corollary 2.2 that both \(\{\Vert u^k - u^\dag \Vert _G^2\}\) and \(\{\Vert u^k - u^*\Vert _G^2\}\) are monotonically decreasing and thus converge as \(k \rightarrow \infty \). By taking \(k = k_j\) and \(k=l_j\) in (2.19) respectively and letting \(j \rightarrow \infty \) we can see that, for the both cases, the right hand side tends to the same limit. Therefore
which implies \(\Vert u^*-u^\dag \Vert _G^2 =0\). \(\square \)
Remark 2.2
Theorem 2.7 requires \(\{u^k\}\) to be bounded. According to Corollary 2.2, \(\{\Vert u^k\Vert _G^2\}\) is bounded which implies the boundedness of \(\{\lambda ^k\}\). In the following we will provide sufficient conditions to guarantee the boundedness of \(\{(x^k, y^k)\}\).
-
(i)
From (2.5) it follows that \(\{\sigma _f \Vert x^k\Vert ^2 + \sigma _g \Vert y^k\Vert ^2 + \Vert u^k\Vert _G^2\}\) is bounded. By the definition of G, this in particular implies the boundedness of \(\{\lambda ^k\}\) and \(\{B y^k\}\). Consequently, it follows from \(\Delta \lambda ^k = \rho (A x^k + B y^k - c)\) that \(\{A x^k\}\) is bounded. Putting the above together we can conclude that both \(\{(\sigma _f I + P + A^*A) x^k\}\) and \(\{(\sigma _g I + Q + B^* B) y^k\}\) are bounded. Therefore, if both the bounded linear self-adjoint operators
$$\begin{aligned} \sigma _f I + P + A^*A \quad \text{ and } \quad \sigma _g I + Q + B^*B \end{aligned}$$are coercive, we can conclude the boundedness of \(\{x^k\}\) and \(\{y^k\}\). Here a linear operator \(L: \mathcal V\rightarrow \mathcal H\) between two Hilbert spaces \(\mathcal V\) and \(\mathcal H\) is called coercive if \(\Vert Lv\Vert \rightarrow \infty \) whenever \(\Vert v\Vert \rightarrow \infty \). It is easy to see that L is coercive if and only if there is a constant \(c>0\) such that \(c\Vert v\Vert \le \Vert Lv\Vert \) for all \(v\in \mathcal V\).
-
(ii)
If there exist \(\beta >H_*\) and \(\sigma >0\) such that the set
$$\begin{aligned} \{(x, y) \in \mathcal X\times \mathcal Y: H(x, y)\le \beta \text{ and } \Vert A x + B y -c\Vert \le \sigma \} \end{aligned}$$is bounded, then \(\{(x^k,y^k)\}\) is bounded. In fact, since \(H(x^k, y^k)\rightarrow H_*\) and \(A x^k + B y^k - c\rightarrow 0\) as shown in Theorem 2.6, the sequence \(\{(x^k, y^k)\}\) is contained in the above set except for finite many terms. Thus \(\{(x^k, y^k)\}\) is bounded.
Remark 2.3
It is interesting to investigate under what conditions \(\{u^k\}\) has a unique weak cluster point. According to Theorem 2.7, for any two weak cluster points \(u^*:= (x^*, y^*, \lambda ^*)\) and \(u^\dag := (x^\dag , y^\dag , \lambda ^\dag )\) of \(\{u^k\}\) there hold
By using the definition of G and the monotonicity of \(\partial f\) and \(\partial g\) we can deduce that
Consequently
Therefore, if both \(\sigma _f I + P + A^* A\) and \(\sigma _g I + Q + B^* B\) are injective, then \(x^* = x^\dag \) and \(y^* = y^\dag \) and hence \(\{u^k\}\) has a unique weak cluster point, say \(u^\dag \); consequently \(u^k \rightharpoonup u^\dag \) as \(k \rightarrow \infty \).
Remark 2.4
In [31] the proximal ADMM (with relaxation) has been considered under the condition that
which requires both \((P + \rho A^*A + \partial f)^{-1}\) and \((Q + \rho B^*B + \partial g)^{-1}\) exist as single valued mappings and are Lipschitz continuous. It has been shown that the iterative sequence converges weakly to a KKT point which is its unique weak cluster point. The argument in [31] used the facts that the KKT mapping F(u), defined in (2.21) below, is maximal monotone and maximal monotone operators are closed under the weak-strong topology [2, 3]. Our argument is essentially based on Proposition 2.1, it is elementary and does not rely on any machinery from the maximal monotone operator theory.
Based on Theorem 2.7, we now devote to deriving convergence rates of the proximal ADMM (1.3) under certain regularity conditions. To this end, we introduce the multifuncton \(F: \mathcal X\times \mathcal Y\times \mathcal Z\rightrightarrows \mathcal X\times \mathcal Y\times \mathcal Z\) defined by
Then \(\bar{u}\) is a KKT point of (1.1) means \(0 \in F(\bar{u})\) or, equivalently, \(\bar{u}\in F^{-1}(0)\), where \(F^{-1}\) denotes the inverse multifunction of F. We will achieve our goal under certain bounded (Hölder) metric subregularity conditions of F. We need the following calculus lemma.
Lemma 2.8
Let \(\{\Delta _k\}\) be a sequence of nonnegative numbers satisfying
for all \(k\ge 1\), where \(C>0\) and \(\theta >1\) are constants. Then there is a constant \(\tilde{C}>0\) such that
for all \(k\ge 0\).
Proof
Please refer to the proof of [1, Theorem 2]. \(\square \)
Theorem 2.9
Let Assumptions 1 and 2 hold. Consider the sequence \(\{u^k:=(x^k, y^k, \lambda ^k)\}\) generated by the proximal ADMM (1.3). Assume \(\{u^k\}\) is bounded and let \(u^\dag :=(x^\dag , y^\dag , \lambda ^\dag )\) be a weak cluster point of \(\{u^k\}\). Let R be a number such that \(\Vert u^k - u^\dag \Vert \le R\) for all k and assume that there exist \(\kappa >0\) and \(\alpha \in (0, 1]\) such that
-
(i)
If \(\alpha = 1\), then there exists a constant \(0<q<1\) such that
$$\begin{aligned} \Vert u^{k+1} - u^\dag \Vert _G^2 + \Vert \Delta y^{k+1}\Vert _Q^2 \le q^2 \left( \Vert u^k - u^\dag \Vert _G^2 + \Vert \Delta y^k\Vert _Q^2\right) \end{aligned}$$(2.24)for all \(k \ge 0\) and consequently there exist \(C>0\) and \(0<q<1\) such that
$$\begin{aligned} \begin{aligned} \Vert u^k - u^\dag \Vert _G, \, \Vert \Delta u^k\Vert _G&\le C q^k, \\ \Vert A x^k + B y^k - c\Vert&\le C q^k, \\ |H(x^k, y^k) - H_*|&\le C q^k \end{aligned} \end{aligned}$$(2.25)for all \(k \ge 0\).
-
(ii)
If \(\alpha \in (0, 1)\) then there is a constant C such that
$$\begin{aligned} \Vert u^k - u^\dag \Vert _G^2 + \Vert \Delta y^k\Vert _Q^2 \le C (k+1)^{-\frac{\alpha }{1-\alpha }} \end{aligned}$$(2.26)and consequently
$$\begin{aligned} \begin{aligned} \Vert \Delta u^k \Vert _G&\le C (k+1)^{-\frac{1}{2(1-\alpha )}}, \\ \Vert A x^k + B y^k - c\Vert&\le C (k+1)^{-\frac{1}{2(1-\alpha )}}, \\ |H(x^k, y^k) - H_*|&\le C (k+1)^{- \frac{1}{2(1-\alpha )}} \end{aligned} \end{aligned}$$(2.27)for all \(k \ge 0\).
Proof
According to Theorem 2.7, \(u^\dag \) is a KKT point of (1.1). Therefore we may use Lemma 2.4 with \(\bar{u} = u^\dag \) to obtain
where \(\eta \in (0, 1)\) is any number. According to (2.3),
Thus, by using \(\Delta \lambda ^{k+1} = \rho (A x^{k+1} + B y^{k+1}-c)\) we can obtain
where
Combining this with (2.28) gives
Since \(\Vert u^k - u^\dag \Vert \le R\) for all k and F satisfies (2.23), one can see that
Consequently
For any \(u =(x, y, \lambda ) \in \mathcal X\times \mathcal Y\times \mathcal Z\) let
which measures the “distance" from u to \(F^{-1}(0)\) under the semi-norm \(\Vert \cdot \Vert _G\). It is easy to see that
where \(\Vert G\Vert \) denotes the norm of the operator G. Then we have
Now let \(\bar{u}\in F^{-1}(0)\) be any point. Then
Since \(u^\dag \) is a weak cluster point of \(\{u^k\}\), there is a subsequence \(\{u^{k_j}\}\) of \(\{u^k\}\) such that \(u^{k_j} \rightharpoonup u^\dag \). Thus
which implies \(\Vert u^\dag - \bar{u}\Vert _G \le \liminf _{j\rightarrow \infty } \Vert u^{k_j} - \bar{u}\Vert _G\). From Corollary 2.2 we know that \(\{\Vert u^k - \bar{u}\Vert _G^2\}\) is monotonically decreasing. Thus
Since \(\bar{u}\in F^{-1}(0)\) is arbitrary, we thus have
Therefore
By using the fact \(\Vert \Delta u^k\Vert _G\rightarrow 0\) established in Proposition 2.5, we can find a constant \(C>0\) such that
Note that \(\Vert \Delta u^{k+1}\Vert _G^2 \ge \Vert \Delta y^{k+1}\Vert _Q^2\). Thus
Choose \(\eta \) such that
Then
Using the inequality \((a+b)^p \le 2^{p-1}(a^p + b^p)\) for \(a,b\ge 0\) and \(p\ge 1\), we then obtain
(i) If \(\alpha =1\), then we obtain the linear convergence
which is (2.24) with \(q = 1/(1 + C \eta )\). By using Lemma 2.4 and (2.24) we immediately obtain the first estimate in (2.25). By using (2.9) and (2.11) we then obtain the last two estimates in (2.25).
(ii) If \(\alpha \in (0, 1)\), we may use (2.30) and Lemma 2.8 to obtain (2.26). To derive the first estimate in (2.27), we may use Lemma 2.4 to obtain
for all integers \(1 \le l < k\). By using the monotonicity of \(\{\Vert \Delta u^j\Vert _G^2\}\) shown in Lemma 2.3 and the estimate (2.26) we have
Taking \(l = [k/2]\), the largest integers \(\le k/2\), gives
with a possibly different generic constant C. This shows the first estimate in (2.27). Based on this, we can use (2.9) and (2.11) to obtain the last two estimates in (2.27). The proof is therefore complete. \(\square \)
Remark 2.5
Let us give some comments on the condition (2.23). In finite dimensional Euclidean spaces, it has been proved in [30] that for every polyhedral multifunction \(\Psi : {\mathbb R}^m \rightrightarrows {\mathbb R}^n\) there is a constant \(\kappa >0\) such that for any \(y \in {\mathbb R}^n\) there is a number \(\varepsilon >0\) such that
This result in particular implies the bounded metric subregularity of \(\Psi \), i.e. for any \(r>0\) and any \(y \in {\mathbb R}^n\) there is a number \(C>0\) such that
Therefore, if \(\partial f\) and \(\partial g\) are polyhedral multifunctions, then the multifunction F defined by (2.21) is also polyhedral and thus (2.23) with \(\alpha =1\) holds. The bounded metric subregularity of polyhedral multifunctions in arbitrary Banach spaces has been established in [34].
On the other hand, if \(\mathcal X\), \(\mathcal Y\) and \(\mathcal Z\) are finite dimensional Euclidean spaces, and if f and g are semi-algebraic convex functions, then the multifunction F satisfies (2.23) for some \(\alpha \in (0, 1]\). Indeed, the semi-algebraicity of f and g implies that their subdifferentials \(\partial f\) and \(\partial g\) are semi-algebraic multifunctions with closed graph; consequently F is semi-algebraic with closed graph. According to [24, Proposition 3.1], F is bounded Hölder metrically subregular at any point \((\bar{u}, \bar{\xi })\) on its graph, i.e. for any \(r>0\) there exist \(\kappa >0\) and \(\alpha \in (0,1]\) such that
which in particular implies (2.23).
By inspecting the proof of Theorem 2.9, it is easy to see that the same convergence rate results can be derived with the condition (2.23) replaced by the weaker condition: there exist \(\kappa >0\) and \(\alpha \in (0,1]\) such that
Therefore we have the following result.
Theorem 2.10
Let Assumptions 1 and 2 hold. Consider the sequence \(\{u^k:=(x^k, y^k, \lambda ^k)\}\) generated by the proximal ADMM (1.3). Assume \(\{u^k\}\) is bounded. If there exist \(\kappa >0\) and \(\alpha \in (0, 1]\) such that (2.31) holds, then, for any weak cluster point \(u^\dag \) of \(\{u^k\}\), the same convergence rate results in Theorem 2.9 hold.
Remark 2.6
Note that the condition (2.31) is based on the iterative sequence itself. Therefore, it makes possible to check the condition by exploring not only the property of the multifunction F but also the structure of the algorithm. The condition (2.31) with \(\alpha = 1\) has been introduced in [27] as an iteration based error bound condition to study the linear convergence of the proximal ADMM (1.3) with \(Q =0\) in finite dimensions.
Remark 2.7
The condition (2.31) is strongly motivated by the proof of Theorem 2.9. We would like to provide here an alternative motivation. Consider the proximal ADMM (1.3). We can show that if \(\Vert \Delta u^k\Vert _G =0\) then \(u^k\) must be a KKT point of (1.1). Indeed, \(\Vert \Delta u^k\Vert _G^2=0\) implies \(P\Delta x^k =0\), \({{\widehat{Q}}} \Delta y^k=0\) and \(\Delta \lambda ^k=0\). Since \({{\widehat{Q}}} = Q +\rho B^T B\) with Q positive semi-definite and \(\Delta \lambda ^k = \rho (A x^k + B y^k-c)\), we also have \(B \Delta y^k=0\), \(Q\Delta y^k=0\) and \(A x^k+B y^k-c=0\). Thus, it follows from (2.3) that
which shows that \(u^k=(x^k, y^k, \lambda ^k)\) is a KKT point, i.e., \(u^k \in F^{-1}(0)\). Therefore, it is natural to ask, if \(\Vert \Delta u^k\Vert _G\) is small, can we guarantee \(d_G(u^k, F^{-1}(0))\) to be small as well? This motivates us to propose a condition like
for some function \(\varphi : [0, \infty ) \rightarrow [0, \infty )\) with \(\varphi (0) =0\). The condition (2.31) corresponds to \(\varphi (s) = \kappa s^\alpha \) for some \(\kappa >0\) and \(\alpha \in (0, 1]\).
In finite dimensional Euclidean spaces some linear convergence results on the proximal ADMM (1.3) have been established in [9] under various scenarios involving strong convexity of f and/or g, Lipschitz continuity of \(\nabla f\) and/or \(\nabla g\), together with further conditions on A and/or B, see [9, Theorem 3.1 and Table 1]. In the following theorem we will show that (2.31) with \(\alpha = 1\) holds under any one of these scenarios and thus the linear convergence in [9, Theorem 3.1 and Theorem 3.4] can be established by using Theorem 2.10. Therefore, the linear convergence results based on the bounded metric subregularity of F or the scenarios in [9] can be treated in a unified manner.
Actually our next theorem improves the results in [9] by establishing the linear convergence of \(\{u^k\}\) and \(\{H(x^k, y^k)\}\) and relaxing the Lipschitz continuity of gradient(s) to the local Lipschitz continuity. Furthermore, Our result is established in general Hilbert spaces. To formulate the scenarios from [9] in this general setting, we need to replace the full row/column rank of matrices by the coercivity of linear operators. We also need the linear operator \(M: \mathcal X\times \mathcal Y\rightarrow \mathcal Z\) defined by
which is constructed from A and B. It is easy to see that the adjoint of M is \(M^* z = (A^* z, B^* z)\) for any \(z \in \mathcal Z\).
Theorem 2.11
Let Assumptions 1 and 2 hold. Let \(\{u^k\}\) be the sequence generated by the proximal ADMM (1.3). Then \(\{u^k\}\) is bounded and there exists a constant \(C>0\) such that
for all \(k\ge 1\), provided any one of the following conditions holds:
-
(i)
\(\sigma _g>0\), A and \(B^*\) are coercive, g is differentiable and its gradient is Lipschitz continuous over bounded sets;
-
(ii)
\(\sigma _f>0\), \(\sigma _g>0\), \(B^*\) is coercive, g is differentiable and its gradient is Lipschitz continuous over bounded sets;
-
(iii)
\(\lambda ^0=0\), \(\sigma _f>0\), \(\sigma _g>0\), \(M^*\) restricted on \(\mathcal N(M^*)^\perp \) is coercive, both f and g are differentiable and their gradients are Lipschitz continuous over bounded sets;
-
(iv)
\(\lambda ^0=0\), \(\sigma _g>0\), A is coercive, \(M^*\) restricted on \(\mathcal N(M^*)^\perp \) is coercive, both f and g are differentiable and their gradients are Lipschitz continuous over bounded sets;
where \(\mathcal N(M^*)\) denotes the null space of \(M^*\). Consequently, there exist \(C>0\) and \(0< q<1\) such that
for all \(k \ge 0\), where \(u^\dag :=(x^\dag , y^\dag , \lambda ^\dag )\) is a KKT point of (1.1).
Proof
We will only consider the scenario (i) since the proofs for other scenarios are similar. In the following we will use C to denote a generic constant which may change from line to line but is independent of k.
We first show the boundedness of \(\{u^k\}\). According to Corollary 2.2, \(\{\Vert u^k\Vert _G^2\}\) is bounded which implies the boundedness of \(\{\lambda ^k\}\). Since \(\sigma _g>0\), it follows from (2.5) that \(\{y^k\}\) is bounded. Consequently, it follows from \(\Delta \lambda ^k = \rho (A x^k + B y^k -c)\) that \(\{A x^k\}\) is bounded. Since A is coercive, \(\{x^k\}\) must be bounded.
Next we show (2.32). Let \(u^\dag :=(x^\dag , y^\dag , \lambda ^\dag )\) be a weak cluster point of \(\{u^k\}\) whose existence is guaranteed by the boundedness of \(\{u^k\}\). According to Theorem 2.7, \(u^\dag \) is a KKT point of (1.1). Let \((\xi , \eta , \tau ) \in F(u^k)\) be any element. Then
By using the monotonicity of \(\partial f\) and \(\partial g\) we have
Since \(\sigma _g>0\), it follows from (2.33) and the Cauchy-Schwarz inequality that
Note that \(A (x^k - x^\dag ) = - B(y^k - y^\dag ) + \frac{1}{\rho } \Delta \lambda ^k\). Since A is coercive, we have
By the differentiability of g we have \(-B^*\lambda ^\dag = \nabla g(y^\dag )\) and \(-B^* \lambda ^k - Q \Delta y^k = \nabla g(y^k)\). Since \(B^*\) is coercive and \(\nabla g\) is Lipschitz continuous over bounded sets, we thus obtain
Adding (2.35) and (2.36) and then using (2.34), it follows
which together with the Cauchy-Schwarz inequality then implies
Combining (2.34) and (2.37) we can obtain
Since \((\xi , \eta , \tau ) \in F(u^k)\) is arbitrary, we therefore have
With the help of (2.29), we then obtain
Thus
which shows (2.32).
Because \(\{u^k\}\) is bounded and (2.32) holds, we may use Theorem 2.10 to conclude the existence of a constant \(q \in (0, 1)\) such that
Finally we may use (2.38) to obtain \(\Vert u^k-u^\dag \Vert \le C q^k\). \(\square \)
Remark 2.8
If \(\mathcal Z\) is finite-dimensional, the coercivity of \(M^*\) restricted on \(\mathcal N(M^*)^\perp \) required in the scenarios (iii) and (iv) holds automatically. If it is not, then there exists a sequence \(\{z^k\}\subset \mathcal N(M^*)^\perp {\setminus }\{0\}\) such that
By rescaling we may assume \(\Vert z^k\Vert =1\) for all k. Since \(\mathcal Z\) is finite-dimensional, by taking a subsequence if necessary, we may assume \(z^k \rightarrow z\) for some \(z \in \mathcal Z\). Clearly \(z\in \mathcal N(M^*)^\perp \) and \(\Vert z\Vert =1\). Note that \(\Vert M^* z^k\Vert \le 1/k\) for all k, we have \(\Vert M^* z\Vert = \lim _{k\rightarrow \infty } \Vert M^* z^k\Vert =0\) which means \(z \in \mathcal N(M^*)\). Thus \(z \in \mathcal N(M^*) \cap \mathcal N(M^*)^\perp = \{0\}\) which is a contradiction.
3 Proximal ADMM for Linear Inverse Problems
In this section we will consider the method (1.11) as a regularization method for solving (1.9) and establish a convergence rate result under a benchmark source condition on the sought solution. Throughout this section we will make the following assumptions on the operators Q, L, A, the constraint set \(\mathcal C\) and the function f:
Assumption 3
-
(i)
\(A: \mathcal X\rightarrow \mathcal H\) is a bounded linear operator, \(Q: \mathcal X\rightarrow \mathcal X\) is a bounded linear positive semi-definite self-adjoint operator, and \(\mathcal C\subset \mathcal X\) is a closed convex subset.
-
(ii)
L is a densely defined, closed, linear operator from \(\mathcal X\) to \(\mathcal Y\) with domain \(\textrm{dom}(L)\).
-
(iii)
There is a constant \(c_0>0\) such that
$$\begin{aligned} \Vert A x\Vert ^2 + \Vert L x\Vert ^2 \ge c_0 \Vert x\Vert ^2, \qquad \forall x\in \textrm{dom}(L). \end{aligned}$$ -
(iv)
\(f: \mathcal {Y}\rightarrow (-\infty , \infty ]\) is proper, lower semi-continuous, and strongly convex.
This assumptions is standard in the literature on regularization methods and has been used in [21, 22]. Based on (iii), we can define the adjoint \(L^*\) of L which is also closed and densely defined; moreover, \(z\in \text{ dom }(L^*)\) if and only if \(\langle L^* z, x\rangle =\langle z, L x\rangle \) for all \(x\in \text{ dom }(L)\). Under Assumption 3, it has been shown in [21, 22] that the proximal ADMM (1.11) is well-defined and if the exact data b is consistent in the sense that there exists \({\hat{x}}\in \mathcal X\) such that
then the problem (1.9) has a unique solution, denoted by \(x^\dag \). Furthermore, there holds the following monotonicity result, see [22, Lemma 2.3]; alternatively, it can also be derived from Lemma 2.3..
Lemma 3.1
Let \(\{z^k, y^k, x^k, \lambda ^k, \mu ^k, \nu ^k\}\) be defined by the proximal ADMM (1.11) with noisy data and let
Then \(\{E_k\}\) is monotonically decreasing with respect to k.
In the following we will always assume the exact data b is consistent. We will derive a convergence rate of \(x^k\) to the unique solution \(x^\dag \) of (1.9) under the source condition
Note that when \(L = I\) and \(\mathcal C= \mathcal X\), (3.2) becomes the benchmark source condition
which has been widely used to derive convergence rate for regularization methods, see [7, 13, 23, 29] for instance. We have the following convergence rate result.
Theorem 3.2
Let Assumption 3 hold, let the exact data b be consistent, and let the sequence \(\{z^k, y^k, x^k, \lambda ^k, \mu ^k, \nu ^k\}\) be defined by the proximal ADMM (1.11) with noisy data \(b^\delta \) satisfying \(\Vert b^\delta - b\Vert \le \delta \). Assume the unique solution \(x^\dag \) of (1.9) satisfies the source condition (3.2). Then for the integer \(k_\delta \) chosen by \(k_\delta \sim \delta ^{-1}\) there hold
as \(\delta \rightarrow 0\).
In order to prove this result, let us start from the formulation of the algorithm (1.11) to derive some useful estimates. For simplicity of exposition, we set
According to the definition of \(z^{k+1}\), \(y^{k+1}\) and \(x^{k+1}\) in (1.11), we have the optimality conditions
By using the last two equations in (1.11), we have from (3.4) and (3.5) that
Letting \(y^\dag = L x^\dag \). From the strong convexity of f, the convexity of \(\iota _C\), and (3.6) it follows that
where \(\sigma _f\) denotes the modulus of convexity of f; we have \(\sigma _f>0\) as f is strongly convex. By taking the inner product of (3.3) with \(z^{k+1} - x^\dag \) we have
Therefore we may use the definition of \(\lambda ^{k+1}, \mu ^{k+1}, \nu ^{k+1}\) in (1.11) and the fact \(A x^\dag = b\) to further obtain
Subtracting (3.7) by (3.8) gives
Note that under the source condition (3.2), there exist \(\mu ^\dag \), \(\nu ^\dag \) and \(\lambda ^\dag \) such that
Thus, it follows from the above equation and the last two equations in (1.11) that
By using (3.9), \(b = A x^\dag \) and the convexity of f, we can see that
Consequently, by using the fourth equation in (1.11), we have
By using the polarization identity and the last two equations in (1.11) we further have
Let
Then
where \(E_k\) is defined by (3.1).
Lemma 3.3
For all \(k = 0, 1, \cdots \) there hold
and
Proof
By using (3.6) and the monotonicity of the subdifferentials \(\partial f\) and \(\partial \iota _{\mathcal C}\) we have
This together with (3.10) implies (3.11). From (3.11) it follows immediately that
which shows (3.12). By the non-negativity of \(E_{k+1}\) we then obtain from (3.12) that
which clearly implies (3.13). \(\square \)
In order to derive the estimate on \(\Phi _k\) from (3.13), we need the following elementary result.
Lemma 3.4
Let \(\{a_k\}\) and \(\{b_k\}\) be two sequences of nonnegative numbers such that
where \(c \ge 0\) is a constant. If \(\{b_k\}\) is non-decreasing, then
Proof
We show the result by induction on k. The result is trivial for \(k =0\) since the given condition with \(k=0\) gives \(a_0 \le b_0\). Assume that the result is valid for all \(0\le k \le l\) for some \(l\ge 0\). We show it is also true for \(k = l+1\). If \(a_{l+1} \le \max \{a_0, \cdots , a_l\}\), then \(a_{l+1} \le a_j\) for some \(0\le j\le l\). Thus, by the induction hypothesis and the monotonicity of \(\{b_k\}\) we have
If \(a_{l+1} > \max \{a_0, \cdots , a_l\}\), then
which implies that
Taking square roots shows \(a_{l+1} \le b_{l+1} + c (l+1)\) again. \(\square \)
Lemma 3.5
There hold
and
Proof
Based on (3.13), we may use Lemma 3.4 with \(a_k = \Phi _k^{1/2}\), \(b_k = \Phi _0^{1/2}\) and \(c = (2\rho _2)^{1/2} \delta \) to obtain (3.14) directly. Next, by using the monotonicity of \(\{E_k\}\), (3.12) and (3.14) we have
which shows (3.15). \(\square \)
Now we are ready to complete the proof of Theorem 3.2.
Proof (Proof of Theorem 3.2)
Let \(k_\delta \) be an integer such that \(k_\delta \sim \delta ^{-1}\). From (3.14) and (3.15) in Lemma 3.5 it follows that
where \(C_0\) and \(C_1\) are constants independent of k and \(\delta \). In order to use (3.11) in Lemma 3.3 to estimate \(\Vert y^{k_\delta } - y^\dag \Vert \), we first consider \(\Phi _k - \Phi _{k+1}\) for all \(k\ge 0\). By using the definition of \(\Phi _k\) and the inequality \(\Vert u\Vert ^2 - \Vert v\Vert ^2 \le (\Vert u\Vert + \Vert v\Vert ) \Vert u - v\Vert \), we have for \(k \ge 0\) that
By virtue of the Cauchy-Schwarz inequality and the inequality \((a+b)^2 \le 2(a^2 + b^2)\) for any numbers \(a, b \in {\mathbb R}\) we can further obtain
This together with (3.16) in particular implies
Therefore, it follows from (3.11) that
Thus
where \(C_2\) is a constant independent of \(\delta \) and k. By using the estimate \(E_{k_\delta } \le C_0 \delta \) in (3.16), the definition of \(E_{k_\delta }\), and the last three equations in (1.11), we can see that
Therefore
By virtue of (iii) in Assumption 3 on A and L we thus obtain
This means there is a constant \(C_3\) independent of \(\delta \) and k such that
Finally we obtain
The proof is thus complete. \(\square \)
Remark 3.1
Under the benchmark source condition (3.2), we have obtained in Theorem 3.2 the convergence rate \(O(\delta ^{1/4})\) for the proximal ADMM (1.11). This rate is not order optimal. It is not yet clear if the order optimal rate \(O(\delta ^{1/2})\) can be achieved.
Remark 3.2
When using the proximal ADMM to solve (1.9) with \(L = I\), i.e.
it is not necessary to introduce the y-variable as is done in (1.11) and thus (1.11) can be simplified to the scheme
where
The source condition (1.9) reduces to the form
If the unique solution \(x^\dag \) of (3.17) satisfies the source condition (3.19), one may follow the proof of Theorem 3.2 with minor modification to deduce for the method (3.18) that
whenever the integer \(k_\delta \) is chosen such that \(k_\delta \sim \delta ^{-1}\).
We conclude this section by presenting a numerical result to illustrate the semi-convergence property of the proximal ADMM and the convergence rate. We consider finding a solution of (1.8) with minimal norm. This is equivalent to solving (3.17) with \(f(y) = \frac{1}{2} \Vert y\Vert ^2\). With a noisy data \(b^\delta \) satisfying \(\Vert b^\delta - b\Vert \le \delta \), the corresponding proximal ADMM (3.18) takes the form
where \(P_\mathcal C\) denotes the orthogonal projection of \(\mathcal X\) onto \(\mathcal C\). The source condition (3.19) now takes the form
which is equivalent to the projected source condition \(x^\dag \in P_\mathcal C(\text{ Ran }(A^*))\).
Example 3.6
In our numerical simulation we consider the first kind integral equation
on \(L^2[0,1]\), where the kernel \(\kappa \) is continuous on \([0,1]\times [0,1]\). Such equations arise naturally in many linear ill-posed inverse problems, see [12, 18]. Clearly A is a compact linear operator from \(L^2[0,1]\) to itself. We will use
with \(d = 0.1\). The corresponding equation is a 1-D model problem in gravity surveying. Assume the equation (3.22) has a nonnegative solution. We will employ the method (3.20) to determine the unique nonnegative solution of (3.22) with minimal norm in case the data is corrupted by noise. Here \(\mathcal C:=\{x \in L^2[0,1]: x\ge 0 \text{ a.e. }\}\) and thus \(P_\mathcal C(x) = \max \{x, 0\}\).
a Plots the true solution \(x^\dag \), b, c plot the relative errors versus the number of iterations for the method (3.20) using noisy data with noise level \(\delta = 10^{-2}\) and \(10^{-4}\) respectively
In order to investigate the convergence rate of the method, we generate our data as follows. First take \(\omega ^\dag \in L^2[0,1]\), set \(x^\dag := \max \{A^* \omega ^\dag , 0\}\) and define \(b:= A x^\dag \). Thus \(x^\dag \) is a nonnegative solution of \(A x = b\) satisfying \(x^\dag = P_\mathcal C(A^* \omega ^\dag )\), i.e. the source condition (3.21) holds. We use \(\omega ^\dag = t^3(0.9-t)(t-0.35)\), the corresponding \(x^\dag \) is plotted in Fig. 1a. We then pick a random data \(\xi \) with \(\Vert \xi \Vert _{L^2[0,1]} = 1\) and generate the noisy data \(b^\delta \) by \(b^\delta := b + \delta \xi \). Clearly \(\Vert b^\delta - b\Vert _{L^2[0,1]} = \delta \).
For numerical implementation, we discretize the equation by the trapzoidal rule based on partitioning [0, 1] into \(N-1\) subintervals of equal length with \(N = 600\). We then execute the method (3.20) with \(Q =0\), \(\rho _1 = 10\), \(\rho _2=1\) and the initial guess \(x^0 = \lambda ^0 = \nu ^0 = 0\) using the noisy data \(b^\delta \) for several distinct values of \(\delta \). In Fig. 1b and c we plot the relative error \(\Vert x^k- x^\dag \Vert _{L^2}/\Vert x^\dag \Vert _{L^2}\) versus k, the number of iterations, for \(\delta = 10^{-2}\) and \(\delta = 10^{-4}\) respectively. These plots demonstrate that the proximal ADMM always exhibits the semi-convergence phenomenon when used to solve ill-posed problems, no matter how small the noise level is. Therefore, properly terminating the iteration is important to produce useful approximate solutions. This has been done in [21, 22].
In Table 1 we report further numerical results. For the noisy data \(b^\delta \) with each noise level \(\delta = 10^{-i}\), \(i = 1, \cdots , 7\), we execute the method and determine the smallest relative error, denoted by \(\texttt {err}_{\min }\), and the required number of iterations, denoted by \(\texttt {iter}_{\min }\). The ratios \(\texttt {err}_{\min }/\delta ^{1/2}\) and \(\texttt {err}_{\min }/\delta ^{1/4}\) are then calculated. Since \(x^\dag \) satisfies the source condition (3.21), our theoretical result predicts the convergence rate \(O(\delta ^{1/4})\). However, Table 1 illustrates that the value of \(\texttt {err}_{\min }/\delta ^{1/2}\) does not change much while the value of \(\texttt {err}_{\min }/\delta ^{1/4}\) tends to decrease to 0 as \(\delta \rightarrow 0\). This strongly suggests that the proximal ADMM admits the order optimal convergence rate \(O(\delta ^{1/2})\) if the source condition (3.21) holds. However, how to derive this order optimal rate remains open.
Data Availibility
Enquiries about data availability should be directed to the author.
References
Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. Ser. B 116, 5–16 (2009)
Attouch, H., Soueycatt, M.: Augmented Lagrangian and proximal alternating direction methods of multipliers in Hilbert spaces. Applications to games, PDE’s and control. Pac. J. Optim. 5(1), 17–37 (2009)
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, New York (2011)
Beck, A.: First-Order Methods in Optimization, MOS-SIAM Series on Optimization. Society for Industrial and Applied Mathematics, Philadelphia (2017)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3(1), 1–122 (2011)
Bredies, K., Sun, H.: A proximal point analysis of the preconditioned alternating direction method of multipliers. J. Optim. Theory Appl. 173(3), 878–907 (2017)
Burger, M., Osher, S.: Convergence rates of convex variational regularization. Inverse Prob. 20(5), 1411–1421 (2004)
Davis, D., Yin, W.: Convergence rate analysis of several splitting schemes. In: Splitting Methods in Communication, Imaging, Science, and Engineering. Science Computing, pp. 115–163. Springer, Cham (2016)
Deng, W., Yin, W.: On the global and linear convergence of the generalized alternating direction method of multipliers. J. Sci. Comput. 66, 889–916 (2016)
Eckstein, J., Bertsekas, D.P.: On the Douglas–Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 55(1–3), 293–318 (1992)
Ekeland, I., Temam, R.: Convex Analysis and Variational Problems. North Holland, Amsterdam (1976)
Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems. Kluwer, Dordrecht (1996)
Frick, K., Scherzer, O.: Regularization of ill-posed linear equations by the non-stationary augmented Lagrangian method. J. Integral Equ. Appl. 22(2), 217–257 (2010)
Gabay, D.: Applications of the method of multipliers to variational inequalities. Stud. Math. Appl. 15, 299–331 (1983)
Gabay, D., Mercier, B.: A dual algorithm for the solution of nonlinear variational problems via finite element approximation. Comput. Math. Appl. 2, 17–40 (1976)
Glowinski, R., Marrocco, A.: Sur l’approximation, par éléments finis d’ordre un, et la résolution, par pénalisation-dualité, d’une classe de problémes de Dirichlet non linéaires. ESAIM Math. Model. Numer. Anal. 9(R2), 41–76 (1975)
Goldstein, T., Bresson, X., Osher, S.: Geometric applications of the split Bregman method: segmentation and surface reconstruction. J. Sci. Comput. 45(1), 272–293 (2010)
Groetsch, C.W.: The Theory of Tikhonov Regularization for Fredholm Equations of the First Kind, Research Notes in Mathematics, vol. 105. Pitman (Advanced Publishing Program), Boston, MA (1984)
He, B., Yuan, X.: On the \(O(1/n)\) convergence rate of Douglas–Rachford alternating direction method. SIAM J. Numer. Anal. 50, 700–709 (2012)
He, B., Yuan, X.: On non-ergodic convergence rate of Douglas–Rachford alternating direction method of multipliers. Numer. Math. 130, 567–577 (2015)
Jiao, Y., Jin, Q., Lu, X., Wang, W.: Alternating direction method of multipliers for linear inverse problems. SIAM J. Numer. Anal. 54(4), 2114–2137 (2016)
Jiao, Y., Jin, Q., Lu, X., Wang, W.: Preconditioned alternating direction method of multipliers for solving inverse problems with constraints. Inverse Probl. 33, 025004 (2017)
Jin, Q.: Convergence rates of a dual gradient method for constrained linear ill-posed problems. Numer. Math. 151(4), 841–871 (2022)
Lee, J.H., Pham, T.S.: Openness, Hölder metric regularity, and Hölder continuity properties of semialgebraic set-valued maps. SIAM J. Optim. 32(1), 56–74 (2022)
Lin, T., Ma, S., Zhang, S.: On the sublinear convergence rate of multi-block ADMM. J. Oper. Res. Soc. China 3(3), 251–274 (2015)
Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16(6), 964–979 (1979)
Liu, Y., Yuan, X., Zeng, S., Zhang, J.: Partial error bound conditions and the linear convergence rate of the alternating direction method of multipliers. SIAM J. Numer. Anal. 56(4), 2095–2123 (2018)
Natterer, F.: The Mathematics of Computerized Tomography. SIAM, Philadelphia (2001)
Resmerita, E., Scherzer, O.: Error estimates for non-quadratic regularization and the relation to enhancement. Inverse Prob. 22(3), 801–814 (2006)
Robinson, S.M.: Some continuity properties of polyhedral multifunctions. Math. Program. Study 14, 206–214 (1981)
Sun, H.: Analysis of fully preconditioned alternating direction method of multipliers with relaxation in Hilbert spaces. J. Optim. Theory Appl. 183(1), 199–229 (2019)
Yang, W.H., Han, D.R.: Linear convergence of alternating direction method of multipliers for a class of convex optimization problems. SIAM J. Numer. Anal. 54(2), 625–640 (2016)
Zhang, X., Burger, M., Osher, S.: A unified primal-dual algorithm framework based on Bregman iteration. J. Sci. Comput. 46, 20–46 (2011)
Zheng, X.Y., Ng, K.F.: Metric subregularity of piecewise linear multifunctions and applications to piecewise linear multiobjective optimization. SIAM J. Optim. 24(1), 154–174 (2014)
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions. The work of Qinian Jin is partially supported by the Future Fellowship of the Australian Research Council (FT170100231).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jin, Q. On Convergence Rates of Proximal Alternating Direction Method of Multipliers. J Sci Comput 97, 66 (2023). https://doi.org/10.1007/s10915-023-02383-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02383-3