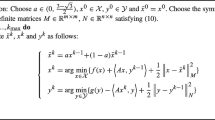An Adaptive Superfast Inexact Proximal Augmented Lagrangian Method for Smooth Nonconvex Composite Optimization Problems

Abstract

This work presents an adaptive superfast proximal augmented Lagrangian (AS-PAL) method for solving linearly-constrained smooth nonconvex composite optimization problems. Each iteration of AS-PAL inexactly solves a possibly nonconvex proximal augmented Lagrangian (AL) subproblem obtained by an aggressive/adaptive choice of prox stepsize with the aim of substantially improving its computational performance followed by a full Lagrange multiplier update. A major advantage of AS-PAL compared to other AL methods is that it requires no knowledge of parameters (e.g., size of constraint matrix, objective function curvatures, etc) associated with the optimization problem, due to its adaptive nature not only in choosing the prox stepsize but also in using a crucial adaptive accelerated composite gradient variant to solve the proximal AL subproblems. The speed and efficiency of AS-PAL is demonstrated through extensive computational experiments showing that it can solve many instances more than ten times faster than other state-of-the-art penalty and AL methods, particularly when high accuracy is required.

Appendices

ADAP-FISTA Algorithm

1.1 ADAP-FISTA Method

This subsection presents an adaptive ACG variant, called ADAP-FISTA, which is an important tool in the development of the AS-PAL method. We first introduce the assumptions on the problem it solves. ADAP-FISTA considers the following problem

$$\begin{aligned} \min \{ \psi (x):= \psi _s(x) + \psi _n(x): x \in \Re ^n\} \end{aligned}$$

(A.1)

where $\psi _s$ and $\psi _n$ are assumed to satisfy the following assumptions:

(I):

$\psi _n:\Re ^n \rightarrow \Re \cup \{+\infty \}$ is a possibly nonsmooth convex function;

(II):

$\psi _s: \Re ^n\rightarrow \Re$ is a differentiable function and there exists ${{\bar{L}}} \ge 0$ such that

$$\begin{aligned} \Vert \nabla \psi _s(z') - \nabla \psi _s(z)\Vert \le {{\bar{L}}} \Vert z'-z\Vert \quad \forall z,z' \in \Re ^n. \end{aligned}$$

(A.2)

We now describe the type of approximate solution that ADAP-FISTA aims to find.

Problem A: Given $\psi$ satisfying the above assumptions, a point $x_0 \in \textrm{dom}\,\psi _n$, a parameter $\sigma \in (0,\infty )$, the problem is to find a pair $(y,u) \in \textrm{dom}\,\psi _n \times \Re ^n$ such that

$$\begin{aligned} \Vert u\Vert \le \sigma \Vert y-x_0\Vert , \quad u \in \nabla \psi _s(y)+\partial \psi _n(y). \end{aligned}$$

(A.3)

We are now ready to present the ADAP-FISTA algorithm below.

We now make some remarks about ADAP-FISTA. First, usual FISTA methods for solving the strongly convex version of (A.1) consist of repeatedly invoking only steps 2 and 3 of ADAP-FISTA either with a static Lipschitz constant (of the gradient), namely, $L_{j+1}=L$ for all $j \ge 0$ for some $L\ge {{\bar{L}}}$, or by adaptively searching for a suitable Lipschitz $L_{j+1}$ (as in step 2 of ADAP-FISTA) satisfying a condition similar to (A.6). Second, the pair $(y_{j+1},u_{j+1})$ always satisfies the inclusion in (A.3) (see Lemma A.3 below) so if ADAP-FISTA stops successfully in step 5, or equivalently (A.12) holds, the pair solves Problem A above. Finally, if condition (A.10) in step 4 is never violated, ADAP-FISTA must stop successfully in step 5 (see Proposition A.1 below).

We now discuss how ADAP-FISTA compares with existing ACG variants for solving (A.1) under the assumption that $\psi _s$ is $\mu$-strongly convex. Under this assumption, FISTA variants have been studied, for example, in [3, 11, 12, 28, 30], while other ACG variants have been studied, for example, in [7, 8, 31]. A crucial difference between ADAP-FISTA and these variants is that: (i) ADAP-FISTA stops based on a different relative criterion, namely, (A.12) (see Problem A above) and attempts to approximately solve (A.1) in this sense even when $\psi _s$ is not $\mu$-strongly convex, and (ii) ADAP-FISTA provides a key and easy to check inequality whose validity at every iteration guarantees its successful termination. On the other hand, ADAP-FISTA shares similar features with these other methods in that: (i) it has a reasonable iteration complexity guarantee regardless of whether it succeeds or fails, and (ii) it successfully terminates when $\psi _s$ is $\mu$-strongly convex (see Propositions A.1–A.2 below). Moreover, like the method in [3], ADAP-FISTA adaptively searches for a suitable Lipschitz estimate $L_{j+1}$ that is used in (A.5).

We now present the main convergence results of ADAP-FISTA, which is invoked by AS-PAL for solving the sequence of subproblems (1.4). The first result, namely Proposition A.1 below, gives an iteration complexity bound regardless if ADAP-FISTA terminates with success or failure and shows that if ADAP-FISTA successfully stops, then it obtains a stationary solution of (A.1) with respect to a relative error criterion. The second result, namely Proposition A.2 below, shows that ADAP-FISTA always stops successfully whenever $\psi _s$ is $\mu$-strongly convex.

Proposition A.1

The following statements about ADAP-FISTA hold:

• (a) if $L_0 = {{{\mathcal {O}}}}({{\bar{L}}})$, it always stops (with either success or failure) in at most

  $$\begin{aligned} {{\mathcal {O}}}_1\left( \sqrt{\frac{{{\bar{L}}}}{\mu }}\log ^+_1 ({{\bar{L}}}) \right) \end{aligned}$$

  iterations/resolvent evaluations;

• (b) if it stops successfully, it terminates with a triple $(y,u,L) \in \textrm{dom}\,\psi _{n} \times \Re ^{n}$ satisfying

  $$\begin{aligned}&u \in \nabla \psi _s(y)+\partial \psi _n(y), \quad \Vert u\Vert \le \sigma \Vert y-x_0\Vert , \quad L \le \max \{L_0, \omega {{\bar{L}}}\} . \end{aligned}$$

  (A.13)

Proposition A.2

If $\psi _s$ is $\mu$-convex, then ADAP-FISTA always terminates with success and its output (y, u, L), in addition to satisfying (A.13) also satisfies the inclusion $u \in \partial (\psi _s+\psi _n)(y)$.

The rest of this section is broken up into two subsections which are dedicated to proving Propositions A.1 and A.2, respectively.

1.2 Proof of Proposition A.1

This subsection is dedicated to proving Proposition A.1. The first lemma below presents key definitions and inequalities used in the convergence analysis of ADAP-FISTA.

Lemma A.3

Define

$$\begin{aligned} \omega =2\beta /(1-\chi ), \quad \zeta :={{\bar{L}}}+\max \{L_0,\omega {{\bar{L}}}\}. \end{aligned}$$

(A.14)

Then, the following statements hold:

• (a) $\{L_j\}$ is nondecreasing;

• (b) for every $j \ge 0$, we have

  $$\begin{aligned}&\tau _j = 1+A_j\mu , \quad \frac{\tau _j A_{j+1}}{ a_j^2}=L_{j+1}-\mu ; \end{aligned}$$

  (A.15)
  $$\begin{aligned}&L_0\le L_j\le \max \{L_0,\omega {{\bar{L}}}\}; \end{aligned}$$

  (A.16)
  $$\begin{aligned}&u_{j+1} \in \nabla \psi _s(y_{j+1}) + \partial \psi _n(y_{j+1}), \quad \Vert u_{j+1}\Vert \le \zeta \Vert y_{j+1}-{\tilde{x}}_{j}\Vert . \end{aligned}$$

  (A.17)

Proof

(a) It is clear from the update rule in the beginning of Step 1 that $\{L_j\}$ is nondecreasing.

(b) The first equality in (A.15) follows directly from both of the relations in (A.7). The second equality in (A.15) follows immediately from the definition of $a_j$ in (A.4) and the first relation in (A.7).

We prove (A.16) by induction. It clearly holds for $j=0$. Suppose now (A.16) holds for $j \ge 0$ and let us show that it holds for $j+1$. Note that if $L_{j+1}=L_j$, then relation (A.16) immediately holds. Assume then that $L_{j+1}>L_j$. It then follows from the way $L_{j+1}$ is chosen in step 1 that (A.6) is not satisfied with $L_{j+1}/\beta$. This fact together with the inequality (A.2) at the points $(y_{j+1},{\tilde{x}}_j)$ imply that

$$\begin{aligned}{} & {} \ell _{\psi _s}(y_{j+1};{\tilde{x}}_j)+\frac{(1-\chi ) L_{j+1}}{4\beta }\Vert y_{j+1}-{\tilde{x}}_j\Vert ^2 \nonumber \\{} & {} \quad < \psi _s(y_{j+1}) \overset{\mathrm{(A.2)}}{\le } \ell _{\psi _s}(y_{j+1};{\tilde{x}}_j)+\frac{{{\bar{L}}}}{2}\Vert y_{j+1} -{\tilde{x}}_j\Vert ^2. \end{aligned}$$

(A.18)

The relation in (A.16) then immediately follows from the definition of $\omega$ in (A.14).

Now, by the definition of $u_{j+1}$ in (A.11), triangle inequality, (A.2), the bound (A.16) on $L_{j+1}$, and the definition of $\zeta$ we have

$$\begin{aligned} \frac{\Vert u_{j+1}\Vert }{\Vert y_{j+1}- {\widetilde{x}}_{j}\Vert } \overset{\mathrm{(A.11)}}{\le } \frac{ \Vert \nabla \psi _s(y_{j+1}) - \nabla \psi _s({\widetilde{x}}_{j}) \Vert }{\Vert y_{j+1}- {\widetilde{x}}_{j}\Vert }+ L_{j+1} \overset{\mathrm{(A.2)}}{\le } {{\bar{L}}}+L_{j+1} \overset{\mathrm{(A.16)}}{\le } \zeta \end{aligned}$$

which immediately implies the inequality in (A.17). It follows from (A.5) and its associated optimality condition that $0 \in \nabla \psi _s({\widetilde{x}}_{j}) + \partial \psi _n(y_{j+1})-L_{j+1}({\tilde{x}}_j-y_{j+1})$, which in view of the definition of $u_{j+1}$ in (A.11) implies the inclusion in (A.17). $\square$

The result below gives some estimates on the sequence $\{A_j\}$, which will be important for the convergence analysis of the method.

Lemma A.4

Define

$$\begin{aligned} Q:= 2 \sqrt{ \frac{\max \{L_0,\omega {{{\bar{L}}}}\}}{\mu }} \end{aligned}$$

(A.19)

where $\omega$ is as in (A.14). Then, for every $j \ge 1$, we have

(A.20)

Proof

Let integer $j \ge 1$ be given. Define $\xi _{j}=1/(L_{j}-\mu )$. Using the first equality in (A.7) and the definition of $a_j$ in (A.4), we have that for every $i \le j$,

$$\begin{aligned} A_{i} \overset{\mathrm{(A.7)}}{=} A_{i-1}+ a_{i-1} \overset{\mathrm{(A.4)}}{\ge } A_{i-1} + \left( \frac{\tau _{i-1} \xi _{i}}{2} + \sqrt{\tau _{i-1} \xi _{i} A_{i-1}} \right) \ge \left( \sqrt{A_{i-1}} + \frac{1}{2} \sqrt{\tau _{i-1} \xi _{i}} \right) ^2. \end{aligned}$$

Passing the above inequality to its square root and using Lemma A.3(a) and the fact that (A.15) implies that $\tau _{i-1} \ge \max \{1,\mu A_{i-1}\}$, we then conclude that for every $i \le j$,

$$\begin{aligned} \sqrt{A_{i}} - \sqrt{A_{i-1}}&\ge \frac{1}{2} \sqrt{ \xi _{i}} \ge \frac{1}{2} \sqrt{ \xi _{j} } \end{aligned}$$

(A.21)

$$\begin{aligned} \sqrt{\frac{A_{i}}{A_{i-1}}}&\ge 1 + \frac{1}{2} \sqrt{\mu \xi _{i}} \ge 1 + \frac{1}{2} \sqrt{\mu \xi _{j}}\ge 1 + Q^{-1} \end{aligned}$$

(A.22)

where the last inequality in (A.22) follows from the definition of $\xi _j$, the relation in (A.16), and the definition of Q in (A.19). Adding the inequality in (A.21) from $i=1$ to $i=j$ and using the fact that $A_0=0$, we conclude that $\sqrt{A_j} \ge j \sqrt{\xi _j} /2$ and hence that the first bound in (A.20) holds in view of the fact that $\xi _j \ge 1/L_j$. Now, multiplying the inequality in (A.22) from $i=2$ to $i=j$ and using Lemma A.3(a) and the fact that $A_1= \xi _1$, we conclude that $\sqrt{A_j} \ge \sqrt{\xi _1} (1+Q^{-1})^{j-1} \ge \sqrt{\xi _j} (1+Q^{-1})^{j-1}$, and hence that the second bound in (A.20) holds in view of the fact that $\xi _j \ge 1/L_j$. $\square$

Proposition A.5

Let $\zeta$ and Q be as in (A.14) and (A.19), respectively. ADAP-FISTA always stops (with either success or failure) and does so by performing at most

(A.23)

iterations/resolvent evaluations.

Proof

Let l denote the first quantity in (A.23). Using this definition and the inequality $\log (1+ \alpha ) \ge \alpha /(1+\alpha )$ for any $\alpha >-1$, it is easy to verify that

$$\begin{aligned} \left( 1+Q^{-1}\right) ^{2(l-1)} \ge \frac{\zeta ^2}{\chi \sigma ^2}. \end{aligned}$$

(A.24)

We claim that ADAP-FISTA terminates with success or failure in at most l iterations. Indeed, it suffices to show that if ADAP-FISTA has not stopped with failure up to (and including) the l-th iteration, then it must stop successfully at the l-th iteration. So, assume that ADAP-FISTA has not stopped with failure up to the l-th iteration. In view of step 4 of ADAP-FISTA, it follows that (A.10) holds with $j=l-1$.

This observation together with the inequality in (A.17) with $j=l-1$, (A.20) with $j=l$, and (A.24), then imply that

$$\begin{aligned}{} & {} \Vert y_{l}-x_{0}\Vert ^{2} \overset{\mathrm{(A.10)}}{\ge } \chi A_{l}L_{l} \Vert y_{l}-{\tilde{x}}_{l-1}\Vert ^2 \overset{\mathrm{(A.17)}}{\ge } \frac{\chi }{\zeta ^2}A_lL_l \Vert u_{l}\Vert ^2\overset{\mathrm{(A.20)}}{\nonumber }\\{} & {} \qquad \qquad \qquad \quad \ge \frac{\chi }{\zeta ^2} \left( 1+Q^{-1} \right) ^{2(l-1)} \Vert u_l\Vert ^2 \overset{\mathrm{(A.24)}}{\ge } \frac{1}{\sigma ^2}\Vert u_l\Vert ^2, \end{aligned}$$

(A.25)

and hence that (A.12) is satisfied. In view of Step 5 of ADAP-FISTA, the method must successfully stop at the end of the l-th iteration. We have thus shown that the above claim holds. Moreover, in view of (A.16), it follows that the second term in (A.23) is a bound on the total number of times $L_j$ is multiplied by $\beta$ and step 2 is repeated. Since exactly one resolvent evaluation occurs every time step 2 is executed, the desired conclusion follows. $\square$

We are now ready to give the proof of Proposition A.1.

Proof of Proposition A.1

• (a) The result immediately follows from Proposition A.5 and the assumption that $L_0 = {{{\mathcal {O}}}}({{\bar{L}}})$.

• (b) This is immediate from the termination criterion (A.12) in step 5 of ADAP-FISTA, the inclusion in (A.17), and relation (A.16).

$\square$

1.3 Proof of Proposition A.2

This subsection is dedicated to proving Proposition A.2. Thus, for the remainder of this subsection, assume that $\psi _s$ is $\mu$-strongly convex. The first lemma below presents important properties of the iterates generated by ADAP-FISTA.

Lemma A.6

For every $j\ge 0$ and $x \in \Re ^n$, define

$$\begin{aligned} \gamma _j(x)&:=\ell _{\psi _s}(y_{j+1},{\tilde{x}}_j) + \psi _n(y_{j+1})+\langle s_{j+1},x - y_{j+1}\rangle \nonumber \\ {}&\quad +\frac{\mu }{2}\Vert y_{j+1}-{\tilde{x}}_j\Vert ^2 + \frac{\mu }{2} \Vert x-y_{j+1}\Vert ^2, \end{aligned}$$

(A.26)

where $\psi :=\psi _s+\psi _n$ and $s_{j+1}$ are as in (A.1) and (A.8), respectively. Then, for every $j \ge 0$, we have:

$$\begin{aligned} y_{j+1}&= {{\mathrm{arg\,min}}}_{x}\left\{ \gamma _{j}(x)+\frac{L_{j+1}-\mu }{2}\left\| x-\tilde{x}_{j}\right\| ^{2}\right\} ; \end{aligned}$$

(A.27)

$$\begin{aligned} x_{j+1}&=\underset{x \in \Re ^n}{{{\mathrm{arg\,min}}}}\left\{ a_{j} \gamma _{j}(x)+\tau _j \left\| x-x_{j}\right\| ^{2} /2 \right\} . \end{aligned}$$

(A.28)

Proof

Since $\nabla \gamma _j(y_{j+1})=s_{j+1}$, it follows from (A.8) that $y_{j+1}$ satisfies the optimality condition for (A.27), and thus the relation in (A.27) follows. Furthermore, we have that:

$$\begin{aligned} a_j \nabla \gamma _j(x_{j+1})+\tau _j(x_{j+1}-x_j)&=a_js_{j+1}+a_j\mu (x_{j+1}-y_{j+1})+\tau _j(x_{j+1}-x_{j})\\&\overset{\mathrm{(A.7)}}{=} a_j s_{j+1} -\mu a_jy_{j+1}-\tau _jx_j+ \tau _{j+1}x_{j+1} \overset{\mathrm{(A.9)}}{=}0 \end{aligned}$$

and thus (A.28) follows. $\square$

Before stating the next lemma, recall that if a closed function $\varPsi :\Re ^n\rightarrow \Re \cup \{+\infty \}$ is $\nu$-convex with modulus $\nu >0$, then it has an unique global minimum $z^*$ and

$$\begin{aligned} \varPsi (z^*) +\frac{\nu }{2}\Vert \cdot - z^*\Vert ^2\le \varPsi (\cdot ). \end{aligned}$$

(A.29)

Lemma A.7

For every $j\ge 0$ and $x \in \Re ^n$, we have

$$\begin{aligned}&A_j\gamma _j(y_j) + a_j\gamma _j(x) + \frac{\tau _j}{2} \Vert x_j - x\Vert ^2 - \frac{\tau _{j+1}}{2} \Vert x_{j+1} - x\Vert ^2 \nonumber \\&\quad \ge A_{j+1}\psi (y_{j+1})+\frac{\chi A_{j+1} L_{j+1}}{2}\Vert y_{j+1}-{\tilde{x}}_{j}\Vert ^2. \end{aligned}$$

(A.30)

Proof

Using (A.28), the second identity in (A.7), and the fact that $\varPsi _j:=a_j\gamma _j(\cdot )+\tau _j \Vert \cdot -x_j\Vert ^2/2$ is $(\tau _j+\mu a_j)$-convex, it follows from (A.29) with $\varPsi =\varPsi _j$ and $\nu =\tau _{j+1}$ that

$$\begin{aligned}&a_j\gamma _j(x) + \frac{\tau _j}{2} \Vert x-x_j\Vert ^2 - \frac{\tau _{j+1}}{2} \Vert x-x_{j+1}\Vert ^2\\ {}&\quad \ge a_j\gamma _j(x_{j+1}) + \frac{\tau _j}{2} \Vert x_{j+1}-x_j\Vert ^2 \quad \forall x \in \Re ^n. \end{aligned}$$

Using the convexity of $\gamma _j$, the definitions of $A_{j+1}$ and ${\widetilde{x}}_j$ in (A.7) and (A.4), respectively, and the second equality in (A.15), we have

$$\begin{aligned} A_j\gamma _j(y_j)&+ a_j\gamma _j(x_{j+1}) + \frac{\tau _j}{2} \Vert x_{j+1}-x_j\Vert ^2 \\&\ge A_{j+1} \gamma _j\left( \frac{A_jy_j+a_jx_{j+1}}{A_{j+1}} \right) + \frac{\tau _jA^2_{j+1}}{2a_j^2}\left\| \frac{A_jy_j+a_jx_{j+1}}{A_{j+1}}- \frac{A_jy_j+a_jx_{j}}{A_{j+1}} \right\| ^2\\&\overset{\mathrm{(A.4)}}{\ge } A_{j+1} \min _{x}\left[ \gamma _j\left( x \right) + \frac{\tau _jA_{j+1}}{2a_j^2} \left\| x-{\widetilde{x}}_j\right\| ^2\right] \\&\overset{\mathrm{(A.15)}}{=} A_{j+1}\min _{x}\left\{ \gamma _j(x) + \frac{L_{j+1}-\mu }{2}\Vert x-{\widetilde{x}}_j\Vert ^2\right\} \\&\overset{\mathrm{(A.27)}}{=} A_{j+1}\left[ \gamma _j(y_{j+1}) + \frac{L_{j+1}-\mu }{2}\Vert y_{j+1}-{\widetilde{x}}_j\Vert ^2\right] \\&\overset{\mathrm{(A.26)}}{=} A_{j+1}\left[ \ell _{\psi _s}(y_{j+1};{\tilde{x}}_j) +\psi _n(y_{j+1})+ \frac{L_{j+1}}{2}\Vert y_{j+1}-{\widetilde{x}}_j\Vert ^2 \right] \\&\overset{\mathrm{(A.6)}}{\ge } A_{j+1}\left[ \psi (y_{j+1}) + \frac{\chi L_{j+1}}{2}\Vert y_{j+1}-{\widetilde{x}}_j\Vert ^2 \right] . \end{aligned}$$

The conclusion of the lemma now follows by combining the above two relations. $\square$

Lemma A.8

For every $j \ge 0$, we have $\gamma _j \le \psi$.

Proof

Define:

$$\begin{aligned} {{\tilde{\gamma }}}_j(x):= \ell _{\psi _s}(x;{\tilde{x}}_j) + \psi _n(x)+\frac{\mu }{2}\Vert x-{\tilde{x}}_j\Vert ^2 . \end{aligned}$$

(A.31)

It follows immediately from the fact that $\psi _s$ is $\mu$-convex that ${{\tilde{\gamma }}}_j \le \psi$. Furthermore, immediately from the definition of $y_{j+1}$ in (A.5), we can write:

$$\begin{aligned} y_{j+1}= {{\mathrm{arg\,min}}}_{x}\left\{ {\tilde{\gamma }}_{j}(x)+\frac{L_{j+1} -\mu }{2}\left\| x-\tilde{x}_{j}\right\| ^{2}\right\} . \end{aligned}$$

(A.32)

Now, clearly from (A.32) and the definition of $s_{j+1}$ in (A.8), we see that $s_{j+1} \in \partial {{\tilde{\gamma }}}_j(y_{j+1})$. Furthermore, since ${{\tilde{\gamma }}}_j$ is $\mu$-convex, it follows from the subgradient rule for the sum of convex functions that the above inclusion is equivalent to $s_{j+1} \in \partial \left( {{\tilde{\gamma }}}_j(\cdot )-\frac{\mu }{2}\Vert \cdot -y_{j+1}\Vert ^2\right) (y_{j+1}).$ Hence, the subgradient inequality and the fact that ${{\tilde{\gamma }}}_j(x) \le \psi (x)$ imply that for all $x\in \Re ^{n}$:

$$\begin{aligned} \psi (x)\ge {{\tilde{\gamma }}}_j(x)&\ge {{\tilde{\gamma }}}_j(y_{j+1}) +\langle s_{j+1},x-y_{j+1}\rangle +\frac{\mu }{2}\Vert x-y_{j+1}\Vert ^2=\gamma _j(x) \end{aligned}$$

and thus the statement of the lemma follows. $\square$

Lemma A.9

For every $j \ge 0$ and $x \in \textrm{dom}\,\psi _n$, we have

$$\begin{aligned} \eta _j(x) - \eta _{j+1} (x) \ge \frac{\chi A_{j+1}L_{j+1}}{2} \Vert y_{j+1} - {\widetilde{x}}_j \Vert ^2 \end{aligned}$$

where

$$\begin{aligned} \eta _j(x):= A_j [ \psi (y_j) - \psi (x) ] + \frac{\tau _j}{2} \Vert x-x_j\Vert ^2. \end{aligned}$$

Proof

Subtracting $A_{j+1} \psi (x)$ from both sides of the inequality in (A.30) and using Lemma A.8 we have

$$\begin{aligned}&A_j \psi (y_j) + a_j\psi (x)-A_{j+1}\psi (x) + \frac{\tau _j}{2} \Vert x_j - x\Vert ^2 - \frac{\tau _{j+1}}{2} \Vert x_{j+1} - x\Vert ^2 \\&\quad \ge A_{j+1} \psi (y_{j+1})-A_{j+1}\psi (x) + \frac{\chi A_{j+1}L_{j+1}}{2} \Vert y_{j+1} - {\widetilde{x}}_j \Vert ^2 . \end{aligned}$$

The result now follows from the first equality in (A.7) and the definition of $\eta _j(x)$. $\square$

We now state a result that will be important for deriving complexity bounds for ADAP-FISTA.

Lemma A.10

For every $j \ge 0$ and $x \in \textrm{dom}\,\psi _n$, we have

$$\begin{aligned} A_j [ \psi (y_j) - \psi (x) ] + \frac{\tau _j}{2} \Vert x-x_j\Vert ^2 \le \frac{1}{2} \Vert x-x_0\Vert ^2 - \frac{\chi }{2} \sum _{i=0}^{j-1} A_{i+1}L_{i+1} \Vert y_{i+1} - {\widetilde{x}}_i \Vert ^2. \end{aligned}$$

(A.33)

Proof

Summing the inequality of Lemma A.9 from $j=0$ to $j=j-1$, using the facts that $A_0=0$ and $\tau _0=1$, and using the definition of $\eta _j(\cdot )$ in Lemma A.9 gives us the inequality of the lemma. $\square$

We are now ready to give the proof of Proposition A.2.

Proof of Proposition A.2

Since $\psi _s$ is $\mu$-convex, Lemma A.10 holds. Thus, using (A.33) with $x=y_j$, it follows that for all $j\ge 0$:

$$\begin{aligned} \Vert y_j-x_0\Vert ^2 \overset{\mathrm{(A.33)}}{\ge }\chi \sum _{i=1}^{j}A_{i}L_{i} \Vert y_{i}-{\tilde{x}}_{i-1}\Vert ^2 \ge \chi A_jL_j\Vert y_{j}-{\tilde{x}}_{j-1}\Vert ^2. \end{aligned}$$

(A.34)

Hence, for all $j\ge 0$, relation (A.10) in step 4 of ADAP-FISTA is always satisfied and thus ADAP-FISTA never fails. In view of this observation and Proposition A.1, it follows that if $\psi _s$ is $\mu$-convex then ADAP-FISTA always terminates successfully with a (y, u, L) satisfying relation (A.13) in a finite number of iterations. The inclusion $u\in (\psi _s+\psi _n)(y)$ then follows immediately from the inclusion in (A.13) and the subgradient rule for the sum of convex functions. $\square$

Technical Results for Proof of Lagrange Multipliers

The following basic result is used in Lemma B.3. Its proof can be found, for instance, in [4, Lemma A.4]. Recall that $\nu ^+_A$ denotes the smallest positive singular value of a nonzero linear operator A.

Lemma B.1

Let $A:\Re ^n \rightarrow \Re ^l$ be a nonzero linear operator. Then,

$$\begin{aligned} \nu ^+_A\Vert u\Vert \le \Vert A^*u\Vert , \quad \forall u \in A(\Re ^n). \end{aligned}$$

The following technical result, whose proof can be found in Lemma 3.10 of [16], plays an important role in the proof of Lemma B.3 below.

Lemma B.2

Let h be a function as in (C1). Then, for every $\delta \ge 0$, $z\in {{\mathcal {H}}}$, and $\xi \in \partial _{\delta } h(z)$, we have

$$\begin{aligned} \Vert \xi \Vert {\textrm{dist}}(u,\partial {{\mathcal {H}}}) \le \left[ \textrm{dist}(u,\partial {{\mathcal {H}}})+\Vert z-u\Vert \right] M_h + \langle \xi ,z-u\rangle +\delta \quad \forall u \in {{\mathcal {H}}} \end{aligned}$$

(B.1)

where $\partial {{{\mathcal {H}}}}$ denotes the boundary of ${{{\mathcal {H}}}}$.

Lemma B.3

Assume that h is a function as in condition (C1) and $A:\Re ^n \rightarrow \Re ^l$ is a linear operator satisfying condition (C2). Assume also that the triple $(z,q,r) \in \Re ^{n} \times A(\Re ^{n}) \times \Re ^{n}$ satisfy $r \in \partial h(z)+A^{*}q$. Then:

• (a) there holds

  $$\begin{aligned} {\bar{d}}\nu _A^{+}\Vert q\Vert \le 2 D_h\left( M_h + \Vert r\Vert \right) - \langle q,Az-b\rangle ; \end{aligned}$$

  (B.2)

• (b) if, in addition,

  $$\begin{aligned} q=q^-+\chi (Az-b) \end{aligned}$$

  (B.3)

  for some $q^-\in \Re ^l$ and $\chi >0$, then we have

  $$\begin{aligned} \Vert q\Vert \le \max \left\{ \Vert q^-\Vert ,\frac{2D_h(M_h+\Vert r\Vert )}{{{\bar{d}}} \nu ^{+}_A} \right\} . \end{aligned}$$

  (B.4)

Proof

(a) The assumption on (z, q, r) implies that $r-A^{*}q \in \partial h(z)$. Hence, using the Cauchy-Schwarz inequality, the definitions of ${{\bar{d}}}$ and ${{\bar{z}}}$ in (2.15) and (C2), respectively, and Lemma B.2 with $\xi =r-A^{*}q$, $u={{\bar{z}}}$, and $\delta =0$, we have:

$$\begin{aligned} {{\bar{d}}}\Vert r-A^{*}q\Vert -\left[ {{\bar{d}}}+\Vert z-{{\bar{z}}}\Vert \right] M_h&\overset{\mathrm{(B.1)}}{\le } \langle r-A^{*}q,z-{{\bar{z}}}\rangle \le \Vert r\Vert \Vert z-{{\bar{z}}}\Vert - \langle q,Az-b\rangle . \end{aligned}$$

(B.5)

Now, using the above inequality, the triangle inequality, the definition of $D_h$ in (C1), and the facts that ${{\bar{d}}} \le D_h$ and $\Vert z-{{\bar{z}}}\Vert \le D_h$, we conclude that:

$$\begin{aligned} {{\bar{d}}} \Vert A^*q\Vert + \langle q,Az-b\rangle&\overset{\mathrm{(B.5)}}{\le } \left[ {{\bar{d}}}+\Vert z-{{\bar{z}}}\Vert \right] M_h + \Vert r\Vert \left( D_h + {{\bar{d}}}\right) \le 2 D_h\left( M_h + \Vert r\Vert \right) . \end{aligned}$$

(B.6)

Noting the assumption that $q \in A(\Re ^n)$, inequality (B.2) now follows from the above inequality and Lemma B.1.

(b) Relation (B.3) implies that $\langle q,Az-b\rangle =\Vert q\Vert ^2/\chi -\langle q^-,q\rangle /\chi$, and hence that

$$\begin{aligned} {{\bar{d}}} \nu ^{+}_A\Vert q\Vert +\frac{\Vert q\Vert ^2}{\chi }\le 2D_h(M_h+\Vert r\Vert )+\frac{\langle q^-,q\rangle }{\chi }\le 2D_h(M_h+\Vert r\Vert )+\frac{\Vert q\Vert }{\chi }\Vert q^-\Vert ,\nonumber \\ \end{aligned}$$

(B.7)

where the last inequality is due to the Cauchy-Schwarz inequality. Now, letting K denote the right hand side of (B.4) and using (B.7), we conclude that

$$\begin{aligned} \left( {{\bar{d}}} \nu ^+_A+\frac{\Vert q\Vert }{\chi } \right) \Vert q\Vert \overset{\mathrm{(B.7)}}{\le } \left( \frac{2D_h(M_h+\Vert r\Vert )}{K}+\frac{\Vert q\Vert }{\chi }\right) K\le \left( {{\bar{d}}} \nu ^+_A+\frac{\Vert q\Vert }{\chi } \right) K, \end{aligned}$$

(B.8)

and hence that (B.4) holds. $\square$