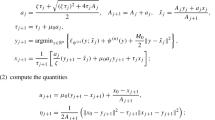An accelerated inexact dampened augmented Lagrangian method for linearly-constrained nonconvex composite optimization problems

Abstract

This paper proposes and analyzes an accelerated inexact dampened augmented Lagrangian (AIDAL) method for solving linearly-constrained nonconvex composite optimization problems. Each iteration of the AIDAL method consists of: (i) inexactly solving a dampened proximal augmented Lagrangian (AL) subproblem by calling an accelerated composite gradient (ACG) subroutine; (ii) applying a dampened and under-relaxed Lagrange multiplier update; and (iii) using a novel test to check whether the penalty parameter of the AL function should be increased. Under several mild assumptions involving the dampening factor and the under-relaxation constant, it is shown that the AIDAL method generates an approximate stationary point of the constrained problem in $\mathcal{O}(\varepsilon ^{-5/2}\log \varepsilon ^{-1})$ iterations of the ACG subroutine, for a given tolerance $\varepsilon >0$. Numerical experiments are also given to show the computational efficiency of the proposed method.

Appendices

A Key technical bounds

The appendix presents a key technical bound that is used in the analysis of AIDAL.

Lemma A.1

For every $(\tau ,\theta )\in [0,1]^{2}$ satisfying $\tau \le \theta ^{2}$ and every $a,b\in \mathbb {R}^{n}$, we have that

$$\begin{aligned} \Vert a-(1-\theta )b\Vert ^{2}-\tau \Vert a\Vert ^{2}\ge \left[ \frac{(1-\tau )- (1-\theta )^{2}}{2}\right] \left( \Vert a\Vert ^{2}-\Vert b\Vert ^{2}\right) . \end{aligned}$$

(40)

Proof

Let $a,b\in \mathbb {R}^{n}$ be fixed and define

$$\begin{aligned} z=\left[ \begin{array}{c} \Vert a\Vert \\ \Vert b\Vert \end{array}\right] ,\quad M=\left[ \begin{array}{cc} (1-\tau )+(1-\theta )^{2} &{} -2(1-\theta )\\ -2(1-\theta ) &{} (1-\tau )+(1-\theta )^{2} \end{array}\right] . \end{aligned}$$

(41)

Moreover, using our assumption of $\tau \le \theta ^{2}\le 1$, observe that

$$\begin{aligned} \det M&=\left[ (1-\tau )+(1-\theta )^{2}-2(1-\theta )\right] \left[ (1-\tau )+(1-\theta )^{2}+2(1-\theta )\right] \\&=\left[ \theta ^{2}-\tau \right] \left[ (1-\tau )+(1-\theta )^{2}+2(1-\theta )\right] \ge 0, \end{aligned}$$

and hence, by Sylvester’s criterion, it follows that $M\succeq 0$. Combining this fact with the Cauchy–Schwarz inequality and (41), we thus have that

$$\begin{aligned} \Vert a-(1-\theta )b\Vert ^{2}-\tau \Vert a\Vert ^{2}&\ge (1-\tau ) \Vert a\Vert ^{2}-2(1-\theta )\Vert a\Vert \cdot \Vert b\Vert +(1-\theta )^{2}\Vert b\Vert ^{2}\\&=\frac{1}{2}z^{T}Mz+\left[ \frac{(1-\tau )-(1-\theta )^{2}}{2}\right] \left( \Vert a\Vert ^{2}-\Vert b\Vert ^{2}\right) \\ {}&\ge \left[ \frac{(1-\tau )-(1-\theta )^{2}}{2}\right] \left( \Vert a\Vert ^{2}-\Vert b\Vert ^{2}\right) . \end{aligned}$$

$\square$

B Statement and analysis of the ACG algorithm

Recall from Sect. 1 that our interest is in solving (1) by inexactly solving NCO subproblems of the form in (3). This subsection presents an ACG algorithm for inexactly solving latter type of problem and it considers the more general class of NCO problems

$$\begin{aligned} \min _{u\in \mathbb {R}^{n}}\left\{ \psi (u):= \psi _{s}(u)+\psi _{n}(u)\right\} , \end{aligned}$$

(42)

where the functions $\psi _{s}$ and $\psi _{n}$ are assumed to satisfy the following assumptions:

• (B1) $\psi _{n}:\mathbb {R}^{n}\mapsto (-\infty ,\infty ]$ is a proper closed convex function.

• (B2) $\psi _{s}$ is $\mu$-strongly convex and continuously differentiable on $\mathbb {R}^{n}$ and satisfies

  $$\begin{aligned} \Vert \nabla \psi _s(z) - \nabla \psi _s(z')\Vert \le L\Vert z-z'\Vert \end{aligned}$$

  (43)

  for every $z',z\in \mathbb {R}^{n}$ and some $L > 0$ and $\mu \in (0, L]$.

Clearly, problem (3) is a special case of (42), and hence, any result that is stated in the context of (42) also applies to (3). It is also well-known that assumption (B2) implies

$$\begin{aligned} \frac{\mu }{2} \Vert z'-z\Vert ^{2} \le \psi _{s}(z')-\ell _{\psi _{s}}(z';z)\le \frac{L}{2}\Vert z'-z\Vert ^{2}, \end{aligned}$$

(44)

for every $z,z'\in \mathbb {R}^{n}$.

The pseudocode for the ACG algorithm is stated in Algorithm B.1 which, for a given a pair $({\sigma },x_{0})\in \mathbb {R}_{++}\times \textrm{dom}\psi _{n}$, inexactly solves (42) by obtaining a pair (z, v) satisfying

$$\begin{aligned} v\in \nabla \psi _{s}(z)+ \partial \psi _{n}(z),\quad \Vert v\Vert \le {\sigma }\Vert z-x_{0}\Vert . \end{aligned}$$

(45)

Note that if ACG algorithm obtains the aforementioned triple with ${\sigma }=0$ then the first component of the triple is, in fact, a global solution of (42). Indeed, if ${\sigma }=0$ then the above inequality implies that $v=0$, and the above inclusion reduces to $0\in \partial (\psi _{s}+\psi _{n})(z)$, which in view of (7) clearly implies that z is a global solution of (42).

We now devote the remainder of the section to proving the following properties about the ACG algorithm. Variations of the arguments that follow can also be found in [9, 28].

Proposition B.1

The following properties hold about the ACG algorithm:

• (a) for every $j\ge 0$, it holds that

  $$\begin{aligned} u_{j+1}\in \nabla \psi _{s}(x_{j+1}) + \partial \psi _{n}(x_{j+1}) = {\partial }(\psi _s + \psi _n)(x_{j+1}); \end{aligned}$$

• (b) it stops in a number of iterations bounded above by

  $$\begin{aligned} \left\lceil 1 + 2\sqrt{\frac{L}{\mu }}\log _{1}^{+} \left\{ \frac{4L(L+\mu )^2}{\mu \sigma ^2} \right\} \right\rceil , \end{aligned}$$

  (46)

  and its output (z, v) satisfies (45).

We first present some technical properties about the generated iterates of Algorithm B.1.

Lemma B.2

Define the quantities

$$\begin{aligned}&\tau _{j} := 1 + \mu A_{j}, \end{aligned}$$

(47)

$$\begin{aligned}&\tilde{q}_{j+1}(\cdot ) := \ell _{\psi _s}(\cdot ;\tilde{x}_j) + \psi _n(\cdot ) + \frac{\mu }{2}\Vert \cdot -\tilde{x}_j\Vert ^2 \end{aligned}$$

(48)

$$\begin{aligned}&q_{j+1}(\cdot ) := \tilde{q}_j(x_{j+1}) + L \langle \tilde{x}_j - x_{j+1}, \cdot - x_{j+1} \rangle + \frac{\mu }{2}\Vert \cdot - x_{j+1}\Vert ^2, \end{aligned}$$

(49)

for every $j\ge 0$. Then, for every $j\ge 1$, the following statements hold:

• (a) $A_{j+1} \ge \left[ 1 + \sqrt{\mu }/(2\sqrt{L})\right] ^{2j} / L$;

• (b) $x_{j+1} = \textrm{argmin}_{x} \{{q}_{j+1}(x) + L\Vert x-\tilde{x}_j\Vert ^2/2\}$;

• (c) $y_{j+1} = \textrm{argmin}_y\{a_j q_{j+1}(y) + \tau _{j} \Vert y-y_j\Vert ^2/2\}$;

• (d) $q_{j+1}(\cdot ) \le \psi (\cdot )$.

Proof

(a) See, for example, [23, Lemma 4].

(b) Since $\nabla q_{j+1}(x_{j+1}) = L(\tilde{x}_j - x_{j+1})$, it follows that $x_{j+1}$ satisfies the optimality condition of the given minimization problem. Hence, the desired identity follows.

(c) It follows from the definition of ${q}_{j+1}(\cdot )$ and the update rule of $y_{j+1}$ that $a_j \nabla q_{j+1}(y_{j+1}) = \tau _{j+1} (y_{j+1}-y_j)$. The conclusion now follows from the optimality condition for the desired identity.

(d) In view of (44) and the definition of $\tilde{q}_{j+1}$, we first have that $\tilde{q}_{j+1}(\cdot ) \le \psi (\cdot )$. On the other hand, it follows from the optimality condition of $\tilde{x}_{j+1}$ in Algorithm B.1, the convexity of $\psi _n$, and the definition of $q_j(\cdot )$ that $L(\tilde{x}_j - x_{j+1}) \in \partial \tilde{q}_{j+1}(x_{j+1})$. Furthermore, since $\tilde{q}_{j+1}$ is $\mu$-strongly convex, we also have $L(\tilde{x}_j - x_{j+1}) \in \partial (\tilde{q}_{j+1} - \mu \Vert \cdot -x_{j+1}\Vert ^2/2)(x_{j+1})$. Combining all these facts with the definition of the subdifferential, we thus conclude that

$$\begin{aligned} \psi (\cdot ) \ge \tilde{q}_{j+1}(\cdot ) \ge \tilde{q}_{j+1}(x_{j+1}) + L\langle \tilde{x}_j - x_{j+1}, \cdot - x_{j+1} \rangle + \frac{\mu }{2}\Vert \cdot -x_{j+1}\Vert ^2 = q_{j+1}(\cdot ). \end{aligned}$$

$\square$

The next result establishes an important technical bound.

Lemma B.3

For every $j\ge 0$ and $y\in \mathbb {R}^{n}$, it holds that

$$\begin{aligned} \begin{gathered} A_{j} q_{j+1}(x_j) + a_j q_{j+1}(y) + \frac{\tau _{j}}{2}\Vert y_j - y\Vert ^2 - \frac{\tau _{j+1}}{2}\Vert y_{j+1}-y\Vert ^2 \\ \quad \ge A_{j+1} \left[ \psi (x_{j+1}) + \frac{\mu }{2}\Vert x_{j+1} - \tilde{x}_j\Vert ^2 \right] , \end{gathered} \end{aligned}$$

(50)

where $\tau _j$ and $q_j(\cdot )$ are as in (47) and (49), respectively.

Proof

Using the update rule for $A_{j+1}$ we first note that $\tau _{j+1} = \tau _j + \mu a_j$. Combining this fact, the optimality condition in Lemma B.2(c) and the fact that $a_j q_{j+1}(\cdot ) + \tau _{j}\Vert \cdot -y_j\Vert ^2/2$ is $\tau _{j+1}$-strongly convex, we then have that

$$\begin{aligned} a_j q_{j+1}(y)+\frac{\tau _{j}}{2}\Vert y-y_j\Vert ^2 - \frac{\tau _{j+1}}{2}\Vert y-y_{j+1}\Vert ^2 \ge a_j q_{j+1}(y_{j+1})+\frac{\tau _{j}}{2}\Vert y_{j+1}-y_j\Vert ^2\qquad \end{aligned}$$

(51)

for every $y\in \mathbb {R}^{n}$. On the other hand, using the convexity of $q_{j+1}(\cdot )$, the second bound in (44), Lemma B.2(b), and the quadratic subproblem associated with $a_j$, we have

$$\begin{aligned}&A_{j}q_{j+1}(x_{j})+a_{j}q_{j+1}(y_{j+1})+\frac{\tau _{j}}{2}\Vert y_{j+1}-y_{j}\Vert ^{2} \nonumber \\&\quad \ge A_{j+1}q_{j+1}\left( \frac{A_{j}x_{j}+a_{j}y_{j+1}}{A_{j+1}}\right) +\frac{\tau _{j}A_{j+1}^{2}}{2a_{j}^{2}}\left\| \frac{A_{j}x_{j}+a_{j}y_{j+1}}{A_{j+1}}-\frac{A_{j}x_{j}+a_{j}y_{j}}{A_{j+1}}\right\| ^{2} \nonumber \\&\quad \ge A_{j+1}\min _{x\in \mathbb {R}^{n}}\left\{ q_{j+1}(x)+\frac{\tau _{j}A_{j+1}^{2}}{2a_{j}^{2}}\Vert x-\tilde{x}_{j}\Vert ^{2}\right\} =A_{j+1}\min _{x\in \mathbb {R}^{n}}\left\{ q_{j+1}(x)+\frac{L}{2}\Vert x-\tilde{x}_{j}\Vert ^{2}\right\} \nonumber \\&\quad =A_{j+1}\left[ q_{j+1}(x_{j+1})+\frac{L}{2}\Vert x_{j+1}-\tilde{x}_{j}\Vert ^{2}\right] \ge A_{j+1} \left[ \psi (x_{j+1}) + \frac{\mu }{2}\Vert x_{j+1}-\tilde{x}_{j}\Vert ^{2} \right] .\qquad \end{aligned}$$

(52)

The conclusion follows from combining (51) and (52). $\square$

We now derive a general telescopic bound on the quantity $\Vert x_{j+1} - \tilde{x}_j\Vert ^2$.

Lemma B.4

For every $j\ge 0$ and $x\in \mathbb {R}^{n}$, it holds that

$$\begin{aligned} \frac{\mu A_{j+1}}{2}\Vert x_{j+1} - \tilde{x}_j\Vert ^2 \le \eta _j(x) - \eta _{j+1}(x), \end{aligned}$$

(53)

where the potential $\eta _i(\cdot )$ is given by

$$\begin{aligned} \eta _i(\cdot ):= A_i [\psi (x_i) - \psi (\cdot )] + \frac{\tau _i}{2} \Vert \cdot - y_i\Vert ^2 \quad \forall i\ge 0. \end{aligned}$$

(54)

Proof

Subtracting $A_{j+1} \psi (y)$ from (50) and using Lemma B.2(d), we have that

$$\begin{aligned}&\frac{A_{j+1}}{2}\Vert x_{j+1}-\tilde{x}_j\Vert ^2 + A_{j+1}\left[ \psi (x_{j+1}) - \psi (y)\right] \\&\quad \le A_{j} q_{j+1}(x_j) + a_j q_{j+1}(y) - A_{j+1} \psi (y) + \frac{\tau _{j}}{2}\Vert y_j - y\Vert ^2 - \frac{\tau _{j+1}}{2}\Vert y_{j+1}-y\Vert ^2 \\&\quad \le A_{j} \psi (x_j) + a_j \psi (y) - A_{j+1} \psi (y) + \frac{\tau _{j}}{2}\Vert y_j - y\Vert ^2 - \frac{\tau _{j+1}}{2}\Vert y_{j+1}-y\Vert ^2. \end{aligned}$$

The conclusion follows by re-arranging the above bound and using the update rule for $A_{j+1}$ and the definition of $\eta _i(\cdot )$. $\square$

Specializing the above result, we establish a bound for the residuals $\{u_{j+1}\}_{j\ge 0}$ in terms of the prox residual $\Vert x_{j+1} - x_0\Vert ^2$.

Lemma B.5

For every $j \ge 0$, it holds that

$$\begin{aligned} \Vert u_{j+1}\Vert ^2 \le \frac{4(L+\mu )^2}{\mu A_{j+1}} \Vert x_{j+1}-x_0\Vert ^2. \end{aligned}$$

(55)

Proof

Using assumption (B2), the definition of $u_{j+1}$, the bound $(a+b)^2 \le 2a^2 + 2b^2$ for $a,b\in \mathbb {R}$, (53) at $x=x_j$, and the fact that $(A_0,\tau _0)=(0,1)$, we have that

$$\begin{aligned}&\frac{\mu A_{j+1}\Vert u_{j+1}\Vert ^{2}}{2}\\ {}&\quad \le \frac{\mu \sum _{i=0}^{j}A_{i+1}\Vert u_{i+1}\Vert ^{2}}{2}\\&\quad =\frac{\mu \sum _{i=0}^{j}A_{i+1}\Vert \nabla \psi _{s}(x_{i+1})-\nabla \psi _{s}(\tilde{x}_{i})+(L+\mu )(\tilde{x}_{i}-x_{i+1})\Vert ^{2}}{2}\\&\quad \overset{\text {(B2)}}{\le } \mu \sum _{i=0}^{j}A_{i+1}\left[ \Vert \nabla \psi _{s}(x_{i+1})-\nabla \psi _{s}(\tilde{x}_{i})\Vert ^{2}+(L+\mu )^2\Vert \tilde{x}_{i}-x_{i+1}\Vert ^{2}\right] \\&\quad \overset{(53)}{\le }\ 2\mu (L+\mu )^2\sum _{i=0}^{j}A_{i+1}\Vert \tilde{x}_{i}-x_{i+1}\Vert ^{2}\le 4(L+\mu )^2\left[ \eta _{0}(x_{j+1})-\eta _{k+1}(x_{j+1})\right] \\&\quad \overset{(A_{0}, \tau _{0}) = (0,1)}{=}4(L+\mu )^2\left[ \frac{1}{2}\Vert x_{0}-x_{j+1}\Vert ^{2}-\frac{\tau _{j+1}}{2}\Vert x_{0}-x_{j+1}\Vert ^{2}\right] \\&\quad \le 2(L+\mu )^2\Vert x_{0}-x_{j+1}\Vert ^{2}. \end{aligned}$$

$\square$

We are now ready to prove Proposition B.1.

Proof of Proposition B.1

(a) Using the optimality of $x_{j+1}$ the definition of $u_{j+1}$ in Algorithm B.1, we have that

$$\begin{aligned} 0&\in \nabla \psi _s({\tilde{x}_j}) + {\partial }\psi _n(x_{j+1}) + (L+\mu )(x_{j+1} - \tilde{x}_j)\\ {}&= -u_{j+1} + \nabla \psi _s({x}_{j+1}) + {\partial }\psi _n(x_{j+1})\\&= -u_{j+1} + {\partial }(\psi _s + \psi _n)(x_{j+1}) \end{aligned}$$

where the last identity follows from the fact that $\psi _s$ and $\psi _n$ are convex (see (B1)–(B2)).

(b) Let J denote the quantity in (46). Using Lemma B.2(a) and the bound $\log (1+t) \ge t/2$ for $t\in [0,1]$, it is straightforward to verify that $4(L+\mu )^2/(\mu A_{J+1}) \le \sigma ^2$. It then follows from the previous bound and (55) that

$$\begin{aligned} \Vert u_{J+1}\Vert ^2 \le \frac{4(L+\mu )^2}{\mu A_{J+1}} \Vert x_{J+1}-x_0\Vert ^2 \le \sigma ^2 \Vert x_{J+1}-x_0\Vert ^2. \end{aligned}$$

Consequently, it follows from the above bound, part (a), and the termination condition of Algorithm B.1 that the ACG algorithm stops in a number of iterations bounded above by J. $\square$

C Necessary optimality conditions

This appendix shows that if $\hat{z}$ local minimum of (1) then condition (11) holds. Throughout this appendix, we denote

$$\begin{aligned} \psi '(x;d) = \lim _{t\downarrow 0} \frac{\psi (x+td)-\psi (x)}{t} \end{aligned}$$

as the directional derivative of a function $\psi$ at x in the direction d.

The first useful result presents a relationship between directional derivatives of composite functions and the usual first-order necessary conditions.

Lemma C.1

Let $g:\mathbb {R}^{n}\mapsto (-\infty ,\infty ]$ be a proper convex function, and let f be a differentiable function on $\textrm{dom}g$. Then, for every $x\in \textrm{dom}g$, the following statements hold:

• (a) $\inf _{\Vert d\Vert \le 1} (f+g)'(x;d) = -\inf _{u\in \mathbb {R}^{n}} \{\Vert u\Vert : u \in \nabla f(x) +\partial g(x)\}$;

• (b) if x is a local minimum of $f+h$ then $0 \in \nabla f(x)+\partial h(x)$.

Proof

(a) See [14, Lemma 15] with $({{\mathcal {X}}}, h)=(\mathbb {R}^{n}, g)$.

(b) This follows immediately from (a) and the fact that $(f+h)'(x;d)\ge 0$ for every $d\in \mathbb {R}^{n}$.

We now establish the aforementioned necessary condition.

Proposition C.2

Let (f, h, A, b) be as in (A1)-(A4). If $\hat{z}$ is a local minimum of (1), then there exists a multiplier $\hat{p}$ such that (11) holds.

Proof

We first establish an important technical identity. Let $S=\{z \in \mathbb {R}^{n}: Az=b\}$, let $\delta _S$ denote the indicator function of S, i.e., the function that takes value 0 if its input is in S and $+\infty$ otherwise, and let ${\text {*}}{ri}X$ denote the relative interior of a set X. Since assumptions (A3)–(A4) imply that ${\text {*}}{ri}{{\mathcal {H}}} \cap {\text {*}}{ri}{S} = \textrm{int}{{\mathcal {H}}} \cap {S} \ne \emptyset$, it follows from [26, Theorem 23.8] that for every $x\in {{\mathcal {H}}} \cap S$ we have

$$\begin{aligned} \partial (\delta _S + h)(x) = \partial \delta _S(x) + \partial h(x) = N_S(x) + \partial h(x) = \{\xi + A^*p: \xi \in \partial h(x)\}. \qquad \end{aligned}$$

(56)

The conclusion follows from the above identity and Lemma C.1(b) with $g=h+\delta _{S}$.

D Adaptive AIDAL

This appendix presents an adaptive version of AIDAL where we choose the prox stepsize adaptively.

Before presenting the algorithm, we first motivate its construction under the assumption that the reader is familiar with the notation and results of Sect. 3. To begin, the careful reader may notice that the special choice of $\lambda =1/(2m)$ in AIDAL (Algorithm 2.1) is only needed to ensure that the function $\lambda {{\mathcal {L}}}_c^\theta (\cdot ;p) + \Vert \cdot \Vert ^2$ is strongly convex with respect to the norm $\Vert x\Vert _Q = \langle x, [(1-\lambda m)I + c\lambda A^*A]x \rangle$ for every $c>0$ and $p\in A(\mathbb {R}^{n})$. Moreover, this global property is only needed to show that:

• (i) the $k{\textrm{th}}$ ACG call of AIDAL stops with a pair $(z_k, v_k)$ satisfying $\Vert v_k\Vert \le \sigma \Vert z_k - z_{k-1}\Vert$;

• (ii) $\lambda \Vert \hat{v}_i\Vert \lesssim \Psi _{k-1}^\theta - \Psi _{k}^\theta$.

The other technical details of Sect. 3, such as the boundedness of $\Psi _i^\theta$, are straightforward to show as long as the prox stepsize is bounded. As a consequence, a natural relaxation of AIDAL is to employ a line search at its $k{\textrm{th}}$ outer iteration for the largest $\lambda$ within a bounded range satisfying conditions (i) and (ii) above.

In Algorithm D.1, we present one possible relaxation. Specifically, the $k{\textrm{th}}$ prox stepsize $\lambda _k$ is chosen from a set of candidates in the range $(0, \lambda _{k-1}]$.

We now make a few remarks about Algorithm D.1. First, the candidate search space for the $k{\textrm{th}}$ prox stepsize forms a geometrically decreasing sequence and $\lambda _k \le \lambda _{k-1}$. Second, the first condition of (57) corresponds to condition (i), while the second condition corresponds to condition (ii). Moreover, the second condition of (57) always holds when $\lambda = 1/(2\,m)$ due to Lemma 3.4, Lemma 3.5, and the definition of $\hat{v}_i$ which imply (cf. the proof of Proposition 3.3) that

$$\begin{aligned} \Vert v_{k}+z_{k-1}-z_{k}\Vert ^{2}&= \lambda ^{2}\Vert \hat{v}_{k}\Vert ^{2}\le 9\lambda (\Psi _{k-1}^{\theta }-\Psi _{k}^{\theta }). \end{aligned}$$

Third, in view of the previous remark, since conditions (i) and (ii) are always satisfied whenever $\lambda \le 1/(2m)$, we also have that $\lambda _k \in [1/(2\gamma m), \lambda _0]$ and, hence, the sequence $\{\lambda _k\}_{k\ge 1}$ is bounded.

Notice that it is not immediately clear how one obtains $\beta _k$ at the $k{\textrm{th}}$ outer iteration. One possible approach is to apply an adaptive ACG variant to the stepsize sequence $\{\lambda _{k-1}\beta ^{-j}\}_{j\ge 0}$ in which the variant has a mechanism to determine if at least one of the conditions in (57) is reachable. This is so that if none of the conditions in (57) are reachable for some candidate $\lambda$, then the variant can be called again with a smaller stepsize. One example is the adaptive ACG variant in [9], which contains a mechanism for determining the reachability of the first condition in (57) and can even adaptively choose its other curvature parameters, such as L in Algorithm B.1. Note that if the ACG has already been called with the $\beta _k$ satisfying (57) during the $\beta _k$ line search, then it does not need to be called again when executing the steps of Algorithm 2.1.

Before closing this section, we briefly discuss the convergence and iteration complexity of the method. Convergence of the method is straightforward to establish using the same techniques of Sect. 3 and the fact that $\lambda _k$ is bounded (see the remarks above). On the other hand, it can be shown that the iteration complexity of the method is on the same order of complexity as in Theorem 2.3. Without going through the cumbersome technical details, we assert that this follows from the boundedness of the stepsizes $\lambda _k$, the fact that the search for the next stepsize is done geometrically, and arguments similar to other adaptive augmented Lagrangian/penalty methods such as the one in [11].