Multidimensional WENO-AO Reconstructions Using a Simplified Smoothness Indicator and Applications to Conservation Laws

Abstract

Finite volume, weighted essentially non-oscillatory (WENO) schemes require the computation of a smoothness indicator. This can be expensive, especially in multiple space dimensions. We consider the use of the simple smoothness indicator $\sigma ^{\textrm{S}}= \frac{1}{N_{\textrm{S}}-1}\sum _{j} ({\bar{u}}_{j} - {\bar{u}}_{m})^2$, where $N_{\textrm{S}}$ is the number of mesh elements in the stencil, ${\bar{u}}_j$ is the local function average over mesh element j, and index m gives the target element. Reconstructions utilizing standard WENO weighting fail with this smoothness indicator. We develop a modification of WENO-Z weighting that gives a reliable and accurate reconstruction of adaptive order, which we denote as SWENOZ-AO. We prove that it attains the order of accuracy of the large stencil polynomial approximation when the solution is smooth, and drops to the order of the small stencil polynomial approximations when there is a jump discontinuity in the solution. Numerical examples in one and two space dimensions on general meshes verify the approximation properties of the reconstruction. They also show it to be about 10 times faster in two space dimensions than reconstructions using the classic smoothness indicator. The new reconstruction is applied to define finite volume schemes to approximate the solution of hyperbolic conservation laws. Numerical tests show results of the same quality as standard WENO schemes using the classic smoothness indicator, but with an overall speedup in the computation time of about 3.5–5 times in 2D tests. Moreover, the computational efficiency (CPU time versus error) is noticeably improved.

1 Introduction

Weighted essentially non-oscillatory (WENO) reconstructions approximate a function $u({\textbf{x}})$, usually arising as the solution of a differential equation, by a linear combination of stencil approximations. The weights are defined in a nonlinear way based on the smoothness of the stencil approximations so as to bias the reconstruction to the smooth stencils, and thereby make the approximation essentially non-oscillatory.

Classic WENO reconstructions [24] require an additional property, namely, that there be linear weights associated with each stencil so that this linear combination of all the stencils gives a higher order approximation. The essentially non-oscillatory property is achieved by modifying the linear weights to create the nonlinear weights based on the smoothness of the stencil approximations. The requirement for carefully defined linear weights effectively restricts the definition of classic WENO to rectangular computational meshes.

Weighted essentially non-oscillatory reconstructions with adaptive order (WENO-AO) [4, 8, 20] overcome this difficulty by including stencil approximations of two or more orders of accuracy. That is, the higher order approximation is included directly in the linear combination, rather than having it arise from the weighting procedure. The advantage is that now the linear weights can be chosen arbitrarily, which means that extensions to general computational meshes in multiple dimensions is feasible. Of course, the disadvantage is that the large stencil, high order approximation and its smoothness indicator must be computed.

In this paper, we will use finite volume polynomial approximations over the stencils, although it is possible to use nonpolynomial stencil approximations (see, e.g., [1, 3, 9, 24, 26, 28]). We will also consider only two-level approximations.

For the stencil $S_\ell$ (for some set of indices $\ell$), let the polynomial approximation of the function $u({\textbf{x}})$ to be reconstructed be denoted $p_\ell ({\textbf{x}})$. If ${\bar{u}}_j$ denotes the average of u over the jth element $E_j$, i.e.,

$$\begin{aligned} {\bar{u}}_j = \frac{1}{|E_j|} \int _{E_j} u({\textbf{x}})\,d{\textbf{x}}, \end{aligned}$$

(1)

then the stencil polynomial $p_\ell ({\textbf{x}})$ is defined by requiring that its average over each $E_j$ in the stencil $S_\ell$ equals ${\bar{u}}_j$. (In case the number of polynomial coefficients is less than the number of elements in the stencil, this requirement is imposed in a least-squares sense [21].)

The key to the nonlinear weighting is to define a smoothness indicator for $p_\ell$. There are many ways to do this, but the most popular and classic way is due to Jiang and Shu [16]. If $p_\ell$ is of degree k, its smoothness indicator over a mesh element E is given by

$$\begin{aligned} \sigma ^{\textrm{JS}}_{\ell } = \sum _{1\le |\alpha |\le k} \int _{E}|E|^{|\alpha |-1}\big (\mathscr {D}^\alpha p_\ell ({\textbf{x}})\big )^2\,d{\textbf{x}}, \end{aligned}$$

(2)

where $\alpha$ is a multi-index, $\mathscr {D}$ is the derivative operator, and |E| is the d-dimensional volume of E.

This smoothness indicator works beautifully in one space dimension. It can be computed in a simple way in terms of the finite volume averages of the solution [24], and so it is quite efficient. However, in multiple space dimensions on general computational meshes, it is relatively difficult to develop computer implementations, and they are computationally expensive, especially as the degree of the polynomial k increases. For example, in d-dimensions, there are $\bigg (\begin{matrix}k+d\\ d\end{matrix}\bigg )-1 = {\mathscr {O}}(k^d)$ terms in the summation in (2). Each term requires the evaluation of a derivative of a polynomial, and each derivative has ${\mathscr {O}}(k^d)$ terms. Moreover, on a general mesh, we need to use an accurate numerical integration over the element E, which requires many quadrature points. The total computational effort is proportional to $k^{2d}$. (We interject that in this paper, we concentrate on implementations with $k=4$ and $d=2$, so the workload is proportional to 256.)

Perhaps a more efficient approach to implementation of the stencil polynomials in multidimensions is to precompute the dual polynomial basis $p_{\ell ,j}({\textbf{x}})$, where j ranges over the elements in the stencil $S_\ell$ (see, e.g., [2, 5]). Then the stencil polynomial is simply $p_\ell ({\textbf{x}}) = \sum _j {\bar{u}}_j\,p_{\ell ,j}({\textbf{x}})$. Moreover, one can use this expansion to see that $\sigma ^{\textrm{JS}}_\ell = \sum _j \sum _k {\bar{u}}_j\, {\bar{u}}_k\,\sigma _{\ell ,j,k}$ for appropriately defined and precomputed “base smoothness indicators” $\sigma _{\ell ,j,k}$. However, in d-dimensions, the number of terms in this expression is ${\mathscr {O}}(k^{2d})$, and so the computational effort is of the same order as a direct implementation (not counting the pre-computation cost, which is considerable).

The computational cost of the smoothness indicator (2) is very high for multidimensional problems and WENO-AO reconstructions, which require the large stencil (high polynomial degree) smoothness indicators. In this paper we seek to reduce the cost by using a much simpler smoothness indicator. Some works in this direction include [15, 19]; however, the approaches taken in these papers do not result in substantially simpler smoothness indicators. Instead, we use the smoothness indicator suggested by Liu and Jiao [21]. For the stencil $S_\ell$ on which $p_\ell$ is posed, we define the simplified smoothness indicator as

$$\begin{aligned} \sigma _\ell ^{\textrm{S}}= \frac{1}{N_{\textrm{S}}-1}\sum _{j} ({\bar{u}}_{j} - {\bar{u}}_{m})^2, \end{aligned}$$

(3)

where $N_{\textrm{S}}$ is the number of elements in the stencil, j ranges over the elements in the stencil, and the target (“middle”) element is $E=E_m$. The overall computational effort for $\sigma _\ell ^{\textrm{S}}$ is only ${\mathscr {O}}(k^d)$ in d-dimensions. It is also very simple to implement in a computer code.

Unfortunately, this simple smoothness indicator is not very robust in general. If ${\bar{u}}_j=1$ except for a single element where the value is 0, $\sigma _\ell ^{\textrm{S}}=\frac{1}{N_{\textrm{S}}-1}$. This is not large, particularly when $N_{\textrm{S}}$ is large (as it will be in multidimensions), and so it incorrectly indicates that there is not a lot of oscillation in the polynomial approximation. We must compensate for this deficiency, and we will use an alternate weighting strategy similar to that proposed by Castro, Costa, and Don [10, 11] known as WENO-Z weighting. We denote our new WENO-AO reconstruction using the simplified smoothness indicator as SWENOZ-AO, where S stands for simplified.

We also develop a finite volume scheme using SWENOZ-AO reconstructions to solve a system of hyperbolic conservation laws

$$\begin{aligned} u_t + \nabla \cdot F(u) = 0, \quad t > 0, \end{aligned}$$

(4)

where $u = u({\textbf{x}}, t)\in {\mathbb R}^d$. As we will see, our strategy allows $\sigma _\ell ^{\textrm{S}}$ to give good results, with improved overall speedup and computational efficiency (CPU time versus error).

In the next section we develop the SWENOZ-AO reconstruction. We discuss its convergence behavior in Sect. 3. We prove that it maintains the order of accuracy of the largest stencil when the solution is smooth, and drops to the order of the small stencils otherwise. In Sect. 4, we provide numerical tests of the reconstruction which verify our theoretical results. In Sect. 5, we develop our SWENOZ-AO finite volume scheme for conservation laws. Applications to problems posed in one and two space dimensions are given in Sects. 6, 7, respectively. We close with a section summarizing our results and conclusions.

2 Finite Volume WENO-AO Reconstructions

Suppose that we have a domain $\varOmega \subset {\mathbb R}^{d}$ and a computational mesh of elements partitioning the domain. We fix the large stencil $S_0=\{E_1,\ldots ,E_{N_0}\}$, where each $E_j$ is an element of the mesh, and we fix the target element $E_m\in S_0$ for some m. We fix small stencils $S_\ell \subset S_0$ of $N_\ell <N_0$ elements such that $E_m\in S_\ell$ for all $\ell =1,2,\ldots ,L_{{\textrm{S}}}$.

For $\ell =0,1,\ldots ,L_{{\textrm{S}}}$, let $p_{\ell }({\textbf{x}})$ denote the stencil polynomial approximation of the solution $u({\textbf{x}})$ on the stencil $S_\ell$. Then the WENO-AO approximation of $u({\textbf{x}})$ for ${\textbf{x}}$ in the target element $E_m$ is

$$\begin{aligned} {\mathscr {R}}_m({\textbf{x}}) = \frac{{\tilde{\omega }}_{0}}{\omega _{0}}\bigg [p_{0}({\textbf{x}}) - \sum _{\ell =1}^{L_{\textrm{S}}}\omega _{\ell }\,p_{\ell }({\textbf{x}})\bigg ] + \sum _{\ell =1}^{L_{\textrm{S}}}\tilde{\omega }_{\ell }\,p_{\ell }({\textbf{x}}), \end{aligned}$$

(5)

where $\omega _{\ell }$ and $\tilde{\omega }_{\ell }$ are the linear and the corresponding nonlinear weights, respectively. The $\omega _{\ell }$ can be chosen arbitrarily, such that they are positive and sum to one.

The classic definition of the nonlinear weights [16] says that

$$\begin{aligned} {\tilde{\omega }}^{\textrm{JS}}_{\ell } = \frac{{\hat{\omega }}^{\textrm{JS}}_{\ell }}{\sum _{k=0}^{L_{\textrm{S}}}{\hat{\omega }}^{\textrm{JS}}_{k}} \quad \text {where}\quad \hat{\omega }^{\textrm{JS}}_{\ell } = \frac{\omega _{\ell }}{(\sigma ^{\textrm{JS}}_{\ell }+\epsilon _h)^\eta }, \end{aligned}$$

(6)

for some $\epsilon _h>0$ and $\eta >0$, where $\epsilon _{h} = \epsilon _0h^2$ for some fixed $\epsilon _0>0$, or simply $\epsilon _{h} = \epsilon _0$ [2, 4]. We call the reconstruction using this weighting WENO-AO.

A straightforward substitution of the simplified smoothness indicator $\sigma ^{\textrm{S}}_{\ell }$ for the classic one $\sigma ^{\textrm{JS}}_{\ell }$ in (6) does not lead to the required convergence properties of WENO schemes. To see this fact, one can follow the proof of Theorem 4 in Sect. 3. Result (22) fails to hold when one uses the simple smoothness indicator in (6). (That is, the perturbation of the linear weights from the nonlinear ones is not accurate enough.) We therefore modify the definition of the nonlinear weights. Motivated by the WENO-Z weighting procedure of Castro, Costa, and Don [10, 11], we define the nonlinear weights in (5) as

$$\begin{aligned} \tilde{\omega }^{{\textrm{Z}},{\textrm{S}}}_{\ell } = \frac{\hat{\omega }^{{\textrm{Z}},{\textrm{S}}}_{\ell }}{\sum _{k=0}^{L_{\textrm{S}}}\hat{\omega }^{{\textrm{Z}},{\textrm{S}}}_{k}} \quad \text {where}\quad \hat{\omega }^{{\textrm{Z}},{\textrm{S}}}_{\ell } = {\omega _{\ell }}\,\bigg (1 + \frac{\tau ^{\eta _1}}{(\sigma ^{\textrm{S}}_{\ell }+\epsilon _h)^{\eta _2}}\bigg ), \end{aligned}$$

(7)

for some $\epsilon _h>0$, $\tau >0$, $\eta _1>0$, and $\eta _2>0$, where $\tau$ is defined below in (8). Here we take $\epsilon _{h} = \epsilon _0h^2$ for some fixed $\epsilon _0>0$. Standard WENO-Z weighting uses $\eta _1 = \eta _2$, but for our reconstructions, these parameters need to take on different values. We call the reconstruction using (7) SWENOZ-AO.

The choice of $\tau$ is subtle. We take

$$\begin{aligned} \tau = \sum _{\ell =1}^{L_{\textrm{S}}} \left| \sigma ^{\textrm{S}}_\ell - \sigma ^{\textrm{S}}_0\right| , \end{aligned}$$

(8)

although there are other choices. Our numerical tests suggest that (8) works the best among the three choices that we tried, the others being $\tau _1 = \frac{1}{L_{\textrm{S}}}\sum _{\ell =1}^{L_{\textrm{S}}} \left| \sigma ^{\textrm{S}}_\ell - \sigma ^{\textrm{S}}_0\right|$ and $\tau _2 = \frac{1}{L_{\textrm{S}}}\sum _{\ell =0}^{L_{\textrm{S}}} \sigma ^{\textrm{S}}_\ell$. The question of what is the optimal choice of $\tau$ remains open.

Of course, we also have the weighting given by WENO-Z weighting (7) and (8) but using the classic smoothness indicator $\sigma ^{\textrm{JS}}_{\ell }$. In this case, $\eta _1=\eta _2$. The weights would be denoted $\tilde{\omega }^{{\textrm{Z}},{\textrm{JS}}}_{\ell }$. We call this reconstruction WENOZ-AO.

The values one should take for $\eta >0$ in (6) and $\eta _i>0$, $i=1, 2$, in (7) are determined by the convergence theory discussed in the next section.

3 Convergence Behavior of SWENOZ-AO

It is known that WENO-AO and WENOZ-AO reconstructions have the appropriate convergence properties for use in schemes approximating conservation laws [2, 4, 12, 18]. We show in this section the same properties for SWENOZ-AO. Similar to [3], we will need to verify three conditions to obtain the results given in [4]. The first condition is to require the proper accuracy by each stencil polynomial approximation.

Condition 1

Let $h=\max _{E\in S_0}\text {diam}(E)$. For $\ell =0,1,\ldots ,L_{\textrm{S}}$, when u is smooth on the stencil $S_\ell$, we require that for some constant $C>0$, the approximation $p_\ell$ on the target element $E_m$ satisfies

$$\begin{aligned} \Vert p_{0} - u\Vert _{L^\infty (E_m)} \le C h^r,\quad \ell =0, \quad \text {and}\quad \Vert p_{\ell } - u\Vert _{L^\infty (E_m)} \le C h^s,\quad \ell \ge 1, \end{aligned}$$

(9)

for some integers $r>s\ge 1$.

In the context of Condition 1, we refer to our reconstruction as SWENOZ-AO(r, s). This condition places reasonable restrictions on the computational mesh, such as requiring that it be quasiuniform and shape regular.

Condition 2

In the case that u is smooth on the stencil $S_\ell$, we require that for some constant $C>0$, the smoothness indicator $\sigma ^{\textrm{S}}_{\ell }$ and $\tau$ satisfy

$$\begin{aligned} \sigma ^{\textrm{S}}_{\ell }&= {\mathscr {O}}(h^2), \end{aligned}$$

(10)

$$\begin{aligned} \tau&= {\mathscr {O}}(h^{2}). \end{aligned}$$

(11)

The notation $f(h) = \varTheta (h^t)$ means that there are lower and upper bounds $C_1$ and $C_2$ such that

$$\begin{aligned} C_1h^t \le |f(h)|\le C_2h^t \quad \text {as }h\rightarrow 0^+. \end{aligned}$$

(12)

Condition 3

In the case that u has a jump discontinuity on the stencil $S_\ell$, we require that the smoothness indicator $\sigma ^{\textrm{S}}_{\ell }$ and $\tau$ satisfy

$$\begin{aligned} \sigma ^{\textrm{S}}_{\ell }&= \varTheta (1), \end{aligned}$$

(13)

$$\begin{aligned} \tau&= \varTheta (1). \end{aligned}$$

(14)

Our SWENOZ-AO reconstructions using definitions (3) and (8) obviously satisfy Condition 2. Condition 3, however, requires the discontinuities to be bounded away from the gridpoints as the mesh spacing goes to 0 (see [4]).

Theorem 4

Let Conditions 1–2 hold. Suppose that $\epsilon _h=\epsilon _0h^2$ for some $\epsilon _0 > 0$ in the definition of the nonlinear weights (7). Assume that $r>s\ge 2$ and $\eta _1 - \eta _2 \ge (r -s)/2$. If the function u is smooth on $S_0$, then the SWENOZ-AO(r, s) approximation ${\mathscr {R}}_m^{r,s}$, defined in (5), on the target element $E_m$ satisfies

$$\begin{aligned} \Vert {\mathscr {R}}_m^{r,s} - u\Vert _{L^\infty (E_m)} \le C h^{r}. \end{aligned}$$

(15)

Moreover, let Condition 3 hold and assume further that $\eta _2 \ge s/2$. If u is smooth except for a jump discontinuity in the interior of $S_0$ but not in some stencil $S_\ell$, then

$$\begin{aligned} \Vert {\mathscr {R}}_m^{r,s} - u\Vert _{L^\infty (E_m)} \le Ch^s. \end{aligned}$$

(16)

Proof

Our proof follows and combines various arguments found in [4]. Assume first that u is smooth on $S_0$, i.e., on all the stencils. By Condition 2 and our choice of $\epsilon _h$, $\tau ={\mathscr {O}}(h^2)$ and $\sigma ^{\textrm{S}}_{\ell }+\epsilon _h=\varTheta (h^2)$. For any $\ell$, let

$$\begin{aligned} \rho _{\ell } = \frac{\tau ^{\eta _1}}{(\sigma ^{\textrm{S}}_{\ell }+\epsilon _h)^{\eta _2}} = \frac{{\mathscr {O}}(h^{2\eta _1})}{\varTheta (h^{2\eta _2})} = {\mathscr {O}}\left( h^{2(\eta _1 - \eta _2)}\right) . \end{aligned}$$

(17)

Now (7) gives that

$$\begin{aligned} \tilde{\omega }_{\ell }^{{\textrm{Z}},{\textrm{S}}} = \tilde{\omega }_{\ell } = \frac{\omega _{\ell }(1+\rho _{\ell })}{\sum \limits _{k} \omega _{k}(1+\rho _{k})} = \frac{\omega {_\ell }(1+\rho _{\ell })}{1+ \sum \limits _{k} \omega _{k}\rho _{k}}. \end{aligned}$$

(18)

Since we require that $\eta _1-\eta _2\ge (r-s)/2>0$, $\rho _{\ell }\rightarrow 0$ as $h\rightarrow 0^+$, and we see from elementary asymptotic theory that

$$\begin{aligned} \begin{aligned} \tilde{\omega }_{\ell }&\sim \omega _{\ell }(1+\rho _{\ell })\Big (1- \sum _{k}\omega _{k}\rho _{k}\Big )\\&\sim \omega _{\ell } \Big (1+\rho _{\ell } - \sum _{k}\omega _{k}\rho _{k}\Big ) \\&= \omega _{\ell }\Big ( 1+ \sum \limits _{k} \omega _{k}(\rho _{\ell } - \rho _{k})\Big ).\\ \end{aligned} \end{aligned}$$

(19)

The mean value theorem shows that

$$\begin{aligned} \begin{aligned} \rho _{\ell } - \rho _{k}&= \frac{\tau ^{\eta _1}}{(\sigma ^{\textrm{S}}_{\ell }+\epsilon _{h})^{\eta _2}} - \frac{\tau ^{\eta _1}}{(\sigma ^{\textrm{S}}_{k}+\epsilon _{h})^{\eta _2}} \\&= \frac{\tau ^{\eta _1}\left( (\sigma ^{\textrm{S}}_{k}+\epsilon _{h})^{\eta _2} - (\sigma ^{\textrm{S}}_{\ell }+\epsilon _{h})^{\eta _2} \right) }{(\sigma ^{\textrm{S}}_{\ell }+\epsilon _{h})^{\eta _2}\,(\sigma ^{\textrm{S}}_{k}+\epsilon _{h})^{\eta _2}} \\&= \frac{\tau ^{\eta _1}\,\eta _2\,\xi ^{\eta _2-1} (\sigma ^{\textrm{S}}_{k} - \sigma ^{\textrm{S}}_{\ell })}{(\sigma ^{\textrm{S}}_{\ell }+\epsilon _{h})^{\eta _2}\,(\sigma ^{\textrm{S}}_{k}+\epsilon _{h})^{\eta _2}} \end{aligned} \end{aligned}$$

(20)

for some $\xi$ between $\sigma ^{\textrm{S}}_{\ell }+\epsilon _{h}$ and $\sigma ^{\textrm{S}}_{k}+\epsilon _{h}$. Note that by Condition 2, $\xi ={\mathscr {O}}(h^2)$. Thus, for all $\ell$ and k,

$$\begin{aligned} \rho _{\ell }-\rho _{k} = \frac{{\mathscr {O}}(h^{2 \eta _1})\,{\mathscr {O}}(h^{2(\eta _2-1)})\,{\mathscr {O}}(h^{2})}{\varTheta (h^{4 \eta _2})} = {\mathscr {O}}\left( h^{2 (\eta _1 - \eta _2)}\right) . \end{aligned}$$

(21)

We conclude from (19) and (21) that

$$\begin{aligned} {\tilde{\omega }}_\ell - \omega _\ell \sim \omega _{\ell }\sum _{k} \omega _{k}(\rho _{\ell } - \rho _{k}) = {\mathscr {O}}(h^{2(\eta _1 - \eta _2)}). \end{aligned}$$

(22)

Because $\sum _{\ell =0}^{L_{\textrm{S}}}\omega _\ell =\sum _{\ell =0}^{L_{\textrm{S}}}\tilde{\omega }_\ell =1$, we have on $E_m$ that

$$\begin{aligned} \begin{aligned} {\mathscr {R}}_m^{r,s} - u&= \frac{\tilde{\omega }_0}{\omega _0}\bigg [ (p_{0}-u) - \sum _{\ell =1}^{L_{\textrm{S}}} \omega _\ell (p_{\ell }-u)\bigg ] + \sum _{\ell =1}^{L_{\textrm{S}}} \tilde{\omega }_\ell (p_{\ell }-u) \\&= \frac{\tilde{\omega }_0}{\omega _0}(p_{0}-u) - \sum _{\ell =1}^{L_{\textrm{S}}}\bigg [\frac{\tilde{\omega }_0-\omega _0}{\omega _0}\omega _\ell - (\tilde{\omega }_\ell -\omega _\ell )\bigg ]\,(p_{\ell }-u). \end{aligned} \end{aligned}$$

(23)

Invoking Condition 1 and (22), we see that

$$\begin{aligned} \big |{\mathscr {R}}_m^{r,s} - u\big |= & {} {\mathscr {O}}(h^r) + \sum _{\ell =1}^{L_{\textrm{S}}} \big [{\mathscr {O}}({\tilde{\omega }}_0-\omega _0) + {\mathscr {O}}({\tilde{\omega }}_\ell -\omega _\ell )\big ]\,{\mathscr {O}}(h^s)\nonumber \\= & {} {\mathscr {O}}(h^r) + {\mathscr {O}}(h^{2(\eta _1 - \eta _2) + s}), \end{aligned}$$

(24)

and we have our result (15) provided $2(\eta _1 - \eta _2) + s \ge r$, as we have assumed.

We now treat the case in which u has a discontinuity. First of all, Conditions 2, 3 give that $\tau = \varTheta (1)$ and $\sigma ^{\textrm{S}}_\ell + \epsilon _{h} = {\mathscr {O}}(h^2)$ if u is smooth on $S_\ell$ and $\sigma ^{\textrm{S}}_\ell + \epsilon _{h} = \varTheta (1)$ otherwise. Thus,

$$\begin{aligned} \rho _{\ell } = \frac{\tau ^{\eta _1}}{(\sigma ^{\textrm{S}}_{\ell }+\epsilon _h)^{\eta _2}} = {\left\{ \begin{array}{ll} \varTheta (h^{-2\eta _2}), &{} \text {if }u \text { is smooth on }S_{\ell },\\ \varTheta (1), &{} \text {if } u \text { jumps on }S_{\ell }. \end{array}\right. } \end{aligned}$$

(25)

We conclude that the denominator in (18) is dominated by terms that are $\varTheta (h^{-2\eta _2})$, and so we obtain

$$\begin{aligned} \begin{aligned} \tilde{\omega }_\ell = {\left\{ \begin{array}{ll} \varTheta (1), &{} \text {if }u \text { is smooth on }S_{\ell },\\ \varTheta (h^{2\eta _2}), &{} \text {if } u \text { jumps on }S_{\ell }. \end{array}\right. } \end{aligned} \end{aligned}$$

(26)

Returning to (23), we see that

$$\begin{aligned} \begin{aligned} \big |{\mathscr {R}}_m^{r,s} - u\big |&\le \bigg |\frac{\tilde{\omega }_0}{\omega _0}\bigg [(p_{0}-u) - \sum _{\ell =1}^{L_{\textrm{S}}}\omega _\ell (p_{\ell }-u)\bigg ]\bigg | + \sum _{\ell =1}^{L_{\textrm{S}}}\tilde{\omega }_\ell \big |p_{\ell }-u\big |\\&= {\mathscr {O}}(\tilde{\omega }_0)\,{\mathscr {O}}(1) + \bigg \{\sum _{\begin{array}{c} u \text { discontin-}\\ \text {uous on }S_\ell \end{array}}{\mathscr {O}}(\tilde{\omega }_\ell )\,{\mathscr {O}}(1) + \!\sum _{\begin{array}{c} u\text { smooth}\\ \text { on }S_\ell \end{array}}{\mathscr {O}}(h^s)\bigg \}\\&= {\mathscr {O}}(h^{2\eta _2}) + {\mathscr {O}}(h^s), \end{aligned} \end{aligned}$$

(27)

which implies the result (16), since we assumed $2\eta _2\ge s$. $\square$

4 Numerical Tests of the Reconstructions

In this section, we test the three reconstructions SWENOZ-AO, WENO-AO, and WENOZ-AO, as described in Sect. 2, independent of their application to solving conservation laws. For these tests, we use a computer code written in C++, compiled using the Gnu compiler (version 11.3.0 with optimization -O2), and run on a Dell Precision 3650 Tower workstation using an Intel Core i7-10700 CPU running at 2.90 GHz.

4.1 Reconstruction Near Jump Discontinuities in 1D

We begin with the case in which the solution contains a jump (as in [2, 13, 18]). Let H denote the Heaviside function. For some fixed point $x_{\text {jump}}$, let the solution

$$\begin{aligned} u(x) = x^3+\sin (x) +H(x_{\text {jump}}-x). \end{aligned}$$

For refinement level $L=0,1,2,\ldots$, let $h = 2^{-L-6}$. Let the large mesh stencil be $\{-2h$, $-h$, 0, h, 2h, $3h\}$ of five elements with target element $E=[0,h]$, and the three small stencils of three contiguous elements. We test the accuracy of only the new SWENOZ-AO(5,3) reconstruction at $x = 0$ when $x_{\text {jump}} = 0$, $-h$, $-2h$. The solution is smooth on the large stencil for the latter case $x_{\text {jump}} = -2h$, but in the other two cases there is a discontinuity in the large stencil and either one or two of the small stencils.

Theorem 4 predicts that we should see the accuracy of the stencil without a shock, provided $\eta _1$ and $\eta _2$ are chosen properly. The theory implies that SWENOZ-AO(5,3) requires the condition $\eta _1 - \eta _2 \ge 1$, and also the condition $\eta _2 \ge 3/2$ when there is a jump in the solution.

Table 1 Example 4.1. SWENOZ-AO(5,3) errors and convergence orders using various values for $\eta _1$ and $\eta _2$

Our numerical test results are shown in Table 1, using various values for $\eta _1$ and $\eta _2$. When there is no jump in the solution, i.e., $x_{\text {jump}}=-2h$, we see fifth order convergence when $\eta _1 - \eta _2 \ge 1$ ($\eta _1=3$ and $\eta _2=2$, or $\eta _1=2$ and $\eta _2=1$). However, when $\eta _1=2$ and $\eta _2=2$, the condition is violated, and we see only third order convergence.

When there is a jump in the solution, i.e., $x_{\text {jump}}=0,-h$, we see third order convergence when $\eta _2 \ge 3/2$ ($\eta _1=3$ and $\eta _2=2$), but the convergence drops to second order when either of the two conditions is violated ($\eta _1=2$ and $\eta _2=1$, or $\eta _1=2$ and $\eta _2=2$).

All of our results are consistent with Theorem 4, and they suggest that our two conditions are sharp.

4.2 WENO Reconstructions of Adaptive Order in 2D

In two dimensions, the test function to be reconstructed (the true solution) is $u(x,y)=2(1+\cos (2\pi x))e^{xy-y}$, possibly with the addition of a jump term. We consider two reconstructions of adaptive order (5,3).

We consider the large stencil of 15 elements and three small stencils of 6 elements each as depicted in Fig. 1. The large and small stencils support polynomials of degree 4 and 2, respectively. We refine the mesh by contracting the mesh vertices to a fixed point in the central target element by a factor of $2^{-L}$, where the level $L=0,1,\ldots$. The linear weights in the reconstructions are all taken to be equal to each other.

Fig. 1

Example 4.2. The initial mesh, which is the large stencil, and three small stencils

Table 2 Example 4.2. Discrete $L_h^1$ and $L_h^\infty$ errors and convergence orders for a smooth solution using the stencils in Fig. 1

With no jump in the true solution, we see good fifth order convergence of all three reconstructions in Table 2, where we give the $L_h^1$ and $L_h^\infty$ errors and convergence orders over the target element. Moreover, the three sets of errors are comparable. The advantage of SWENOZ-AO is that its (average) computation time is only 1484 ns, compared to over 19,300 ns for the other two reconstructions. That is, in this test the new reconstruction is about 13 times faster, due mainly to the fact that SWENOZ-AO uses the new simplified smoothness indicator (3), while WENO-AO, and WENOZ-AO use the classic smoothness indicator computed as in (2).

We evaluate the inner-workings of the reconstructions by considering the values of the smoothness indicators and effective nonlinear weights. The latter are denoted $\gamma _\ell$ and defined by

$$\begin{aligned} \gamma _0 = \frac{\tilde{\omega }_0}{\omega _0} \quad \text {and}\quad \gamma _\ell = \tilde{\omega }_\ell - \frac{\tilde{\omega }_0}{\omega _0}\omega _\ell ,\quad \ell >0, \end{aligned}$$

(28)

so that

$$\begin{aligned} {\mathscr {R}}_m({\textbf{x}}) = \gamma _0\,p_{0}({\textbf{x}}) + \sum _{\ell =1}^{L}\gamma _{\ell }\,p_{\ell }({\textbf{x}}). \end{aligned}$$

(29)

We see in Table 3 that the simple smoothness indicator agrees rather well with the classic one. Moreover, the three reconstructions strongly bias the effective nonlinear weights to emphasize the large stencil. We note that although some of the effective nonlinear weights $\gamma _\ell$ are negative (and then only slightly), all of the actual nonlinear weights $\omega _\ell$ are positive.

Table 3 Example 4.2. Smoothness indicators ($\sigma _\ell$) and effective nonlinear weights ($\gamma _\ell$) of the reconstructions of a smooth solution for using the stencils in Fig. 1

Table 4 Example 4.2. Discrete $L_h^1$ and $L_h^\infty$ errors and convergence orders for a discontinuous solution using the stencils in Fig. 1

A jump discontinuity of size one is now added to the smooth solution. The discontinuity is a line that cuts all the stencils except the third one. The line is adjusted on each refinement level so that it appears stationary in the mesh (much like as is done in 1D). In Table 4, we see third order convergence and comparable errors for all three reconstructions. For these runs, the (average) computation time of SWENOZ-AO is 1646 ns, compared to over 19,700 ns for the other two reconstructions. That is, for these runs we saw that the new reconstruction is about 12 times faster.

Table 5 Example 4.2. Smoothness indicators ($\sigma _\ell$) and effective nonlinear weights ($\gamma _\ell$) for the reconstructions of a discontinuous solution using the stencils in Fig. 1

The smoothness indicators and effective nonlinear weights are given in Table 5. We see that the simple smoothness indicator agrees approximately with the classic one. Moreover, the three reconstructions strongly bias the nonlinear weights to stencil number 3, as they should.

The two tests suggest that the SWENOZ-AO(5,3) reconstruction is on the order of 10 times faster to compute than the classic WENO-AO(5,3) reconstruction. As noted in the Introduction (§1), the computational cost of the classic reconstruction is ${\mathscr {O}}(k^{2d})$, while the simple reconstruction is ${\mathscr {O}}(k^d)$. Therefore in 2D the classic reconstruction workload for the one polynomial of degree 4 and three polynomials of degree 2 is proportional to $4^4 + 3\times 2^4=304$, whereas the simple reconstruction workload is only $4^2+3\times 2^2=28$. Indeed, we should have expected to see about a tenfold speedup.

5 Application to Conservation Laws

Let $\{E_{j}\}$ be the computational mesh of the domain of interest, where $E_{j}$ is a polytopal element in ${\mathbb R}^d$ and $d>1$. Let $\partial E_{j,i}$, $i = 1,\cdots ,N_j$ be the $N_j$ facets of $E_j$, and let $|\partial E_{j,i}|$ be its volume in $(d-1)$-dimensions. Let us also assume that the mesh is quasiuniform; that is, with $h=\max _j|E_j|^{1/d}$, we have $|E_j|=\varTheta (h^d)$ and $|\partial E_{j,i}|=\varTheta (h^{d-1})$, where the bounds are independent of j and i.

The integral form of the conservation law (4) over the element $E_{j}$ gives

$$\begin{aligned} \frac{d{\bar{u}}_{j}}{dt} + \frac{1}{|E_{j}|}\oint _{\partial E_{j}} F \cdot \nu _j\,ds = 0, \end{aligned}$$

(30)

where $\nu _j$ stands for the outward unit normal vector to $\partial E_{j}$. The boundary integral on each facet is approximated by a sufficiently accurate quadrature rule, where ${\textbf{x}}_{j,i,q}$ and $|\partial E_{j}|w_{j,i,q}$ are the quadrature points and weights on facet $\partial E_{j,i}$, respectively. That is, we approximate the boundary integral by

$$\begin{aligned} \oint _{\partial E_{j}}F\cdot \nu _j\,ds \approx \sum _{i = 1}^{N_j}|\partial E_{j,i}|\sum _{q} w_{j,i,q}\hat{F}_{j,i,q}(t), \end{aligned}$$

(31)

where $\hat{F}_{j,i,m}(t) = \hat{F}\big (u({\textbf{x}}_{j,i,m},t)\big )\cdot \nu _j$ is the numerical flux.

The Lax-Friedrichs numerical flux is used, which is given by

$$\begin{aligned} \hat{F}_{j,i,q}(t)&= \hat{F}\big (u_{j,i,q}^{-}(t),u_{j,i,q}^{+}(t),\nu _j\big )\nonumber \\&= \frac{1}{2}\Big [\Big (F\big (u_{j,i,q}^{-}(t)\big ) +F\big (u_{j,i,q}^{+}(t)\big )\Big )\cdot \nu _{j,i} -\alpha \big (u_{j,i,q}^{+}(t)-u_{j,i,q}^{-}(t)\big )\Big ], \end{aligned}$$

(32)

where $\alpha$ is bounds the absolute value of the eigenvalues of the Jacobian of F in the direction of $\nu _{j,i}=\nu _j\big |_{\partial E_{j,i}}$, and $u_{j,i,q}^{-}$ and $u_{j,i,q}^{+}$ are reconstructed values of u inside the element and in the neighboring element at the quadrature point ${\textbf{x}}_{j,i,q}$, respectively. We use one of the reconstructions defined in Sect. 2, i.e., SWENOZ-AO, WENO-AO, or WENOZ-AO, using a set of stencils and parameters to be discussed later when we give numerical results,

The time discretization of the SWENOZ-AO scheme is implemented by a high order Runge–Kutta method. Although other time integrators could be used, the third order, three stage total variation diminishing explicit Runge–Kutta method (TVD RK-3) [16] is used, except for the various convergence tests, which use the standard fourth order, four stage Runge–Kutta method (nonTVD RK-4).

All the numerical results appearing below in Sects. 6, 7 were obtained with a computer program compiled using the intel Fortran compiler. The tests were run on an ASUS workstation ESC8000G4 with 256 gigabytes of memory and dual Intel Xeon gold processors running at 2.30 GHz.

6 Numerical Results in One Space Dimension

In one space dimension, we describe our computational mesh as a set of points $\cdots<x_{-1/2}< x_{1/2}< x_{3/2}< \cdots$ which partition space into elements $E_{j} = [x_{j-1/2},x_{j+1/2}]$ with length $\varDelta x_j = x_{j+1/2}-x_{j-1/2}$ and midpoint $x_j=(x_{j+1/2}+x_{j-1/2})/2$. Now $h=\max _i\varDelta x_i$ and our assumption of a quasiuniform mesh says that there is some $\rho >0$ such that $\rho h\le \min _j\varDelta x_j$.

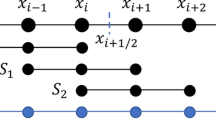
We use the SWENOZ-AO(5, 3) reconstruction in this section. It is defined for a target element $E_m$ using the large stencil $S_0=\{E_{m-2}, E_{m-1}, E_{m}, E_{m+1}, E_{m+2}\}$ and the three small stencils $S_{1}=\{E_{m-2}, E_{m-1}, E_{m}\}$, $S_{2}=\{E_{m-1}, E_{m}, E_{m+1}\}$, and $S_{3}=\{E_{m}, E_{m+1}, E_{m+2}\}$. Condition 1 holds for the stencil polynomial approximations with $r=5$ and $s=3$. Following Theorem 4, we take $\eta _2=2\ge s/2$ and then $\eta _1=(r-s)/2+\eta _2=3$. We arbitrarily choose to use $\omega _0= 1/2$, $\omega _\ell = 1/6$ for $\ell = 1, 2, 3$, and $\epsilon _0=1$.

Below we test the scheme described in Sect. 5 using SWENOZ-AO(5, 3). For comparison, we also test the scheme using classic WENO-AO(5,3) and WENOZ-AO(5,3) reconstructions (with $\eta =2$ for both).

6.1 Linear Equation

To determine the rate of convergence, we start with a linear equation, i.e., the problem

$$\begin{aligned} u_t + u_x = 0\quad \text {and}\quad u(x,0) = 0.5 + \sin (\pi x)\quad \text {for}\quad x\in (0,2). \end{aligned}$$

We ran tests over gradually refined, uniform meshes up to time $t=2$ using $\varDelta t= 0.1 h$ (i.e., CFL number = 0.1). We compare the SWENOZ-AO(5,3), WENO-AO(5,3), and WENOZ-AO(5,3) schemes in terms of discrete $L_h^1$ errors (i.e., the $L^1$ errors of the element averages) and convergence orders in Table 6. The discrete $L_h^\infty$ errors and convergence orders are also given in the table. All schemes are fifth order accurate. The errors are smallest for WENOZ-AO, followed by SWENOZ-AO, and then WENO-AO. This is perhaps expected, since WENO-Z weighting biases the nonlinear weights to the linear ones more than classic weighting. Results using the simple smoothness indicator (3) combined with the standard WENO weights (6) (SWENO-AO(5,3)) are provided in the last two columns in Table 6. This scheme does not lead to the required convergence properties.

Table 6 Example 6.1, linear equation. Discrete $L_h^1$ and $L_h^\infty$ errors and convergence orders at $t=2$ on uniform meshes using $\varDelta t= 0.1 h$, $h=2/m$

6.2 Burgers Equation

We now solve the scalar Burgers equation with 2-periodic boundary conditions to evaluate the convergence rates; that is, we solve the nonlinear problem

$$\begin{aligned} u_t + (u^2/2)_x = 0\quad \text {and}\quad u(x,0) = 0.5 + \sin (\pi x)\quad \text {for}\quad x\in (0,2). \end{aligned}$$

We ran the computation over gradually refined, uniform meshes using $\varDelta t= 0.1 h$ (i.e., CFL number = 0.15) up to time $t=0.25$. This is before the time $t=1/\pi \approx 0.32$ when shocks develop. The discrete errors and convergence orders for the three schemes are given in Table 7. We see that the schemes all approach a fifth order convergence rate.

Table 7 Example 6.2, Burgers equation with no shocks. Error and convergence order at $t=0.25$ using using $\varDelta t= 0.1 h$, $h=2/m$

Fig. 2

Example 6.2, Burgers equation with a shock. Solutions using SWENOZ-AO(5,3) (circles), WENO-AO(5,3) (crosses) and WENOZ-AO(5,3) (squares) at time $t=3/(2\pi )$ on uniform meshes using $\varDelta t= 0.1h$, $h=2/m$. The solid line is the reference solution

The circles are SWENOZ-AO(5,3), the crosses are WENO-AO(5,3) and the squares are WENOZ-AO(5,3) results at time $t=3/(2\pi )$ in Fig. 2. The shock is formed at time $1/\pi < 3/(2\pi )\approx 0.48$. We do not see oscillation in the shock transition zone.

6.3 Buckley–Leverett Equation

The next scalar equation is the Buckley–Leverett one which uses the flux function

$$\begin{aligned} f(u) = \frac{u^2}{u^2+(1-u)^2}. \end{aligned}$$

(33)

Shocks and rarefactions interact in this test, for which the initial condition is

$$\begin{aligned} u(x,0)={\left\{ \begin{array}{ll} 1-20x&{}\text {for }0\le x\le 0.05,\\ 0.5&{}\text {for }0.25\le x\le 0.4,\\ 0&{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

(34)

The problem is solved on [0, 1] using $m=100$ mesh elements and $\varDelta t= 0.1h$ (i.e., CFL number = 0.2). The results are shown in Fig. 3 for the SWENOZ-AO(5,3) (circles), WENO-AO(5,3) (crosses) and WENOZ-AO(5,3) (squares) schemes. All schemes handle the merging of the two pulses quite well and with comparable accuracy.

Fig. 3

Example 6.3, Buckley–Leverett. The solid line is the reference solution. The circles are SWENOZ-AO(5,3), the crosses are WENO-AO(5,3) and the squares are WENOZ-AO(5,3) results on a uniform mesh using $m=100$ and $\varDelta t= 0.1h$

6.4 The Euler System

We solve the one-dimensional nonlinear system of Euler equations for gas dynamics

$$\begin{aligned} \left( \!\! \begin{array}{c} \rho \\ \rho u\\ E \end{array} \!\!\right) _{t} +\, \left( \!\! \begin{array}{c} \rho u \\ \rho u^2 + p\\ u(E+p) \end{array} \!\!\right) _{x} =0. \end{aligned}$$

(35)

Here $\rho$ is the density, u is the velocity, E is the total energy, and p is the pressure related to the total energy by $E = \frac{p}{\gamma -1} +\frac{1}{2}\rho (u^2)$, $\gamma =1.4$. To avoid spurious oscillations, a local characteristic decomposition over the conserved variables is perform before applying SWENOZ-AO to the characteristic variables.We use Roe’s flux as an approximate Riemann solver.

6.4.1 A Smooth Problem for the Euler Equations

In this example, the initial condition is $\rho (x,0) = 1+ 0.2\sin (\pi x)$, $u(x,0)=1$, and $p(x,0)=1$, with 2-periodic boundary conditions over the spatial domain (0, 2). The exact solution is $\rho (x,t) = 1+ 0.2\sin (\pi (x-t))$, $u=1$, and $p=1$. We compute the numerical solution up to time $t=2$ using $\varDelta t$ with CFL number = 0.4 and $h=2/m$. In Table 8, we report the discrete errors and convergence orders for the density. We observe a clean fifth order accuracy using uniform meshes.

From Fig. 4, we see that the computational efficiency (CPU time versus error) of WENO-AO and WENOZ-AO are about the same, while SWENOZ-AO is a bit more efficient. The speedup results of Table 8 confirm this observation as well. It should be noted that in 1D (using uniform meshes), there are explicit formulas for the classic low order smoothness indicators, so the simple smoothness indicator is not expected to gain much speedup. Nevertheless, SWENOZ-AO is the most efficient scheme among the three.

Table 8 Example 6.4.1, Euler equations. Error and convergence order at $t=2$, and computational speedup compared to SWENOZ-AO(5,3)

Fig. 4

Example 6.4.1, Euler equations. Computational efficiency comparison of the schemes: $L_h^1$ error (left) and $L_h^\infty$ error (right) versus CPU-time for the 1D Euler equations. Shown are results for SWENOZ-AO(5,3) (circles), WENOZ-AO(5,3) (squares) and WENO-AO(5,3) (crosses)

6.4.2 Riemann Problems for the Euler Equations

Next, we solve 1D shock tube test problems. The primitive variables specify a discontinuous initial condition

$$\begin{aligned} (\rho , u, p) ={\left\{ \begin{array}{ll} (\rho _l,\ u_l,\ p_l),&{}\text {for } 0< x< 1/2,\\ (\rho _r,\ u_r,\ p_r),&{}\text {for } 1/2< x < 1. \end{array}\right. } \end{aligned}$$

The first test case is Sod’s problem, ($\rho _l=1$, $u_l=0$, $p_l=1$) and ($\rho _r=1/8$, $u_r=0$, $p_r=1/10$), and the second test is proposed by Lax, ($\rho _l=0.445$, $u_l=0.698$, $p_l=3.528$) and ($\rho _r=0.5$, $u_r=0$, $p_r=0.571$). We show in Fig. 5 the density $\rho$ at time $t=0.16$. We use $\varDelta t$ with CFL number = 0.3 and $h = 1/100$ i.e. a uniform mesh of $m = 100$. The three schemes give very similar results.

Fig. 5

Example 6.4.2, Sod and Lax 1D shock tube tests. The density profile at time $t=0.16$ using a uniform mesh of $m = 100$ elements ($h=1/m$) and $\varDelta t$ with CFL number = 0.3. Shown are results for SWENOZ-AO(5,3) (circles), WENOZ-AO(5,3) (squares) and WENO-AO(5,3) (crosses). The solid line is the reference solution

6.4.3 Shu and Osher’s Shock Interaction with Entropy Waves

To show the advantage of a higher order schemes, we present a problem with a shock interacting with entropy waves due to Shu and Osher [25]. The problem is scaled to the domain (0, 1), and the initial condition is

$$\begin{aligned} (\rho , u, p) ={\left\{ \begin{array}{ll} (\rho _l = 3.857143,\ u_l=2.629369,\ p_l=10.333333),\!&{}\text {for } 0< x< 1/10,\\ (\rho _r = 1 + 0.2\sin (5(10 x -5)),\ u_r=0,\ p_r=1),&{}\text {for } 1/10 \le x < 1. \end{array}\right. } \end{aligned}$$

The results at time $t = 0.18$ are reported in Fig. 6, using $\varDelta t$ with CFL number = 0.4 and $h = 1/400$ i.e. $m=400$ uniform mesh elements. It can be seen that SWENOZ-AO(5,3) (circles) performs better than WENO-AO(5,3) (crosses), and perhaps slightly better than WENOZ-AO(5,3) (squares).

Fig. 6

Example 6.4.3, Shu and Osher’s test. The density profile for SWENOZ-AO(5,3) (circles), WENOZ-AO(5,3) (squares), and WENO-AO(5,3) (crosses) at time $t=0.18$ using $\varDelta t$ with CFL number = 0.4, $h=1/400$ i.e. a uniform mesh of $m=400$ elements, as well as the fine resolution reference solution (solid line)

6.4.4 Woodward and Colella’s Double Blast Test

We end our 1D tests with the blast wave problem of Woodward and Colella, which uses the initial condition

$$\begin{aligned} (\rho , u, p) ={\left\{ \begin{array}{ll} (\rho _l=1,\ u_l=0,\ p_l=1000),&{}\text {for } 0< x< 1/10,\\ (\rho _m=1,\ u_m=0,\ p_m=1/100),&{}\text {for } 1/10< x< 9/10,\\ (\rho _r=1,\ u_r=0,\ p_r=100),&{}\text {for } 9/10< x < 1. \end{array}\right. } \end{aligned}$$

This problem involves the interaction of two blast waves. The density component of the solution is shown in Fig. 7 for the time $t=0.038$. A reference solution (the fine black line) is obtained by using the MUSCL scheme with $m=4000$. Unlike the other tests, here we show convergence of our SWENOZ-AO(5,3) scheme using $m=400$, 800, and 1600 mesh elements and $\varDelta t$ with CFL number = 0.2, $h = 1/m$. For comparison, we also show the result using $m = 800$ and classic WENO5 reconstructions (not using adaptive order), which matches the SWENOZ-AO(5,3) scheme on that mesh quite well.

Fig. 7

Example 6.4.4, Woodward and Colella’s double blast test. The density profile at time $t=0.038$ on uniform meshes using $m = 400$, 800, and 1600 for SWENOZ-AO(5,3), shown in black, blue, and red circles, respectively. Also shown is the result using $m = 800$ using classic WENO5 reconstructions (green plus signs) and the reference solution (fine black line)

7 Numerical Results in Two Space Dimensions

We consider now the extension of our SWENOZ-AO reconstructions to the finite volume scheme (30)–(32) for solving conservation laws in more than one space dimension. We present only the case of two space dimensions, since extension to three (or more) dimensions is straightforward. It is well known that implementing WENO schemes on general meshes in multiple space dimensions has been problematic. Most importantly, one must either define a set of “good stencils” [7, 14] or use least squares polynomial fitting [21]. Since these issues have nothing to do with the use of SWENOZ-AO reconstructions, we avoid these unrelated issues by testing only schemes on logically rectangular computational meshes.

A logically rectangular mesh of quadrilaterals has the advantages of being able to define its index space as rectangular. The description and implementation of the reconstruction can therefore be simplified significantly. We define our SWENOZ-AO(5,3) reconstruction on such logically rectangular meshes. Detailed ideas are described in [6].

Fig. 8

Stencils for WENO-AO(5,3) reconstruction. Depicted (three times) is the large stencil $S_0$ of 25 elements centered around $E_{m,n}$. On the left, we also see two of the small stencils of 9 elements centered about $E_{m-1,n-1}$ (pink) and $E_{m+1,n+1}$ (light blue). In the center, we see the two small stencils centered at $E_{m-1,n+1}$ (orange) and $E_{m+1,n-1}$ (green). On the right is the small stencil centered at $E_{m,n}$ (gray) (Color figure online)

The computational mesh consists of quadrilateral elements $\{E_{i,j}\}$, where $i=1,2,\ldots ,N_1$ and $j=1,2,\ldots ,N_2$. As shown in Fig. 8 for target element $E_{m,n}$, the large stencil of 25 elements including it and its surrounding elements is

$$\begin{aligned} S_0=\{E_{m+i,n+j} : i=-2,-1,0,1,2, j=-2,-1,0,1,2\}. \end{aligned}$$

It is perhaps unclear what small stencils should be taken. We found good results using five small stencils of 9 elements each, a center element and its surrounding elements. The center elements are $E_{m-1+i,n-1+j}$, $E_{m+1+i,n-1+j}$, $E_{m-1+i,n+1+j}$, $E_{m+1+i,n+1+j}$, and $E_{m+i,n+j}$, respectively, and so

$$\begin{aligned} S_1&= \{E_{m-1+i,n-1+j} : i=-1,0,1; j=-1,0,1\},\\ S_2&= \{E_{m+1+i,n-1+j} : i=-1,0,1; j=-1,0,1\},\\ S_3&= \{E_{m-1+i,n+1+j} : i=-1,0,1; j=-1,0,1\},\\ S_4&= \{E_{m+1+i,n+1+j} : i=-1,0,1; j=-1,0,1\},\\ S_5&= \{E_{m+i,n+j} : i=-1,0,1; j=-1,0,1\}. \end{aligned}$$

In particular, inclusion of $S_5$ improved the results for the Riemann problems of Sect. 7.3.2 below.

The SWENOZ-AO(5,3) reconstruction is then as described in Sect. 2, with one important exception. We impose that the number of elements in the stencil matches the number of coefficients in the polynomial by using tensor product polynomials ${\mathbb P}_{k,k}=\text {span}\{x^i\,y^j: i,j=0,1,\ldots ,k\}$. Thus the large stencil uses polynomials in ${\mathbb P}_{4,4}$ and the small stencils use polynomials in ${\mathbb P}_{2,2}$.

Our choice of stencil polynomials implies that the SWENOZ-AO(5,3) reconstruction will indeed be ${\mathscr {O}}(h^5)$ when u is smooth and reduce to ${\mathscr {O}}(h^3)$ when u has a discontinuity. We take $\epsilon _h = |E_{i,j}|$, $\eta _2=2$, and $\eta _1=3$. The linear weights are $\omega _{0} = 1/2$, and $\omega _{j} = 1/10$ for $j=1,2,3,4,5$. When computed, we use the same parameters for the WENO-AO(5,3) and WENOZ-AO(5,3) schemes, except that now we have simply $\eta =2$.

Note that the one dimensional integrals on each edge in (31) need to be approximated properly. In order to maintain the overall fifth order accuracy of our scheme, a locally sixth order accurate 3-point Gauss-Legendre quadrature rule is applied.

Three types of meshes are used in the computational studies:

• Type I. Uniform rectangular meshes.

• Type II. Nonuniform, perturbed logically rectangular meshes. Starting from a uniform rectangular mesh (Type I), we randomly perturb the points of the uniform mesh. The random perturbation of each point is set to be within $\pm 10\%$ of the uniform mesh spacing h. Also, in order to maintain periodicity on the mesh, the boundary points are perturbed only in the tangential direction.

• Type III. Nested logically rectangular meshes. Type III meshes are used for convergence tests on nonuniform meshes. We start from a Type II (coarse) mesh ($m\times m$, $m=40$). The next level (fine, $2m\times 2m$) mesh is obtained as follows. First of all, the fine mesh inherits all points of the coarse mesh. Secondly, the fine mesh includes a perturbation of the midpoint of two consecutive coarse mesh points. Finally, we perturb and include the average of the four vertices of every coarse in the fine mesh. The random perturbation is set to be within $\pm 5\%$ of one half of the coarse mesh spacing $h_{\text {coarse}}$ and the resulting meshes have to maintain periodicity.

7.1 Linear Equation in 2D

Our first 2D test is for $u_t + u_x + u_y = 0$ on $[0,2]^2$, with the initial condition

$$\begin{aligned} u(x,y,0) = \sin ^2(\pi x)\,\sin ^2(\pi y), \quad (x,y)\in [0,2]^2. \end{aligned}$$

(36)

We use Type III meshes. As shown in Table 9, the discrete error and convergence rates at time $t = 2$, using $\varDelta t= 0.1h$ and, approximately, $h = 2/m$ (so CFL number $\approx$ 0.1). A clean fifth order of convergence for all three schemes is obtained.

Table 9 Example 7.1, Linear equation. Discrete error and convergence order at $t=2$ on Type III meshes using $\varDelta t= 0.1 h$

7.2 Burgers Equation in 2D

We now test a two dimensional Burgers equation

$$\begin{aligned} u_t + (u^2/2)_x + (u^2/2)_y = 0. \end{aligned}$$

We first impose the initial condition (36) on $[0,2]^2$. A $160 \times 160$ Type II mesh is used. We take $\varDelta t= 0.1 h$ (CFL number $\approx$ 0.1), $h=1/80$. Figure 9 shows the results for SWENOZ-AO(5,3) at $t = 0$, 0.75, and 1.5. The shocks are well resolved by the new scheme.

Fig. 9

Example 7.2, Burgers equation with initial condition (36) solved with the SWENOZ-AO(5,3) scheme using Type II mesh with $m = 160$ and $\varDelta t= 0.1 h$, $h=1/80$, at times $t = 0$, 0.75, and 1.5

Table 10 Example 7.2, timing results for the three schemes, and the speedup for SWENOZ-AO(5,3)

For this 2D test, we report the solution times in Table 10. Our computer program solved the overall problem using the SWENOZ-AO scheme in about 182.7 s. This number includes all the time stepping computations, not just the time computing the reconstructions. We contrast it to the time taken to compute the WENOZ-AO solution, 950.2 s, and the WENO-AO solution, 941.8 s. We see that the entire computation is speeded up by a factor of about 5 using the simplified smoothness indicator.

Next, we consider a problem posed by Jiang and Tadmor [17] using the initial data

$$\begin{aligned} u(x,y,0) = {\left\{ \begin{array}{ll} 0.5, \quad &{}x< 0.5, y< 0.5,\\ 0.8, \quad &{}x> 0.5, y< 0.5,\\ -0.2, \quad &{}x < 0.5, y> 0.5,\\ -1.0, \quad &{}x> 0.5, y > 0.5.\\ \end{array}\right. } \end{aligned}$$

(37)

In order to obtain a reliable solution on the domain of $[0,1]^2$ using periodic boundary conditions, we use the larger region $[-0.5,1.5]^2$. Good results are shown in Fig. 10 on $[0,1]^2$ at time 0.5 using $\varDelta t= 0.2 h$ (with CFL number $\approx$ 0.2, $h = 1/160$ and 1/320) on a $160\times 160$ Type II mesh ($320\times 320$ on $[-0.5,1.5]^2$). Even though the mesh is not rectangular, the solution shows no spurious oscillations on all four fronts. We remark that the WENOZ-AO(5,3) and WENO-AO(5,3) schemes give results that are the same to the naked eye.

Fig. 10

Example 7.2. Burgers equation with initial data (37) solved with the SWENOZ-AO(5,3) scheme using Type II mesh with $m =160$ and $\varDelta t= 0.2h$ to time $t=0.5$. The contour plot has 21 level lines

7.3 The 2D Euler Equations

We solve the nonlinear system of Euler equations

$$\begin{aligned} \xi _t + f(\xi )_x + g(\xi )_y = 0, \end{aligned}$$

(38)

where

$$\begin{aligned}&\xi = (\rho , \rho u, \rho v, E)^T,\quad f(\xi ) = (\rho u, \rho u^2 + p, \rho u v, u(E + p))^T\\&\text {and}\quad g(\xi ) = (\rho v, \rho u v, \rho v^2 + p, v(E + p))^T. \end{aligned}$$

Here $\rho$ is the density, (u, v) is the velocity, and E is the total energy, with the pressure p being related to the total energy by $E = \frac{p}{\gamma -1} +\frac{1}{2}\rho (u^2+v^2)$ (again $\gamma =1.4$).

The extension of the finite volume scheme to the Euler System in two space dimensions follows closely what is described in [14, Section 4.4]. The eigenvalue matrix for the two-dimensional Euler system can be found in [22].

7.3.1 A Test of Convergence

We first test the convergence of the scheme. We consider the solution of the 2D Euler equations (38) in the domain $[0,2]^2$. The initial condition is set to be $\rho (x,y,0) = 1+0.2 \sin (\pi (x+y))$, $u(x,y,0) = 0.7$, $v(x,y,0) = 0.3$, and $p(x,y,0) = 1$, with 2-periodic boundary conditions. The exact solution is $\rho (x,y,t) = 1 + 0.2 \sin (\pi (x + y - (u + v)t))$, $u = 0.7$, $v = 0.3$, and $p = 1$.

Table 11 Example 7.3.1, 2D Euler convergence. Error and convergence order at $t=2$ for the three schemes on Type I and III meshes using $\varDelta t$ with CFL number = 0.6, $h=2/m$. Also shown is the computational speedup compared to SWENOZ-AO(5,3)

Table 12 Example 7.3.1, 2D Euler convergence. Computational speedup compared to SWENOZ-AO(5,3) on uniform and nonuniform meshes

The simulation is run to final time 2 using $\varDelta t$ with CFL number = 0.6, $h=2/m$ on a Type I $m\times m$ mesh, as well as a Type III mesh. The discrete errors and orders of convergence are reported in Table 11 for our new SWENOZ-AO(5,3) scheme and for the WENO-AO(5,3) and WENOZ-AO(5,3) schemes. All three schemes show the same convergence behavior. We see a clean fifth order convergence using uniform meshes, and a less clean fifth order convergence using nonuniform meshes, as we should expect.

Table 12 provides the speedup information. We see better speedup results than the 1D results, as we should have expected. They are not as good as the speedup in Table 2 (pure reconstruction) and Table 10 (scalar equation). This should also be expected, since we include the entire CPU time for solving the system of Euler equations, which requires more computation and therefore the portion of computing the nonlinear weights is reduced. We also observe that the speedups for nonuniform meshes are better than those for uniform meshes, since the latter needs only one computation of the dual basis [2]. Figures 11 and 12 display the CPU time versus error (the computational efficiency) of the three schemes using uniform and nonuniform meshes. SWENOZ-AO is clearly the most efficient scheme among the three.

Fig. 11

Example 7.3.1, Euler equations. Computational efficiency comparison of the schemes using Type I (uniform) mesh: $L_h^1$ error (left) and $L_h^\infty$ error (right) versus CPU-time for the 2D Euler equations. Shown are results for SWENOZ-AO(5,3) (circles), WENOZ-AO(5,3) (squares) and WENO-AO(5,3) (crosses)

Fig. 12

Example 7.3.1, Euler equations. Computational efficiency comparison of the schemes using Type III (nonuniform) mesh: $L_h^1$ error (left) and $L_h^\infty$ error (right) versus CPU-time for the 2D Euler equations. Shown are results for SWENOZ-AO(5,3) (circles), WENOZ-AO(5,3) (squares) and WENO-AO(5,3) (crosses)

7.3.2 A Riemann Problem

Our next test problem is the 2D Euler equation Riemann problem identified as Configuration F from [23], which has four interacting elementary planar waves. On the computational domain $[0,2]^2$, the initial condition is given in Table 13. The solution is symmetric about the diagonal $x=y$.

Table 13 Example 7.3.2, initial data for the 2D Riemann problem

Fig. 13

Example 7.3.2, The 2D Euler equation Riemann problem. Density using a $600\times 600$ Type II nonuniform mesh plotted as thirty equally spaced density contours from 0.56 to 1.67. Plots show SWENOZ-AO(5,3), WENO-AO(5,3) and WENOZ-AO(5,3) using $\varDelta t$ with CFL number = 0.4, $h=2/600$

The mesh size is taken to be $600\times 600$ for Type II meshes. We compute the solutions up to the final time 0.52 using $\varDelta t$ with CFL number = 0.4 and show the results in Fig. 13. We see nearly the same solutions for results from SWENOZ-AO(5,3), WENO-AO(5,3) and WENOZ-AO(5,3), with only small differences between them. We remark that the results for the uniform mesh appear to be nearly identical.

7.3.3 Mach-3 Wind Tunnel with a Step

This model problem is from [27]. The tunnel’s height and length is 1 unit by 3 units, and it has within it a forward-facing step appearing at the bottom 0.6 length units from the left side of the tunnel and being 0.2 length units high. The problem is initialized by a Mach 3 flow moving to the right. The boundary conditions are taken to be reflective along the walls of the tunnel, inflow on the left, and outflow on the right.

The corner of the step is a singular point and we treat it based on the assumption of a nearly steady flow in the region near the corner suggested by Woodward and Colella [27]. Square cells (greens cells in Fig. 14) are used locally near the corner of the step so that additional boundary conditions suggested in [27] and ghost cells for setting reflective boundary conditions could be easily prescribed. We reset the solution in the first four cells starting from the right of the corner and two cells above this row (cells marked with a cross in Fig. 14) based on the solution in the cell left and below the corner (marked with a circle in Fig. 14) after every iteration. The density of each crossed cell is re-initialized so the entropy has the same value as the circle cell while keeping the pressure unchanged. The velocity magnitude of the crossed cell is also reset so that the enthalpy has the same value as the circle cell using the corrected density and pressure.

The results are shown in Fig. 15 at $t=4$ using CFL number 0.4 and a $960\times 320$ Type II mesh. The three schemes give very comparable results.

Fig. 14

Example 7.3.3, Mach-3 wind tunnel with a step. Local mesh and special treatment of the expansion corner

Fig. 15

Example 7.3.3, Mach-3 wind tunnel with a step at $t=4$ using CFL number 0.4 and $960\times 320$ Type II mesh. The density is plotted as thirty equally spaced density contours from 0.32 to 6.15

7.3.4 Double Mach Reflection

Finally, the double Mach reflection problem was proposed by Woodward and Colella [27]. The computational domain of the problem is $[0,4]\times [0, 1]$. A shock of Mach 10 is located at $(x,y) = (1/6,0)$ and moves diagonally to the right, making a 60 degree angle with the horizontal axis. See [27] for a detailed description of this problem.

Fig. 16

Example 7.3.4, Double Mach reflection at $t=0.2$ using CFL number 0.4 and $1600\times 400$ Type II mesh. The density is plotted as thirty equally spaced density contours from 1.731 to 20.92

Fig. 17

Example 7.3.4, Double Mach reflection blow-up of results at $t=0.2$ using CFL number 0.4 and $1600\times 400$ Type II mesh. The density is plotted as thirty equally spaced density contours from 1.731 to 20.92

Using a CFL number of 0.4 , the simulation is run on a $1600\times 400$ mesh to a final time of 0.2. We show results in Fig. 16 on $[0,3]\times [0, 1]$ for the nonuniform mesh (Type II), since we do not see significant differences between the uniform (Type I) and nonuniform meshes. We also show in Fig. 17 a blow-up of the results on $[2,3]\times [0, 0.5]$. The results compare favorably with those found in the scientific literature (e.g., in [14]).

8 Summary and Conclusions

Classic WENO reconstruction is basically restricted to rectangular computational meshes, and so we concentrated on WENO reconstructions with adaptive order. These require the computation of the large stencil polynomial. Computation of the classic smoothness indicator (2), is quite expensive in d space dimensions, especially for a polynomial of high degree k (such as the large stencil polynomial). In fact, the workload is proportional to $k^{2d}$. To reduce the computational work, we proposed using the simple smoothness indicator (3), which has workload proportional to $k^d$.

It turns out that the simple smoothness indicator is not as robust as the classical one. Reconstructions based on the simple smoothness indicator combined with standard WENO weighting do not work well in practice. We therefore developed a modification of WENO-Z weighting (7)–(8) that, when combined with the simple smoothness indicator, gives a reliable and accurate reconstruction. We called the reconstruction SWENOZ-AO, and it requires two parameters $\eta _1$ and $\eta _2$.

We proved in Theorem 4 that SWENOZ-AO(r, s) attains ${\mathscr {O}}(h^r)$ accuracy when the solution is smooth, and drops to ${\mathscr {O}}(h^s)$ when there is a jump discontinuity in the solution, provided one takes $\eta _1 - \eta _2 \ge (r -s)/2$ and $\eta _2 \ge s/2$. These results were verified in numerical tests. Moreover, the 2D tests showed that SWENOZ-AO(5,3) was more than ten times faster to compute than the classic WENO-AO(5,3) reconstruction.

We defined finite volume schemes to approximate the solution of hyperbolic conservation laws using the new reconstruction. Numerical tests in 1D and 2D showed results of the same quality as standard WENO schemes using the classic smoothness indicator, but with an overall speedup in the computation time by a factor of about 3.5–5 in 2D tests. The computational efficiency (CPU time versus error) was also noticeably improved.

Due to limitations of the computer programs used, the numerical results were conducted in two space dimensions. The new smoothness indicator will clearly be much more efficient in three and higher dimensions, but it is difficult to say exactly how well it will perform without extensive numerical tests. Moreover, the two dimensional tests of the reconstruction in isolation given in Section 4 used general meshes, but the numerical tests of conservation laws given in Section 7 were conducted only on logically rectangular meshes. Testing of the new smoothness indicator in more general settings would need to be reserved for future work.