Abstract
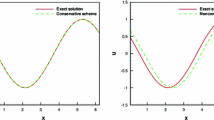
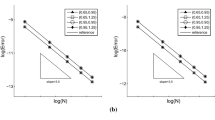
In this paper, semi-discrete numerical scheme for the approximation of the periodic Vlasov-viscous Burgers’ system is developed and analyzed. The scheme is based on the coupling of discontinuous Galerkin approximations for the Vlasov equation and local discontinuous Galerkin approximations for the viscous Burgers’ equation. Both these methods use generalized numerical fluxes. The proposed scheme is both mass and momentum conservative. Based on generalized Gauss–Radau projections, optimal rates of convergence in the case of smooth compactly supported initial data are derived. Finally, computational results confirm our theoretical findings.








Similar content being viewed by others
Data Availability
The codes during the current study are available from the corresponding author on reasonable request.
References
Brenner, S., Scott, R.: The mathematical theory of finite element methods, Texts in Applied Mathematics, vol. 15. Springer Science & Business Media, London (2007)
Cheng, Y., Chou, C.-S., Li, F., Xing, Y.: \(L^2\) stable discontinuous Galerkin methods for one-dimensional two-way wave equations. Math. Comp. 86(303), 121–155 (2017)
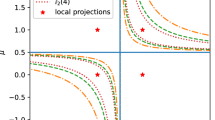
Cheng, Yao, Meng, Xiong, Zhang, Qiang: Application of generalized Gauss–Radau projections for the local discontinuous Galerkin method for linear convection-diffusion equations. Math. Comp. 86(305), 1233–1267 (2017)
Cockburn, B., Shu, C.-W.: Tvb Runge–Kutta local projection discontinuous Galerkin finite element method for conservation laws. ii. General framework. Math. Comp. 52(186), 411–435 (1989)
Cockburn, B., Shu, C.-W.: The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 35(6), 2440–2463 (1998)
Cao, W., Shu, C.-W., Zhang, Z.: Superconvergence of discontinuous Galerkin methods for 1-D linear hyperbolic equations with degenerate variable coefficients. ESAIM Math. Model. Numer. Anal. 51(6), 2213–2235 (2017)
De Ayuso Dios, B., Carrillo, J.A., Chi-Wang, S.: Discontinuous Galerkin methods for the one-dimensional Vlasov–Poisson system. Kinet Relat Models 4(4), 955–989 (2009)
DiPerna, R.J., Lions, P.-L.: Ordinary differential equations, transport theory and sobolev spaces. Invent. Math. 98(3), 511–547 (1989)
Daniele Antonio, D.P., Alexandre, E.: Mathematical aspects of discontinuous Galerkin methods. In: Mathématiques & Applications (Berlin) [Mathematics & Applications], vol. 69. Springer, Heidelberg (2012)
Domelevo, K., Roquejoffre, J.-M.: Existence and stability of travelling wave solutions in a kinetic model of two-phase flows. Comm. Partial Differ. Equ. 24(1–2), 61–108 (1999)
Goudon, T.: Asymptotic problems for a kinetic model of two-phase flow. Proc. Roy. Soc. Edinburgh Sect. A 131(6), 1371–1384 (2001)
Gottlieb, S., Shu, C.-W.: Total variation diminishing Runge–Kutta schemes. Math. Comp. 67(221), 73–85 (1998)
Hamdache, K.: Global existence and large time behaviour of solutions for the Vlasov–Stokes equations. Jpn. J. Ind. Appl. Math. 15(1), 51–74 (1998)
Han-Kwan, D., Miot, É., Moussa, A., Moyano, I.: Uniqueness of the solution to the 2D Vlasov–Navier–Stokes system. Rev. Mat. Iberoam. 36(1), 37–60 (2020)
Hopf, E.: The partial differential equation \(u_t+uu_x=\mu u_{xx}\). Comm. Pure Appl. Math. 3, 201–230 (1950)
Liu, H., Ploymaklam, N.: A local discontinuous Galerkin method for the Burgers–Poisson equation. Numer. Math. 129(2), 321–351 (2015)
Liu, M., Wu, B., Meng, X.: Optimal error estimates of the discontinuous Galerkin method with upwind-biased fluxes for 2D linear variable coefficients hyperbolic equations. J. Sci. Comput. 83(1), 1–19 (2020)
Li, J., Zhang, D., Meng, X., Wu, B., Zhang, Q.: Discontinuous Galerkin methods for nonlinear scalar conservation laws: Generalized local Lax-Friedrichs numerical fluxes. SIAM J. Numer. Anal. 58(1), 1–20 (2020)
Li, J., Zhang, D., Meng, X., Wu, B.: Analysis of discontinuous Galerkin methods with upwind-biased fluxes for one dimensional linear hyperbolic equations with degenerate variable coefficients. J. Sci. Comput. 78(3), 1305–1328 (2019)
Meng, X., Shu, C.-W., Wu, B.: Optimal error estimates for discontinuous Galerkin methods based on upwind-biased fluxes for linear hyperbolic equations. Math. Comp. 85(299), 1225–1261 (2016)
Meng, X., Shu, C.-W., Zhang, Q., Wu, B.: Superconvergence of discontinuous Galerkin methods for scalar nonlinear conservation laws in one space dimension. SIAM J. Numer. Anal. 50(5), 2336–2356 (2012)
P. J. O’ROURKE. Collective drop effects on vaporizing liquid sprays. PhD thesis, Princeton University, (1981)
Ploymaklam, N., Kumbhar, P.M., Pani, A.K.: A priori error analysis of the local discontinuous Galerkin method for the viscous Burgers–Poisson system. Int. J. Numer. Anal. Model. 14(4–5), 784–807 (2017)
Ploymaklam, N.: A local discontinuous Galerkin method for the reduced Burgers–Poisson equation. Thai J. Math. 17(2), 515–525 (2019)
Reed, W. H., Hill, T. R.: Triangular mesh methods for the neutron transport equation. Technical report, Los Alamos Scientific Lab., N. Mex.(USA), (1973)
Williams, F.A.: Combustion theory. CRC Press, Baco Ranton (1985)
Wang, H., Zhang, Q., Shu, C.-W.: Implicit-explicit local discontinuous Galerkin methods with generalized alternating numerical fluxes for convection-diffusion problems. J. Sci. Comput. 81(3), 2080–2114 (2019)
Acknowledgements
Authors are grateful to anonymous referees for their valuable comments and suggestions which help to improve the revised manuscript. K.K. and H.H. thank Laurent Desvillettes for introducing them to the fluid-kinetic equations modelling the thin sprays during the Junior Trimester Program on Kinetic Theory organised at the Hausdorff Research Institute for Mathematics, Bonn. K.K. and H.H. thank the Hausdroff Institute of Mathematics, Bonn, for hosting them during the Junior Trimester program on Kinetic theory (Summer of 2019) where this work was initiated. K.K. further acknowledges the financial support of the University Grants Commission (UGC), Government of India.
Funding
The second author acknowledges the financial support of the University Grants Commission (UGC), Government of India. the first and second authors thank the Hausdroff Institute of Mathematics, Bonn, for hosting them during the Junior Trimester program on Kinetic theory (Summer of 2019) where this work was initiated.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to prepare this manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A.
Appendix A.
The following lemma yields estimate for \(u_x\) in \(L^\infty \)-norm which helps us to prove the regularity result for viscous Burgers’ equation.
Lemma A.1
For a periodic function u with \(u \in C^2(I)\), there holds
Proof
As u is periodic. Hence, \(\int _I u_x\,{\textrm{d}}x = 0\) and there is some \(x_0 \in I\) such that \(u_x(x_0) = 0\)
Here, in first step use fundamental theorem of Calculus and in last step use the Cauchy-Schwarz inequality. After taking square root on both side and supremum over \(x \in I\) completes the proof. \(\square \)
The following lemma shows the regularity result for the solution of viscous Burgers’ equation.
Lemma A.2
Let \(\int _{{\mathbb R}}\int _I\,|v|^pf_0\,{\textrm{d}}x\,{\textrm{d}}v < \infty \) for \(0 \le p \le 3\) and \(u_0 \in H^1(I)\). Then
Proof
Multiplying Eq. (1.2) by \(- u_{xx}\) and integrate with respect to x to obtain
A use of the Hölder inequality with Lemma A.1 and the Young’s inequality yields
From Eq. (A.2) after a use of the Hölder inequality, the Young’s inequality and Eq. (A.3) with kickback argument, we obtain
A use of Sobolev inequality and an integration in time from 0 to t leads to
A use of (2.2) and (2.5) shows
After taking supremum over \(t \in [0,T]\), we obtain the first result.
Now, multiply Eq. (1.2) by \(u_t\) and integration with respect to x follows
A use of the Hölder inequality with the Young’s inequality, kickback argument and an integration in time completes the rest of the proof. \(\square \)
As a consequence of above lemma, it follows that
Here, in second step use Sobolev inequality and in third step use the Hölder inequality.
The following result is on the propagation of velocity moments which is crucial for the proof of existence and uniqueness of strong solution.
Lemma A.3
Let \(u \in L^1(0,T;W^{1,\infty }(I))\) and let \(f_0 \ge 0\) be such that
for \(k \ge 0\). Then, the solution f of the Vlasov equation satisfies
for \(k \ge 0\) and for all \(t>0\).
Proof
Consider the equation for \(\partial _xf\)
Multiplying the above equation by \(\left( 1 + |v|^k\right) \partial _xf\) and integrating with respect to x, v yields
where
and
After using the Young’s inequality in \(I_1\), we obtain
An integration by parts yields
with
A use of the Young’s inequality shows
Next, consider the equation for \(\partial _vf\)
Multiplying the above equation by \(\left( 1 + \vert v\vert ^k\right) \partial _vf\) and integrating with respect to x, v yields
where
After using the Young’s inequality in \(I_5\), we obtain
An integration by parts yields
with
An integration by parts shows
with
A use of the Young’s inequality leads to
Altogether, we obtain
Let \( F(t) = \int _{{\mathbb R}}\int _I\left( 1 + \vert v\vert ^k\right) \left( \left| \partial _xf\right| ^2 + \left| \partial _vf\right| ^2\right) \,{\textrm{d}}x\,{\textrm{d}}v\), then
this implies
This completes our proof. \(\square \)
Theorem A.4
(Existence and Uniqueness of strong solution) Let the initial data \(\left( f_0,u_0\right) \) be such that
for \(0 \le p \le 4\) and \(u_0 \in H^1(I)\). Then, there exists a unique global-in-time strong solution \(\left( f,u\right) \) to the Vlasov-viscous Burgers’ system (1.1)–(1.2).
Proof
Let \(0< T < \infty \) and set \(X = L^\infty (0,T;H^1(I))\), with norm
We now consider the map
defined by the following scheme.
-
Solve the Vlasov equation
$$\begin{aligned} \partial _t f + v\,\partial _x f + \partial _v \left( \left( u^* - v\right) f\right) = 0, \end{aligned}$$(A.5)with initial data \(f_0\).
-
Solve the viscous Burgers’ equation
$$\begin{aligned} \begin{aligned} \left( u_t,\phi \right) + \left( uu_x, \phi \right) + \epsilon \left( u_x,\phi _x\right) = \left( \rho V - \rho u, \phi \right) , \quad \forall \,\, \phi \in H^1(I) \end{aligned} \end{aligned}$$(A.6)with initial data \(u_0\). Here \(\rho \) and \(\rho V\) are the local density and the momentum associated with the solution f of (A.5).
To begin with, we show that the above map \(\mathcal {T}\) is well-defined. For a given \(u^* \in X\) and a given initial datum \(f_0\), the Vlasov equation (A.5) is uniquely solvable (see Lemma A.5 below for details). Having solved (A.5) for \(f(u^*)\), one gather that the corresponding local density \(\rho \in L^\infty \) (see Lemma 2.5) and the corresponding momentum \(\rho V \in L^2\) (see Lemma 2.3). Hence, classical theory for the viscous Burgers’ problem [15] yields a unique solution \(u \in X\) for the problem (A.6). Thus, the map \(\mathcal {T}: X \rightarrow X\) that takes \(u^*\) to \(\mathcal {T}(u^*) = u\) is well-defined. Our next step in the proof is to show that \(\mathcal {T}\) is a contraction map and that has been demonstrated in Lemma A.6 below. Therefore, an application of the Banach fixed-point theorem ensures the existence of a unique solution (f, u) in a short time interval \((0,T^0)\). As the solution (f, u) stays bounded at \(t = T^0\), thanks to a priori estimates, we can employ continuation argument to extend the interval of existence upto (0, T]. As T is arbitrary, we get global-in-time well-posedness of our system. \(\square \)
Next we deal with Lemmata A.5 and A.6 which played a crucial role in the above proof.
Lemma A.5
Let \(u^* \in X\) and let \(f_0 \in L^1(I\times {\mathbb R})\cap L^\infty (I\times {\mathbb R})\). Then, there exists a unique solution \(f \in L^\infty (0,T;L^1(I\times {\mathbb R})\cap L^\infty (I\times {\mathbb R}))\) to (A.5).
Proof
Note that (A.5) can be rewritten as
where \(b = (v, u^*(t,x) - v)\), which lies in
Note that div\(_{x,v}b = -1 \in L^\infty ((0,T) \times \Omega )\). Furthermore, \(|b|/(1 + |v|)\) is bounded. This setting appeals to the general results in [8]. In particular, we can apply [8, Corollaries II-1 and II-2, p.518] to arrive at the existence of the unique solution. \(\square \)
Lemma A.6
The map defined by (A.5) and (A.6) is a contraction map.
Proof
Let for given \(u_i^*\) there exist a unique solution \(f_i\) for equation (A.5). Define \(\bar{u} = u_1 - u_2, \bar{u}^* = u_1^* - u_2^*\) and \(\bar{f} = f_1 - f_2\), then from (A.5) and (A.6) we find that
and
with \(\quad \bar{u}(0,x) = 0.\)
Choose \(\phi = \bar{u} - \bar{u}_{xx}\) in (A.8) to obtain
a use of the Hölder inequality with the Young’s inequality, a kickback argument and integration in time yields
Now, the Hölder inequality followed by Sobolev imbedding shows
and
For a sufficiently small \(T > 0\)
Using Eqs. (A.9)–(A.12), we obtain
Now, a similar calculation as in proof of Lemma 2.3 shows
and
Multiplying Eq. (A.7) by \(|v|^k\frac{\bar{f}}{\sqrt{\bar{f}^2 + \delta }}\); \(k \ge 1\), we obtain
Then, an integrate with respect to x, v yields
A use of Sobolev inequality with integration in time shows
Here,
and
As \(\bar{f} \in L^1(0,T;L^\infty (I\times {\mathbb R}))\) and as fourth order velocity moments of \(\left| \partial _vf\right| ^2\) and \(\bar{f}\) are bounded (see Lemma A.3), \(\left| T_k^1\right| \rightarrow 0\) and \(\left| T_k^2\right| \rightarrow 0\) as \(\delta \rightarrow 0\) for \(k = 1,2,3\). Next, we multiply Eq. (A.7) by \(\frac{\bar{f}}{\sqrt{\bar{f}^2+\delta }}\) and integrate with respect to x, v and t variables to obtain
with \(\bar{f}(0,x,v) = 0\). Arguing as we did with the \(T_k^1\) and \(T_k^2\) terms, in the \(\delta \rightarrow 0\) limit in above equation, we arrive at
A use of Eq. (A.16) for \(k = 1\) in Eq. (A.15) and \(\delta \rightarrow 0\) shows
Using Eq. (A.14) and by induction from Eq. (A.16), we deduce
Using (A.18)–(A.19) for a sufficiently small \(T > 0\) from (A.13), we obtain
This shows that \(\mathcal {T}\) is a contraction map. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Hutridurga, H., Kumar, K. & Pani, A.K. Discontinuous Galerkin Methods with Generalized Numerical Fluxes for the Vlasov-Viscous Burgers’ System. J Sci Comput 96, 7 (2023). https://doi.org/10.1007/s10915-023-02230-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-023-02230-5
Keywords
- Vlasov-viscous Burgers’ system
- Discontinuous Galerkin method
- LDG method
- Generalized numerical fluxes
- Discrete mass and momentum conservation
- Generalized Gauss–Radau projection
- Optimal error estimates
- Numerical experiments