Guidelines for RBF-FD Discretization: Numerical Experiments on the Interplay of a Multitude of Parameter Choices

Abstract

There exist several discretization techniques for the numerical solution of partial differential equations. In addition to classical finite difference, finite element and finite volume techniques, a more recent approach employs radial basis functions to generate differentiation stencils on unstructured point sets. This approach, abbreviated by RBF-FD (radial basis function-finite difference), has gained in popularity since it enjoys several advantages: It is (relatively) straightforward, does not require a mesh and generalizes easily to higher spatial dimensions. However, its application is not quite as blackbox as it may appear at first sight. The computed solution might suffer severely from various sources of errors if RBF-FD parameters are not selected carefully. Through comprehensive numerical experiments, we study the influence of several of these parameters on the condition numbers of intermediate (local) weight matrices, on the condition number of the resulting (global) stiffness matrix and ultimately on the approximation error of the computed discrete solution to the partial differential equation. The parameters of investigation include the type of RBF (and its shape or other parameters if applicable), the degree of polynomial augmentation, the discretization stencil size, the underlying type of point set (structured/unstructured), and the total number of (interior and boundary) points to discretize the PDE, here chosen as a three-dimensional Poisson’s problem with Dirichlet boundary conditions. Numerical tests on a sphere as well as tests for the convection-diffusion equation are included in a supplement and demonstrate that the results obtained for the Laplace problem on a cube generalize to wider problem classes. The purpose of this paper is to provide a comprehensive survey on the various components of the basic algorithms for RBF-FD discretization and steer away from potential pitfalls such as computationally more expensive setups which not always lead to more accurate numerical solutions. We guide toward a compatible selection of the multitude of RBF-FD parameters in the basic version of RBF-FD. For many of its components we refer to the literature for more advanced versions.

1 Introduction

(Linear) partial differential equations can be solved numerically by a suitable discretization followed by the solution of a linear system of equations. Among possible discretization techniques, the radial basis function-finite difference (RBF-FD) method can be viewed as a generalization of the finite difference (FD) method to unstructured point sets. The earlier papers on RBF-FD include [72, 73]. Since then, it has gained in popularity and entered into several applications including geosciences [25, 26], heat flow [44], the financial sector [45], linear elasticity [66], fluid mechanics [11, 36], and neuronal dynamics [52].

As in classical finite difference methods, RBF-FD replaces (linear) differential operators by differentiation stencils which encode formulas for weighted sums of function values at neighboring points. The weights are chosen such that the formulas become exact for a set of test functions which typically include radial as well as polynomial functions.

The discretization error in the numerical solution of a boundary value problem is affected by several aspects of the solution process including the underlying point set (the number of interior/boundary nodes and their distribution), the number (and distribution) of nodes in the discretization stencil as well as the RBF (including its shape or other parameters) and the degree of polynomial augmentation used to generate the stencil weights.

The application of RBF-FD discretization can lead to (auxiliary) highly ill-conditioned linear systems of equations to be solved for the weights, resulting in instability which prevents convergence of the numerical to the exact solution [24, 25, 39]. One possibility to address the ill-conditioning lies in a scaling of the shape parameter which, however, leads to a stagnation effect [1]. Another possibility lies in the use of hybrid kernels [46, 47], another in the transition to stable versions of RBFs, e. g. RBF-GA [27, 41, 42], RBF-RA [31, 80] or RBF-QR [39]. These, however, typically incur increased computational costs. A computationally even more expensive possibility to address the ill-conditioning is provided by (sufficiently high) extended precision [23]. Further possibilities to address the ill-conditioning are spatially variable shape parameters [8, 29, 56], Tikhonov regularization [69] or smoothing splines [20, 82]. More recent papers often suggest to use polyharmonic splines (PHS) in combination with high order polynomials to generate the stencil weights. In [23, 25], the Gaussian (GA) and PHS generating functions are studied and compared with respect to polynomial augmentation, extended precision and stable algorithms. In [58], PHS with polynomial augmentation (for a fixed stencil size and a numerically determined optimal degree of polynomial augmentation) is compared to the stable RBF-GA method with a small shape parameter (i. e., representing the limit case $\varepsilon \rightarrow 0$). The advantages and disadvantages of the choice of parameters and the performance of the PHS generating function with polynomial augmentation are further studied in [2,3,4, 22, 35, 62].

In this paper, we will review some of these approaches with a focus on the most commonly used and (to us) most promising ones. We will discuss the multitude of involved parameter choices, illustrate their influence through numerical tests, and draw comparisons between the different approaches. There already exist quite a few numerical studies for the performance of RBF interpolation, approximation [7] and the solution of partial differential equations, but we address yet another angle that we have not found in the literature yet. Namely, the novel contributions of this paper consist of

• A comprehensive view and comparison of the basic but often still competitive RBF-FD methods from the literature, in particular comprehensive numerical tests to illustrate the condition numbers of weight and stiffness matrices side-by-side with the discretization errors for a broad set of parameter choices across the landscape of RBF-FD discretization; the intention is to illustrate the ill-conditioning of weight matrices as a cause for numerical instabilities and the scaling of the shape parameter which is introduced to control this ill-conditioning as a cause for stagnation, show both the potential and limitations of individual RBF classes and offer a comparison to alternative RBF-FD setups (see Sects. 4.2–4.4);

• A new scaling law for the stencil size and the degree of polynomial augmentation for PHS and HYB generating functions on Cartesian node distributions (see Sect. 4.3);

• A detailed (numerical) comparison of the hybrid (HYB) [46] and the PHS generating functions for the case of polynomial augmentation (see Sect. 4.4);

• General recommendations for parameter setups in the basic version of RBF-FD discretizations (see Sect. 4.5).

While in this paper all linear systems are solved directly, our focus on condition numbers of the resulting stiffness matrices will also be of interest for the subsequent development of iterative solvers for the systems.

The remainder of this paper is organized as follows. In Sect. 2, we review RBFs, RBF-FD approximation of linear differential operators and its application to the discretization of linear partial differential equations. The details pertaining to the node generation, the stencil formation and computation of the stencil weights, the choice of the RBF and the role of polynomial augmentation are discussed in Sect. 3. Section 4 is devoted to comprehensive numerical tests for a multitude of parameter choices in RBF-FD discretization applied to our model problem, the three-dimensional Poisson’s equation with Dirichlet boundary conditions. In order to illustrate that qualitative results also apply to a wider class of model problems, we provide a supplement with numerical results on a different domain, i. e., a sphere, as well as for a different partial differential equation, i. e., the convection-diffusion equation with a recirculating convection. Finally, a conclusion and an outlook are presented in Sect. 5.

2 The RBF-FD Method

In this section, we introduce radial basis functions as a tool for the approximation of linear differential operators (Sect. 2.1), explain the discretization of a partial differential equation with Dirichlet boundary conditions by means of the RBF-FD method (Sect. 2.2) and summarize the various types of errors that may and typically do occur in the overall numerical RBF-FD solution process (Sect. 2.3).

2.1 RBF and RBF-FD Approximation

Radial basis functions typically refer to a set of functions that are characterized by individual centers but are otherwise identical and radial in shape, i. e., shifted copies of one another, the function value at a point depending only on its distance to the center. Formally, they can be defined as follows).

Definition 2.1

For a spatial dimension $d\in {\mathbb {N}}$, an open domain $\Omega \subseteq {\mathbb {R}}^d$, a shape parameter $\varepsilon > 0$, a set of pairwise distinct nodes $X := \{x_1,\ldots , x_n\} \subset \Omega$ with $n \in {\mathbb {N}}$, and a generating function $\phi _{\varepsilon } :[0,\infty ) \rightarrow {\mathbb {R}}$, we define radial basis functions (RBFs) centered at a node $x_i$ as

$$\begin{aligned} \Phi _{\varepsilon ,x_i}:\Omega \rightarrow {\mathbb {R}}, \;\;\;\; \Phi _{\varepsilon ,x_i}(x) := \phi _{\varepsilon }\left( \Vert x-x_i\Vert _2\right) , \quad ~i\in \{1,\ldots , n\}. \end{aligned}$$

Sometimes, the generating function $\phi _{\varepsilon }$ is referred to as a kernel function or even as a radial basis function itself. Ideally, the functions $\Phi _{\varepsilon ,x_i}$ are linearly independent and hence form a basis of their span so that the terminology basis function is justified. Furthermore, in order to later be able to guarantee the existence of unique solutions of (discrete) interpolation problems using radial basis functions, we will require the kernel function to be (conditionally) positive definite, see Definition 2.2. Typical examples for such kernel functions are listed in Table 1.

We list several reasons for the popularity of RBFs for multivariate interpolation and approximation [78]:

• RBFs can be used in any spatial dimension.

• RBFs are applicable to arbitrarily scattered data. In particular, no mesh is required.

• Interpolants/approximants have a simple representation and inherit thesmoothness of the radial basis functions.

RBFs can be used to approximate the action of a linear differential operator as follows. Let ${\mathcal {L}}$ denote a linear differential operator, $u:\Omega \rightarrow {\mathbb {R}}$ be a sufficiently smooth function, and let

$$\begin{aligned} X_\Omega := \{x_1, \ldots , x_{N_I}\} \subset \Omega , \qquad X_{\partial \Omega } := \{x_{N_I+1}, \ldots , x_N\} \subset \partial \Omega \end{aligned}$$

be sets of distinct interior and boundary nodes, resp., with $N_I, N \in {\mathbb {N}}, ~N_I\le N$ (see Sect. 3.1 for more details about possibilities for the generation of these node sets). Such node sets $X := X_\Omega \cup X_{\partial \Omega }$ also occur in finite difference discretizations, but now the nodes may be scattered and need not be connected by edges of a (structured tensor product) grid.

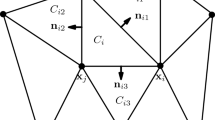
For a node $x_j \in X_\Omega$, $j \in \{1, \ldots , N_I\}$, and stencil size $n\le N$, let $X_j \subseteq X$ be a stencil associated to the (stencil) center $x_j$ (see Sect. 3.2 for more information on the stencil computation). We use ${\mathcal {I}}_j \subseteq \{1, \ldots , N\}$ to denote the index set of nodes included in the stencil $X_j$, i. e.,

$$\begin{aligned} X_j = \left\{ x_{s_1^j}, \ldots , x_{s_n^j} \right\} = \left\{ x_i \in X: i \in {\mathcal {I}}_j \right\} ~~\text { for } {\mathcal {I}}_j := \left\{ s_1^j, \ldots , s_n^j \right\} . \end{aligned}$$

(2.1)

The goal is to determine weights $\{w_1^j,\ldots ,w_n^j\}\subset {\mathbb {R}}$ such that the differential operator applied to the function u and evaluated at $x_j$ can be expressed (approximately) as a weighted sum of function values at the nodes in the stencil $X_j$, i. e.,

$$\begin{aligned} {\mathcal {L}} u(x_j) := \left. {\mathcal {L}} u(x) \right| _{x = x_j} \approx \sum _{i = 1}^n w_i^j u \left( x_{s_i^j} \right) . \end{aligned}$$

(2.2)

The stencil weights are determined such that the weighted sum yields the correct result for the interpolant w. r. t. the stencil nodes, i. e., equality is enforced for (basis) functions $k_1, \ldots , k_n :\Omega \rightarrow {\mathbb {R}}$. If these are cardinal basis functions w. r. t. the stencil nodes in $X_j$, i. e., if there holds $k_{\ell }(x_{s_i^j}) = \delta _{\ell i}$ with the Kronecker delta, then $p_u :\Omega \rightarrow {\mathbb {R}}, ~p_u (x) = \sum _{i=1}^n u(x_{s_i^j}) k_i (x)$ is the interpolant of u, and the application of a differential operator ${\mathcal {L}}$ at some $x_c\in \Omega$ is given by

$$\begin{aligned} {\mathcal {L}} p_u (x_c)&= \sum _{i=1}^n u \left( x_{s_i^j} \right) {\mathcal {L}} k_i (x_c) =: \sum _{i=1}^n u \left( x_{s_i^j} \right) w_i \end{aligned}$$

(2.3)

for weights defined by $w_i := {\mathcal {L}} k_i (x_c)$, $i \in \{1\ldots ,n\}$.

We will next illustrate the computation of these weights for typical RBF spaces with (or without) polynomial augmentation. Let $\{\Phi _{\varepsilon ,x_i} \mid i\in {{{\mathcal {I}}}}_j\}$ denote the n radial basis functions associated with the nodes of the stencil $X_j$, and let

$$\begin{aligned} \Pi _{\ell } := \text {span} \bigg \{ p ~:\Omega \rightarrow {\mathbb {R}}, ~p(x) = \prod _{j = 1}^d x_j^{k_j} \mid k_j\in {\mathbb {N}}_0, \sum \limits _{j = 1}^d k_j \le \ell \bigg \} \end{aligned}$$

(2.4)

denote the space of d-variate polynomials of degree at most $\ell \in {\mathbb {N}}_0$. There holds

$$\begin{aligned} \dim \Pi _{\ell } = \left( {\begin{array}{c}\ell +d\\ d\end{array}}\right) =: M, \end{aligned}$$

(2.5)

and we denote a basis of $\Pi _{\ell }$ by $\{p_1,\ldots , p_M\}$. The n-dimensional constrained function space of RBFs associated with the stencil $X_j$ (2.1) and augmented by polynomials up to degree $\ell$ is defined by

$$\begin{aligned}&{{{\mathcal {R}}}}_j := \bigg \{ s ~:\Omega \rightarrow {\mathbb {R}}, ~s(x) = \sum _{i=1}^n \lambda _i^j \Phi _{\varepsilon ,x_{s_i^j}}( x ) + \sum _{k=1}^M {\widetilde{\lambda }}_k^j p_k( x ) \mid \lambda _i^j, {\widetilde{\lambda }}_k^j \in {\mathbb {R}} \\&\quad \text { such that } \sum _{i=1}^n \lambda _i^j p_k(x_{s_i^j} ) = 0 \text { for all } k\in \{1,\ldots ,M\} \bigg \}. \end{aligned}$$

It is straightforward that (the weights of) an interpolant $s\in {{{\mathcal {R}}}}_j$ of a function $f :\Omega \rightarrow {\mathbb {R}}$ can be computed as the solution of the linear system

$$\begin{aligned} \begin{bmatrix} A_j &{}\quad P_j \\ P^T_j &{}\quad {\textbf{0}} \end{bmatrix} \begin{bmatrix} \lambda ^j \\ {\widetilde{\lambda }}^j \\ \end{bmatrix} = \begin{bmatrix} f^j \\ 0_M \end{bmatrix} \end{aligned}$$

with coefficient and right hand side vectors

$$\begin{aligned} \lambda ^j := \begin{bmatrix} \lambda _1^j \\ \vdots \\ \lambda _n^j\end{bmatrix}, ~~{{\widetilde{\lambda }}}^j := \begin{bmatrix} {{\widetilde{\lambda }}}_1^j \\ \vdots \\ \widetilde{\lambda }_M^j\end{bmatrix}, ~~f^j := \begin{bmatrix} f\left( x_{s_1^j}\right) \\ \vdots \\ f\left( x_{s_n^j}\right) \end{bmatrix}, ~~0_M := \begin{bmatrix} 0 \\ \vdots \\ 0 \end{bmatrix}\in {\mathbb {R}}^M \end{aligned}$$

and system matrix

$$\begin{aligned} \widetilde{A_j} := \begin{bmatrix} A_j &{}\quad P_j \\ P^T_j &{}\quad {\textbf{0}} \end{bmatrix} := \begin{bmatrix} \Phi _{\varepsilon ,x_{s_1^j}}( x_{s_1^j} ) &{}\quad \cdots &{}\quad \Phi _{\varepsilon ,x_{s_n^j}}( x_{s_1^j} ) &{}\quad p_1( x_{s_1^j} ) &{}\quad \cdots &{}\quad p_M( x_{s_1^j} ) \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \Phi _{\varepsilon ,x_{s_1^j}}( x_{s_n^j} ) &{}\quad \cdots &{}\quad \Phi _{\varepsilon ,x_{s_n^j}}( x_{s_n^j}) &{}\quad p_1( x_{s_n^j} ) &{}\quad \cdots &{}\quad p_M( x_{s_n^j} ) \\ p_1( x_{s_1^j} ) &{}\quad \cdots &{}\quad p_1( x_{s_n^j} ) &{}\quad 0 &{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ p_M( x_{s_1^j} ) &{}\quad \cdots &{}\quad p_M( x_{s_n^j} ) &{}\quad 0 &{}\quad \cdots &{}\quad 0 \end{bmatrix}. \end{aligned}$$

(2.6)

The interpolation problem has a unique solution if this matrix ${{\widetilde{A}}}_j$ is regular. This can be guaranteed if the kernel function and node set X satisfy the properties given in Definitions 2.2 and 2.3, resp.

Definition 2.2

The generating function $\phi : [0,\infty )\rightarrow {\mathbb {R}}$ is called conditionally positive definite of order $\ell \in {\mathbb {N}}$ if

$$\begin{aligned} \sum _{j=1}^N\sum _{k=1}^N \lambda _j \lambda _k \phi (\Vert x_j - x_k\Vert _2) >0 \end{aligned}$$

(2.7)

for any (finite) set $X=\{x_1,\ldots ,x_N\}\subset {\mathbb {R}}^n$ of distinct nodes and coefficients $\lambda _j, j=1,\ldots , N$, $\lambda _j\ne 0$ for at least one $j\in \{1,\ldots ,N\}$, satisfying

$$\begin{aligned} \sum _{j=1}^N \lambda _j p(x_j) = 0 \end{aligned}$$

for all polynomials $p \in \Pi _{\ell -1}$.

The generating function $\phi$ is called positive definite if (2.7) holds without any restrictions on $\lambda _j$ imposed through polynomials.

Definition 2.3

A (finite) set $X=\{x_1,\ldots ,x_N\}\subset {\mathbb {R}}^n$ of distinct nodes is called $\Pi _{\ell }$-unisolvent if there is no nonzero polynomial in $\Pi _{\ell }$ that vanishes on all nodes in X, i. e., if

$$\begin{aligned} p(x_j) = 0 \quad \forall j\in \{1,\ldots ,N\} \quad \Longrightarrow \quad p=0. \end{aligned}$$

More details concerning (conditionally) positive definite functions are included in most textbooks on radial basis functions, see e. g. [9, 77]. In terms of matrices, $\Pi _{\ell }$-unisolvency guarantees that the submatrix $P_j$ in (2.6) has full column rank, and if in addition the generating function is conditionally positive definite (of order $\ell +1$ or less), then ${{\widetilde{A}}}_j$ is regular.

The cardinal functions of the space ${{{\mathcal {R}}}}_j$ may now be represented by

$$\begin{aligned} k_i (x)&= \begin{bmatrix} \Phi _{\varepsilon ,x_{s_1^j}}( x )&\cdots&\Phi _{\varepsilon ,x_{s_n^j}}( x )&p_1(x)&\cdots&p_M(x) \end{bmatrix} \widetilde{A_j}^{-1} \begin{bmatrix} e_i\\ 0_M \end{bmatrix} \end{aligned}$$

where $e_i\in {\mathbb {R}}^n$ denotes the i’th unit vector. Application of the differential operator and evaluation at the stencil center $x_c:=x_j$ yields

for a single weight and

$$\begin{aligned} \left[ w_1^j~\ldots ~w_n^j\right] = \left[ \left( {\mathcal {L}} \mathbf {\Phi }_j\right) ^T ~ \left( {\mathcal {L}} {\textbf{p}}_j\right) ^T \right] \widetilde{A_j}^{-1} \begin{bmatrix} I_n\\ 0_{M\times n} \end{bmatrix} \end{aligned}$$

for all weights with identity matrix $I_n\in {\mathbb {R}}^{n\times n}$ and zero matrix $0_{M\times n} \in {\mathbb {R}}^{M\times n}$. Augmentation of the matrix on the right to an $(n+M)\times (n+M)$ identity matrix and introduction of dummy variables ${\widetilde{w}}_i^j$ (which may later be discarded since they originated from the arbitrary augmentation to the identity matrix) leads to the linear system of equations

$$\begin{aligned} \underbrace{\begin{bmatrix} A_j &{}\quad P_j \\ P_j^T &{}\quad {{\textbf{0}}} \end{bmatrix}}_{=\widetilde{A_j} (2.6)} \begin{bmatrix} w^j \\ {\widetilde{w}}^j \end{bmatrix} = \begin{bmatrix} {\mathcal {L}} \vec {\Phi }_j\\ {\mathcal {L}} {\textbf{p}}_j \end{bmatrix} \quad \text {with}\quad w^j := \begin{bmatrix} w_1^j \\ \vdots \\ w_n^j \end{bmatrix}, ~~{\widetilde{w}}^j := \begin{bmatrix} {\widetilde{w}}_1^j \\ \vdots \\ {\widetilde{w}}_M^j \end{bmatrix} \end{aligned}$$

(2.8)

for the desired stencil weights $w_i^j$ in the approximation (2.2) [25]. Without polynomial augmentation, the saddle point system (2.8) simplifies to $A_j w^j = {\mathcal {L}} \vec {\Phi }_j$. However, there exist several reasons to add polynomials in RBF-FD interpolation and approximation [23, 25], including the following.

• For some RBFs, the matrix $A_j$ in (2.8) is guaranteed to be positive definite. For other RBFs, it can be shown that $A_j$ is positive definite on the subspace that satisfies the constraints for an appropriately chosen polynomial degree $\ell$ (this is e. g. the case for conditionally positive definite generating functions and a unisolvent stencil).

• Exact/accurate interpolation of low order polynomials (in particular constants) instead of an oscillatory representation which is often obtained without polynomial augmentation.

• The accuracy of the approximation in (2.2) may be significantly improved.

• Stagnation errors may be reduced.

2.2 RBF-FD for Partial Differential Equations

In the previous subsection, we derived an approximation of the application of a linear differential operator to a function and its evaluation at a fixed node by a sum of weighted function values at stencil nodes. We next extend this approach to the discretization of a linear partial differential equation

$$\begin{aligned} {\mathcal {L}} u(x)&= f(x) \;\;\;\;\; \forall x \in \Omega , \end{aligned}$$

(2.9a)

$$\begin{aligned} u(x)&= g(x) \qquad \forall x \in \partial \Omega , \end{aligned}$$

(2.9b)

where $f:\Omega \rightarrow {\mathbb {R}}$ is a sufficiently smooth function and $g:\partial \Omega \rightarrow {\mathbb {R}}$ is a function to specify the Dirichlet boundary conditions.

For each interior node $x_j \in X_\Omega ,~j \in \{1, \ldots , N_I\}$, of the point set $X=X_\Omega \cup X_{\partial \Omega } \subset {\overline{\Omega }}$, we compute a stencil $X_j\subset X$ of size n (2.1) and stencil weights $\{w_1^j, \ldots , w_n^j\}$ by solving (2.8). The stencil weights are used to compute approximations $u_{i}$ to the solution $u(x_{i})$ of (2.9a), (2.9b) at all interior nodes $x_{i} \in X_\Omega$, i. e., $u_{i} \approx u(x_{i})$ for all $x_{i} \in X_\Omega , i \in \{1, \ldots , N_I\}$ by enforcing equality in (2.2), i. e.

$$\begin{aligned} \sum _{i = 1}^n w_i^j u_{s_i^j} = f(x_j), \quad j\in \{1,\ldots ,N_I\}. \end{aligned}$$

(2.10)

Given the Dirichlet boundary data from (2.9b), we set $u_{s_i^j} := g(x_{s_i^j})$ for all $x_{s_i^j} \in \partial \Omega$, substitute this boundary information into (2.10) and obtain

$$\begin{aligned} \sum _{{\mathop {\text {s.t. } x_{s_i^j} \in \Omega }\limits ^{i\in \{1,\ldots ,n\}}}} w_i^j u_{s_i^j} = \underbrace{f(x_j) - \sum _{{\mathop {\text {s.t. } x_{s_i^j} \in \partial \Omega }\limits ^{i\in \{1,\ldots ,n\}}}} w_i^j g(x_{s_i^j})}_{=:{\widetilde{f}}_j} , \qquad j\in \{1,\ldots , N_I\}. \end{aligned}$$

Hence, we define the right hand side vector ${\widetilde{f}} := ({\widetilde{f}}_1, \ldots , {\widetilde{f}}_{N_I})^T \in {\mathbb {R}}^{N_I}$ and the global stiffness matrix $B \in {\mathbb {R}}^{N_I \times N_I}$, containing row-wise the weights of the interior nodes of the j’th stencil,

$$\begin{aligned} B_{j, \ell } := {\left\{ \begin{array}{ll} w_i^j &{}: \exists i \in \{1, \ldots , n\} \text { such that } \ell = s_i^j \in {{{\mathcal {I}}}}_j,\\ &{}~~\text {i. e., the interior node } x_{\ell }=x_{s_i^j} \text { is in the stencil } X_j, \\ 0 &{}: \text {else, } \end{array}\right. } \end{aligned}$$

(2.11)

for all $j,\ell \in \{1, \ldots , N_I\}$. The solution $u \in {\mathbb {R}}^{N_I}$ of the linear system of equations

$$\begin{aligned} B u = {\widetilde{f}} \end{aligned}$$

(2.12)

yields the RBF-FD approximation $u_j \approx u(x_j)$ to the solution of the partial differential equation (2.9a), (2.9b) at the interior nodes $x_j$ for $j \in \{1, \ldots , N_I\}$.

2.3 Sources for Errors in the RBF-FD Method

There are several sources that contribute to (numerical) approximation errors $|u_j - u(x_j)|, \, j \in \{1,\ldots ,N_I\}$ in the RBF-FD method where $u\in {\mathbb {R}}^{N_I}$ denotes the computed solution of (2.12). First of all, there occurs a discretization error when approximating the differential operator by a weighted sum of function values at the stencil nodes (2.2). The computation of the weights requires the solution of (small, possibly ill-conditioned) linear systems of equations subject to floating point arithmetic [33]. The subsequent computation of the RBF-FD approximate solution u requires the solution of another (now large and sparse) linear system of equations whose matrix coefficients consist of those weights, i. e., solutions of ill-conditioned systems. Errors in u can hence be attributed to errors in the stiffness matrix B as well as errors in the right hand side ${\widetilde{f}}$ in (2.12) which might result in amplified relative errors in u if the stiffness matrix B is ill-conditioned.

To illustrate the propagation of errors, we recall the well-known result from numerical linear algebra bounding the relative error between the solution ${{\hat{x}}}$ of a perturbed linear system of equations ${{\hat{A}}} {{\hat{x}}} = {{\hat{b}}}$ and the solution x of $Ax=b$ with respect to the relative errors in the matrix entries, $\epsilon _A$, and right hand side, $\epsilon _b$,

$$\begin{aligned} \frac{\Vert {\widehat{x}}-x\Vert }{\Vert x\Vert }\le \frac{{\mathcal {K}}(A)}{1-\epsilon _A\cdot {\mathcal {K}}(A)}(\epsilon _A+\epsilon _b), \end{aligned}$$

if $\epsilon _A\cdot \kappa (A) <1$. If we assume for the weight matrices and right hand sides in (2.8) relative errors of order $\epsilon _{A_j}, \epsilon _{b_j} \in {{{\mathcal {O}}}}(10^{-16})$ (e. g. rounding errors when computing in double precision accuracy), then the relative error in the computed weights is bounded by $\kappa (A_j)\cdot 10^{-16}$. Hence, we might lose up to $\lfloor \log _{10} \kappa (A_j)\rfloor$ digits of accuracy in the weights which in turn define via (2.11) the matrix entries of the stiffness matrix B in (2.12), leading to a possibly large relative error $\epsilon _{B}$ in these matrix entries. Hence, both the condition numbers of the weight matrices ${\widetilde{A}}_j$ in (2.8) and the stiffness matrix B in (2.12) give insight into the numerical approximation errors observed in the RBF-FD solution of a partial differential equation.

3 Node and Stencil Generation, Choice of RBFs and Polynomial Augmentation

In this section, we discuss some methods for the node generation (Sect. 3.1), the stencil formation (Sect. 3.2), the choice of the RBF (Sect. 3.3) and the role of polynomial augmentation in RBF-FD (Sect. 3.4).

3.1 Generation of Node Distributions

The underlying application may already provide the set of (scattered) nodes. However, we may have the luxury to generate our own node set for a given domain and its boundary which is typically the case for the numerical solution of partial differential equations. We discuss several options to do so and refer to the literature for further sophisticated methods that may be necessary for more complex applications.

The different ways to generate a node distribution can be roughly classified as regular/structured (e. g., Cartesian, Chebyshev or hexagonal) [46] or irregular/unstructured/scattered (e. g., coordinates generated by some type of random number generator). There are also variants that are neither structured nor (completely) unstructured such as node sets generated by a sequence of quasi-random numbers, or initially regular node distributions that have been subsequently perturbed [55]. Sophisticated algorithms to create node distributions with variable node density or strategies for local modification and refinement can be found in [19, 25, 48, 51, 63, 67, 75], and an overview of generation methods for node distributions, focusing on meshless finite difference methods including RBF-FD, is given in [70].

Two important quantities which are relevant for the RBF approximation error are the fill distance and separation distance of a point set.

Definition 3.1

Given a node set X in a domain $\Omega$, the fill distance $h_{X, \Omega }$ (radius of largest circle not intersecting with X) and the separation distance $q_X$ (shortest distance of two disjoint nodes) are defined by

$$\begin{aligned} h_{X, \Omega } := \sup _{x\in \Omega } \min _{x_j\in X} \Vert x - x_j\Vert _2 \quad \text { and } \quad q_X := \frac{1}{2} \min _{{\mathop {j \ne i}\limits ^{x_i, x_j \in X}}} \Vert x_j - x_i\Vert _2, \quad \text {resp.} \end{aligned}$$

In general, the (global) RBF approximation error depends on the fill distance (the smaller the better) as well as the separation distance (the larger the better for stability reasons) of the node set [67, 74, 78], hence these two aspects should be kept in mind for its construction.

We will use the following four prototypes for node distributions in our numerical tests in Sect. 4: regular Cartesian node distributions, a recently introduced node placing algorithm based on Poisson disk sampling which rejects nodes that are too close to each other (according to a user-defined minimal spacing) abbreviated as PNP [67] (created by [65]), Halton node distributions [21, 32] (created by [10]) and irregular random node distributions (created by [53]).

The construction of these four types of node sets in the interior of our model domain $(0,1)^d$ is straightforward. The extension of the Cartesian node set to the boundary $\partial \Omega$ is also straighforward whereas different variants exist in the case of PNP, Halton or random nodes, both with respect to the number and location of boundary nodes. One could e. g. use PNP/Halton/random nodes in a lower spatial dimension. We will use the same number of boundary nodes (as determined by the Cartesian grid) for all four types of node sets. The PNP and Halton interior node sets are complemented with boundary nodes of the Cartesian grid whereas the random interior node set is complemented with $d-1$ dimensional random boundary nodes.

Figure 1 illustrates these four types of node distributions for $d = 2$ spatial dimensions (even though all our numerical experiments will be performed for $d = 3$ spatial dimensions).

Fig. 1

Example node distributions and stencils for $\Omega =(0,1)^2$, $N = 100$ (total number of nodes), $N_I = 64$ (number of interior nodes) and $n = 5$ (stencil size)

3.2 Generation of Stencils

There are several aspects to take into consideration when selecting the number and location of nodes in a stencil. If a partial differential equation is to be solved, then the stencil will be used to approximate partial/directional derivatives or more general differential operators. Since these describe local characteristics of a function, it is natural to include nodes that are close to the stencil center, e. g. the n nearest neighbors or all neighbors within a certain distance to the center.

Finite difference stencils often have a symmetric structure, i. e., node $x_i$ belongs to stencil $X_j$ if and only if node $x_j$ belongs to stencil $X_i$ (possibly even with identical weights $w_i^j=w_j^i$, e. g. for self-adjoint differential operators). This symmetry property typically no longer holds if upwinding is used for convection-type operators [64] or if a node lies near the boundary. In this case, one may use an extrapolation approach, introducing new nodes outside the closure ${\overline{\Omega }}$, or asymmetric stencils [76]. For scattered node sets, we cannot expect any symmetry for RBF-FD stencils.

In the finite difference method, the stencil size n is typically fixed for all nodes. In the RBF-FD method, it is easily possible (and sometimes advantageous) to utilize different stencil sizes $n_j$ for different stencils $X_j$, e. g., by selecting a fixed radius and choosing stencils that consist of all nodes within this radius with respect to the stencil center [46]. Further propositions and algorithms to form stencils can be found in [14, 15, 51, 60] but are not pursued in more detail here.

Figure 1 illustrates nearest neighbor stencils (marked in red) for stencil centers (marked in black) for the four types of node distributions. The remaining nodes are marked green if they lie on the boundary or blue if they lie in the interior.

If stencil nodes are very close to each other, the small separation distance often results in high condition numbers of the weight matrices. The criteria for good node distributions for (global) RBF approximations as mentioned in Sect. 3.1 carry over to the local RBF-FD approach, i. e., a good stencil $X_j$ should consist of a small fill distance (w. r. t. a suitable domain $\Omega _j$ containing $x_j$) and a large separation distance (see Definition 3.1) but does not necessarily have to be structured.

In the case of a structured grid, the weights and resulting truncation errors of RBF-FD may be computed analytically [5, 6]. Stencils may be optimized with respect to these truncation errors, e. g. for the discretization of the Laplace operator on Cartesian (tensor product) nodes, we observed that so-called sparse stencils along the coordinate axes can be advantageous compared to nearest neighbor stencils. However, these advantages typically disappear (or are hard to exploit) on unstructured node sets. Stencils on structured grids more likely run into problems with unisolvency (Definition 2.3) than stencils on unstructured grids. A typical example of a node set that is not $\Pi _2$-unisolvent in ${\mathbb {R}}^2$ consists of any three nodes that are collinear, i. e., lying on a line. In [77, Theorem 2.7], a criterion is provided that guarantees for certain (subsets of Cartesian) node sets in ${\mathbb {R}}^2$ to be $\Pi _{\ell }$-unisolvent, a generalization to higher spatial dimensions along with additional information on polynomial interpolation in several variables is given in [30, 43]. Here we will pursue only the nearest neighbor approach (with a fixed stencil size for all nodes). For more advanced stencil selection algorithms (which may lead to different conclusions for the choice of RBF-FD parameters) and a machine learning approach to classify the quality of stencils we refer to [13, 14, 17, 51, 57].

If not only the nodes but an underlying, possibly unstructured mesh is available, then a nearest neighbor search could be performed on the graph with the Euclidean distance between nodes being replaced by the shortest path in the graph.

In the case of an unstructured node distribution without a mesh, nearest neighbor stencils may be determined efficiently using a kd-tree [81]. However, especially in the case of randomly distributed nodes, problems may occur if, as illustrated in Fig. 1 (right), the nearest neighbors are located in a somewhat imbalanced way around the stencil center, possibly with relatively large fill distance and small separation distance. Lop-sided stencils may also occur on structured grids for stencil centers close to the boundary $\partial \Omega$.

3.3 Choice of RBF

Table 1 shows some of the most commonly used generating functions which can be roughly classified as

• Leading to infinitely smooth RBFs and depending on a shape parameter (e. g., GA, GMQ, MQ, IMQ, IQ),

• Leading to not infinitely smooth RBFs and (possibly) independent of a shape parameter (e. g., PHS(k)),

• And a hybridization of both (e. g., $\textrm{HYB}(\gamma ) = \textrm{GA} + \gamma \, \textrm{PHS}(2)$) [46, 47].

Additional generating functions can be found in [9, 25], including compactly supported generating functions which lead to a sparse matrix $A_j$ (2.8).

Table 1 Commonly used generating functions

For the first class of generating functions, a major challenge in interpolation and approximation is the selection of a suitable shape parameter $\varepsilon$. Choosing it too large results in poor approximation accuracies since the RBFs either form peaks (GA, IMQ, IQ) or approximate piecewise polynomials (GMQ($\nu$) with $\nu > 0$) [18]. On the other side, as the shape parameter $\varepsilon$ goes to zero, the RBFs converge to a constant function and the matrix $A_j$ in (2.8) becomes increasingly ill-conditioned, rendering a solution in finite floating point arithmetic numerically infeasible. However, the underlying interpolants/approximants may still exist in the limit and be determined analytically in which case they are related to multivariate polynomials [28, 59] (which also explains why polynomial augmentation is not needed for small shape parameters [39]). E. g., for $d=1$, the Lagrange minimal-degree interpolating polynomial can be obtained for the underlying interpolant/approximant in the limit $\varepsilon \rightarrow 0$. Hence, the FD method can be seen as the limit $\varepsilon \rightarrow 0$ in the RBF-FD method [5, 6, 18]. On the other hand, this explains the occurrence of the Runge phenomenon (i. e., large boundary oscillations in interpolations with higher degree polynomials) in (global) RBF interpolation with small shape parameters. In the context of RBFs, the Runge phenomenon can also be observed if the separation distance becomes very small [29].

For each node set X and stencil $X_j$, there typically exists a shape parameter $\varepsilon _j>0$ that is optimal for the numerical computation of the corresponding stencil weights (2.8). Such an $\varepsilon _j$ depends on several factors such as the function to be approximated, the generating function, the stencil nodes and even the machine precision [38]. Hence, using spatially varying (i. e., stencil dependent) shape parameters $\varepsilon _j$ can be (theoretically) advantageous [8, 25, 29], especially for functions with gradient discontinuities [56], but it is not pursued any further here since it adds even more parameters/choices into the setting of RBF-FD. On Cartesian grids, optimal shape parameters can be derived analytically [5, 6].

Another way to address the problem of ill-conditioning is using the hybrid kernel HYB$(\gamma )$ [46, 47]. The idea is to achieve numerical stability (i. e., lower condition numbers of the weight and stiffness matrices as well as no large spurious eigenvalues of the stiffness matrix for smaller shape parameters) in a direct approach, i. e., with lower computational costs than a stable RBF algorithm. HYB($\gamma$) typically leads to smaller errors and larger condition numbers by decreasing $\gamma$ and vice versa (i. e., a too small as well as a too large $\gamma$ value can be problematic in terms of stability or accuracy, respectively). Hence, often

$$\begin{aligned} \gamma \in [10^{-6}, 10^{-3}] \end{aligned}$$

(3.1)

is utilized [46, 52].

Yet another (computationally more expensive) possibility to address the ill-conditioning is to switch to stable versions of RBFs, e. g., RBF-GA [27, 41, 42], RBF-RA [31, 80] or RBF-QR [39]. These stable algorithms typically increase the computational costs by at least a factor of 10 [61]. Using (sufficiently high) extended precision is another approach, but in general not advisable for large scale problems since it is computationally even more expensive [23, 39].

3.4 Polynomial Augmentation in RBF-FD

Polynomial interpolation can be viewed as a special case of RBF-FD with polynomial augmentation in which the dimension of the polynomial space M equals the stencil size n, but no radial basis functions are used, i. e., the stencil weights are computed as the solution of $P_j^T w_j = {{\mathcal {L}}} \textbf{p}_j$ (2.8). As mentioned in Sect. 2.1, polynomial interpolation can lead to a singular $P_j$ if $\min \{d,n\}>1$. If polynomial augmentation is used in RBF-FD, necessary (but not sufficient) criteria for the weight matrix ${{\widetilde{A}}}_j$ in (2.8) to be regular are given by $n\ge M$ and rank$(P_j)=M$ (full column rank).

Often, for a numerically stable computation, a lower bound $n_{\textrm{min}}=n_{\textrm{min}}(\ell )$ is suggested for the stencil size n that depends on the degree $\ell$ of polynomial augmentation (or, equivalently, the dimension M of the respective polynomial space (2.4)). In [23], the lower bound $n_{\textrm{min}} = M$ is suggested for RBF-FD interpolation and approximation. For the solution of elliptic and hyperbolic PDEs, $n_{\textrm{min}} \approx 2M$ has been proposed [4, 22, 35]. A slightly different bound, $n_{\textrm{min}} \approx 2M + \lfloor \ln (2M) \rfloor$ is proposed in [62] for the advection-diffusion equation. In [22, 58], it is observed that unstructured node distributions allow for smaller $n_{\textrm{min}}$ than Cartesian node distributions with an increasing difference as $\ell$ increases (e. g., $n_{\textrm{min}} \approx 2M$ is too small for Cartesian nodes with $\ell > 4$ whereas unstructured nodes can achieve lowest errors for $n \approx M + \lfloor \ln (2M) \rfloor$ [58]. In general, the optimal relation between polynomial degree $\ell$ and stencil size n depends on the underlying problem [62].

There are different effects of polynomial augmentation in the RBF-FD method which depend on the type of generating function that they complement. Polynomial augmentation (with close too maximal permissible degree $\ell$) is studied in [23, 25] for RBF-FD interpolation and approximation for the GA generating function (with a shape parameter $\varepsilon$, leading to infinitely smooth RBFs) and the PHS(k) generating function (without a shape parameter, leading to not infinitely smooth RBFs). In both cases, stagnation errors disappear and higher accuracies (for the same convergence order) compared to polynomial least squares approximation with the same $\ell$ are observed (for sufficiently large $\ell$). The convergence order for $\ell \ge D$ (3.2) is then

$$\begin{aligned} {\mathcal {O}}\left( N^{(D - \ell - 1)/d} \right) , \quad D := \text { order of the linear differential operator } {\mathcal {L}} \end{aligned}$$

(3.2)

if the approximated function is sufficiently smooth [63, 74] (i. e., $D=0$ for function interpolation/approximation and $D=2$ for the Laplace operator ${\mathcal {L}} = \Delta$ or the convection-diffusion operator ${\mathcal {L}} = \Delta + b^T \nabla$) and (approximate) internodal spacing $N^{-1/d}$ [2, 23, 39]. Hence, the convergence order depends on $\ell$ (which is connected to n as a larger $\ell$ requires a larger n). While $n, ~\varepsilon$ and k do not enter into the above order of convergence, varying these parameters can still lead to significant changes in the accuracy [23], i. e., affect the constants hidden in the ${\mathcal {O}}$ notation.

For GA, the accuracy can be significantly increased by polynomial augmentation for shape parameters larger than the optimal one [27] (while possibly increasing the condition number of ${\widetilde{A}}_j$ in (2.8)) and the optimal shape parameter is (similar to the case without polynomial augmentation) mostly invariant with respect to refinement (i. e., the number of nodes N).

For PHS (or other only conditionally positive definite RBFs), polynomial augmentation is typically needed for convergence [35, 46]. The condition number of the matrix ${\widetilde{A}}_j$ in (2.8) may increase (also for PHS) when increasing the polynomial degree $\ell$. Furthermore, when increasing the stencil size n, the stencil weights become larger (by absolute value) near the stencil center and smaller elsewhere, and if the stencil size n is large enough, then there is no Runge phenomenon [2, 3].

Infinitely smooth RBFs have the potential for spectral accuracy in global RBF approaches [29], but this benefit is typically sacrificed in the local RBF-FD approach [5] since the stencil size n is significantly smaller than the number of nodes N. Additionally, GA and PHS with polynomial augmentation (and n only slightly larger than M) can achieve (especially for unstructured nodes since they allow for smaller $n_{\textrm{min}}$ than Cartesian nodes [58]) comparable accuracies with lower computational costs than stable RBF variants. Using the GA generating function (with a stable algorithm or close to maximal permissible degree of polynomial augmentation) leads to the challenge of choosing an appropriate shape parameter, and using extended precision is computationally too expensive for RBF-FD approximation. Hence, the PHS generating function with close to maximal permissible degree of polynomial augmentation is recommended (taking into consideration the approximation accuracy and computational cost) [23, 25].

Many results for RBF-FD approximation using PHS with polynomial augmentation carry over to the solution of elliptic and hyperbolic PDEs, i. e., stagnation errors disappear, the convergence order is again given by (3.2), hence depends on the polynomial degree $\ell$ (which requires a minimal stencil size $n_{\textrm{min}}$). Increasing the PHS degree determined by k and stencil size n may lead to slight improvements of accuracy. The stencil weights become larger (by absolute value) near the stencil center and smaller elsewhere by increasing the stencil size n. If the stencil size n is large enough, then there is no Runge phenomenon [4, 22].

For the Poisson problem (involving a differential operator ${{\mathcal {L}}}$ of order $D = 2$ (3.2)), a convergence order of ${\mathcal {O}}(N^{-\ell / d})$ is numerically observed for $\ell \in \{2, 4, 6, 8\}$ (and no convergence for $\ell = 0$) [35], i. e., slightly higher than the (theoretical) convergence order for RBF-FD interpolation and approximation (3.2). Additionally, it is observed in [4, 22] that using PHS in the form $r^{2k-1}$ or $r^{2k}\log (r)$ leads to similar results (thus the form $r^{2k-1}$ is preferred), quasi-uniform node distributions lead to similar (often even higher) accuracies compared to Cartesian node distributions, and if the stencil size n is sufficiently large, then no ghost nodes (i. e., additional nodes outside the domain $\Omega$ to increase stability and accuracy by avoiding lop-sided stencils near the boundary $\partial \Omega$) are needed. It has been observed in [74] that ghost nodes can increase stability and accuracy especially in the presence of Neumann boundary conditions. Moreover, whereas a larger PHS degree can lead to a higher accuracy (accompanied by the potential for more numerical instabilities such as larger spurious eigenvalues of the stiffness matrix and larger absolute values of the stencil weights), a PHS degree that is chosen too small can also be problematic. Hence, given the degree of augmentation $\ell \in {\mathbb {N}}$, in [62] it is suggested to select k in the PHS $r^{2k-1}$ according to

$$\begin{aligned} k= {\left\{ \begin{array}{ll} \frac{\ell + 1}{2}, &{} \text {if }\ell \text { is odd,}\\ \frac{\ell }{2}, &{} \text {if }\ell \text { is even}. \end{array}\right. } \end{aligned}$$

(3.3)

While the optimal choice for the relation between PHS exponent k and polynomial degree $\ell$ could depend on the type of the node distribution, the relation

$$\begin{aligned} k \le {k_{\textrm{max}} :=} \; \ell + 1 \end{aligned}$$

(3.4)

has to be satisfied to prove unisolvency in this setting [62]. Furthermore, there has to hold

$$\begin{aligned} D \le k \end{aligned}$$

(3.5)

for the order D of the differential operator (3.2) to ensure that the right hand side ${\mathcal {L}} \Phi _{\varepsilon ,x_{s_i^j}}(x_j)$ in (2.8) is defined for all stencil nodes $x_{s_i^j}$, in particular for the center $s_i^j=j$. Since (3.3) contradicts (3.5) for the case $\ell = 2$, we modify (3.3) and define (with D as in (3.2))

$$\begin{aligned} {k_{\textrm{min}} :=}{\left\{ \begin{array}{ll} \max \{D, \frac{\ell + 1}{2}\}, &{} \text {if }\ell \text { is odd,}\\ \max \{D, \frac{\ell }{2}\}, &{} \text {if }\ell \text { is even} \end{array}\right. } \end{aligned}$$

(3.6)

and propose to select $k \in [k_{\textrm{min}}, k_{\textrm{max}}]$ depending on the model problem and number of points N (see also (4.1) for our choice in the numerical experiments).

A different idea lies in the use of variable degrees of polynomial augmentation $\ell _j$ and variable sizes $n_j$ for each stencil $X_j$ [49]. While it can reduce the computational costs and increase the accuracy, it adds even more parameters/choices into the setup of RBF-FD, hence this approach is not pursued any further here.

4 Numerical Results

This section contains numerical tests for the RBF-FD discretization of Poisson’s equation in $d=3$ spatial dimensions on a unit cube, i. e., in (2.9a), (2.9b), we set $\Omega = (0,1)^3$ and ${\mathcal {L}} = \Delta$. We refer to the supplement for numerical tests for further model problems. We choose the right hand side functions f,  g such that the analytical solution u is given by the three-dimensional version of Franke’s function $F :{\mathbb {R}}^3 \rightarrow {\mathbb {R}}$ [40, 54] with

$$\begin{aligned} F(x)&= 0.75 \exp \left[ -\left( (9x_1 - 2)^2 + (9x_2 - 2)^2 + (9x_3 - 2)^2\right) / 4 \right] \\&\quad + 0.75 \exp \left[ -(9x_1 + 1)^2 / 49 - (9x_2 + 1) / 10 - (9x_3 + 1) / 10 \right] \\&\quad + 0.5 \exp \left[ -\left( (9x_1 - 7)^2 + (9x_2 - 3)^2 + (9x_3 - 5)^2\right) / 4 \right] \\&\quad - 0.2 \exp \left[ -(9x_1 - 4)^2 - (9x_2 - 7)^2 - (9x_3 - 5)^2 \right] . \end{aligned}$$

We will study the influence of the following parameters on the performance of the RBF-FD method to illustrate causes for potential pitfalls and hopefully steer away from them:

• The type of the node distribution (i. e., Cartesian, PNP, Halton or random);

• The stencil size n;

• The total number of nodes N;

• The generating function $\phi _{\varepsilon }$ and its intrinsic parameters (shape parameter $\varepsilon$, the parameter $\gamma$ in HYB($\gamma$), the PHS degree specified by k);

• the degree of polynomial augmentation $\ell$.

We will illustrate the resulting approximation errors of the discrete approximate solution side-by-side with the condition numbers of the involved weight and stiffness matrices. To this end, all of the following Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and 14 consist of three columns of plots, showing

• The errors between the exact and computed solution of the PDE (left column),

• The (maximum of the) condition numbers of the weight matrices (2.8) (middle column),

• The condition numbers of the stiffness matrices (2.11), (2.12) (right column).

In Sect. 4.1, we present general information about the setting of the numerical tests such as node and stencil generation, solution of the arising linear systems of equations and the computation of the approximation error. In Sect. 4.2, we focus on the pitfalls for infinitely smooth (GA) RBFs related to the choice of the shape parameter. We concentrate in Sect. 4.3 on the (shape parameter independent) PHS generating function. In Sect. 4.4, we utilize the HYB generating function in the same setups as in Sect. 4.2 and compare HYB to infinitely smooth RBFs as well as to PHS. The conclusions are summarized in Sect. 4.5, along with recommendations for the various components of RBF-FD discretization.

4.1 General Information

In order to compare results for the different types of node distributions (see Sect. 3.1), we generate PNP, Halton and random node distributions with the same number of interior and boundary nodes as in a typical Cartesian grid, i. e., $N_I=\nu ^d$ interior nodes and $N=(\nu +2)^d$ total nodes for some $\nu \in {\mathbb {N}}$. While the construction of Halton or random nodes with a prescribed number $N_I$ of interior nodes is straighforward, it is slightly more complicated for PNP nodes since their construction is based on a local distance function $h:\Omega \rightarrow (0, \infty )$ that specifies the minimal nodal spacing at point $x \in \Omega$ via h(x). A constant nodal spacing function $h \equiv (\nu + 1)^{-1}$ (i. e., the same spacing as for the Cartesian nodes) leads to fewer nodes than $N_I$. Hence, we use a scaled version $h \equiv \alpha (\nu + 1)^{-1}$ with $\alpha \in [0.9256, 0.9284]$ experimentally determined such that exactly $N_I$ nodes are generated. (The tests with $h \equiv (\nu + 1)^{-1}$ lead to qualitatively comparable observations as $h \equiv \alpha (\nu + 1)^{-1}$ with slightly increased errors and decreased condition numbers due to the typically larger fill and separation distances).

When showing results on Cartesian grids, for comparison we also include test results (for the error (4.2) and the condition number of the stiffness matrix) obtained for finite difference discretizations with a standard central 7-point stencil (i. e., second-order approximation) as well as for a compact/Hermite 19-point stencil (i. e., the 19 stencil nodes consist of the $3 \times 3 \times 3$ nodes around the center without the 8 corner nodes, and not only function values but also derivatives are included in the approximation in (2.2), leading to a fourth-order approximation, see [68, 79]).

For the computation of stencils (see Sect. 3.2), we use a library [50] that utilizes a kd-tree for the nearest neighbor search with respect to the norm $\Vert \cdot \Vert _\mu$ for some $\mu \in {\mathbb {N}}$. In our experiments, we use the Euclidean norm by setting $\mu =2$.

We focus on the generating functions in Table 1, i. e., we consider the generating functions GA, MQ, IMQ, IQ, HYB($\gamma$) and PHS(k) of the form $r^{2k-1}$ with $k \ge 2$ determined by

$$\begin{aligned} k={\left\{ \begin{array}{ll} \ell + 1, &{} \text {if }\ell \le 3\text {,}\\ \ell , &{} \text {if }\ell \ge 4 \end{array}\right. } \end{aligned}$$

(4.1)

for polynomial augmentation $\ell \ge 2$ (which is required for convergence, see (3.2)).

Even though some generating functions (e. g., GA, IMQ, IQ [25]) guarantee the resulting matrices $A_j$ in (2.8) to be symmetric positive definite, they might be highly ill-conditioned so that a direct solver based on a Cholesky factorization may break down in practice. Hence, for solving linear systems, we will always use direct solvers based on LU factorizations with pivoting. For stencils that are not unisolvent, the matrix block $P_j$ in (2.8) may no longer have full column rank, hence ${{\widetilde{A}}}_j$ is no longer regular but (2.8) may still have (no longer unique) solutions. These can be computed by a nullspace approach [12, 15] which may also be beneficial in the unisolvent case. For the computation of (lower bounds of) condition numbers $\kappa _1$ of the arising matrices, we use the LAPACK [37] function dgecon with the 1-norm (we also computed $\kappa _\infty$ which led to qualitatively similar observations for the stiffness matrix and made no difference for the symmetric weight matrices, hence these results are not reported here).

In order to measure the approximation accuracy of the RBF-FD computed discrete solution, we determine the relative 2-norm error between the exact solution of the PDE (2.9a),(2.9a) evaluated at the nodes, $u_s:=\left( u(x_j)\right) _{j=1}^{N_I}$, and the computed solution u obtained from solving the system in (2.12),

$$\begin{aligned} e_2 := \frac{\Vert u_s - u \Vert _2}{\Vert u_s \Vert _2}. \end{aligned}$$

(4.2)

We have also performed numerical experiments and measured the error in the (relative) infinity as well as the (relative) 1-norm but do not report these results here since they are qualitatively very similar (see also [19, 35] for results in different error norms).

Fig. 2

Pointwise relative error $|(u_s(\cdot ) - u(\cdot )) / u_s(\cdot )|$ (top row) and absolute error $|u_s(\cdot ) - u(\cdot )|$ (bottom row) with respect to their $\Vert \cdot \Vert _\infty$ norm distance to the center $(0.5, 0.5, 0.5)^T$ of the domain $[0, 1]^3$ for Halton node distributions with $N = 8000$ nodes and $N_I = 5832$ interior nodes. PHS with stencil size $n = 116$, polynomial augmentation of degree $\ell = 5$; GA and HYB($10^{-5}$) with $n = 131$, shape parameter $\varepsilon = 3.5$, no polynomial augmentation

Since the error $e_2$ in (2.12) does not provide insight into the component-wise absolute or relative errors $|(u_s(\cdot ) - u(\cdot ))|$ or $|(u_s(\cdot ) - u(\cdot )) / u_s(\cdot )|$, resp., we include Fig. 2 which illustrates these pointwise errors with respect to their distance to the center $(0.5, 0.5, 0.5)^T$ of the domain $[0, 1]^3$ for three different types of generating functions on a Halton grid. While we observe that the pointwise errors possess a significant deviation from their mean and tend to become smaller closer to the (Dirichlet) boundary, we argue that the error $e_2$ (added as a horizontal line to all plots, scaled by $1/\sqrt{N_I}$ for the bottom row) is a reasonable measure to assess the overall RBF-FD discretization error.

4.2 Numerical Results for (Infinitely Smooth) Gaussian RBFs

In this subsection, we provide numerical tests using the GA generating function which leads to infinitely smooth RBFs. We have also performed the same tests for generalized multiquadric $\textrm{GMQ}(\nu )$ for $\nu \in \{1, -1, -2\}$ (i. e., for MQ, IMQ and IQ) generating functions but do not report on these results since they were qualitatively similar (with adjusted shape parameters and constants c in (4.3)).

Similarly, since random nodes lead to qualitatively comparable observations as Halton nodes (with slightly increased errors and condition numbers due to the typically larger fill distance and smaller separation distance), we also do not include our test results for random nodes here.

We will later (in Sect. 4.4) provide numerical results comparing several generating functions, including MQ, IMQ and IQ, on all four types of grids (Cartesian, PNP, Halton, random).

We begin with an overview of the numerical tests before a more detailed discussion of the results. In all of these tests, we show plots for the RBF-FD discretization error (4.2), the (maximum of the) condition numbers of the weight matrices (2.8) and the condition numbers of the stiffness matrices defined by (2.11).

• Figure 3: Influence of the shape parameter $\varepsilon$ on different grid types (Cartesian, PNP, Halton) for different stencil sizes n, fixed problem size N.

• Figure 4: Influence of the stencil size n on different grid types (Cartesian, PNP, Halton) for different shape parameters $\varepsilon$, fixed problem size N, polynomial augmentation of degree $\ell =0$ (a constant term).

• Figure 5: Influence of the problem size N on different grid types (Cartesian, PNP, Halton) for different stencil sizes n, a problem size dependent shape parameter $\varepsilon$ (4.3), polynomial augmentation of degree $\ell =0$.

We will now present the tests and discuss the results. In Fig. 3, we show results with respect to the shape parameter $\varepsilon \in \{0.2m : m = 1, 2, \ldots , 30\}$ for the GA generating function, stencil sizes $n \in \{7, 35, 50, 90, 131\}$ and node distributions (Cartesian, PNP, Halton) with $N = 20^3=8000$ total nodes ($N_I = 18^3=5832$ interior and $N-N_I=2168$ boundary nodes). Each color/marker represents a different stencil size.

Fig. 3

Error (4.2) and condition numbers as a function of the shape parameter $\varepsilon$ for the GA generating function, stencil sizes $n \in \{7, 35, 50, 90, 131\}$ and node distributions (Cartesian, PNP, Halton) with $N = 8000$ nodes and $N_I = 5832$ interior nodes

In the three left plots, we see that there exists an optimal shape parameter $\varepsilon \in (1,4)$ that increases with increasing stencil size, especially on the Cartesian and PNP grids. For (much) larger shape parameters, the discretization error increases since the basis functions turn more and more into spikes so that the spanned function space does not offer accurate approximations. For (much) smaller shape parameters, numerical instabilities occur which become apparent in the middle and right plots showing condition numbers for both the weight and stiffness matrices. Larger stencil sizes incur larger condition numbers in the weight matrices but also have the potential to reach smaller discretization accuracies for suitably chosen shape parameters. In particular, the (best possible) RBF-FD discretization accuracies obtained on the PNP and Halton grids are comparable to the ones on the Cartesian grid (or even better) as long as the stencil size is large enough.

Fig. 4

Error (4.2) and condition numbers as a function of the stencil size n for the GA generating function, shape parameters $\varepsilon \in \{1, 2, 3, 4, 5\}$, polynomial augmentation of degree $\ell = 0$ and node distributions (Cartesian, PNP, Halton) with $N = 8000$ nodes and $N_I = 5832$ interior nodes

Fig. 5

Error (4.2) and condition numbers as a function of the number of nodes for the GA generating function with polynomial augmentation of degree $\ell = 0$, $c = 0.15$ (4.3) and stencil sizes $n \in \{7, 33, 50, 90, 131\}$

In Fig. 4, the setting is similar to the one in Fig. 3, only that now the stencil size $n \in \{7, \ldots , 200\}$ is shown along the x-axis and each color/marker represents a different shape parameter $\varepsilon \in \{1, 2, 3, 4, 5\}$. Furthermore, polynomial augmentation of degree $\ell = 0$ (i. e., a constant term) has been added. This choice typically increases the accuracy slightly with only marginal increase in the computational cost (see Sect. 3.4 for more details). This figure once more illustrates the numerical instabilities that occur for (too) small shape parameters. On the Cartesian grid, one can observe a noticeable jump that occurs when increasing the stencil size from $n\le 32$ to $n\ge 33$ which was also observed in [5] and coincides with the following observation: The stencil nodes that are most valuable for the approximation of the Laplace operator on the Cartesian grid appear to be those along the coordinate axes. The first 27 nodes in a nearest neighbor search are those in the $3\times 3\times 3$ grid around the stencil center, the next 6 are the extensions to both sides along the respective three coordinate axes. When all 6 are added and a stencil of 33 nodes is formed, one sees the jumping improvement in the approximation accuracy. On the Cartesian grid, a further increase in the stencil size leads to hardly any improvement. On the Halton grid, stagnation sets in for a stencil size around $n=100$ whereas the error continues to (slowly) decrease up to a stencil size around $n=150$.

In Fig. 5, we show plots with respect to $\root 3 \of {N}$ where $N \in \{(\nu +2)^3: \nu \in {\mathbb {N}},\, 6\le \nu \le 25\}$ denotes the number of total nodes with $N_I=\nu ^3\in [216, 15,625]$ interior nodes. As before, we use the GA generating function with polynomial augmentation of degree $\ell = 0$. For the shape parameter, we follow the strategy to increase it along with the problem size as in

$$\begin{aligned} \varepsilon := c N^{1/d} \end{aligned}$$

(4.3)

for a constant c to avoid increasing ill-conditioning in the weight matrices [22, 24, 46, 71]. The constant c influences the shape parameter, a smaller c leads to larger condition numbers of the weight (stiffness) matrices, a larger c leads to “spiky” basis functions that no longer provide good approximations on finer grids. A similar approach using two constants $c_1, c_2$ with $\varepsilon = c_1 N^{1/d} - c_2>0$ (and the determination of these constants) has been studied in [24].

We have performed several tests for constants $c \in \{0.05, 0.1, 0.15, 0.2, 0.25\}$ (not reported here) and found $c=0.15$ to yield the best results for a stencil size $n=50$ (and good results for a wider range of stencil sizes). In the plots in the middle of Fig. 5, using (4.3) to determine the shape parameter, it is confirmed that with such a choice of shape parameter, the condition numbers of the weight matrices remain (close to) constant (with different constants for different c) as N increases while the condition numbers of the stiffness matrix still increase with N.

On a Cartesian grid, the RBF-FD error for a stencil of size $n=7$ is comparable to the 7-point-FD error (even better up to $\root 3 \of {N}\approx 25$ and worse for larger N since $c = 0.15$ is too large for this n), and stencil sizes $n > 33$ appear to lead to no further advantage compared to $n=33$. On PNP and Halton grids, RBF-FD with stencil size $n=7$ performs worse than on a Cartesian grid. For larger stencils, the error decreases both with increasing stencil and problem sizes n, N, reaching accuracies even better than the finite difference 19-point-stencil.

4.3 Numerical Results for Polyharmonic Spline (PHS) RBFs

An attractive feature of the PHS generating function with polynomial augmentation lies in their simplicity due to the lack of a shape parameter $\varepsilon$ to be finetuned and their scalability. In fact, it can be shown [16, 34] that the weight vector $w^j$ in the solution of the system (2.8) can be recovered from the solution $w^j_h$ of a scaled (and typically much better conditioned) system

$$\begin{aligned} \begin{bmatrix} A^h_j &{}\quad P^h_j \\ (P^h_j)^T &{}\quad {{\textbf{0}}} \end{bmatrix} \begin{bmatrix} w_h^j \\ {\widetilde{w}}_h^j \end{bmatrix} = \begin{bmatrix} {\mathcal {L}} \vec {\Phi }^h_j\\ {\mathcal {L}} {\textbf{p}}^h_0 \end{bmatrix} \end{aligned}$$

(4.4)

via $w^j = h^{-D}w_h^j$ with D denoting the order of the differential operator. The matrices $A_j^h, P_j^h$ and right hand side vectors ${\mathcal {L}} \vec {\Phi }^h_j, {\mathcal {L}} {\textbf{p}}^h_0$ are now computed for the shifted and scaled point sets $X_j^h := h^{-1}(X_j - x_j)$ where the scaling parameter $h\in {\mathbb {R}}$ is selected such that the maximum distance from the center $x_j$ to another stencil node is one. Since the new center node after the shift is the origin, the evaluation of ${\mathcal {L}} {\textbf{p}}^h_0$ greatly simplifies in the case of a monomial basis of $\Pi _{\ell }$: For the Laplace operator, the entries corresponding to $x^2$ and $y^2$ are 2, all others are zero.

Since the high condition numbers in (2.8) hence can be reduced by a (row and column) scaling, they are harmless in actual computations and have no negative effect on the computed interpolant. This has also been observed in Sect. 5.2 of [23]. We will illustrate the (lack of) difference between the numerical solutions with and without shift-and-scale in Fig. 7 (last two rows of plots) and use (4.4) instead of (2.8) in all other numerical tests involving PHS.

However, even without a shape parameter, there still remain several parameters to choose such as the stencil size n, the exponent in the polyharmonic spline determined by k and the degree $\ell$ of polynomial augmentation. Similarly as in the previous subsection, PNP leads to results somewhat between those for Cartesian and Halton nodes while random nodes lead to worse, but qualitatively comparable observations as Halton nodes. Hence, we do not include test results for PNP and random nodes (Sect. 4.4 will include results for PHS on PNP and random nodes in comparison to other RBFs). In this subsection, we provide the following numerical results to illustrate the interplay of these quantities and their resulting discretization errors.

• Figure 6: Influence of the stencil size n on a Halton grid for the PHS(k) generating function and different degrees $\ell$ of polynomial augmentation where k is determined by $\ell$ via (3.6) or (4.1).

• Figure 7: Influence of the problem size N on different grid types (Cartesian, Halton) for different k in PHS(k) and degrees $\ell$ of polynomial augmentation which in turn determine the stencil size n via (4.5).

• Figure 8: Influence of the problem size N on different grid types (Cartesian, Halton) for different degrees $\ell$ of polynomial augmentation which in turn determine k in PHS(k) and the stencil size n via (4.1) and (4.5), resp.

In Fig. 6, each color/marker represents a different degree of polynomial augmentation $\ell \in \{2,3,4,5,6,7,8\}$. For a given $\ell$, we use the generating function PHS(k) with k selected via (3.6) (top row) and via (4.1) (bottom row) and use stencil sizes $n \in \{2M + \lfloor 2M/15 \rfloor i ~:~ i \in \{-4, \ldots , 17\}\} \subset [\lfloor 22M/15 \rfloor , \lfloor 64M/15 \rfloor ]$ (where M (2.5) denotes the dimension of the space of augmented polynomials, see also Table 2).

Fig. 6

Error (4.2) and condition numbers as a function of the quotient of stencil size n and the number of augmented polynomials M (2.5) for the PHS(k) generating function with $k \in \{2,3,4\}$ given by (3.6) (top row) and $k \in \{3,4,5,6,7,8\}$ given by (4.1) (bottom row), degree of polynomial augmentation $\ell \in \{2,3,4,5,6,7,8\}$ and $N = 8000$ Halton nodes ($N_I = 5832$)

The comparison between plots in the two rows demonstrates that larger PHS degrees can decrease the error but may eventually lead to numerical instabilities. Larger degrees than given by (3.6) seem to be especially beneficial for smaller polynomial degrees $\ell \le 4$ while (4.1) can lead to numerical instabilities for $\ell \ge 5$.

We do not show plots for our results on Cartesian grids but only briefly summarize our findings: For Cartesian nodes and $\ell \in \{2, 3, 5\}$, there occured breakdowns in the solver (i. e., in the LU factorization of the weight matrices) for some of the smaller stencil sizes. The nullspace approach of [12, 15] could have been used instead of an LU factorization to compute weights but was not pursued here. The second column in Table 2 summarizes the minimal stencil sizes $n_{\textrm{min}}$ which were necessary in these setups.

Table 2 Required and recommended stencil sizes for PHS on a three-dimensional Cartesian grid

As discussed in Sect. 3.4, using a stencil size of approximately $n \approx 2M$ seems reasonable for Cartesian nodes with $\ell \le 3$ or unstructured nodes. Further tests on unstructured grids (not included here) have shown an only slight advantage when using $n = 2M + \lfloor \ln (2M) \rfloor$ compared to $n = 2M$ for the error (4.2) and the condition numbers of the weight and stiffness matrices, especially in the case of larger degrees of polynomial augmentation (or on random nodes). Since the difference between $n = 2M$ and $n = 2M + \lfloor \ln (2M) \rfloor$ (or some similar stencil size) is typically rather small (as long as $\ell$ is sufficiently large (3.2)), we recommend (and will use ourselves in subsequent tests) the following stencil sizes,

$$\begin{aligned} n = {\left\{ \begin{array}{ll} (\ell - 1)M, &{} \text {if Cartesian nodes are used and }\ell \ge 4,\\ 2M + \lfloor \ln (2M) \rfloor , &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(4.5)

A larger stencil size not only increases the computational cost to compute the stencil weights but also leads to more non-zero entries in the stiffness matrix. We hence conclude that RBF-FD using PHS and polynomial augmentation with a large degree $\ell$ is not suitable/efficient for Cartesian nodes since the stencil size should increase with the degree $\ell$ of polynomial augmentation as for example suggested in (4.5). Compared to the search for a best shape parameter in infinitely smooth RBFs, the sensitivity of the results when moving away from the optimal setting is much reduced here.

In Fig. 7, we show results for the PHS(k) generating functions with stencil sizes given by (4.5), polynomial augmentation of degree $\ell = 3$ with $k \in \{2, \ldots , 5\}$, $\ell = 5$ with $k \in \{2, \ldots , 7\}$ and $\ell \; {\in \{6,} \; 8\}$ with $k \in \{2, \ldots , 8\}$ ($\ell \ge 5$ only for Halton nodes since the stencil size for Cartesian nodes according to (4.5) would be rather large). In particular, in these tests k and $\ell$ are no longer connected via (3.6) or (4.1). However, the polynomial degree $\ell$ now determines the stencil size via (4.5). These tests show that violating the unisolvency condition (3.4) (by using $(k,\ell )$ combinations (5, 3), (7, 5), (8, 6)) significantly increases the error (4.2) and the condition numbers of the weight and stiffness matrices. The results for $\ell = 8$ in combination with $k = 2$ show that additionally (as mentioned in [62]) it can be problematic if k is too small. Furthermore, it can be observed that using higher values of k than those given by (3.6) can further decrease the error. The equation (3.2) for the convergence order can be interpreted in the way that for increasing N and $\ell$, the other parameters n and k become less influential. Our numerical tests indicate that for our settings (4.1) leads to smaller approximation errors compared to (3.6). However, [62] points out that using a larger k than given by (3.6) can lead to numerical instabilities (especially for a large degree $\ell$).

The plots in the last row show results that have been computed without scaling and shifting, i. e., using (2.8) instead of (4.4). Comparing with the plots directly above, it can be seen that shifting and scaling has an effect on the condition numbers of the weight matrices but leads to hardly noticible changes in the approximation errors (except for $k=2$).

Fig. 7

Error (4.2) and condition numbers as a function of the number of nodes for the PHS(k) generating function $r^{2k-1}$ with polynomial augmentation of degree $\ell = 3$ with $k \in \{2, \ldots , 5\}$, $\ell = 5$ with $k \in \{2, \ldots , 7\}$ and $\ell \; \in \{6, \; 8\}$ with $k \in \{2, \ldots , 8\}$ (last row without scaling and shifting, i. e., using (2.8) instead of (4.4)) and stencil sizes n given by (4.5)

In Fig. 8, we show results with respect to the total number of nodes N for the generating function PHS(k). Each color/marker represents a different degree of polynomial augmentation $\ell \in \{2, 3, 4, 5, 6, 7, 8\}$. This degree $\ell$ determines k by (4.1) and n by (4.5). Further tests (not included here) on unstructured nodes with stencil sizes n determined via $n \in \{2M, 3M\}$ instead of (4.5) do not lead to significant changes in the error (4.2) or the condition numbers of the weight or stiffness matrices whereas $n = M + \lfloor \ln (2M) \rfloor$ turned out to be too small (in most cases), leading to significantly larger errors and condition numbers of the weight and stiffness matrices.

For Cartesian nodes, we show results only for $\ell \le 5$ since larger degrees require very large stencil sizes, rendering the RBF-FD approach computationally very costly and hence not competitive (e. g., $n = 420$ for $\ell = 6$ on a Cartesian grid versus $n = 335$ for $\ell = 8$ on a Halton grid).

We find that for $\ell \in \{2, 3, 4, 5\}$, we obtain comparable errors on Cartesian and Halton node sets (for significantly larger stencil sizes on Cartesian grids for $\ell \ge 4$ (4.5)). Larger degrees of polynomial augmentation (and with it larger stencils) lead to smaller discretization errors but larger condition numbers in the weight matrices.

Fig. 8

Error (4.2) and condition numbers as a function of the number of nodes for PHS(k) generating function, degrees of polynomial augmentation $\ell \in \{2, 3, 4, 5, 6, 7, 8\}$ (k and stencil size n are determined by (4.1) and (4.5), respectively, for a fixed $\ell$)

The tests in this subsection illustrated that the PHS(k) generating function can be used successfully as long as the parameter k, the degree $\ell$ of polynomial augmentation and the stencil size n are adjusted correspondingly.

4.4 Numerical Results for Hybrid (HYB) RBFs and Comparison with Other RBFs

In this subsection, we show numerical results for hybrid generating functions HYB($\gamma$) and comparisons to GA, IMQ, IQ, MQ and PHS (see Table 1). We will mostly use $\gamma =10^{-5}$ (which fulfills (3.1)) but also include some numerical experiments with $\gamma =10^{-9}$ or $\gamma = 10^{-1}$. The results of this subsection are presented through the following Figures.

• Figure 9 (as Fig. 3, with HYB($10^{-5}$) instead of GA): Influence of the shape parameter $\varepsilon$ on different grid types (Cartesian, PNP, Halton) for different stencil sizes n, fixed problem size N.

• Figure 10 (as Fig. 4, with HYB($10^{-5}$) instead of GA): Influence of the stencil size n on different grid types (Cartesian, PNP, Halton) for different shape parameters $\varepsilon$, fixed problem size N, polynomial augmentation of degree $\ell =0$ (a constant term).

• Figure 11 (as Fig. 5, with HYB($10^{-5}$) instead of GA): Influence of the problem size N on different grid types (Cartesian, PNP, Halton) for different stencil sizes n, a problem size dependent shape parameter $\varepsilon$ (4.3), polynomial augmentation of degree $\ell =0$.

• Figure 12: Influence of the problem size N on different grid types (Cartesian, PNP, Halton, random) for different generating functions (GA, IMQ, IQ, MQ, HYB($10^{-9}$), HYB($10^{-5}$), HYB($10^{-1}$)), a problem size dependent shape parameter $\varepsilon$ (4.3), stencil size $n \in \{ 50, 131 \}$, polynomial augmentation of degree $\ell = 0$.

• Figure 13: Influence of the shape parameter $\varepsilon$ for HYB($10^{-5}$) on different grid types (Cartesian, Halton) for different degrees of polynomial augmentation, stencil size $n=90$, fixed problem size N.

• Figure 14: Influence of the problem size N on different grid types (Cartesian, PNP, Halton, random) for HYB($10^{-9}$), HYB($10^{-5}$), HYB($10^{-1}$) (with a problem size dependent shape parameter $\varepsilon$ (4.3)) and PHS(k) with k given by (4.1), stencil size n given by (4.5), degree of polynomial augmentation $\ell \in \{3, \; {5,} \; 8\}$.

The results of Fig. 9 may be compared to those in Fig. 3 since we have only exchanged the Gaussian generating function and now use HYB($10^{-5}$). A noticeable difference can be observed as the shape parameter $\varepsilon$ goes to zero: the condition numbers of weight and stiffness matrices now remain bounded, and while there still is an optimal shape parameter $\varepsilon \in (1,4)$, the errors/condition numbers no longer blow up for $\varepsilon \rightarrow 0$.

Fig. 9

Error (4.2) and condition numbers as a function of the shape parameter $\varepsilon$ for the HYB($10^{-5}$) generating function, stencil sizes $n \in \{7, 35, 50, 90, 131\}$ and node distributions (Cartesian, PNP, Halton) with $N = 8000$ nodes and $N_I = 5832$ interior nodes

Figure 10 compares to Fig. 4 in the same sense that only the Gaussian generating function has been replaced by HYB($10^{-5}$). On the Cartesian grid, we observe the same jump in accuracy at the stencil size $n=33$. When increasing the stencil size n, the condition numbers now remain bounded (and significantly smaller than for the Gaussian) so that the discretization error no longer blows up due to ill-conditioning for large n.

Fig. 10

Error (4.2) and condition numbers as a function of the stencil size n for the HYB($10^{-5}$) generating function, shape parameters $\varepsilon \in \{1, 2, 3, 4, 5\}$, polynomial augmentation of degree $\ell = 0$ and node distributions (Cartesian, PNP, Halton) with $N = 8000$ nodes and $N_I = 5832$ interior nodes

Figure 11 shows test results for the same setting as in Fig. 5, again for HYB($10^{-5}$) instead of GA. It shows that HYB($10^{-5}$) can lead to similar errors as the GA generating function with the additional benefit of numerical stability for smaller shape parameters, larger stencil sizes and finer discretizations.

Fig. 11

Error (4.2) and condition numbers as a function of the number of nodes for the HYB($10^{-5}$) generating function with polynomial augmentation of degree $\ell = 0$, $c = 0.15$ (4.3) and stencil sizes $n \in \{7, 33, 50, 90, 131\}$

In Fig. 12, we use stencil sizes $n=50$ (top four rows) and $n=131$ (bottom two rows) to compare results for the generating functions GA, IMQ, IQ, MQ, HYB($10^{-9}$), HYB($10^{-5}$), HYB($10^{-1}$) on Cartesian, PNP, Halton and random nodes. For each combination of generating function, grid type and stencil size, we beforehand numerically determined the constant $c \in \{0.05, 0.1, 0.15, 0.2, 0.25\}$ in (4.3) leading to the smallest approximation errors over a wide range of tested problem sizes N, see Table 3. We observe that on all except the random node sets, the RBF-FD variants lead to more accurate approximations than the 7-point FD stencil (except for very small problem sizes N). On PNP and Halton grids, all except HYB($10^{-1}$) lead to approximation errors comparable or even better than the 19-point FD stencil on the Cartesian grid.

Fig. 12

Error (4.2) and condition numbers as a function of the number of nodes for several generating functions with shape parameter $\varepsilon = c \root 3 \of {N}$, c as in Table 3, polynomial augmentation of degree $\ell = 0$, stencil size $n = 50$ for Cartesian, PNP, Halton and random nodes and stencil size $n = 131$ for PNP and Halton nodes

Comparing the three hybrid versions, we note that HYB($10^{-1}$) (compared to HYB($10^{-5}$)) reduces the condition numbers but increases the error, while HYB($10^{-9}$) leads to condition numbers and approximation errors comparable to those for the infinitely smooth RBFs.

For $n = 131$, we include only results for PNP and Halton nodes since there is no improvement on Cartesian nodes compared to $n = 50$ (or, in fact, $n = 33$), and the results for random nodes are qualitatively similar to those for Halton nodes. Increasing from $n = 50$ to $n = 131$ on PNP or Halton nodes leads to a significant reduction in the error (accompanied by an increase in the condition numbers of the weight matrices) for all generating functions except for HYB($10^{-1}$). (HYB($10^{-1}$) behaves similar to PHS, i. e., the error is mainly decreased by increasing the polynomial degree $\ell$ and not the stencil size n.)

Table 3 Summary of constants c in (4.3) for tests in Fig. 12

In Fig. 13, we add polynomial augmentation to the HYB($10^{-5}$) generating function. We also add two horizontal (dashed gray/green) lines for the (shape parameter independent) PHS(2) results using the two polynomial augmentation degrees $\ell \in \{3, 5\}$, resp. (and otherwise identical setting). On the Cartesian grid, HYB($10^{-5}$) with $\ell = 5$ failed for $\varepsilon \in \{0.5, 1\}$ (with a breakdown in the LU factorization of the weight matrices) which we indicate by the dummy values $10^{39}$ and $10^{22}$ for the condition numbers of the weight and stiffness matrices, resp. We recall that a minimal stencil size n depending on the polynomial augmentation degree $\ell$ is necessary for the weight matrices to be non-singular. For $\ell =6$, the polynomial space $\Pi _{6}$ (2.4) for $d=3$ has dimension 84 (2.5), hence the fixed stencil size $n = 90$ satisfies this constraint for all degrees of polynomial augmentation $\ell \in \{-1,0,\ldots ,6\}$. Here, $\ell = -1$ denotes the case of no polynomial augmentation.

The best results in terms of the error (4.2) and condition numbers of the weight and stiffness matrices are obtained for Cartesian nodes for $\ell = 2$ and for Halton nodes for $\ell = 4$. Larger degrees $\ell$ do not appear advisable since they increase the computational complexity without reducing the approximation error. The magnitude of the optimal shape parameter increases (and the range of suitable shape parameters widens) as the degree of polynomial augmentation increases (especially on the Halton grid), and an appropriately chosen shape parameter leads to significantly better results than PHS(2) by itself. While $\varepsilon \rightarrow 0$ leads to blow-up (and no improvement though polynomial augmentation) for the Gaussian kernel, HYB($\gamma$) with polynomial augmentation behaves similar to PHS with polynomial augmentation as $\varepsilon \rightarrow 0$ (since the Gaussian approximates a constant contained in the polynomial augmentation).

This figure as well as many additional tests (not included here) with a setting as in Fig. 6 but for HYB($\gamma$) for $\gamma \in \{10^{-9}, 10^{-5}, 10^{-1}\}$ have shown that some results for PHS regarding polynomial augmentation carry over to HYB (e. g., Cartesian nodes need larger stencil sizes than unstructured nodes). Hence, for the remaining tests, we use (4.5) to determine the stencil size n for HYB when used in combination with larger degrees $\ell$.

Fig. 13

Error (4.2) and condition numbers as a function of the shape parameter $\varepsilon$ for the HYB($10^{-5}$) generating function, stencil size $n = 90$, polynomial augmentation of degree $\ell \in \{-1, 0, \ldots , 6\}$ and node distributions (Cartesian, Halton) with $N = 8000$ nodes and $N_I = 5832$ interior nodes. (Horizontal gray/green dashed lines show results for $\varepsilon$-independent PHS(2) with $\ell \in \{3, 5\}$ for comparison)

The setup in Fig. 14 is similar to Fig. 12 with PHS instead of the generating functions GA, IMQ, IQ, MQ, and now larger degrees $\ell$. Each color/marker represents a different generating function (HYB($10^{-9}$), HYB($10^{-5}$), HYB($10^{-1}$) and PHS(k)). The top four rows of plots show results for $\ell =3$ on Cartesian, PNP, Halton and random nodes, resp. The polynomial degree determines k and n via (4.1) and (4.5), leading to $(\ell , n, k) = (3, 43, {4} )$. In the bottom two rows, we show results for the two parameter combinations $(\ell , n, k) \in \{(5, 116, 5), (8, 335, 8)\}$. For each combination of $\gamma$ value in HYB($\gamma$), grid type and degree of polynomial augmentation, we beforehand numerically determined the constant $c \in \{0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4\}$ for the problem size dependent shape parameter in (4.3) leading to the smallest approximation errors over a wide range of tested problem sizes N, see Table 4. The PHS generating function needs polynomial augmentation of degree $\ell \ge D$ (3.2) in order to converge and we use respective degrees for the HYB($\gamma$) generating function as well. The $\gamma$ value seems to be mainly important for the numerical stability and not so much for the error in the case of larger degrees $\ell$. Tests with $\ell = 5$ (not included here) showed that Cartesian nodes are not an advisable option for RBF-FD with HYB in combination with larger degrees of polynomial augmentation $\ell$ since the required stencil sizes are significantly larger than for unstructured nodes without leading to smaller errors, similar to the PHS case studied in Sect. 4.3. Tests for $\ell \in \{5, 8\}$ with k according to (4.1) show a decrease in the approximation error as $\ell$ increases with hardly any noticible difference between HYB($10^{-9}$) and PHS. However, for large $\ell$, PHS seems to be the better option in terms of numerical stability.

Fig. 14

Error (4.2) and condition numbers as a function of the number of nodes for several generating functions with fixed $(\ell , n, k) = (3, 43, {4} )$ for Cartesian, PNP, Halton and random nodes (top four rows) and $(\ell , n, k) \in \{(5, 116, 5), (8, 335, 8)\}$ (i. e., given $\ell$, then n and k follow by (4.5) and (4.1)) and shape parameter $\varepsilon = c \root 3 \of {N}$, c as in Table 4, for the HYB generating functions on Halton nodes (bottom two rows)

4.5 Summary

In Sect. 4.2, we focused on the main difficulty of the (infinitely smooth) GA generating function: the selection of a shape parameter.

We concentrated in Sect. 4.3 on the PHS generating function. Tests on Cartesian nodes (not included here) exhibited problems for larger $\ell$ (and required excessively large stencil sizes). For non-Cartesian grids, determining the stencil size via (4.5) and the PHS degree via (4.1) (or in case of numerical instabilities via the smaller (3.6)) seems reasonable in terms of accuracy and numerical stability.

In Sect. 4.4, we showed tests for the HYB generating function which combines GA with PHS(2) and compared results with those obtained for several infinitely smooth RBFs and PHS. On one hand, we repeated the tests in Sect. 4.2 with HYB($\gamma$) instead of GA. Our observations (in the setup with no or only small degrees of polynomial augmentation) agree with [46] that typically smaller errors and larger condition numbers are obtained by decreasing $\gamma$. Additionally, we showed that HYB($\gamma$), GA, IQ, IMQ and MQ generating functions can lead to comparable errors (for carefully selected shape parameters, see Table 3, Table 4 and (4.3) for general guidelines) and if $\gamma$ is chosen according to (3.1).

Table 4 Summary of constants c in (4.3) for tests in Fig. 14

We also focused on the role of polynomial augmentation. For GA, IQ, IMQ and MQ generating functions, typically a small degree $\ell$ (e. g., $\ell \le 2$) is suggested. For HYB($\gamma$), with a sufficiently large $\gamma$, we observed that increasing $\ell$ can lead to smaller errors than small $\ell$ (always paired with suitable shape parameters).

Therefore, we compared PHS and HYB generating functions with larger degrees of polynomial augmentation. These tests showed that $\ell > 3$ on Cartesian nodes is also not advisable for HYB. For $\ell \le 5$ on PNP and Halton nodes, HYB can lead to smaller errors than PHS. For sufficiently large $\ell$, HYB converges to PHS(2) as $\varepsilon \rightarrow 0$ which is reflected in the illustrated approximation errors (the condition numbers of the weight and stiffness matrices depend on $\gamma$). An advantage of using degrees $\ell \ge 3$ for HYB is the decrease of sensitivity with respect to the choice of $\gamma$ or the shape parameter.

When it comes to the underlying nodes, one observes “PNP $\le$ Halton $\le$ random” where “$\le$” relates the approximations errors (as well as condition numbers of the weight and stiffness matrices) obtained for those node sets. However, for PHS and HYB generating functions with larger degrees of polynomial augmentation, the differences are rather small, making HYB and PHS good options for adaptive node refinement and stencil selection as long as stencil sizes according to (4.5) (or larger) are used (for nearest neighbor stencils).

Hence, our recommendations for a good RBF-FD discretization setup using basic algorithms as described in this paper may be summarized as follows:

• If Cartesian nodes are used, then a standard finite difference discretization or HYB with a small degree $\ell \in \{0, 1, 2\}$ of polynomial augmentation and $\gamma$ according to (3.1) should be used. (Alternatives such as stabilized RBF-GA [58] may also be viable.)

• On unstructured nodes, PHS with polynomial augmentation offers a shape-parameter-independent approach. The required parameters $\ell , n, k$ may be determined via (3.2), (4.5) and (4.1) (or (3.6) if numerical instabilities occur), resp.. Best results are observed for large exponents and polynomial degrees $k=\ell =8$ which require rather large stencils.

• On unstructured nodes, GA, MQ, IMQ, IQ or HYB with carefully finetuned parameters and constant polynomial augmentation provide options to achieve similar accuracies as PHS with smaller stencils and hence may decrease the computational time or memory compared to the PHS setup.

• (Unstructured) PNP node sets often lead to the best results (smallest approximation error) among the various node sets included in our tests and are a promising option for more complicated domains $\Omega$, adaptive node refinement or variable density node sets.

These recommendations almost certainly will have to be adjusted when more advanced algorithms for node generation or stencil selection, stable versions of radial basis functions or computation of weights for deficient sets, etc., are used which are beyond the scope of this paper.

5 Conclusion and Outlook

RBF-FD provides a meshfree and relatively easy to implement approach for the discretization of partial differential equations. Its realization, however, involves a multitude of parameter choices, many of which (but by far not all) have been tested and illustrated in this work. Our conclusions for these have been summarized at the end of the previous section. It turns out that several methods work well if parameters are chosen accordingly, and there is no clear winner (at least not among the tested variants). However, if parameters are not selected carefully, there are many “losers” leading to stagnation/divergence of the approximation error.

A straightforward extension of this work would lie in the consideration of further RBF-FD variants, including stabilized versions, variable shape parameters, other than nearest neighbor stencils, further types of generating functions or their combinations. It would furthermore be of interest to extend our study to other types of partial differential equations.

We have focused on the discretization process and resulting approximation errors of RBF-FD discretization and mostly left out considerations of computational complexity. The computation of stencil weights may be executed in parallel, hence an increase in stencil size (or polynomial augmentation degree) may not be a severe drawback with respect to computational time for the setup phase. However, it will lead to a less sparse and worse conditioned stiffness matrix and hence increase the computational time required for solving it (directly or iteratively). We plan to design and analyse iterative solvers for linear systems arising in RBF-FD discretization next.