Non-linear System of Multi-order Fractional Differential Equations: Theoretical Analysis and a Robust Fractional Galerkin Implementation

Abstract

This paper presents a comprehensive study of non-linear systems of multi-order fractional differential equations from aspects of theory and numerical approximation. In this regard, we first establish the well-posedness of the underlying problem by investigations concerning the existence, uniqueness, and influence of perturbed data on the behavior of the solutions as well as smoothness of the solutions under some assumptions on the given data. Next, from the numerical perspective, we develop and analyze a well-conditioned and high-order numerical approach based on an operational spectral Galerkin method. The main advantage of our strategy is that it characterizes the approximate solution via some recurrence formulas, instead of solving a complex non-linear block algebraic system that requires high computational costs. Moreover, the familiar spectral accuracy is justified in a weighted $L^2$-norm, and some practical test problems are provided to approve efficiency of the proposed method.

1 Introduction

Recently the fractional calculus has attracted the attention of many researchers due to its capability in the modeling of problems influenced by memory properties and having non-local behavior [18]. Among them, there are diverse physical phenomena for which their separated elements make tight contact with each other. Thus, their mathematical modeling of these phenomena may result in the systems of fractional differential equations (FDEs). These systems appear in numerous fields of science and technology, such as the fractional-order SEIR epidemic model [1], pollution problems [4], hepatitis B disease [5], HIV/AIDS fractional model [12], nuclear magnetic resonance (NMR) [13], magnetic resonance imaging (MRI) [15], fractional-order COVID-19 model [16] and electron spin resonance (ESR) [19].

It turned out that the process of finding the analytical solution for systems of FDEs is a challenging task, and even in some cases is impossible. Therefore, designing efficient numerical methods plays a crucial role in examining the solutions of these equations. Systems of FDEs are generally divided into single-order and multi-order categories, which contain fixed and various orders of fractional derivative operators, respectively. Researchers have recently developed different approximate methods for the numerical solution of systems of single-order FDEs (SSFDEs), such as fractional-order generalized Laguerre pseudo-spectral method [2], Petrov-Galerkin method [9], fractional-order Jacobi Tau method [3], hybrid non-polynomial collocation method [10], spline Collocation method [14] and Jacobi-Gauss collocation method [20].

Systems of multi-order fractional differential equations (SMFDEs) seem to be investigated less frequently than SSFDEs. For example, in papers [7, 8] Chebyshev Tau and fractional collocation methods have introduced for the numerical solution of constant and variable coefficients linear SMFDEs, respectively. Most of the used methods for obtaining the approximate solutions of non-linear SMFDEs suffer from the following crucial items, which play a key role in establishing an efficient numerical scheme:

• Lack of comprehensive analysis regarding the well-posedness of the problem, including existence, uniqueness, the effects of perturbations on the solutions and absence of a robust smoothness investigation which is essential in designing high-order approaches such as spectral methods.

• Solving complex non-linear algebraic systems with high computational costs that significantly affects the accuracy of approximate solutions. Clearly, this weakness typically causes even efficient numerical methods can not provide suitable approximations for the solutions of equations arising from real-world phenomena, which are mostly considered on the long integration domain.

• Ignoring the singularity arising from the fractional derivative operators in adopting appropriate basis functions that leads to characterize the approximate solutions by a linear combination of infinitely smooth basis functions such as polynomials. In fact, one of the requirements of producing high-order methods is to establish a consistency between the asymptotic behavior of the exact solution, and the degree of smoothness of the basis functions, which has been ignored in many of the methods presented so far.

In this paper, we intend to provide a comprehensive study taking the approach of removing the above drawbacks to the following non-linear SMFDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\gamma _j}_C z_j(x)=g_j(x,{\mathbf {z}}(x)),\quad j \in \aleph _{n}=\{1,2,\ldots ,n\},\\ z_j^{(k)}(0)=z_{j,0}^{(k)},~k=0,1,\ldots , \lceil \gamma _j \rceil -1,~ x \in \chi =[0,X], \end{array}\right. } \end{aligned}$$

(1.1)

where $\gamma _{j}=\frac{\eta _{j}}{\lambda _{j}}$ is a positive rational number with the co-prime integers $\eta _{j} \ge 1$ and $\lambda _{j} \ge 2$, X is a finite positive real number, and $\lceil . \rceil$ is the ceiling function. $g_j(x,\mathbf{z }(x)): \chi \times {\mathbb {R}}^n \rightarrow {\mathbb {R}}$ are continuous functions, and $\mathbf{z }(x)=[z_{1}(x),z_{2}(x),\ldots ,z_{n}(x)]^{T}: \chi \rightarrow {\mathbb {R}}^n$ is the vector of unknowns. $D^{\gamma _{j}}_{C}$ is Caputo fractional derivative of order $\gamma _{j}$ defined by

$$\begin{aligned} D^{\gamma _j}_C (.)=I^{\lceil \gamma _j \rceil -\gamma _{j}}\partial _x^{\lceil \gamma _j \rceil }(.), \end{aligned}$$

in which $I^{\lceil \gamma _j \rceil -\gamma _{j}}$ denotes the Riemann–Liouville fractional integral operator of order $\lceil \gamma _j \rceil -\gamma _{j}$ [6].

To this end, we first present a comprehensive analysis around the existence, uniqueness, smoothness properties, and influence of perturbed data of (1.1), and then an efficient spectral approximation using the fractional Jacobi functions is introduced to (1.1). Although spectral methods are capable of providing highly accurate solutions to smooth problems, there are some disadvantages, including the need to solve complex and ill-conditioned algebraic systems. Moreover, the accuracy of the solutions would be significantly reduced in attacking the problems with non-smooth solutions. However, during this investigation, the numerical scheme is designed in such a way that it incorporates both high accuracy in dealing with non-smooth solutions and computing approximate solutions through recurrence relations rather than solving non-linear complex algebraic systems.

The rest of this paper is organized as follows. In Sect. 2, the well-posedness of (1.1) including existence, uniqueness, and influence of perturbed data along with some smoothness properties of (1.1) are established. Our analysis will reveal that the problem (1.1) is well-posed, and some derivatives of the solutions may have a discontinuity at the origin. In Sect. 3, a novel spectral Galerkin method based on the fractional Jacobi basis functions for the numerical solution of (1.1) is implemented. In this regard, the numerical solvability and complexity analysis of the corresponding non-linear block algebraic system are investigated. In Sect. 4, the convergence analysis of the proposed method is rigorously studied. To support our analysis, some examples are illustrated in Sect. 5. Finally, some concluding remarks are expressed in Sect. 6.

2 Well-Posedness and Smoothness Properties

Before implementing our numerical approach, we investigate some results on the well-posedness and smoothness of solutions of (1.1). Commonly, a problem is called well-posed if it has a unique solution, and the solution depends on the given data continuously. In this regard, we first recall the following existence and uniqueness theorem.

Theorem 2.1

(Existence and uniqueness [6]) Let the continuous functions $g_j$ in (1.1) satisfy a Lipschitz condition with respect to all their variables except for the first one, i.e.,

$$\begin{aligned} |g_{j}(x,\mathbf{u }_{1})-g_{j}(x,\mathbf{u }_{2})| \le L ||\mathbf{u }_{1}-\mathbf{u }_{2}||_{\infty },\quad \mathbf{u }_{1},~\mathbf{u }_{2} \in {\mathbb {R}}^{n}, \end{aligned}$$

with some constant $L>0$, where $||.||_{\infty }$ is the max norm on ${\mathbb {R}}^{n}$, i.e.,

$$\begin{aligned} ||\mathbf{u }_1||_{\infty }=\max \{|u_{1,1}|,|u_{1,2}|,\ldots ,|u_{1,n}|\}, \end{aligned}$$

for all $\mathbf{u }_{1}=[u_{1,1},u_{1,2},\ldots ,u_{1,n}]^{T} \in {\mathbb {R}}^{n}$. Then, the problem (1.1) has a unique continuous solution on $\chi$.

Now, we investigate the dependence of the exact solution on some small perturbations in the input data. Clearly, this is an important factor in the numerical solution of (1.1) because the influence of perturbations on the discretized equation is a fundamental item in determining the effect of roundoff errors. The next theorems will show that the solution of (1.1) depends continuously on the given data. First, we investigate the dependence of the solution of (1.1) on the initial values and the given function of the right-hand side.

Theorem 2.2

Assume that the conditions of Theorem 2.1 hold for both equation (1.1) and the perturbed equation

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\gamma _j}_C {\tilde{z}}_j(x)={\tilde{g}}_j(x,\tilde{\mathbf{z }}(x)),\quad j \in \aleph _{n},\\ {\tilde{z}}_j^{(k)}(0)={\tilde{z}}_{j,0}^{(k)},~k=0,1,\ldots , \lceil \gamma _j \rceil -1,~ x \in \chi . \end{array}\right. } \end{aligned}$$

(2.1)

In addition, let

$$\begin{aligned} \epsilon _j^{1}=\max _{k=0,1,\ldots , \lceil \gamma _j \rceil -1}|z_{j,0}^{(k)}-{\tilde{z}}_{j,0}^{(k)}|,\quad \quad \epsilon _{j}^{2}=\max _{(x,\mathbf{u }) \in \chi \times {\mathbb {R}}^{n}}|g_j(x,\mathbf{u })-{\tilde{g}}_j(x,\mathbf{u })|. \end{aligned}$$

If $\epsilon _j^{1}$ and $\epsilon _{j}^{2}$ are sufficiently small, then we have

$$\begin{aligned} \max _{x \in \chi }|z_j(x)-{\tilde{z}}_j(x)|=O(\epsilon _j^{1}+\epsilon _j^{2}), \quad j \in \aleph _{n}. \end{aligned}$$

(2.2)

Proof

Subtracting (2.1) from (1.1), and defining $\varDelta _{j}(x)=z_j(x)-{\tilde{z}}_j(x)$, we find that

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\gamma _j}_C \varDelta _j(x)=g_j(x,\mathbf{z }(x))-{\tilde{g}}_j(x,\tilde{\mathbf{z }}(x)),\quad j \in \aleph _{n},\\ \varDelta _j^{(k)}(0)=z_{j,0}^{(k)}-{\tilde{z}}_{j,0}^{(k)},~k=0,1,\ldots , \lceil \gamma _j \rceil -1,~ x \in \chi , \end{array}\right. } \end{aligned}$$

which is equivalent to the following system involving Volterra integral equations of the second kind

$$\begin{aligned} \varDelta _j(x)=\sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{x^k}{k!}\Big (z_{j,0}^{(k)}-{\tilde{z}}_{j,0}^{(k)}\Big )}+I^{\gamma _j}\Big (g_j(x,\mathbf{z }(x))- {\tilde{g}}_j(x,\tilde{\mathbf{z }}(x))\Big ),\quad j \in \aleph _{n}. \end{aligned}$$

It can be concluded that

$$\begin{aligned} |\varDelta _j(x)|\le & {} \epsilon _j^{1}\sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{X^k}{k!}}+\frac{1}{\varGamma {(\gamma _j)}}\\&\int _{0}^{x}(x-t)^{\gamma _j-1}\Big (\big |g_j(t,\mathbf{z }(t))-g_j(t,\tilde{\mathbf{z }} (t))\big |+\big |g_j(t,\tilde{\mathbf{z }}(t))-{\tilde{g}}_j(t,\tilde{\mathbf{z }}(t))\big | \Big )dt. \end{aligned}$$

In view of the Lipschitz assumption on $g_{j}$ and definition of max norm on ${\mathbb {R}}^{n}$, we have

$$\begin{aligned} \big |g_j(t,\mathbf{z }(t))-g_j(t,\tilde{\mathbf{z }} (t))\big | \le L ||\mathbf{z }(t)-\tilde{\mathbf{z }} (t)||_{\infty } \le L \sum \limits _{i=1}^{n}|\varDelta _{i}(t)|, \end{aligned}$$

(2.3)

and thereby

$$\begin{aligned} |\varDelta _j(x)|\le & {} \epsilon _j^{1}\sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{X^k}{k!}}+\frac{L}{\varGamma {(\gamma _j)}}\sum \limits _{i=1}^{n}\int _{0}^{x}(x-t)^{\gamma _j-1}|\varDelta _{i}(t)|dt+ \frac{\epsilon _{j}^{2}}{\varGamma {(\gamma _j)}}\int _{0}^{x}(x-t)^{\gamma _j-1}dt\\\le & {} \epsilon _j^{1}\sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{X^k}{k!}}+\frac{L}{\varGamma {(\gamma _j)}}\sum \limits _{i=1}^{n}\int _{0}^{x}(x-t)^{\gamma _j-1}| \varDelta _{i}(t)|dt+\epsilon _{j}^{2}\frac{X^{\gamma _{j}}}{\varGamma {(\gamma _{j}+1)}}\\\le & {} \epsilon _j^{1}\sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{X^k}{k!}}+{\widetilde{L}} \sum \limits _{i=1}^{n}\int _{0}^{x}(x-t)^{\min \limits _{1 \le s \le n}\lbrace \gamma _{s}\rbrace -1}| \varDelta _{i}(t)|dt+\epsilon _{j}^{2}\frac{X^{\gamma _{j}}}{\varGamma {(\gamma _{j}+1)}}, \end{aligned}$$

where ${\widetilde{L}}=L \max \limits _{j \in \aleph _{n}}\frac{X^{\gamma _{j}-\min \limits _{1 \le s \le n}\{\gamma _{s}\}}}{\varGamma {(\gamma _j)}}$. The above inequality can be rewritten as the following vector-matrix form

$$\begin{aligned} {\underline{\varDelta }}(x) \le {\underline{\Pi }}+{\widetilde{L}}I \int _{0}^{x}(x-t)^{\min \limits _{1 \le s \le n}\lbrace \gamma _{s}\rbrace -1}{\underline{\varDelta }}(t)dt, \end{aligned}$$

where I denotes a matrix of order n with entries one. In addition, we have ${\underline{\varDelta }}(x)=\big [\vert \varDelta _{1}(x)\vert ,\vert \varDelta _{2}(x)\vert ,\ldots ,\vert \varDelta _{n}(x)\vert \big ]^{T}$ and ${\underline{\Pi }}=\big [ \Pi _{1} , \Pi _{2} ,\ldots , \Pi _{n} \big ]^T$ with

$$\begin{aligned} \Pi _{j}=\epsilon _j^{1}\sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{X^k}{k!}}+\epsilon _{j}^{2}\frac{X^{\gamma _{j}}}{\varGamma {(\gamma _{j}+1)}}. \end{aligned}$$

Equivalently, we arrive at

$$\begin{aligned} {\underline{\varDelta }}(x) \le {\underline{\Pi }}+n {\widetilde{L}}\int _{0}^{x}(x-t)^{\min \limits _{1 \le s \le n}\lbrace \gamma _{s}\rbrace -1}{\underline{\varDelta }}(t)dt, \end{aligned}$$

in view of the fact that n is the max norm of matrix I on ${\mathbb {R}}^{n \times n}$. Gronwall’s inequality [7] yield

$$\begin{aligned} {\underline{\varDelta }}(x) \le C |{\underline{\Pi }}|, \end{aligned}$$

where C is a generic positive constant, and equivalently

$$\begin{aligned} |\varDelta _j(x)| \le C |\Pi _{j}| \le C(\epsilon _j^{1}+\epsilon _j^{2}), \end{aligned}$$

which proves the theorem. $\square$

Next, we survey the influence of changes in the fractional derivative orders.

Theorem 2.3

Suppose that the assumptions of Theorem 2.1 hold for both equation (1.1) and the perturbed equation

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{{\tilde{\gamma }}_j}_C {\tilde{z}}_j(x)=g_j(x,\tilde{\mathbf{z }}(x)),\quad j \in \aleph _{n},\\ {\tilde{z}}_j^{(k)}(0)=z_{j,0}^{(k)},~k=0,1,\ldots , \lceil {\tilde{\gamma }}_j \rceil -1,~ x \in \chi , \end{array}\right. } \end{aligned}$$

(2.4)

where ${\tilde{\gamma }}_{j} > \gamma _{j}$. Moreover, let $\epsilon _j^{3}={\tilde{\gamma }}_{j}-\gamma _{j}$ and

$$\begin{aligned} \epsilon _{j}^{4}={\left\{ \begin{array}{ll} 0,\quad \lceil \gamma _j \rceil = \lceil {\tilde{\gamma }}_j \rceil ,\\ \max \{|z_{j,0}^{(k)}|:\lceil \gamma _j \rceil \le k \le \lceil {\tilde{\gamma }}_j \rceil -1\},\quad \quad \text {else}. \end{array}\right. } \end{aligned}$$

If $\epsilon _j^{3}$ and $\epsilon _{j}^{4}$ are sufficiently small, then for $j \in \aleph _{n}$, we have

$$\begin{aligned} \max _{x \in \chi }|z_j(x)-{\tilde{z}}_j(x)|=O(\epsilon _j^{3})+O(\epsilon _j^{4}). \end{aligned}$$

(2.5)

Proof

Rewriting the equation (1.1) and the perturbed equation (2.4) as equivalent systems of Volterra integral equations and subtracting the tow resulting systems from each other yields

$$\begin{aligned} \varDelta _j(x)= & {} -\sum \limits _{k=\lceil \gamma _j \rceil }^{\lceil {\tilde{\gamma }}_j \rceil -1}{\frac{x^k}{k!}z_{j,0}^{(k)}}+\frac{1}{\varGamma {(\gamma _j)}}\int _{0}^{x}(x-t)^{\gamma _j-1}g_j(t,\mathbf{z }(t))dt\\&-\frac{1}{\varGamma {({\tilde{\gamma }}_j)}}\int _{0}^{x}(x-t)^{{\tilde{\gamma }}_j-1}g_j(t,\tilde{\mathbf{z }}(t))dt\\= & {} -\sum \limits _{k=\lceil \gamma _j \rceil }^{\lceil {\tilde{\gamma }}_j \rceil -1}{\frac{x^k}{k!}z_{j,0}^{(k)}}+\frac{1}{\varGamma {(\gamma _j)}}\int _{0}^{x}(x-t)^{\gamma _j-1}(g_j(t,\mathbf{z }(t))-g_j(t,\tilde{\mathbf{z }}(t)))dt\\&\quad +\int _{0}^{x}\Big (\frac{(x-t)^{\gamma _j-1}}{\varGamma (\gamma _{j})}-\frac{(x-t)^{{\tilde{\gamma }}_j-1}}{\varGamma ({\tilde{\gamma }}_{j})}\Big )g_j(t,\tilde{\mathbf{z }}(t))dt. \end{aligned}$$

From (2.3), we have

$$\begin{aligned} |\varDelta _j(x)|\le & {} \sum \limits _{k=\lceil \gamma _j \rceil }^{\lceil {\tilde{\gamma }}_j \rceil -1}{\frac{X^k}{k!}|z_{j,0}^{(k)}}|+\frac{L}{\varGamma {(\gamma _j)}}\sum \limits _{i=1}^{n}\int _{0}^{x}(x-t)^{\gamma _j-1}|\varDelta _{i}(t)|dt \nonumber \\&+\max _{(x,\mathbf{u })\in \chi \times {\mathbb {R}}^{n}}|g_{j}(x,\mathbf{u })|\int _{0}^{x}\Big |\frac{(x-t)^{\gamma _j-1}}{\varGamma (\gamma _{j})}-\frac{(x-t)^{{\tilde{\gamma }}_j-1}}{\varGamma ({\tilde{\gamma }}_{j})}\Big |dt. \end{aligned}$$

(2.6)

Proceeding in exactly the same way as the previous theorem, we can rewrite (2.6) as the following vector-matrix form

$$\begin{aligned} {\underline{\varDelta }}(x) \le {\underline{\varPsi }}+n {\widetilde{L}} \int _{0}^{x}(x-t)^{\min \limits _{1 \le s \le n}\lbrace \gamma _{s}\rbrace -1}{\underline{\varDelta }}(t)dt, \end{aligned}$$

in which ${\underline{\varPsi }}=\big [ \varPsi _{1} , \varPsi _{2} ,\ldots , \varPsi _{n} \big ]^T$, with

$$\begin{aligned} \varPsi _{j}=\sum \limits _{k=\lceil \gamma _j \rceil }^{\lceil {\tilde{\gamma }}_j \rceil -1}{\frac{X^k}{k!}|z_{j,0}^{(k)}}|+\max _{(x,\mathbf{u })\in \chi \times {\mathbb {R}}^{n}}|g_{j}(x,\mathbf{u })|\int _{0}^{x}\Big |\frac{(x-t)^{\gamma _j-1}}{\varGamma (\gamma _{j})}-\frac{(x-t)^{{\tilde{\gamma }}_j-1}}{\varGamma ({\tilde{\gamma }}_{j})}\Big |dt.\qquad \end{aligned}$$

(2.7)

Now, we can bound the integral on the right-hand side of $\varPsi _{j}$ in accordance with

$$\begin{aligned} \int _{0}^{x}\Big |\frac{(x-t)^{\gamma _j-1}}{\varGamma (\gamma _{j})}-\frac{(x-t)^{{\tilde{\gamma }}_j-1}}{\varGamma ({\tilde{\gamma }}_{j})}\Big |dt&=\int _{0}^{x}\Big |\frac{w^{\gamma _j-1}}{\varGamma (\gamma _{j})}-\frac{w^{{\tilde{\gamma }}_j-1}}{\varGamma ({\tilde{\gamma }}_{j})}\Big |dw\\&\le \int _{0}^{X}\Big |\frac{w^{\gamma _j-1}}{\varGamma (\gamma _{j})}-\frac{w^{{\tilde{\gamma }}_j-1}}{\varGamma ({\tilde{\gamma }}_{j})}\Big |dw \le C \epsilon _j^{3}. \end{aligned}$$

Indeed, the integral can be computed explicitly: One first has to find the zero of the integrand, which is located at $(\varGamma (\tilde{\gamma _{j}})/\varGamma (\gamma _{j}))^{1/(\tilde{\gamma _{j}}-\gamma _{j})}$. If X is smaller than this value, then the integrand has no change of sign, and we can move the absolute value operation outside the integral. Otherwise we must split the interval of integration at this point, and each integral can be handled in this way. In either case, we may use the Mean Value Theorem of Differential Calculus to see that the resulting expression is bounded by $O(\tilde{\gamma _{j}}-\gamma _{j})=O(\epsilon _j^{3})$. Using Gronwall’s inequality [7], we have

$$\begin{aligned} {\underline{\varDelta }}(x) \le C |{\underline{\varPsi }}|, \end{aligned}$$

where C is a generic positive constant, and thereby

$$\begin{aligned} |\varDelta _j(x)| \le C |\varPsi _{j}| \le C(\epsilon _j^{3}+\epsilon _j^{4}), \end{aligned}$$

which concludes the relation (2.5). $\square$

Clearly, Theorems 2.1–2.3 deduce the well-posedness of (1.1). In particular, Theorems 2.2 and 2.3 assert that small perturbations in the input data cannot have a meaningful effect on the exact solution. Indeed, the existence of small perturbations in the right-hand sides of (2.2) and (2.5) will translate into small discrete perturbations in the numerical solution due to roundoff errors, and the well-posedness property does not allow a meaningful effect to enter the accuracy of the approximate solution. In what follows, we will discuss the properties dealing with the solution smoothness of the problem (1.1). Since the Caputo fractional derivative is a weakly singular integral operator, we cannot typically expect the solutions of FDEs to be smooth, even for smooth input functions. Clearly, this can lead to a challenge of constructing the numerical methods with reasonable orders of convergence. Hence, recognizing the singularity behavior of the solutions under imposing some conditions on the given functions $g_{j}$ is crucial to design high-order numerical methods. In this regard, in the next theorem, the regularity of solutions of (1.1) is explored by obtaining their series representations in a neighborhood of the origin.

Theorem 2.4

(Smoothness of the solutions) Under the assumptions of Theorem 2.1, suppose that

$$\begin{aligned} g_j(x,\mathbf{z }(x))={\bar{g}}_j(x^{1/\lambda },\mathbf{z }(x)), \quad j \in \aleph _{n}, \end{aligned}$$

where $\lambda$ is the least common multiple of $\lambda _{j}$, and ${\bar{g}}_j$ is an analytic function in the neighborhood of $(0,z_{1,0}^{(0)},\ldots ,z_{n,0}^{(0)})$. Then the solution $z_j(x)$ has the following series representation around the origin

$$\begin{aligned} z_j(x)=\psi _j(x)+\sum \limits _{\rho =\gamma _j \lambda }^{\infty }{{\bar{z}}_{j,\rho }~x^{\frac{\rho }{\lambda }}},\quad j \in \aleph _{n}, \end{aligned}$$

(2.8)

where $\psi _j(x)=\sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{z_{j,0}^{(k)}}{k!}x^k}$, and ${\bar{z}}_{j,\rho }$ are known coefficients.

Proof

Let us assume the following representation of $z_j(x)$

$$\begin{aligned} z_j(x)=\sum \limits _{\rho =0}^{\infty }{{\bar{z}}_{j,\rho }~x^{\frac{\rho }{\lambda }}},\quad j \in \aleph _{n}. \end{aligned}$$

(2.9)

We find the unknown coefficients $\{{\bar{z}}_{j,\rho }\}_{j=1}^{n}$ such that the representation (2.9) converges and satisfies (1.1). Using the series expansion of ${\bar{g}}_j$ around the point $(0,z_{1,0}^{(0)},\ldots ,z_{n,0}^{(0)})$, we obtain

$$\begin{aligned} g_j(x,\mathbf{z }(x))={\bar{g}}_j(x^{1/\lambda },\mathbf{z }(x))=\sum \limits _{\begin{array}{c} \rho =0\\ \{\theta _k\}_{k=1}^{n}=0 \end{array}}^{\infty }{g_{j,\rho ,\{\theta _k\}_{k=1}^n}~x^{\frac{\rho }{\lambda }} \prod _{k=1}^{n}\bigg (z_{k}(x)-z_{k,0}^{(0)}\bigg )^{\theta _k}}.\qquad \end{aligned}$$

(2.10)

By rearranging, it can be concluded that

$$\begin{aligned} \bigg (z_{k}(x)-z_{k,0}^{(0)}\bigg )^{\theta _k}=\bigg (\sum \limits _{\rho =1}^{\infty }{{\bar{z}}_{k,\rho } x^{\frac{\rho }{\lambda }}}\bigg )^{\theta _k}= \sum \limits _{\sigma _k=0}^{\infty }{C_{\sigma _k}^{\theta _k} x^{\frac{\sigma _k}{\lambda }}}, \end{aligned}$$

(2.11)

where

$$\begin{aligned} {C}_{\sigma _k}^{\theta _k}={\left\{ \begin{array}{ll} 1,\quad \theta _k=0,~\sigma _k=0,\\ 0,\quad \theta _k=0,~\sigma _k \ge 1,\\ \sum \limits _{\rho _{1}+\ldots +\rho _{\theta _k}=\sigma _k}{\bar{z}}_{k,\rho _{1}} \ldots {\bar{z}}_{k,\rho _{\theta _k}},\quad \quad \quad \theta _k \ne 0,~\sigma _k \ge 1. \end{array}\right. } \end{aligned}$$

(2.12)

The case $\sigma _k = 0$ in the sum on the right-hand side only occurs for $\theta _{k} = 0$. Meanwhile, the equation (1.1) can be considered as the following system involving Volterra integral equations of the second kind

$$\begin{aligned} z_j(x)=\psi _j(x)+I^{\gamma _j} g_j(x,\mathbf{z }(x)),~~ j \in \aleph _{n}. \end{aligned}$$

(2.13)

Therefore, substituting the relation (2.11) into (2.10), we find

$$\begin{aligned} \sum \limits _{\rho =0}^{\infty }{{\bar{z}}_{j,\rho }~x^{\frac{\rho }{\lambda }}}=\psi _j(x)+I^{\gamma _j}\left( \sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _k\}_{k=1}^n=0 \end{array}}^{\infty }{g_{j,\rho ,\{\theta _k\}_{k=1}^n}~x^{\frac{\rho }{\lambda }}\prod _{k=1}^{n}\left( \sum \limits _{\sigma _k=0}^{\infty }{{C}_{\sigma _k}^{\theta _k}~x^{\frac{\sigma _k}{\lambda }}}\right) }\right) . \end{aligned}$$

Assuming uniform convergence, the coefficients ${\bar{z}}_{j,\rho }$ satisfy the following equality

$$\begin{aligned} \sum \limits _{\rho =0}^{\infty }{{\bar{z}}_{j,\rho }~x^{\frac{\rho }{\lambda }}}= \psi _j(x)+\zeta _{j}\left( \sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _{k},\sigma _{k}\}_{k=1}^n=0 \end{array}}^{\infty }g_{j,\rho ,\{\theta _k\}_{k=1}^n} \left( \prod _{k=1}^{n}{C}_{\sigma _k}^{\theta _k}\right) ~x^{\gamma _{j}+\frac{\rho +\sum \limits _{k=1}^{n}{\sigma _{k}}}{\lambda }}\right) , \end{aligned}$$

(2.14)

where $\zeta _{j}=\frac{\varGamma (\frac{\rho +\sum \limits _{k=1}^{n}{\sigma _{k}}}{\lambda }+1)}{\varGamma (\gamma _{j}+\frac{\rho +\sum \limits _{k=1}^{n}{\sigma _{k}}}{\lambda }+1)}$. Inserting $\rho =\rho -\gamma _j \lambda -\sum \limits _{k=1}^{n}{\sigma _{k}}$ in the series of the right-hand side of (2.14), we obtain

$$\begin{aligned} \sum \limits _{\rho =0}^{\infty }{{\bar{z}}_{j,\rho }~x^{\frac{\rho }{\lambda }}}= \psi _j(x)+{\bar{\zeta }}_{j}\left( \sum \limits _{\begin{array}{c} \rho =\gamma _j \lambda +\sum \limits _{k=1}^{n}{\sigma _{k}} \\ \{\theta _{k},\sigma _{k}\}_{k=1}^n=0 \end{array}}^{\infty }g_{j,\rho -\gamma _j \lambda -\sum \limits _{k=1}^{n}{\sigma _{k}},\{\theta _k\}_{k=1}^n}\left( \prod _{k=1}^{n}{C}_{\sigma _k}^{\theta _k} \right) ~x^{\frac{\rho }{\lambda }}\right) , \end{aligned}$$

(2.15)

in which ${\bar{\zeta }}_{j}=\frac{\varGamma (\frac{\rho }{\lambda }-\gamma _{j}+1)}{\varGamma (\frac{\rho }{\lambda }+1)}$. Now, by comparing the coefficients of $x^{\frac{\rho }{\lambda } }$ on both sides of (2.15), the unknown coefficients ${\bar{z}}_{j,\rho }$ can be derived. Clearly for $\rho <\gamma _{j} \lambda$, we have

$$\begin{aligned} {\bar{z}}_{j,\rho }=\left\{ \begin{array}{l} \frac{z_{j,0}^{(\frac{\rho }{\lambda })}}{(\frac{\rho }{\lambda })!},\quad \rho =0,\lambda , \ldots , (\lceil \gamma _j \rceil -1)\lambda ,\\ 0,\text { else}, \end{array}\right. \end{aligned}$$

and for $\rho \ge \gamma _{j} \lambda$, the following recursive formula is inferred

$$\begin{aligned} {\bar{z}}_{j,\rho }={\bar{\zeta }}_{j}\left( \sum \limits _{\{\theta _{k},\sigma _{k}\}_{k=1}^n=0}^{\infty }g_{j,\rho -\gamma _j \lambda - \sum \limits _{k=1}^{n}{\sigma _{k}},\{\theta _k\}_{k=1}^n}\left( \prod _{k=1}^{n}{C}_{\sigma _k}^{\theta _k}\right) \right) , \end{aligned}$$

such that the coefficients $g_{j,\rho -\gamma _j \lambda - \sum \limits _{k=1}^{n}{\sigma _{k}},\{\theta _k\}_{k=1}^n}$ with negative indices are considered as zero, and in the case $\rho -\gamma _j \lambda - \sum \limits _{k=1}^{n}{\sigma _{k}} \ge 0$, we have

$$\begin{aligned} \rho \ge \gamma _j \lambda -\sum \limits _{k=1}^{n}{\sigma _{k}}>\sigma _{l}=\rho _{1}+\ldots +\rho _{\theta _l}\ge \rho _{i}, \quad l \in \aleph _{n}, \quad i=1,2,\ldots ,\theta _l. \end{aligned}$$

In other words, ${\bar{z}}_{j,\rho }$ can be expressed in terms of coefficients with lower indices. This means, the solution of the problem (1.1) can be described by the series representation (2.8).

Now, we verify that the series converges uniformly and absolutely in the neighborhood of origin. To this, we apply a suitable modification of Lindelof’s majorant method [6]. Let us consider the following system involving Volterra integral equations of the second kind

$$\begin{aligned} Z_j(x)={\bar{\psi }}_j(x)+I^{\gamma _j}G_j(x,\mathbf{Z }(x)),~~j \in \aleph _{n}, \end{aligned}$$

where ${\bar{\psi }}_j(x)=\sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{x^k}{k!}|z_{j,0}^{(k)}|}$, and

$$\begin{aligned} G_j(x,\mathbf{Z }(x))={\bar{G}}_j(x^{1/\lambda },\mathbf{Z }(x))=\sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _k\}_{k=1}^{n}=0 \end{array}}^{\infty }{|g_{j,\rho ,\{\theta _k\}_{k=1}^n}|~x^{\frac{\rho }{\lambda }} \prod _{k=1}^{n}\bigg (Z_{k}(x)-|z_{k,0}^{(0)}|\bigg )^{\theta _k}}. \end{aligned}$$

Clearly, $\{Z_j(x)\}_{j=1}^n$ is a majorant for $\{z_j(x)\}_{j=1}^n$, and that all coefficients of $\{Z_j(x)\}_{j=1}^n$ are positive. The formal solution $\{Z_j(x)\}_{j=1}^n$ may be computed in exactly the same way as the previous step. Thus, we now need to prove that the series $Z_j(x)$ converges absolutely over $[0,\eta _j]$, with some $\eta _j>0$. For this purpose, it suffices to show that the finite partial sum of $Z_j(x)$ is uniformly bounded on $[0,\eta _j]$. Considering

$$\begin{aligned} S_{j,{\mathscr {L}}+1}(x)={\bar{\psi }}_j(x)+\sum \limits _{\rho =\gamma _j \lambda }^{{\mathscr {L}}+1}{{\bar{Z}}_{j,\rho }~x^{\frac{\rho }{\lambda }}}, \end{aligned}$$

as the finite partial sum of $Z_j(x)$, we have

$$\begin{aligned} S_{j,{\mathscr {L}}+1}(x) \le {\bar{\psi }}_j(x)+I^{\gamma _j}G_j(x,S_{j,{\mathscr {L}}}(x)),~~j \in \aleph _{n}, \end{aligned}$$

that follows from the recursive computation of the coefficients. Indeed, if we expand the right-hand side of the above inequality, all coefficients ${\bar{Z}}_{j,\rho }$ with indices satisfying the inequality $\frac{\rho }{\gamma }\le \frac{({\mathscr {L}}+1)}{\gamma }$ are omitted from both sides, while there will in general be additional positive terms of higher-order in the right-hand side. Assuming

$$\begin{aligned} B_{1,j}= & {} \sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{X^{k}}{k!}|z_{j,0}^{(k)}|},\\ B_{2,j}= & {} \max _{(x,W)\in \chi \times [0 ,2B_{1,1}]\times \ldots \times [0,2B_{1,n}]}{\frac{\big |G_{j}(x,W)\big |}{\varGamma {(\gamma _j+1)}}},~~j \in \aleph _{n}, \end{aligned}$$

we define

$$\begin{aligned} \eta _j=\min \bigg \{X,\bigg [\frac{B_{1,j}}{B_{2,j}}\bigg ]^{\frac{1}{\gamma _j}}\bigg \},~~j \in \aleph _{n}. \end{aligned}$$

Now, we show that $|S_{j,{\mathscr {L}}}(x)| \le 2 B_{1,j}$ for $j \in \aleph _{n}, x \in [0, \eta _j]$. The proof is done using mathematical induction on ${\mathscr {L}}$. The statement for ${\mathscr {L}}=0$ is evident since

$$\begin{aligned} S_{j,0}(x)=|z_{j,0}^{(0)}| \le B_{1,j},~~j \in \aleph _{n}. \end{aligned}$$

We assume that it holds for ${\mathscr {L}}$ and transit to ${\mathscr {L}}+1$ as

$$\begin{aligned} |S_{j,{\mathscr {L}}+1}(x)|= & {} S_{j,{\mathscr {L}}+1}(x) \le {\bar{\psi }}_j(x)+I^{\gamma _j}G_j(x,S_{j,{\mathscr {L}}}(x)) \\\le & {} \sum \limits _{k=0}^{\lceil \gamma _j \rceil -1}{\frac{\eta _j^k}{k!}|z_{j,0}^{(k)}|}+\max _{t \in [0,x]}{\big |G_j(t,S_{j,{\mathscr {L}}}(t))\big |} \frac{x^{\gamma _j}}{\varGamma {(\gamma _j+1)}}\\\le & {} B_{1,j}+\max _{(t,W) \in [0,\eta _j]\times [0 ,2B_{1,1}]\times \ldots \times [0,2B_{1,n}]}{\big |G_j(t,W)\big |} \frac{\eta _{j}^{\gamma _j}}{\varGamma {(\gamma _j+1)}}\\\le & {} B_{1,j}+\eta _j^{\gamma _j} B_{2,j}\le 2 B_{1,j},~~j \in \aleph _{n}, \end{aligned}$$

which proves that $S_{j,{\mathscr {L}}+1}(x)$ is uniformly bounded over interval $[0, \eta _j]$. Since all its coefficients are positive, it is also monotone. Hence, in view of the power series structure of $Z_j(x)$, it is absolutely and uniformly convergent on $[0,\eta _j]$ and the compact subsets of $[0,\eta _j)$, respectively. Thanks to Lindelof’s theorem, it ultimately concludes the same properties for series representation $z_j(x)$. Thus, it allows us to interchange integration and series. $\square$

Indeed, Theorem 2.4 shows that the $\lceil \gamma _j \rceil$-th derivative of $z_{j}(x)$ may have a discontinuity at the initial point. This would have a great impact on accuracy in implementing the classical spectral methods to approximate the solutions. In this sense, we are going to introduce a new spectral method to calculate better approximate solutions for the problem (1.1) having non-smooth behavior. In what follows, we will construct our numerical approach under the conditions of Theorems 2.1–2.4.

3 Numerical Approach

This section is going to develop an effective and applicable numerical scheme based on the operational fractional Jacobi Galerkin method to estimate the solution of problem (1.1). In order to do so, we first discuss some imperative theoretical consequences dealt with the classical Jacobi polynomials and fractional Jacobi functions.

3.1 Jacobi Polynomials

The Jacobi polynomials $J_n^{(\mu ,\nu )}(s)$ with the parameters $\mu ,\nu >-1$, and $s \in I=[-1,1]$ are orthogonal associated with the weight function $w^{(\mu ,\nu )}(s)=(1-s)^{\mu }(1+s)^{\nu }$, i.e., [17]

$$\begin{aligned} \int _{I}J_{m}^{(\mu ,\nu )}(s)J_{n}^{(\mu ,\nu )}(s)w^{(\mu ,\nu )}(s)ds=\lambda _{n}^{(\mu ,\nu )}\delta _{mn}, \quad m,n\ge 0, \end{aligned}$$

(3.1)

where

$$\begin{aligned} \lambda _{n}^{(\mu ,\nu )}=\Vert J_{n}^{(\mu ,\nu )}\Vert _{w^{(\mu ,\nu )}}^{2}=\dfrac{2^{\mu +\nu +1}\varGamma (n+\mu +1)\varGamma (n+\nu +1)}{(2n+\mu +\nu +1)n!\varGamma (n+\mu +\nu +1)}, \end{aligned}$$

and $\delta _{mn}$ is known as the Kronecker delta function. These polynomials are explicitly signified as follows

$$\begin{aligned} J_{n}^{(\mu ,\nu )}(s)=\sum _{j=0}^{n}\varUpsilon _{j}^{(\mu ,\nu ,n)}\left( \frac{s+1}{2}\right) ^{j}, \end{aligned}$$

(3.2)

where

$$\begin{aligned} \varUpsilon _{j}^{(\mu ,\nu ,n)}=\dfrac{(-1)^{n-j}\varGamma (n+\nu +1)\varGamma (n+\mu +\nu +j+1)}{\varGamma (\nu +j+1)j!\varGamma (n+\mu +\nu +1)(n-j)!}. \end{aligned}$$

Since $\{J_n^{(\mu ,\nu )}\}_{n \ge 0}$ forms a complete $L_{w^{(\mu ,\nu )}}^2(I)$-orthogonal system, defining

$$\begin{aligned} \mathbf{U }_{N}^{(\mu ,\nu )}=\text {Span}\{J_n^{(\mu ,\nu )}: ~n= 0,1,\ldots ,N\}, \end{aligned}$$

along with the related orthogonal projection $\pi _{N}^{(\mu ,\nu )}:L_{w^{(\mu ,\nu )}}^2(I)\rightarrow \mathbf{U }_{N}^{(\mu ,\nu )}$ given by

$$\begin{aligned} \left( F-\pi _{N}^{(\mu ,\nu )}F,\varPhi \right) _{w^{(\mu ,\nu )}}=0, \quad \quad \forall \varPhi \in \mathbf{U }_{N}^{(\mu ,\nu )}, \end{aligned}$$

concludes

$$\begin{aligned} \pi _{N}^{(\mu ,\nu )}F=\sum \limits _{n=0}^{N}{F_n J_{n}^{(\mu ,\nu )}(s)}, \quad F_n=\frac{1}{\lambda _{n}^{(\mu ,\nu )}}(F,J_{n}^{(\mu ,\nu )})_{w^{(\mu ,\nu )}}. \end{aligned}$$

Considering the Sobolev space

$$\begin{aligned} H_{w^{(\mu ,\nu )}}^m(I)=\{F : \Vert F\Vert _{m,w^{(\mu , \nu )}}< \infty ,~ m \in {\mathbb {N}}\}, \end{aligned}$$

associated with the norm and semi-norm

$$\begin{aligned} \Vert F\Vert _{m,w^{(\mu ,\nu )}}^2=\sum \limits _{l=0}^{m}{\Vert \partial _s^l F\Vert _{w^{(\mu +l,\nu +l)}}^2},\quad |F|_{m,w^{(\mu ,\nu )}}=\Vert \partial _s^m F\Vert _{w^{(\mu +m,\nu +m)}}, \end{aligned}$$

a suitable bound of the truncation error $\pi _{N}^{(\mu ,\nu )}F-F$ can be established as follows.

Theorem 3.1

[17] For each $F \in H_{w^{(\mu ,\nu )}}^{m}(I)$, $0 \le m \le N+1$, and $m \in {\mathbb {N}}$, the following inequality is satisfied

$$\begin{aligned} \Vert \pi _{N}^{(\mu ,\nu )}F-F\Vert _{w^{(\mu ,\nu )}} \le C N^{-m}|F|_{m,w^{(\mu ,\nu )}}, \end{aligned}$$

where C is a positive constant independent of N.

In order to find more properties of the Jacobi polynomials, one can refer to [17].

3.2 Fractional Jacobi Functions

The essence of the fractional Jacobi functions (FJFs) $J_n^{(\mu ,\nu ,\tau )}(x)$ with $\tau \in (0,1]$ and $x \in \chi$ comes from the Jacobi polynomials with coordinate transformation $s=2 (\frac{x}{X})^{\tau }-1$ as [3, 21]

$$\begin{aligned} J_n^{(\mu ,\nu ,\tau )}(x)=J_n^{(\mu ,\nu )}\left( 2 \left( \frac{x}{X}\right) ^{\tau }-1\right) . \end{aligned}$$

(3.3)

From (3.1), one can check that these functions are mutually orthogonal with respect to the weight function $w^{(\mu ,\nu ,\tau )}(x)= x^{\tau \nu +\tau -1}(X^{\tau }-x^{\tau })^{\mu }$, i.e.,

$$\begin{aligned} \int _{\chi }J_{m}^{(\mu ,\nu ,\tau )}(x)J_{n}^{(\mu ,\nu ,\tau )}(x)w^{(\mu ,\nu ,\tau )}(x)dx= \lambda _{n}^{(\mu ,\nu ,\tau )}\delta _{mn}, \quad m,n\ge 0, \end{aligned}$$

(3.4)

where $\lambda _{n}^{(\mu ,\nu ,\tau )}=\frac{X^{\tau (\mu +\nu +1)}}{\tau 2^{\mu +\nu +1}}\lambda _{n}^{(\mu ,\nu )}$. Regarding (3.2), the FJFs satisfy the following explicit formula

$$\begin{aligned} J_{n}^{(\mu ,\nu ,\tau )}(x)=\sum _{j=0}^{n}\frac{1}{X^{\tau j}}\varUpsilon _{j}^{(\mu ,\nu ,n)}x^{\tau j}=\text {Span}\{1,x^{\tau },\ldots ,x^{n\tau }\}. \end{aligned}$$

Due to the completeness of the FJFs in $L_{w^{(\mu ,\nu ,\tau )}}^2(\chi )$, we state

$$\begin{aligned} \mathbf{U }_{N}^{(\mu ,\nu ,\tau )}=\text {Span}\{J_n^{(\mu ,\nu ,\tau )}: ~n= 0,1,\ldots ,N\}, \end{aligned}$$

and define the corresponding orthogonal projection $\pi _{N}^{(\mu ,\nu ,\tau )}:L_{w^{(\mu ,\nu ,\tau )}}^2(\chi )\rightarrow \mathbf{U }_{N}^{(\mu ,\nu ,\tau )}$ as

$$\begin{aligned} \left( f-\pi _{N}^{(\mu ,\nu ,\tau )}f,\phi \right) _{w^{(\mu ,\nu ,\tau )}}=0, \quad \quad \forall \phi \in \mathbf{U }_{N}^{(\mu ,\nu ,\tau )}. \end{aligned}$$

(3.5)

Trivially, by the relations (3.4) and (3.5), we have

$$\begin{aligned} \pi _{N}^{(\mu ,\nu ,\tau )}f=\sum \limits _{n=0}^{N}{f_n J_{n}^{(\mu ,\nu ,\tau )}(x)}, \quad f_n=\frac{1}{\lambda _{n}^{(\mu ,\nu ,\tau )}}(f,J_{n}^{(\mu ,\nu ,\tau )})_{w^{(\mu ,\nu ,\tau )}}. \end{aligned}$$

Now, we try to find an appropriate error bound of the truncation error $f-\pi _{N}^{(\mu ,\nu ,\tau )}f$. To this end, we suppose that the functions f(x) and F(s) are related by coordinate transformation $s = 2 (\frac{x}{X})^{\tau }-1$. Their derivatives are related in the following sense

$$\begin{aligned} D_x f:=\partial _s F(s)= & {} \partial _s x~ \partial _x f,\\ D_x^2 f:=\partial _s^2 F(s)= & {} \partial _s x~\partial _x(D_x f)~,\\ \vdots \\ D_x^n f:=\partial _s^n F(s)= & {} \partial _s x~\partial _x(\partial _s x~ \partial _x(\cdots (\partial _s x~ \partial _x f)\cdots )), \end{aligned}$$

in which $\partial _s x=\frac{X}{2\tau }\big (\frac{x}{X}\big )^{1-\tau }$. Moreover, it can be readily inferred that

$$\begin{aligned} \Vert F(s)\Vert _{w^{(\mu ,\nu )}}^2= & {} \int _{I}{|F(s)|^2 w^{(\mu ,\nu )}(s)ds}\nonumber \\= & {} d^{(\mu ,\nu )}\int _{\chi }{|f(x)|^2 w^{(\mu ,\nu ,\tau )}(x)dx}=d^{(\mu ,\nu )}\Vert f(x)\Vert _{w^{(\mu ,\nu ,\tau )}}^2,\nonumber \\ \Vert \partial _s^m F(s)\Vert _{w^{(\mu ,\nu )}}^2= & {} \int _{I}{|\partial _s^m F(s)|^2 w^{(\mu ,\nu )}(s)ds}=d^{(\mu ,\nu )}\int _{\chi }{|D_x^m f(x)|^2 w^{(\mu ,\nu ,\tau )}(x)dx}\nonumber \\= & {} d^{(\mu ,\nu )}\Vert D_x^m f(x)\Vert _{w^{(\mu ,\nu ,\tau )}}^2, \end{aligned}$$

(3.6)

where $d^{(\mu ,\nu )}=\frac{\tau 2^{\mu +\nu +1}}{X^{\tau (\mu +\nu +1)}}$.

To obtain the upper bound for truncation error $\pi _{N}^{(\mu ,\nu ,\tau )}f-f$, we define the transformed space

$$\begin{aligned} H_{w^{(\mu ,\nu ,\tau )}}^m(\chi )=\{f:~ \Vert f\Vert _{m,w^{(\mu ,\nu ,\tau )}} < \infty \}, \end{aligned}$$

equipped with the following norm and semi-norm

$$\begin{aligned} \Vert f\Vert _{m,w^{(\mu ,\nu ,\tau )}}^2= & {} \sum \limits _{l=0}^{m}{d^{(\mu +l,\nu +l)}\Vert D_x^l f\Vert _{w^{(\mu +l,\nu +l,\tau )}}^2},\\ |f|_{m,w^{(\mu ,\nu ,\tau )}}= & {} \sqrt{d^{(\mu +m,\nu +m)}}\Vert D_x^m f\Vert _{w^{(\mu +m,\nu +m,\tau )}}, \end{aligned}$$

and give the following theorem.

Theorem 3.2

For $f \in H_{w^{(\mu ,\nu ,\tau )}}^{m}(\chi ),~ 0 \le m \le N+1$, and $m \in {\mathbb {N}}$, the following inequality holds

$$\begin{aligned} \Vert \pi _{N}^{(\mu ,\nu ,\tau )}f-f\Vert _{w^{(\mu ,\nu ,\tau )}} \le C N^{-m}|f|_{m,w^{(\mu ,\nu ,\tau )}}, \end{aligned}$$

where C is a positive constant independent of N.

Proof

Applying coordinate transformation $s = 2 (\frac{x}{X})^{\tau }-1$ and also relation (3.6), one has

$$\begin{aligned} \Vert \pi _{N}^{(\mu ,\nu ,\tau )}f-f\Vert _{w^{(\mu ,\nu ,\tau )}}=\frac{1}{\sqrt{d^{(\mu ,\nu )}}} \Vert \pi _{N}^{(\mu ,\nu )}F-F\Vert _{w^{(\mu ,\nu )}}. \end{aligned}$$

The desired consequence can be derived by Theorem 3.1 and the relation (3.6). $\square$

3.3 Operational Fractional Jacobi Galerkin Method

The aim of this section is to establish the operational fractional Jacobi Galerkin method to approximate the solutions of (1.1). In this scheme, the Galerkin approximate solutions are presented as a linear combination of fractional Jacobi functions, and the corresponding non-linear algebraic representation of the problem is constructed utilizing a sequence of matrix operations. Due to the equivalence of the equation (1.1) and (2.13), we implement our strategy on the equivalent equation (2.13). Inserting $\tau =\frac{1}{\lambda }$ into (3.3), the fractional Jacobi Galerkin approximation $z_{j,N}(x)$ of the exact solution $z_{j}(x)$ is defined in the following sense

$$\begin{aligned} z_{j,N}(x)=\sum \limits _{i=0}^{\infty }{v_{j,i}J_{i}^{(\mu ,\nu ,\tau )}(x)}={\underline{v}}_j{\underline{J}}= {\underline{v}}_j J {\underline{X}}_x,\quad j \in \aleph _{n}, \end{aligned}$$

(3.7)

where ${\underline{v}}_j=[v_{j,0},v_{j,1},\ldots ,v_{j,N},0,\ldots ]$, and

$$\begin{aligned} {\underline{J}}=[J_{0}^{(\mu ,\nu ,\tau )}(x),J_{1}^{(\mu ,\nu ,\tau )}(x), \ldots ,J_{N}^{(\mu ,\nu ,\tau )}(x),\ldots ]^{T}, \end{aligned}$$

indicating the vector of fractional Jacobi basis functions with degree $(J_{i}^{(\mu ,\nu ,\tau )}(x))\le i \tau$, J is an infinite order lower-triangular matrix and ${\underline{X}}_x=[1,x^{\tau },x^{2\tau },\ldots ,x^{N\tau },\ldots ]^{T}$. Assume that

$$\begin{aligned} \psi _j(x)=\sum \limits _{i=0}^{\infty }\psi _{j,i}x^{i\tau }={\underline{\psi }}_j{\underline{X}}_{x},\quad \quad {\underline{\psi }}_j=[ \psi _{j,0},\psi _{j,1},\ldots ,\psi _{j,N},0,\ldots ]. \end{aligned}$$

(3.8)

Moreover, the relation (2.10) can be rewritten as

$$\begin{aligned} g_j(x,\mathbf{z }(x))= & {} \sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _k\}_{k=1}^n=0 \end{array}}^{\infty } g_{j,\rho ,\{\theta _k\}_{k=1}^n}~x^{\rho \tau }~ \Bigg (\prod \limits _{k=1}^n{z_{k}^{\theta _{k}}(x)}\Bigg )\nonumber \\= & {} \sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _k\}_{k=1}^n=0 \end{array}}^{\infty } g_{j,\rho ,\{\theta _k\}_{k=1}^n}~x^{\rho \tau }~ \Bigg (\prod \limits _{k=1}^r{z_{l_{k}}^{\theta _{l_{k}}}(x)}\Bigg ), \end{aligned}$$

(3.9)

where $\{l_{1},l_{2},\ldots ,l_{r}\} \subseteq \aleph _{n}$, and for $r \in \aleph _{n}$, we have $\theta _{l_{1}}, \theta _{l_{2}},\ldots ,\theta _{l_{r}}\ne 0$.

Inserting the relations (3.7), (3.8) into (2.13) and using (3.9), we obtain

$$\begin{aligned} z_{j,N}(x)={\underline{\psi }}_j{\underline{X}}_{x}+\sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _k\}_{k=1}^n=0 \end{array}}^{\infty }g_{j,\rho ,\{\theta _k\}_{k=1}^n} I^{\gamma _j} \left( x^{\rho \tau }~\prod \limits _{k=1}^r{z_{l_{k},N}^{\theta _{l_{k}}}(x)}\right) . \end{aligned}$$

(3.10)

Now, we intend to derive a matrix representation for the right-hand side of (3.10). To this end, we first give the following lemma which transforms $z_{l_{k},N}^{\theta _{l_{k}}}(x),~k=1,2,\ldots ,r$ into a suitable matrix form.

Lemma 3.1

The following relation holds

$$\begin{aligned} z_{l_{k},N}^{\theta _{l_{k}}}(x)={\underline{v}}_{l_{k}} J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1} {\underline{X}}_x,\quad k=1,2,\ldots ,r, \end{aligned}$$

where ${\mathscr {M}}_{l_{k}}$ is the following infinite upper-triangular matrix

$$\begin{aligned} {\mathscr {M}}_{l_{k}}= \begin{bmatrix} {\underline{v}}_{l_{k}} J_{0}&{}{\underline{v}}_{l_{k}} J_{1}&{}{\underline{v}}_{l_{k}} J_{2}&{}\ldots \\ 0&{}{\underline{v}}_{l_{k}} J_{0}&{}{\underline{v}}_{l_{k}} J_{1}&{}\ldots \\ 0&{}0&{}{\underline{v}}_{l_{k}} J_{0}&{}\ldots \\ \vdots &{}\vdots &{}\vdots &{}\ddots \end{bmatrix}, \end{aligned}$$

with $J_{s}=\{J_{m,s}\}_{m=0}^{\infty },~s=0,1,\ldots ~$.

Proof

We proceed using mathematical induction on $\theta _{l_{k}}$. For $\theta _{l_{k}}=1$, the lemma is valid. We assume that it holds for $\theta _{l_{k}}$, and transit to $\theta _{l_{k}}+1$ as follows

$$\begin{aligned} z_{l_{k},N}^{\theta _{l_{k}}+1}(x)= & {} z_{l_{k},N}^{\theta _{l_{k}}}(x)\times z_{l_{k},N}(x)=\big ({\underline{v}}_{l_{k}} J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1} {\underline{X}}_x\big )\times ({\underline{v}}_{l_{k}} J {\underline{X}}_x)\nonumber \\= & {} {\underline{v}}_{l_{k}} J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1}( {\underline{X}}_x \times ({\underline{v}}_{l_{k}} J {\underline{X}}_x)). \end{aligned}$$

(3.11)

Next, it is enough to show that

$$\begin{aligned} {\underline{X}}_x \times ({\underline{v}}_{l_{k}} J {\underline{X}}_x)={\mathscr {M}}_{l_{k}} {\underline{X}}_x. \end{aligned}$$

(3.12)

For this purpose, it can be written

$$\begin{aligned} {\underline{X}}_x \times ({\underline{v}}_{l_{k}} J {\underline{X}}_x)= & {} {\underline{X}}_x \times \left( \sum \limits _{h=0}^{\infty }{\sum \limits _{i=0}^{\infty }{v_{l_{k},i}J_{i,h}~x^{h\tau }}}\right) =\left[ \sum \limits _{h=0}^{\infty }{\sum \limits _{i=0}^{\infty }{v_{l_{k},i}J_{i,h}~x^{(h+m)\tau }}}\right] _{m=0}^{\infty }\nonumber \\= & {} \left[ \sum \limits _{s=m}^{\infty }{\left( \sum \limits _{i=0}^{\infty }{v_{l_{k},i}J_{i,s-m}~x^{s\tau }}\right) }\right] _{m=0}^{\infty }, \end{aligned}$$

(3.13)

which deduces (3.12). Clearly, substituting (3.12) into (3.11) concludes the desired result. $\square$

Now, we can construct the matrix representation of $\prod \limits _{k=1}^r{z_{l_{k},N}^{\theta _{l_{k}}}(x)}$. To this end, let us consider the following lemma.

Lemma 3.2

We have

$$\begin{aligned} \prod \limits _{k=1}^r{z_{l_{k},N}^{\theta _{l_{k}}}(x)}={\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\Bigg (\prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\Bigg ){\underline{X}}_x, \end{aligned}$$

in which matrix $\{{\mathscr {M}}_{\theta _{l_{k}}}^{*}\}_{k=2}^r$ has the following upper-triangular structure

$$\begin{aligned} {\mathscr {M}}_{\theta _{l_{k}}}^{*}= \begin{bmatrix} {\underline{v}}_{l_{k}} (J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1})_{0}&{}{\underline{v}}_{l_{k}} (J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1})_{1}&{}{\underline{v}}_{l_{k}} (J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1})_{2}&{}\ldots \\ 0&{}{\underline{v}}_{l_{k}} (J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1})_{0}&{}{\underline{v}}_{l_{k}} (J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1})_{1}&{}\ldots \\ 0&{}0&{}{\underline{v}}_{l_{k}} (J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1})_{0}&{}\ldots \\ \vdots &{}\vdots &{}\vdots &{}\ddots \end{bmatrix}, \end{aligned}$$

where $(J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1})_{s},~s=0,1,\ldots$ denotes the s-th column of the matrix $J{\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1}$.

Proof

We apply the principle of mathematical induction on r. In view of Lemma 3.1, the induction basis $r = 1$ is evident. We will show that if the statement is hold up for r, then it is also hold up for $r+1$. We have

$$\begin{aligned} \prod \limits _{k=1}^{r+1}{z_{l_{k},N}^{\theta _{l_{k}}}(x)}= & {} \Bigg ({\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\Big (\prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\Big ) {\underline{X}}_x\Bigg )\times \Bigg ({\underline{v}}_{l_{r+1}} J{\mathscr {M}}_{l_{r+1}}^{\theta _{l_{r+1}}-1} {\underline{X}}_x\Bigg ) \nonumber \\= & {} {\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\Big (\prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\Big ) \Bigg ({\underline{X}}_x\times \big ({\underline{v}}_{l_{r+1}} J{\mathscr {M}}_{l_{r+1}}^{\theta _{l_{r+1}}-1} {\underline{X}}_x\big )\Bigg ). \end{aligned}$$

(3.14)

Proceeding the same way as (3.13), we derive

$$\begin{aligned} {\underline{X}}_x\times \big ({\underline{v}}_{l_{r+1}} J{\mathscr {M}}_{l_{r+1}}^{\theta _{l_{r+1}}-1} {\underline{X}}_x\big )={\mathscr {M}}_{\theta _{l_{r+1}}}^{*}{\underline{X}}_x, \end{aligned}$$

(3.15)

which completes the proof by employing (3.15) into (3.14). $\square$

In this stage, we apply Lemmas 3.1 and 3.2 to the second term of the right-hand side of (3.10) which yields

$$\begin{aligned}&\sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _k\}_{k=1}^n=0 \end{array}}^{\infty }{g_{j,\rho ,\{\theta _k\}_{k=1}^n} I^{\gamma _j}\left( x^{\rho \tau } \prod \limits _{k=1}^{r}{z_{l_{k},N}^{\theta _{l_{k}}}(x)}\right) }\nonumber \\&\quad =\sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _k\}_{k=1}^n=0 \end{array}}^{\infty }{g_{j,\rho ,\{\theta _k\}_{k=1}^n} I^{\gamma _j}\left( x^{\rho \tau }~{\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\left( \prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\right) {\underline{X}}_x\right) }\nonumber \\&\quad =\sum \limits _{\{\theta _k\}_{k=1}^n=0}^{\infty }{{\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\left( \prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\right) \left( \sum \limits _{\rho =0}^{\infty }g_{j,\rho ,\{\theta _k\}_{k=1}^n}\left[ I^{\gamma _j}x^{(\rho +m) \tau }\right] _{m=0}^{\infty }\right) }. \end{aligned}$$

(3.16)

Evidently, we have [6]

$$\begin{aligned} \left[ I^{\gamma _j}x^{(\rho +m) \tau }\right] _{m=0}^{\infty }=\left[ {A}_{j,\rho }^{m}~x^{(\rho +m) \tau +\gamma _j}\right] _{m=0}^{\infty }, \quad j \in \aleph _{n}, \end{aligned}$$

in which ${A}_{j,\rho }^{m}=\frac{\varGamma ((\rho +m) \tau +1)}{\varGamma ((\rho +m) \tau +\gamma _j+1)}$. Therefore, the equality (3.16) can be rewritten as

$$\begin{aligned}&\sum \limits _{\begin{array}{c} \rho =0 \\ \{\theta _k\}_{k=1}^n=0 \end{array}}^{\infty }{g_{j,\rho ,\{\theta _k\}_{k=1}^n} I^{\gamma _j}\left( x^{\rho \tau } \prod \limits _{k=1}^{r}{z_{l_{k},N}^{\theta _{l_{k}}}(x)}\right) }\nonumber \\&\quad =\sum \limits _{\{\theta _k\}_{k=1}^n=0}^{\infty }{{\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\left( \prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\right) \left( \sum \limits _{\rho =0}^{\infty }g_{j,\rho ,\{\theta _k\}_{k=1}^n}\left[ {A}_{j,\rho }^{m}~x^{(\rho +m) \tau +\gamma _j}\right] _{m=0}^{\infty }\right) }\nonumber \\&\quad =\left( \sum \limits _{\{\theta _k\}_{k=1}^n=0}^{\infty }{{\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\left( \prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\right) Q_{j,\{\theta _k\}_{k=1}^n}}\right) {\underline{X}}_x, \quad j \in \aleph _{n}, \end{aligned}$$

(3.17)

where ${Q}_{j,\{\theta _k\}_{k=1}^n}$ is an infinite upper-triangular matrix with the following entries

$$\begin{aligned} \big [Q_{j,\{\theta _k\}_{k=1}^n}\big ]_{\alpha ,\beta =0}^{\infty }={\left\{ \begin{array}{ll} 0,\,\alpha \ge \beta -\gamma _{j}\lambda +1,\\ g_{j,\beta -\alpha -\gamma _{j}\lambda ,\{\theta _k\}_{k=1}^n}~{A}_{j,\beta -\alpha -\gamma _{j}\lambda }^{\alpha },\quad \quad ~~ \alpha < \beta -\gamma _{j}\lambda +1. \end{array}\right. } \end{aligned}$$

In this step, to derive the algebraic form of the fractional Jacobi Galerkin discretization of (2.13), it suffices to insert the relations (3.7) and (3.17) into (3.10). Thus, we have

$$\begin{aligned} {\underline{v}}_j J {\underline{X}}_x={\underline{\psi }}_j{\underline{X}}_{x}+\left( \sum \limits _{\{\theta _k\}_{k=1}^n=0}^{\infty }{{\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\left( \prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\right) Q_{j,\{\theta _k\}_{k=1}^n}}\right) {\underline{X}}_x, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} {\underline{v}}_j {\underline{J}}=\left( {\underline{\psi }}_j+\left( \sum \limits _{\{\theta _k\}_{k=1}^n=0}^{\infty }{{\underline{v}}_{l_{1}} J{\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\left( \prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*}}\right) Q_{j,\{\theta _k\}_{k=1}^n}}\right) \right) J^{-1} {\underline{J}}. \end{aligned}$$

(3.18)

Projecting (3.18) onto $\langle J_{0}^{(\mu ,\nu ,\tau )}(x), J_{1}^{(\mu ,\nu ,\tau )}(x),\ldots , J_{N}^{(\mu ,\nu ,\tau )}(x)\rangle$ concludes

$$\begin{aligned} {\underline{v}}_j^{N}=\left( {\underline{\psi }}_j^{N}+\left( \sum \limits _{\{\theta _k\}_{k=1}^n=0}^{\infty }{{\underline{v}}_{l_{1}}^{N} J^{N}\big ({\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\big )^{N} \left( \prod \limits _{k=2}^{r}{{\mathscr {M}}_{\theta _{l_{k}}}^{*^{N}}}\right) {Q}_{j,\{\theta _k\}_{k=1}^n}^{N}}\right) \right) (J^{N})^{-1}, \end{aligned}$$

(3.19)

where the index N at the top of the vectors and matrices dictates the principle sub-vectors and sub-matrices of order $N+1$ respectively. Here, we point out that the unknown vectors can be found by solving a system of $n(N + 1)$ non-linear algebraic equations (3.19). In the next section, we present more details regarding the numerical solvability and practical implementation of this system.

3.4 Numerical Solvability and Practical Implementation

Trivially, the non-linear algebraic system (3.19) is complex, and its solution requires high computational costs, especially for large values of n and N, and thereby possibly low accuracy. In this subsection, to overcome this weakness, we proceed with a well-conditioned and practical implementation that finds the unknowns of (3.19) using some recurrence formulas without the need to solve any non-linear algebraic system. In this regard, multiplying both sides of (3.19) by $J^{N}$ and defining

$$\begin{aligned} \underline{{\underline{v}}}_j={\underline{v}}_j^{N} J^{N}=[\underline{{\underline{v}}}_{j,0},\underline{{\underline{v}}}_{j,1},\ldots ,\underline{{\underline{v}}}_{j,N}],\quad j \in \aleph _{n}, \end{aligned}$$

(3.20)

yields

$$\begin{aligned} \underline{{\underline{v}}}_j={\underline{\psi }}_j^{N}+\left( \sum \limits _{\{\theta _k\}_{k=1}^n=0}^{\infty } {\underline{{\underline{v}}}_{l_{1}}\big ({\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\big )^{N}\left( \prod \limits _{k=2}^{r} {{\mathscr {M}}_{\theta _{l_{k}}}^{*^{N}}}\right) {Q}_{j,\{\theta _k\}_{k=1}^n}^{N}}\right) . \end{aligned}$$

(3.21)

In view of Lemma 3.1, we can write

$$\begin{aligned} {\mathscr {M}}_{l_{k}}= \begin{bmatrix} {\underline{v}}_{l_{k}} J_{0}&{}{\underline{v}}_{l_{k}} J_{1}&{}{\underline{v}}_{l_{k}} J_{2}&{}\ldots \\ 0&{}{\underline{v}}_{l_{k}} J_{0}&{}{\underline{v}}_{l_{k}} J_{1}&{}\ldots \\ 0&{}0&{}{\underline{v}}_{l_{k}} J_{0}&{}\ldots \\ \vdots &{}\vdots &{}\vdots &{}\ddots \end{bmatrix}=\begin{bmatrix} \underline{{\underline{v}}}_{l_{k},0}&{}\underline{{\underline{v}}}_{l_{k},1}&{}\underline{{\underline{v}}}_{l_{k},2}&{}\ldots \\ 0&{}\underline{{\underline{v}}}_{l_{k},0}&{}\underline{{\underline{v}}}_{l_{k},1}&{}\ldots \\ 0&{}0&{}\underline{{\underline{v}}}_{l_{k},0}&{}\ldots \\ \vdots &{}\vdots &{}\vdots &{}\ddots \end{bmatrix}. \end{aligned}$$

From [11], we observe that $\{\big ({\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1}\big )^{N}\}_{k=1}^r$ has the following upper-triangular Toeplitz structure

$$\begin{aligned}&\big ({\mathscr {M}}_{l_{k}}^{\theta _{l_{k}}-1}\big )^{N}\nonumber \\&\quad =\begin{bmatrix} \left( \underline{{\underline{v}}}_{l_{k},0}\right) ^{\theta _{l_{k}}-1}&{}(\theta _{l_{k}}-1)\left( \underline{{\underline{v}}}_{l_{k},0}\right) ^{\theta _{l_{k}}-2}\underline{{\underline{v}}}_{l_{k},1} &{}\ldots &{}\ldots \\ 0&{}\left( \underline{{\underline{v}}}_{l_{k},0}\right) ^{\theta _{l_{k}}-1}&{}(\theta _{l_{k}}-1)\left( \underline{{\underline{v}}}_{l_{k},0}\right) ^{\theta _{l_{k}}-2}\underline{{\underline{v}}}_{l_{k},1}&{}\ldots \\ 0&{}0&{}\left( \underline{{\underline{v}}}_{l_{k},0}\right) ^{\theta _{l_{k}}-1}&{}\ldots \\ \vdots &{}\vdots &{}\vdots &{}\vdots \\ 0&{}\ldots &{}0&{}\left( \underline{{\underline{v}}}_{l_{k},0}\right) ^{\theta _{l_{k}}-1} \end{bmatrix}\nonumber \\&\quad =\begin{bmatrix} {\mathscr {M}}_{l_{k},0,0}^{\theta _{l_{k}}-1}&{}{\mathscr {M}}_{l_{k},0,1}^{\theta _{l_{k}}-1}&{}\ldots &{}{\mathscr {M}}_{l_{k},0,N}^{\theta _{l_{k}}-1}\\ 0&{}{\mathscr {M}}_{l_{k},0,0}^{\theta _{l_{k}}-1}&{}\ldots &{}{\mathscr {M}}_{l_{k},0,N-1}^{\theta _{l_{k}}-1}\\ \vdots &{}\vdots &{}\ldots &{}\vdots \\ 0&{}0&{}\ldots &{}{\mathscr {M}}_{l_{k},0,0}^{\theta _{l_{k}}-1} \end{bmatrix}, \end{aligned}$$

(3.22)

where $\{{\mathscr {M}}_{l_{k},0,s}^{\theta _{l_{k}}-1}\}_{s=0}^N$ are non-linear functions of the elements $\underline{{\underline{v}}}_{l_{k},0},~\underline{{\underline{v}}}_{l_{k},1},\ldots ,~\underline{{\underline{v}}}_{l_{k},s}$.

In addition, from (3.20) and (3.22), the matrices $\{{\mathscr {M}}_{\theta _{l_{k}}}^{*^{N}}\}_{k=2}^r$ can be rewritten as the following upper-triangular Toeplitz structure

$$\begin{aligned} {\mathscr {M}}_{\theta _{l_{k}}}^{*^{N}}= \begin{bmatrix} {\mathscr {M}}_{\theta _{l_{k},0,0}}^{*}&{}{\mathscr {M}}_{\theta _{l_{k},0,1}}^{*}&{}\ldots &{}{\mathscr {M}}_{\theta _{l_{k},0,N}}^{*}\\ 0&{}{\mathscr {M}}_{\theta _{l_{k},0,0}}^{*}&{}\ldots &{}{\mathscr {M}}_{\theta _{l_{k},0,N-1}}^{*}\\ \vdots &{}\vdots &{}\ldots &{}\vdots \\ 0&{}0&{}\ldots &{}{\mathscr {M}}_{\theta _{l_{k},0,0}}^{*} \end{bmatrix}, \end{aligned}$$

in which

$$\begin{aligned} {\mathscr {M}}_{\theta _{l_{k},0,s}}^{*}=\sum \limits _{i=0}^{s} {\underline{{\underline{v}}}_{l_{k},i}~{\mathscr {M}}_{l_{k},0,s-i}^{\theta _{l_{k}}-1}},~~s=0,1,\ldots ,N, \end{aligned}$$

are non-linear functions of the components $\underline{{\underline{v}}}_{l_{k},0},~\underline{{\underline{v}}}_{l_{k},1},\ldots ,~\underline{{\underline{v}}}_{l_{k},s}$.

Consequently, the matrix $\varOmega ^{\{l_{k}\}_{k=1}^{r}}$ defined by

$$\begin{aligned} \varOmega ^{\{l_{k}\}_{k=1}^{r}}=\big ({\mathscr {M}}_{l_{1}}^{\theta _{l_{1}}-1}\big )^{N}{\mathscr {M}}_{\theta _{l_{2}}}^{*^{N}}.~\ldots ~.{\mathscr {M}}_{\theta _{l_{r}}}^{*^{N}}=\begin{bmatrix} \varOmega _{0,0}^{\{l_{k}\}_{k=1}^{r}}&{}\varOmega _{0,1}^{\{l_{k}\}_{k=1}^{r}}&{}\ldots &{}\varOmega _{0,N}^{\{l_{k}\}_{k=1}^{r}}\\ 0&{}\varOmega _{0,0}^{\{l_{k}\}_{k=1}^{r}}&{}\ldots &{}\varOmega _{0,N-1}^{\{l_{k}\}_{k=1}^{r}}\\ \vdots &{}\vdots &{}\ldots &{}\vdots \\ 0&{}0&{}\ldots &{}\varOmega _{0,0}^{\{l_{k}\}_{k=1}^{r}} \end{bmatrix}, \end{aligned}$$

has an upper-triangular Toeplitz structure, in which $\{\varOmega _{0,s}^{\{l_{k}\}_{k=1}^{r}}\}_{s=0}^N$ are non-linear functions of the elements

$$\begin{aligned} \underline{{\underline{v}}}_{l_{1},0},~\underline{{\underline{v}}}_{l_{2},0},\ldots ,~\underline{{\underline{v}}}_{l_{r},0},\\ \underline{{\underline{v}}}_{l_{1},1},~\underline{{\underline{v}}}_{l_{2},1},\ldots ,~\underline{{\underline{v}}}_{l_{r},1},\\ \vdots \,\\ \underline{{\underline{v}}}_{l_{1},s},~\underline{{\underline{v}}}_{l_{2},s},\ldots ,~\underline{{\underline{v}}}_{l_{r},s}, \end{aligned}$$

and obtained by

$$\begin{aligned} \varOmega _{0,s}^{\{l_{k}\}_{k=1}^{r}}=\sum \limits _{i_{1}=0}^{s}\sum \limits _{i_{2}=0}^{i_{1}}\ldots \sum \limits _{i_{r-1}=0}^{i_{r-2}}{{\mathscr {M}}_{l_{1},0,s-i_{1}}^{\theta _{l_{1}}-1}. {\mathscr {M}}_{\theta _{l_{2},0,i_{1}-i_{2}}}^{*}.~\ldots ~.{\mathscr {M}}_{\theta _{l_{r},0,i_{r-1}}}^{*}}. \end{aligned}$$

Finally, defining $\varLambda _{j}^{\{\theta _k\}_{k=1}^n}=\varOmega ^{\{l_{k}\}_{k=1}^{r}} {Q}_{j,\{\theta _k\}_{k=1}^n}^{N}$, $j \in \aleph _{n}$, it can be derived

$$\begin{aligned} \big [\varLambda _{j}^{\{\theta _k\}_{k=1}^n}\big ]_{\alpha ,\beta =0}^{N}={\left\{ \begin{array}{ll} 0,\,\alpha \ge \beta -\gamma _{j}\lambda +1,\\ \sum \limits _{s=0}^{\beta -\alpha -\gamma _{j}\lambda }\varOmega _{0,s}^{\{l_{k}\}_{k=1}^{r}}~\big [{Q}_{j,\{\theta _k\}_{k=1}^n}^{N}\big ]_{\alpha +s,\beta },\quad \quad \quad ~\alpha < \beta -\gamma _{j}\lambda +1. \end{array}\right. } \end{aligned}$$

Next, in accordance with the structure of the upper-triangular matrix $\varLambda _{j}^{\{\theta _k\}_{k=1}^n}$, we have

$$\begin{aligned}&\underline{{\underline{v}}}_{l_{1}} \varLambda _{j}^{\{\theta _k\}_{k=1}^n}\\&\quad =\underline{{\underline{v}}}_{l_{1}}\begin{bmatrix} \overbrace{0 \ldots 0}^{\gamma _{j}\lambda }&{}\big [ \varLambda _{j}^{\{\theta _k\}_{k=1}^n}\big ]_{0,\gamma _{j}\lambda }&{}\big [ \varLambda _{j}^{\{\theta _k\}_{k=1}^n}\big ]_{0,\gamma _{j}\lambda +1}&{}\ldots &{}\big [ \varLambda _{j}^{\{\theta _k\}_{k=1}^n}\big ]_{0,N}\\ \vdots &{}0&{}\big [ \varLambda _{j}^{\{\theta _k\}_{k=1}^n}\big ]_{1,\gamma _{j}\lambda +1}&{}\cdots &{}\big [ \varLambda _{j}^{\{\theta _k\}_{k=1}^n}\big ]_{1,N}\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\ddots \\ 0&{}0&{}\ddots &{}0&{}\big [ \varLambda _{j}^{\{\theta _k\}_{k=1}^n}\big ]_{N-\gamma _{j}\lambda ,N}\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}0&{}0 \end{bmatrix}. \end{aligned}$$

Now, considering the above relation, for $j \in \aleph _{n}$ we can write

$$\begin{aligned} \bigg [\underline{{\underline{v}}}_{l_{1}} \varLambda _{j}^{\{\theta _k\}_{k=1}^n}\bigg ]_{\beta =0}^{N}= & {} {\left\{ \begin{array}{ll} 0,\,\beta < \gamma _{j}\lambda ,\\ \sum \limits _{\alpha =0}^{\beta -\gamma _{j}\lambda }\underline{{\underline{v}}}_{l_{1},\alpha }\big [\varLambda _{j}^{\{\theta _k\}_{k=1}^n}\big ]_{\alpha ,\beta },\quad \quad \quad \beta \ge \gamma _{j}\lambda , \end{array}\right. } \nonumber \\= & {} [\overbrace{0 \ldots 0}^{\gamma _{j}\lambda },\mathbf{G }_{\gamma _{j}\lambda }^{\{\theta _k\}_{k=1}^n}, \mathbf{G }_{\gamma _{j}\lambda +1}^{\{\theta _k\}_{k=1}^n},\ldots ,\mathbf{G }_{N}^{\{\theta _k\}_{k=1}^n}], \end{aligned}$$

(3.23)

where $\{\mathbf{G }_{\gamma _{j}\lambda +s}^{\{\theta _k\}_{k=1}^n}\}_{s=0}^{N-\gamma _{j}\lambda }$ are non-linear functions of the elements

$$\begin{aligned}&\underline{{\underline{v}}}_{l_{1},0},~\underline{{\underline{v}}}_{l_{2},0},\ldots ,~\underline{{\underline{v}}}_{l_{r},0},\\&\underline{{\underline{v}}}_{l_{1},1},~\underline{{\underline{v}}}_{l_{2},1},\ldots ,~\underline{{\underline{v}}}_{l_{r},1},\\&\vdots \,\\&\underline{{\underline{v}}}_{l_{1},s},~\underline{{\underline{v}}}_{l_{2},s},\ldots ,~\underline{{\underline{v}}}_{l_{r},s}. \end{aligned}$$

Substituting (3.23) into (3.21), the unknown components of the unknown vectors $\{\underline{{\underline{v}}}_j\}_{j=1}^{n}$ can be evaluated by the following recurrence relations

$$\begin{aligned}\left\{ \begin{array}{l} \underline{{\underline{v}}}_{j,0}=\psi _{j,0},\\ \vdots \\ \underline{{\underline{v}}}_{j,\gamma _{j}\lambda -1}=\psi _{j,\gamma _{j}\lambda -1},\\ \underline{{\underline{v}}}_{j,\gamma _{j}\lambda }=\sum \limits _{\{\theta _k\}_{k=1}^n=0}^ {\infty }\mathbf{G }_{\gamma _{j}\lambda }^{\{\theta _k\}_{k=1}^n}+\psi _{j,\gamma _{j}\lambda },\\ \vdots \\ \underline{{\underline{v}}}_{j,N}=\sum \limits _{\{\theta _k\}_{k=1}^n=0}^{\infty }\mathbf{G }_{N}^{\{\theta _k\}_{k=1}^n}+\psi _{j,N},\quad \quad j \in \aleph _{n}. \end{array}\right. \end{aligned}$$

Finally, the unknowns $\{{\underline{v}}_j^{N}\}_{j=1}^{n}$ are achieved by solving the lower-triangular system (3.20), and thereby the fractional Jacobi Galerkin solutions (3.7) can be computed.

4 Convergence Analysis

The aim of this section is to provide convergence properties for the presented method via establishing a suitable error bound in a weighted $L^{2}$- norm.

Theorem 4.1

Suppose that $z_{j,N}(x)$ given by (3.7) are the approximate solutions of (1.1). If we have

$$\begin{aligned} I^{\gamma _{j}}g_j \in H_{w^{(\mu ,\nu ,\tau )}}^{\varepsilon _j}(\chi ),~~D_x^{\varepsilon _j+1}(I^{\gamma _{j}}g_j) \in C(\chi ),~~ \varepsilon _{j} \ge 0, \end{aligned}$$

then for sufficiently large values of N the following inequality holds

$$\begin{aligned} \Vert e_{j,N}(x)\Vert _{w^{(\mu ,\nu ,\tau )}} \le C N^{-\varepsilon _j}|I^{\gamma _{j}}g_j|_{\varepsilon _j,w^{(\mu ,\nu ,\tau )}},\quad j \in \aleph _{n}, \end{aligned}$$

where $e_{j,N}(x)=z_{j}(x)-z_{j,N}(x)$ denotes the error function, and $C>0$ is a constant independent of N.

Proof

In according to the proposed numerical scheme in Sect. 3, we first consider (3.10) and substitute the approximate solutions (3.7) into the equation (2.13) and obtain

$$\begin{aligned} z_{j,N}(x)-\psi _j(x)-I^{\gamma _{j}} g_j(x,\mathbf{z }_{N}(x))=0, \end{aligned}$$

(4.1)

where $\mathbf{z }_{N}(x)=[z_{1,N}(x),z_{2,N}(x),\ldots ,z_{n,N}(x)]^{T}$. Then, from (3.19), we multiply both sides of (4.1) by $J_k^{(\mu ,\nu ,\tau )}(x) w^{(\mu ,\nu ,\tau )}(x)$ and integrate on $\chi$, which concludes

$$\begin{aligned} (z_{j,N}(x)-\psi _j(x)-I^{\gamma _{j}} g_j(x,\mathbf{z }_{N}(x)), J_k^{(\mu ,\nu ,\tau )})_{w^{(\mu ,\nu ,\tau )}}=0,~~ k=0,1,\ldots ,N. \end{aligned}$$

(4.2)

Now, multiplying both sides of (4.2) by $\frac{J_k^{(\mu ,\nu ,\tau )}(x)}{\lambda _k^{(\mu ,\nu ,\tau )}}$ and summing up from $k=0$ to $k=N$ deduces

$$\begin{aligned} \pi _{N}^{(\mu ,\nu ,\tau )} \big (z_{j,N}(x)-\psi _j(x)-I^{\gamma _{j}} g_j(x,\mathbf{z }_{N}(x))\big )=0, \end{aligned}$$

and equivalently we have

$$\begin{aligned} z_{j,N}(x)=\psi _j(x)+\pi _{N}^{(\mu ,\nu ,\tau )} \big (I^{\gamma _{j}} g_j(x,\mathbf{z }_{N}(x))\big ), \end{aligned}$$

(4.3)

since we have $z_{j,N}(x),~ \psi _j(x) \in \text {Span}\{J_0^{(\mu ,\nu ,\tau )}, J_1^{(\mu ,\nu ,\tau )},\ldots ,J_N^{(\mu ,\nu ,\tau )}\}$. Subtracting (4.3) from (2.13) yields

$$\begin{aligned} e_{j,N}(x)=I^{\gamma _{j}}g_j(x,\mathbf{z }(x))-\pi _{N}^{(\mu ,\nu ,\tau )} \big (I^{\gamma _{j}} g_j(x,\mathbf{z }_{N}(x))\big ), \end{aligned}$$

which can be rewritten in the following sense

$$\begin{aligned} e_{j,N}(x)=I^{\gamma _{j}}(g_j-{\bar{g}}_j)+e_{\pi _{N}^{(\mu ,\nu ,\tau )}}(I^{\gamma _{j}}{\bar{g}}_j), \end{aligned}$$

where $e_{\pi _{N}^{(\mu ,\nu ,\tau )}} (f)=f-\pi _{N}^{(\mu ,\nu ,\tau )}(f)$ and ${\bar{g}}_j=g_j(x,\mathbf{z }_{N}(x))$. Similar to (2.3), we infer that

$$\begin{aligned} \vert e_{j,N}(x) \vert \le L \sum _{i=1}^{n}\bigg ( \frac{1}{\varGamma {(\gamma _{j})}}\int _{0}^{x} (x-t)^{\gamma _{j}-1} \vert e_{i,N}(t) \vert dt\bigg )+\vert {B}_j \vert , \end{aligned}$$

(4.4)

where ${B}_j=e_{\pi _{N}^{(\mu ,\nu ,\tau )}}(I^{\gamma _{j}}{\bar{g}}_j)$. Defining the vectors

$$\begin{aligned} {\underline{E}}(x)=\big [\vert e_{1,N}(x)\vert ,\vert e_{2,N}(x)\vert ,\ldots ,\vert e_{n,N}(x)\vert \big ]^{T},\quad \quad \underline{{B}}=\big [ \vert {B}_1\vert ,\vert {B}_2\vert ,\ldots ,\vert {B}_n\vert \big ]^T, \end{aligned}$$

and proceeding in exactly the same way as the proof of Theorem 2.2, we can rewrite the equation (4.4) as the following matrix formulation

$$\begin{aligned} {\underline{E}}(x) \le n {\widetilde{L}} \int _{0}^{x}(x-t)^{\min \limits _{1 \le s \le n}\lbrace \gamma _{s}\rbrace -1} {\underline{E}}(t)dt+\underline{{B}}. \end{aligned}$$

Applying Gronwall’s inequality [7] concludes

$$\begin{aligned} \Vert {\underline{E}}\Vert _{w^{(\mu ,\nu ,\tau )}} \le C \left\| \underline{{B}}\right\| _{w^{(\mu ,\nu ,\tau )}}, \end{aligned}$$

and consequently

$$\begin{aligned} \Vert e_{j,N}(x)\Vert _{w^{(\mu ,\nu ,\tau )}} \le C \Vert {B}_j\Vert _{w^{(\mu ,\nu ,\tau )}} \le C \Vert e_{\pi _{N}^{(\mu ,\nu ,\tau )}}(I^{\gamma _{j}}{\bar{g}}_j)\Vert _{w^{(\mu ,\nu ,\tau )}}. \end{aligned}$$

(4.5)

Using Theorem 3.2, we deduce

$$\begin{aligned} \Vert e_{\pi _{N}^{(\mu ,\nu ,\tau )}}(I^{\gamma _{j}}{\bar{g}}_j)\Vert _{w^{(\mu ,\nu ,\tau )}}\le & {} C N^{-\varepsilon _j} |I^{\gamma _{j}}{\bar{g}}_j|_{\varepsilon _j,w^{(\mu ,\nu ,\tau )}}\nonumber \\\le & {} C N^{-\varepsilon _j} \Big (|I^{\gamma _{j}}g_j|_{\varepsilon _j,w^{(\mu ,\nu ,\tau )}}+\Vert D_x(D_x^{\varepsilon _j} I^{\gamma _{j}}g_j)\Vert _\infty \Vert g_j-{\bar{g}}_j \Vert _{w^{(\mu ,\nu ,\tau )}}\Big ) \nonumber \\\le & {} C N^{-\varepsilon _j} \Big (|I^{\gamma _{j}}g_j|_{\varepsilon _j,w^{(\mu ,\nu ,\tau )}}+\sum _{i=1}^{n}\Vert e_{i,N}\Vert _{w^{(\mu ,\nu ,\tau )}}\Big ), \end{aligned}$$

(4.6)

in view of employing the first order Taylor formula. Inserting (4.6) into (4.5) gives

$$\begin{aligned} \Vert e_{j,N}(x)\Vert _{w^{(\mu ,\nu ,\tau )}} -C N^{-\varepsilon _j} \sum _{i=1}^{n}\Vert e_{i,N}(x)\Vert _{w^{(\mu ,\nu ,\tau )}}\le C H_{j}, \end{aligned}$$

(4.7)

in which $H_{j}=N^{-\varepsilon _j}|I^{\gamma _{j}}g_j|_{\varepsilon _j,w^{(\mu ,\nu ,\tau )}}$.

Trivially, the relation (4.7) can be rewritten as the following vector-matrix form

$$\begin{aligned} P {\underline{e}} \le C {\underline{H}}, \end{aligned}$$

(4.8)

where

$$\begin{aligned} {\underline{e}}= & {} [\Vert e_{1,N}\Vert _{w^{(\mu ,\nu ,\tau )}}, \Vert e_{2,N}\Vert _{w^{(\mu ,\nu ,\tau )}},\ldots ,\Vert e_{n,N}\Vert _{w^{(\mu ,\nu ,\tau )}}]^{T},\\ {\underline{H}}= & {} [H_1, H_2, \ldots , H_n]^{T}, \end{aligned}$$

and P is a diagonal matrix of order n with the entries

$$\begin{aligned} \big [P\big ]_{i,j=1}^{n}={\left\{ \begin{array}{ll} 1-CN^{-\varepsilon _j},\quad i=j,\\ 0,\quad \quad \quad \quad ~~~~ i \ne j. \end{array}\right. } \end{aligned}$$

Evidently, for sufficiently large values of N, the matrix P tends to the identity matrix. Therefore, the inequality (4.8) yields

$$\begin{aligned} \Vert e_{j,N}\Vert _{w^{(\mu ,\nu ,\tau )}} \le C H_{j}, \end{aligned}$$

which is the desired result. $\square$

5 Illustrative Examples

In this section, to confirm the accuracy and efficiency of the strategy, the numerical results obtained from the implementation of the proposed scheme are illustrated for some non-linear systems of FDEs. For this purpose, we organize this section as follows

• Some crucial items such as numerical errors $(\mathbf{E }(N))$ and CPU-time used are reported to monitor the computational performance of the suggested method. In all of the examples, the numerical errors are calculated through $L^{2}_{w^{(\mu ,\nu ,\tau )}}(\chi )$ -norm by

  $$\begin{aligned} \mathbf{E }(N)=\max \limits _{j \in \aleph _{n}}\Vert e_{j,N}\Vert _{w^{(\mu ,\nu ,\tau )}}, \end{aligned}$$

  and in the lack of access to the exact solutions, the numerical errors are estimated by means of

  $$\begin{aligned} \mathbf{E }(N)=\max \limits _{j \in \aleph _{n}}\Vert z_{j,2N}(x)-z_{j,N}(x)\Vert _{w^{(\mu ,\nu ,\tau )}}. \end{aligned}$$

• To approve the superiority of the proposed method over other existed methods, we compare our results with those obtained by the spectral collocation method introduced in [20].

• To demonstrate the applicability of the method, some examples are selected from real-world problems.

• To confirm the stability of the approach, the performance of this strategy is investigated for problems with the long integration domain $\chi$ and large degrees of approximation N.

The process of calculations is done via Mathematica v11.2, running in a computer system with an Intel (R) Core (TM) i5-4210U CPU @ 2.40 GHz.

Example 5.1

Consider the following non-linear SMFDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\gamma _{1}}_Cz_1(x)=z_1^{3}(x)+x^{\frac{5}{2}}z_1(x)z_2(x)+q_1(x),\\ D^{\gamma _{2}}_Cz_2(x)=z_2^{4}(x) z_{3}(x)+\frac{1}{2}J_{0}(x^{\frac{7}{4}})\sin {(z_2(x))}+q_2(x),\\ D^{\gamma _{3}}_Cz_3(x)=xz_1(x)z_3^{2}(x)-{_{2}F_{2}}\left( \left\{ \frac{1}{4},\frac{3}{4}\right\} ;\left\{ \frac{1}{5},\frac{2}{5}\right\} ; -\frac{x^{\frac{3}{4}}}{2}\right) z_2(x)z_3(x)+q_3(x), \\ z_1(0)=z_2(0)=0,\quad z_3(0)=\frac{1}{2},\\ z_{2}^{(1)}(0)=z_{3}^{(1)}(0)=0, \quad x \in [0,1], \end{array}\right. } \end{aligned}$$

(5.1)

where $\gamma _{1}=\frac{3}{4},~ \gamma _{2}=\frac{5}{4},~ \gamma _{3}=\frac{3}{2}$ and the source functions $q_{j}(x)$ with $j=1,2,3$ are chosen in a way that the exact solutions are as follows

$$\begin{aligned} z_1(x)=\sin {x^{\frac{3}{4}}},\quad z_2(x)=x^{\frac{7}{4}}+x^{\frac{10}{4}},\quad z_3(x)=\frac{1}{2}E_{\frac{3}{2}}(x^{\frac{3}{2}}). \end{aligned}$$

Trivially, we have

$$\begin{aligned} z_1(x)=O(x^{\frac{3}{4}}), \quad z_2(x)=O(x^{\frac{7}{4}}), \quad z_3(x)=\frac{1}{2}+O(x^{\frac{3}{2}}), \end{aligned}$$

which confirms Theorem 2.4. $E_{\delta }(x)$ is known for Mittag-Leffler function, $J_{c}(x)$ denotes the Bessel function for integer number c, and ${_{\xi }F_{\xi }}(\{a_{1},\ldots ,a_{\xi }\};\{b_{1},\ldots ,b_{\xi }\};x)$ is generalized hypergeometric function.

This problem is solved by our method, and the obtained results are presented in Table 1 and Fig. 1. From Table 1, one can deduce that the proposed strategy provides approximate solutions with high accuracy, mainly because the numerical errors are considerably reduced in short elapsed CPU-time corresponding to the large values of N. Moreover, the semi-log representation of the numerical errors with $\mu =\nu =-\frac{1}{2}$ depicted in Fig. 1, justifies the familiar spectral accuracy which predicted in Theorem 4.1 because the numerical errors in the semi-log report linearly varied versus N (note that we have $\{\varepsilon _{j}\}_{j=1}^{3}=\infty$ in Theorem 4.1).

Table 1 The numerical results of Example 5.1 for various values of $\mu$, $\nu$ and N

Fig. 1

Illustration for semi-log errors of Example 5.1 in the case of fixed $\mu =\nu =-\frac{1}{2}$

To solve a more challenging problem, we set $\gamma _{1}=\frac{1}{3},~ \gamma _{2}=\frac{5}{4},~ \gamma _{3}=\frac{13}{5}$ in (5.1), and the forcing functions $q_{j}(x)$ with $j=1,2,3$ are chosen such that the exact solutions are

$$\begin{aligned} z_1(x)=\sin {x^{\frac{3}{4}}},\quad z_2(x)=x^{\frac{7}{4}}+x^{\frac{10}{4}},\quad z_3(x)=\frac{1}{2}E_{\frac{13}{5}}(x^{\frac{13}{5}}). \end{aligned}$$

The numerical errors and the approximate solutions obtained by applying the introduced method are presented in Tables 2 and 3, respectively. Notably, in this case, we have $\tau =1/\lambda =1/60$ and we can’t expect the numerical errors to decay very fast. However, From Table 2, it can be seen that the effective computational performance of our method lets us give reasonable errors even for a large degree of approximation $N=320$.

Table 2 The numerical errors of Example 5.1 for $\gamma _{1}=\frac{1}{3},~ \gamma _{2}=\frac{5}{4},~ \gamma _{3}=\frac{13}{5}$ and various values of $\mu$, $\nu$ and N

Table 3 Approximate solutions of Example 5.1 for $\gamma _{1}=\frac{1}{3},~ \gamma _{2}=\frac{5}{4},~ \gamma _{3}=\frac{13}{5}$ and various values of N

In the next example, we will compare our method with the proposed method in [20].

Example 5.2

[20] Consider the following non-linear SSFDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\gamma }_Cz_1(x)=-2z_{1}^{2}(x)+x^{3}E_{\gamma }(-x^{\gamma })z_2^{2}(x)+q_1(x),\\ D^{\gamma }_Cz_2(x)=x^{3}E_{\gamma }(-x^{\gamma })z_{1}^{2}(x)-z_{2}^{2}(x)+q_2(x), \\ z_1(0)=z_2(0)=0,\quad \gamma \in (0,1),\quad x \in [0,1], \end{array}\right. } \end{aligned}$$

(5.2)

where the functions $q_{j}(x)$, $j=1,2$ are chosen in a way that the true solutions are

$$\begin{aligned} z_{1}(x)=x^{\gamma }, \quad \quad \quad z_{2}(x)=x^{\gamma }+x^{2\gamma }. \end{aligned}$$

The equation (5.2) is solved via the implemented scheme for the values $\gamma =\frac{1}{5}, \frac{1}{2}, \frac{3}{4}$, and the parameters $\mu =\nu =-\frac{1}{2}$ and $\mu =0,\nu =\frac{1}{2}$. Implementing the proposed scheme, the exact solutions are obtained with the degree of approximations 2,  2,  6, respectively. Also, in [20], the approximate solutions of (5.2) are computed by applying a spectral collocation method, and the numerical errors are obtained in $L^{\infty }$-norm. The maximum of the errors presented in Ref. [20] for different values of N and $\gamma$ are listed in Table 4. Clearly, comparison results confirm the superiority of our proposed scheme over the method presented in [20].

Table 4 The maximum of the errors of Example 5.2 for various values of N and $\gamma$ using the method mentioned in [20]

Example 5.3

(Hepatitis B [5]) The fractional-order model for hepatitis B with drug therapy can be written as the following non-linear SSFDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{{\bar{\tau }}^{1-\gamma }}D^{\gamma }_CT(t)={\bar{s}}-{\bar{d}}T(t)-(1-{\bar{\eta }}){\bar{\alpha }}V(t)T(t)+{\bar{\rho }}I(t),\\ \frac{1}{{\bar{\tau }}^{1-\gamma }}D^{\gamma }_CI(t)=(1-{\bar{\eta }}){\bar{\alpha }}V(t)T(t)-{\bar{\delta }}^{\prime }I(t)-{\bar{\rho }}I(t), \\ \frac{1}{{\bar{\tau }}^{1-\gamma }}D^{\gamma }_CV(t)=(1-{\bar{\epsilon }}){\bar{p}}I(t)-{\bar{c}}V(t),\\ T(0)=T_{0},\quad I(0)=I_{0}, \quad V(0)=V_{0},\quad \gamma \in (0,1],\quad t \in \chi , \end{array}\right. } \end{aligned}$$

(5.3)

considering three state variables at time t: target cells T(t), infected cells I(t), and free virus V(t).

Following [5], the description of parameters and their values are given in Table 5. We note that the units of all the parameters are $(\text {day}^{-1})$.

Table 5 Description of the parameters of model (5.3)

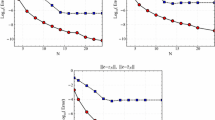
We set $T_{0}=14$, $I_{0}=13$, $V_{0}=10$ and $\gamma =\frac{7}{10}$, and solve the problem via the proposed approach. Table 6 and Fig. 2 report the attained numerical results. Undeniably, the reported results indicate the high accuracy of the presented scheme in solving real-world problems due to the absence of unwanted oscillation in errors, in particular for long integration domain $\chi$ and large values of N. Obviously, obtaining the regular error reduction in a complex non-linear problem, despite the large integration domain, especially in a short CPU time and large degrees of approximation, is a very powerful feature that has been presented in fewer numerical approaches so far.

Table 6 The numerical results of Example 5.3 for various values of $\mu$, $\nu$, $\chi$ and N

Fig. 2

Illustration for semi-log errors of Example 5.3 for $\chi =[0,10]$ (the left one) and $\chi =[0,20]$ (the right one) in the case of fixed $\mu =\nu =-\frac{1}{2}$

Example 5.4

(COVID-19 [16]) Consider the following non-linear dynamical model of COVID-19 disease

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\gamma }_CS(t)={\bar{a}}-{\bar{K}}I(t)S(t)(1+{\hat{\alpha }}I(t))-{\bar{d}}_{0}S(t),\\ D^{\gamma }_CE(t)={\bar{K}}I(t)S(t)(1+{\hat{\alpha }}I(t))-({\bar{d}}_{0}+{\bar{\kappa }})E(t), \\ D^{\gamma }_CI(t)={\bar{b}}+{\hat{\alpha }}E(t)-({\bar{\beta }}+{\bar{d}}_{0}+{\bar{\delta }})I(t),\\ D^{\gamma }_CR(t)={\bar{\delta }}I(t)-{\bar{d}}_{0}R(t),\\ S(0)=S_{0},\quad E(0)=E_{0}, \quad I(0)=I_{0},\quad R(0)=R_{0}, \quad \gamma \in (0,1],\quad t \in [0,15], \end{array}\right. } \end{aligned}$$

(5.4)

Table 7 Description of the parameters of model (5.4)

Table 8 The numerical results of Example 5.4 for various values of $\mu$, $\nu$, $\gamma$ and N

Fig. 3

Illustration for semi-log errors of Example 5.4 for $\gamma =\frac{1}{2}$ (the left one) and $\gamma =\frac{2}{3}$ (the right one) for $\mu =\nu = -\frac{1}{2}$

where ${\bar{K}}=\frac{R_{0}{\bar{d}}_{0}({\bar{d}}_{0}+{\bar{\kappa }})({\bar{\beta }}+{\bar{d}}_{0}+{\bar{\delta }})}{{\hat{\alpha }}{\bar{a}}}$ is proportionality constant. This model contains four compartments at time t (day): healthy or susceptible population S(t), the exposed class E(t), the infected population I(t) and the removed class R(t).

The details of the parameters written in the model (5.4) and their values are given in Table 7.

Applying the proposed method, we evaluate this example by setting the initial conditions $S(0)=0.323$, $E(0)=0.21$, $I(0)=0.22$ and $R(0)=0.21$ scaled in million. The numerical results are illustrated in Table 8 and Fig. 3. From these results, one is thus led to conclude that the numerical errors are decreased as N is increased. Furthermore, the decay of the errors in short elapsed CPU-time corresponding to the large values of N reveals that the introduced strategy is well-conditioned.

Example 5.5

(HIV/AIDS [12]) Let us consider the HIV/AIDS epidemic model with treatment as

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\gamma }_CS(t)={\hat{\beta }}{\hat{k}}-{\hat{c}}{\hat{\nu }}(I(t)+{\hat{a}}J(t))S(t)-{\hat{\beta }}S(t),\\ D^{\gamma }_CI(t)={\hat{c}}{\hat{\nu }}(I(t)+{\hat{a}}J(t))S(t)-({\hat{\beta }}+{\hat{k}}_{1})I(t)+{\hat{\delta }}J(t), \\ D^{\gamma }_CJ(t)={\hat{k}}_{1}I(t)-({\hat{\beta }}+{\hat{k}}_{2}+{\hat{\delta }})J(t),\\ D^{\gamma }_CA(t)={\hat{k}}_{2}J(t)-({\hat{\beta }}+{\hat{d}})A(t),\\ S(0)=S_{0},\quad I(0)=I_{0}, \quad J(0)=J_{0},\quad A(0)=A_{0}, \quad \gamma \in (0,1],\quad t \in [0,5]. \end{array}\right. } \end{aligned}$$

(5.5)

The total population is divided into a susceptible class of size S, an infectious class before the onset of AIDS, and a full-blown AIDS group of size A, which is removed from the active population. The infection population is classified into two groups, the asymptomatic stage of size I and the symptomatic stage of size J. ${\hat{\beta }}{\hat{k}}$ represents the recruitment rate of the population, and the parameter ${\hat{a}} > 1$ captures the fact that the individuals in the symptomatic stage J are more infectious than the asymptomatic stage I. The description and values of the other parameters are depicted in Table 9. It is noticed that the unit of time is the year. For more explanations about the model, we also refer to [12].

Table 9 Description of the parameters of model (5.5)

Inserting $S(0)=300,~I(0)=60,~J(0)=30,~A(0)=5,~{\hat{k}}=120,~{\hat{a}}=0.3$ and $\gamma =\frac{4}{5}$, we compute the approximate solutions of (5.5), and the numerical results are illustrated in Table 10 and Fig. 4.

Table 10 The numerical results of Example 5.5 for various values of $\mu$, $\nu$ and N

Fig. 4

Illustration for semi-log errors of Example 5.5 in the case of fixed $\mu =\nu =-\frac{1}{2}$

6 Conclusion

In this paper, the well-posedness and smoothness properties of the solutions of (1.1) were presented. Furthermore, a suitable operational Galerkin approach based on the fractional Jacobi functions was presented, and a practical implementation process was introduced which finds the unknowns via some recurrence relations without solving any non-linear algebraic system. Convergence analysis of the presented method was justified that confirmed the high accuracy of the scheme without enforcing the problematic regularity assumptions on the given data. Finally, through the numerical solution of various examples, the well-conditioning and high-order accuracy of the presented method was emphasized.