1 Introduction

The shallow water equations (SWE) with non-flat bottom geometry problems suppose a hyperbolic system of conservation laws with a source term, also called balance laws. In these problems we can achieve steady state solutions in which the flux gradients are not zero, but rather they are exactly cancelled by the contribution of the source term. In practice, the exact cancellation of the flux gradients with the source term is difficult to achieve numerically, if there are no additional considerations when it comes to discretize the source term [1,2,3,4,5,6,7].

When a non-well-balanced scheme is used in SWE with variable bathymetry some fixed-valued artificial perturbations will appear throughout the domain [8]. These perturbations are proportional to the mesh size or to the distance between particles in meshless methods. Well-balanced schemes [9] or schemes that satisfy the C-property, as they were called in early works [10, 11], are those which can successfully compensate (balance) the source term with the flux gradients and reproduce steady state solutions. Hence, a well-balanced scheme should preserve static states over time regardless of the bathymetry. Balancing the SWE is a problem that has gained a lot of attention during the past few decades to date and it has been faced using many different numerical methods [1, 6, 7, 12].

Smoothed Particle Hydrodynamics (SPH) methods were originally designed by Gingold and Monaghan [13] and, Lucy [14] to be used in the field of astrophysics in the late seventies. This use was soon after extended into many other fields of hydrodynamics. SPH methods have been notably used in the solution of problems involving huge deformations or moving boundaries, considering their Lagrangian approach and the absence of geometrical limitations of classical mesh-based methods [15, 16].

The method presented in this work is based on the SPH Arbitrary Lagrangian-Eulerian (SPH-ALE) scheme proposed by Vila and Ben Moussa [17,18,19]. Unlike classical SPH formulations [20], this meshless formulation is based on Riemann solvers. The use of Riemann solvers avoids the need for explicit artificial dissipation and, the accuracy of the resulting scheme is increased with the aid of Moving Least Squares (MLS) [21,22,23,24,25,26].

Moreover, the SPH-ALE method has an Arbitrary Eulerian-Lagrangian nature and thus, it combines the advantages of the Lagrangian and Eulerian methods.

Nonetheless, the use of meshless SPH methods to solve well balanced SWE has not been widely developed yet. We can refer to previous works from Vacondio et al [27, 28], Xia et al [29] and Berthon et al [30] . To the authors’ knowledge, the work of Rossi et al [31] is the only successful attempt employing the SPH-ALE formulation. In their work, Rossi et al. presented a path-conservative scheme. This scheme introduces an additional discretization term to obtain the well-balance property. This term considers the contribution of the non-conservative terms based on Roe-matrix integrated through a straight line path. In the present work, we obtain the well-balancedness by an alternative new discretization of the source term based on splitting the source term into two different terms. This procedure is based on the approach presented in [6, 7] for Finite Differences, Finite Volumes and Discontinuous Galerkin schemes. The aim of the present work is to design a well-balanced, high-order SPH-ALE scheme to solve the SWE. The proposed method is designed to solve problems with non-smooth flows and variable bathymetry with high accuracy and preserving steady states and, static solutions over time.

Stabilization is achieved using the Multi-Order Optimal Detection (MOOD) procedure [24, 32, 33]. In common limiting procedures, the limiting is performed a priori, that is, predicting the troubled particles of the next time step. In MOOD the limiting procedure is performed a posteriori, and thus, the prediction of the troubled particles is substituted by the precise determination of the particles requiring limitation. In this work, we adapt the approach proposed in [24] for the Euler equations to the SWE.

This paper is organized as follows: in Sect. 2 the SWE equations are presented. Section 3 is devoted to show the proposed discretization, with particular attention on the discretization of the source term, required to achieve a well-balanced method (Sect. 3.2). Several numerical tests are presented in Sect. 4, to test the accuracy and robustness of the proposed method. Finally, in Sect. 5, some concluding remarks are drawn.

2 Governing Equations

The SWE with non-flat bottom geometry suppose a hyperbolic system of balance laws defined as follows:

$$\begin{aligned} \dfrac{\partial \pmb {U}}{\partial t} + \nabla \cdot \pmb {\mathcal {F}}(\pmb {U})= \pmb {S}(\pmb {U}), \end{aligned}$$
(1)

where \(\pmb {U}\) is the vector of conservative variables and \(\pmb {\mathcal {F}}=(\pmb {F}_{x}(\pmb {U}),\pmb {F}_{y}(\pmb {U}))\) is the flux tensor, that are defined as

$$\begin{aligned} \pmb {U}=\left( \begin{array}{c} h\\ hu\\ hv \end{array}\right) \;;\qquad \pmb {F}_{x}(\pmb {U})=\left( \begin{array}{c} hu\\ hu^{2}+\dfrac{g}{2}h^{2}\\ huv \end{array}\right) \;; \qquad \pmb {F}_{y}(\pmb {U})=\left( \begin{array}{c} hv\\ huv\\ hv^{2}+\dfrac{g}{2}h^{2} \end{array}\right) . \end{aligned}$$

The source term vector, \(\pmb {S}(\pmb {U})\), accounts for the effects of the bottom bathymetry and is defined as

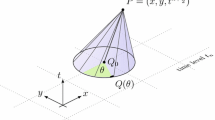
$$\begin{aligned} \pmb {S}(\pmb {U})=\left( \begin{array}{c} 0\\ \\ -gh\dfrac{\partial b}{\partial x}\\ \\ -gh\dfrac{\partial b}{\partial y} \end{array}\right) . \end{aligned}$$

The terms h and g stand for the water height and the gravity acceleration. The position is defined by \(\pmb {r}=(x,y)^T\), and the elevation of the bottom bathymetry is defined by a smooth function \(b(\pmb {r})\) that is included in the source term. The water flow velocity vector is \(\pmb {u}=(u,v)^T\), and the elevation of water surface is denoted as \(\eta =h+b\). In Figure 1 a schematic diagram with \(h(\pmb {r})\), \(b(\pmb {r})\) and \(\eta (\pmb {r})\) is shown.

Fig. 1
figure 1

Schematic diagram of water at rest over irregular bottom bathymetry

Full size image

3 A Well-Balanced, High-Order SPH-ALE Scheme

In SPH-ALE methods the problem’s domain is discretized into a set of particles that hold the values of the variables in their positions. We can solve the SWE described in section 2 for a given particle i as the weighted sum of the interactions between this particle i and the neighbouring particles j within its influence domain, denoted as stencil. This interaction between particles is conceived as a Riemann problem (RP) at the integration point ij at midpoint between particles i and j. In Figure 2 a schematic representation of the fluid particles, the particle i, its stencil, the neighbour particle j, and the integration point ij located at midpoint between i and j are shown. The positions of these points are denoted by \(\pmb {r}_i\), \(\pmb {r}_j\) and \(\pmb {r}_{ij}\) respectively. The normal vector of the ij path is noted as \(\pmb {n}_{ij} = \frac{\pmb {r}_j -\pmb {r}_i}{|| \pmb {r}_j -\pmb {r}_i || }\).

Fig. 2
figure 2

Schematic 2D diagram of particle i and its neighbour particles within its stencil

Full size image

In the present work, we use the SPH-ALE formulation [17,18,19] with the correction term proposed in [34]:

$$\begin{aligned} \dfrac{d}{dt}\left( V_{i}\pmb {U}_{i}\right)= & {} -\sum _{j=1}^{N_i}2\left( \pmb {G}_{ij}-\pmb {H}_{i}\right) \;V_{i}V_{j}\;\nabla W_{ij}\;+\;V_{i}\;\pmb {S}_i \;; \end{aligned}$$
(2)
$$\begin{aligned} \dfrac{dV_{i}}{dt}= & {} \sum _{j=1}^{N_i}2V_{i}V_{j}\left( \pmb {w}_{ij}-\pmb {w}_{i}\right) \nabla W_{ij}\;; \end{aligned}$$
(3)
$$\begin{aligned} \dfrac{d\pmb {r}_{i}}{dt}= & {} \dfrac{\sum \nolimits _{j=1}^{N_i}\pmb {w}_{j}\;V_{j}W_{ij}}{\sum \nolimits _{j=1}^{N_i}V_{j}W_{ij}}\;, \end{aligned}$$
(4)

where \(\pmb {r}_{i}\) is the position vector of particle i, \(\pmb {G}_{ij}\) is the numerical flux tensor computed by a Riemann solver in the integration point ij, which will be defined later, and \(\pmb {H}_i = \pmb {H}(\pmb {U}_i,\pmb {w}_i)\) is the Lagrangian flux tensor of the SWE in a reference moving frame with velocity \(\pmb {w}\). It is defined as

$$\begin{aligned} \pmb {H}_{i}=\pmb {\mathcal {F}}(\pmb {U}_i)-\pmb {w}_i\otimes {\pmb {U}_i}. \end{aligned}$$
(5)

The terms \(\pmb {w}_i, \pmb {w}_j\) refer to the Lagrangian velocity of particles i, j, while the Lagrangian velocity at the integration point ij is \(\pmb {w}_{ij}\), which will be defined in section 3.1. In an Eulerian frame \(\pmb {w}_i= \pmb {w}_j=0\), and in a Lagrangian frame they are coincident with particle velocities \(\pmb {u}_i\),\(\pmb {u}_j\). The flux tensor defined in Eq. (5) leads to a flux difference formulation of the SPH-ALE scheme [34].

In Eqs. (2), (3) and (4), the term \(V_j\) represent the volume associated to the particle j, and \(W_{ij}\) is a kernel function. Here, the kernel function is defined as

$$\begin{aligned} W_{ij}=\dfrac{C}{l_{ij}^{D}}{\left\{ \begin{array}{ll} 1-\dfrac{3}{2}q_{ij}^{2}+ {{\dfrac{3}{4}q_{ij}^{3}}} &{} q_{ij}\le 1\\ \dfrac{1}{4}\left( 2-q_{ij}\right) ^{3} &{} 1\le q_{ij}\le 2\\ 0 &{} q_{ij}>2 \end{array}\right. }. \end{aligned}$$
(6)

In Eq. (6), D is the number of space dimensions. The value of the kernel depends on the positions of the particle i and its neighbouring particles j, as \(q_{ij}=\dfrac{||\pmb {r}_{j}-\pmb {r}_{i}||}{l_{ij}}\) . The value of \(l_{ij}\) is defined from the smoothing lengths associated to the particle i and particle j and related to their volume as

$$\begin{aligned} l_{ij}=\dfrac{1}{2}(l_i +l_j)\,, \qquad l_{i}=2\,V_{i}^{\frac{1}{D}}\, . \end{aligned}$$

The value of the constant C depends on the number of spatial dimensions. We use \(C=1\) for 1D problems and \(C=\dfrac{10}{7\pi }\) for 2D problems. We refer to [24] and its references for a more exhaustive and complete description of the SPH kernel formulations used in this work.

3.1 Discretization of the Numerical Fluxes

The numerical flux tensor \(\pmb {G}_{ij}\) is computed by a Riemann solver, considering that the left and right states of the RP at the integration point ij are given by the polynomial reconstructions of the variables at the integration point ij. In the following, for a given variable \(\alpha \), we consider \(\alpha _{ij}^-\) and \(\alpha _{ij}^+\) as the left and right states of the RP respectively. In Fig. 3 a schematic diagram of the mentioned RP and the reconstructions at ij is shown. In this work, the Rusanov flux is considered [35].

Fig. 3
figure 3

Schematic diagram of the reconstruction at midpoint (ij) between two particles i and j. A 1D Riemann problem is solved at ij. The left and right Riemann states (\(\alpha ^-(x)\) and \(\alpha ^+(x)\)) are computed from Taylor polynomial reconstructions of the variable \(\alpha (x)\). These reconstructions are computed separately, using the information of the stencils associated to particles i (for the left state) and j (for the right state). Note that \(\alpha \) stands for any of the variables of the problem, either h, u or b

Full size image
$$\begin{aligned} \pmb {G}_{ij}=\dfrac{1}{2}\left( \pmb {H}_{ij}^+ +\pmb {H}_{ij}^-\right) -\dfrac{1}{2}\left| S_{ij}^{*}\right| \left( \pmb {U}_{ij}^+ -\pmb {U}_{ij}^- \right) \cdot \pmb {n}_{ij}^T \,. \end{aligned}$$
(7)

In Eq. (7) the term \(\left| S_{ij}^{*}\right| \) is the maximum eigenvalue of the flux’s Jacobian matrix [35], which in the ALE framework reads as

$$\begin{aligned} S^{*}_{ij}=\max \left( (\pmb {u}_{ij}^+-\pmb {w}_{ij})\cdot \pmb {n}^T_{ij}+c^+_{ij}\;,\;(\pmb {u}_{ij}^--\pmb {w}_{ij})\cdot \pmb {n}^T_{ij}-c^-_{ij})\right) , \end{aligned}$$
(8)

where \(\pmb {w}_{ij}=\frac{1}{2}\left( \pmb {w}_{ij}^+ +\pmb {w}_{ij}^- \right) \) is the Lagrangian velocity associated to the integration point, \(c^\pm _{ij}=\sqrt{g \cdot h^\pm _{ij}}\) denotes the left and right states of the wave celerities in the RP. Moreover, \(\pmb {H}_{ij}^- =\pmb {H}(\pmb {U}_{ij}^- ,\pmb {w}_{ij})\) and \(\pmb {H}_{ij}^+ =\pmb {H}(\pmb {U}_{ij}^+ ,\pmb {w}_{ij})\) are the flux approximations of \(\pmb {H}\) on the left and right sides of the integration point (located at the midpoint between particles i and j), \(\pmb {r}_{ij}\) with the positive orientation given by \({\pmb {r}_j-\pmb {r}_i}\) and represented by the normalized vector \(\pmb {n}_{ij}\), while \(\pmb {U}_{ij}^+ -\pmb {U}_{ij}^- \) is the jump of the reconstructed conservative variables.

3.1.1 High Order Reconstructions with Moving Least Squares

The left and right states at integration points of the conservative variables (\(\pmb {U}_{ij}^-\) and \(\pmb {U}_{ij}^+\)) and the bathymetry (\(b_{ij}^-\) and \(b_{ij}^+\)) are computed using a cubic Taylor polynomial. These polynomial reconstructions are used to calculate the fluxes \(\pmb {H}_{ij}^-\) and \(\pmb {H}_{ij}^+\) in equation (7), as well as the source term (that will be described in the next section).

The derivatives required to compute the Taylor polynomials are obtained using MLS approximations. In the following, we present very succinctly the MLS approximations approach, and we refer the reader to [21, 23,24,25,26] for a complete description of the method.

We can approximate the value of the variables \(\pmb {U}\) at a given point, \(\pmb {r}= (x, y)^T\), using MLS reconstruction as

$$\begin{aligned} \pmb {{\widehat{U}}_i}(\pmb {r})=\sum ^{N_i}_{j=1}\phi _{j}(\pmb {r})\,\pmb {U}_{j}, \end{aligned}$$
(9)

where \(N_i\) is the number of neighbour particles in the stencil of particle i and \(\phi _j(\pmb {r})\) are each of the MLS shape functions associated o the neighbour particles j [21, 25]. These shape functions, are calculated in function of the relative positions of the particles j and i and they are weighted by a kernel function. The shape functions, gathered in vector \(\pmb {\varPhi } = (\phi _1,\phi _2,\ldots ,\phi _{N_i} ) \in {\mathbb {R}}^{N_i}\), are computed as follows

$$\begin{aligned} \pmb {\varPhi }^{T}(\pmb {r})=\pmb {p}^{T}(\pmb {r})\;\pmb {M}^{-1}(\pmb {r})\;\pmb {P}(\pmb {r})\;\pmb {W}_{D}(\pmb {r}), \end{aligned}$$

where \(\pmb {p}^T (\pmb {r}) = (1, x, y, x^2, y^2, xy, ...) \in {\mathbb {R}}^m\) is the m-dimensional basis functions vector, \(\pmb {P}\) is a \(m \times N_i\) matrix where the basis functions are evaluated at each point of the stencil, namely \(\pmb {P} = [\pmb {p}^T (\pmb {r}_j )]_i\) and \(\pmb {M}(\pmb {r})\) is the \(m \times m\) moment matrix given by

$$\begin{aligned} \pmb {M}(\pmb {r})=\pmb {P}(\pmb {r})\;\pmb {W}_{D}(\pmb {r})\pmb {\;P}^{T}(\pmb {r}), \end{aligned}$$

where \(\pmb {W}_{D}(\pmb {r})\) is a diagonal matrix which is obtained from the kernel function evaluated at \(\pmb {r}_j - \pmb {r}_i\) for the \(N_i\) neighbouring particles. In the numerical applications of the present work, we use the truncated exponential kernel function [23, 24]

$$\begin{aligned} W_{ij}=W(\pmb {r}_{i},\pmb {r}_{j})=\frac{e^{1 - \beta ^2} -1}{e-1};\qquad \beta =\dfrac{|\pmb {r}_j - \pmb {r}_i |}{{2}\cdot \max (|\pmb {r}_k - \pmb {r}_i|)}, {\forall k \in {N_i}} \end{aligned}$$

3.2 Well Balanced Methods: Source Term Discretization

In order to obtain a well balanced scheme, a new discretization of the source term is presented. The proposed discretization is based on the splitting of the source term, and it adapts to the SPH-ALE scheme the source term separation procedure presented by Xing and Shu for FD methods [7] and to FV and DG methods [6].

If we consider the contribution of the non-flat bathymetry and no other external forces, such as bed friction, the source term on a 2D SWE scheme reads:

$$\begin{aligned} \pmb {S}(\pmb {U})=\left( \begin{array}{c} S_{1}\\ S_{2}\\ S_{3} \end{array}\right) =\left( \begin{array}{c} 0\\ \\ -gh\dfrac{\partial b}{\partial x}\\ \\ -gh\dfrac{\partial b}{\partial y} \end{array}\right) . \end{aligned}$$
(10)

The discretization of \(S_2\) and \(S_3\) components of the vector (10) is the same, so in the following only the \(S_2\) term is derived. First, we proceed to separate the source term into two different terms:

$$\begin{aligned} S_2= & {} -gh\dfrac{\partial b}{\partial x}=-g(\eta -b)\dfrac{\partial b}{\partial x}=g\left( \dfrac{1}{2}\dfrac{\partial b^{2}}{\partial x}-\eta \dfrac{\partial b}{\partial x}\right) , \nonumber \\ S_{2}= & {} S_{2}^{A}+S_{2}^{B};\qquad {\left\{ \begin{array}{ll} S_{2}^{A}=\dfrac{g}{2}\dfrac{\partial b^{2}}{\partial x}\\ S_{2}^{B}=-g\eta \dfrac{\partial b}{\partial x}\end{array}\right. }. \end{aligned}$$
(11)

Usual kernel approximations of a function and its gradient, read as

$$\begin{aligned} \begin{aligned} f(\pmb {r}_i)&\approx \sum \limits _{j=1}^{N_i} f(\pmb {r}_j) V_j W_{ij};\\ \nabla f(\pmb {r}_i)&\approx \sum \limits _{j=1}^{N_i} f(\pmb {r}_j) V_j \nabla W_{ij}. \end{aligned} \end{aligned}$$

In order to ensure zeroth-order consistency, it is usual to approximate the gradient as [17, 36].

$$\begin{aligned} \nabla f(\pmb {r}_i) \approx \sum \limits _{j=1}^{N_i}\left( f(\pmb {r}_j)-f(\pmb {r}_i)\right) V_j \nabla W_{ij} \approx \sum \limits _{j=1}^{N_i}2\left( f(\pmb {r}_{ij})-f(\pmb {r}_i)\right) V_j \nabla W_{ij}. \end{aligned}$$

The value of a function at the midpoint between particles can be computed as

$$\begin{aligned} f(\pmb {r}_{ij}) =\dfrac{f(\pmb {r}_{ij}^+ )+f(\pmb {r}_{ij}^- )}{2}, \end{aligned}$$

and then,

$$\begin{aligned} \nabla f(\pmb {r}_{i}) \approx \sum \limits _{j=1}^{N_i}\left( f(\pmb {r}_{ij}^+ ) + f(\pmb {r}_{ij}^- )-2f(\pmb {r}_{i})\right) V_j \nabla W_{ij}. \end{aligned}$$

Thus, applying this approximation to the gradient of b, \(\nabla b = (\frac{\partial b}{\partial x}, \frac{\partial b}{\partial y})^T\), the term \(S_2^A\), only involving the first component of the gradient, can be expressed as:

$$\begin{aligned} \begin{aligned} S_{2}^{A}&=\dfrac{g}{2}\sum _{j=1}^{N_i}\left( b_{j}^{2}-b_{i}^{2}\right) V_{j}\dfrac{\partial W_{ij}}{\partial x}\\&=\dfrac{g}{2}\sum _{j=1}^{N_i}\left( (b_{ij}^+)^{2}+(b_{ij}^- )^{2}-2b_{i}^{2}\right) V_{j}\dfrac{\partial W_{ij}}{\partial x}. \end{aligned} \end{aligned}$$
(12)

An analogous procedure applied to the \(S_{2}^{B}\) term leads to:

$$\begin{aligned} \begin{aligned} S_{2}^{B}&=-g\eta _{i}\sum _{j=1}^{N_i}\left( b_{j}-b_{i}\right) V_{j}\dfrac{\partial W_{ij}}{\partial x}\\&= -g\eta _{i}\sum _{j=1}^{N_i}\left( b_{ij}^+ +b_{ij}^- -2b_{i}\right) V_{j}\dfrac{\partial W_{ij}}{\partial x}. \end{aligned} \end{aligned}$$
(13)

If we add both split terms (12,13) into a single sum, we finally obtain \(S_{2}\), and \(S_{3}\) as the proposed discretization of the source term:

$$\begin{aligned} \begin{aligned} S_{2}&=\dfrac{g}{2}\sum _{j=1}^{N_i}\left[ \left( (b_{ij}^+)^{2}+(b_{ij}^-)^{2}-2b_{i}^{2}\right) -2\eta _{i}\left( b_{ij}^+ + b_{ij}^- -2b_{i}\right) \right] \;V_{j}\dfrac{\partial W_{ij}}{\partial x}\;;\\ S_{3}&=\dfrac{g}{2}\sum _{j=1}^{N_i}\left[ \left( (b_{ij}^+)^{2}+(b_{ij}^-)^{2}-2b_{i}^{2}\right) -2\eta _{i}\left( b_{ij}^+ + b_{ij}^- -2b_{i}\right) \right] \;V_{j}\dfrac{\partial W_{ij}}{\partial y}\;. \end{aligned} \end{aligned}$$
(14)

Applying the following discretization of the source term to the SWE hyperbolic system (7), the flux gradient is explicitly canceled by the source term when water at rest conditions are considered (\(h+b=\eta =\)constant; \(u=v=0\) for all the particles). This is strictly true for the equations derived from the conservation of momentum (those that consider \(S_2\) and \(S_3\) respectively). The equation of the water height, derived from mass conservation, is examined in the following. We consider the water height equation, and we define

$$\begin{aligned} \pmb {H}_{i\; 1} =\left( \begin{array}{c} H_{i\; 1x} \\ H_{i\; 1y} \end{array}\right) =\pmb {F}_{i\; 1} - h_{i} \,\pmb {w}_{i} =\left( \begin{array}{c} hu_{i} \\ hv_{i} \end{array} \right) - h_{i} \,\pmb {w}_{i}\;; \end{aligned}$$

and the high-order reconstructions

$$\begin{aligned} \pmb {H}_{ij\; 1}^\pm =\left( \begin{array}{c} H_{ij\; 1x}^\pm \\ \\ H_{ij\; 1y}^\pm \end{array}\right) =\pmb {F}_{ij\; 1}^\pm - h_{ij}^\pm \,\pmb {w}_{ij} =\left( \begin{array}{c} hu_{ij}^\pm \\ \\ hv_{ij}^\pm \end{array} \right) - h_{ij}^\pm \,\pmb {w}_{ij}\;; \end{aligned}$$

Then, the water height equation reads as

$$\begin{aligned} \begin{aligned} \dfrac{d}{dt}\left( V_{i}h_{i}\right) =&-\sum _{j=1}^{N_i}\left( H_{ij\;1x}^+ +H_{ij\;1x}^- -\left| S_{ij}^{*}\right| \left( h_{ij}^+ -h_{ij}^- \right) n_{x}-2H_{i\; 1x}\right) \;V_{i}V_{j}\dfrac{\partial W_{ij}}{\partial x}\\&-\sum _{j=1}^{N_i}\left( H_{ij\; 1y}^+ +H_{ij\; 1y}^- -\left| S_{ij}^{*}\right| \left( h_{ij}^+ -h_{ij}^- \right) n_{y}-2H_{i\; 1y}\right) \;V_{i}V_{j}\dfrac{\partial W_{ij}}{\partial y}\;, \end{aligned} \end{aligned}$$
(15)

Considering water at rest conditions, we obtain:

$$\begin{aligned} \begin{aligned} \dfrac{d}{dt}\left( V_{i}h_{i}\right)&=\sum _{j=1}^{N_i}\left| S_{ij}^{*}\right| \left( h_{ij}^+ -h_{ij}^- \right) n_{x}\; V_{i}V_{j}\dfrac{\partial W_{ij}}{\partial x}\\&\quad +\sum _{j=1}^{N_i}\left| S_{ij}^{*}\right| \left( h_{ij}^+ -h_{ij}^- \right) n_{y}\; V_{i}V_{j}\dfrac{\partial W_{ij}}{\partial y}\;. \end{aligned} \end{aligned}$$
(16)

Note that \(\pmb {w}_{ij}=\pmb {0}\) and \(\pmb {w}_i=\pmb {0}\) for the water at rest conditions for both Lagrangian and Eulerian approaches. Eq. (16) shows that the difference of the jump term is not exactly neglected for the water at rest conditions, as the reconstructed values of the water height (h) may be different in the presence of non-flat bottom bathymetry, and the resulting numerical scheme is not well-balanced.

In this work, following the works presented in [5, 37], we propose a well-balanced SPH-ALE discretization of the mass conservation equation. We consider a non-erodible bathymetry hypothesis, and under this hypothesis, the transport operators of the water height (h) and the bathymetry (b) can be expressed as

$$\begin{aligned} L_{w}\left( h\right)= & {} \dfrac{\partial h}{\partial t}+\nabla \cdot \left( h\pmb {w}\right) \;; \\ L_{w}\left( b\right)= & {} \dfrac{\partial b}{\partial t}+\nabla \cdot \left( b\pmb {w}\right) =\nabla b\cdot \pmb {w}+b\nabla \cdot \pmb {w}\;; \end{aligned}$$

Then, the mass conservation equation in terms of h reads

$$\begin{aligned} \dfrac{\partial h}{\partial t}+\nabla \cdot \pmb {\mathcal {F}}_1 \left( \pmb {U}\right) =0\;; \end{aligned}$$

and, introducing the operator \(L_{w}\left( h\right) \) and the flux \(\pmb {H}_{1} \left( \pmb {U}\right) =\pmb {\mathcal {F}}_1 \left( \pmb {U}\right) -h\pmb {w}\), this equation can be written as

$$\begin{aligned} L_{w}\left( h\right) +\nabla \cdot \pmb {H}_{1}\left( \pmb {U}\right) =0\;. \end{aligned}$$

Since \(\eta =h+b\) and the bathymetry is non-erodible we can rewrite the mass conservation equation in terms of \(\eta \) as

$$\begin{aligned} L_{w}\left( \eta \right) =L_{w}\left( h\right) +L_{w}\left( b\right) =-\nabla \cdot \pmb {H}_{1}\left( \pmb {U}\right) +L_{w}\left( b\right) \;; \end{aligned}$$
(17)

We can discretize Eq. (17) in particle i approximating the ALE flux term as a numerical flux [17] including the kernel gradient correction [34] as follows

$$\begin{aligned} \dfrac{1}{V_{i}}\dfrac{d\left( V_{i}\eta _{i}\right) }{dt}=-\sum _{j=1}^{N_i}V_{j}2\,\left( \widehat{\pmb {G}}_{ij1} - \pmb {H}_i \right) \cdot \nabla W_{ij}+\sum _{j=1}^{N_i}V_{j}\left( b_{i}\pmb {w}_{j}+b_{j}\pmb {w}_{i}\right) \cdot \nabla W_{ij}\;, \end{aligned}$$

Note that we use the Rusanov numerical flux [35] considering the water surface elevation \(\eta \) as the updating variable on time, since Eq. (17) is written in terms of this variable.

$$\begin{aligned} \widehat{\pmb {G}}_{ij1}= & {} \dfrac{\pmb {H}_{ij1}^{+}+\pmb {H}_{ij1}^{-}}{2}-\dfrac{\left| S^{*}_{ij}\right| }{2}\left( \eta _{ij}^{+}-\eta _{ij}^{-}\right) \pmb {n}^T_{ij}\;. \nonumber \\ \dfrac{d\left( V_{i}\eta _{i}\right) }{dt}= & {} -\sum _{j=1}^{N_i}V_{i}V_{j}\,2\left( \dfrac{\pmb {H}_{ij1}^{+}+\pmb {H}_{ij1}^{-}}{2}-\dfrac{\left| S^{*}_{ij}\right| }{2}\left( \eta _{ij}^{+}-\eta _{ij}^{-}\right) \pmb {n}^T_{ij} -\pmb {H}_i\right) \cdot \nabla W_{ij}\nonumber \\&+\sum _{j=1}^{N_i}V_{i}V_{j}\left( b_{i}\pmb {w}_{j}+b_{j}\pmb {w}_{i}\right) \cdot \nabla W_{ij}\;. \end{aligned}$$
(18)

We can now revert the change of variables to write Eq. (18) in terms of water height h before proceeding with the time discretization

$$\begin{aligned} \dfrac{d\left( V_{i}\eta _{i}\right) }{dt} =\dfrac{d\left( V_{i}(h_{i}+b_i)\right) }{dt}=\dfrac{d\left( V_{i}h_{i}\right) }{dt}+\dfrac{d\left( V_{i}b_{i}\right) }{dt}\;, \end{aligned}$$

Using that

$$\begin{aligned} \dfrac{d\left( V_{i}b_{i}\right) }{dt} =V_{i}\dfrac{db_{i}}{dt}+\dfrac{dV_{i}}{dt}b_{i} =V_{i}\left( \dfrac{\partial b_{i}}{\partial t}+\nabla b\cdot \pmb {w}_{i}\right) +\left( V_{i}\nabla \cdot \pmb {w}_{i}\right) b_{i}\;, \end{aligned}$$

we can write

$$\begin{aligned} \dfrac{d\left( V_{i}\eta _{i}\right) }{dt} =\dfrac{d\left( V_{i}h_{i}\right) }{dt}+\sum _{j=1}^{N_i}V_{i}V_{j}\left( b_{i}\pmb {w}_{j}+b_{j}\pmb {w}_{i}\right) \cdot \nabla W_{ij}\;. \end{aligned}$$

Finally, substituting in Eq. (18) we get

$$\begin{aligned} \dfrac{d\left( V_{i}h_{i}\right) }{dt}=-\sum _{j=1}^{N_i}V_{i}V_{j}\,2\left( \dfrac{\pmb {H}_{ij1}^{+}+\pmb {H}_{ij1}^{-}}{2}-\dfrac{\left| S^{*}_{ij}\right| }{2}\left( \eta _{ij}^{+}-\eta _{ij}^{-}\right) \pmb {n}^T_{ij}-\pmb {H}_i\right) \cdot \nabla W_{ij}\;. \end{aligned}$$

When water at rest conditions are considered, we obtain

$$\begin{aligned} \dfrac{d}{dt}\left( V_{i}h_{i}\right) =\sum _{j=1}^{N_i} \left| S_{ij}^{*}\right| \left( \eta _{ij}^+ -\eta _{ij}^-\right) V_{i}V_{j}\nabla W_{ij} \cdot \mathbf{n} \end{aligned}$$

Hence, since \(\eta \) is constant, an exact zero mass flux is granted. Thus, we have derived a new SPH-ALE method in which the numerical flux for the mass conservation equation is discretized considering the water surface elevation \(\eta \) as the updated variable, instead of h. It is important to note that in the proposed method the conservative variable is h. This is different of the procedure followed by the pre-balanced methods [38,39,40,41] in which the conservative variable is changed for the water elevation \(\eta \).

3.3 Final Discretization

To summarise, and for the sake of clarity, we write down the system of equations to be solved and discretizations adopted in the presented method.

$$\begin{aligned} \dfrac{d}{dt}\left( V_{i}\pmb {U}_{i}\right)= & {} -\sum _{j=1}^{N_i}2\left( \pmb {G}_{ij}-\pmb {H}_{i}\right) \;V_{i}V_{j}\;\nabla W_{ij}\;+\;V_{i}\;\pmb {S}_{i}\;;\nonumber \\ \dfrac{dV_{i}}{dt}= & {} \sum _{j=1}^{N_i}2V_{i}V_{j}\left( \pmb {w}_{ij}-\pmb {w}_{i}\right) \nabla W_{ij}\;; \nonumber \\ \dfrac{d\pmb {r}_{i}}{dt}= & {} \dfrac{\sum \limits _{j=1}^{N_i}\pmb {w}_{j}\;V_{j}W_{ij}}{\sum \limits _{j=1}^{N_i}V_{j}W_{ij}}\;. \end{aligned}$$
(19)

And the source term is discretized as

$$\begin{aligned} \begin{aligned} S_{1}&=0\;;\\ S_{2}&=\dfrac{g}{2}\sum _{j=1}^{N_i}\left[ \left( (b_{ij}^+)^{2}+(b_{ij}^-)^{2}-2b_{i}^{2}\right) -2\eta _{i}\left( b_{ij}^+ + b_{ij}^- -2b_{i}\right) \right] \;V_{j}\dfrac{\partial W_{ij}}{\partial x}\;;\\ S_{3}&=\dfrac{g}{2}\sum _{j=1}^{N_i}\left[ \left( (b_{ij}^+)^{2}+(b_{ij}^-)^{2}-2b_{i}^{2}\right) -2\eta _{i}\left( b_{ij}^+ + b_{ij}^- -2b_{i}\right) \right] \;V_{j}\dfrac{\partial W_{ij}}{\partial y}\;. \end{aligned} \end{aligned}$$

3.3.1 Time Discretization

A TVD third-order Runge-Kutta time discretization [42] is used in this work

$$\begin{aligned} \begin{aligned} \alpha ^{I}&=\alpha ^{N_i} + \varDelta t {\mathcal {F}}(\alpha ^n)\;; \\ \alpha ^{II}&=\dfrac{3}{4}\alpha ^{N_i} +\dfrac{1}{4}\left( \alpha ^{I} + \varDelta t {\mathcal {F}} \left( \alpha ^I \right) \right) \;;\\ \alpha ^{N_i+1}&=\dfrac{1}{3}\alpha ^{N_i} +\dfrac{2}{3}\left( \alpha ^{II} + \varDelta t {\mathcal {F}}\left( \alpha ^{II} \right) \right) \;,\\ \end{aligned} \end{aligned}$$

where \({\mathcal {F}}(\alpha )\) is the spatial operator, and \(\alpha \) is any of the time dependant variables from Eq. (19).

In this work the time step is defined according to

$$\begin{aligned} \varDelta t = CFL \cdot \min \left( \dfrac{V_i^{1/D}}{ ||\pmb {u}_i||+ c_i } \right) . \end{aligned}$$

3.3.2 MOOD Method: A posteriori stabilization

High order reconstruction methods, such as the fourth-order MLS polynomial reconstruction employed in this method, may produce artificial oscillations in the vicinity of shocks or discontinuities of the solution. In order to avoid these non-physical oscillations, some kind of stabilization procedures must be introduced. The classic approaches for stabilization are based on artificial viscosity terms or slope limiters, that are estimated a priori. This means that the method predicts at time step n the cells/particles/elements that will become problematic in the next time step \(n+1\).

In the present work, the a posteriori paradigm is used. In particular, we use the multi-dimensional Optimal Order Detection (MOOD) limiting procedure [24, 32, 33, 43,44,45,46]. In this a posteriori method, a candidate solution is obtained by solving the system of equations using the most accurate method at disposal without any stabilization mechanism.

This candidate solution may contain NaN values or excessive numerical oscillations. In order to prevent that, some detection chains are applied to that candidate solution to identify the troubled particles.

After the MOOD detecting procedure, the fluxes are recalculated considering a lower reconstruction order for those particles which were detected. This procedure (MOOD loop) continues until all the particles of the candidate solution successfully pass the detection chain. It has been shown that the schemes built with this approach are convergent and stable, provided that the last scheme used is convergent and stable. Thus, the last scheme (termed as the parachute scheme [32]), must be convergent and stable. In our case, the parachute or base scheme is the first-order SPH-ALE method. In the present implementation of the MOOD procedure, if a particle is marked as problematic, the order of the reconstructions switches from fourth to first order.

In this work, we implemented a MOOD loop based on the method proposed in [24]. The first detector of the detection chain is the Physical Admissible Detector (PAD). The PAD ensures the positivity of the water height and of the particle volume, and also search for NaN values. The second detector is the Discrete Maximum Principle (DMP) that detects local maximum of the water elevation (\(\eta \)) as a potential numerical oscillation. Finally, the Plateau Detector (PD) relax the DMP detector by admitting oscillations under a margin of \(10^{-15}\), that is, machine truncating errors that would mistakenly trigger the DMP detector. For a comprehensive explanation of the implementation of the MOOD method in the SPH-ALE scheme, we refer the interested reader to [24].

3.3.3 Bathymetry Reconstruction

When a Lagrangian approach is considered, the location of the particles changes over time and thus, the points where the bottom bathymetry must be evaluated are different each time step. At the same time, in practical applications of the SWE, the bottom bathymetry is only known at a discrete set of points. Hence, a SWE method must consider a procedure to obtain the bathymetry at any given point inside the problem’s domain.

In order to design an algorithm able to deal with scattered bathymetry data, we propose a new procedure to reconstruct the bathymetry from a discrete set of points. We consider that the bathymetry is only known at a discrete set of points that we call bathymetry points. In our numerical tests the bathymetry points are coincident with the initial location of the fluid particles but, any other locations are also valid for the proposed algorithm. We approximate the bathymetry at any given position \(\pmb {r}_i\) inside of the problem’s domain employing \(m^{th}\)-order Taylor polynomial reconstructions, namely \(\overline{b_{p}}(\pmb {r})\) where the gradients and derivatives are computed with MLS from its closest bathymetry point \(\pmb {r}_p\)

$$\begin{aligned} b(\pmb {r}_{i})\approx \overline{b_{p}}(\pmb {r}_{i})= & {} b_{p}^0 +\sum _{j=1 }^{m-1}\varPsi _{j}\;;\\ \varPsi _{j}= & {} \dfrac{1}{j}\left( \nabla \varPsi _{j-1}\right) ^{T}\cdot \left( \pmb {r}_{p}-\pmb {r}_{i}\right) \;; \qquad \varPsi _{0}=b_{p}^0,\\ \nabla ^n b(\pmb {r}_{p})\approx & {} \nabla ^n \widehat{b_{p}^{0}}=\sum _{k=1}^{M_p} \nabla ^n \varPhi _{k}^{0}(\pmb {r}_{k})\cdot b_{k}^{0}\;; \end{aligned}$$

where \(\nabla ^n \widehat{b_{p}^0}(\pmb {r})\) are the MLS derivatives of the bathymetry at \(\pmb {r}_p\), \(b_k^0\) are the values of the bathymetry at the bathymetry points \(\pmb {r}_k\), and \(\varPhi _k^0\) are the MLS shape functions of each neighbouring bathymetry point of \(\pmb {r}_p\), \(M_p\). The \(m^{th}\)-order polynomial reconstruction of the bathymetry based on \(\pmb {r}_p\) is denoted as \(\overline{b_{p}}(\pmb {r})\). Note that we use this procedure even though in the proposed numerical examples, an analytical expression for the bathymetry is known.

Then, a MOOD procedure for the bathymetry approximation starts with a candidate bathymetry computed using a fourth-order polynomial reconstruction. Then, the DMP and PD detectors are applied to assess that the approximation is valid in terms of smoothness. If the approximation is identified as troubled by the detectors, a new candidate approximation employing a lower order MLS reconstruction is checked. This MOOD loop continues until the candidate solution successfully passes the detection chain. This MOOD procedure grants a smooth bathymetry reconstruction, compatible with the formulation presented in Sect. 2.

4 Numerical Results

This section presents the numerical results for several benchmark problems which aim to assess the accuracy and efficiency of the proposed method. These problems also aim to assess the Well Balancedness of the method for both, the high-order reconstruction scheme and also the first-order base scheme. Thus, in the following test cases we are employing and comparing the performance of the proposed method, labelled as SPH-ALE-MOOD, with the first-order SPH-ALE scheme which is labelled as the Base scheme.

A Lagrangian approach and homogeneous boundary conditions are used for the proposed test cases, unless indicated in the text. The boundary conditions in this work were implemented using the mirroring ghost particles procedure, as in [47, 48].

4.1 Convergence Test: Steady Subcritical Flow Over a Bump

In this test the order of convergence of our scheme is checked for a smooth solution. This test case presents a steady subcritical flow over a bump with a smooth bathymetry and it is commonly use to analyze the accuracy and convergence of the numerical methods [30, 49, 53]. The bathymetry is given by

$$\begin{aligned} b(x)= 0.2 \;exp{\left( -0.16(x-10)^2 \right) }\;, \quad x\in [0,20]\;. \end{aligned}$$

Considering a steady state, we can obtain the analytical solution of the problem as

$$\begin{aligned} {\left\{ \begin{array}{ll} hu=q_c\\ \dfrac{q_c^2}{2h^2}+g(h+b)=E_o\\ \end{array}\right. }\;;\qquad E_o= \dfrac{q_c^2}{2h_o^2}+g\,h_o\;. \end{aligned}$$

As initial conditions, all the particles are started with \(\eta =2\) and \(hu=q_c =4.42\). On the left boundary (inlet), a null Neumann boundary condition is imposed for the water height h, while a Dirichlet boundary condition (\(hu=q_c=4.42\)) is imposed for the discharge. On the right boundary (outlet), null Neumann is imposed to the discharge, while a Dirichlet boundary condition (\(h_o=2\)) is imposed on the water height.

This problem was computed until convergence with different refinements, using a SPH-ALE scheme with fourth-order MLS reconstructions.

Table 1 Convergence test
Full size table

In table 1, the \(L^2-norm\) of h and u and the obtained order of convergence are presented for several particle discretizations. In the first set of particles, until 160, tends to fourth-order convergence, but after it decays to the expected second-order [17]. This behaviour is due the fourth-order reconstruction of the variables and the second-order spatial integration of the scheme.

4.2 Lake at Rest Test Cases

This set of cases is widely used to test the well balancedness of numerical methods [1, 29, 50]. These problems test the ability of the schemes to preserve the water at rest solution (null velocity and constant water surface elevation) over time for an arbitrary bottom bathymetry .

In the following test cases, the proposed method is compared with an SPH-ALE method with a non-well balanced discretization of its source term. This non-WB source term is discretized as

$$\begin{aligned} \begin{aligned} S_{2}^{NonWB}&=-g h_i\sum _{j=1}^{N_i}\left( b_{ij}^+ + b_{ij}^- -2b_{i}\right) \;V_{j}\dfrac{\partial W_{ij}}{\partial x}\;;\\ S_{3}^{NonWB}&=-g h_i\sum _{j=1}^{N_i}\left( b_{ij}^+ + b_{ij}^- -2b_{i}\right) \;V_{j}\dfrac{\partial W_{ij}}{\partial y}\;. \end{aligned} \end{aligned}$$

4.2.1 1D Lake at Rest Test Cases

In this first test case, we tested two different bottom bathymetries. The first bathymetry \(b_1(x)\), consists of a single bump [1, 29, 51, 52]. The second bottom bathymetry \(b_2(x)\), is more complex and considers a variable ground elevation [53].

The two bottom bathymetries are defined as follows:

$$\begin{aligned} b_1(x)= & {} {\left\{ \begin{array}{ll} 0.25 \left[ 1+ \cos ( 10 \pi (x-0.5) ) \right] , \quad &{}\text {if } \, 0.4\le x \le 0.6 \\ 0, \quad &{}\text {otherwise} \\ \end{array}\right. }; \quad \varOmega _1:x\in [0,1]. \end{aligned}$$
(20)
$$\begin{aligned} b_2(x)= & {} \dfrac{1}{20}\Big ( 10 \exp (-x^2)+ 15 \exp (-(x-2.5)^2) +10 \exp (-0.5(x-5)^2)\nonumber \\&+ 6 \exp (-2(x-7.5)^2) + 16 \exp (-(x-10)^2) \Big ); \nonumber \\&\text {for:} \;\varOmega _2:x\in [0,10]. \end{aligned}$$
(21)

For these cases, 200 particles were equally distributed throughout the computational domain. All of the particles were given the same water surface elevation \(\eta =1\) and null velocity as initial conditions. The CFL number was set to \(CFL=0.9\).

The results of the two bathymetries test cases for \(T=1\) are shown in Figs. 4 and 5 . As it is shown in the mentioned figures, the non-well-balanced methods introduce artificial perturbations. The high order non-well-balanced method reduce the magnitude of the oscillations, but it still fails to obtain an exact flat surface. The proposed well-balanced SPH-ALE method is able to preserve the stationary static solution over time for both, the high-order and the base schemes, keeping the relative error of water surface elevation at the order of \(10^{-16}\), which is at the level of the machine precision.

Fig. 4
figure 4

Water surface elevation and bottom bathymetry of the Lake at rest over a single bump (bathymetry \(b_1\)) for the base scheme and the SPH-ALE-MOOD method at \(T=1\). Top row: General view. Bottom row: Close up view of the difference between the numerical results and the exact water elevation \(\eta _{exact}=1\). Left column: Non-Well-balanced methods. Right column: Well-balanced methods

Full size image
Fig. 5
figure 5

Water surface elevation and bottom bathymetry of the Lake at rest over a variable bathymetry (bathymetry \(b_2\)) for the base scheme and the SPH-ALE-MOOD methods at \(T=1\). Top row: General view. Bottom row: Close up view of the difference between the numerical results and the exact water elevation \(\eta _{exact}=1\). Left column: Non-Well-balanced methods. Right column: Well-balanced methods

Full size image

4.2.2 2D Lake at Rest Over a Bump

We consider a test case that takes the lake at rest conditions for a 2D domain. This test case involves a circular domain with a radius of \(R=45\) discretized with 60429 scattered particles. All particles were initialized with lake at rest conditions with \(\eta =1\). The CFL number was set to \(CFL=0.9\). The bottom bathymetry is defined as follows:

$$\begin{aligned} b(r)={\left\{ \begin{array}{ll} 0.25 \left[ 1+ \cos \left( \dfrac{\pi r}{9} \right) \right] , \quad &{}\text {if } \, r \le 9 \\ 0, \quad &{}\text {otherwise} \\ \end{array}\right. } ; \quad r= \sqrt{x^2 + y^2}\;. \end{aligned}$$
(22)

We run the simulation until a final time of \(T=1\). Figure 6 shows that the proposed method is able to preserve the stationary static solution over time for both, the base scheme and the SPH-ALE-MOOD methods. Note that all the particles are represented in the figure. The relative error of water surface elevation is of the order of \(10^{-16}\).

Fig. 6
figure 6

2D Lake at rest over a bump test case for \(T=1\). Water surface elevation and bottom bed for the base scheme and the SPH-ALE-MOOD methods. a 3D view. b Radial representation of the water surface elevation and bathymetry of all the fluid particles. The horizontal axis represents the radial distance of each particle to the center of the domain. c Difference between exact water surface elevation and the result of the proposed methods. The horizontal axis represents the radial distance of each particle to the center of the domain

Full size image

4.3 Propagation of Small Water Surface Perturbations on Water at Rest Cases

The goal of these problems is to asses the Well Balancedness of the presented method when a small water perturbation is present on the water at rest initial conditions.

We consider initial null velocity and constant water surface elevation for all the particles, except in a subregion of the domain, in which a small perturbation is added to the water surface as initial conditions.

The setup of the following test cases were taken from [1]. These test cases have been widely used by other researchers to test different mesh-based numerical methods, in 1D [6, 49, 54] and in 2D [6, 12, 54, 55]. For SPH methods, these test cases have been used in [29, 31]. A \(CFL=0.15\) was employed in these cases.

4.3.1 Propagation of Small Water Surface Perturbations on 1D Lake at Rest Cases

In this test case, we consider a domain \(\varOmega : x\in [0,1]\) . The bottom bathymetry is

$$\begin{aligned} b(x)={\left\{ \begin{array}{ll} 0.25 \left[ 1+ \cos ( 10 \pi (x-0.5) ) \right] , \quad &{}\text {if } \, 0.4\le x \le 0.6 \\ 0, \quad &{}\text {otherwise} \\ \end{array}\right. }. \end{aligned}$$
(23)

Throughout the problem’s domain, we set 200 particles with null velocity and the following water height

$$\begin{aligned} h(x)={\left\{ \begin{array}{ll} \left( 1-b(x)\right) +\varepsilon , \quad &{}\text {if } \, 0.1\le x \le 0.2 \\ 1-b(x) , \quad &{}\text {otherwise} \\ \end{array}\right. }. \end{aligned}$$
(24)

Two different cases were considered, imposing different initial perturbations: (a) \(\varepsilon =0.2\) and (b) \(\varepsilon =0.01\). The numerical results and the reference solution for both initial perturbations at time \(T=0.7\) are presented in Fig. 7.

Fig. 7
figure 7

water surface elevation of the propagation of a small perturbation on water at rest. Results for the base scheme and the SPH-ALE-MOOD methods for \(T=0.7\). Left: Initial water surface perturbation of \(\varepsilon =0.2\), right: initial water surface perturbation of \(\varepsilon =0.01\). The results of Xia et al. have been digitized from [29]

Full size image

In Fig. 7 our results are compared with a reference solution obtained by LeVeque [1] employing a finite volume method with a very fine grid. For the small perturbation case, we also plot the results obtained in [29] using a well-balanced SPH scheme with 400 particles. Neither of the proposed methods show any artificial perturbation due to the bathymetry bump, in consonance with the well-balanced behaviour of the schemes. The SPH-ALE-MOOD method obtains a very accurate representation of the solution. It is also important to remark that the MOOD method is employing two different reconstruction orders in different particles simultaneously (fourth-order reconstruction in non-troubled cells and first-order reconstruction in troubled cells) throughout the domain. Despite this, the method is able to keep the well-balanced behaviour. For the small perturbation case, we note that the result of the proposed SPH-ALE-MOOD method is comparable to that of [29], using half of the particles.

4.3.2 Propagation of Small Water Surface Perturbations on 2D Lake at Rest Case

In this test case, we consider a rectangular domain \(\varOmega :(x,y)\in [0,2]\times [0,1]\) and the bottom bathymetry reads as

$$\begin{aligned} b(x,y)= 0.8 \exp (-5(x- 0.9)^2 - 50(y-0.5)^2). \end{aligned}$$
(25)

The computational domain is discretized with an equally distributed set of \(200\times 100\) particles, with initial null velocity and the water height defined as

$$\begin{aligned} h(x,y)={\left\{ \begin{array}{ll} \left( 1-b(x,y)\right) +\varepsilon , \quad &{}\text {if } \, 0.05\le x \le 0.15 \\ 1-b(x,y) , \quad &{}\text {otherwise} \\ \end{array}\right. } ; \quad \varepsilon = 0.01\;. \end{aligned}$$
(26)

The numerical results for \(T=0.6\), \(T=1.2\) and \(T=1.8\) are presented in Fig. 8 both for the SPH-ALE Base scheme and for the SPH-ALE-MOOD methods. In Fig. 9 a 3D view of the results from the SPH-ALE-MOOD method are shown.

Fig. 8
figure 8

Elevation of the water surface at the propagation of a small perturbation through water at rest in 2D. From top to bottom, we present the results at \(T=0.0\), \(T=0.6\), \(T=1.2\) and \(T=1.8\). Left: SPH-ALE Base scheme. Right: SPH-ALE-MOOD method

Full size image
Fig. 9
figure 9

3D view of the elevation of the water surface and bathymetry at the propagation of a small perturbation through water at rest in 2D. The represented vertical scale of \(\eta \) is augmented 20 times the bathymetry’s vertical scale. Results from the SPH-ALE-MOOD method for different times: a \(T=0.0\), b \(T=0.6\), c \(T=1.2\) and d \(T=1.8\)

Full size image

Figures 8 and 9 show the results obtained using the base scheme and the SPH-ALE-MOOD methods. We notice that both methods obtains a solution free of spurious oscillations, showing the well-balanced character of the proposed schemes. Moreover, the proposed SPH-ALE-MOOD method obtains a very accurate solution, which is comparable to those obtained in the literature [29, 55].

4.4 Moving Fluid with Height Discontinuity over Constant Bed Slope

This academic numerical test was set to check the performance of the proposed method in an extreme situation when water height discontinuities, fluid velocity and, non-flat bathymetry are present at the same time. Here, we examine if the scheme preserves the well-balance property when shocks, contact discontinuities and, rarefactions are present in the solution. This test case was first proposed in [57] as a modified version of a test from [56]. The initial conditions are defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} h_l=1.3, \quad u_l=-2.0, \quad &{}\text {if } \, x \le 0.5 \\ h_r=0.1, \quad u_r=-2.0, \quad &{}\text {if } \, x >0.5 \\ \end{array}\right. }. \end{aligned}$$

The bottom bathymetry is given by

$$\begin{aligned} b(x)= 0.4-0.4x, \quad x \in [0,1]. \end{aligned}$$

The discretization is performed using 240 particles, initially distributed in an extended domain \(\varOmega _0:x\in [0,1.2]\). We did this in order to get 200 particles on the computational domain (\(\varOmega :x\in [0,1]\)) at the final computing time \(T=0.1\), as it is shown in Fig. 10.The CFL number was set to \(CFL=0.6\). In Fig. 10 the results of this problem are shown for the SPH-ALE-MOOD method compared to reference solution from [57]. It is observed that the proposed method captures accurately the position of the shock. The MOOD procedure is able to prevent the appearance of non-physical oscillations at the surroundings of the shock.

Fig. 10
figure 10

Numerical test: Moving fluid with height discontinuity over constant bed slope at \(T=0.1\). SPH-ALE-MOOD method and reference solution [57]. Left: Elevation of water surface \(\eta \) and bottom bathymetry. Right: u velocity

Full size image

4.5 2D Circular Dam Break on Flat Bathymetry

Dam break tests are a classic way to test the accuracy of SWE methods and specially, their ability to correctly solve problems with discontinuities and shock waves. This test case was introduced in [58] and has been used in many different works since then, i.e. [12, 59, 60]. This problem considers a squared domain \([-25,25]\times [-25,25]\) in which we distribute 40090 particles with an scattered disposition. All of the particles were initialized with null velocity, null bottom bathymetry, and the following water height as initial condition:

$$\begin{aligned} h(r)={\left\{ \begin{array}{ll} 10, \quad &{}\text {if } \, r \le 11 \\ 1, \quad &{}\text {otherwise} \\ \end{array}\right. } ; \quad r= \sqrt{x^2 + y^2}\;. \end{aligned}$$
(27)

The final results for different times are shown in Figs. 11 and 12 . The CFL number was set to \(CFL=0.90\).

In Fig. 11 the results obtained with the SPH-ALE Base scheme and SPH-ALE-MOOD methods for \(T=0.69\) are compared with \([100 \times 100]\) FV-HLLC first-order and second-order-MUSCL reference solutions from [60], respectively. We can see that the SPH-ALE-MOOD method’s results agree well with the HLLC-MUSCL FV method reference solution. In Fig. 12, the 3D view of the water surface elevation obtained with the SPH-ALE-MOOD method for six different times \(T= 0.0,0.2,0.4,0.6,0.8,1.0 \) is shown.

Fig. 11
figure 11

2D circular dam break problem over a flat bathymetry: Elevation of water surface for \(T =0.69\) of the particles contained in the cut \([-25,25]\times [-1,1]\) of the domain. Left: SPH-ALE Base scheme method compared with a FV-HLLC first order method [60]. Right: SPH-ALE-MOOD method compared with a FV-HLLC MUSCL method. [60]

Full size image
Fig. 12
figure 12

2D circular dam break problem with over a flat bathymetry: 3D view of the elevation of water surface for the SPH-ALE-MOOD method. a Initial condition. b Solution for \(T=0.2\). c Solution for \(T=0.4\). d Solution for \(T=0.6\). e Solution for \(T=0.8\). f Solution for \(T=1.0\)

Full size image

4.6 2D Circular Dam Break Problem on a Non-Flat Bed

This 2D dam break benchmark problem was firstly introduced in [61], and it was later reproduced in different SWE works such as [12, 59, 62]. This test case considers a \([0,2]\times [0,2]\) domain in which \(201\times 201\) particles are equally distributed along both axis. All of the particles were given null velocity and the following water surface elevation as initial condition:

$$\begin{aligned} \eta (x,y)={\left\{ \begin{array}{ll} 1.1, \quad &{}\text {if } \, (x-1.25)^2 + (y-1)^2 \le 0.01 \\ 0.6, \quad &{}\text {otherwise} \\ \end{array}\right. }. \end{aligned}$$

And the bathymetry is given by:

$$\begin{aligned} b(x,y)={\left\{ \begin{array}{ll} b_{1}(x,y), \quad &{}\text {if } \, (x-1.5)^2 + (y-1)^2 \le 0.25 \\ 0, \quad &{}\text {otherwise} \\ \end{array}\right. }, \end{aligned}$$

with:

$$\begin{aligned} b_{1}(x,y)=\dfrac{1}{8}\left[ 1+\cos \left( 2 \pi (x-0.5) \right) \right] \left[ 1+\cos \left( 2 \pi y \right) \right] \;. \end{aligned}$$

The initial condition and the results for \(T=0.05\), \(T=0.1\) and \(T=0.15\) from the SPH-ALE-MOOD method are shown in Figs. 13 and 14 . The CFL number was set to \(CFL=0.6\). Solid wall boundary conditions were considered at the \(y=0\) and \(y=2\) contours, as null Neumann boundary conditions were considered at the \(x=0\) and \(x=2\) contours.

The results obtained with the SPH-ALE-MOOD method are compared in Fig. 13 with a reference solution (fourth-order FV \(800\times 800\) grid method) digitized from [59]. We see that the presented method provides accurate solutions, specially at detecting the position and strength of the shock wave.

Fig. 13
figure 13

2D circular dam break problem on a non-flat bed: Elevation of water surface of points at \(y=1\). Results from the SPH-ALE-MOOD method. The reference solution is obtained by a fourth-order FV method using a \(800\times 800\) grid and it was digitized from [59]. a General view of initial conditions. b Close up of solution at \(T = 0.05\). c Close up of solution at \(T = 0.10\). d) Close up of solution at \(T = 0.15\)

Full size image
Fig. 14
figure 14

2D circular dam break problem on a non-flat bed: Cut at \(y=1\) of 3D view of the elevation of water surface and bathymetry. Results from SPH-ALE-MOOD method. a Solution at \(T = 0\). b Solution at \(T = 0.05\). c Solution at \(T = 0.10\). d Solution at \(T = 0.15\)

Full size image

4.7 Steady Flow Over a Bump Test Cases

The following cases were first proposed by Goutal and Maurel in [51] and, since then, they have become classic benchmark test problems to test the behaviour of new numerical schemes for the SWE [3, 6, 30, 63].

For this test case we consider a purely Eulerian approach, using 200 particles which are equally distributed in the domain \(\varOmega : x\in [0,25]\). The gravity acceleration is \(g=9.812\). The CFL number was set to \(CFL=0.9\). The bathymetry of the problems is defined as follows

$$\begin{aligned} b(x)={\left\{ \begin{array}{ll} 0.2-0.05(x-10)^2, \quad &{}\text {if } \, 8\le x \le 12 \\ 0, \quad &{}\text {otherwise} \\ \end{array}\right. }. \end{aligned}$$
(28)

We consider three different flow cases using the same bottom bathymetry: A subcritical flow (SF), a Transcritical flow without a shock (TF), and a Transcritical flow with a shock(TFsh). The Dirichlet boundary conditions and initial conditions for each of the three different flow cases are shown in Table 2. Note that the boundary conditions that are not determined in the table for the inlet and the outlet are considered as null Neumann boundary conditions.

Table 2 Boundary and initial conditions for the three different cases of Steady flow over a bump. Subcritical flow (SF), Transcritical flow without a shock (TF), and Transcritical flow with a shock (TFsh). * : when the flow is subcritical
Full size table

The subcritical flow case (SF) remains in the subcritical regime all along the problem’s domain. However, in the steady solution of the transcritical flow without a shock case (TF) the flow regime changes from subcritical at the inlet, to supercritical downstream the bump. In the steady solution of the transcritical flow with a shock (TFsh), the flow regime changes from subcritical at the inlet, to supercritical downstream the bump and then abruptly changes again into subcritical thorugh a shock wave.

The results of the calculations are presented in Fig. 15. As we can see, the presented SPH-ALE-MOOD method obtains solutions in very close agreement with the analytical solution. The method is able to reach and preserve the steady state solution over time. No artificial perturbations due to the bottom bathymetry are observed, in consonance with the well balanced behaviour of the proposed scheme. The presented solutions are comparable to those obtained using mesh-based methods [2, 3, 6, 53, 55] or SPH methods like [30].

Fig. 15
figure 15

Steady flow over a bump. water surface elevation for subcritical flow at \(T=40\) (left), transcritical flow without a shock at \(T=25\) (center) and transcritical flow with a shock at \(T=60\) (right)

Full size image

5 Conclusions

A new well balanced SPH-ALE-MOOD scheme to solve the SWE is presented in this work. The presented numerical method is accurate and provides well-balanced solutions. The well-balanced behavior is obtained through a new discretization of the source term. The proposed discretization of the source term is able to exactly cancel the contribution of the flux gradient for water at rest conditions.

A series of 1D and 2D benchmark problems were considered to assess the performance of the proposed method. It is shown that the proposed methodology is able to solve the SWE with variable bottom bathymetry and discontinuities in the solution. Moreover, the ALE formulation allows to consider Lagrangian and Eulerian approaches to solve the SWE, and provides high-accurate, well-balanced and robust solutions for both purely Eulerian and Lagrangian approaches. The MOOD limiting procedure is able to prevent artificial oscillations in the vicinity of discontinuities and shocks, preserving the well-balanced behaviour of the proposed scheme.