Abstract
We present a new rank-adaptive tensor method to compute the numerical solution of high-dimensional nonlinear PDEs. The method combines functional tensor train (FTT) series expansions, operator splitting time integration, and a new rank-adaptive algorithm based on a thresholding criterion that limits the component of the PDE velocity vector normal to the FTT tensor manifold. This yields a scheme that can add or remove tensor modes adaptively from the PDE solution as time integration proceeds. The new method is designed to improve computational efficiency, accuracy and robustness in numerical integration of high-dimensional problems. In particular, it overcomes well-known computational challenges associated with dynamic tensor integration, including low-rank modeling errors and the need to invert covariance matrices of tensor cores at each time step. Numerical applications are presented and discussed for linear and nonlinear advection problems in two dimensions, and for a four-dimensional Fokker–Planck equation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
High-dimensional partial differential equations (PDEs) arise in many areas of engineering, physical sciences and mathematics. Classical examples are equations involving probability density functions (PDFs) such as the Fokker–Planck equation [49], the Liouville equation [13, 14, 58], and the Boltzmann equation [8, 11, 18]. More recently, high-dimensional PDEs have also become central to many new areas of application such as optimal mass transport [27, 59], random dynamical systems [57, 58], mean field games [19, 52], and functional-differential equations [55, 56]. Computing the numerical solution to high-dimensional PDEs is an extremely challenging problem which has attracted substantial research efforts in recent years. Techniques such as sparse collocation methods [4, 9, 12, 25, 41], high-dimensional model representations [3, 10, 37], deep neural networks [46, 47, 60], and numerical tensor methods [2, 7, 28, 31, 33, 51] were proposed to mitigate the exponential growth of the degrees of freedom, the computational cost and the memory requirements.
In this paper, we build upon our recent work on dynamical tensor approximation [16, 17], and develop new rank-adaptive temporal integrators to compute the numerical solution of high-dimensional initial/boundary value problems of the form
where \(\varvec{x}\in \Omega \subseteq \mathbb {R}^d\) (\(\Omega \) compact, \(d\ge 1\)), and G is a nonlinear operator which may take into account boundary conditions. A well-known challenge of dynamic tensor approximations to (1) is that the curvature of the tensor manifold in which we compute the PDE solution is inversely proportional to the energy of the tensor modes. This means that the smaller the energy of the tensor modes the higher the curvature. Hence, to integrate a solution characterized by tensor modes with a wide range of energies one has to consider time stepping schemes that can effectively handle geometric features associated with the curvature of the manifold. In projection-based approaches [16, 17, 34, 43] the computational challenge posed by the curvature of the tensor manifold translates into the need to invert the positive semi-definite covariance matrices of the tensor cores at each time step. A time-integration scheme constructed in this way may become numerically unstable in the presence of tensor modes with small energy, or even singular when modes with zero energy are present (e.g., at a time instant in which we increase the tensor rank by adding a mode with zero energy). To mitigate this problem, Babaee et al. [1] introduced a matrix pseudo-inverse approximation method that can handle potential singularities in the covariance matrices of the tensor cores, in particular when adding modes with zero energy to the tensor series expansion of the PDE solution.
A mathematically rigorous framework to integrate dynamical tensors over manifolds with arbitrary curvature was developed by Lubich et al. in [32, 38, 39]. The key idea is to integrate the evolution equation generating the tensor dynamics using operator splitting schemes, e.g., the Lie–Trotter or the Strang time integrators (see [32, 39] for details). This results in a scheme that does not suffer from the curvature of the tensor manifold, and even provides an exact representation in the presence of tensor modes with zero energy. The numerical method presented in this work combines all these features, i.e., functional tensor train (FTT) series expansions, operator splitting time integration, and a new rank-adaptive algorithm to add and remove tensor modes from the PDE solution based on a thresholding criterion that limits the component of the velocity vector normal to the FTT tensor manifold.
This paper is organized as follows. In Sect. 2 we briefly review finite-rank functional tensor train (FTT) expansions of high-dimensional functions. In Sect. 3 we discuss dynamic tensor approximation of nonlinear PDEs of the form (1) and develop robust temporal integration schemes based on operator splitting methods. We also discuss step-truncation algorithms [50, 51] and prove that dynamic tensor approximation and step-truncation are at least order one consistent to one another. In Sect. 4 we develop new rank-adaptive time integrators on rank-structured FTT tensor manifolds and prove that the resulting scheme is consistent. In Sect. 5 we present and discuss various numerical applications of the proposed rank-adaptive tensor method, and demonstrate its accuracy and computational efficiency. The main findings are summarized in Sect. 6.
2 The Manifold of Fixed-Rank FTT Tensors
Let us consider the weighted Hilbert spaceFootnote 1
where \(\Omega \subseteq \mathbb {R}^d\) is a separable domain such as a d-dimensional flat torus \(\mathbb {T}^d\) or a Cartesian product of d real intervals \(\Omega _i=[a_i,b_i]\)

and \(\mu \) is a finite product measure on \(\Omega \)
Let \(\tau \) be the counting measure on \(\mathbb {N}\). Each element \(u \in L^2_{\mu }(\Omega )\) admits a functional tensor train (FTT) expansion of the form
where \(\{\psi _i(\alpha _{i-1};x_i;\alpha _i)\}_{\alpha _{i}}\) is an orthonormal basis for the space \(L^2_{\tau \times \mu _i}(\mathbb {N} \times \Omega _i)\). It can be shown that \(\psi _i(\alpha _{i-1};x_i;\alpha _i)\) are eigenfunctions for a self-adjoint compact operator and \( \lambda (1)\ge \lambda (2) \ge \cdots \ge 0\) is a sequence of real numbers converging to zero (see [6, 17] for more details). By truncating (5) so that only the largest singular values are retained, we obtain the approximation of \(u(\varvec{x})\)
where \(\varvec{r} = (r_0, r_1, \ldots , r_{d-1}, r_d)\) is the FTT rank. It is convenient to write (6) in a more compact form as
where \({\varvec{\Psi }}_i(x_i)\) is a \(r_{i-1} \times r_i\) matrix with entries \(\left[ {\varvec{\Psi }}_i(x_i)\right] _{j k} = \psi _i(j;x_i;k)\) and \({\varvec{\Lambda }}\) is a diagonal matrix with entries \(\lambda (\alpha _{d-1})\) (\(\alpha _{d-1}=1,\ldots ,r_{d-1}\)). The matrix-valued functions \({\varvec{\Psi }}_i(x_i)\) will be referred to as FTT cores, and we denote by \(M_{r_{i-1} \times r_i}(L_{\mu _i}^2(\Omega _i))\) the set of all \(r_{i-1} \times r_i\) matrices with entries in \(L_{\mu _{i-1}}^2(\Omega _i)\). To simplify notation even more, we will often suppress explicit tensor core dependence on the spatial variable \(x_i\), allowing us to simply write \({\varvec{\Psi }}_i={\varvec{\Psi }}_i(x_i)\) and \(\psi _i(\alpha _{i-1},\alpha _i)=\psi _i(\alpha _{i-1};x_i;\alpha _i)\) as the spatial dependence is indicated by the tensor core subscript.
2.1 Orthogonalization and Truncation of FTT Tensors
For any tensor core \({\varvec{\Psi }}_i \in M_{r_{i-1} \times r_i} (L_{\mu _i}^2(\Omega _i))\) we define the matrix
with entriesFootnote 2
The FTT representation (7) is given in terms of FTT cores \({\varvec{\Psi }}_i\) satisfyingFootnote 3
Other orthogonal representations can be computed, e.g., based on recursive QR decompositions. To describe different orthogonalizations of FTT tensors, let \({\varvec{\Psi }}_i \in M_{r_{i-1} \times r_i} (L^2_{\mu _i}(\Omega _i))\) and consider each column of \({\varvec{\Psi }}_i\) as a vector in  . Performing an orthogonalization process (e.g. Gram–Schmidt) on the columns of the FTT core \({\varvec{\Psi }}_i\) relative to the inner product (8) yields a QR-type decomposition of the form
. Performing an orthogonalization process (e.g. Gram–Schmidt) on the columns of the FTT core \({\varvec{\Psi }}_i\) relative to the inner product (8) yields a QR-type decomposition of the form
Where \(\varvec{Q}_i\) is an \(r_{i-1} \times r_i\) matrix with elements in \(L^2_{\mu _i}(\Omega _i)\) satisfying \(\left\langle \varvec{Q}_i^{\text {T}}\varvec{Q}_i \right\rangle _i = \varvec{I}_{r_{i} \times r_i}\), and \(\varvec{R}_i\) is an upper triangular \(r_i \times r_i\) matrix with real entries. Next consider an arbitrary FTT tensor \({u_{\varvec{r}}} = {\varvec{\Psi }}_1 {\varvec{\Psi }}_2 \cdots {\varvec{\Psi }}_d\), where the matrix \(\langle \varvec{\Psi }_i^{\text {T}} {\varvec{\Psi }}_i \rangle _i\) may be singular. For notational convenience, we define the partial products
One way to orthogonalize \({u_{\varvec{r}}}\) is by performing QR decompositions recursively from left to right as we will now describe. Begin by decomposing \({\varvec{\Psi }}_1\) as
Now we may write \({u_{\varvec{r}}} = \varvec{Q}_1 \varvec{R}_1 {\varvec{\Psi }}_2 \cdots {\varvec{\Psi }}_d\). Next, perform another QR decomposition
Proceeding recursively in this way we obtain a representation for \({u_{\varvec{r}}}\) of the form
where each \(\varvec{Q}_i \in M_{r_{i-1} \times r_i}(L^2_{\mu _i}(\Omega _i))\) satisfies \(\left\langle \varvec{Q}_i^{\text {T}} \varvec{Q}_i\right\rangle _{i} = \varvec{I}_{r_i \times r_i}\). We refer to such a representation as a left orthogonalization of \({u_{\varvec{r}}}\). We may stop orthogonolizing at any step in the recursive process to obtain the partial left orthogonalization
Similar to orthogonalizing from the left, we may also orthogonalize \({u_{\varvec{r}}}\) from the right. To do so, begin by performing a QR decomposition
A substitution of (17) into (7) yields the expansion \(u_{\varvec{r}} = {\varvec{\Psi }}_1 \cdots {\varvec{\Psi }}_{d-1} \varvec{W}_d^{\text {T}} \varvec{K}_d^{\text {T}}\). Next perform a QR decomposition
Proceeding recusively in this way we obtain the right orthogonalization
We may have stopped the orthogonalization process at any point to obtain the partial right orthogonalization
It is also useful to orthogonalize from the left and right to obtain expansions of the form
where the rank of the matrix \(\varvec{R}_i \varvec{W}_{i+1}^{\text {T}}\) is the i-th component of the true FTT rank of the tensor \({u_{\varvec{r}}}\).
Another important operation is truncation of FTT tensors to smaller rank. Efficient algorithms to perform this operation for TT tensors can be found in [44, section 3] and in [15]. Such algorithms are easily adapted to FTT tensors by replacing QR decompositions of matrices with the QR of FTT cores given in (11) and SVD decomposition of matrices with Schmidt decompositions. In numerical implementations, this adaptation amounts to introducing appropriate quadrature weight matrices into the algorithms.
2.2 Tangent and Normal Spaces of Fixed-Rank FTT Manifolds
Let us denote by \(V_{r_{i-1} \times r_i}^{(i)}\) the set of all tensor cores \({\varvec{\Psi }}_i \in M_{r_{i-1} \times r_{i}}(L^2_{\mu _i}(\Omega _i))\) with the property that the autocovariance matrices \(\left\langle {\varvec{\Psi }}_i^{\text {T}}{\varvec{\Psi }}_i \right\rangle _{i} \in M_{r_i \times r_i}(\mathbb {R})\) and \(\left\langle {\varvec{\Psi }}_i{\varvec{\Psi }}_i^{\text {T}} \right\rangle _{i} \in M_{r_{i-1} \times r_{i-1}}(\mathbb {R})\) are invertible for \(i =1,\ldots ,d\). The set
consisting of fixed-rank FTT tensors, is a smooth Hilbert submanifold of \(L^2_{\mu }(\Omega )\) (see [17]). We represent elements in the tangent space, \({T_{u_{\varvec{r}}} \mathcal {M}_{\varvec{r}}}\), of \(\mathcal {M}_{\varvec{r}}\) at the point \({u_{\varvec{r}}} \in \mathcal {M}_{\varvec{r}}\) as equivalence classes of velocities of continuously differentiable curves on \(\mathcal {M}_{\varvec{r}}\) passing through \({u_{\varvec{r}}}\)
Sketch of the tensor manifold \(\mathcal {M}_{\varvec{r}}\) and the tangent space \(T_{{u_{\varvec{r}}}}\mathcal {M}_{\varvec{r}}\) at \({u_{\varvec{r}}} \in \mathcal {M}_{\varvec{r}}\). The tangent space is defined as equivalence classes of velocities of continuously differentiable curves \(\gamma (s)\) on \(\mathcal {M}_{\varvec{r}}\) passing through \({u_{\varvec{r}}}\)
A sketch of \(\mathcal {M}_{\varvec{r}}\) and \(T_{{u_{\varvec{r}}}}\mathcal {M}_{\varvec{r}}\) is provided in Fig. 1. Since \(L^2_{\mu }(\Omega )\) is an inner product space, for each \(u \in L^2_{\mu }(\Omega )\) the tangent space \(T_u L^2_{\mu }(\Omega )\) is canonically isomorphic to \(L^2_{\mu }(\Omega )\). Moreover, for each \({u_{\varvec{r}}} \in \mathcal {M}_{\varvec{r}}\) the normal space to \(\mathcal {M}_{\varvec{r}}\) at the point \({u_{\varvec{r}}}\), denoted by \({N}_{{u_{\varvec{r}}}} \mathcal {M}_{\varvec{r}}\), consists of all vectors in \(L^2_{\mu }(\Omega )\) that are orthogonal to \(T_{{u_{\varvec{r}}}} \mathcal {M}_{\varvec{r}}\) with respect to the inner product in \(L^2_{\mu }(\Omega )\)
Since the tangent space \(T_{{u_{\varvec{r}}}} \mathcal {M}_{\varvec{r}}\) is closed, for each point \({u_{\varvec{r}}} \in \mathcal {M}_{\varvec{r}}\) the space \(L^2_{\mu }(\Omega )\) admits a decomposition into tangential and normal components
3 Dynamic Tensor Approximation of Nonlinear PDEs
The idea of dynamic tensor approximation is to project the time derivative of a low-rank tensor onto the tangent space of the corresponding low-rank tensor manifold at each time. Such a projection results in evolution equations on the low-rank tensor manifold, and can be used to solve initial/boundary value problem of the form (1). This approximation technique is known in the quantum physics community as Dirac–Frenkel/Mclachlan variational principle [26, 40, 45]. Dynamic approximation has been recently studied by Lubich et al. [34, 35, 38, 43] for finite-dimensional rank-structured manifolds embedded in Euclidean spaces. There have also been extensions to the Tucker format on tensor Banach spaces [21] and tree-based tensor formats on tensor Banach spaces [22].
3.1 Dynamic Tensor Approximation on Low-Rank FTT Manifolds
Let us briefly describe the method of dynamic tensor approximation for the low-rank FTT manifold (22). First we define a projection onto the tangent space of \(\mathcal {M}_{\varvec{r}}\) at \({u_{\varvec{r}}}\) by
For fixed \({u_{\varvec{r}}}\), the map \(P_{{u_{\varvec{r}}}}\) is linear and bounded. Each \(v \in {L^2_{\mu }(\Omega )}\) admits a unique representation as \(v = v_t + v_n\) where \(v_t \in T_{{u_{\varvec{r}}}} \mathcal {M}_{\varvec{r}}\) and \(v_n \in N_{{u_{\varvec{r}}}} \mathcal {M}_{\varvec{r}}\) (see Eq. 25). From this representation it is clear that \(P_{{u_{\varvec{r}}}}\) is an orthogonal projection onto the tangent space \(T_{{u_{\varvec{r}}}} \mathcal {M}_{\varvec{r}}\). If the initial condition \({u_0(\varvec{x})}\) is on the manifold \(\mathcal {M}_{\varvec{r}}\), then the solution to the initial/boundary value problem
remains on the manifold \(\mathcal {M}_{\varvec{r}}\) for all \(t \ge 0\). Here G is the nonlinear operator on the right hand side of equation (1). The solution to (27) is known as a dynamic approximation to the solution of (1). In the context of separable Hilbert spaces, the dynamic approximation problem (27) can be solved using dynamically orthogonal or bi-orthogonal constraints on tensor modes [16, 17]. Such constraints, also referred to as gauge conditions, provide the unique solution of the minimization problem (26) with different FTT cores. However, in the presence of repeated eigenvalues the bi-orthogonal constraints result in singular equations for the tangent space projection (26). Hereafter we recall the equations which allow us to compute (26) with FTT cores subject to dynamically orthogonal (DO) constraints.
First, expand \({u_{\varvec{r}}} \in \mathcal {M}_{\varvec{r}}\) in terms of FTT cores \({u_{\varvec{r}}} = {\varvec{\Psi }}_1 {\varvec{\Psi }}_2 \cdots {\varvec{\Psi }}_d\), where \({\varvec{\Psi }}_i\) are orthogonalized from the left, i.e., \(\left\langle {\varvec{\Psi }}_i^{\text {T}} {\varvec{\Psi }}_i \right\rangle _i = \varvec{I}_{r_i \times r_i}\), for all \(i = 1,\ldots ,d-1\). With this ansatz, an arbitrary element of the tangent space \(T_{{u_{\varvec{r}}}}\mathcal {M}_{\varvec{r}}\) can be expressed as
where \({\dot{u}_{\varvec{r}}}=\partial {u_{\varvec{r}}}/\partial t\) and \(\dot{{\varvec{\Psi }}}_i=\partial {\varvec{\Psi }}_i/\partial t\). The DO constraints are given by
which ensures that \(\left\langle {\varvec{\Psi }}_i^{\text {T}}(t) {\varvec{\Psi }}_i(t) \right\rangle _i = \varvec{I}_{r_i \times r_i}\) for all \(i = 1,\ldots ,d-1\) and for all \(t \ge 0\). We have shown in [17] that under these constraints, the convex minimization problem (26) admits a unique minimum for vectors in the tangent space (28) satisfying the PDE system
Here, \({u_{\varvec{r}}}={\varvec{\Psi }}_1 {\varvec{\Psi }}_2 \cdots {\varvec{\Psi }}_d\in \mathcal {M}_r\) and we have introduced the notation
for any matrix \({\varvec{\Psi }}(\varvec{x}) \in M_{r \times s}\left( L^2_{\mu }\left( \Omega \right) \right) \). The DO-FTT system (30) involves several inverse covariance matrices \(\left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle _{\ge k}^{-1}\), which can become poorly conditioned in the presence of tensor modes with small energy (i.e. autocovariance matrices with small singular values). This phenomenon has been shown to be a result of the fact that the curvature of the tensor manifold at a tensor is inversely proportional to the smallest singular value present in the tensor [34, section 4]. A slight improvement to the numerical stability of (30) can be obtained by right orthogonalizing the partial products
Using the orthogonality of \(\varvec{Q}_k\) it can easily be verified that \(\varvec{R}_k = \left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle _{\ge k}^{1/2}\). With these right orthogonalized cores, the DO-FTT system (30) can be written as
where \(\left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle _{k,\ldots ,d}^{-1/2}\) denotes the inverse of the matrix square root. Since the condition number of \(\left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle _{\ge k}\) is larger than the condition number of \(\left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle _{\ge k}^{1/2}\), the inverse covariances at the right hand side of (33) can be computed more accurately than the ones in (30) in the presence of small singular values.
3.1.1 Temporal Integration Using Operator Splitting Methods
As we mentioned previously, one of the challenges of dynamic approximation of PDEs on low-rank tensor manifolds relates to the curvature of the manifold, which is proportional to the inverse of the smallest singular value of \(\left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle _{\ge k}\) [34, section 4]. Such curvature appears naturally at the right hand side of the DO-FTT system (30) in the form of inverse covariances \(\left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle ^{-1}_{\ge k}\). Clearly, if the tensor solution is comprised of cores with small singular values, then the covariance matrices \(\left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle _{\ge k}\) are ill-conditioned and therefore not easily invertible. Moreover, it is desirable to add and remove tensor modes adaptively during temporal integration, and adding a mode with zero energy immediately yields singular covariance matrices (see [16]). The problem of inverting the covariance matrices \(\left\langle {\varvec{\Psi }}_{\ge k} {\varvec{\Psi }}_{\ge k}^{\text {T}} \right\rangle _{\ge k}\) when integrating (30) or (33) can be avoided by using projector-splitting methods. These methods were originally proposed for integration on tensor manifolds by Lubich et al. in [32, 38, 39]. The key idea is to apply an exponential operator splitting scheme, e.g., the Lie–Trotter scheme, directly to the projection operator onto the tangent space defining the dynamic approximation (see Eq. 26). To describe the method, we begin by introducing a general framework for operator splitting of dynamics on the FTT tangent space. We first rewrite the right hand side of (27) as
where in the second line we used the right orthogonalizations in Eq. (32). A substitution of the expressions for \(\dot{{\varvec{\Psi }}}_k\) we obtained in (33) into (34) yields
where we defined the following projection operators from \(L^2_{\mu }(\Omega )\) onto \(T_{{u_{\varvec{r}}}} \mathcal {M}_{\varvec{r}}\)
for any \(z(\varvec{x}) \in L^2_{\mu }(\Omega )\). Also we set \({\varvec{\Psi }}_0 = 1\). The key point in (35) is that inverse covariance matrices no longer appear. To establish a general operator splitting framework, let us assume that there exists an evolution operator \(\mathcal {E}_{P_{{u_{\varvec{r}}}} G}\) for the solution of the initial/boundary value problem (27), where \(P_{{u_{\varvec{r}}}} G\) is given in (35). Such an evolution operator \(\mathcal {E}_{P_{{u_{\varvec{r}}}} G}: L^2_{\mu }(\Omega ) \times [0,T] \rightarrow L^2_{\mu }(\Omega )\) satisfies a semi-group property and it maps the initial condition \(u_0(\varvec{x})\) into the solution to (27) at a later time
We write such an evolution operator formally as an exponential operator with generator \(D_{P_{{u_{\varvec{r}}}} G}\) (see e.g. [36])
where \(D_{P_{{u_{\varvec{r}}}} G}\) is the Lie derivative associated with \(P_{{u_{\varvec{r}}}} G\). We now discretize the temporal domain of interest [0, T] into \(N+1\) evenly-spaced time instants,
An approximation to the exact solution of (27) is then obtained by the recurrence relation
where \(\mathcal {S}\) is an exponential splitting operator that approximates the exact evolution operator
Setting \(s = 1\) and \(\gamma _{1,j} = 1\) for all \( j = 1,\ldots ,d\) in (41) yields the well-known Lie–Trotter splitting, which is first-order in time. The discrete time version of this scheme can be written as
This allows us to compute \(u_{\varvec{r}}(t_{i+1})\) given \(u_{\varvec{r}}(t_i)\). Although each equation in (42) involves a FTT tensor, it was shown in [38, Theorem 4.1] that each equation only updates one tensor core. Clearly this is computationally more efficient than updating a full tensor. Moreover, in (42) there is no need to invert covariance matrices, which is a distinct advantage over iterating a discrete form of (30) or (33).
Regarding computational cost, suppose we discretize the d-dimensional domain \(\Omega \) using a tensor product grid with n points per dimension. It was pointed out in [38] that the computational complexity of the sweeping algorithm to update the tensor cores for the Lie–Trotter scheme (42) applied to a linear PDE (i.e. Eq. 27 with linear G) is linear in the dimension d but has high polynomial complexity in the tensor rank. On the other hand, discretizing such linear PDE on the same tensor product grid and performing one time step with a first-order time stepping scheme (e.g. Euler forward) has computational complexity which scales exponentially with the dimension d. Specifically, assuming that the operator G in (1) is linear with rank \(r_{G}\) (see [5]), the computational cost of one time step of Euler forward is \(d n^{d+1} r_{G} + n^d r_{G}\) floating point operations, hence exponential in d.
3.2 Step-Truncation Temporal Integration Methods
Another methodology to integrate nonlinear PDEs on fixed-rank tensor manifolds \(\mathcal {M}_{\varvec{r}}\) is step-truncation [33, 50, 51]. The idea is to integrate the solution off of \(\mathcal {M}_{\varvec{r}}\) for short time, e.g., by performing one time step of the full equation with a conventional time-stepping scheme, followed by a truncation operation back onto \(\mathcal {M}_{\varvec{r}}\). To describe this method further let us define the truncation operator
which provides the best approximation of u on \(\mathcal {M}_{\varvec{r}}\). Such a map is known as a metric projection or closest point function and in general it may be multivalued, i.e., the set of \(u_{\varvec{r}} \in \mathcal {M}_{\varvec{r}}\) which minimize \(\Vert u - u_{\varvec{r}} \Vert _{{L^2_{\mu }(\Omega )}}\) is not a singleton set. However, since \(\mathcal {M}_{\varvec{r}}\) is a smooth submanifold of \({L^2_{\mu }(\Omega )}\), we have by [53, Proposition 5.1] that for each \(u_0 \in \mathcal {M}_{\varvec{r}}\) there exists an open neighborhood U of \(u_0\) such that \(\mathfrak {T}_{\varvec{r}}\) is well-defined and smooth on U. Let
be a convergent one-step time integration schemeFootnote 4 approximating the solution to the initial value problem (1). Assume that the solution \(u(\varvec{x},t_0)\) at time \(t_0\) is on \(\mathcal {M}_{\varvec{r}}\).Footnote 5 In order to guarantee the solution \(u(\varvec{x},t_k)\) at time step \(t_k\) is an element of the manifold \(\mathcal {M}_{\varvec{r}}\) for each \(k = 1,2,\ldots \), we apply the truncation operator to the right hand side (44). This yields the following step-truncation method
3.3 Consistency of Dynamic Approximation and Step-Truncation Methods
Next we ask what happens in the step-truncation algorithm in the limit of time step \(\Delta t\) approaching zero. The result of such a limiting procedure results in a scheme which keeps the solution \(u(\varvec{x},t)\) on the manifold \(\mathcal {M}_{\varvec{r}}\) for all time \(t \ge t_0\) in an optimal way. We now show that this limiting procedure in fact results in precisely the dynamic approximation method described in Sect. 3.1. In other words, by sending \(\Delta t\) to zero in (45) we obtain a solution of (27). For similar discussions connecting these two approximation methods in closely related contexts see [23, 24, 33]. To prove consistency between step-truncation and dynamic approximation methods we need to compute \(\mathfrak {T}_{\varvec{r}}(u(\varvec{x},t))\) for t infinitesimally close to \(t_0\). Such a quantity depends on the derivative
The following proposition provides a representation of the derivative \(\partial \mathfrak {T}_{\varvec{r}}(u(\varvec{x},t))/\partial t\) in terms of \(G(u(\varvec{x},t))\) and the Fréchet derivative [56] of the operator \(\mathfrak {T}_{\varvec{r}}(u)\).
Proposition 3.1
If the solution \(u_0 = u(\varvec{x},t_0)\) to (1) at time \(t_0\) is on the manifold \(\mathcal {M}_{\varvec{r}}\), then
where \((\mathfrak {T}_{\varvec{r}})'_{u_0}\) is the Fréchet derivative of the nonlinear operator \(\mathfrak {T}_{\varvec{r}}\) at the point \(u_0\).
Proof
Express the solution of (1) at time \(t \ge t_0\) as
where
Expanding \(\mathfrak {T}_{\varvec{r}}(u(\varvec{x},t))\) in a Taylor series around \(u_0(\varvec{x})\) we obtain [42, Theorem 6.1]
Differentiating (50) with respect to t and evaluating at \(t = t_0\) we obtain
where we assumed that \(\partial /\partial t\) commutes with \((\mathfrak {T}_{\varvec{r}})'_{u_0}\) and used the fact that \(\partial h(\varvec{x},t)/\partial t = G(u(\varvec{x},t))\) for the first order term. All of the higher order terms are seen to be zero by commuting \(\partial /\partial t\) with \((\mathfrak {T}_{\varvec{r}})^{(n)}_{u_0}\) and using chain rule. \(\square \)
Since \(\mathfrak {T}_{\varvec{r}}(u(\varvec{x},t))\) is an element of \(\mathcal {M}_{\varvec{r}}\) for all \(t \ge t_0\), it follows that (47) is an element of \(T_{u_0}\mathcal {M}_{\varvec{r}}\). Arguing on the optimality of the tangent space element \((\mathfrak {T}_{\varvec{r}})'_{u_0} G(u(\varvec{x},t_0))\) it is seen that (51) is the same problem as dynamic approximation (27), i.e., \((\mathfrak {T}_{\varvec{r}})'_{u_0} = P_{u_0}\). Now consider the scheme (45) and use a Taylor expansion of \(\mathfrak {T}_{\varvec{r}}\) around \(u_{\varvec{r}}(\varvec{x},t_k)\) on the right hand side
Discarding higher order terms in \(\Delta t\) yields
Moreover if the increment function \(\Phi \) defines the Euler forward scheme
then the scheme (53) is equivalent to the scheme in (27). Thus, we just proved the following lemma.
Lemma 3.1
Step-truncation and dynamic approximation methods are consistent at least to first-order in \(\Delta t\).
This Lemma applies to any first-order time integrator for dynamic approximation and step-truncation, including the Lie–Trotter splitting integrator we discussed in Sect. 3.1.1.
4 Rank-Adaptive Integration
The solution to the initial/boundary value problem (1) is often not accurately represented on a tensor manifold with fixed rank, even for short integration times. In this section we discuss effective methods to adaptively add and remove tensor modes from the solution based on appropriate criteria.
In the context of step-truncation algorithms, if the solution rank naturally decreases in time then the operator \(\mathfrak {T}_{\varvec{r}}\) in (45) is no longer well-defined. In this situation, replacing the operator \(\mathfrak {T}_{\varvec{r}}\) with \(\mathfrak {T}_{\varvec{s}}\) for an appropriateFootnote 6\(\varvec{s} \le \varvec{r}\) allows for integration to continue. On the other hand, if the solution rank increases in during integration then the operator \(\mathfrak {T}_{\varvec{r}}\) will still be well-defined for small enough \(\Delta t\) but the approximation on \(\mathcal {M}_{\varvec{r}}\) will not retain accuracy. To address this problem of constant rank integration we shall introduce a criterion for rank increase of the FTT solution. Both decreasing and increasing rank are based on FTT orthogonalization and truncation (see Sect. 2.1). For the remainder of this section let \(u(\varvec{x},t)\) be the solution to (1) and \(u_{\varvec{r}}(\varvec{x},t) \in \mathcal {M}_{\varvec{r}}\) an approximation of \(u(\varvec{x},t)\) obtained by either the solution of the dynamical approximation problem (27) or step-truncation methods (see Sect. 3.2).
4.1 Decreasing Tensor Rank
For decreasing tensor rank at time t, we are interested in determining if \(u_{\varvec{r}}(\varvec{x},t) \in \mathcal {M}_{\varvec{r}}\) is close to an element \(u_{\varvec{s}}(\varvec{x},t) \in \mathcal {M}_{\varvec{s}}\) for \(\varvec{s} \le \varvec{r}\). This can be achieved by simply performing a FTT truncation on \(u_{\varvec{r}}(\varvec{x},t)\) with small threshold \(\epsilon _{\mathrm {dec}}\). Since the splitting integrator described in Sect. 3.1.1 is robust to over approximation by tensor rank, it may not be strictly necessary to decrease rank during integration. However, it is desirable to have solutions of the lowest rank possible (while retaining accuracy) when solving high dimensional problems. For these reasons it is advisable not to perform a FTT truncation at each time step (as this would be unnecessary and inefficient when using an operator splitting integrator) but only every once and a while. One may choose a criterion for when to check for rank decrease based on the problem, step size, current rank, and dimension. If one is using a step-truncation method with a tolerance based FTT truncation algorithm such as the one described in Sect. 2.1 then rank decrease is already built into each time step.
4.2 Increasing Tensor Rank
As a general heuristic one would like to increase rank at the time when the error between the low-rank approximation \(u_{\varvec{r}}(\varvec{x},t)\) and the PDE solution \(u(\varvec{x},t)\) will become large after the subsequent time step. Such critical time instant for rank increase can be determined by examining the normal component of the dynamics
To describe this situation further, suppose we are integrating one time step forward from \(t_i\) to \(t_{i+1}\). The error at \(t_{i+1}\) is given by
If \(u(\varvec{x},t_i) \in \mathcal {M}_{\varvec{r}}\) then
For small \(\Delta t\) the above integral can be approximated by the left endpoint
where \(N_{u_{\varvec{r}}(\varvec{x},\tau )}\) denotes the orthogonal projection onto the normal space of \(\mathcal {M}_{\varvec{r}}\) at the point \(u_{\varvec{r}}(\varvec{x},t)\). Hence, up to first-order in \(\Delta t\) we have that
From this approximation we see that a reasonable criterion for increasing rank at time \(t_i\) is when the norm of the normal component of \(G(u_{\varvec{r}}(\varvec{x},t_i))\) is larger than some threshold \(\epsilon _{\mathrm {inc}}\) (see Fig. 2)
To efficiently compute the normal component \(N_{u_{\varvec{r}}\varvec{x},t_i)}G(u_{\varvec{r}}(\varvec{x},t_i))\) at each time instant \(t_i\) we use the formula
where \(N_{\varvec{r}}G(u_{\varvec{r}})\) and \(P_{u_{\varvec{r}}}G(u_{\varvec{r}})\) represent the normal and tangential components of \(G(u_{\varvec{r}})\). The tangential component can be approximated at a low computational cost via backward differentiation formulas (BDF) as
With a p-point backward difference approximation of the tangent space projection available at \(t_i\) we easily obtain an approximation of the normal component of \(G(u_{\varvec{r}})\) at \(t_i\)
which allows us to implement the criterion (60) for rank increase at time \(t_i\). Clearly, the p-point formula (64), and the corresponding approximation of the normal component (65), are effectively of order p in \(\Delta t\) if and only if the time snapshots \(u_{\varvec{r}}(\varvec{x},t_i)\) are computed via a temporal integrator of order p. We emphasize that this method of using a finite difference stencil based on the temporal grid for approximating the tangential component of the dynamics (and thus the normal component) creates a lower bound for the choice of normal vector threshold \(\epsilon _{\mathrm {inc}}\). In particular, we must have that \(K_1(\Delta t)^p \ge \epsilon _{\text {inc}}\) for some constant \(K_1\) otherwise the error incurred from our approximation of the normal component may trigger unnecessary mode addition. This approximation of the normal component is cheap but only informs on whether or not it is appropriate to add modes at time instant \(t_i\).
Tangent and normal components of \(G\left( u_{\varvec{r}}\right) = \partial u_{\varvec{r}}/\partial t\) at \(u_{\varvec{r}}\). The tensor rank of the solution is increased at time \(t_i\) if the norm of the normal component \(N_{u_{\varvec{r}}}G(u_{\varvec{r}})\) is larger than a specified threshold \(\epsilon _{\mathrm {inc}}\)
The subsequent question is which entries of the rank vector \(\varvec{r}\) need to be increased. In order to make such a determination we expand the approximate solution at time t as
where \({\varvec{\Gamma }}_1(t) \cdots {\varvec{\Gamma }}_d(t) = 0\) for all \(t \in [0,T]\). Differentiating (66) with respect to time yields
Subtracting off the tangential component (28) we have the normal component at time t
Next, orthogonalize the partial product \({\varvec{\Gamma }}_{\le i-1}(t)\) from the left and the partial product \({\varvec{\Gamma }}_{\ge i}(t)\) from the right to obtain
where \(\varvec{C}_i = \varvec{0}_{r_{i-1} \times r_i}\) and \(\left\langle {\varvec{\Gamma }}_i^{\text {T}} {\varvec{\Gamma }}_i \right\rangle _i = \varvec{I}\) for all \(i = 1,2,\ldots ,d\). Expand (69) using a product rule and evaluate at \(t = t_i\)
From the previous equation we see that the FTT autocorrelation matrices of the normal component at time instant \(t_i\) are the time derivatives of the zero energy modes in the current solution. Thus, if the normal component has FTT rank \(\varvec{n}\) then the solution \(u_{\varvec{r}}(\varvec{x},t)\) at time \(t_i\) should be represented by an FTT tensor of rank \(\varvec{r} + \varvec{n}\). Certainly, the solution will be over represented at \(t_i\) with rank \(\varvec{r}+ \varvec{n}\). However, after one step of the splitting integrator the additional ranks will ensure that the low-rank solution \(u_{\varvec{r}+\varvec{n}}(\varvec{x},t) \in \mathcal {M}_{\varvec{r}+\varvec{n}}\) retains its accuracy.
The main steps of the algorithm we propose to adaptively increase the tensor rank are summarized in Algorithm 1. The operation “\(*\)” appearing within the conditional statement if/end denotes scalar times FTT tensor, and is meant to indicate that the multiplication is done by scaling the first core of the tensor with the scalar 0 and leaving the remainder of the cores unchanged [44]. As we will demonstrate in Sect. 5, Algorithm 1 is robust and it yields accurate results that do no require ad-hoc approximations such the matrix pseudo-inverse approximation introduced in [1].

4.3 Order of the Rank-Adaptive Tensor Scheme
Let us choose the threshold \(\epsilon _{\mathrm {inc}}\) in (60) to satisfy
and assume that the condition
is satisfied for all \( t \in [0,T]\). Then we have the following bound for the local truncation error
In particular, we have that the continuous-time rank-adaptive scheme is order one consistent in \(\Delta t\) if the normal vector threshold is set as in (71).
When implementing the adaptive scheme we usually discretize the time domain [0, T] into a mesh of time instants as in (39). Therefore, we do not necessarily have control over the normal vector for all \(t \in [0,T]\) but rather only at a finite number of time instants. However, an analogous argument as we have made for order one consistency in the continuous time rank-adaptive scheme holds for the discrete time rank-adaptive scheme by considering the first-order approximation of the local truncation error given in (58). In particular by using the equality in (58) and discrete time thresholding of the normal component
we have that
This proves that the discrete time rank-adaptive scheme with normal threshold given by (74) is consistent with order one in \(\Delta t\). Higher-order consistency results can be obtained with higher-order time integration methods and higher-order estimators for the normal vector \({N_{u_{\varvec{r}}}} G(u_{\varvec{r}})\).
5 Numerical Examples
In this section we demonstrate the proposed rank-adaptive FTT tensor method on linear and nonlinear PDEs. In all examples the rank-adaptive scheme relies on first-order Lie–Trotter operator splitting time integration (42), and the thresholding criterion (60). For each PDE we rigorously assess the accuracy of the proposed rank-adaptive tensor method by comparing it with benchmark solutions computed with well-established numerical methods.
5.1 Two-Dimensional Variable Coefficient Advection Equation
Let us begin with the two-dimensional variable coefficient advection problem
on the flat torus \(\Omega =\mathbb {T}^2\). We have shown in previous work [16] that the tensor solution to the PDE (76) increases in rank as time increases.
As is well known, the PDE (76) can be reduced to the trivial ODE \(du/dt=0\) along the flow generated by the dynamical system (see, e.g., [48])
With the flow \(\{x_1(t,x_{01},x_{02}),x_1(t,x_{01},x_{02})\}\) available, we can write the analytical solution to (76) as
where \(\{x_{01}(x_1,x_2,t), x_{02}(x_1,x_2,t)\}\) denotes the inverse flow generated by (77). We obtain a semi-analytical solution to the PDE (76) by solving the characteristic system (77) numerically for different initial conditions and then evaluating (78). A few time snapshots of the semi-analytical solution (78) are plotted in Fig. 3 (middle row).
Variable coefficient advection equation (76). Time snapshots of the rank-adaptive FTT solution \({u_{\varvec{r}}}(x_1,x_2,t)\) obtained with threshold \(\epsilon _{\mathrm {inc}} = 10^{-2}\) (top), the semi-analytical solution \(u_{\text {ref}}(x_1,x_2,t)\) (middle), and the pointwise error between the two solutions (bottom)
We also solve the PDE (76) using the proposed rank-adaptive tensor method with first-order Lie–Trotter operator splitting and thresholding criterion (60). The initial condition is approximated by an FTT tensor \({u_{\varvec{r}}}(x_1,x_2,0)\) with multivariate rank \(\varvec{r} = \begin{bmatrix} 1&15&1 \end{bmatrix}\)
where
Each tensor mode \(\psi _i\) is discretized on a grid of 81 evenly-spaced points in the interval \(\Omega _i = [0,2\pi ]\). One-dimensional Fourier pseudo-spectral quadrature rules and differentiation matrices [29] are used to compute inner products and derivatives when needed. We run three simulations with the initial tensor decomposition (79) and time step \(\Delta t = 10^{-4}\). In the first simulation we do not use any rank adaptation, in the second simulation we set the normal vector threshold to \(\epsilon _{\mathrm {inc}} = 10^{-1}\) and in the third simulation we set \(\epsilon _{\mathrm {inc}} = 10^{-2}\). At each time step the component of \(G({u_{\varvec{r}}}(\varvec{x},t_i))\) normal to the tensor manifold is approximated with the two-point BDF formula (Sect. 4.2). In Fig. 5 we plot a few time snapshots of the singular values of the rank-adaptive FTT solution with \(\epsilon _{\text {inc}} = 10^{-2}\).
Figure 4a–c summarize the performance and accuracy of the proposed rank-adaptive FTT solver. In particular, in Fig. 4a we plot the time-dependent \(L^2(\Omega )\) error between the rank-adaptive FTT solution and the reference solution we obtained with method of characteristics. It is seen that decreasing the threshold \(\epsilon _{\text {inc}}\) on the norm of the component of \(G({u_{\varvec{r}}})\) normal to the FTT tensor manifold (Fig. 4b) yields addition of more tensor mores to the FTT solution (Fig. 4c). This, in turn, results in better accuracy as demonstrated in Fig. 4a.
5.2 Two-Dimensional Kuramoto–Sivashinsky Equation
a Global \(L^2(\Omega )\) error of the FTT solution \({u_{\varvec{r}}}\) relative to the benchmark solution \(u_{\mathrm {ref}}\); b Norm of the two-point BDF approximation to the normal component \(N_{{u_{\varvec{r}}}}G({u_{\varvec{r}}}(\varvec{x},t))\) (note the effect of thresholding); c tensor rank versus time of the constant-rank FTT solution and adaptive rank solutions with \(\epsilon _{\mathrm {inc}} = 10^{-1}\) and \(\epsilon _{\mathrm {inc}} = 10^{-2}\)
In this section we demonstrate the rank-adaptive FTT integrator on the two-dimensional Kuramoto–Sivashinsky equation [30]
where
Here, \(\nu _1\), \(\nu _2\) are bifurcation parameters. For our demonstration we set \(\nu _1 = 0.25\), \(\nu _2 = 0.04\) and solve (81) on the two-dimensional flat torus \(\mathbb {T}^2\). The initial condition can be written as rank \(\varvec{r} = \begin{bmatrix} 1&2&1 \end{bmatrix}\) FTT tensor
where
and
Kuramoto–Sivashinsky equation (81). Time snapshots of the rank-adaptive FTT solution \({u_{\varvec{r}}}(x_1,x_2,t)\) obtained with threshold \(\epsilon _{\mathrm {inc}} = 10^{-2}\) (top), the Fourier pseudo-spectral solution \(u_{\mathrm {ref}}(x_1,x_2,t)\) (middle), and the pointwise error between the two solutions (bottom)
We compute a benchmark solution by using a Fourier pseudo-spectral method [29] with 33 evenly-spaced grid points per spatial dimension (1089 total number of points). Derivatives and integrals are approximated with well-known pseudo-spectral differentiation matrices and Gauss quadrature rules. The resulting ODE system is integrated forward in time using an explicit fourth-order Runge–Kutta method with time step \(\Delta t = 10^{-5}\).
As before, we performed multiple simulations using the proposed rank-adaptive FTT algorithm with different thresholds for the component of \(G({u_{\varvec{r}}})\) normal to the tensor manifold. Specifically, we ran one simulation with no mode addition and three simulations with adaptive mode addition based on Algorithm 1, and thresholds set to \(\epsilon _{\mathrm {inc}} = 10\), \(\epsilon _{\mathrm {inc}} = 10^{-1}\), and \(\epsilon _{\mathrm {inc}} = 10^{-2}\). We used the two-point BDF formula (62) to approximate the component of the solution normal to the tensor manifold at each time step and the Lie–Trotter operator splitting scheme (42) with time step \(\Delta t = 10^{-5}\) to integrate in time the rank-adaptive FTT solution. In Fig. 6 we compare the time snapshots of the rank-adaptive FTT solution with \(\epsilon _{\mathrm {inc}} = 10^{-2}\) with the benchmark solution obtained by the Fourier pseudo-spectral method. As before, Fig. 7a–c demonstrate that the rank-adaptive FTT algorithm is effective in controlling the \(L^2(\Omega )\) error of the FTT solution. Interestingly, the solution to the PDE (81) has the property that any tensor approximation with sufficient rank yields a normal component that does not grow in time. In fact, as seen in Fig. 7b the tensor rank becomes constant for each threshold \(\epsilon _{\text {inc}}\) after a transient of approximately 0.5 dimensionless time units.
In Fig. 7 we observe that the error associated with the constant rank 2 FTT solution increases significantly during temporal integration. This suggests that projecting the nonlinear Kuramoto–Sivashinsky equation (81) onto a rank 2 FTT manifold yields a reduced-order PDE which does not accurately capture the dynamics of the full system. A similar phenomenon occurs in other areas of reduced-order modeling, e.g., when projecting nonlinear PDEs onto proper orthogonal decomposition (POD) bases [54].
a Global \(L^2(\Omega )\) error between the FTT solution \({u_{\varvec{r}}}\) to equation (81) and the benchmark solution \(u_{\mathrm {ref}}\). b Norm of the approximation to \(N_{{u_{\varvec{r}}}}G({u_{\varvec{r}}}) = {\dot{u}_{\varvec{r}}} - G({u_{\varvec{r}}})\) where the tangent space projection is computed with a two-point BDF formula at each time. c Rank versus time of the constant rank FTT solution and rank-adaptive FTT solutions with \(\epsilon _{\mathrm {inc}} = 10,10^{-1},10^{-2}\)
5.3 Four-Dimensional Fokker–Planck Equation
Finally, we demonstrate the proposed rank-adaptive FTT integrator on a four-dimensional Fokker–Planck equation with non-constant drift and diffusion coefficients. As is well known [49], the Fokker–Planck equation describes the evolution of the probability density function (PDF) of the state vector solving the Itô stochastic differential equation (SDE)
Here, \(\varvec{X}_t\) is the d-dimensional state vector, \({\varvec{\mu }}(\varvec{X}_t,t)\) is the d-dimensional drift, \({\varvec{\sigma }}(\varvec{X}_t,t)\) is an \(d \times m\) matrix and \(\varvec{W}_t\) is an m-dimensional standard Wiener process. The Fokker–Planck equation that corresponds to (86) has the form
where \(p_0(\varvec{x})\) is the PDF of the initial state \(\varvec{X}_0\), \(\mathcal {L}\) is a second-order linear differential operator defined as
and \(\varvec{D}(\varvec{x},t)={\varvec{\sigma }}(\varvec{x},t) {\varvec{\sigma }}(\varvec{x},t)^{\text {T}}/2\) is the diffusion tensor. For our numerical demonstration we set
where \(g(x)=\sqrt{1 + k \sin (x)}\). With the drift and diffusion matrices chosen in (89) the operator (88) takes the form
Clearly \(\mathcal {L}\) is a linear, time-independent separable operator of rank 9, since it can be written as
where each \(L_i^{(j)}\) operates on \(x_j\) only. Specifically, we have
Time snapshots of marginal PDF \(p_{\varvec{r}}(x_1,x_2,t)\) corresponding to the solution to the Fokker–Planck equation (87). We plot marginals computed with the rank-adaptive FTT integrator using \(\epsilon _{\mathrm {inc}} = 10^{-4}\) (top row) and with the full tensor product Fourier pseudo-spectral method (middle row). We also plot the pointwise error between the two numerical solutions (bottom row). The initial condition is the FTT tensor (93)
and all other unspecified \(L_i^{(j)}\) are identity operators. We set the parameters in (89) as \(\alpha = 0.1\), \(\beta = 2.0\), \(k = 1.0\) and solve (87) on the four-dimensional flat torus \(\mathbb {T}^4\). The initial PDF is set as
Note that (93) is a four-dimensional FTT tensor with multilinear rank \(\varvec{r} = \begin{bmatrix} 1&2&2&2&1 \end{bmatrix}\). Upon normalizing the modes appropriately we obtain the left orthogonalized initial condition required to begin integration
where
All other tensor modes are equal to \(1/\sqrt{2 \pi }\), and \(\sqrt{\lambda (2)} = 1/(2\pi ^2)\). To obtain a benchmark solution with which to compare the rank-adaptive FTT solution, we solve the PDE (87) using a Fourier pseudo-spectral method on the flat torus \(\mathbb {T}^4\) with \(21^4=194481\) evenly-spaced points. As before, the operator \(\mathcal {L}\) is represented in terms of pseudo-spectral differentiation matrices [29], and the resulting semi-discrete approximation (ODE system) is integrated with an explicit fourth-order Runge Kutta method using time step \(\Delta t = 10^{-4}\). The numerical solution we obtained in this way is denoted by \(p_{\text {ref}}(\varvec{x},t)\). We also solve the Fokker–Planck using the proposed rank-adaptive FTT method with first-order Lie–Trotter time integrator (Sect. 3.1.1) and normal vector thresholding (Sect. 4.2). We run three simulations all with time step \(\Delta t = 10^{-4}\): one with no rank adaption, and two with rank-adaptation and normal component thresholds set to \(\epsilon _{\mathrm {inc}} = 10^{-3}\) and \(\epsilon _{\mathrm {inc}} = 10^{-4}\). In Fig. 8 we plot three time snapshots of the two-dimensional solution marginal
computed with the rank-adaptive FTT integrator (\(\epsilon _{\mathrm {inc}} = 10^{-4}\)) and the full tensor product pseudo-spectral method (reference solution). In Fig. 9a we compare the \(L^2(\Omega )\) errors of the rank-adaptive method relative to the reference solution. It is seen that as we decrease the threshold the solution becomes more accurate. In Fig. 9b we plot the component of \(\mathcal {L} {p_{\varvec{r}}}\) normal to the tensor manifold, which is approximated using the two-point BDF formula (62). Note that in the rank-adaptive FTT solution with thresholds \(\epsilon _{\text {inc}}=10^{-3}\) and \(\epsilon _{\text {inc}}=10^{-4}\) the solver performs both mode addition as well as mode removal. This is documented in Fig. 10. The abrupt change in rank observed in Fig. 10a–c near time \(t=0.4\) corresponding to the rank-adaptive solution with threshold \(\epsilon _{\text {inc}} = 10^{-4}\) is due to the time step size \(\Delta t\) being equal to \(\epsilon _{\text {inc}}\). This can be justified as follows. Recall that the solution is first order accurate in \(\Delta t\) and therefore the approximation of the component of \(\mathcal {L} p_{\varvec{r}}\) normal to the tensor manifold \(\mathcal {M}_{\varvec{r}}\) is first-order accurate in \(\Delta t\). If we set \(\epsilon _{\text {inc}} \le \Delta t\), then the rank-adaptive scheme may overestimate the number of modes needed to achieve accuracy on the order of \(\Delta t\). This does not affect the accuracy of the numerical solution due to the robustness of the Lie–Trotter integrator to over-approximation [38]. Moreover we notice that the rank-adaptive scheme removes the unnecessary modes ensure that the tensor rank is not unnecessarily large (see Sect. 4.1). In fact, the diffusive nature of the Fokker–Plank equation on the flat torus \(\mathbb {T}^4\) yields relaxation to a statistical equilibrium state that depends on the drift and diffusion coefficients in (87). In this case such an equilibrium state is well-approximated by a low-rank FTT tensor.
a The \(L^2(\Omega )\) error of the FTT solution \({p_{\varvec{r}}}(\varvec{x},t)\) relative to the benchmark solution \(p_{\text {ref}}(\varvec{x},t)\) computed with a Fourier pseudo-spectral method on a tensor product grid. b Norm of the component of \(\mathcal {L} {p_{\varvec{r}}}\) normal to the tensor manifold (see Fig. 2). Such component is approximated with a two-point BDF formula at each time step
Tensor rank \(\varvec{r}=[ 1 \, r_1 \, r_2\,r_3 \, 1]\) of the adaptive FTT solution to the four dimensional Fokker–Planck equation (87)
6 Summary
We presented a new rank-adaptive tensor method to integrate high-dimensional nonlinear PDEs. The new method is based on functional tensor train (FTT) expansions [6, 17, 44], operator splitting time integration [32, 39], and a new rank-adaptive algorithm to add and remove tensor modes from the PDE solution based on thresholding the component of the velocity vector normal to the FTT tensor manifold. We tested the proposed new algorithm on three different initial/boundary value problems including a 2D variable-coefficient first-order linear PDE, a 2D Kuramoto–Sivashinsky equation, and a 4D Fokker–Planck equation. In all cases the adaptive FTT solution was compared to a benchmark numerical solution constructed with well-established numerical methods. The numerical results we obtained demonstrate that the proposed rank-adaptive tensor method is effective in controlling the temporal integration error, and outperforms known integration methods for multidimensional PDEs in terms of accuracy, robustness and computational cost. We also proved that the new method is consistent with recently proposed step-truncation algorithms [33, 50, 51] in the limit of small time steps.
Data availability statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Code availability
The code generated during the current study is available from the corresponding author on reasonable request.
Notes
The averaging operation in (9) can be viewed as a an inner product on the space
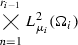 .
.Equation (10) follows immediately from the orthonormality of \(\{\psi _i(\alpha _{i-1};x_i;\alpha _i)\}_{\alpha _{i}}\) relative to the inner product in \(L^2_{\tau \times \mu _i}(\mathbb {N} \times \Omega _i)\).
If \(u(\varvec{x},t_0)\) is not on \(\mathcal {M}_{\varvec{r}}\) then it may be mapped onto \(\mathcal {M}_{\varvec{r}}\) by evaluating \(\mathfrak {T}_{\varvec{r}}(u(\varvec{x},t_0))\).
Here \(\le \) denotes component-wise inequality of rank vectors, i.e., \(\varvec{s}<\varvec{r}\) if and only if \(s_i \le r_i\) for all \(i = 0,1,\ldots ,d\).
References
Babaee, H., Choi, M., Sapsis, T.P., Karniadakis, G.E.: A robust bi-orthogonal/dynamically-orthogonal method using the covariance pseudo-inverse with application to stochastic flow problems. J. Comput. Phys. 344, 303–319 (2017)
Bachmayr, M., Schneider, R., Uschmajew, A.: Tensor networks and hierarchical tensors for the solution of high-dimensional partial differential equations. Found. Comput. Math. 16(6), 1423 (2016)
Baldeaux, J., Gnewuch, M.: Optimal randomized multilevel algorithms for infinite-dimensional integration on function spaces with ANOVA-type decomposition. SIAM J. Numer. Anal. 52(3), 1128–1155 (2014)
Barthelmann, V., Novak, E., Ritter, K.: High dimensional polynomial interpolation on sparse grids. Adv. Comput. Mech. 12, 273–288 (2000)
Beylkin, G., Mohlenkamp, M.J.: Numerical operator calculus in higher dimensions. Proc. Natl. Acad. Sci. USA 99(16), 10246–10251 (2002)
Bigoni, D., Engsig-Karup, A.P., Marzouk, Y.M.: Spectral tensor-train decomposition. SIAM J. Sci. Comput. 38(4), A2405–A2439 (2016)
Boelens, A.M.P., Venturi, D., Tartakovsky, D.M.: Parallel tensor methods for high-dimensional linear PDEs. J. Comput. Phys. 375, 519–539 (2018)
Boelens, A.M.P., Venturi, D., Tartakovsky, D.M.: Tensor methods for the Boltzmann–BGK equation. J. Comput. Phys. 421, 109744 (2020)
Bungartz, H.J., Griebel, M.: Sparse grids. Acta Numer. 13, 147–269 (2004)
Cao, Y., Chen, Z., Gunzbuger, M.: ANOVA expansions and efficient sampling methods for parameter dependent nonlinear PDEs. Int. J. Numer. Anal. Model. 6, 256–273 (2009)
Cercignani, C.: The Boltzmann Equation and Its Applications. Springer, Berlin (1988)
Chkifa, A., Cohen, A., Schwab, C.: High-dimensional adaptive sparse polynomial interpolation and applications to parametric PDEs. Found. Comput. Math. 14, 601–633 (2014)
Cho, H., Venturi, D., Karniadakis, G.E.: Statistical analysis and simulation of random shocks in Burgers equation. Proc. R. Soc. A 2171(470), 1–21 (2014)
Cho, H., Venturi, D., Karniadakis, G.E.: Numerical methods for high-dimensional probability density function equations. J. Comput. Phys. 315, 817–837 (2016)
Al Daas, H., Ballard, G., Benner, P.: Parallel algorithms for tensor train arithmetic. arXiv:2011.06532, pp. 1–31 (2020)
Dektor, A., Venturi, D.: Dynamically orthogonal tensor methods for high-dimensional nonlinear PDEs. J. Comput. Phys. 404, 109125 (2020)
Dektor, A., Venturi, D.: Dynamic tensor approximation of high-dimensional nonlinear PDEs. J. Comput. Phys. 437, 110295 (2021)
di Marco, G., Pareschi, L.: Numerical methods for kinetic equations. Acta Numer. 23, 369–520 (2014)
Han, W .E,J., Li, Q.: A mean-field optimal control formulation of deep learning. Res. Math. Sci. 6(10), 1–41 (2019)
Falcó, A., Hackbusch, W., Nouy, A.: Geometric structures in tensor representations. arXiv:1505.03027, pp. 1–50 (2015)
Falcó, A., Hackbusch, W., Nouy, A.: On the Dirac–Frenkel variational principle on tensor Banach spaces. Found. Comput. Math. 19(1), 159–204 (2019)
Falcó, A., Hackbusch, W., Nouy, A.: Geometry of tree-based tensor formats in tensor banach spaces. ArXiv 2011(08466), 1–14 (2020)
Feppon, F., Lermusiaux, P.F.J.: A geometric approach to dynamical model order reduction. SIAM J. Matrix Anal. Appl. 39(1), 510–538 (2018)
Feppon, F., Lermusiaux, P.F.J.: The extrinsic geometry of dynamical systems tracking nonlinear matrix projections. SIAM J. Matrix Anal. Appl. 40(2), 814–844 (2019)
Foo, J., Karniadakis, G.E.: Multi-element probabilistic collocation method in high dimensions. J. Comput. Phys. 229, 1536–1557 (2010)
Frenkel, J.: Wave Mechanics: Advanced General Theory. Oxford University Press, Oxford (1934)
Gangbo, W., Li, W., Osher, S., Puthawala, M.: Unnormalized optimal transport. J. Comput. Phys. 399, 108940 (2019)
Hackbusch, W.: Tensor Spaces and Numerical Tensor Calculus. Springer, Berlin (2012)
Hesthaven, J.S., Gottlieb, S., Gottlieb, D.: Spectral methods for time-dependent problems, volume 21 of Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge (2007)
Kalogirou, A., Keaveny, E.E., Papageorgiou, D.T.: An in-depth numerical study of the two-dimensional Kuramoto–Sivashinsky equation. Proc. A. 471(2179):20140932 (2015)
Khoromskij, B.N.: Tensor numerical methods for multidimensional PDEs: theoretical analysis and initial applications. In: CEMRACS 2013—Modelling and Simulation of Complex Systems: Stochastic and Deterministic Approaches, volume 48 of ESAIM Proc. Surveys, pp. 1–28. EDP Sci., Les Ulis (2015)
Kieri, E., Lubich, C., Walach, H.: Discretized dynamical low-rank approximation in the presence of small singular values. SIAM J. Numer. Anal. 54(2), 1020–1038 (2016)
Kieri, E., Vandereycken, B.: Projection methods for dynamical low-rank approximation of high-dimensional problems. Comput. Methods Appl. Math. 19(1), 73–92 (2019)
Koch, O., Lubich, C.: Dynamical low-rank approximation. SIAM J. Matrix Anal. Appl. 29(2), 434–454 (2007)
Koch, O., Lubich, C.: Dynamical tensor approximation. SIAM J. Matrix Anal. Appl. 31(5), 2360–2375 (2010)
Koch, O., Neuhauser, C., Thalhammer, M.: Error analysis of high-order splitting methods for nonlinear evolutionary Schrödinger equations and application to the MCTDHF equations in electron dynamics. ESAIM Math. Model. Numer. Anal. 47(5), 1265–1286 (2013)
Li, G., Rabitz, H.: Regularized random-sampling high dimensional model representation (RS-HDMR). J. Math. Chem. 43(3), 1207–1232 (2008)
Lubich, C., Oseledets, I.V., Vandereycken, B.: Time integration of tensor trains. SIAM J. Numer. Anal. 53(2), 917–941 (2015)
Lubich, C., Vandereycken, B., Walach, H.: Time integration of rank-constrained Tucker tensors. SIAM J. Numer. Anal. 56(3), 1273–1290 (2018)
McLachlan, A.D.: A variational solution of the time-dependent Schrödinger equation. Mol. Phys. 8, 39–44 (1964)
Narayan, A., Jakeman, J.: Adaptive Leja sparse grid constructions for stochastic collocation and high-dimensional approximation. SIAM J. Sci. Comput. 36(6), A2952–A2983 (2014)
Nashed, M.Z.: Differentiability and related properties of nonlinear operators: Some aspects of the role of differentials in nonlinear functional analysis. In: Nonlinear Functional Anal. and Appl. (Proc. Advanced Sem., Math. Res. Center, Univ. of Wisconsin, Madison, WI, 1970), pp. 103–309. Academic Press, New York (1971)
Nonnenmacher, A., Lubich, C.: Dynamical low-rank approximation: applications and numerical experiments. Math. Comput. Simul. 79(4), 1346–1357 (2008)
Oseledets, I.V.: Tensor-train decomposition. SIAM J. Sci. Comput. 33(5), 2295–2317 (2011)
Raab, A.: On the Dirac–Frenkel/Mclachlan variational principle. Chem. Phys. Lett. 319, 674–678 (2000)
Raissi, M., Karniadakis, G.E.: Hidden physics models: machine learning of nonlinear partial differential equations. J. Comput. Phys. 357, 125–141 (2018)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 606–707 (2019)
Rhee, H.-K., Aris, R., Amundson, N.R.: First-Order Partial Differential Equations, Volume 1: Theory and Applications of Single Equations. Dover, New York (2001)
Risken, H.: The Fokker–Planck Equation: Methods of Solution and Applications, vol. 60, 2nd edn. Springer (1989)
Rodgers, A., Dektor, A., Venturi, D.: Adaptive integration of nonlinear evolution equations on tensor manifolds. arXiv:2008.00155:1–22 (2020)
Rodgers, A., Venturi, D.: Stability analysis of hierarchical tensor methods for time-dependent PDEs. J. Comput. Phys. (2020). https://doi.org/10.1016/j.jcp.2020.109341
Ruthotto, L., Osher, S., Li, W., Nurbekyan, L., Fung, S.W.: A machine learning framework for solving high-dimensional mean field game and mean field control problems. PNAS 117(17), 9183–9193 (2020)
Salas, D., Thibault, L.: On characterizations of submanifolds via smoothness of the distance function in Hilbert spaces. J. Optim. Theory Appl. 182(1), 189–210 (2019)
Sirisup, S., Karniadakis, G.E.: A spectral viscosity method for correcting the long-term behavior of pod models. J. Comput. Phys. 194(1), 92–116 (2004)
Venturi, D.: The numerical approximation of nonlinear functionals and functional differential equations. Phys. Rep. 732, 1–102 (2018)
Venturi, D., Dektor, A.: Spectral methods for nonlinear functionals and functional differential equations. Res. Math. Sci. 8(27), 1–39 (2021)
Venturi, D., Karniadakis, G.E.: Convolutionless Nakajima–Zwanzig equations for stochastic analysis in nonlinear dynamical systems. Proc. R. Soc. A 470(2166), 1–20 (2014)
Venturi, D., Sapsis, T.P., Cho, H., Karniadakis, G.E.: A computable evolution equation for the joint response-excitation probability density function of stochastic dynamical systems. Proc. R. Soc. A 468(2139), 759–783 (2012)
Villani, C.: Optimal Transport: Old and New. Springer, Berlin (2009)
Zhu, Y., Zabaras, N., Koutsourelakis, P.-S., Perdikaris, P.: Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 394, 56–81 (2019)
Funding
This research was supported by the U.S. Air Force Office of Scientific Research (AFOSR) Grant FA9550-20-1-0174 and by the U.S. Army Research Office (ARO) Grant W911NF-18-1-0309.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dektor, A., Rodgers, A. & Venturi, D. Rank-Adaptive Tensor Methods for High-Dimensional Nonlinear PDEs. J Sci Comput 88, 36 (2021). https://doi.org/10.1007/s10915-021-01539-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-021-01539-3














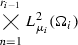 .
.