Poly-Sinc Solution of Stochastic Elliptic Differential Equations

Abstract

In this paper, we introduce a numerical solution of a stochastic partial differential equation (SPDE) of elliptic type using polynomial chaos along side with polynomial approximation at Sinc points. These Sinc points are defined by a conformal map and when mixed with the polynomial interpolation, it yields an accurate approximation. The first step to solve SPDE is to use stochastic Galerkin method in conjunction with polynomial chaos, which implies a system of deterministic partial differential equations to be solved. The main difficulty is the higher dimensionality of the resulting system of partial differential equations. The idea here is to solve this system using a small number of collocation points in space. This collocation technique is called Poly-Sinc and is used for the first time to solve high-dimensional systems of partial differential equations. Two examples are presented, mainly using Legendre polynomials for stochastic variables. These examples illustrate that we require to sample at few points to get a representation of a model that is sufficiently accurate.

1 Introduction

In many applications the values of the parameters of the problem are not exactly known. These uncertainties inherent in the model yield uncertainties in the results of numerical simulations. Stochastic methods are one way to model these uncertainties by using random fields [1]. If the physical system is described by a partial differential equation (PDE), then the combination with the stochastic model results in a stochastic partial differential equation (SPDE). The solution of the SPDE is again a random field, describing both the expected response and quantifying its uncertainty. SPDEs can be interpreted mathematically in several ways.

In the numerical framework, the stochastic regularity of the solution determines the convergence rate of numerical approximations, and a variational theory for this was earlier devised in [2]. The ultimate goal in the solution of SPDEs is usually the computation of response statistics, i.e. a functional of the solution. Monte Carlo (MC) methods can be used directly for this purpose, but they require a high computational effort [3, 4]. Quasi Monte Carlo (QMC) and variance reduction techniques [3] may reduce the computational effort considerably without requiring much regularity. However, often we have high regularity in the stochastic variables, and this is not exploited by QMC methods.

Alternatives to MC methods have been developed, for example, perturbation methods [5], methods based on Neumann-series [6], or the spectral stochastic finite element method (SSFEM) [7, 8]. Stochastic Galerkin methods have been applied to various linear problems, see [7, 9, 10]. Nonlinear problems with stochastic loads have been tackled in [11]. These Galerkin methods yield an explicit functional relationship between the independent random variables and the solution. In contrast with common MC methods, subsequent evaluations of functional statistics like the mean and covariance are very cheap.

In this paper, we do not consider (classical) stochastic differential equations driven by Wiener processes, cf. [12]. Alternatively, we investigate an elliptic PDE in space including a random field as material parameters. The polynomial chaos approach and the stochastic Galerkin method yield a deterministic system of PDEs in space [13]. We introduce a spatial collocation technique based on polynomial approximation by Lagrange interpolation. For the interpolation points we use a specific set of non-uniform points created by conformal maps, called Sinc points. Later, we use a small number of Sinc points as collocation points to compute a very accurate solution of the PDEs, see [14]. This technique is called Poly-Sinc collocation that was used to solve a single elliptic PDE in [15]. Recently it has been used to solve coupled system of parabolic equations [16]. In this paper, we use Poly-Sinc collocation to solve a high-dimensional system of PDEs resulting from a Galerkin projection, which shows that with a small degree of freedom we can get a highly accurate solution.

The paper is organized as follows: In Sect. 2, we introduce a model problem, the structure of its polynomial chaos model and the stochastic Galerkin solution. In Sect. 3, we illustrate the main theorem of Poly-Sinc approximation. In Sect. 4, we review a Poly-Sinc collocation technique with the main collocation theorem. Finally, in Sect. 5, we investigate numerical examples. We start with a simple example in one stochastic variable and then we discuss the model with multiple stochastic variables from Sect. 2.

2 Stochastic Model Problem

In this paper, we are interested to solve the following stochastic partial differential equations:

$$\begin{aligned} \begin{aligned} \mathcal {L}(u)\equiv -\nabla \cdot (a(x,y,\Theta )\nabla u(x,y,\Theta ))&=f(x,y) \text { in } Q \times \Omega \text { and }\\ u&=0 \text { on } \partial Q \times \Omega , \end{aligned} \end{aligned}$$

(1)

where $\Theta =\left( \xi _1,\xi _2,\ldots ,\xi _K\right)$ is a vector of stochastic parameters. These parameters are independent and uniformly distributed in $I=[-1,1]$ and thus $\Theta :\Omega \longrightarrow [-1,1]^K$ with an event space $\Omega$. Moreover the domain of the spatial variables $x$ and $y$ is $Q =(0,1)^2$ or $Q =(-1,1)^2$. The function $a(x,y,\Theta )$ is defined as

$$\begin{aligned} a(x,y,\Theta )=a_0(x,y)+b_0\sum _{k=1}^K \xi _k a_k(x,y), \end{aligned}$$

(2)

where $a_k$’s are functions in $x$ and $y$ only, $b_0$ is a constant and, $\xi _k$’s are the random variables. Without loss of generality, we consider $a_0=1$ and $b_0=1/2$. We assume that $a(x,y,\Theta )\ge \alpha > 0$ for all $(x,y)\in Q$ and all $\Theta \in [-1,1]^K$. Thus the differential operator in (1) is always uniformly elliptic. Equation (2) is a truncated form of a Karhunen-Loeve expansion where the spatial functions $a_k$ can be eigenfunctions of a covariance operator and the random variables $\xi _k$ are uncorrelated, see [17]. Alternatively, we will define these spatial functions ourselves. In addition, the random variables are independent in our case.

In the rest of the section, we introduce the main concepts used in the solution of (1) with (2). Basically, we discuss the polynomial chaos in one- and multidimensional cases and the stochastic Galerkin method.

2.1 Polynomial Chaos Expansion

Generalized Polynomial Chaos (gPC) is a particular set of polynomials in a given random variable, with which an approximation of a random variable with finite second moments is computed. This procedure is named Polynomial Chaos Expansion (PCE). This technique exploits orthogonal properties of polynomials involved, to detect a representation of random variables as series of functionals. Now, the function $u$ can be expressed as an infinite series of orthogonal basis functions $\Phi _{i}$ with suitable coefficient functions $u_i$ as

$$\begin{aligned} u(x,y,\Theta ) = \sum _{i=0}^{\infty } u_i(x,y)\Phi _{i}(\Theta ). \end{aligned}$$

(3)

The expansion in (3) converges in the mean square of the probability space. The truncation form including $m+1$ basis functions leads to

$$\begin{aligned} u(x,y,\Theta )\simeq {\widetilde{u}}(x,y,\Theta )= \sum _{i=0}^m u_i(x,y)\Phi _{i}(\Theta ) \end{aligned}$$

(4)

with coefficients functions

$$\begin{aligned} u_i(x,y)= \left\langle u(x,y,\Theta ),\,\Phi _{i}(\Theta )\right\rangle , \,\,\, i=0,1,\ldots , m. \end{aligned}$$

A fundamental property of the basis functions is the orthogonality,

$$\begin{aligned} \left\langle \Phi _{i}(\Theta ),\,\Phi _{j}(\Theta )\right\rangle =\int _{I^K}\Phi _{i}(\Theta )\,\Phi _{j}(\Theta )\,W(\Theta )d\Theta = c_{i}\,\delta _{i j}, \,\, \text {for all } {i}, {j}, \end{aligned}$$

(5)

where $c_{i}$ are real positive numbers and $\delta _{i j}$ is the Kronecker-delta. In general, the inner product in (5) can be defined for different types of weighting function $W$; however, it is possible to prove that the optimal convergence rate of a gPC model can be achieved when the weighting function $W$ agrees to the joint probability density function (PDF) of the random variables considered in a standard form [9, 18]. In this framework, an optimal convergence rate means that a small number of basis functions is sufficient to obtain an accurate PC model (4). Hence, the choice of the basis functions depends only on the probability distribution of the random variables $\Theta$, and it is not influenced by the type of system under study. In particular, if the random variables $\Theta$ are independent, their joint PDF corresponds to the product of the PDFs of each random variable: in this case, the corresponding basis functions $\Phi _{i}$ can be calculated as product combinations (tensor product) of the orthogonal polynomials corresponding to each individual random variable [13, 17, 19, 20]:

$$\begin{aligned} \Phi _{i}(\Theta )=\Phi _{\mathbf {i}}(\Theta ):= \prod ^{K}_{r=1}\Phi _{i_r}^{(r)}(\xi _r),\,\, \mathbf {i}=(i_1,\ldots ,i_K), \end{aligned}$$

(6)

where $\Phi _{i_r}^{(r)}$ represents the univariate basis polynomial of degree $i_r$ associated to the $r$th random variable and with one-to-one correspondence between the integers $i$ and the multi-indices $\mathbf {i}$. We assume $\mathrm{{degree}}(\Phi _i) \le \mathrm{{degree}}(\Phi _{i+1})$ for each $i$. Now let

$$\begin{aligned} \mathcal {R}_P=\left\{ \Phi _{i}(\Theta ): \sum ^{K}_{r=1}i_r \le P\right\} , \end{aligned}$$

(7)

be the set of all multivariate polynomials up to total degree $P$. Furthermore, for random variables with specific PDFs, the optimal basis functions are known and are formed by the polynomials of the Wiener-Askey scheme [9]. For example, in the uniform probability distribution, the basis functions are the Legendre polynomials.

Using (6) and (7), it is possible to show that the total number of basis functions $m+1$ in (4) is expressed as

$$\begin{aligned} m+1=\frac{(K+P)!}{K!P!}. \end{aligned}$$

(8)

The total degree of the PC (the maximum degree) P can be chosen relatively small to achieve the desired accuracy in the solution.

In the case of the orthogonal polynomials, we can see that $\Phi _0 (\Theta )=1$ and for orthonormal polynomials

$$\begin{aligned} \left\langle \Phi _{i}(\Theta ),\,\Phi _{i}(\Theta )\right\rangle =1. \end{aligned}$$

(9)

Once a PC model in the form of (4) is obtained, stochastic moments like the mean $E(u)$ and the variance $V(u)$ can be analytically calculated by the PC expansion coefficients, see [17]. The expected value reads as

$$\begin{aligned} E\left( u(x,y,\Theta )\right) =u_0(x,y). \end{aligned}$$

The variance can be approximated by

$$\begin{aligned} V(u(x,y,\Theta )) \approx \sum ^{m}_{i=1}u^{2}_{i}(x,y). \end{aligned}$$

It is clear now that, in order to obtain a PC model in (4) and the stochastic moments, the coefficients functions $u_i (x,y)$ must be computed. The PC coefficient estimation depends on the type of the resulting system from the chaos expansion, not only the PC truncation.

2.2 Stochastic Galerkin Method

To solve the problem in (1) and (2), a Galerkin method is used along side the PC. The main idea is to assume that the solution of (1) and (2) is written as expansion in (4) and then use the PC theory introduced in the previous section. This process transform the SPDE (1) and (2) into a deterministic system of PDEs.

To recover the coefficient functions $u_i(x,y)$ we apply the inner product of (1) with the basis polynomial $\Phi _{j}(\Theta )$

$$\begin{aligned} \left\langle \mathcal {L}(\widetilde{u}) - f(x,y),\Phi _{j}(\Theta )\right\rangle =0 \,\,\,\,\, \text {for } j=0,1,\ldots ,m. \end{aligned}$$

(10)

Substituting (4) in (1) we obtain

$$\begin{aligned} \mathcal {L}(\widetilde{u})=-\nabla \cdot \left( \nabla \sum _{i=0}^m u_i(x,y)\Phi _{i}(\Theta )\right) -\frac{1}{2}\sum _{k=1}^K \xi _k \nabla \cdot \left( a_k\nabla \sum _{i=0}^m u_i(x,y)\Phi _{i}(\Theta )\right) . \end{aligned}$$

Now applying the inner residual product in (10) and use the orthogonality property of the multivariate basis $\Phi _{i}$’s to get

$$\begin{aligned} -\nabla ^2u_j-\frac{1}{2}\sum _{k=1}^K \sum _{i=0}^m \left\langle \xi _k \Phi _{i}(\Theta ),\Phi _{j}(\Theta )\right\rangle \nabla \cdot \left( a_k\nabla u_i\right) =F_j \end{aligned}$$

(11)

where $F_j(x,y) = \left\langle f(x,y),\Phi _{j}(\Theta )\right\rangle$ forms an $(m+1)$ vector and the array $\left\langle \xi _k\Phi _{i},\Phi _{j} \right\rangle$ is a triple tensor of dimension $K \times (m+1)\times (m+1)$. (11) is a system of elliptic PDEs with unknown variables $u_i(x,y)$, $i=0,1,2,\ldots ,m$. With large number of random variables $K$ (say $K \ge 5$) the size of the system in (11) becomes huge due to (8). One of our targets in the solution of the system in (11) is to use a collocation method to achieve a high accuracy with small numbers of collocation points. The proposed method in this report is to use Sinc points in a Lagrange interpolation.

2.3 Quadrature

The inner product (5) is defined by an integral. For the integration of polynomials analytic methods are used. Alternatively, we can use highly accurate quadrature techniques to evaluate the integrals exactly except for round-off errors. We omit the details of these techniques, since they can be easily found in several textbooks. For example, descriptions of Gaussian quadrature can be found in most texts on numerical analysis [21], while [22] contains descriptions of Sinc quadratures over finite, semi-infinite, infinite intervals and contours.

3 Poly-Sinc Approximation

A novel family of polynomial-like approximations that interpolate given Sinc data of the form $\left\{ (x_j , u_j)\right\} _{j=- M}^N$ where the $x_j$ are Sinc points was derived in [22] and extended in [23]. The interpolation to this data is of course accurate, provided that the function $u$ with $u_j = u (x_j)$ belongs to a suitable space of functions. We also desire approximations of the derivative of the function $u$. On the one hand, this approximation can be obtained straightforward by a differentiation of the interpolant. On the other hand, this type of approximation of the derivative may not be very accurate, as it can happen in the case of Chebyshev polynomial, or Sinc approximation. The main purpose of this interpolation was to be able to get a more accurate method of obtaining an approximation for the derivative of the function $u$ and to improve a wavelet or other method of approximation by a very simple procedure, see [23]. In [14, 24, 25], a complete theory of this approximation has been introduced where the error analysis for the function approximation, quadrature and stability have been studied. Moreover, this polynomial-like approximation (Poly-Sinc) has been used to solve singular boundary value problems based on ordinary differential equations (ODEs) and PDEs [14, 15, 26, 27].

Let us first establish some mathematical notation which we shall require. Let $\mathbb {Z}$ denote the set of all integers, $\mathbb {R}$ the real line, and $\mathbb {C}$ the complex plane $\left\{ \chi + \mathrm{i}\, \tau : \chi \in \mathbb {R}, \tau \in \mathbb {R} \right\}$. Given a number $d > 0$, we define the strip $\mathcal{{D}}_d$ as

$$\begin{aligned} \mathcal{{D}}_d = \left\{ z \in \mathbb {C} \,:\, \left| \mathcal{{I}} z\right| < d\right\} . \end{aligned}$$

Let $\mathcal {D} \subset \mathbb {C}$ be a simply connected domain having a boundary $\partial \mathcal{{D}}$, and let $a$ and $b$ denote two distinct points of $\partial \mathcal{{D}}$. Let $\phi : \mathcal{{D}} \longrightarrow \mathcal{{D}}_d$ denote a conformal map such that $\lim _{z\rightarrow a}\phi (z) = - \infty$ and $\lim _{z \rightarrow b}\phi (z) = \infty$, and let us define the inverse conformal map by $\psi ={\phi }^{-1}$, $\psi :\mathcal{{D}}_d \longrightarrow \mathcal {D}$. In addition, let $\Gamma$ be an arc defined by

$$\begin{aligned} \Gamma = \left\{ z \in [a,\,b] \,:\, z = \psi (x),\, x \in \mathbb {R} \right\} . \end{aligned}$$

For real numbers $a$ and $\Gamma \subseteq \mathbb {R}$, a one-dimensional Poly-Sinc approximation for a function $u$ defined on an arc $\Gamma$ using $n=M+N+1$ Sinc points can be obtained by applying the following Lagrange interpolation formula:

$$\begin{aligned} u(x) \approx P_n(x)=\sum _{k=-M}^N b_k(x) \, u(x_k), \, x \in \Gamma \end{aligned}$$

(12)

where $x_k = \psi (kh)$ are Sinc points on $\Gamma$ and $b_k(x)$ are Lagrange basis polynomials. These polynomial basis are defined as follows

$$\begin{aligned} b_k(x)=\frac{g(x)}{(x-x_k)\,g'(x_k)},\,\,\, g(x)=\prod _{j=-M}^{N} \left( x-x_j\right) . \end{aligned}$$

Using the interpolation (12) in calculations generates an accurate approximation with an exponentially decaying error rate which for $h = (\pi d/N)^{1/2}$ and $M = N$, by

$$\begin{aligned} \left\| u(x)-P_n(x)\right\| \le A\frac{\sqrt{N}}{B^{2N}}\, \, \exp \left( \frac{-\pi ^2 N^{\frac{1}{2}}}{2}\right) , \end{aligned}$$

(13)

and

$$\begin{aligned} \left\| u'(x)-P'_n(x)\right\| \le C\frac{\sqrt{N}}{B^{2N}}\, \, \exp \left( \frac{-\pi ^2 N^{\frac{1}{2}}}{2}\right) , \end{aligned}$$

(14)

where $\left\| .\right\|$ denotes the supremum norm on $\Gamma$ and $A>0$, $C>0$, $B>1$ are three constants, independent of $N$. For the proof of (13) and (14), see [23].

If $a$ and $b$ are finite real numbers then $\phi (x)=\log \left( (x-a)/(b-x)\right)$ and the Sinc points are $x_j=(b e^{jh}+a)/(1+e^{jh})$. For the full list of conformal maps and Sinc points, see [22, 23].

Another criterion to discuss the convergence and stability of the Poly-Sinc approximation is the Lebesgue constant. In [25] an estimate of the Lebesgue constant for Lagrange approximation at Sinc points has been derived as

$$\begin{aligned} \Lambda _{n} \approx \frac{1}{\pi }\log (n+1)+1.07618 \end{aligned}$$

(15)

where $n=M+N+1$ is the number of Sinc points in (12). The upper bound of Lebesgue constant in (15) is better than the bounds using Chebyshev and Legendre points [25]. Besides the advantage of exponential decaying of the error from using Sinc points as interpolation points in Lagrange interpolation formula, especially in a finite interval, we can see that Lagrange approximation at Sinc points delivers approximation results closer to the conjectured optimal approximation than using Chebyshev or Legendre points [25].

An extention of the one-dimensional Poly-Sinc approximation to the multi-dimensional case has been introduced in [24]. Let $X=(x_1, \ldots ,x_l)$ be a point in an l-dimensional domain Q, then Poly-Sinc approximation of a function u(X) can be defined by a nested operator as

$$\begin{aligned} u(X) \approx (P_n u)(X)=\sum _{k_1=-M_1}^{N_1} \sum _{k_2=-M_2}^{N_2} \ldots \sum _{k_l=-M_l}^{N_l} u(X_{\pmb {k}})\, b_{k_1}(x_1)b_{k_2}(x_2) \cdots b_{k_l}(x_l), \end{aligned}$$

(16)

where $X_{\pmb {k}}=(x_{1,k_1}, \ldots ,x_{l,k_l} )$ with $k_i=-M_i,\ldots ,N_i$ and $x_{i,k_i}$ are the Sinc points in one-dimension.

Next, we assume $M_i=N_i=N,\, i=1,\ldots ,l$ and $n=2N+1$ is the number of Sinc points in each dimension $i=1,2,\ldots ,l$. The convergence and stability of the approximation (16) are discussed in [24] and [25]. For the upper bound of the error $E_n$, we have

$$\begin{aligned} E_n=\left\| u(X)- (P_n u)(X) \right\| \le \sum _{i=0}^{l-1} {\left( C_i \log ^i{N}\right) \frac{\sqrt{N}}{\gamma _i^{2N}}\, \exp \left( \frac{-\pi ^2 N^{\frac{1}{2}}}{2}\right) }, \end{aligned}$$

(17)

where $C_i>0$, $\gamma _i>1$, $i=0, \ldots , l-1$ are two sets of constants, independent of $N$.

The notation $\Lambda _{n,l}$ is used to denote the Lebesgue constant using n interpolation points in each dimension $i=1,2,\ldots ,l$, i.e. $n^l$ Sinc points in total. If $P_n(X)$ is defined as in (16), then:

$$\begin{aligned} \Lambda _{n,l}\le \left( \frac{1}{\pi }\log (n+1)+1.07618\right) ^l . \end{aligned}$$

(18)

We can write the interpolation scheme in (12) and (16) in simple operator form, as

$$\begin{aligned}&u(x)\simeq \varvec{B}(x) \, U \end{aligned}$$

(19)

$$\begin{aligned}&u(X)\simeq \bigodot ^{l}_{i=1} {\varvec{B}}_i(X) \, U, \end{aligned}$$

(20)

where $U$ is vector/matrix including data of the function $u$ calculated at Sinc points.

4 Poly-Sinc Collocation Method

In [15], a collocation method based on the use of bivariate Poly-Sinc interpolation defined in (20) is introduced to solve elliptic equations defined on rectangular domains. In [26], Poly-Sinc collocation domain decomposition method for elliptic boundary value problems is investigated on complicated domains. In [27], a collocation method is introduced to solve certain type of singular differential equations. The idea of the collocation method is to reduce the boundary value problem to a system of algebraic equations which have to be solved subsequently. To start let us introduce the following collocation theorem.

Theorem 1

Let $u:\overline{Q}\rightarrow \mathbb {R}$ be an analytic bounded function on the compact domain $\overline{Q}$. Let $U=\left\{ u(x_j,y_k)\right\} ^{N}_{j,k=-N}$ be a vector, where $x_j$ and $y_k$ are the Sinc points. If ${\widetilde{U}}=\left\{ {\widetilde{u}_{j k}}\right\} ^{N}_{j,k=-N}$ is a vector satisfying

$$\begin{aligned} \left\| U-\widetilde{U}\right\| _{\infty }=\max _{j,\,k}\,\left| u_{j k}-\widetilde{u}_{j k}\right| < \delta , \end{aligned}$$

then

$$\begin{aligned} \left\| u(x,y)- \bigodot ^{2}_{i=1} {\varvec{B}}_i(x,y)\, \widetilde{U}\right\| < E_n \, + \, \delta \, \Lambda _{n,2}, \end{aligned}$$

(21)

where $n=2N+1$, $E_n$ from (17), and $\Lambda _{n,2}$ from (18).

Proof

We apply triangle inequality

$$\begin{aligned} \left\| u(x,y)-\bigodot ^{2}_{i=1} {\varvec{B}}_i(x,y)\, \widetilde{U}\right\|&\le \left\| u(x,y)-\bigodot ^{2}_{i=1} {\varvec{B}}_i(x,y)\, U \right\| \\&\quad + \left\| \bigodot ^{2}_{i=1} {\varvec{B}}_i(x,y)\, U-\bigodot ^{2}_{i=1} {\varvec{B}}_i(x,y)\, \widetilde{U} \right\| \\&\le E_n + \delta \, \left\| \bigodot ^{2}_{i=1} {\varvec{B}}_i(x,y)\right\| \\&\le E_n + \delta \, \Lambda _{n,2}, \end{aligned}$$

which is the statement of the theorem. $\square$

This theorem guarantees an accurate final approximation of $u$ on its domain of definition provided that we know a good approximation to $u$ at the Sinc points.

To set up the collocation scheme, let us consider the following partial differential operator,

$$\begin{aligned} \mathcal{{L}}u \equiv u_{x\,x}+u_{y\,y}&=f(x,y),\,\, (x,y)\in Q,\\ u(x,y)&=u_{ex}(x,y),\,\, (x,y)\in \partial Q, \nonumber \end{aligned}$$

(22)

where $Q=\left\{ a<x<b,\, c<y<d \right\}$ and $u_{x\,x}=\frac{\partial ^2 u}{\partial {x^2}}$, $u_{y\,y}=\frac{\partial ^2 u}{\partial {y^2}}$.

The first step in the collocation algorithm is to replace $u(x,y)$ in Eq. (22) by the Poly-Sinc approximation defined in (16). Next, we collocate the equation by replacing x and y by Sinc points

$$\begin{aligned} x_i=\frac{a+b\, \mathrm{{e}}^{i\, h}}{1+ \mathrm{{e}}^{i\, h}},\, i=-M,\ldots ,N \end{aligned}$$

and

$$\begin{aligned} y_q=\frac{c+d \, \mathrm{{e}}^{q\, h}}{1+\mathrm{{e}}^{q h}},\, q=-M,\ldots ,N. \end{aligned}$$

In this case, we have,

$$\begin{aligned} u_{x\,x}(x_i,y_q)\approx \sum _{k=-M}^{N}\sum _{j=-M}^N u_{j k}\, B^{''}(j,h)(x_i) B(k,h)(y_q), \end{aligned}$$

where

$$\begin{aligned} B(j,h)(x_i)=\delta _{j\,i}={\left\{ \begin{array}{ll} 0 &{} j\ne i. \\ 1 &{} j=i, \end{array}\right. } \end{aligned}$$

and $B^{''}(j,h)(x_i)$ defines an $n \times n$ matrix, with $n=M+N+1$

$$\begin{aligned} B^{''}(j,h)(x_i)=[b_{j i}]={\left\{ \begin{array}{ll} \frac{-2 g'(x_i)}{(x_i-x_j){}^2g'(x_j)}+\frac{g''(x_i)}{(x_i-x_j)g'(x_j)} &{} \text {if}\, j\ne i \\ \\ {\sum }^N_{s=-M} \, {\sum }^N_{\begin{array}{c} l=-M\\ l,s\ne i \end{array}} \frac{1}{(x_i-x_l)(x_i-x_s)}&\text {if}\, j=i. \end{array}\right. } \end{aligned}$$

So,

$$\begin{aligned} \mathcal{{U}}_{x\,x} = \left( u_{x\,x}(x_i,y_q)\right) _{i,q=-M,\ldots ,N}= \mathcal{{M}}_{1} \, \mathcal{{U}}, \end{aligned}$$

where $\mathcal{{M}}_{1}$ is a $n^2 \times n^2$ matrix defined as,

$$\begin{aligned} \mathcal{{M}}_{1}={\left\{ \begin{array}{ll} b_{j i} &{} k=q \wedge \, i,\, j,\, k,\, q=-M,\,\ldots ,\,N\\ \\ 0 &{} k\ne q \wedge \, i,\, j,\, k,\, q=-M,\,\ldots ,\,N, \end{array}\right. } \end{aligned}$$

and where $\mathcal{{U}}_{x\,x}$ is collected in a vector of of length $n^2$. Likewise, it holds that

$$\begin{aligned} \mathcal{{U}}_{y\,y} = \left( u_{y\,y}(x_i,y_q)\right) _{i,q=-M,\ldots ,N}= \mathcal{{M}}_{2} \, \mathcal{{U}}, \end{aligned}$$

where $\mathcal{{M}}_{2}$ is defined in the same way as $\mathcal{{M}}_{1}$.

The differential equation (22) has been transformed to a system of $n^2$ algebraic equations,

$$\begin{aligned} \mathcal{{A}} \, \mathcal {U}=\mathcal {F}, \end{aligned}$$

where $\mathcal {U}$ is the vector of length $n^2$ including the unknowns $u_{i q}=u(x_i , y_q)$ and

$$\begin{aligned} \mathcal{{A}}=\mathcal{{M}}_{1} +\mathcal{{M}}_{2}. \end{aligned}$$

The right hand side $\mathcal {F}$ is a vector of Length $n^2$ and defined as

$$\begin{aligned} \mathcal {F}=f(x_i,\,y_q), \, i,\, q=-M, \ldots , N. \end{aligned}$$

Now the PDE (22) was transformed to a system of $n^2$ algebraic equations in $n^2$ unknowns. The boundary conditions are collocated separately to yield 4n algebraic equations. More precisely,

$$\begin{aligned} u(a,y_j)&=u_{ex}(a,y_j) \\ u(b,y_j)&=u_{ex}(b,y_j) \\ u(x_i,c)&=u_{ex}(x_i,c) \\ u(x_i,d)&=u_{ex}(x_i,d), \end{aligned}$$

where $x_i$ and $y_j$ are the Sinc points defined on (a, b) and (c, d), respectively. Adding these 4n equations to the $n^2 \times n^2$ algebraic system, produced from the collocation of the PDE, yields a system of linear equations given by a rectangular matrix. Finally, solving this least squares problem produces the desired numerical solution.

Notes:

• In our calculations, we multiplied the algebraic equations associated to the boundary conditions by a factor $\tau = 10^3$. This scaling emphasizes the boundary values and improve the error behavior at the boundaries.

• The Poly-Sinc collocation technique is based on the collocation of the spatial variables using Sinc points. This means that it is valid also for PDEs with space-dependent coefficients. Moreover, it can be generalized to solve a system of PDEs.

5 Numerical Results

In this section, we present the computational results. Mainly, we discuss two examples. The first simple example includes one stochastic parameter. In the second example we solve the model problem introduced in Sect. 2.

5.1 One Stochastic Variable

Consider the Poisson equation in two spatial dimensions with one random parameter. This problem is described by the following SPDE

$$\begin{aligned} a(\xi )\left( u_{xx}(x,y,\xi )+u_{yy}(x,y,\xi )\right)= & {} f(x,y) \,\, \text{ on } Q\times \Omega \nonumber \\ u(x,y,\xi )= & {} 0 \,\, \text{ on } \partial Q\times \Omega , \end{aligned}$$

(23)

where $Q=(-1,1)^2$ is the spatial domain and $\Omega$ is an event space and $\xi :\Omega \rightarrow [-1,1]$ is a random variable. The function $a(\xi )=\xi + 2$ is a linear function of a uniformly distributed random variable $\xi$ and $f(x,y)=1$ for all $(x,y)\in Q$.

Now, we use the PC representation in (4) with $m=3$ to have

$$\begin{aligned} u(x,y,\xi )=\sum ^{3}_{i=0}{u_i(x,y)\,\Phi _i(\xi )}, \end{aligned}$$

(24)

where $\Phi _i$’s are the univariate orthonormal Legendre polynomials defined on $[-1,1]$. Substitution of (24) in the SPDE (23) yields the residual

$$\begin{aligned} R=(\xi + 2) \sum ^{3}_{i=0}{\left( (u_i)_{xx}+(u_i)_{yy}\right) \,\Phi _i(\xi )} - 1. \end{aligned}$$

We then perform a Galerkin projection and use the orthogonality of Legendre polynomials, which yields the system of elliptic PDEs

$$\begin{aligned} \sum ^{3}_{i=0}{\left\langle (\xi + 2)\, \Phi _i, \, \Phi _k\right\rangle }\mathcal {L}{u_i}&=\left\langle 1, \Phi _k\right\rangle \text { for } k=0,1,2,3,\,\, \text {on } Q\nonumber \\ u_i&= 0 \text { for } i=0,1,2,3\,\, \text {on } \partial Q, \end{aligned}$$

(25)

where $\mathcal {L}{u_i}=(u_i)_{xx}+(u_i)_{yy}$. It holds that $\left\langle 1, \Phi _k \right\rangle =\delta _{1 k}$.

The computational results of this example are given in the following experiments.

Experiment 1

E(u) and V(u) In this experiment, we use Poly-Sinc collocation from Sect. 4 to solve the system of PDEs in (25). In our computation, we use $N=5$, i.e. $11 \times 11$ of 2D grid of Sinc points defined on the domain Q. As a result of the Poly-Sinc solution, the coefficient functions $u_i(x,y)$ are obtained. In Fig. 1, the expectation $E(u)=u_0(x,y)$ and its contour plot are represented while in Fig. 2, the variance calculations are presented.

Fig. 1

The expectation, E(u), using $m=3$ and Poly-Sinc with $N=5$

Fig. 2

The variance, V(u), using $m=3$ and Poly-Sinc with $N=5$

Experiment 2

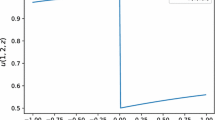
Coefficients functions As we mentioned above, to get an accurate result, just a small number of orthogonal polynomials, $\Phi _i$, is needed. In our computations, we used $m=3$, i.e. The four coefficient orthonormal Legendre polynomials. The 4 coefficients functions, $u_i (x,y),\, i=0,\ldots ,3$, are given in Fig. 3. In addition, we verify that this number is sufficient by showing that the coefficient functions $u_i$ tend to zero as m increases. The results are given in Fig. 4. In Fig. 4, the dots represent the maximum of the coefficient functions $u_i(x,y)$ on the spatial domain. We then use these maximum values in a least square estimation to find the coefficients of the decaying rate function $\alpha \, \exp (-\beta i)$, where $\alpha$ and $\beta$ are constants. In Fig. 4, the solid line represents the best fitting function with $\alpha =0.135$ and $\beta =1.2$. This means that the coefficient functions $u_i(x,y)$ follow an exponentially decay relation.

Fig. 3

Coefficients functions, $u_i (x,y),\, i=0,\ldots ,3$

Fig. 4

Logarithmic plot of maximum of coefficient functions $u_i,\,\, i=0,\ldots ,3$. The dots are the calculated maximum and the solid line represent the exponential fitting function $0.135\,e^{-1.2 \, i}$

Experiment 3

Error To discuss the convergence of Poly-Sinc solution, we need a reference (nearly exact) solution. For that, we create a discrete list of PDEs of the equation (23) at a finite set of instances of $\xi \in [-1,1]$. We choose 100 points of Gauss-Legendre nodes as values of $\xi \in [-1,1]$ and create corresponding 100 PDEs. To solve each one of these 100 equations we use Mathematica Package NDSolve. NDSolve uses a combination of highly accurate numeric schemes to solve initial and boundary value PDEs¹. We then calculate the expectation and variance of the solutions of our set of boundary value problems of PDEs. In Fig. 5, the errors in the calculations of E(u) and V(u) using $m=3$ (with orthonormal Legendre polynomials) and Poly-Sinc and the references from the 100 PDEs are presented. Using the spatial $L_2$-norm error, calculating the error in both E(u) and V(u) delivers error of order $\mathcal {O}(10^{-4})$ and $\mathcal {O}(10^{-6})$, respectively. In Fig. 6, the error between the solution of the SPDE in (23), using the method in this paper, and the reference solution is presented. We choose four instances of $\xi$.

Fig. 5

Absolute error between the Poly-Sinc calculation and the calculations obtained from 100 solutions

Fig. 6

Absolute error in u for some discrete $\xi \in \left\{ -0.757, 0, 0.757, 0.989\right\}$

Experiment 4

Comparison In this experiment we compare the Poly-Sinc solution with the classical finite difference (FD) solution. In 5-point-star FD method [28], we use an $11 \times 11$ meshing with constant step size for the spatial variables x and y, which is the same number of Sinc points used in the Poly-Sinc solution. The error between finite difference solution and the reference exact solution is given in Fig. 7. Using the spatial $L_2$-norm error, calculating the error in both E(u) and V(u) delivering error of order $\mathcal {O}(10^{-2})$. These calculations shows that for the same number of points, Poly-Sinc delivers better approximation for the solution of the SPDE. In Fig. 8 we run the calculations for different numbers of Sinc points $n=2N+1$ and use the same number of points in the FD method. In addition, we use Chebyshev and Legengdre points as interpolation points in Lagrange polynomials (Poly-Chebyshev and Poly-Legendre) and as collocation points to solve the system of the PDEs. We then calculate the $L_2$-norm errors. Figure 8 shows the decaying rates of the error, in both mean and variance, using Poly-Sinc, FD method, Poly-Chebyshev, and Poly-Legendre. We can see that the decaying rate of Poly-Sinc is better than the other methods. The comparison between Sinc points and Chebyshev points confirms the results in [23] and [25] that while increasing the number of interpolation points, Sinc points are creating less error and more stable approximation than Chebyshev points. Moreover, in [29] it has been shown that the entries of the Chebyshev differentiation matrix can be computed by explicit formulas. Some of these formulas are numerically unstable (from practical point of view) as the number of Chebyshev points increases. This might cause ill conditioned matrix or non-uniform error at the boundaries. This error affecting the overall solution of the system of the PDEs.

Fig. 7

Absolute error between the FD calculation and the calculations obtained from 100 solutions

Fig. 8

Results for Poly-Sinc method (dots), FD method with uniform meshes (rhombus), Poly-Chebyshev (squares) and, Poly-Legendre (triangles)

5.2 Multiple Stochastic Variables

We solve the model problem defined in Sect. 2 for five stochastic variables, cf. [30]. Consider the SPDE defined in (1) with $K=5$ in (2) and where,

$$\begin{aligned} a_1(x,y)&= {\frac{1}{4}} \cos (2 \pi x)\\ a_2(x,y)&= {\frac{1}{4}} \cos (2 \pi y)\\ a_3(x,y)&= {\frac{1}{16}} \cos (4 \pi x)\\ a_4(x,y)&= {\frac{1}{16}} \cos (4 \pi y)\\ a_5(x,y)&= {\frac{1}{8}} \cos (2 \pi x) \cos (2 \pi y). \end{aligned}$$

$\Theta =\left\{ \xi _k\right\} ^{5}_{k=1}$ is a set of independent random variables uniformly distributed in $[-1,1]$ and $Q=(0,1)$. For this SPDE we run four experiments.

Experiment 5

E(u) and V(u) In this experiment, we perform the Galerkin method along side the multivariate PC. For the PC parameters, we choose $K=5$ and $P=3$. Due to (8), the number of multivariate Legendre polynomials is $m+1=56$. As a result the three-dimensional array $\left\langle \xi _k \Phi _i(\Theta ),\Phi _j(\Theta )\right\rangle$ is of dimension $5 \times 56\times 56$. For the Poly-Sinc solution of the resulting system of PDEs, we use $N=5$, i.e. $n=11$ Sinc points. In Figs. 9 and 10 the expectation and variance plots are presented.

Fig. 9

The expectation, E(u), using $K=5,\, P=3$ and Poly-Sinc with $N=5$

Fig. 10

The variance, V(u), using $K=5,\, P=3$ and Poly-Sinc with $N=5$

Experiment 6

Coefficients Functions Similar to the second experiment in Example 1, we would like to study the accuracy of the polynomial expansion. In other words, study the decaying rate, to zero, of these functions. In Fig. 11, the first six coefficients functions of the Poly-Sinc solution are given. These six coefficient functions are associated to the basis polynomials of degree zero and one. In Fig. 12, the logarithmic plot of the maximum of the absolute value of the coefficient functions $u_{i-1}(x,y),\,\,i=1,\ldots ,56$ on the spatial domain is presented. We can see the fast decaying rate to zero.

Fig. 11

Coefficients functions $u_{i}(x,y),\,\,i=0,1,\ldots ,5$

Fig. 12

Logarithmic plot of maximum of coefficient functions $u_{i-1}(x,y)$ for $i=1,\ldots ,56$. The dotted lines separate the degrees of basis polynomials

Experiment 7

Error The idea of creating a set of (exact) instance solutions we used in the previous example is not applicable here as we have a set of 5 random variables. For that we need to find a different reference to check the accuracy of our solution. We use the Finite Element (FE) solution with cell meshing $10^{-3}$ to solve the stochastic Galerkin system of PDEs. The FE element method is a part of the package NDSolve“FEM” in Mathematica 11 that uses the rectangular meshing of the domain and Dirichlet boundary conditions². In Fig. 13, the error for the expectation and variance is presented. Using the $L_2$-norm error, calculating the errors in both E(u) and V(u) delivers errors of order $\mathcal {O}(10^{-4})$ and $\mathcal {O}(10^{-8})$, respectively.

Fig. 13

Absolute error between the Poly-Sinc calculation and the FE

Fig. 14

Spatial $L_2$-error. The red dots for Poly-Sinc calculations and the blue circles for FD method colour figure online (Color figure online)

Experiment 8

Comparison In this experiment we compare the Poly-Sinc solution with the 5-point-star FD method. The reference solution is the Finite Element (FE) solution with cell meshing $10^{-3}$. In Fig. 14 we run the calculations for different numbers of Sinc points $n=2N+1$ and use the same number of points in FD. We then calculate the $L_2$-norm error. These calculations show that the decaying rate of the error, in both mean and variance, is better in Poly-Sinc than the FD method. Moreover, the Poly-Sinc decaying rates of errors are following qualitatively the exponential decaying rate in (21).

6 Conclusion

In this work we have formulated an efficient and accurate collocation scheme for solving a system of elliptic PDEs resulting from an SPDE. The idea of the scheme is to use a small number of collocation points to solve a large system of PDEs. We introduced the collocation theorem based on the error rate and the Lebesgue constant of the 2D Poly-Sinc approximation. As applications, we discussed two examples, the first example with one random variable while the other with five random variables. For each case the expectation, variance, and error are discussed. The experiments show that using Poly-Sinc approximation to solve the system of PDEs is an efficient method. The number of Sinc points needed to get this accuracy is small and the error decays faster than in the classical techniques, as the finite difference method.