Abstract
Conventional reduced order modeling techniques such as the reduced basis (RB) method (relying, e.g., on proper orthogonal decomposition (POD)) may incur in severe limitations when dealing with nonlinear time-dependent parametrized PDEs, as these are strongly anchored to the assumption of modal linear superimposition they are based on. For problems featuring coherent structures that propagate over time such as transport, wave, or convection-dominated phenomena, the RB method may yield inefficient reduced order models (ROMs) when very high levels of accuracy are required. To overcome this limitation, in this work, we propose a new nonlinear approach to set ROMs by exploiting deep learning (DL) algorithms. In the resulting nonlinear ROM, which we refer to as DL-ROM, both the nonlinear trial manifold (corresponding to the set of basis functions in a linear ROM) as well as the nonlinear reduced dynamics (corresponding to the projection stage in a linear ROM) are learned in a non-intrusive way by relying on DL algorithms; the latter are trained on a set of full order model (FOM) solutions obtained for different parameter values. We show how to construct a DL-ROM for both linear and nonlinear time-dependent parametrized PDEs. Moreover, we assess its accuracy and efficiency on different parametrized PDE problems. Numerical results indicate that DL-ROMs whose dimension is equal to the intrinsic dimensionality of the PDE solutions manifold are able to efficiently approximate the solution of parametrized PDEs, especially in cases for which a huge number of POD modes would have been necessary to achieve the same degree of accuracy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The solution of a parametrized system of partial differential equations (PDEs) by means of a full-order model (FOM), whenever dealing with real-time or multi-query scenarios, entails prohibitive computational costs if the FOM is high-dimensional. In the former case, the FOM solution must be computed in a very limited amount of time; in the latter one, the FOM must be solved for a huge number of parameter instances sampled from the parameter space. Reduced order modeling techniques aim at replacing the FOM by a reduced order model (ROM), featuring a much lower dimension, which is still able to express the physical features of the problem described by the FOM. The basic assumption underlying the construction of such a ROM is that the solution of a parametrized PDE, belonging a priori to a high-dimensional (discrete) space, lies on a low-dimensional manifold embedded in this space. The goal of a ROM is then to approximate the solution manifold– that is, the set of all PDE solutions when the parameters vary in the parameter space—through a suitable, approximated trial manifold.
A widespread family of reduced order modeling techniques relies on the assumption that the reduced order approximation can be expressed by a linear combination of basis functions, built starting from a set of FOM solutions, called snapshots. Among these techniques, proper orthogonal decomposition (POD) exploits the singular value decomposition of a suitable snapshot matrix (or the eigen-decomposition of the corresponding snapshot correlation matrix), thus yielding linear ROMs, that is ROMs employing linear trial spaces, in which the ROM approximation is given by the linear superimposition of POD modes. In this case, the solution manifold is approximated through a linear trial manifold, that is, the ROM approximation is sought in a low-dimensional linear trial subspace.
Projection-based methods are linear ROMs in which the ROM approximation of the PDE solution, for any new parameter value, results from the solution of a low-dimensional (nonlinear, dynamical) system, whose unknowns are the ROM degrees of freedom (or generalized coordinates). Despite the PDE (and thus the FOM) being linear or not, the operators appearing in the ROM are obtained by imposing that the projection of the FOM residual evaluated on the ROM trial solution is orthogonal to a low-dimensional, linear test subspace, which might coincide with the trial subspace. Hence, the resulting ROM manifold is linear, that is, the ROM approximation is expressed as the linear combination of a set of basis functions. In particular, in projection-based ROMs, the reduced dynamics is obtained through a projection process onto a linear subspace [9, 10, 48]. However, linear ROMs might experience computational bottlenecks at different extents when dealing with parametrized problems featuring coherent structures (possibly dependent on parameters) that propagate over time, namely in transport and wave-type phenomena, or convection-dominated flows, as soon as the physical behavior under analysis is strongly affected by parametric dependence. Indeed, fluid flows past complex geometries, featuring either turbulence effects or shocks and boundary layers, have been addressed by linear ROMs, showing extremely good performance when the ROM is tested for the same parameter values used to collect simulation data offline [15], or when the solution exhibits a mild dependence on parametric variations [64]. For larger parametric variations, or stronger dependence of coherent structures from parameters, the dimension of the linear trial manifold can easily become extremely large (if compared to the intrinsic dimension of the solution manifold) thus compromising the ROM efficiency. To overcome this issue, ad-hoc extensions of the POD strategy have been considered, see, e.g., [43, 45].
In this paper, we propose a computational, non-intrusive approach based on deep learning (DL) algorithms to deal with the construction of efficient ROMs (which we refer to as DL-ROMs) in order to tackle parameter-dependent PDEs; in particular, we consider PDEs that feature wave-type phenomena. A comprehensive framework is presented for the global approximation of the map \((t, \varvec{\mu }) \mapsto {\mathbf {u}}_h(t, \varvec{\mu })\), where \(t \in (0,T)\) denotes time, \(\varvec{\mu } \in \mathcal {P} \subset \mathbb {R}^{n_{\mu }}\) a vector of input parameters and \( {\mathbf {u}}_h(t, \varvec{\mu }) \in \mathbb {R}^{N_h}\) the solution of a large-scale dynamical system arising from the space discretization of a parametrized, time-dependent (non)linear PDE. Several recent works have shown possible applications of DL techniques to parametrized PDEs – thanks to their approximation capabilities, their extremely favorable computational performance during online testing phases, and their relative ease of implementation – both from a theoretical [35] and a computational standpoint. Regarding this latter aspect, artificial neural networks (ANNs), such as feedforward neural networks, have been employed to model the reduced dynamics in a data-driven [55], and less intrusive way (avoiding, e.g., the costs entailed by projection-based ROMs), but still relying on a linear trial manifold built, e.g., through POD. For instance, in [26, 27, 29, 59] the solution of a (nonlinear, time-dependent) ROM for any new parameter value has been replaced by the evaluation of ANN-based regression models; similar ideas can be found, e.g., in [32, 41, 62]. Few attempts have been made in order to describe the reduced trial manifold where the approximation is sought (avoiding, e.g., the linear superimposition of POD modes) through ANNs, see, e.g., [37, 40].
For instance, a projection-based ROM technique has been introduced in [37], in which the FOM system is projected onto a nonlinear trial manifold identified by means of the decoder function of a convolutional autoencoder. However, the ROM is defined by a minimum residual formulation, for which the quasi-Newton method herein employed requires the computation of an approximated Jacobian of the residual at each time instant. A ROM technique based on a deep convolutional recurrent autoencoder has been proposed in [40], where a reduced trial manifold is generated through a convolutional autoencoder; the latter is then used to train a Long Short-Term Memory (LSTM) neural network modeling the reduced dynamics. However, even if in principle LSTMs can handle parameters through the input at each time instance or the initial hidden state, explicit parameter dependence in the PDE problem is not considered in [40], apart from \(\varvec{\mu }\)-dependent initial data. LSTMs have been recently employed in [63] to realize efficient closure models based on the Mori-Zwanzig formalism, in order to improve the stability and accuracy of projection-based ROMs; in particular, LSTMs are used as the regression model of the memory integral which represents the impact of the unresolved scales. Another promising application of machine learning techniques within a ROM framework deals with the efficient evaluation of ROM errors, see, e.g., [22, 44, 46, 61].
Our goal is to set up nonlinear ROMs whose dimension is nearly equal (if not equal) to the intrinsic dimension of the solution manifold that we aim at approximating. Our DL-ROM approach combines and improves the techniques introduced in [37, 40] by shaping an all-inclusive DL-based ROM technique, where we both (1) construct the reduced trial manifold and (2) model the reduced dynamics on it by employing ANNs. The former task is achieved by using the decoder function of a convolutional autoencoder; the latter task is instead carried out by considering a feedforward neural network and the encoder function of a convolutional autoencoder. Moreover, we set up a computational procedure performing the training of both network architectures simultaneously, by minimizing a loss function that weights two terms, one dedicated to each single task. In this respect, we are able to design a flexible framework capable of handling parameters affecting both PDE operators and data, which avoids both the expensive projection stage of [37] and the training of a more expensive LSTM network. In our technique, the intrusive construction of a ROM is replaced by the evaluation of the ROM generalized coordinates through a deep feedforward neural network taking only \((t, \varvec{\mu })\) as inputs. The proposed technique is purely data-driven, that is, it only relies on the computation of a set of FOM snapshots—in this respect, we do not replace standard numerical methods to solve the FOM by DL algorithms as, e.g., in the works by Karniadakis and coauthors [50,51,52,53,54] where the FOM is replaced by a physics-informed neural network (PINN) trained by minimizing the residual of the PDE; rather, DL techniques are built upon the high-fidelity FOM, to enhance its repeated evaluation for different values of the parameters.
The structure of the paper is as follows. In Sect. 2 we show how to generate nonlinear ROMs by reinterpreting the classical ideas behind linear ROMs for parametrized PDEs. In Sect. 3 we detail the construction of the proposed DL-ROM, whose accuracy and efficiency are numerically assessed in Sect. 4 by considering three different test cases of increasing complexity (with respect to the parametric dependence, the nature of the PDE, and the spatial dimension). Finally, the conclusions are drawn in Sect. 5. A quick overview of useful facts about neural networks is reported in the Appendix A to make the paper self-contained.
2 From Linear to Nonlinear Dimensionality Reduction
Starting from the well-known setting of linear (projection-based) ROMs, in this section we generalize this task to the case of nonlinear ROMs.
2.1 Problem Formulation
We formulate the construction of ROMs in algebraic terms, starting from the high-fidelity (spatial) approximation of nonlinear, time-dependent, parametrized PDEs. By introducing suitable space discretizations techniques (such as, e.g., the Finite Element method, Isogeometric Analysis or the Spectral Element method) the high-fidelity, full order model (FOM) can be expressed as a nonlinear parametrized dynamical system. Given \(\varvec{\mu } \in \mathcal {P}\), we aim at solving the initial value problem
where the parameter space \(\mathcal {P} \subset \mathbb {R}^{n_{\varvec{\mu }}}\) is a bounded and closed set, \(\mathbf {u}_h:[0,T) \times \mathcal {P} \rightarrow \mathbb {R}^{N_h}\) is the parametrized solution of (1), \(\mathbf {u}_0 : \mathcal {P} \rightarrow \mathbb {R}^{N_h}\) is the initial datum and \(\mathbf {f} : (0,T) \times \mathbb {R}^{N_h} \times \mathcal {P} \rightarrow \mathbb {R}^{N_h}\) is a (nonlinear) function, encoding the system dynamics.
The FOM dimension \(N_h\) is related with the finite dimensional subspaces introduced for the space discretization of the PDE – here \(h>0\) usually denotes a discretization parameter, such as the maximum diameter of elements in a computational mesh – and can be extremely small whenever the PDE problem shows complex physical behaviors and/or high degrees of accuracy are required to its solution. The parameter \(\varvec{\mu } \in \mathcal {P}\) may represent physical or geometrical properties of the system, like, e.g., material properties, initial and boundary conditions, or the shape of the domain. In order to solve problem (1), suitable time discretizations are employed, such as backward differentiation formulas [49].
Our goal is the efficient numerical approximation of the whole set
of solutions to problem (1) when \((t ; \varvec{\mu } )\) varies in \([0, T) \times \mathcal {P} \), also referred to as solution manifold (a sketch is provided in Fig. 1). Assuming that, for any given parameter \(\varvec{\mu } \in \mathcal {P}\), problem (1) admits a unique solution, for each \(t \in (0,T)\), the intrinsic dimension of the solution manifold is at most \(n_{\varvec{\mu }} + 1 \ll N_h\), where \(n_{\varvec{\mu }}\) is the number of parameters (time plays the role of an additional coordinate). This means that each point \(\mathbf {u}_h(t ; \varvec{\mu } )\) belonging to \(\mathcal {S}_h\) is completely defined in terms of at most \(n_{\varvec{\mu }} + 1\) intrinsic coordinates, or equivalently, the tangent space to the manifold at any given \(\mathbf {u}_h(t ; \varvec{\mu } )\) is spanned by \(n_{\varvec{\mu }} + 1\) basis vectors.
2.2 Linear Dimensionality Reduction: Projection-Based ROMs
The most common way to build a ROM for approximating problem (1) relies on the introduction of a reduced linear trial manifold, that is of a subspace \(\tilde{\mathcal {S}}_n = \text {Col}(V)\) of dimension \(n \ll N_h\), spanned by the n columns of a matrix \(V \in \mathbb {R}^{N_h \times n}\). Hence, a linear ROM looks for an approximation \({\tilde{\mathbf {u}}}_h(t; \varvec{\mu }) \approx \mathbf {u}_h(t; \varvec{\mu })\) in the form
where \({\tilde{\mathbf {u}}}_h : [0,T) \times \mathcal {P} \rightarrow \tilde{\mathcal {S}}_n\).
Here \(\mathbf {u}_n(t; \varvec{\mu }) \in \mathbb {R}^n\) for each \(t \in [0,T)\), \(\varvec{\mu } \in \mathcal {P}\) denotes the vector of intrinsic coordinates (or degrees of freedom) of the ROM approximation; note that the map
that, given the (low-dimensional) intrinsic coordinates, returns the (high-dimensional) approximation of the FOM solution \({\mathbf {u}}_h(t; \varvec{\mu })\), is linear.
POD is one of the most widely employed techniques to generate the linear trial manifold [48]. Considering a set of \(N_{train}\) instances of the parameter \(\varvec{\mu }\in \mathcal {P}\), we introduce the snapshot matrix \(S \in \mathbb {R}^{N_h \times N_s}\),
considering a partition of [0, T] in \(N_t\) time steps \(\{t^k\}_{{k=1}}^{N_t}\), \(t^k = k \Delta t\), of size \(\Delta t =T/N_t\) and \(N_s = N_{train}N_t\). Moreover, let us introduce a symmetric and positive definite matrix \(X_h \in \mathbb {R}^{N_h \times N_h}\) encoding a suitable norm (e.g., the energy norm) on the high-dimensional space and admitting a Cholesky factorization \(X_h = H^T H\). POD computes the singular value decomposition (SVD) of HS,
where \(U = [\varvec{\zeta }_1| \ldots | \varvec{\zeta }_{N_h}] \in \mathbb {R}^{N_h \times N_h}\), \(Z = [\varvec{\psi }_1| \ldots | \varvec{\psi }_{N_s}] \in \mathbb {R}^{N_s \times N_s}\) and \(\Sigma = \text {diag}(\sigma _1, \ldots , \sigma _r) \in \mathbb {R}^{N_h \times N_s}\) with \(\sigma _1 \ge \sigma _2 \ge \ldots \ge \sigma _r\), and \(r \le \min (N_h, N_s)\), and sets the columns of V in terms of the first n left singular vectors of S that is, \(V = [H^{-1} \varvec{\zeta }_1 | \ldots | H^{-1} \varvec{\zeta }_n]\). By construction, the columns of V are orthonormal (with respect to the scalar product \(( \, \cdot \, , \, \cdot \,)_{X_h}\)) and among all possible n-dimensional subspaces spanned by the column of a matrix \(W \in \mathbb {R}^{N_h \times n}\), V provides the best reconstruction of the snapshots, that is,
where \(\mathcal {V}_{n} = \{ W \in \mathbb {R}^{N_h \times n} : W^T X_h W = I \}\); here \(V V^T X_h \mathbf {u}_h(t; \varvec{\mu })\) is the optimal-POD reconstruction of \(\mathbf {u}_h(t; \varvec{\mu })\) onto a reduced subspace of dimension \(n < N_h\).
To model the reduced dynamics of the system, that is, the time-evolution of the generalized coordinates \(\mathbf {u}_n(t; \varvec{\mu })\), we can replace \(\mathbf {u}_h(t; \varvec{\mu })\) by (3) in system (1),
and impose that the residual
associated to the first equation of (5) is orthogonal to an n-dimensional subspace spanned by the column of a matrix \(Y \in \mathbb {R}^{N_h \times n}\), that is, \(Y^T \mathbf {r}_h(V\mathbf {u}_n) = \mathbf{0}\). This condition yields the following ROM
If \(Y=V\), a Galerkin projection is performed, while the case \(Y \ne V\) yields a more general Petrov-Galerkin projection. Note that choosing Y such that \(Y^T V = I \in \mathbb {R}^{N_h \times N_h}\) does not automatically ensure ROM stability on long time intervals.
Although POD-(Petrov-)Galerkin methods have been successfully applied to a broad range of parametrized time-dependent (non)linear problems (see, e.g., [39, 45]), they usually provide low-dimensional subspaces of dimension \(n \gg n_{\mu } + 1\) much larger than the intrinsic dimension of the solution manifold – relying on a linear, global trial manifold thus represents a major bottleneck to computational efficiency [43, 45]. The same difficulty may also affect hyper-reduction techniques, such as the (discrete) empirical interpolation method [8, 16]. Such hyper-reduction techniques are essential to assemble the operators appearing in the ROM (7) in order not to rely on expensive \(N_h\)-dimensional arrays [20].
2.3 Nonlinear Dimensionality Reduction
A first attempt to overcome the computational issues entailed by the use of a linear, global trial manifold is to build a piecewise linear trial manifold, using local reduced bases whose dimension is smaller than the one of the global linear trial manifold. Clustering algorithms applied on a set of snapshots can be employed to partition them into \(N_c\) clusters from which POD can extract a subspace of reduced dimension; the ROM is then obtained by following the strategy described above on each cluster separately [5, 6]. An alternative approach based on classification binary trees has been introduced in [4]. These strategies have been employed (and compared) in [45] in order to solve parametrized problems in cardiac electrophysiology. Using a piecewise linear trial manifold only partially overcomes the limitation of linear ROMs; indeed local bases might still have a dimension which is much higher than the intrinsic dimension of the solution manifold \(\mathcal {S}_h\). An approach based on a dictionary of solutions, computed offline, has been developed in [2] as an alternative to using POD modes, together with an online \(L^1\)-norm minimization of the residual.
Other possible options involving nonlinear transformations of modes might rely on a reconstruction of the POD modes at each time step using Lax pairs [23], on the solution of Monge-Kantorovich optimal transport problems [31], on a problem-dependent change of coordinates requiring the solution of an optimization problem repeatedly [14], on shifted POD modes [56] after multiple transport velocities have been identified and separated, or again basis updates are derived from querying the FOM at a few selected spatial coordinates [47]. Despite providing remarkable improvements compared to the classic (Petrov-)Galerkin-POD approach, all these strategies exhibit some drawbacks, such as: (1) the high computational costs entailed during the online testing evaluation stage of the ROM – which is not restricted to the intensive offline training stage; (2) performance and settings are highly dependent on the problem at hand; (3) the need to deal only with a linear superimposition of modes (which characterizes linear ROMs), yielding low-dimensional spaces whose dimension is still (much) higher than the intrinsic dimension of the solution manifold.
Motivated by the need of avoiding the drawbacks of linear ROMs and setting a general paradigm for the construction of efficient, extremely low-dimensional ROMs, we resort to nonlinear dimensionality reduction techniques.
We build a nonlinear ROM to approximate \( \mathbf {u}_h(t; \varvec{\mu }) \approx {\tilde{\mathbf {u}}}_h(t; \varvec{\mu })\) by
where \(\varvec{\varPsi }_h : \mathbb {R}^{n} \rightarrow \mathbb {R}^{N_h}\), \(\varvec{\varPsi }_h : \mathbf {s}_n \mapsto \varvec{\varPsi }_h(\mathbf {s}_n)\), \(n \ll N_h\), is a nonlinear, differentiable function; similar approaches can be found in [37, 40]. As a matter of fact, the solution manifold \(\mathcal {S}_h\) is approximated by a reduced nonlinear trial manifold
so that \({\tilde{\mathbf {u}}}_h : [0,T) \times \mathcal {P} \rightarrow \tilde{\mathcal {S}}_n\). As before, \(\mathbf {u}_n: [0,T) \times \mathcal {P} \rightarrow \mathbb {R}^{n}\) denotes the vector-valued function of two arguments representing the intrinsic coordinates of the ROM approximation. Our goal is to set a ROM whose dimension n is as close as possible to the intrinsic dimension \(n_{\varvec{\mu }} + 1\) of the solution manifold \(\mathcal {S}_h\), i.e. \(n \ge n_{\varvec{\mu }} + 1\), in order to correctly capture the solution of the dynamical system by containing the size of the approximation spaces [37].
To model the relationship between each couple \((t, \varvec{\mu }) \mapsto \mathbf {u}_n(t, \varvec{\mu })\), and to describe the system dynamics on the reduced nonlinear trial manifold \(\tilde{\mathcal {S}}_n\) in terms of the intrinsic coordinates, we consider a nonlinear map under the form
where \(\varvec{\varPhi }_n : [0, T) \times \mathbb {R}^{n_{\varvec{\mu }}} \rightarrow \mathbb {R}^{n}\) is a differentiable, nonlinear function. No additional assumptions such as, e.g., the (exact, or approximate) affine \(\varvec{\mu }\)-dependence as in the RB method, are required.
3 A Deep Learning-Based Reduced Order Model (DL-ROM)
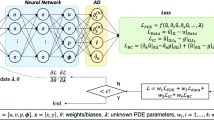
We now detail the construction of the proposed nonlinear ROM. In this respect, we define the functions \(\varvec{\varPsi }_h\) and \(\varvec{\varPhi }_n\) in (8) and (10) by means of DL algorithms, exploiting neural network architectures. Besides their ability of effectively approximating nonlinear maps, learning from data, and generalizing to unseen data, neural networks enable us to build non-intrusive, purely data-driven ROMs. In particular, the construction of DL-ROMs only requires to access the snapshot matrix and the corresponding parameter values, but not the high-dimensional FOM operators appearing in (1). The DL-ROM technique is composed by two main blocks responsible, respectively, for the reduced dynamics learning and the reduced trial manifold learning (see Fig. 2). Hereon, we denote by \(N_{train}\), \(N_{test}\) and \(N_t\) the number of training-parameter, testing-parameter, and time instances, respectively, and set \(N_{s} = N_{train} N_t\). The dimension of both the FOM solution and the ROM approximation is \(N_h\), while \(n \ll N_h\) denotes the number of intrinsic coordinates.
For the description of the system dynamics on the reduced nonlinear trial manifold (reduced dynamics learning), we employ a deep feedforward neural network (DFNN) with L layers, that is, we define the function \(\varvec{\varPhi }_n\) in (10) as
thus yielding the map
where \(\varvec{\phi }_n^{DF}\) takes the form (31), with \({t \in [0,T)}\), and results from the subsequent composition of a nonlinear activation function, with a linear transformation of the input, L times. Here \(\varvec{\theta }_{DF}\) denotes the vector of parameters of the DFNN.
Regarding instead the description of the reduced nonlinear trial manifold \(\tilde{\mathcal {S}}_n\) defined in (9) (reduced trial manifold learning), we employ the decoder function of a convolutional autoencoder (AE), that is, we define the function \(\varvec{\varPsi }_h\) appearing in (8) and (9) as
thus yielding the map
where \(\mathbf {f}_{h}^D\) results from the composition of several (possibly, convolutional) layers, overall depending on the vector \(\varvec{\theta }_{D}\) of parameters of the decoder function.
Combining the two former stages, the DL-ROM approximation is given by
where \(\varvec{\phi }_n^{DF} (\cdot ; \cdot , \varvec{\theta }_{DF}) : [0, T) \times \mathbb {R}^{n_{\varvec{\mu }}} \rightarrow \mathbb {R}^{n}\) and \(\mathbf {f}_{h}^D (\cdot ; \varvec{\theta }_{D}) : \mathbb {R}^{n} \rightarrow \mathbb {R}^{N_h}\) are defined as in (11) and (12), respectively, and \(\varvec{\theta } = (\varvec{\theta }_{DF}, \varvec{\theta }_{D})\) are the parameters defining the neural network. The architecture of DL-ROM is shown in Fig. 2.
Computing the ROM approximation (13) for any new value of \(\varvec{\mu } \in \mathcal {P}\), at any given time, requires evaluation of the map \((t, \varvec{\mu }) \rightarrow {\tilde{\mathbf {u}}}_h(t; \varvec{\mu }, \varvec{\theta })\) at the testing stage, once the parameters \(\varvec{\theta } = (\varvec{\theta }_{DF}, \varvec{\theta }_{D})\) have been determined, once and for all, during the training stage. The training stage consists in solving an optimization problem (in the variable \(\varvec{\theta }\)) after a set of snapshots of the FOM have been computed. More precisely, provided the parameter matrix \(M \in \mathbb {R}^{(n_{\varvec{\mu }} + 1) \times N_{s}}\) defined as
and the snapshot matrix S, we find the optimal parameters \(\varvec{\theta }^*\) solution of
where
To solve the optimization problem (15 and 16) we use the ADAM algorithm [33] which is a stochastic gradient descent method [57] computing an adaptive approximation of the first and second momentum of the gradients of the loss function. In particular, it computes exponentially weighted moving averages of the gradients and of the squared gradients. We set the starting learning rate to \(\eta = 10^{-4}\), the batch size to \(N_b = 20\) and the maximum number of epochs to \(N_{epochs} = 10000\). We perform cross-validation, in order to tune the hyperparameters of the DL-ROM, by splitting the data in training and validation sets, with a proportion 8:2. Moreover, we implement an early-stopping regularization technique to reduce overfitting [25], arresting the training if the loss does not decrease over 500 epochs. As nonlinear activation function we employ the ELU function [18] defined as
No activation function is applied at the last convolutional layer of the decoder neural network, as usually done when dealing with AEs. The parameters, weights and biases, are initialized through the He uniform initialization [28].
As we rely on a convolutional AE to define the function \(\varvec{\varPsi }_h\), we also exploit the encoder function
which maps each FOM solution associated to \((t; \varvec{\mu }) \in \text {Col}(M)\) provided as inputs to the feedforward neural network (11), onto a low-dimensional representation \(\tilde{\mathbf {u}}_n(t; \varvec{\mu }, \varvec{\theta }_E)\) depending on the parameters vector \(\varvec{\theta }_E\) defining the encoder function.
Indeed, the actual architecture of DL-ROM used only during the training and the validation phases, but not during testing, is the one shown in Fig. 3.
In practice, we add to the DL-ROM architecture introduced above the encoder function of the convolutional AE. This produces an additional term in the per-example loss function (16), yielding the following optimization problem:
where
and \(\varvec{\theta } = (\varvec{\theta }_{E}, \varvec{\theta }_{DF}, \varvec{\theta }_{D})\), with \(\omega _h \in [0,1]\). The per-example loss function (19) combines the reconstruction error (that is, the error between the FOM solution and the DL-ROM approximation) and the error between the intrinsic coordinates and the output of the encoder.
Remark 1
Training the convolutional AE and the DFNN simultaneously by including in the loss function the second term appearing in (19) allows to improve the overall DL-ROM performance. Indeed, feeding the intrinsic coordinates (provided as outputs by the DFNN) as inputs to the decoder function \(\mathbf {f}_h^D\), enhances the model robustness, making the neural network stable with respect to possible perturbations affecting the output of the DFNN \(\mathbf {u}_n\). Moreover, training the neural networks all at once results in updates of the DFNN parameters \(\varvec{\theta }_{DF}\) depending not only on the gradients of the error between the intrinsic coordinates and the encoder output, but also on the gradients of the reconstruction error. On the test cases presented in this work, training the convolutional AE and the DFNN simultaneously impacts both on the accuracy and computational times. For instance, as we will see in Test 3.1, training the convolutional AE and the DFNN separately, which consists in training the convolutional AE, projecting the FOM snapshots onto the latent space to generate training data for the DFNN, and finally training the DFNN, entails a 15\(\%\) more expensive training stage, however yielding a higher error indicator \(\epsilon _{rel} = 7.2 \times 10^{-3}\) (compared to the value reported in Fig. 19).
3.1 Training and Testing Algorithms
Let us now detail the algorithms through which the training and testing phases of the networks are performed. First of all, data normalization and standardization enhance the training phase of the network by rescaling all the dataset values to a common frame. For this reason, the inputs and the output of DL-ROM are rescaled in the range [0, 1] by applying an affine transformation. In particular, provided the training parameter matrix \(M^{train} \in \mathbb {R}^{(n_{\varvec{\mu }} + 1) \times N_s}\), we define
so that data are normalized by applying the following transformation
Each feature of the training parameter matrix is rescaled according to its maximum and minimum values. Regarding instead the training snapshot matrix \(S^{train} \in \mathbb {R}^{N_h \times N_s}\), we define
and apply transformation (21) by replacing \(M_{max}^i, M_{min}^i\) with \(S_{max}, S_{min} \in \mathbb {R}\), respectively, that is. we use the same maximum and minimum values for all the features of the snapshot matrix, as in [37, 40]. Using the latter approach or employing each feature’s maximum and minimum values, for the matrix \(S^{train}\), does not lead to remarkable changes in the DL-ROM performance. Transformation (21) is applied also to the validation and testing sets, but considering as maximum and minimum the values computed over the training set. In order to rescale the reconstructed solution to the original values, we apply the inverse transformation of (21). We point out that the input of the encoder function, the FOM solution \(\mathbf {u}_h = \mathbf {u}_h(t^k; \varvec{\mu }_i)\) for a given (time, parameter) instance \((t^k, \varvec{\mu }_i)\), is reshaped into a matrix. In particular, starting from \(\mathbf {u}_h \in \mathbb {R}^{N_h}\), we apply the transformation \(\mathbf {u}_h^R\)=reshape\((\mathbf {u}_h)\) where \(\mathbf {u}_h^R \in \mathbb {R}^{N_h^{1/2} \times N_h^{1/2}}\). If \(N_h \ne 4^{m}\), \(m \in \mathbb {N}\), the input \(\mathbf {u}_h\) is zero-padded [25]. For the sake of simplicity, we continue to refer to the reshaped FOM solution as to \(\mathbf {u}_h\). The inverse reshaping transformation is applied to the output of the last convolutional layer in the decoder function, yielding the ROM approximation. Note that applying one of the functions (11, 12, 17) to a matrix means applying it row-wise. The reduced dimension is chosen through hyperparameters tuning, i.e. we start from \(n =n_{\mu } + 1\) and select a different value of n only if it leads to a significant increase of the performance of the neural network.
The training algorithm referring to the DL-ROM architecture of Fig. 3 is reported in Algorithm 1. During the training phase, the optimal parameters of the DL-ROM neural network are found by solving the optimization problem (18 and 19) through back-propagation and ADAM algorithms.

At testing time, the encoder function is instead discarded (the DL-ROM architecture is the one shown in Fig. 2) and the testing algorithm is provided by Algorithm 2. The testing phase corresponds to a forward step of the DL-ROM neural network in Fig. 2. We remark that with \(\widetilde{S}_n\) we refer to a matrix collecting column-wise the output of the encoder function of the convolutional AE (17) applied to each column of the snapshot matrix S. In the same way, the columns of \({S}_n\) collect the intrinsic coordinates, output of the DFNN (12), for each sample in the parameter matrix M, and \(\widetilde{S}_h\) is a matrix whose columns are the ROM approximations, outputs of the decoder function of the convolutional AE (13), associated to the columns of \({S}_n\).

We implement the neural networks required by the DL-ROM technique by means of the Tensorflow DL framework [1]; numerical simulations are performed on a workstation equipped with an Nvidia GeForce GTX 1070 8 GB GPU.
4 Numerical Results
In this section, we report the numerical results obtained by applying the proposed DL-ROM technique to three parametrized, time-dependent PDE problems, namely (1) Burgers equation, (2) a linear transport equation, and (3) a coupled PDE-ODE system arising from cardiac electrophysiology; this latter is a system of time dependent, nonlinear equations, whose solutions feature a traveling wave behavior. We deal with problems set in \(d=1, 2\) (spatial) dimensions. In the one-dimensional test cases we aim at assessing the numerical accuracy of the DL-ROM approximation, comparing it to the solution provided by a POD-Galerkin ROM, which features linear (possibly, piecewise linear) trial manifolds. In the two-dimensional test case we instead focus on computational efficiency, by comparing the computational times of DL-ROM to the ones entailed by a POD-Galerkin method.
To evaluate the performance of DL-ROM we rely on the loss function (19) and on the following error indicator
4.1 Test 1: Burgers Equation
Let us consider the parametrized one-dimensional nonlinear Burgers equation
where
with \(A_0 = \exp (\mu / 8)\), \(L = 1\) and \(T =2\). System (24) has been discretized in space by means of linear finite elements, with \(N_h =256\) grid points, and in time by means of the Backward Euler scheme, with \(N_t = 100\) time instances. The parameter space, to which belongs the single (\(n_{\mu } = 1\)) parameter, is given by \(\mathcal {P} = [100, 1000]\). We consider \(N_{train} = 20\) training-parameter instances uniformly distributed over \(\mathcal {P}\) and \(N_{test} = 19\) testing-parameter instances, each of them corresponding to the midpoint between two consecutive training-parameter instances.
The configuration of the DL-ROM neural network used for this test case is the following. We choose a 12-layer DFNN equipped with 50 neurons per hidden layer and n neurons in the output layer, where n corresponds to the dimension of the reduced trial manifold. The architectures of the encoder and decoder functions are instead reported in Tables 1 and 2, and are similar to the ones used in [37]. The total number of parameters (i.e., weights and biases) of the neural network is equal to 393051.
Problem (24) does not represent a remarkably challenging task for linear ROMs, such as the POD-Galerkin method. Indeed, by using the POD method on the snapshot matrix (the latter built by collecting the solution of (24) for \(N_s = N_{train}N_t\) training-parameter instances), we find that a linear trial manifold of dimension 20 is enough to capture more than the 99.99\(\%\) of the energy of the system [48, 59]. In order to assess the DL-ROM performance, we compute the DL-ROM solution by fixing the dimension of the nonlinear trial manifold to \(n=20\). In Fig. 4 we compare the DL-ROM and the FOM solutions, with the optimal-POD reconstructions as measured by the discrete 2-norm (that is, the projection of the FOM solution onto the POD linear trial manifold of dimension 20 for \(t = 0.02\) and the testing-parameter instance \(\mu _{test} = 976.32\)).
The latter testing value has been selected as the instance of \(\mu \) for which the reconstruction task results to be the most difficult both for POD and DL-ROM, being the diffusion term in (24) smaller and the solution closer to the one of a purely hyperbolic system. In particular, for \(\mu _{test} = 976.32\), employing the DL-ROM technique allows us to halve the error indicator \(\epsilon _{rel}\) associated to the optimal-POD reconstruction. Referring to Fig. 4, the DL-ROM approximation is more accurate than the optimal-POD reconstruction, indeed it mostly fits the FOM solution, even in correspondence of its maximum, as shown in Fig. 4. The same comparison of Fig. 4, but with a reduced dimension \(n=10\), is shown in Fig. 5, where the difference in terms of accuracy is even more remarkable.
Finally, in Fig. 6 we highlight the accuracy properties of both the DL-ROM and POD techniques by displaying the behavior of the error indicator \(\epsilon _{rel}\), defined in (23), with respect to the dimension n of the corresponding reduced trial manifold. For \(n < 20\) the DL-ROM approximation is more accurate than the one provided by POD, and only for \(n = 20\) the two techniques provide almost the same accuracy. The lack of convergence of the DL-ROM technique, with respect to n, is related to the almost unchanged capacity of the neural network. In particular, by increasing the dimension n, for example, from 2 to 20, the total number of parameters of the DL-ROM neural network varies from 393051 to 403203, that is we are increasing the total number of weights and biases by almost the 2.5\(\%\), thus resulting in a slightly enhancement of the network capacity. Moreover, similar trends of suitable indicators of the error between the FOM and the ROM approximation with respect to the reduced dimension can also be observed in [11, 29].
4.2 Test 2: Linear Transport equation
4.2.1 Test 2.1: \(n_{\mu } = 1\) Input Parameter
First, we consider the parametrized one-dimensional linear transport equation
whose solution is \(u(x, t) = u_0(x - \mu t)\); here \(u_0(x) = (1/\sqrt{2 \pi \sigma }) e^{-x^2/2 \sigma }\) and \(T = 1\).
Here the parameter represents the velocity of the traveling wave, varying in the parameter space \(\mathcal {P} = [0.775, 1.25]\); we set \(\sigma = 10^{-4}\). The dataset is built by uniformly sampling the exact solution in the domain \((0, L) \times (0, T)\), with \(L = 1\), considering \(N_h = 256\) degrees of freedom in the space discretization and \(N_t = 200\) time instances. We consider \(N_{train} = 20\) training-parameter instances uniformly distributed over \(\mathcal {P}\) and \(N_{test} = 19\) testing-parameter instances such that \(\mu _{test,i}= ( \mu _{train,i}+ \mu _{train,i+1})/2\), for \(i = 1, \ldots , N_{test}\). This test case, and more in general hyperbolic problems, are examples in which the use of a linear approach to ROM might yield a loss of accuracy. Indeed, the dimension of the linear trial manifold must be very large, if compared to the dimension of the solution manifold, in order to capture the variability of the FOM solution over the parameter space \(\mathcal {P}\).
Figure 7 shows the exact solution and the DL-ROM approximation for the testing-parameter instance \(\mu _{test} = 0.8625\); here, we set the dimension of the nonlinear trial manifold to \(n = 2\), equal to the dimension \(n_{\mu } + 1\) of the solution manifold. Moreover, in Fig. 7 we also report the relative error \(\varvec{\epsilon }_k \in \mathbb {R}^{N_h}\), for \(k = 1, \ldots , N_t\), associated to the selected \(\varvec{\mu }_{test} \in \mathcal {P}\), defined as
whose largest values are found in proximity of the largest variations of the solution.
In Fig. 8 we report the exact solution and the DL-ROM approximation with \(n = 2\), at three particular time instances. To compare the performance of DL-ROM with a linear ROM, we performed POD on the snapshot matrix and report, for the same testing-parameter instance, the optimal-POD reconstruction as measured by the 2-norm (that is, the projection of the exact solution onto the POD linear trial manifold). Still with \(n=50\) POD modes, the optimal-POD reconstruction is affected by spurious oscillations. On the other hand, the DL-ROM approximation with \(n = 2\) yields an error indicator \(\epsilon _{rel} = 8.74 \times 10^{-3}\); to achieve the same accuracy obtained through DL-ROM over the testing set, a linear trial manifold should have dimension \(n = 90\).
Figure 9 shows the behavior of the error indicator (23) with respect to the reduced dimension n. By increasing the dimension n of the nonlinear trial manifold there is a mild improvement of the DL-ROM performance, i.e. the error indicator slightly decreases; however, such an improvement is not significant, in general: in this range of n, indeed, the number of parameters of the DL-ROM neural network slightly increases, thus implying almost the same approximation capability.
Remark 2
(Hyperparameters tuning). The hyperparameters of the DL-ROM neural network are tuned by evaluating the loss function over the validation set and by setting each of them equal to the value minimizing the generalization error on the validation set. In particular, we show the tests performed to choose the size of the (transposed) convolutional kernels in the (decoder) encoder function, the number of hidden layers in the DFNN and the number of neurons for each hidden layer. The hyperparameters evaluation starts from the default configuration in Table 3.
Then, the best values are found iteratively by inspecting the impact of the variation of a single hyperparameter at a time on the validation loss. Once the best value of each hyperparameter is found, it replaces the default value from that point on. For each hyperparameter the tuning is performed in a range of values for which the training of the network is computationally affordable.
In Fig. 10, we show the impact of the size of the convolutional kernels on the loss over the validation and testing sets, the number of hidden layers in the DFNN and the number of neurons in each hidden layer by varying the reduced dimension in order to find the best value of such hyperparameter over n. The final configuration of the DL-ROM neural network is the one provided in Table 4.
4.2.2 Test 2.2: \(n_{\mu } = 2\) Input Parameters
Here we consider again the parametrized one-dimensional transport equation (25), whose exact solution is \(u(x, t) = u_0(x - t; \varvec{\mu })\); however, we now take
as initial datum, where \(\varvec{\mu }=[\mu _1, \mu _2]^T\). The \(n_{\mu }=2\) parameters belong to the parameter space \(\mathcal {P} = \mathcal {P}_{\mu _1} \times \mathcal {P}_{\mu _2} = [0.025, 0.25] \times [0.5, 1]\). We build the dataset by uniformly sampling the exact solution in the domain \((0, L) \times (0, T)\), with \(L = 1\) and \(T=1\), and by considering \(N_h = 256\) grid points for the space discretization and \(N_t = 100\) time instances. We collect, both for \(\mu _1\) and \(\mu _2\), \(N_{train} = 21\) training-parameter instances uniformly distributed in the parameter space \(\mathcal {P}\) and \(N_{test} = 20\) testing-parameter instances, selected as in the other test cases. Equation (25), completed with the initial datum (27), represents a challenging test bed for linear ROMs because of the difficulty to accurately reconstruct the jump discontinuity of the exact solution as a linear combination of basis functions computed from the snapshots, for a testing-parameter instance. The architecture of the DL-ROM neural network used here is the one presented in the Test 2.1.
In Fig. 11 we show the exact solution and the DL-ROM approximation obtained by setting \(n=3\) (thus equal to \(n_{\mu } + 1\)) for the testing-parameter instance \(\varvec{\mu }_{test} = (0.154375, 0.6375)\), along with the relative error \(\varvec{\epsilon }_k\), defined in (26). Also in this case, the relative error is larger close to the solution discontinuity.
In Fig. 12 we report the DL-ROM approximation, the optimal-POD reconstruction, as measured in the 2-norm, and the exact solution, for the time instances \(t = 0.245, 0.495\) and 0.745, and the testing-parameter instance \(\varvec{\mu }_{test} = (0.154375, 0.6375)\). The dimension of the reduced manifolds are \(n = 3\) and \(n = 50\) for the DL-ROM and the POD techniques, respectively. Also in this case, even by setting the dimension of the linear manifold equal to \(n = 50\), the reconstructed solution presents spurious oscillations. Moreover, the optimal-POD reconstruction is not able to fit the discontinuity of the exact solution in a sharp way. These oscillations are significantly mitigated by the use of our DL-ROM technique, which is able to fit the jump discontinuity accurately, as shown in Fig. 12.
Finally, we remark how the relative error with respect to the reduced dimension n behaves as in the previous test case (see Fig. 13). The DL-ROM approximation yields an error indicator \(\epsilon _{rel} = 2.85 \times 10^{-2}\) with \(n = 3\); a similar accuracy would be achieved by POD only through a linear trial manifold of dimension \(n = 165\).
4.3 Test 3: Monodomain Equation
4.3.1 Test 3.1: \(d = 1\) Spatial Dimension
We now consider a one-dimensional coupled PDE-ODE nonlinear system
where \(L = 1\), \(T = 2\), \(\gamma = 2\) and \(\beta = 0.5\); the parameter \(\mu \) belongs to the parameter space \(\mathcal {P} = 5 \cdot [10^{-3}, 10^{-2}]\). This system consists in a parametrized version of the Monodomain equation coupled with the FitzHugh-Nagumo cellular model, describing the excitation-relaxation of the cell membrane in the cardiac tissue [21, 42]. In such a model, the ionic current is a cubic function of the electrical potential u and linear in the recovery variable w. System (28) has been discretized in space through linear finite elements, by considering \(N_h = 256\) grid points and using a one-step, semi-implicit, first order scheme for time discretization; see, e.g., [45]Footnote 1. The solution of the former problem consists in a \(\mu \)-dependent traveling wave, which exhibits sharper and sharper fronts as \(\mu \) gets smaller (see Fig. 14).
We consider \(N_{train} = 20\) training-parameter instances uniformly distributed in the parameter space \(\mathcal {P}\) and \(N_{test} = 19\) testing-parameter instances, each of them corresponding to the midpoint between two consecutive training parameter instances. Figure 15 shows the FOM solution and the DL-ROM one obtained by setting \(n=2\), the dimension of the solution manifold, for the testing-parameter instance \(\mu _{test} = 0.0062\). We also report in Fig. 15 the relative error \(\varvec{\epsilon }_k\) (26), which takes larger values close to the points where the FOM solution shows steeper gradients. The accuracy obtained by our DL-ROM technique with \(n = 2\), and measured by the error indicator on the testing set, is \(\epsilon _{rel} = 3.42 \times 10^{-3}\).
In order to assess the performance of the DL-ROM against a linear ROM, we consider a POD-Galerkin ROM exploiting local reduced bases; these latter are obtained by applying POD to a set of clusters which partition the original snapshot set. In particular, we employ the k-means clustering algorithm [38], an unsupervised statistical learning technique for finding clusters and cluster centers in an unlabeled dataset, to partition into \(N_c\) clusters the snapshots, i.e. the columns of S, such that those within each cluster are more closely related to one another than elements assigned to different clusters. In Table 5 we report the maximum number of basis functions among all the clusters, i.e. the dimension of the largest linear trial manifold, required by the (local) POD-Galerkin ROM, in order to achieve the same accuracy obtained through a DL-ROM. By increasing the number \(N_c\) of clusters, the dimension of the largest linear trial subspace decreases; this does not hold as long as the number of clusters is larger than \(N_c=32\). Indeed, the dimension of some linear subspaces become so small that the error might increase compared to the one obtained with fewer clusters.
In particular, in Figs. 16 and 17 the POD-Galerkin ROM approximations obtained by considering \(n=2\) and \(n =66\) basis functions, and \(N_c = 16\) and \(N_c = 32\), where the largest local linear trial manifold dimension is reported in Table 5, are shown. In Fig. 18 we compare the FOM solution for \(\mu _{test} = 0.0157\) at \(t = 0.4962, 0.9975\) and 1.4987, with the DL-ROM approximation obtained for \(n = 2\), and the POD-Galerkin approximation with a global (\(N_c=1\)) linear trial manifold, of dimension \(n = 2, 20\) and 66, respectively.
The convergence of the error indicator (23) as a function of the reduced dimension n is shown in Fig. 19. For the (local) POD-Galerkin ROM, by increasing the dimension of the largest linear trial manifold, the error indicator decreases; this also occurs for the DL-ROM technique for \(n \le 20\), although the error decay in this latter case is almost negligible, for the same reason pointed out in Test 2.1. By considering larger values of n, e.g. \(n = 40\), overfitting might then occur, meaning that the neural network model is too complex with respect to the amount of data provided to it during the training phase. This might explain the slight increase of the error indicator \(\epsilon _{rel}\) for \(n = 40\).
Finally, in Fig. 20 we report the behavior of the loss function and of the error indicator \(\epsilon _{rel}\) with respect to the number of training-parameter instances, i.e. the size of the training dataset. By providing more data to the DL-ROM neural network, its approximation capability increases, thus yielding a decrease in the generalization error and the error indicator. In particular, the loss decay with respect to the number of training-parameter instances \(N_{train}\) is of about order \(1/N_{train}^3\), while the decay of the error indicator (23) is of about order \(1/N_{train}^2\).
Remark 3
(Hyperparameters tuning). In order to perform hyperparameters tuning we follow the same procedure used for Test 2.1. We start from the default configuration and we tune the size of the (transposed) convolutional kernels in the (decoder) encoder function, the number of hidden layers in the feedforward neural network and the number of neurons for each hidden layer. In Fig. 21 we show the impact of the hyperparameters on the validation and testing losses. The final configuration of the DL-ROM neural network is the one provided in Table 6.
Remark 4
(Sensitivity with respect to the weight \(\omega _h\)). For all the test cases, we set the parameter \(\omega _h\) in the loss function (19) equal to \(\omega _h = 1/2\). To justify this choice, we performed a sensitivity analysis for problem (28) as shown in Fig. 22. For extreme values of \(\omega _h\), the error indicator (23) worsens of about one order of magnitude. In particular, the case \(\omega _h = 1\) (that is, not considering the contribution of the encoder function \(\mathbf {f}_n^E\) in the loss) yields worse DL-ROM performance; similarly, the case \(\omega _h = 0\) would neglect the reconstruction error (that is, the first term in the per-example loss function (19)) – this is why the error indicator is large for \(\omega _h = 0.1\). All the values of \(\omega _h\) in the range [0.2, 0.9] do not yield significant differences in terms of error indicator, so we decided to set \(\omega _h = 1/2\).
4.3.2 Test 3.2: \(d = 2\) Spatial Dimensions
We now consider a two-dimensional coupled PDE-ODE nonlinear system, in which the Monodomain equation is coupled to the Aliev-Panfilov ionic model [3],
Here, we consider a square domain \(\varOmega = (0, 10) \; \text {cm}\) and two \((n_{\mu }=2)\) parameters, consisting in the electric conductivities in the longitudinal and the transversal directions to the fibers, i.e., the conductivity tensor \(\mathbf {D}(\mathbf {x}; \varvec{\mu }) \) takes the form
where \(\mathbf {f}_0=(1, 0)^T\) and the parameters space is \(\mathcal {P} = 12.9 \cdot [0.02, 0.2] \times 12.9 \cdot [0.01,0.1 ] \text {cm}^{2}/\text {ms}\). The applied current is defined as
where \(C = 100\) mA, \(\alpha = 1\), \(\beta = 1\) cm\(^{2}\) and \(t = 2\) ms. The parameters of the Aliev-Panfilov ionic model are set to \(K = 8\), \(a = 0.01\), \(b = 0.15\), \(\varepsilon _0 = 0.002\), \(c_1 = 0.2\), and \(c_2 = 0.3\), see, e.g., [24]. The equations have been discretized in space through linear finite elements by considering \(N_h = 4096\) grid points. For the time discretization and the treatment of nonlinear terms, we use a one-step, semi-implicit, first order scheme (see [45] for further details) by considering a time step \(\Delta t = 0.1\) ms over the interval (0, T), with \(T=400\) ms.
For the training phase, we uniformly sample \(N_t = 1000\) time instances in the interval (0, T) and consider \(N_{train} = 25\) training-parameter, i.e. \(\varvec{\mu }_{train}=12.9 \cdot (0.02 + i 0.045, 0.01 + j 0.0225)\) with \(i,j = 0, \ldots , 4\). For the testing phase, \(N_{test} = 16\) testing-parameter instances have been considered, each of them given by \(\varvec{\mu }_{test}=12.9 \cdot (0.0425 + i 0.045, 0.0212 + j 0.0225)\) with \(i,j = 0, \ldots , 3\). The maximum number of epochs is \(N_{epochs} = 10000\), the batch size is \(N_b = 40\) and, regarding the early-stopping criterion, we stop the training if the loss function does not decrease along 500 epochs.
In Fig. 23 we show the FOM and the DL-ROM solutions, the latter obtained with \(n = 3\), for the testing-parameter instances \(\varvec{\mu }_{test}=12.9 \cdot (0.088, 0.066)\) cm\(^{2}\)/ms and \(\varvec{\mu }_{test}=12.9 \cdot (0.178, 0.066)\) cm\(^{2}\)/ms, respectively, at \(t = 47.7\) ms, together with the relative error \(\varvec{\epsilon }_k\). We remark the variability of the solution of (29) over \(\mathcal {P}\), characterized by the propagation of a sharp front across the domain, depending on the parameter values.
Test 3.2: FOM solution (left), DL-ROM solution with \(n=3\) (center) and relative error \(\varvec{\epsilon }_k\) (right) for the testing-parameter instances \(\varvec{\mu }_{test}=12.9 \cdot (0.088, 0.066)\) cm\(^{2}\)/ms (above) and \(\varvec{\mu }_{test}=12.9 \cdot (0.178, 0.066)\) cm\(^{2}\)/ms (bottom) at \(t = 47.4\) ms
Finally, we focus on the performance of our DL-ROM technique, in terms of computational efficiency. In Table 7 we compare the computational timesFootnote 2 required to compute the solution for a randomly sampled testing-parameter instance, over the entire time interval (0, T), by the FOM, the (local) POD-Galerkin ROM (for different values of \(N_c\)) and the DL-ROM, keeping for the three models the same degree of accuracy achieved by DL-ROM, i.e. \(\epsilon _{rel} = 5.87 \times 10 ^{-3}\).
We emphasize that the DL-ROM solution can be queried at any desired time instance \(\bar{t} \in [0,T]\), without involving the solution of a dynamic system to determine its evolution up to \(\bar{t}\), unlike the FOM or the POD-Galerkin ROM. This latter still requires solving for whole range of discrete times in the interval \([0,\bar{t}]\), with time-step size \(\Delta t\) dependent on the desired level of accuracy. In other words, when using the DL-ROM we are free to choose a larger time resolution, to reach the same degree of accuracy, with respect to the time stepping required in the solution of the POD-Galerkin ROM dynamical system. Indeed, the underlying nature of the FOM in the test case at hand implies very small time step sizes when both solving the POD-Galerkin ROM and sampling the FOM solution for the snapshot matrix assembling. This feature allows to drastically reduce the testing computational time of DL-ROM with respect to the ones required to compute the FOM or the POD-Galerkin ROM solutions at a given time.
The speed up introduced by the DL-ROM technique with respect to the FOM is about 138 times, provided that we evaluate the solution at \(N_t=4000\) time steps as in the FOM; the speedup increases to 536 times if the DL-ROM approximation is computed instead, ensuring the same degree of accuracy, at \(N_t=1000\) time steps. Compared to the use of the local POD-Galerkin ROM in the best case (i.e., with \(N_c = 6\) or 8 local bases) leads to almost 30 times faster computations.
The computational gain is even more remarkable regarding the evaluation of the solution at the final time \(\bar{t}=T\): the DL-ROM directly provides it, as \(\bar{t}\) is an input of the neural network, whereas a POD-Galerkin ROM still require solving for hundreds or thousands of discrete time instances. In Fig. 24 (right) we show the DL-ROM, FOM and POD-Galerkin ROM CPU time needed to compute the approximated solution at \(\bar{t}\), for \(\bar{t} =\) 1, 10, 100 and 400 ms averaged over the testing set. We perform the training phase of the POD-Galerkin ROM over the original time interval (0, T) ms and we report the results for \(N_c =8\) local bases, for which the smallest computational time is obtained in Table 7. The DL-ROM CPU time to compute \(\tilde{\mathbf {u}}_h(\bar{t})\) does not vary over \(\bar{t}\) and by choosing \(\bar{t} = T\) ms the DL-ROM speed ups are equal to \(7.1 \times 10^{4}\) and \(2.4 \times 10^{3}\) with respect to the FOM and the POD-Galerkin ROM with \(N_c=8\) local basesFootnote 3. In Fig. 24 (left) we also show the comparison between the FOM solution and the DL-ROM approximation (with \(n = 3\)) computed at \(P_1 = (9.52, 4.76)\) cm and \(P_2 = (1.9, 1.11)\) cm, for the testing-parameter instance \(\varvec{\mu }_{test}=12.9 \cdot (0.132, 0.066)\) cm\(^{2}\)/ms. The time evolution of the FOM solution is sharply captured by our DL-ROM technique at both locations.
Test 3.2: FOM and DL-ROM solutions for the testing-parameter instance \(\varvec{\mu }_{test}=12.9 \cdot (0.088, 0.066)\) cm\(^{2}\)/ms at \(P_1\) and \(P_2\) (left). FOM, (local) POD-Galerkin ROM and DL-ROM computational times to compute \(\tilde{\mathbf {u}}_h(\bar{t})\) vs. \(\bar{t}\) averaged over the testing set (right)
Last but not least, the weaker constraint on time stepping used in the DL-ROM also has a positive impact on the size of the dataset used for its training phase. For the case at hand, (i) we can train the DL-ROM on a snapshot matrix containing only \(25\%\) of the snapshots used to train the POD-Galerkin ROM – taking \(N_t = 1000\) instead of 4000 as in the POD-Galerkin case.
Remark 5
(Unstructured mesh). The FOM solution needs to be reshaped before entering the encoder function. However, the fact that neighboring cells do not always have close cell indices on unstructured meshes does not affect the DL-ROM performance. To show this fact, we consider the previous test case on an unstructured mesh featuring \(N_h = 3964\) degrees of freedom. In order to recover a FOM dimension \(N_h = 4^{m}\), \(m \in \mathbb {N}\), we zero-padded the snapshot matrix. In Fig. 25 we show the FOM and the DL-ROM solutions, the latter obtained with \(n = 3\), for the testing-parameter instance \(\varvec{\mu }_{test}=12.9 \cdot (0.088, 0.066)\) cm\(^{2}\)/ms at \(t = 47.7\) ms, and the relative error \(\varvec{\epsilon }_k\). Note that larger errors no longer occur at locations where the solution exhibits larger gradients. Moreover, almost the same number of epochs is required on unstructured and structured meshes, and the same accuracy is reached – for the case of Fig. 25, the error indicator is \(\epsilon _{rel} = 4.84 \times 10 ^{-3}\).
Test 3.2: FOM solution (left), DL-ROM solution with \(n=3\) (center) and relative error \(\varvec{\epsilon }_k\) (right) for the testing-parameter instance \(\varvec{\mu }_{test}=12.9 \cdot (0.088, 0.066)\) cm\(^{2}\)/ms at \(t = 47.4\) ms on an unstructured mesh. The mesh elements have been highlighted
5 Conclusions
In this work we proposed a novel technique to build low-dimensional ROMs by exploiting DL algorithms to overcome typical computational bottlenecks shown by classical, linear projection-based ROM techniques when dealing with problems featuring coherent structures propagating over time. Our DL-ROM technique allows approximating both the solution manifold of a given parametrized nonlinear, time-dependent PDE by means of a low-dimensional, nonlinear trial manifold, and the nonlinear dynamics of the generalized coordinates on such reduced trial manifold, as a function of the time coordinate and the parameters. Both (1) the nonlinear trial manifold and (2) the reduced dynamics are learnt in a non-intrusive way; the former is learnt by means of the decoder function of a convolutional AE neural network, whereas the latter through a DFNN, and the encoder function of the convolutional AE. The numerical results obtained for three different test cases show that DL-ROMs provide sufficiently accurate solutions to the parametrized PDEs involving a low-dimensional solution manifold whose dimension is equal to (or slightly larger than) the solution manifold \(n_{\mu }+1\). The proposed DL-ROM outperforms linear ROMs such as the RB method (relying on a global POD basis), as well as nonlinear approaches exploiting local POD bases, when applied both to (1) problems which are challenging for linear ROMs, such as the linear transport equation or nonlinear diffusion-reaction PDEs coupled to ODEs, and (2) problems which are more tractable using a linear ROM, like Burgers equation, however featuring POD bases with much higher dimension.
Regarding numerical accuracy, DL-ROMs provide approximations that are orders of magnitude more accurate than the ones provided by linear ROMs, when keeping the same dimension. Error decrease is moderate when considering low-dimensional spaces of increasing dimensions, thus making, in the numerical tests considered, the accuracy of both approximations comparable when dealing with \(\mathcal {O}(10^2)\) POD basis functions. Regarding computational efficiency, we have numerically assessed the computational speed up provided by DL-ROMs compared to POD-Galerkin ROMs with local bases, obtaining a remarkable computational gain when dealing with a parametrized coupled nonlinear PDE-ODE system on a two-dimensional domain. This is motivated by the fact that DL-ROMs allow us to build an approximated manifold by keeping its dimension extremely small and the use of a larger time resolution than the POD-Galerkin ROM, thus decreasing the size of the training snapshot matrix and discarding solutions whose variation in time is not significant for preserving the same degree of accuracy. Moreover, DL-ROMs are also able to directly approximate the solution at any given time instance, without computing the whole dynamics until that time, as it occurs instead with POD-Galerkin ROMs. In addition, compared to these latter, DL-ROMs completely avoids the use of (very often, expensive) hyper-reduction techniques.
Numerical results show that DL-ROMs allow us to generate approximation spaces of dimension close to the intrinsic dimension of the solution manifold, by providing remarkable improvements in terms of computational efficiency when dealing with parametrized nonlinear time-dependent PDEs defined in \(d\ge 2\) dimensional domains, yet at the same degree of accuracy. This is a fundamental step toward the application of DL-ROMs to nonlinear PDEs whose high-fidelity discretization involves a larger number \(N_h\) of degrees of freedom, a task that represents the object of our ongoing research activities.
Data Availibility
The code used in this work is available at: https://github.com/stefaniafresca/DL-ROM-Meth. The training and testing datasets will be made available upon request to the authors.
Notes
The Matlab library used to compute snapshots and to implement the (local) POD-Galerkin method for problem (28) is available at https://github.com/StefanoPagani/LocalROM
Here we performed our simulations on a full 64 GB node (20 Intel\(^{\textregistered }\) Xeon\(^{\textregistered }\) E5-2640 v4 2.4GHz cores) of the HPC cluster available at MOX, Politecnico di Milano.
We did not investigate the case \(N_c > 8\) due to the fact that the employing \(N_c = 6\) or \(N_c = 8\) clusters lead to the same testing computational time.
References
Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., Devin, M., Ghemawat, S., Irving, G., Isard, M., Kudlur, M., Levenberg, J., Monga, R., Moore, S., Murray, D.G., Steiner, B., Tucker, P., Vasudevan, V., Warden, P., Wicke, M., Yu, Y., Zheng, X.: Tensorflow: A system for large-scale machine learning pp. 265–283 (2016). https://www.usenix.org/system/files/conference/osdi16/osdi16-abadi.pdf
Abgrall, R., Amsallem, D., Crisovan, R.: Robust model reduction by \(l^1\)-norm minimization and approximation via dictionaries: application to nonlinear hyperbolic problems. Adv. Model. Simul. Eng. Sci. (2016). https://doi.org/10.1186/s40323-015-0055-3
Aliev, R.R., Panfilov, A.V.: A simple two-variable model of cardiac excitation. Chaos Solitons Fractals 7(3), 293–301 (1996)
Amsallem, D., Haasdonk, B.: PEBL-ROM: Projection-error based local reduced-order models. Adv. Model. Simul. Eng. Sci. 3(1), 6 (2016)
Amsallem, D., Zahr, M.J., Farhat, C.: Nonlinear model order reduction based on local reduced-order bases. Int. J. Numer. Methods Eng. 92(10), 891–916 (2012)
Amsallem, D., Zahr, M.J., Washabaugh, K.: Fast local reduced basis updates for the efficient reduction of nonlinear systems with hyper-reduction. Adv. Comput. Math. 41(5), 1187–1230 (2015)
Antipov, G., Baccouche, M., Dugelay, J.: Face aging with conditional generative adversarial networks. Presented at the (2017)
Barrault, M., Maday, Y., Nguyen, N.C., Patera, A.T.: An ‘empirical interpolation’ method: Application to efficient reduced-basis discretization of partial differential equations. Comptes Rendus Mathématique de l’Académie des Sciences 339(9), 667–672 (2004)
Benner, P., Cohen, A., Ohlberger, M., Willcox, K.: Model Reduction and Approximation: Theory and Algorithms. SIAM, Philadelphia (2017)
Benner, P., Gugercin, S., Willcox, K.: A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev. 57(4), 483–531 (2015)
Bhattacharya, K., Hosseini, B., Kovachki, N.B., Stuart, A.: Model reduction and neural networks for parametric PDEs. arXiv preprint arXiv:2005.03180 (2020)
Bourlard, H., Kamp, Y.: Auto-association by multilayer perceptrons and singular value decomposition. Biol. Cybern. 59, 291–294 (1998)
Bourlard, H., Wellekens, C.: Speech pattern discrimination and multi-layered perceptrons. Comput. Speech Lang. 3, 1–19 (1989)
Cagniart, N., Maday, Y., Stamm, B.: Model order reduction for problems with large convection effects. Contributions to Partial Differential Equations and Applications. Computational Methods in Applied Sciences, vol. 47, pp. 131–150. Springer, Cham (2019)
Carlberg, K., Farhat, C., Cortial, J., Amsallem, D.: The gnat method for nonlinear model reduction: effective implementation and application to computational fluid dynamics and turbulent flows. J. Comput. Phys. 242, 623–647 (2013)
Chaturantabut, S., Sorensen, D.C.: Nonlinear model reduction via discrete empirical interpolation. SIAM J. Sci. Comput. 32(5), 2737–2764 (2010)
Chung, J.S., Senior, A.W., Vinyals, O., Zisserman, S.: Lip reading sentences in the wild. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) pp. 3444–3453 (2017)
Clevert, D., Unterthiner, T., Hochreiter, S.: Fast and accurate deep network learning by exponential linear units (elus). arXiv preprint arXiv:1511.07289 (2015)
Devlin, J., Chang, M., Lee, K., Toutanova, K.: BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 (2018)
Farhat, C., Grimberg, S., Manzoni, A., Quarteroni, A.: Computational bottlenecks for PROMs: Pre-computation and hyperreduction. In: P. Benner, S. Grivet-Talocia, A. Quarteroni, G. Rozza, W. Schilders, L. Silveira (eds.) Model Order Reduction. Volume 2: Snapshot-Based Methods and Algorithms. De Gruyter, Berlin (2020, in press)
FitzHugh, R.: Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1(6), 455–466 (1961)
Freno, B.A., Carlberg, K.T.: Machine-learning error models for approximate solutions to parameterized systems of nonlinear equations. arXiv preprint arXiv:1808.02097 (2018)
Gerbeau, J.F., Lombardi, D.: Approximated lax pairs for the reduced order integration of nonlinear evolution equations. J. Comput. Phys. 265, 246–269 (2014)
Göktepe, S., Wong, J., Kuhl, E.: Atrial and ventricular fibrillation: computational simulation of spiral waves in cardiac tissue. Arch. Appl. Mech. 80, 569–580 (2010). https://doi.org/10.1007/s00419-009-0384-0
Goodfellow, I., Bengio, Y., Courville, A.: Deep Learning. MIT Press, Cambridge (2016)
Guo, M., Hesthaven, J.S.: Reduced order modeling for nonlinear structural analysis using gaussian process regression. Comput. Methods Appl. Mech. Eng. 341, 807–826 (2018)
Guo, M., Hesthaven, J.S.: Data-driven reduced order modeling for time-dependent problems. Comput. Methods Appl. Mech. Eng. 345, 75–99 (2019)
He, K., Zhang, X., Ren, S., Sun, J.: Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. Proceedings of the IEEE International Conference on Computer Vision (ICCV) pp. 1026–1034 (2015)
Hesthaven, J., Ubbiali, S.: Non-intrusive reduced order modeling of nonlinear problems using neural networks. J. Comput. Phys. 363, 55–78 (2018)
Hinton, G.E., Zemel, R.S.: Autoencoders, minimum description length, and Helmholtz free energy. Proceedings of the 6th International Conference on Neural Information Processing Systems (NIPS’1993) (1994)
Iollo, A., Lombardi, D.: Advection modes by optimal mass transfer. Phys. Rev. E 89, 022923 (2014)
Kani, J.N., Elsheikh, A.H.: DR-RNN: A deep residual recurrent neural network for model reduction. arXiv preprint arXiv:1709.00939 (2017)
Kingma, D.P., Ba, J.: Adam: A method for stochastic optimization. Presented at the (2015)
Krizhevsky, A., Sutskever, I., Hinton, G.E.: Imagenet classification with deep convolutional neural networks. Proceedings of the 25th International Conference on Neural Information Processing Systems (NIPS’2012) 1, 1097–1105 (2012)
Kutyniok, G., Petersen, P., Raslan, M., Schneider, R.: A theoretical analysis of deep neural networks and parametric PDEs. arXiv preprint arXiv:1904.00377 (2019)
LeCun, Y., Bottou, L., Bengio, Y., Haffner, P.: Gradient based learning applied to document recognition. Proceedings of the IEEE pp. 533–536 (1998)
Lee, K., Carlberg, K.: Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J. Comput. Phys. 404, 108973 (2020)
Likas, A., Vlassis, N., Verbeek, J.J.: The global k-means clustering algorithm. Pattern Recognit 36(2), 451–461 (2003)
Manzoni, A., Pagani, S., Lassila, T.: Accurate solution of Bayesian inverse uncertainty quantification problems combining reduced basis methods and reduction error models. SIAM/ASA J. Uncertain. Quantif. 4(1), 380–412 (2016)
Miranda González, F.J., Balajewicz, M.: Deep convolutional recurrent autoencoders for learning low-dimensional feature dynamics of fluid systems. arXiv preprint (2018)
Mohan, A., Gaitonde, D.V.: A deep learning based approach to reduced order modeling for turbulent flow control using LSTM neural networks. arXiv preprint arXiv:1804.0926 (2018)
Nagumo, J., Arimoto, S., Yoshizawa, S.: An active pulse transmission line simulating nerve axon. Proc. IRE 50(10), 2061–2070 (1962)
Ohlberger, M., Rave, S.: Reduced basis methods: Success, limitations and future challenges. Proceedings of ALGORITMY pp. 1–12 (2016)
Pagani, S., Manzoni, A., Carlberg, K.: Statistical closure modeling for reduced-order models of stationary systems by the ROMES method. arXiv preprint arXiv:1901.02792 (2019)
Pagani, S., Manzoni, A., Quarteroni, A.: Numerical approximation of parametrized problems in cardiac electrophysiology by a local reduced basis method. Comput. Methods Appl. Mech. Eng. 340, 530–558 (2018)
Parish, E., Carlberg, K.: Time-series machine-learning error models for approximate solutions to parameterized dynamical systems. arXiv preprint arXiv:1907.11822 (2019)
Peherstorfer, B.: Model reduction for transport-dominated problems via online adaptive bases and adaptive sampling. arXiv preprint arXiv:1812.02094 (2018)
Quarteroni, A., Manzoni, A., Negri, F.: Reduced Basis Methods for Partial Differential Equations: An Introduction, vol. 92. Springer, Cham (2016)
Quarteroni, A., Sacco, R., Saleri, F.: Matematica Numerica. Springer Milan (2008)
Raissi, M.: Deep hidden physics models: deep learning of nonlinear partial differential equations. J. Mach. Learn. Res. 19, 1–24 (2018)
Raissi, M., Karniadakis, G.E.: Hidden physics models: machine learning of nonlinear partial differential equations. J. Comput. Phys. 357, 125–141 (2018)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv preprint arXiv:1711.10561 (2017)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics informed deep learning (part ii): Data-driven discovery of nonlinear partial differential equations. arXiv preprint arXiv:1711.10566 (2017)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)
Regazzoni, F., Dede’, L., Quarteroni, A.: Machine learning for fast and reliable solution of time-dependent differential equations. J. Comput. Phys. 397, 108852 (2019)
Reiss, J., Schulze, P., Sesterhenn, J., Mehrmann, V.: The shifted proper orthogonal decomposition: a mode decomposition for multiple transport phenomena. SIAM J. Sci. Comput. 40(3), A1322–A1344 (2018)
Robbins, H., Monro, S.: A stochastic approximation method. Ann. Math. Stat. 22, 400–407 (1951)
Rumelhart, D., Hinton, G., Williams, R.: Learning representations by back-propagating errors. Nature 323, 533–536 (1986)
San, O., Maulik, R.: Neural network closures for nonlinear model order reduction. Adv. Comput. Math. 44, 1717 (2018)
Sutskever, I., Vinyals, O., Le, Q.V.: Sequence to sequence learning with neural networks. Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS’2014) 2, 3104–3112 (2014)
Trehan, S., Carlberg, K.T., Durlofsky, L.J.: Error modeling for surrogates of dynamical systems using machine learning. Int. J. Numer. Methods Eng. 112(12), 1801–1827 (2017)
Wan, Z., Vlachas, P., Koumoutsakos, P., Sapsis, T.: Data-assisted reduced-order modeling of extreme events in complex dynamical systems. PLOS ONE 13, e0197704 (2018). https://doi.org/10.1371/journal.pone.0197704
Wang, Q., Ripamonti, N., Hesthaven, J.: Recurrent neural network closure of parametric pod-galerkin reduced-order models based on the mori-zwanzig formalism. J. Comput. Phys. 410, 109402 (2020)
Washabaugh, K.M., Zahr, M.J., Farhat, C.: On the use of discretenonlinear reduced-order models for the prediction of steady-stateflows past parametrically deformed complex geometries. In: 54th AIAAAerospace Sciences Meeting (2016). https://doi.org/10.2514/6.2016-1814
Acknowledgements
We gratefully acknowledge Prof. A. Quarteroni (MOX, Politecnico di Milano) for his valuable comments, Dr. S. Pagani and M. Salvador (MOX, Politecnico di Milano) for their useful remarks.
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Basic Concepts of Deep Learning
Basic Concepts of Deep Learning
Deep learning (DL) techniques have gained great attention in recent years in several areas like computer vision [7, 34], natural language processing [19, 60] and speech recognition [13, 17], due to their ability to discover pattern and extract features from massive datasets, in order to make predictions without providing hand-crafted features. In this section we provide an overview of those deep-learning models which the proposed DL-ROM technique relies on.
1.1 Deep Feedforward Neural Network
A remarkable example of DL model is the deep feedforward neural network (DFNN). A DFNN is a mathematical function modeling the relationship between a set of input values and some output values [25]. This mathematical function is obtained through composition of simpler (nonlinear) functions, or layers, and allows to learn complex hierarchies of features. More formally, provided an input \(\mathbf {x} \in \mathbb {R}^{N_0}\) a DFNN with L layers takes the form
where \(\varvec{\phi }_i(\cdot ; \varvec{\theta }_i) : \mathbb {R}^{N_i-1} \mapsto \mathbb {R}^{N_i}\), \(i = 1, \ldots , L\), refers to the activation function applied at layer i of the DFNN and \(\varvec{\theta }_i = (W_i, \mathbf {b}_i)\), with \(W_i \in \mathbb {R}^{N_i \times N_{i-1}}\) and \(\mathbf {b}_i \in \mathbb {R}^{N_i}\), \(i = 1, \ldots , L\), are the weights and the bias of layer i such that \(\varvec{\theta }_{DF} = (\varvec{\theta }_1, \ldots , \varvec{\theta }_L)\). We usually refer to the collection of all weights and biases as to the parameters vector. Each layer of the network corresponds to a matrix whose values are computed by applying a linear transformation to the previous layer followed by the application of a nonlinear activation function. In particular, referring to Fig. 26, \(\mathbf {y}_0 = \mathbf {x} \in \mathbb {R}^{N_0}\) is the input layer, \(\mathbf {y}_L = \varvec{\phi }^{DF}(\mathbf {x}; \varvec{\theta }_{DF}) \in \mathbb {R}^{N_L}\) is the output layer, and each hidden layer \(\mathbf {y}_i \in \mathbb {R}^{N_i}\), \(i = 1, \ldots , L - 1\), takes the form
Given a set of M input-output pair observations \(\{( \mathbf {x}^i, \mathbf {y}^i) \}_{i=1}^M\) and considering a supervised learning paradigm [25], the learning task consists in finding the optimal parameters vector \(\varvec{\theta }_{DF}^*\) by solving the optimization problem
where \(\mathcal {J}\) is the loss (or cost) function, and \(\mathcal {L}\) is the per-example loss function, measuring the mismatch between the desired observed output \(\mathbf {y}^i\) and the approximated one \(\mathbf {y}_L^i\). Problem (32) is usually solved by means of the gradient descent method exploiting the back-propagation algorithm [58] to compute the derivatives of the loss function with respect to parameters. In particular, the gradient descent method requires to evaluate
a task which might easily become prohibitive when the size M of the training dataset is very large, thus causing a single step of the gradient descent method to require a huge amount of time. The stochastic gradient descent (SGD) method allows to reduce the computational cost associated to the computation of the gradient of the loss function, by exploiting the fact that (33) can be considered as an expectation over the entire training dataset. Such an expectation can be approximated using a small set (or minibatch) of samples; hence, at each iteration the SGD method samples a minibatch of \(m < M\) data points, drawn (e.g., uniformly) from the training dataset [25], and approximates the gradient (33) of the loss function by
1.2 Convolutional Neural Network
Convolutional neural networks (CNNs) [36] are the standard neural network architecture in computer vision tasks, since they are well-suited to high-dimensional and spatially distributed data like images. This is due to the local approach of convolutional layers which enables them to exploit spatial correlations among pixels in order to extract low-level features of the input to carry out the task. The main ingredients of a convolutional layer are convolutional kernels, or filters, which consist in tensors of smaller dimensions with respect to the input. Each element of a feature map is obtained by sliding the kernel over the image and by computing the discrete convolution, as shown in Fig. 27.
Considering a 3-dimensional input \(Y_0 = X \in \mathbb {R}^{N_0^1 \times N_0^2 \times N_0^3}\) and a bank of \(K_i\) convolutional filters in layer i denoted as \(W_i^k \in \mathbb {R}^{n_i^1 \times n_i^2 \times n_i^3}\), \(i = 1, \ldots , L\) and \(k = 1, \ldots , K_i\), the k-th feature map is computed as
where \(Y_i \in \mathbb {R}^{N_i^1 \times N_i^2 \times N_i^3}\) (or, equivalently, \(Y_i^k \in \mathbb {R}^{N_i^1 \times N_i^2}\)) with \(N_i^1\) and \(N_i^2\) depending on \(n_i^1\) and \(n_i^2\), respectively, the padding and the striding strategies, and \(N_i^3 = K_i\).
Convolutional layers are characterized by shared parameters, that is, weights are shared by all the elements (neurons) in a particular feature map, and local connectivity, that is, each neuron in a feature map is connected only to a local region of the input. Parameter sharing allows convolutional layers to enjoy another property: translation invariance or, more precisely, translation equivariance. This means that if the input varies, the output changes accordingly [25]. In particular, if we apply a transformation to the input \(Y_0\) and then compute the convolution, the result is the same we would obtain by computing the convolution and then applying the transformation to the output. The two properties above increase efficiency of CNNs, both in terms of memory and computational costs, with respect to DFNNs, thus making them preferable to the latter when dealing with extremely high-dimensional data.
1.3 Autoencoder Neural Network
Autoencoders (AEs) [12, 30] are a particular type of feedforward neural networks aiming at learning, under suitable constraints, the identity function
Internally, an autoencoder has a hidden layer consisting in a code used to represent the input. We focus on undercomplete autoencoders [25] where the constraint imposed is the reduction of the dimension of the code with respect to the input and output dimension.
By considering the input \(\mathbf {y}_0 = \mathbf {x}_h \in \mathbb {R}^{N_h}\) and the output \(\mathbf {y}_L = {\tilde{\mathbf {x}}}_h \in \mathbb {R}^{N_h}\), an autoencoder is composed by two main parts (see Fig. 28)
-
The encoder function \(\mathbf {f}_{n}^E(\cdot ; \varvec{\theta }_E) : \mathbf {x}_h \mapsto {\tilde{\mathbf {x}}}_n = \mathbf {f}_{n}^E( \mathbf {x}_h; \varvec{\theta }_E)\), where \(\mathbf {f}_{n}^E (\cdot ; \varvec{\theta }_E) : \mathbb {R}^{N_h} \rightarrow \mathbb {R}^{n}\) and \(n \ll N_h\), mapping the high-dimensional input \(\mathbf {x}_h\) onto the low-dimensional code \({\tilde{\mathbf {x}}}_n\). The encoder function depends on a vector of parameters \(\varvec{\theta }_E \in \mathbb {R}^{N_E}\) collecting all the weights and biases specifying the function itself;
-
The decoder function \(\mathbf {f}_{h}^D(\cdot ; \varvec{\theta }_D) : {\tilde{\mathbf {x}}}_n \mapsto {\tilde{\mathbf {x}}}_h = \mathbf {f}_{h}^D({\tilde{\mathbf {x}}}_n; \varvec{\theta }_D)\), where \(\mathbf {f}_{h}^D(\cdot ; \varvec{\theta }_D) : \mathbb {R}^{n} \rightarrow \mathbb {R}^{N_h}\), mapping the code \(\tilde{\mathbf {x}}_n\) to an approximation of the original high-dimensional input \({\tilde{\mathbf {x}}}_h\). Similarly to the encoder function, the decoder function depends on a vector of parameters \(\varvec{\theta }_D \in \mathbb {R}^{N_D}\) collecting all the weights and biases specifying the function itself.
The autoencoder is then defined as
Autoencoder learning lays within the unsupervised learning paradigm [25] since its goal is to reconstruct the input being the target output an approximation of the input. An autoencoder not only learns a low-dimensional representation of the high-dimensional input but also learns how to reconstruct the input from the code through the encoder and the decoder functions.
When dealing with large inputs, as the ones arising from the discretization of system (1), the use of a feedforward autoencoder may become prohibitive as the number of parameters (weights and biases) required may be very large. As pointed out in A.2, parameter sharing and local connectivity allow to reduce the numbers of parameters of the network and the number of associated computations, both in the forward and in the backward pass, hence the idea of relying on convolutional autoencoders for the sake of building our DL-ROM technique.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fresca, S., Dede’, L. & Manzoni, A. A Comprehensive Deep Learning-Based Approach to Reduced Order Modeling of Nonlinear Time-Dependent Parametrized PDEs. J Sci Comput 87, 61 (2021). https://doi.org/10.1007/s10915-021-01462-7
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-021-01462-7
Keywords
- Parametrized PDEs
- Nonlinear time-dependent PDEs
- Reduced order modeling
- Deep learning
- Proper orthogonal decomposition