Abstract
The implicit mid-point rule is a Runge–Kutta numerical integrator for the solution of initial value problems, which possesses important properties that are relevant in micromagnetic simulations based on the Landau–Lifshitz–Gilbert equation, because it conserves the magnetization length and accurately reproduces the energy balance (i.e. preserves the geometric properties of the solution). We present an adaptive step size version of the integrator by introducing a suitable local truncation error estimator in the context of a predictor-corrector scheme. We demonstrate on a number of relevant examples that the selected step sizes in the adaptive algorithm are comparable to the widely used adaptive second-order integrators, such as the backward differentiation formula (BDF2) and the trapezoidal rule. The proposed algorithm is suitable for a wider class of non-linear problems, which are linearised by Newton’s method and require the preservation of geometric properties in the numerical solution.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Background and Context
Initial value problems (IVP) arise in mathematical models of many important physical and engineering processes and phenomena. They either appear as stand-alone problems (as ordinary differential equations (ODEs), where the unknown functions depend only on a single variable, for example describing the motion in classical mechanics or chemical reactions), or in the context of applying the method of lines to partial differential equations (PDE), i.e. the problems where unknown functions have both spatial and time variation [1, p. 8]. The solutions of such problems frequently exhibit multiple spatio-temporal scales. In such cases implicit solvers allow the deployment of larger step sizes, while maintaining stability. Efficient integrators should also involve adaptivity [2, p. 73,74], which can be realised both with explicit and implicit methods. The design and development of these algorithms has been the topic of much previous research (see, for example [3, Sect. 3.16],[4,5,6,7]). Many publicly available codes for the solution of IVPs (for example CVODE [8], or the various solvers in Matlab [9]) involve some adaptivity strategy. Adaptive IVP solvers allow the selection of the right step sizes at each stage of the solution process to satisfy the required accuracy, thus removing the need for a “trial-and-error” approach. This also improves the computational efficiency and robustness of the overall algorithm.
In some problems the governing equations dictate that the solution vectors should have constant magnitude, and that the system’s energy should either be conserved or accurately reproduced. In such cases IVP solvers should preserve these properties at the discrete level, while computational efficiency is achieved by using the adaptive implicit methods. As an example, we consider micromagnetics [10]. Dynamical micromagnetic models are based on the Landau–Lifshitz–Gilbert (LLG) equation, a time-dependent differential equation modelling the magnetization evolution in a ferromagnetic body. The classical LLG equation models the magnetization at zero temperature, which implies that the magnetization vector length is constant at any point of the domain. The second important property of the LLG equation is the energy conservation in the non-damped case, or equivalently, under a constant applied field the energy decreases at a rate proportional to the damping factor. Solutions of the LLG equation in practical cases often exhibit multiple spatio-temporal scales favouring the use of adaptive implicit time integration schemes [11]. An integration scheme that preserves (or, in the damped case, accurately reproduces) the length/energy properties of the solution is referred to as a geometric integrator. Most commonly used implicit schemes (such as the second-order backward differentiation formula BDF2 or the trapezoidal rule (TR)) do not possess this property. By contrast, the implicit mid-point rule (IMR), combined with an appropriate spatial discretisation in the PDE cases, is a geometric integrator [12, 13]. The proposed adaptive version of IMR retains this favourable property. Some alternative numerical techniques aimed at preserving the magnetization length include peiodic renornalisation [14], length constraints imposed through Lagrange multipliers [15], penalty formulations [16], and the self-correcting LLG equation used by Nmag [16]. However, all these formulations change the energy of the system.
The implicit mid-point rule (IMR) is a well-known second order implicit Runge–Kutta method [17, p. 204],[3, p. 262], that has been applied in fixed-step form to micromagnetic problems [12]. In this paper we present an adaptive version of the IMR based on the new local truncation error estimator in the context of a predictor-corrector scheme. We demonstrate the efficiency of the adaptive version of IMR by comparing its accuracy and computational cost with the fixed step version of the method [12], and with the adaptive versions of the BDF2 [3, p. 649] and the TR [3, p. 647] when applied to both ODE and PDE problems that arise in computational micromagetics.
The paper is organised as follows. In Sect. 2 we introduce the LLG equation and describe a method for its discretisation that is used in this paper. Section 3 introduces the IMR and details some of its properties. In Sect. 4 we present the new local truncation error (LTE) estimator for the IMR and introduce the adaptive integrator. Finally, in Sect. 5 we evaluate the effectiveness of the adaptive IMR when applied to ODE and PDE problems associated with the LLG equation. We also compare the adaptive IMR to adaptive BDF2 and the standard version of TR in terms of the computational cost, accuracy and the preservation of geometric properties.
2 The Dynamical Micromagnetic Model
2.1 The Landau–Lifshitz–Gilbert Equation
Micromagnetics is a semi-continuum theory of ferromagnetic materials that covers the lengthscales between the atomistic spin dynamics and the classical Maxwell’s theory. Its aim is to describe the behaviour of a magnetic body, expressed by its magnetization vector \({\mathbf {m}}\), under various external conditions and internal material properties. This can be achieved either by calculating the minimum energy of a magnetic body [10], or by modelling the magnetization dynamics. In the latter case the time evolution of the magnetization is modelled by a differential equation. Given a space of k-continuous functions \(C^k(\cdot )\), the evolution of the magnetization vector denoted by \({\mathbf {m}}\in [C^2(\Omega )]^3\times C^1(T)\) in a magnetic body \(\Omega \subset \mathbb {R}^d\), \(d=2,3\) with a smooth boundary \(\partial \Omega \) over a time interval T follows the Landau-Lifshitz (LL) equation, which, in non-dimensional form, reads
\(d=2,3\), subject to the Neumann-type boundary conditions (BCs) [10, p. 178]
and the initial condition
In (1) \({\mathbf {h}}\in [C(\Omega )]^3\times C(T)\) is the effective magnetic field, and \(\alpha \) is an empirical damping parameter. In (2) \({\hat{\mathbf {n}}}\) denotes the outward normal vector on \(\partial \Omega \). The first term on the right-hand side of (1) determines the precession of \({\mathbf {m}}\), while the second term is responsible for damping. A mathematically equivalent form of (1), referred to as the Landau–Lifshitz–Gilbert (LLG) equation is frequently used, which in non-dimensional form reads
The effective field \({\mathbf {h}}\) in (1) and (4) has several components [18, p. 306], namely
where \({\mathbf {h}}_{{\text {ap}}}\) is the applied (external) field, \({\mathbf {h}}_{{\text {ex}}}=\nabla ^2{\mathbf {m}}\) is the is a phenomenological exchange field that represents the effect of quantum mechanical exchange, which acts to align the magnetic moments of neighbouring atoms in ferromagnetic materials, \({\mathbf {h}}_{{\text {ms}}}=\nabla \phi \) is the magnetostatic (demagnetisation or stray) field expressed in terms of the magnetostatic potential \(\phi \), and \({\mathbf {h}}_{{\text {mc}}}=k_1({\mathbf {m}}\cdot {{\hat{\mathbf {e}}}}){\hat{\mathbf {e}}}\) is the magnetocrystaline anisotropy field associated with the easy magnetization axis \({\hat{\mathbf {e}}}\) of a ferromagnetic material [18, p. 306]. The magnetostatic potential \(\phi ({\mathbf {x}})\), \({\mathbf {x}}\in \mathbb {R}^3\) is related to the magnetization vector through the equation
where \(\Omega ^*\) is the exterior of a ferromagnetic body \(\Omega \). Boundary conditions associated with (6) are of the form
on \(\partial \Omega \), where \(\phi ^{{\text {int}}}\) and \(\phi ^{{\text {ext}}}\) are the values of the potential just inside and outside of \(\Omega \), respectively, and
The fact that (6) is posed over an infinite domain, together with the BC (9) at infinity cause difficulties with the discretisation of this part of the problem.
2.2 Finite Element Discretisation
The weak formulation of (4) in a residual form is to find \({\mathbf {m}}\in [H^1(\Omega )]^3\) such that \({\mathbf {r}}({\mathbf {m}},{\mathbf {v}})={\mathbf {0}}\) for all functions \({\mathbf {v}}\in [H^1(\Omega )]^3\), i.e.
where \(H^1(\Omega )\) is the standard Sobolev space. The discrete problem is obtained by restricting this space to a finite element space \(S_h\) associated with the subdivision of \(\Omega \) into a set of quadrilateral elements and adopting piecewise bi/trilinear polynomial approximation \({\mathbf {m}}_h\) for the solution \({\mathbf {m}}\) over the elements, i.e. \(S_h={\text {span}}\{\psi _k\}_{k=1}^N\), \(N=N_i+N_b\) (\(N_i\) is the number of nodes in the interior of \(\Omega \) and \(N_b\) the number of nodes on \(\partial \Omega \)). Then we have
with \({\mathbf {m}}_k=[m_{k,x}\ m_{k,y}\ m_{k,z}]^t\) representing the values of \({\mathbf {m}}\) at node k. This process results in a semi-discrete problem, which is fully discretised approximating the time derivatives in (10). We use the IMR method in this context (see Sect. 3). The linearisation of the non-linear discrete problem at each time step is done using the Newton method, leading to the solution of a sequence of linear algebraic systems of the form \(J_\ell \bar{\delta m}_\ell =-\bar{r}_\ell \), \(\bar{m}_{\ell +1}=\bar{m}_\ell +\bar{\delta m}_\ell \), \(\ell =0,1,\ldots \). The Jacobian matrix with elements \(J_{mk}=\frac{\partial r_m}{\partial m_k}\) can be written in block form
where \(\tilde{M}\) is a matrix similar to a mass matrix [19, p. 55], while the blocks \(K_*\) are sums of mass and Laplacian-like matrices (for detailed expressions see [13, pp. 97–102]).
The Jacobian matrices are assembled from the elemental contributions with their coefficients calculated two ways: either using standard Gaussian quadratures [19, p. 30], or nodal (Newton–Cotes) quadratures [20]. The former approach is standard in FE computations and gives optimal order of accuracy per amount of computational work. However, it does not lead to the conservation of the magnetization length.Footnote 1 The nodal quadrature (also known in micromagnetic literature as the “reduced integration” [21]) for an integral over an element \(\Omega _e\) is defined by
where \(\varphi _\ell ^{(e)}\) is the local basis function associated with the local node \(\ell \) and \(V(\Omega _e)\) is the set of nodes of an element \(\Omega _e\). The nodal quadratures use element’s nodes as the knots, thus allowing the point-wise magnetization length conservation when the weak formulation of the problem is used as the basis for spatial discretisation [20]. In order for this procedure to be effective, we need to set a tight tolerance \(\epsilon _N\) in the stopping criterion of Newton’s method ( e.g. \(\epsilon _N<10^{-10}\)).
Notice that J in (12) is a block skew-symmetric matrix. Linear systems with the coefficient matrix J are solved either directly, or by preconditioned Krylov solvers. In our experiments reported in Sects. 5.2 and 5.3 GMRES preconditioned by ILU(1) method is used [22].
2.3 Hybrid Finite-Boundary Element Method for the Exchange Field
Spatial discretisation of (6) with BCS (7)–(9) is problematic, as the domain \(\Omega ^*\) is infinite. The application of FEM in this context would require so-called “infinite elements” [23]. An alternative is to truncate the domain \(\Omega ^*\) or to use asymptotic BCs [24]. The asymptotic accuracy of such approaches is usually low. An alternative approach is to apply the hybrid finite/boundary element method, in which the external domain is replaced by a dipole layer placed on \(\partial \Omega \), which simulates the correct BC (9) [25]. Standard FEM is used to calculate the potentials in \(\Omega \).
We use the linearity of the problem (6)–(9) to introduce two new potentials \(u({\mathbf {x}})\) and \(v({\mathbf {x}})\), such that \(\phi =u+v\), and u is defined to be non-zero only in \(\Omega \). Therefore, \(u({\mathbf {x}})\) satisfies
Thus, u is calculated in the domain \(\Omega \) using the FEM and the double layer charge distribution on \(\partial \Omega \) simulates the potential v in \(\Omega ^*\) and is solved by BEM. After setting the conditions for v [13, p. 114–116], we obtain the following problem:
subject to the BCs
where \({\mathcal {G}}[\,\cdot \,]\) is defined as
In (20) \(\mathbb {G}({\mathbf {x}},{\mathbf {y}})\) denotes the Green’s function of the Laplacian, and \(\gamma ({\mathbf {x}})\) is the fractional (space) angle, where for any smooth part of \(\partial \Omega \) we have \(\gamma =\frac{1}{2}\). After discretisation, Eq. (18) becomes a matrix-vector product \(\bar{\phi }=G\bar{u}\), where the elements of the BEM matrix G are obtained as
In (21) \(\psi _j\) is the basis function, \(d=2,3\) is the spatial dimension, and \(\delta _{ji}\) is the Kronecker delta.
The accuracy of the FEM/BEM method is better than that of the asymptotic BCs method [26]. The main drawback of the hybrid method is that it produces a dense coefficient matrix of size \(N_b\), leading to both the computational and storage cost of \(O(N^2_b)\) (in the discrete version of (18) the BEM matrix needs to be multiplied by a vector to impose the BCs). This cost can be prohibitive when modelling micromagnetic problems posed over thin domains, where \(N_b=O(N)\). This problem was circumvented by the approximation of the BEM matrix by low rank hierarchical matrices, as implemented in the library HLib [27, 28], reducing both the storage and computational cost from \(O(N_{b}^{2})\) to \(O(N_b\log N_b)\).
3 The Implicit Mid-Point Rule
Consider a system of N coupled IVPs
for \(t\in T=[0,t_{\max }]\), where \({\mathbf {y}}(t)\in [C^1(T)]^N\) is a vector function, \({\mathbf {y}}_0\) is the initial condition, and \({\mathbf {f}}\) is a locally Lipshitz-continuous function. We denote an approximation to \({\mathbf {y}}(t_n)\) by \({\mathbf {y}}_n\) and write \(\Delta _n=t_{n+1}-t_n\) for the size of n-th time step, and introduce three commonly used second-order implicit methods for numerical integration of (22).
The IMR is defined by [17, p. 204]
With the notation \(t_{n+1/2}=\frac{t_{n+1}+t_n}{2}=t_n+\frac{\Delta _n}{2}\) , \({\mathbf {y}}_{n+1/2}= \frac{{\mathbf {y}}_{n+1}+{\mathbf {y}}_n}{2}\) for the mid-point approximations of t and \({\mathbf {y}}\), (23) becomes
The trapezoidal rule (TR) [3, p. 260] is given by
and the second order backward difference formula (BDF2) [3, p. 715] by
where \(w_n=\frac{\Delta _{n+1}}{\Delta _n}\), \(\Delta _{n+1}=t_{n+1}-t_n\), \(\Delta _n=t_n-t_{n-1}\).
3.1 Local Truncation Errors and the Order of Convergence
The local truncation error (LTE) of an integration scheme is the error due to a single integration step [1, p. 40]:
where \({\hat{{\mathbf {y}}}}_{n+1}\) is an approximation to \({\mathbf {y}}(t_{n+1})\) obtained by the integration method with all the history values \({\mathbf {y}}_n,{\mathbf {y}}_{n-1},\ldots \) being exact (i.e. \({\mathbf {y}}_{n-i}={\mathbf {y}}(t_{n-i})\)). The LTE expression for the IMR is more complex than those of TR or BDF2 due to the approximation \({\mathbf {y}}\approx \frac{{\mathbf {y}}_n+{\mathbf {y}}_{n+1}}{2}\). To derive it, we apply Taylor expansions of \({\mathbf {y}}(t_{n+1})\) and \({\mathbf {y}}(t_n)\) about the midpoint \(t_{n+1/2}\):
and
Substituting (28) and (29) into
gives
The LTE expression (31) has two terms: terms similar to (I) feature in LTEs of many other second-order integrators [cf. (32) and (33)], while the term (II) arises from the use of the approximation to \({\mathbf {y}}(t_{n+1/2})\) in the evaluation of \({\mathbf {f}}\) (i.e. it reflects the Runge–Kutta nature of the IMR). The IMR is asymptotically second-order accurate (i.e. the global error behaves as \(O(\Delta ^2_n)\) when \(\Delta _n\rightarrow 0\)) [29, p. 152]. For completeness, we present the LTE expressions for the TR [3, p. 261] and the BDF2 methods [3, p. 715], respectively:
and
3.2 Properties of the IMR
The IMR has two important properties that makes it a method of choice for the time integration of semi-discretised PDEs:
-
It is A-stable [17, p. 43,251], i.e. it can be applied to stiff problems.
-
It requires only one evaluation of the function \({\mathbf {f}}\) per step (a one-step method, unlike many other Runge–Kutta methods).
These properties of the IMR method are shared with TR and BDF2. However, the IMR does not introduce spurious damping of oscillatory solutions (TR does possess this property, although it is lost in the modified versions of it [4, 30], introduced to avoid the locking effect in the step size selection caused by the accumulation of the round-off errors). All backward differentiation formulae are damping [3, p. 265]. When applied to the time integration of the LLG equation, the IMR has geometric properties, related to the conservation of the magnetization length and reproduces a correct energy behaviour of the system. It is also worth noticing that when applied to the integration of linear problems, IMR and standard TR will produce exactly the same numerical solutions, i.e. the two methods are equivalent (by virtue of \({\mathbf {f}}_{n+1/2}= \frac{1}{2} ({\mathbf {f}}_{n+1}+{\mathbf {f}}_n)\) for linear functions \({\mathbf {f}}\) [3, p. 650]).
4 Adaptive Implicit Mid-Point Rule
Implicit time integration of ODEs or semi-discretised PDEs is a computationally intensive task. Numerically effective integrators employ adaptivity, which enables an integrator to take steps of the size governed, within the prescribed tolerance, by the physics of the problem, rather than artificial (method-specific) constraints. Adaptive step selection algorithms rely on computable estimates of the LTE. In this section we discuss the difficulties in applying the commonly used LTE estimation schemes to IMR and introduce the new approach.
4.1 Local Truncation Error Estimation
Typical LTE estimators used in implicit IVP integrators (such as TR or BDF2) are based on the solution estimate \({\mathbf {y}}^{{\text {E}}}_{n+1}\sim {\mathbf {y}}(t_{n+1})\) computed by an explicit method with the same asymptotic order of accuracy, using the history values computed by an implicit method. This is referred to as the predictor step. Algebraic rearrangements of the analytical expressions for the LTEs of an explicit and an implicit method lead to a computable estimate of the implicit LTE with a desired order of accuracy. This approach is known as Milne’s device [3, p. 707–716]. It is not straightforward to apply this approach to estimating the LTE of the IMR, due to the presence of the term II in (31). The difficulty of constructing a Milne device in this case lies in finding a suitable predictor which LTE involves the term II from (31). In the case of linear or linearised problems (such as the Simo-Armero linearisation of the Navier–Stokes equations [31]), the IMR is numerically equivalent to TR, which implies that the use of the standard AB2 predictor will produce the same behaviour (in terms of the number and the size of the selected steps) for both AB2-TR and AB2-IMR integrators. This is no longer the case when \({\mathbf {f}}\) is non-linear and we focus on this scenario in the remainder of this paper.
Adaptivity in explicit Runge–Kutta methods is achieved by finding a pair of methods of different orders and to obtain a LTE estimate by comparing the two solutions [17, p. 165]. The effectiveness of this approach relies on the existence of pairs of methods that share the most of their function evaluation points – the so-called embedded methods (the examples include the Dormand-Prince pair of order 4/5 deployed in Matlab’s function ode45 [9]). To deploy this approach in the context of the IMR would require a third order implicit method that involve a function evaluation in addition to \({\mathbf {f}}(t_{n+1/2},{\mathbf {y}}_{n+1/2})\). However, the function evaluation \({\mathbf {f}}(t_{n+1/2},{\mathbf {y}}_{n+1/2})\) at the “mid-point” of the interval \([t_n,t_{n+1}]\) leads to the cancellation of the second-order terms in (28)–(29), and an additional function evaluation at a point in \([t_n,t_{n+1}]\) would break this symmetry. To restore it, we would require two additional function evaluations.
In order to bypass these problems, we consider explicit third order methods as predictors in the non-linear case. Suitable candidates are AB3 [1, p. 127], RK3 [1, p. 73], and the eBDF3 method [17, p. 378]. The first two of these methods are computationally more expensive and/or require the storage of more history values than the AB2 method. This is, however, not the case with the eBDF3 method. In order to be a competitive predictor, it should lead either to the overall reduction in the number of time steps in non-linear cases for a set LTE tolerance, or a better accuracy for a fixed number of steps performed compared to the AB2 predictor. In particular, the AB2 method requires the storage of the function values (the solution derivatives) at two history points. In the non-linear case this ammounts to either storing the Jacobians at these points or assembling them on the fly. We notice that the function evaluations at multiple points also introduce additional implementation complications in ODE/PDE cases where the time derivative is given implicitly (such as in the LLG equation). The situation is even worse for AB3 and RK3 methods that require the computation or storage of the function values at three history points. Neither of these predictors is self-starting, which is a drawback for a self-starting IMR method. The eBDF3 method is not self-starting either, but requires the storage of three history solution values, rather than its derivatives, and only one function evaluation (at \(\Delta _n\)). This makes it a competitive alternative to the AB2 method and the other two third order methods. The computational cost of applying the eBDF3 predictor consists of one sparse matrix-vector multiplication (where we assume that a dense matrix block obtained in the BEM discretisation of the magnetostatic field is sparsified prior to its use) and, in PDE cases, the solution of one trivial linear system with a diagonal mass matrix (assuming that reduced quadratures are used). The eBDF3 predictor is therefore judiciously chosen among the other alternatives (AB2, AB3, RK3) due to its low computational and/or storage overhead.
The eBDF3 method is unstable for fixed step sizes [17, p. 378], however this is not an issue when used as a predictor, as we only perform a single step of it using IMR-computed history values. Thus, the eBDF3 method can be viewed as an extrapolation of \({\mathbf {y}}\) at \(t_{n+1}\) using the history values.
The LTE estimate of a generic explicit third-order method at the time step \(\Delta _n=t_{n+1}-t_n\) is given by:
and the LTE of the IMR can be written as
Expressing \({\mathbf {y}}(t_{n+1})\) from (34) and substituting to (35) gives
i.e. we have an estimate:
4.2 The Variable Step eBDF3 Method
Both explicit and implicit BDF methods are derived from a divided difference representation of an interpolation polynomial \({\mathbf {p}}(t)\) through \({\mathbf {y}}_{n+1}\) and a number of history values. Setting \({\mathbf {p}}'(t_{n+1})={\mathbf {f}}(t_{n+1},{\mathbf {y}}_{n+1})\) leads to implicit BDF methods, while \({\mathbf {p}}(t_n)={\mathbf {f}}(t_n,{\mathbf {y}}_{n})\) gives the family of the explicit BDF methods [17, p. 364]. The Lagrange interpolation polynomial of degree k [17, p. 400] can be written in terms of the backward Newton divided differences \({\mathbf {y}}[t_{n+1},\ldots ,t_{n+1-j}]\), \(j=1,\ldots ,k\) as
Differentiating (38) yields
Equation (39) can be simplified by noticing that the product on the right-hand side evaluated at \(t=t_n\) (for \(i=1\)) is zero. This gives
For \(k=1\) and \(k=2\) (40) reduces to the well-known forward Euler and the leapfrog (explicit mid-point rule) methods, respectively [3, p. 715]. For larger values of k the complexity of (40) increases significantly. The eBDF3 method is obtained for \(k=3\):
The rearrangement of (41) for \({\mathbf {y}}_{n+1}\) was done using the symbolic library SymPy [32, 33] resulting in
where
For constant step size (\(\Delta _n=\Delta _{n-1}=\Delta _{n+1}=\Delta \)) (43) reduces to the scheme given in [17, p. 364] with \(b=3\Delta \), \(c_n=-\frac{3}{2}\), \(c_{n-1}=3\), \(c_{n-2}=-\frac{1}{2}\). The computational cost of (43) can be high for linear scalar IVPs. However, if non-linear IVP systems are solved in the context of the method of lines, the cost of computing (43) is small compared to the (repeated) solution of a linear system required by an implicit corrector.
The LTE estimate for IMR (37) is used to predict the next step size via the standard heuristics that involves the user-prescribed tolerance \(\varepsilon _T\) [3, p. 268]:
where \(\Vert \cdot \Vert \) is a suitable norm of the LTE (e.g. a mass matrix norm, see [3, p. 708]). In the example from Sect. 5.1 we do not introduce any further restrictions in the step selection while in the cases from Sects. 5.2 and 5.3 we make the criterion (44) more robust by adding the following two heuristical rules, which are in line with the recommendations from [19, p. 432]: i) if \(\Delta _{n+1}/\Delta _n\) is smaller than 0.7, we adopt \(\Delta _n= \Delta _n/2\) and repeat the calculation for the step \(\Delta _n\) (the step cancellation), and ii) we limit the step size growth factor \(\Delta _{n+1}/ \Delta _n\) by 4 to improve numerical stability.
We notice that some public IVP solvers, such as CVODE [8, Sect. 2.1] keep the step size constant as long as feasible. This allows the use of the inexact Newton’s method, which does not require the assembly of the Jacobians at every iteration, thus reducing the computational cost. However, if the associated linear systems are solved by a preconditioned Krylov method, the gains in convergence speed obtained using exact Newton’s method can outweigh the savings obtained by not assembling the Jacobian matrices [34, p. 128]. The adaptive high-order explicit method from [7] also selects fairly constant time steps over long time intervals.
5 Numerical Examples
In this section we present numerical experiments that demonstrate the effectiveness, accuracy, and geometric properties of the proposed adaptive IMR scheme. The first case study is an ODE system modelling a magnetization reversal in a small spherical (both isotropic and anisotropic) ferromagnetic particle, while the two further cases are the PDE problems which involve spatial variation of the magnetization vector and are discretised using finite element method and the method of lines is applied to the semi-discretised system of IVPs [35]. The implementation of the ODE example in Sect. 5.1 is done in Matlab, while the PDE examples are implemented in oomph-lib, an object-oriented multi-physics finite element library [36].
5.1 The Magnetic Reversal of a Spherical Particle
This is a widely used model-problem from micromagnetics which is represented by an ODE system. We consider the magnetization of a small spherical particle made of either an isotropic or anisotropic ferromagnetic material under a spatially uniform applied field \({\mathbf {h}}_{\text{ ap }}\). The evolution of the magnetization vector \({\mathbf {m}}\in C^1(T)\) follows the LL Eq. (1) with \({\mathbf {h}}={\mathbf {h}}_{\text{ ap }}+k_1({\mathbf {m}}\cdot {\mathbf {e}}){\mathbf {e}}\) is the effective field. In case of an isotropic material (\(k_1=0\)) \({\mathbf {h}}\) has only the applied field component [18, p. 306]. For a sufficiently small sphere the magnetization is spatially uniform, i.e. \({\mathbf {m}}={\mathbf {m}}(t)\) and the problem (1) is a system of three ODEs for the unknown Cartesian components of \({\mathbf {m}}\). The problem has an analytical solution [37], which describes the process of the magnetization switching and can be expressed in spherical polar coordinates \((\theta ,\phi )\) as \(\theta =\cos ^{-1}(m_z/1)\), \(\phi =\tan ^{-1}(m_y/m_x)\), where \(\theta \) is the angle between \({\mathbf {m}}\) and \({\mathbf {h}}_{\text{ ap }}\). The energy of the system is in this case given by \(E=-{\mathbf {m}}\cdot {\mathbf {h}}_{\text{ ap }}\). In the ideal non-damped case (\(\alpha =0\)) the energy remains conserved throughout the magnetization reversal (i.e. the process of the realignment of \({\mathbf {m}}\) from the initial configuration \({\mathbf {m}}_0\) to the external field \({\mathbf {h}}_{\text{ ap }}\)) – the property that needs to be replicated by the time integrator. For anisotropic materials (\(k_1>0\)) we study the behaviour of the time integrators for the realistic values of the phenomenological anisotropy parameter \(k_1\in [0,4]\).
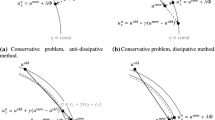
a) Isotropic case (\(k_1=0\)). We consider the damping value \(\alpha = 0.01\). In this case the problem (1) is only mildly non-linear. Thus, we would expect that the AB2-IMR method performs well, and its step size selection to be comparable to that obtained with a third-order predictor. We choose \({\mathbf {h}}_{\text{ ap }}=(0,0,-1.1)^t\), which is a sufficient magnetic field strength to reverse the initial magnetization \({\mathbf {m}}_0={\hat{{\mathbf {m}}}}_0/\Vert {\hat{{\mathbf {m}}}}_0\Vert \), where \({\hat{{\mathbf {m}}}}_0=(0.01,0,1)^t\). In all our experiments it took 1–2 iterations for the exact Newton method to converge to a prescribed tolerance \(\varepsilon _N=10^{-14}\). The system (1) is integrated over the interval \(T=[0,1000]\), which is sufficient to reach a steady state after the reversal. The time evolution of the Cartesian components of the magnetization vector \({\mathbf {m}}=(m_x,m_y,m_z)^t\) is presented in Fig. 1.
We first examine the efficiency of the step size selection procedure and the magnetization length conservation properties of different integration schemes as a function of the LTE tolerance \(\epsilon _T\). The results are summarised in Table 1. From these figures we see that the adaptive step IMR method conserves \(|{\mathbf {m}}|\) to the level of Newton’s tolerance \(\varepsilon _N\), while this is not the case for the BDF2 and TR methods. TR is more accurate in this context than BDF2, which can also be seen from Fig. 2, which depicts the time evolution of the magnetization length for the three time integrators. Comparing the number of time steps required to complete the integration, it follows that AB2-TR and AB2-IMR have the same behaviour (which is expected in the case of linear and mildly non-linear problems). The combination eBDF3-IMR leads to approximately \(40\%\) higher number of time steps than the AB2 predictor for a fixed value of \(\epsilon _T\). The time step evolution for various integrators is presented in Fig. 3.
Next we test the accuracy of the proposed time integrators. To this end, we record the time \(t_1\) for which \(m_z(t_1)=0\) (cf. Fig. 1), i.e. the time \(t_1\) for which \({\mathbf {m}}\cdot \hat{\mathbf k}=0\). The reference solution for this problem is calculated by both adaptive TR and IMR with a tight tolerance (\(\epsilon _T=10^{-10}\)) as \(t_s=481.72\). In Table 2 we present the accuracy results when all the tested methods take the same number of steps to perform the simulation over the interval \(T=[0,490]\). This is achieved by adjusting the LTE tolerance \(\epsilon _T\) for each method separately. The rationale behind this experiment is to evaluate the quality of the integration points distribution for each of the predictors considered.
From these results we see that the combination eBDF3-IMR is as accurate as AB2-TR. This is due to the character of the problem, which is only weakly non-linear, implying a near equivalence of the TR and IMR schemes. Indeed, for the tight LTE tolerances \(\epsilon _T\) the TR and IMR schemes are virtually indistinguishable.
b) Anisotropic case (\(k_1\ne 0\)). This case involves material anisotropy, expressed by an additional field component (the anisotropic field). We test the efficiency and accuracy of the proposed time integrators when the non-linearity in the problem, controlled by the parameter \(k_1\), increases. In particular, there is no equivalence between the TR and the IMR method in these cases, and we expect that the third order predictor for IMR leads to a better accuracy when the number of time steps is fixed, when compared to AB2-TR and AB2-IMR methods. As in the previous example, we choose \({\mathbf {h}}_{\text{ ap }}=(0,0,-1.1)^t\), \({\mathbf {m}}_0={\hat{{\mathbf {m}}}}_0/\Vert {\hat{{\mathbf {m}}}}_0\Vert \), where \({\hat{{\mathbf {m}}}}_0=(0.01,0,1)^t\), and select the direction of the material anisotropy as \(\hat{\mathbf {e}}={{\mathbf {e}}}/\Vert {{\mathbf {e}}}\Vert \) where \(\mathbf {e}=(1,-0.3,0)^t\). The remaining problem and algorithm parameters are the same as in the isotropic case. The size of the time interval required to complete the reversal varies for different values of \(k_1\) and is selected to be sufficiently long for the system to reach a steady state. For any non-zero value of \(k_1\) the steady-state position of the magnetization vector after the reversal is no longer aligned with \({\mathbf {h}}_{\text{ ap }}.\) The time evolution of the magnetization vector components with \(k_1=4\) is presented in Fig. 4.
In Table 3 we present the numbers of time steps N required to complete the integration for the LTE tolerance \(\epsilon _T=10^{-5}\) and the bounds for the magnetization length \(|{\mathbf {m}}|\) for different values of \(k_1\) and different integrators. From the table we see that the increase in \(k_1\) leads to the poorer magnetization length preservation (although the used level of toletance \(\epsilon _T\) gives fairly good values for all integrators, looser values of \(\epsilon _T\) will cause problems for BDF2 and TR, with notable loss of accuracy in \(|{\mathbf {m}}|\), see Fig. 5 for the case \(\epsilon _T=10^{-4}\)). As \(k_1\) is increased, the combination AB2-IMR requires fewer steps than AB2-TR.
The time step size history for three different combinations of time integrators is presented in Fig. 6. Comparing to the isotropic case, where a smooth variation in step sizes is observed in all time integrators, we see that the step size selection exhibits a considerably more dynamic behaviour, which is the consequence of a more complex dynamics in the problem.
Next, we report the accuracy of the first zero crossing in the z component of the magnetization for \(k_1=4\) (i.e. the smallest time \(t_1\) for which \(m_z(t_1)=0\)). We do this with respect to two different criteria: fixed number of time steps and fixed execution time for all tested integrators. The first criterion reflects the quality of a predictor, i.e. how the distribution of a prescribed number of the integration points that it produces affects the solution accuracy. The second criterion tests whether the computational overhead associated with adaptive step selection leads to a more accurate method than computationally cheaper fixed step counterpart within a set amount of wall clock time.
For the first criterion we consider three different levels of precision, determined by a fixed number of steps \(N_1\) required to cover the interval [0, 150] for all methods. These levels are \(N_1= 4142\), 8967, and 19,336, obtained by setting \(\epsilon _T\) in AB2-TR method to \(10^{-5}\), \(10^{-6}\), and \(10^{-7}\), respectively, and adjusting it in other integrators to match this number of steps. The reference solution \(t^{{\text {ref}}}_1=145.038\) is obtained by the eBDF3-IMR and AB2-TR methods with \(\epsilon _T=10^{-10}\). The results are presented in Table 4. From the results we observe that the eBDF3-IMR combination is the most accurate, although for very tight tolerances \(\epsilon _T\) the differences to AB2-TR and AB2-IMR methods become less pronounced.
For the second criterion (fixed execution time) we compare only the adaptive and the fixed step versions of the IMR integrator. We consider again three different levels of precision for adaptive IMR and adjust the number of time steps for the fixed step variant so that both methods have the same execution time to perform the integration over the time interval [0, 500]. In Table 5 we report the values of \(t_1\) at which the first zero crossing \(m_z(t_1)\) occurs. From these figures it can be concluded that fixed step IMR completes more steps in a set amount of time (due to an increased computational cost per step in the adaptive method), but still has lower accuracy, justifying the additional costs of the adaptive version. We remark that the number of steps reported in Table 5 suggest that the computational cost of an adaptive step is only \(5{-}10\%\) larger than that of a fixed step. This is expected in the case of non-linear problems, with the cost of computing a predictor consists of a matrix-vector multiplication, while the cost of the corrector is dominated by multiple linear system solves that are costly.
Finally, in Table 6 we report the energy \(E=-{\mathbf {m}}\cdot ({\mathbf {h}}_{\text{ ap }}+{\mathbf {h}}_{\mathrm{mc}})\) at the time \(t=600\) of the simulation with \(k_1=4\) as the function of the LTE tolerance \(\epsilon _T\). This time is sufficient for the magnetization vector to reach the steady-state after the reversal. We observe from the results that for the larger values of \(\epsilon _T\) there is a notable error in the computed energy (more than 5% for the BDF2 method with \(\epsilon _T=10^{-4}\)). By contrast, the computed energy remains constant with the IMR method, irrespectively of the LTE tolerance.
5.2 The PDE Example with an Analytical Solution
This model problem is defined in the domain \(\Omega \subset \mathbb {R}^2\), and is modelled by the non-dimensional form of the LLG equation (4). In this example we consider only the exchange coupling, hence \({\mathbf {h}}=\nabla ^2{\mathbf {m}}\). We report on the behaviour of the adaptive IMR when applied to a problem whose analytical solution has a non-trivial spatial variation. A more detailed description can be found in [38, 39]. We consider an infinite two-dimensional domain, which is reduced to a finite counterpart by applying periodic BCs. For chosen constants \(c\in \mathbb {R}\) and \({\mathbf {k}}\in \mathbb {R}^3\), define
Then the components of the magnetization are given by
For large intervals of the values of c and \({\mathbf {k}}\) (46) represents a damped periodic precession tending to a steady state \({\mathbf {m}}=[0\ 0\ \pm 1]^t\) as \(t\rightarrow \infty \), reducing to a simple wave in space and time for \(\alpha \rightarrow 0\).
The domain \(\Omega =[0,1]^2\subset \mathbb {R}^2\) is used in our simulations with periodic BCs. Spatial discretisation is performed by finite elements (uniform quadrilateral elements with the resolution \(80\times 80\) resulting in 1681 nodes). Our spatial discretisation is similar to that used in [20]. The difference between the two approaches is that instead of a provably convergent, but restrictive linearisation procedure (the convergence is proved under a time step size restriction \(\Delta =O(h^2)\)), we use the standard Newton method with a tolerance linked to the desired level of error in the magnetization length and/or energy, leaving to the adaptive eBDF3-IMR procedure to select the appropriate time step sizes. The initial condition is set according to (46) for \(t=0\) and \({\mathbf {h}}_{{\text {ap}}}={\mathbf {0}}\). The solution parameters are \({\mathbf {k}}=[2\pi , 2\pi ]^t\), \(c=0.1\pi \) and \({\mathbf {h}}_{\text{ ap }}=0.01\). For the energy conservation experiments we set \(\alpha =0\).
The snapshot of the solution at \(t=0.1\) is given in Fig. 7. In Fig. 8 we depict the error in the nodal magnetization
where \({\mathbf {m}}_{j,n}\) are the FE approximations at the nodes j of the magnetization vector at \(t=t_n\) and V is the set of all nodes in the mesh. We consider four different configurations: BDF2, TR and IMR with Gaussian integration, and IMR with nodal (reduced) integration. When IMR with nodal quadrature is used the error (47) remains small and controlled by the adopted Newton’s tolerance \(\varepsilon _N\). When Gaussian quadratures are used, the error (47) grows rapidly up to \(10^{-4}\) at which level it remains fairly constant, irrespective of the time integration scheme.
We next examine the energy conservation properties for different schemes for the non-damped case \(\alpha =0\). The only energy component in this example is the exchange energy defined by [13, Ch. 2]
The integral in (48) can be evaluated exactly by both the Gaussian and the nodal quadratures when piecewise linear elements are used, since \(\nabla {\mathbf {m}}\) is a constant in each element. The results are summarised in Fig. 9. We observe that BDF2 does not conserve energy, but both TR and IMR with Gaussian quadratures perform well for this particular problem. The best results are obtained, however, when IMR and nodal quadratures in FE discretisation are used. Accurate results for the length and energy conservation with Gaussian quadratures are not observed for any of the time integrators in more general cases (see, for example, [13, Sect. 8.2] for the test-problem with a non-uniform external field).
5.3 The NIST \(\mu \)MAG Standard Problem #4
The \(\mu \)MAG standard problem #4 [40] is a widely used benchmark for testing various micromagnetic methods and models. It involves modelling the reversal of the magnetization in a thin film of a permalloy material under an applied field. The problem is modelled by a PDE system (4)–(9), where we consider an isotrpic case (\(k_1=0\)). The damping parameter is \(\alpha =0.02\) and we consider two cases of applied field: \(\mu _0{\mathbf {h}}_{\text{ ap }, 1}=[-24.6\ 4.3\ 0.0]^t\,mT\) and \(\mu _0{\mathbf {h}}_{\text{ ap }, 2}=[-35.5\ -6.3\ 0.0]^t\,mT\), where \(\mu _0=4\pi \cdot 10^{-7}\,H\cdot m^{-1}\). The non-dimensionalisation of the LLG equation results in the unit length of 5.69 nm and the unit time of 5.65 ps. Hence, the non-dimensional domain is of size \(87.94\times 21.98\times 0.53\).
The evolution of the Cartesian components of the mean magnetization and the time step size \(\Delta _n\) for the \(\mu \)MAG problem #4 for \({\mathbf {h}}_{\text{ ap }, 1}\) obtained with adaptive IMR and FEM (red) and the solution plotted using the raw data from [12] (green). One non-dimensional time unit is equal to 5.65 ps (Color figure online)
The initial condition \({\mathbf {m}}_0\) is the S-state obtained by slowly relaxing the magnetization from the state obtained by a saturating field in the \([1\ 1\ 1]^t\) direction [40]. The S-state is obtained by applying the field
over the non-dimensional time interval \([-300,0]\) to the initial state \({\mathbf {m}}=[1\ 1\ 1]^t\) with \(\alpha =1\). This choice allows the system to reach the initial condition quickly.
The domain \(\Omega \) is discretised by a structured uniform mesh of hexahedral elements with a single layer of elements in the z-direction. Then we apply the hybrid FEM/BEM method described in Sect. 2.3. The parameters used in the eBDF3-IMR method are \(\Delta _0=10^{-4}\) and \(\epsilon _T=10^{-5}\). Newton’s method tolerance is \(\epsilon _N=10^{-11}\). We comment briefly on the computational cost of the FEM/BEM method. At each time step the eBDF3 predictor requires one sparse matrix-vector multiplication (recall that we use hierarchical approximation of the BEM matrix) at a cost \(O(N+N_b\log N_b)\) and a trivial solution of a linear system with a mass coefficient matrix with a cost O(N) (when reduced integration is used, the mass matrix is diagonal by construction [13, p. 104]). The Newton iteration in the corrector takes 2–3 steps to converge [13, Fig. 8.24]. The cost of assembling the Jacobian is O(N), as the BEM matrix does not need to be reassembled. The Krylov solver is preconditioned by a general algebraic, rather than a problem-specific, preconditioner, leading to an inevitable growth in iteration counts as N is increased. For our simulations GMRES converged in 10–25 iterations. Therefore, we pessimistically estimate the computational cost per time step of the eBDF3-IMR method as \(150 C_{mv}\), where \(C_{mv}\) is the cost of a sparse matrix-vector multiplication.
The evolution of the Cartesian components of the mean magnetization and the time step size \(\Delta _n\) for the \(\mu \)MAG problem #4 for \({\mathbf {h}}_{\text{ ap }, 2}\) obtained with adaptive IMR and FEM (red) and the solution plotted using the raw data from [12] (green). One non-dimensional time unit is equal to 5.65 ps (Color figure online)
We compare the accuracy of the solutions obtained by the adaptive IMR scheme to the results from [12] obtained by the IMR scheme with fixed step sizes and finite difference method applied to spatial discretisation (magnetostatic effects are handled by the FFT and monolithically coupled to the LLG model). In Fig. 10 we present the mean magnetization and the time step sizes \(\Delta _n\) generated by the proposed adaptive scheme for the field \({\mathbf {h}}_{\text{ ap }, 1},\) while Fig. 11 plots the same results for \({\mathbf {h}}_{\text{ ap }, 2}.\)
The results obtained by adaptive IMR (in red) are superimposed to those in green plotted using the raw data from [12]. The two solutions agree reasonably well, except in the interval [100, 200] for \({\mathbf {h}}_{\text{ ap }, 2}.\) It is worth noticing that this is the interval where all the solutions submited to \(\mu \)MAG repository [40] exhibit different behaviour. The upshot is that the proposed adaptive algorithm correctly identifies this difficult part of the time interval and responds by cutting the stepsize to a value significantly below the fixed steps adopted in [12]. After the oscillations in \({\mathbf {m}}\) are damped out for \(t>200\), the step size increases steadily. In Fig. 12 we present the mean value of \(m_y\) in the critical part of the time interval calculated with two different spatial resolutions (the number of grid points in x direction is equal to the number assigned to the quadrature rule in the figure legend) and two different types of numerical quadratures.
When compared to adaptive BDF2 and TR methods, IMR selects significantly smaller steps during the initial relaxation phase (for \(t<0\)). This effect may be attributed to order reduction observed in IMR when applied to very stiff problems. For \(t>0\) time steps selected by all three methods are commensurate. We notice that recently introduced adaptive high-order explicit midpoint method [7] keeps the step size fairly constant both in the highlighted time interval [100, 200] and during the entire simulation for the case \({\mathbf {h}}_{\text{ ap }, 1}.\) The time step of \(200\,fs\) reported in [7] is between 3 and 20 times smaller than the step sizes taken by the eBDF3-IMR method for \(t>0\) (cf. Fig. 10).
The comparison of the computational cost per time step between the explicit method from [7] and the coupled FEM/BEM method is not straightforward. Results from Table 1 in [7] indicate approximately between 25 and 40 total (effective and stray) field evaluations per time step. If we assume that the cost of one field computation is proportional to \(C_{mv}\), we can conclude that the overall computational times of both methods are broadly comparable in this particular case.Footnote 2
The maximum pointwise error (47) in the magnetization length observed during the simulation was in both cases \(4\cdot 10^{-10}\), in line with the adopted Newton’s tolerance.
6 Conclusions
In this paper we have introduced an adaptive IMR method. Using the example domain of micromagnetic problems we have shown that the method conserves the magnetisation length and accurately reproduces the energy balance (i.e. it preserves the geometric properties of the solution even for loose LTE tolerances). The method uses a computationally efficient and reliable method for the LTE estimation in the IMR and is based on the use of a third-order explicit method as the predictor. In our experiments the selected step sizes of the adaptive IMR were commensurate to the other commonly used second-order methods, while the geometric integration properties were preserved. We also remark that geometric integrator properties of IMR are relevant for other problems (for example, if the Navier–Stokes problem is solved, the kinetic energy \({\mathbf {u}}^t{\mathbf {u}}\) will be correctly reproduced independently of the step size, where \({\mathbf {u}}\) is the fluid velocity [3, p. 651], provided that an appropriate spatial discretisation is used, see [41]). This makes the proposed adaptive integrator suitable choice for a much wider class of problems than studied in this paper.
The codes used to produce the results in Sect. 5.1 are publicly available at https://github.com/davidshepherd7/Landau--Lifshitz--Gilbert-ODE-model, and for the PDE examples from Sects. 5.2 and 5.3 at https://github.com/davidshepherd7/oomph-lib-micromagnetics.
Notes
In this case the magnetization is conserved in an “element-wise”, rather than “point-wise” fashion.
The cost of an implicit step is between 4 and 6 times higher than the cost of an explicit step, but the implicit step sizes are between 3 and 20 times larger than that of the explicit integrator.
References
Ascher, U., Petzold, L.: Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. SIAM, Philadelphia (1998)
Ascher, U., Mattehij, R., Russell, R.: Numerical Solution of Boundary Value Problems for Ordinary Differential Equations. SIAM, Philadelphia (1995)
Gresho, P.M., Sani, R.L.: Incompressible Flow and the Finite Element Method: Advection-Diffusion and Isothermal Laminar Flow, 1st edn. Wiley, Chichester (1998)
Gresho, P.M., Griffiths, D.F., Silvester, D.J.: Adaptive time-stepping for incompressible flow part I: scalar advection-diffusion. SIAM J. Sci. Comput. 30(4), 2018–2054 (2008)
Kay, D., Gresho, P., Griffiths, D., Silvester, D.: Adaptive time stepping for incompressible flow; part II: Navier–Stokes equations. SIAM J. Sci. Comput. 32, 111–128 (2010). https://doi.org/10.1137/070688018
Elman, H., Mihajlović, M., Silvester, D.: Fast iterative solvers for buoyancy driven flow problems. J. Comput. Phys. 230, 3900–3914 (2011). https://doi.org/10.1016/j.jcp.2011.02.014
Exl, L., Mauser, N., Schrefl, T., Suess, D.: The extrapolated explicit midpoint scheme for variable order and step size controlled integration of the Landau–Lifshitz–Gilbert equation. J. Comput. Phys. 346, 14–24 (2017). https://doi.org/10.1016/j.jcp.2017.06.005
Hindmarsh, A.C., Serban, R.: User Documentation for \(\mathtt {cvode}\) v2.7.0 (2012)
MathWorks, ode45 (2014). http://www.mathworks.co.uk/help/matlab/ref/ode45.html
Aharoni, A.: Introduction to the Theory of Ferromagnetism, 2nd edn. Oxford University Press, Oxford (1996)
Shepherd, D., Miles, J., Heil, M., Mihajlović, M.: Discretisation induced stiffness in micromagnetic simulations. IEEE Trans. Magn. 50, 7201304 (2014). https://doi.org/10.1109/TMAG.2014.2325494
d’Aquino, M., Serpico, C., Miano, G.: Geometrical integration of Landau–Lifshitz–Gilbert equation based on the mid-point rule. J. Comput. Phys. 209(2), 730–753 (2005). https://doi.org/10.1016/j.jcp.2005.04.001
Shepherd, D.: Numerical methods for dynamical micromagnetics, Ph.D. thesis, The University of Manchester (2015)
Fidler, J., Schrefl, T.: Micromagnetic modelling—the current state of the art. J. Phys. D Appl. Phys. 33(15), R135–R156 (2000). https://doi.org/10.1088/0022-3727/33/15/201
Szambolics, H., Buda-Prejbeanu, L., Toussaint, J., Fruchart, O.: A constrained finite element formulation for the Landau–Lifshitz–Gilbert equations. Comput. Mater. Sci. 44, 253–258 (2008). https://doi.org/10.1016/j.commatsci.2008.03.019
Fischbacher, T., Fangohr, H.: Continuum multi-physics modeling with scripting languages: the Nsim simulation compiler prototype for classical field theory, arXiv (2009) 1–50. arXiv:0907.1587v1
Hairer, E., Morsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I: Nonstiff Problems, 2nd edn. Springer, Berlin (1991)
Coey, J.: Magnetism and Magnetic Materials, 1st edn. Cambridge University Press, Cambridge (2010)
Elman, H., Silvester, D., Wathen, A.: Finite Elements and Fast Iterative Solvers, 2nd edn. Oxford University Press, Oxford (2014)
Bartels, S., Prohl, A.: Convergence of an implicit finite element method for the Landau–Lifshitz–Gilbert equation. SIAM J. Numer. Anal. 44(4), 1405 (2006). https://doi.org/10.1137/050631070
Cimrák, I.: A survey on the numerics and computations for the Landau–Lifshitz equation of micromagnetism. Arch. Comput. Methods Eng. 15(3), 277–309 (2008). https://doi.org/10.1007/s11831-008-9021-2
Suess, D., Tsiantos, V., Schrefl, T., Fidler, J., Scholtz, W., Forster, H., Dittrich, R., Miles, J.: Time resolved micromagnetics using a preconditioned time integration method. J. Magn. Magn. Mater. 248(2), 298–311 (2002). https://doi.org/10.1016/S0304-8853(02)00341-4
Ying, L.: Infinite Element Methods. Springer, Berlin (1995)
Yang, B.: Numerical studies of dynamical micromagnetics, Ph.D. thesis, University of California (1997)
Fredkin, D., Koehler, T.: Hybrid method for computing demagnetizing fields. IEEE Trans. Magn. 26(2), 415–417 (1990)
Bottauscio, O., Chiampi, M., Manzin, A.: A finite element procedure for dynamic micromagnetic computations. IEEE Trans. Magn. 44(11), 3149–3152 (2008). https://doi.org/10.1109/TMAG.2008.20016
Knittel, A., Franchin, M., Bordignon, G., Fischbacher, T., Bending, S., Fangohr, H.: Compression of boundary element matrix in micromagnetic simulations. J. Appl. Phys. 105(7), 07D542 (2009)
Borm, S., Grasedyck, L.: HLib. http://www.hlib.org/
Atkinson, K.E., Han, W., Stewart, D.E.: Numerical Solution of Ordinary Differential Equations, 1st edn. Wiley, Hoboken (2009)
Lee, J., Nam, J., Pasquali, M.: A new stabilization of adaptive step trapezoid rule based on finite difference interrupts. SIAM J. Sci. Comput. 37, A725–A746 (2015). https://doi.org/10.1137/140966915
Simo, J., Armero, F.: Unconditional stability and long-term behaviour of transient algorithms for the incompressible Navier–Stokes and Euler equations. Comput. Methods Appl. Mech. Eng. 111, 111–154 (1994). https://doi.org/10.1016/0045-7825(94)90042-6
SymPy: Python library for symbolic mathematics. http://www.sympy.org/
Shepherd, D.: sym-bdf3.py. https://github.com/davidshepherd7/Landau-Lifshitz-Gilbert-ODE-model/blob/master/algebra/sym-bdf3.py
Iserles, A.: A First Course in the Numerical Analysis of Differential Equations, 2nd edn. Cambridge University Press, Cambridge (2009)
Gilbert, T.: A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 40(6), 3443–3449 (2004). https://doi.org/10.1109/TMAG.2004.836740
Heil, M., Hazel, A.L.: oomph-lib—An object-oriented multi-physics finite-element library. In: Fluid-Structure Interaction, Lecture Notes in Computational Science and Engineering, vol. 53, pp. 19–49. Springer, Berlin (2006)
Mallinson, J.: Damped gyromagnetic switching. IEEE Trans. Magn. 36(4), 1976–1981 (2000)
Jeong, D., Kim, J.: An accurate and robust numerical method for micromagnetics simulations. Curr. Appl. Phys. 14(3), 476–483 (2014). https://doi.org/10.1016/j.cap.2013.12.028
Fuwa, A., Ishiwata, T., Tsutsumi, M.: Finite difference scheme for the Landau–Lifshitz equation. Proc. Czech-Jpn. Semin. Appl. Math. 29, 107–113 (2006)
McMichael, B.: \(\mu \)MAG – Micromagnetic modelling activity group. http://www.ctcms.nist.gov/rdm/mumag.org.html
Cliffe, K.: On conservative finite element formulations of the inviscid Boussinesq equations. Int. J. Numer. Methods Fluids 1(2), 117–127 (1981)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shepherd, D., Miles, J., Heil, M. et al. An Adaptive Step Implicit Midpoint Rule for the Time Integration of Newton’s Linearisations of Non-Linear Problems with Applications in Micromagnetics. J Sci Comput 80, 1058–1082 (2019). https://doi.org/10.1007/s10915-019-00965-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-019-00965-8