1 Introduction

Devised by Dahlquist, the linear test equation \(\dot{x} = \lambda x\), with parameter \(\lambda \in {\mathbb {C}}\), is the standard problem for analyzing numerical stability of time stepping methods for initial value problems of ordinary differential equations (ODEs). Although numerical stability depends both on the problem parameter \(\lambda \) and the method’s step size \(h>0\), it only depends on their product \(z = h\lambda \in {\mathbb {C}}\). Thus, it can be analyzed in terms of a single parameter, the scaled vector field z. For example, integrating the test equation by a Runge–Kutta (RK) method, we obtain the recursion

$$\begin{aligned} x_{n+1} = S(z)\,x_n, \end{aligned}$$

where the stability function S(z) is a polynomial P(z) if the method is explicit, and a rational function R(z) if the method is implicit. The method’s stability region consists of the set of \(z\in {\mathbb {C}}\) which are mapped by the stability function S into the unit circle, i.e., \(|R(z) |\le 1\) in the implicit case, and \(|P(z) |\le 1\) in the explicit case.

Since \(P(z)\rightarrow \infty \) when \(z\rightarrow \infty \), all explicit methods have bounded stability regions. Thus, explicit methods will do as long as \(|z |\ll 1\), corresponding to nonstiff problems, but only implicit methods can be stable for large vales of z. To be useful for stiff differential equations, implicit methods are typically designed so that the stability region \(\{z\in {\mathbb {C}} \,:\, |R(z) |\le 1\}\) covers a large portion, possibly all, of \({\mathbb {C}}^-\). This way numerical stability can be maintained without severe step size restrictions.

Although simple, the linear test equation has strong implications. In a broader context \({\text {Re}}(z) < 0\) corresponds to uniform negative monotonicity and dissipation. Likewise, \(|z |\gg 1\) corresponds to problems with large scaled Lipschitz constants. The idea of this paper is to transform the scaled vector field into another vector field, which can be handled by an explicit method. We seek a map \({\mathcal {M}}:{\mathbb {C}} \rightarrow {\mathbb {C}}\) such that

$$\begin{aligned} {\text {Re}}(z) \le 0 \implies |{\mathcal {M}}(z) |\lessapprox 1. \end{aligned}$$

The simplest choice is a Möbius transformation

$$\begin{aligned} z \mapsto w = \frac{z}{1 - \gamma z}, \end{aligned}$$

where \(\gamma > 0\) is chosen so that the left half-plane \({\text {Re}}(z) \le 0\) is mapped into a disk of moderate radius,

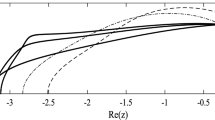
$$\begin{aligned} \left|w + \frac{1}{2\gamma } \right|\le \frac{1}{2\gamma }. \end{aligned}$$

Here the imaginary axis in the z-plane is mapped to the boundary of the disk, and \(z=-1\) to its inside (see Fig. 1).

Fig. 1
figure 1

Image of the Möbius map. Half-planes \({\text {Re}}{z}< a < 0\) are mapped by the transformation \(z \mapsto w = \frac{z}{1-\gamma z}\) into circles centered at \(-\frac{1}{2\gamma } \frac{1 - 2a\gamma }{1 - a\gamma }\) with radius \(\frac{1}{2\gamma }\frac{4a\gamma - 1}{a\gamma - 1}\). Depicted is the \(\gamma = 1\) case, with color shades corresponding to different values of a. In particular, for \(a=0\), the left half plane \({\text {Re}}{z} \le 0\) is mapped into a subset of the unit circle, \(|z + \frac{1}{2} |\le \frac{1}{2}\)

Full size image

The motivation is that a polynomial P(w) is then equivalent to a rational function,

$$\begin{aligned} P(w) = P\left( \frac{z}{1 - \gamma z}\right) = R(z). \end{aligned}$$

Thus, applying an explicit Runge–Kutta (ERK) method (with a bounded stability region) to the modified vector field (which has a moderate scaled Lipschitz constant) is equivalent to applying a particular kind of implicit RK method with unbounded stability region to the original vector field, which is only assumed to be dissipative.

We shall demonstrate that for a single parameter \(\gamma \), this procedure is equivalent to a singly diagonally implicit Runge–Kutta (SDIRK) method, while, if several different parameters \(\gamma \) are chosen, it is equivalent to a DIRK method. We then use this equivalence to explore the behaviour of SDIRK methods on linear problems. This leads us to an expansion of the exponential function in terms of modified Laguerre polynomials. We explore how a similar transformation may be used to define a family of RK methods with B-stability and consistency that are easy to characterize.

A useful review of general purpose DIRK-type methods is given by [6], where many examples are given of the different method properties, and what aspects have to be considered in the choice of methods. A full treatment of explicit and implicit RK methods is given in [2, 4, 5]. This also includes the special topic of B-stability [1], and its relation to A-stability [3].

2 From the test equation to systems of ODEs

The transformation applied to the linear test equation can be adapted to linear and nonlinear systems of ordinary differential equations.

2.1 The linear case

The linear scalar test equation provides a sufficient model for diagonalizable systems of ODEs. If \(A \in {\mathbb {R}}^{n\times n}\) represents the vector field and \(A = T^{-1} \Lambda T\) is its spectral decomposition, then, taking \(y(t) = Tx(t)\), the systems

$$\begin{aligned} \dot{x}(t) = A x(t) \quad \text {and} \quad {\dot{y}}(t) = \Lambda y(t) \end{aligned}$$

are equivalent. The latter system is merely a collection of scalar equations, whose solutions decrease monotonically if and only if the eigenvalues reside in the left complex half plane, i.e.,

$$\begin{aligned} \alpha [A] = \max \limits _{1\le j \le n} {\text {Re}}{\lambda _j(A)} \le 0, \end{aligned}$$

where \(\alpha [A]\) is the spectral abscissa of A.

Integrating this system with an RK method yields the recursion

$$\begin{aligned} x_{n+1} = S(hA) x_n, \end{aligned}$$

where S is the method’s stability function and \(h = t_{n+1}-t_n\) is the time step, with \(x_n \approx x(t_n)\). This recursion is equivalent to \(y_{n+1} = S(h\Lambda ) y_n\), with \(y_n \approx y(t_n)\).

Therefore, the condition for stability is

$$\begin{aligned} |S(h\lambda _j(A)) |\le 1. \end{aligned}$$

In other words, if the stability function S maps the negative half plane \({\text {Re}}z \le 0\) into the unit circle (the A-stability condition), then the numerical solution is stable whenever the differential equation is.

This result generalizes to systems of equations using the Euclidean logarithmic norms and matrix norms to replace the real part and absolute value, respectively. Thus, if S satisfies the A-stability condition above, any matrix having a nonpositive Euclidean logarithmic norm \(M_2[hA] \le 0\) will map to a contraction, \(\Vert S(hA)\Vert _2\le 1\), and guarantee stability. Here, the logarithmic norm is defined by

$$\begin{aligned} M_2[A] = \sup _{u\ne 0} {\frac{u^*Au}{u^*u}}. \end{aligned}$$

This pattern also generalizes to the nonlinear case, with certain restrictions on A- and B-stability. Following [8], for a vector field \(f:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) we define its least upper bound (lub.) logarithmic Lipschitz constant

$$\begin{aligned} M_2[f] = \sup \limits _{u \ne v} \frac{\left\langle u - v, f(u) - f(v) \right\rangle }{\left\langle u - v, u - v \right\rangle }, \end{aligned}$$

and its Lipschitz constant

$$\begin{aligned} L_2[f] = \sup \limits _{u \ne v} \frac{\left\langle f(u) - f(v), f(u) - f(v) \right\rangle }{\left\langle u - v, u - v \right\rangle }. \end{aligned}$$

We remark that a greatest lower bound logarithmic Lipschitz constant can be defined similarly, with \(\inf \) in place of \(\sup \) in the former equation. We will not use this quantity directly, therefore we omit the lub. qualifier, i.e., by the logarithmic Lipschitz constant we will understand \(M_2\).

Given \(\gamma > 0\), let us define \({\mathcal {M}}_{\gamma }: {\mathbb {R}}^{n\times n} \rightarrow {\mathbb {R}}^{n \times n}\), a mapping between matrix spaces, such that

$$\begin{aligned} {\mathcal {M}}_{\gamma }(hA) = hA(I - \gamma hA)^{-1}. \end{aligned}$$

Theorem 2.1

If \(h, \gamma > 0\) and \(A \in {\mathbb {R}}^{n \times n}\) is a matrix, then the implication chain

$$\begin{aligned} M_2[hA] \le 0 \quad \implies \quad \left\| \frac{1}{2\gamma } I + {\mathcal {M}}_{\gamma }(hA)\right\| _2 \le \frac{1}{2\gamma } \quad \implies \quad \left\| {\mathcal {M}}_{ \gamma }(hA) \right\| _2 \le \frac{1}{\gamma } \end{aligned}$$

holds.

In other words, the nonnegative definiteness of hA implies a circle condition on \({\mathcal {M}}_{\gamma }(hA)\) which leads to the h-independent bound on the latter.

Instead of proving this theorem separately, we show how the same chain of implications holds in a general, nonlinear setting, where a scaled uniformly negative monotone vector field is transformed by the Möbius map to a vector field with small scaled Lipschitz constant.

2.2 The nonlinear case

Let us fix a \(\gamma > 0\) and introduce the function spaces

$$\begin{aligned} {\text {Lip}}_\gamma ({\mathbb {R}}^{n})&= \left\{ f \in {\text {Lip}}({\mathbb {R}}^{n}): L_2[f] \le \gamma ^{-1} \right\} , \\ {\text {Mon}}_{-}({\mathbb {R}}^{n})&= \left\{ f:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n: L_2[f] < \infty , M_2[f] \le 0 \right\} . \end{aligned}$$

Using these we can extend the Möbius map to the nonlinear case as

$$\begin{aligned} {\mathcal {M}}_{\gamma }&: {\text {Mon}}_{-}({\mathbb {R}}^n) \rightarrow {\text {Lip}}_\gamma ({\mathbb {R}}^n), \\ hf&\mapsto hf\circ (I - \gamma hf)^{-1}. \end{aligned}$$

The domain and range in this definition are justified by the following theorem.

Theorem 2.2

If \(f: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) is a vector field, then the implication chain

$$\begin{aligned} M_2[hf] \le 0 \implies L_2\left[ \frac{1}{2\gamma } I + hf \circ (I - \gamma hf)^{-1} \right] \le \frac{1}{2\gamma } \implies L_2\left[ hf \circ (I - \gamma hf)^{-1} \right] \le \frac{1}{\gamma } \end{aligned}$$

holds.

Proof

Let hg denote \(\gamma hf \circ (I - \gamma hf)^{-1}\). Then our chain reads

$$\begin{aligned} M_2[hf] \le 0 \quad \implies \quad L_2\left[ I + 2 hg \right] \le 1 \quad \implies \quad L_2\left[ hg \right] \le 1. \end{aligned}$$

The second implication follows from a reverse triangle inequality. To show the first, we start from the inequality defining \(M_2[hf]\). We have that

$$\begin{aligned} \langle u-v, hf(u) - hf(v) \rangle \le M_2[hf]\cdot \langle u-v, u-v \rangle \end{aligned}$$

holds for all u, v in some suitably chosen domain. To further simplify notation, we will use capital letters to refer to these differences: \(F = hf(u) - hf(v), G = hg(u) - hg(v), J = u - v\). Then this inequality (intended in the “for all possible pairs of n-vectors” sense) becomes

$$\begin{aligned} \langle J, F \rangle \le M_2[hf] \cdot \langle J,J \rangle . \end{aligned}$$

Our goal is to show that

$$\begin{aligned} \langle J, F \rangle \le 0 \implies \langle J + 2G, J + 2G \rangle - \langle J, J \rangle \le 0. \end{aligned}$$

Obviously \( \langle J, \gamma F \rangle \le 0\) follows from the inequality on the left, thus by the polarization identity

$$\begin{aligned} \langle J + \gamma F , J + \gamma F \rangle - \langle J - \gamma F, J-\gamma F \rangle \le 0. \end{aligned}$$

Writing this as

$$\begin{aligned} \langle J - \gamma F + 2\gamma F , J - \gamma F + 2 \gamma F \rangle - \langle J - \gamma F, J-\gamma F \rangle \le 0, \end{aligned}$$

and momentarily regarding J, F, G as functions to compose them from the right by \((I - \gamma hf)^{-1}\), or equivalently, making a change of variables of the form \( u - \gamma hf(u) = x\) we get

$$\begin{aligned} \langle J + 2G, J + 2G \rangle - \langle J, J \rangle \le 0. \end{aligned}$$

\(\square \)

3 SDIRK \(\Leftrightarrow \) ERK + \({\mathcal {M}}_\gamma \)

Let us consider the Möbius transform of a step size scaled vector field hf

$$\begin{aligned} hg = {\mathcal {M}}_\gamma (hf) = hf \circ (I-\gamma hf)^{-1}. \end{aligned}$$

Here, as we have seen, the modified vector field has an h-independently small scaled Lipschitz constant, in the sense that even if hf has a large Lipschitz constant, hg has a small scaled Lipschitz constant. Therefore it is possible to solve the modified problem numerically using an explicit Runge–Kutta method.

This leads us to our main equivalence result, stated in the following theorem.

Theorem 3.1

SDIRK methods are equivalent to ERK methods combined with the Möbius transformation \({\mathcal {M}}_\gamma \) in the sense that taking a single numerical step in the solution of the transformed equation using an explicit method yields the same result as taking a single numerical step in the solution of the original equation using an SDIRK method.

Proof

Let us take a single step of step size h from \(x_0\) to \(x_1\) using a general s-stage explicit Runge–Kutta method given by its Butcher-tableau \((a_{ij})_{i,j = 1}^s, (b_i)_{i=1}^s\), applied to the transformed vector field

$$\begin{aligned} hg = hf \circ (I-\gamma hf)^{-1}. \end{aligned}$$

A step with the explicit method takes the form of

$$\begin{aligned} X_i&= x_0 + \sum _{j=1}^{i-1}a_{ij} hg(X_j) \quad (i= 1,\ldots ,s),\\ x_1&= x_0 + \sum _{i=1}^s b_i hg(X_i). \end{aligned}$$

Introducing the variables \(Y_i = (I-\gamma hf)^{-1}(X_i)\), these equations become

$$\begin{aligned} (I-\gamma hf)(Y_i)&= x_0 + \sum _{j=1}^{i-1}a_{ij}hf(Y_j) \quad (i= 1,\ldots ,s),\\ x_1&= x_0 + \sum _{i=1}^s b_i hf(Y_i), \end{aligned}$$

which is equivalent to

$$\begin{aligned} Y_i&= x_0 + \sum _{j=1}^{i-1}a_{ij}hf(Y_j) + \gamma hf(Y_i) \quad (i= 1,\ldots ,s),\\ x_1&= x_0 + \sum _{i=1}^s b_i hf(Y_i). \end{aligned}$$

Here we recognize the formula of a time step by an SDIRK method with Butcher-tableau

$$\begin{aligned} \begin{array}{@{}|cccc@{}} \gamma &{} &{} &{}\\ a_{21} &{} \gamma &{} &{} \\ \vdots &{} &{} \ddots &{}\\ a_{s1} &{} a_{s2} &{} a_{s,s-1} &{} \gamma \\ \hline b_1 &{} b_2 &{} \dots &{} b_s \end{array} \end{aligned}$$

applied to the original vector field. \(\square \)

Let us remark that a similar argument works in the DIRK case, however the transformation is more complicated. When we are at step n and time \(t_n\), we may define hg such that

$$\begin{aligned} hg(t_n + h\sum _{j=1}^s a_{ij}, x) = \left( hf \circ (I - \gamma _ihf)^{-1}\right) (x)\quad (i=1,\ldots ,s) \end{aligned}$$

holds. Then the above argument can be repeated with the appropriate \(\gamma _i\) in place of \(\gamma \).

4 SDIRK methods through the Möbius transformation

In this section we investigate the behaviour of SDIRK methods on linear problems through the Möbius transformation.

The two fundamental topics of interest are stability and consistency. In the linear case, both of these are studied through \({\tilde{R}}\), the stability function of the method. The first is related to the magnitude of \({\tilde{R}}\), the second is to the ability of \({\tilde{R}}\) to approximate the (complex) exponential map.

4.1 Stability

In Sect. 1 we have argued that if the ERK method’s stability function is R, then the stability function of the method obtained by first transforming the vector field, then applying this ERK method to it is

$$\begin{aligned} {\tilde{R}}(z) = R\left( \frac{z}{1-\gamma z}\right) . \end{aligned}$$

A-stability then becomes

$$\begin{aligned} z \in {\mathbb {C}}^- \implies \left|{\tilde{R}}(z) \right|\le 1. \end{aligned}$$

Therefore it is enough to require that the image of the left half plane by the Möbius transformation is contained in the stability region of the explicit method. The previous set is the disk centered at \(-\frac{1}{2\gamma }\) with radius \(\frac{1}{2\gamma }\), thus A-stability may be written as

$$\begin{aligned} |z |\le 1 \implies \left|R\left( \frac{-1 + z}{2\gamma }\right) \right|\le 1. \end{aligned}$$

Letting \(P(z) = R\left( \frac{-1 + z}{2\gamma } \right) \), the condition becomes that P should map the unit disk into itself.

Assuming that the coefficients of P are \(c_k\), we have

$$\begin{aligned} c_k = \frac{1}{k!}R^{(k)}(-(2\gamma )^{-1}) (2\gamma )^{-k}. \end{aligned}$$

Forming a vector c of these coefficients, we have the following. Due to Parseval’s theorem, a necessary condition is that \(\Vert c\Vert _2 \le 1\). On the other hand, one sufficient condition is that \(\Vert c\Vert _{1} \le 1\), implying that \(\Vert c\Vert _2 \le \frac{1}{\sqrt{\deg P + 1}}\) is enough.

4.2 Consistency

As we have already mentioned, the order of consistency depends on how well the stability function approximates the exponential map. More precisely, the SDIRK method satisfying the linear order conditions up to order p can be expressed briefly as

$$\begin{aligned} {\tilde{R}}(z) = \exp (z) + {\mathcal {O}}(z^{p+1}). \end{aligned}$$

This implies that we are facing the approximation problem

$$\begin{aligned} {\tilde{R}}(z) = R\left( \frac{z}{1-\gamma z}\right) \approx \mathrm e^z \end{aligned}$$

for some polynomial R.

4.3 Möbius–Laguerre expansion of \(\mathrm e^z\)

Let us introduce the modified Laguerre polynomials

$$\begin{aligned} {\tilde{L}}_n(\gamma ) = {\left\{ \begin{array}{ll} 1, &{} n = 0,\\ \frac{1}{n}(-\gamma )^{n-1}L_{n-1}(\gamma ^{-1}), &{} n \ge 1, \end{array}\right. } \end{aligned}$$

where \(L_n\) is the nth Laguerre polynomial [7, with \(\alpha = 1\)]. Then the following theorem holds.

Theorem 4.1

   

$$\begin{aligned} \sum _{n=0}^{\infty }{\tilde{L}}_n(\gamma ) \left( \frac{z}{1 - \gamma z} \right) ^n = \mathrm e^z. \end{aligned}$$

Proof

The generating function of \(L_n\) is

$$\begin{aligned} \sum \limits _{n=0}^{\infty }L_n(x) t^n = \frac{1}{(1-t)^{2}}\exp \left( - \frac{tx}{1-t} \right) , \quad |t |< 1. \end{aligned}$$

Multiplying both sides by \((1-t)^2\), this is equivalent to

$$\begin{aligned} L_0(x) + (L_1(x) - 2L_0(x))t + \sum _{n=2}^{\infty }(L_{n-2}(x) - 2L_{n-1}(x) + L_n(x)) t^n = \exp \left( \frac{tx}{t - 1}\right) , \quad |t |< 1. \end{aligned}$$

The recursion

$$\begin{aligned} L_{n}(x) = {\left\{ \begin{array}{ll} 1 &{} n = 0 \\ 2 - x &{} n = 1 \\ \left( 2 - \frac{x}{n}\right) L_{n-1}(x) - L_{n-2}(x) &{} n \ge 2 \end{array}\right. } \end{aligned}$$

implies that this can be rewritten as

$$\begin{aligned} 1 - xt + \sum _{n=2}^{\infty }\left( -\frac{x}{n}L_{n-1}(x) \right) t^n = \exp \left( \frac{tx}{t - 1}\right) , \quad |t |< 1, \end{aligned}$$

where the term \(-xt\) can be moved into the sum with \(n=1\). Substituting

$$\begin{aligned} t = \frac{z\gamma }{\gamma z - 1}, \quad x = \frac{1}{\gamma }, \end{aligned}$$

and using that \(t(t-1)^{-1}\) is an involution, we arrive at our result

$$\begin{aligned} 1 + \sum _{n=1}^{\infty }\left( -\frac{1}{n\gamma } L_{n-1}(\gamma ^{-1}) \right) \left( \frac{z\gamma }{\gamma z - 1} \right) ^n = \mathrm e^z. \end{aligned}$$

\(\square \)

We remark that the relation between Laguerre polynomials and the stability function of the SDIRK methods has been explored previously [5], but not through the Möbius transformation perspective.

4.4 A remark on implementation

The mathematical equivalence outlined in this paper is well mirrored in code.

In a fairly standard imperative style implementation of an SDIRK method one has three main layers — loops — of computation. First there are the time steps. Inside each of these are the stage steps, which calculate the stage values and derivatives. Inside each of these calculations one has to solve a typically nonlinear equation of the form

$$\begin{aligned} k_i = f\left( \sum _{j=1}^{i-1} a_{ij} h k_j + \gamma hk_i\right) . \end{aligned}$$

This is usually done using an iterative Newton-like method, which becomes our last layer of computation, below this lie the majority of vector field evaluations.

If implemented in the Runge–Kutta–Möbius sense, the layers stay the same with the distinction that the iterative solver is moved down to the layer of vector field evaluations.

The reason for this is twofold. Firstly, in an explicit method there is no need for equation solving during the stage steps. Secondly, implementing an inversion such as \((I - \gamma hf)^{-1}(c)\) is in practice done by solving the equation \(c = (I - \gamma hf)(x)\).

Therefore the two viewpoints yield similar codes. This brings similar computational costs. However, when the evaluation of the map

$$\begin{aligned} hf \circ (I - \gamma hf)^{-1} \end{aligned}$$

is cheaper than the solution of the corresponding nonlinear equation, the Möbius style dominates.

5 A family of Runge–Kutta–Möbius methods

In this section we are going to construct a family of Runge–Kutta methods. We describe their B-stability and look at their order conditions.

5.1 Construction

Assume a fixed \(\gamma > 0\). Let us introduce the elementary Runge–Kutta–Möbius method \(N_1(\alpha )\) identified with its step function

$$\begin{aligned} N_1(\alpha ) = (I - (\gamma - \alpha ) hf) \circ (I - \gamma hf)^{-1}. \end{aligned}$$

This is a single stage implicit Runge–Kutta method since

$$\begin{aligned} N_1(\alpha ) = I + \alpha hf \circ (I - \gamma hf)^{-1}. \end{aligned}$$

We define the s-stage elementary Runge–Kutta–Möbius (RKM) method as a composition of these

$$\begin{aligned} N_s(b_1, \ldots , b_s) = \prod _{j=s {\mathop {\ldots }\limits ^{\rightarrow }} 1}^{\circ } N_1(b_j). \end{aligned}$$

We will use the following remark in showing that these are Runge–Kutta methods.

Corollary 5.1

The stage value functions \(S_i(a_{1:i, 1:i-1})\) of an SDIRK method satisfy the recursion

$$\begin{aligned} S_i(a_{1:i, 1:i-1}) = (I-\gamma hf)^{-1}\left( I + \sum _{j=1}^{i-1}a_{ij} S_j(a_{1:j, 1:j-1})\right) \quad 1 \le i \le s. \end{aligned}$$

The pre-stage value functions \(P_i(a_{1:i, 1:i-1})\) of an SDIRK method satisfy the recursion

$$\begin{aligned} P_i(a_{1:i, 1:i-1}) = I + \sum _{j=1}^{i-1} a_{ij} hf (I-\gamma hf)^{-1} P_j(a_{1:j, 1:j-1}) \quad 1 \le i \le s. \end{aligned}$$

SDIRK methods are themselves pre-stage value functions.

Proof

This is the functional form of Theorem 3.1. \(\square \)

Theorem 5.2

An s-stage SDIRK method satisfying the constant off-diagonal columns condition

$$\begin{aligned} a_{ij} = b_j \quad \text {for}\quad 1 \le j < i \le s \end{aligned}$$

is an s-stage elementary RKM method

$$\begin{aligned} N_s(b_1, \ldots , b_s) = N_s(b_{1:s}). \end{aligned}$$

Proof

We proceed by induction. The one-stage case is clear. If \(G = hf(I-\gamma hf)^{-1}\), then

$$\begin{aligned} N_{s}(b_{1:s})&= I + \sum _{i=1}^{s}b_i G P_i(a_{1:i, 1:i-1}) \\&= I + \sum _{i=1}^{s}b_i G P_i(b_{1:i-1}) \\&= I + \sum _{i=1}^{s-1}b_i G P_i(b_{1:i-1}) + b_s G P_s(b_{1:s-1}) \\&= N_{s-1}(b_{1:s-1}) + b_s G N_{s-1}(b_{1:s-1}) \\&= (I+b_sG) N_{s-1}(b_{1:s-1}) \\&= N_1(b_s)N_{s-1}(b_{1:s-1}). \end{aligned}$$

\(\square \)

5.2 Stability

The stability function of these methods takes the form

$$\begin{aligned} \frac{\det (I-zA + z 1 \otimes b^T)}{\det (I-zA)} = \frac{1}{(1 - z\gamma )^{s}}\prod _{i=1}^s (1 - z\gamma + z b_i) = \prod _{i=1}^s\frac{1 - (\gamma -b_i)z}{1 - z\gamma }, \end{aligned}$$

since \(I + z1\otimes b^T - zA\) is upper triangular with diagonal elements \(1 - z\gamma + z b_i\). Clearly, since this is the product of the stability functions of the components.

Due to the construction, both A- and B-stability can be guaranteed by requiring the components to be A- and B-stable, respectively.

Let us characterize the B-stability of the components.

Theorem 5.3

When \(0 < \gamma \), the statements

  1. i)

    \(M_2[F] < 0 \implies L_2[(I - \alpha F)(I - \gamma F)^{-1}] \le 1 \),

  2. ii)

    \(|\alpha |\le \gamma \)

are equivalent.

Proof

The inequality of the first point is equivalent to

$$\begin{aligned} \Vert (I-\alpha F)(I-\gamma F)^{-1}(x) - (I-\alpha F)(I-\gamma F)^{-1}(y) \Vert _2^2 \le \Vert x - y\Vert _2^2, \end{aligned}$$

for all suitable \(x \ne y\) in a suitable domain. We introduce \(u = (I -\gamma F)^{-1}(x)\) and \(v = (I-\gamma F)^{-1}(y)\) to rewrite this as

$$\begin{aligned} \Vert (I-\alpha F)(u) - (I-\alpha F)(v) \Vert _2^2 \le \Vert (I-\gamma F)(u) - (I-\gamma F)(v)\Vert _2^2. \end{aligned}$$

If \(J = u - v, H = F(u) - F(v)\), then this is just

$$\begin{aligned} \Vert J - \alpha H \Vert _2^2 - \Vert J - \gamma H \Vert _2^2 \le 0. \end{aligned}$$

Solving

$$\begin{aligned} J - \alpha H = X + Y, \quad J - \gamma H = X - Y \end{aligned}$$

we get

$$\begin{aligned} X = J - \frac{\alpha + \gamma }{2}H, \quad Y = \frac{\gamma - \alpha }{2}H. \end{aligned}$$

So we continue with the polarization identity,

$$\begin{aligned} \left\langle J - \frac{\alpha + \gamma }{2}H, \frac{\gamma - \alpha }{2}H \right\rangle \le 0, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \frac{\gamma - \alpha }{2}\langle J, H \rangle \le \frac{\gamma ^2 - \alpha ^2}{4}\langle H, H \rangle . \end{aligned}$$

From the assumptions we have that \(\langle J, H \rangle \le 0 \le \langle H, H \rangle \). Considering the signs of \(\gamma - \alpha \) and \(\gamma + \alpha \), there are four cases.

On the one hand, when \(\gamma \ge \alpha \) and \(\gamma \ge -\alpha \), the inequality holds.

On the other hand, setting \(f = c I\), and dividing both sides by \(\langle J, J \rangle > 0 \), we get

$$\begin{aligned} \frac{\gamma - \alpha }{2} c \le \frac{\gamma ^2 - \alpha ^2}{4}c^2. \end{aligned}$$

Thus, picking \(c < 0\) constants appropriately, we see that the case where \(\gamma \ge \alpha \) and \(\gamma \ge -\alpha \) hold is the only possible one. \(\square \)

Corollary 5.4

The elementary RKM method \(N_1(\alpha )\) is B-stable if and only if

$$\begin{aligned} |\gamma - \alpha |\le \gamma . \end{aligned}$$

Proof

Apply Theorem 5.3 to the elementary RKM method

$$\begin{aligned} N_1(\alpha ) = (I- (\gamma - \alpha )hf) \circ (I - \gamma hf)^{-1}. \end{aligned}$$

\(\square \)

5.3 Consistency

In Theorem 5.2, we have seen that these are SDIRK methods. Therefore, the \(\Phi _s(t)\) weight of a t rooted tree can be expressed as a polynomial in \(\gamma \), where the coefficients do not depend on \(\gamma \), and these coefficients can be expressed in terms of tree weights of the underlying ERK method [2]. We are going to concentrate on the latter.

More precisely, we shall provide formulae for separating the last k of the \(b_i\) parameters from the rest in the order conditions. Firstly, one might separate \(b_s\) from the rest using the formula

$$\begin{aligned} \Phi _s(t) = b_s \prod _{t' \in {\text {unroot}}(t)}\Phi _{s-1}(t') + \Phi _{s-1}(t), \end{aligned}$$

where \({\text {unroot}}\) maps a tree to a forest by removing its root node (and the corresponding edges). We will use \(t' \in t\) to denote the same thing.

We are going to need the elementary symmetric polynomials

$$\begin{aligned} e_j(x_1, \ldots , x_n) = \sum \limits _{1\le i_1< i_2< \cdots < i_j \le n} x_{i_1}x_{i_2}\ldots x_{i_j}. \end{aligned}$$

For example,

$$\begin{aligned} \begin{aligned} e_0(x, y, z)&= 1, \\ e_1(x, y, z)&= x + y + z, \\ e_2(x, y, z)&= xy + xz + yz, \\ e_3(x, y, z)&= xyz. \end{aligned} \end{aligned}$$

These have the property that

$$\begin{aligned} e_{k+1}(x_1, \ldots , x_{n+1}) = e_k(x_1, \ldots , x_{n})x_{n+1} + e_{k+1}(x_1, \ldots , x_{n}). \end{aligned}$$

We introduce the formal expressions

$$\begin{aligned} E_j(x_1, \ldots , x_n)\Phi (t) = \sum \limits _{1\le i_1< i_2< \cdots < i_j \le n} x_{i_1}\prod _{t' \in t} x_{i_2} \prod _{t'' \in t'}\cdots x_{i_{j}} \prod _{t^{(j)} \in t^{(j-1)}}\Phi (t^{(j)}). \end{aligned}$$

We will use the shorter notation and write this expression as

$$\begin{aligned} E_j(x_1, \ldots , x_n) = \sum \limits _{1\le i_1< i_2< \cdots < i_j \le n} {}_{x_1}{\Pi }' {}_{x_2}{\Pi }''\cdots {}_{x_j}{\Pi }^{(j)}. \end{aligned}$$

For example,

$$\begin{aligned} \begin{aligned} E_0(x, y, z)&= 1, \\ E_1(x, y, z)&= {}_{x}{\Pi }' + {}_{y}{\Pi }' + {}_{z}{\Pi }', \\ E_2(x, y, z)&= {}_{x}{\Pi }'{}_{y}{\Pi }'' + {}_{x}{\Pi }'{}_{z}{\Pi }'' + {}_{y}{\Pi }'{}_{z}{\Pi }'', \\ E_3(x, y, z)&= {}_{x}{\Pi }'{}_{y}{\Pi }''{}_{z}{\Pi }'''. \end{aligned} \end{aligned}$$

These satisfy the recursion

$$\begin{aligned} E_{k+1}(x_1, \ldots , x_{n+1}) = E_{k}(x_1, \ldots , x_n) {}_{x_{n+1}}{\Pi }^{(k+1)}+ E_{k+1}(x_1, \ldots , x_n). \end{aligned}$$

Theorem 5.5

If \(k \le s\), then

$$\begin{aligned} \Phi _s(t) = \sum _{j=0}^k E_j\left( b_s, \ldots , b_{s-k+1}\right) \Phi _{s-k}(t). \end{aligned}$$

Proof

The \(k=0\) case is clear. We proceed by induction.

$$\begin{aligned} \Phi _s(t)&= \sum _{j=0}^{k}E_j\left( b_s, \ldots , b_{s-k+1}\right) \Phi _{s-k}(t) \\ {}&= \sum _{j=0}^{k}E_j\left( b_s, \ldots , b_{s-k+1}\right) \left( {}_{b_{s-k}}{\Pi }^{(j+1)} + 1 \right) \Phi _{s-k-1}(t) \\ {}&= \left( \sum _{j=0}^{k}E_j\left( b_s, \ldots , b_{s-k+1}\right) {}_{b_{s-k}}{\Pi }^{(j+1)} + E_{j+1}\left( b_s, \ldots , b_{s-k+1}\right) \right) \Phi _{s-k-1}(t) \\ {}&\quad + \left( \sum _{j=0}^{k}E_j\left( b_s, \ldots , b_{s-k+1}\right) - E_{j+1}\left( b_s, \ldots , b_{s-k+1}\right) \right) \Phi _{s-k-1}(t) \\ {}&= \left( \sum _{j=1}^{k+1} E_j(b_s, \ldots , b_{s-k}) + E_0(b_s, \ldots , b_{s-k+1}) - E_{k+1}(b_s, \ldots , b_{s-k+1})\right) \Phi _{s-k-1}(t) \\ {}&= \left( \sum _{j=1}^{k+1} E_j(b_s, \ldots , b_{s-k}) + 1 - 0\right) \Phi _{s-k-1}(t). \end{aligned}$$

\(\square \)

Corollary 5.6

If \(k \le s\), then, for any lanky tree \(t_l\),

$$\begin{aligned} \Phi _s(t_l) = \sum _{j=0}^k e_j\left( b_s, \ldots , b_{s-k+1}\right) \Phi _{s-k}(t_l) \end{aligned}$$

holds.

Proof

Unrooting a lanky tree yields a forest that has a single member, a lanky tree of size one less. Thus, \(\Pi ^{(k)}\) can be removed from the formula, and we are left with the elementary symmetric polynomials. \(\square \)

Corollary 5.7

Given \(\gamma \) and the first \(s-k\) of the \(b_i\) coefficients, it is possible to construct a polynomial such that choosing its roots as the last k of the \(b_i\) coefficients, the method satisfies the first k linear order conditions.

Proof

Apply the previous formula to the first k lanky trees one by one to recursively get equations of the form

$$\begin{aligned} e_j(b_s, \ldots , b_{s-k+1}) = c_j \quad (j=1, \ldots , k). \end{aligned}$$

These are Viète-formulae that provide the coefficients of the polynomial. \(\square \)

6 Conclusion

In this paper we have considered a complex Möbius transformation

$$\begin{aligned} {\mathcal {M}}_\gamma : {\mathbb {C}} \rightarrow {\mathbb {C}}, \quad z \mapsto \frac{z}{1-\gamma z} \end{aligned}$$

for some \(\gamma > 0\). This maps the left complex half plane to the inside of a circle of radius \(\gamma ^{-1}\).

Firstly, we have extended this transformation to linear systems. In Theorem 2.1, we have shown that this extension maps matrices with nonpositive spectral abscissa to matrices with 2-norm at most \(\gamma ^{-1}\).

Secondly, we have extended this transformation to the nonlinear system case via the formula

$$\begin{aligned} hf \mapsto hf \circ (I - \gamma hf)^{-1}. \end{aligned}$$

In Theorem 2.2, we have shown that this extension maps uniformly negative monotone, Lipschitz-continous vector fields to ones with a Lipschitz-constant at most \(\gamma ^{-1}\).

Thirdly, we have argued that a step size scaled vector field hf transformed this way will therefore have an h-independent, small bound on its Lipschitz constant. Therefore an ERK method may be applied to the transformed vector field. In Theorem 3.1, we have shown the equivalence

$$\begin{aligned} \text {SDIRK} \Leftrightarrow \text {ERK} +{\mathcal {M}}_\gamma , \end{aligned}$$

which says that applying an ERK method and transforming the step size scaled vector field with \({\mathcal {M}}_\gamma \) yields the same numerical solution as applying the corresponding SDIRK method.

Fourthly, we have used the Möbius transformation to view the stability function of SDIRK methods, and by consequence their linear order and stability conditions in a new light. The transformation led us to prove a Möbius–Laguerre expansion of the exponential function in Theorem 4.1:

$$\begin{aligned} \sum _{n=0}^{\infty } {\tilde{L}}_n(\gamma ) \left( \frac{z}{1 - \gamma z} \right) ^n = \mathrm e^z. \end{aligned}$$

Then, we have remarked that the transformation viewpoint isolates the equation solver, and speeds up calculation when \(hf(I-\gamma hf)^{-1}\) has a known closed form.

Lastly, we have used another Möbius transformation to define a new family of RKM methods. We have shown that these are SDIRK methods. In Theorem 5.3, we have extended the proof of Theorem 2.2 to characterize their B-stability, and lastly, explored their order conditions.