Abstract
We propose and analyse a finite element method with mass lumping (LESFEM) for the numerical approximation of reaction–diffusion systems (RDSs) on surfaces in \({\mathbb {R}}^3\) that evolve under a given velocity field. A fully-discrete method based on the implicit–explicit (IMEX) Euler time-discretisation is formulated and dilation rates which act as indicators of the surface evolution are introduced. Under the assumption that the mesh preserves the Delaunay regularity under evolution, we prove a sufficient condition, that depends on the dilation rates, for the existence of invariant regions (i) at the spatially discrete level with no restriction on the mesh size and (ii) at the fully-discrete level under a timestep restriction that depends on the kinetics, only. In the specific case of the linear heat equation, we prove a semi- and a fully-discrete maximum principle. For the well-known activator-depleted and Thomas reaction–diffusion models we prove the existence of a family of rectangles in the phase space that are invariant only under specific growth laws. Two numerical examples are provided to computationally demonstrate (i) the discrete maximum principle and optimal convergence for the heat equation on a linearly growing sphere and (ii) the existence of an invariant region for the LESFEM–IMEX Euler discretisation of a RDS on a logistically growing surface.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Reaction–diffusion systems (RDSs) are a well-known class of partial differential equations that arise from the mathematical modelling of numerous phenomena taking place on a space-time domain, see for instance [31]. In many applications the spatial domain is a curved surface rather than a flat domain, which may be time-dependent. Among the applications of RDSs on surfaces we mention brain growth [26], cell migration [3], chemotaxis [12], developmental biology [28], electrodeposition [24] and phase field modeling [42]. The growing interest toward PDEs on evolving surfaces has stimulated the development of several numerical methods for such problems, among which we mention (but not limited to) embedding methods [2], kernel methods [18], implicit boundary integral methods [5, 35], surface finite element methods (SFEM) [10] and some of their recent variations and extensions [13, 16, 17, 20, 23, 40].
An interesting property of some RDSs is the existence of invariant regions. An invariant region is a subset \(\Sigma \) of the phase-space such that, if the initial condition takes values in \(\Sigma \), then the solution of the RDS takes values in \(\Sigma \) at all times. We recall that, for scalar equations, the well-known notion of maximum principle is equivalent to the invariance of all the regions of the form [0, M], \(M>0\). For RDSs on a stationary surface, sufficient conditions have been found for a region to be invariant at the continuous level, see [39]. To the best of the authors’ knowledge, the extension of these results to RDSs on evolving surfaces has not been considered in the literature. In this paper we will focus on surfaces that evolve according to a prescribed material velocity field. More complicated forms of the evolution law are beyond the scope of this manuscript and are a subject of our current studies.
For a numerical method it is interesting to understand if the invariant regions of the continuous problem are preserved under discretisation. In [15, 16] we proved that, for RDSs on stationary surfaces, the lumped surface finite element method (LSFEM), combined with an implicit–explicit (IMEX) Euler method, preserves the invariant regions of the continuous problem. The purpose of the present paper is to extend these results to the case of evolving surfaces, in particular (i) we prove a semi- and a fully-discrete maximum principle for the heat equation with a linear source term and (ii) we provide sufficient conditions under which a region is invariant at the semi- and fully-discrete levels when a lumped evolving surface finite element method (LESFEM) and an IMEX Euler timestepping are considered. In particular we quantify the impact of surface evolution (measured through the dilation rate) on the existence of invariant regions and we find that surface growth or contraction respectively fosters or inhibits the invariance of a given region in the phase-space.
Crucial in our analysis is the assumption that the mesh preserves the Delaunay property under evolution, which is not true for an arbitrary surface evolution law. A class of surface evolution laws for which the Delaunay property is automatically preserved is that of isotropic growth [29], which has biological applications [7, 27, 33, 36]. To the best of the authors’ knowledge, an adaptive strategy for the preservation of the Delaunay property under a generic evolution law is still an open problem. An attempt in this direction is the work in [22]. For the special case of isotropic growth, we provide fully practical sufficient conditions for the existence of invariant regions at the semi- and fully-discrete levels. As an application of our general theory, we classify some classes of invariant regions, depending on the growth rate of the evolving surface, for two well-known RD models in the literature: the activator-depleted (or Schnakenberg, also known as the Brusselator model) and the Thomas models. Finally, we provide two numerical examples. In the first example we experimentally show that the LESFEM–IMEX Euler method, applied to the heat equation with a linear source term on a linearly growing sphere, exhibits optimal convergence rates in space and time. In the second example we consider the Thomas RDS on an exponentially growing Dupin ring cyclide thereby showing (i) the existence of invariant regions for the fully discretised model and (ii) the violation of this region in the absence of mass lumping.
The present paper is structured as follows. First, in Sect. 2 we recall (i) the derivation of RDSs on evolving surfaces and (ii) some basic notions about invariant regions and we introduce the notion of dilation rate, which is crucial in our analysis. In Sect. 3 we introduce the LESFEM for the space discretisation of RDSs on evolving surfaces and we carry out a fully-discrete scheme using the IMEX Euler timestepping. Section 4 deals with the characterisation of the dilation rate in terms of the material velocity. In particular, we compute exactly the dilation rate for the class of isotropic growth laws. In Sect. 5 we prove a semi- and a fully-discrete maximum principle for the linear heat equation on evolving surfaces with a linear source term. We prove, in Sect. 6, sufficient conditions for the existence of invariant regions for RDSs of arbitrarily many equations on evolving surfaces at the semi- and fully-discrete levels. Section 7 presents some classes of invariant regions for the activator-depleted and the Thomas RD models on evolving surfaces, respectively. Numerical examples are presented in Sect. 8. Finally, in Sect. 9 we conclude and discuss our findings with an eye for future extensions of the present work.
2 Reaction–Diffusion Equations on an Evolving Surface
2.1 Preliminaries and Basic Results
For \(t\in [0,T]\), let \(\varGamma (t)\) be a \({\mathscr {C}}^2\) orientable surface in \({\mathbb {R}}^3\), represented as the zero-level set of a signed distance function \(d\in {\mathscr {C}}^1([0,T], {\mathscr {C}}^2({\mathbb {R}}^3))\), i.e. \(\varGamma (t) = \{\mathbf {x}\in {\mathbb {R}}^3 \; | \; d(\mathbf {x},t) = 0\}\), with \(\nabla d(\mathbf {x},t) \ne 0\) for \(t\in [0,T]\) and \(\mathbf {x}\in \varGamma (t)\). Hence, the outward unit normal vector field on \(\varGamma (t)\) is given by
where \(\Vert \cdot \Vert \) denotes the Euclidean norm in \({\mathbb {R}}^3\). Following [10, Section 5], we assume that there exists a mapping \(G: \varGamma (0) \times [0,T] \rightarrow {\mathbb {R}}^3\), \(G\in {\mathscr {C}}^1([0,T], {\mathscr {C}}^2(\varGamma (0)))\), such that for all \(t\in [0,T]\), \(G(\varGamma (0), t) = \varGamma (t)\) and \(G(\cdot ,t)\) is a diffeomorphism between \(\varGamma (0)\) and \(\varGamma (t)\). The space-time surface \({\mathscr {G}}_T\) is defined by \({\mathscr {G}}_T := \bigcup _{t\in [0,T]} \varGamma (t) \times \{t\}\). The material velocity \(\mathbf {v}: {\mathscr {G}}_T \rightarrow {\mathbb {R}}^3\) of \(\varGamma (t)\) is defined by
Vice-versa, if \({\tilde{\mathbf {v}}}\in {\mathscr {C}}^1([0,T], {\mathscr {C}}^2({\mathbb {R}}^3))\) is an extension of \(\mathbf {v}\), i.e. \({\tilde{\mathbf {v}}}(G(\mathbf {x}_0,t),t) = \mathbf {v}(G(\mathbf {x}_0,t),t)\) for \(\mathbf {x}_0\in \varGamma (0)\) and \(t\in [0,T]\), the mapping G (and thus the time-dependent surface \(\varGamma (t)\)) is recovered by solving, for each \(\mathbf {x}_0\in \varGamma (0)\), the Cauchy problem
For \(t\in [0,T]\) and \(\delta > 0\), let \(U_\delta (t)\) be the open neighbourhood of \(\varGamma (t)\) defined by
We recall from [10] the following property.
Lemma 1
(Fermi coordinates) For any \(t\in [0,T]\) there exists \(\delta > 0\) such that for any \(\mathbf {x}\in \varGamma (t)\) there exists a unique \(\mathbf {a}(\mathbf {x}) \in \varGamma (t)\) that fulfils
Hence, for \(t\in [0,T]\), every point \(\mathbf {x}\in U_\delta (t)\) can be described by \(d(\mathbf {x})\) and \(\mathbf {a}(\mathbf {x})\), which are called normal coordinates or Fermi coordinates of \(\mathbf {x}\). The function \(\mathbf {a}(\cdot ,t): U_\delta (t) \rightarrow \varGamma (t)\) is called the normal projection onto \(\varGamma (t)\).
For any sufficiently smooth \(g: {\mathscr {G}}_T \rightarrow {\mathbb {R}}\) and \(\mathbf {g}: {\mathscr {G}}_T \rightarrow {\mathbb {R}}^3\), let \(\nabla _{\varGamma (t)} g\), \(\varDelta _{\varGamma (t)} g\) and \(\nabla _{\varGamma (t)}\cdot \mathbf {g}\) denote the tangential gradient, the Laplace-Beltrami operator and the tangential divergence of \(\mathbf {g}\) on \(\varGamma (t)\), respectively (see [10] for the details). In the following, we will write \(\varGamma \) instead of \(\varGamma (t)\) to simplify the notation. Furthermore, let \(\partial ^\bullet g\) denote the material derivative of g defined by
where \(\nabla \) is the standard gradient in \({\mathbb {R}}^3\) and \({\tilde{g}}\) is any differentiable extension of g defined on a neighborhood of \({\mathscr {G}}_T\). Definition (6) is intrinsic, i.e. it does not depend on the choice of the extension \({\tilde{g}}\) (see [11] for further details). Let us recall some basic results from [10].
Lemma 2
(Integration by parts) If \(\mathbf {g}: {\mathscr {G}}_T \rightarrow {\mathbb {R}}^3\) is sufficiently smooth and \(t\in [0,T]\), it holds that
where \({\mathsf {\mu }}: \partial {\varGamma }(t)\rightarrow {\mathbb {R}}^3\) is the outward conormal unit vector on \(\partial {\varGamma }(t)\), i.e. normal to \(\partial {\varGamma }(t)\) and tangent to \({\varGamma }(t)\). Specifically, if \(\mathbf {g}\) is tangent to \(\varGamma \), i.e. \(\mathbf {g}\cdot \mathbf {n}=0\), it holds that
\(\square \)
Lemma 3
(Transport formula) For sufficiently smooth \(g:{\mathscr {G}}_T \rightarrow {\mathbb {R}}\), it holds that
\(\square \)
Lemma 4
(Green’s formula on surfaces) For sufficiently smooth \(f,g: {\mathscr {G}}_T \rightarrow {\mathbb {R}}\), it holds that
\(\square \)
Remark 1
(Surfaces without boundary) Lemmas 2–4 hold on surfaces with or without boundary, i.e. \(\partial \varGamma (t) \ne \emptyset \) or \(\partial \varGamma (t) = \emptyset \), respectively. Specifically, if \(\partial \varGamma (t) = \emptyset \), then the boundary integrals in (7), (8) and (10) vanish.
2.2 Derivation of the Reaction–Diffusion Model in Strong Form
Suppose we are given \(r\in {\mathbb {N}}\) species \(u_k: \varGamma (t) \rightarrow {\mathbb {R}}\), \(k=1,\ldots ,r\), and let \(\mathbf {q}_k:\varGamma (t)\rightarrow {\mathbb {R}}^3\), \(k=1,\ldots ,r\), be their fluxes tangent to \(\varGamma (t)\). We recall from [1] the derivation of a system of r equations for \(\mathbf {u}:= (u_1,\ldots , u_r)\) that accounts for (i) the diffusion on the surface, (ii) the flux across the boundary (if non-empty) and (iii) the production rates \(f_k(\mathbf {u})\), \(k=1,\ldots ,r\), of the given species. To this end, let \({\mathscr {R}}(0)\) be a portion of \(\varGamma (0)\) and let \({\mathscr {R}}(t) = G({\mathscr {R}}(0),t)\) be the portion of \(\varGamma (t)\) corresponding to the initial portion \({\mathscr {R}}(0)\). Notice that \({\mathscr {R}}(t)\) is itself an evolving surface, hence formulae (7) through (10) still hold if \(\varGamma (t)\) is replaced by \({\mathscr {R}}(t)\). We consider a mass balance on \({\mathscr {R}}(t)\) of the form
Since the fluxes \(\mathbf {q}_k\), \(k=1,\ldots ,r\), are tangent to \(\varGamma (t)\), we can apply the integration-by-parts formula (8) to the first term on the right hand side of (11). Then (11) becomes
By applying the transport formula (9) to the left hand side of (12), we obtain
where \(\mathbf {v}\) is the material velocity defined in Sect. 2.1. Since \({\mathscr {R}}(t)\) is an arbitrary portion, we conclude that
We assume \(\mathbf {q}_k\) corresponds to a diffusive flux according to Fick’s law as follows:
where \(d_k\), \(k=1,\ldots ,r\), are positive diffusivity constants. Inserting (15) into (14), we end up with the reaction–diffusion system of the form
2.3 Invariant Regions and Maximum Principle
In this section we recall basic notions concerning invariant regions for systems of the form (16) and conjecture a sufficient condition under which system (16) possesses an invariant region. To this end, we give the following definitions.
Definition 1
(Dilation rates) The minimum and maximum instantaneous dilation rates are defined by
respectively. When the minimum and maximum instantaneous dilation rates coincide, we call \(H^*(t) := H^*_{min}(t) = H^*_{max}(t)\) the instantaneous dilation rate. The minimum and maximum global dilation rates are defined by
respectively. When the minimum and maximum global dilation rates coincide, we call \(\mu ^* := \mu ^*_{min} = \mu ^*_{max}\) the global dilation rate.
Definition 2
(Invariant regions) For the system (16), a region \(\Sigma \) in the phase-space \({\mathbb {R}}^r\) is said to be an invariant region if, whenever the initial condition \(\mathbf {u}_0\) is in \(\Sigma \), the solution u stays in \(\Sigma \) as long as it exists and is unique.
We focus our attention on regions \(\Sigma \subset {\mathbb {R}}^r\) of hyper rectangular shape, that is to say of the form
where \({\underline{\sigma }}_k\in {\mathbb {R}}\cup \{-\infty \}\) and \({\overline{\sigma }}_k \in {\mathbb {R}}\cup \{+\infty \}\) for all \(k=1,\ldots ,r\). For instance, if \({\underline{\sigma }}_k=0\) and \({\overline{\sigma }}_k=+\infty \) for all \(k=1,\ldots , r\), then \(\Sigma \) is the positive orthant in \({\mathbb {R}}^r\), which means that the solution of the RDS stays positive at all times. Consider the \((r-1)\)-dimensional hyperfaces
For \(k=1,\ldots ,r\), we define the constants
where \(\mu _{min}^*\) and \(\mu _{max}^*\) are defined in (18).
Next, we conjecture a criterion under which a hyper-rectangle is invariant for system (16). This criterion holds true in the stationary cases (when \(\mu ^*=0\)): (i) when \(\varGamma \) is a stationary monodimensional domain in \({\mathbb {R}}\) (see [38]), (ii) when \(\varGamma \) is a stationary k-dimensional domain in \({\mathbb {R}}^k\), \(k\in {\mathbb {N}}\) (see [6]) and (iii) when \(\varGamma \) is a stationary Riemannian manifold without boundary (see [39]). In the case of isotropically evolving flat domains, the invariance of the positive orthant was studied in [41]. To the best of the author’s knowledge, the case of evolving surfaces has not been studied at the continuous level. Hence, we introduce at the continuous level the following conjecture.
Conjecture 1
Let \(\Sigma \) be a hyper-rectangle as in (19) in the phase space of (16) and let \(\mathbf {f}\) be Lipschitz on \(\Sigma \). If
then \(\Sigma \) is an invariant region for (16). In particular, when \({\overline{\sigma }}_k = +\infty \) and \({\underline{\sigma }}_k = -\infty \), then \({\overline{\Sigma }}_k \cap {\mathbb {R}}^r\) and \({\underline{\Sigma }}_k \cap {\mathbb {R}}^r\) are respectively empty, and so (21) and (22) are automatically fulfilled, respectively.
Notice that on stationary surfaces, since \({\overline{\mu }}_k^* = {\underline{\mu }}_k^*=0\), then conditions (21)–(22) reduce to the inward flux condition considered in [39, Chapter 4]. In Sect. 4 next, we will prove the discrete counterpart of Conjecture 1 obtained by discretizing the RDS in space with the lumped version of the ESFEM method [10] and IMEX Euler in time.
We remark that, on stationary domains, some systems are known to possess an invariant region which do not meet the strict inequalities (21)–(22). For instance, for many mass-action laws, the positive orthant is invariant [4, 16] even though the flux of \(\mathbf {f}\) is tangent to this region, instead of strictly inward. For the scalar case \(k=1\), the notion of invariant region reduces to the well-known concept of maximum principle.
Definition 3
(Maximum principle) For \(k=1\), the scalar equation (16) fulfils the maximum principle if, for any initial condition, i.e. \(u(\cdot ,0) \), the solution u fulfils
In particular, if the initial condition is nonnegative, \(u(\mathbf {y},0) \ge 0\) for \(\mathbf {y}\in \varGamma (0)\), the solution fulfils
Notice that the maximum principle corresponds to the fact that every (monodimensional) region of the form \(\Sigma = [{\underline{\sigma }},{\overline{\sigma }}]\), with \({\underline{\sigma }} \le 0\), \({\overline{\sigma }} \ge 0\), is invariant.
2.4 Derivation of the Variational Formulation
Following [1], we derive the variational formulation of system (16). To this end, for each \(t\in [0,T]\) we multiply equations (16) by the respective test functions \(\varphi _1,\ldots , \varphi _r \in L^2([0,T]; H^1(\varGamma (t)))\) with \(\partial ^\bullet {\varphi }_1,\ldots , \partial ^\bullet {\varphi }_r\in L^2([0,T]; H^{-1}(\varGamma (t)))\) and integrate over \(\varGamma (t)\):
for all \(k=1,\ldots , r\). For the rigorous definition of the Sobolev spaces \(H^1\) and \(H^{-1}\) on a manifold see [21], while for the Bochner spaces \(L^2([0,T]; B)\), with B being any Banach space, see [34]. By applying the Green formula (10) to the right hand side of (25) we obtain
for all \(k=1,\ldots , r\). We assume that either \(\varGamma (t)\) has no boundary, i.e. \(\partial \varGamma (t) = \emptyset \), or homogeneous Neumann boundary condition are enforced, i.e. \(\nabla _\varGamma u_k\cdot {\mathsf {\mu }}= 0\) on \(\partial \varGamma (t)\), so that the last term in (26) vanishes (see Remark 1). Furthermore, by observing that \(\partial ^\bullet (\varphi _k u_k) = \varphi _k\partial ^\bullet u_k + u_k\partial ^\bullet \varphi _k\), (26) becomes
for all \(k=1,\ldots , r\). By applying the transport property to the first term on the left hand side of (27), we have
for all \(k=1,\ldots , r\). Therefore, the variational formulation seeks to find \(u_1,\ldots , u_r\in L^2([0,T]; H^1(\varGamma (t)))\) with \(\partial ^\bullet u_1,\ldots , \partial ^\bullet u_r\in L^2([0,T]; H^{-1}(\varGamma (t)))\) such that, for each \(t\in [0,T]\),
for all \(\varphi _1,\ldots , \varphi _r \in L^2([0,T]; H^1(\varGamma (t)))\) with \(\partial ^\bullet {\varphi }_1,\ldots , \partial ^\bullet {\varphi }_r\in L^2([0,T]; H^{-1}(\varGamma (t)))\).
3 Lumped Evolving Surface Finite Element Method
Following the evolving surface finite element method (ESFEM) studied in [1] for the approximation of the variational problem (29), we present its lumped counterpart, the lumped evolving surface finite element method (LESFEM).
3.1 Surface Triangulation and Some Definitions
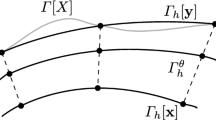
Following [9], given \(h>0\), called meshsize, a triangulation \(\varGamma _h(t)\) of the evolving surface \(\varGamma (t)\) is defined by
where \({\mathscr {Z}}_h(t)\) is a set of evolving triangles, with \(\mathbf {x}_i(t), i=1,\ldots ,N\in {\mathbb {N}}\), being the overall evolving nodes, such that
-
The nodes evolve with the exact material velocity, i.e. \({\dot{\mathbf {x}}}_i(t) = \mathbf {v}(\mathbf {x}_i(t),t)\) for \(t\in [0,T]\) and \(i=1,\ldots ,N\);
-
For all \(t\in [0,T]\) and for any two distinct triangles \(Z_1(t)\) and \(Z_2(t)\) in \({\mathscr {Z}}_h(t)\), the intersection \(Z_1(t) \cap Z_2(t)\) is either empty, or a node, or a complete edge;
-
For all \(t\in [0,T]\) and \(Z(t) \in {\mathscr {Z}}_h(t)\), \(Z(t) \subset U_\delta (t)\), where \(U_\delta \) is as defined in Lemma 1;
-
For all \(t\in [0,T]\), the normal projection \(\mathbf {a}(\cdot ,t): U_\delta (t) \rightarrow \varGamma (t)\) defined in Lemma 1 is a one-to-one mapping between \(\varGamma _h(t)\) and \(\varGamma (t)\), i.e. \(\mathbf {a}(\varGamma _h(t),t) = \varGamma (t)\).
We assume that, for each \(t\in [0,T]\), \(\varGamma _h(t)\) meets the Delaunay condition, defined as follows. Let e be an edge of \(\varGamma _h(t)\) and let \(Z_1\) and \(Z_2\) be the faces of \(\varGamma _h(t)\) sharing the edge e. Let \(\alpha _1\) and \(\alpha _2\) be the angles in \(Z_1\) and \(Z_2\) opposite to e, respectively. The triangulation \(\varGamma _h(t)\) is said to meet the Delaunay condition if, for all \(t\in [0,T]\) and for any edge e of \(\varGamma _h(t)\), it holds that
see for instance [16]. The space-time triangulated surface \({\mathscr {G}}_{h,T}\) is defined by
Since \(\varGamma _h(t)\) is piecewise planar, there exists a time-differentiable mapping \(G_h: \varGamma _h(0) \times [0,T] \rightarrow {\mathbb {R}}^3\) such that, for all \(t\in [0,T]\), \(G_h(\varGamma _h(0), t) = \varGamma _h(t)\) and, for every facet \(Z\in {\mathscr {Z}}_h\), \(G_h(\cdot ,t)\) is a diffeomorphism between Z(0) and Z(t).
For a fixed time \(t\in [0,T]\), let \({\mathbb {V}}_h(t)\) be the space of piecewise linear functions on \(\varGamma _h(t)\) defined by
Let \({\mathbb {V}}_h\) be the space of time-dependent, spatially piecewise linear functions defined by
Given \(t\in [0,T]\) and a function \(\eta \in {\mathscr {C}}^0(\varGamma _h(t))\), its linear interpolant \(I_h\eta \) is the unique function in \({\mathbb {V}}_h(t)\) such that
The discrete material derivative of a sufficiently smooth function \(U\in {\mathbb {V}}_h\) is defined by
where \(\mathbf {v}\) is the material velocity. For our purposes, we define the discrete counterpart of the dilation rates introduced in Definition 1.
Definition 4
(Discrete dilation rates) The minimum and maximum discrete instantaneous dilation rates are defined by
respectively. When the minimum and maximum discrete instantaneous dilation rates coincide, we call \(H(t) := H_{min}(t) = H_{max}(t)\) the discrete instantaneous dilation rate. The minimum and maximum discrete global dilation rates are defined by
respectively. When the minimum and maximum discrete global dilation rates coincide, we call \(\mu := \mu _{min} = \mu _{max}\) the discrete global dilation rate.
For every \(i=1,\ldots ,N\), the i-th Lagrange basis function \(\chi _i\) is the unique \({\mathbb {V}}_h\) function such that
where \(\delta _{ij}\) is the usual Kronecker symbol. The components \(U_1,\ldots , U_r\in {\mathbb {V}}_h\) of the spatially discrete solution may be expressed in the Lagrange basis as
3.2 Preliminary Results on Triangulated Surfaces
We recall from [9] the following property of the basis functions.
Lemma 5
(Transport property of the basis functions) The basis functions \(\chi _i\), \(i=1,\ldots ,N\), defined in (35) fulfil
Hence, for the functions \(U_k\), \(k=1,\ldots ,r\) defined in (36) it holds that
\(\square \)
We recall from [10, Lemma 5.6 and Remark 5.7] the following preliminary result.
Lemma 6
(Leibniz formula on triangulated surfaces) For any time-differentiable \(U,V\in {\mathbb {V}}_h\), it holds that
\(\square \)
3.3 Lumped Evolving Surface Finite Element Method
The lumped evolving surface finite element method (LESFEM), applied to the variational formulation (29), seeks to find \(U_1,\ldots , U_r \in {\mathbb {V}}_h\) such that
for all \(k=1,\ldots ,r\) and \(i=1,\ldots ,N\). Thanks to the transport property (37) of the basis functions, formulation (40) is equivalent to: find \(U_1,\ldots , U_r \in {\mathbb {V}}_h\) such that
for all \(k=1,\ldots ,r\) and \(i=1,\ldots ,N\). The LESFEM method (41) differs from the evolving surface finite element method (ESFEM) in [1] due to the presence of the interpolant operator on the first and the last terms in (41). By expressing \(U_1,\ldots , U_r\) according to (36), the matrix form of (41) is
where A and M are the (time-dependent) stiffness and lumped mass matrices defined by
for \(t\in [0,T]\), respectively. Notice that the lumped mass matrix M is diagonal. The Delaunay condition (30) holds if and only if
The above fact, together with the structure of the lumped mass matrix implies that, for any \(s\ge 0\),
See [16] for further details.
3.4 Time Discretisation
We are now concerned with the time discretisation of the spatially discrete system (42) arising from the LESFEM. We discretise system (42) by means of the IMEX (IMplicit–EXplicit) Euler method, i.e by treating diffusion implicitly and reaction terms explicitly. To this end, let \(\tau >0\) be a timestep, let \(t_n := n\tau \) for all \(n = 0,\ldots , N_T\) with \(N_T = \left\lfloor \frac{T}{\tau }\right\rfloor \), let \(A^n\) and \(M^n\) be the stiffness and lumped mass matrices at time \(t_n\), respectively, let \(({\mathsf {\xi }}_1^n,\ldots , {\mathsf {\xi }}_r^n)\) be the coefficients of the numerical solution at time \(t_n\), and let \(\mathbf {f}_k^n := f_k({\mathsf {\xi }}_1^n,\ldots , {\mathsf {\xi }}_n^n)\) for each \(k=1,\ldots ,r\). If \(({\mathsf {\xi }}_1^0,\ldots , {\mathsf {\xi }}_r^0)\) are the coefficients of the spatially discrete initial datum, the IMEX Euler time discretisation of (42) is
or equivalently
4 Characterisation of Surface Growth
The purpose of this section is to characterise surface growth in terms of the material velocity \(\mathbf {v}\), with specific regard to isotropic growth. In fact, the lumped mass M(t) and stiffness A(t) matrices depend on \(\mathbf {v}\). In particular:
-
1.
For an arbitrary triangulated surface that evolves with an arbitrary material velocity, we bound the time derivative \(\frac{\mathrm {d}M}{\mathrm {d}t}\) of the lumped mass matrix in terms of the constants \(\mu _{min}\) and \(\mu _{max}\) defined in (34), i.e. in terms of the divergence \(\nabla _{\varGamma _h}\cdot I_h(v)\) of the discrete material velocity. We will need this result to prove a sufficient condition for the existence of invariant regions for the semi- and fully-discrete schemes;
-
2.
For an arbitrary smooth or triangulated surface that evolves with an arbitrary material velocity, we characterise the velocity flows \(\nabla _\varGamma \cdot \mathbf {v}\) and \(\nabla _{\varGamma _h}\cdot I_h(\mathbf {v})\) in terms of the mappings G and \(G_h\) introduced in Sects. 2.1 and 3.1, respectively;
-
3.
For an arbitrary smooth or triangulated surface that evolves isotropically in space, that is
$$\begin{aligned} \mathbf {v}(\mathbf {x},t) = S(t)\mathbf {x}, \quad (\mathbf {x},t) \in {\mathbb {R}}^3 \times [0,T], \end{aligned}$$(48)where \(S: [0,T] \rightarrow {\mathbb {R}}\) is an arbitrary smooth function, we compute exactly \(\nabla _\varGamma \cdot \mathbf {v}\) and \(\nabla _{\varGamma _h}\cdot I_h(\mathbf {v})\) in terms of \(\mathbf {v}\). This result will yield a fully practical criterion to detect the invariant regions of a given RDS in the case of isotropic surface evolution.
4.1 Bounding the Rate of Change of the Mass Matrix in Terms of the Dilation Rates
In this section we bound the time derivative \(\frac{\mathrm {d}M}{\mathrm {d}t}\) of M in terms of the discrete dilation rates defined in (34). To this end, we prove the following characterisation of \(\frac{\mathrm {d}M}{\mathrm {d}t}\).
Lemma 7
(Transport formula for the lumped mass matrix M) The entries of the lumped mass matrix M fulfil the following property
Proof
By choosing \(U=I_h(\chi _i\chi _j)\) for any \(i,j=1,\ldots ,N\) and \(V=1\) in the Leibniz formula (39) we have
Now, if \(i=j\), then \(I_h(\chi _i\chi _j) = \chi _i\), otherwise, if \(i\ne j\), \(I_h(\chi _i\chi _j)=0\). Then, from the transport property (37) we have \(\partial ^\bullet I_h(\chi _i\chi _j)=0\) for all \(i,j=1,\ldots ,N\). Equation (50) thus implies the desired result (49). \(\square \)
In some proofs we will need the following corollary of Lemma 7.
Corollary 1
(Consequence of the transport formula for the lumped mass matrix M) The diagonal matrix \(\frac{\mathrm {d}M}{\mathrm {d}t}\) fulfils the estimates
where \(\mu _{min}\) and \(\mu _{max}\) are defined in (34). \(\square \)
4.2 Characterising Velocity Flows in Terms of the Mappings G and \(G_h\)
We wish to characterise the continuous and discrete velocity flows \(\nabla _\varGamma \cdot \mathbf {v}\) and \(\nabla _{\varGamma _h}\cdot I_h(\mathbf {v})\) in terms of the mappings G and \(G_h\) introduced in Sects. 2.1 and 3.1, respectively, for arbitrary smooth or triangulated surfaces that evolve under an arbitrary material velocity. To this end, let \(\varGamma (t)\) be an arbitrary evolving smooth surface and let (A, X) be any local parametrisation of \(\varGamma (0)\), where \(A\subset {\mathbb {R}}^2\) is an open connected set and \(X : A \rightarrow \varGamma (0)\) is a differentiable map such that its Jacobian J is full-rank on A. Let B be a measurable subset of A. For all t, the portion X(B) of \(\varGamma (0)\) evolves into \(G(X(B),t) \subset \varGamma (t)\). By choosing \(f(\mathbf {x},t) = 1\) for each \((\mathbf {x},t) \in {\mathscr {G}}_T\) in the transport formula (9), we have
Let \({\hat{e}}_i\), \(i=1,2,3\), be the standard basis vectors in \({\mathbb {R}}^3\). For \(({\mathsf {\theta }},t) \in B \times [0,T]\), let \(J(\mathbf {x},t) \in {\mathbb {R}}^{2,3}\) be the (spatial) Jacobian of the function \(G(X({\mathsf {\theta }}), t)\) and let

The surface integrals in (52) can be written as integrals on the planar domain B by using the parametrisation \(G(X(\cdot ),t): B \rightarrow G(X(B),t)\). Hence, (52) becomes
where \(\Vert \cdot \Vert \) denotes the Euclidean norm in \({\mathbb {R}}^3\), or equivalently,
Since (55) holds for any measurable subset B of A, then it holds that
By applying the chain rule, (56) is equivalent to
Given any triangulated surface \(\varGamma _h(t)\) (which evolves under the discrete velocity field \(I_h(\mathbf {v})\)), we notice that every facet \(Z(t)\in {\mathscr {Z}}_h(t)\) is smooth and thus parametrisable. For any facet of the initial triangulated surface, \(Z(0) \in {\mathscr {Z}}_h(0)\), let (A, X) be a parametrisation of Z(0), as described above. For \(({\mathsf {\theta }}, t) \in A\times [0,T]\), let \(J_h({\mathsf {\theta }},t) \in {\mathbb {R}}^{2,3}\) be the Jacobian of the function \(G_h(X({\mathsf {\theta }}),t)\) and let

A similar reason as above yields the following discrete counterpart of (57).
Relations (57) and (59) are useful in that they (i) express the velocity flow without tangential derivatives and (ii) can be computed exactly when G and \(G_h\) are known explicitly, e.g. for the isotropic growth as discussed in the next subsection.
4.3 Computing the Dilation Rates for the Isotropic Growth
In this section we compute the dilation rates defined in (18) and (34), respectively, for arbitrary surfaces that evolve with the material velocity (48). The velocity field (48) corresponds to the specific case of isotropic evolution, see for instance [8, 29] for the case of evolving planar domains and [1, 32] for the general case. In particular, for suitable choices of the function S(t), the growth law (48) admits some specific cases such as uniform, exponential, logistic and periodic growth, see [1, 8, 29, 32]. From (3), it is easy to show that, with the velocity field (48), each \(\mathbf {x}_0\in \varGamma _0\) evolves to the point
therefore the evolution induced by an isotropic growth is a time-dependent dilation of the initial surface. The function
that appears in (60) is known as the growth function, see for instance [29].
Remark 2
(Properties of isotropic growth) Isotropic growth preserves the angles of triangulated surfaces. This has two consequences:
-
1.
if \(\varGamma _h(0)\) meets the Delaunay condition, then \(\varGamma _h(t)\) retains the Delaunay condition for all \(t\in [0,T]\);
-
2.
if A(0) and M(0) are the stiffness and the mass matrices at \(t=0\), then
$$\begin{aligned} A(t) = A(0),\quad M(t) = \phi ^2(t)M(0),\quad t\in [0,T]. \end{aligned}$$(62)Hence, in implementations, A(t)and M(t) need not be computed at each time step.
In the following result we compute the dilation rates \(\mu _{min}\), \(\mu _{max}\), \(\mu _{min}^*\) and \(\mu _{max}^*\) on an arbitrary smooth or triangulated surface that evolves with the material velocity (48), in terms of S(t).
Theorem 1
(Velocity flow on isotropically growing smooth or triangulated surfaces) Let \(\varGamma (t)\) be a smooth surface that evolves with the velocity field (48) and let \(\varGamma _h(t)\) be the corresponding triangulated surface. Then, the instantaneous dilation rates satisfy
Hence, it follows that
Proof
Let \(\varGamma _h(t)\) be an evolving smooth surface and let (A, X), \(J({\mathsf {\theta }},t)\) and \({\tilde{J}}({\mathsf {\theta }},t)\) as defined in Sect. 4.2. From (60) and (61), \(J({\mathsf {\theta }},t)\) fulfils
where \(J_X: A\rightarrow {\mathbb {R}}^{2,3}\) is the Jacobian of X. It follows that
which implies that
By differentiating (67), we have
By combining (57), (68) and dropping the parameterised coordinates \({\mathsf {\theta }}\), we have
which proves the first equality in (63). Analogously, we prove the second equality in (63) by using (59). This completes the proof. \(\square \)
For the uniform, exponential, logistic and periodic growths, the functions \(\phi (t)\), S(t) and the dilation rates \(\mu _{min}\), \(\mu _{min}^*\), \(\mu _{max}\) and \(\mu _{max}^*\) are detailed in Table 1, see also [29, Table 1] for the case of evolving planar domains, while the corresponding plots are depicted in Fig. 1.
Plots of the growth functions \(\phi (t)\) (top row) and the corresponding S(t) functions (bottom row) listed in Table 1 for \(K=2\) and \(r=0.5,1,1.5\). From left to right: linear, exponential, logistic and periodic growth profiles
5 Linear Heat Equation and Discrete Maximum Principles
We consider, for \(k=1\), the specific case of linear heat equation on an evolving surface \(\varGamma (t)\):
and we prove the semi- and fully-discrete maximum principles for the case when \(\mu _{min}+\beta \ge 0\). Equation (70) is a special case of the general system (16) that we are interested in. However, we start with this specific case as (i) it provides more insights on the effect of growth on stability, (ii) we are able to prove a better timestep stability condition and (iii) to make the reader familiar with the demonstrative techniques.
The following result, that we proved in [16, Theorem 2.1] for the special case of stationary surfaces, addresses the maximum principle at the semi-discrete level.
Theorem 2
(Semi-discrete maximum principle for the linear heat equation (70)) If the velocity field \(\mathbf {v}\) fulfils
with \(\mu _{min}\) as defined in (34), and the triangulation \(\varGamma _h(t)\) meets the Delaunay condition for all \(t\in [0,T]\), then the LESFEM solution of (70) fulfils the following discrete maximum principle
Proof
From (42), the LESFEM spatial discretisation of (70) is
By applying the chain rule, (73) becomes
By multiplying (74) on the left by \(M^{-1}\), we have
All we have to prove is that the ODE (75) is dissipative, i.e. \(-dM^{-1}A|{\mathsf {\xi }}| -M^{-1}\frac{\mathrm {d}M}{\mathrm {d}t}|{\mathsf {\xi }}| - \beta |{\mathsf {\xi }}| \le \mathbf {0}\). For every \(t\in [0,T]\), M is diagonal with positive diagonal entries and A fulfils (43) from the Delaunay condition. Then, it follows that \(-dM^{-1}A|{\mathsf {\xi }}| \le \mathbf {0}\). Hence, it suffices to prove that \(-(M^{-1}\frac{\mathrm {d}M}{\mathrm {d}t} + \beta I)|{\mathsf {\xi }}| \le \mathbf {0}\), that is true provided
By using (51), condition (76) is true if
which holds true from assumption (71). This completes the proof. \(\square \)
The next theorem shows the same result for the LESFEM–IMEX Euler full-discretisation of (70), under a timestep restriction. This result holds true for the special case of stationary surfaces (see [16, Theorem 2.2]).
Theorem 3
(Fully-discrete maximum principle for the linear heat equation (70)) If the velocity field \(\mathbf {v}\) fulfils
with \(\mu _{min}\) as defined in (34), and the triangulation \(\varGamma _h\) meets the Delaunay condition for all \(t>0\), then the LESFEM–IMEX Euler solution of (70) fulfils the following minimum-maximum principle
if the timestep satisfies
In particular, there is no timestep restriction if \(\beta \le 0\).
Proof
The full-discretisation (47) of the heat equation (70) can be written as
Then scheme (81) fulfils the discrete maximum principle if
Since \((M^{n+1})^{-1}M^n\) is diagonal with strictly positive diagonal entries, conditions (84)–(85) are true provided
Condition (86) is true under assumption (80). In order to prove (87), we need to estimate \(M^{n+1}\) as a function of \(M^n\). To this end, by applying Gronwall’s lemma to the first inequality in (51), we have
By using (88), condition (87) is true if
Let us now define \(f(\tau ) := 1-\tau \beta \) and \(g(\tau ) = e^{\tau \mu _{min}}\). These functions fulfil \(f(0) = g(0) = 1\), f is linear and g is non-concave for all \(\mu _{min}\in {\mathbb {R}}\). Then
-
if \(f'(0) > g'(0)\), then condition (89) is not fulfilled for any sufficiently small \(\tau \).
-
if \(f'(0) \le g'(0)\), then condition (89) is fulfilled for every \(\tau > 0\).
Now, condition \(f'(0) \le g'(0)\) means \(-\beta \le \mu _{min}\), which is true from assumption (78). This completes the proof. \(\square \)
Remark 3
(Interplay between material velocity and source term) Relation (71) implies that
-
domain growth (\(\mu _{min} > 0\)) can enable the discrete maximum principle even for \(\beta <0\);
-
local domain contraction (\(\mu _{min} < 0\)) can prevent the discrete maximum principle even for \(\beta \ge 0\).
This interplay is justified by observing that domain evolution implies a dilution effect, explained as follows. By choosing \(\varphi =1\) in the variational formulation (29) with \(k=1\) and \(f_1(u) = -\beta u\), we obtain
If \(|\varGamma (t)|\) denotes the surface area of \(\varGamma (t)\) and \(\langle u(t)\rangle := \frac{1}{|\varGamma (t)|}\int _{\varGamma (t)} u\) denotes the mean value of u, (90) becomes
By solving (91) for \(\frac{\mathrm {d}}{\mathrm {d}t} \langle u(t)\rangle \), we obtain
By choosing \(g=1\) in the transport formula (9), we have
By combining (92) and (93) we have
From (94), the dilution effect arising from surface growth can be interpreted as the dampening or uplifting effect of \(\mu _{min}^*\) on \(\langle u(t)\rangle \). The estimate (94) implies that \(\langle u(t)\rangle \) is non-increasing if
which is the continuous counterpart of (71). We conclude that condition (71) is consistent with the interpretation of surface growth in terms of dilution effect.
Remark 4
(Interplay between timestep restriction and source term) Relation (80) implies that the timestep restriction needed for guaranteeing the discrete maximum principle is independent of the material velocity and it only depends on the stiffness parameter \(\beta \) of the source term. In particular, when the source term is nonnegative (i.e. when \(\beta \le 0\)), the LESFEM–IMEX Euler fully-discrete scheme unconditionally fulfils the discrete maximum principle.
6 Reaction–Diffusion Systems and Invariant Regions
In this section we prove, for the semi- and full-discretisations of RDSs of the form (16), a criterion to test if a hyper-rectangle in the phase-space is invariant. In the case \(k=1\) of scalar equations, the notion of invariant region collapses to that of minimum-maximum principle, considered in the previous section for the special case of the linear heat equation. We assume that the Delaunay regularity of the mesh is preserved under evolution. For \(k=1,\ldots ,r\), we define the constants
where \(\mu _{min}\) and \(\mu _{max}\) are the dilation rates defined in (34). In the following theorem we prove that, under similar assumptions of Conjecture 1, \(\Sigma \) is an invariant region for the solution obtained from the semi-discrete scheme (42). Hence, the following theorem extends [16, Theorem 3.3] to the case of evolving surfaces.
Theorem 4
(Invariant rectangles for (42)) Let \(\Sigma \) be a hyper-rectangle as in (19) in the phase space of (42), let \(\mathbf {f}\) be Lipschitz on \(\Sigma \). If the triangulation \(\varGamma _h(t)\) satisfies the Delaunay condition for all \(t\ge 0\) and
then \(\Sigma \) is an invariant region for (42).
Proof
The semi-discrete method (42) can be written, after applying the chain rule to the term \(\frac{\mathrm {d}}{\mathrm {d}t}(M{\mathsf {\xi }}_k)\) and multiplying on the left by \(M^{-1}\) as
Since M is diagonal with positive diagonal entries and \(A_{ij}\le 0\) for \(i\ne j\) from the assumption of Delaunay regularity, proceeding as in the proof of [16, Theorem 3.3], it suffices to verify that, for all \((U_1,\ldots , U_r)\in \Sigma \), \(k=1,\ldots ,r\), and \(i=1,\ldots ,N\),
where \({\underline{\sigma }}_k\) and \({\overline{\sigma }}_k\) are as in (19). Using relation (51), conditions (100)–(101) hold if, for all \(k=1,\ldots ,r\),
with \({\underline{\mu }}_k\) and \({\overline{\mu }}_k\) as in (96), that is true from assumptions (97)–(98). This completes the proof. \(\square \)
The following theorem provides a sufficient condition for regions to be invariant for the LESFEM–IMEX Euler scheme (47) and extends [16, Theorem 3.4]. In contrast to the semi-discrete case, we relax the strict inequalities (21)–(22) with conditions (105)–(106), in which we use the perturbed dilation rates \({\tilde{\mu }}_k\) and  given by
given by

respectively, and \(\mu _{min}\) and \(\mu _{max}\) are defined in (34). Observe that \({\tilde{\mu }}_k \rightarrow {\overline{\mu }}_k\) and  as \(\tau \rightarrow 0\).
as \(\tau \rightarrow 0\).
Theorem 5
(Invariant rectangles for (47)) Let \(\Sigma \) be a hyper-rectangle as in (19) in the phase space of (42), let \(\mathbf {f}\) be Lipschitz on \(\Sigma \). If the triangulation \(\varGamma _h(t)\) meets the Delaunay condition for all \(t\ge 0\) and

then \(\Sigma \) is an invariant region for (47) if the timestep \(\tau \) fulfils
where, for all \(k=1,\ldots ,r\), \(L_k\) is the Lipschitz constant of \(f_k\).
Proof
The fully-discrete scheme (47) can be written as
\(n\in {\mathbb {N}}\cup \{ 0\}\), \(k=1,\ldots ,r\). Since the mesh meets the Delaunay assumption at all times, the matrix properties (82)–(83) hold. Then, it suffices to prove that
where \(\mathbf {1}\) is the column vector of ones. We will prove the two inequalities in (109) in turn. From (51), the inequality on the right side of (109) holds true if
with \({\overline{\mu }}_k\) as defined in (96). Suppose \({\overline{\sigma }}_k\ge 0\). From assumption (105) we can estimate \(\mathbf {f}_k^n\) as follows
From (111), condition (110) holds true provided
From assumption (107), since \({\mathsf {\xi }}_k^n \le {\overline{\sigma }}_k \mathbf {1}\), then (112) holds true if
that is to say
which holds true for each \(\tau \in {\mathbb {R}}\). Suppose, instead, \({\overline{\sigma }}_k < 0\). From assumption (105) we can estimate \(\mathbf {f}_k^n\) as follows
From (115), condition (110) holds true provided
From assumption (107), since \({\mathsf {\xi }}_k^n \le {\overline{\sigma }}_k \mathbf {1}\), then (116) holds true if
As (117) always holds with the equality, we conclude that the second inequality in (109) is true under assumptions (105) and (107). Similarly, the inequality on the left side of (109) holds under assumptions (106) and (107). This completes the proof. \(\square \)
Remark 5
(Sharper timestep restriction) In the specific case of the linear heat equation (70), estimate (80) in Theorem 3 is sharper than estimate (107) in Theorem 5. In fact, since the Lipschitz constant of the source term is \(L=|\beta |\), the timestep restriction (107) is fulfilled for \(\tau |\beta | \le 1\), that is more restrictive than condition (80).
7 Velocity-Induced Invariant Regions for RD Models
Now, we consider two different RDSs that are well-known in the literature and prove, at the discrete level, the existence of discrete invariant hyper-rectangles for these RDSs, depending on the global discrete dilation rates \(\mu _{min}\) and \(\mu _{max}\) defined in (18). The results in this section are confined to the spatially discrete level, but from Conjecture 1, we claim that the same results holds at the continuous level. In the special case of stationary surfaces (i.e. when \(\mu _{min} = \mu _{max} = 0\)), we obtain invariant hyper-rectangles that have been studied in the literature (see [4, 6, 19]). It is worth remarking that, even though we consider two RD models for illustrative purposes, the following analysis can be easily extended to other types of RDSs. To mention two examples, for the well-known Hodgkin-Huxley model and for the DIB model for electrodeposition considered in [24, 25], the invariant region study is carried out in [14].
7.1 RDS with Activator-Depleted Kinetics
Let us consider an RDS with the well-known non-dimensional activator-depleted kinetics, also known as Schnakenberg or Brusselator kinetics (see for instance [1, 37]), on evolving surfaces
where a, b and \(\gamma \) are positive parameters and d is a positive diffusion rate. The model describes a system of two interacting chemicals, in which \(u_1\ge 0\) and \(u_2\ge 0\) are the respective concentrations. For this reason, we focus our attention on invariant regions contained in the positive ortant. In the following theorem we prove that: (i) the positive orthant is invariant for (118) regardless of \(\mu _{min}\) and \(\mu _{max}\). At the continuous level, the result holds in the specific case of stationary planar domains, see [4]. (ii) when \(\mu _{min} > 0\), the model possesses invariant stripes (depending on \(\mu _{min}\)) in the positive orthant.
Theorem 6
(Velocity-induced invariant regions for the activator-depleted model (118)) For the LESFEM spatial discretisation of (118), the following statements hold:
-
1.
For any value of the constants \(\mu _{min}\), and \(\mu _{max}\) defined in (34), the positive orthant \(\Sigma ^+ := [0,+\infty [^2\) is invariant.
-
2.
If \(\mu _{min} >0\) and \({\overline{\sigma }}_2\) is a constant such that
$$\begin{aligned}&{\overline{\sigma }}_2 \ge \frac{\gamma b}{\mu _{min}}, \end{aligned}$$(119)then the stripe \(\Sigma = [0, +\infty [\times [0, {\overline{\sigma }}_2]\) is invariant.
Proof
In order to prove Statements (1) and (2) we have to verify conditions (21)–(22). For Statement (1), we observe that
-
\({\underline{\Sigma }}_1 := \{0\}\times [0,{\overline{\sigma }}_2] \subset {\underline{\Sigma }}_1^+ := \{0\}\times [0,+\infty [\) and, for \((u_1,u_2)\in {\underline{\Sigma }}_1^+\), we have \({\underline{f}}_1 (u_1,u_2) = f_1(u_1,u_2)=\gamma a>0\);
-
\({\underline{\Sigma }}_2 := [0,{\overline{\sigma }}_1]\times \{0\} \subset {\underline{\Sigma }}_2^+ := [0,+\infty [\times \{0\}\) and, for \((u_1,u_2)\in {\underline{\Sigma }}_2^+\), we have \({\underline{f}}_2 (u_1,u_2) = f_2(u_1,u_2)=\gamma b>0\).
This proves Statement (1). For Statement (2), let \(\mu _{min}>0\) and we assume for the moment that the strict inequality holds in (119). Then the set \({\overline{\Sigma }}_1 := [0,+\infty [ \times \{{\overline{\sigma }}_2\}\) is contained in the region
in which \({\overline{f}}_1(u_1,u_2) := f_1(u_1,u_2) - \mu _{min} u_1 <0\). This proves Statement (2) when the strict inequality holds in (119). Otherwise, observe that
i.e. \(\Sigma \) is the intersection of invariant regions and is thus invariant. This completes the proof of Statement (2). \(\square \)
7.2 RDS with Thomas kinetics
Let us consider an RDS with the non-dimensional Thomas kinetics (see for instance [31, p. 78]), on evolving surfaces
where \(\alpha \), a, b, \(\gamma \), K and \(\rho \) are positive constants and d is a positive diffusion rate. The model describes a system of two interacting chemicals, in which \(u_1\ge 0\) and \(u_2\ge 0\) are the respective concentrations. For this reason, we focus our attention on invariant regions contained in the positive orthant.
Theorem 7
(Velocity-induced invariant regions for the Thomas model (121))
For the LESFEM spatial discretisation of (121), the following statements hold:
-
1.
For any value of the constants \(\mu _{min}\), and \(\mu _{max}\) defined in (34), the positive orthant \(\Sigma ^+ := [0,+\infty [^2\) is invariant.
-
2.
If \(\mu _{min} > -\gamma \min (1,\alpha )\) and \({\overline{\sigma }}_1\) and \({\overline{\sigma }}_2\) are two constants such that
$$\begin{aligned} {\overline{\sigma }}_1 \ge \frac{\gamma a}{\gamma +\mu _{min}}, \quad {\overline{\sigma }}_2 \ge \frac{\gamma \alpha b}{\gamma \alpha + \mu _{min}}, \end{aligned}$$(122)then the region \(\Sigma = [0, {\overline{\sigma }}_1]\times [0, {\overline{\sigma }}_2]\) is invariant.
Proof
To prove Statements (1) and (2), we have to verify conditions (21)–(22). For Statement (1), observe that
-
for \((u_1,u_2)\in {\underline{\Sigma }}_1 := \{0\}\times [0,{\overline{\sigma }}_2]\), we have \({\underline{f}}_1 (u_1,u_2) = f_1(u_1,u_2)=a>0\);
-
for \((u_1,u_2)\in {\underline{\Sigma }}_2 := [0,{\overline{\sigma }}_1]\times \{0\}\), we have \({\underline{f}}_2 (u_1,u_2) = f_2(u_1,u_2)=\alpha b>0\).
This proves Statement (1). For Statement (2), let \(\mu _{min} > -\gamma \min (1,\alpha )\) and we assume for the moment that the strict inequalities hold in (122). Then, observe that
-
the set \({\overline{\Sigma }}_1 := \{{\overline{\sigma }}_1\}\times [0,{\overline{\sigma }}_2]\) is contained in the region
$$\begin{aligned} \left\{ (u,v) \in {\mathbb {R}}^2 | u> 0, v > (\gamma a-(\mu _{min}+\gamma )u)\dfrac{1+u+Ku^2}{\gamma \rho u}\right\} , \end{aligned}$$in which \({\overline{f}}_1(u_1,u_2) := f_1(u_1,u_2) - \mu _{min} u_1 <0\);
-
the set \({\overline{\Sigma }}_2 := [0,{\overline{\sigma }}_1]\times \{{\overline{\sigma }}_2\}\) is contained in the region
$$\begin{aligned} \left\{ (u,v) \in {\mathbb {R}}^2 | u>0, v > \dfrac{\gamma \alpha b(1+u+Ku^2)}{\gamma \rho u + (\gamma \alpha +\mu _{min})(1+u+Ku^2)} \right\} , \end{aligned}$$in which \({\overline{f}}_2(u_1,u_2) := f_2(u_1,u_2) - \mu _{min} u_2 <0\).
This proves Statement (2) when the strict inequalities hold in (122). Otherwise, we have that
i.e. \(\Sigma \) is the intersection of invariant regions and is thus invariant. \(\square \)
8 Numerical Examples
The purpose of this section is to provide two numerical examples in which we (i) estimate the experimental order of convergence of the LESFEM and (ii) experimentally show the ability of Theorem 5 to find invariant regions of RDSs on evolving surfaces at the discrete level.
8.1 Numerical Example 1: Linear Heat Equation on an Evolving Sphere
In this example, we wish to estimate the experimental order of convergence of the LESFEM. As a test problem, we consider the linear heat equation given by
We choose \(T=1\) to be the final time. The initial domain \(\varGamma (0)\) is the unit sphere \({\mathscr {S}}^2\), that evolves under the velocity field
and undergoes linear growth for \(r=1\), see Table 1. In particular, the domain \(\varGamma (t)\) at time \(t \in [0,T]\) is a sphere whose radius is given by the growth function \(\phi (t) = t+1\) and the minimum dilation rate fulfils \(\mu _{min} = \frac{2r}{rT+1}=1\) (see Table 1).
In order to determine the experimental order of convergence, we consider the analytical solution to (124) given by
See “Appendix” for the derivation of the solution (126).
The constants \(\beta = -1\) and \(\mu _{min} = 1\) fulfill (78) and (80) for each \(\tau > 0\). Hence, the LESFEM–IMEX Euler solution to (124) fulfils a discrete maximum principle unconditionally on \(\tau \). In order to appreciate the quadratic convergence in space we solve the problem on a sequence of eight Delaunay meshes \(\varGamma _i\), \(i=1,\ldots ,8\), whose mesh sizes at \(t=0\) fulfil \(h_1(0) = 0.4013\) and \(h_{i}(0) \approx \frac{h_{i-1}(0)}{\sqrt{2}}\), \(i=2,\ldots ,8\). The corresponding timesteps \(\tau _i\) fulfil \(\tau _1 = 4e\)-2 and \(\tau _{i} = \left( \frac{h_i}{h_{i-1}}\right) ^2\tau _{i-1}\), \(i=2,\ldots ,8\). In Fig. 2 we show a sequence of snap shots of the evolution of the numerical solution on the finest mesh \(\varGamma _8\). The experimental order of convergence is computed by measuring the error, in \(L^\infty ([0,T],L^2(\varGamma _h(t)))\) norm, between the numerical solution U and the piecewise linear interpolant \(I_h(u)\) of the exact solution. The result is shown in Fig. 3: the convergence is experimentally optimal in that it is quadratic in the meshsize and linear in the timestep.
Numerical Example 1 on the linear heat equation (124): numerical solution at different times obtained on the finest mesh \(\varGamma _8\) with \(N=16962\) gridpoints, initial meshsize \(h_8 = 3.542\hbox {e}{-}2\) and timestep \(\tau = 3.116\hbox {e}{-}4\). Plotted values range from \(-0.1924\) (blue) to 0.1924 (red) (Color figure online)
Numerical Example 1 on the linear heat equation (124): Error in \(L^\infty (0,T,L^2(\varGamma _h(t)))\) norm (left) and experimental rate of convergence (right). The quadratic convergence in space is optimal
8.2 Numerical Example 2: RDS with Thomas Kinetics and Invariant Regions
In this example, we show that the LESFEM–IMEX Euler preserves the invariant regions of RDSs on evolving surfaces. Let us consider the following RDS with Thomas kinetics
considered in Sect. 7.2, with \(a=150\), \(b=100\), \(\rho = 13\), \(K=0.05\) as in [30] and \(\gamma =1\) for illustrative purposes. With these parameters, system (127) admits, in the absence of domain growth, the homogeneous steady state \(P \approx (37.7382, 25.1588)\) calculated using Newton-Raphson method on a stationary domain. Notice that the diffusion coefficient for \(u_2\) has been normalised to 1 for convenience, and we choose \(d_1=0.01\). The initial domain \(\varGamma (0)\) is the Dupin ring cyclide considered in [18, Appendix B], rescaled for convenience, given by
an orientable surface without boundary that is topologically equivalent to a torus. The surface evolves under the velocity field (48) with \(S(t) = \frac{rK(K-1)}{K-1 +\exp (Krt)}>0\), \(t\in [0,T]\), with \(r=0.2\), \(K=3\) and undergoes a logistic growth, see Table 1. As final time we choose \(T=100\). From Theorem 1, it follows that the corresponding dilation rates fulfil
From Theorem (), model (127) possesses arbitrarily large bounded invariant regions contained in the positive orthant. Let
be the smallest bounded region that (i) contains P and (ii) meets the modified inward flux conditions (105)–(106) with \(\tau = \bar{\tau } := 2e\)-3 and thus (105)–(106) hold for all \(0 < \tau \le \bar{\tau }\). As illustrated in Fig. 4, \(\Sigma \) is obtained by considering the nullclines of the modified kinetics
It is easy to see that, on a region of the form \(\Sigma = [{\underline{\sigma }}_1,{\overline{\sigma }}_1]\times [{\underline{\sigma }}_2, {\overline{\sigma }}_2]\), the Lipschitz constants \(L_1\) and \(L_2\) of the kinetics \(f_1\) and \(f_2\) of (127) fulfil
Hence, the timestep restriction (107) becomes \(\tau \le \frac{1}{\max ({\hat{L}}_1,{\hat{L}}_2)} \approx 1.676e\)-3. It follows that \(\Sigma \) is invariant for the LESFEM–IMEX Euler full discretisation under the timestep restriction \(0 < \tau \le \min \left( {\bar{\tau }}, \frac{1}{\max ({\hat{L}}_1,{\hat{L}}_2)}\right) \approx 1.676e\)-3. We choose \(\tau = 1e\)-3. The region \(\Sigma \) is smaller than the invariant region provided in Theorem 7, which has a simple analytical expression but is not optimal. The following initial condition
where \(\psi (x,y,z) := \sqrt{1-25(\min (|y|, \frac{1}{5}))^2}\) fulfils \((u_{1,0}(\mathbf {x}), u_{2,0}(\mathbf {x})) \in \Sigma \) for all \(\mathbf {x}\in \varGamma (0)\) and is shown in the first snap shot of Fig. 5. We solve the problem with \(\tau = 1e\)-3 on a sequence of seven meshes \(\varGamma _{h,i}(t)\), \(i=1,\ldots ,7\), with decreasing initial meshsizes \(h_i(0)\), \(i=1,\ldots ,7\), with both the LESFEM–IMEX Euler and ESFEM-IMEX Euler methods. Snap shots of the LESFEM–IMEX Euler numerical solution obtained on the finest mesh \(\varGamma _{h,7}\) at different times are shown in Fig. 5. In particular, at the final time \(T=100\) (see the last snap shot of Fig. 5), the surface is stationary up to machine precision and the numerical solution has reached a stationary pattern. For a given numerical solution \((U_1,U_2)\) on the mesh \(\varGamma _{h,i}\), \(i=1,\ldots ,7\), consider the following functions
These functions are the oriented distances of the numerical solution \((U_1,U_2)\) from the edges of \(\Sigma \). If the oriented distances \({\underline{\eta }}_k\) and \({\overline{\eta }}_k\), \(k=1,2\), stay positive at all times, it means that \((U_1,U_2)\) is in \(\Sigma \) at all times. For all \(i=1,\ldots ,7\), we show the minima over the time interval \([\tau , T]\) (i.e. excluding the initial data) of \({\underline{\eta }}_k\) and \({\overline{\eta }}_k\), \(k=1,2\), for both the ESFEM-IMEX Euler and LESFEM–IMEX Euler methods in Tables 2 and 3, respectively. We observe that ESFEM-IMEX Euler violates \(\Sigma \) for all \(i=1,\ldots ,7\), while LESFEM–IMEX Euler preserves \(\Sigma \) for all \(i=1,\ldots ,7\).
Numerical Example 2 on the Thomas RDS (127): snap shots of the \(U_1\) component of the LESFEM–IMEX Euler numerical solution at different times
9 Conclusions
In this paper we have considered a lumped evolving surface finite element method for the spatial discretisation of reaction–diffusion systems on evolving surfaces, by extending substantially the counterpart on stationary surfaces studied in [16]. We have obtained a fully-discrete scheme by applying the IMEX Euler timestepping to the spatially discrete method. In Sect. 4 we have presented a characterisation of the tangential flow of the continuous and discrete material velocities on evolving smooth and triangulated surfaces, respectively. As a consequence we have obtained, in Theorem 1, an explicit expression for the dilation rates for the special case of isotropic growth. In Theorems 2 and 3 of Sect. 5 we have presented sufficient conditions for the linear heat equation on evolving surfaces to fulfil the maximum principle at the semi- and fully-discrete levels, respectively. In particular, at the fully-discrete level, no timestep restriction is needed if the source parameter \(\beta \) in (70) is nonpositive. In Theorems 4 and 5 of Sect. 6 we provided sufficient conditions under which a hyper-rectangle in the phase space of an RDS on evolving surfaces is invariant at the semi- and fully-discrete levels, respectively. In particular, at the fully-discrete level, a timestep restriction depending on the Lipschitz constants of the kinetics is needed. In Sect. 7 we classified some families of invariant regions for two well-known RD models on evolving surfaces: the activator-depleted and the Thomas models. Two numerical examples are presented in Sect. 8 that experimentally show (i) the optimal convergence (i.e. quadratic in space and linear in time) of the proposed method for the linear heat equation on a linearly evolving sphere and (ii) the existence of a bounded invariant region for an RDS with Thomas kinetics on a logistically growing Dupin ring cyclide at the discrete level.
The mathematical and numerical analysis of more complicated settings such as non-isotropic chemically driven is a non-trivial exercise that requires new mathematical tools and techniques. Such a study is beyond the scope of this paper. In order to provide a first step in this direction, we have considered the simplest form of growth, uniform isotropic, which has allowed us to state precisely the conditions necessary for the preservation of invariant regions as well as stating the conditions for positivity of solutions.
In future studies we wish to extend the method by considering an ALE approach as in [13] in order to preserve good mesh properties under evolution. This would involve the study of convection RDSs on evolving surfaces, where the convection term arises from the ALE mapping.
References
Barreira, R., Elliott, C.M., Madzvamuse, A.: The surface finite element method for pattern formation on evolving biological surfaces. J. Math. Biol. 63(6), 1095–1119 (2011)
Bertalmıo, M., Cheng, L.T., Osher, S., Sapiro, G.: Variational problems and partial differential equations on implicit surfaces. J. Comput. Phys. 174(2), 759–780 (2001)
Blazakis, K.N., Madzvamuse, A., Reyes-Aldasoro, C.C., Styles, V., Venkataraman, C.: Whole cell tracking through the optimal control of geometric evolution laws. J. Comput. Phys. 297, 495–514 (2015)
Chellaboina, V., Bhat, S.P., Haddad, W.M., Bernstein, D.S.: Modeling and analysis of mass-action kinetics. IEEE Control Syst. 29, 60–78 (2009)
Chen, C, Kublik, C, Tsai, R.: An implicit boundary integral method for interfaces evolving by Mullins–Sekerka dynamics. In: Maekawa, Y., Jimbo, S. (eds.) Mathematics for Nonlinear Phenomena—Analysis and Computation, pp. 1–21. Springer (2017)
Chueh, K.N., Conley, C.C., Smoller, J.A.: Positively invariant regions for systems of nonlinear diffusion equations. Indiana Univ. Math. J. 26, 373–392 (1977)
Corson, F., Hamant, O., Bohn, S., Traas, J., Boudaoud, A., Couder, Y.: Turning a plant tissue into a living cell froth through isotropic growth. Proc. Nat. Acad. Sci. 106(21), 8453–8458 (2009)
Crampin, E.J., Gaffney, E.A., Maini, P.K.: Reaction and diffusion on growing domains: scenarios for robust pattern formation. Bull. Math. Biol. 61(6), 1093–1120 (1999)
Dziuk, G., Elliott, C.M.: Finite elements on evolving surfaces. IMA J. Numer. Anal. 27(2), 262–292 (2007)
Dziuk, G., Elliott, C.M.: Finite element methods for surface PDEs. Acta Numer. 22, 289–396 (2013)
Dziuk, G., Elliott, C.M.: L\(^2\)-estimates for the evolving surface finite element method. Math. Comput. 82(281), 1–24 (2013)
Elliott, C.M., Stinner, B., Venkataraman, C.: Modelling cell motility and chemotaxis with evolving surface finite elements. J. R. Soc. Interface 9(76), 3027–3044 (2012)
Elliott, C.M., Venkataraman, C.: Error analysis for an ALE evolving surface finite element method. Numer. Methods Partial Differ. Equ. 31(2), 459–499 (2015)
Frittelli, M: Numerical Methods for Partial Differential Equations on Stationary and Evolving Surfaces. Ph.D. thesis, Dipartimento di Matematica e Fisica “E. De Giorgi”, Università del Salento (2018) (to appear)
Frittelli, M., Madzvamuse, A., Sgura, I., Venkataraman, C.: Lumped finite elements for reaction-cross-diffusion systems on stationary surfaces. Comput. Math. Appl. 74(12), 3008–3023 (2017). https://doi.org/10.1016/j.camwa.2017.07.044
Frittelli, M., Madzvamuse, A., Sgura, I., Venkataraman, C.: Preserving invariance properties of reaction–diffusion systems on stationary surfaces. IMA J. Numer. Anal. (2017). https://doi.org/10.1093/imanum/drx058
Frittelli, M., Sgura, I.: Virtual element method for the Laplace–Beltrami equation on surfaces. ESAIM Math. Model. Numer. Anal. (2017). https://doi.org/10.1051/m2an/2017040
Fuselier, E.J., Wright, G.B.: A high-order kernel method for diffusion and reaction–diffusion equations on surfaces. J. Sci. Comput. 56(3), 535–565 (2013)
González-Olivares, E., Ramos-Jiliberto, R.: Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability. Ecol. Model. 166, 135–146 (2003)
Grande, J., Reusken, A.: A higher order finite element method for partial differential equations on surfaces. SIAM J. Numer. Anal. 54(1), 388–414 (2016)
Hebey, E., Robert, F.: Sobolev spaces on manifolds. In: Krupka, D., Saunders, D. (eds.) Handbook of Global Analysis, pp. 375–415 (2008)
Kovács, B.: Computing arbitrary Lagrangian Eulerian maps for evolving surfaces. arXiv preprint arXiv:1612.01701 (2016)
Kovács, B., Li, B., Lubich, C., Guerra, C.A.P.: Convergence of finite elements on an evolving surface driven by diffusion on the surface. Numer. Math. 137(3), 643–689 (2017)
Lacitignola, D., Bozzini, B., Frittelli, M., Sgura, I.: Turing pattern formation on the sphere for a morphochemical reaction–diffusion model for electrodeposition. Commun. Nonlinear Sci. Numer. Simul. 48, 484–508 (2017). https://doi.org/10.1016/j.cnsns.2017.01.008
Lacitignola, D., Bozzini, B., Sgura, I.: Spatio-temporal organization in a morphochemical electrodeposition model: Hopf and Turing instabilities and their interplay. Eur. J. Appl. Math. 26(2), 143–173 (2015)
Lefèvre, J., Mangin, J.F.: A reaction–diffusion model of human brain development. PLoS Comput. Biol. 6(4), e1000,749 (2010)
Li, H., Lin, Y., Heath, R.M., Zhu, M.X., Yang, Z.: Control of pollen tube tip growth by a rop gtpase-dependent pathway that leads to tip-localized calcium influx. Plant Cell 11(9), 1731–1742 (1999)
Madzvamuse, A., Barreira, R.: Exhibiting cross-diffusion-induced patterns for reaction-diffusion systems on evolving domains and surfaces. Phys. Rev. E 90(4), 043,307 (2014)
Madzvamuse, A., Gaffney, E.A., Maini, P.K.: Stability analysis of non-autonomous reaction-diffusion systems: the effects of growing domains. J. Math. Biol. 61(1), 133–164 (2010)
Madzvamuse, A., Wathen, A.J., Maini, P.K.: A moving grid finite element method applied to a model biological pattern generator. J. Comput. Phys. 190(2), 478–500 (2003)
Murray, J.D.: Mathematical Biology. II Spatial Models and Biomedical Applications (Interdisciplinary Applied Mathematics), vol. 18. Springer, New York (2001)
Plaza, R.G., Sanchez-Garduno, F., Padilla, P., Barrio, R.A., Maini, P.K.: The effect of growth and curvature on pattern formation. J. Dyn. Differ. Equ. 16(4), 1093–1121 (2004)
Pruyne, D., Bretscher, A.: Polarization of cell growth in yeast. I. Establishment and maintenance of polarity states. J. Cell Sci. 113(3), 365–375 (2000)
Quarteroni, A., Valli, A.: Numerical Approximation of Partial Differential Equations, vol. 23. Springer, New York (2008)
Ren, K., Tsai, R., Zhong, Y.: An implicit boundary integral method for computing electric potential of macromolecules in solvent. arXiv:1709.08070v4 (2018)
Sahlin, P., Jönsson, H.: A modeling study on how cell division affects properties of epithelial tissues under isotropic growth. PLoS ONE 5(7), e11,750 (2010)
Schnakenberg, J.: Simple chemical reaction systems with limit cycle behaviour. J. Theor. Biol. 81(3), 389–400 (1979)
Smoller, J.: Shock Waves and Reaction Diffusion Equations. Springer, New York (1994)
Taylor, M.E.: Partial Differential Equations. III. Springer, New York (2011)
Tuncer, N., Madzvamuse, A.: Projected finite elements for systems of reaction–diffusion equations on closed evolving spheroidal surfaces. Commun. Comput. Phys. 21(3), 718–747 (2017)
Venkataraman, C., Lakkis, O., Madzvamuse, A.: Global existence for semilinear reaction–diffusion systems on evolving domains. J. Math. Biol. 64(1–2), 41–67 (2012)
Yang, F.W., Venkataraman, C., Styles, V., Madzvamuse, A.: A robust and efficient adaptive multigrid solver for the optimal control of phase field formulations of geometric evolution laws. Commun. Comput. Phys. 21(1), 65–92 (2017)
Acknowledgements
The authors (MF, AM, IS CV) would like to thank the Isaac Newton Institute for Mathematical Sciences for its hospitality during the programme [Coupling Geometric PDEs with Physics for Cell Morphology, Motility and Pattern Formation] supported by EPSRC Grant Number EP/K032208/1. MF’s and IS’s research work has been performed under the auspices of the Italian National Group for Scientific Calculus (GNCS-INdAM). This work (AM, CV) is partly supported by the EPSRC Grant Number EP/J016780/1 and the Leverhulme Trust Research Project Grant (RPG-2014-149). AM acknowledges funding from the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreement No. 642866, the Commission for Developing Countries, and was partially supported by a grant from the Simons Foundation. AM is a Royal Society Wolfson Research Merit Award Holder funded generously by the Wolfson Foundation.
Author information
Authors and Affiliations
Corresponding author
Appendix: Derivation of the Analytical Solution to Experiment 8.1
Appendix: Derivation of the Analytical Solution to Experiment 8.1
Let \(\psi : \mathscr {S}^2\rightarrow \mathbb {R}\) be an eigenfunction of the Laplace-Beltrami operator on \(\mathscr {S}^2\) with eigenvalue \(\lambda \in \mathbb {R}\), i.e. \(\varDelta _{\mathscr {S}^2} \psi = \lambda \psi \). Let the surface evolve with an arbitrary isotropic velocity field (48) and let \(\phi (t)\) be the respective growth function, as defined in (61). For each \(t\in [0,T]\), \(\varGamma (t)\) is a sphere of radius \(\phi (t)\). By using the chain rule, it is easy to show that
i.e. \(\psi \left( \frac{\cdot }{\phi (t)}\right) \) is an eigenfunction of \(\varDelta _{\varGamma (t)}\) and its eigenvalue decays quadratically with the growth function. We look for solutions to (124) of the form
where \(\eta (t)\) is an unknown time-dependent coefficient. By using (63), (131) and (132) in (124), and cancelling \(\psi \left( \frac{\mathbf {x}}{\phi (t)}\right) \) on both sides, we have
which leads to
In (134) we choose
-
a linear growth with \(r=1\) (hence \(S(t) = \frac{1}{t+1}\) and \(\phi (t) = t+1\) for \(t\in [0,1]\), see Table 1);
-
\(\eta (0)=1\), \(\beta = -1\) and \(d = \frac{1}{12}\) for illustrative purposes.
The profile \(\eta (t)\) defined in (134) thus becomes
By combining (132) with (135), we have
Finally, we choose the eigenfunction \(\psi (x,y,z) := xyz\), \((x,y,z)\in \mathscr {S}^2\), whose eigenvalue is \(\lambda = -12\). Hence, (136) becomes
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Frittelli, M., Madzvamuse, A., Sgura, I. et al. Numerical Preservation of Velocity Induced Invariant Regions for Reaction–Diffusion Systems on Evolving Surfaces. J Sci Comput 77, 971–1000 (2018). https://doi.org/10.1007/s10915-018-0741-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0741-7