Abstract
An evolving surface finite element discretisation is analysed for the evolution of a closed two-dimensional surface governed by a system coupling a generalised forced mean curvature flow and a reaction–diffusion process on the surface, inspired by a gradient flow of a coupled energy. Two algorithms are proposed, both based on a system coupling the diffusion equation to evolution equations for geometric quantities in the velocity law for the surface. One of the numerical methods is proved to be convergent in the \(H^1\) norm with optimal-order for finite elements of degree at least two. We present numerical experiments illustrating the convergence behaviour and demonstrating the qualitative properties of the flow: preservation of mean convexity, loss of convexity, weak maximum principles, and the occurrence of self-intersections.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we propose and analyse an evolving surface finite element semi-discretisation of a geometric partial differential equation (PDE) system that couples a forced mean curvature flow to a diffusion equation on the surface. The unknowns are a time dependent two-dimensional closed, orientable, immersed surface \(\varGamma \subset {\mathbb {R}}^3\), and a time and spatially varying surface concentration u.
The coupled mean curvature–diffusion flow system is
where F and \({\mathcal {D}}\) are given sufficiently smooth functions. Associated with the surface \(\varGamma \) are the geometric quantities the mean curvature H, the oriented continuous unit normal field of the surface \(\nu \), and v the velocity of the evolving surface \(\varGamma \), where \(V = v \cdot \nu \) denotes the normal velocity. In the case that \(\varGamma \) encloses a domain we always choose the unit outward pointing normal field.
A special case, inspiring this work, with \(F(u,H)=g(u)H\), \({\mathcal {D}}(u)=G''(u)\) where \(g(u) = G(u) - G'(u)u\) and \(G(\cdot )\) is given arises as the \((L^2,H^{-1})\)-gradient flow of the coupled energy, [1, 2, 15],
yielding
It is important to note that (1.1) contains not only the gradient flow of [1, 2, 15] as a special case, but numerous other geometric flows as well. Examples are pure mean curvature flow [34], the generalised mean curvature flows \(v=-V(H)\nu \), see, e.g., [33], examples in [12] and [11], additively forced mean curvature flow [9, 16], and [38] (see also the references therein). Also it arises as a sub-system in coupled bulk–surface models such as that for tumour growth considered in [30].
1.1 Notation for evolving hypersurfaces
We adopt commonly used notation for surface and geometric partial differential equations. Our setting is that the evolution takes an initial \(C^k\) hypersurface \(\varGamma ^0\subset {\mathbb {R}}^3\) and an initial distribution \(u^0 :\varGamma ^0\rightarrow \mathbb R\) and evolves the surface so that \(\varGamma (t)\equiv \varGamma [X]\subset {\mathbb {R}}^3\) is the image
of a smooth mapping \(X:\varGamma ^0\times [0,T]\rightarrow {\mathbb {R}}^3\) such that \(X(\cdot ,t)\) is the parametrisation of an orientable, immersed hypersurface for every t. We denote by \(v(x,t)\in {\mathbb {R}}^3\) at a point \(x=X(p,t)\in \varGamma [X(\cdot ,t)]\) the velocity defined by
For a function \(\eta (x,t)\) (\(x\in \varGamma [X]\), \(0\le t \le T\)) we denote the material derivative (with respect to the parametrization X) as
On any regular surface \(\varGamma \subset {\mathbb {R}}^3\), we denote by \(\nabla _{\varGamma }\eta :\varGamma \rightarrow {\mathbb {R}}^3\) the tangential gradient of a function \(\eta :\varGamma \rightarrow {\mathbb {R}}\), and in the case of a vector-valued function \(\eta =(\eta _1,\eta _2,\eta _3)^T:\varGamma \rightarrow {\mathbb {R}}^3\), we let \(\nabla _{\varGamma }\eta = (\nabla _{\varGamma }\eta _1, \nabla _{\varGamma }\eta _2, \nabla _{\varGamma }\eta _3)\). We thus use the convention that the gradient of \(\eta \) has the gradient of the components as column vectors, (in agreement with gradient of a scalar function is a column vector). We denote by \(\nabla _{\varGamma } \cdot \eta = \text {tr}(\nabla _{\varGamma }\eta )\) the surface divergence of a vector field \(\eta \) on \(\varGamma \), and by \(\varDelta _{\varGamma } \eta =\nabla _{\varGamma }\cdot \nabla _{\varGamma }\eta \) the Laplace–Beltrami operator applied to \(\eta :\varGamma \rightarrow {\mathbb {R}}\); see the review [17] or [27, Appendix A], or any textbook on differential geometry for these notions.
We suppose that \(\varGamma (t)\) is an orientable, immersed hypersurface for all t. In the case that \(\varGamma \) is the boundary of a bounded open set \(\varOmega \subset {\mathbb {R}}^3\) we orient the unit normal vector field \(\nu :\varGamma \rightarrow {\mathbb {R}}^3\) to point out of \(\varOmega \). The surface gradient of the normal field contains the (extrinsic) curvature data of the surface \(\varGamma \). At every \(x\in \varGamma \), the matrix of the extended Weingarten map,
is symmetric and of size \(3\times 3\) (see, e.g., [50, Proposition 20]). Apart from the eigenvalue 0 (with eigenvector \(\nu \)), its other two eigenvalues are the principal curvatures \(\kappa _1\) and \(\kappa _2\). They determine the fundamental quantities
where |A| denotes the Frobenius norm of the matrix A. Here, the mean curvature H is, as in most of the literature, taken without the factor 1/2. In this setting, the mean curvature of a sphere is positive.
For an evolving surface \(\varGamma \) with normal velocity \(v=V\nu \), using that \(\nabla _{\varGamma }f \cdot \nu = 0\) for any function f, we have the fundamental equation
The following geometric identities hold for any sufficiently smooth evolving surface \(\varGamma (t)\), (see for example [11, 27, 34]):
They are fundamental in the derivation of the system of evolution equations discretised in this paper.
1.2 Our approach
The key idea of our approach is that it is based on a system of evolution equations coupling the two Eqs. (1.1a) and (1.1b) to parabolic equations for geometric variables in the velocity law. This approach was first used for mean curvature flow [37]. The system is derived using the geometric identities (1.7), (1.8) and (1.9). Using the notation \(\partial _i\cdot ,\; i=1,2\) for appropriate partial derivatives, we prove the following lemma.
Lemma 1.1
Let \(\varGamma [X]\) and u be sufficiently smooth solutions of the Eqs. (1.1a)–(1.1b). Suppose that \(F,K:{\mathbb {R}}^2\rightarrow {\mathbb {R}}\) are sufficiently smooth, satisfy
and in addition assume that \(\partial _2 F(u,H)\) is positive. Then the normal vector \(\nu \), the mean curvature H and the normal velocity V satisfy the two following systems of non-linear parabolic evolution equations:
and
Proof
These two sets of equations are an easy consequence of the geometric identities (1.5), (1.7)–(1.9), and the following calculations
as well as
\(\square \)
Employing the lemma above we see that a sufficiently smooth solution of the original initial value problem (1.1) also satisfies two other different problems involving parabolic PDE systems in which the dependent variables are a parametrised surface \(\varGamma [X]\), the velocity v of \(\varGamma \), a surface concentration field u, and either the variables \(\nu \) and V or \(\nu \) and H. In these problems the variables \(\nu ,V\) or \(\nu ,H\) are considered to be independently evolving unknowns, rather than being determined by the associated geometric quantities of the surface \(\varGamma [X]\) (in contrast to the methods of Dziuk [26] or Barrett, Garcke, and Nürnberg [10], etc.).
Problem 1.1
Given \(\{\varGamma ^0,u^0,\nu ^0,V^0\}\), find for \(t\in (0,T]\) functions \( \{ X(\cdot , t):\varGamma ^0\rightarrow {\mathbb {R}}^3,\; v(\cdot ,t):\varGamma [X(\cdot ,t)] \rightarrow {\mathbb {R}}^3,\; u:\varGamma [X(\cdot ,t)] \rightarrow {\mathbb {R}},\; \nu (\cdot ,t):\varGamma [X(\cdot ,t)]\rightarrow {\mathbb {R}}^3\), \(V(\cdot ,t):\varGamma [X(\cdot ,t)]\rightarrow {\mathbb {R}}\}\) such that
with initial data
where \(\nu ^0\) is the unit normal to \(\varGamma ^0\) and \(V^0 = -F(u^0,H^0)\) with \(H^0\) being the mean curvature of \(\varGamma ^0\).
Problem 1.2
Given \(\{\varGamma ^0,u^0,\nu ^0,H^0\}\), find for \(t\in (0,T]\) the functions \( \{X(\cdot ,t):\varGamma ^0\rightarrow \mathbb R^3,u:\varGamma [X(\cdot ,t)] \rightarrow {\mathbb {R}}, v(\cdot ,t):\varGamma [X(\cdot ,t)] \rightarrow {\mathbb {R}}^3\), \(\nu (\cdot ,t):\varGamma [X(\cdot ,t)]\rightarrow {\mathbb {R}}^3\), \(V(\cdot ,t):\varGamma [X(\cdot ,t)]\rightarrow \mathbb R\}\) such that
with initial data
where \(\nu ^0\) and \(H^0\) are, respectively, the unit normal to and mean curvature of \(\varGamma ^0\).
The idea is to discretise these systems using the evolving surface finite element method, see, e.g., [18], and also [21, 41]. The same approach was successfully used previously for mean curvature flow [37], also with additive forcing [38], and in arbitrary codimension [13], for Willmore flow [39], and for generalised mean curvature flows [12].
1.3 Main results
In Theorem 7.1, we state and prove optimal-order time-uniform \(H^1\) norm error estimates for the spatial semi-discretisation, with finite elements of degree at least 2, in all variables of Problem 1.1, over time intervals on which the solution remain sufficiently regular. This excludes the formation of singularities, but not self-intersections. We expect that an analogous proof would suffice for the other system Problem 1.2 but due to length this is not presented here. The convergence proof separates the questions of consistency and stability. Stability is proved via energy estimates, testing with the errors and also with their time derivatives. Similarly to previous works, the energy estimates are performed in the matrix–vector formulation, and they use technical lemmas comparing different quantities on different surfaces, cf. [37, 40]. Due to the non-linear structure of the evolution equations in the coupled system we will also need similar but new lemmas estimating differences of solution-dependent matrices, cf. [12]. A key issue in the stability proof is to establish a \(W^{1,\infty }\) norm error bounds for all variables. These are obtained from the time-uniform \(H^1\) norm error estimates via an inverse inequality.
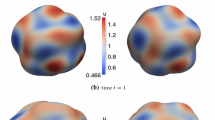
In [15, Chapter 5] Bürger proved qualitative properties for the continuous coupled flow (1.3) with energy (1.2), for example the preservation of mean convexity, the possible loss of convexity, the existence of a weak maximum principle for the diffusion equation, the decay of energy, and the existence of self-intersections. These properties are enjoyed by our evolving surface finite element method as illustrated in the numerical simulations in Sect. 10.
1.4 Related numerical analysis
Numerical methods for related problems have been proposed and studied in many papers. We first restrict our literature overview for numerical methods for at least two-dimensional surface evolutions.
Algorithms for mean curvature flow were proposed, e.g., by Dziuk in [26], in [10], and in [29] based on the DeTurck trick. The first provably convergent algorithm was proposed and analysed in [37], while [38] extends these convergence results to additively forced mean curvature flow coupled to a semi-linear diffusion equation on the surface. Recently, Li [43] proved convergence of Dziuk’s algorithm, for two-dimensional surfaces requiring surface finite elements of degree \(k \ge 6\).
Evolving surface finite element based algorithms for diffusion equations on evolving surface were analysed, for example, in [18, 20], in particular non-linear equations were studied in [36, 42]. On the numerical analysis of both problems we also refer to the comprehensive survey articles [17, 19], and [11]. For curve shortening flow coupled to a diffusion on a closed curve optimal-order finite element semi-discrete error estimates were shown in [47], while [8] have proved convergence of the corresponding backward Euler full discretisation. The case of open curves with a fix boundary was analysed in [49]. For forced-elastic flow of curves semi-discrete error estimates were proved in [48]. For mean curvature flow coupled to a diffusion process on a graph optimal-order fully discrete error bounds were recently shown in [24].
1.5 Outline
The paper is organised as follows. Section 1 introduces basic notation and geometric quantities, and it is mainly devoted to the derivation of the two coupled systems. In Sect. 2 we present the weak formulations of the coupled problems, and explore the properties of the coupled flow. In Sect. 3 we briefly recap the evolving surface finite element method, define interpolation operators and Ritz maps. Sect. 4 presents important technical results relating different surfaces. In Sect. 5 we present the semi-discrete systems, while Sect. 6 presents their matrix–vector formulations, and the error equations. Section 7 contains the most important results of the paper: consistency and stability analysis, as well as our main result which proves optimal-order semi-discrete error estimates. Sections 8 and 9 are devoted to the proofs of the results presented in Sect. 7. Finally, in Sect. 10 we describe an efficient fully discrete scheme, based on linearly implicit backward differentiation formulae. Then we present numerical experiments which illustrate and complement our theoretical results. We present numerical experiments testing convergence, and others which preserve mean convexity, but lose convexity, report on weak maximum principles, energy decay, and on an experiment with self-intersection.
2 Weak formulation, its properties, and examples
Throughout the paper we will assume the following properties of the nonlinear functions:
-
1.
\( \frac{\partial _1F}{\partial _2 F}\) is locally Lipschitz continuous,
-
2.
\(\frac{1}{\partial _2 F}\) is positive and locally Lipschitz continuous,
-
3.
\(\partial _1 K\) and \(\partial _2 K\) are locally Lipschitz continuous,
-
4.
\(\partial _2 K(u,V)\) is positive,
-
5.
\({\mathcal {D}}\) satisfies \(0 < D_0 \le {\mathcal {D}}(\cdot ) \le D_1\) and \( {\mathcal {D}}'\) is locally Lipschitz continuous.
The domain of definitions of the above nonlinearities are depending on the particular problem at hand. These properties hold on a compact neighbourhood of the exact smooth solution, on which \(\partial _2 K(u,V)\) and \(1/\partial _2F(u,H)\) are bounded from above and below by positive constants, and all functions are Lipschitz continuous.
2.1 Weak formulations
2.1.1 Weak formulation of Problem 1.1
The weak formulation of Problem 1.1 reads: Find \(X:\varGamma ^0 \rightarrow {\mathbb {R}}^3\) defining the (sufficiently smooth) surface \(\varGamma [X]\) with velocity v, and \(\nu \in L^2_{H^1(\varGamma [X])^3}\) with \(\partial ^{\bullet }\nu \in L^2_{L^2(\varGamma [X])^3}\), \(V \in L^2_{H^1(\varGamma [X])}\) with \(\partial ^{\bullet }V \in L^2_{L^2(\varGamma [X])}\), and \(u \in L^2_{H^1(\varGamma [X])}\) with \(\partial ^{\bullet }u \in L^2_{L^2(\varGamma [X])}\) such that, denoting \(A = \nabla _{\varGamma [X]} \nu \) and \(|\cdot |\) the Frobenius norm,
holds for all test functions \(\varphi ^\nu \in L^2_{H^1(\varGamma [X])^3}\), \(\varphi ^V \in L^2_{H^1(\varGamma [X])}\), and \(\varphi ^u \in L^2_{H^1(\varGamma [X])}\) with \(\partial ^{\bullet }\varphi ^u \in L^2_{L^2(\varGamma [X])}\), together with the ODE for the positions (1.4). The coupled weak system is endowed with initial data \(\varGamma ^0\), \(\nu ^0\), \(V^0\), and \(u^0\). For the definition of the Bochner-type spaces \(L^2_{L^2(\varGamma [X])}\) and \(L^2_{H^1(\varGamma [X])}\), which consist of time-dependent functions spatially defined on an evolving hypersurface, we refer to [4].
2.1.2 Weak formulation of Problem 1.2
The weak formulation of Problem 1.2 reads: Find \(X:\varGamma ^0 \rightarrow {\mathbb {R}}^3\) defining the (sufficiently smooth) surface \(\varGamma [X]\) with velocity v, and \(\nu \in L^2_{H^1(\varGamma [X])^3}\) with \(\partial ^{\bullet }\nu \in L^2_{L^2(\varGamma [X])^3}\), \(H\in L^2_{L^2(\varGamma [X])}\) with \(\partial ^{\bullet }H \in L^2_{L^2(\varGamma [X])}\), \(V \in L^2_{H^1(\varGamma [X])}\), and \(u \in L^2_{H^1(\varGamma [X])}\) with \(\partial ^{\bullet }u \in L^2_{L^2(\varGamma [X])}\) such that, denoting \(A = \nabla _{\varGamma [X]} \nu \) and \(|\cdot |\) the Frobenius norm,
holds for all test functions \(\varphi ^\nu \in L^2_{H^1(\varGamma [X])^3}\), \(\varphi ^H \in L^2_{H^1(\varGamma [X])}\), \(\varphi ^V \in L^2_{L^2(\varGamma [X])}\), and \(\varphi ^u \in L^2_{H^1(\varGamma [X])}\) with \(\partial ^{\bullet }\varphi ^u \in L^2_{L^2(\varGamma [X])}\), together with the ODE for the positions (1.4). The coupled weak system is endowed with initial data \(\varGamma ^0\), \(\nu ^0\), \(H^0\), and \(u^0\).
2.2 Properties of the weak solution
-
1.
Conservation of mass: This is easily seen by testing the weak formulation (2.1d) with \(\varphi ^u \equiv 1\).
-
2.
Weak maximum principle: By testing the diffusion equation with \(\min {(u,0)}\) and assuming that
$$\begin{aligned} 0\le u^0\le M^0,~~\text{ a.e. } \text{ on }~~\varGamma ^0 , \end{aligned}$$we find, cf. [15, Sect. 5.4],
$$\begin{aligned} 0\le u(\cdot ,t),~~\text{ a.e. } \text{ on }~~\varGamma [X]. \end{aligned}$$(2.3) -
3.
Energy bounds: Let G be any convex function, for which \(g(u) = G(u) - G'(u)u \ge 0\). Taking the time derivative of the energy \(\int _{\varGamma [X]} G(u)\), and using the diffusion equation (1.1b) and (1.6), we obtain,
$$\begin{aligned}&\frac{\text {d}}{\text {d}t}\bigg ( \int _{\varGamma [X]} G(u) \bigg ) \\&\quad = \int _{\varGamma [X]} G'(u) \partial ^{\bullet }u + \int _{\varGamma [X]} (\nabla _{\varGamma [X]} \cdot v) G(u) \\&\quad = \int _{\varGamma [X]} G'(u) \Big ( \nabla _{\varGamma [X]} \cdot \big ( {\mathcal {D}}(u) \nabla _{\varGamma [X]} u \big ) - u (\nabla _{\varGamma [X]} \cdot v) \Big ) + \int _{\varGamma [X]} (\nabla _{\varGamma [X]} \cdot v) G(u) \\&\quad = \int _{\varGamma [X]} G'(u) \Big ( \nabla _{\varGamma [X]} \cdot \big ( {\mathcal {D}}(u) \nabla _{\varGamma [X]} u \big ) - u V H \Big ) + \int _{\varGamma [X]} V H G(u) \\&\quad = \int _{\varGamma [X]} G'(u) \nabla _{\varGamma [X]} \cdot \big ( {\mathcal {D}}(u) \nabla _{\varGamma [X]} u \big ) + \int _{\varGamma [X]} \big (G(u)- G'(u) u ) \big ) V H \\&\quad = - \int _{\varGamma [X]} {\mathcal {D}}(u) G''(u) |\nabla _{\varGamma [X]} u|^2 + \int _{\varGamma [X]} g(u) V H \end{aligned}$$yielding
$$\begin{aligned} \frac{\text {d}}{\text {d}t}\bigg ( \int _{\varGamma [X]} G(u) \bigg ) + \int _{\varGamma [X]} {\mathcal {D}}(u) G''(u) |\nabla _{\varGamma [X]} u|^2 = \int _{\varGamma [X]} g(u) V H. \end{aligned}$$(2.4)Energy decrease and a priori estimates follow provided that \(VH \le 0\), (note that \({\mathcal {D}}(u) G''(u) \ge 0\), \(g(u) = G(u) - G'(u)u \ge 0\) are already assumed). This inequality holds assuming \(K(u,V)V\ge 0\) and \(F(u,H)H\ge 0\), respectively, for Problem 1.1 and Problem 1.2. For system (1.3) the energy identity (2.4) leads to the natural energy decrease for the gradient flow [15, Sects. 3.3–3.4], [1].
3 Finite element discretisation
3.1 Evolving surface finite elements
For the spatial semi-discretisation of the weak coupled systems (2.1) and (2.2) we will use the evolving surface finite element method (ESFEM) [18, 25]. We use curved simplicial finite elements and basis functions defined by continuous piecewise polynomial basis functions of degree k on triangulations, as defined in [21, Sect. 2], [41] and [31].
3.1.1 Surface finite elements
The given smooth initial surface \(\varGamma ^0\) is triangulated by an admissible family of triangulations \({\mathcal {T}}_h\) of degree k [21, Sect. 2], consisting of curved simplices of maximal element diameter h; see [18] and [31] for the notion of an admissible triangulation, which includes quasi-uniformity and shape regularity. Associated with the triangulation is a collection of unisolvent nodes \(p_j\) \((j=1,\dots ,N)\) for which nodal variables define the piecewise polynomial basis functions \(\{\phi _j\}_{j=1}^N\).
Throughout we consider triangulations \(\varGamma _h[{{\mathbf {y}}}]\) isomorphic to \(\varGamma _h^0\) with respect to the labelling of the vertices, faces, edges and nodes. We use the notation \({{\mathbf {y}}}\in {\mathbb {R}}^{3N}\) to denote the positions \(y_j = {{\mathbf {y}}}|_j\), of nodes mapped to \(p_j\) so that
That is we assume there is a unique pullback \({{\tilde{p}}} \in \varGamma _h^0\) such that for each \(q\in \varGamma _h[{{\mathbf {y}}}]\) it holds \(q=\sum _{j=1}^Ny_j\phi _j({{\tilde{p}}})\).
We define globally continuous finite element basis functions using the pushforward
such that
Thus they have the property that on every curved triangle their pullback to the reference triangle is polynomial of degree k, which satisfy at the nodes \(\phi _i[{{\mathbf {y}}}](y_j) = \delta _{ij}\) for all \(i,j = 1, \dotsc , N\). These basis functions define a finite element space on \(\varGamma _h[{{\mathbf {y}}}]\)
We associate with a vector \({{\mathbf {z}}}=\{z_j\}_{j=1}^N\in \mathbb R^N\) a finite element function \(z_h\in S_h[{{\mathbf {y}}}]\) by
For a finite element function \(z_h\in S_h[{{\mathbf {y}}}]\), the tangential gradient \(\nabla _{\varGamma _h[{{\mathbf {y}}}]}z_h\) is defined piecewise on each curved element.
3.1.2 Evolving surface finite elements
We set \(\varGamma _h^0\) to be an admissible initial triangulation that interpolates \(\varGamma ^0\) at the nodes \(p_j\) and we denote by \({{\mathbf {x}}}^0\) the vector in \({\mathbb {R}}^{3N}\) that collects all nodes so \(x_j^0=p_j\). Evolving the jth node \(p_j\) in time by a velocity \(v_j(t)\in C([0,T])\), yields a collection of surface nodes denoted by \({{{\mathbf {x}}}}(t) \in {\mathbb {R}}^{3N}\), with \( x_j(t)={{\mathbf {x}}}(t)|_j\) at time t and \({{\mathbf {x}}}(0)={{\mathbf {x}}}^0\). Given such a collection of surface nodes we may define an evolving discrete surface by
That is, the discrete surface at time t is parametrized by the initial discrete surface via the map \(X_h(\cdot ,t):\varGamma _h^0\rightarrow \varGamma _h[{{\mathbf {x}}}(t)]\)
which has the properties that \(X_h(p_j,t)=x_j(t)\) for \(j=1,\dots ,N\), \(X_h(p_h,0) = p_h\) for all \(p_h\in \varGamma _h^0\) and for each \(q\in \varGamma _h[{{\mathbf {x}}}(t)]\) there exists a unique pullback \(p(q,t)\in \varGamma _h^0\) such that \(q=\sum _{j=1}^Nx_j(t)\phi _j(p(q,t)).\) We assume that the discrete surface remains admissible, which – in view of the \(H^1\) norm error bounds of our main theorem – will hold provided the flow map X is sufficiently regular, see Remark 7.4.
We define globally continuous finite element basis functions using the pushforward
such that
Thus they have the property that on every curved evolving triangle their pullback to the reference triangle is polynomial of degree k, and which satisfy at the nodes \(\phi _i[{{\mathbf {x}}}(t)](x_j) = \delta _{ij}\) for all \(i,j = 1, \dotsc , N\). These basis functions define an evolving finite element space on \(\varGamma _h[{{\mathbf {x}}}(t)]\)
We define a material derivative, \(\partial ^{\bullet }_h\cdot \), on the time dependent finite element space as the push forward of the time derivative of the pullback function. Thus the basis functions satisfy the transport property [18]:
It follows that for \(\eta _h(\cdot ,t) \in S_h[{{\mathbf {x}}}(t)]\), (with nodal values \((\eta _j(t))_{j=1}^N\)), we have
where the dot denotes the time derivative \(\text {d}/\text {d}t\). The discrete velocity \(v_h(q,t) \in {\mathbb {R}}^3\) at a point \(q=X_h(p,t) \in \varGamma [X_h(\cdot ,t)]\) is given by
Definition 3.1
(Interpolated-surface) Let \({{\mathbf {x}}}^*(t)\in \mathbb R^{3N}\) and \({{\mathbf {v}}}^*(t)\in {\mathbb {R}}^{3N}\) be the vectors with components \(x_j^*(t)=X(p_j,t)\), \(v^*_j(t):=\dot{X}(p_j,t)\) where \(X(\cdot ,t)\) solves Problem 1.1 and 1.2. The evolving triangulated surface \(\varGamma _h[{{\mathbf {x}}}^*(t)]\) associated with \(X_h^*(\cdot ,t)\) is called the interpolating surface, with interpolating velocity \(v_h^*(t)\).
The interpolating surface \(\varGamma _h[{{\mathbf {x}}}^*(t)]\) associated with \(X_h^*(\cdot ,t)\) is assumed to be admissible for all \(t\in [0,T]\), which indeed holds provided the flow map X is sufficiently regular, see Remark 7.4.
3.2 Lifts
Any finite element function \(\eta _h\) on the discrete surface \(\varGamma _h[{{\mathbf {x}}}(t)]\), with nodal values \((\eta _j)_{j=1}^N\), is associated with a finite element function \({\widehat{\eta }}_h\) on the interpolated surface \(\varGamma _h[{{\mathbf {x}}}^*(t)]\) with the exact same nodal values. This can be further lifted to a function on the exact surface by using the lift operator \(\,^\ell \), mapping a function on the interpolated surface \(\varGamma _h[{{\mathbf {x}}}^*(t)]\) to a function on the exact surface \(\varGamma [X(\cdot ,t)]\), via the identity, for \(x \in \varGamma _h[{{\mathbf {x}}}^*(t)]\),
using a signed distance function d, provided that the two surfaces are sufficiently close. For more details on the lift \(\,^\ell \), see [19, 21, 25]. The inverse lift is denoted by \(\eta ^{-\ell }:\varGamma _h[{{\mathbf {x}}}^*(t)] \rightarrow {\mathbb {R}}\) such that \((\eta ^{-\ell })^\ell = \eta \).
Then the composed lift operator \(\,^L\) maps finite element functions on the discrete surface \(\varGamma _h[{{\mathbf {x}}}(t)]\) to functions on the exact surface \(\varGamma [X(\cdot ,t)]\), see [37], via the interpolated surface \(\varGamma _h[{{\mathbf {x}}}^*(t)]\), by
We introduce the notation
where, for \(p_h \in \varGamma _h^0\), from the nodal vector \({{\mathbf {x}}}(t)\) we obtain the function \(X_h(p_h,t) = \sum _{j=1}^N x_j(t)\phi _j[{{\mathbf {x}}}(0)](p_h)\), while from \({{\mathbf {u}}}(t)\), with \(x_h \in \varGamma _h[{{\mathbf {x}}}(t)]\), we obtain \(u_h(x_h,t) = \sum _{j=1}^N u_j(t)\phi _j[{{\mathbf {x}}}(t)](x_h)\), and similarly for any other nodal vectors.
3.3 Surface mass and stiffness matrices and discrete norms
For a triangulation \(\varGamma _h[{{\mathbf {y}}}]\) associated with the nodal vector \({{\mathbf {y}}}\in {\mathbb {R}}^{3N}\), we define the surface-dependent positive definite mass matrix \({{\mathbf {M}}}({{\mathbf {y}}}) \in {\mathbb {R}}^{N \times N}\) and surface-dependent positive semi-definite stiffness matrix \({{\mathbf {A}}}({{\mathbf {y}}}) \in {\mathbb {R}}^{N \times N}\):
and then set
For a pair of finite element functions \(z_h,w_h\in S_h[{{\mathbf {y}}}]\) with nodal vectors \({{\mathbf {z}}},{{\mathbf {w}}}\) we have
These finite element matrices induce discrete versions of Sobolev norms on the discrete surface \(\varGamma _h[{{\mathbf {y}}}]\). For any nodal vector \({{\mathbf {z}}}\in {\mathbb {R}}^{N}\), with the corresponding finite element function \(z_h \in S_h[{{\mathbf {y}}}]\), we define the following (semi-)norms:
3.4 Ritz maps
Let the nodal vectors \({{\mathbf {x}}}^*(t)\in {\mathbb {R}}^{3N}\) and \({{\mathbf {v}}}^*(t)\in {\mathbb {R}}^{3N}\), collect the nodal values of the exact solution \(X(\cdot ,t)\) and \(v(\cdot ,t)\). Recalling Definition 3.1, the corresponding finite element functions \(X_h^*(\cdot ,t)\) and \(v_h^*(\cdot ,t)\) in \(S_h[{{\mathbf {x}}}^*(t)]^3\) are the finite element interpolations of the exact solutions.
The two Ritz maps below are defined following [41, Definition 6.1] (which is slightly different from [20, Definition 6.1] or [31, Definition 3.6]) and – for the quasi-linear Ritz map – following [42, Definition 3.1].
Definition 3.2
For any \(w \in H^1(\varGamma [X])\) the generalised Ritz map \({\widetilde{R}}_hw \in S_h[{{\mathbf {x}}}^*]\) uniquely solves, for all \(\varphi _h \in S_h[{{\mathbf {x}}}^*]\),
Definition 3.3
For any \(u \in H^1(\varGamma [X])\) and an arbitrary (sufficiently smooth) \(\xi :\varGamma [X] \rightarrow {\mathbb {R}}\) the \(\xi \)-dependent Ritz map \({\widetilde{R}}_h^\xi u \in S_h[{{\mathbf {x}}}^*]\) uniquely solves, for all \(\varphi _h \in S_h[{{\mathbf {x}}}^*]\),
where \(^{-\ell }\) denotes the inverse lift operator, cf. Sect. 3.2.
We will also refer to \({\widetilde{R}}_h^\xi \) as quasi-linear Ritz map, since it is associated to a quasi-linear elliptic operator.
Definition 3.4
The Ritz maps \(R_h\) and \(R_h^\xi \) are then defined as the lifts of \({\widetilde{R}}_h\) and \({\widetilde{R}}_h^\xi \), i.e. \(R_h u = ({\widetilde{R}}_hu)^\ell \in S_h[{{\mathbf {x}}}^*]^\ell \) and \(R_h^\xi u = ({\widetilde{R}}_h^\xi u)^\ell \in S_h[{{\mathbf {x}}}^*]^\ell \).
4 Relating different surfaces
In this section from [37, 40] we recall useful inequalities relating norms and semi-norms on differing surfaces. First recalling results in a general evolving surface setting, and then proving new results for the present problem.
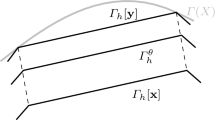
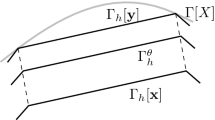
Given a pair of triangulated surfaces \(\varGamma _h[{{\mathbf {x}}}]\) and \(\varGamma _h[{{\mathbf {y}}}]\) with nodal vectors \({{\mathbf {x}}}, {{\mathbf {y}}}\in {\mathbb {R}}^{3N}\), we may view \(\varGamma _h[{{\mathbf {x}}}]\) as an evolution of \(\varGamma _h[{{\mathbf {y}}}]\) with a constant velocity \({{\mathbf {e}}}= (e_j)_{j=1}^N = {{\mathbf {x}}}- {{\mathbf {y}}}\in {\mathbb {R}}^{3N}\) yielding a family of intermediate surfaces.
Definition 4.1
For \(\theta \in [0,1]\) the intermediate surface \(\varGamma _h^\theta \) is defined by
For the vectors \({{\mathbf {x}}}= {{\mathbf {e}}}+ {{\mathbf {y}}}, {{\mathbf {w}}},{{\mathbf {z}}}\in {\mathbb {R}}^N\), we define the corresponding finite element functions on \(\varGamma _h^\theta \):
Figure 1 illustrates the described construction.
It follows from the evolving surface transport theorems for the \(L^2\) and Dirichlet inner products, [19], that for arbitrary vectors \({{\mathbf {w}}}, {{\mathbf {z}}}\in {\mathbb {R}}^N\):
where \(D_{\varGamma _h^\theta } e_h^\theta = \text {tr}(E^\theta ) I_3 - (E^\theta +(E^\theta )^T)\) with \(E^\theta =\nabla _{\varGamma _h^\theta } e_h^\theta \in {\mathbb {R}}^{3\times 3}\).
The following results relate the mass and stiffness matrices for the discrete surfaces \(\varGamma _h[{{\mathbf {x}}}]\) and \(\varGamma _h[{{\mathbf {y}}}]\), they follow by the Leibniz rule, and are given in [40, Lemma 4.1], [37, Lemma 7.2].
Lemma 4.1
In the above setting, if
then the following hold:
-
1.
For \(0\le \theta \le 1\) and \(1 \le p \le \infty \) with a constant \(c_p > 0\) independent of h and \(\theta \):
$$\begin{aligned} \begin{aligned}&\Vert w_h^\theta \Vert _{L^p(\varGamma _h^\theta )} \le c_p \, \Vert w_h^0 \Vert _{L^p(\varGamma _h^0)} , \qquad \Vert \nabla _{\varGamma _h^\theta } w_h^\theta \Vert _{L^p(\varGamma _h^\theta )} \le c_p \, \Vert \nabla _{\varGamma _h^0} w_h^0 \Vert _{L^p(\varGamma _h^0)}. \end{aligned}\nonumber \\ \end{aligned}$$(4.4) -
2.
$$\begin{aligned} \begin{aligned}&\text {The norms }\Vert \cdot \Vert _{{{\mathbf {M}}}({{\mathbf {y}}}+\theta {{\mathbf {e}}})}\text { and the norms }\Vert \cdot \Vert _{{{\mathbf {A}}}({{\mathbf {y}}}+\theta {{\mathbf {e}}})}\\&\text {are }h\text {-uniformly equivalent for }0\le \theta \le 1. \end{aligned} \end{aligned}$$(4.5)
-
3.
For any \({{\mathbf {w}}}, {{\mathbf {z}}}\in {\mathbb {R}}^N\), with an h-independent constant \(c>0\), we have the estimates
$$\begin{aligned} \begin{aligned} {{\mathbf {w}}}^T ({{\mathbf {M}}}({{\mathbf {x}}})-{{\mathbf {M}}}({{\mathbf {y}}})) {{\mathbf {z}}}&\le \ c \, \varepsilon \, \Vert {{\mathbf {w}}}\Vert _{{{\mathbf {M}}}({{\mathbf {y}}})} \Vert {{\mathbf {z}}}\Vert _{{{\mathbf {M}}}({{\mathbf {y}}})} , \\ {{\mathbf {w}}}^T ({{\mathbf {A}}}({{\mathbf {x}}})-{{\mathbf {A}}}({{\mathbf {y}}})) {{\mathbf {z}}}&\le \ c \, \varepsilon \, \Vert {{\mathbf {w}}}\Vert _{{{\mathbf {A}}}({{\mathbf {y}}})} \Vert {{\mathbf {z}}}\Vert _{{{\mathbf {A}}}({{\mathbf {y}}})} . \end{aligned} \end{aligned}$$(4.6) -
4.
If \(z_h \in W^{1,\infty }(\varGamma _h[{{\mathbf {y}}}])\) then, for any \({{\mathbf {w}}}, {{\mathbf {z}}}\in {\mathbb {R}}^N\), with an h-independent constant \(c>0\), we have
$$\begin{aligned} \begin{aligned} {{\mathbf {w}}}^T ({{\mathbf {M}}}({{\mathbf {x}}})-{{\mathbf {M}}}({{\mathbf {y}}})) {{\mathbf {z}}}&\le \ c \, \Vert {{\mathbf {w}}}\Vert _{{{\mathbf {M}}}({{\mathbf {y}}})} \Vert {{\mathbf {e}}}\Vert _{{{\mathbf {A}}}({{\mathbf {y}}})} \Vert z_h\Vert _{L^{\infty }(\varGamma _h[{{\mathbf {y}}}])} , \\ {{\mathbf {w}}}^T ({{\mathbf {A}}}({{\mathbf {x}}})-{{\mathbf {A}}}({{\mathbf {y}}})) {{\mathbf {z}}}&\le \ c \, \Vert {{\mathbf {w}}}\Vert _{{{\mathbf {A}}}({{\mathbf {y}}})} \Vert {{\mathbf {e}}}\Vert _{{{\mathbf {A}}}({{\mathbf {y}}})} \Vert z_h\Vert _{W^{1,\infty }(\varGamma _h[{{\mathbf {y}}}])}. \end{aligned} \end{aligned}$$(4.7)
4.1 Time evolving surfaces
-
Let \({{\mathbf {x}}}:[0,T]\rightarrow {\mathbb {R}}^{3N}\) be a continuously differentiable vector defining a triangulated surface \(\varGamma _h[{{\mathbf {x}}}(t)]\) for every \(t\in [0,T]\) with time derivative \({{\mathbf {v}}}(t)={\dot{{{\mathbf {x}}}}}(t)\) whose finite element function \(v_h(\cdot ,t)\) satisfies
$$\begin{aligned} \Vert \nabla _{\varGamma _h[{{\mathbf {x}}}(t)]}v_h(\cdot ,t) \Vert _{L^{\infty }(\varGamma _h[{{\mathbf {x}}}(t)])} \le K_v, \qquad 0\le t \le T. \end{aligned}$$(4.8)With \({{\mathbf {e}}}={{\mathbf {x}}}(t)-{{\mathbf {x}}}(s)=\int _s^t {{\mathbf {v}}}(r) \text {d}r\), the bounds (4.6) then yield the following bounds, which were first shown in Lemma 4.1 of [23]: for \(0\le s, t \le T\) with \(K_v|t-s| \le \tfrac{1}{4}\), for arbitrary vectors \({{\mathbf {w}}}, {{\mathbf {z}}}\in {\mathbb {R}}^N\), we have with \(C=c K_v\)
$$\begin{aligned} \begin{aligned} {{\mathbf {w}}}^T \bigl ({{\mathbf {M}}}({{\mathbf {x}}}(t)) - {{\mathbf {M}}}({{\mathbf {x}}}(s))\bigr ){{\mathbf {z}}}&\le \ C \, |t-s| \, \Vert {{\mathbf {w}}}\Vert _{{{\mathbf {M}}}({{\mathbf {x}}}(t))}\Vert {{\mathbf {z}}}\Vert _{{{\mathbf {M}}}({{\mathbf {x}}}(t))} , \\ {{\mathbf {w}}}^T \bigl ({{\mathbf {A}}}({{\mathbf {x}}}(t)) - {{\mathbf {A}}}({{\mathbf {x}}}(s))\bigr ){{\mathbf {z}}}&\le \ C\, |t-s| \, \Vert {{\mathbf {w}}}\Vert _{{{\mathbf {A}}}({{\mathbf {x}}}(t))}\Vert {{\mathbf {z}}}\Vert _{{{\mathbf {A}}}({{\mathbf {x}}}(t))}. \end{aligned} \end{aligned}$$(4.9)Letting \(s\rightarrow t\), this implies the bounds stated in Lemma 4.6 of [40]:
$$\begin{aligned} \begin{aligned} {{\mathbf {w}}}^T \frac{\text {d}}{\text {d}t}\big ( {{\mathbf {M}}}({{\mathbf {x}}}(t)) \big ) {{\mathbf {z}}}&\le \ C \, \Vert {{\mathbf {w}}}\Vert _{{{\mathbf {M}}}({{\mathbf {x}}}(t))}\Vert {{\mathbf {z}}}\Vert _{{{\mathbf {M}}}({{\mathbf {x}}}(t))} , \\ {{\mathbf {w}}}^T \frac{\text {d}}{\text {d}t}\big ( {{\mathbf {A}}}({{\mathbf {x}}}(t)) \big ) {{\mathbf {z}}}&\le \ C \, \Vert {{\mathbf {w}}}\Vert _{{{\mathbf {A}}}({{\mathbf {x}}}(t))}\Vert {{\mathbf {z}}}\Vert _{{{\mathbf {A}}}({{\mathbf {x}}}(t))} . \end{aligned} \end{aligned}$$(4.10)Moreover, by patching together finitely many intervals over which \(K_v|t-s| \le \tfrac{1}{4}\), we obtain that
$$\begin{aligned} \begin{aligned}&\ \text {the norms }\Vert \cdot \Vert _{{{\mathbf {M}}}({{\mathbf {x}}}(t))}\text { and the norms }\Vert \cdot \Vert _{{{\mathbf {A}}}({{\mathbf {x}}}(t))} \\&\ \text {are }h\text {-uniformly equivalent for }0\le t \le T. \end{aligned} \end{aligned}$$(4.11)
4.2 Variable coefficient matrices
Given \({{\mathbf {u}}}, {{\mathbf {V}}}\in {\mathbb {R}}^N\) with associated finite element functions \(u_h,V_h\) we define variable coefficient positive definite mass matrix \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {V}}}) \in {\mathbb {R}}^{N \times N}\) and positive semi-definite stiffness matrix \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}) \in {\mathbb {R}}^{N \times N}\):
for \(i,j = 1, \dotsc ,N\).
The following lemma is a variable coefficient variant of the estimates above relating mass matrices, i.e. (4.6) and (4.7).
Lemma 4.1
Let \({{\mathbf {u}}}, {{\mathbf {u}}}^*\in {\mathbb {R}}^N\) and \({{\mathbf {V}}}, {{\mathbf {V}}}^*\in {\mathbb {R}}^N\) be such that the corresponding finite element functions \(u_h, u_h^*\) and \(V_h, V_h^*\) have \(L^\infty \) norms bounded independently of h. Let (4.3) hold. Then the following bounds hold, for arbitrary vectors \({{\mathbf {w}}}, {{\mathbf {z}}}\in {\mathbb {R}}^N\):
and
The constant \(C > 0\) is independent of h and t, but depends on \(\partial _2 K(u_h,V_h)\) for (i)–(ii) and on \(\partial _2 K(u_h^*,V_h^*)\) for (iii)–(iv).
Proof
The proof is an adaptation of the proof in [12, Lemma 6.1], and it uses similar techniques as the proof of Lemma 4.2 below. \(\square \)
We will also need the stiffness matrix analogue of Lemma 4.1.
Lemma 4.2
Let \({{\mathbf {u}}}\in {\mathbb {R}}^N\) and \({{\mathbf {u}}}^*\in {\mathbb {R}}^N\) be such that the corresponding finite element functions \(u_h\) and \(u_h^*\) have bounded \(L^\infty \) norms. Let (4.3) hold. Then the following bounds hold:
and
The constant \(C > 0\) is independent of h and t.
Proof
The proof is similar to the proof of [12, Lemma 6.1].
(i) Using the fundamental theorem of calculus and the Leibniz formula [18, Lemma 2.2], and recalling (4.2), we obtain
where we used that the due to the \(\theta \)-independence of \(u_h^{*,\theta }\) we have \(\partial ^{\bullet }_{\varGamma _h^\theta } u_h^{*,\theta } = 0\), and hence \(\partial ^{\bullet }_{\varGamma _h^\theta } ( {\mathcal {D}}(u_h^{*,\theta })) = 0\).
For the first two terms we use the interchange formula [22, Lemma 2.6], for any \(w_h :\varGamma _h \rightarrow {\mathbb {R}}\):
where \(e_h^\theta \) is the velocity and \(\nu _{\varGamma _h^\theta }\) is the normal vector of the surface \(\varGamma _h^\theta \), the material derivative associated to \(e_h^\theta \) is denoted by \(\partial ^{\bullet }_{\varGamma _h^\theta }\).
Using (4.15) and recalling \(\partial ^{\bullet }_{\varGamma _h^\theta } w_h^\theta = \partial ^{\bullet }_{\varGamma _h^\theta } z_h^\theta = 0\), for (4.14) we obtain the estimate
where for the last estimate we used the norm equivalences (4.4), and the assumed \(L^\infty \) bound on \(u_h^*\).
(ii) The second estimate is proved using a similar idea, now working only on the surface \(\varGamma _h[{{\mathbf {x}}}]\):
using the \(L^\infty \) boundedness of \(u_h\) and \(u_h^*\) together with the local Lipschitz continuity of \({\mathcal {D}}\). \(\square \)
As a consequence of the boundedness below of the nonlinear functions \( \partial _2 K(\cdot ,\cdot )\) and \({\mathcal {D}}(\cdot )\), we note here that the matrices \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {V}}})\) and \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}})\) (for any \({{\mathbf {u}}}\) and \({{\mathbf {V}}}\), with corresponding \(u_h\) and \(V_h\) in \(S_h[{{\mathbf {x}}}]\)) generate solution-dependent (semi-)norms:
equivalent (independently of h and t) to \(\Vert \cdot \Vert _{{{\mathbf {M}}}({{\mathbf {x}}})}\) and \(\Vert \cdot \Vert _{{{\mathbf {A}}}({{\mathbf {x}}})}\), respectively. The following h-independent equivalence between the \({{\mathbf {A}}}({{\mathbf {x}}})\) and \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}})\) norms follows by Assumption 5 on \({\mathcal {D}}(\cdot )\): for any \({{\mathbf {z}}}\in {\mathbb {R}}^N\)
The equivalence for the \({{\mathbf {M}}}({{\mathbf {x}}})\) and \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {V}}})\) norms will be proved later on.
4.3 Variable coefficient matrices for time evolving surfaces
Similarly to (4.9), we will need a result comparing the matrices \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}^*)\) at different times. Particularly important will be the \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}^*)\) variant of (4.10).
Lemma 4.3
Let \({{\mathbf {u}}}^*:[0,T] \rightarrow {\mathbb {R}}^N\) be such that for all t the corresponding finite element function \(u_h^*\) satisfies \(\Vert \partial ^{\bullet }_h u_h^* \Vert _{L^\infty (\varGamma _h[{{\mathbf {x}}}])} \le R\) and \(\Vert {\mathcal {D}}'(u_h^*)\Vert _{L^\infty (\varGamma _h[{{\mathbf {x}}}])} \le R\) for \(0 \le t \le T\). Then the following bounds hold, for \(0\le s, t \le T\) with \(K_v|t-s| \le \tfrac{1}{4}\),
where the constant \(C > 0\) is independent of h and t, but depends on \(R^2\).
Proof
We follow the ideas of the proofs of [23, Lemma 4.1] and [40, Lemma 4.1]. Similarly to the proof of Lemma 4.1 (see [37]), by the fundamental theorem of calculus and the Leibniz formula, and recalling that \(\partial ^{\bullet }_h w_h = \partial ^{\bullet }_h z_h = 0\), we obtain
where the first order differential operator \(D_{\varGamma _h[{{\mathbf {x}}}]}\) is given after (4.2).
Similarly as for (4.9), using the bound (4.8) we obtain that
On the other hand, using the uniform upper bound on the growth of the diffusion coefficient \({\mathcal {D}}\) (Assumption 5) and the assumed \(L^\infty \) bound \(\Vert \partial ^{\bullet }_h u_h^* \Vert _{L^\infty (\varGamma _h[{{\mathbf {x}}}])} \le R\), we have the bound
By applying the Hölder inequality to (4.19), and combining it with the above estimates, we obtain
The proof of (4.17) is then finished using the h-uniform norm equivalence in time (4.11).
Dividing (4.17) by \(t-s\) and letting \(s \rightarrow t\) yields (4.18). \(\square \)
5 Finite element semi-discretisations of the coupled problem
We present two evolving surface finite element discretisations of Problems 1.1, 1.2. In the following we use the notation \(A_h = \frac{1}{2}(\nabla _{\varGamma _h[{{\mathbf {x}}}]} \nu _h + (\nabla _{\varGamma _h[{{\mathbf {x}}}]} \nu _h)^T)\) for the symmetric part of \(\nabla _{\varGamma _h[{{\mathbf {x}}}]} \nu _h\), \(|\cdot |\) for the Frobenius norm and the abbreviations \(\partial _j K_h := \partial _j K(u_h,V_h)\), \(\partial _j F_h := \partial _j F(u_h,V_h)\) (\(j = 1,2\)). We set \({{\widetilde{I}}}_h = {{\widetilde{I}}}_h[{{\mathbf {x}}}] :C(\varGamma _h[{{\mathbf {x}}}]) \rightarrow S_h(\varGamma _h[{{\mathbf {x}}}])\) to be the finite element interpolation operator on the discrete surface \(\varGamma _h[{{\mathbf {x}}}]\).
Problem 5.1
Find the finite element functions \(X_h(\cdot ,t)\in S_h[{{\mathbf {x}}}^0]^3\), \(\nu _h(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]^3\), \(V_h(\cdot ,t) \in S_h[{{\mathbf {x}}}(t)]\) and \(u_h(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]\) such that for \(t>0\) and for all \(\varphi _h^\nu (\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]^3\), \(\varphi _h^V(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]\), and \(\varphi _h^u(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]\) with discrete material derivative \(\partial ^{\bullet }_h \varphi _h^u(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]\):
The initial values for the finite element functions solving this system are chosen to be the Lagrange interpolations on the initial surface of the corresponding data for the PDE, \(X^0, \nu ^0,V^0 \) and \(u^0\). The initial data is assumed consistent to be with the equation \(V^0=-F(u^0,H^0)\).
Problem 5.2
Find the finite element functions \(X_h(\cdot ,t)\in S_h[{{\mathbf {x}}}^0]^3\), \(\nu _h(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]^3\), \(H_h(\cdot ,t) \in S_h[{{\mathbf {x}}}(t)]\) and \(u_h(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]\) such that for \(t>0\) and for all \(\varphi _h^\nu (\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]^3\), \(\varphi _h^H(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]\), and \(\varphi _h^u(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]\) with discrete material derivative \(\partial ^{\bullet }_h \varphi _h^u(\cdot ,t)\in S_h[{{\mathbf {x}}}(t)]\):
The initial values for the finite element functions solving this system are chosen to be the Lagrange interpolations on the initial surface of the corresponding data for the PDE, \(X^0, \nu ^0,H^0 \) and \(u^0\).
Remark 5.1
– We note that, in view of the discrete transport property (3.1), the last term in each of (5.1d) and (5.2d) vanishes for all basis functions \(\varphi _h^u = \phi _j[{{\mathbf {x}}}]\).
– Also by testing (5.1d) and (5.2d) by \(\varphi _h^u \equiv 1 \in S_h[{{\mathbf {x}}}]\) we observe that both semi-discrete systems preserve the mass conservation property of the continuous flow, cf. Sect. 2.2.
Remark 5.2
Note that the approximate normal vector \(\nu _h\) and the approximate mean curvature \(H_h\) are finite element functions \(\nu _h(\cdot ,t) = \sum _{j=1}^N\nu _j(t) \, \phi _j[{{\mathbf {x}}}(t)] \in S_h[{{\mathbf {x}}}]^3\) and \(H_h(\cdot ,t) = \sum _{j=1}^NH_j(t) \, \phi _j[{{\mathbf {x}}}(t)] \in S_h[{{\mathbf {x}}}]^3\), respectively, and are not the normal vector and the mean curvature of the discrete surface \(\varGamma _h[{{\mathbf {x}}}(t)]\). Similarly \(V_h(\cdot ,t) = \sum _{j=1}^NV_j(t) \, \phi _j[{{\mathbf {x}}}(t)] \in S_h[{{\mathbf {x}}}]\) is not the normal velocity of \(\varGamma _h[{{\mathbf {x}}}(t)]\).
6 Matrix–vector formulations
The finite element nodal values of the unknown semi-discrete functions \(v_h(\cdot ,t)\), \(\nu _h(\cdot ,t)\) and \(V_h(\cdot ,t)\), \(u_h(\cdot ,t)\), and (if needed) \(H_h(\cdot ,t)\) are collected, respectively, into column vectors \({{\mathbf {v}}}(t)= (v_j(t)) \in {\mathbb {R}}^{3N}\), \({{\mathbf {n}}}(t)= (\nu _j(t)) \in {\mathbb {R}}^{3N}\), \({{\mathbf {V}}}(t)= (V_j(t)) \in {\mathbb {R}}^N\), \({{\mathbf {u}}}(t)= (u_j(t)) \in {\mathbb {R}}^N\), and \({{\mathbf {H}}}(t)= (H_j(t)) \in {\mathbb {R}}^N\). If it is clear from the context, the time dependencies will be often omitted.
6.1 Matrix vector evolution equations
Recalling the notation \(A_h = \frac{1}{2}(\nabla _{\varGamma _h[{{\mathbf {x}}}]} \nu _h + (\nabla _{\varGamma _h[{{\mathbf {x}}}]} \nu _h)^T)\), \(\partial _j K_h = \partial _j K(u_h,V_h)\), and \(\partial _j F_h = \partial _j F(u_h,V_h)\) from the previous section, it is convenient to introduce the following non-linear maps:
for \(j = 1, \dotsc , N\) and \(\ell =1,2,3\). Since \({{\mathbf {f}}}_2\) is linear in \({\dot{{{\mathbf {u}}}}}\), we highlight this by the use of a semi-colon in the list of arguments.
For convenience we introduce the following notation. For \(d \in {{\mathbb {N}}}\) (with the identity matrices \(I_d \in {\mathbb {R}}^{d \times d}\)), we define by the Kronecker products:
When no confusion can arise, we will write \({{\mathbf {M}}}({{\mathbf {x}}})\) for \({{\mathbf {M}}}^{[d]}({{\mathbf {x}}})\), \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}})\) for \({{\mathbf {M}}}^{[d]}({{\mathbf {x}}},{{\mathbf {u}}})\), and \({{\mathbf {A}}}({{\mathbf {x}}})\) for \({{\mathbf {A}}}^{[d]}({{\mathbf {x}}})\). We will use both concepts for other matrices as well. Moreover, we use \(\bullet \) to denote the coordinate-wise multiplication for vectors \({{\mathbf {y}}}\in \mathbb R^{N}, {{\mathbf {z}}}\in {\mathbb {R}}^{3N}\)
Problem 6.1
(Matrix–vector formulation of Problem 5.1) Using these definitions, and the transport property (3.1) for (5.1d), the semi-discrete Problem 5.1 can be written in the matrix–vector form:
Problem 6.2
(Matrix–vector formulation of Problem 5.2) The semi-discrete Problem 5.2 can be written in the matrix–vector form (with non-linear matrix \({{\mathbf {F}}}\) and vectors \({{\mathbf {f}}}_3, {{\mathbf {f}}}_4\), defined according to (5.2)):
Remark 6.1
Upon noticing that the equations for \({{\mathbf {n}}}\) and \({{\mathbf {V}}}\) in Problem 6.1 are almost identical, we collect
Motivated by this abbreviation, we set \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {w}}}) := {{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {V}}})\) (using these two notations interchangeably, if no confusion can arise), we then rewrite the system into
Problem 6.3
(Equivalent matrix–vector formulation of Problem 5.1)
We remind that \({{\mathbf {f}}}= ({{\mathbf {f}}}_1,{{\mathbf {f}}}_2)^T\) is linear in \({\dot{{{\mathbf {u}}}}}\).
Remark 6.2
We compare the above matrix–vector formulation (6.3) to the same formulas for forced mean curvature flow [38], with velocity law \(v = -H\nu + g(u)\nu \), here \({{\mathbf {w}}}\) collects \({{\mathbf {w}}}= ({{\mathbf {n}}},{{\mathbf {H}}})^T\):
and to generalised mean curvature flow [12, Eq. (3.4)], with velocity law \(v = -V(H) \nu \), here \({{\mathbf {w}}}\) collects \({{\mathbf {w}}}= ({{\mathbf {n}}},{{\mathbf {V}}})^T\):
The coupled system (6.3) has a similar structure to those of (6.2) and (6.2). Due to these similarities, in the stability proof we will use similar arguments to [38] and [12] as wells as those in [37].
Compared to previous works, the concentration dependency in the mass matrix \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {w}}})\) and in the stiffness matrix \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}})\) requires extra care in estimating the corresponding terms in the stability analysis. For which the results of Sect. 4.2 will play a key role.
6.2 Defect and error equations
We set \({{\mathbf {u}}}^*\) to be the nodal vector of the Ritz projection \({\widetilde{R}}_h^u u\) defined by (3.4) on the interpolated surface \(\varGamma _h[{{\mathbf {x}}}^*(t)]\). The vectors \({{\mathbf {n}}}^*\in {\mathbb {R}}^{3N}\) and \({{\mathbf {V}}}^*\in {\mathbb {R}}^N\) are the nodal vectors associated with the Ritz projections \({\widetilde{R}}_h\nu \) and \({\widetilde{R}}_hV\) defined by (3.3) of the normal and the normal velocity of the surface solving the PDE system. We set
It is convenient to introduce the following equations that define defect quantities \({{\mathbf {d}}}_{{\mathbf {v}}},{{\mathbf {d}}}_{{\mathbf {w}}},{{\mathbf {d}}}_{{\mathbf {u}}}\) which occur when surface finite element interpolations and Ritz projections of the exact solution (i.e. \({{\mathbf {x}}}^*\), \({{\mathbf {v}}}^*\) and \({{\mathbf {w}}}^*\), \({{\mathbf {u}}}^*\)) are substituted into the matrix–vector equations defining the numerical approximations (6.3).
Definition 6.1
(Defect equations) The defects \({{\mathbf {d}}}_{{\mathbf {v}}},{{\mathbf {d}}}_{{\mathbf {w}}},{{\mathbf {d}}}_{{\mathbf {u}}}\) are defined by the following coupled system:
The following error equations for the nodal values of the errors between the exact and numerical solutions are obtained by subtracting (6.1) from (6.3) where the errors are set to be
with corresponding finite element functions, respectively,
Definition 6.2
(Error equations) The error equations are defined by the following system:
Note that by definition the initial data \({{\mathbf {e}}}_{{\mathbf {x}}}(0) = {{\mathbf {0}}}\) and \({{\mathbf {e}}}_{{\mathbf {v}}}(0) = {{\mathbf {0}}}\) whereas \({{\mathbf {e}}}_{{\mathbf {u}}}(0) \ne {{\mathbf {0}}}\) and \({{\mathbf {e}}}_{{\mathbf {w}}}(0) \ne {{\mathbf {0}}}\) in general.
7 Consistency, stability, and convergence
In this section we prove the main results of this paper. We begin in Sect. 7.1.1 by noting the uniform boundedness of some coefficients as a consequence of the approximation properties of the Ritz projections. In Sect. 7.2.1 we address the consistency of the finite element approximation by bounding the \(L^2\) norms of the defects.
7.1 Uniform bounds
7.1.1 Boundedness of the Ritz projections
We start by proving h- and t-uniform \(W^{1,\infty }(\varGamma _h[{{\mathbf {x}}}^*(t)])\) norm bounds for the finite element projections of the exact solutions (see Sect. 6.2).
Lemma 7.1
The finite element interpolations \(x_h^*\) and \(v_h^*\) and the Ritz maps \(w_h^*\), and \(u_h^*\) of the exact solutions satisfy
uniformly in h.
Proof
The \(W^{1,\infty }\) bounds for the interpolations, \({\widetilde{I}}_hX = x_h^*\) and \({\widetilde{I}}_hv = v_h^*\), follow from the error estimates in [21, Sect. 2.5].
On the other hand, the \(W^{1,\infty }\) bounds on the Ritz maps (\({\widetilde{R}}_hw = w_h^*\) and \({\widetilde{R}}_h^u u = u_h^*\)) are obtain, using an inverse estimate [14, Theorem 4.5.11], above interpolation error estimates of [21], and the Ritz map error bounds [41] and [42], by
with \(k - d/2 \ge 0\), in dimension \(d = 3\) here. Where for the last term we used the (sub-optimal) interpolation error estimate of [21, Proposition 2.7] (with \(p=\infty \)). \(\square \)
7.1.2 A priori boundedness of numerical solution
We note here that, by Assumption 4, along the exact solutions u, V in the bounded time interval [0, T] the factor \(\partial _2 K(u,V)\) is uniformly bounded from above and below by constants \(K_1 \ge K_0 > 0\).
For the estimates of the non-linear terms we establish some \(W^{1,\infty }\) norm bounds.
Lemma 7.2
Let \(\kappa > 1\). There exists a maximal \(T^* \in (0,T]\) such that the following inequalities hold:
Then for h sufficiently small and for \(0 \le t \le T^*\),
Furthermore, the functions \(\partial _2 K_h^*=\partial _2 K(u_h^*,V_h^*)\) and \(\partial _2 K_h = \partial _2 K(u_h,V_h)\) satisfy the following bounds
Then these h- and time-uniform upper and lower bounds imply that the norms \(\Vert \cdot \Vert _{{{\mathbf {M}}}({{\mathbf {x}}})}\) and \(\Vert \cdot \Vert _{{{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {w}}})}\) are indeed h- and t-uniformly equivalent, for any \({{\mathbf {z}}}\in {\mathbb {R}}^N\):
Proof
(a) Since we have assumed \(\kappa >1\) we obtain that \(T^*\) exists and is indeed positive. This is a consequence of the initial errors \(e_x(\cdot ,0) = 0\), \(e_v(\cdot ,0) = 0\), and, by an inverse inequality [14, Theorem 4.5.11],
and for the last inequalities using the error estimates for the Ritz maps \(R_h w\) and \(R_h^u u\), [41, Theorem 6.3 and 6.4] and the generalisations of [42, Theorem 3.1 and 3.2], respectively.
The uniform bounds on numerical solutions over \([0,T^*]\) (7.4) is directly seen using (7.3), (7.1), and a triangle inequality.
(b) We now show the h- and t-uniform upper- and lower-bounds for the coefficient functions \(\partial _2 K_h^*=\partial _2 K(u_h^*,V_h^*)\) and \(\partial _2 K_h = \partial _2 K(u_h,V_h)\). We use a few ideas from [12], where similar estimates were shown.
As a first step, it follows from applying inverse inequalities (see, e.g., [14, Theorem 4.5.11]) on the finite element spaces and \(H^1\) norm error bounds on the Ritz maps \(R_h\) and \(R_h^u\) and \(H^1\) and \(L^\infty \) error bounds for interpolants (e.g. [21, 31, 41] and [42]) that the following \(L^\infty \) norm error bounds hold in dimension \(d = 2\) (but stated for a general d for future reference):
By the definition of the lift map we have the equality \(\eta _h^*(x,t) = (\eta _h^*)^\ell (x^\ell ,t)\) for any function \(\eta _h^*:\varGamma _h[{{\mathbf {x}}}^*] \rightarrow {\mathbb {R}}\), and then by the triangle and reversed triangle inequalities and using the local Lipschitz continuity of \(\partial _2 K\) in both variables and its uniform upper and lower bounds, in combination with (7.1), we obtain (with the abbreviations \(\partial _2 K = \partial _2 K(u,V)\) and \(\partial _2 K_h^* = \partial _2 K(u_h^*,V_h^*)\)), written here for a d dimensional surface (we will use \(d=2\)),
and
which proves (7.5) on [0, T], independently of (7.3).
A similar argument comparing \(\partial _2 K_h\) with \(\partial _2 K_h^*\) now, using (7.3) (which only hold for \(0 \le t \le T^*\)) instead of (7.8), together with (7.5), yields the bounds (7.6).
In view of (7.6) the norm equivalence (7.7) is straightforward. \(\square \)
7.2 Consistency and stability
7.2.1 Consistency
For evolving surface finite elements of polynomial degree k, the defects satisfy the following consistency bounds:
Proposition 7.1
For \(t\in [0,T]\), it holds that
Proof
The consistency analysis is heavily relying on [12, 37, 39, 42], and the high-order error estimates of [41].
For the defect in the velocity v, using the \(O(h^k)\) error estimates of the finite element interpolation operator in the \(H^1\) norm [21, 41], similarly as they were employed in [39, Sect. 6], we obtain the estimate \(\Vert d_v(\cdot ,t)\Vert _{H^1(\varGamma _h[{{\mathbf {x}}}^*(t)])} = \Vert {{\mathbf {d}}}_{{\mathbf {v}}}(t)\Vert _{{{\mathbf {K}}}({{\mathbf {x}}}^*(t))} \le c h^k\).
Regarding the geometric part, (1.15c)–(1.15d), the additional terms on the right-hand side compared to those in the evolution equations of pure mean curvature flow in [37] do not present additional difficulties in the consistency error analysis, while the non-linear weights on the left-hand side are treated exactly as in [12]. Therefore, by combining the techniques and results of [37, Lemma 8.1] and [12, Lemma 8.1] we directly obtain for \(d_w = (d_\nu ,d_V)^T\) the consistency estimate \(\Vert d_w(\cdot ,t)\Vert _{L^2(\varGamma _h[{{\mathbf {x}}}^*(t)])} = \Vert {{\mathbf {d}}}_{{\mathbf {w}}}(t)\Vert _{{{\mathbf {M}}}({{\mathbf {x}}}^*(t))} \le c h^k\).
For the nonlinear diffusion equation on the surface, (1.15e), consistency is shown by the techniques of [42, Theorem 5.1], and yields the bound \(\Vert d_u(\cdot ,t)\Vert _{L^2(\varGamma _h[{{\mathbf {x}}}^*(t)])} = \Vert {{\mathbf {d}}}_{{\mathbf {u}}}(t)\Vert _{{{\mathbf {M}}}({{\mathbf {x}}}^*(t))} \le c h^k\). \(\square \)
7.2.2 Stability
The stability proof is based on the following three key estimates for the surface, concentration, and velocity-law, whose clever combination is the key to our stability proof. These results are energy estimates proved by testing the error equations with the time derivatives of the error, cf. [37]. The first two stability bounds may formally look similar to those in [12, 37, 38], yet their proofs are different and are based on the new results of Sect. 4.2. The proofs are postponed to Sect. 8.
Lemma 7.3
For the time interval \([0,T^*]\), where Lemma 7.2 holds, there exist constants \(c_0>0\) and \(c>0\) independent of h and \(T^*\) such that the following bounds hold:
-
1.
Surface estimate:
$$\begin{aligned} \begin{aligned}&\ \frac{c_0}{2} \Vert {\dot{{{\mathbf {e}}}}}_{{\mathbf {w}}}\Vert _{{{\mathbf {M}}}}^2 + \frac{1}{2} \frac{\text {d}}{\text {d}t}\Vert {{\mathbf {e}}}_{{\mathbf {w}}}\Vert _{{{\mathbf {A}}}}^2 \\&\le \ c_1 \Vert {\dot{{{\mathbf {e}}}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {M}}}}^2 + c\, \big ( \Vert {{\mathbf {e}}}_{{\mathbf {x}}}\Vert _{{{\mathbf {K}}}}^2 + \Vert {{\mathbf {e}}}_{{\mathbf {v}}}\Vert _{{{\mathbf {K}}}}^2 + \Vert {{\mathbf {e}}}_{{\mathbf {w}}}\Vert _{{{\mathbf {K}}}}^2 + \Vert {{\mathbf {e}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {K}}}}^2 \big ) + c \, \Vert {{\mathbf {d}}}_{{\mathbf {w}}}\Vert _{{{\mathbf {M}}}^*}^2 \\&\quad - \frac{\text {d}}{\text {d}t}\Big ( {{\mathbf {e}}}_{{\mathbf {w}}}^T \big ( {{\mathbf {A}}}({{\mathbf {x}}}) - {{\mathbf {A}}}({{\mathbf {x}}}^*) \big ) {{\mathbf {w}}}^*\Big ) . \end{aligned} \end{aligned}$$(7.12) -
2.
Concentration estimate:
$$\begin{aligned} \begin{aligned} \frac{1}{4} \Vert {\dot{{{\mathbf {e}}}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {M}}}}^2 + \frac{1}{2} \frac{\text {d}}{\text {d}t}\Vert {{\mathbf {e}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}^*)}^2&\le \ c \, \big ( \Vert {{\mathbf {e}}}_{{\mathbf {x}}}\Vert _{{{\mathbf {K}}}}^2 + \Vert {{\mathbf {e}}}_{{\mathbf {v}}}\Vert _{{{\mathbf {K}}}}^2 + \Vert {{\mathbf {e}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {K}}}}^2 \big ) + c \, \Vert {{\mathbf {d}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {M}}}^*}^2 \\&\quad - \frac{1}{2}\frac{\text {d}}{\text {d}t}\Big ( {{\mathbf {e}}}_{{\mathbf {u}}}^T \big ({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}) - {{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}^*)\big ) {{\mathbf {e}}}_{{\mathbf {u}}}\Big ) \\&\quad - \frac{\text {d}}{\text {d}t}\Big ( {{\mathbf {e}}}_{{\mathbf {u}}}^T \big ({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}) - {{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}^*)\big ) {{\mathbf {u}}}^*\Big ) \\&\quad - \frac{\text {d}}{\text {d}t}\Big ( {{\mathbf {e}}}_{{\mathbf {u}}}^T \big ({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}^*) - {{\mathbf {A}}}({{\mathbf {x}}}^*,{{\mathbf {u}}}^*)\big ) {{\mathbf {u}}}^*\Big ) . \end{aligned} \end{aligned}$$(7.13) -
3.
Velocity-law estimate:
$$\begin{aligned} \begin{aligned} \Vert {{\mathbf {e}}}_{{\mathbf {v}}}\Vert _{{{\mathbf {K}}}}&\le \ c \Vert {{\mathbf {e}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {K}}}} + c \Vert {{\mathbf {d}}}_{{\mathbf {v}}}\Vert _{{{\mathbf {K}}}^*} . \end{aligned} \end{aligned}$$(7.14)
Remark 7.1
Regarding notational conventions: By c and C we will denote generic h-independent constants, which might take different values on different occurrences. In the norms the matrices \({{\mathbf {M}}}({{\mathbf {x}}})\) and \({{\mathbf {M}}}({{\mathbf {x}}}^*)\) will be abbreviated to \({{\mathbf {M}}}\) and \({{\mathbf {M}}}^*\), i.e. we will write \(\Vert \cdot \Vert _{{{\mathbf {M}}}}\) for \(\Vert \cdot \Vert _{{{\mathbf {M}}}({{\mathbf {x}}})}\) and \(\Vert \cdot \Vert _{{{\mathbf {M}}}^*}\) for \(\Vert \cdot \Vert _{{{\mathbf {M}}}({{\mathbf {x}}}^*)}\), and similarly for the other norms.
The following result provides the key stability estimate.
Proposition 7.2
(Stability) Assume that, for some \(\kappa \) with \(1 < \kappa \le k\), the defects are bounded, for \(0 \le t \le T\), by
and that also the errors in the initial errors satisfy
Then, there exists \(h_0>0\) such that the following stability estimate holds for all \(h\le h_0\) and \(0\le t \le T\):
where C is independent of h and t, but depends exponentially on the final time T.
The proof to this result is obtained by an adept combination of the three estimates of Lemma 7.3 and a Gronwall argument, and is postponed to Sect. 9. We also note that by the consistency result, Proposition 7.1, the estimates (7.15) hold with \(\kappa = k\).
7.3 Convergence
We are now in the position to state the main result of the paper, which provide optimal-order error bounds for the finite element semi-discretisation (5.1a), for finite elements of polynomial degree \(k \ge 2\).
Theorem 7.1
Suppose Problem 1.1 admits a sufficiently regular exact solution \((X,v,\nu ,V,u)\) on the time interval \(t \in [0,T]\) for which the flow map \(X(\cdot ,t)\) is non-degenerate so that \(\varGamma [X(\cdot ,t)]\) is a regular orientable immersed hypersurface. Then there exists a constant \(h_0 > 0\) such that for all mesh sizes \(h \le h_0\) the following error bounds, for finite elements of polynomial degree \( k \ge 2\), for the lifts of the discrete position, velocity, normal vector, normal velocity and concentration over the exact surface \(\varGamma [X(\cdot ,t)]\) for \(0 \le t \le T\):
furthermore, by (1.10) and the smoothness of K, for the mean curvature we also have
The constant C is independent of h and t, but depends on bounds of higher derivatives of the solution \((X,v,\nu ,V,u)\) of the coupled problem, and exponentially on the length T of the time interval.
Proof
The errors are decomposed using the interpolation \(I_h\) for X and v, using the Ritz map \(R_h\) (3.3) for \(w = (\nu ,V)^T\), and using the quasi-linear Ritz map \(R_h^u\) (3.4) for u. For a variable \(z \in \{X,v,w,u\}\) and the appropriate ESFEM projection operator \({{\mathcal {P}}}_h\) (with \({{\mathcal {P}}}_h = (\widetilde{{{\mathcal {P}}}}_h)^\ell \)), we rewrite the error as
In each case, the second terms are bounded as \(c h^k\) by the error estimates for the above three operators, [21, 31, 41, 42]. By the same arguments, the initial values satisfy the \(O(h^k)\) bounds of (7.16).
The first terms on the right-hand side are bounded using the stability estimate Proposition 7.2 together with the defect bounds of Proposition 7.1 (and the above error estimates in the initial values), to obtain
Combining the two estimates completes the proof. \(\square \)
Sufficient regularity assumptions are the following: with bounds that are uniform in \(t\in [0,T]\), we assume \(X(\cdot ,t) \in H^{k+1}(\varGamma ^0)^3\), \(v(\cdot ,t) \in H^{k+1}(\varGamma [X(\cdot ,t)])^3\), and for \(w=(\nu ,V,u)\) we assume \(\ w(\cdot ,t), \partial ^{\bullet }w(\cdot ,t) \in W^{k+1,\infty }(\varGamma [X(\cdot ,t)])^5\).
Remark 7.2
Under these regularity conditions on the solution, for the numerical analysis we only require local Lipschitz continuity of the non-linear functions in Problem 1.1. These local-Lipschitz conditions are, of course, not sufficient to ensure the existence of even just a weak solution. For regularity results we refer to [15] and [2]. Here we restrict our attention to cases where a sufficiently regular solution exists, excluding the formation of singularities but not self-intersections, which we can then approximate with optimal-order under weak conditions on the nonlinearities.
Remark 7.3
We note here that the above theorem remains true if we add a non-linear term \(f(u,\nabla _{\varGamma }u)\) (locally Lipschitz in both variables) to the diffusion equation (1.1b). This is due to the fact that we already control the \(W^{1,\infty }\) norm of both the exact and numerical solutions (see (7.1) and (7.4)). Hence the corresponding terms in the stability analysis can be estimated analogously to the non-linear terms in the geometric evolution equations, see Sect. 8.1.
Remark 7.4
The remarks made after the convergence result in [37, Theorem 4.1] apply also here, which we briefly recap here.
– A key issue in the proof is to ensure that the \(W^{1,\infty }\) norm of the position error of the surfaces remains small. The \(H^1\) error bound and an inverse estimate yield an \(O(h^{k-1})\) error bound in the \(W^{1,\infty }\) norm. For two-dimensional surfaces, this is small only for \(k \ge 2\), which is why we impose the condition \(k \ge 2\) in the above result. For higher-dimensional surfaces a larger polynomial degree is required.
– Provided the flow map X parametrises sufficiently regular surfaces \(\varGamma [X]\), the admissibility of the numerical triangulation over the whole time interval [0, T] is preserved for sufficiently fine grids.
8 Proof of Lemma 7.3
The proof Lemma 7.3 is separated into three subsections for the three estimates.
The proofs extend the main ideas of the proof of Proposition 7.1 of [37] to the coupled mean curvature flow and diffusion system. Together they form the main technical part of the stability analysis. The first two estimates are based on energy estimates testing the error Eqs. (6.9b) and (6.9c) with the time-derivative of the corresponding error. The third bound for the error in the velocity is shown using Lemma 5.3 of [39]. The proofs combines the approach of [37, Proposition 7.1] with those of [38, Theorem 4.1] on handling the time-derivative term in \({{\mathbf {f}}}\) in (6.9b), of [12, Proposition 7.1] on dealing with the solution-dependent mass matrix \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {w}}})\) in (6.9b).
The estimates for the terms with \({{\mathbf {u}}}\)-dependent stiffness matrices in (6.9c) require new and more elaborate techniques, which are developed here, slightly inspired by the estimates for the stiffness-matrix differences in [40].
Due to these reasons, a certain degree of familiarity with these papers (but at least [37]) is required for a concise presentation of this proof.
Remark 8.1
In addition to Remark 7.1, throughout the present proof we will use the following conventions: References to the proof Proposition 7.1 in [37] are abbreviated to [37], unless a specific reference therein is given. For example, (i) in part (A) of the proof of Proposition 7.1 of [37] is referenced as [37, (A.i)].
8.1 Proof of (7.12)
Proof
We test (6.9b) with \({\dot{{{\mathbf {e}}}}}_{{\mathbf {w}}}\) and obtain:
(i) For the first term on the left-hand side, by the definition of \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {w}}}) = {{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {V}}})\) and the h-uniform lower bound from (7.6), we have
with the constant \(c_0 = \tfrac{1}{2} K_0\), see Lemma 7.2.
(ii) By the symmetry of \({{\mathbf {A}}}\) and (4.10) we obtain
(iii) On the right-hand side the two terms with differences of the solution-dependent mass matrix (recall the notation \({{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {w}}}) = {{\mathbf {M}}}({{\mathbf {x}}},{{\mathbf {u}}},{{\mathbf {V}}})\)) are estimated using Lemma 4.1, together with (7.3) and (7.1), (7.4).
For the first term, by Lemma 4.1 (iv) (with \({\dot{{{\mathbf {e}}}}}_{{\mathbf {w}}}\), \({\dot{{{\mathbf {w}}}}}^*\), and \({{\mathbf {u}}}\), \({{\mathbf {u}}}^*\) in the role of \({{\mathbf {w}}}\), \({{\mathbf {z}}}\), and \({{\mathbf {u}}}\), \({{\mathbf {u}}}^*\), respectively), together with (7.3), the uniform bounds (7.1) and (7.4), and the \(W^{1,\infty }\) bound on \(\partial ^{\bullet }_h u_h^*\), proved in [37, (A.iii)]. Using the norm equivalence (4.5), we altogether obtain
For the other term we apply Lemma 4.1 (ii) (with \({\dot{{{\mathbf {e}}}}}_{{\mathbf {w}}}\), \({\dot{{{\mathbf {w}}}}}^*\), and \({{\mathbf {u}}}^*\) in the role of \({{\mathbf {w}}}\), \({{\mathbf {z}}}\), and \({{\mathbf {u}}}\), respectively), and obtain
where we again used the norm equivalence (4.5).
(iv) The third term on the right-hand side is estimated exactly as in [37, (A.iv)] by (recalling \({{\mathbf {K}}}= {{\mathbf {M}}}+ {{\mathbf {A}}}\))
(v) Before estimating the non-linear terms \({{\mathbf {f}}}\), let us split off the part which depends linearly on \(\dot{{{\mathbf {u}}}}\), cf. (6.2):
Since the estimates for the non-linear term [37, (A.v)] were shown for a general locally Lipschitz function, they apply for the estimates for the difference \(\widetilde{{{\mathbf {f}}}} - \widetilde{{{\mathbf {f}}}}^*\) as well (note, however, that \({{\mathbf {f}}}\) defined in [37, Sect. 3.3] is different from the one here), and yield
The remaining difference is bounded
where for the first term we have used (6.2) and the \(W^{1,\infty }\) boundedness of the numerical solutions (7.4), while the second term is bounded by the same arguments used for the previous estimate.
(vi) The defect term is simply bounded by the Cauchy–Schwarz inequality and a norm equivalence (4.5):
Altogether, collecting the estimates in (i)–(vi), and using Young’s inequality and absorptions to the left-hand side, we obtain the desired estimate (7.12). \(\square \)
8.2 Proof of (7.13)
Proof
We test (6.9c) with \({\dot{{{\mathbf {e}}}}}_{{\mathbf {u}}}\), and obtain:
To estimate these terms we again use the same techniques as in Sect. 8.1.
(i) For the first term on the left-hand side, using (4.10) and the Cauchy–Schwarz inequality, we obtain
Then Young’s inequality yields
(ii) The second term on the left-hand side is bounded, using the symmetry of \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}^*)\) and (4.18), (via a similar argument as in (A.ii)), by
For the estimate (4.18), which follows from Lemma 4.3, the latter requires the bounds
The first estimate is proved exactly as in [37, (A.iii)], while the second one is shown (by a similar idea) using the local Lipschitz continuity of \({\mathcal {D}}'\) (Assumption 5) and the bounds (7.1), for sufficiently small h:
(iii) The time-differentiated mass matrix difference, the first term on the right-hand side of (8.2), is bounded, by the techniques for the analogous term in (A.iii) of the proof of [40, Proposition 6.1], by
For the last inequality we use (8.4).
(iv) By the symmetry of the matrices \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}})\) and \({{\mathbf {A}}}({{\mathbf {x}}},{{\mathbf {u}}}^*)\), and the product rule, we obtain
The first term will be estimated later after an integration in time, while the second term is bounded similarly to [37, (A.iv)].
Lemma 4.3 and the Leibniz formula yields, for any vectors \({{\mathbf {w}}}, {{\mathbf {z}}}\in {\mathbb {R}}^N\) (which satisfy \(\partial ^{\bullet }_h w_h = \partial ^{\bullet }_h z_h = 0\)),
Here \(v_h\) is the velocity of the discrete surface \(\varGamma _h[{{\mathbf {x}}}]\) with nodal values \({{\mathbf {v}}}\).
We now estimate the four terms separately. For the first term in \(J_1\), we compute
The local Lipschitz continuity of \({\mathcal {D}}'\) and (8.4), together with a Hölder inequality then yields
The two middle terms are estimated by first interchanging \(\partial ^{\bullet }_h\) and \(\nabla _{\varGamma _h[{{\mathbf {x}}}]}\) via the formula (4.15). Using (4.15) together with \(\partial ^{\bullet }_h w_h = \partial ^{\bullet }_h z_h = 0\) and the boundedness of \(\nu _{\varGamma _h[{{\mathbf {x}}}]}\) and \(v_h\) (7.4), we obtain the estimate
The last term \(J_4\) is estimated by a similar argument as the first, now using the local Lipschitz continuity of \({\mathcal {D}}'\) and the h-uniform \(W^{1,\infty }\) boundedness of \(v_h\) (7.4):
By combining these bounds, and recalling the \(W^{1,\infty }\) norm bounds (7.3) and (7.4), we obtain
Altogether we obtain
which does not contain a critical term \(\Vert {\dot{{{\mathbf {e}}}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {A}}}}\).
(v) Almost verbatim as the argument in (iv) we rewrite and estimate the third term on the right-hand side of (8.2) as
For the non-differentiated term here we used Lemma 4.2 (ii) (together with (7.1) and (7.4)) and the \(W^{1,\infty }\) variant of (8.4). The latter is shown (omitting the argument t) by
Here we subsequently used the norm equivalence for the lift operator (see [21, (2.15)–(2.16)]) in the first inequality, an inverse inequality [14, Theorem 4.5.11] in the second inequality, and the known error bounds for interpolation (see [21, Proposition 2]) and for the Ritz map \(u_h^* = {\widetilde{R}}_h^u u\) (a direct modification of [42, Theorem 3.1]) in the last inequality.
(vi) The argument for the fourth term on the right-hand side of (8.2) is slightly more complicated since it compares stiffness matrices on different surfaces. We will estimate this term by a \({\mathcal {D}}\)-weighted extension of the argument of [37, (A.iv)].
We start by rewriting this term as a total derivative
where we now used Lemma 4.2 (i) (together with (7.1) and (7.4)).
The remaining term is bounded similarly to (8.6). In the setting of Sect. 4, analogously to Lemma 4.1, using Leibniz formula we obtain, for any vectors \({{\mathbf {w}}}, {{\mathbf {z}}}\in {\mathbb {R}}^N\), but for a fixed \({{\mathbf {u}}}^*\in {\mathbb {R}}^N\) in both matrices,
We recall from Sect. 4 that \(\varGamma _h^\theta (t)\) is the discrete surface with nodes \({{\mathbf {x}}}^*(t)+\theta {{\mathbf {e}}}_{{\mathbf {x}}}(t)\) (with unit normal field \(\nu _h^\theta := \nu _{\varGamma _h^\theta }\)), and with finite element space \(S_h[{{\mathbf {x}}}^*(t)+\theta {{\mathbf {e}}}_{{\mathbf {x}}}(t)]\). The function \(u_h^{*,\theta }=u_h^{*,\theta }(\cdot ,t) \in S_h[{{\mathbf {x}}}^*(t)+\theta {{\mathbf {e}}}_{{\mathbf {x}}}(t)]\) with \(\theta \)-independent nodal values \({{\mathbf {u}}}^*(t)\).
We denote by \(w_h^\theta (\cdot ,t)\) and \(z_h^\theta (\cdot ,t)\) the finite element functions in \(S_h[{{\mathbf {x}}}^*(t)+\theta {{\mathbf {e}}}_{{\mathbf {x}}}(t)]\) with the time- and \(\theta \)-independent nodal vectors \({{\mathbf {w}}}\) and \({{\mathbf {z}}}\), respectively. The velocity of \(\varGamma _h^\theta (t)\) is \(v_{\varGamma _h^\theta }(\cdot ,t)\) (as a function of t), which is the finite element function in \(S_h[{{\mathbf {x}}}^*(t)+\theta {{\mathbf {e}}}_{{\mathbf {x}}}(t)]\) with nodal vector \({\dot{{{\mathbf {x}}}}}^*(t) + \theta {\dot{{{\mathbf {e}}}}}_{{\mathbf {x}}}(t) = {{\mathbf {v}}}^*(t) + \theta {{\mathbf {e}}}_{{\mathbf {v}}}(t)\). Related to this velocity, \(\partial ^{\bullet }_{\varGamma _h^\theta }\) denotes the corresponding material derivative on \({\varGamma _h^\theta }\). We thus have
The various time- and \(\theta \)-independencies imply
and since for the nodal vectors we have \({\dot{{{\mathbf {e}}}}}_{{\mathbf {x}}}= {{\mathbf {e}}}_{{\mathbf {v}}}\) (6.9d) we also have
The terms \(J_k^\theta \) for \(k = 0,\dotsc ,4\) are bounded almost exactly as the analogous terms in [37, (A.iv)].
For the first term we have \(\partial ^{\bullet }_{\varGamma _h^\theta } \big ( {\mathcal {D}}(u_h^{*,\theta }) \big ) = {\mathcal {D}}'(u_h^{*,\theta }) \, \partial ^{\bullet }_{\varGamma _h^\theta } u_h^{*,\theta }\), this together with (8.4) and recalling that \(u_h^{*,\theta }\) is \(\theta \)-independent yields \(\Vert {\mathcal {D}}'(u_h^{*,\theta }) \, \partial ^{\bullet }_{\varGamma _h^\theta } u_h^{*,\theta }\Vert _{L^\infty (\varGamma _h^\theta )} \le R^2\), cf. the proof of Lemma 4.3. We then obtain bound
The identities in (8.10) in combination with the interchange formula (4.15) yield
where we have used the uniform boundedness of K (5).
The interchange formula for \(\partial ^{\bullet }_{\varGamma _h^\theta }\) and \(D_{\varGamma _h^\theta }\), cf. [37, Eq. (7.27)], analogous to (4.15), and reads
with \({\bar{E}}^\theta = - \bigl (\nabla _{\varGamma _h^\theta } v_{\varGamma _h^\theta } - \nu _h^\theta (\nu _h^\theta )^T(\nabla _{\varGamma _h^\theta } v_{\varGamma _h^\theta } )^T \bigr ) \nabla _{\varGamma _h^\theta } e_x^\theta \), as follows from [22, Lemma 2.6] and the definition of the first order linear differential operator \(D_{\varGamma _h^\theta }\).
The interchange identity (8.12) and (8.11) (together with (5)) then yields
The last term is directly bounded, using the \(W^{1,\infty }\) boundedness of \(v_h\), as
Using the norm equivalences (4.4) for the bounds of \((J_k^\theta )_{k=0}^4\) we obtain
Altogether, using the bound (8.7), we obtain
(vii) Finally, the defect terms are bounded by
Altogether, collecting the above estimates in (i)–(vii), and using Young’s inequality and absorptions to the left-hand side, we obtain the desired estimate (recalling \({{\mathbf {K}}}= {{\mathbf {M}}}+ {{\mathbf {A}}}\)). \(\square \)
8.3 Proof of (7.14)
Proof
The error equation for the velocity law is estimated exactly as the velocity error equation for Willmore flow [39, (B)] (based on Lemma 5.3 therein), and recalling \({{\mathbf {u}}}= ( {{\mathbf {n}}}, {{\mathbf {V}}})^T \in {\mathbb {R}}^{4N}\), we obtain
where for the last inequality we used a norm equivalence (4.5). \(\square \)
9 Proof of Proposition 7.2
Proof
The aim is to to combine the three estimates of Lemma 7.3, following the main ideas of [37].
First we use the differential equation \({\dot{{{\mathbf {e}}}}}_{{\mathbf {x}}}= {{\mathbf {e}}}_{{\mathbf {v}}}\) (6.9d), using (4.10), to show the bound
We first take the weighted linear combination of (7.12) and (7.13) with weights 1 and \(8 c_1\), respectively, to absorb the term \(c_1 \Vert {\dot{{{\mathbf {e}}}}}_{{\mathbf {u}}}\Vert _{{{\mathbf {M}}}}^2\) from (7.12). We then obtain
We now connect \(\Vert {\dot{{{\mathbf {e}}}}}\Vert _{{{\mathbf {M}}}}^2\) with \(\text {d}/ \text {d}t \, \Vert {{\mathbf {e}}}\Vert _{{{\mathbf {M}}}}^2\), and will use the result either for \({{\mathbf {e}}}_{{\mathbf {x}}}\) or for \({{\mathbf {e}}}_{{\mathbf {u}}}\) in place of \({{\mathbf {e}}}\). We estimate, using (4.10), by
where for the last step we used Young’s inequality with an arbitrary number \(\varrho > 0\), to be chosen later on independently of h. We will also use its time-integrated version:
Using (9.3) for \({{\mathbf {e}}}= {{\mathbf {e}}}_{{\mathbf {w}}}\) with \(\varrho = 1\), the left-hand side of (9.2) simplifies to
with additional terms on the right-hand side which already appeared before.
In order to estimate the remaining time derivatives on the left-hand side of (9.2) we integrate both sides form 0 to t and use the norm equivalence (4.16), recalling \({{\mathbf {K}}}= {{\mathbf {M}}}+ {{\mathbf {A}}}\) we obtain (after factoring out a constant and dividing through):
where for the four time-differentiated terms on the right-hand side (cf. (9.2)), we used, in order, (4.7), Lemma 4.2 (ii) twice, and Lemma 4.2 (i), in combination with the uniform \(W^{1,\infty }\) norm bounds (7.3) and (7.1), (7.4).
Using Young’s inequality and absorptions to the left-hand side yields (after factoring out a constant and dividing through)
In order to apply Gronwall’s inequality we need to estimate the last two terms of (9.6): The first of which is bounded by (9.1). The second is estimated using (9.4) for \({{\mathbf {e}}}= {{\mathbf {e}}}_{{\mathbf {u}}}\) with a factor \(\varrho > 0\) such that \(c_2 \varrho < c_1 / 2\), allowing an absorption to the left-hand side. This, and using (9.4) for \({{\mathbf {e}}}= {{\mathbf {e}}}_{{\mathbf {u}}}\) with a factor \(\varrho = 1\) now on the left-hand side, yields
Substituting (9.7) into the right-hand side of (7.14), and then summing up the resulting estimate with (9.7) with (9.1) (analogously as in [37, (C)]), and using the norm equivalence (4.5), and then finally using Gronwall’s inequality we obtain the stated stability estimate (7.17) for all \(0 \le t \le T^*\).
Finally, it remains to show that in fact \(T^*= T\) for h sufficiently small, i.e. that Lemma 7.2 holds for thw whole time interval [0, T]. Upon noting that by the assumed defect bounds (7.15) and (7.16), combined with the obtained stability bound (7.17), yields
and therefore by an inverse inequality [14, Theorem 4.5.11] we obtain, for \(t \in [0,T^*]\),
for sufficiently small h. This means that the bounds (7.3), (and hence all other estimates in Lemma 7.2), can be extended beyond \(T^*\), contradicting the maximality of \(T^*\), unless \(T^*= T\) already. Therefore we have show the stability bound (7.17) over the whole time interval [0, T]. \(\square \)
10 Numerical experiments
We performed numerical simulations and experiments for the flow (1.1) formulated as Problem 1.1 in which:
-
The rate of convergence in an example involving a radially symmetric exact solution is studied in order to illustrate the theoretical results of Theorem 7.1.
-
Flows decreasing the energy \({{\mathcal {E}}}(\varGamma ,u) = \int _\varGamma G(u)\) and their qualitative properties, see Sect. 2.2, are investigated in several simulations.
-
Numerical experiments exhibiting loss of convexity and self-intersection are presented. This is in contrast to mean curvature flow which preserves convexity, and for which self-intersections are not possible.
-
The preservation under discretisation of mass conservation and the existence of a weak maximum principle together with the energy decay, and mean convexity properties enjoyed by the underlying PDE system are studied.
The numerical experiments use quadratic evolving surface finite elements. Quadratures of sufficiently high order are employed to compute the finite element vectors and matrices so that the resulting quadrature error does not feature in the discussion of the accuracies of the schemes. Similarly, sufficiently high-order linearly implicit BDF time discretisations, see the next Sect. 10.1, with small time steps were employed for the solution of the time dependent ODE system. The parametrisation of the quadratic elements was inspired by [7]. The initial meshes were all generated using DistMesh [46], without taking advantage of any symmetry of the surface.
10.1 Linearly implicit backward difference full discretisation
For the time discretisation of the system of ordinary differential equations (6.3) we use a q-step linearly implicit backward difference formula (BDF method). For a step size \(\tau >0\), and with \(t_n = n \tau \le T\), we determine the approximations to all variables \({{\mathbf {x}}}^n\) to \({{\mathbf {x}}}(t_n)\), \({{\mathbf {v}}}^n\) to \({{\mathbf {v}}}(t_n)\), \({{\mathbf {w}}}^n = ({{\mathbf {n}}}^n,{{\mathbf {V}}}^n)^T\) to \({{\mathbf {w}}}(t_n) = ({{\mathbf {n}}}(t_n),{{\mathbf {V}}}(t_n))^T\), and \({{\mathbf {u}}}^n\) to \({{\mathbf {u}}}(t_n)\) by the fully discrete system of linear equations, for \(n \ge q\),
where we denote the discretised time derivatives
while by \({\widetilde{{{\mathbf {x}}}}}^n\) we denote the extrapolated values
Both notations are used for all other variables, in particular note the BDF time derivative of the the product \(({{\mathbf {M}}}({\widetilde{{{\mathbf {x}}}}}^n) {{\mathbf {u}}}^n)^{\varvec{\cdot }}\).
The starting values \({{\mathbf {x}}}^i\) and \({{\mathbf {u}}}^i\) (\(i=0,\dotsc ,q-1\)) are assumed to be given. Furthermore, we set \({\widetilde{{{\mathbf {x}}}}}^i = {{\mathbf {x}}}^i\) and \({\widetilde{{{\mathbf {u}}}}}^i = {{\mathbf {u}}}^i\) (\(i=0,\dotsc ,q-1\)). The initial values can be precomputed using either a lower order method with smaller step sizes or an implicit Runge–Kutta method.
The method is determined by its coefficients, given by
The classical BDF method is known to be zero-stable for \(q\le 6\) and to have order q; see [35, Chapter V]. This order is retained, for \(q \le 5\) see [44], also by the linearly implicit variant using the above coefficients \(\gamma _j\); cf. [5, 6]. In [3], the multiplier techniques of [45] have been recently extended, via a new approach, to the six-step BDF method.
We again point out that the fully discrete system (10.1) is extremely similar to the fully discrete system for the mean curvature flow [37, Eqs. (5.1)–(5.4)], and Theorem 6.1 in [37] proves optimal-order error bounds for the combined ESFEM–BDF full discretisation of the mean curvature flow system, for finite elements of polynomial degree \(k \ge 2\) and BDF methods of order \(2 \le q \le 5\).
We note that in each time step the method decouples and hence only requires solving a few linear systems (with symmetric positive definite matrices): first (10.1c) is solved with \(\delta _0 {{\mathbf {M}}}({\widetilde{{{\mathbf {x}}}}}^n) + \tau {{\mathbf {A}}}(\widetilde{{\mathbf {x}}}^n,{\widetilde{{{\mathbf {u}}}}}^n)\), then, since \({\dot{{{\mathbf {u}}}}}^n\) is already known for \({{\mathbf {f}}}\), (10.1b) is solved with \(\delta _0 {{\mathbf {M}}}({\widetilde{{{\mathbf {x}}}}}^n,{\widetilde{{{\mathbf {u}}}}}^n,{\widetilde{{{\mathbf {w}}}}}^n) + \tau {{\mathbf {A}}}({\widetilde{{{\mathbf {x}}}}}^n)\), and finally (10.1d) with (10.1a) is computed.
10.2 Convergence experiment
We will construct a radially symmetric solution to Problem 1.1 of the form \(u(\cdot ,t) \equiv u(t)\) on \(\varGamma [X(\cdot ,t)]\), where the surface \(\varGamma [X(\cdot ,t)] \subset {\mathbb {R}}^{m+1}\) is a sphere of radius \(R(t)\) with \(R(0) = R_0\). We choose \({\mathcal {D}}(u) \equiv 1\) and \(F(u,H)=-g(u) H\), so that \(K(u,V)= - V / g(u)\). The positive function g here will be chosen later on.
Since the flow preserves the radial symmetry of \(\varGamma [X]\), it remains a sphere of radius \(R(t)\), and inspection of the diffusion equation yields that \(u(\cdot ,t)\) remains spatially constant. For more details on this example we refer to [15, Sect. 3.4].
The velocity and mean curvature of the evolving sphere in \(\mathbb R^m\) of radius R(t) are \(V = \dot{R}\), and \(H = m/R(t)\) so that
yields
On the other hand, by mass conservation, see Sect. 2.2, we have
and together with (10.4) this yields
We set, with \(\alpha \in {\mathbb {R}}\) to be chosen later on,
which corresponds to the energy density
recalling that \(g(r) = G(r) - G'(r)r\) for the gradient flow (1.3). With these coefficient functions this problem satisfies our assumptions from Sect. 2.
By choosing (10.7) in the ODE (10.6), we obtain
where the constant b collects all time-independent factors. Note that for \(\alpha = 0\) we recover the classical mean curvature flow (\(b = m\)). The solution of the above separable ODE, with initial value \(R(0) = R_0\), is
on the time interval \([0,T_{\max }]\). In the m-dimensional case, if \(2 - \alpha m \ge 0\) the sphere \(\varGamma [X]\) shrinks to a point in finite time, \(T_{\max } = R_0^{2 - \alpha m} \, (b (2 - \alpha m))^{-1}\), while if \(2 - \alpha m < 0\) a solution exists for all times.
For the convergence experiment we chose the following initial values and parameters: The initial surface \(\varGamma ^0\) is a two-dimensional sphere of radius \(R_0 = 1\), the initial concentration is \(u^0(x,0) = 1\) for all \(x \in \varGamma ^0\). The parameter \(\alpha \) in (10.8)–(10.7) is chosen to be \(\alpha = 2\). That is we are in a situation where a solution exists on \([0,\infty )\). The exact solutions for \(\varGamma [X]\) and \(u(\cdot ,t)\) are given in (10.10) and (10.5), respectively. We started the algorithms from the nodal interpolations of the exact initial values \(\varGamma [X(\cdot ,t_i)]\), \(\nu (\cdot ,t_i)\), \(V(\cdot ,t_i) = -g(u(\cdot ,t_i)) H(\cdot ,t_i)\), and \(u(\cdot ,t_i)\), for \(i=0,\dotsc ,q-1\). In order to illustrate the convergence results of Theorem 7.1, we have computed the errors between the numerical solution (10.1) and (the nodal interpolation of the) exact solutions of Problem 1.1 for the above radially symmetric geometric solution in dimension \(m=2\). The solutions are plotted in Fig. 2.
In Figs. 3 and 4 we report the errors between the numerical solution and the interpolation of the exact solution until the final time \(T=1\), for a sequence of meshes (see plots) and for a sequence of time steps \(\tau _{k+1} = \tau _k / 2\). The logarithmic plots report on the \(L^\infty (H^1)\) norm of the errors against the mesh width h in Fig. 3, and against the time step size \(\tau \) in Fig. 4. The lines marked with different symbols and different colours correspond to different time step sizes and to different mesh refinements in Figs. 3 and 4, respectively.
In Fig. 3 we can observe two regions: a region where the spatial discretisation error dominates, matching the \(O(h^2)\) order of convergence of Theorem 7.1 (see the reference lines), and a region, with small mesh size, where the temporal discretisation error dominates (the error curves flatten out). For Fig. 4, the same description applies, but with reversed roles. Convergence of fully discrete methods is not shown, but \(O(\tau ^2)\) is expected for the 2-step BDF method, cf. [37].
The convergence in time and in space as shown by Figs. 3 and 4, respectively, is in agreement with the theoretical convergence results (note the reference lines).
Spatial convergence of the BDF2 / quadratic ESFEM discretisation for Problem 1.1 with \(T = 1\) and \(\alpha = 2\)
Temporal convergence of the BDF2 / quadratic ESFEM discretisation for Problem 1.1 with \(T = 1\) and \(\alpha = 2\)
10.3 Convexity/non-convexity along the flow
It is well known that for mean curvature flow, [34], a strictly convex surface shrink to a round point in finite time, and stays strictly convex throughout. For the flow (1.1) this is not true. In Figs. 5 and 6, \(F(u,H) = g(u)H\) and \({\mathcal {D}}(u) \equiv 1\) where \(g(u) = G(u) - G'(u)u = 3 u^{-2}\), which corresponds to the energy density \(G(u) = u^{-2}\). This problem satisfies our assumptions from Sect. 2. We respectively report on the evolution of an elongated ellipsoid as initial surface with an initial value \(u^0\) (concentrated along the tips with \(\text {values} \approx 5\) decreasing in the middle to 0.5), and on the mass conservation, weak maximum principle, energy decay, and the mean convexity along the flow. The plots of Fig. 5 show the flow until final time \(T=7.5\), where a pinch singularity occurs. The simulations used \(\text {dof} =4002\) for the number of degrees of freedom and a time step \(\tau = 0.01\), (the colorbar applies to all plots). We point out the crucial observation that the approaching singularity is detectable on the mass conservation plot. Note that in Remark 5.1 only the mass conservation of the spatial semi-discretisation was studied, but not that of the fully discrete numerical method (10.1). For Fig. 6 (and the other experiments as well) the mass and energy were computed by quadratures.
Unlike for mean curvature flow, convex surfaces do not remain convex along the flow (1.1) with \(F(u,H) = g(u)H = 3 u^{-2} H\) (the colorbar applies to all plots)
10.4 Slow diffusion through a tight neck
The diffusion speed on surfaces is greatly influenced by the geometry, see, e.g., the insightful paper of Ecker [28]. To report on such an experiment for the flow (1.1a)–(1.1b), as an initial surface we take a dumbbell (given by [32, Eq. (2.3)]) and initial data \(u^0\) which is 0.8 from the neck above and smoothly transitioning to \(10^{-4}\) for the neck and below. The experiment takes \({\mathcal {D}}(u) \equiv 1\) and \(F(u,H) = uH\). In view of these choices, and the initial data \(u^0\), the bottom part barely moves, while the top part quickly shrinks before the concentration could pass through the neck. We note that for pure mean curvature flow of this initial surface a pinch-off singularity would occur in finite time, cf. [37, Fig. 4] which uses the exact same initial surface \(\varGamma ^0\).
The experiment uses a mesh with \(\text {dof} =10522\) and a time step size \(\tau = 0.001\). In Fig. 7 we observe that, since the diffusion speed at the neck is rather slow, the concentration \(u_h\) cannot equidistribute before the top part is vanishing. A pinch-off does not occur, contrary to standard mean curvature flow, see [37, Sect. 13.2] (using the same initial surface). Similarly as before, Fig. 8 reports on the mass conservation, weak maximum principle, and the mean convexity along the flow, we note however that the initial surface is not mean convex: \(\min \{H(\cdot ,0)\} \approx -1.72 \cdot 10^{-12}\). Note the axis-limits in Fig. 8.
The diffusion speed is slow at a tight neck, and hence the large concentration differences cannot equilibrate before the top part shrinks along the flow (1.1) with \(F(u,H) = uH\) and \({\mathcal {D}}(u) \equiv 1\)
Snapshots (cross section at the \(x = 0\) plane) of a self-intersecting evolution (1.1) with \(F(u,H) = g(u) H = 5u^{-4} H\) and \({\mathcal {D}}(u) \equiv 1\)
Snapshots of the surface \(\varGamma _h[{{\mathbf {x}}}]\) and the concentration \(u_h\) (bottom view of the x–y-projection) of a self-intersecting evolution (1.1) with \(F(u,H) = g(u) H = 5u^{-4} H\) and \({\mathcal {D}}(u) \equiv 1\)
10.5 A self-intersecting flow
The flow (1.1) may describe surface evolutions where \(\varGamma [X]\) is self intersecting, i.e. \(X(\cdot ,t) :\varGamma ^0 \rightarrow {\mathbb {R}}^3\) is not a parametrisation, but an immersion, see the similar construction in [15, Figs. 5.3–5.5]. We consider the flow (1.1) with \(F(u,H) = g(u)H\) and \({\mathcal {D}}(u) \equiv 1\) where \(g(u) = G(u) - G'(u)u = 5 u^{-4}\), which corresponds to the energy density \(G(u) = u^{-4}\). This problem satisfies our assumptions from Sect. 2.
For a cup shaped surfaceFootnote 1 (with \(\text {dof} =4002\)) and a suitably chosen initial value self-intersections are possible. The initial datum is chosen such that \(u^0\) is constant 10 over the whole surface \(\varGamma ^0\), except on the outer-bottom where it is gradually decreased to a smaller \(\text {value} \approx 1\) as shown in the leftmost plot in Fig. 10. In Figs. 9 and 10 we present the numerical solution obtained by the 2-step BDF method with \(\tau = 10^{-3}\). The self-intersection is clearly observable on both figures, e.g., note the bright patch in Fig. 10 after the self intersection. Of course the self-intersection does not influence the mass conservation, weak maximum principle, and energy decay, see Fig. 11. (The initial surface is clearly not convex.)
Notes
Generated in Blender: blender.org.
References
Abels, H., Bürger, F., Garcke, H.: Qualitative properties for a system coupling scaled mean curvature flow and diffusion. arXiv:2205.02493, (2022)
Abels, H., Bürger, F., Garcke, H.: Short time existence for coupling of scaled mean curvature flow and diffusion. arXiv:2204.07626, (2022)
Akrivis, G., Chen, M., Yu, F., Zhou, Z.: The energy technique for the six-step BDF method. SIAM J. Math. Anal. 59, 2449–2472 (2021)
Alphonse, A., Elliott, C.M., Stinner, B.: An abstract framework for parabolic PDEs on evolving spaces. Port. Math. 72(1), 1–46 (2015)
Akrivis, G., Lubich, C.: Fully implicit, linearly implicit and implicit-explicit backward difference formulae for quasi-linear parabolic equations. Numer. Math. 131(4), 713–735 (2015)
Akrivis, G., Li, B., Lubich, C.: Combining maximal regularity and energy estimates for time discretizations of quasilinear parabolic equations. Math. Comp. 86(306), 1527–1552 (2017)
Bartels, S., Carstensen, C., Hecht, A.: P2Q2Iso2D=2D isoparametric FEM in Matlab. J. Comput. Appl. Math. 192(2), 219–250 (2006)
Barrett, J.W., Deckelnick, K., Styles, V.: Numerical analysis for a system coupling curve evolution to reaction diffusion on the curve. SIAM J. Numer. Anal. 55(2), 1080–1100 (2017)
Barreira, R., Elliott, C.M., Madzvamuse, A.: The surface finite element method for pattern formation on evolving biological surfaces. J. Math. Biol. 63(6), 1095–1119 (2011)
Barrett, J.W., Garcke, H., Nürnberg, R.: On the parametric finite element approximation of evolving hypersurfaces in \({\mathbb{R}}^3\). J. Comput. Phys. 227(9), 4281–4307 (2008)
Barrett, J.W., Garcke, H., Nürnberg, R.: Handb. Numer. Anal. In: Bonito, Andrea, Nochetto, Ricardo H. (eds.) Parametric finite element approximations of curvature driven interface evolutions, vol. 21, pp. 275–423. Elsevier, Amsterdam (2020)
Binz, T., Kovács, B.: A convergent finite element algorithm for generalized mean curvature flows of closed surfaces. IMA J. Numer. Anal. (2021). https://doi.org/10.1093/imanum/drab043
Binz, T., Kovács, B.: A convergent finite element algorithm for mean curvature flow in higher codimension. arXiv:2107.10577, (2021)
Brenner, S.C., Scott, R.: The mathematical theory of finite element methods. Texts in Applied Mathematics, vol. 15. Springer, New York (2008)
Bürger, F.: Interaction of mean curvature flow and diffusion. PhD thesis, University of Regensburg, Regensburg, Germany, https://doi.org/10.5283/epub.51215 (2021)
Chaplain, M.A.J., Ganesh, M., Graham, I.G.: Spatio-temporal pattern formation on spherical surfaces: numerical simulation and application to solid tumour growth. J. Math. Biol. 42(5), 387–423 (2001)
Deckelnick, K., Dziuk, G., Elliott, C.M.: Computation of geometric partial differential equations and mean curvature flow. Acta Numer 14, 139–232 (2005)
Dziuk, G., Elliott, C.M.: Finite elements on evolving surfaces. IMA J. Numer. Anal. 27(2), 262–292 (2007)
Dziuk, G., Elliott, C.M.: Finite element methods for surface PDEs. Acta Numer 22, 289–396 (2013)
Dziuk, G., Elliott, C.M.: \(L^2\)-estimates for the evolving surface finite element method. Math. Comp. 82(281), 1–24 (2013)
Demlow, A.: Higher-order finite element methods and pointwise error estimates for elliptic problems on surfaces. SIAM J. Numer. Anal. 47(2), 805–807 (2009)
Dziuk, G., Kröner, D., Müller, T.: Scalar conservation laws on moving hypersurfaces. Interfaces Free Bound. 15(2), 203–236 (2013)
Dziuk, G., Lubich, C., Mansour, D.E.: Runge-Kutta time discretization of parabolic differential equations on evolving surfaces. IMA J. Numer. Anal. 32(2), 394–416 (2012)
Deckelnick, K., Styles, V.: Finite element error analysis for a system coupling surface evolution to diffusion on the surface. Interfaces Free Bound. 24, 63–93 (2022)
Dziuk, G.: Finite elements for the Beltrami operator on arbitrary surfaces. Partial differential equations and calculus of variations, Lecture Notes in Math., 1357, Springer, Berlin, pages 142–155, (1988)
Dziuk, G.: An algorithm for evolutionary surfaces. Numer. Math. 58(1), 603–611 (1990)
Ecker, K.: Regularity Theory for Mean Curvature Flow. Progress in Nonlinear Differential Equations and their Applications, vol. 57. Birkhäuser Boston, Boston, MA (2004)
Ecker, K.: Heat equations in geometry and topology. Jahresber. Deutsch. Math.-Verein. 110(3), 117–141 (2008)
Elliott, C.M., Fritz, H.: On approximations of the curve shortening flow and of the mean curvature flow based on the DeTurck trick. IMA J. Numer. Anal. 37(2), 543–603 (2017)
Eyles, J., King, J.R., Styles, V.: A tractable mathematical model for tissue growth. Interfaces Free Bound. 21(4), 463–493 (2019)
Elliott, C.M., Ranner, T.: A unified theory for continuous-in-time evolving finite element space approximations to partial differential equations in evolving domains. IMA J. Numer. Anal. 41, 1696–1845 (2021)
Elliott, C.M., Styles, V.: An ALE ESFEM for solving PDEs on evolving surfaces. Milan J. Math. 80(2), 469–501 (2012)
Huisken, G., Polden, A.: Geometric evolution equations for hypersurfaces. In Calculus of variations and geometric evolution problems (Cetraro, 1996), volume 1713 of Lecture Notes in Math., pages 45–84. Springer, Berlin (1999)
Huisken, G.: Flow by mean curvature of convex surfaces into spheres. J. Differential Geometry 20(1), 237–266 (1984)
Hairer, E., Wanner, G.: Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems., 2nd edn. Springer, Berlin (1996)
Kovács, B., Li, B.: Maximal regularity of backward difference time discretization for evolving surface PDEs and its application to nonlinear problems. arXiv:2106.07951, (2021)
Kovács, B., Li, B., Lubich, C.: A convergent evolving finite element algorithm for mean curvature flow of closed surfaces. Numer. Math. 143, 797–853 (2019)
Kovács, B., Li, B., Lubich, C.: A convergent algorithm for forced mean curvature flow driven by diffusion on the surfaces. Interfaces Free Bound. 22(4), 443–464 (2020)
Kovács, B., Li, B., Lubich, C.: A convergent evolving finite element algorithm for Willmore flow of closed surfaces. Numer. Math. 149(4), 595–643 (2021)
Kovács, B., Li, B., Lubich, C., Power Guerra, C.A.: Convergence of finite elements on an evolving surface driven by diffusion on the surface. Numer. Math. 137(3), 643–689 (2017)
Kovács, B.: High-order evolving surface finite element method for parabolic problems on evolving surfaces. IMA J. Numer. Anal. 38(1), 430–459 (2018)
Kovács, B., Power Guerra, C.A.: Error analysis for full discretizations of quasilinear parabolic problems on evolving surfaces. NMPDE 32(4), 1200–1231 (2016)
Li, B.: Convergence of Dziuk’s semidiscrete finite element method for mean curvature flow of closed surfaces with high-order finite elements. SIAM J. Numer. Anal. 59(3), 1592–1617 (2021)
Lubich, C., Mansour, D.E., Venkataraman, C.: Backward difference time discretization of parabolic differential equations on evolving surfaces. IMA J. Numer. Anal. 33(4), 1365–1385 (2013)
Nevanlinna, O., Odeh, F.: Multiplier techniques for linear multistep methods. Numer. Funct. Anal. Optim. 3(4), 377–423 (1981)
Persson, P.-O., Strang, G.: A simple mesh generator in MATLAB. SIAM Rev. 46(2), 329–345 (2004)
Pozzi, P., Stinner, B.: Curve shortening flow coupled to lateral diffusion. Numer. Math. 135(4), 1171–1205 (2017)
Pozzi, P., Stinner, B.: Elastic flow interacting with a lateral diffusion process: the one-dimensional graph case. IMA J. Numer. Anal. 39(1), 201–234 (2019)
Styles, V., Van Yperen, J.: Numerical Analysis for a System Coupling Curve Evolution Attached Orthogonally to a Fixed Boundary, to a Reaction-diffusion Equation on the Curve. Num. Meth, PDE (2021)
Walker, S.W.: The Shape of Things: A Practical Guide to Differential Geometry and the Shape Derivative. SIAM, Philadelphia (2015)
Acknowledgements
We thank Stefan Schmidt for his Blender magic regarding the initial cup surface. The work of Harald Garcke and Balázs Kovács is supported by the DFG Graduiertenkolleg 2339 IntComSin – Project-ID 321821685. The work of Balázs Kovács is funded by the Heisenberg Programme of the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 446431602.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Elliott, C.M., Garcke, H. & Kovács, B. Numerical analysis for the interaction of mean curvature flow and diffusion on closed surfaces. Numer. Math. 151, 873–925 (2022). https://doi.org/10.1007/s00211-022-01301-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-022-01301-3