Abstract
Stochastic Galerkin finite element methods (SGFEMs) are commonly used to approximate solutions to PDEs with random inputs. However, the study of a posteriori error estimation strategies to drive adaptive enrichment of the associated tensor product spaces is still under development. In this work, we revisit an a posteriori error estimator introduced in Bespalov and Silvester (SIAM J Sci Comput 38(4):A2118–A2140, 2016) for SGFEM approximations of the parametric reformulation of the stochastic diffusion problem. A key issue is that the bound relating the true error to the estimated error involves a CBS (Cauchy–Buniakowskii–Schwarz) constant. If the approximation spaces associated with the parameter domain are orthogonal in a weighted \(L^2\) sense, then this CBS constant only depends on a pair of finite element spaces \(H_{1}, H_{2}\) associated with the spatial domain and their compatibility with respect to an inner product associated with a parameter-free problem. For fixed choices of \(H_{1}\), we investigate non-standard choices of \(H_{2}\) and the associated CBS constants, with the aim of designing efficient error estimators with effectivity indices close to one. When \(H_1\) and \(H_2\) satisfy certain conditions, we also prove new theoretical estimates for the CBS constant using linear algebra arguments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The motivation for this work is the design of efficient a posteriori error estimators for adaptive Galerkin finite element approximation of solutions to partial differential equations (PDEs). In particular, we are interested in PDEs with random inputs and so-called stochastic Galerkin finite element methods (SGFEMs) (see [4, 5, 14, 22, 24, 31]). When the inputs are represented by a finite, or countably infinite number of random variables \(\xi _{m}: \varOmega \rightarrow \mathbb {R}\), \(m=1,2,\ldots ,\) where \(\varOmega \) is a sample space, it is conventional to reformulate the stochastic problem of interest as a high-dimensional deterministic one, whose solution depends on a set of parameters \(y_{m}=\xi _{m}(\omega )\). Unlike sampling methods such as Monte Carlo, in the SGFEM approach, an approximation is sought in a tensor product space of the form \(H_1 \otimes P\) where \(H_1\) is an appropriate finite element space associated with the spatial domain and P is a set of polynomials associated with the parameter domain. When the number of active parameters is high, the dimension of \(H_1 \otimes P\) for standard choices of \(H_1\) and P can become unwieldy. To remedy this, we can either work with standard approximation spaces and deal with the resulting very large discrete systems by using smart linear algebra techniques (see [20, 21, 25, 26, 32, 33]), or we can use an adaptive approach, starting in a low-dimensional space \(H_1^{0} \otimes P^{0}\), and using a posteriori error estimators to decide whether it is necessary to enrich \(H_1^{0}\) or \(P^{0}\), or both. This allows us to build up a tailored sequence of approximation spaces \(H_1^{\ell } \otimes P^{\ell }, \ell =0,1, \ldots \) incrementally, so that the dimension of the final space is balanced against an error tolerance for a quantity of interest.
We consider the steady-state stochastic diffusion problem. Let \(D\subset \mathbb {R}^{2,3}\) be a bounded spatial domain and let \(\mathbf {y}=[y_1,y_2,\dots ]\) be a vector-valued parameter which takes values in \(\varGamma = \prod _{m=1}^{\infty }\varGamma _m\) (the parameter domain). We want to approximate the function \(u:D\times \varGamma \rightarrow \mathbb {R}\) that satisfies
For simplicity, we assume that \(f=f(\mathbf {x})\) is independent of \(\mathbf {y}\), but the methodologies discussed herein can be extended to accommodate \(f = f(\mathbf {x},\mathbf {y})\). We also assume that the parameters are bounded, with \(y_{m} \in \varGamma _m = [-1,1]\). We denote by \(\pi (\mathbf {y})\) a product measure on \((\varGamma ,\mathcal {B}(\varGamma ))\), where \(\mathcal {B}(\varGamma )\) is the Borel \(\sigma \)-algebra on \(\varGamma \), so that \(\pi (\mathbf {y})=\prod _{m=1}^{\infty }\pi _m(y_m),\) where \(\pi _m(y_m)\) is a measure on \((\varGamma _m,\mathcal {B}(\varGamma _m))\). In addition,
which is true when \(y_m\) is the image of a mean zero random variable and \(\pi _m(y_m)\) is the associated probability measure.
Assumption 1
The coefficient \(a(\mathbf {x},\mathbf {y})\) admits the decomposition
with \(a_0(\mathbf {x}),a_m(\mathbf {x})\in L^{\infty }(D)\). Moreover, there exist real positive constants \(a_{\min }^0\) and \(a_{\max }^0\) such that
and \(||a_m||_{L^\infty (D)}\) converges sufficiently quickly to zero as \(m\rightarrow \infty \) so that
The parameter-free function \(a_0(\mathbf {x})\) typically represents the mean with each term \(a_m(\mathbf {x})y_m\) representing a perturbation away from the mean, while (5) helps ensure the well posedness of the weak formulation of (1a)–(1b).
Next, we recall the classical strengthened Cauchy–Buniakowskii–Schwarz (CBS) inequality (see [1, Theorem 5.4]), a key tool in many areas of numerical analysis.
Theorem 1
Let H be a Hilbert space equipped with inner product \((\cdot ,\cdot )\) and induced norm \(||\cdot ||\) and let U, V be a pair of finite-dimensional subspaces of H satisfying \(U\cap V=\{0\}\). Then, there exists a constant \(\gamma \in [0,1)\), depending only on U and V such that
The smallest constant \(\gamma \in [0,1)\) satisfying (6) is
and is known as the CBS constant. In particular, CBS constants appear in the analysis of hierarchical preconditioners (see [2, 3, 30]) and certain types of a posteriori error estimators for Galerkin finite element approximations to PDEs. See, for example, [1, 19, 27, 28].
The design of error estimators for SGFEMs for parameter-dependent PDEs is still under development. However, there have been a few recent works (see [8,9,10,11,12, 16,17,18, 29]) for the model problem (1a)–(1b). In [12] and [11], algorithms constructing so-called sparse SGFEM approximations are driven by a priori error analysis, where the error associated with each discretisation parameter is balanced against the total number of degrees of freedom. In [16] and [17] a general framework for an explicit residual-based error estimation strategy for SGFEMs is proposed, where the selection of hierarchical approximation spaces is driven by a Dörfler marking strategy [15] on both the spatial and parameter domains. In both works, overestimation up to a factor of 10 of the true error is reported. In [18] a similar approach is taken, where residuals are computed using an equilibrated fluxes strategy and overestimation up to a factor of 5 is reported.
We focus on the (implicit) approach taken in [8,9,10] which is based on solving local subproblems for the error over a ‘detail’ space. The bound for the effectivity index of the resulting error estimators depends on a CBS constant. In [8,9,10] no insight into which choices of detail space result in a sharp error bound (effectivity indices close to one) is given. In this paper we provide that analysis. Specifically, we provide detailed information about the CBS constant and derive theoretical bounds for it, for certain choices of SGFEM solution and detail spaces. Due to the way that the spaces associated with the parameter domain are chosen, the CBS constants needed to analyse the estimators in [8,9,10] depend only on a pair of finite element spaces on the spatial domain. Hence, our results are also applicable to the design of adaptive finite element schemes for deterministic PDEs. We investigate which choices of detail FEM space result in CBS constants close to zero, to help ensure a sharp error bound. In particular, due to cost restrictions imposed to avoid high-dimensional detail spaces, we investigate non-standard choices that aren’t typically considered in the deterministic setting. The error estimation strategy in [29] also relies on a CBS constant, but in a different setting. Enrichment of the finite element space is not considered.
1.1 Outline
In Sect. 2, for the benefit of readers who are not familiar with the area, we review classical results from [1, 6] concerning a posteriori error estimation for Galerkin approximation. In Sect. 3 we demonstrate how those results are applied to SGFEM approximations of (1a)–(1b), leading to a simplified analysis of the error estimator introduced in [10] and the associated error bound. In particular, we show how the bound depends on a CBS constant associated with two finite element spaces \(H_{1}\) and \(H_{2}\). In Sect. 4 we first remind the reader how to compute CBS constants numerically. We then study some (non-standard) pairs of \(H_{1}\) and \(H_{2}\) and compute the associated CBS constants. In Sect. 5 we demonstrate that if \(H_1\) is the space of piecewise bilinear (\(\mathbb {Q}_{1}\)) functions, theoretical estimates for the CBS constant can be obtained using a novel linear algebra approach for several choices of \(H_2\). Finally, in Sect. 6 we present numerical results demonstrating the quality of the aforementioned error estimator, and the vital importance of choosing the right detail spaces.
2 Classical a Posteriori Error Estimation
The following classical results from [1, 6], along with Theorem 1, form the foundations of our main investigation in Sects. 3, 4, 5, 6. Let V be a Hilbert space with norm \(||\cdot ||_V\) and let \(B:V\times V\rightarrow \mathbb {R}\) and \(F:V\rightarrow \mathbb {R}\) denote a bounded and coercive bilinear form and linear functional, respectively. Consider the problem:
We assume that \(B(\cdot ,\cdot )\) is an inner product on V with the ‘energy’ norm
and that (8) is uniquely solvable. We now seek a Galerkin approximation to \(u\in V\). Let X be an \(N_X\)–dimensional subspace of V. We then solve:
Computing the error \(e = u-u_X\in V\) is a non-trivial task. Our goal is to estimate the energy error \(||e||_B\). Clearly, e satisfies the problem:
where \(u_X\in X\) is the Galerkin approximation satisfying (9).
Now suppose we choose a second subspace \(W\subset V\) of dimension \(N_W\), where \(X \subset W\) (i.e., W is richer than X) and consider the following problem:
By letting \(e_W = u_{W} - u_X\) we see that
Note that (12) is simply a restatement of (10) over W. We deduce then that the function \(e_W\in W\) satisfying (12) estimates the true error \(e\in V\) satisfying (10). Whilst we do not compute \(u_W\), it is clear that the quality of that Galerkin approximation (and hence the choice of W) determines the quality of the estimator \(e_W\). To analyse this, we require the following assumption.
Assumption 2
Let the functions \(u,u_X\) and \(u_W\) satisfy (8), (9) and (11) respectively. There exists a constant \(\beta \in [0,1)\) (the saturation constant) such that
In many applications, Assumption 2 is reasonable (see [1, p. 88]). The relationship between \(||e||_B\) and \(||e_W||_B\) is summarised in the next result.
Theorem 2
(See [1, p. 89]) Let Assumption 2 hold and let \(e\in V\) and \(e_W\in W\) satisfy (10) and (12) respectively, then
where \(\beta \in [0,1)\) is the saturation constant satisfying (13).
The interpretation of (14) is as follows; \(||e_W||_B\) will never overestimate the true error \(||e||_B\), but could underestimate it by a factor of \((1-\beta ^2)^{-1/2}\).
Problem (12) leads to a linear system of \(N_W\) equations which may be too expensive to solve. This is the case for the problem considered in Sect. 3. Suppose then that \(B_0:V\times V\rightarrow \mathbb {R}\) is an inner product with induced norm \(||\cdot ||_{B_0} = B_0(\cdot ,\cdot )^{1/2}\), whose matrix representation on W is more convenient to work with. We may then consider the alternative problem:
The next result summarises the relationship between \(||e_W||_B\) and \(||e_0||_{B_0}\).
Theorem 3
(See [1, Theorem 5.3]) Let \(e_W\in W\) and \(e_0\in W\) satisfy (12) and (15) respectively and suppose that there exist \(\lambda ,\varLambda \in \mathbb {R}^+\) such that
(the norms are equivalent) then
Even after replacing \(B(\cdot , \cdot )\) with \(B_{0}(\cdot , \cdot )\), since \(W\supset X\), it may be more expensive to compute \(e_0\in W\) satisfying (15) than \(u_X\in X\) satisfying (9). To reduce the cost further, we insist that
where the ‘detail’ space \(Y\subset V\) has dimension \(N_Y\) and consider the lower-dimensional problem:
Does \(||e_Y||_{B_0}\) provide a good estimate for \(||e||_{B}\)? To answer this, we require Theorem 1. Since \(X\cap Y = \{0\}\), there exists a constant \(\gamma \in [0,1)\) such that
The estimates \(||e_Y||_{B_0}\) and \(||e_0||_{B_0}\) are then related by the following theorem.
Theorem 4
(See [1, Theorem 5.2]) Let \(e_0\in W\) and \(e_Y\in Y\) satisfy (15) and (19) respectively and suppose that (18) holds. Then
where \(\gamma \in [0,1)\) satisfies (20).
If X and Y are orthogonal with respect to the inner product \(B_0(\cdot ,\cdot )\) then \(\gamma = 0\) and \(||e_Y||_{B_0} = ||e_0||_{B_0}\). Consolidating Theorems 2–4 yields the final result.
Theorem 5
Let \(e\in V\) and \(e_Y\in Y\) satisfy (10) and (19) respectively, where (18) holds. If Assumption 2 holds, and there exist \(\lambda ,\varLambda \in \mathbb {R}^+\) such that (16) holds, then
where \(\gamma \in [0,1)\) satisfies (20) and \(\beta \in [0,1)\) satisfies (13).
In summary, the quality of the energy error estimate \(||e_Y||_{B_0}\) is determined by two constants \(\beta \) and \(\gamma \), which both depend on X and Y. Ideally, we want \(\sqrt{1-\beta ^2}\sqrt{1-\gamma ^2} \approx 1\). Given a fixed initial approximation space X, what is the best choice of detail space Y, from the point of view of obtaining the best possible error estimate? This is the essence of our investigation.
3 The Parametric Diffusion Problem
The variational formulation of (1a)–(1b) is:
where \(H_{0}^{1}(D)\) is the usual Hilbert space and \(L_{\pi }^2(\varGamma )\) is given by
V is equipped with the norm \(|| \cdot ||_V\), where \(||v||_V^2 = \int _{\varGamma }||v(\cdot ,\mathbf {y})||_{H_0^1(D)}^2\ d\pi (\mathbf {y})\) and the bilinear form \(B:V\times V\rightarrow \mathbb {R}\) and the linear functional \(F:V\rightarrow \mathbb {R}\) are given by
To ensure that (23) is well-posed, we make the following assumption.
Assumption 3
There exist real positive constants \(a_{\min }\) and \(a_{\max }\) such that
If Assumption 3 holds, the bilinear form \(B(\cdot ,\cdot )\) defined in (24) induces a norm \({||\cdot ||_B = B(\cdot ,\cdot )^{1/2}}\) (the energy norm). Note that due to (3), we have the decomposition
for all \(u,v\in V\), where the component bilinear forms are defined by
If (4) in Assumption 1 holds, then \(B_0(\cdot ,\cdot )\) in (27a) also induces a norm \(||\cdot ||_{B_0} = B_0(\cdot ,\cdot )^{1/2}\). Moreover, the following norm equivalence holds:
where \(0< \lambda< 1< \varLambda < \infty \) and
3.1 SGFEM Approximation
We now seek a Galerkin approximation to \(u\in V\) satisfying (23). As in Sect. 2, we denote by X an \(N_X\)–dimensional subspace of V. Here, we exploit the tensor product structure of V and choose \(X:=H_1\otimes P\), where \(H_1\subset H_0^1(D)\) and \(P\subset L^2_{\pi }(\varGamma )\). We then look for \(u_X\in X\) satisfying (9).
We choose \(H_{1}=\text {span}\{\phi _{i}(\mathbf {x})\}_{i=1}^n\) to be a space of finite element functions associated with a mesh on D and \(P=\text {span}\{\varphi _{i}(\mathbf {y})\}_{i=1}^s\) to be a space of global (multivariate) polynomials on \(\varGamma \), so that \(N_{X}=ns\). We choose the basis functions for P to be orthonormal with respect to \(\langle \cdot ,\cdot \rangle _{L_{\pi }^2(\varGamma )}\). To this end, we introduce the set of finitely supported multi-indices; \(J:=\{\mu = (\mu _1,\mu _2,\dots )\in \mathbb {N}_0^{\mathbb {N}};\ \#\ \text {supp}(\mu ) < \infty \}\), where \(\text {supp}(\mu ) :=\{m\in \mathbb {N};\ \mu _m\ne 0\}\). For a given multi-index \(\mu \in J\) we then construct
where the families of univariate polynomials \(\{\varphi _{\mu _{m}}(y_{m}),\ \mu _{m}=0,1,2 \ldots \},\) for \(m=1, \ldots , \infty ,\) are chosen to be orthonormal with respect to the inner product associated with \(\pi _m(y_m)\). We also assume that \(\varphi _{0}(y_{m})=1\) so that \(\varphi _\mu (\mathbf {y}) = \prod _{\mu _m\ne 0}\varphi _{\mu _m}(y_m)\) for any \(\mu \in J\). Clearly, choosing the subspace P is equivalent to choosing a set of multi-indices \(J_P\subset J\) with cardinality \(\text {card}(J_P)=s\).
To compute a Galerkin approximation \(u_{X} \in X\) satisfying (9), it is essential that the sum in (26) has a finite number of nonzero terms. It is not necessary to truncate the diffusion coefficient a priori. We need only assume that P contains polynomials in which a finite number of parameters \(y_{m}\) are ‘active’. If we assume that the first M parameters are active, then, provided (2) holds, \(B_m(u_{X},v) = 0\) for \(u_{X}, v \in X\) for all \(m >M\) (e.g., see [8]). In other words, the projection onto \(X=H_{1} \otimes P\) truncates the sum after M terms.
3.2 A Posteriori Error Estimation
Suppose we now choose a second SGFEM space \(W\subset V=H_{0}^{1}(D) \otimes L_{\pi }^{2}(\varGamma )\) such that \(W \supset X:=H_{1} \otimes P\) and solve (12) to obtain an estimator \(e_{W} \in W\) for the error \(e=u-u_{X}\). If Assumption 2 holds for the chosen spaces X and W, then (14) also holds, where \(||\cdot ||_B \) is the energy norm induced by the bilinear form defined in (24). In addition, due to the norm equivalence (28), the bound (17) also holds, where \(e_{0} \in W\) satisfies (15) and \(||\cdot ||_{B_0}\) is the norm induced by the bilinear form defined in (27a).
There are several possible ways to construct W. Following [10], we choose
with \(H_2 \subset H_0^1(D)\) and \(Q \subset L^2_{\pi }(\varGamma )\). Consequently \(Y_1\cap Y_2 = \{0\}\) for the spaces \(Y_1:= H_2\otimes P\) and \(Y_2 := H_1\otimes Q\). Let \(J_Q\) denote the set of finitely supported multi-indices which correspond to the subspace Q. If \(J_P\cap J_Q = \emptyset \), then we have \(P\cap Q = \{0\}\) as required. In this case, P and Q are mutually orthogonal with respect to \(\langle \cdot ,\cdot \rangle _{L_{\pi }^2(\varGamma )}\) since
for all \(\mu \in J_P\) and \(\nu \in J_Q\). Furthermore, due to the tensor product structure of \(Y_1\) and \(Y_2\) and the fact that \(P\cap Q=\{0\}\), it can be shown that
To see this, expand \(u\in Y_1\) and \(v\in Y_2\) in the chosen bases and use (32). Given Y, we can then compute the error estimate \(\eta := ||e_Y||_{B_0}\) by solving (19) and the bound (21) holds. Combining all these results yields the result of Theorem 5. For completeness, we restate this for our parametric diffusion problem.
Theorem 6
Let \(u\in V=H_{0}^{1}(D) \otimes L_{\pi }^{2}(\varGamma )\) satisfy the variational problem (8) associated with the parametric diffusion problem (1a)–(1b) and let \(u_X\in X:=H_{1}\otimes P\) satisfy (9). Choose \(H_2\), Q and Y as in (31). Let \(e_Y \in Y\) satisfy (19). If Assumptions 1–3 hold, then \(\eta := ||e_Y||_{B_0}\) satisfies
where \(\lambda \) and \(\varLambda \) are defined in (29), \(\gamma \in [0,1)\) satisfies (20), and \(\beta \in [0,1)\) satisfies (13).
When Y is chosen as in (31), problem (19) decouples. Since \(Y_1 \cap Y_2 = \{0\}\), \(e_Y = e_{Y_1} + e_{Y_2}\) for some \(e_{Y_1}\in Y_1\), \(e_{Y_2}\in Y_2\) and thus \(B_0(e_Y,v) = B_0(e_{Y_1}+e_{Y_2},v) = B_0(e_{Y_1},v) + B_0(e_{Y_2},v)\) for all \(v\in Y\). By choosing test functions \(v \in Y_{1}\) and \(v \in Y_{2}\) in (19) and considering the identity (33), we find that \(e_Y \in Y\) satisfying (19) can be determined by solving the lower-dimensional problems
Moreover, since \(B_{0}(e_{Y_{1}}, e_{Y_{2}})=0\), we have
This is precisely the estimator considered in [10]. In [10] however, (31) is rearranged as \(W = ((H_1 \oplus H_2)\otimes P) \oplus (H_2\otimes Q)\). The analysis in that work relies on the orthogonality of P and Q, and the decoupling of (15) into two smaller problems over \(((H_1 \oplus H_2)\otimes P)\) and \((H_2\otimes Q)\). A CBS constant is introduced into the analysis by splitting the former into \(H_1\otimes P\) and \(H_2\otimes P\). Our approach is subtly different. We introduce a CBS constant by splitting the augmented space W into X and Y, as would be done for the analogous deterministic problem (for which \(X = H_1\) and \(Y = H_2\)).
If (4) holds, then \(H_0^1(D)\) is a Hilbert space with respect to the inner product
and since \(H_1\cap H_2 = \{0\}\), by Theorem 1, there exists a \(\gamma \in [0,1)\) such that
In [8, Lemma 3.1], it is shown that the \(\gamma \) that features in (39) also satisfies
Now consider (20). For each \(v \in Y\), we have \(v = v_1+v_2\), with \(v_1\in Y_1\) and \(v_2\in Y_2\). Since P and Q are orthogonal with respect to \(\left<\cdot , \cdot \right>_{L_{\pi }^{2}}\), \(Y_{1}\) and \(Y_{2}\) are orthogonal with respect to \(B_{0}(\cdot , \cdot )\) and so \(B_0(u,v) = B_0(u,v_1)\) for all \(u \in X\) and \(v \in Y\). Hence, using \(||v_1||_{B_0}^2 = ||v||^2_{B_0} - ||v_2||^2_{B_0}\), we have \(|B_0(u,v)| \le \gamma ||u||_{B_0}||v_1||_{B_0} \le \gamma ||u||_{B_0}||v||_{B_0}\), for all \(u\in X,\) and \(v\in Y\), where \(\gamma \in [0,1)\) is the same constant satisfying (39). Consequently, \(\gamma \) in (34) can be determined by analyzing the spaces \(H_1\) and \(H_2\). P and Q do not play a role. They do, of course, affect the saturation constant \(\beta \), and this will be discussed in Sect. 6.
3.3 Estimated Error Reductions
The constant \(\gamma \) also plays an important role in adaptivity. Given \(u_X\in X\), how do we choose an enriched space \(X^*\supset X\) in which to compute a new approximation \(u^{*}\) which yields a reduced energy error? Consider the problems;
where \(W_1 := (H_1\oplus H_2)\otimes P\) and \(W_2 := H_1\otimes (P\oplus Q)\). Let \(e_{W_1} = u - u_{W_1}\) denote the error corresponding to the enhanced approximation \(u_{W_1}\in W_1\). Due to Galerkin orthogonality we find;
Hence, \(||u_{W_1} - u_X||_B\) characterises the energy error reduction that would be achieved by enriching only the subspace \(H_1\subset H_0^1(D)\). Similarly, \(||u_{W_2} - u_X||_B\) characterises the energy error reduction that would be achieved by enriching only the subspace \(P\subset L_{\pi }^2(\varGamma )\). Fortunately, the two components \(||e_{Y_1}||_{B_0}\) and \(||e_{Y_2}||_{B_0}\) of our error estimator provide estimates of these error reductions, see [8, Theorem 5.1].
Theorem 7
Let \(u_X\in X=H_{1} \otimes P\) be the Galerkin approximation satisfying (9) and let \(u_{W_1} \in W_{1}\) and \(u_{W_2} \in W_{2}\) satisfy (41) and (42). Then,
where \(e_{Y_1}\) and \(e_{Y_2}\) satisfy (35) and (36), respectively, \(\lambda \) and \(\varLambda \) are the constants in (28), and \(\gamma \in [0,1)\) is the constant satisfying (39).
Given \(H_{2}\) and Q, Theorem 7 allows us to assess whether enrichment of \(H_1\) (with functions in \(H_2\)) is more beneficial than enrichment of P (with functions in Q). We may choose \(X^* = W_1\) or \(X^* = W_2\). Our choice is determined by which space offers the greatest estimated error reduction per additional degree of freedom. Note that the bound (44) is independent of the saturation constant \(\beta \), and choosing \(H_2\) in (31) so that the constant \(\gamma \) in (39) is small tightens the bound (44). That is, if the CBS constant is small, we can have more confidence in our decisions when performing adaptivity. We now study this constant for various choices of \(H_1\) and \(H_2\).
4 Numerical Estimates of CBS Constants
The constant \(\gamma \in [0, 1)\) in (34) and (44), which is equivalent to the constant \(\gamma \in [0, 1)\) satisfying (39), is not unique. Given \(H_1\) and \(H_2\), we want to find the smallest such constant, the CBS constant. We now recall a standard result from [19] which leads to a numerical method for computing the CBS constant associated with (39).
Suppose first that \(M\in \mathbb {R}^{N\times N}\) is symmetric and positive definite with \(N:=m+n\) for \(m,n\in \mathbb {N}\). Then \((\mathbb {R}^N,(\cdot ,\cdot )_{M})\) is a Hilbert space with respect to the inner product \((\mathbf {u},\mathbf {v})_{M}:=\mathbf {u}^\top M\mathbf {v}\). Now consider \(U,V\subset \mathbb {R}^N\) given by
which satisfies \(U\cap V = \{\mathbf{0}\}\). When M has a particular block structure, Theorem 1 along with U and V in (46), leads to the following result (see [19] for a proof).
Corollary 1
Let \(M\in \mathbb {R}^{N\times N}\) be symmetric and positive definite with
where \(N=m+n,\) \(B\in \mathbb {R}^{m\times m}\) and \(A\in \mathbb {R}^{n\times n}\). There exists a constant \(\gamma \in [0,1)\) such that
Furthermore, the smallest such constant, \(\gamma _{\min }\in [0,1)\) (the CBS constant), satisfying (48) is the square root of the largest eigenvalue \(\theta _{\max }\) of the generalised eigenvalue problem
We now demonstrate that the CBS constant associated with (39) for various choices of \(H_1\) and \(H_2\) can be computed by solving an eigenvalue problem of the form (49). Recall that \(H_1, H_2\subset H_{0}^{1}(D)\) with \(H_1\cap H_2 = \{0\}\). For now, we assume \(a_0(\mathbf {x}) = 1\). Note that due to the symmetry of (38) we may compute the CBS constant associated with the equivalent result; there exists a \(\gamma \in [0,1)\) such that
Given \(H_1 := \text {span}\{\phi _i(\mathbf {x})\}_{i=1}^n\) and \(H_2 := \text {span}\{\psi _i(\mathbf {x})\}_{i=1}^m\), we can define the augmented subspace
of dimension \(N=m+n\). We have \(H = \text {span}\{\varPhi _i(\mathbf {x})\}_{i=1}^N\), where \(\varPhi _i = \psi _i,\) for \(i=1,2,\dots ,m\), and \(\varPhi _{m+i} = \phi _i\), for \(i=1,2,\dots ,n.\) Then, for all \(u\in H_2\) and \(v\in H_1\), \(\langle u,v\rangle = \mathbf {u}^{\top }M\mathbf {v}\) for some \(\mathbf {u}\in U\) and \(\mathbf {v}\in V\) in (46).
The matrix \(M\in \mathbb {R}^{N\times N}\) is symmetric and positive definite and has the structure (47) with \([A]_{ij} = \langle \phi _{i}, \phi _{j}\rangle \), for \(i,j=1,\ldots ,n\), \([B]_{ij} = \langle \psi _{i}, \psi _{j}\rangle \) for \(i,j=1,\ldots , m\) and \([C]_{ij} = \langle \phi _{i}, \psi _{j}\rangle \) for \(i=1,\ldots , n\) and \(j=1,\ldots , m\). By Corollary 1, there exists a constant \(\gamma \in [0,1)\) such that (48) holds, which is equivalent to (50). Therefore, the CBS constant \(\gamma _{\min }\) satisfying (50) can be computed numerically by solving the eigenvalue problem (49).
Given a fixed space \(H_1\) associated with a uniform mesh \(\mathcal {T}_h\) on the spatial domain D, we construct \(H_2\) element-wise. That is, we insist that \(H_2\) admits the decomposition
where \(\Box _k\) denotes an element in \(\mathcal {T}_h\). We choose the functions \(\psi _{i}^{k}\) to be bubble functions so that \(H_{k,2}\) contains functions which only have non-zero support on \(\square _{k}\). The linear system associated with the estimator \(e_{Y_{1}}\) satisfying (35) then decouples. Since \(e_{Y_{1}} \in Y_{1}:=H_2\otimes P\), on each \(\Box _{k}\), we have to solve a problem of size \(m_{k} \times \text {dim}(P)\). Since \(\text {dim}(P)\) may be large, to keep costs reasonable, we must restrict the dimension of \(H_{k,2}\). Note that the necessity to restrict the dimension of \(H_2\) is not as prevalent in the deterministic PDE setting, where each local problem for the analogous error estimate is of dimension \(m_k\), not \(m_{k} \times \text {dim}(P)\). The goal is to find the best space (the one leading to the tightest error bound), of a fixed small dimension. Below, we fix \(H_{1}\) and consider various choices of \(H_{2}\) of the same dimension. We vary the mesh size h, and estimate the CBS constant by solving the eigenvalue problem (49).
Example 1
Let \(D=[-1,1]^2\) and let \(\mathcal {T}_{h}\) denote a uniform mesh of square elements, with edge length h. Now let \(H_1\) be the space of continuous functions that are piecewise bilinear on \(\mathcal {T}_h\) (denoted \(H_{1}=\mathbb {Q}_1(h)\)). On each \(\square _{k}\) we construct a local space \(H_{k,2}\) of dimension \(m_{k} \le 5\), by defining bubble functions at the edge midpoints and the element centroid (the \(\mathbb {Q}_{1}\) nodes that would be introduced by a uniform mesh refinement). We consider the following options. The name given to the resulting space \(H_{2}\) is shown in brackets.
-
1.
Biquadratic bubble functions (\(\mathbb {Q}_{2}(h)\)) Consider the standard set of nine biquadratic (\(\mathbb {Q}_{2}\)) element basis functions and keep only those associated with the five selected nodes.
-
2.
Biquartic bubble functions (\(\mathbb {Q}_{4}(h)\)) Consider the standard set of twenty-five biquartic (\(\mathbb {Q}_{4}\)) element basis functions and keep only the desired five.
-
3.
Piecewise bilinear bubble functions (\(\mathbb {Q}_{1}(h/2)\)) Subdivide each element into four smaller ones of size h / 2, and concatenate the standard \(\mathbb {Q}_{1}\) basis functions associated with each new element at the five chosen nodes.
-
4.
Piecewise biquadratic bubble functions (\(\mathbb {Q}_{2}(h/2)\)) This is the same as option 3 but with \(\mathbb {Q}_{2}\) basis functions.
Figure 1 displays an arbitrary internal, edge, and corner element. In Table 1 we record \(\gamma _{\min }^2\) for each choice of \(H_2\) for varying h. In [8], the authors choose \(H_{2}=\mathbb {Q}_{1}(h/2)\) to define the error estimator \(\eta =\Vert e_{Y} \Vert _{B_{0}}\) described in Sect. 3 when \(u_{X}\) is computed with \(H_{1}=\mathbb {Q}_{1}(h)\). Hence, when \(a_{0}=1\), the associated CBS constant is \(\gamma _{\min }\le \sqrt{0.375}= \sqrt{3/8}\). However, of the four choices considered, \(H_{2}=\mathbb {Q}_{4}(h)\) yields the smallest CBS constant.
Example 2
Let \(D=[-1,1]^2\) and let \(\mathcal {T}_{h}\) denote a uniform mesh of square elements. Now let \(H_1\) be the set of continuous functions that are piecewise biquadratic on \(\mathcal {T}_h\) (denoted \(H_{1}=\mathbb {Q}_2(h)\)). On each \(\square _{k}\) we construct a local space \(H_{k,2}\) of dimension \(m_{k} \le 16\), by defining a set of bubble functions associated with the additional \(\mathbb {Q}_{2}\) nodes that would be introduced by performing a uniform mesh refinement (see Fig. 2). We consider the following options.
-
1.
Biquartic bubble functions (\(\mathbb {Q}_{4}(h)\)) Consider the set of twenty-five \(\mathbb {Q}_{4}\) element basis functions associated with \(\square _{k}\) but retain only those associated with the nodes indicated by the clear and grey markers in Fig. 2.
-
2.
Piecewise biquadratic bubble functions (\(\mathbb {Q}_{2}(h/2)\)) Subdivide each element into four smaller ones of size h / 2, and concatenate the standard \(\mathbb {Q}_{2}\) basis functions associated with the new elements at the nodes indicated by the clear and grey markers in Fig. 2.
For our third and fourth choices of \(H_{2}\) we modify the first two spaces by removing the basis functions associated with the nodes indicated by the grey markers in Fig. 2. This configuration is motivated by error estimation results presented in [23, p. 39]. We denote the resulting ‘reduced’ spaces by \(\mathbb {Q}_{4}^{r}(h)\) and \(\mathbb {Q}_{2}^{r}(h/2)\) and denote the number of degrees of freedom by \(N_{r}\).
In Table 2 we record \(\gamma _{\min }^2\) for each choice of \(H_2\) for varying h. In [10], the authors choose \(H_{2}=\mathbb {Q}_{4}^{r}(h)\) to define the error estimator \(\eta =\Vert e_{Y} \Vert _{B_{0}}\) described in Sect. 3, when \(u_{X}\) is computed with \(H_{1}=\mathbb {Q}_{2}(h)\). When \(a_{0}=1\), the CBS constant is \(\gamma _{\min }\le \sqrt{0.36}\). Of the four spaces considered, \(H_{2}=\mathbb {Q}_{4}^{r}(h)\) yields the smallest CBS constant.
4.1 Local CBS Constants
Solving the eigenvalue problem (49) to compute the CBS constant when N is large is not practical. Alternatively, we may derive a small eigenvalue problem associated with a single element. For all \(u\in H_2\) and \(v\in H_1\) we have
where \(u_k:=u|_{k}\in H_{k,2} := H_2|_{k},\) and \(v_k:=v|_{k}\in H_{k,1} := H_1|_{k}\) with \(H_{k,1},H_{k,2}\subset H^1(\Box _k)\) having dimensions \(n_k = \text {dim}(H_{k,1})\) and \(m_k = \text {dim}(H_{k,2})\) (recall that we now list functions in \(H_2\) before functions in \(H_1\)). Here, \(|_{k}\) denotes the restriction to element \(\square _{k}\). For all \(u_k\in H_{k,1}\) and \(v_k\in H_{k,2}\), \(\langle a_0 u_k,v_k\rangle _k = \mathbf {u}_k^{\top }M_k\mathbf {v}_k\), where the matrix \(M_k \in \mathbb {R}^{N_{k} \times N_{k}}\) for \(N_k:= n_k + m_k\) has the same \(2 \times 2\) block structure as before with \(A_{k} \in \mathbb {R}^{n_{k} \times n_{k}}\), \(B_{k} \in \mathbb {R}^{m_{k} \times m_{k}}\) and \(C_{k} \in \mathbb {R}^{n_{k} \times m_{k}}\). Since \(\langle a_0\cdot ,\cdot \rangle _k\) only induces a seminorm on \(H^1(\Box _k)\), \(M_k\) is positive semidefinite and Corollary 1 is not applicable. For our block matrices of interest, we require the following result from [19].
Corollary 2
Let \(M_k\in \mathbb {R}^{N_k\times N_k}\) be symmetric and positive semidefinite with
where \(N_k=m_k+n_k,\) \(B_k\in \mathbb {R}^{m_k\times m_k}\) is invertible and \(A_k\in \mathbb {R}^{n_k\times n_k}\). Let \(U_k,V_k\subset \mathbb {R}^{N_k}\) have the same structure as U and V in (46), but for \(n_k\) and \(m_k\) in place of n and m. Then, there exists a constant \(\gamma _k\in [0,1)\) such that
If \(H_{k,1}\) and \(H_{k,2}\) are chosen so that \(M_k\) satisfies the conditions of Corollary 2, there exists a constant \(\gamma _k\in [0,1)\) such that (55) holds, or equivalently
Furthermore, the local CBS constant \(\gamma _{k,\min }\) associated with (56) is the square root of \(\theta _{\max }\) satisfying
see [19]. It is straightforward to show that
and comparing with (39) gives \(\gamma _{\min }\le \sup _{\Box _k}\gamma _{k,\min }\). When the mesh is uniform and \(a_{0}(\mathbf {x})\) is constant on each element, \(\gamma _{k,\min }\) does not depend on h or \(a_{0}|_{k}\). To estimate \(\gamma _{\min }\), we only need to compute \(\gamma _{k,\min }\) for a single internal element (as this is larger than the constant associated with corner/edge elements).
We now revisit Example 1 and compute local CBS constants associated with \(\Box _{\text {ref}} := [-1,1]^2\). We choose \(H_{k,1}\) to be the local \(\mathbb {Q}_{1}\) finite element space whose basis functions are associated with the black markers shown in Fig. 3, and ordered as shown. Then, \(\text {dim}(H_{k,1}) = 4\) and, if \(a_{0}=1\), we have
For the four choices of \(H_{k,2}\) considered in Example 1 (which all have dimension five), we construct the matrix \(M_k\) in (54) and calculate \(\gamma ^2_{k,\min }\) by solving the eigenvalue problem (57). The ordering of the basis functions of \(H_{k,2}\) is as illustrated by the clear markers in Fig. 3.
First, let \(H_{k,2}=\mathbb {Q}_{2}(h)\). The matrices \(C_k\) and \(B_k\) are
where we define
Solving (57) gives \(\gamma _{k,\min }^2 = \frac{5}{11}\approx 0.4545\), which agrees with the bound reported in [28]. If we choose \(H_{k,2}=\mathbb {Q}_{4}(h)\) (a non-standard choice), we have
and \(\gamma _{k,\min }^2 \approx 0.0121\). Next, if \(H_{k,2}=\mathbb {Q}_{1}(h/2)\), we have
and \(\gamma _{k,\min }^2 = \frac{3}{8}=0.3750\), which agrees with [27]. Finally, let \(H_{k,2}=\mathbb {Q}_{2}(h/2)\) (another non-standard choice). Then,
and \(\gamma _{k,\min }^2 \approx 0.0446\). Comparing with the results in Table 1, we confirm the relationship \(\gamma _{\min }^{2}\le \gamma _{\min ,k}^{2}\).
Remark 1
If \(a_0(\mathbf {x})\) varies in space, we may assume that \(a_0(\mathbf {x})\) can be approximated by a function \(a_{0}^h(\mathbf {x})\) that is constant in each element in \(\mathcal {T}_h\). Then, on each \(\Box _k\), we have a symmetric and positive semidefinite matrix
where \(B_k\) is invertible and \(B_k,C_k,A_k\) do not depend on \(\alpha _k\). The local eigenvalue problem, equivalent to (57), is \((\alpha _{k} C_k)(\alpha _{k} B_k)^{-1}(\alpha _{k} C_k^{\top })\mathbf {v}_2 = \theta ( \alpha _{k}A_k)\mathbf {v}_2\) for \(\mathbf {v}_2\notin \mathcal {N}(A_k)\), and thus the local CBS constant \(\gamma _{k,\min }\) satisfying (56) is independent of \(\alpha _{k}\) and \(a_{0}^{h}(\mathbf {x})\).
5 Theoretical Estimates of the CBS Constant
In this section we fix \(H_{k,1}\) to be the local \(\mathbb {Q}_{1}\) finite element space so that \(A_k\) is given by (58) and assume that the degrees of freedom are numbered as shown in Fig. 3. We also assume that \(H_{k,2}\) is chosen so that dim\((H_{k,2})=5\) and the resulting matrices \(B_k\) and \(C_k\) have a particular structure. Exploiting this structure, and using only linear algebra arguments, we show that the local CBS constant \(\gamma _{k,\min }\) can be calculated analytically without assembling and solving (57). To simplify notation, we drop the subscript k.
Theorem 8
Let \(M\in \mathbb {R}^{9\times 9}\) be a symmetric and positive semidefinite matrix with the \(2\times 2\) block structure (47), where \(B \in \mathbb {R}^{5\times 5}\) is symmetric and positive definite and A is the \(\mathbb {Q}_1\) element stiffness matrix defined in (58). If the matrix \(CB^{-1}C^{\top }\in \mathbb {R}^{4\times 4}\) is of the form
for some constant \(\beta \in \mathbb {R}^{+}\), then there exists a constant \(\gamma \in [0,1)\) such that
Proof
It is sufficient to show that \(\mathcal {N}(M)\) is given by the definition in (54). The result then follows from Corollary 2. Let \(\mathbf {x}^T=(\mathbf {u}_1^T,\mathbf {v}_2^T)\in \mathbb {R}^9\) for \(\mathbf {u}_1\in \mathbb {R}^{5}\) and \(\mathbf {v}_2\in \mathbb {R}^{4}\) be such that \(M\mathbf {x}=\mathbf {0}\). Then
and \(S\mathbf {v}_2 = \mathbf {0}\) for the Schur complement \(S = A - CB^{-1}C^T = A - \beta Q\). Since
and A are circulant matrices with zero row sums, we have
and thus \(\mathbf {v}_2\in \mathcal {N}(A)\). We now show that \(\mathbf {u}_1 = \mathbf {0}\) and \(C^T\mathbf {v}_2 = \mathbf {0}\) for all \(\mathbf {v}_2\in \mathcal {N}(A)\). If \(\mathbf {v}_2\in \mathcal {N}(A)\), from (63) it follows that \(C\mathbf {u}_1 = \mathbf {0}\). Since B is invertible, (62) gives \(0 = \mathbf {v}_2^TC\mathbf {u}_1 = -(C^T\mathbf {v}_2)^TB^{-1}(C^T\mathbf {v}_2)\) and \((B\mathbf {u}_1)^TB^{-1}(B\mathbf {u}_1)=0.\) Since \(B^{-1}\) is also invertible, we conclude that \(B\mathbf {u}_1=\mathbf {0}\) and \(\mathbf {u}_1 = \mathbf {0}\). Finally, \(\mathbf {u}_1 = \mathbf {0}\) and (62) gives \(C^T\mathbf {v}_2 = \mathbf {0}\). \(\square \)
Theorem 9
Let \(M\in \mathbb {R}^{9\times 9}\) be as in Theorem 8, then the smallest constant \(\gamma \in [0,1)\) satisfying (61), denoted \(\gamma _{\min }\) (the CBS constant), is given by
where \(\beta \in \mathbb {R}^+\) is the constant in (60).
Proof
Recall from (57) that \(\gamma ^2_{\min }\) is the largest eigenvalue \(\theta _{\max }\) satisfying
By considering the expression \(Q\mathbf {u}=\mathbf {0}\) it is easy to show that
and so \(\mathcal {N}(A)\subset \mathcal {N}(Q)\). Under the stated assumptions, we have
and the set of eigenvalues is \(\{2\beta ,2\beta ,0,0\}\). The basis vectors of \(\mathcal {N}(Q)\) in (67) are eigenvectors corresponding to the zero eigenvalues. In addition,
is an eigenvector corresponding to \(\theta =2\beta \). To see this, note that
The same is true for \(\mathbf {P}_2= [-1, 1, 1, -1]^{\top }\). Furthermore, the vectors \(\mathbf {P}_1\) and \(\mathbf {P}_2\) also satisfy \(A\mathbf {P}_1=\mathbf {P}_1\) and \(A\mathbf {P}_2=\mathbf {P}_2\) (and clearly do not belong to \(\mathcal {N}(A)\), see (64)) and hence are eigenvectors of A with eigenvalue \(\theta =1\). Thus
That is, \(\mathbf {P}_1\) and \(\mathbf {P}_2\) are eigenvectors in (66) with \(\theta =2\beta \). If we take \(\mathbf {u}\) to be a member of \(\mathcal {N}(Q)\) but not \(\mathcal {N}(A)\), then (66) is trivially satisfied with \(\theta =0\). Hence, \(\gamma _{\min }^2 = \max \{0,2\beta \} = 2\beta \).
\(\square \)
The next results show that if the matrices B and C have certain structures, then \(CB^{-1}C^{\top }\) always has the structure (60) and an explicit expression is available for the constant \(\beta \) in (65), and hence the CBS constant.
Lemma 1
If the matrix \(C \in \mathbb {R}^{4 \times 5}\) has the form
for some \(\alpha \in \mathbb {R}^{+}\) and if \(B\in \mathbb {R}^{5\times 5}\) is an invertible bordered matrix of the form
where \(\bar{B}\in \mathbb {R}^{4\times 4}\) is a symmetric circulant matrix, \(\mathbf {b}\in \mathbb {R}^4\) is a constant vector, and \(\mu \in \mathbb {R}\) is a constant, then the matrix \(CB^{-1}C^{\top }\) has the form (60).
Proof
First we show that if B has the form (69) then so does \(B^{-1}\). We have
where \(\nu :=\mu -\mathbf {b}^{\top }\bar{B}^{-1}\mathbf {b}\in \mathbb {R}\) is the Schur complement. Since \(\bar{B}\) is symmetric and circulant, so is its inverse (see [13]). Consequently, \(\mathbf {q}:=\bar{B}^{-1}\mathbf {b}\in \mathbb {R}^{4\times 1}\) is a constant vector and \(\mathbf {q}\mathbf {q}^{\top }\in \mathbb {R}^{4\times 4}\) is a constant matrix. This is because \(\mathbf {b}\) is a constant vector and the row sums of a circulant matrix are equal. Therefore
where \(\hat{B} := \bar{B}^{-1} +\nu ^{-1}\mathbf {q}\mathbf {q}^{\top } \in \mathbb {R}^{4\times 4}\) is a symmetric circulant matrix bordered by \(\hat{\mathbf {b}} := -\nu ^{-1}\mathbf {q}\in \mathbb {R}^{4\times 1}\) and \(\nu \in \mathbb {R}\) is a constant. Hence, \(B^{-1}\) has the form
for some \(\alpha _1,\alpha _2,\alpha _3\in \mathbb {R}\) and, for the rest of the proof, the elements marked with \(\times \) are not important. Now, elementary matrix multiplication with C gives
(again the elements marked with \(\bar{\times }\) are not important) and
with \(\beta := 4(\alpha _1-\alpha _3)\alpha ^2\). \(\square \)
Combining the last two results, we see that to compute the CBS constant, we only need to know \(\alpha \) (one entry of C) and \(\alpha _{1}\) and \(\alpha _{3}\) (two entries of the first column of \(B^{-1}\)). We can determine the latter analytically by exploiting the spectral decomposition for circulant matrices. Lemma 2 is standard (for example, see [13]) and we apply it to \(\bar{B}\) in (69) in Lemma 3.
Lemma 2
Let \(D\in \mathbb {R}^{n\times n}\) be a circulant matrix with first column given by \(\mathbf d =[d_0,d_1,\dots ,d_{n-1}]^{\top }\in \mathbb {R}^n\). The eigenvalues \(\lambda _{j}\) and eigenvectors \(\mathbf v _j\) of D are
where \(\omega _j=\exp (2\pi \text {i}j/n)\) and \(\text {i}=\sqrt{-1}\).
Lemma 3
Let the principle minor \(\bar{B}\) in (69) of the matrix B be given by
Then the eigenvalues of \(\bar{B}\) are
and the eigenvectors of \(\bar{B}\) are given by the columns of the unitary matrix
Moreover, \(\bar{B} = F^*\text {diag}(\varvec{\lambda })F\), where \(\varvec{\lambda }=[\lambda _{1}, \lambda _{2}, \lambda _{3}, \lambda _{4}]^{\top }\).
Proof
Since \(\bar{B}\) is circulant, its eigenpairs are given by (72). Here, \(n=4\) and we have \(\omega _1 = \text {i}, \omega _2 = -1, \omega _3=-\text {i}\), and \(\omega _4=1\). The decomposition is standard (see [34, Corollary 5.16]). \(\square \)
Combining the above results, gives the following final result.
Theorem 10
Let the assumptions of Theorem 8 and Lemma 1 hold, with the entries of \(\bar{B}\) labelled as in (73). Then, the square of the CBS constant associated with (61) is given by
Proof
From Lemma 1, we have \(CB^{-1}C^\top =\beta Q\) with \(\beta =4 \alpha ^{2}(\alpha _{1}-\alpha _{3})\) where \(\alpha _1\) and \(\alpha _3\) are elements of the matrix \(\hat{B}\) in (70), which depends on the inverse of \(\bar{B}\) in (69). By Lemma 3,
Since \(\bar{B}^{-1}\) is circulant, its entries are known once we specify its first column \(\bar{\mathbf{c }}\). Furthermore, since
we have \(\bar{\mathbf{c }}:=\bar{B}^{-1}{} \mathbf e _1=F^*\text {diag}(1./\varvec{\lambda })F\mathbf e _1=\tfrac{1}{2}F^*(1./\varvec{\lambda })\). It follows that
Now, since \(\hat{B} := \bar{B}^{-1} +\nu ^{-1}{} \mathbf q {} \mathbf q ^{\top }\) in Lemma 1, we know that \(\alpha _1 = [\bar{\mathbf{c }}]_1 + \tau \) and \(\alpha _3 = [\bar{\mathbf{c }}]_3 + \tau \) for some \(\tau \in \mathbb {R}\), and consequently, by considering (76) and the eigenvalues (74), we have
Since B is symmetric and positive definite, so is \(\bar{B}\). Consequently, \(\lambda _{1}>0\) and \(\beta =4 \alpha ^{2} \left( b_1-b_3\right) ^{-1} >0\). The result follows by Theorem 9. \(\square \)
The matrices B and C associated with the examples in Sect. 4.1 (corresponding to the four choices of \(H_{k,2}\) from Example 1) all have the desired structure. The associated values of \(\alpha , b_{1}\) and \(b_{3},\) and the squares of the CBS constants are recorded in Table 3 (to stress that these are local quantities we reintroduce the subscript k). The results match the numerical estimates obtained in Sect. 4.1. With the new approach, the matrices A, B and C do not need to be assembled, and no eigenvalue problem needs to be solved.
6 Numerical Results
We now return to (1a)–(1b) and assess the quality of the energy error estimator \(\eta \) in (37), extending the discussion in [8] and [10]. First, we select \(X= H_1\otimes P\) and compute \(u_X\in X\) by solving (9). We choose either \(H_1=\mathbb {Q}_1(h)\) or \(H_1=\mathbb {Q}_2(h)\) on a uniform square partition of D and fix P to be the space of global polynomials with total degree less than or equal to p in \(y_1,y_2,\dots , y_M\). Each parameter \(y_{m}\) is assumed to be the image of a mean zero uniform random variable. Hence, for a given multi-index \(\mu \in J_P\) we construct the basis functions in (30) by tensorizing univariate Legendre polynomials. Next, we compute \(\eta = \eta (u_X)\) in (37) by solving (35) and (36), choosing \(H_2\) and Q so that the conditions in (31) are satisfied. For \(H_{2}\), we consider the spaces from Examples 1 and 2. We choose Q to be the space of polynomials associated with \(J_Q:= \hat{J}_{Q}\backslash J_P\) where \(\hat{J}_Q\) is the set of multi-indices associated with the space of polynomials with total degree less than or equal to \(p+1\) in \(y_1,y_2,\dots , y_M, y_{M+1}\).
By Theorem 6, the effectivity index \(\theta _{\text {eff}}:= \eta (u_X)/||u-u_X||_B\) satisfies
Since \(||u-u_X||_B\) cannot be computed, we examine \({\hat{\theta }_{\text {eff}} := \eta (u_X)/||u_{\text {ref}}-u_X||_B}\), where \(u_{\text {ref}}\in X_{\text {ref}}\) is a surrogate solution obtained by solving (9) over a sufficiently rich subspace \(X_{\text {ref}}\subset V\) where \(X_{\text {ref}}\supset X\). We define \(X_\text {ref}\) in the same way as X, with \(M_{\text {ref}}=10\), \(h_{\text {ref}} = 2^{-7}\) and \(p_{\text {ref}}= 8\). Fixing \(H_1\), P and Q, we investigate which choice of \(H_2\) consistently leads to \(\hat{\theta }_{\text {eff}}\approx 1\).
6.1 Test Problem 1
To start, we consider a test problem from [8]. We choose \(f(\mathbf {x})=\frac{1}{8}(2 - x_1^2 - x_2^2)\) for \(\mathbf {x}=(x_1,x_2)^T\in D:=[-1,1]^2\) and assume that \(a(\mathbf {x},\mathbf {y})\) is the parametric form of a second order random field with mean \(\mathbb {E}[a](\mathbf {x})\) and covariance function
We may then expand \(a(\mathbf {x},\mathbf {y})\) using the Karhunen-Loève expansion, namely;
where \((\lambda _m,\phi _m)\) are the eigenpairs of the covariance operator. We choose \(\mathbb {E}[a](\mathbf {x}) = 1\) (the mean), \(\sigma = 0.15\) (the standard deviation) and \(l_1=l_2= 2\) (the correlation lengths). In [8], (79) is truncated a priori after M terms, so that the problem is posed on \(D\times \bar{\varGamma }\), where \(\bar{\varGamma } = \prod _{m=1}^M\varGamma _m\). In that case, \(u_{X}\) and \(u_{\text {ref}}\) are both functions of M parameters. Here, u depends on infinitely many parameters and \(u_{\text {ref}}\) is a function of \(M_{\text {ref}} > M\) parameters.
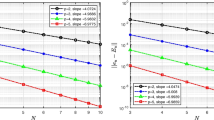
In our first experiment we choose \(H_1 = \mathbb {Q}_1(h)\) and fix \(M=5\) in the definition of P. In Table 4 we record \(\hat{\theta }_{\text {eff}}\) for varying h with fixed \(p=4\), and varying p with fixed \(h=2^{-3}\). We see that \(H_{2}=\mathbb {Q}_2(h/2)\) yields the best error estimator. Interestingly, \(H_{2}=\mathbb {Q}_4(h)\) defines the worst estimator, despite the fact that its associated CBS constant is the smallest (\(\gamma _{\min }^2 \le 0.0121\)). Recall from Theorem 7 that \(||e_{Y_1}||_{B_0} \) and \(||e_{Y_2}||_{B_0}\) provide estimates of the energy error reductions associated with augmenting \(H_{1}\) with \(H_{2}\), and P with Q, respectively. When \(H_{2}=\mathbb {Q}_4(h)\), since the CBS constant is small, we know \(||e_{Y_1}||_{B_0}\) is a good estimate. When both \(||e_{Y_1}||_{B_0} \) and \(||e_{Y_2}||_{B_0}\) are much smaller than \(||e||_B\) (which is true when we use the stated Q and \(H_{2}=\mathbb {Q}_{4}(h)\)), the saturation constant \(\beta \approx 1\). This causes \(\eta \) to be much smaller than \(||e||_B\), resulting in a poor effectivity index.
We now repeat the experiment with \(H_1 = \mathbb {Q}_2(h)\). Note that for a fixed h, the spatial error associated with \(u_{X}\) is smaller than for \(H_1 = \mathbb {Q}_1(h).\) Results are presented in Table 5. Now, as we vary both h (for p=4 fixed) and p (for \(h=2^{-3}\) fixed), the error \(||u_{\text {ref}}-u_X||_B\) stagnates. The estimated errors behave the same way, but \(\hat{\theta }_{\text {eff}}\) is not close to one. There is little benefit in computing a new Galerkin solution by augmenting either \(H_{1}\) with \(H_{2}\) (for any of the choices of \(H_{2}\)) or P with Q. The saturation constant is close to one in all cases. However, if introducing more parameters into the approximation space leads to a smaller saturation constant, a better estimate of the error should be obtained by modifying Q to include more parameters.
We fix P as before with \(M=5\) but now choose Q to be the space of polynomials associated with \(J_Q:= \hat{J}_{Q}\backslash J_P\) where \(\hat{J}_Q\) is the set of multi-indices associated with polynomials with total degree less than or equal to \(p+1\) in the first \(M+3\) parameters. Results are presented in Table 6. The effectivity indices are much improved. It is well known that the eigenvalues \(\lambda _m\) associated with (78) decay very slowly (\(\sqrt{\lambda _{m}} = O(m^{-1})\), see [24]). To achieve a small saturation constant, and hence an accurate error estimator, a large number of parameters need to be incorporated into Q. We now study a problem with faster decaying coefficients.
6.2 Test Problem 2
We consider a problem as in [10], first introduced in [16]. We choose \(f(\mathbf {x})=1\) for \(\mathbf {x}=(x_1,x_2)^T\in D:=[0,1]^2\) and
where \(\beta _m^1 = m - k_m(k_m+1)/2\) and \(\beta _m^2 = k_m - \beta _m^1\) for \( m\in \mathbb {N}\) with \(k_m = \big \lfloor {-1/2 + (1/4 + 2m)^{1/2}\big \rfloor }\). As in [16] we select \(\alpha _m = 0.547m^{-2}\). We conduct the same experiments as in Sect. 6.1 using the original definition of \(\hat{J}_Q\) (with \(M+1\) parameters). Effectivity indices are shown in Tables 7 and 8. When \(H_1 = \mathbb {Q}_1(h)\), \(H_{2}=\mathbb {Q}_2(h)\) yields the best estimator, very closely followed by \(\mathbb {Q}_2(h/2)\). When \(H_1 = \mathbb {Q}_2(h)\), \(H_{2}=\mathbb {Q}_4(h)\) yields the best error estimator, closely followed by \(\mathbb {Q}_2^r(h/2)\) (recall that \(\mathbb {Q}_4^r(h)\) has the smallest CBS constant).
7 Summary and Conclusions
Using classical theory from [1, 6] for Galerkin approximation, we provided an alternative derivation of an error estimator from [10] and the associated bound. Our approach highlights the straightforward extension of an error estimation strategy for standard Galerkin FEMs for deterministic PDEs to SGFEMs for parameter-dependent PDEs. The quality of the estimator depends on a CBS constant associated with two finite element spaces \(H_1\) and \(H_2\). For \(H_1 = \mathbb {Q}_1(h)\) and \(H_{1}=\mathbb {Q}_2(h)\) we investigated non-standard choices of \(H_2\) which lead to small CBS constants. When \(H_1 = \mathbb {Q}_1(h)\) and \(H_2\) satisfies certain conditions, we derived new theoretical estimates for the CBS constant. In Sect. 6 we demonstrated that the best choice of \(H_2\) for constructing an effective error estimator is not necessarily the space that leads to the smallest CBS constant. Through numerical experiments, we demonstrated that Q must also be carefully selected and tailored to properties of the diffusion coefficient. When both \(H_2\) and Q are chosen appropriately, the estimator exhibits effectivity indices close to one.
Choosing \(H_{2}\) and Q so that the effectivity index is close to one is not the end of the story. If the estimated error associated with \(u_{X} \in X=H_{1} \otimes P\) is too high, we need to decide how to enrich X and compute a new approximation. The error estimate needs to be accurate, but to derive adaptive algorithms using (44)–(45), we should only work with spaces \(H_2\) and Q such that it is straight-forward to compute new SGFEM approximations in \((H_{1}\oplus H_{2}) \otimes P\) and/or \(H_{1} \otimes (P \oplus Q)\). For example, when \(H_1 = \mathbb {Q}_1(h)\), choosing \(H_2=\mathbb {Q}_2(h)\) yields an accurate error estimate for the current approximation, but does not give a feasible spatial adaptive enrichment strategy. Choosing \(H_{2}=\mathbb {Q}_1(h/2)\) is more natural. Fortunately, this space also yields a good error estimator. When \(H_1 = \mathbb {Q}_2(h)\), \(H_{2}=\mathbb {Q}_2^r(h/2)\) yields an excellent estimator. Although using \(H_{2}=\mathbb {Q}_2(h/2)\) is more natural for adaptivity, we recommend using \(H_{2} =\mathbb {Q}_2^r(h/2)\) to estimate the error. Not only is this cheapest option of all those considered, since \(\mathbb {Q}_2(h/2)\) is richer, the estimated spatial error reduction \(||e_{Y_1}||_{B_0}\) obtained using \(H_{2}=\mathbb {Q}_2^r(h/2)\) is still informative, if we wish to assess the benefit of computing a new approximation in \(\left( \mathbb {Q}_2(h)\oplus \mathbb {Q}_2(h/2)\right) \otimes P\).
References
Ainsworth, M., Oden, J.T.: A Posteriori Error Estimation in Finite Element Analysis. Wiley, New York (2000)
Axelsson, O., Blaheta, R., Neytcheva, M., Pultarová, I.: Preconditioning of iterative methods–theory and applications. Numer. Linear Algebra Appl. 22, 901–902 (2015)
Axelsson, O., Vassilevski, P.S.: Algebraic multilevel preconditioning methods. II. SIAM J. Numer. Anal. 27, 1569–1590 (1990)
Babuška, I.M., Tempone, R., Zouraris, G.E.: Galerkin finite element approximations of stochastic elliptic partial differential equations. SIAM J. Numer. Anal. 42, 800–825 (2004)
Babuška, I.M., Tempone, R., Zouraris, G.E.: Solving elliptic boundary value problems with uncertain coefficients by the finite element method: the stochastic formulation. Comput. Methods Appl. Mech. Eng. 194, 1251–1294 (2005)
Bank, R.E., Weiser, A.: Some a posteriori error estimators for elliptic partial differential equations. Math. Comput. 44, 283–301 (1985)
Bespalov, A., Powell, C.E., Silvester, D.: Stochastic IFISS (S-IFISS) version 1.1. http://www.manchester.ac.uk/ifiss/s-ifiss1.0.tar.gz (2016). Accessed 6 Mar 2018
Bespalov, A., Powell, C.E., Silvester, D.: Energy norm a posteriori error estimation for parametric operator equations. SIAM J. Sci. Comput. 36, A339–A363 (2014)
Bespalov, A., Rocchi, L.: Efficient adaptive algorithms for elliptic PDEs with random data. SIAM/ASA J. Uncertain. Quantif. 6, 243–272 (2018)
Bespalov, A., Silvester, D.: Efficient adaptive stochastic Galerkin methods for parametric operator equations. SIAM J. Sci. Comput. 38, A2118–A2140 (2016)
Bieri, M., Andreev, R., Schwab, C.: Sparse tensor discretization of elliptic SPDEs. SIAM J. Sci. Comput. 31, 4281–4304 (2009)
Bieri, M., Schwab, C.: Sparse high order FEM for elliptic sPDEs. Comput. Methods Appl. Mech. Eng. 198, 1149–1170 (2009)
Davis, P.J.: Circulant Matrices. Wiley, New York (1979)
Deb, M.K., Babuška, I.M., Oden, J.T.: Solution of stochastic partial differential equations using Galerkin finite element techniques. Comput. Methods Appl. Mech. Eng. 190, 6359–6372 (2001)
Dörfler, W.: A convergent adaptive algorithm for Poisson’s equation. SIAM J. Numer. Anal. 33, 1106–1124 (1996)
Eigel, M., Gittelson, C.J., Schwab, C., Zander, E.: Adaptive stochastic Galerkin FEM. Comput. Methods Appl. Mech. Eng. 270, 247–269 (2014)
Eigel, M., Gittelson, C.J., Schwab, C., Zander, E.: A convergent adaptive stochastic Galerkin finite element method with quasi-optimal spatial meshes. ESAIM Math. Model. Numer. Anal. 49, 1367–1398 (2015)
Eigel, M., Merdon, C.: Local equilibration error estimators for guaranteed error control in adaptive stochastic higher-order Galerkin finite element methods. SIAM/ASA J. Uncertain. Quantif. 4, 1372–1397 (2016)
Eijkhout, V., Vassilevski, P.: The role of the strengthened Cauchy–Buniakowskiĭ-Schwarz inequality in multilevel methods. SIAM Rev. 33, 405–419 (1991)
Ernst, O.G., Powell, C.E., Silvester, D.J., Ullmann, E.: Efficient solvers for a linear stochastic Galerkin mixed formulation of diffusion problems with random data. SIAM J. Sci. Comput. 31, 1424–1447 (2008)
Ernst, O.G., Ullmann, E.: Stochastic Galerkin matrices. SIAM J. Matrix Anal. Appl. 31, 1848–1872 (2009)
Ghanem, R.G., Spanos, P.D.: Stochastic Finite Elements: A Spectral Approach. Springer, New York (1991)
Liao, Q.: Error estimation and stabilization for low order finite elements. Ph.D. Thesis. The University of Manchester, Manchester (2010)
Lord, G.J., Powell, C.E., Shardlow, T.: An Introduction to Computational Stochastic PDEs. Cambridge University Press, New York (2014)
Powell, C.E., Elman, H.C.: Block-diagonal preconditioning for spectral stochastic finite-element systems. IMA J. Numer. Anal. 29, 350–375 (2009)
Powell, C.E., Ullmann, E.: Preconditioning stochastic Galerkin saddle point systems. SIAM J. Matrix Anal. Appl. 31, 2813–2840 (2010)
Pultarová, I.: The strengthened C.B.S. inequality constant for second order elliptic partial differential operator and for hierarchical bilinear finite element functions. Appl. Math. 50, 323–329 (2005)
Pultarová, I.: Preconditioning and a posteriori error estimates using \(h\)- and \(p\)-hierarchical finite elements with rectangular supports. Numer. Linear Algebra Appl. 16, 415–430 (2009)
Pultarová, I.: Adaptive algorithm for stochastic Galerkin method. Appl. Math. 60, 551–571 (2015)
Pultarová, I.: Hierarchical preconditioning for the stochastic Galerkin method: upper bounds to the strengthened CBS constants. Comput. Math. Appl. 71, 949–964 (2016)
Schwab, C., Gittelson, C.J.: Sparse tensor discretizations of high-dimensional parametric and stochastic PDEs. Acta Numer. 20, 291–467 (2011)
Silvester, D.: Pranjal: an optimal solver for linear systems arising from stochastic FEM approximation of diffusion equations with random coefficients. SIAM/ASA J. Uncertain. Quantif. 4, 298–311 (2016)
Ullmann, E.: A Kronecker product preconditioner for stochastic Galerkin finite element discretizations. SIAM J. Sci. Comput. 32, 923–946 (2010)
Vogel, C.R.: Computational Methods for Inverse Problems. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2002)
Acknowledgements
We thank David Silvester and Alexei Bespalov for valuable discussions and contributions to the MATLAB toolbox S-IFISS [7], which we used to produce our numerical results.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Crowder, A.J., Powell, C.E. CBS Constants & Their Role in Error Estimation for Stochastic Galerkin Finite Element Methods. J Sci Comput 77, 1030–1054 (2018). https://doi.org/10.1007/s10915-018-0736-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0736-4
Keywords
- Error estimation for stochastic PDE problems
- Stochastic finite element method
- Stochastic Galerkin method
- Strengthened Cauchy–Schwarz inequality
- CBS constants