Abstract
A general review of quantum molecular similarity structure and applications is presented. The backbone of the discussion corresponds to the general problem of the data structure associated with the mathematical representation of a molecular set. How to standardize, and how to compare it to any other problem. This computational track describes the exact isometric vectors of the similarity matrix in a Minkowskian space. The further aim is to construct a set of origin-shifted vectors forming the vertices of a molecular polyhedron. From here, one can calculate a set of statistical-like momenta, providing a set of scalars that describe in a compact form the attached molecular set. Finally, the definition of a quantum QSPR operator permits building up a system of equations that can be further employed to determine the unknown properties of molecules in the original set. This last achievement leads to a quantum QSPR algorithm comparable with the classical QSPR counterpart but described in molecular space, not parameter space.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The present paper will deal with a general analysis of QSPR.Footnote 1 Circumscribing the discussion on the issue of using molecular spaces,Footnote 2 not descriptor or parameter spaces, is a usual framework in the main literature trend.
Since the dawn of the twenty-first century, several assorted papers [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40] have attracted our attention and have been published dealing with classical QSPR (CQSPR); in the same way, work around the associated mathematical problems appearing in this class of techniques are included in the same list.
Since the humble origin of quantum similarity [41], in the subsequent quantum QSPR (QQSPR) studies collection [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94], as far as the present author can tell, no particular recommendations about how to prepare the whole set of data, which is usually involved in the QSPR procedures, have been discussed so far. The situation can be considered an intriguing fact, which we’ll try to revise in the present study.
Previous papers have discussed some QSPR processing recommendations; reference [95]. But perhaps some essential clues on data rearrangement are still missing from the list of alleged actions, which one might suggest based on the QSPR available information.
If present, such data rearrangements must be constructed as a collection of simple procedures, leading to a reproducible computational structure. While simultaneously setting the possibility of systematic comparison with any QSPR problems appearing in the future. Reproducibility in CQSPR seems to be not a strongly contemplated issue. For example, examine the contributions in reference [7]. Nevertheless, it is undoubtedly an essential requirement in scientific endeavors.
Intermediate data preparation procedures also seem not well-defined in the QSAR-QSPR literature. Therefore, one will discuss this subject in the present work. This author opines that one needs to ensure QSPR results are reproducible and comparable and that data preparation in QSPR procedures could be a first step all-purpose way to obtain such a goal.
This point of view will need or lead to new data manipulation and algorithmic description, which one will also discuss. In this sense, this study will provide a general isometry algorithm helpful in calculating the molecular set momenta and provide the basis of the QSPR operator construction.
Finally, there is no claim that this study’s algebraic proposals described below shall be taken as a final nor a unique possibility to obtaining reliable and well-structured QSPR. On the contrary: they might be considered an open way to the perfection of generic QSPR algorithms in molecular spaces.
Thus, we are opening the possibility of describing an alternative path to the parameter space calculations in current QSPR procedures.
2 Preliminary considerations
The QSPR methodological proposal considered here can start by admitting the following points as a working background:
-
(a)
Suppose known a set of \(M\) molecular structures, which in principle, one might consider as arbitrarily ordered and thus numbered accordingly:
-
(b)
Suppose some known property values are associated with the molecular set \({\mathbb{M}}: {\mathbf{P}} = \left\{ {p_{I} \left| {I = 1,M} \right.} \right\}\). Then, one standardizes the available property values according to the reference [95] suggestions, transforming them into values within the unit interval.
Therefore, from now on, one can also take for granted that in any QSPR procedure, the property set lies on the compact unit interval: \({\mathbf{P}} \Rightarrow {{\varvec{\Pi}}} \subset \left[ {0,1} \right].\)
Such a transformation is essential for comparing the predicted property results obtained by applying QSPR algorithms. One suggested this standardization [95] to carry a given QSPR problem into the most accessible comparative form with any other QSPR problem in the future.
Such property values transformation will make any QSPR problem homogeneous concerning any other problem property.
-
(c)
Suppose the preparation of a QSPR procedure so that the molecular set’s descriptors are employed to construct a molecular space noted as: \({\mathbb{V}}_{D \ge M}\), and bearing a dimension D imposed by the number of different descriptors of the molecular structuresFootnote 3 [85].
This point is systematically ignored in CQSPR, as the usual classical procedures describe such problems as belonging to the descriptor or parameter space.
In principle, one must arrange molecular descriptors so that every molecule of the set \(\mathbb{M}\) becomes associated with a vector of sufficient arbitrary dimensions. Defining in this manner, a column vector set: \({\mathbb{D}} = \left\{ {\left| {{\mathbf{d}}_{I} } \right\rangle \left| {I = 1,M} \right.} \right\},\) is connected in a one-to-one correspondence with the molecular set \({\mathbb{M}}\), that is:
Consequently, this is equivalent to assuming that in a general QSPR formalism, one describes every molecule by a finite-dimensional vector in CQSPR or by an infinite-dimensional density function in QQSPR.
Such description prepares the molecular structures of point (a) to be considered elements of a molecular spaceFootnote 4 of the appropriate dimension.
Despite that, in the usual literature, such a molecular vector space definition appears systematically ignored; however, one cannot avoid the presence of the molecular structures described as vectors in QSPR calculations.
Even if AI manipulations lead to black box QSPR-like results, one cannot avoid this vector-molecule information source; for example, see references [6, 25, 26, 31, 32, 34, 36] for more evidence.
3 Systematic ordering of any molecular set
Admitting to start the discussion of the QQSPR problems with the three points of the previous section as a sound working foundation, one can systematically achieve a general QSPR ordering procedure.
First, one can compute the self-similarities of the molecular set, employing their description elements. Then one can order them according to their values. Therefore, this simple process generates a new order in the original molecular set.
Hypothetically, the ordering of the whole QSPR data set, as accepted by definition in point (a) of the previous paragraph, might be considered arbitrarily chosen as is usual in the QSPR literature.
Nevertheless, in parallel to the previous reordering, after unit interval standardization of the known property values as indicated in point (b) of the previous section, it is not too difficult to assume that this will allow us to easily compare the data of a particular QSPR calculation with any other one.
One could perform this kind of systematic standardization even if the compared problems correspond to different molecular sets or possess diverse inhomogeneous elements.
Therefore, as it seems from a logical point of view, it could be very interesting that one might systematically prepare QSPR procedures. And one performs this groundwork in the same way before obtaining the QSPR operator or function, relating the structure of the molecular set algebraic representation with their properties, regardless of the nature of the studied problem property.
One can thus consider every QSPR calculation comparable with any other. Not only might one transform the molecular property values set \({\mathbb{P}}\) into a normalized one, as indicated in reference [95], but one can also propose that one might standardize the molecular ordering, using selfsimilarities for this task.
A systematic reordering of the involved QSPR molecular set \({\mathbb{M}}\) would permit us to easily compare a particular calculation with any other submitted to an equivalent treatment.
3.1 QSPR ordering algorithm
Thus, one can propose obtaining a simple and effective universal ordering of the descriptor data set \(\mathbb{D}\) of any QSPR problem. To arrive to achieve this purpose, one might apply the following procedure.
One can start a QSPR ordering algorithm by using the elements of the molecular descriptor set \(\mathbb{D}\). One can easily obtain the norms of the vector representation of every molecule and further define their values as an additional set, like:
where one defines the metric signature matrix \(\Gamma_{M}\) as a diagonal matrix:
such that all the non-null diagonal elements contain only positive or negative units. That is, one can consider the definition of the following dimensions and diagonal matrices:
Thus, one can also consider the diagonal matrix \(\Gamma_{M}\) as isomorphic to an M-dimensional column vector \(\left| {\Gamma_{M} } \right\rangle\), with its elements containing the diagonal elements of the matrix \(\Gamma_{M}\), or as a matrix signature in the sense of reference [96].
On the other hand, one can also consider the norm set \(\mathbb{S}\) in the Eq. (2) as connected with a one-to-one correspondence to the molecular set: \({\mathbb{M}} \Leftrightarrow {\mathbb{S}}.\)
Admitting norms can be calculated for every molecular descriptor vector; this corresponds to associating such vectors, as defined within a Banach space, to the QSPR studied problem.
Proceeding in this way, not only the QSPR working space is a Banach space, but also a Minkowski space, which one can transform into a Euclidian oneFootnote 5 if needed. This possibility will be accomplished when the negative part role of the metric signature matrix \(\Gamma_{N}\) is absent, and thus the following equality holds:
where
is the \(\left( {M \times M} \right)\) unit matrix.Footnote 6
Now, adopting the vocabulary of quantum similarity, the \(\mathbb{S}\) set of the norms of the molecular vector representations contains the selfsimilarities attached to each element of the molecular set.
Suppose each molecular descriptor corresponds to a function, like in QQSPR, where electronic density functions are employed as molecular descriptor vectors; see, for example, references [42,43,44, 86]. In that case, the Euclidian norm of a finite-dimensional CQSPR vector is substituted by the integral of such squared QQSPR function.
According to the above definition, the norm set \(\mathbb{S}\) is made by a (sometimes positive) definite set of real (in computational practice, rational) numbers.
Hence, it is evident that one can easily reorder the set \(\mathbb{S}\) from, say, the smaller to the more significant (or vice versa) norm. Therefore, one can consider that the reordered subindices now mean that:
the symbol\(... \, m_{I} \prec m_{I + 1} \, ...\) means that the molecule \(m_{I}\) on the left precedes the molecule \(m_{I + 1}\) on the right.
From now on, we can suppose, before performing any proper QSPR calculation, that such supplementary order conditioning of the molecular set \(\mathbb{M}\) is complete.
Then one can consider that one now reorders the set \(\mathbb{M}\) in such a way that:
while:
or the other way around if necessary.
Proceeding in this manner, after knowing the possibility of ordering the QSPR data and elements of the set \(\mathbb{M}\), one can add a fourth term to the three initial conditions proposed in the previous section:
-
(d)
One might always perform QSPR calculations systematically on a molecular set \(\mathbb{M}\), ordered according to the increasing (alternatively: decreasing) values of the molecular selfsimilarities.
Moreover, according to the previous point (b), this will also be made in the company of a set of standardized property values, which shall be accordingly reordered.
4 Selfsimilarities and the similarity matrix (re-) and (de-) construction
Self-similarities thus play an essential role in QSPR procedures as a simple source of systematic data reordering. They have been studied deeply in the QQSPR framework [54, 97], but have been apparently ignored in CQSPR. This circumstance is due perhaps to molecular space oblivion in classical procedures.
Within this section, one will now develop a general procedure valid for both QSPR practical computational branches.
4.1 Definition of the similarity matrix
The selfsimilarity set \(\mathbb{S}\) corresponds to the diagonal elements of a symmetric matrix, the so-called similarity matrix; see for more information, for example, reference [60], which is an \(\left( {M \times M} \right)\) array that one can supposedly construct holding all the possible scalar products between the molecular descriptor vector pairs:
where one has explicitly used the diagonal metric signature matrix \(\Gamma_{M}\) to obtain, in this manner, a general picture of the similarity matrix computation.
Owing to this definition, one can also write the selfsimilarities set \(\mathbb{S}\) as the diagonal elements of the similarity matrix:
The possibility of constructing the similarity matrix, as in the Eq. (10), allows the molecular space to be associated with a Minkowskian pre-Hilbert space [83].
4.2 Similarity matrix properties
Moreover, the similarity matrix is coincident with the metric matrix of the vector (sub)space generated by the descriptor set \(\mathbb{D}\). This is so because in case every molecule in the set \(\mathbb{M}\) is different from the rest (which strictly corresponds to a more than a reasonable general situation in any QSPR data setup), then every molecular descriptor vector must be linearly independent of the other descriptor vectors. See for a discussion of this relevant point, for example, reference [84].
If the elements of set \(\mathbb{D}\) do not bear such an algebraic characteristic, then, in CQSPR procedures, one faces the so-called dimensionality paradox [85].
One might state such a condition attached to the descriptor set \(\mathbb{D}\) as a point added to the four previously discussed ones:
-
(e)
The molecular descriptor set \(\mathbb{D}\) in each QSPR problem must always be constructed as a set of linearly independent vectors in the molecular space.
As commented before, to avoid the dimensionality paradox, the dimension D of the vector space containing them must be: \(D \ge M\).
This necessary condition has no connection with the possibility of handling the CQSAR problem as a subject of statistical studies in parameter space. Constitutes instead an unavoidable preliminary condition that shall be attached to any molecular set mathematical description.
4.3 Successive approximations to the similarity matrix
Once the set of descriptor vectors \(\mathbb{D}\) is constructed and computed the similarity matrix via the Eq. (10), one might put forward some nuances related to the successive approximations of the matrix Z.
One can accept the set of the diagonal elements of the similarity matrix as an approximation of order zero. For this reason, we can also represent such a zeroth-order similarity matrix with the symbol \({\mathbf{Z}}_{0}\).
Starting with the diagonal zeroth-order similarity matrix, we can also consider as the next step the non-zero elements of the similarity matrix first sub-diagonals:
One constructs in this manner a tridiagonal matrix. Then, we can name the resultant matrix the first-order similarity matrix and represent it as: \({\mathbf{Z}}_{1}\).
Consequently, proceeding in this way and adding to the first-order matrix the next non-zero subdiagonals, larger band matrices can be stepwise constructed. Then one can obtain a sequence of M similarity matrices, which can be written as follows:
To adequately describe a simple algorithm leading to the above sequence (13) of approximate similarity matrices, we can first define a sequence of M matrices initially holding the diagonal and the successive sub-diagonals as the unique non-zero elements:
In this way, one can easily write the sequence of approximate similarity matrices (13), concerning the P-th order approximation as follows:
Therefore, such simple (re-)construction permits to build of a sequential set of similarity matrix approximations, which starts from the self-similarity diagonal and ends up with the full similarity matrix. A final approximation stage leading to the exact similarity matrix is reached when \(P = M - 1\). In this last step, the matrix \({\mathbf{D}}_{M - 1}\) possesses two non-zero elements only: \(z_{1,M - 1} = z_{M - 1,1} .\)
One can obtain a convenient (de-)construction of the similarity matrix by subtracting from the original similarity matrix the sequence of sub-diagonal matrices defined in the Eq. (14).
4.4 Eigenvalues and eigenvectors of the similarity matrix
One has postulated the eigenvalues and eigenvectors of the similarity matrix as building blocks to algebraically construct statistical-like moments of the molecular set \(\mathbb{M}\) [88].
One can use the momenta of the molecular set to construct a QSPR operator, too, see reference [78], able to compute a chosen molecular property. Furthermore, one might use condensed scalar momenta to represent geometrically and numerically the molecular set \(\mathbb{M}\) [88,89,90].
Still, by transforming the eigenvectors of the quantum similarity matrix into an isometric vector set, the resultant M-dimensional vector set can be admitted as the finite-dimensional representation of the infinite-dimensional quantum representation of the molecular set \(\mathbb{M}\).
A most interesting computational fact to be highlighted now corresponds to the zeroth-order approximation.
Indeed, the matrix \({\mathbf{Z}}_{0}\) is diagonal; thus, their eigenvalues are the diagonal elements themselves and the eigenvectors corresponding to \({\mathbf{I}}_{M}\), the unit matrix of the adequate dimension, which is, in fact, a \(\left( {M \times M} \right)\) matrix, like any eigenvector matrix related to higher-order approximations.
Therefore, calculating the moments of this zeroth-order similarity matrix becomes equivalent to computing the statistical moments of a scalar set made by the self-similarities \(\mathbb{S}\).
Besides the tridiagonal first-order matrix, the higher-order elements in the sequences (13) and (15) correspond to so-called symmetric band matrices.
4.5 Spectral indefiniteness of the similarity matrices and isometric vector representations
One can provide a remark now concerning the eigenvalues of the approximate similarity matrix sequence (13).
The zeroth order and the final exact similarity matrix are by construction positive definite whenever one chooses a Euclidian metric signature matrix \(\Gamma_{M} = {\mathbf{I}}_{M}\).
In some molecular QQSPR cases, the superposition of the involved molecules performed to obtain optimal similarity integrals [97, 98] might result in a non-definite exact similarity matrix [91, 92].
Such circumstantial spectral non-definiteness might also appear in part or all of the intermediate band similarity matrices. Thus, it may start in the tridiagonal form of the first-order approximation.
In all the cases of non-definite eigensystem sets, one can compute the isometric vectors [89] necessary to obtain the statistical-like moments of the molecular descriptor set (for a résumé of the computational details, see reference [91]), via a so-called synisometry procedure [92], where one uses the absolute values of the negative eigenvalues to avoid complex algebra.
However, a better way to proceed consists in using the scalar products definition, leading to computing the elements of the similarity matrices into a Minkowskian Banach space, as explained before in Sect. 3.1. For this purpose, a diagonal metric signature matrix holding the appropriate signs is assigned to the space directions; see [99] for extended mathematical details.
Of course, one retrieves the usual Euclidian space when the diagonal metric matrix coincides with the appropriate dimension unit matrix.
The possibility of working within a Minkowskian metric Banach space has been ignored in CQSPR, while this possible framework has been recently put forward in QQSPR [99].
Working in Minkowskian spaces in both QSPR contexts could enhance the possibilities of finding better ways to obtain ameliorated functions, relating molecular structure with their properties, with a simple mathematical variation.
4.6 Numerical problems concerning the similarity matrix when considered as a metric matrix
The computational problems about numerical instability of matrix diagonalization are well-known in numerical linear algebra and have been studied since old times; see, for example, reference [100].
Also, as a typical case study, the Hilbert matrix [101] corresponds to a positive definite metric matrix made of scalar products, defined with the basis set elements of a polynomial vector space. Depending on the machine’s precision and the chosen dimension, the Hilbert matrix becomes non-definite, even singular, for practical computational purposes.
Even if the similarity matrix elements are well-defined for a given QSPR problem, some weird numerical behavior is produced when diagonalization or inversion is involved.
The dimension of the manipulated matrix and the finite machine precision could produce that a positive definite matrix numerically behaves as a non-definite one.
A similar problem also occurs in systematic quantum chemical calculations involving large basis sets. In these cases, the overlap matrix is nothing else than a metric matrix attached to the atomic basis set and has well-defined elements. Consequently, it has to be positive definite but computationally becomes non-definite or even singular in some cases due to numerical instabilities of the same sort as previously discussed here.
The quantum similarity representation of the periodic table of the elements, with the use of Gaussian atomic densities attached to each atom, was presented in previous work[102].Footnote 7 This study generates the same numerical problem when computing the similarity matrix, even with a simple function used as an atomic quantum descriptor.
Thus, one must be aware that in molecular spaces, when handling large numbers of molecules in a QSPR problem, the complete similarity matrix could become numerically singular. In those cases, deconstructing the similarity matrix could be good advice.
5 Isometric QQSPR molecular spaces
CQSPR and QQSPR Molecular Spaces can be associated with a similarity matrix constructed using the implicit algorithm in the Eq. (10).
However, the similarity matrix in the QQSPR environment can only be constructed via a set of positive integrals, holding a volume or measure, which are not so easy to compute, using pairs of molecular electronic density functions.
It could be interesting without leaving the QQSPR framework to obtain an isometric finite-dimensional representation of the involved molecular set, emulating the CQSPR background structure, but providing a general automated way to construct the molecular description vectors.
In obtaining this isometric description, both CQSPR and QQSPR ways will appear on the same footing to describe the involved molecular set algebraically.
Some attempts to reach this goal have been described recently [91, 92], but a new study [99] contains the most general and exact algorithm, as far as we know.
For effectiveness, this procedure, developed from the vantage point of the inward vector products, will be sketched from a matrix point of view.
5.1 Towards the construction of an isometric vector set
The quantum similarity matrix Z, as defined in the Eq. (10), is a symmetric one, that is: \({\mathbf{Z}} = {\mathbf{Z}}^{T}\). As such, always exists to it an attached secular equation, which one can write in matrix form:
where \({\mathbf{U}}\) corresponds to an orthonormal matrix:
containing the eigenvectors of Z as columns, and the matrix \(\Theta\) is diagonal:
it contains the eigenvalues of Z, ordered the same way as the column vectors in U.
As commented, when issued from a computed quantum similarity matrix, the diagonal matrix \(\Theta\) could be non-definite. But one can rewrite it with a metric signature matrix \(\Gamma_{M}\), as described early in the Eqs. (3) and (4).
First, defining the auxiliary definite positive diagonal matrix:
then one can retrieve the original eigenvalues matrix and write:
In this case, one can construct the metric signature matrix with the aid of a pair of logical Kronecker’s deltas:
With this eigenvalue rearrangement, one can also define the square root of the unsigned eigenvalues matrix:
and using the commutativity of the product of diagonal matrices, one can write:
thus, rearranging the Eq. (16), plus taking into account the Eqs. (17), (19), (20), (22), and (23), one can write:
where a new matrix, holding the isometric vectors as columns, is defined as:
The column vector set \({\mathbb{D}} = \left\{ {\left| {{\mathbf{d}}_{I} } \right\rangle \left| {I = 1,M} \right.} \right\} \subset {\mathbb{V}}_{M}\), which has to be used to compute the scalar products with the appropriate metric signature matrix via the Eq. (24), can be seen in the same manner as the elements described in the Eq. (10). They constitute a set of vectors isometric to the quantum density functions representing the molecules in the studied set.
The earlier synisometric vectors, see reference [99] for more details, are constructed by transforming the metric signature matrix into a Euclidian metric matrix. That is: simply performing the substitution: \(\Gamma_{M} \to {\mathbf{I}}_{M}\), in the Eq. (24), thus, constituting an obvious simplification and ignoring the presence of a possible Minkowskian metric, which can be crucial in some cases to obtain a suitable molecular structure–property relation.
5.2 The discrete representation of a molecular set nature
As a consequence of the discussion in the preceding Sect. 5.1, in both QSPR environments, one can arrive at the description of a molecular set constructed as a set of vectors belonging to a vector space of similar characteristics and dimensions. However, even if the set of discrete vectors \(\mathbb{D}\) seems equivalent in both classical and quantum procedures, their nature is quite different.
The construction of the classical \(\mathbb{D}\) vector set is, in many aspects, arbitrary, as it contains intrinsic difficulties in distinguishing and including as descriptors some molecular attributes, like conformation structures, electronic states, and optical isomers…, to mention some obvious ones. Even if the algorithms operating in CQSPR and AI claim a quantum origin of the parameters or descriptors employed in the molecular description, see the already cited papers [6, 25, 26, 31, 32, 34, 36].
Such drawbacks are not necessarily present in the quantum way of determining the elements of \(\mathbb{D}\). The precise, general character connected to quantum procedures must always be present in the systematic construction and use of the vector set \(\mathbb{D}\).
Even being aware of this classical drawback in front of the quantum algorithm, one can additionally enunciate a new point in the data manipulation of a QSPR molecular set representation:
-
(f)
One can transform the vector representation \(\mathbb{D}\), attached to any molecular set \(\mathbb{M}\), into an isometric vector set that generates the original similarity matrix and can be further used to describe \(\mathbb{M}\).
6 The vector set \(\mathbb{D}\) geometric connection: construction of a molecular polyhedron and the statistical-like manipulation of its elements
Here will be summarized the theoretical background of constructing a set of statistical-like parameters, which can be employed to describe in a condensed manner any molecular set \(\mathbb{M}\) via the vectors of the descriptor set \(\mathbb{D}\).
Such statistical-like parameters can also be associated with a set of collective distances [90].
Theoretical, computational, and practical details of this issue have been published in many instances [88, 89, 93, 94, 98, 99, 102], so only one will describe here the backbone of this general possibility.
6.1 Molecular polyhedra: centroid and origin shift
The first element of this descriptor transformation considers the set \(\mathbb{D}\) as a many-dimensional polyhedron or polytope (here, one will select the first name in front of the second). That is: a mathematical object containing M vertices associated with every vector in the set \(\mathbb{D}\). One can also name this geometric image of the set \(\mathbb{D}\) as a molecular polyhedron.
Admitting this, the centroid of this geometrical structure is easily calculated by:
From there, one can follow the systematic transformation of the description of the set \(\mathbb{M}\) by defining a new vector descriptor set possessing a cero centroid, namely:
this result generally corresponds to an algorithm transforming any molecular descriptor set into a new vector set \(\mathbb{G}\) possessing a null centroid.
In general, one can perform this redescription on any molecular set. It corresponds to obtaining a molecular polyhedron with a unique origin at the vector \(\left| {\mathbf{0}} \right\rangle\).
One can refer to this transformation as an origin shift of the initial molecular polyhedron described by the vector elements of the set \(\mathbb{D}\). Such a possibility allows to add of a new point to the already described set of conditions of QSPR data:
-
(g)
Knowing an isometric vector representation \(\mathbb{D}\) of a molecular set \(\mathbb{M}\) is the same as defining a molecular polyhedron. Then a centroid can be calculated. Hence, an origin shift can be performed on \(\mathbb{D}\), producing a new descriptor set, the origin-shifted molecular polyhedron \(\mathbb{G}\), bearing a zero centroid.
This M-dimensional possibility corresponds to the origin shift one can perform in one-dimensional scalar sets, as is usual in statistical lore, by subtracting the arithmetic mean from every set element.
6.2 Momenta of the molecular polyhedron
Once generating an origin-shifted molecular polyhedron \(\mathbb{G}\), one can use its elements to construct a set of statistical-like momenta, a set of vectors that condensate the information contained in the vector representation of the molecular set \(\mathbb{M}\).
One can describe the set of vector momenta as the average sum of the successive inward powers of the vectors in the origin-shifted polyhedron. One can define such inward powers as:
remarking diagonal metric matrix presence associated with the QSPR problem.
In the Eq. (28), one can easily define by the following algorithm, see for example [89] for more details, the inward P-th power of a vectorFootnote 8:
Owing to the vector power definition (29), the molecular polyhedron momenta, as defined in the Eq. (28), represent in the framework of vector spaces the same as the statistical momenta of a set of scalars. Thus, one can call the vectors described in the Eq. (28) the statistical-like vector momenta of the molecular polyhedron.
Then, the centroid corresponds to a first-order momentum: \(P = 1\), and becomes null for the origin-shifted molecular polyhedra. The vector momenta calculated with the values \(P = 2,3,4\) have the roles of variance, skewness, and kurtosis but in the framework of vector sets instead of scalar sets.
One can reduce the vector moments into scalars just by performing the complete sum of the elementsFootnote 9 of every momentum vector, as we can define, see for example [89], the complete sum of the elements of any vector as:
Knowing that, by calculating the complete sum of a vector, also one can describe the contribution of every molecular structure to the total momentum. One can use the metric matrix as a vector submitted to a scalar product, that is:
Then, the set of elements:
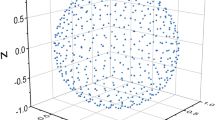
can be reordered, forming a column vector: \(\left| {{{\varvec{\upgamma}}}^{\left( P \right)} } \right\rangle = \left( {\gamma_{1}^{\left( P \right)} ,\gamma_{2}^{\left( P \right)} ,...\gamma_{M}^{\left( P \right)} } \right)^{T}\) which can be used as coordinates to locate the molecules of the set \(\mathbb{M}\) as a set of points in some Cartesian plot. For example, one can draw the molecular set’s elements: \(P = 2,3,4\) as a set of three-dimensional points: \(\left\{ {\gamma_{J}^{\left( 2 \right)} ,\gamma_{J}^{\left( 3 \right)} ,\gamma_{J}^{\left( 4 \right)} } \right\}\left( {J = 1,M} \right)\), representing every molecule in the set \(\mathbb{M}\).
Therefore, one can use origin-shifted molecular polyhedra momenta to characterize a molecular set and, in this manner, visualize a possible reordering within the molecular set \(\mathbb{M}\) by drawing each molecule as a point in a 1-, 2-, or 3-dimensional graph.
7 The QQSPR operator
From the first published applied quantum similarity developments, the possibility of defining a QQSPR operator has been repeated speculation; for example, see references [44, 45, 50, 60, 65]. Recently, one has discussed the possibility of defining some operator that, applied to the density function, provides an expectation value connected with a given property of interest. Some examples were given [78].
That is, one could construct some Hermitian operator \(\Omega \left( {\mathbf{r}} \right)\) in such a way that, using a quantum mechanical molecular electronic density function \(\rho \left( {\mathbf{r}} \right)\), acting as a distribution function, one can compute the expectation value of some property \(\pi\) through the integral:
When solving a QQSPR problem, as has been done at the beginning of the present work, recalling the nature, properties, and mathematical description of a molecular set \(\mathbb{M}\), one supposedly knows a set of electronic density functions: \({\mathbb{P}} \left\{ {\rho_{I} \left( {\mathbf{r}} \right)\left| {I = 1,M} \right.} \right\}\), associated in a one-to-one correspondence with the molecular set elements, that is: \({\mathbb{M}} \Leftrightarrow {\mathbb{P}}\).
7.1 Quantum similarity matrices
Quantum similarity permits the construction of the so-called similarity matrix via volume integrals, which in this case, one can generally write as:
where one can choose the weight operator \(O\left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} } \right)\) positive definite. Usually, one uses Dirac’s function \(\delta \left( {{\mathbf{r}}_{1} - {\mathbf{r}}_{2} } \right)\), which transforms the integral in the Eq. (34) into a so-called quantum overlap similarity matrix:
Thus, one habitually computes the quantum similarity matrix as the integral array:
an expression formally connected with the discrete construction of the Eq. (10). The manipulation described in Sect. 5 is applicable because Z is a symmetric \(\left( {M \times M} \right)\) matrix. Then a discrete isometric vector set of quantum mechanical origin can be obtained, as described in Sect. 5.1, connecting in this way CQSPR with QQSPR.
One computes the integrals entering the Eq. (36) by superimposing (rotating and translating) the attached different molecular pairs \(\left\{ {m_{I} ,m_{J} } \right\}\),Footnote 10 until each integral becomes maximal; for example, see reference [103].
This manipulation of the molecular pairs produces overlap quantum similarity matrices that are not definite, leading to the presence of a metric signature matrix \(\Gamma_{M}\), as defined in the Eq. (21), in the posterior use of the isometric vector set \(\mathbb{D}\).
7.2 The QQSPR operator
To solve any QQSPR problem, it is not sufficient to construct the quantum similarity matrix. One must use the Eq. (33) to build an algorithm to evaluate the unknown property values of some molecular elements present in a molecular set.
A possible way to obtain an adequate QQSPR algorithm corresponds to constructing the QQSPR operator as a Taylor-like series [110] inspired by some old Lowdin’s work [104,105,106], with each molecular density function acting as a variable. Assuming this option, we can write:
the coefficient set \(\left\{ {\omega_{P} \left| {P = 0,\infty } \right.} \right\}\), considered constant among the whole molecular set, characterizes the operator (37) for a given problem as a set of expectation values and is attached to the powers of any density function adequate for the operator and associated with each molecule in the set \(\mathbb{M}\).
The Eq. (37) represents a general Taylor-like expression of the function representing the sought QQSPR operator; therefore, one can explicitly write the inverses of the factorials, substituting the coefficient set \(\left\{ {\omega_{P} \left| {P = 0,\infty } \right.} \right\}\) by the set:
however, this possibility will not be explicitly used in this discussion. Yet, it might be advantageous to scale Taylor-like series coefficients in practical computations.
The Eq. (33) now can be written for a specific molecular structure \(m_{I}\) using the Eq. (37), yielding:
a result that demands computation of the density function powers up to some value. Estimating some molecular property needs the calculation of self-similarities up to some chosen order Q + 1, truncating the Taylor series in this way (37).
One must note here that the expectation values set: \({{\varvec{\Pi}}} = \left\{ {\pi_{I} \left| {I = 1,M} \right.} \right\}\), are not the same as the initial property values set P described in point (b) of Sect. 2.
As explained before, the integrals shown in the expression (39) do not present the superposition problem when calculated as in the overlap quantum similarity matrix. Because all of them belong to the same molecular structure, as density function powers grew, integral computation times might present a problem, even with simplified densities and modern computer facilities.
7.3 QQSPR equations
The following array can contain the integrals described in the Eq. (39):
so using the vectors: \(\left| {{\varvec{\uppi}}} \right\rangle = \left( {\pi_{1} ,\pi_{2} ,...\pi_{M} } \right)^{T}\) and \(\left| {{\varvec{\upomega}}} \right\rangle = \left( {\omega_{0} ,\omega_{1} ,...\omega_{P} ,...} \right)^{T}\), one can compactly rewrite the Eq. (39) as:
One can solve the Eq. (41) by constructing a pseudoinverse matrix. Just multiply the Eq. (41) on the left by \({\mathbf{Q}}^{T}\), obtaining the expression:
That is a matrix expression permitting to compute the coefficient vector \(\left| {{\varvec{\upomega}}} \right\rangle ,\) which allows the construction of the QQSPR operator.
7.4 Practical use of the QQSPR equation
There are two aspects of the QQSPR Eq. (39) to obtain unknown values from the density function and the QQSPR operator. Equation (42) permits to obtain the coefficients defining the operator up to some approximation, for instance: \(\left\{ {P = 0,Q} \right\}\), by using the elements of the matrix Q obtained by the Eq. (40) and some known values of the property.
7.4.1 Approximate matrix Q
The first aspect one has to consider corresponds to how to plausibly compute the elements of the matrix Q. One will study it here in some detail.
One can easily construct the matrix Q with the aid of ASA approximate electronic density functions [107, 108] and an extension of the Gaussian product theorem, published some years ago [109].
But a better way to overcome the large amount of computation needed to implement the Eq. (40), corresponds to using the set of isometric vectors, as previously defined in Sects. 5.1 and 6.1.
One can use both kinds of vectors. In case one chooses the raw isometric vector set \(\mathbb{D}\) as a finite-dimensional vector set representing the molecular set, then one can rewrite the Eq. (40) as:
It is also considering the Eq. (43) that the inward power of the isometric vectors must bear the signature metric matrix.
One can obtain a similar expression with the vertices of the molecular polyhedron \(\mathbb{G}\), which, as earlier described, are the isometric vectors of the set \(\mathbb{D}\) origin-shifted by the centroid. Because this substitution is trivial, it will no longer be mentioned in the following, but one has to keep in mind both possible alternative uses of the sets \(\mathbb{D}\) or \(\mathbb{G}\).
Obtaining an approximate Q matrix via Eq. (43) permits finding the QQSPR operator coefficients in the same way as in the exact solution (42).
One has to account for another parameter: the limit that has to be reached in the series leading to the QQSPR operator. We can admit that for a given problem, the maximal value of the power is \(\max \left( P \right) = Q\), and then construct the matrices and vectors accordingly. From now on, this limit will be used in the appropriate places of the equations bearing it.
7.4.2 Use of the QQSPR operator to estimate unknown values of some property
The second aspect one has to be aware of corresponds to applying the QQSPR operator over the density of a molecule with an unknown property to evaluate it. One has already studied and published [SS] various facets of this problem, contemplating variants and the general case. Here, one will only sketch and circumscribe it to the case where one evaluates a unique molecular property.
The preliminary step corresponds to suppose that to the molecular set M of known property values, one adds a new structure with an unknown property value: \(\pi_{u}\). The problem can be analyzed considering that now one deals with \(M + 1\) molecular structures and that one has to dimension the matrix Q accordingly, having in this manner the structure:
where the row vector \(\left\langle {{\mathbf{q}}_{u} } \right|\) now contains the new elements involving the added molecule, that is:
or using the isometric vectors:
Then one can rewrite the Eq. (41) as follows:
and now: \(\left\{ {\left| {{\varvec{\upomega}}} \right\rangle ;\pi_{u} } \right\}\) are the unknowns to be found.
One can easily prepare an iterative procedure in this case. Supposing that the order of the density power series is Q, then starting with an approximate value of the unknown property, using the Q-dimensional coefficients calculated without the unknown property molecule, say \(\left| {{{\varvec{\upomega}}}^{0} } \right\rangle\):
or
Using the approximate property value obtained by the Eqs. (48) or (49) in the Eq. (47), then one can solve the Eq. (47) to obtain new component values for the vector \(\left| {{\varvec{\upomega}}} \right\rangle\):
Note that the dimension of the coefficient vector doesn’t change if one keeps the approximation order of Eqs. (39) or (43) to a constant value Q.
However, keeping the order Q constant is not compulsory, so the approximation order can be considered free to vary within the iteration cycles.
Now one can obtain a restored value of the unknown property using alternatively up to convergence Eq. (50) while using the refreshed coefficient vector \(\left| {{\varvec{\upomega}}} \right\rangle\) in the corresponding equation:
or
The iteration process can stop when values of the variation of the estimated unknown property in two successive iterations appear below a given threshold.
One can easily generalize the procedure when the unknown property is associated with several newly added molecular structures; for more details, see reference [103].
8 Conclusions
One has discussed a complete review of the mathematical structure and algorithms used to solve QSPR problems in molecular spaces.
Along the development of this study, one can observe that classical or quantum procedures can be brought to the same footing and associated with the isometric description of the molecular vectors representing the elements of a molecular set.
One has described in the present study the whole algorithmic structure of molecular spaces QSPR. One can resume it in seven points enumerated with the seven first letters of the alphabet within the text: [(a), (b), (c), (d), (e), (f), (g)}. Such seven points summarize the body of molecular space QSPR procedures.
They can be summarized as follows:
-
One knows a molecular set associated with some property.
-
One can construct an appropriate dimension molecular space.
-
One can compute molecular selfsimilarities to reorder the molecular data.
-
One can assemble a molecular descriptor-independent vector set in molecular space.
-
One can build an isometric vector set.
-
One can construct a molecular polyhedron.
Finally, with the data resulting from the previous manipulations, one can set up the algorithm of QSPR in molecular space.
In future work, one will present applications of the various proposed algorithms.
Notes
The acrostic QSPR will be used in the present study, as it is preferable to the less general QSAR. However, it must be remarked that both mean the same intent of finding a relationship between molecular properties and some chosen mathematical representation of molecular structures.
Certainly not in chemical spaces, see for example the discussion on chemical spaces in reference [1], as it appears to be the wrong attributed name in the current literature, which is systematically given to the representation subsets of molecular structures, susceptible to manipulation within QSPR techniques, see for example. Molecular spaces appear to be the logically correct name for collecting molecular study sets represented by some mathematical vector structure.
The dimension D choice is imposed by the number of molecules, as the molecular space dimension has to be such that the vectorial molecular description makes all the molecules linearly independent. This asseveration comes from the fact that in a QSPR problem, all the molecules are chosen as being different. Therefore, their mathematical representations shall differ, and consequently, the attached vectors representing the molecules shall form a linearly independent set.
It must be repeated here that the current literature associated with QSPR publications generally uses the concept of chemical space to name the construct described here as molecular space. As previously commented, this last terminology is preferable to the former one in the present author’s opinion.
Such a possibility corresponds to a general procedure where the metric signature matrix is transformed into the unit matrix, according to the synisometry algorithm of reference [91].
Here is used a logical Kronecker delta definition; in general, by writing: \(\delta \left( {.expression.} \right)\). If the logical.expression. is true then \(\delta \left( {.T.} \right) = 1\) or if false, then \(\delta \left( {.F.} \right) = 0\).
This problem was avoided in the cited work using a raw zeroth order approach to the similarity matrix.
The inward product or power of a vector is also known as diagonal, Hadamard, or Schur product or power.
The complete sum of the elements of a vector is a well-defined linear operator acting on any vector space element.
Except for the diagonal selfsimilarities that do not need superimposition.
References
J.-L. Reymond, The chemical space project. Acc. Chem. Res. 48, 722–730 (2015)
Ch.A. Lipinski, F. Lombardo, B.W. Dominy, P.J. Feeney, Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Adv. Drug Deliv. Rev. 46, 3–26 (2001)
V. Venkatraman, P.R. Chakravarthy, D. Kihara, Application of 3D Zernike descriptors to shape-based ligand similarity analysis. J. Cheminform. 1, 1–19 (2009)
I. Mitra, P.P. Roy, S. Kar, P.K. Ojha, K. Roy, On further application of as a metric for validation of QSAR models. J. Chemometr. 24, 22–33 (2010)
M. Devereux, P.L. Popelier, In silico techniques for the identification of bioisosteric replacements for drug design. Curr. Top. Med. Chem. 10, 657–658 (2010)
M.A. Nielsen, I.L. Chuang, Quantum computation and quantum information (Cambridge University Press, Cambridge, 2010)
T. Puzyn, J. Leszczynski, M.T.D. Cronin, Recent advances in QSAR studies. Methods and applications (Springer, Heidelberg, 2010). https://doi.org/10.1007/978-1-4020-9783-6
A. Varnek, I.I. Baskin, Chemoinformatics as a theoretical chemistry discipline. Mol. Inf. 30, 20–32 (2011)
P. Gramatica, S. Cassani, P.P. Roy, S. Kovarich, Ch.W. Yap, E. Papa, QSAR modelling is not ‘push a button and find a correlation’: a case study of toxicity of (benzo-)triazoles on algae. Mol. Inf. 31, 817–835 (2012)
W.-H. Shin, X. Zhu, M.G. Bures, D. Kihara, Three-dimensional compound comparison methods and their application in drug discovery. Molecules 20, 12841–12862 (2015). https://doi.org/10.3390/molecules200712841
R.N. Das, T. Sintra, J.A.P. Coutinho, S.P.M. Ventura, K. Roy, P.L. Popelier, Development of predictive QSAR models for Vibrio fischeri toxicity of ionic liquids and their true external and experimental validation tests. Toxicol. Res. 5, 1388–1399 (2016). https://doi.org/10.1039/C6TX00180G
N. Sizochenko, A. Gajewicz, J. Leszczynskib, T. Puzyn, Causation or only correlation? Application of causal inference graphs for evaluating causality in nano-QSAR models. Nanoscale 8, 7203 (2016)
F. Pizzo, A. Lombardo, A. Manganaro, E. Benfenati, A new structure-activity relationship (SAR) model for predicting drug-induced liver injury, based on statistical and expert-based structural alerts. Front. Pharmacol. 7, 442 (2016). https://doi.org/10.3389/fphar.2016.00442
H.A. Gaspar, I.I. Baskin, A. Varnek, Visualization of a multidimensional descriptor space, in Frontiers in molecular design and chemical information science—Herman Skolnik Award Symposium 2015. ACS Symposium Series. (American Chemical Society, Washington, DC, 2016)
P. Wang, X. Xu, S. Liao, J. Song, G. Fan, S. Chen, Z. Wang, Quantitative structure–activity relationship study of amide mosquito repellents. SAR QSAR Environ. Res. 28, 341–353 (2017)
B.J. Neves, R.C. Braga, C.C. Melo-Filho, J.T. Moreira-Filho, E.N. Muratov, C.H. Andrade, “QSAR-based virtual screening” advances and applications in drug discovery. Front. Pharmacol. 9, 1275 (2018). https://doi.org/10.3389/fphar.2018.01275
A.A. Toporov, R. Carbó-Dorca, A.P. Toporova, Index of ideality of correlation: a criterion of predictability of QSAR models for toxicity to fathead minnow (Pimephales promelas). Struct. Chem. 29, 33–38 (2018)
S. Kausar, A.O. Falcao, Analysis and comparison of vector space and metric space representations in QSAR modeling. Molecules 24, 1698–1720 (2019)
I.I. Baskin, N.I. Zhokhova, Continuous molecular fields and the concept of molecular co-fields in structure-activity studies. Future Med. Chem. (2019). https://doi.org/10.4155/fmc-2018-0360
C.L. Bellera, A. Talevi, Quantitative structure-activity relationship models for compounds with anticonvulsant activity. Expert Opin. Drug Discov. (2019). https://doi.org/10.1080/17460441.2019.1613368
S. Brogi, T.C. Ramalho, J.L. Medina-Franco, K. Kuca, M. Valko, In silico methods for drug design and discovery (Frontiers Media SA, Lausanne, 2020). https://doi.org/10.3389/978-2-88966-057-5
S.C. Basak, Some comments on the three-pronged chemobiodescriptor approach to QSAR- a historical view of the emerging integration. Curr. Comput.-Aided Drug Des. 17, 703 (2021)
A.G. Atanasov, S.B. Zotchev, V.M. Dirsch et al., Natural products in drug discovery: advances and opportunities. Nat. Rev. Drug Discov. 20, 200–216 (2021). https://doi.org/10.1038/s41573-020-00114-z
R.A. Miranda-Quintana, J. Smiatek, Electronic properties of amino acids and nucleobases: similarity classes and pairing principles from chemical reactivity indices. Phys. Chem. Chem. Phys. 24, 22477 (2022)
J. Bajorath, A.L. Chávez-Hernández, M. Duran-Frigola, E. Fernández de Gortari, J. Gasteiger, E. López-López, G.M. Maggiora, J.L. Medina-Franco, O. Méndez-Lucio, J. Mestres, R.A. Miranda-Quintana, T.I. Oprea, F. Plisson, F.D. Prieto-Martínez, R. Rodríguez-Pérez, P. Rondón-Villarreal, F.I. Saldívar-Gonzalez, N. Sánchez-Cruz, M. Valli, Chemoinformatics and artificial intelligence colloquium: progress and challenges in developing bioactive compounds. J. Cheminform. 14, 82 (2022)
S. Gugler, M. Reiher, Quantum chemical roots of machine-learning molecular similarity descriptors. J. Chem. Theory Comput. 18, 6670–6689 (2022). https://doi.org/10.1021/acs.jctc.2c00718
M. Manathunga, A.W. Götz, K.M. Merz Jr., Computer-aided drug design, quantum-mechanical methods for biological problems. Curr. Opin. Struct. Biol. 75, 102417 (2022). https://doi.org/10.1016/j.sbi.2022.102417
F.I. Saldívar-González, J.L. Medina-Franco, Approaches for enhancing the analysis of chemical space for drug discovery. Expert Opin. Drug Discov. (2022). https://doi.org/10.1080/17460441.2022.2084608
E. López-López, E. Fernández de Gortari, J.L. Medina-Franco, Yes SIR! On the structure-inactivity relationships in drug discovery. Drug Discov. Today (2022). https://doi.org/10.1016/j.drudis.2022.05.005
K. Nesmerák, A. Toporov, I. Yildiz, QSAR based on optimal descriptors as a tool to predict antibacterial activity against Staphylococcus aureus. Front. Biosci. (Landmark Ed) 27, 112–125 (2022)
C. Gorgulla, A. Kumar Nigam, M. Koop, S. Selim Cınaroglu, Ch. Secker, M. Haddadnia, A. Kumar, Y. Malets, A. Hasson, M. Li, M. Tang, R. Levin-Konigsberg, D. Radchenko, A. Kumar, M. Gehev, P. Aquilanti, H. Gabb, A. Alhossary, G. Wagner, A. Aspuru-Guzik, Y.S. Moroz, K. Fackeldey, H. Arthanari, VirtualFlow 2.0—the next generation drug discovery platform enabling adaptive screens of 69 billion molecules. bioRxiv (2023). https://doi.org/10.1101/2023.04.25.537981
N.-M. Koutroumpa, K.D. Papavasileiou, A.G. Papadiamantis, G. Melagraki, A.A. Afantitis, Systematic review of deep learning methodologies used in the drug discovery process with emphasis on in vivo validation. Int. J. Mol. Sci. 24, 6573 (2023). https://doi.org/10.3390/ijms24076573
R. Pal, P.K. Chattaraj, Development of quantitative structure-activity relationship models based on electrophilicity index: a conceptual DFT-based descriptor, in Big data analytics in chemoinformatics and bioinformatics. (Elsevier, Amsterdam, 2023), pp.219–229. https://doi.org/10.1016/B978-0-323-85713-0.00020-7
E. López-López, J.L. Medina-Franco, Towards decoding hepatotoxicity of approved drugs through navigation of multiverse and consensus chemical spaces. Biomolecules 13, 176 (2023). https://doi.org/10.3390/biom13010176
A. Ousaa, A.I. Taourati, M. Chiban, S. Chtita, M. Ghamali, F. Guenoun, T. Lakhlifi, M. Bouachrine, Discovery of new inhibitors of Sars-CoV: QSAR study using density functional theory (DFT) and statistical methods. J. Mater. Environ. Sci. 14, 326–336 (2023)
M. Moret, I. Pachon Angona, L. Cotos, S. Yan, K. Atz, C. Brunner, M. Baumgartner, F. Grisoni, G. Schneider, Leveraging molecular structure and bioactivity with chemical language models for de novo drug design. Nat. Commun. 14, 114 (2023). https://doi.org/10.1038/s41467-022-35692-6
M.J. Falaguera, J. Mestres, Illuminating the chemical space of untargeted proteins. J. Chem. Inf. Model. (2023). https://doi.org/10.1021/acs.jcim.2c01364
D. Paul, M. Arockiaraj, K. Jacob, J. Clement, Multiplicative versus scalar multiplicative degree-based descriptors in QSAR/QSPR studies and their comparative analysis in entropy measures. Eur. Phys. J. Plus 138, 323 (2023). https://doi.org/10.1140/epjp/s13360-023-03920-7
A.P. Toropova, A.A. Toropov, A. Roncaglioni, E. Benfenati, The system of self-consistent models: QSAR analysis of drug-induced liver toxicity. Toxics 11, 419 (2023). https://doi.org/10.3390/toxics11050419
A.A. Toropov, D. Barnes, A.P. Toropova, A. Roncaglioni, A.R. Irvine, R. Masereeuw, E. Benfenati, CORAL models for drug-induced nephrotoxicity. Toxics 11, 293 (2023). https://doi.org/10.3390/toxics11040293
R. Carbó, L. Leyda, M. Arnau, How similar is a molecule to another? An electron density measure of similarity between two molecular structures. Int. J. Quant. Chem. 17, 1185–1189 (1980)
R. Carbó, B. Calabuig, Molecular quantum similarity measures and N-dimensional representation of quantum objects. I. Theoretical foundations. Int. J. Quant. Chem. 42, 1681–1693 (1992)
R. Carbó, B. Calabuig, Quantum similarity measures, molecular cloud description and structure-properties relationships. J. Chem. Inf. Comput. Sci. 32, 600–606 (1992)
R. Carbó, E. Besalú, B. Calabuig, L. Vera, Molecular quantum similarity: theoretical framework, ordering principles, and visualization techniques. Adv. Quant. Chem. 25, 253–313 (1994)
R. Carbó, E. Besalú, Theoretical foundation of quantum similarity, in Molecular similarity and reactivity: from quantum chemical to phenomenological approaches. Understanding chemical reactivity, vol. 14, ed. by R. Carbó (Kluwer Academic Publishers, Amsterdam, 1995), pp.3–30
R. Carbó, E. Besalú, L. Amat, X. Fradera, Quantum molecular similarity measures (QMSM) as a natural way leading towards a theoretical foundation of quantitative structure-properties relationships (QSPR). J. Math. Chem. 18, 237–246 (1995)
L. Amat, E. Besalú, X. Fradera, R. Carbó-Dorca, Application of molecular quantum similarity to QSAR. Quant. Struct.—Act. Relat. 16, 25–32 (1997)
L. Amat, D. Robert, E. Besalú, R. Carbó-Dorca, Molecular quantum similarity measures tuned QSAR: an antitumoral family validation study. J. Chem. Inf. Comput. Sci. 38, 624–631 (1998)
L. Amat, R. Carbó-Dorca, R. Ponec, Molecular quantum similarity measures as an alternative to log P values in QSAR studies. J. Comput. Chem. 19, 1575–1583 (1998)
R. Carbó-Dorca, E. Besalú, A general survey of molecular quantum similarity. J. Mol. Struct. (Theochem) 451, 11–23 (1998)
X. Gironés, L. Amat, R. Carbó-Dorca, Using molecular quantum similarity measures as descriptors in quantitative structure-toxicity relationships. SAR QSAR Environ. Res. 10, 545–556 (1999)
D. Robert, L. Amat, R. Carbó-Dorca, 3D QSAR from tuned molecular quantum similarity measures: prediction of the CBG binding affinity for a steroids family. J. Chem. Inf. Comput. Sci. 39, 333–344 (1999)
D. Robert, R. Carbó-Dorca, Aromatic compounds aquatic toxicity QSAR using molecular quantum similarity measures. SAR QSAR Environ. Res. 10, 401–422 (1999)
L. Amat, R. Carbó-Dorca, R. Ponec, Simple linear QSAR models based on quantum similarity measures. J. Med. Chem. 42, 5169–5180 (1999)
X. Gironés, L. Amat, R. Carbó-Dorca, Descripció de propietats moleculars i activitats biològiques emprant l’energia de repulsió electró-electró. Sci. Gerund. 24, 197–208 (1999)
X. Gironés, L. Amat, R. Carbó-Dorca, Use of electron-electron repulsion energy as a molecular description in QSAR or QSPR studies. J. Comput. Aided Mol. Des. 14, 477–485 (2000)
R. Carbó-Dorca, L. Amat, E. Besalú, X. Gironés, D. Robert, Quantum mechanical origin of QSAR: theory and applications. J. Mol. Struct. (Theochem) 504, 181–228 (2000)
R. Carbó-Dorca, Quantum QSAR and the eigensystems of stochastic quantum similarity matrices. J. Math. Chem. 27, 357–376 (2000)
D. Robert, X. Gironés, R. Carbó-Dorca, Molecular quantum similarity measures as descriptors for quantum QSAR. Polycycl. Aromat. Comp. (ISPAC17) 19, 51–71 (2000)
R. Carbó-Dorca, E. Besalú, Quantum theory of QSAR. Contrib. Sci. 1, 399–422 (2000)
R. Carbó-Dorca, Inward matrix products: extensions and applications to quantum mechanical foundations of QSAR. J. Mol. Struct. (Teochem) 537, 41–54 (2001)
E. Besalú, X. Gironés, L. Amat, R. Carbó-Dorca, Molecular quantum similarity and the fundaments of QSAR. Acc. Chem. Res. 35, 289–295 (2002)
R. Carbó-Dorca, E. Besalú, Fundamental quantum QSAR (Q2SAR) equation: extensions, non-linear terms, and generalizations within extended Hilbert-Sobolev spaces. Int. J. Quant. Chem. 88, 167–182 (2002)
X. Gironés, R. Carbó-Dorca, Molecular similarity and quantitative structure-activity relationships, in Computational medicinal chemistry for drug discovery. ed. by P. Bultinck, H. De Winter, W. Langenaeker, J.P. Tollenaere (Marcel Dekker Inc., New York, 2004), pp.365–385
R. Carbó-Dorca, Non-linear terms and variational approach in quantum QSPR. J. Math. Chem. 36, 241–260 (2004)
R. Carbó-Dorca, X. Gironés, Foundation of quantum similarity measures and their relationship to QSPR: density function structure, approximations, and application examples. Int. J. Quant. Chem. 101, 8–20 (2005)
P. Bultinck, X. Gironés, R. Carbó-Dorca, Molecular quantum similarity: theory and applications, in Reviews in computational chemistry, vol. 21, ed. by K.B. Lipkowitz, R. Larter, T. Cundari (Wiley, Hoboken, 2005), pp.127–207
X. Gironés, R. Carbó-Dorca, Modelling toxicity using molecular quantum similarity measures. QSAR Comb. Sci. 25, 579–589 (2006)
R. Carbó-Dorca, Theoretical foundations of quantum-quantitative structure-properties relationships. SAR QSAR Environ. Res. 18, 265–284 (2007)
R. Carbó-Dorca, S. Van Damme, Solutions to the quantum QSPR problem in molecular spaces. Theor. Chem. Acc. 118, 673–679 (2007)
R. Carbó-Dorca, S. Van Damme, Riemann spaces, molecular density function semispaces, quantum similarity measures, and quantum quantitative structure-properties relationships (QQSPR). Afinidad 64, 147–153 (2007)
R. Carbó-Dorca, S. Van Damme, A new insight on the quantum quantitative structure-properties relationships (QQSPR). Int. J. Quant. Chem. 108, 1721–1734 (2007)
R. Carbó-Dorca, A. Gallegos, Quantum similarity and quantum QSPR (QQSPR), in Encyclopedia of complexity and systems science, vol. 8, ed. by R.A. Meyers (Springer, New York, 2009), pp.7422–7480
R. Carbó-Dorca, Notes on quantitative structure-properties relationships (QSPR) (3): density functions origin shift as a source of quantum QSPR (QQSPR) algorithms in molecular spaces. J. Comput. Chem. 34, 766–779 (2013)
R. Carbó-Dorca, S. González, Notes in QSPR (4): quantum multimolecular polyhedra, collective vectors, quantum similarity, and quantum QSPR fundamental equation. Manage. Stud. 4, 33–47 (2016)
R. Carbó-Dorca, Least squares estimation of unknown molecular properties and quantum QSPR fundamental equation. J. Math. Chem. 53, 1651–1656 (2015)
R. Carbó-Dorca, S. González, Molecular space quantitative structure-properties relations (MSQSPR): a quantum mechanical comprehensive theoretical framework. Int. J. QSPR 1(2), 1–22 (2016)
R. Carbó-Dorca, Towards a universal quantum QSPR operator. Int. J. Quant. Chem. 118, 1–17 (2018)
R. Carbó-Dorca, About the concept of chemical space: a concerned reflection on some trends of modern scientific thought within theoretical chemical lore. J. Math. Chem. 51, 413–419 (2013)
R. Carbó-Dorca, Molecular quantum similarity measures in Minkowski metric vector semispaces. J. Math. Chem. 44, 628–636 (2008)
R. Carbó-Dorca, Diagonal coefficient representation of density functions and quantum similarity measures. J. Math. Chem. 44, 621–627 (2008)
R. Carbó-Dorca, Definition of norm coherent generalized scalar products and quantum similarity. J. Math. Chem. 47, 331–334 (2010)
R. Carbó-Dorca, Generalized scalar products in Minkowski metric spaces. J. Math. Chem. 59, 1029–1045 (2021)
R. Carbó-Dorca, A. Gallegos, Á.J. Sánchez, Notes on quantitative structure-properties relationships (QSPR) (1): a discussion on a QSPR dimensionality paradox (QSPR DP) and its quantum resolution. J. Comput. Chem. 30, 1146–1159 (2008)
R. Carbó-Dorca, Molecular spaces and the dimension paradox. Pure Appl. Chem. 93, 1189–1196 (2021)
L.D. Mercado, R. Carbó-Dorca, Quantum similarity and discrete representation of molecular sets. J. Math. Chem. 49(1), 558–1572 (2011)
R. Carbó-Dorca, E. Besalú, EMP as a similarity measure: a geometric point of view. J. Math. Chem. 51, 382–389 (2013)
R. Carbó-Dorca, Collective Euclidian distances and quantum similarity. J. Math. Chem. 51, 338–353 (2013)
R. Carbó-Dorca, Quantum polyhedra, definitions, statistics and the construction of a collective quantum similarity index. J. Math. Chem. 53, 171–182 (2015)
R. Carbó-Dorca, D. Barragán, Communications on quantum similarity (4): collective distances computed by means of similarity matrices, as generators of intrinsic ordering among quantum multimolecular polyhedra. WIREs Comput. Mol. Sci. 5, 380–404 (2015)
R. Carbó-Dorca, An isometric representation problem related with quantum multimolecular polyhedra and similarity. J. Math. Chem. 53, 1750–1758 (2015)
R. Carbó-Dorca, An isometric representation problem in quantum multimolecular polyhedra and similarity: (2) synisometry. J. Math. Chem. 53, 1867–1884 (2015)
R. Carbó-Dorca, Quantum molecular polyhedra in LCAO-MO theory. Mol. Phys. 114(7–8), 1236–1249 (2016)
R. Carbó-Dorca, Aromaticity, quantum molecular polyhedra and quantum QSPR. J. Comput. Chem. 37, 78–82 (2016)
R. Carbó-Dorca, Universal transformation and non-linear connection between experimental and calculated property vectors in QSPR. J. Math. Chem. 57, 1075–1087 (2019)
R. Carbó-Dorca, About some questions relative to the arbitrariness of signs: their possible consequences in matrix signatures definition and quantum chemical applications. J. Math. Chem. 33, 227–244 (2003)
R. Carbó-Dorca, A. Gallegos, Notes on quantitative structure-properties relationships (QSPR) part 2: the role of the number of atoms as a molecular descriptor. J. Comput. Chem. 30, 2099–2104 (2009)
R. Carbó-Dorca, E. Besalú, L.D. Mercado, Communications on quantum similarity, part 3: a geometric-quantum similarity molecular superposition algorithm. J. Comput. Chem. 32, 582–599 (2011)
R. Carbó-Dorca, Quantum similarity and QSPR in Euclidean-, and Minkowskian-Banach spaces. J. Math. Chem. 61, 1016–1035 (2023)
J.H. Wilkinson, The algebraic eigenvalue problem (Clarendon Press, Oxford, 1965)
J.H. Wilkinson, C. Reinsch, Linear algebra, in Handbook for automatic computation. ed. by F.L. Bauer (Springer, Berlin, 1971)
R. Carbó-Dorca, T. Chakraborty, Divagations about the periodic table: Boolean hypercube and quantum similarity connections. J. Comput. Chem. 40, 2653–2663 (2019)
R. Carbó-Dorca, Determination of unknown molecular properties in molecular spaces. J. Math. Chem. 60, 353–359 (2022)
P.O. Löwdin, Quantum theory of many-particle systems. I. Physical interpretations by means of density matrices, natural spin-orbitals, and convergence problems in the method of configuration interaction. Phys. Rev. 97, 1474–1489 (1955)
P.O. Löwdin, Quantum theory of many-particle systems. II. Study of the ordinary Hartree-Fock approximation. Phys. Rev. 97, 1490–1508 (1955)
P.O. Löwdin, Quantum theory of many-particle systems. III. Extension of the Hartree-Fock scheme to include degenerate systems and correlation effects. Phys. Rev. 97, 1509–1520 (1955)
L. Amat, R. Carbó-Dorca, Quantum similarity measures under atomic shell approximation: first order density fitting using elementary Jacobi rotations. J. Comput. Chem. 18, 2023–2029 (1997)
L. Amat, R. Carbó-Dorca, Fitted electronic density functions from H to Rn for use in quantum similarity measures: Cis-diamminedichloroplatinum (II) complex as an application example. J. Comput. Chem. 20, 911–920 (1999)
E. Besalú, R. Carbó-Dorca, The general Gaussian product theorem. J. Math. Chem. 49, 1769–1784 (2011)
R. Carbó-Dorca, Shadows’ hypercube, vector spaces, and non-linear optimization of QSPR procedures. J. Math. Chem. 60, 283–310 (2022)
Acknowledgements
The author wants to thank his wife, Blanca Cercas, for her support. Without her, this and other related works could not have been performed.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Contributions
I did the whole manuscript construction.
Corresponding author
Ethics declarations
Conflict of interest
The author state that this work has no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carbó-Dorca, R. QSPR in molecular spaces: ordering data, {de- & re-} constructing molecular similarity matrices, building their isometric vectors defining statistical-like momenta of molecular polyhedra, and analyzing the structure of a quantum QSPR operator. J Math Chem (2023). https://doi.org/10.1007/s10910-023-01501-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10910-023-01501-8