1 Introduction

Most chemical reaction problems have been known to be stiff in nature, little wonder they have attracted the attention of mathematicians recently. According to [1, 2], chemical reactions in alive species, atmospheric phenomena, mechanics and molecular dynamics, and chemical kinetics, extensively describe the stiff systems. If the time constants fluctuate significantly in magnitude, then the system is known as stiff. The time constants here refer to the rates of decay of perturbations [3]. If a system diverges considerably in terms of time constants, we must use smaller time steps to deal with expeditiously decaying terms.

In this paper, an implicit 3-Point Block Backward Differentiation Formula with one off-step point (3POBBDF) is derived for the solutions of stiff chemical reaction problems of the form,

$${y}^{{\prime}}\left(x\right)=f\left(x,y\right), y\left(a\right)={y}_{0}, x\in [a,b]$$
(1.1)

where \(f\) is assumed to be continuous and satisfies the existence and uniqueness theorem.

For Ordinary Differential Equations (ODEs) such as non-linear or linear, stiff or non-stiff ODEs, different numerical methods have been developed [4,5,6]. It must be noted that employing the wrong method for a model can result in a slow or incorrect solution [7]. Problems with the form (1.1) are generally divided into two categories. The first category is a non-stiff ODEs, in which explicit methods are employed together with certain error control. Another category is stiff ODEs. [8] was the first to use the term "stiff" in a scenario requiring chemical kinetics. The only way to find answers to stiff problems is to employ implicit methods because explicit methods are slow and sometimes fail to deliver an accurate solution [9]. The Backward Differentiation Formula (BDF) is one of the well-known classes of implicit methods for finding the solution of stiff ODEs. Developing a mathematical model for stiff ODEs considers a few factors such as selection of step size, stability, accuracy, and computational cost [10, 11].

Stiffness is defined in different ways in literature as it does not have a specific definition. Equation (1.1) is said to be stiff according to Lambert [12] if the Jacobian matrix \(\frac{\partial f}{\partial y}\) for the eigenvalues \({\lambda }_{t}\)(x) satisfies these conditions:

$$Re\left({\lambda }_{t}\left(x\right)\right)<0, t=\mathrm{1,2},\ldots ,n$$
$$\underset{t}{\mathrm{max}}|Re\left({\lambda }_{t}\left(x\right)\right)|\gg \underset{t}{\mathrm{min}}|Re\left({\lambda }_{t}\left(x\right)\right)|$$

where \({\lambda }_{t}\) are the eigenvalues and the ratio \(\frac{{max}_{t=\mathrm{1,2},\ldots ,m}\left|Re\left({\lambda }_{t}\right)\right|}{{min}_{t=\mathrm{1,2},\ldots ,m}\left|Re\left({\lambda }_{t}\right)\right|}\) is called stiffness ratio.

Many studies have been directed into the improvement of multistep block methods for the solution of (1.1). Several studies have recently focused on improving the performance of different forms of multistep block methods encompassing estimated solution accuracy and computational time; see [10, 13,14,15,16,17,18,19]. While several block methods (based on Adams formulas) were proposed previously emphasizing ODEs of non-stiff systems, the challenge has always been how to find an appropriate implicit method for solving stiff ODEs that have A-stability properties. Since block methods' most serious flaw appears to be their ability to sustain stability [20], it is necessary to develop algorithms with suitable stability properties.

Gear [21] initially introduced the BDF, which is known to be efficient in handling complex stiff ODE problems. This BDF approach has been extended in papers such as [15, 22,23,24,25]. Single-step and multi-step block techniques are the two types of block methods. Rosser [26] introduced the standard single-step method known as the Runge–Kutta method. [27] explored the single-step implicit A-stable r-block approach. [28] developed a fourth-order block approach for multistep methods that can be used as a predictor–corrector method. [29] proposed a Modified extended BDF method for numerical solutions of stiff ODEs. [15] devised a method for solving first-order ODEs using 2-point and 3-point block BDF. [30] developed the 5th order 2-Point Block Backward Differentiation Formula to improve the existing BBDF. Authors in articles [31,32,33] also improved the BBDF method by extending the method and adding future points. Many researchers have explored other block methods such as [34] who developed a seven-step block method for the solution of first order IVPs in ODEs and [35] considered the approximate solutions to third-order boundary value problems (BVPs) of ODEs.

Despite having many advantages, the block method also possessed a major setback which pointed out that the order of interpolation points must not exceed the order of the differential equations [36, 37]. Because of this setback, addition of off-step points in the block were introduced and named as hybrid method. Hybrid methods are highly efficient and have been reported to circumvent the “Dahlquist Zero-Stability Barrier” condition by introducing function evaluation at off-step points which takes some time in its development but provides better approximation than two conventional methods (Runge–Kutta and linear multistep methods) [13, 36]. [38] proposed function evaluation at an off-step and named as “Hybrid” method. [9] derived higher-order method with more than one off-step point. [39] were the first who introduce BDF methods with some off-step points. The hybrid Obrechkof BDF methods with some off-step points were presented in [40]. Hybrid Block Second Derivative Backward Differentiation Formula (HBSDBDF) is proposed by [41] which provides simultaneous solutions of IVPs in each block without any predictor formula. [42] formulated Block Backward Differentiation Formula with two off-step points (BBDFO(6)). [23] have studied block methods with various off-step points. [43,44,45] have described a closely related methods that involves off-step points. In modifying the selection of the most acceptable off-step points, a similar method is used from [46, 47].

Motivated from the above literature, this study is aimed at developing a 3-Point Block Backward Differentiation Formula with one off-step point (3POBBDF) using Lagrange polynomials as basis function to solve chemical reactions problems comprising stiff first order ODEs. The method will be employed in solving stiff chemical reaction problems of the form (1.1). Several points have been examined for the selection of off-step points and hence it was concluded that selecting the points where the step is halved will lead to zero-stable formulae. Compared to the methods developed by Khalsaraei and Molayi [48], and Ismail [49], the advantage of the proposed method is that the solutions are approximated with off-step points concurrently and provide better accuracy. The organization of the paper is as follow; Section 2 briefly describes the formulation of the method. Analysis of convergence properties is examined in Section 3. Section 4 elaborates the implementation of the derived method. List of tested problems with results are presented in section 5. Section 6 includes discussions of the results. Graphical representation of the results is displayed in section 7. consists of Numerical problems with their results respectively. Furthermore, Sections 8 describes the conclusions.

2 Derivation of the 3POBBDF

This section consists of a detailed explanation of how the proposed 3POBBDF for solving (1.1) is formulated. The two starting values, \({x}_{n-1}\) and \({x}_{n}\) of identical step size which is fixed as \({h=x}_{n+1}-{x}_{n}\) and one off-step point at \({x}_{n+\frac{5}{2}}\) is considered, as shown in Fig. 1.

Fig. 1
figure 1

3-Point Block Backward Differentiation Formula with one off-step point

Full size image

The interval \([a, b]\) in (1.1) is split into a sequence of blocks in a 3-point block method (see Fig. 1). For finding out the solution of (1.1), \({y}_{n-1}\) and \({y}_{n}\) are used as the values of previous block to evaluate the future points at \({y}_{n+1, }{y}_{n+2}\), \({y}_{n+\frac{5}{2}}\) and \({y}_{n+3}\) with constant step size simultaneously. The off-step point \({y}_{n+\frac{5}{2}}\) is added to all three formulas to increase the accuracy. The 3POBBDF we shall derive is a k-step Linear Multistep Method (LMM) defined according to [12] as,

$$\sum_{j=0}^{k}{\alpha }_{j}{y}_{n+j}=h\sum_{j=0}^{k}{\beta }_{j}\,{f}_{n+j},$$
(2.1)

h represents the step size, \({\alpha }_{j}\) and \({\beta }_{j}\) are the unknown constants that needs to be decided and k indicates the number of steps of the method. Presuming that \({\alpha }_{j}\ne 0\), and both \({\alpha }_{0}\) and \({\beta }_{0}\) are not equal to zero. The LMM (2.1) is extended by adding an off-step point to generate a new form of LMM given by,

$$\sum_{j=0}^{4}{\alpha }_{j-1}{y}_{n+(j-1)}+{\alpha }_\frac{5}{2}{y}_\frac{5}{2}=h{\beta }_{T,T}{f}_{n+T}, for T=\mathrm{1,2},\frac{5}{2},3$$
(2.2)

The function \({f}_{n+T}\) in Eq. (2.2) is evaluated by using Lagrange interpolation polynomial \((P(x))\) with interpolation points such as (\({x}_{n-1},{y}_{n-1}\)), (\({x}_{n},{y}_{n}\)), (\({x}_{n+1},{y}_{n+1}\)), (\({x}_{n+2},{y}_{n+2}\)), (\({x}_{n+\frac{5}{2}},{y}_{n+\frac{5}{2}}\)) and (\({x}_{n+3},{y}_{n+3}\)). The process is given as,

$$P(x)={\sum }_{j=0}^{4}{L}_{j}(x)f({x}_{n+3-j}),$$
(2.3)

whereas,

$${L}_{j}=\prod_{\begin{array}{c}i=0\\ i\ne j\end{array}}^{4}\frac{x-{x}_{n+3-i}}{{x}_{n+3-j}-{x}_{n+3-i}} for i=0,\frac{1}{2},\mathrm{1,2},\mathrm{3,4}$$

Expanding the polynomial \({L}_{j}\) by substituting \(s=\frac{x-{x}_{n+3}}{h}\) implying \(x=sh+{x}_{n+3}\). The interpolating polynomial is further differentiated with respect to \(s\) provides the coefficient values of \(\alpha\) and \(\beta\) as presented in Table 1.

Table 1 Coefficients of 3POBBDF
Full size table

Furthermore, (2.2) is shaped up after substituting all values taken from Table 1. Hence, the corresponding formulas for the points \({y}_{n+1},{y}_{n+2},{y}_{n+5/2},\) and \({y}_{n+3}\) take the following form:

$${y}_{n+1}=\frac{3}{56}{y}_{n-1}-\frac{3}{5}{y}_{n}+3{y}_{n+2}-\frac{64}{35}{y}_{n+\frac{5}{2}}+\frac{3}{8}{y}_{n+3}-\frac{3}{2}h{f}_{n+1},\quad {y}_{n+2}=-\frac{1}{98}{y}_{n-1}+\frac{3}{35}{y}_{n}-\frac{3}{7}{y}_{n+1}+\frac{384}{245}{y}_{n+\frac{5}{2}}-\frac{3}{14}{y}_{n+3}-\frac{6}{7}h{f}_{n+2},\quad {y}_{n+\frac{5}{2}}=-\frac{75}{9088}{y}_{n-1}+\frac{147}{2272}{y}_{n}-\frac{1225}{4544}{y}_{n+1}+\frac{3675}{2272}{y}_{n+2}-\frac{3675}{9088}{y}_{n+3}+\frac{105}{142}h{f}_{n+\frac{5}{2}}\quad {y}_{n+3}=\frac{3}{343}{y}_{n-1}-\frac{16}{245}{y}_{n}+\frac{12}{49}{y}_{n+1}-\frac{48}{49}{y}_{n+2}+\frac{3072}{1715}{y}_{n+\frac{5}{2}}+\frac{12}{49}h{f}_{n+3}.$$
(2.4)

Equation (2.4) is the 3POBBDF for the solution of stiff chemical reaction problems of the form (1.1).

3 Analysis of basic properties of the 3POBBDF

The following section comprises the analysis of basic properties of the proposed method. These properties include order, consistency, zero-stability and convergence. The region of absolute stability of the method shall also be determined.

3.1 Order and error constant of the method

Definition 3.1

(Order and Error Constant)

The LMM (2.1) associated with the linear difference operator is said to be of order p if \({C}_{1}={C}_{2}=\ldots ={C}_{p}=0\) and \({C}_{p+1}\ne 0\). The term \({C}_{p+1}\ne 0\) is called the error constant of the method

According to [12] and [50], the local truncation error related with (2.1), for determining the order and error constant of the proposed method is well-defined by the linear difference operator \(L\left(y\left(x\right)\right)\) as,

$$L\left(y\left(x\right)\right)=\sum_{j=0}^{k+s-1}({a}_{j-1}y\left(x+Th\right)-h{\beta }_{T,T}y(x+Th))$$
(3.1)

The function \(y(x + Th)\) with its derivative \(y^{\prime}(x + Th)\) are expanded and collecting terms in (3.1) will be obtained such as,

$$L\left[y\left(x\right);h\right]={C}_{0}y\left(x\right)+{C}_{1}{y}^{{\prime}}\left(x\right)+...+{C}_{q}{h}^{q}{y}^{\left(q\right)}\left(x\right)+.\ldots$$
(3.2)

On the application of Eq. (3.2) on 3POBBDF derived in Eq. (2.4) using the coefficients presented in Table 1, we obtain

$${C}_{0}=\sum_{j=0}^{k+s-1}{\alpha }_{j-\left(k-1\right),T}={[0 0 0 0]}^{T},{C}_{1}=\sum_{j=0}^{k+s-1}t{\alpha }_{j-\left(k-1\right),T}-{\beta }_{T,T}={[0 0 0 0]}^{T},{C}_{2}=\sum_{j=0}^{k+s-1}\frac{{t}^{2}}{2!}{\alpha }_{j-\left(k-1\right),T}-{T\beta }_{T,T}={[0 0 0 0]}^{T},\vdots {C}_{5}=\sum_{j=0}^{k+s-1}\frac{{t}^{5}}{5!}{\alpha }_{j-\left(k-1\right),T}-{\frac{{(T)}^{4}}{4!}\beta }_{T,T}={[0 0 0 0]}^{T},$$
$${C}_{6}=\sum_{j=0}^{k+s-1}\frac{{t}^{6}}{6!}{\alpha }_{j-\left(k-1\right),T}-{\frac{{\left(T\right)}^{5}}{5!}\beta }_{T,T}={[\frac{1}{80} -\frac{1}{280} \frac{21}{6250} -\frac{1}{245}]}^{T}\ne {[0 0 0 0]}^{T}$$
(3.3)

As a result, the error constant of the proposed method is obtained as

$${C}_{6}=\left[\begin{array}{c}\begin{array}{c}\frac{1}{80}\\ -\frac{1}{280}\\ \frac{21}{6250}\end{array}\\ -\frac{1}{245}\end{array}\right].$$

According to Definition 3.1, \({c}_{0}={c}_{1}=\ldots ={c}_{5}={[0 0 0 0]}^{T}\). The term \({c}_{6}\) represents the error constant. Therefore, this can be demonstrated that the proposed method is of order five.

3.1.1 Consistency of the method

Definition 3.2

(Consistency)

The LMM (2.1) is said to be consistent if it is of order \(p\ge 1\).

It is therefore clear that the 3POBBDF is consistent since it has order p = 5 which satisfies Definition 3.2

3.1.2 Zero-stability of the method

Definition 3.3

(Zero-stable)

If no root of the characteristic polynomial has a modulus greater than one and every root with modulus one is simple, then LMM (2.2) is said to be zero-stable

To be a convergent method, zero-stability is one of the main criteria which will be discussed here. [13] proposed the scalar test to determine the stability of the method (2.4) as

$${y}^{{{\prime}}}=\lambda y,\quad \lambda <0,$$
(3.4)

where λ represents the complex constant with Re(λ) < 0. Equation (3.4) is substituted in Eq. (2.4), therefore it precedes as,

$${y}_{n+1}=\frac{3}{56}{y}_{n-1}-\frac{3}{5}{y}_{n}+3{y}_{n+2}-\frac{64}{35}{y}_{n+\frac{5}{2}}+\frac{3}{8}{y}_{n+3}-\frac{3}{2}h\lambda {y}_{n+1},$$
(3.5)
$${y}_{n+2}=-\frac{1}{98}{y}_{n-1}+\frac{3}{35}{y}_{n}-\frac{3}{7}{y}_{n+1}+\frac{384}{245}{y}_{n+\frac{5}{2}}-\frac{3}{14}{y}_{n+3}-\frac{6}{7}h\lambda {y}_{n+2},$$
$${y}_{n+\frac{5}{2}}=-\frac{75}{9088}{y}_{n-1}+\frac{147}{2272}{y}_{n}-\frac{1225}{4544}{y}_{n+1}+\frac{3675}{2272}{y}_{n+2}-\frac{3675}{9088}{y}_{n+3}+\frac{105}{142}h\lambda {y}_{n+\frac{5}{2}},$$
$${y}_{n+3}=\frac{3}{343}{y}_{n-1}-\frac{16}{245}{y}_{n}+\frac{12}{49}{y}_{n+1}-\frac{48}{49}{y}_{n+2}+\frac{3072}{1715}{y}_{n+\frac{5}{2}}+\frac{12}{49}h\lambda {y}_{n+3}$$

The matrix is then created by inscribing Eq. (3.5) into the matrix form as follows:

$$\left[\begin{array}{cccc}-\frac{3}{8}& \frac{64}{35}& -3& 1+\frac{3}{2}h\lambda \\ \frac{3}{14}& -\frac{384}{245}& 1+\frac{6}{7}h\lambda & \frac{3}{7}\\ \frac{3675}{9088}& 1-\frac{105}{142}h\lambda & -\frac{3675}{2272}& \frac{1225}{4544}\\ 1-\frac{12}{49}h\lambda & -\frac{3072}{1715}& \frac{48}{49}& -\frac{12}{49}\end{array}\right]\left[\begin{array}{c}{y}_{n+3}\\ {y}_{n+\frac{5}{2}}\\ {y}_{n+2}\\ {y}_{n+1}\end{array}\right]=\left[\begin{array}{cccc}-\frac{3}{5}& 0& \frac{3}{56}& 0\\ \frac{3}{35}& 0& -\frac{1}{98}& 0\\ \frac{147}{2272}& 0& -\frac{75}{9088}& 0\\ -\frac{16}{245}& 0& \frac{3}{343}& 0\end{array}\right]\left[\begin{array}{c}{y}_{n}\\ {y}_{n-\frac{1}{2}}\\ {y}_{n-1}\\ {y}_{n-2}\end{array}\right],$$

which is equivalent to,

$$C{Y}_{n}=D{Y}_{n-1},$$
(3.6)

\(C\) and \(D\) are appropriately selected \(m \times m\) matrix coefficients, \({Y}_{n}={\left[{{y}_{n+3},{y}_{n+\frac{5}{2}},{y}_{n+2},y}_{n+1}\right]}^{T}\) and \({Y}_{n-1}={\left[{y}_{n},{y}_{n-\frac{1}{2}},{y}_{n-1},{y}_{n-2}\right]}^{T}\). The stability polynomial \(R\left(t, H\right)\) correlated with the method in (2.2) is defined by

$$R\left(t, H\right)=|Ct-D|,$$
$$R\left(t, H\right)=\frac{-13977{t}^{2}}{79147250}+\frac{44523H{t}^{2}}{158294500}+\frac{9{H}^{2}{t}^{2}}{97412}-\frac{2883852{t}^{3}}{344125}-\frac{811134{Ht}^{3}}{807625}-\frac{15070599{H}^{2}{t}^{3}}{39573625}-\frac{2889{H}^{3}{t}^{3}}{48706}+\frac{41616{t}^{4}}{48706}-\frac{179199H{t}^{4}}{97412}+\frac{159417{H}^{2}{t}^{4}}{97412}-\frac{40851{H}^{3}{t}^{4}}{48706}+\frac{810{H}^{4}{t}^{4}}{3479}.$$
(3.7)

Based on the stability polynomial in (3.7), the zero-stability is obtained by replacing \(H = h\lambda =0\) into (3.7), this yield,

$$R\left(t,0\right)=\frac{-13977{t}^{2}}{79147250}-\frac{2883852{t}^{3}}{344125}+\frac{41616{t}^{4}}{48706} .$$
(3.8)

Solving \(R\left(t,0\right)=0\), gives the roots for \(t\), as \(t = \mathrm{0,0},-0.000186375, 0.999767\). Since all the roots lie within \(|t| \le 1\) described in Definition 4.1; hence, it is concluded that the method 3POBBDF is zero-stable.

3.1.3 Convergence of the method

Definition 3.4

(Convergence)

Consistency and zero-stability are required conditions for the LMM (2.1) to be convergent

Therefore, we conclude that the newly derived 3POBBDF is convergent since it is consistent and zero-stable.

3.1.4 Stability region of the method

Definition 3.5

(A-stable)

The term "A-stable" refers to a method that is stable for all λ in the left-half plane \((Re(\lambda )\le 0)\). The stability region for A-stable method covers up the complete negative left-half plane

In this section, the stability region of the 3POBBDF(5) presented in Eq. (2.4) is plotted by using the stability polynomial given in (3.7). The boundary of the stability region is described by the set of points defined by \(t={e}^{i\theta }\),\(0 \le \theta \le 2\pi\). The root condition \((|t| \le 1)\) of the stability polynomial must be tested at multiple grid points in order to determine the boundary of the stability region. Figure 2 shows the region of absolute stability for the system in (2.4).

Fig. 2
figure 2

Stability region of 3POBBDF(5)

Full size image

It is observed from this figure that the stability region lies outside of the bounded region. Since most of the region is in the left half-plane therefore, according to Definition 3.5, the method is A-stable. Thus, it can be implied that the constructed 3POBBDF method is appropriate for solving stiff problems.

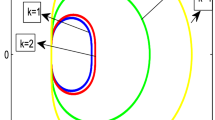
3.1.5 Comparison of stability regions

The stability region of the proposed 3POBBDF(5) is depicted in the Fig. 3 below, as opposed to the existing stability region of the Block Backward Differentiation Formula of Order 6 (BBDFO(6)) developed by [42]. On the complex \(h\lambda\) plane, Fig. 3 illustrates the region including both methods, namely the 3POBBDF(5) and the BBDFO(6).

Fig. 3
figure 3

Regions of Stability for 3POBBDF(5)and BBDFO(6)

Full size image

The interval of instability of the current 3POBBDF(5) and the BBDFO(6) [42] are then compared. The derived 3POBBDF(5) has a larger stability area, as shown in Table 2. This implies that the proposed 3POBBDF(5) is more computationally reliable than BBDFO(6) developed by [42].

Table 2 Comparison of instability region of 3POBBDF(5) with BBDFO(6)
Full size table

4 Implementation and Algorithm of the 3POBBDF

This section discusses the implementation and algorithms of the proposed method.

4.1 Implementation of the 3POBBDF

By using Newton iteration, implementation of the 3POBBDF(5) method having one off-step is briefly mentioned in the generalized form. An increment notation is introduced for stipulating the iteration. In which \({y}_{n+1}^{(i+1)}\) will represent the \((i+1)\) th iterative value of \({y}_{n+1}\)[51].

The main limitation for the implementation of the 3POBBDF(5) predominantly is that it is not self-starting. The back values are therefore calculated using the Euler method in this case.

By applying Newton's iteration, (2.4) is solved and the number of iterations is limited to two. Newtons’ iteration for \({y}_{(n+1)}^{(i+1)}\), \({y}_{(n+2)}^{(i+1)}\), \({y}_{(n+\frac{5}{2})}^{(i+1)}\), \({y}_{(n+3)}^{(i+1)}\) points in the block takes the form

$${y}_{(n+1)}^{(i+1)}={y}_{n+1}^{(i)}-\frac{{F}_{1}{y}_{n+1}^{(i)}}{{F}_{1}^{{{\prime}}}{y}_{n+1}^{(i)}},$$
$${y}_{(n+2)}^{(i+1)}={y}_{n+2}^{(i)}-\frac{{F}_{2}{y}_{n+2}^{(i)}}{{F}_{2}^{{{\prime}}}{y}_{n+2}^{(i)}},$$
$${y}_{(n+\frac{5}{2})}^{(i+1)}={y}_{n+\frac{5}{2}}^{(i)}-\frac{{F}_\frac{5}{2}{y}_{n+\frac{5}{2}}^{(i)}}{{F}_{n+\frac{5}{2}}^{{{\prime}}}{y}_{n+\frac{5}{2}}^{(i)}},$$
$${y}_{(n+3)}^{(i+1)}={y}_{n+3}^{(i)}-\frac{{F}_{3}{y}_{n+3}^{\left(i\right)}}{{F}_{3}^{{\prime}}{y}_{n+3}^{\left(i\right)}}.$$
(4.1)

where \(i=\mathrm{0,1}\).

We need to set the formula for \({y}_{n+1}\)

$${y}_{n+1}=\frac{3}{56}{y}_{n-1}-\frac{3}{5}{y}_{n}+3{y}_{n+2}-\frac{64}{35}{y}_{n+\frac{5}{2}}+\frac{3}{8}{y}_{n+3}-\frac{3}{2}h{f}_{n+1}.$$

Let

$${F}_{1}={y}_{n+1}-3{y}_{n+2}+\frac{64}{35}{y}_{n+\frac{5}{2}}-\frac{3}{8}{y}_{n+3}+\frac{3}{2}{hf}_{n+1}-{\psi }_{1},$$

where \({\psi }_{1}\) represent the back values

$${\psi }_{1}=\frac{3}{56}{y}_{n-1}-\frac{3}{5}{y}_{n},$$

Referring to (4.1), \({F}_{1}^{{\prime}}\) for \({y}_{n+1}\) is also required which is,

$${F}_{1}^{{{\prime}}}=1+\frac{3h}{2}\frac{\partial {f}_{n+1}}{\partial {y}_{n+1}},$$

So, the (4.1) for \({y}_{n+1}^{(i+1)}\) becomes,

$${y}_{n+1}^{(i+1)}-{y}_{n+1}^{\left(i\right)}=-\frac{({y}_{n+1}^{\left(i\right)}-3{y}_{n+2}^{\left(i\right)}{+\frac{64}{35}y}_{n+\frac{5}{2}}^{\left(i\right)}-{\frac{3}{8}y}_{n+3}^{\left(i\right)}+\frac{3}{2}h{f}_{n+1}^{\left(i\right)}-{\psi }_{1})}{1+\frac{3}{2}\frac{h\partial {f}_{n+1}}{\partial {y}_{n+1}}},$$
$$\left(1+\frac{3}{2}\frac{h\partial {f}_{n+1}}{\partial {y}_{n+1}}\right)\left({y}_{n+1}^{\left(i+1\right)}-{y}_{n+1}^{\left(i\right)}\right)=-{y}_{n+1}^{\left(i\right)}+3{y}_{n+2}^{\left(i\right)}{-\frac{64}{35}y}_{n+\frac{5}{2}}^{\left(i\right)}+{\frac{3}{8}y}_{n+3}^{\left(i\right)}-\frac{3}{2}h{f}_{n+1}^{\left(i\right)}+{\psi }_{1},$$
(4.2)

Similarly, Newton iteration for \({y}_{n+2}\),\({y}_{n+\frac{5}{2}}\), and \({y}_{n+3}\)

$$\left(1+\frac{6h}{7}\frac{\partial {f}_{n+2}}{\partial {y}_{n+2}}\right)\left({y}_{n+2}^{\left(i+1\right)}-{y}_{n+2}^{\left(i\right)}\right)=-{\frac{3}{7}y}_{n+1}^{\left(i\right)}-{y}_{n+2}^{\left(i\right)}{+\frac{384}{245}y}_{n+\frac{5}{2}}^{\left(i\right)}-{\frac{3}{14}y}_{n+3}^{\left(i\right)}-\frac{6}{7}h{f}_{n+2}^{\left(i\right)}+{\psi }_{2}),$$
(4.3)
$$\left(1-\frac{105h}{142}\frac{\partial {f}_{n+\frac{5}{2}}}{\partial {y}_{n+\frac{5}{2}}}\right)\left({y}_{n+\frac{5}{2}}^{\left(i+1\right)}-{y}_{n+\frac{5}{2}}^{\left(i\right)}\right)=-{\frac{1225}{4544}y}_{n+1}^{\left(i\right)}+\frac{3675}{2272}{y}_{n+2}^{\left(i\right)}{-y}_{n+\frac{5}{2}}^{\left(i\right)}-{\frac{3675}{9088}y}_{n+3}^{\left(i\right)}+\frac{105}{142}h{f}_{n+\frac{5}{2}}^{\left(i\right)}+{\psi }_\frac{5}{2}),$$
(4.4)
$$\left(1-\frac{12h}{49}\frac{\partial {f}_{n+3}}{\partial {y}_{n+3}}\right)\left({y}_{n+3}^{\left(i+1\right)}-{y}_{n+3}^{\left(i\right)}\right)={\frac{12}{49}y}_{n+1}^{\left(i\right)}-\frac{48}{49}{y}_{n+2}^{\left(i\right)}{+\frac{3072}{1715}y}_{n+\frac{5}{2}}^{\left(i\right)}-{y}_{n+3}^{\left(i\right)}+\frac{12}{49}h{f}_{n+3}^{\left(i\right)}+{\psi }_{3}).$$
(4.5)

Let \({e}_{n+1}^{(i+1)}={y}_{n+1}^{(i+1)}-{y}_{n+1}^{(i)}\) be the increment value from \(i\) th to \((i+1)\) th iterations. Therefore, Eqs. (4.2)-(4.5) are then represented in matrix form as

$$\left[\begin{array}{cccc}1+\frac{3h}{2}\frac{\partial {f}_{n+1}}{\partial {y}_{n+1}}& -3& \frac{64}{35}& -\frac{3}{8}\\ \frac{3}{7}& 1+\frac{6}{7}h\frac{\partial {f}_{n+2}}{\partial {y}_{n+2}}& -\frac{384}{245}& \frac{3}{14}\\ \frac{1225}{4544}& -\frac{3675}{2272}& 1-\frac{105}{142}h\frac{\partial {f}_{n+\frac{5}{2}}}{\partial {y}_{n+\frac{5}{2}}}& \frac{3675}{9088}\\ -\frac{12}{49}h\lambda & \frac{48}{49}& -\frac{3072}{1715}& 1-\frac{12}{49}\frac{\partial {f}_{n+3}}{\partial {y}_{n+3}}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{e}_{n+1}^{\left(i+1\right)}\\ {e}_{n+2}^{\left(i+1\right)}\\ {e}_{n+\frac{5}{2}}^{\left(i+1\right)}\end{array}\\ {e}_{n+3}^{\left(i+1\right)}\end{array}\right]=\left[\begin{array}{cccc}-1& 3& -\frac{64}{35}& \frac{3}{8}\\ -\frac{3}{7}& -1& \frac{384}{245}& -\frac{3}{14}\\ -\frac{1225}{4544}& \frac{3675}{2272}& -1& -\frac{3675}{9088}\\ \frac{12}{49}& -\frac{48}{49}& \frac{3072}{1715}& -1\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{y}_{n+1}^{\left(i\right)}\\ {y}_{n+2}^{\left(i\right)}\\ {y}_{n+\frac{5}{2}}^{\left(i\right)}\end{array}\\ {y}_{n+3}^{\left(i\right)}\end{array}\right]+\left[\begin{array}{cccc}-\frac{3}{2}& 0& 0& 0\\ 0& \frac{-6}{7}& 0& 0\\ 0& 0& \frac{105}{142}& 0\\ 0& 0& 0& \frac{12}{49}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{f}_{n+1}^{\left(i\right)}\\ {f}_{n+2}^{\left(i\right)}\\ {f}_{n+\frac{5}{2}}^{\left(i\right)}\end{array}\\ {f}_{n+3}^{\left(i\right)}\end{array}\right]+\left[\begin{array}{c}\begin{array}{c}{\psi }_{1}\\ {\psi }_{2}\\ {\psi }_\frac{5}{2}\end{array}\\ {\psi }_{3}\end{array}\right]$$

Consequently, we will get the approximation values of \({y}_{n+1}, {y}_{n+2}, {y}_{n+\frac{5}{2}}\) and \({y}_{n+3}\) as

$${y}_{n+1}^{(i+1)}={y}_{n+1}^{(i)}+{e}_{n+1}^{(i+1)},$$
$${y}_{n+2}^{(i+1)}={y}_{n+2}^{(i)}+{e}_{n+2}^{(i+1)},$$
$${y}_{n+\frac{5}{2}}^{(i+1)}={y}_{n+\frac{5}{2}}^{(i)}+{e}_{n+\frac{5}{2}}^{(i+1)},$$

and

$${y}_{n+3}^{(i+1)}={y}_{n+3}^{(i)}+{e}_{n+3}^{(i+1)}.$$

4.1.1 Algorithm of the 3POBBDF in Code

This section will elaborate on how the developed code works with the proposed method. Initially, the code will begin with three points having one off-step block method. It is employed in \({PE(CE)}^{r}\), the type where P and C stand for predictor and corrector correspondingly. Whereas E indicates the evaluation of function \(f\).The power \(r=2\) shows the number of iterations as presented by [51] that is required to converge three points having one off-step block method corrector formulae. The algorithm of the proposed method in the code is given below,

Step 1: \(P=\) Predictor values \({y}_{n+m}\) for \(m=\mathrm{1,2},\frac{5}{2},3\),

Step 2: E \(=\) Evaluate \({f}_{n+m}\) for \(m=\mathrm{1,2},\frac{5}{2},3\),

Step 3: \(C=\) Corrector value \({y}_{n+m}\) for \(m=\mathrm{1,2},\frac{5}{2},3\),

Step 4: E \(=\) Evaluate \({f}_{n+m}\) for \(m=\mathrm{1,2},\frac{5}{2},3\).

5 Test problems

To test the reliability of the proposed 3POBBDF(5) method, some numerical results are obtained by applying the method on some well-known chemical reaction problems. Comparison is done with other multistep methods. The 3POBBDF(5) method has been coded in C +  + .

Problem 5.1

(Stiff Chemical Reaction Problem)

A chemistry problem with a stiff system is considered below,

$${y}_{1}^{{{\prime}}}={-0.013y}_{2}-1000{y}_{1}{y}_{2}-2500{y}_{1}{y}_{3},$$
$${y}_{2}^{{{\prime}}}={-0.013y}_{2}-1000{y}_{1}{y}_{2},$$
$${y}_{3}^{{{\prime}}}=-2500{y}_{1}{y}_{3},$$

with initial value\({y}_{1}=0\),\({y}_{2}=1\) and \({y}_{3}=1\), \(0\le x\le 2.\)

This problem is solved using \(h={10}^{-5}\) for 3POBBDF(5). Table 3 shows the integration results for this problem at \(x=2\). Compared with the formulas of two-step hybrid method by Khalsaraei and Molayi [48], and Ismail’s method [49], the 3POBBDF(5) method provides more accurate results in terms of Absolute error.

Table 3 Numerical results of Problem 5.1
Full size table

Problem 5.2

(Chemical AKZO Nobel Problem)

The chemical AKZO noble problem is a chemical process given by a stiff system with six non-linear differential equations taken from [52] is considered. Mathematically the problem is described as,

$$\frac{dy}{dx}=F(y), \quad y\left(0\right)={y}_{0},\quad y\in {\mathbb{R}}^{6},\quad 0\le x\le 180.$$

The function \(F(y)\) is defined by

$$\frac{dy}{dx}=\left(\begin{array}{c}-2{r}_{1}+{r}_{2}-{r}_{3}-{r}_{4}\\ \frac{1}{2}{r}_{1}-{r}_{4}-\frac{1}{2}{r}_{5}+{F}_{in}\\ {r}_{1}-{r}_{2}+{r}_{3}\\ -{r}_{2}+{r}_{3}-{2r}_{4}\\ {-r}_{2}-{r}_{3}+{r}_{5}\\ -{r}_{5}\end{array}\right),$$

where \({r}_{i}\) and \({F}_{in}\) are auxiliary variables given by

$${r}_{1}={k}_{1}{y}_{1}^{4}{y}_{2}^\frac{1}{2},\quad {k}_{1}=18.7,\quad {r}_{2}={k}_{2}{y}_{3}{y}_{4}{k}_{2}=0.58,\quad {r}_{3}=\frac{{k}_{2}}{K}{y}_{3}{y}_{5}K=34.4,\quad {r}_{4}={k}_{3}{y}_{1}{y}_{4}^{2},\quad {k}_{3}=0.09,\quad {r}_{5}={k}_{4}{y}_{6}^{2}{y}_{2}^\frac{1}{2},\quad {k}_{4}=0.42,$$
$${F}_{in}=klA\left(\frac{p\left({O}_{2}\right)}{H}-{y}_{2}\right)klA=3.3p\left({O}_{2}\right)=0.9H=737,$$

The initial vector \({y}_{0}={(0.437, 0.00123, 0, 0, 0, 0.367)}^{T}\).

Background of the Chemical AKZO Nobel Problem: This problem comes from AKZO Nobel Central Research in Arnhem, the Netherlands. It defines a chemical process that mixes MBT and CHA with a continuous supply of oxygen. The important consequent species is CBS. AKZO Nobel problem contains following reaction equations,

$$2MBT+\frac{1}{2}{O}_{2}\stackrel{{k}_{1}}{\to } MBTS+{H}_{2}O$$
$$CBS+MBT{\leftrightarrows }_{{k}_{1}}^{\frac{{k}_{2}}{K}}MBTS+CHA$$
$$MBT+2CHA+{O}_{2}\stackrel{{k}_{3}}{\to } BT+sulfate$$
$$MBT+CHA+\frac{1}{2}{O}_{2}\stackrel{{k}_{4}}{\to } CBS+{H}_{2}O$$
$$MBT+CHA\rightleftarrows MBT.CHA$$

An equilibrium is explained by the last equation

$${Ks}^{1}=\frac{\left[MBT.CHA\right]}{\left[MBT\right].{\left[CHA\right]}^{{\prime}}},$$

while the velocities of others describe reactions are given by

$${r}_{1}={k}_{1}{\left[MBT\right]}^{4}.{\left[{O}_{2}\right]}^\frac{1}{2},$$
$${r}_{2}={k}_{2}\left[MBTS\right].\left[CHA\right],$$
$${r}_{3}=\frac{{k}_{2}}{K}\left[MBT\right].\left[CBS\right],$$
$${r}_{4}={k}_{3}\left[MBT\right]. {\left[CHA\right]}^{2},$$
$${r}_{5}={k}_{4}{\left[MBT.CHA\right]}^{2}.{\left[{O}_{2}\right]}^\frac{1}{2},$$

respectively. Here the concentration is denoted by square brackets ‘[.]’. \({F}_{in}\) indicated the inflow of oxygen per unit volume and satisfies.a

$${F}_{in}=klA\left(\frac{p\left({O}_{2}\right)}{H}-\left[{O}_{2}\right]\right),$$

where \(klA\) is the coefficient of mass transfer, \(H\) represents Henry constant, and the partial oxygen pressure is denoted by \(p\left({O}_{2}\right)\). \(p\left({O}_{2}\right)\) is supposed to be independent of \(\left[{O}_{2}\right]\). The parameters \({k}_{1}\), \({k}_{2}\), \({k}_{3}\), \({k}_{4}\), \(K\), \(klA\), \(p\left({O}_{2}\right)\) and \(H\) are given constants. The procedure begins with a mixture of 0.437 mol/L [MBTS] and 0.367 mol/L [\(MBTS.CHA\)]. At the start, the oxygen concentration is 0.00123 mol/L. There is no additional presence of species at first. The simulation is completed in the time interval [0 180 min]. The mathematical formulation of the above description is simply obtained by identifying the concentrations [\(MBT\)], [\({O}_{2}\)], [\(MBTS\)], [\(CHA\)], [\(CBS\)], [\(MBT.CHA\)] with \({y}_{1}\),…,\({y}_{6}\), respectively. The numerical results by proposed method at the end point.

(\({x}_{end}=180\)) are shown in Table 4.

Table 4 Numerical results of Problem 5.2
Full size table

Problem 5.3

(Robertson Problem)

A stiff system of three non-linear ODEs is involved in the Robertson problem. In 1966, Robertson proposed it [53]. [9] came up with the name ROBER. The file rober.f contained the software part of the problem which can be found in [54]. The problem is described mathematically in the form.

$$\frac{dy}{dx}=F(y),\quad y\left(0\right)={y}_{0},$$

with \(y\in {\mathbb{R}}^{3}\), \(x\in [0, X]\) and the function \(F\) is specified by \(({{f}_{1},{f}_{2},{f}_{3})}^{T}\) where,

$${f}_{1}=-0.04{y}_{1}+{10}^{4}{y}_{2}{y}_{3},$$
$${f}_{2}=0.04{y}_{1}-{10}^{4}{y}_{2}{y}_{3}-3\times {10}^{7}{y}_{2}^{2},$$
$${f}_{3}=3\times {10}^{7}{y}_{2}^{2},$$

with the initial value \({y}_{1}=1\),\({y}_{2}=0\) and \({y}_{3}=0\).

Origin of the Problem: Robertson [53] defined the ROBER problem as the kinetics of an autocatalytic reaction. The composition of the reactions is as follows:

$$A\stackrel{{k}_{1}}{\to } B$$
$$B+B \stackrel{{k}_{2}}{\to } C+B$$
$$B+C \stackrel{{k}_{3}}{\to } A+C$$

\(A\), \(B,\) and \(C\) are the chemical species and \({k}_{1}\), \({k}_{2}\) and \({k}_{3}\) are the rate constants. The following mathematical model, consisting of a set of three ODEs, can be put up under some ideal conditions [55] and the assumption that the mass action law is implemented to the rate functions.

$$\left(\begin{array}{c}{y}_{1}^{{\prime}}\\ {y}_{2}^{{\prime}}\\ {y}_{3}^{{\prime}}\end{array}\right)=\left(\begin{array}{c}{-k}_{1}{y}_{1}+{k}_{3}{y}_{2}{y}_{3}\\ {k}_{1}{y}_{1}-{k}_{2}{y}_{2}^{2}-{k}_{3}{y}_{2}{y}_{3}\\ {k}_{2}{y}_{2}^{2}\end{array}\right),$$

with \(({{y}_{1}(0),{y}_{2}(0),{y}_{3}(0))}^{T}=({{y}_{01},{y}_{02},{y}_{03})}^{T}\), where \({y}_{1}\), \({y}_{2}\) and \({y}_{3}\) refers to the concentrations of \(A, B,\) and \(C\) respectively, and \({y}_{01}\), \({y}_{02}\) and \({y}_{03}\) are concentrations at time \(t=0\). In the test problem, \({k}_{1}=0.04\), \({k}_{2}=3\times {10}^{7}\) and \({k}_{3}={10}^{4}\) are the numerical values of rate constants with the initial concentrations \({y}_{01}=1\), \({y}_{02}=0\) and \({y}_{03}=0\).

The cause for stiffness is the substantial variation in reaction rate constants. This system features a modest, very rapid initial transient phase for problems arising from chemical kinetics. This is followed by a highly smooth fluctuation of the components, which would be acceptable for a numerical technique with a large stepsize. For \(x\in\) [0,4000], the ODE system is integrated. The numerical results by proposed method at the points.

\(x=0.4, 40, 4000\) are shown in Table 5.

Table 5 Numerical results of Problem 5.3
Full size table

Problem 5.4

(Stiff Chemical Reaction Problem)

Consider the stiff system IVPs.

$${y}_{1}^{{{\prime}}}=-1002{y}_{1}+1000{y}_{2}^{2}$$
$${y}_{2}{{^{\prime}}}={y}_{1}-{y}_{2}(1+{y}_{2}),$$

with the initial conditions as \({y}_{1}\left(0\right)=1\) and \({y}_{2}\left(0\right)=1\) having exact solutions as,

$${y}_{1}=\exp (-2x)$$
$${y}_{2}=\exp (-x)$$

This problem is solved at \(x=50\) by the new method and compared the results with forth order Two step hybrid method with one off-step point [48]. Here the stepsize \(h=0.05\) is used for compared and proposed methods. The smaller stepsize can also be used to get more accurate results. Table 6 shows the numerical results.

Table 6 Numerical results of Example 5.4
Full size table

6 Discussion

The results generated by the developed 3POBBDF(5) method are displayed in Tables 3, 4, 5, 6. In Table 3, comparison on the basis of absolute error was made using the 3POBBDF(5) of order 5 at the point \(x = 2\) with the methods of Khalsaraei and Molayi [48] and Ismail’s method [49] at the stepsize\(h={10}^{-5}\). In Table 4, 3POBBDF(5) method is integrated at \({h=10}^{-5}\) and the direct comparison has been made with the two step hybrid method with one off-step point [48] by taking the solution points at\(x=180\). Table 3 shows that the 3POBBDF(5) is more accurate and performs relatively better than the method [48] and significantly better than the method [49]. However, Table 4 shows the superiority of 3POBBDF(5) over the method [48]. Table 5 shows the numerical integration results for the problem 7.3 at \(x = 0.4, 40\) and 4000 using the proposed 3POBBDF(5) approach in comparison to that of [48] at \(h = 0.001\). The comparison of the absolute errors in Table 5 for different points of \(x\) demonstrates the dominancy of 3POBBDF(5) over the method given in [48] in terms of accuracy at\(h=0.05\). According to Table 6, it is observed that the 3POBBDF(5) method of order 5 is more effective than the two-step hybrid method of forth order with one off-step point [48]. In Table 6, it can be seen that the 3POBBDF(5) method of order 5 performs better than the fourth order Two step hybrid method with one off-step point [48]. As shown by tables (3–6), 3POBBDF(5) is well suited to nonlinear chemical reaction problems of a stiff nature.

7 Graphical representations of numerical results

The tested chemical reaction problems (5.1)–(5.4) are also compared with ode15s. Figures 4, 5, 6, and 7 are the graphs demonstrating the accuracy of the 3POBBDF(5) compared with the stiff solver ode15s. It can be examined from the graphs that the results of the 3POBBDF(5) method and the results of ode15s are nearly identical at specific intervals. These figures demonstrate that the proposed method is well suited for stiff chemical reaction problems, since the solutions produced by the 3POBBDF(5) coincide with the well-known ode15s code of MATLAB.

Fig. 4
figure 4

Graphs of intervals vs solution values for Problem 5.1

Full size image
Fig. 5
figure 5

Graphs of intervals vs solution values for Problem 5.2

Full size image
Fig. 6
figure 6

Graphs of intervals vs solution values for Problem 5.3

Full size image
Fig. 7
figure 7

Graphs of intervals Vs solution values for Problem 5.4

Full size image

8 Conclusion

In the present paper, an implicit 3POBBDF(5) method has been derived for the numerical solution of stiff systems of first-order IVPs arising from chemical reactions such as Chemical AKZO, Robertson problem, and stiff chemical problems. The approach is based on the block BDF, in which at each step of the integration, three approximate solutions are generated instantaneously. Based on stability analysis of the 3POBBDF(5), the method is consistent and zero-stable; thus, the 3POBBF(5) is convergent. Since it has an A-stability property, the method is declared suitable for solving stiff ODEs. Comparison between the stability regions was also made which shows that the 3POBBDF(5) has a smaller interval of instability than the BBDFO(6) suggested by [42]. The numerical results obtained through the 3POBBDF(5) and compared to [48] and [49] evidenced that by applying the 3POBBDF(5) method, the accuracy of the numerical solutions in terms of absolute error at specific points is improved. Hence, the proposed method can be successfully applied on stiff systems generated from chemical reactions because of their high order accuracy and wider stability region. Therefore, it can be concluded that the 3POBBDF(5) could be an appropriate substitute solver for stiff ODEs. To improve efficiency, further research can be implemented by using variable step sizes for solving ODEs would be beneficial.