A new type OF hybrid multistep multiderivative formula for solving stiff IVPs

Abstract

We present a new class of higher-order multistep multiderivative methods for the numerical solution of stiff initial value problems. These methods are obtained based on free parameters and off-point. The methods have minimum error bounds. The constructed class is A-stable for orders 3 and 4, and $A(\alpha)$-stable for orders 5 and 6. The new class is L-stable for all orders. They are suitable for solving stiff systems of initial value problems with large eigenvalues lying close to the imaginary axis. The stability regions of the new class are plotted, and some problems are solved, which show the superiority of the class in efficiency and accuracy.

1 Introduction

Consider the initial value problems for the first-order ordinary differential equation

$$\begin{aligned} y'(x) = f\bigl(x;y(x)\bigr);\qquad y(a) = \eta ;\quad x \in [x_{0},b]. \end{aligned}$$

(1)

Here $y: [x _{0}; b] \rightarrow R^{\mathrm{d}}$ and $f: [x _{0}; b] \times R^{{d}} \rightarrow R^{{d}}$ are assumed to be sufficiently smooth, and $y _{0} \in R^{{d}}$ is the given initial value. Without any loss of generality we assume the step-size $h > 0$ to be constant, and we define the grid points along the x-axis by $x _{{n}} = x _{0} + nh; n = 0; 1; 2; \ldots;N$, where $Nh = b - x_{0}$, and the set of equally spaced points on the integration interval is defined by $x _{0} < x _{1}< x _{2}< \cdots <x_{n+1}= b$.

Equations having highly oscillatory solution or stiff problems are very common problems in many fields, such as biology, celestial mechanics, control, fluids, heat transfer [20], chemical kinetics, lasers, and mechanics; see [7]. In general, any physical system modeled by an ordinary differential equation and having physical components with greatly different time constants leads to a stiff problem. In the literature of ordinary differential equations (ODEs), various definitions are seen for the stiffness [3, 9, 13, 17, 19], one being somewhat more precise than another. The essence of stiffness is that the solution to be computed is slowly varying but there exist rapidly damped perturbations.

The numerical solution of these kinds of problems is a central task in all simulation environments for mechanical, electrical, and chemical systems. From discussion on the relative merits of linear multistep and Runge–Kutta methods it emerged that the former class of methods, though generally more efficient in terms of accuracy and weak stability properties for a given number of functions evaluations per step, suffered the disadvantage of requiring additional starting values and special procedures for changing step length. These difficulties would be reduced, without sacrifice, if we could lower the step number of the linear multistep methods without reducing their order. The difficulty here lies in satisfying the essential condition of zero-stability. This “zero-stability barrier” was circumvented by the introduction of modified linear multistep formula, which incorporates a function evaluation at off-step point. Such formula, simultaneously proposed by Agarwal, Ibrahim, and Yousry [2], Butcher [4], Gear [11], Gragg and Stetter [12], Ibrahim and Yousry [15], and Shokri [18] were christened “hybrid” by the last author since, whilst retaining certain linear multistep characteristics, hybrid methods share with Runge–Kutta methods the property of utilizing data at points other than the step points [5, 6]. Thus, we may regard the introduction of hybrid formula as an important step by Kopal [16]. In this paper, our objective is to construct stable multistep multiderivative methods with off-points and good stability characteristic properties, fewer function evaluations, and rapid convergence to the exact solution.

The k-step classical hybrid method formula is as follows:

$$\begin{aligned} \sum_{i = o}^{k} \alpha _{i} y_{n + i} = h\sum_{i = 0}^{k} \beta _{k} f _{n + i} + h \beta _{s} f_{n + s}, \end{aligned}$$

(2)

where $\alpha _{{k}} = +1$, $\alpha _{0}$ and $\beta _{0}$ are not both zero, $s\notin \{0, 1, \dots, k\}$, and $f_{n+s}= f(x_{n+s},y_{n+s})$. These methods are similar to linear multistep methods but with one essential modification: an additional predictor is introduced at the off-step point. This greater generality allows the consequences of the Dahlquist barrier to be avoided, and it is actually possible to obtain convergent k-step methods with order $2k+1$ up to $k= 7$. Even higher orders are available if two or more off-step points are used. The other independent discoveries of this approach were reported in [3, 8, 10, 11].

Another important class of linear multistep methods for the numerical solution of first-order ordinary differential equations is the classical Obrechkoff methods. The k-step classical Obrechkoff method using the first l derivatives of y for solution of (1) is given by [12]

$$\begin{aligned} \sum_{j=0}^{k} \alpha _{j} y_{n+j} = \sum_{i=1}^{l} h^{i} \sum_{j=0}^{k} \beta _{ij} y_{n+j}^{(i)},\quad \alpha _{k} = 1. \end{aligned}$$

(3)

According to [17], the error constant decreases more rapidly with increasing l rather than with increasing k. It is difficult to satisfy the zero-stability for large k. The weak stability interval appears to be small.

For many problems, such explicit differentiation is intolerably complicated, but when it is feasible to evaluate the first few total derivatives of y, then generalizations of linear multistep methods that employ such derivatives can be very efficient [1].

2 Construction of the new hybrid superimplicit method

The main aim of this section is to consider the numerical integration of (1). We consider k-step methods with first l derivatives of y and ν off-step points of the form

$$\begin{aligned} \sum_{j = 0}^{k} \alpha _{j} y_{n + j} = \sum_{i = 1}^{l} h^{i} \sum_{j = 0}^{k} \beta _{ij} y_{n + j}^{(i)} + h\sum _{j = 1}^{\nu } \gamma _{j} f_{n + s_{j}},\quad \alpha _{k} = 1, \end{aligned}$$

(4)

where $\alpha _{{i}}$, $\beta_{ij}$, $\gamma _{{j}}$ are arbitrary constants to be determined, and $0 < s< k$ are parameters. Formula (4) can only be used if we know the values of the solution $y(x)$ and associated derivatives at k successive points. These k values will be assumed to be given.

For $s > k$, the methods are called superimplicit because they require the knowledge of functions not only at past and present but also at future steps (off-points).

The next work concerns the parametric formula with one off-point as follows:

$$\begin{aligned} \sum_{i=0}^{k} \alpha _{i} y_{n+i} = h \beta _{k} ( f_{n+k} - \beta _{s} f_{n+s} )+ h^{2} \gamma _{k} ( g_{n+k} - \gamma _{s} g_{n+s} ),\quad \alpha _{k} = 1. \end{aligned}$$

(5)

The associative formula to obtain the first and second derivatives at the superfuture points is

$$\begin{aligned} y_{n + s} = h \mu y'_{n + k} + \sum _{j = 0}^{k} \nu _{j} y_{n + j}, \end{aligned}$$

(6)

where $y'= f (x,y)$ and $y''= g(x, y) = f_{{x}} + f_{ {y}} f$, and the coefficients are chosen so that (5) and (6) have orders $k+1$ and $k-1$, respectively.

The associated polynomials are given by

$$\begin{aligned} \rho (z)= \sum_{i=0}^{k} \alpha _{i} z^{i},\qquad \sigma (z)= \beta _{k} \bigl( z^{k} - \beta _{s} z^{s} \bigr),\qquad \eta ( z ) = \gamma _{k} \bigl( z^{k} - \gamma _{s} z ^{s} \bigr). \end{aligned}$$

We can assume that the functions $\rho (z ), \sigma (z)$, and $\eta(z)$ have no common factors.

We use a Taylor series expansion to determine all the coefficients of (5), for which we have

$$\begin{aligned} L\bigl[y(x),h\bigr] = C_{0} y(x) + C_{1} h y^{(1)}(x) +\cdots + C_{q} h^{q} y^{(q)}(x) +\cdots. \end{aligned}$$

(7)

Definition 1

The new multistep method (5) is said to be of order p if

$$\begin{aligned} C_{0} = C_{1} = C_{2} =\cdots = C_{p} = 0, \qquad C_{p + 1} \ne 0. \end{aligned}$$

Hence for any function $y(x)\in C^{(p+2)}$ and for some nonzero constant $C_{p+1}$, we have

$$\begin{aligned} L\bigl(y(x),h\bigr) ={}& \sum_{i = 0}^{k} (\alpha _{i} y(x_{n} + ih) - h \beta _{k} \bigl(y'(x _{n} + k h) - \beta _{s}y'(x_{n} + sh)\bigr) - h^{2} \gamma _{k}\bigl(y''(x_{n} + kh) \\ &{} - \gamma _{s}y''(x_{n} + sh)\bigr) + C_{p + 1} h^{p + 1} y^{(p + 1)}(x_{n}) + O\bigl(h^{p + 2}\bigr), \end{aligned}$$

(8)

where $C_{p+1}$ is called the error constant.

In particular, $L(y(x),h)$ vanishes identically when $y(x)$ is a polynomial whose degree is less than or equal to p.

Lemma 1

The new multistep method (5) is consistent if and only if

$$\begin{aligned} \rho (1)= 0, \qquad \rho '(1)=\sigma (1). \end{aligned}$$

(9)

Proof

We know that the general linear multistep methods are consistent if and only if they have the order $p \geq 1$. This implies $C _{0} = C _{1} = 0$. Therefore by a simple calculation we get (9). □

3 Stability analysis

In this section, we introduce different types of stability. We study A, $A(\alpha)$, and L-stability of the new superfuture methods (5)–(6) for $k= 2-5$ with one off-point.

Definition 2

(Lambert [17])

A numerical method is said to be A-stable if its region of absolute stability S contains the whole complex left-half plane.

Definition 3

(Lambert [17])

A k-step method is said to be L-stable if it is A-stable and has a stability matrix with vanishing eigenvalues at infinity.

If we apply (5)–(6) to the test equation $y' = \lambda y$ for which $y'' = \lambda ^{2} y$, then we get

$$\begin{aligned} &\sum_{i = 0}^{k} \alpha _{i} y_{n + i} = \chi \beta _{k}(y_{n + k} - \beta _{s}y_{n + s}) + \chi ^{2} \gamma _{k} (y_{n + k} - \gamma _{s}y_{n + s}), \end{aligned}$$

(10)

$$\begin{aligned} &y_{n + s} = \chi \mu y_{n + k} + \sum _{j = 0}^{k} \nu _{j} y_{n + j}, \end{aligned}$$

(11)

where $\chi = h \lambda$ Substituting (11) inti (10), we obtain

$$\begin{aligned} \sum_{i = 0}^{k} \alpha _{i} y_{n + i} = {}&\chi \beta _{k}\Biggl(y_{n + k} - \beta _{s}\Biggl(\chi \mu y_{n + k} + \sum _{j = 0}^{k} \nu _{j} y_{n + j} \Biggr)\Biggr) \\ &{} + \chi ^{2} \gamma _{k}\Biggl(y_{n + k} - \gamma _{s}\Biggl(\chi \mu y_{n + k} + \sum _{j = 0}^{k} \nu _{j} y_{n + j} \Biggr)\Biggr). \end{aligned}$$

(12)

This equation can be written as

$$\begin{aligned} &y_{n + k}\bigl(\gamma _{k} \gamma _{s} \mu \chi ^{3} + \beta _{k}\beta _{s} \mu \chi ^{2} - \chi \beta _{k} + \alpha _{k} + \beta _{k}\beta _{s} \nu _{k} - \gamma _{k}\bigr) \\ &\quad{} + \sum_{i = 0}^{k} \bigl(\alpha _{i} - \nu _{i} \beta _{k} \beta _{s} \chi - \gamma _{k} \gamma _{s} \nu _{i} \chi ^{2}\bigr)y_{n + i} = 0, \end{aligned}$$

(13)

$$\begin{aligned} & y_{n + k} = \frac{ - \sum_{i = 0}^{k} (\alpha _{i} - \nu _{i}\beta _{k} \beta _{s} \chi - \gamma _{k}\gamma _{s}\nu _{i} \chi ^{2})}{(\gamma _{k} \gamma _{s} \mu \chi ^{3} + \beta _{k}\beta _{s} \mu \chi ^{2} - \chi \beta _{k} + \alpha _{k} + \beta _{k}\beta _{s}\nu _{k} - \gamma _{k})}y_{n + i}. \end{aligned}$$

(14)

The associated characteristic equation takes the form

$$\begin{aligned} \sum_{i = 0}^{k} \alpha _{i} \xi ^{i} ={}& \chi \beta _{k}\Biggl(\xi ^{k} - \beta _{s}\Biggl(\chi \mu \xi ^{k} + \sum _{j = 0}^{k} \nu _{n - j} \xi ^{k - j} \Biggr)\Biggr) \\ &{}+ \chi ^{2} \gamma _{k}\Biggl( \xi ^{k} - \gamma _{s}\Biggl(\chi \mu \xi ^{k} + \sum_{j = 0}^{k} \nu _{n - j} \xi ^{k - j} \Biggr)\Biggr). \end{aligned}$$

(15)

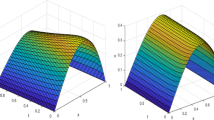
For stability, ξ must satisfy the condition $|\xi |\leq1$, with strict inequality for multiple roots; see [17]. We use the boundary locus method to determine the absolute stability region; for $\xi = e^{i\theta}$, a cubic equation gives rise to three roots locus curves, which together describe the stability domain. The stability regions of method (5)–(6) for steps $k=2$ up to 5 are plotted in Fig. 1. The method (5)–(6) is A-stable for $k=2$ and 3, and is $A(\alpha)$ stable for $k=4$ and 5, where $\alpha =85.1^{\circ}$ for $k=4$ and $\alpha = 75.7^{\circ}$ for $k=5$. From (14) it is clear that since the power of χ in the denominator is higher than that in the numerator, the solution tends to zero, and so (5)–(6) is L-stable or $L(\alpha)$-stable according to its A-stability or $A(\alpha)$-stability.

Figure 1

Absolute stability region for formulas (4)–(5) with $k= 2, 3, 4, 5$

4 Four-step methods with one off-step point

We are going to discuss in details method (4)–(5) for $k=4$. The coefficients of method (5)–(6) for $k=2, 3, 5$, the error constants, and the values of the parameters that minimize the truncation error are listed in the Appendix.

Upon choosing $k = 4$ in (5)–(6), we get

$$\begin{aligned} &\sum_{i = 0}^{4} \alpha _{i} y_{n + i} = h \beta _{4}(f_{n + 4} - \beta _{s}f_{n + s}) + h^{2} \gamma _{4}(g_{n + 4} - \gamma _{s}g_{n + s}),\quad \alpha _{4} = 1, \end{aligned}$$

(16)

$$\begin{aligned} &y_{n + s} = h \mu y'_{n + 4} + \sum _{j = 0}^{4} \nu _{j} y_{n + j}. \end{aligned}$$

(17)

The coefficients of (16) and (17) are as follows:

$$\begin{aligned} \alpha _{0} ={}& {-} \bigl( - 6 \bigl(1660 + ( - 5 + s) s \bigl(906 + 5 ( - 5 + s) s \bigl(33 + 2 ( - 5 + s) s\bigr)\bigr)\bigr) \\ &{}+ \beta _{4} ( - 4 + s) 2 \bigl(1421 + s \bigl( - 3080 + s \bigl(2469 + 10 s ( - 86 + 11 s)\bigr)\bigr) \bigr) \\ &{}+2 ( - 4 + s) \bigl( - 4669 + s \bigl(10{,}856 + 5 s \bigl( - 1946 + 3 s \bigl(276 + s ( - 55 + 4 s)\bigr)\bigr)\bigr)\bigr) \gamma _{4}\bigr)\\ &{}/ \bigl(6 \bigl(36 + ( - 3 + s) s \bigl(66 + 5 ( - 3 + s) s \bigl(9 + 2 ( - 3 + s) s\bigr)\bigr)\bigr)\bigr); \\ \alpha _{1} ={}& \bigl(\beta _{4} ( - 4 + s)2 \bigl(324 + s \bigl( - 864 + s \bigl(972 +5 s ( - 89 + 14 s)\bigr)\bigr)\bigr) \\ &{}- 4 \bigl(576 + s \bigl( - 1872 + s \bigl(2676 + 5 s \bigl( - 384 + s \bigl(144 + s ( - 27 + 2 s)\bigr)\bigr) \bigr)\bigr)\bigr)\\ &{} + ( - 4 + s) \bigl( - 2088 + s \bigl(5832 + 5 s \bigl( - 1392 + s \bigl(746 + 7 s ( - 25 + 2 s)\bigr)\bigr)\bigr)\bigr) \gamma _{4}\bigr)\\ &{}/ \bigl(36 + ( - 3 + s) s \bigl(66 + 5 ( - 3 + s) s \bigl(9 + 2 ( - 3 + s) s\bigr) \bigr)\bigr); \\ \alpha _{2} ={}& {-} \bigl( - 12 \bigl(144 + ( - 4 + s) s \bigl(171 + 5 ( - 4 + s) s \bigl(15 + 2 ( - 4 + s) s\bigr)\bigr)\bigr) \\ &{}+ \beta _{4} ( - 4 + s)2 \bigl(225 + s \bigl( - 936 + s \bigl(1569 + 10 s ( - 94 + 19 s)\bigr)\bigr)\bigr)\\ &{} + 2 ( - 4 + s) \bigl( - 657 + s \bigl(2808 + 5 s \bigl( - 978 + s \bigl(664 + s ( - 185 + 16 s)\bigr)\bigr)\bigr)\bigr) \gamma _{4} \bigr)\\ &{}/ \bigl(2\bigl(36 + ( - 3 + s)s\bigl(66 + 5( - 3 + s)s\bigl(9 + 2( - 3 + s) s \bigr)\bigr)\bigr)\bigr); \\ \alpha _{3} = {}&\bigl(\beta _{4} ( - 4 + s)2 \bigl(76 + s \bigl( - 352 + s \bigl(672 + 5 s ( - 101 + 26 s)\bigr)\bigr)\bigr) \\ &{}- 12 \bigl(64 + s \bigl( - 336 + s \bigl(756 + 5 s \bigl( - 160 + s \bigl(84 + s ( - 21 + 2 s)\bigr)\bigr)\bigr) \bigr)\bigr) \\ &{}+ ( - 4 + s) \bigl( - 376 + s \bigl(1784 + 5 s \bigl( - 704 + 3 s \bigl(194 + s ( - 65 + 6 s)\bigr)\bigr)\bigr)\bigr) \gamma _{4} \bigr)\\ &{}/ \bigl(3 \bigl(36 + ( - 3 + s) s \bigl(66 + 5 ( - 3 + s) s \bigl(9 + 2 ( - 3 + s) s\bigr)\bigr)\bigr)\bigr); \\ \gamma _{s} ={}& (12 \bigl(24 + 5 ( - 4 + s) s \bigl(5 + ( - 4 + s) s \bigr)\bigr) - \beta _{4} ( - 4 + s) \bigl( - 168 + s \bigl(649 + s ( - 548 + 125 s)\bigr)\bigr) \\ &{}- 5 \bigl(228 + 5 s \bigl( - 184 + s \bigl(183 + s ( - 64 + 7 s)\bigr)\bigr) \gamma _{4}\bigr)\\ &{}/ \bigl(\bigl(36 + ( - 3 + s) s \bigl(66 + 5 ( - 3 + s) s \bigl(9 + 2 ( - 3 + s) s \bigr)\bigr)\bigr) z\bigr); \\ \beta _{s} ={}& \bigl(2 \bigl( - 60 ( - 2 + s) \bigl(5 + 2 ( - 4 + s) s \bigr) + \beta _{4} \bigl( - 1382 + s \bigl(2841 + 2 s ( - 786 + 125 s)\bigr)\bigr) \\ &{}+ 25 ( - 4 + s) \bigr)23 + 2 s ( - 20 + 7 s)\bigr) \gamma _{4}))\\ &{}/ \bigl(\beta _{4} \bigl(36 + ( - 3 + s) s \bigl(66 + 5 ( - 3 + s) s \bigl(9 + 2 ( - 3 + s) s\bigr)\bigr)\bigr)\bigr); \\ v_{1} ={}& \frac{1}{6} \bigl(24 - 26 s + 9 s^{2} - s^{2} + 2 \mu - 24 v_{0}\bigr);\\ v _{2} ={}& \frac{1}{2} \bigl( - 12 + 19 s - 8 s^{2} + s^{3} - 3 \mu + 12 v_{0}\bigr); \\ v_{3} = {}&\frac{1}{2}\bigl(8 - 14 s + 7 s^{2} - s^{3} + 6 \mu - 8 v_{0}\bigr);\\ v _{4} ={}& \frac{1}{6} \bigl( - 6 + 11 s - 6 s^{2} + s^{3} - 11 \mu + 6 v_{0}\bigr). \end{aligned}$$

Here $\beta _{4}$, $\gamma _{4}$, s, μ, $\nu _{0}$ are free parameters, and the error constant of the local truncation error is

$$\begin{aligned} T ={}& {-} ( - 12\bigl(576 + 5( - 4 + s)s\bigl(180 + ( - 4 + s)s\bigl(114 + ( - 4 + s)s\bigl(31 + 3( - 4 + s)s\bigr)\bigr)\bigr)\bigr) \\ &{}+ \beta _{4}( - 4 + s)^{2} \bigl(1116 + s\bigl( - 6336 + s \bigl(15{,}690 + s\bigl( - 18{,}620 \\ &{}+ s\bigl(11{,}195 - 3288s + 375s^{2}\bigr)\bigr) \bigr)\bigr)\bigr) \\ &{}+ ( - 4 + s) \bigl( - 8856 + s\bigl(51{,}624 + 5s\bigl( - 26{,}424 + s \bigl(33{,}502\\ &{} + s\bigl( - 22{,}640 + s\bigl(8233 + 15s( - 100 + 7s)\bigr)\bigr)\bigr)\bigr) \bigr)\bigr)\gamma _{4})\\ &{}/ (360\bigl(36 + ( - 3 + s)s\bigl(66 + 5( - 3 + s) s\bigl(9 + 2( - 3 + s)s\bigr) \bigr)\bigr). \end{aligned}$$

The values, $s=4$ and $\gamma _{4}= -72/415$ minimize the truncation error, and the error constant becomes $\frac{24}{2075}$.

5 Stability analysis

We study the stability analysis of method (4)–(5) for $k=4$.

Definition 4

(Lambert [17])

An LMM is called $A( \alpha)$-stable ($0 < \alpha <\pi/2$) if $S \supseteq S_{\alpha } = \{ \mu , \vert \arg ( - \mu ) < \alpha , \mu \ne 0\} \vert$.

To analyze the method for the absolute stability, the associated characteristic equation of the method (16)–(17) takes the form

$$\begin{aligned} &\xi ^{4}\bigl(1 + \beta _{4}\chi ( - 1 + \beta _{s} \mu \chi ) + \gamma _{4} \chi ^{2}( - 1 + \gamma _{s} \mu \chi )\bigr) + \alpha _{0} + \chi (\beta _{4} \beta _{s} + \gamma _{4}\gamma _{s} \chi )v_{0} \\ &\quad + \xi \bigl(\alpha _{1} + \xi \alpha _{2}+ \xi ^{2}\alpha _{3} \\ &\quad{}+ \chi (\beta _{s} \gamma _{s} + \gamma _{4}\gamma _{s}\chi ) \bigl(v_{1} + \xi \bigl(v_{2} + \xi (v_{3} + \xi v_{4})\bigr)\bigr)\bigr) . \end{aligned}$$

(18)

By using boundary locus method and Wolfram Mathematica the absolute stability region is plotted. The figure shows that the method is $A( \alpha)$-stable with $\alpha =85.1^{\circ}$. The absolute stability region is plotted in Fig. 1.The methods are unstable at the shaded region.

From equation (14) we have

$$\begin{aligned} y_{n + 4} = {}&{-} \sum_{i = 0}^{4} \bigl(\alpha _{i} - \nu _{i}\beta _{k}\beta _{s}\chi - \gamma _{k}\gamma _{s}\nu _{i} \chi ^{2}\bigr)y_{n + i} \\ &{}/ \bigl(\gamma _{k} \gamma _{s}\mu \chi ^{3} + \beta _{k}\beta _{s} \mu \chi ^{2} - \chi \beta _{k} + \alpha _{k} + \beta _{k}\beta _{s}\nu _{k} - \gamma _{k}\bigr). \end{aligned}$$

(19)

This equation shows that method (16)–(7) is $L(\alpha)$-stable.

6 Numerical examples

In this section, we present some numerical results obtained by our new methods (5)–(6) with step $k=3$. The values of the parameters used are $\beta _{3} = 0.2, \gamma _{3} = 0.2, s = 4,\mu = - 0.6, \nu _{0} = 0.3$, and the numerical results are compared with those of other multistep methods.

Test 1

(Robertson chemical kinetics problem, Hojjati [14])

Consider the stiff initial value problem

$$\begin{aligned} &y_{1}^{\prime } (x) = - 0.04 y_{1}(x) + 10^{4} y_{2}(x)y_{3}(x), \\ &y_{2}^{\prime } (x) = - 0.04 y_{1}(x) - 10^{4}y_{2}(x)y_{3}(x) - 3*10^{7}y _{2}^{2}(x), \\ &y_{3}^{\prime } (x) = 3*10^{7}y_{2}^{2}(x),\qquad y_{1}(0) = 1, \qquad y_{2}(0) = 1,\qquad y _{3}(0) = 1. \end{aligned}$$

Numerical results for the Robertson problem by method (5)–(6) are compared with those of the parallel SDMM method in Table 1. The solution curves are displayed in Fig. 2.

Figure 2

The solution curves of Test 1

Table 1 Numerical results for Test 1

Test 2

The following stiff initial value problem arises from a chemistry problem:

$$\begin{aligned} &y_{1}'(x) = - 0.013 y_{2}(x) - 1000 y_{1}(x)y_{2}(x) - 2500 y_{1}(x)y_{3}(x), \\ &y_{2}'(x) = - 0.013y_{2}(x) - 10 00y_{1}(x)y_{2}(x), \\ &y_{3}'(x) = - 2500y _{1}(x) y_{3}(x), \end{aligned}$$

with $y _{1} (0) = 0$, $y _{2} (0) = 1$, $y _{3} (0) =1$. For $x=2$, the exact solution is

$$\begin{aligned} &y_{1}(2) = - 0.3616933169289 *10^{-5}, \\ &y_{2}(2)=0.9815029948230, \\ &y_{3}(2)= 1.018493388244. \end{aligned}$$

This problem is solved by method (5)–(6), and the second derivative BDF method (SDBDF) with $h=0.0001$. The absolute errors of the numerical integration at $x=2$ are tabulated in Table 2.

Table 2 The absolute errors for Test 2

Test 3

Consider the stiff system

$$\begin{aligned} &y_{1}'(x) = - 10 y_{1}(x) + 21 y_{2}(x),\qquad y_{1}(0) = 1, \\ &y_{2}'(x) = - 21 y_{1}(x) - 10 y_{2}(x),\qquad y_{2}(0) = 1, \\ &y_{3}'(x) = - 10 y_{3}(x),\qquad y_{3}(0) = 1. \end{aligned}$$

The exact solution is given by

$$\begin{aligned} &y_{1}(x) = e^{ - 10 x} (\cos 21 x + \sin 21 x),\\ &y_{2}(x) = e^{ - 10 x}(\cos 21 x - \sin 21 x),\\ & y_{3}(x) = e^{ - 10 x}. \end{aligned}$$

This problem is solved by method (5)–(6), and the sixth-order method given by [19]

$$\begin{aligned} \begin{aligned} y_{n+1} ={}& y_{n} + \frac{h}{120} [900 f_{n+1} -780 f_{n+2} )+ \frac{h ^{2}}{120} (372 g_{n+1} +348 g_{n+2} )\\ &{}+ \frac{h^{3}}{120} (111 l _{n+1} -49 l_{n+2} ),\\ y_{n+2} ={}& y_{n} + \frac{h}{15} [120 f_{n+1} -90 f_{n+2} )+ \frac{h ^{2}}{15} (48 g_{n+1} +428 g_{n+2} )\\ &{}+ \frac{h^{3}}{15} ( 14 l_{n+1} -6 l _{n+2} ). \end{aligned} \end{aligned}$$

(20)

The absolute errors of the numerical integration are illustrated in Table 3.

Table 3 The absolute errors for Test 3

7 Conclusion

Multiderivative methods are used to solve stiff problems effectively. This paper has been able to develop implicit formulas of linear multistep methods to hybrid superimplicit formulas for the solution of initial value problems. Here a hybrid multistep multiderivative method is derived with parameters that control stability and the degree of accuracy. It is clear from the tables that our new methods are accurate. However, choosing the values of the parameter such that the method is super implicit, the new method has large stability regions. The method is L-stable for $k=2$ and 3 and $L( \alpha)$-stable with large α for $k=4$ and 5. The parameters are determined to minimize the truncation errors for different k.

Appendix

The coefficients of (5) and (6) for $k=2$ are

$$\begin{aligned} &\alpha _{0} = 1 - \beta _{2} + \bigl(2(\beta _{2} + 3\gamma _{2})\bigr)/\bigl(2 + 3( - 2 + s)s\bigr), \\ &\alpha _{1} = - 2 + \beta _{2} - \bigl(2(\beta _{2} + 3\gamma _{2})\bigr)/\bigl(2 + 3( - 2 + s)s\bigr), \\ &\beta _{s} = \bigl(2(\beta _{2} + 3\gamma _{2}) \bigr)/\bigl(\beta _{2}\bigl(2 + 3( - 2 + s)s\bigr)\bigr). \\ &\gamma _{s} = \bigl(\beta _{2}( - 2 + s) ( - 4 + 9s) + 2\bigl( - 2 + 3s\bigl(2 + s( - 1 + \gamma _{2}) - 4\gamma _{2}\bigr) + 5\gamma _{2}\bigr)\bigr)\\ &\phantom{\gamma _{s} =}{}/\bigl(2 \bigl(2 + 3( - 2 + s)s\bigr)\gamma _{2}\bigr), \\ &v_{1} = 2 - s + \mu - 2v_{0},\qquad v_{2} = - 1 + s - \mu + v_{0}. \end{aligned}$$

The error constant of the local truncation error is

$$\begin{aligned} T = {}&\bigl(\beta _{2}( - 2 + s) \bigl(8 + s( - 23 + 8s) \bigr) + 2\bigl(2 - 21\gamma _{2} \\ &{}+3s\bigl( - 2 + s + 2\bigl(12 + s( - 9 + 2s)\bigr)\gamma _{2}\bigr) \bigr)\bigr)/24\bigl(2 + 3( - 2 + {s}){s}\bigr). \end{aligned}$$

The values $s=2$ and $\beta _{2} = - 3\gamma _{2}$ minimize the truncation error, and the error constant becomes $\frac{1}{48}$.

The coefficients of (5) and (6) for $k=3$ are

$$\begin{aligned} \alpha _{0} ={}& \bigl(\beta _{3}( - 3 + s)^{2} \bigl(39 + 2s( - 26 + 9s)\bigr) + 2\bigl( - 85 + 243 \gamma _{3} \\ &{}+3s \bigl(60 - 147 \gamma _{3} + s\bigl( - 47 + 2s\bigl(8 + s( - 1 + \gamma _{3}) - 12 \gamma _{3}\bigr) 94\gamma _{3}\bigr)\bigr)\bigr)\bigr)\\ &{}/\bigl(8 + 6( - 2 + s)s \bigl(3 + 2( - 2 + s)s\bigr)\bigr), \\ \alpha _{1} ={}& \bigl( - 8\beta _{3}( - 3 + s)^{2}\bigl(3 + s( - 5 + 3s)\bigr) + 3\bigl(36 - 90 s + 93 s^{2} - 40 s^{3} + 6 s^{4} \\ &{}- 4 ( - 3 + s) \bigl( - 8 + ( - 7 + s) ( - 2 + s)s\bigr) \gamma _{3}\bigr)\bigr)\\ &{}/ \bigl(4 + 3 ( - 2 + s)s \bigl(3 + 2 ( - 2 + s)\bigr)\bigr)), \\ \alpha _{2} ={}& \bigl(\beta _{3}( - 3 + s)^{2}\bigl(9 - 28 s + 30 s^{2}\bigr) + 6 \bigl( - 9 + 15 \gamma _{3} + s \bigl(36 - 53 \gamma _{3} \\ &{}+ s \bigl( - 57 + 32 s - 6 s^{2} + 2( - 7 + s) ( - 5 + s) \gamma _{3}\bigr)\bigr)\bigr)\bigr)\\ &{}/\bigl(8 + 6 ( - 2 + s) s \bigl(3 + 2 ( - 2 + s) s\bigr)\bigr), \\ \beta _{s} ={}& \bigl(\beta _{3} \bigl(139 + 6 s( - 36 + 11 s)\bigr) + 6\bigl( - 11 + 33 \gamma _{3} + s \bigl(18 - 47 \gamma _{3} + 6 s ( - 1 + 2 \gamma _{3})\bigr)\bigr) \bigr)\\ &{}/ \bigl(\beta _{3} \bigl(4 + 3 ( - 2 + s) s \bigl(3 + 2 ( - 2 + s) s \bigr)\bigr)\bigr), \\ \gamma _{s} ={}& {- }\bigl(18 + \beta _{3}( - 3 + s) \bigl(13 - 42 s + 22 s^{2}\bigr) - 58 \gamma _{3} \\ &{}+ 3 s\bigl( - 22 + 66 \gamma _{3} + s\bigl(18 - 47 \gamma _{3} + s ( - 4 + 8 \gamma _{3})\bigr)\bigr) \bigr)\\ &{}/ \bigl(\bigl(4 + 3( - 2 + s)s\bigl(3 + 2( - 2 + s)s\bigr)\bigr)\gamma _{3}\bigr), \\ v_{1} ={}& \frac{1}{2}\bigl(6 - 5 s + s^{2} - \mu - 6 v_{0}\bigr), \\ v_{2} ={}&{ -} 3 + 4 s - s^{2} + 2 \mu + 3 v_{0}, \\ v_{3} ={}& \frac{1}{2}\bigl(2 - 3 s + s^{2} - 3 \mu - 2 v_{0}\bigr). \end{aligned}$$

The error constant of the local truncation error is

$$\begin{aligned} T ={}&{ - }\bigl( - 6\bigl(36 + ( - 3 + s)s\bigl(66 + 5( - 3 + s)s\bigl(9 + 2( - 3 + s)s\bigr)\bigr)\bigr) \\ &{}+ \beta _{3}( - 3 + s)^{2}\bigl(60 + s\bigl( - 282 + s \bigl(549 + 10s( - 42 + 11s)\bigr)\bigr)\bigr) \\ &{}+ 2( - 3 + s) \bigl( - 168 + s\bigl(816 + 5s\bigl( - 332 + 3s\bigl(96 + s( - 35 + 4s)\bigr)\bigr)\bigr)\bigr) \gamma _{3}\bigr)\\ &{}/\bigl(120\bigl(4 + 3( - 2 + s)s\bigl(3 + 2( - 2 + s)s\bigr)\bigr)\bigr). \end{aligned}$$

The values $s=3$ and $\gamma _{3} = - 18/85$ minimize the truncation error, and the error constant becomes $\frac{9}{425}$.

The coefficients of (5) and (6) for $k=5$ are

$$\begin{aligned} \alpha _{0} ={}& ( - 12 \bigl(48{,}076 + 5 ( - 6 + s) s \bigl(5145 + ( - 6 + s) s \bigl(1029 + ( - 6 + s) s \bigl(91 + 3 ( - 6 + s) s\bigr)\bigr)\bigr)\bigr)\\ &{} + \beta _{5} ( - 5 + s)^{2} \bigl(56{,}620 + s \bigl( - 157{,}046 + s \bigl(177{,}225 \\ &{}+ s \bigl( - 103{,}780 + s \bigl(33{,}260 - 5538 s + 375 s^{2}\bigr)\bigr)\bigr)\bigr)\bigr)\\ &{} + ( - 5 + s) \bigl( - 522{,}500 + s \bigl(1\text{,}525{,}694 + 5 s \bigl( - 369{,}805 + s \bigl(240{,}067 \\ &{}+ s \bigl( - 89{,}980 + s \bigl(19{,}438 + 15 s ( - 149 + 7 s)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr) \gamma _{5})\\ &{}/(12 \bigl(576 + 5 ( - 4 + s) s \bigl(180 + ( - 4 + s) s\bigl(\bigl(114 + ( - 4 + s) s \bigl(31 + 3 ( - 4 + s) s\bigr)\bigr) \bigr)\bigr)\bigr); \\ \alpha _{1} ={}& {-} (\beta _{5} ( - 5 + s)^{2} \bigl(42{,}048 + s \bigl( - 142{,}992 + s \bigl(215{,}940 + s \bigl( - 161{,}656 \\ &{}+ s \bigl(62{,}642 + 3 s ( - 4022 + 305 s)\bigr)\bigr)\bigr) \bigr)\bigr) - 30 \bigl(14{,}400 + s \bigl( - 55{,}440 \\ &{}+ s \bigl(96{,}708 + s \bigl( - 90{,}832 + s \bigl(49{,}650 + s \bigl( - 16{,}296 + s \bigl(3167 + 3 s ( - 112 + 5 s)\bigr)\bigr)\bigr)\bigr) \bigr)\bigr)\bigr) \\ &{}+ 2 ( - 5 + s) \bigl( - 191{,}808 + s \bigl(676{,}944 + 5 s \bigl( - 213{,}732 + s \bigl(173{,}836 \\ &{}+ s \bigl( - 77{,}608 + s \bigl(19{,}147 + 3 s ( - 811 + 41 s)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr) \gamma _{5})\\ &{}/ \bigl(6\bigl(576 + 5 ( - 4 + s)s\bigl(180 + ( - 4 + s) s \bigl(114 + ( - 4 + s) s \bigl(31 + 3 ( - 4 + s) s\bigr)\bigr)\bigr)\bigr) \bigr); \\ \alpha _{2} ={}& (3 \beta _{5} ( - 5 + s)^{2} \bigl(2256 + s \bigl( - 11{,}052 + s \bigl(23{,}075 + s \bigl( - 21{,}734 \\ &{}+ s \bigl(10{,}114 + s ( - 2266 + 195 s)\bigr)\bigr)\bigr)\bigr)\bigr) - 20 \bigl(3600 + s \bigl( - 19{,}260\\ &{} + s \bigl(44{,}967 + s \bigl( - 52{,}064 + s \bigl(33{,}405 + s \bigl( - 12{,}468 + s \bigl(2693 + 3 s ( - 104 + 5 s)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr) \\ &{}+ 3 ( - 5 + s) \bigl( - 19{,}632 + s \bigl(98{,}628 + 5 s \bigl( - 42{,}557 + s\bigl(43{,}063 \\ &{}+ s\bigl( - 22{,}712 + s\bigl(6388 + s( - 899 + 49s) \bigr)\bigr)\bigr)\bigr)\bigr)\bigr) \gamma _{5}) \\ &{}/\bigl(2 \bigl(576 + 5 ( - 4 + s) s \bigl(180 + ( - 4 + s) s \bigl(114 + ( - 4 + s) s \bigl(31 + 3 ( - 4 + s) s\bigr)\bigr)\bigr)\bigr)\bigr); \\ \alpha _{3} ={}& {- }(\beta _{5} ( - 5 + s)^{2} \bigl(8384 + s \bigl( - 45{,}232 + s \bigl(105{,}420 + s \bigl( - 115{,}304 + s \bigl(62{,}566 \\ &{}+ 3 s ( - 5402 + 535 s)\bigr)\bigr)\bigr)\bigr)\bigr) - 60 \bigl(1600 + s \bigl( - 9360 + s \bigl(24{,}132 \\ &{}+ s \bigl( - 31{,}536 + s \bigl(22{,}830 + s \bigl( - 9522 + s \bigl(2273 + 3 s ( - 96 + 5 s)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr) \\ &{}+ 2( - 5 + s) \bigl( - 33{,}344 + s \bigl(183{,}824 + 5s \bigl( - 88{,}084 \\ &{}+ s\bigl(102{,}076 + s\bigl( - 61{,}564 + s \bigl(19{,}489 + 3s( - 1009 + 59 s)\bigr)\bigr) \bigr)\bigr)\bigr)\bigr)\gamma _{5})\\ &{}/ \bigl(6 \bigl(576 + 5 ( - 4 + s) s \bigl(180 + ( - 4 + s) s \bigl(114 + ( - 4 + s) s \bigl(31 + 3 ( - 4 + s) s\bigr)\bigr)\bigr)\bigr) \bigr); \\ \alpha _{4} ={}& (\beta _{5} ( - 5 + s)^{2} \bigl(3636 + s \bigl( - 20{,}466 + s \bigl(50{,}145 + s \bigl( - 58{,}928 \\ &{}+ s \bigl(35{,}104 + 3 s ( - 3406 + 385 s)\bigr)\bigr)\bigr)\bigr)\bigr) - 60 \bigl(900 + s \bigl( - 5490 + s \bigl(14{,}853 \\ &{}+ s \bigl( - 20{,}668 + s \bigl(16{,}125 + s \bigl( - 7314 + s \bigl(1907 + 3 s ( - 88 + 5 s)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr) \\ &{}+ ( - 5 + s) ( - 24{,}732 + s )142{,}074 + 5 s \bigl( - 71{,}433 + s \bigl(88{,}447\\ &{} + s \bigl( - 57{,}892 + s \bigl(20{,}122 + 3 s ( - 1141 + 71 s)\bigr)\bigr)\bigr)\bigr))) \gamma _{5})\\ &{}/\bigl(12 \bigl(576 + 5 ( - 4 + s) s \bigl(180 + ( - 4 + s) s \bigl(114 + ( - 4 + s) s \bigl(31 + 3 ( - 4 + s) s\bigr)\bigr) \bigr)\bigr)\bigr); \\ \beta _{s} ={}& (2 \bigl( - 60 \bigl(274 + 15 ( - 5 + s) s \bigl(9 + ( - 5 + s) s\bigr) + \beta _{5} \bigl(40{,}538 + 15 s \bigl( - 6585 \\ &{}+ s \bigl(4898 + s ( - 1410 + 137 s)\bigr) \bigr)\bigr)\\ &{} + 5 ( - 5 + s) \bigl( - 3014 + s \bigl(6623 + s ( - 3923 + 675 s)\bigr)\bigr) \gamma _{5}\bigr)\bigr)\\ &{}/ \bigl(\beta _{5} \bigl(576 + 5 ( - 4 + s) s \bigl(180 + (4 + s) s \bigl(114 + ( - 4 + s) s \bigl(31 + 3 ( - 4 + s) s\bigr)\bigr)\bigr)\bigr)\bigr); \\ \gamma _{s} ={}& \bigl(60 ( - 5 + 2 s) \bigl(24 + ( - 5 + s) s \bigl(20 + 3 ( - 5 + s) s\bigr)\bigr) - \beta _{5} ( - 5 + s) \bigl(3576 \\ &{}+ s \bigl( - 15{,}500 + s \bigl(16{,}655 - 6465 s + 822 s^{2}\bigr)\bigr)\bigr) \\ &{}+ \bigl(33{,}576 - 5 s \bigl(30{,}140 + s \bigl( - 36{,}129 + s \bigl(17{,}492 + s ( - 3649 + 270 s)\bigr)\bigr)\bigr)\bigr) \gamma _{5}\bigr)\\ &{}/\bigl(\bigl(576 + 5 ( - 4 + s) s\bigl(180 + ( - 4 + s)s\bigl(114 + ( - 4 + s) s \bigl(31 + 3( - 4 + s) s\bigr) \bigr)\bigr)\bigr)\gamma _{5}\bigr); \\ v_{1} ={}& \bigl(120 - 154 s + 71 s^{2} - 14 s^{3} + s^{4} - 6 \mu - 120 v _{0}\bigr)/24; \\ v_{2} = {}&\bigl( - 60 + 107 s - 59 s^{2} + 13 s^{3} - s^{4} + 8 \mu + 60 v _{0}\bigr)/6; \\ v_{3} ={}& \bigl(40 - 78 s + 49 s^{2} - 12 s^{3} + s^{4} - 12 \mu - 40 v_{0}\bigr)/4; \\ v_{4} ={}& \bigl( - 30 + 61 s - 41 s^{2} + 11 s^{3} - s^{4} + 24 \mu + 30 v _{0}\bigr)/6; \\ v_{5} ={}& \bigl(24 - 50 s + 35 s^{2} - 10 s^{3} + s^{4} - 50 \mu - 24 v_{0}\bigr)/24. \end{aligned}$$

The error constant of the local truncation error is

$$\begin{aligned} T ={}& {-} \bigl( - 180\bigl(4800 + ( - 5 + s)s\bigl(6576 + ( - 5 + s)s \bigl(3820 \\ &{}+ 7( - 5 + s) s\bigl(152 + ( - 5 + s)s\bigl(20 + ( - 5 + s)s\bigr)\bigr)\bigr)\bigr)\bigr) + 3 \beta _{5}( - 5 + s)^{2} \bigl(30{,}912 \\ &{}+ s\bigl( - 198{,}000 + s\bigl(567{,}740 + s( - 841{,}720 + s)704{,}268 + s\bigl( - 345{,}575\\ &{} + s\bigl(98{,}505 + 7s( - 2155 + 137s)\bigr)\bigr)\bigr)\bigr) \bigr)\bigr))\\ &{} + ( - 5 + s) \bigl( - 977{,}472 + s\bigl(6\text{,}397{,}200 + s\bigl( - 18{,}824{,}100 \\ &{}+ s\bigl(29{,}186{,}060 + 7s\bigl( - 3\text{,}739{,}208 + 5s\bigl(407{,}305 + s\bigl( - 136{,}318 \\ &{}+ s\bigl(27{,}268 + s( - 2974 + 135s)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr)\bigr) \gamma _{5})\\ &{}/ \bigl(2520\bigl(576 + 5( - 4 + s)s\bigl(180 + ( - 4 + s)s\bigl(114 + ( - 4 + s) s\bigl(31 + 3( - 4 + s)s\bigr)\bigr)\bigr)\bigr)\bigr). \end{aligned}$$

The values ${s}=5$ and $\gamma _{5} = - 1800/12{,}019$ minimize the truncation error, and the error constant becomes $\frac{600}{84{,}133}$.