Abstract
This paper studies a class of power-law kinetics, PL-ILK, for whose subset, PL-TIK, analogues of the Deficiency Zero Theorem and the Deficiency One Theorem (DOT) for mass action systems are valid. The DOT also includes the necessary and sufficient condition of Boros for uniqueness in the non-weakly reversible case. To our knowledge, this is the first set of kinetics beyond mass action kinetics (MAK) for which the DOT has been shown to be valid. A further interesting property of PL-TIK is a certain “robustness” relative to dependence of linkage classes: existence of a positive equilibrium for each linkage class implies the existence of a positive equilibrium for the whole network. For MAK systems, the PL-ILK property is equivalent to the reactant deficiency of the linkage class containing the zero complex being one, and zero for all other linkage classes. As shown in the Supplementary Materials, an initial survey of MAK and BST systems already reveals numerous examples with PL-ILK kinetics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The concept of deficiency, which was introduced by Feinberg and Horn in back-to-back papers in 1972, has played a central role in the development of Chemical Reaction Network Theory, particularly in its first three decades. This non-negative integer is, as Shinar and Feinberg pointed out in [16], essentially a measure of the linear dependency of the network’s reactions. The two main Theorems, the Deficiency Zero Theorem (DZT) and the Deficiency One Theorem (DOT), describe the set of positive equilibria \(E_+({\mathscr {N}},K)\) of MAK systems on networks of low deficiency (we will hence call these two results the Low Deficiency Theorems for MAK systems). The DZT includes the equivalence \(E_+({\mathscr {N}},K) \ne \emptyset \) if and only if \({\mathscr {N}}\) is weakly reversible, the parametrization

with \(x^*\) a positive equilibrium and S the stoichiometric subspace, and the uniqueness of positive equilibria in each stoichiometric class. As M. Feinberg emphasized in [10], the Deficiency One Theorem generalizes most of the DZT’s content: it shows that, for t-minimal networks with independent linkage classes (ILC) and linkage class deficiencies bounded by 1 (in zero deficiency, ILC and linkage class deficiency bounded by 0 are automatically fulfilled), monostationarity holds in each stoichiometric class and weak reversibility is a sufficient condition for the existence of a unique equilibrium in each class. The DZT was developed by Horn, Jackson and Feinberg in the seventies while a complete proof of the DOT was published by Feinberg in 1995. In 2012, Boros completed the DOT scenario by deriving a necessary and sufficient condition for uniqueness in the non-weakly reversible case.
Although the pioneers of CRNT studied kinetics beyond mass action from the beginning (the fundamental work of Horn and Jackson in 1972 was entitled “General Mass Action Kinetics”), it was not until 2012 that Müller and Regensburger extended the Deficiency Zero Theorem to a set of power-law kinetic systems they called “Generalized Mass Action Kinetics” (GMAK) systems. In this and a subsequent paper in 2014, GMAK systems were characterized by their kinetic deficiency which, when equal to zero, implies that their underlying networks have zero deficiency. They provided a characterization of \(E_+({\mathscr {N}},K)\), which in this case consists entirely of complex balanced equilibria, and an analogous parametrization. They also provided conditions for uniqueness using the sign vector spaces associated with certain subspaces. A detailed discussion of their results in comparison with this paper’s results is provided in Sect. 6.
In this paper, we introduce the set PL-ILK kinetics, which is characterized by the linear independence of the kinetic order matrix rows per linkage class, with branching reactions represented as one row and the zero row of inflow reactions (if present) excluded (s. T matrix definition in Sect. 3). Our main results include the Deficiency Zero Theorem and the Deficiency One Theorem (including the non-weakly reversible extension) for a subset of this kinetics set. The study started with the impression of the last author that the methods used by Boros in his PhD thesis to prove the DZT and DOT for MAK systems—with their strong digraph theory flavor - could work for more general kinetics. The first author undertook this exploration in his MS thesis and discovered the set PL-LLK (PL-ILK for CRNs without inflow reactions) and, mixing extensions of Boros’ techniques with his own, established fundamental properties of its subset, PL-RLK. By fortuitous circumstance, the kinetics set generalized concepts and results of the last two authors on the theory of reactant subspaces discussed in [1], so that some of those (e.g. kinetic flux subspaces) could be used in this paper. The extension to PL-TIK, including the final Low Deficiency Theorems, was then completed in collaborative effort. To our knowledge, the Deficiency One Theorem for PL-TIK is the first extension of Feinberg’s result beyond mass action kinetics.
The set PL-TIK exhibits a further remarkable property, a certain “robustness” relative to dependency of linkage classes: \(E_+({\mathscr {L}}^i,K^i) \ne \emptyset \) for each linkage class \({\mathscr {L}}^i\) implies that \(E_+({\mathscr {N}},K) \ne \emptyset \) (s. Theorem 4). On the other hand, without independence of linkage classes, even the PL-TIK property does not guarantee the converse result (s. Example 4).
We document in Supplementary Materials the results of an initial survey of biochemical systems, which showed that numerous examples of MAK and BST systems display linkage class linearly independent kinetics. However, almost all of them have higher deficiency, so they are outside of the scope of the Low Deficiency Theorems—this finding highlights the need for further research.
The paper is organized as follows: In Sect. 2, we collect all the concepts and previous results needed in the Introduction and the later sections. In Sect. 3, we introduce the set PL-ILK and its relevant subsets in the overall context of power law kinetics. In Sect. 4, we prove our first main result that, for a PL-TIK system, the existence of positive equilibria for each linkage class implies the existence of such for the whole network, even without independence of the linkage classes. We also, after developing tools we need for the Low Deficiency Theorems, derive the Deficiency Zero Theorem for PL-TIK systems. In Sect. 5, we prove the Deficiency One Theorem for PL-TIK systems. We conduct a detailed comparison with the results of Müller and Regensburger in Secion 6 and provide concluding remarks in Sect. 7. In the Supplementary Materials to this paper, we discuss examples of MAK and BST networks of biological systems which exhibit linear independent kinetics.
We provide a list of frequently used abbreviations in Table 1.
2 Fundamental concepts of chemical reaction networks and chemical kinetic systems
In this section, we collect the fundamental concepts and propositions about chemical reaction networks and chemical kinetic systems (CKS) needed for our results. In particular, we expound the standpoint that a CRN is a digraph with a vertex-labelling, i.e., its stoichiometry. In our view, this approach enables easier application of (general) digraph theory results to CRNT as well as better appreciation of CRNT in the graph theory community, particularly of its novel contributions to (general) digraph theory. We focus on the CKS side of power-law kinetics (PLK) systems.
2.1 Chemical reaction networks as vertex-labelled digraphs
Our first object of interest is the following:
Definition 1
A chemical reaction network (CRN) is a digraph \(\left( {\mathscr {C}},{\mathscr {R}} \right) \) where each vertex has positive degree and stoichiometry, i.e., there is a finite set \({\mathscr {S}}\) (whose elements are called species) such that \({\mathscr {C}}\) is a subset of \({\mathbb {R}}^{{\mathscr {S}}}_{\ge }\). Each vertex is called a complex and its coordinates in \({\mathbb {R}}^{{\mathscr {S}}}_{\ge }\) are called stoichiometric coefficients. The arcs are called reactions.
The property of stoichiometry, which can be viewed as a vertex labelling, is what makes a CRN special: it allows the embedding of the graph’s vertices in the real vector space \({\mathbb {R}}^{{\mathscr {S}}}_{\ge }\), called species composition space (or simply, species space). The elements of the latter are interpreted as (chemical) compositions, i.e., the coordinate values are concentrations of the different (chemical) species. Since the species set \({\mathscr {S}}\) plays an important role in the theory, it is standard notation to specify a CRN as a triple \(\left( {\mathscr {S}},{\mathscr {C}},{\mathscr {R}} \right) \) to indicate the pair \(\left( \left( {{\mathscr {C}}},{\mathscr {R}} \right) ,{\mathscr {S}} \right) \).
If \({\mathscr {S}} = \left\{ X_1, X_2,\cdots ,X_m \right\} \), then each \(X_i\) can be identified with the vector with 1 in the ith coordinate and zero elsewhere. One often then adds the property that \({\mathscr {S}} = \bigcup _{y \in {{\mathscr {C}}}} {{\mathrm{supp}}}y\), i.e., each species appears in at least one complex.
In chemistry, the stoichiometric coefficients are integers, but we do not require this in the CRN definition since it is rarely used in the proofs. We explicitly add the integer property as an assumption in propositions where it is needed.
We denote the number of species with m, the number of complexes with n, and the number of reactions with r.
Two useful maps are associated with each reaction:
Definition 2
The reactant map \(\rho : {\mathscr {R}} \rightarrow {{\mathscr {C}}} \) maps a reaction to its reactant complex while the product map \(\pi : {\mathscr {R}} \rightarrow {{\mathscr {C}}} \) maps it to its product complex. We denote \(\left| \rho ({\mathscr {R}}) \right| \) with \(n_r\), i.e., the number of reactant complexes.
2.1.1 Stoichiometry-independent properties of CRNs
Connectivity in a digraph constitutes one of its fundamental properties, and they apply to CRNs, but have slightly differing names since a connected component is traditionally called a linkage class in CRNT. Hence, a strong linkage class is a subset of a linkage class where any two elements are connected by a directed path in each direction. A terminal strong linkage class is a strong linkage class such that there is no reaction from a complex in the strong linkage class to a complex not in the strong linkage class. We denote the number of linkage classes with l, those of the strong linkage class with sl, and the number of terminal strong linkage classes with t. Clearly \(sl \ge t \ge l\).
Each linkage class \({\mathscr {L}}^{i}\) forms a subnetwork and we designate the number of complexes and reactions in \({\mathscr {L}}^{i}\) with \(n^i\) and \(r^i\), respectively, \(i = 1,\). Let
be the characteristic vectors of the sets \({{\mathscr {C}}}^{1}\),\({{\mathscr {C}}}^{2}\),...,\({{\mathscr {C}}}^{l}\), respectively, where \({{\mathscr {C}}}^{i}\) is the set of complexes in linkage class \({\mathscr {L}}^{i}\).
Definition 3
A chemical reaction network is weakly reversible if \(sl = l\). It is called t-minimal if \(t = l\). The non-negative integer \(t-l\) is called the terminality of the CRN, i.e., it is t-minimal if it has zero terminality.
Remark 1
A weakly reversible network is easily translated into digraph theory terminology: it is a digraph whose connected components are strong digraphs. On the contrary, there seems to be no digraph theory concept corresponding to a t-minimal network.
The terminal strong linkage classes can be of two kinds: cycles (not necessarily simple) and singletons (which we call “terminal points”). We have the following useful classification of CRNs according to the types of their terminal strong linkage classes.
Definition 4
Let \(n_r\) be the number of reactant complexes of a CRN. Then \(n - n_r\) is the number of terminal points. A CRN is called cycle-terminal if and only if \(n - n_r = 0\), i.e., each complex is a reactant complex. It is called point-terminal if and only if \(n - n_r = t\) and point- and cycle-terminal if \(n - n_r < t\).
The incidence matrix, a central concept in digraph theory, is defined as follows:
Definition 5
The incidence matrix \(I_a\) is an \(n \times r\) matrix where each row corresponds to a complex and each column to a reaction, satisfying
Note that in most graph theory books, the incidence matrix is defined as \(I_a\). A well-documented result in graph theory provides the following facts about \({{\mathrm{Im}}}I_a\):
Proposition 1
([4]) \({{\mathrm{rank}}}I_a=n-l\) and \({{\mathrm{Im}}}I_a = \left( {{\mathrm{span}}} \left( e^1,e^2,\ldots ,e^l \right) \right) ^\perp .\)
The following Proposition from M. Feinberg [9] is a novel contribution of CRNT to digraph theory:
Proposition 2
A network is weakly reversible if and only if \(\ker I_a\) contains a positive vector.
If the CRN also has an arc labeling, i.e., a map \(k: {\mathscr {R}} \rightarrow {\mathbb {R}}_{>}\), then we can associate to it a k-Laplacian matrix as follows:
Definition 6
The k-Laplacian matrix of an arc CRN is an \(n \times n\) matrix such that
where \(k_{ji}\) is the label (often called the rate constant) associated to the reaction from \(C_j\) to \(C_i\).
The following theorem, denoted as the Structure Theorem of the k-Laplacian Kernel (STLK) in [3], is not only the basis for important results in early CRNT (cf. [9]), it is also its most significant contribution to (general) digraph theory to date. For \(t \in {\mathbb {N}}\), \(\overline{1,t}:=\left\{ 1,2,\ldots ,t \right\} \).
Theorem 1
(Structure Theorem of the Laplacian Kernel) Let \(({{\mathscr {C}}},{\mathscr {R}},k)\) be a labeled directed graph with \(k: {\mathscr {R}} \rightarrow {\mathbb {R}}\). Let

. Denote by \(A_k''\) the submatrix of \(A_k\) with rows and columns corresponding to \(V''\). Then
-
1.
\(A_k''\) is invertible,
-
2.
\(\dim \ker A_k=t\), and
-
3.
there exists a basis \(y^1,y^2,\ldots ,y^t \in {\mathbb {R}}^n_{\ge 0}\) in \(\ker A_k\) such that supp\((y^k)={{\mathscr {C}}}^k \quad \forall k \in \overline{1,t}\) (i.e., \(k \in \left\{ 1, 2, \ldots , t \right\} \)).
Computations show that the determinant of \(A_k''\) is nonzero, implying that it is invertible. It is important to take note that each column is a linear combination of some columns of \(I_a\). Hence, we have the following corollary.
Corollary 1
If \({\mathscr {N}}\) is t-minimal, then \({{\mathrm{Im}}}I_a= {{\mathrm{Im}}}A_k\).
2.1.2 Stoichiometry-dependent properties of a CRN
In a CRN, a matrix of complexes Y holds the stoichiometry information: it is well-defined after an indexing of the complexes, say \(y_1, \ldots , y_n\), is set. We call the i-th coordinate of \(y_j\) its stoichiometric coefficient with respect to the species \(X_i\).
Definition 7
The matrix of complexes Y is the \(m \times n\) matrix whose (i, j)th element is the stoichiometric coefficient of \(y_j\) with respect to \(X_i\).
We now introduce two matrices which play important roles in the Linear Geometry of species (composition) space:
Definition 8
The stoichiometric matrix N is the \(m \times r\) matrix defined by \(N = Y I_a\). Its columns are the reaction vectors \(\pi (R_i)-\rho (R_i)\) for \(i = 1,..,r\). Its image \({{\mathrm{Im}}}N\) is called the stoichiometric subspace S, whose dimension s is called the rank of the network. Clearly S is generated by the reaction vectors.
The cosets with respect to the stoichiometric subspace form the basis for the concept of stoichiometric classes:
Definition 9
For \(x \in {\mathbb {R}}^{m}_{\ge }\), the set \((x + S) \cap {\mathbb {R}}^{m}_{\ge 0}\) is called a stoichiometric class.
Definition 10
The reactant matrix \(Y_{res}\) is the \(m \times n_r\) matrix Y without the columns of the terminal points. Its columns are the reactant complexes \(\rho (R_1)\), \(\rho (R_2)\), \( \ldots \), \(\rho (R_r)\). Its image \({{\mathrm{Im}}}Y_{res}\) is called the reactant subspace R, whose dimension q is called the reactant rank of the CRN. Clearly R is generated by the reactant complexes.
Arceo et al. [1] conducted an initial systematic study of the reactant subspace R’s connection to kinetic behavior and identified the set of RSS networks as particularly interesting.
Definition 11
A CRN has the RSS (reactant-determined stoichiometric subspace) property (or type RSS) if S is contained in R.
Example 1
Any cycle-terminal network is an RSS network. There are however many RSS networks with terminal points. A simple example from [6] is the following:
\(R_1: 2X_1 \rightarrow X_1+X2\)
\(R_2: X_1+X_2 \rightarrow 2X_1\)
\(R_3: X_1+X_2 \rightarrow 2X_2\)
\(S = \left\langle X_1 - X_2 \right\rangle \) is one-dimensional while \(R = \left\langle X_1 + X_2, 2X_1 \right\rangle = {\mathbb {R}}^2\).
A characterization of RSS networks is easily found in [1]:
Proposition 3
Let \({\mathscr {N}}\) be a network with matrix of complexes Y and reactant subspace R. Then \({\mathscr {N}}\) is RSS if and only if \(R = {{\mathrm{Im}}}Y\).
In other words, in an RSS network, every complex is a linear combination of reactant complexes. RSS networks will be studied in more detail in Sect. 5.
Since linkage classes partition both the set of complexes and the set of reactions, the linear maps Y, \(I_a\) and N can be decomposed by restricting their domains to the complexes or reactions in a linkage class. Hence we can write \(Y = \left[ Y^1,\ldots ,Y^l \right] \), \(I_a = \left[ I_a^1,\ldots ,I_a^l \right] \) and \(N = \left[ N^1,\ldots ,N^l \right] \).
Alignment with linkage classes also determines an interesting subset of RSS networks:
Definition 12
An RSS network is linkage class aligned if for each linkage class, the stoichiometric subspace of the linkage class is contained in its reactant subspace.
Example 2
For any cycle-terminal CRN, S is contained in R. Since every linkage class of a cycle-terminal network is also cycle-terminal, then a cycle-terminal network is a linkage class aligned RSS network.
2.1.3 Deficiency and reactant deficiency
Definition 13
The deficiency of a CRN is the integer \(\delta = n - l - s\).
The non-negativity of a CRN’s deficiency follows from its geometric interpretation:
Proposition 4
([7]) \(\delta = \dim (\ker Y \cap {{\mathrm{Im}}}I_a)\).
To introduce an alternative way way of defining deficiency, Boros [6] constructed the \(n \times l\) matrix \(L = \left[ e^1,e^2,\ldots ,e^l \right] \) and the matrix \(\hat{Y}\) defined as:
The matrix \(\hat{Y}\) is called the augmented matrix of complexes. The rank of \(\hat{Y}\) is the deficiency, as shown by the proposition below.
Proposition 5
\(\delta = \dim \ker \hat{Y}\) and \(\ker \hat{Y} =\ker Y \cap {{\mathrm{Im}}}I_a\)
For t-minimal networks, one has an alternative for the definition of the deficiency, as shown by the corollary that follows. This will be very useful for our development of deficiency theory for power-law kinetics.
Corollary 2
If \({\mathscr {N}}\) is t-minimal, then \(\ker \hat{Y} =\ker Y \cap {{\mathrm{Im}}}A_k\) and \(\delta = \dim (\ker Y \cap {{\mathrm{Im}}}A_k)\).
Furthermore, we can define the deficiency not only for the whole network, but also for each linkage class \({\mathscr {L}}^i\). Considering the stoichiometric matrix N in block form, i.e., \(N=\left[ N^1,\ldots ,N^l \right] \), we let \(s^i={{\mathrm{rank}}}N^i\).
Definition 14
The deficiency of linkage class \({\mathscr {L}}^i\) (denoted by \(\delta ^{i}\)) is defined by the formula \(\delta ^{i}=n^i-1-s^i\).
Moreover, if we consider \(\hat{Y}\) in block form, such as
we obtain directly the following result.
Proposition 6
\(\delta ^i = \dim \ker \hat{Y}^i\).
We next introduce the concepts of reactant deficiency and rank difference from [1]:
Definition 15
The reactant deficiency \(\delta _\rho := n_r - q\), i.e., the difference between the number of reactant complexes and the reactant rank q. Furthermore, the rank difference \(\varDelta ({\mathscr {N}})\) is defined as \(s - q\).
The following result summarizes the relationship between deficiency and reactant deficiency of a CRN.
Theorem 2
([1]) Let \({\mathscr {N}}\) be a CRN with terminality \(\tau ({\mathscr {N}})\), rank difference \(\varDelta ({\mathscr {N}})\), deficiency \(\delta \) and reactant deficiency \(\delta _\rho \).
-
1.
If \({\mathscr {N}}\) is cycle-terminal, then \(0 \le \delta - \delta _\rho = l + \varDelta ({\mathscr {N}}) \le l\).
-
2.
If \({\mathscr {N}}\) is point-terminal, then \(\delta - \delta _\rho = \tau ({\mathscr {N}}) - \varDelta ({\mathscr {N}})\).
-
3.
If \({\mathscr {N}}\) is point- and cycle-terminal, then \(\delta - \delta _\rho < \tau ({\mathscr {N}}) - \varDelta ({\mathscr {N}})\).
2.1.4 Independence of linkage classes
A network property of considerable importance in our further discussion is that of independence of linkage classes (ILC).
Definition 16
A CRN \({\mathscr {N}}\) with the property \(\delta = \delta ^1 + \delta ^2 + \cdots + \delta ^l\) is called a network with independent linkage classes, ILC or ILC-network. Otherwise, if \(\delta \ne \delta ^1 + \delta ^2 + \cdots + \delta ^l\), it is called a network with dependent linkage classes or DLC-network.
The following characterization is well-established in CRNT:
Proposition 7
\(\delta \ge \delta ^1 + \cdots + \delta ^l\). Moreover, the following are equivalent:
-
1.
\({\mathscr {N}}\) is an ILC-network.
-
2.
\({{\mathrm{Im}}}N = {{\mathrm{Im}}}N^1 \oplus {{\mathrm{Im}}}N^2 \oplus \cdots \oplus {{\mathrm{Im}}}N^l\).
-
3.
\({{\mathrm{Im}}}\hat{Y} = {{\mathrm{Im}}}\hat{Y}^1 \oplus {{\mathrm{Im}}}\hat{Y}^2 \oplus \cdots \oplus {{\mathrm{Im}}}\hat{Y}^l\).
2.2 Fundamentals of chemical kinetic systems
2.2.1 Basic concepts
Definition 17
A kinetics K for a reaction network \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}})\) is an assignment to each reaction \(j \in {\mathscr {R}}\) of a rate function \(K_j:\varOmega _K \rightarrow {\mathbb {R}}_{\ge 0}\) where \(\varOmega _K\) is a set such that \({\mathbb {R}}^m_{>0} \subseteq \varOmega _K \subseteq {\mathbb {R}}^m_{\ge 0}\), \(c\wedge d \in \varOmega _K\), and
The pair \(({\mathscr {N}},K)\) is called a chemical kinetic system (CKS).
We add the definition relevant to our context:
Definition 18
A chemical kinetics is a kinetics K satisfying the positivity condition: for each reaction \(j:y \rightarrow y', K_j(c)>0\) if and only if \({{\mathrm{supp}}}y \subset {{\mathrm{supp}}}c\).
Definition 19
The species formation rate function (SFRF) of a CKS is the vector field \(f(x) = NK(x) = \displaystyle \sum _{y\rightarrow y'} K_{y\rightarrow y'}(x) (y'- y).\)
is the ODE or dynamical system of the CKS. A zero of f is an element c of \(\mathbb R^{{\mathscr {S}}}\) such that \(f(c) = 0.\) A zero of f is an equilibrium or steady state of the ODE system. For a differentiable f, a steady state c is called non-degenerate if the \(Ker(J_c(f))\cap S=\{ 0\}\), where \(J_c(f)\) is the Jacobian matrix of f at c.
The function \(g = I_aK: \mathbb R^{\mathscr {S}}\rightarrow \mathbb R^{\mathscr {C}}\) is called the “complex formation rate function”, as its value is the difference between production and degradation for each complex. Consequently, a positive vector in \(\ker I_a\) results in “complex balancing”, justifying the term that will be used in Definition 21. The positive vectors in \(\ker I_a\), which are in \({{\mathrm{Im}}}K\), will be highlighted by the definitions in the next section.
Recall that we introduced decompositions for the maps Y, \(I_a\), N with respect to the set of linkage classes and wrote them in the form \(Y = \left[ Y^1,\ldots ,Y^l \right] \), \(I_a = \left[ I_a^1,\ldots ,I_a^l \right] \) and \(N = \left[ N^1,\ldots ,N^l \right] \). We now use the partition of the reaction set into subsets \({\mathscr {R}}^i\) for each linkage class to obtain the corresponding decomposition \(K = \left[ K^1,\ldots ,K^l \right] \), with \(K^i : {\mathbb {R}}^{{\mathscr {S}}} \rightarrow {\mathbb {R}}^{{\mathscr {R}}}\). We then define a linkage class decomposition for SFRF \(f=f^1+f^2+\cdots +f^l\) with \(f^i=N^i K^i\).
2.2.2 Positive equilibria of chemical kinetic systems
Definition 20
A positive equilibrium x is an element of \({\mathbb {R}}^{m}_{>}\) for which \(f(x) = 0\). The set of positive equilibria of a chemical kinetic system is denoted by \(E_+({\mathscr {N}}, K)\).
Definition 21
A positive vector c in \({\mathbb {R}}^{{\mathscr {S}}}\) is called complex balanced (CB) if K(x) is contained in \(\ker I_a\). A CKS is called complex balanced if it has complex balanced equilibria.
Complex balanced systems played an essential role in the development of CRNT, and in the following propositions, we recall useful results from the early work of F. Horn, R. Jackson and M. Feinberg ([12],[11],[7]). A very instructive review can also be found in [8].
Proposition 8
([11]) If a chemical kinetic system has complex balanced equilibria, then the underlying CRN is weakly reversible.
Proposition 9
([7]) If a chemical kinetic system has deficiency 0, then its equilibria are all complex balanced.
Given the decomposition of the SFRF \(f = f^1 +\cdots + f^l\) with respect to the linkage classes, we can consider the sets of positive equilibria \(E_+({\mathscr {N}}^i, K^i)\) of the \(f^i\) and their relationships to the positive equilibria of the whole system. Clearly, for any network and any kinetics, the intersection \(\cap _i E_+({\mathscr {L}}^i,K^i)\) is contained in \(E_+({\mathscr {N}},K)\). The following theorem demonstrates the impact of the structural property of ILC on the kinetic behavior of the system:
Theorem 3
Let \({\mathscr {N}}\) be a network with ILC, and K a chemical kinetics on \({\mathscr {N}}\). Then \(E_+({\mathscr {N}},K) = \cap _i E_+({\mathscr {N}}^i, K^i)\). In particular, \(E_+({\mathscr {N}},K) \ne \emptyset \) implies \(E_+({\mathscr {N}}^i, K^i) \ne \emptyset \) for each linkage class \(L^i\).
Proof
An element f(x) in \({{\mathrm{Im}}}f = {{\mathrm{Im}}}(NK) = N({{\mathrm{Im}}}K)\) lies in \({{\mathrm{Im}}}N = S\). Since S is the direct sum of the \(S^i\), then f(x) has a unique representation as a sum of elements of the \(S^i\). Hence \(f(x)=0\) if and only if \(f^i(x)=0\) for each linkage class \(L^i\). \(\square \)
In general, \(E_+({\mathscr {N}}^i, K^i) \ne \emptyset \) for each linkage class \(L^i\) does not imply the existence of a positive equilibrium for the whole system, even under ILC. Hence identifying kinetics sets with this property is an interesting research area. Furthermore, for most biochemical systems, the underlying networks have dependent linkage classes (DLC), further enhancing the challenge to understand the relationships between positive equilibria on the linkage classes and those of the whole network.
2.3 Power-law kinetics
Definition 22
A kinetics \(K: {\mathbb {R}}^m_> \rightarrow {\mathbb {R}}^r\) is a power-law kinetics if
with \(k_i, F_{ij} \in {\mathbb {R}}_+\). Power-law kinetics is defined by an \(r \times m\) matrix \(F=[F_{ij}]\), called the kinetic order matrix, and vector \(k \in {\mathbb {R}}^r\), called the rate vector.
Power-law kinetics form a large group of kinetics [12]. Arceo et al. [2] present a kinetics landscape with algebraic properties which include power-law systems. The general form of PLK systems make it flexible for modeling purposes in many areas of science such as chemistry, ecology and epidemics [17].
Furthermore, the SFRF of a PLK system can be written as
where \(N_{\cdot ,i}\) is the ith column of stoichiometric matrix N.
An example of PLK is the well-known Mass Action Kinetics (MAK) where the kinetic order matrix is the transpose of the molecularity matrix [6, 9]. Hence, we can write the SFRF of a MAK as:
In [3], the set of power-law kinetics with Reactant-Determined Kinetic orders of a network \({\mathscr {N}}\) (\(\mathscr {PL-RDK(N)}\)) is introduced. It is defined as follows:
Definition 23
A PLK system has reactant-determined kinetics (of type PL-RDK) if for any two reactions i, j with identical reactant complexes, the corresponding rows of kinetic orders in F are identical, i.e., \(f_{ik}=f_{jk}\) for \(k = 1,\ldots ,m.\)
If the given kinetics is of type PL-RDK, we can define the factor map of a CKS. The definition below comes from Arceo et al. [3].
Definition 24
The factor map \(\psi _K: {\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{n}\) is defined as
Another set of power-law kinetics of special interest for us is the set of factor span surjective systems \(\mathscr {PL-FSK(N)}\). We use the following characterization which was derived in [2] as our working definition:
Definition 25
A PL-RDK kinetics is factor span surjective if and only if all rows with different reactant complexes in the kinetic order matrix F are pairwise different (i.e., \(\rho (r) \ne \rho (r')\) implies \(F_{r,\cdot } \ne F_{r',\cdot }\)).
The SFRF of a PL-RDK kinetics has the following decomposition:
\(\mathscr {PL-FSK(N)}\) is a large and important subset of \(\mathscr {PL-RDK(N)}\) which reflects important properties of its subset of MAK systems. For example, as shown in [2], the Feinberg-Horn Theorem on the coincidence of kinetic and stoichiometric subspaces extends precisely to this set of power-law kinetics
The Power-Law Kinetics Landscape in Fig. 1 provides an overview of kinetics subsets studied so far in CRNT.
3 The set of PL-ILK kinetics: definition and basic properties
In this section, we present new subsets of PL-RDK systems to which we extend some results of Deficiency Theory for MAK systems. To define these classes of kinetics, a T-matrix from the kinetic order matrix of PL-RDK system is derived.
3.1 Notations
Let \(n_r\) be the number of distinct reactant complexes. Recall the notion of factor maps in Definition 24. The corresponding components of non-reactant complexes are zero. Hence, we truncate some of our main objects in CRNT. Notations are summarized by Table 2. We emphasize that the truncated parts of \(Y_{res}\) and \(A_{k,res}\) are the non-reactant columns. On the other hand, non-reactant rows are those neglected in \(\psi _{K,pr}\) and \(L_{pr}\).
3.2 Definition of the PL-ILK kinetic set
Recall the kinetic order matrix in Definition 22. From Müller and Regensburger [15], we introduce the matrix \(\widetilde{Y}\). It is an \(m \times n\) matrix defined as:
In order to focus on the reactant complexes and related spaces, we define the T-matrix as follows:
Definition 26
The \(m \times n_r\) T-matrix is the truncated \(\widetilde{Y}\) where the non-reactant columns are deleted. The block matrix \(\hat{T} \in {\mathbb {R}}^{(m+l)\times n_{r}}\) is defined as
where \(L_{pr}^\top \) is the truncated matrix L as in Table 2.
The T-matrix defines a map \(T: {\mathbb {R}}^{\rho ({\mathscr {R}})} \rightarrow {\mathbb {R}}^{\mathscr {S}}\) which defines a new important subspace of \({\mathbb {R}}^{\mathscr {S}}\):
Definition 27
The kinetic reactant subspace \(\tilde{R}\) is the image of T. Its dimension is called the kinetic reactant rank \(\tilde{q}\) and the cosets \(x + \tilde{R}\), \(x \in {\mathbb {R}}^{\mathscr {S}}\), are the kinetic reactant classes.
Analogous to the other CRNT matrices, we consider \(\hat{T}\) and T in block form \(\hat{T}=\left[ \hat{T}^1,\ldots ,\hat{T}^l \right] \) and \(T=\left[ T^1,\ldots ,T^l \right] \), where \(\hat{T}^i\) and \(T^i\) correspond to the linkage class \({\mathscr {L}}^i\).
We are now in the position to define the first two classes of power-law reactant-determined kinetics: linkage class linear independent power-law kinetics (PL-LLK) and reactant set linear independent power-law kinetics (PL-RLK).
Definition 28
A chemical kinetics K is called linkage class linear independent (of type PL-LLK) if the columns of T corresponding to each linkage class are linearly independent.
Definition 29
A chemical kinetics K is said to be reactant set linear independent (of type PL-RLK) if the columns of T are linearly independent.
Clearly, \(\mathscr {PL-LLK(N)}\) contains \(\mathscr {PL-RLK(N)}\). In [1], Arceo et al. relate LLK and RLK properties to mass action kinetics. They state that in order for a MAK system to have the RLK property, the reactant deficiency must be zero. On the other hand, the LLK property in MAK implies that the reactant deficiency for each linkage class is zero.
One of the immediate concerns regarding these classes of power-law kinetics is their applicability. Note that some MAK systems and most of the chemical reaction networks of BST systems studied by Arceo et al. [2] have inflow reactions. These reactions have zero kinetic orders, making the columns of T linearly dependent, thus implying the limitations of PL-LLK and PL-RLK. In order to address this issue, we introduce another two classes of power-law kinetics: PL-ILK and PL-IRK. Here, inflow reactions are excluded.
Definition 30
A kinetics K is called inflow-excluded linkage class linear independent (of type PL-ILK) if the non-inflow columns (i.e., columns of the complexes associated to non-inflow reactions) of T corresponding to each linkage class are linearly independent.
Definition 31
A kinetics K is said to be inflow-excluded reactant set linear independent (of type PL-IRK) if the non-inflow columns (i.e., columns of the complexes associated to non-inflow reactions) of T are linearly independent.
It turns out that our main results hold for a set of kinetics between \(\mathscr {PL-ILK}\mathscr {(N)}\) and \(\mathscr {PL-IRK(N)}\) (and correspondingly between \(\mathscr {PL-LLK(N)}\) and \(\mathscr {PL- RLK(N)}\)) which we now define:
Definition 32
A PL-ILK kinetics is \(\hat{T}\)-rank maximal (to type PL-TIK) if its column rank is maximal. The subset PL-TLK of PL-LLK kinetics is analogously defined.
Example 3
The following simple network shows that PL-TIK is a proper subset of PL-ILK:
\(R_1: 0 \rightarrow X_1\)
\(R_2: X_1 \rightarrow X_2\)
\(R_3: X_2 \rightarrow X_1\)
\(R_4: 2X_1 \rightarrow 2X_2\)
\(R_5: 2X_2 \rightarrow 2X_1\)
Solving for Y and T, we have

Clearly, under mass action, the kinetic system is PL-ILK since the columns of each linkage class associated with non-inflow complexes are linearly independent. However, constructing \(\hat{T}\) shows that it is not PL-TIK since the column rank is 3.

Example 4
In the Supplementary Materials, we show that the MAK-system of calcium dynamics of olfactory cilia is in PL-LLK, but not in PL-TLK.
Clearly, \(\mathscr {PL-IRK(N)}\) is contained in \(\mathscr {PL-ILK(N)}\). Figure 2 illustrates the connections between the presented classes of PL-RDK systems. For networks without inflow, we have:
-
1.
\(\mathscr {PL-ILK(N)} = \mathscr {PL-LLK(N)}\),
-
2.
\(\mathscr {PL-IRK(N)}= \mathscr {PL-RLK(N)}\), and
-
3.
\(\mathscr {PL-IRK(N)}\) is contained in \(\mathscr {PL-ILK}(N)\).
On the other hand, if there are inflows, the results will be:
-
1.
\(\mathscr {PL-ILK(N)}\) contains \(\mathscr {PL-IRK(N)}\), and
-
2.
\(\mathscr {PL-LLK(N)} = \mathscr {PL-RLK (N)} = \emptyset \).
Moreover, if we have only one linkage class,
-
1.
\(\mathscr {PL-TIK(N)} = \mathscr {PL-IRK(N)} = \mathscr {PL-ILK(N)}\), and correspondingly
-
2.
\(\mathscr {PL-TLK(N)} = \mathscr {PL-RLK(N)} = \mathscr {PL-LLK(N)}\).
Proposition 10
Let K be a PL-TIK. Then
-
1.
\(\dim (\ker (\hat{T}))=0\); and
-
2.
\({{\mathrm{Im}}}\hat{T} = {{\mathrm{Im}}}\hat{T}^1 \oplus {{\mathrm{Im}}}\hat{T}^2 \oplus \cdots \oplus {{\mathrm{Im}}}\hat{T}^l\).
Proof
Statement (1) is a direct consequence of columns of \(\hat{T}\) being linearly independent. For statement (2), linear independence of columns implies \({{\mathrm{Im}}}\hat{T} = {{\mathrm{Im}}}\hat{T}_1 \oplus {{\mathrm{Im}}}\hat{T}_2 \oplus \cdots \oplus {{\mathrm{Im}}}\hat{T}_{n_r}\) (\(\hat{T}_{i}\) is the ith column of \(\hat{T}\)). Hence, \({{\mathrm{Im}}}\hat{T} = {{\mathrm{Im}}}\hat{T}^1 \oplus {{\mathrm{Im}}}\hat{T}^2 \oplus \cdots \oplus {{\mathrm{Im}}}\hat{T}^l\). \(\square \)
Example 5
Consider the BST model of a “linear pathway with inhibition” (taken from Voit [18]). In [3], Arceo et al. provide the total CRN representation of this model:
\(R_1: 0 \rightarrow X_4\)
\(R_2: X_4+X_3 \rightarrow X_1+X_3\)
\(R_3: X_1 \rightarrow X_2\)
\(R_4: X_2 \rightarrow X_3\)
\(R_5: X_3 \rightarrow 0.\)
Table 3 provides the network properties of this CRN system. Clearly, this is a t-minimal network. Moreover, we have two linkage classes. The first linkage class contains \(X_1\), \(X_2\), \(X_3\), \(X_4\) and the zero-complex, and the other includes only two complexes, namely, \(X_4+X_3\) and \(X_1 + X_3\). Both linkage classes have deficiency zero, making the CRN a DLC network. The kinetic order matrix provided by Voit [18] is given as:

It is easy see that this example is of type PL-RDK. Furthermore, we want to examine if the example is of type PL-ILK. The \(\widetilde{Y}\) and T-matrix are provided below:


Due to the existence of an inflow reaction, the system is neither PL-LLK nor PL-RLK. However, it can be verified that if we neglect the zero column of T corresponding to the inflow reaction to \(X_4\), columns of T are linearly independent. Thus, the kinetics of the biological model is of types PL-ILK and PL-IRK.


It is easy to see that the kinetics is PL-TIK. A manual check shows that all the properties in Proposition 10 hold.
Recall the truncated CRNT objects presented in Table 2 and the notion of SFRF in Sect. 2. Since \(A_{k,\rho } \cdot \psi _{K,pr}=A_k \cdot \psi _K\), we can modify the set of positive equilibria \(E_+\) as

and the set of positive equilibria for the linkage class \({\mathscr {L}}^i\) as

4 Positive equilibria of PL-TIK systems
4.1 Non-emptiness of the set of positive equilibria of a PL-TIK system
We saw in Theorem 3 that, for any kinetics on a network with ILC, the existence of a positive equilibrium of the whole system implies the existence of a positive equilibrium for each linkage class. For MAK systems on a network with ILC, Boros showed in [6] Theorem 3.6 that the converse holds: \(E_{+}({\mathscr {L}}^i,K) \ne \emptyset \) for each linkage class \({\mathscr {L}}^i\) implies \(E_+({\mathscr {N}},K)\ne \emptyset \). A striking property of PL-ILK kinetics is that the converse property also holds, even without ILC. We adopt some of his techniques to show this remarkable “DLC-robustness” in the next theorem.
Theorem 4
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be PL-TIK. If for each linkage class \({\mathscr {L}}^i\) (considered as a subnetwork) \(E_{+}({\mathscr {L}}^i,K)\ne \emptyset \), then \(E_+({\mathscr {N}},K)\ne \emptyset \).
Proof
Consider Y, \(A_{k,\rho }\), \(\psi _{K,pr}(x)\), \(\hat{T}\) and T in block forms:
where \(Y^i\), \((A_{k,\rho })^i\), \(\psi ^{i}_{K,\pi }(x)\), \(\hat{T}^i\) and \(T^i\) correspond to linkage class \({\mathscr {L}}^i\).
Assume \(E_{+}({\mathscr {L}}^i,K) \ne \emptyset \) for all \(i \in \overline{1,l}\) (i.e., \(i \in \left\{ 1, 2, \ldots , l \right\} \)). Without loss of generality, we fix \(r \in \overline{1,l}\). We obtain that \(E_{+}({\mathscr {L}}^r,K)\ne \emptyset \) if and only if there exists \(v^{r} \in {\mathbb {R}}^{n^r}_+\) such that \((\psi _{K,pr})^{r}(x)=v^{r}\) and \(Y^{r}\cdot (A_{k,\rho })^{r} \cdot v^{r}=0.\) Equivalently, since \(\log ((\psi _{K,pr})^{r}(x))=(T^r)^{\top } \log (x)\) and \(\log :{\mathbb {R}}^{n}_+ \rightarrow {\mathbb {R}}^{n}\) is a bijection, \(E_{+}({\mathscr {L}}^r,K)\ne \emptyset \) if and only if there exists \(v^{r} \in {\mathbb {R}}^{n^r}_+\) such that \(\log (v^{r}) \in {{\mathrm{Im}}}(T^r)^{\top }\) and \(Y^{r}\cdot (A_{k,\rho })^{r} \cdot v^{r}=0\). We define \(\mathbf 1 ^{r}\) as a vector in \({\mathbb {R}}^{n^r}_+\) with all coordinates having value equal to one. In order to proceed, we need the following claim:
Indeed, since \({{\mathrm{Im}}}(\hat{T}^{r})^{\top }={{\mathrm{Im}}}\left[ (T^{r})^{\top } \mathbf 1 ^{r} \right] \), \({{\mathrm{Im}}}(T^{r})^{\top } \subset {{\mathrm{Im}}}(\hat{T}^{r})^{\top }\). Thus, if \(\log (v^{r}) \in {{\mathrm{Im}}}(T^r)^{\top }\), then \(\log (v^{r}) \in {{\mathrm{Im}}}(\hat{T}^r)^{\top }\).
For the converse, consider the fact that \(\log (\gamma ^r v^{r})=\log (v^{r})+\log (\gamma ^r \mathbf 1 ^{r})\) for all \(\gamma ^r\in {\mathbb {R}}_{+}\). Hence if \(\log (\gamma ^r v^{r}) \in {{\mathrm{Im}}}(\hat{T}^r)^{\top }\), we see that there exists \(\left[ \begin{array}{c} \log x \\ \log \gamma ^r \end{array} \right] \) such that
In particular, if \(\gamma ^r=1\), we have
Thus, \(\log (v^{r}) \in {{\mathrm{Im}}}(T^r)^{\top }\).
Because of this claim, we see that \(E_{+}({\mathscr {L}}^r,K)\ne \emptyset \) if and only if there exists \(v^{r} \in {\mathbb {R}}^{n^r}_+\) such that \(\log (v^{r}) \in {{\mathrm{Im}}}(\hat{T}^r)^{\top }\) and \(Y^{r} (A_{k,\rho })^{r} v^{r}=0\). Fix \(v^{1},\ldots , v^{l}\) such that \(\log (v^{r}) \in {{\mathrm{Im}}}(\hat{T}^r)^{\top }\) and \(Y^{r}\cdot (A_{k,\rho })^{r} \cdot v^{r}=0\) for all \(r \in \overline{1,l}\). Hence,  .
.
Moreover, Proposition 10 implies that \({{\mathrm{Im}}}\hat{T} = {{\mathrm{Im}}}\hat{T}_1 \oplus {{\mathrm{Im}}}\hat{T}_2 \oplus \cdots \oplus {{\mathrm{Im}}}\hat{T}_l\). Using Corollary B.2 of [5], we have

Thus, there exist \(u \in {\mathbb {R}}^{m}\) and \(w \in {\mathbb {R}}^{l}\) such that
Let \(x \in {\mathbb {R}}^{n}_+\) and \(\gamma ^{1},\ldots ,\gamma ^{l} \in {\mathbb {R}}_+\) such that \(\log (x)=u\) and \(-\log (\gamma ^{r})=w_r\) for all \(r \in \overline{1,l}\).
Hence, for all \(r \in \overline{1,l}\) and for all \(i \in {{\mathscr {C}}}^r\), we have
Thus, \((\psi _{K,pr})^{r}(x)=\gamma ^{r} v^{r}\) and it follows that
Hence, \(x \in E_+({\mathscr {N}},K).\) \(\square \)
Remark 2
Proposition 10 shows that \(\hat{T}\)-rank-maximality is analogous to ILC because the latter case is defined as \(S = {{\mathrm{Im}}}N\) being the direct sum of the \({{\mathrm{Im}}}N = {{\mathrm{Im}}}N_1 \oplus {{\mathrm{Im}}}N_2 \oplus \cdots \oplus {{\mathrm{Im}}}N_l\). Thus, all MAK systems with ILC are PL-TIK.
Example 6
We consider a counterexample to the converse of Theorem 4. It is shown in the Supplementary Materials that the S-system model of anti-inflammatory signaling in macrophages is of type PL-TIK. According to A-matrix theory of S-systems discussed in Chapter 6 of [18], there is a positive steady state for all rate constants, but at least one of the 7 linkage classes (\(X_2 \rightarrow 0\)) is not weakly reversible and has deficiency 0 and, hence, does not have any positive equilibrium.
4.2 Kinetic spaces associated with PL-RDK systems
For the formulation of the Low Deficiency Theorems for PL-TIK kinetics, we need kinetic analogues of subspaces of the stoichiometric subspace of the network.
Definition 33
A reaction j has a reactant product complex (of type \({\mathscr {R}}_R\)) if its product complex is also a reactant complex, i.e., \(\pi (j) \in \rho ({\mathscr {R}})\). Otherwise, it is said to have non-reactant product complex (of type \({\mathscr {R}}_{NR}\)). The partition \({\mathscr {R}} = {\mathscr {R}}_{R} \cup {\mathscr {R}}_{NR}\) is called the reactant product partition of \({\mathscr {R}}\).
The reactant product partition generates a network decomposition \({\mathscr {N}} = {\mathscr {N}}_{R} + {\mathscr {N}}_{NR}\) and a concomitant expression for the stoichiometric subspace \(S = S_R + S_{NR}\). We call \(S_R\) the reactant stoichiometric subspace. Since each reaction vector of \(S_R\) is also in R, \(S_R\) is a subspace of \(S \cap R\) and hence can be the nullspace (e.g. for TRS networks, s. Fig. 3).
Example 7
Even if \(S_R\) is non-trivial, it can be a proper subspace of S as in the deficiency zero network \(2X_1 \leftrightarrow X_1 + X_2 \rightarrow X_2\), where \(S = {\mathbb {R}}^2\) and \(S_R = \left\langle X1 - X2 \right\rangle \). Note that the CRN is RES, i.e. \(S = R\).
Note also that \(S = S_R\) implies that the network is RSS.
For the incidence matrix, we have the following variant:
Definition 34
The restricted incidence matrix \(I_{a,R}\) is the restriction of \(I_a\) to the subspace \({\mathbb {R}}^{{\mathscr {R}}_{R}}\). Its image is contained in \({\mathbb {R}}^{\rho ({\mathscr {R}})}\).
We can now introduce the kinetic analogue of \(S_R\), which is used in the abovementioned parametrization and unique intersection results of the DOT:
Definition 35
The kinetic reactant flux subspace \(\tilde{S}_R\) is the subspace \(T ({{\mathrm{Im}}}(I_{a,R}))\) of the kinetic reactant space \(\tilde{R}\). For \(q \in {\mathbb {R}}^{m}_{\ge }\), the set \((q + \tilde{S}_R) \cap {\mathbb {R}}^{m}_{\ge }\) is called the kinetic reactant flux class. A kinetic reactant flux class \(\mathbf Q \) is said to be positive if \(\mathbf Q \cap {\mathbb {R}}^{m}_{>} \ne \emptyset \).
Arceo et al. [1] introduced the kinetic flux subspace \(\tilde{S}\) of a PL-RDK system on an RSS network. It is defined as follows:
Definition 36
For a PL-RDK system on an RSS network, the kinetic flux subspace \(\tilde{S}\) is the subspace \(T(Y_{res}^{-1}(S))\) of \(\tilde{R}\). \(\tilde{s} = \dim \tilde{S}\) is called the kinetic rank.
As shown in [1], for a PL-RDK on a cycle-terminal network, the kinetic flux subspace coincides with the kinetic order subspace \(\tilde{S}_{MR}\) introduced by Müller and Regensburger in [15]. Moreover, for a MAK system on an RSS network, it coincides with the stoichiometric subspace.Recall also from [1] that a PL-RDK kinetics is called Y-kernel aligned (YKA) if \(\ker Y_{res} \subset \ker T\).
The following proposition describes the relationship between \(\tilde{S}_R\) and the kinetic flux subspace \(\tilde{S}\) of PL-RDK kinetics on RSS networks:
Proposition 11
Let \({\mathscr {N}}\) be an RSS network and \(({\mathscr {N}}, K)\) be a PL-RDK system with T-matrix T.
-
1.
\(\tilde{S}_R\) is a subspace of \(\tilde{S}\).
-
2.
If \(S_R = S\), then \(\tilde{S} = \tilde{S}_R + T(\ker Y_{res})\). In particular, if K is YKA-aligned, then \(\tilde{S} = \tilde{S}_R\).
Proof
-
1.
\({{\mathrm{Im}}}(I_{a,R})\) is a subspace of \(Y_{res}^{-1}(S_R)\), which is contained in \(Y_{res}^{-1}(S)\). Hence the images under T have the same containment relation.
-
2.
This is also straightforward. \(\square \)
Corollary 3
If \({\mathscr {N}}\) has zero reactant deficiency and \(S = S_R\), then for any PL-RDK kinetics, \(\tilde{S}_R = \tilde{S}\).
Remark 3
If \({\mathscr {N}}\) is cycle terminal, \(S_R=S\) and \(\tilde{S}_R=\tilde{S}_{MR}\) (since \(I_{a,R} =I_a\)) and hence \(\tilde{S}_R=\tilde{S}\). It follows from Proposition 11 that, in this case \(T(\ker Y_{res}) \subset \tilde{S}_R\).
4.3 Tools on the finiteness and uniqueness of positive equilibria
In this section, we will use the kinetic reactant flux subspace to examine the finiteness and uniqueness of positive equilibria.
Remark 4
Each column of \(T (I_{a,R})\) corresponds to a reaction (i, j), where j is a reactant product complex in such a way that the corresponding column is \(T_{\cdot ,j}-T_{\cdot ,i}\).
The following proposition and corollaries make claims similar to Boros’ Proposition 4.3 and its consequences [6].
Proposition 12
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a PL-ILK system. Let \(Pr_{1}:{\mathbb {R}}^{m} \times {\mathbb {R}}^{l} \rightarrow {\mathbb {R}}^{m}\) be the first projection map, i.e., \(Pr_1 (v) = v^{1}\) for \(v=\left[ \begin{array}{*{20}c} v^{1} \\ v^{2} \\ \end{array} \right] \in {\mathbb {R}}^{m} \times {\mathbb {R}}^{l}\). Then \(Pr_{1}|_{\ker \hat{T}^\top }\) is a bijection between \(\ker \hat{T}^{\top }\) and \((\tilde{S}_R)^{\perp }\).
Proof
We want to show \(Pr_{1}|_{\ker \hat{T}^\top }\) is both surjective and injective. Let \(w \in (\tilde{S}_R)^{\perp }\). Remark 4 implies
Hence, \(\left\langle T_{.,j},w \right\rangle =\left\langle T_{.,i},w \right\rangle \). Clearly, \(\left\langle T_{.,i},w \right\rangle \) depends only on the linkage class \({\mathscr {L}}^i\) of complex \(C_i \in {{\mathscr {C}}}\). Let \(\xi _{r}=\left\langle T_{.,i},w \right\rangle \) for the linkage class \({\mathscr {L}}^r\).
To prove surjectivity, we want to show that for \(w \in (\tilde{S}_R)^{\perp },\) there exists \(v \in \ker \hat{T}^{\top }\) such that \(Pr_1(v) = w\). From arguments found in [6], let \(v \in {\mathbb {R}}^{m+l}\) such that \(v=\left[ w^{\top },-\xi _1,\ldots -\xi _l \right] ^{\top }\). This implies that
Therefore, \(v \in \ker \hat{T}^{\top }\) and \(Pr_1(v)=w\). On the other hand, to prove injectivity, we want to show that if \(Pr_1(v_1)=Pr_1(v_2)\), then \(v_1=v_2\). Let \(w=Pr_1(v_1)=Pr_1(v_2)\). We can write \(v_1=[w^{\top }, u^{\top }_1]^{\top }\) and \(v_2=[w^{\top }, u^{\top }_2]^{\top }\). Thus, it suffices to show that \(u_1=u_2\). Since \(v_1 \in \ker \hat{T}^{\top }\),
Note that \(\left\langle T_{.,i},w \right\rangle \) depends on the linkage class of complex \(C_i\). Thus, the equation above can be written as
It implies that \(Lu_1 = \left[ \begin{array}{c} -\xi _1 \\ \vdots \\ -\xi _l \\ \end{array} \right] \). Analogously, \(Lu_2 = \left[ \begin{array}{c} -\xi _1 \\ \vdots \\ -\xi _l \\ \end{array} \right] \). Therefore \(Lu_1=Lu_2\). Since columns of L are linearly independent, L is of full column rank. Thus, \(u_1=u_2\), implying \(Pr_1|_{\ker \hat{T}^{\top }}\) is injective. \(\square \)
The connection presented by Proposition 12 will be the key for Corollaries 4 and 5.
Corollary 4
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a PL-ILK system. Fix \(w \in (\tilde{S}_R)^{\perp }\) and \(x^* \in {\mathbb {R}}^{m}_+\) such that there exists \(\gamma ^{*} \in {\mathbb {R}}^{l}_{+}\) such that \(\hat{T}^{\top } \left[ {\begin{array}{*{20}r} \log (x^*) \\ -\log (\gamma ^{*}) \\ \end{array} } \right] =w\). Then for \(x \in {\mathbb {R}}^{m}_+\) the following are equivalent:
-
1.
There exists \(\gamma \in {\mathbb {R}}^{l}_+\) such that \(\hat{T}^{\top } \left[ {\begin{array}{*{20}r} \log (x) \\ -\log (\gamma ) \end{array} } \right] =w.\)
-
2.
The vector \(\log (x)-\log (x^*) \in (\tilde{S}_R)^{\perp }.\)
Proof
The equivalence is an immediate consequence of Proposition 12. \(\square \)
Corollary 5
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a PL-ILK system. Fix \(w \in (\tilde{S}_R)^{\perp }\). Then for all \(q \in {\mathbb {R}}^{m}_+,\) there exists \((x,\gamma ) \in {\mathbb {R}}^{m}_+ \times {\mathbb {R}}^{l}_+\) such that \(x \in (q + \tilde{S}_R)\) and \(\hat{T}^{\top } \left[ {\begin{array}{*{20}r} \log (x) \\ -\log (\gamma ) \\ \end{array} } \right] =w.\)
Proof
The statement is an immediate consequence of Corollary 4 and Lemma 3.3 of [6]. \(\square \)
4.4 A Deficiency Zero Theorem for PL-TIK system
In this part, we use the results in the previous sections to prove a Deficiency Zero Theorem for both a single linkage class and multiple linkage classes. As can be observed, properties of \(\hat{T}\), from Proposition 10, play important roles.
Remark 5
Theorem 5 below restates Boros’ Theorem 4.6 [6] for the PL-TIK case.
Theorem 5
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a PL-TIK system which satisfies \(l=1\) and \(\delta =0\). Then
-
1.
\(E_+({\mathscr {N}},K)\ne \emptyset \) if and only if \({\mathscr {N}}\) is strongly connected;
-
2.
if \(E_+({\mathscr {N}},K)\ne \emptyset \) and \(x^* \in E_+({\mathscr {N}},K)\), then

-
3.
if \(E_+({\mathscr {N}},K)\ne \emptyset \), then \(|E_+({\mathscr {N}},K) \cap \mathbf Q |=1\) for each positive kinetic class \(\mathbf Q \).
Proof
By Proposition 4, \(\delta =\dim (\ker Y \cap {{\mathrm{Im}}}I_a)\). Hence, if \(\delta =0\), then \(\ker Y \cap {{\mathrm{Im}}}I_a =\left\{ \mathbf 0 \right\} \). Clearly,

We now prove (1). The forward direction was proven by Feinberg in 1972 [9]. For the converse, assume \({\mathscr {N}}\) is strongly connected. Thus, we have only one terminal strong linkage class. By Theorem 1, we can find a \(y\in {\mathbb {R}}^{n}_+\) such that \(\ker A_k= {{\mathrm{span}}} y\). Because \(\psi _K \in {\mathbb {R}}^{n}_\ge \) for all \(x\in {\mathbb {R}}^{m}_+\), finding an element in \(E_+({\mathscr {N}},K)\) is equivalent to finding some \(\gamma \in {\mathbb {R}}_+\) and \(x\in {\mathbb {R}}^{m}_+\) such that \(\gamma y = \psi _K (x)\). Note that \(\psi _K= \psi _{K,pr}\) and \(n=n_r\) since our network is strongly connected. Taking the logarithm of \(\gamma y = \psi _K (x)\) coordinate-wise yields \(\log (\gamma )e+\log (y) = T^{\top }\), where e is the vector in \({\mathbb {R}}^{n}\) whose coordinates are all equal to 1. Hence, \(x \in E_+({\mathscr {N}},K)\) if and only if there exists \(\gamma \in {\mathbb {R}}_+\) such that
Since \(\dim (\ker (\hat{T}))=0\), \(\hat{T}^{\top }\) has full range, \(\log (y) \in {{\mathrm{Im}}}\hat{T}^{\top }\). Because \(\log \) and \(-\log \) are bijective, we obtain \(E_+({\mathscr {N}},K)\ne \emptyset \).
Statements (2) and (3) follow immediately from Corollaries 4 and 5, respectively.
Note that, in this strongly connected case, \(S_R=S\) and \(\tilde{S}_R=\tilde{S}_{MR}\) \(\square \)
Example 8
To illustrate Theorem 5, we consider the system
\(R_1: X_1 \rightarrow 2X_2\)
\(R_2: 2X_2 \rightarrow X_1\)
The kinetic order matrix is \(F=\left[ \begin{array}{cc} 0.01 &{} 0 \\ 0 &{} 0.5 \end{array} \right] \). Hence, \(\widetilde{Y}\) and T will be
This system is of type PL-TIK. By Theorem 5, \(E_+ \ne \emptyset \). For statements (2) and (3) of Theorem 5, we compute the kinetic reactant flux subspace \(\tilde{S}_R\).
Furthermore, one can easily check that if \(k_{12}=k_{21}=1\), then
Clearly, \(\left[ \begin{array}{c} 1 \\ 1 \\ \end{array} \right] \in E_+\). Thus, by statement (2),

Statement (3) is illustrated by Fig. 4 where \(\mathbf Q _1, \mathbf Q _2 \in \mathbf Q \).
The following corollary extends the previous result to CRN with multiple linkage classes.
Corollary 6
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a PL-TIK system and \(\delta =0\). Then \(E_+({\mathscr {N}},K)\ne \emptyset \) if and only if \(({{\mathscr {C}}},{\mathscr {R}})\) is weakly reversible.
Proof
Note that because of Proposition 7, all deficiency-zero networks have ILC. Hence, this result is a direct consequence of Theorems 4 and 5. \(\square \)
5 Deficiency One Theorem for PL-TIK
In the next two sections, we will prove the DOT for PL-TIK systems under the weakly reversible and non-weakly reversible conditions. Though we extend Boros’ statements [6] to the PL-TIK systems, the proofs are very different.
5.1 Weakly reversible case
We prove the DOT for a single linkage class deficiency-one PL-TIK system. As with the DZT, we will extend it to weakly reversible systems. To start, we have this lemma from [6]. Note that, in this case, \(S_R=S\) and \(\tilde{S}_R=\tilde{S}_{MR}\)
Lemma 1
(Remark 4.8 of [6]) Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a single linkage class PL-TIK system and \({\mathscr {N}}\) be strongly connected. Let \(0 \ne h \in {\mathbb {R}}^{n}\) such that \(h \in \ker Y \cap {{\mathrm{Im}}}A_k\). Then there exist \(\bar{y} \in {\mathbb {R}}^{n}_+\) and \(y^{*} \in {\mathbb {R}}^{n}_{\ge 0}\) such that \(A_k \bar{y}=0\) and \(A_k y^{*}=h\).
These \(\bar{y}\) and \(y^{*}\) will play a significant role in the proof of the following theorem.
Theorem 6
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a single linkage class PL-TIK system which satisfies \(\delta =1\), and \({\mathscr {N}}\) be strongly connected. Then
-
1.
\(E_+({\mathscr {N}},K)\ne \emptyset \);
-
2.
if \(x^* \in E_+({\mathscr {N}},K)\), then

-
3.
\(|E_+({\mathscr {N}},K) \cap \mathbf Q |=1\) for each positive kinetic class \(\mathbf Q \).
Proof
Since \({\mathscr {N}}\) is strongly connected, we have \(l=t=1\), \(\psi _{K,pr}=\psi _K\), \(A_{k,res}=A_k\), \({{\mathscr {C}}}={{\mathscr {C}}}_r\) and \(n=n_r\). Since \(\delta = 1\), Corollary 2 implies \(\dim (\ker Y \cap {{\mathrm{Im}}}A_k)=1\). Let \(0 \ne h \in {\mathbb {R}}^{n}\) such that \(h \in \ker Y \cap {{\mathrm{Im}}}A_k\). By Lemma 1, there exist \(\bar{y} \in {\mathbb {R}}^{n}_+\) and \(y^{*} \in {\mathbb {R}}^{n}_{\ge 0}\) such that \(A_k \bar{y}=0\) and \(A_k y^{*}=h\). Let \(x \in {\mathbb {R}}^{m}_+\). Recall that \(x\in E_+({\mathscr {N}},K)\) if and only if \(Y \cdot A_k \cdot \psi _K (x) =0\). Hence, \(x\in E_+({\mathscr {N}},K)\) if and only if \(A_k \cdot \psi _K (x) \in \ker Y\). To proceed, we need the following claim:
Multiplying both sides of the expression \(\psi _K (x) = \alpha y^* + \gamma \bar{y}\) by \(A_k\) results in \(\alpha h = A_k \cdot \psi _K (x)\). Since \(\alpha h \in \ker Y\), \(A_k \cdot \psi _K (x) \in \ker Y\). For the other direction, note that \(A_k \cdot \psi _K (x), h \in \ker Y \cap {{\mathrm{Im}}}A_k\) and \(\dim (\ker Y \cap {{\mathrm{Im}}}A_k)=1\). Thus, there exists \(\alpha \in {\mathbb {R}}\) such that \(A_k \cdot \psi _K (x)=\alpha h = \alpha A_k y^*\). This implies \(A_k \cdot (\psi _K (x)- \alpha y^*) = 0\). But \(\dim \ker A_k =1\) and \(\bar{y} \in \ker A_k\). Hence, there exists \(\gamma \in {\mathbb {R}}\) such that \(\psi _K (x)- \alpha y^* = \gamma \bar{y}\).
Therefore, using the claim, \(x\in E_+({\mathscr {N}},K)\) if and only if there exist \(\alpha , \gamma \in {\mathbb {R}}\) such that \(\psi _K (x) = \alpha y^* + \gamma \bar{y}\). Taking the logarithm of both sides of \(\psi _K(x)= \alpha y^* + \gamma \bar{y}\) yields \(T^{\top } \log (x) = \log (\alpha y^* + \gamma \bar{y})\) for some \(\alpha , \gamma \in {\mathbb {R}}\). It is equivalent to \(\hat{T}^{\top } \left[ \begin{array}{c} \log (x) \\ -\log (\gamma ) \\ \end{array} \right] = \log \left( \dfrac{\alpha }{\gamma } y^* + \bar{y} \right) \). Thus, \(x \in E_+({\mathscr {N}},K)\) if and only if there exist \(\alpha , \gamma \in {\mathbb {R}}\) such that
Since \(\dim (\ker (\hat{T}))=0\), \(\hat{T}^{\top }\) has full range. Thus, \(\log \left( \dfrac{\alpha }{\gamma } y^* + \bar{y}\right) \in {{\mathrm{Im}}}\hat{T}^{\top }\). Because \(\log \) and \(-\log \) are bijective, we can find \(\alpha , \gamma \in {\mathbb {R}}\) and \(x \in {\mathbb {R}}^m\) satisfying (34). Thus, \(E_+({\mathscr {N}},K)\ne \emptyset \). Statements (2) and (3) follow immediately from Corollaries 4 and 5, respectively. \(\square \)
Corollary 7
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a PL-TIK system which satisfies \(\delta =1\). If \({\mathscr {N}}\) is weakly reversible then \(E_+({\mathscr {N}},K) \ne \emptyset \).
Proof
This is a direct consequence of Theorems 4 and 6. \(\square \)
5.2 Non-weakly reversible case
For this subsection, we need to define the following:
-
1.
\({{\mathscr {C}}}_{r}\)—set of reactant complexes
-
2.
\({{\mathscr {C}}}'\)—set of complexes in the terminal strong linkage class
Let

. Let \(n_{r} = |{{\mathscr {C}}}_{r}|\), \(n' = |{{\mathscr {C}}}'|\), and \(n'' = |{{\mathscr {C}}}''|\). Consider \(A_k \in {\mathbb {R}}^{n \times n}\), \(\psi _K: {\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{n}\) and a vector \(h \in {\mathbb {R}}^{n}\) in the block forms
Let \(h \in \ker Y \cap {{\mathrm{Im}}}A_k\). Denote as \(\mathbf H ''\) the product of \((A_k '')^{-1}\) and \(h''\).
Lemma 2
[Remark 4.8 of [6]] Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a single linkage class PL-TIK system and \({\mathscr {N}}\) be not strongly connected. Let \(0 \ne h \in {\mathbb {R}}^{n}\) such that \(h \in \ker Y \cap {{\mathrm{Im}}}A_k\) and \(\mathbf H '' \in {\mathbb {R}}^{n''}_+ \cup {\mathbb {R}}^{n''}_-\) (i.e., either all the coordinates of \(\mathbf H ''\) are positive or all the coordinates of \(\mathbf H ''\) are negative). Then
-
1.
there exists \(\bar{y} \in {\mathbb {R}}^{n}_+\) such that \(A_k \bar{y}=0\);
-
2.
if \(\mathbf H '' \in {\mathbb {R}}^{n''}_+\) then there exists \(y^{*} \in {\mathbb {R}}^{n}_{\ge 0}\) such that \(A_k y^{*}=h\); and
-
3.
if \(\mathbf H '' \in {\mathbb {R}}^{n''}_-\) then there exists \(y^{*} \in {\mathbb {R}}^{n}_{\ge 0}\) such that \(A_k y^{*}=-h\).
Having in hand Lemma 2, we can prove the Deficiency One Theorem for the non-strongly connected case using arguments very similar to those used in the proof of Theorem 6.
Theorem 7
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a PL-TIK system which satisfies \(\delta =1\), \(l=t=1\), and \({\mathscr {N}}\) be not strongly connected. Then
-
1.
\(E_+({\mathscr {N}},K)\ne \emptyset \) if and only if \(\mathbf H ''\in {\mathbb {R}}^{n''}_+ \cup {\mathbb {R}}^{n''}_-\);
-
2.
if \(E_+({\mathscr {N}},K)\ne \emptyset \), and \(x^* \in E_+({\mathscr {N}},K)\), then
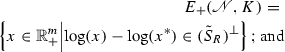
-
3.
if \(E_+({\mathscr {N}},K)\ne \emptyset \), then \(|E_+({\mathscr {N}},K) \cap \mathbf Q |=1\) for each positive kinetic reactant flux class \(\mathbf Q \).
Proof
Since \(\delta = 1\) and \(l=t\), Corollary 2 implies \(\dim (\ker Y \cap {{\mathrm{Im}}}A_k)=1\).
For the forward direction, suppose \(E_+({\mathscr {N}},K) \ne \emptyset \). Let h be a nonzero element of \(\ker Y \cap {{\mathrm{Im}}}A_k\). Since \(E_+({\mathscr {N}},K) \ne \emptyset \), there exist \(x^* \in E_+({\mathscr {N}},K)\) and \(\alpha \in {\mathbb {R}}\) such that \(A_k \psi _K (x^*) = \alpha h\). Then \(A_k'' \psi _K'' (x^*) = \alpha h''\). Because of Equation 35 and Theorem 1, \(\alpha (A_k '')^{-1}h'' = \psi _K'' (x^*)\). Moreover, \(\mathbf H ''= \dfrac{1}{\alpha } (\psi _K'')_r (x^*)\) where \((\psi _K'')_r (x^*)\) is the vector of reactant complexes from \(\psi _K''(x^*)\). Since \((\psi _K'')_r (x^*) \in {\mathbb {R}}^{n''}_+\), we obtain \(\mathbf H '' \in {\mathbb {R}}^{n''}_+ \cup {\mathbb {R}}^{n''}_-\).
For the converse, we assume \(\mathbf H '' \in {\mathbb {R}}^{n''}_+\). By Lemma 2, there exists \(\bar{y} \in {\mathbb {R}}^{n}_+\) and \(y^{*} \in {\mathbb {R}}^{n}_{\ge 0}\) such that \(A_k \bar{y}=0\) and \(A_k y^{*}=h\). Let \(x \in {\mathbb {R}}^{m}_+\). Recall that \(x \in E_+({\mathscr {N}},K)\) if and only if \(A_k \cdot \psi _K (x) \in \ker Y\) (or \(Y \cdot A_k \cdot \psi _K (x) =0\)). Hence, as the claim in the proof of Theorem 6 implies, \(x\in E_+({\mathscr {N}},K)\) if and only if there exist \(\alpha , \gamma \in {\mathbb {R}}\) such that \(\psi _K (x) = \alpha y^* + \gamma \bar{y}\). Equivalently, \(x\in E_+({\mathscr {N}},K)\) if and only if there exist \(\alpha , \gamma \in {\mathbb {R}}\) such that \(\psi _{K,pr} (x) = \alpha z^* + \gamma \overline{z}\) where \(z^*\) and \(\overline{z}\) are the truncated \(y^*\) and \(\bar{y}\) respectively. (i.e., the components corresponding to non-reactant complexes are deleted). The same argument follows as in the proof of Theorem 6. We take the logarithm of both sides of \(\psi _{K,pr}(x)= \alpha z^* + \gamma \bar{z}\). This yields \(T^{\top } \log (x) = \log (\alpha z^* + \gamma \bar{z})\) for some \(\alpha , \gamma \in {\mathbb {R}}\). This is equivalent to \(\hat{T}^{\top } \left[ \begin{array}{c} \log (x) \\ -\log (\gamma ) \\ \end{array} \right] = \log \left( \dfrac{\alpha }{\gamma } z^* + \bar{z}\right) \). Thus, \(x \in E_+({\mathscr {N}},K)\) if and only if there exist \(\alpha , \gamma \in {\mathbb {R}}\) such that
Since \(\dim (\ker (\hat{T}))=0\), \(\hat{T}^{\top }\) has full range. Thus, \(\log \left( \dfrac{\alpha }{\gamma } z^* + \bar{z}\right) \in {{\mathrm{Im}}}\hat{T}^{\top }\). Because \(\log \) and \(-\log \) are bijective, we can find \(\alpha , \gamma \in {\mathbb {R}}\) and \(x \in {\mathbb {R}}^m\) satisfying (36). Thus, \(E_+({\mathscr {N}},K)\ne \emptyset \). Analogously, if \(\mathbf H '' \in {\mathbb {R}}^{n''}_-\) holds, take \(0 \ne -h \in \ker Y \cap {{\mathrm{Im}}}A_k\) instead of h. \(\square \)
We extend Theorem 7 to a t-minimal non-weakly reversible PL-ILK system. Let \((\mathbf H '')^i\) be the vector with values from \(\mathbf H ''\) associated to linkage class \({\mathscr {L}}^i\).
Corollary 8
Let \(({\mathscr {S}},{{\mathscr {C}}},{\mathscr {R}},K)\) be a t-minimal non-weakly reversible PL-TIK system where each linkage class has deficiency 0 or 1. \(E_+({\mathscr {N}},K)\ne \emptyset \) if
-
1.
each linkage class \({\mathscr {L}}^i\) with \(\delta =0\) is strongly connected; and
-
2.
each non-strongly connected linkage class \({\mathscr {L}}^i\) has \(\delta =1\) and contains a terminal strong linkage class which satisfies \((\mathbf H '')^i \in {\mathbb {R}}^{(n^i)''}_+ \cup {\mathbb {R}}^{(n^i)''}_-\).
Proof
This is a direct consequence of Theorems 4, 6 and 7. \(\square \)
Example 9
To illustrate Corollary 8 , we consider a system with CRN as shown below.
\(R_1, L_1: 2X1 \rightarrow X1 + X2\), \(k_{12}\)
\(R_2, L_2: X1 +X_2 \rightarrow 2X1\), \(k_{21}\)
\(R_3, L_3: X1 +X_2 \rightarrow 2X2\), \(k_{23}\)
\(R_4, L_4: X1 \rightarrow X2\), \(k_{45}\)
\(R_5, L_5: X2 \rightarrow X1\), \(k_{54}\)
It is important to note that the deficiency of the whole network is 2 while the deficiency of the first and second linkage classes are 1 and 0, respectively. Hence, the network has dependent linkage classes.
The kinetic order matrix is

Clearly, this is a PL-RDK system. Matrices \(\widetilde{Y}\) and T will be

Constructing \(\hat{T}\), we have
Thus, this system is of type PL-TLK but not PL-RLK. Note that the network under consideration is t-minimal (i.e., \(l=t=2\)) and the columns are linearly independent. Taking into account the first condition of Corollary 8 , the strongly connected linkage class (e.g. the second linkage class) has zero deficiency. For the second condition, note that \(({{\mathscr {C}}}^1)'={2X_2}\), \(({{\mathscr {C}}}^1)''={2X_1, X_1+X_2}\), and
Therefore, to satisfy the last condition of Corollary 8 , \(E_+ \ne \emptyset \) if \(k_{21}>k_{23}\).
6 Relationships between PL-TIK and GMAK systems
6.1 The bijection between PL-RDK and GMAK systems
S. Müller and G. Regensburger developed their theory of Generalized Mass Action Kinetics (GMAK) systems in a 2012 paper [14] and a subsequent one in 2014 [15]. The GMAK concepts in those papers are different, hence we denote them GMAK-12 and GMAK, respectively. We show below that in cycle-terminal networks, a GMAK-12 system is a special case of a GMAK system.
We recall the definitions for a GMAK system [15]:
Definition 37
A Generalized Chemical Reaction Network (GCRN) \(\left( G,y,\tilde{y} \right) \) is given by a digraph \(G=\left( V,E \right) \) without self-loops, and two functions
assigning to each vertex a (stoichiometric) complex and to each source a kinetic complex.
In the above definition, \(V=\left\{ 1,\ldots ,n\right\} \) is a finite set of vertices and \(E \subseteq V \times V\) is a finite set of edges. An edge \(e=\left( i,j \right) \in E\) is denoted by \(i \rightarrow j\) to emphasize that it is directed from the source i to a target j. Moreover, the set \(V_s\) is the set of source vertices, that is,

Müller and Regensburger do not require the map y to be injective. However, for compatibility with the commonly used definition of a CRN, we restrict ourselves to GCRNs where y is the inclusion, i.e. the pair \(\left( G,y \right) \) is a CRN in the sense of Definition 1, with \({{\mathscr {C}}} = V\), \({\mathscr {R}} = E\) and \(\rho \left( {\mathscr {R}} \right) = V_s\).
Furthermore, for a digraph with an inflow reaction \(0 \rightarrow X\), Müller and Regensburger allow the image of the zero complex under the kinetic complex map \(\tilde{y}\) to be non-zero. This property has useful applications, e.g. it was used by Johnston for his method of network translation [13]. Again, for compatibility with models of biochemical systems, we focus on GCRNs with the property that \(\tilde{y}(0)=0\).
The image of a reactant complex under \(\tilde{y}\) is called a kinetic complex, as it is used to define part of the kinetics in the following definition:
Definition 38
A generalized mass action system \(\left( G_k,y,\tilde{y} \right) \) is a GCRN \(\left( G,y,\tilde{y} \right) \) where edges \((i,j) \in E\) are labeled with constants \(k_{ij} \in {\mathbb {R}}_{>}\). Assuming GMAK, the rate of the reaction is determined by the source kinetic complex \(\tilde{y}(i)\) and the positive rate constant \(k_{ij}\):
Remark 6
A GMAK-12 system is a 5-tuple \(\left( {\mathscr {S}}, {{\mathscr {C}}}, \tilde{{{\mathscr {C}}}}, {\mathscr {R}}, k \right) \), whereby \(\left( {\mathscr {S}}, {{\mathscr {C}}},{\mathscr {R}} \right) \) is a CRN, \(k \in {\mathbb {R}}^{{\mathscr {R}}}_{>}\) is an edge-labeling, a bijection \(\tilde{y}: {{\mathscr {C}}} \rightarrow \tilde{{{\mathscr {C}}}}\) is given, and the rate function is given as in a GMAK-system. On a cycle-terminal network, i.e., \({{\mathscr {C}}} = \rho ( {\mathscr {R}} )\), embed \(\tilde{{{\mathscr {C}}}}\) in \({\mathbb {R}}^{{\mathscr {S}}}\), then we obtain a bijection between GMAK-12 systems and GMAK systems with injective \(\tilde{y}\).
Definition 39
A GMAK system \((G, y, \tilde{y}, k)\) is an element of GMAK\(_c\) (called the set of compatible GMAK systems) if its GCRN \((G, y, \tilde{y})\) has the following “compatibility” properties:
-
1.
y is injective.
-
2.
If the digraph G has an inflow reaction \(0 \rightarrow X\), then \(\tilde{y}(0) = 0\).
We next prove that GMAK\(_c\) systems can be identified with PL-RDK\(({\mathscr {N}})\), where \({\mathscr {N}} = (G,y)\).
Proposition 13
The set of GMAK\(_c\) systems for a pair (G, y) maps bijectively to \(\mathscr {PL-RDK(N)}\), where \({\mathscr {N}} = (G,y)\). Under this bijection, those with injective \(\tilde{y}\) are mapped to \(\mathscr {PL-FSK(N)}\).
Proof
Given a GMAK\(_c\) system \((G, y, \tilde{y}, k)\), we can define the CRN \({\mathscr {N}} = (G,y)\) since y is injective. To define the PL-RDK system, we set the T-matrix column for a reactant complex y equal to \(\tilde{y}(y)\). If there is an inflow reaction, T maps \(w_0\) to 0 since \(\tilde{y}(0) = 0\). The kinetics \(K = I_k \psi _K\), with k the rate vector from the GMAK system and the factor map \(\psi _K (x) = xT^\top \). The mapping is clearly injective. Surjectivity follows from the reverse process, setting \((G,y) = N\), \(\tilde{y}(y) = T(_y)\) and taking k from \(I_k\). The injectivity of \(\tilde{y}\) is equivalent to the columns of the T-matrix being pairwise different, which was shown in [5] (Corollary 3) to be equivalent to factor span surjectivity. \(\square \)
Remark 7
On a cycle-terminal network G, the set of GMAK-12 systems are bijectively mapped to GMAK systems with injective \(\tilde{y}\). Consequently, we can define GMAK\(_c\)-12 as the image of GMAK\(_c\) under this bijection. This also induces a bijection between GMAK\(_c\)-12 and PL-FSK\(({\mathscr {N}})\) on cycle-terminal networks.
Focusing on GMAK\(_c\) and using our PL-RDK terminology, we recall further concepts and results of Müller-Regensburger which we need in the following discussion.
Definition 40
Let \({\mathscr {N}}\) be a cycle-terminal network with n complexes and l linkage classes and K a PL-RDK kinetics. The kinetic order subspace \(\tilde{S}\) of the system \(({\mathscr {N}}, K)\) is the  , where T is the T-matrix map. If \(\tilde{s} = \dim \tilde{S}\), then the kinetic deficiency is defined as \(\tilde{\delta }= n - l - \tilde{s}\).
, where T is the T-matrix map. If \(\tilde{s} = \dim \tilde{S}\), then the kinetic deficiency is defined as \(\tilde{\delta }= n - l - \tilde{s}\).
The first main result in [15] is Theorem 1, which characterizes the set of complex balanced equilibria of a PL-RDK system and hence could be denoted as the Complex Balancing Theorem (CBT) for PL-RDK systems. We reformulate part (1) in a slightly more general framework:
Definition 41
Let \(\mathscr {K}\) be a set of PL-RDK kinetics on a cycle-terminal CRN \({\mathscr {N}}\). We say \({\mathscr {N}}\) has kinetic deficiency \(= i\) for \(\mathscr {K}\) if and only if for all kinetics in \(\mathscr {K}\), the kinetic deficiency of \(({\mathscr {N}},K)\) is equal to i. If \(\mathscr {K} = PL-RDK({\mathscr {N}})\), we will simply say “ \({\mathscr {N}}\) has kinetic deficiency \(= i\)”.
Remark 8
Associating a property to a CRN if all kinetic systems of a certain type on it possess that property has a long tradition in CRNT. For example, a network is called injective if all MAK systems on it are injective.
We can thus reformulate statement (1) of Theorem 1 in [15] as follows:
Theorem 8
(Kinetic Deficiency Zero Theorem) Let \({\mathscr {N}}\) be a weakly reversible network and \(\mathscr {K}\) a PL-RDK kinetics with T-matrix T on \({\mathscr {N}}\). Then \(\tilde{\delta }=0\) implies that all PL-RDK systems with T-matrix T are complex balanced.
Corollary 9
A weakly reversible CRN that has zero kinetic deficiency implies that all PL-RDK systems on it are complex balanced
Proof
If we denote all PL-RDK systems with a (fixed) T-matrix T as PL-RDK\(({\mathscr {N}}, T)\), then we have \(PL-RDK({\mathscr {N}}) = \bigcup _{T} PL-RDK({\mathscr {N}},T)\), the union being taken over all \(m \times n_r\) real-valued matrices. Any PL-RDK system with kinetic deficiency 0 will belong to at least one set in the union, implying complex balancing for all with that T-matrix. On the other hand, any complex balanced system must belong to such a set, hence completing the forward direction. We use similar arguments to prove the converse. \(\square \)
Remark 9
If one replaces “all PL-RDK systems with the same T-matrix T” with the stronger condition “all GMAK systems with same map \(\tilde{y}\)” in Theorem 8, then one obtains an equivalence, since the latter is also sufficient. Consequently, the statement in Corollary 9 would also become an “if and only if” statement.
We can further derive the following relationship from the KDZT:
Proposition 14
For a weakly reversible network, zero kinetic deficiency implies zero deficiency.
Proof
If the kinetic deficiency is zero then all PL-RDK systems are complex balanced, which implies that all MAK systems are complex balanced. Hence, the deficiency is zero. \(\square \)
The converse will not always hold as the following simple non-PL-LLK counterexample shows:
Example 10
Define the cyclic network with 2 species X1, X2 as follows:
\(R_1: 2X1 + X2 \rightarrow X1 + 2X2\)
\(R_2: X1 + 2X2 \rightarrow X1 + X2\)
\(R_3: X1 + X2 \rightarrow 2X1 + X2.\)
Its reaction vectors are \((-1,1)\), \((0,-1)\) and (1, 0), so s =2 and therefore \(\delta = 0\). Define the T-matrix T as

The network is nonbranching and weakly reversible. The reaction vectors of the kinetic complexes are (2, 1), \((-2,-1)\), (0, 0), so that the kinetic deficiency \(= 1\).
The second main result of GMAK theory is the parametrization of \(Z_+ ({\mathscr {N}}, K)\) for PL-RDK systems. In Proposition 2.21 of [14], they prove the following:
Proposition 15
Let \({\mathscr {N}}\) be a a weakly reversible network and K a factor span surjective kinetics with a nonempty set \(Z_+ ({\mathscr {N}}, K)\) of complex balancing equilibria. Then

for any \(c^* \in Z_+ ({\mathscr {N}}, K)\).
In [15], the proposition is extended to all PL-RDK kinetics on a weakly reversible network.
The third useful result, Proposition 3.1 from [14], provides a condition on sign vector sets for the intersection of two interesting sets derived from two arbitrary subspaces of a finite dimensional real linear space.
Proposition 16
Let S, \(\tilde{S}\) be subspaces of \({\mathbb {R}}^n\). Then the following statements are equivalent:
-
1.
For all \(c^*>0\) and \(c'>0\), the intersection
 contains at most one element.
contains at most one element. -
2.
\(\sigma (S) \cap \sigma (\tilde{S}^\perp ) = \left\{ 0 \right\} \)
Finally, we formulate the application of the Generalized Birch’s Theorem (Theorem 2 of [15]) to the zero kinetic deficiency case as follows:
Proposition 17
(Müller-Regensburger) Let \({\mathscr {N}}\) be weakly reversible, conservative, and have \(\tilde{\delta }=0\). Then any PL-RDK kinetics with \(\sigma (S) = \sigma (\tilde{S})\) has a unique equilibrium in any stoichiometric class.
6.2 Relationships between PL-TIK and GMAK\(_c\) systems on deficiency zero networks
Since for any kinetics on a deficiency zero network, all equilibria are complex balanced (Feinberg 1972), then in this section, we use the notation \(Z_+ ({\mathscr {N}}, K)\) instead of \(E_+ ({\mathscr {N}}, K)\).
6.2.1 Parametrization of the set of complex balanced equilibria \(Z_+\)
The parametrization in Theorem 5 (2) is a special case of the above-mentioned characterization of \(Z_+ ({\mathscr {N}}, K)\) for all PL-RDK systems.
6.2.2 Existence of a positive equilibrium \((Z_+ \ne \emptyset )\)
In Corollary 6, we showed that for a PL-TIK system on a weakly reversible, deficiency zero network, \(Z_+\) is non-empty. If the network satisfies the stronger condition that \(\tilde{\delta }=0\), then this result follows from the Corollary of the KDZT. Otherwise, it is a new result.
6.2.3 Uniqueness and monostationarity
The uniqueness of the complex balanced equilibrium in a kinetic class for any PL-TIK kinetics is a new result. One can use the sign vector condition above to formulate the following monostationarity result with respect to a stoichiometric class (since \(S_R=S\) and \(\tilde{S}_R=\tilde{S}_{MR}\)):
Proposition 18
Let \({\mathscr {N}}\) be a weakly reversible network with \(\delta =0\) and K a PL-TIK kinetics with \(\sigma (S) = \sigma (\tilde{S})\). Then K is monostationary in each stoichiometric class.
Comparing this with the Proposition 18 above, we see that for PL-TIK kinetics, we obtain a result for non-conservative networks as well as the more general \(\delta = 0\), but cannot guarantee the existence of the equilibrium.
6.3 Relationships between PL-TIK and GMAK\(_c\) systems on deficiency one networks
The comparison in the Deficiency One case is more challenging since the relationship between \(\delta = 1\) and the various kinetic deficiency values is not clear.
6.3.1 Parametrization of \(E_+ ({\mathscr {N}}, K)\)
This result extends the characterization of positive equilibria beyond complex balanced ones since such may exist in deficiency one networks. Moreover, it is also valid for t-minimal, non-weakly reversible networks and PL-ILK systems satisfying the appropriate conditions.
6.3.2 Existence of a positive equilibrium \((E_+ ({\mathscr {N}}, K) \ne \emptyset )\)
The result is, to our knowledge, the first for a class of power-law kinetics on deficiency one networks.
6.3.3 Uniqueness and monostationarity
The uniqueness for a PL-TIK kinetics on cycle-terminal networks with respect to a kinetic class and monostationarity of a PL-TIK kinetics with \(\sigma (S_R) = \sigma (\tilde{S}_{R})\) with respect to a reactant stoichiometric class are, to our knowledge, new.
7 Conclusion
In conclusion, we summarize our main results and outline some perspectives for future research.
-
1.
We identified the set of PL-ILK kinetic systems, which exhibits interesting structural and dynamical properties and significantly occur in models of biochemical systems.
-
2.
We proved a remarkable property of the subset PL-TIK of these kinetic systems, that even without linear independence of their linkage classes, the existence of positive equilibria for each linkage class implies the existence of positive equilibria for the whole network.
-
3.
We showed that the Deficiency Zero Theorem holds for this class of power-law kinetics and compared our results with the Kinetic Deficiency Zero Theorem of Müller and Regensburger.
-
4.
We derived the existence of positive equilibria for PL-TIK systems whose underlying networks satisfy the Deficiency One Theorem conditions as well as the Boros condition in the non-weakly reversible case. Moreover, the parametrization and uniqueness properties also hold.
-
5.
The need for parametrization and uniqueness considerations to introduce a subspace of \(\tilde{R}\), which on a non-cycle terminal RSS network is a subspace of the kinetic flux space but not necessarily equal) is a new phenomenon which merits further study. The frequent occurrence among the biological examples in the Supplementary Materials of networks with high deficiency and hence outside of scope of the results presented here also highlights an area for further research.
Abbreviations
- \(\delta \) :
-
Deficiency of a CRN
- \(\psi _K\) :
-
Factor map of a complex factorizable kinetics K
- \( I_a\) :
-
Incidence matrix of a CRN
- \(A_k\) :
-
k-Laplacian matrix
- \(\tilde{S}\) :
-
Kinetic flux subspace
- \(\tilde{R}\) :
-
Kinetic reactant subspace
- K :
-
Kinetic subspace of a CKS
- Y :
-
Molecularity map/matrix of complexes
- \(\pi \) :
-
Product map
- \(\rho \) :
-
Reactant map
- \(Y_{res}\) :
-
Reactant matrix
- \(S_{R}\) :
-
Reactant stoichiometric subspace.
- \({\mathscr {K}}({\mathscr {N}})\) :
-
Set of all chemical kinetics on a CRN \({\mathscr {N}}\)
- \(E_+\) :
-
Set of positive equilibria
- f :
-
Species formation rate function of a CKS
- S :
-
Stoichiometric subspace of a CRN
References
C. Arceo, E. Jose, A. Lao, E. Mendoza, Reactant subspaces and kinetics of chemical reaction networks. J. Math. Chem. (2017, accepted)
C. Arceo, E. Jose, A. Lao, E. Mendoza, Reaction networks and kinetics of biochemical systems. Math. Biosci. 283, 13–29 (2017)
C. Arceo, E. Jose, A. Sanguino, E. Mendoza, Chemical reaction network approaches to biochemical systems theory. Math. Biosci. 269, 135–152 (2015)
B. Bollobas, Graph Theory: An Introductory Course (Springer, New York Inc., New York, Heidelberg, 1979)
B. Boros, Notes on the deficiency-one theorem: multiple linkage classes. Math. Biosci. 235, 110–122 (2011)
B. Boros, On the positive equilibria of deficiency one mass action systems. Ph.D. thesis, Eotvos Lorand Universiti (2013)
M. Feinberg, Complex balancing in general kinetic system. Arch. Ration. Mech. Anal. 49(3), 187–194 (1972)
M. Feinberg, Mathematical aspects of mass action kinetics. in Chemical Reactor Theory: A Review, ed. by N. Amundson, L. Lapidus (Prentice-Hall, Englewood Cliffs, NJ, 1977)
M. Feinberg, Lectures on chemical reaction networks. Univesity of Wisconsin, written version of the lectures given at the mathematical research center (1979)
M. Feinberg, The existence and uniqueness of steady states for a class of chemical reaction networks. Arch. Ration. Mech. Anal. 132(4), 311–370 (1995)
F. Horn, Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal. 49, 172–186 (1972)
F. Horn, R. Jackson, General mass action kinetics. Arch. Ration. Mech. Anal. 47, 81–116 (1972)
M. Johnston, D. Siegel, G. Szederkényi, Computing weakly reversible linearly conjugate chemical reaction networks with minimal deficiency. Math. Biosci. 241(1), 88–98 (2013)
S. Müller, G. Regensburger, Generalized mass action systems: complex balancing equilibria and sign vectors of the stoichiometric and kinetic order subspaces. SIAM J. Appl. Math. 72(6), 1926–1947 (2012)
S. Müller, G. Regensburger, Generalized mass action systems and positive solutions of polynomial equations with real and symbolic exponents. Proceedings of CASC 2014, (eds. V.P. Gerdt, W. Koepf, W.M. Seiler, E.H. Vorozhtsov), Lecture Notes in Comput. Sci. pp. 302–323 (2014)
G. Shinar, M. Feinberg, Design principles for robust biochemical reaction networks: what works, what cannot work, and what might almost work. Math. Biosci. 231(1), 39–48 (2011)
G. Shinar, M. Feinberg, Concordant chemical reaction networks and the species-reaction graph. Math. Biosci. 241(1), 1–23 (2012)
E. Voit, Computational Analysis of Biochemical Systems (Cambridge University Press, Cambridge, 2000)
Acknowledgements
Open access funding provided by Max Planck Society. The authors thank S. Müller for his email clarifying aspects of the GCRN concept.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Talabis, D.A.S.J., Arceo, C.P.P. & Mendoza, E.R. Positive equilibria of a class of power-law kinetics. J Math Chem 56, 358–394 (2018). https://doi.org/10.1007/s10910-017-0804-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10910-017-0804-2











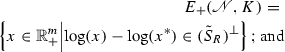
 contains at most one element.
contains at most one element.