Iterative averaging of spectra as a powerful way of suppressing spurious resonances in signal processing

Abstract

The fast Padé transform (FPT) was applied to magnetic resonance spectroscopic (MRS) time signals encoded in vivo on a 1.5 T scanner from the parietal-temporal brain region of a pediatric patient who had suffered cerebral asphyxia. An iterative averaging procedure was implemented to the 9th iteration, whereby spurious structures on the total shape spectra were effectively suppressed. The parametric and non-parametric $\hbox {FPT}^{(\pm )}$ were verified to reconstruct equivalent total shape spectra. Via the parametric FPT, the spectral region of interest was chosen to bypass the giant water resonance, automatically generating spectral envelopes without the need for windowing. The dense component spectra were reliably reconstructed by the $\hbox {FPT}^{(+)}$, in the “usual” mode (mixture of absorption and dispersion components) and “ersatz” mode (reconstructed phases set to zero). Via the latter, interference effects were well-visualized for closely-overlapping and hidden resonances. The most stringent test was performed for the complex frequencies and associated complex amplitudes reconstructed by the $\hbox {FPT}^{(+)}$. Exceedingly small variances were obtained for all four Padé-reconstructed parameters per genuine resonance, once convergence was achieved at the 7th to 9th iterated averages. This now fully-validated methodology can generate denoised spectra and accurate spectral parameters for in vivo MRS data encoded within neurodiagnostics. Such a multi-faceted Padé-based strategy for processing the dense spectra of the brain could vitally improve pediatric neurodiagnostics. A wider range of clinical applications becomes within reach, including areas of cancer diagnostics where the added value of in vivo MRS is urgently needed. The broad theoretical underpinnings of incorporating quantum mechanics into signal processing provide the basis for these innovative advances.

1 Introduction

1.1 Quantum mechanical signal processing and rational polynomials

Within signal processing, rational polynomials in the form of the Padé approximant (PA), are the key response function to external perturbations of general systems [1, 2]. According to Prony, the time evolution of all phenomena can be described by a linear combination of real-valued exponentials [3]. Via the auto-correlation functions, quantum-mechanics concordantly also predicts this latter formula, but with an extra feature in that the exponentials are complex-valued. When this time-domain ansatz is transformed into the frequency domain, the PA is directly generated, as was known to Prony. It was actually about 100 years after Prony’s work that Padé, supervised by Frobenius, published his doctoral dissertation on polynomial quotients [4]. For experimental data for which the energy or frequency parametrized description is rooted in the class of rational polynomials, the PA is always exact. Since such experimental signals are abundant across many basic scientific and applied fields, it becomes clear that a model based upon the PA, also termed the fast Padé transform (FPT) in spectral analysis, would be the method of choice for processing these signals [1, 2]. More generally, as per the Cauchy integral formula, any analytical function can be expressed by a Padé rational polynomial to within an arbitrary level of accuracy. In signal processing, an input spectrum is a Maclaurin series (truncated or not), which is an analytic function and, thus, according to Cauchy, expressible by a polynomial quotient with any desired precision.

1.1.1 Nuclear magnetic resonance versus magnetic resonance spectroscopy

Among the most noteworthy examples of multi-disciplinarity is the field of nuclear magnetic resonance (NMR). The methodology of NMR in analytical chemistry and that of magnetic resonance spectroscopy (MRS) in medical diagnostics do not differ essentially. For in vivo medical applications, the term “nuclear” is omitted, and the instrumentation of NMR compared to in vivo MRS differs. For NMR, spectrometers are quite small as per the size of the samples. In contrast, in medicine, the same scanners are used for magnetic resonance imaging (MRI) as well as MRS, and thus need to be large enough to hold patients. Fundamentally, however, NMR and MRS are faced with the same challenges, particularly those related to mathematical analysis of encoded data. In fact, the methods developed herein are even more widely applicable and can be employed for signal processing in areas that have no connection to magnetic resonance (MR) per se [1, 2].

Besides the importance of generating well-resolved spectra and images within MRS and MRI, incorporating quantum mechanics into signal processing supplies the basic framework of a complete theory of physics. In so doing, arbitrary signals can be directly related to the dynamics of the examined system and its time evolution, as per the first principles of physics. The dynamics of very complex systems may not be known and/or may be very elusive. It is via quantum mechanics that the dynamics of the system can be uncovered and the parametrized full spectral information extracted, insofar as experimental data such as time signals are available. The reason for this possibility is the equivalence between quantum-mechanical auto-correlation functions and time signals. Thereby, with this equivalence, rather than confronting the common challenge of nonlinear fitting of experimental data yielding non-unique reconstructions, the task becomes transformed into a quantum-mechanical linear problem for eigen spectra of the examined system. The unique results obtained from the latter problem retrieve the unknown dynamics and interactions in the system which has undergone transitions as a result of perturbations, prior to generating the recorded time signals. In other words, we are confronting an inverse problem in quantum mechanics, namely that the experimentally measured data are available, from which the interaction potentials or, more generally, the underlying causes need to be reconstructed from the observed effects [1, 2].

1.1.2 The quantification problem

The quantification problem (or spectral analysis, as it is called in mathematics) is a critical challenge in MRS. It consists of the retrieval of the unknown, quantitative information which is contained within the measured time signals. This quantitative information can potentially be of diagnostic importance. However, the encoded MRS time signal, containing tightly packed, multiple, damped sinusoidal oscillations, is not clinically interpretable in a direct manner. Mathematical transformation of these encoded data is needed in order to extract the sought information. Thereby, the encoded data are mapped from the time domain into the frequency domain (or the domain of spectra). The latter, complementary domain is where the needed quantitative information can be extracted from the resonances (peaks) that appear in the spectrum. It is invariably stated in the MRS literature that spectra are acquired, i.e. encoded. This is entirely incorrect since it is the MRS time signals that are acquired, whereas the corresponding spectra are computed. In other words, the time and frequency domains are the subjects of measurement and theory, respectively.

1.2 The clinical context

In the present paper, the high-resolution, quantum-mechanical approach is applied to a specific problem within MRS for pediatric neurodiagnostics, the salient clinical aspects of which will be now briefly reviewed. Overall, MRS has enhanced the specificity of MRI by providing insight into the metabolic features of various pathologic tissues. Within pediatric neurodiagnostics, in vivo MRS has been primarily based upon a small number of metabolites and their concentration ratios. Among these is nitrogen acetyl aspartate (NAA), resonating at $\sim$2.0 ppm (parts per million), which indicates the abundance and viability of neurons. Thus, for example, with cerebral asphyxia, which is brain impairment due to oxygen deprivation usually at birth, the concentration of NAA is reduced  [5]. This is due to the marked vulnerability of cerebral neurons to hypoxia. However, NAA can also be lowered with almost any damage to the brain, including brain tumors [6]. Another diagnostically important metabolite is choline (Cho) resonating at $\sim$3.2 ppm, which reflects phospholipid metabolism of cell membranes, and is a marker of membrane damage, cellular proliferation and cell density. In cerebral ischemia/hypoxia, a lactate (Lac) doublet, centered at $\sim$1.3 ppm, is expected, related to the predominance of anaerobic glycolysis. However, Lac can similarly be observed in brain tumors and sometimes in healthy brain tissue [5, 7–9]. Lipids (Lip), also resonating at $\sim$1.3 ppm, often appear, as well, with reperfusion after hypoxia [9]. Cerebral energy metabolism is reflected by creatine (Cr), which resonates at $\sim$3.0 ppm and whose concentration in the brain is usually stable after the first year of life [9].

Normally, brain metabolite concentrations as well as metabolite concentrations ratios depend upon the age, in the pediatric population. Myoinositol (m-Ins) is the dominant brain metabolite in neonates. In older infants, Cho is normally the largest peak. As the child’s brain matures, Cr and NAA concentrations increase. Concordantly, Cho to NAA and Cho to Cr concentration ratios normally fall with the child’s age [10]. One rationale for the clinical focus of the present paper is to enhance pediatric neurodiagnostics through MRS, aiming towards greater accuracy in identifying cerebral hypoxia/ischemia versus other pathology, including brain tumors, which present differential diagnostic dilemmas.

1.2.1 Implications for cancer diagnostics

Broader implications for cancer diagnostics further motivate the present paper. Especially, it should be noted that hypoxic regions often occur within tumors. These regions are particularly resistant to radiation therapy as well as to chemotherapy. Moreover, hypoxia promotes genomic instability and is associated with the invasive/metastatic process [11]. Consequently, identifying hypoxic regions via MRS could contribute overall to better cancer treatment planning.

As will be addressed in more detail later in this paper, phosphocholine (PC), another MR visible metabolite which reflects hypoxia [12], has been detected and quantified via the fast Padé transform, FPT, [13, 14]. In vitro studies have indicated the importance of PC as a biomarker of pediatric brain tumors [15, 16], breast cancer [17] and of ovarian cancer [18].

Taking this wider view motivates efforts to garner maximal diagnostic information from MRS. One priority area is early ovarian cancer diagnostics, where the need for an effective in vivo MRS-based screening method has been underscored for many years  [19–21]. While technological progress is obviously important, mathematical advances in signal processing are the most critical for MRS, as we will demonstrate. To provide the needed context for comparison, we will first briefly examine the current signal processing method used in MRS.

1.3 The current signal processing method within MRS

A digitized free induction decay (FID) curve is the encoded MRS time signal which holds the entire metabolic content of the scanned tissue. However, the tightly packed, harmonically oscillating and exponentially attenuated waveforms are difficult to interpret directly from the FID. By mapping the FID into the frequency domain via mathematical transforms, a spectrum is generated which is more amenable to interpretation. Presently, in MR scanners this mapping is automatic, and is done using the fast Fourier transform (FFT). Mathematically, the generated Fourier spectrum is expressed as a single polynomial (a truncated Maclaurin series):

$$\begin{aligned} \hbox {FFT:}\; F_m =\sum _{n=0}^{N-1} {c_n \exp (-2\pi imn/N)},\quad 0 \le m \le N - 1, \end{aligned}$$

(1a)

where $2 \pi m/T$ is the fixed mth Fourier grid frequency. Here, the expansion coefficients are collected in the set of complex-valued time signal points $\{c_{n} \}$; further, T is the total signal duration or total acquisition time, $T = {N}\tau$, where N is the total signal length and $\tau$ is the sampling time (dwell time, sampling rate), which is the inverse of the bandwidth (BW). The variables $\hbox {exp}(\pm 2\pi imn/N)$ are the undamped sinusoids and cosinusoids $(nm\tau /T = {nm}/{N})$.

The FFT algorithm is speedy for signals lengths of the composite form, $N = 2^{m}\, (m = 1, 2, 3,{\ldots })$. However, the Fourier spectrum is linear, with unaltered noise being imported directly from the time domain to the frequency domain. The resolution of the FFT is low and determined solely by T as 1 / T. Since the Fourier spectrum is constructed only on the fixed grid points, there is no possibility for resolution improvement by interpolation. Moreover, no extrapolation is provided regarding information beyond the final encoded time signal point, $c_{N-1}$. A zero-filling procedure is typically performed. However, this merely produces sinc-type oscillations on the baseline of an FFT spectrum. Particularly for closely-spaced resonances, the sinc side lobes coupled with truncation artefacts can interfere, generating extraneous peaks or dips that are not part of the true information contained in the investigated FID [2].

The inverse Fourier transform (IFFT) from which the time signal is reproduced from the Fourier spectrum is:

$$\begin{aligned} \hbox {IFFT:}\; c_n =\frac{1}{N}\sum _{m=0}^{N-1} {F_m \exp (2\pi imn/N)},\quad 0 \le n \le N - 1. \end{aligned}$$

(1b)

Insofar as N is non-composite, i.e. any positive integer, the FFT and IFFT from (1a) and (1b) become, respectively, the discrete Fourier transform (DFT) and the inverse DFT, as denoted by IDFT.

Only a total shape spectrum (envelope) can be generated by the FFT, since it is non-parametric. The spectral parameters needed for quantification are not provided by the FFT. The next step has generally been to fit the Fourier envelope to a pre-selected set of Lorentzians, Gaussians or their linear combination mimicking the Voigt profile. Via least square free-parameter-adjusting techniques, attempts are made to estimate metabolite concentrations. However, as per Lanczos’ paradox, any number of pre-assigned peaks can be fitted to the given total shape spectrum, such that genuine resonances may be missed (under-modeling), while spurious structures may be produced (over-modeling) [1, 2].

1.3.1 Ensuing diagnostic dilemmas

Notably, several metabolites that are informative for neurodiagnostics and more broadly for cancer diagnostics, such as m-Ins, Lip, glutamate (Glu) and glutamine (Gln)¹ decay rapidly, such that they can be detected only at short echo times (TE) [22, 23]. Due to high spectral density, fitting becomes even more problematic at short TEs. Recall, Lac at $\sim$1.3 ppm generally appears with ischemia/hypoxia and, moreover, is often associated with malignancy. At short echo times, Lac and Lip overlap since they both resonate in the chemical shift region of $\sim$1.3 ppm. Difficulties in identifying these two diagnostically important resonances are frequently encountered at short TEs [23, 24]. The accurate assessment of Lac and Lip is recognized to be tenuous, due to the overlap of these resonances. On the other hand, the use of long TEs causes attenuation of the magnitude of all resonances [24].

Since spin-spin $T_2^*$-relaxation times of various metabolites differ, changes in TEs can affect peak height ratios. Consequently, reliance upon metabolite concentration ratios becomes particularly precarious. For example, in addition to NAA at $\sim$2.05 ppm, metabolites Glu and Gln within 2.1–2.5 ppm may contribute to the spectral area around 2.0 ppm at short TEs  [25]. It thus becomes more difficult to assess NAA levels at short TEs due to heavily overlapping resonances that cannot be reliably identified using the FFT followed by fitting. These difficulties regarding the relation of metabolite concentration ratios and TEs are very relevant for pediatric neurodiagnostics  [5] and for cancer diagnostics, in general [26].

1.4 Advanced signal processing for MRS through the fast Padé transform

Through the fast Padé transform, FPT, many of these problems can be surmounted. In the FPT, a quotient of two frequency-dependent polynomials, $P_K /Q_K$ is extracted from the encoded MRS time signal. A total shape spectrum is produced which is not limited to the pre-assigned grid of the sweep frequencies, such that interpolation is provided by the FPT [1].

An extra degree of freedom results from the numerator $(P_{K})$ and denominator $(Q_{K})$ polynomials, and this helps cancel noise from the Padé spectrum $P_K /Q_K$. This is not surprising, since the common experience is that when e.g. two observables A and B are measured in any experiment or numerically computed with finite precision, errors in A and B are largely cancelled in the ratio A / B which is often used for data interpretation and analysis. The polynomial $P_{K }$ reduces noise through the “moving average”, as per the autoregressive moving average (ARMA) process from statistical mathematics. In fact, the FPT and ARMA are equivalent  [1].

Extrapolation in the FPT is forthcoming from the denominator polynomial $Q_{K}$. The prediction coefficients from the ARMA process are the same as the expansion coefficients of polynomial $Q_{K}$. New signal points $\{c_{n}\}$ for $n>N - 1 (t>T)$ can be computed using these expansion coefficients. Consequently, it becomes possible to predict time signal data at $t=n\tau \;\hbox {for}\;n > N - 1$, i.e. beyond the total acquisition time T. Due to these properties of extrapolation, interpolation and noise suppression, resolution and Signal-noise ratio (SNR) in MRS are improved through the FPT.

1.4.1 Solving the quantification problem

The solution to quantification includes K which is the model order, together with the 4K real-valued spectral parameters (K complex frequencies $\omega _{k}$ and K associated complex amplitudes $d_{k,} 1 \le k \le K)$ for the K resonances. This is a complete parametrization of the encoded FID set $\{c_{n}\}$, given through the sum of K physical resonances, via the geometric progression:

$$\begin{aligned} c_n =\sum _{k=1}^K {d_k } \hbox {exp(}i\omega _k \tau n),\,\, \hbox {Im}(\omega _k )>0\,\, (0\le n\le N-1). \end{aligned}$$

(2)

Recall that since the FID set $\{c_{n}\}\,\, (0 \le n \le N - 1)$ is known, whereas $\{\omega _{k}, d_{k} \}\,\, (1 \le k \le K)$ need to be found, this is an inverse problem. The exponentials in (2) are complex damped harmonics. This harmonic inversion (2) is linear in $\{d_{k}\}$ and non-linear in $\{\omega _{k}\}$. For the given Maclaurin expansion, the Padé spectrum or the response function R (u) in e.g. its diagonal form, is completely and uniquely determined by the rational function as a ratio of two polynomials $P_{K}$ and $Q_{K}$ of the common degree K:

$$\begin{aligned} R(u)=\frac{P_K (u)}{Q_K (u)}, \quad u=\exp (i\omega \tau ). \end{aligned}$$

(3)

This can be obtained for any real linear frequency $\nu$, related to the angular (circular) frequency $\omega$ by $\omega = 2 \pi \nu$. For the encoded FID set $\{c_{n}\}$, polynomials $P_{K}$ and $Q_{K}$ are determined by solving a single system of linear equations deduced from:

$$\begin{aligned} \sum _{n=0}^{N-1} {c_n } z^{-n}=\frac{P_K (u)}{Q_K (u)}, \quad u=z\,\, \hbox {or } \,u=z^{-1}. \end{aligned}$$

(4)

By rooting the denominator polynomial $Q_{K}$, the fundamental frequencies $\{\omega _{k }\}$ are extracted:

$$\begin{aligned} Q_{K} (u) = 0 \Rightarrow \hbox { Spectral pole frequencies }\,\, \omega _{k }\,\, (1 \le k \le K). \end{aligned}$$

(5)

The amplitudes $\{d_{k} \}$ are deduced through the Cauchy analytical formula for the residues of $P_{K} /Q_{K,}$ taken at the frequency of the kth pole $\omega =\omega _{k }$. When the spectrum $P_{K}/Q_{K}$ is non-degenerate, i.e. comprised of simple poles alone, the result for $d_{k}$ is given by:

$$\begin{aligned} d_k =\frac{P_K (u_k )}{{Q}'_K (u_k )},\quad {Q}'_K (u)=\frac{\hbox {d}}{\hbox {d}u}Q_K (u), \quad u_k =\exp (i\omega _k \tau ), \quad 1\le k\le K. \end{aligned}$$

(6)

The reconstructed amplitudes $\{d_{k}\}$ should be corrected for the $T_{1 }$- (spin-lattice) and $T_{2}^{*}$-relaxation times insofar as the FIDs have not fully decayed to zero. The kth metabolite concentration is then computed from these corrected amplitudes $\{d_{k}\}$.

Within the FPT, for the same input finite $z-$transform given by the lhs of (4), there are two versions: the $\hbox {FPT}^{(+)}$and $\hbox {FPT}^{(-)}$, with their initial convergence regions inside $({\vert }z{\vert }< 1)$ and outside $({\vert }z{\vert }> 1)$ the unit circle, respectively. The independent variable u used in (3)–(6) is either variable $z=\exp (i\omega \tau )$ or $z^{-1}=\exp (-i\omega \tau )$, corresponding to $\hbox {FPT}^{(+)}$ or $\hbox {FPT}^{(-)}$, respectively.

Especially within in vivo encoded MRS time signals, a major obstacle is the presence of noise. Moreover, when the spectra are dense, the number of genuine metabolites is a very small percentage of the total number of retrieved resonances. Through the Signal-noise separation (SNS) procedure by which pole-zero coincidences (Froissart doublets) are identified, the FPT algorithm can distinguish genuine from spurious resonances [27, 28]. The mechanism by which this occurs will be elaborated in Sect. 2.2 by an analytical derivation.

1.4.2 Proof-of-principle studies

By exact quantum-mechanical spectral analysis, the FPT accurately examines MRS time signals, yielding quantitative information for a large number of metabolites using synthesized time signals associated with data from cancerous, benign and/or normal brain, prostate, breast and ovary, as demonstrated in benchmarking studies  [2, 13, 21, 26, 29–40]. In investigations applying the FPT to synthesized MRS time signals that were very similar to those encoded in vivo from the brain of a healthy volunteer at 1.5 T, proof-of-concept validation was provided. Namely, the spectral parameters were exactly reconstructed from which the concentrations of metabolites were precisely computed, including for overlapping resonances whose chemical shifts differed by 0.001 ppm or less [2, 29–31].

An MRS study on FIDs encoded from the standard General Electric (GE) phantom head provided an additional proof-of-principle for the FPT  [41]. Therein, extensive examination of the convergence process substantiated the stability of the reconstructed spectral parameters. Statistical analysis, via “parameter averaging” in the FPT confirmed the accuracy and precision of the reconstructed complex fundamental frequencies $\{\omega _{k}\}$ and the associated complex amplitudes $\{d_{k}\}$, including those in the dense regions of the spectrum, where very small and/or very closely overlapping resonances were located.

1.4.3 Applications of the FPT to in vivo encoded MRS time signals

In addition to the earlier cited proof-of-principle studies on synthesized FIDs and time signals encoded from the GE head phantom, the FPT has also been applied to process MRS time signals encoded in vivo on a 1.5 T MR scanner from pediatric brain tumor [14], as well as from normal human brain [1, 2, 42–46]. Further, the FPT clearly provided better resolution than the FFT for total shape spectra generated from MRS time signals encoded from healthy human brain at high magnetic field (4 and 7 T) and clinical scanners (1.5 T). Even more remarkable is the parametric capability of the FPT, particularly in spectrally dense chemical shift regions, where extremely closely-overlapping resonances were resolved and quantified. This includes several diagnostically important metabolites, some of which are identified cancer biomarkers [2, 14].

A practical challenge encountered very frequently in the MRS literature is incomplete suppression of the giant water resonance. Using a step function within the non-parametric FPT, an information-preserving procedure for suppressing residual water via windowing was introduced and validated in our study of pediatric brain tumors [14]. This windowing procedure is superior to the customary Hankel–Lanczos Singular Value Decomposition (HLSVD) procedure, which involves fitting by artificial resonances that add further spuriousness to the already noisy MRS time signal. It was confirmed through subsequent parametric analysis via the FPT that the spectral components within the spectral region of interest (SRI) were not affected by this windowing procedure. It was only at the edges outside the SRI that some expected, but inconsequential discrepancy was found between the water residual suppressed and unsuppressed Padé reconstructions. This windowing procedure was thus seen as helping to bring us further towards more widespread implementation of the FPT in the clinical setting. Parametric signal processing within a chosen SRI can, of course, be performed in any selected window. Advantageously, this can be done without water residual and without any explicit filtering of the content of the chosen window. Such a more effective procedure of altogether avoiding the water residual, which is a nuisance in MRS, will be a part of the present study.

In our most recent work [47], an iterative averaging procedure was introduced in the FPT, with the aim of providing denoised non-parametrically computed total shape spectra from FIDs encoded in vivo using a 1.5 T clinical scanner. This procedure was shown to stabilize envelope spectra which for different model orders K exhibited many large noise-like spikes. These findings motivate further investigation of the Padé-based iterative averaging methodology with the aim of fully benchmarking this stabilization method for clinical use.

1.5 Aim of the present paper

We now will apply the FPT to in vivo MRS time signals encoded using a clinical 1.5 T scanner from a pediatric patient who had suffered cerebral asphyxia. A comparison will be made between the FPT and DFT regarding resolution performance on the total shape spectra or envelopes. We will extensively test the parametric version of the Padé-based iterative averaging procedure for generating not only total shape spectra, but also for reconstructing spectral parameters. In other words, as an alternative to Ref. [47], all the average envelopes will presently be generated from the parametrically reconstructed iterates. One of the aims would thus be to thereby overcome a critical obstacle of all parametric methods: extreme sensitivity of spectral parameters to any change of the model order K. Detailed examination of the convergence of the Padé-reconstructed spectral parameters will be undertaken, within the framework of the iterative averaging procedure. The possibility of a further upgrade of the water suppression procedure will also be examined through the parametric FPT, with the aim of bypassing the need for windowing, as stated. Overall, this paper will bring together a full, multi-faceted testing of the parametric Padé-based iterative averaging procedure with the aim of its validation for broader applications in the clinical setting. This could directly contribute to pediatric neurodiagnostics through MRS, with possibilities to more accurately identify hypoxia/ischemia and the effects of cerebral asphyxia and to better distinguish these from other pathology. This work aims, as well, to soon extend to other applications of in vivo MRS diagnostics, especially, for cancer diagnostics and patient care within oncology. The generic relevance of this approach for the basic sciences and technology is also foreseen, from both a practical and theoretical standpoint. The latter is the focus of the next section of this paper.

2 Theory of quantum mechanical spectral analysis

2.1 Why is the fast Padé transform a quantum-mechanical spectral analyzer?

There are several reasons why the FPT is a quantum-mechanical spectral analyzer. These can be ascertained according to Eqs. (2), (4), (5) and (6). The first reason is the equivalence of form (2) for every data point in the time signal $\{c_n \}$ with the quantum-mechanical auto-correlation function, $(\Phi _0 |\Phi _n )$. The latter is defined by projecting the Schrödinger non-stationary state $\Phi _n$ of the system at time $n \tau$ onto the initial state $\Phi _0$, with an asymmetric scalar product $(a{\vert }b) = (b{\vert }a)$. The second reason is that the finite $z-$ transform is the quantum-mechanical finite-rank Green function $G(z^{-1})=\sum _{n=0}^{N-1} {c_n } z^{-n}$. According to (4), this corresponds to the spectrum $P_K /Q_K$ in the FPT. The third reason is that in the FPT, the fundamental frequencies $\{\omega _k \}$ from (5) are equivalent to the quantum-mechanical eigen frequencies from the stationary Schrödinger eigen value problem, $\Omega \Psi _k =\omega _k \Psi _k$. Here, $\Omega$ is a non-Hermitean system operator, i.e. a complex “Hamiltonian”. This is due to the fact that the corresponding Schrödinger secular equation, which is equivalent to the Schrödinger eigen value problem, is the same as the characteristic polynomial equation $Q_K =0$ from (5) in the FPT. The fourth reason is that the fundamental amplitudes $\{d_k \}$ from (6) in the FPT are equivalent to $(\Phi _0 |\Psi _k )^{2}$, which is their quantum-mechanical counterpart. This equivalence is due to the uniqueness of the amplitudes $\{d_k\}$ for the same frequencies $\{\omega _k\}$. In other words, various algorithms may differ in how they generate the amplitudes, but they must give the same results for $\{d_k\}$ insofar as the reconstructed sets for $\{\omega _k\}$ are identical [1].

Compared to directly solving the Schrödinger eigen value problem on a given set of basis functions, the FPT provides a twofold advantage. The first is with respect to the amplitudes and the second is for Signal-noise separation, SNS. As to the former, the Padé amplitudes $\{d_k \}$ from (5) completely bypass computing the wave functions $\{\Psi _k \}$ required in quantum mechanics for $d_k =(\Phi _0 |\Psi _k )^{2}$. On the one hand, eigen frequencies $\{\omega _k \}$ from the non-stationary Schrödinger equation are variational, such that their estimates have no first-order errors. On the other hand, however, eigen states $\{\Psi _k \}$ are non-variational. Consequently, the latter contain first-order errors that undermine the accuracy of the amplitudes $(\Phi _0 |\Psi _k )^{2}$. By employing a linear combination of a set of reconstructions for the amplitudes of the original type $(\Phi _0 |\Psi _k )^{2}$ these errors can usually be reduced [1]. However, with the FPT, such errors are altogether avoided from the outset.

Regarding SNS, the FPT has a unique capability. As noted, it extricates genuine from spurious resonances by unequivocally identifying Froissart doublets, which are the coincident spectral poles and zeros. The latter are the solutions of the characteristic equations, $Q_{K} = 0$ and $P_{K} = 0$, respectively. The mechanism by which SNS is achieved is presented in the following subsection.

2.2 The mechanism of pole-zero cancellation in the FPT$^{(+)}$

The phenomenon of Froissart doublets, with the underlying pole-zero cancellation, is so vital for the concept of Signal-noise separation, SNS, that its mechanism should be clearly illuminated by analytical means before confirming it in numerical computations of envelope spectrum $P_K^+ (z)/Q_K^+ (z)$ and its components. The most instructive way towards this goal is to consider a model spectrum in the $\hbox {FPT}^{(+)}$ consisting of a single genuine Lorentzian resonance $L_1^+ (z)=d_1^+ z/(z-z_1^+ )$. Here, $z_1^+$ is the genuine signal pole and $d_1^+$ is the corresponding amplitude. Since there is only one resonance, this latter single expression for $L_1^+ (z)$ represents both the total and component shape spectra, rewritten as $L_1^+ (z)=P_1^+ (z)/Q_1^+ (z)$ where $P_1^+ (z)=d_1^+ z$ and $Q_1^+ (z)=z-z_1^+$. The associated model time signal $c_{n}$ has only one component via $c_n =d_1 \exp (in\, \tau \omega _1^+ )$, where $\omega _1^+ =[1/(i\tau )] \hbox { ln }z_1^+$. For a chosen dwell time $\tau$, the signal $\{c_{n}\}$ is sampled for  0 $\le n \le N - 1$, where N is the total signal length. Once the N time signal points $c_{n}\,\, (0 \le n \le N - 1)$ are sampled, the knowledge about this FID being comprised of only one component is deliberately forgotten. This mimics the typical situation in MRS, where at the end of encoding, only the N data points $c_{n}\,\, (0 \le n \le N - 1)$ become available, whereas the components of each $c_{n}$ are unknown and represent the subject of reconstruction by spectral analysis (quantification).

Since we do not know that the model spectrum has a single component, the application of the $\hbox {FPT}^{(+)}$ would result, for the simplest case, in generating one extra Lorentzian $L_2^+ (z)=d_2^+ z/(z-z_2^+ )$ so that the predicted spectrum and the reconstructed FID would be $L^+ (z)=L_1^+ (z)+L_2^+ (z)$ and $\bar{{c}}_n =d_1^+ \exp (in\,\tau \omega _1^+ )+d_2^+ \exp (in\,\tau \omega _2^+ )$, respectively, where $\omega _2^+ =[1/(i\tau )]\, \hbox {ln}\,z_2^+$. The second Lorentzian has a pole $z_2^+$ and the corresponding amplitude is $d_2^+$. However, the input signal $c_{n}$ “knows” that it possesses merely a single component via $c_n =d_1 \exp (in\,\tau \omega _1^+ )$ and, therefore, the extra harmonic $d_2^+ \exp (in\,\tau \omega _2^+ )$ in the predicted time signal $\bar{{c}}_n$ ought to be false, i.e. spurious. To show this, we assume that the predicted 2-component spectrum $L^+ (z)$ is non-degenerate, i.e. its two poles are unequal, $z_2^+ \ne z_1^+$, which implies $d_2^+ \ne d_1^+$. With no approximation, it is convenient to cast $L^+ (z)$ into the form $L^+ (z)= [(z-z_2^+ )L_1^+ (z)+d_2^+ z]/(z-z_2^+ )$. Here, close to the second pole $z_2^+$, the 1st Lorentzian $L_1^+ (z)$ is not written as a partial fraction since therein $L_1^+ (z)$ is a regular, smooth function. Thus, in the vicinity of the 2nd pole, we can set $L_1^+ (z)\approx L_1^+ (z_2^+ )$ and rewrite the 2-component spectrum $L^+ (z)$ in a way which explicitly exhibits only the polar structure of the 2nd Lorentzian via $L^+ (z)\approx P^+ (z)/Q^+ (z)$, where $P^+ (z)=(z-z_2^+ )L_1^+ (z_2^+ )+d_2^+ z$ and $Q^+ (z)=z-z_2^+$.

The foregoing will enable us to see what actually happens with the extra Lorentzian $L_2^+ (z)$. To this end, we first assume that there is a relationship between the two amplitudes $d_1^+$ and $d_2^+$, e.g. the magnitude of the latter is much smaller than that of the former, i.e. ${\vert }d_2^+ {\vert }<< {\vert }d_1^+ {\vert }$, or equivalently, ${\vert }\rho ^{+}{\vert }<< 1$, where $\rho ^{+}$ is the amplitude ratio, $\rho ^{+}=d_2^+ /d_1^+$. Since ${\vert }d_2^+ {\vert }$ is negligible relative to ${\vert }d_1^+ {\vert }$, it is tempting to immediately ignore the 2nd Lorentzian $d_2^+ z/(z-z_2^+ )$, compared to the first component $d_1^+ z/(z-z_1^+ )$ in their sum $L^+ (z)=d_1^+ z/(z-z_1^+ )+d_2^+ z/(z-z_2^+ )$. However, this might be justified only away from the extra pole $z_2^+$, but not close to it, because in the vicinity of $z_2^+$, the 2nd Lorentzian $L_2^+ (z)=d_2^+ z/(z-z_2^+ )$ has a peak.

To peer into the structure of the additional Lorentzian $L_2^+ (z)$, the presence of the numerator polynomial $P^+ (z)$ becomes essential, and to explore its feature we solve the characteristic equation $P^+ (z)=0.$The ensuing zero is denoted by $z_{2,P}^+$, which is given by $z_{2,P}^+ =z_{2,Q}^+ /[1+(z_{1,Q}^+ -z_{2,Q}^+ )\rho ^{+}$] where $z_{1,Q}^+ \equiv z_1^+$ and $z_{2,Q}^+ \equiv z_2^+$. If here we use the assumption ${\vert }\rho ^{+}{\vert }<< 1$ and retain only the first 2 terms in the binomial series, it follows that $z_{2,P}^+ \approx z_{2,Q}^+ [1-(z_{1,Q}^+ -z_{2,Q}^+ )\rho ^{+}]$. We have $z_{1,Q}^+ -z_{2,Q}^+ \ne 0$ for the considered non-degenerate spectrum, but since it is assumed that ${\vert }\rho ^{+}{\vert }<< 1$, we can still neglect the term $(z_{1,Q}^+ -z_{2,Q}^+ )\rho ^{+}$ in the square brackets, and this leads to $z_{2,P}^+ \approx z_{2,Q}^+$. Hence, the small value of the 2nd magnitude ${\vert }d_2^+{\vert }$ from the extra Lorentzian $L_2^+ (z)$ compared to the 1st magnitude ${\vert }d_1^+ {\vert }$ from $L_1^+ (z)$ implies that the 2nd pole $z_{2,Q}^+$ and the zero $z_{2,P}^+$ are approximately the same (pole-zero coincidence).

Conversely, let us now assume that there is a pole-zero coincidence $z_{2,Q}^+ \approx z_{2,P}^+$ in the 2nd Lorentzian $L_2^+ (z)$, and we aim to estimate the relationship between the 2nd and the 1st magnitudes, ${\vert }d_2^+ {\vert }$ and ${\vert }d_1^+{\vert }$, respectively. This can be done by using the formula for the zero $z_{2,P}^+$ via $z_{2,P}^+ =z_{2,Q}^+ /[1+(z_{1,Q}^+ -z_{2,Q}^+ )\rho ^{+}$] to extract the 2nd pole as the expression $z_{2,Q}^+ =z_{2,P}^+ /\eta ^{+}$ where $\eta ^{+}=(1-\rho ^{+}z_{2,P}^+ )/(1-\rho ^{+}z_{1,Q}^+ )$. It follows from here that a pole-zero coincidence $z_{2,Q}^+ \approx z_{2,P}^+$ would occur in the 2nd Lorentzian $L_2^+ (z)$, provided that $\eta ^{+}\approx 1,$ which is satisfied for ${\vert }\rho ^{+}{\vert }<< 1$, i.e. ${\vert }d_2^+ {\vert }<<{\vert }d_1^+ {\vert }$. Therefore, when the pole $z_{2,Q}^+$ and $z_{2,P}^+$ coincide, the extra magnitude ${\vert }d_2^+ {\vert }$ is much smaller than ${\vert }d_1^+ {\vert }$.

Formally, the relation $\eta ^{+}\approx 1$ which gives ${\vert }d_2^+ {\vert }<<{\vert }d_1^+ {\vert }$, would also hold if, alternatively, the numerator cancels the denominator in the quotient $(1-\rho ^{+}z_{2,P}^+ )/(1-\rho ^{+}z_{1,Q}^+ )$ from the definition of $\eta ^{+}$. This would occur for $z_{2,P}^+ =z_{1,Q}^+$ which, by way of the assumed pole-zero coincidence $z_{2,Q}^+ \approx z_{2,P}^+$ implies $z_{2,Q}^+ =z_{1,Q}^+$. However, the expression $z_{2,Q}^+ =z_{1,Q}^+$ contradicts the assumption that the computed 2-component spectrum $L^+ (z)$ is non-degenerate. Thus, it is the first mentioned line of thought which is correct, stating that $\eta ^{+}$ would be close to unity only if ${\vert }\rho ^{+}|<< 1$, or equivalently, ${\vert }d_2^+ {\vert }<< {\vert }d_1^+ {\vert }$, as in the above derivation.

Overall, if the predicted 2-component spectrum $L^+ (z)=L_1^+ (z)+L_2^+ (z)=d_1^+ z/(z-z_{1,Q}^+ )+d_2^+ z/(z-z_{2,Q}^+ )$ is going to reconstruct the input 1-component spectrum $L_1^+ (z)$, the extra Lorentzian $L_2^+ (z)$ must vanish. As we have already stated, this cannot occur by simply dropping $L_2^+ (z)=d_2^+ z/(z-z_2^+ )$ on the basis of the assumption ${\vert }d_2^+ {\vert }<< {\vert }d_1^+ {\vert }$. An alternative is to rewrite $L^+ (z)$ as $L^+ (z)=L_1^+ (z) {S^{+}}(z)$, where $L_1^+ (z)$ is the genuine and $S^{+}(z)$ is the spurious part with $S^{+}(z)=(1+\rho ^{+})(z-z_{2,P}^+ )/(z-z_{2,Q}^+ )$. Here, due to pole-zero confluence, $z_{2,Q}^+ \approx z_{2,P}^+$, the denominator $z-z_{2,Q}^+$ with the extra pole $z_{2,Q}^+$ annihilates the numerator $z-z_{2,P}^+$ which contains the extra zero $z_{2,P}^+$. This explicitly exhibits pole-zero cancellation , and the result is $S^{+}(z)\approx 1+\rho ^{+}$ which further simplifies to $S^{+}(z)\approx 1$, since ${\vert }\rho ^{+}{\vert }<<$ 1. It is in this manner that the spurious contribution $S^{+}(z)$ is washed out, thus enabling the $\hbox {FPT}^{(+)}$ to reconstruct the input spectrum, $L^+ (z)=L_1^+ (z)S^{+}(z)\approx L_1^+ (z)$. Furthermore, for ${\vert }d_2^+ {\vert }<< {\vert }d_1^+ {\vert }$, it is possible at once to neglect the 2nd term $d_2^+ \exp (in\, \tau \omega _2^+ )$ in the predicted FID, $\bar{{c}}_n =d_1^+ \exp (in\, \tau \omega _1^+ )+d_2^+ \exp (in\, \tau \omega _2^+ )$, since the harmonic $\exp (in\, \tau \omega _2^+ )$ is non-singular at $z_2^+$. Therefore, the predicted time signal simplifies to $\bar{{c}}_n \approx d_1^+ \exp (in\, \tau \omega _1^+ )$, which amounts to reconstruction of the input FID, $c_n = d_1^+ \exp (in\, \tau \omega _1^+ )$, i.e. $\bar{{c}}_n \approx c_n$.

It could be argued that pole-zero cancellation might not be the only mechanism for reduction of the 2-component prediction $L^+ (z)$ to the exact input spectrum $L_1^+ (z)$. The alternative could be that the expansion coefficient $p_2^+$ of the predicted numerator polynomial is zero. More generally, one could contend that the exact result in the $\hbox {FPT}^{(+)}$ for the case of K resonances ($K = 1, 2, 3,{\ldots }$), might also be obtained if instead of pole-zero cancellations, all the coefficients $p_k^+$ become zero for $k > K$. To investigate this, we rewrite the predicted 2-component spectrum $L^+ (z)$ as $L^+ (z)=(p_0^+ +p_1^+ z+p_2^+ z^{2})/[(z-z_{1,Q}^+ )(z-z_{2,Q}^+ )]$, where $p_0^+ =0$, $p_1^+ =- (d_1^+ z_{2,Q}^+ +d_2^+ z_{1,Q}^+ )$ and $p_2^+ =d_1^+ +d_2^+$. Evidently, $p_2^+ \ne 0$. Thus, the said possibility as a confounding factor ($p_2^+ =0)$, in fact, does not exist. Therefore, pole-zero cancellation is the only mechanism for reduction of the prediction $L^+ (z)$ to the exact input spectrum $L_1^+ (z)$.

This completes the demonstration of exact reconstruction of the input time signal and spectrum in the $\hbox {FPT}^{(+)}$. The expounded analytical proof uncovers the mechanism of achieving this result: (a) by eliciting the twofold signature (pole-zero coincidence and near-zero amplitude) of a Froissart doublet, which is a pole-zero spurious pair, as well as (b) by explicitly showing how a pole-zero coincidence yields pole-zero cancellation in the reconstructed spectrum. Moreover, the near-zero amplitude of the exemplified spurious resonance enables the exact reconstruction of the input time signal. We shall now proceed to the application of the FPT for processing an actual in vivo encoded MRS time signal.

3 Methods

3.1 MRS time signal acquisition

The MRS encoding was made from the parietal temporal brain region of an 18 month-old child who had suffered cerebral asphyxia. A 1.5 T GE clinical scanner at the Astrid Lindgren Children’s Hospital in Stockholm was used to encode the MRS time signals, which contained 512 data points. The bandwidth, BW, was 1000 Hz, and the Larmor frequency was $\nu _{\mathrm{L}} = 63.87\,\hbox {MHz}$ corresponding to the magnetic field strength $B_{0}= 1.5$ tesla $(B_{0} = 1.5\,\hbox {T})$. The sampling time $\tau$ was 1 ms $(\tau = 1/\hbox {BW} = 1\,\hbox {ms})$. Single-voxel proton MRS with the point-resolved spectroscopy sequence (PRESS) was used. The repetition time (TR) was 2000 ms. A total of 128 encoded FIDs were averaged to improve SNR. Echo times were 22, 136 and 272 ms. In the present paper, all analysis was performed based on the encoding at TE$\,=\,$272 ms. The Fourier analysis was done with zero-filling, so as to double the original FID length, as is the conventional practice within the FFT. Consequently, the total signal length N was 1024, so that $T = N\tau = 1024\,\hbox {ms}$. For consistency, this total signal length $N = 1024$ will also be used for both the FFT (or DFT) and the FPT. Water was partially suppressed through encoding with the use of the standard spin-echo procedure. The Regional Ethics Committee, Karolinska Institutet (Dnr # 2007/708-31/1) stated that they found no ethical issues to preclude implementation of this research.

3.2 Reconstructions

The DFT and the FPT were employed to process the encoded FID. The FID phase was corrected via multiplication of the encoded set $\{c_n \} (0\le n\le 511)$ by $\hbox {exp}(i\varphi _0 )$ via $c_n^{(0)} =c_n\, \hbox {exp}(i\varphi _0 )$. Here, $\varphi _0$ is the zero-order phase which was selected to be 1.7499 rad. This value of $\varphi _0$ is the result of the calculation of the minimum of the real part of the DFT spectrum, $\hbox {min}\{\hbox {Re}(F_m) \}_{m=0}^{511}$, for the originally encoded, raw, phase uncorrected time signal $\{c_n \}$ with no zero-filling. With this phase correction, the FID data set $\{c_n^{(0)} \}$ is relabeled as $\{c_n \}$. Hereafter, only the phase corrected FID reannotated as $\{c_n \}$ will be used.

3.2.1 Non-parametric reconstructions: Comparison of the DFT and the FPT

By using (1a), the spectrum was reconstructed at the fixed Fourier grid frequencies in the DFT, where N is truncated to a non-composite partial signal length $N_{\mathrm{P}} = 760$. For the non-parametric Padé-based reconstructions, we used both variants $\hbox {FPT}^{(\pm )}$ where the variable u was taken to be $z^{\pm 1}$, respectively. All reconstructions from the $\hbox {FPT}^{(+)}$ were produced by the $\hbox {FPT}^{(-)}$.

In the $\hbox {FPT}^{(\pm )}$ the expansion coefficients of the polynomials $P_K^\pm$ and $Q_K^\pm$ are determined first from the time signal $\{c_{n}\}$. This immediately gives the non-parametrically computed total shape spectra as the ratios $P_K^\pm /Q_K^\pm$ at any sweep frequency $\nu$. If all the phases $\varphi _k^\pm$ of the reconstructed FID amplitudes $d_k^\pm =\left| {d_k^\pm } \right| \exp (i\varphi _k^\pm )$ were equal to zero, $\varphi _k^\pm =0\, (1\le k \le K)$, its real and imaginary parts, Re ($P_K^\pm /Q_K^\pm )$ and $\hbox {Im}(P_K^\pm /Q_K^\pm )$, would be purely absorptive and dispersive, respectively. However, in all encoded MRS time signals, the phases $\varphi _k$ of the FID amplitudes $d_{k}$ are typically non-zero $(\varphi _k \ne 0)$, the reason being that dephasing occurs during the course of encoding. Consequently, the reconstructed values $\varphi _k^\pm$ are also such that $\varphi _k^\pm \ne 0$. Thus, absorption and dispersion lineshapes are mixed in both $\hbox {Re}(P_K^\pm /Q_K^\pm )$ and $\hbox {Im}(P_K^\pm /Q_K^\pm )$.

3.2.2 Parametric processing with the $\hbox {FPT}^{(+)}$

For the parametric reconstructions, we will present the results for the $\hbox {FPT}^{(+)}$ alone. Cross-checking with the $\hbox {FPT}^{(-)}$ has been performed, as well.

The roots of the characteristic equations of the numerator $(P_K^+ )$ and denominator $(Q_K^+ )$ polynomials give the zeros and poles of the Padé spectrum, $P_K^+ /Q_K^+$, respectively. This is the case because $P_K^+ /Q_K^+$ has only polar singularities, namely, the roots of $Q_K^+$ are the poles of $P_K^+ /Q_K^+$ [1]. In other words, the Padé spectrum is a meromorphic function  [1]. The fundamental frequencies $\omega _k^+ = [1/(i\tau )]\ln (z_k^+ )$ were reconstructed via the roots of the denominator characteristic equation $Q_K^+ (z)=0$. The amplitudes $d_{k}^{+}$ were generated through (6) [1].

We will present the component spectra in two different modes. Firstly, we have the “usual” (U) component spectra which is a mixture of absorption and dispersion components. Therein, the amplitudes $\{d_k^+ \} (1\le k \le K)$ are all complex-valued since, as noted, their phases $\varphi _k^+$ are non-zero. Particularly in spectrally dense regions, the “absorption” components often appear as skewed Lorentzians. In the so-called “ersatz” (E) mode, the reconstructed phases $\varphi _k^+$ are set “by hand” to zero, such that $\varphi _k^+ \equiv 0 (1\le k \le K)$. Consequently, the interference effects are eradicated via the said external suppression. This generates pure absorptive Lorentzians, that can be helpful for visualization purposes. The “ersatz” mode of the component spectrum for the kth resonance is:

$$\begin{aligned} \left( {\frac{P_K^+ (z)}{Q_K^+ (z)}} \right) _k^{\mathrm{E}} \equiv \quad \frac{\left| {d_k^+ } \right| z}{z-z_{k,Q}^+ }\, (\hbox {Ersatz component } k) \end{aligned}$$

(7)

where $\{z_{k,Q}^+ \}$ is the set of zeros of the characteristic equation $Q_K^+ (z)=0$ with $z_{k,Q}^+ =\exp (i\omega _{^{k,Q}}^+ \tau )$. From now on, $z_k^+$ and $\omega _k^+$ are denoted as $z_{k,Q}^+$ and $\omega _{k,Q}^+$, respectively, where the subscript Q refers to the polynomial $Q_K^+ (z)$. Similarly, the harmonic variable $z_{k,P}^+$ represents the root of the polynomial $P_K^+ (z).$ We obtain the “usual” mode of the component spectra as:

$$\begin{aligned} \left( {\frac{P_K^+ (z)}{Q_K^+ (z)}} \right) _k^{\mathrm{U}} \equiv \quad \frac{d_k^+ z}{z-z_{k,Q}^+ }\, (\hbox {Usual component }k). \end{aligned}$$

(8)

In order to proceed from (8) to (7), i.e. by setting $\varphi _k^+ =0$, we replace $d_k^+ \equiv \left| {d_k^+ } \right| \exp (i\varphi _k^+ )$ with $\left| {d_k^+ } \right|$. Thus, the real part of the component shape spectra of the ersatz form $\hbox {Re}(P_K^+ /Q_K^+ )_k^{\mathrm{E}}$ from (7) is completely in the absorption mode. In contrast, the usual form $\hbox {Re}(P_K^+ /Q_K^+ )_k^{\mathrm{U}}$ from (8) contains both absorption and dispersion modes [14].

The $T_2^*$-relaxation time in the $\hbox {FPT}^{(+)}$ for the kth component is denoted by $T_{2k}^{*+}$. This relates to the imaginary part of the reconstructed complex frequency $\omega _{k,Q}^+$ or $\nu _{k,Q}^+$ via $T_{2k}^{*+} =1/\{\hbox {Im}(\omega _{k,Q}^+ )\}=1/\{2\pi \hbox {Im}(\nu _{k,Q}^+ )\}$. We use this quantity in the expressions for peak heights $(H_k^+ )^{\mathrm{U}}$ and $(H_k^+ )^{\mathrm{E}},$ respectively, as:

$$\begin{aligned}&(H_k^+ )^{\mathrm{U}}\equiv \frac{d_k^+ }{D_k^+ }, \quad (H_k^+ )^{\mathrm{E}}\equiv \frac{\left| {d_k^+ } \right| }{D_k^+ }; D_k^+ =1-\exp (-\tau /T_{2k}^{*+} ), 0<D_k^+ <1, \end{aligned}$$

(9a)

$$\begin{aligned}&\hbox {Re}(H_k^+ )^{\mathrm{U}}=(\left| {d_k^+ } \right| /D_k^+ )\cos (\varphi _k^+ )=(H_k^+ )^{\mathrm{E}}\cos (\varphi _k^+ ), \end{aligned}$$

(9b)

where $(H_k^+ )^{\mathrm{E}}$ is real-valued.

The peak heights $H_k^{\mathrm{c}+}$ of an absorptive conventional Lorentzian, directly expressed via $\omega$ instead of z as $\left| {d_k^+ } \right| \{(\hbox {Im}\omega _{k,Q}^+ )/\tau \}/\{(\omega -\omega _{k,Q}^+ )^{2}+(\hbox {Im}\omega _{k,Q}^+ )^{2}\}$ are given by $H_k^{\mathrm{c}+} \equiv \left| {d_k^+ } \right| /(\tau \hbox {Im}\omega _{k,Q}^+ )$. This latter result can also be deduced from (9a) for narrow resonances (long relaxation times). Thus, for small $\tau /T_{2k}^{*+}$, the series expansion for $\exp (-\tau /T_{2k}^{*+} )$ yields $D_k^+ \approx 1-(1-\tau /T_{2k}^{*+} +\cdots )\approx \tau /T_{2k}^{*+} =\tau \hbox {Im}\omega _{k,Q}^+$. It, therefore, follows from (9a), that $\left| {d_k^+ } \right| /D_k^+ \approx \left| {d_k^+ } \right| /(\tau \hbox {Im}\omega _{k,Q}^+ )=H_k^{\mathrm{c}+}$.

The explicit expressions for the numerator $(P_K^+ )$ and denominator $(Q_K^+ )$ polynomials in (7) and (8) are given by:

$$\begin{aligned} P_K^+ (z)=\sum _{r=1}^K {p_r^+ } z^{r}, \quad Q_K^+ (z)=\sum _{s=0}^K {q_s^+ } z^{s}, \end{aligned}$$

(10)

where $\{p_r^+ \}$ and $\{q_s^+ \}$ are the expansion coefficients with $p_0^+ \equiv 0$. To extract $\{p_r^+, q_s^+ \}$ from $\{c_{n}\}$, either the total signal length N or the partial signal length $N_{\mathrm{P}}$ can be used. When the number $N_{\mathrm{P}}$ of the employed FID points is even, we have $K=N_{\mathrm{P}}/2$. According to (4) for $u=z$, the expansion coefficients $\{q_s^+ \}$ for the polynomial $Q_K^+ (z)$ from (4) are extracted by solving the system of linear equations $\sum _{s=0}^K {q_s^+ } c_{{s}'+s} =0$. Thereafter, the solutions $\{q_s^+ \}$ are refined through Singular Value Decomposition (SVD). The expansion coefficients $\{p_r^+ \}$ in $P_K^+$ are computed from the analytical expression $p_r^+ =\sum _{{r}'=0}^{K-r} {c_{{r}'}q_{{r}'+r}^+ }$ after the set $\{q_s^+ \}$ becomes available. The free term, $q_0^+$ can be set to e.g., 1 or −1 without affecting the spectra or the spectral parameters $\{\omega _{k,Q}^+,d_k^+ \} (1 \le k \le K)$ reconstructed by the $\hbox {FPT}^{(+)}$. The envelopes in the ersatz and usual modes are given by the Heaviside partial fractions:

$$\begin{aligned}&\left( {\frac{P_K^+ (z)}{Q_K^+ (z)}} \right) ^{\mathrm{E}} \equiv \sum _{k=1}^K {\left( {\frac{P_K^+ (z)}{Q_K^+ (z)}} \right) _k^{\mathrm{E}} } =\sum _{k=1}^K {\frac{\left| {d_k^+ } \right| z}{z-z_{k,Q}^+ }}\, (\hbox {Ersatz envelope}), \end{aligned}$$

(11)

$$\begin{aligned}&\left( {\frac{P_K^+ (z)}{Q_K^+ (z)}} \right) ^{\mathrm{U}} \equiv \sum _{k=1}^K {\left( {\frac{P_K^+ (z)}{Q_K^+ (z)}} \right) _k^{\mathrm{U}} } =\sum _{k=1}^K {\frac{d_k^+ z}{z-z_{k,Q}^+ }}\, (\hbox {Usual envelope}), \end{aligned}$$

(12)

respectively. Note that the difference between the lhs of (8) and (12) for the kth usual component $(P_K^+ /Q_K^+ )_k^{\mathrm{U}}$ and the usual envelope $(P_K^+ /Q_K^+ )^{\mathrm{U}}$, respectively, is the omitted subscript k in the latter and similarly for the ersatz modes in (7) and (11).

Recall that ersatz component spectra are helpful due to the lack of interference between the absorption and dispersion modes. Consequently, the overlap of closely lying or hidden resonances becomes apparent. On the other hand, caution is needed in interpreting these ersatz spectra, because ersatz peak heights may not actually reflect the true abundance of the metabolites. The definitive output list of the reconstructed parameters, including the phases $\varphi _k^+ \ne 0$, is needed to obtain the actual abundance of metabolites, whenever the phases $\{\varphi _k^+ \}$ are retrieved as non-zero quantities from the encoded MRS time signal. Even though the kth component resonances $(P_K^+ /Q_K^+ )_k^{\mathrm{U}}$ and $(P_K^+ /Q_K^+ )_k^{\mathrm{E}}$ do correspond to each other, their full widths at half maxima (FWHM) are generally not equal. Thus, the peak areas of a given kth component are likely to differ in the usual and ersatz modes. Only the parameters $\{\omega _{k,Q}^+, d_k^+ \}$ with $\varphi _k^+ \ne 0$ from the usual components $(P_K^+ /Q_K^+ )_k^{\mathrm{U}}$ should be used to estimate the actual metabolite concentrations, because the interference effects occur for $\varphi _k^+ \ne 0$ and this may significantly influence the peak areas and the metabolite concentrations.

It should be pointed out that the derivation of the envelopes in the representation of the Heaviside partial fractions (11) and (12) makes use of the expression $\sum _{n=0}^\infty {(z_{_{k,Q} }^+ } /z)^{n}=z/(z-z_{_{k,Q} }^+ )$ where $\left| {z_{_{k,Q} }^+ /z} \right| <1$. Here, it is assumed that the total length of time signal $\{c_{n}\}$ is infinite $(N=\infty )$. However, time signals are actually finite $(N < \infty )$ such that the latter series should be truncated at $n=N - 1$. This gives $\sum _{n=0}^{N-1} {(z_{_{k,Q} }^+ } /z)^{n}=\left[ {1-(z_{_{k,Q} }^+ /z)^{N}} \right] /(1-z_{_{k,Q} }^+ /z)$. Thus, the peak heights from (9a) should be corrected for the factor $1-(z_{_{k,Q} }^+ /z)^{N}$taken at sweep frequency, $\nu =\hbox {Re}(\nu _{k,Q}^+ )$. The corrected peak heights should be:

$$\begin{aligned} \hbox {Re}(H_k^+ )^{\mathrm{U}}\equiv & {} \frac{\left| {d_{k,T}^+ } \right| \cos (\varphi _k^+ )}{D_k^+ }, \quad (H_k^+ )^{\mathrm{E}}\equiv \frac{\left| {d_{k,T}^+ } \right| }{D_k^+ }, \nonumber \\ \left| {d_{k,T}^+} \right|= & {} \left| {d_k^+ } \right| \{1-\exp (-T/T_{2k}^{*+} )\},T = N\tau , \end{aligned}$$

(13)

where $0<1-\exp (-T/T_{2k}^{*+} )<1$.

Let us now consider the “Stability test” in the FPT. This entails computing successive values of spectra using partial signal lengths for components and envelopes, respectively, in order to verify that the following relationships hold:

$$\begin{aligned}&\left( {\frac{P_{K+m}^+ (z)}{Q_{K+m}^+ (z)}} \right) _k^{\mathrm{U}} =\left( {\frac{P_K^+ (z)}{Q_K^+ (z)}} \right) _k^{\mathrm{U}}\, (m = 1, 2,{\ldots }), \end{aligned}$$

(14)

$$\begin{aligned}&\left( {\frac{P_{K+m}^+ (z)}{Q_{K+m}^+ (z)}} \right) ^{\mathrm{U}} =\left( {\frac{P_K^+ (z)}{Q_K^+ (z)}} \right) ^{\mathrm{U}}\, (m = 1, 2,{\ldots }). \end{aligned}$$

(15)

The retrieved fundamental frequencies and amplitudes $\{\omega _{k,Q }^+, d_k^+ \}$ are acceptable only when convergence has been attained, as the polynomial degree $K + m$ is systematically increased ($m = 1, 2,{\ldots }$). Envelopes from (15) can be computed non-parametrically and parametrically. The non-parametric spectrum is obtained by evaluating $P_K^+ (z)/Q_K^+ (z)$ for $z=\exp (2\pi i\nu \tau )$ at the chosen set of real-valued sweep frequencies $\nu$. For the parametric case, we used (11) and (12) for the ersatz and usual modes, respectively.

3.2.2.1 Iterative averaging within the parametric ${ FPT}^{(+)}$ We will implement the procedure for iterative averaging of spectra, in order to practically handle the stumbling block of harmonic inversion, namely, over-sensitivity to changes in model order K. This stabilization procedure through iterative averaging will be performed for the computed iterates for envelopes through the parametric ${{FPT}^{(+)}}$.

In the Padé rational functions:

$$\begin{aligned} \frac{P_{K+m}^+ (z)}{Q_{K + m}^+ (z)}=\frac{P_K^+ (z)}{Q_{K }^+ (z)}\quad (m = 1,2,3,{\ldots }), \end{aligned}$$

(16)

all the spurious resonances will cancel out with stabilization for systematically and gradually increased polynomial degree $K+m (m=1,2,3,{\ldots })$. As illustrated by analytical means in Sect. 2.2, the mechanism for this is rooted in pole-zero cancellations. This occurs because spurious resonances exhibit coincidence or near-coincidence of their poles and zeros. These confluences (known as Froissart doublets) make such spurious resonances markedly unstable, especially for changes in the model order K. Each envelope $P_{K+m}^+ (z)/Q_{K + m}^+ (z) (m=1,2,3,{\ldots })$ will show different spuriousness due to random distributions of spurious poles and zeros in the complex frequency plane.

The complex-valued 31 usual envelopes $(P_K^+ /Q_K^+ )_{\mathrm{It:}m}^{\mathrm{U}}$, that are the iterates, will be taken for $K = 385,386,{\ldots },415$, with increment $\Delta K = 1$. Each of these envelopes uses the encoded FID zero-filled once to 1024. Next, the arithmetic average will be obtained of these 31 envelopes. The result is denoted by $\{\hbox {FPT}^{(+)}\}_{\mathrm{Av:}m}^{\mathrm{U}}$ where the subscripts It:m and $\hbox {Av:}m\, (m=1,2,3,{\ldots })$ denote the Iteration (It) and Average (Av). The notation m  indicates the iteration number. The complex average envelope $\{\hbox {FPT}^{(+)}\}_{\mathrm{Av:}m}^{\mathrm{U}}$ is then subjected to the IFFT and a new FID is produced, to which the $\hbox {FPT}^{(+)}$ will be applied again. The subsequent set of 31 envelopes will represent the next iteration in which the above-described procedure will be repeated.

3.2.2.2 Water suppression strategy within the parametric ${ FPT^{(+)}}$ Using the parametric $\hbox {FPT}^{(+)}$, the spectral region of interest, SRI, will be chosen as 0.75–4.5 ppm, with the aim of obviating the giant water peak, whose resonance frequency is set to be 4.61 ppm. The envelopes will be reconstructed from the parameters $z_{k,Q}^+$ and $d_k^+$ whose $\nu _{k,Q}^+$ belong to the SRI. The Padé-reconstructed spectral parameters (frequencies and amplitudes) given by the inverted first average envelope will be evaluated to assess the effectiveness of this procedure.

4 Results

4.1 Conventions

We begin with a brief enumeration of the conventions used to present the results. Each figure presented in this paper was designed to be entirely self-contained, with the complete, detailed information included therein. Besides a summarizing title at the top of every figure, the specifics of each panel are fully described, so that the reader need not necessarily refer to the main text. The relevant formulae are displayed for each panel, and the ordinates and abscissae are fully labeled. As was the case for the equations presented in the methods section, in the figures too, the superscript U denotes “usual” and E denotes “ersatz”. Recall that the subscript abbreviations “It” and “Av” indicate, respectively, Iteration and Average. With the exception of the displayed time signals, the total signal length N will always refer to the zero-filled FID with $N = 1024$. The partial signal lengths, $N_{\mathrm{P}}$, employed will always be even, so that $N_{\mathrm{P}}/2 = K$. The standard conventions “Re” and “Im” indicating the real and imaginary parts of complex quantities, will be used throughout. We recall that all the analyses are performed from the FIDs originally encoded at TE$\,=\,$272 ms.

4.2 The encoded MRS time signals

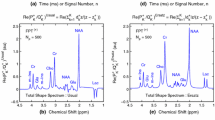
Figure 1 displays the MRS time signals (with the zero-order multiplicative phase correction, $\hbox {e}^{i\varphi _{0 }})$ encoded with 512 data points. The real part of the encoded FID is depicted on the top left panel (a), with the imaginary part on the top right panel (d). A magenta line is drawn across the abscissae, from which it is seen that at end of the encoding (512 ms), the FID has not fully returned to its zero values. Moreover, the waveforms are asymmetric around the abscissae because the residual water peak is still about 500 times more abundant than all the other metabolites.

Fig. 1

The real and imaginary parts (a and d, respectively) of the FID, $\{c_{n}\}$, encoded (and corrected for the zero-order phase, $\varphi _0 )$ in vivo from the parietal-temporal brain region in an 18 month old patient with cerebral asphyxia, using a 1.5 T MR scanner with 512 data points at echo time, TE$\,=\,$272 ms. The horizontal magenta lines are drawn to guide the eye through the departures from the level of the zero-valued amplitudes in the oscillations of the FID. Panels (b), (c), (e) and (f) show the real parts of the total shape spectra at the partial signal length $N_{\mathrm{P}} = 760$ for the encoded FID, zero-filled to $N = 1024$. The envelopes for the full Nyquist range are displayed, from $-3.7$ to 12.5 ppm as reconstructed by the DFT (b) and by the non-parametric $\hbox {FPT}^{(-)}$ (e). The giant resonance at 4.61 ppm represents the residual water peak. Further, the envelopes are shown for the chemical shift window between 0.75 and 4.25 ppm, as generated by the DFT (c) and by the non-parametric $\hbox {FPT}^{(-)}$ (f) (Color online)

4.3 Total shape spectra reconstructed by the DFT and the non-parametric $\hbox {FPT}^{(-)}$

The middle panels (b) and (e) of Fig. 1 display the total shape spectra reconstructed by the DFT and the non-parametric $\hbox {FPT}^{(-)}$ for the full Nyquist range from about −3.7 to 12.5 ppm, at a partial signal length, $N_{\mathrm{P}} = 760 (K = 380)$. As mentioned, this and all other spectral reconstructions used the FID zero-filled once to $N = 1024$ signal points. The dominant resonance in the spectra reconstructed by the DFT and $\hbox {FPT}^{(-)}$ is seen at 4.61 ppm. This represents the water residual resonance which appears to be exclusively in the spectral absorption mode, and pointing downwards. The other metabolites can just barely be seen in the spectral region between 0.75 and 4.25 ppm, due to their relative weakness compared to the water peak which remained giant even after its partial suppression in the course of encoding.

The bottom panels (c) and (f) of Fig. 1 present the total shape spectra reconstructed by the DFT and the non-parametric $\hbox {FPT}^{(-)}$ between 0.75 and 4.25 ppm, at a partial signal length $N_{\mathrm{P}} = 760$. Since the upper bound of the chemical shift region excludes the resonant frequency of water at 4.61 ppm, the other metabolites which appeared as miniscule in panels (b) and (e), now “pop-out” in panels (c) and (f). Still, many of the metabolites have decayed at the used long TE of 272 ms and the baseline is also fairly close to zero due to decay of the relatively immobile macromolecules. With both reconstructions (Fourier, Padé), a tall, narrow peak is seen as centered at $\sim$3.7 ppm which corresponds to m-Ins. The Cho and NAA peaks centered at $\sim$3.2 and $\sim$2.0 ppm, respectively, are notably attenuated in the DFT, compared to the $\hbox {FPT}^{(-)}$. The Cho to Cr metabolite concentration ratio is much lower in the envelopes generated by the DFT than those from the $\hbox {FPT}^{(-)}$. The serrations at $\sim$2.1 and $\sim$3.8 ppm are seen only in the $\hbox {FPT}^{(-)}$. On the whole, the resolution of the total shape spectra from the DFT is markedly inferior to that of the $\hbox {FPT}^{(-)}$, such that many of the peaks in the DFT are blunter and rougher, whereas many more structures appear in the $\hbox {FPT}^{(-)}$. Most vitally, as opposed to the DFT, which can, on its own, generate nothing more than the total shape spectra, the FPT via parametric analysis (to be presented in the next subsection) can provide much more information which may be diagnostically important.

4.4 Iterative averaging of envelopes via the parametric $\hbox {FPT}^{(+)}$

We now will apply the described stabilization procedure within the $\hbox {FPT}^{(+)}$ through iterative averaging of parametrically computed envelopes.

4.4.1 The 1st iteration and its average

The first set of iterates is seen in Fig. 2a, where the real parts of 31 usual envelopes $\text{ Re }(P_K^+ /Q_K^+ )_{\mathrm {It:1}}^{\mathrm {U}}$ are shown for $K = 385,386,{\ldots },415$, with increment $\Delta K = 1$, from the encoded FID and doubled in its length by zero-filling once to $N = 1024$. Therein, many large noise-like spikes are observed. Next, the arithmetic average, labeled by $\{\text{ FPT }^{(+)}\}_{\mathrm {Av:1}}^{\mathrm {U}}$ is taken of the corresponding 31 complex envelopes $(P_K^+ /Q_K^+ )_{\mathrm {It:1}}^{\mathrm {U}}$. In panel (b) of Fig. 2, the result denoted by $\hbox {Re}\{\hbox {FPT}^{(+)}\}_{\mathrm{Av:1}}^{\mathrm{U}}$ is displayed, namely, a “clean” spectrum. Thus, in this average spectrum, the stable structures remain, while the spikes are markedly attenuated or have practically disappeared. Recall that the subscripts It:m and $\hbox {Av:}m\,\, (m=1,2,3,{\ldots })$ denote the Iteration, It, and Average, Av, whereas the notation m indicates the iteration number.

Fig. 2

The real parts of 31 usual envelopes $\hbox {Re}(P_K^+ /Q_K^+ )_{\mathrm{It:1}}^{\mathrm{U}}$ are plotted for $K = 385, 386,{\ldots },415$ $(N_{\mathrm{P}} = 2 K=770, 772,\ldots ,830)$ from the FID with 512 original data points, zero-filled to $N = 1024$ encoded in vivo from the parietal-temporal brain region in an 18 month old patient with cerebral asphyxia, using a 1.5 T MR scanner at TE$\,=\,$272 ms (a). Many noise-like spikes are seen. The associated 31 complex envelopes $(P_K^+ /Q_K^+ )_{\mathrm {It:1}}^{\mathrm {U}}$ are averaged and denoted by $\{\text{ FPT }^{(+)}\}_{\mathrm {Av:1}}^{\mathrm {U}}$ whose real part $\text{ Re }\{\text{ FPT }^{(+)}\}_{\mathrm {Av:1}}^{\mathrm {U}}$ is shown in (b), where a “clean” spectrum is generated. In this average spectrum, the stable structures remain, but the spikes are not seen. The metabolite assignments are shown in (b). See the list of abbreviations for their full names (Color online)

Taking the arithmetic average of a pre-computed sequence of the retrieved envelopes (31 envelopes in Fig. 2) is a straightforward and powerful method for stabilizing total shape spectra. Whereas many sharp, narrow spikes appeared in Fig. 2a, indicating sensitivity of estimation to model order K, in panel (b) the average envelope simultaneously suppresses the instability (spuriousness) and confirms the stability (genuineness) of spectral structures. The mechanism of this finding is the ability of the arithmetic average to damp the unstable (noise-like) peak heights by a significant factor, which is less than or equal to $\sqrt{31}\approx 5.6$ for Fig. 2. This procedure of “spectra averaging” is the frequency-domain concomitant of the well-known SNR-improving “FID averaging” in the time domain where encoding is performed. In MRS, each individually encoded FID is heavily corrupted with noise, which precludes any meaningful estimation. To cope with this obstacle, many FIDs (100–200) are encoded and subsequently averaged. This signal averaging improves the SNR by a factor equal to $\sqrt{{N}'}$, where ${N}'$ is the number of encoded FIDs. However, there are significant advantages of “spectra averaging” relative to the “FID averaging” in that, for example, the former can be iterated to substantially aid the exact reconstructions.

In the average spectrum $\hbox {Re}\{\hbox {FPT}^{(+)}\}_{\mathrm{Av:1}}^{\mathrm{U}}$of Fig. 2b, the metabolite assignments are displayed. Therein, the largest peak in the total shape spectrum is Cho at $\sim$3.2 ppm. Other prominent peaks in the average envelope are Cr at $\sim$3.0 ppm, NAA at $\sim$2.0 ppm, a large component of m-Ins at $\sim$3.75 ppm, a Glx doublet centered at $\sim$3.85 ppm and the component of the Lac doublet resonating at $\sim$1.35 ppm. The other component of the Lac doublet is smaller and wider at $\sim$1.3 ppm, adjacent to which two small, sharp Lip peaks are seen, followed by a serrated valine (Val) peak centered at $\sim$1.0 ppm, and leucine (Leu) at $\sim$0.9 ppm. A number of the larger spectral structures are also serrated, such that, e.g. on the left side of the large Cho peak at $\sim$3.2 ppm, the PC $+$ glycerophosphocholine (GPC) peak appears at $\sim$3.25 ppm. An even more marked NAAG (N-acetyl aspartyl glutamic acid) peak at $\sim$2.1 ppm splits on the left side of NAA at $\sim$2.0 ppm.

In Fig. 2, and afterwards, all the parametrically generated envelopes $(P_K^+ /Q_K^+ )^{\mathrm{U}}$, that are computed using the Heaviside partial fraction sum (12), include only the components $(P_K^+ /Q_K^+ )_k^{\mathrm{U}}$ with chemical shifts from the analyzed SRI, i.e. $\hbox {Re}(\nu _{k,Q}^+ )\in [0.75, 4.5]\, \hbox {ppm}$. The consequence of this procedure can be seen by comparing Figs. 1 and 2. In Fig. 1, the Padé non-parametrically computed envelope includes the residual water peak located at 4.61 ppm, which is outside the SRI, [0.75, 4.5] ppm. The negative peak (i.e. a dip) of the residual water resonance from panel (e) in Fig. 1 pulls down the contributions from the other nearby metabolites, particularly those with chemical shifts above 4.25 ppm. This produces a drop in the envelope below the abscissa as per panel (f) in Fig. 1. Such a drop is absent from the parametrically generated envelopes comprised exclusively of components from the SRI, [0.75, 4.5] ppm, i.e. without water, as seen in Fig. 2. As a result, the Lac quartet centered at 4.25 ppm becomes more distinct in Fig. 2b.

4.4.2 The reconstructed FID built from Padé-reconstructed parameters

In Fig. 3 the originally encoded MRS time signal is compared with the FID reconstructed by the parametric $\hbox {FPT}^{(+)}$ from the 1st average envelope. As a reminder, the real and imaginary parts of the originally encoded FID from Fig. 1, are shown once again in panels (a) and (c) of Fig. 3 where, as before, the phase was corrected via multiplication of the encoded set $\{c_n \} (0\le n\le 511)$ by $\hbox {exp}(i\varphi _0 )$ where $\varphi _0 = 1.7499$ rad. Also, recall that the magenta line is drawn across the abscissa, showing that at end of the encoding (512 ms), the original FID has not completely returned to its zero value and that the waveforms are highly asymmetric around the abscissa, due to the presence of the residual water peak which is, as stated, about 500 times more abundant than all the other metabolites.

Fig. 3

The real (a) and imaginary parts (c), of the FID, $\{c_{n}\}$, encoded (corrected for the zero-order phase, $\varphi _0)$ in vivo from the parietal-temporal brain region in an 18 month old patient with cerebral asphyxia, using a 1.5 T MR scanner with 512 data points at echo time, TE$\,=\,$272 ms. Here, water was partially suppressed through encoding by the standard spin-echo procedure, but the water residual remains, and distorts the waveforms. Real (b) and imaginary (d) parts of the FID given by the inverted complex 1st average envelope in the SRI between 0.75 and 4.5 ppm, with phasing $\varphi _0 = 1.7499\,\hbox {rad}$ preserved. Water is automatically excluded since its resonant frequency 4.61 ppm is above the upper limit of this SRI. The FIDs reconstructed by the parametric $\hbox {FPT}^{(+)}$ are fully centered around the abscissae, with a complete regularization and symmetrization of their shapes. The horizontal magenta lines are drawn to guide the eye through the departures from the level of the zero-valued amplitudes in the oscillations of the FIDs (Color online)

Panels (b) and (d) of Fig. 3 present the real and imaginary parts, respectively, of the FID given by the IFFT-based inversion of the complex 1st average envelope which contains only the components with $\hbox {Re} \nu _{k,Q}^+ \in [0.75, 4.5]\, \hbox {ppm}$. For purposes of comparison with the encoded time signal from panels (a) and (b), the reconstructed FID from panels (c) and (d) is truncated so as to have 512 data points. The phase correction $\varphi _0 = 1.7499\, \hbox {rad}$ of the originally encoded FID being inherently present in the envelope from panels (a) and (c) is also inherited by the reconstructed FID from panels (b) and (d), respectively, of Fig. 3. Recall that the residual water resonance has been automatically excluded from the reconstructed FID on panels (b) and (d) of Fig. 3, since the corresponding resonant frequency 4.61 ppm is above the upper limit of this SRI. It is clearly seen that the reconstruction by the parametric $\hbox {FPT}^{(+)}$ results in an FID with a complete regularization of its shape, which now appears as symmetrical around the abscissa. Because this was achieved through creating the envelopes from the parameters $z_{k,Q}^+$ and $d_k^+$ whose $\nu _{k,Q}^+$ belong to the SRI, there was no need for any windowing procedure, be it through filtering using a box-function [14] or via any other filter. In fact, the outlined procedure of the FID reconstruction amounts to enabling a local spectral analysis with no recourse to windowing at all.

4.4.3 Further iterations and averages: convergence of envelopes

We now proceed to further iterations and testing the robustness of the stability of the average envelopes. The complex first average envelope $\{\text{ FPT }^{(+)}\}_{\mathrm {Av:1}}^{\mathrm {U}}$ is subjected to the IFFT to produce a new FID. The $\hbox {FPT}^{(+)}$ is then applied to this reconstructed FID and the real parts of the new 31 envelopes for $K \in$ [385, 415] are shown on panel (b) of Fig. 4, alongside the 1st iteration repeated on panel (a). The 2nd iteration with the 31 newly obtained envelopes from panel (b) has notably fewer spikes, and these are of much smaller heights compared to the corresponding spurious structures from the 1st iteration, shown in panel (a). Averaging is performed once again, and this time for the 31 complex envelopes whose real parts are from panel (b) of Fig. 4, generating the complex envelope for the 2nd arithmetic average, $\{\text{ FPT }^{(+)}\}_{\mathrm {Av:2}}^{\mathrm {U}}$. This, in the next round, is subjected to the IFFT to produce a new FID. The $\hbox {FPT}^{(+)}$ is then applied to this reconstructed FID and the real parts of the newly generated 31 envelopes for $K \in$ [385, 415] are displayed in panel (c) of Fig. 4. This is the 3rd iteration, whose spurious structures are further attenuated and much sparser compared to the 2nd iteration on panel (b). Using the 31 complex envelopes from iteration #3 with the real parts shown in panel (c), the complex 3rd arithmetic average, $\{\text{ FPT }^{(+)}\}_{\mathrm {Av:3}}^{\mathrm {U}}$, is produced. In panel (d), the real parts of the complex 1st, 2nd and 3rd arithmetic averages are overlain, in the respective colors of green, magenta and blue, following the like colors on panels (a), (b) and (c). It is seen therein that these three curves closely coincide, with just a few scattered small deviations.

Fig. 4

The convergence rate of the first set of 3 iterations $\hbox {Re}(P_K^+ /Q_K^+ )_{\mathrm{It:1,2,3}}^{\mathrm{U}}$ (a), (b) and (c), respectively, are shown. The corresponding three average envelopes $\text{ Re }\{\text{ FPT }^{(+)}\}_{\mathrm {Av:1,2,3}}^{\mathrm {U}}$ displayed on panel (d) are in quite close agreement, as seen by predominant coincidence of the green, magenta and blue curves (Color online)

The entire procedure displayed in Fig. 4 for iterations and averages ## 1-3, is repeated in Fig. 5 for the iterations and averages ## 4-6. The spikes have practically disappeared in panels (a), (b) and (c), for iterations ## 4, 5 and 6, respectively. The 4th, 5th and 6th averages presented in panel (d) of Fig. 5 show even rarer deviations than in Fig. 4, such that it is only with substantial scrutiny that discrepancies among the green, magenta and blue curves can barely be seen.

Fig. 5

The convergence rate of the second set of 3 iterations $\hbox {Re}(P_K^+ /Q_K^+ )_{\mathrm{It:4,5,6}}^{\mathrm{U}}$ (a), (b) and (c), respectively, are shown. The corresponding three average envelopes $\text{ Re }\{\text{ FPT }^{(+)}\}_{\mathrm {Av:4,5,6}}^{\mathrm {U}}$ displayed on panel (d) are in very close agreement, as seen by nearly complete coincidence of the green, magenta and blue curves (Color online)

Fig. 6

The convergence rate of the third set of 3 iterations $\hbox {Re}(P_K^+ /Q_K^+ )_{\mathrm{It:7,8,9}}^{\mathrm{U}}$ (a), (b) and (c), respectively, are shown. The corresponding three average envelopes $\text{ Re }\{\text{ FPT }^{(+)}\}_{\mathrm {Av:7,8,9}}^{\mathrm {U}}$ displayed on panel (d) appear to be in full agreement, as seen by the indistinguishable green, magenta and blue curves (Color online)

Further iterations ## 7, 8 and 9, shown respectively on panels (a), (b) and (c) of Fig. 6, appear to be identical, and no spikes whatsoever can be seen. Moreover, the average spectra ## 7, 8 and 9, displayed in panel (d) cannot be seen to differ at all from their respective iterates from panels (a)–(c). On panel (d) from Fig. 6, no deviations whatsoever can be noted among the green, magenta and blue curves corresponding to averages ## 7, 8 and 9, respectively. Thus, through this iterative averaging of envelopes, convergence can be said to have been fully achieved.

4.5 Equivalence of the Padé-generated parametric and non-parametric envelopes

In Fig. 7 we compare the non-parametrically (panel (b)) and parametrically (panel (c)) computed envelopes in the $\hbox {FPT}^{(+)}$ at $K = 450$. They were reconstructed as follows: via the IFFT-based inversion of the complex 9th average envelope, with its real part displayed in panel (a), the FID is generated first and then used to compute the total shape spectra shown in panels (b) and (c) of Fig. 7. Panels (b) and (c) show the full coincidence of the Padé estimation using non-parametric and parametric analyses. Furthermore, the spectrum from panel (a) coincides with those from panels (b) and (c). This is an essential verification which confirms the correctness of the reconstructed FID which will be subsequently subjected to Padé-based quantification. The same results from panels (b) and (c) for $K = 450$ have also been obtained for the middle of the interval of the K values, i.e. $K = 400 = (385 + 415)/2$. The case with $K = 450$ demonstrates the extrapolation feature of rational polynomials from the Padé approximant, which remains valid beyond the originally selected interval for K. This corroborates our earlier finding using an FID encoded at TE$\,=\,$136, that through the extrapolation feature of the FPT, the same results are generated beyond the originally chosen interval for K [47]. Figure 7 deals explicitly with the 9th average, but the corresponding agreements between the non-parametrically and parametrically retrieved envelopes, similar to panels (b) and (c), have also been recorded in the present reconstructions (not shown) starting with the average envelopes built from lower iterates (8th, 7th, 6th, etc.).

Fig. 7

The complex 9th average envelope $\{\text{ FPT }^{(+)}\}_{\mathrm {Av:9}}^{\mathrm {U}}$ [with its real part shown in (a)] is inverted by the IFFT to obtain the FID from which two envelopes are generated in the mode $\hbox {Re}(P_K^+ /Q_K^+ )^{\mathrm {U}}$, one by the non-parametric $\hbox {FPT}^{(+)}$ (b), and the other by the parametric $\hbox {FPT}^{(+)}$ (c). The envelopes from panels (a)–(c) are essentially indistinguishable (Color online)

4.6 Reconstruction of the component spectra through the FPT

In Fig. 8, from the complex 9th average envelope, with its real part shown in panel (a), an FID is generated from which the component spectra in the usual mode are reconstructed by the parametric $\hbox {FPT}^{(+)}$ as displayed on panel (b). Many absorption spectra are seen with admixtures of dispersion components because the amplitudes $\{d_k^+ \}$ are all complex-valued with their non-zero phases $\varphi _k^+ (1 \le k \le K)$. Panel (c) shows the super-resolution of the component spectra in the ersatz mode, where the abundant closely-overlapping resonances are clearly distinguished. Several underlying and closely overlapping resonances can be seen in association with the most prominent peaks such as Lac at $\sim$1.3 ppm, NAA at $\sim$2.0 ppm, Cr at $\sim$3.0 ppm and Cho at $\sim$3.2 ppm.

Fig. 8

The FID from the IFFT-based inversion of the complex 9th average envelope [with its real part shown in (a)] is subjected to the $\hbox {FPT}^{(+)}$ to generate the usual and ersatz component spectra in (b) and (c), respectively. The usual components (b) mix the absorption and dispersion lineshapes. Ersatz component spectra (c) display many closely-overlapping positively-oriented resonances that are clearly identified, all in the absorption mode. Peak heights computed from the analytical expressions in Eq. (13) are presented as open circles (Color online)

The corrected peak heights shown as open circles on panels (b) and (c) in Fig. 8 for the usual and ersatz component spectra, respectively, are computed from the analytical expressions for $\hbox {Re}(H_k^+ )^{\mathrm{U}}$ and $(H_k^+ )^{\mathrm{E}}$ given in (13). On panel (c) the peak heights $(H_k^+ )^{\mathrm{E}}$ quite closely match the tops of the resonances. On the other hand, the peak heights $\hbox {Re}(H_k^+ )^{\mathrm{U}}$ on panel (b) show two different patterns. For Cr and Cho at $\sim$3.0 and 3.2 ppm, for example, there is quite close matching between the peak heights and the tops of these absorptive resonances. Another pattern is also seen for dispersive lineshapes, wherein the peak heights are somewhat displaced from the tops of the resonances; these departures depend upon the angle $\varphi _k^+$ of the amplitudes of $d_k^+$. The location of the open circles denoting peak heights for dispersive resonances is closer to the dominant of the two lobes (recall the dispersive lineshapes have two lobes).

Figure 9 presents the concept of Signal-noise separation, or SNS, with the underlying pole-zero coincidence, as Froissart doublets, through the $\hbox {FPT}^{(+)}$ from the FID given by the inverted complex 9th average envelope. The Argand plot, as imaginary, $\hbox {Im}(\nu _{k,Q}^+ )$, versus real, $\hbox {Re}(\nu _{k,Q}^+ )$, frequencies is shown on panel (a). Poles and zeros are symbolized by open circles and dots, respectively, that completely coincide for spurious resonances. Open circles for poles of the genuine and spurious resonances are drawn in blue and red colors, respectively. A full separation is seen between genuine and spurious frequencies that lie in the positive and negative imaginary frequency regions, respectively. An auxiliary horizontal green line facilitates visualization of this separation. The pole-zero coincidences result in complete annihilation of the amplitudes for spurious resonances, as seen on panels (b) and (c) for magnitude plots and ersatz component spectra, respectively (recall Sect. 2.2). Note, that poles and zeros can on occasion be quite close for genuine resonances (e.g. the Val doublet close to 1.0 ppm). However, these near pole-zero coincidences are not Froissart doublets since they are located in the positive imaginary frequency region and, most importantly, they are stable against changes in model order K.

Fig. 9

Illustration of Signal-noise separation, or SNS, from the 9th average envelope. The Argand plot of imaginary, $\hbox {Im}(\nu _{k,Q}^+ )$, versus real, $\hbox {Re}(\nu _{k,Q}^+ )$, frequencies, with a complete separation of genuine from spurious frequencies reconstructed by $\hbox {FPT}^{(+)}$ (a). The twofold signature of a spurious resonance is pole-zero coincidence (confluence of an open circle with a dot) as per (a) and a zero-valued amplitude as per (b). Zero-valued magnitudes indicate zero-valued peak heights (c). In panels (a), (b) and (c) circles indicate the genuine (blue) and spurious (red) resonances (Color online)

Fig. 10

Distributions of spectral parameters generated by the $\hbox {FPT}^{(+)}$ from the FIDs given by the inverted complex 1st, 2nd and 3rd average envelopes (whose real parts are in green, magenta and blue, respectively). The ersatz components and their peak heights (a), Argand plot of imaginary, $\hbox {Im}(\nu _{k,Q}^+ ),$ versus real, $\hbox {Re}(\nu _{k,Q}^+ ),$ frequencies (b), magnitudes ${\vert }d_k^+ {\vert }$ versus chemical shifts (c) and phases ${\vert }\varphi _k^+ {\vert }$ versus chemical shifts (d) (Color online)

Observe that in the title of panel (b) of Fig. 9, the expression $|d_k^+ | = |P_K^+ (z_{k,Q}^+ )/[(\hbox {d}/\hbox {d}z_{^{k,Q}}^+ )Q_K^+ (z_{k,Q}^+ )] {\vert }$ is a shortened notation for $d_k^+ =P_K^+ (z_{{k,Q} }^+ )/\{[(\hbox {d}/\hbox {d}z)Q_K^+ (z)]_{z=z_{{k,Q} }^+ } \}$. Here, pole-zero coincidence $(z_{{k,Q} }^+ =z_{k,P}^+ )$ implies $P_K^+ (z_{{k,P} }^+)= 0$ and, consequently, $d_k^+ =0$, as one of the two signatures of Froissart doublets (zero-valued amplitudes). Furthermore, on panel (b), the same amplitude $d_k^+$ is given by the equivalent canonical form $d_k^+ =(p_K^+ /q_K^+ )\prod _{m=1}^K ( z_{k,Q}^+ -z_{m,P}^+ )/\{(z_{_{k,Q} }^+ -z_{_{m,Q} }^+ )_{m\ne k} \}$. In the numerator ($z_{_{k,Q} }^+ -z_{_{m,P} }^+ )$, we can have $m=k$, in which case $d_k^+ =0$. This is in agreement with the same result from the Cauchy residue formula (6) in the $\hbox {FPT}^{(+)}$, i.e. $d_k^+ =P_K^+ (z_{k,Q}^+ ) /\{\left[ {\hbox {(d}} \right. /\hbox {d}z) Q_K^+ \left. {(z)} \right] _{z=z_{k,Q}^+ } \}= 0$ for $z_{k,Q}^+ =z_{k,P}^+$.

4.7 Detailed examination of the convergence of spectral parameters as reconstructed via the FPT$^\mathrm{(+)}$

We now perform the most stringent test of convergence on the level of the parameters reconstructed by the FPT$^{(+) }$for the genuine resonances with the pertinent illustrations shown in Figs. 10, 11 and 12. Figure 10 presents the results generated from the FIDs given by the inverted complex 1st, 2nd and 3rd average envelopes, color-coded as green, magenta and blue, respectively. Quantification is carried out with $K = 450 (N_{\mathrm{P}} = 900)$. The results for $\hbox {Re} (P_k^+ /Q_k^+ )_k^{\mathrm{E}}$, $\nu _{k,Q}^+$, $\left| {d_k^+ } \right|$ and $\varphi _k^+$ are also color-coded (curves, for the ersatz component spectra $\hbox {Re}(P_k^+ /Q_k^+ )_k^{\mathrm{E}}$ and circles, for the reconstructed parameters $\nu _{k,Q}^+, \left| {d_k^+ } \right|$ and $\varphi _k^+$, where $\nu _{k,Q}^+ = [1/(2\pi i\tau )]\ln (z_{k,Q}^+ )$. For these findings of quantification, green, magenta and blue colors are used, respectively, when the 1st, 2nd and 3rd average envelopes have been inverted to generate the corresponding FIDs employed in the Padé quantification. Panel (a) displays the ersatz components $\hbox {Re}(P_k^+ /Q_k^+ )_k^{\mathrm{E}}$ and peak heights $(H_k^+ )_k^{\mathrm{E}}$. Therein, results from the three averages generally coincide, although there are a few discrepancies, at e.g. 1.0 ppm where the magenta peak, which is very small, from the 2nd iteration is about 3 times larger than the blue peak from the 3rd iteration. In the chemical shift region above $\sim$3.9 ppm, four green individual peak heights are noted. Another region of visible discordance in panel (a) is around 2.1–2.2 ppm. The Argand plot in panel (b) shows the imaginary, $\hbox {Im}(\nu _{k,Q}^+ ),$ versus real, $\hbox {Re}(\nu _{k,Q}^+ ),$ frequencies, where a substantial number of discrepancies among the green, magenta and blue circles appear. In particular, isolated green, magenta and blue poles are seen in the chemical shift region from $\sim$2.1 to 2.3 ppm, as well as around 1.65 ppm. In contrast, with a few exceptions, the green, magenta and blue circles are quite close or coincident in the magnitude plot, $\left| {d_k^+ } \right|$ versus chemical shift, shown in panel (c). The plot of phase $\varphi _k^+$ versus chemical shift is shown in panel (d). The lower and upper range of variation from $-\pi$ to $+\pi$, respectively, of the phases $\varphi _k^+$ are demarcated by two black horizontal lines. It can be seen in panel (d) that there are several isolated green, magenta and blue circles indicating lack of concordance in the reconstructed phases from the FIDs given by the 1st, 2nd and 3rd average envelopes.

Fig. 11

Distributions of spectral parameters generated by the $\hbox {FPT}^{(+)}$ from the FIDs given by the inverted complex 4th, 5th and 6th average envelopes (whose real parts are in green, magenta and blue, respectively). The ersatz components and their peak heights (a), Argand plot of imaginary, $\hbox {Im}(\nu _{k,Q}^+ )$, versus real, $\hbox {Re}(\nu _{k,Q}^+ )$, frequencies (b), magnitudes ${\vert }d_k^+ {\vert }$ versus chemical shifts (c) and phases ${\vert }\varphi _k^+ {\vert }$ versus chemical shifts (d) (Color online)

Fig. 12

Distributions of spectral parameters generated by the $\hbox {FPT}^{(+)}$ from the FIDs given by the inverted complex 7th, 8th and 9th average envelopes (whose real parts are in green, magenta and blue, respectively). The ersatz components and their peak heights (a), Argand plot of imaginary, $\hbox {Im}(\nu _{k,Q}^+ ),$ versus real, $\hbox {Re}(\nu _{k,Q}^+ ),$ frequencies (b), magnitudes ${\vert }d_k^+ {\vert }$ versus chemical shifts (c) and phases ${\vert }\varphi _k^+ {\vert }$ versus chemical shifts (d) (Color online)

In Fig. 11, the results for the Padé reconstructions from the FIDs given by the complex inverted 4th, 5th and 6th average envelopes show quite a different picture from those of Fig. 10. Namely, in panel (a) for the ersatz components $\hbox {Re}(P_k^+ /Q_k^+ )_k^{\mathrm{E}}$ and peak heights $(H_k^+ )_k^{\mathrm{E}}$, except for slight discrepancies at 1.0 and at 2.45 ppm, the results are in agreement. The Argand plot in panel (b) shows much more concordance than was the case for Fig. 10b, although there is still one isolated green circle at $\sim$2.45 ppm very close to the zero axis and a few other regions in which the three colored circles are slightly discordant. Other than the one green circle which is of practically zero magnitude at $\sim$2.45 ppm, the magnitude plot in panel (c) indicates agreement among the three reconstructions. The phase plot of panel (d) is substantially less discrepant than was the case for the phase plot in Fig. 10d.

We finally proceed in Fig. 12 to the Padé reconstructions from the FIDs given by the complex inverted 7th, 8th and 9th inverted average envelopes. For all four corresponding panels (a)–(d): ersatz components with peak heights versus chemical shifts, as well as Argand plots, magnitude plots and phase plots, it can be said that convergence has been attained, such that the very minimal deviations are considered to be within the realm of stochasticity.

5 Discussion and conclusion

Using MRS time signals encoded from a pediatric patient with cerebral asphyxia, this study provides further evidence of the super high-resolution features of the fast Padé transform, FPT. The FPT produced better resolved lineshapes compared to the Fourier analysis. The major metabolites such as Cho and NAA were accurately identified by the FPT, whereas in the Fourier envelope, the heights of these peaks were diminished. For the present clinical assessment, reliance upon the Fourier-generated total shape spectrum would thus incorrectly suggest a lower NAA concentration, which could indicate greater damage to cerebral neurons. Moreover, the Fourier envelope underestimated the metabolite concentration ratio of Cho to Cr. It is this ratio which has been very frequently used in neurodiagnostics, including for determining whether a new contrast-enhancing lesion post-radiation therapy is radiation necrosis or recurrence of the primary brain tumor [48]. The results in the present investigation, of an improved resolution of the Padé-generated total shape spectra compared to the Fourier envelope for the same number of in vivo encoded FID points, complements earlier findings [1, 2, 14, 42–45, 47]. Moreover, with fewer FID points, the FPT can achieve the same resolution as that in the Fourier envelope. These two practical advantages of high relevance to the efficiency of MRS in clinical settings stem directly from the use of the Padé quotient of two polynomials instead of a single Fourier polynomial.

The “spectra averaging” procedure in the frequency domain has been thoroughly validated in the current work. This represents a Padé-based counterpart to “signal averaging” as routinely performed in the time domain. In the latter, the SNR is improved by taking typically the arithmetic average of some 128 FIDs, as was the case in the present study. Since noise varies randomly, it diminishes by $\sqrt{{N}'}$ where ${N}'$ denotes the number of transients. However, as opposed to signal averaging in the time domain, spectra averaging in the frequency domain can be carried through iterations that systematically improve the Padé reconstructions. The spectra averaging procedure takes advantage of the stabilization capabilities of the FPT. This is accomplished by the envelope-averaging procedure, using the computed Padé total shape spectra for a sequence of values of the model order K. In the average envelopes, with each iteration, there is an increased level of suppression of spurious spectral structures that are very sensitive to changes in K.

In our earlier studies with the input noise of controlled levels  [26, 36], the query was made as to how can one be certain which of the resonances are spurious and which are genuine, especially for cases when pole-zero coincidence may be either lacking or not complete. The “stability test” was presented as an important step towards handling this problem. Namely, spurious resonances are recognized by their instability with even a slight change in the noise level or model order K. This line of reasoning is now developed further, by iteratively transforming back and forth from the frequency to the time domain, such that ultimately a spectrum is produced which is essentially free from spurious structures. These structures arise not only from the noise associated with encoding, but are also produced by the highly over-determined system of linear equations, as well as from numerical computations themselves whenever the finite arithmetic precision is used, as in our work. This over-determination is, in fact, imposed by both noise and a high spectral density, such as those associated with the MRS data encoded from the brain. Since this procedure is herein fully validated, we can now confidently suggest that iterative averaging could be automatically applied, to suppress the spurious, noise-like spikes and thereby generate the “clean” spectra so vitally needed in clinical MRS for further analyses and interpretations.

For benchmarking purposes, the present study extensively applies the iterative averaging procedure, all the way to the 9th iteration. With regard to the total shape spectra or envelopes, the progressive disappearance of all spurious structures is shown. The 7th, 8th and 9th iterations generate converged envelopes, with the corresponding average envelopes being practically indistinguishable. This finding is particularly remarkable within the $\hbox {FPT}^{(+)}$ whose initial convergence region in the harmonic variable is located inside the unit circle $(\left| z \right| <1)$, implying that, through analytical continuation by numerical means, it must induce convergence into the input series which is divergent in this region [49]. The large spikes seen on Fig. 2a in the 1st iteration reflect the difficulty of this task. The $\hbox {FPT}^{(-)}$ has, in contrast, a less stringent requirement, namely it ought to accelerate convergence of the input series outside the unit circle, which is where its convergence in the harmonic variable $z^{-1}$ already exists. However, with the $\hbox {FPT}^{(-)}$, both the spurious (pole-zero coincidences) and the genuine resonances all reside within the same positive imaginary frequency region in the complex frequency plane. The $\hbox {FPT}^{(+)}$ provides distinct separation of signal from noise, because all the found spurious frequencies lie in the negative imaginary frequency region, while the genuine content resides in the positive imaginary frequency region, as was displayed in the Argand plot of Fig. 9a. In our benchmarking studies based on synthesized data associated with in vitro encoded time signals [50] from benign and cancerous ovary with added noise [21, 51], the powerful noise separation capabilities of the $\hbox {FPT}^{(+)}$ were demonstrated. These capabilities of the $\hbox {FPT}^{(+)}$ are seen to be of vital importance in the clinical setting, as well, in which the FIDs are encoded at quite short total signal lengths using MR scanners of relatively weak magnetic field strength, $B_{0 }= 1.5\, \hbox {T}$.

Cross-validation is provided since the same envelopes are obtained by the two algorithmically different versions of the fast Padé transform, the $\hbox {FPT}^{(+)}$ and $\hbox {FPT}^{(-)},$ that perform signal processing in the complementary domain of the complex plane of the harmonic variable $z \,\mathrm{and}\, z^{-1}$, inside and outside the unit circle, respectively. We have also herein confirmed that parametric and non-parametric Padé reconstructions generate undistinguishable envelopes from the MRS time signals given by the complex inverted average envelopes. This was examined both within the interval [385, 415] of the K values and for K above that interval. The latter case for K further confirms the extrapolation capabilities of the FPT, as a rational polynomial. It should be noted that, in sharp contradistinction to the FPT, when ordinary polynomials are employed (as in Fourier processing) to approximate a function in a given interval, they generally perform inadequately outside that interval. This multiple cross-validation is the prerequisite for estimation reliability which is critical to clinical MRS-based diagnostics.

All the signal processors are vexed with pronounced sensitivity to changes in the otherwise unknown model order K, which is the number of the component metabolites in the spectral analysis (quantification). Via spectra averaging, this sensitivity can be fully suppressed, such that, at convergence, the shape estimations are stabilized.

Verifying that the parametric and non-parametric Padé estimations generate identical total shape spectra allows us to choose which procedure will be used for further analyses. The non-parametric Padé is faster since the set of complex frequencies and amplitudes do not need to be reconstructed. However, the advantage of parametric Padé processing is that after the amplitudes $d_{k }^+$ and harmonics $z_{{k,Q} }^+$ are reconstructed for the full Nyquist range, one can choose the spectral region of interest, SRI, from which to build the envelopes. Since our SRI is between 0.75 and 4.5 ppm, where the main diagnostically important metabolites lie, the envelopes are built only from the components whose chemical shifts $\hbox {Re}(\nu _{{k,Q} }^+ )$ are in this interval. Thereby, the residual and still giant water resonance is automatically bypassed. In contrast, for the non-parametric FPT, it is not possible to pre-select the frequency region of interest without a windowing procedure which is needed to suppress the water residual. In our earlier study [14], we confirmed that within the non-parametric FPT, the windowing procedure with a step function fully preserves the spectral information, excepting the non-consequential part at the edges of the selected window. All told, the advantages of the parametric FPT compensate for the extra processing time needed. Not only is the water suppression problem completely obviated, but the most abiding aim of MRS, namely, quantitative analysis of the metabolic content of the scanned tissue can be accomplished forthwith through the parametric FPT. Moreover, by avoiding the water and other noisy content, the dimensionality of the problem is diminished, i.e. there is less over-determination in the system of linear equations. Overall, the parametric FPT is more powerful in suppressing noise than is the non-parametric FPT.

Going beyond total shape spectra to analyze the components, as achieved through the parametric FPT, is the most important goal, especially given the high density of MR spectra from the brain. Fitting procedures cannot even ascertain the number of peaks underlying, e.g. the prominent Cho at $\sim$3.2 ppm, Cr at $\sim$3.0 ppm or NAA at $\sim$2.0 ppm. The relative abundance of the resonances in these crowded spectral regions would, therefore, be entirely equivocal if one relied upon the conventional Fourier analysis with post-processing via fitting. As noted, the chemical shift region around 1.3 ppm, where lactate and lipids overlap, is of particular importance for identifying hypoxia [9]. Assessment of this spectral region has also been helpful for distinguishing cancerous from non-malignant pathology from the brain  [5, 7–9], and from other organs, such as the ovary  [52] and the breast [53, 54]. However, in vivo proton MRS studies [24, 52] indicate that much uncertainty arises in attempts to assess this chemical shift region. We have seen from the Padé-reconstructed “ersatz” component spectra that in addition to the Lac doublet, a number of other resonances are closely overlapping even at a long TE of 272 ms, when the broad lipid resonances have already decayed. Not only were each of the resonances in the chemical shift region of 1.3 ppm clearly identified through the FPT, but their peak parameters were all precisely ascertained. The latter case was verified by detailed examination of convergence of all four spectral parameters. Phosphocholine, PC, another indicator of hypoxia [12], and which is also a biomarker of malignancy [15–18], was likewise identified and its peak parameters accurately assessed via the FPT. This was the case despite the fact that PC overlaps extremely closely with GPC and the much more prominent free Cho resonance centered at 3.2 ppm. Heretofore, assessment of PC has been limited to in vitro NMR studies.

The present and our most recent results [14, 47] show that parametric Padé-based processing of MRS time signals encoded on 1.5 T scanners is entirely feasible. Wide-ranging possibilities emerge for multivariate exploration to find metabolite patterns that best characterize various types and grades of cancer versus diverse benign pathology which cause differential diagnostic dilemmas. Comparisons with normal, non-infiltrated tissue are also essential. This perspective holds promise for improved clinical diagnostics through in vivo MRS.

In Ref. [5], a quite similar in vivo MRS study was performed on neonates with cerebral hypoxia/ischemia. Nearly the same encoding parameters ($B_{0} = 1.5\, \hbox {T}$, 512 FID points, 128 transients, TE$\,=\,$31, 136 and 272 ms, TR$\,=\,$2000 ms) were used. The FIDs were zero-filled 8 times to a total signal length of 4096 points. Analysis of the computed FFT spectra was also carried out in the interval between 0.75 and 4.5 ppm. This was done through curve fitting by means of AMARES (Advanced Method for Accurate Robust and Efficient Spectral fitting). Altogether, at TE$\,=\,$31 ms, only five metabolites were quantified (NAA, Cr, Cho, Glx, m-Ins) within 2.0–4.5 ppm. Further, fitting in Ref. [5] omitted resonances between 0.8 and 1.3 ppm, with the explanation that this region contains the main contribution from mobile lipids and macromolecules. By comparison, the FPT in the present study at much longer echo time (TE$\,=\,$272 ms) quantified some 49 resonances in the interval 2.0–4.5 ppm, and altogether some 70 resonances between 0.75 and 4.5 ppm.

In our previous paper on the FIDs encoded from the standard GE phantom head [41], we exhaustively examined the convergence of the Padé-reconstructed spectral parameters. Therein a high level of precision was attained, as seen in very small standard deviations obtained from the analysis of the reconstructed parameters from several consecutive values of the model order (or rank) K, after convergence had been reached. A similar approach is applied in the present paper, for the first time, on in vivo MRS time signals encoded from human brain. This provides full corroboration that exceedingly small variances are obtained for all four Padé-reconstructed parameters per resonance once convergence was achieved. By scrutinizing the nine consecutive iterations, progressively fewer and smaller discrepancies appear, until these reach the minimal level which is consistent with stochasticity contained in the encoded time signals. As to the rate of convergence of the spectral parameters, consistent with our previous study [21] on synthesized time signals associated with in vitro data encoded from ovarian lesions [50] and with controlled levels of added noise, the chemical shifts converged most rapidly, whereas the peak widths were the slowest to achieve convergence. These slowly converging peak widths are noted particularly, though not exclusively, as being located deep in the complex frequency plane.

Broadly speaking, we have herein addressed a type of inverse problem, whose basic characteristic is mathematical ill-conditioning or ill-posedness. This difficulty is due to the lack of continual dependence of observables on the independent variables (time in the FID for the studied harmonic inversion problem). Most troublesome is that the solution to an inverse problem is, in principle, non-unique. In other words, this ill-conditioning is seen in that some markedly different solutions are obtained for even a minimal change of the input data (e.g. slightly different truncation of the total acquisition time, etc.). With regard to total shape spectra, this ill-conditioning is reflected in the sensitivity of lineshapes to changes in model order K. The procedure of iterative averaging of envelopes through the FPT computed for a sequence of values of K is shown to be capable of fully stabilizing the total shape spectra. Stabilization of the spectral parameters is the most critical next step, and this is also achieved through Padé reconstructions from the FIDs given by the inverted averaged envelopes. In other words, the set of stabilized fundamental spectral parameters (complex frequencies and complex amplitudes) represent the unique solution to the harmonic inversion problem. We have thus seen that the fast Padé transform is fully capable of unequivocally solving the harmonic inversion problem for encoded time signals that are heavily corrupted with noise.

By parametrizing a general complex system, the system’s performance and dynamics are depicted through a fairly small set of its main features. For quantum mechanics, this complete information is contained in two equivalent concepts: the Schrödinger eigen value problem and the resolvent spectrum. Both approaches generate the frequency or energy spectrum as Heaviside partial fraction decomposition which exactly sums up to the quotient of two polynomials, in other words, to the Padé approximant. The fundamental frequencies and amplitudes are the parameters in the partial fractions that contain the complete information about the examined system. Thereby, quantum mechanics, through its completeness relation, fully and exactly parametrizes any system. Since the quantum mechanical spectrum is the unique ratio of two polynomials, the fast Padé transform is the optimal method of quantitatively describing the system’s performance. Stable dynamical parameters are the key to the stability of a given system, and this is the hallmark of a robust system. This stability can be achieved through the iterative averaging procedure, as has been thoroughly demonstrated herein.