Mathematical analysis of the heterogeneous photo-Fenton oxidation of acetic acid on structured catalysts

Abstract

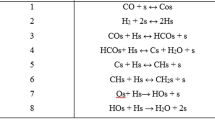
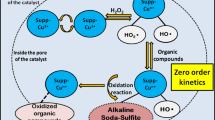
In this paper, we analyse the model for the UV-C photo-Fenton degradation of acetic acid using $LaFeO_{3}$ heterogeneous structured catalyst with a monolithic structure. The model is based on the occurrence of hydrogen peroxide photolysis and acetic acid oxidation in the heterogeneous phase, assumed first-order and Eley–Rideal type kinetics respectively. The main objective is to propose an analytical solution for the concentrations of $\hbox {CH}_{3}\hbox {COOH}$ and $\hbox {H}_{2}\hbox {O}_{2}$. A powerful analytical method called Homotopy Perturbation Method (HPM) has been employed to obtain approximate analytical solutions. The accuracy of the analytical solution is tested with the numerical solution. In this work the numerical solution of the problem is reported using SCILAB program. Stability Analysis of this model is also explained. The obtained analytical solution in comparison with the numerical and stability analysis is found to be in satisfactory agreement.

Appendices

Appendix 1

1.1 Basic idea of homotopy perturbation method

Consider the following non-linear differential equation

$$\begin{aligned} A(y)-f(r)=0, r\in \Omega , \end{aligned}$$

(18)

with the boundary conditions of

$$\begin{aligned} B\left( {y,\frac{\partial y}{\partial n}} \right) =0, r\in \Gamma , \end{aligned}$$

(19)

where A, B, f(r), and $\Gamma$ are a general differential operator, a boundary operator, a known analytic function and the boundary of the domain $\Omega$, respectively.

The operator A can generally be divided into a linear part L and a nonlinear part N. Equation (18) may therefore be written as,

$$\begin{aligned} L(y)+N(y)-f(r)=0, \end{aligned}$$

(20)

By the homotopy technique, we construct a homotopy $v (r,p):\Omega \times [0, 1]\rightarrow R$which satisfies

$$\begin{aligned} H(v,p)=(1-p)[L(v)-L(y_0 )]+p[A(v)-f(r)]=0 \end{aligned}$$

(21)

or

$$\begin{aligned} H(v,p)=L(v)-L(y_0 )+pL(y_0 )+p[N(v)-f(r)]=0, \end{aligned}$$

(22)

where $p\in [0, 1]$ is an embedding parameter, while $y_0$ is an initial approximation of (18), which satisfies the boundary conditions. Obviously, from (21) and (22) we will have

$$\begin{aligned} H(v,0)= & {} L(v)-L(y_0 )=0, \end{aligned}$$

(23)

$$\begin{aligned} H(v,1)= & {} A(v)-f(r)=0. \end{aligned}$$

(24)

The changing process of p from zero to unity is just that of v (r, p) from $y_0$ to y(r). In topology, this is called deformation, while $L(v)-L(y_0 )$ and $A(v)-f(r)$ are called homotopy. If the embedding parameter p is considered as a small parameter, applying the classical perturbation technique, we can assume that the solution of (21) and (22) can be written as a power series in p:

$$\begin{aligned} v=v_0 +pv_1 +p^{2}v_2 +p^{3}v_3 +\cdots \infty . \end{aligned}$$

(25)

Setting $p= 1$ in (25), we have

$$\begin{aligned} y=\mathop {\lim }\limits _{p\rightarrow 1} v=v_0 +v_1 +v_2 +\cdots . \end{aligned}$$

(26)

The combination of the perturbation method and the homotopy method is called the HPM, which eliminates the drawbacks of the traditional perturbation methods while keeping all its advantages. The series (26) is convergent for most cases. However, the convergent rate depends on the nonlinear operator A(v). Moreover, J.H. He made the following suggestions.

• 1. The second derivative of N(v)with respect to v must be small because the parameter may be relatively large, that is, $p\rightarrow 1$.

• 2. The norm of $L^{-1}\left( {\frac{\partial N}{\partial v}} \right)$ must be smaller than one so that the series converges.

Appendix 2

Using homotopy perturbation method, we construct a homotopy for the Eqs. (12) and (13) as follows

$$\begin{aligned} (1-p)\left[ {\frac{df_1 }{dT}+k\mu _1 \mu _2 f_1 } \right] +p\left[ {(1+\mu _1 f_1 )\frac{df_1 }{dT}+k\mu _1 f_1 (g_1 +\mu _2 )} \right] =0\qquad \end{aligned}$$

(27)

and

$$\begin{aligned}&(1-p)\left[ {\frac{dg_1 }{dT}+4k\mu _1 \mu _2 f_1 +g_1 } \right] \nonumber \\&\quad +p\left[ {(1+\mu _1 f_1 )\frac{dg_1 }{dT}+4k\mu _1 f_1 (g_1 +\mu _2 )+g_1 +\mu _1 f_1 g_1 } \right] =0 \end{aligned}$$

(28)

The approximate solution of (27) is as follows:

$$\begin{aligned} f_1 =f_{1,0} +pf_{1,1} +p^{2}f_{1,2} +\cdots \end{aligned}$$

(29)

The approximate solution of (28) is as follows:

$$\begin{aligned} g_1 =g_{1,0} +pg_{1,1} +p^{2}g_{1,2} +\cdots \end{aligned}$$

(30)

Substituting Eqs. (29) and (30) into Eq. (27) and arranging the coefficients of p powers, we have

$$\begin{aligned}&p^{0} : \frac{df_{1,0} }{dT}+k\mu _1 \mu _2 f_{1,0} =0 \end{aligned}$$

(31)

$$\begin{aligned}&p^{1} : \frac{df_{1,1} }{dT}+\mu _1 f_{1,0} \frac{df_{1,0} }{dT}+k\mu _1 \mu _2 f_{1,1} +k\mu _1 f_{1,0} g_{1,0} =0 \end{aligned}$$

(32)

Substituting Eqs. (29) and (30) into Eq. (28) and arranging the coefficients of p powers, we have

$$\begin{aligned}&p^{0} : \frac{dg_{1,0} }{dT}+4k\mu _1 \mu _2 f_{1,0} +g_{1,0} =0 \end{aligned}$$

(33)

$$\begin{aligned}&p^{1} : \frac{dg_{1,1} }{dT}+4k\mu _1 \mu _2 f_{1,1} +g_{1,1} +\mu _1 f_{1,0} \frac{dg_{1,0} }{dT}\nonumber \\&\quad +4k\mu _1 f_{1,0} g_{1,0} +\mu _1 f_{1,0} g_{1,0} =0 \end{aligned}$$

(34)

The initial approximations are as follows:

$$\begin{aligned} T=0 \; f_{1,0} =1 \end{aligned}$$

(35)

and

$$\begin{aligned} T= & {} 0 \; f_{1,i} =0 \hbox { for all } i = 1, 2, 3, \ldots \end{aligned}$$

(36)

$$\begin{aligned} T= & {} 0 \; g_{1,0} =\xi -\mu _2 \end{aligned}$$

(37)

and

$$\begin{aligned} T=0 \; g_{1,i} =0 \; \hbox { for all } \; i = 1, 2, 3, \ldots \end{aligned}$$

(38)

From Eq. (31) we get

$$\begin{aligned} f_{1,0} =e^{-BT} \end{aligned}$$

(39)

From Eq. (33) we get

$$\begin{aligned} g_{1,0} =\frac{1}{B-1}\left[ {4Be^{-BT}-Ae^{-T}} \right] \end{aligned}$$

(40)

Substituting Eqs. (39) and (40) in Eq. (32) we obtain the solution of Eq. (32),

$$\begin{aligned} f_{1,1}= & {} \frac{1}{B-1}\left[ \mu _1 (Ak-4k-1+B)e^{-BT}\right. \nonumber \\&\left. +\mu _1 kAe^{-(1+B)T}+\mu _1 (4k-B+1)e^{-2BT} \right] \end{aligned}$$

(41)

Using Eqs. (39) and (40) in Eq. (34) and then solving we get,

$$\begin{aligned} g_{1,1} =\frac{1}{C}\left[ {De^{-BT}-4Ee^{-(1+B)T}-8Fe^{-2BT}-4Ge^{-T}} \right] \end{aligned}$$

(42)

Adding (39) and (41) we get $f_1$, similarly adding (40) and (42) we get, $g_1$.

$$\begin{aligned} f=f_1 +f_e \hbox { },\hbox { }g=g_1 +g_e \end{aligned}$$

(43)

Using Eq. (43) we get Eq. (16) and Eq. (17) in the text.

Appendix 3

function catalysts

   options= odeset(’RelTol’,1e-6,’Stats’,’on’);

   Xo = [1; 0];

   tspan = [0,5];

   tic

   [t,X] = ode45(@TestFunction,tspan,Xo,options);

   toc

   figure

   hold on

   plot(t, X(:,1),’-’)

   plot(t, X(:,2),’-’)

   return

   function [dx_dt]= TestFunction(t,x)

   y1=0.05;

   y2=50;

   k=1;

   dx_dt(1) =-y1*k*x(1)*x(2)/(1+y1*x(1));

   dx_dt(2) =-4*y1*k*x(1)*x(2)/(1+y1*x(1))-x(2)+y2;

   dx_dt = dx_dt’;