Single-Photon Source with Emission Direction Controlled by a Qubit State

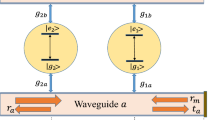
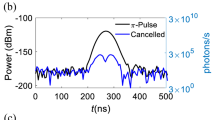
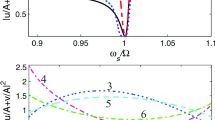
Abstract

We propose an experimentally feasible scheme for a source of itinerant microwave photons. It also features a quantum router that controls the direction of quantum microwave signals. This scheme consists of two superconducting qubits coupled to the transmission line in different regimes (strong and dispersive coupling). The dispersive coupling induces a shift in the resonance frequencies of coupled resonators, which depend on the dispersively coupled qubit state. We use this qubit to switch the direction of photon emission so that one output channel is blocked and the other is open, and vice versa, by changing the qubit state. We tune the bare frequencies of resonators and other system parameters to obtain a high efficient routing of photons. To demonstrate it, we implement a theoretical model of the proposed scheme and use the Jaynes–Cummings approach to describe the photon-matter interaction. We formulate a time-dependent wave function to study the behaviour of the proposed system. We derive and numerically solve a set of equations of motion governing the evolution of a single-photon wave packet. As a result, it is shown that the quantum signal can be routed in one of the two channels with high efficiency—nearly 90%.

Appendices

Appendix A Dynamics of Qubit-Open-Resonator System

Here, we present a model of a qubit and an open-resonator system interaction. This simpler model forms a base for our own. The Hamiltonian of the system, consisting of a qubit, a drain resonator, and a waveguide, is presented as follows

$$\begin{aligned} \begin{aligned} \dfrac{\hat{\mathcal {H}}_{q-r}}{\hbar }=&\omega _{q}\dfrac{\hat{\sigma }_{{z}}}{2} + \omega _{\text{r}}\hat{a}^{\dag }\hat{a}+ g(\hat{\sigma }_{+}\hat{a}+ \hat{a}^{\dag }\hat{\sigma }_{-}) + \int ^{\infty }_{-\infty }\,d\nu \,\nu \hat{b}^{\dag }_{\nu }\hat{b}_{\nu } \\&+ \sqrt{\dfrac{\kappa }{2\pi }} \int ^{\infty }_{-\infty }\,d\nu \,(\hat{a}^{\dag }\hat{b}_{\nu }+\hat{b}^{\dag }_{\nu }\hat{a}). \end{aligned} \end{aligned}$$

(A1)

The time-dependent wave function of the system has the form

$$\begin{aligned} |\psi (t)\rangle = \mathcal {Q}(t)\hat{\sigma }_{+}|\varnothing \rangle +\mathcal {A}(t)\hat{a}^{\dag }|\varnothing \rangle +\int \,d\omega \,\mathcal {B}_{\omega }(t)\hat{b}^{\dag }_{\omega }|\varnothing \rangle , \end{aligned}$$

(A2)

where $|\varnothing \rangle =|g\rangle |0_{r}\rangle |0_{w}\rangle$ means a vacuum state of the system. It defines that there is no excitation in neither resonator $|0_{r}\rangle$ nor waveguide $|0_{w}\rangle$, and the qubit is in a ground state $|g\rangle$. Thus, $\mathcal {Q}(t)$ is the amplitude of the qubit excited-state and vacuum-state resonator $|e\rangle |0_{r}\rangle |0_{w}\rangle =\hat{\sigma }_{+}|\varnothing \rangle$. $\mathcal {A}(t)$ stands for the amplitude of the excitation in the resonator $|g\rangle |1_{r}\rangle |0_{w}\rangle =\hat{a}^{\dag }|\varnothing \rangle$, so the qubit goes to the ground state $|g\rangle$ and emits a single-photon in the resonator field $|1_{r}\rangle$. $\mathcal {B}_{\nu }(t)$ is a continuum of modes of the single-photon wave packet, standing for amplitudes of states $\sum _{j}|g\rangle |0_{r}\rangle |1_{w}^{j}\rangle =\hat{b}^{\dag }_{\nu }|\varnothing \rangle$.

These amplitudes are determined through Heisenberg picture by the following expressions

$$\begin{aligned} \mathcal {Q}(t)&=\langle \varnothing |\hat{\sigma }_{-}(t)|\Psi (0)\rangle , \end{aligned}$$

(A3a)

$$\begin{aligned} \mathcal {A}(t)&=\langle \varnothing |\hat{a}(t)|\Psi (0)\rangle , \end{aligned}$$

(A3b)

$$\begin{aligned} \mathcal {B}_{\omega }(t)&=\langle \varnothing |\hat{b}_{\omega }(t)|\Psi (0)\rangle . \end{aligned}$$

(A3c)

Making use of the Heisenberg method, one can derive a set of coupled equations of motion

$$\begin{aligned}&\left( \dfrac{\partial }{\partial t}+i\omega _{r}+\dfrac{\kappa }{2}\right) \,\mathcal {A}(t)=-ig \mathcal {Q}(t), \end{aligned}$$

(A4a)

$$\begin{aligned}&\left( \dfrac{\partial }{\partial t} +i\omega _{q}\right) \,\mathcal {Q}(t)=-ig \mathcal {A}(t), \end{aligned}$$

(A4b)

$$\begin{aligned}&\left( \dfrac{\partial }{\partial t}+i\nu \right) \,\mathcal {B}_{\nu }(t)=-iU \mathcal {A}(t), \end{aligned}$$

(A4c)

where $\kappa = 2\pi U^{2}$. The solution of the above system reads as

$$\begin{aligned} \mathcal {A}(t)&=g\dfrac{1}{\varepsilon ^{+}-\varepsilon ^{-}}\left( e^{-i(\omega _{q}-\varepsilon ^{-})t}-e^{-i(\omega _{q}-\varepsilon ^{+})t} \right) , \end{aligned}$$

(A5a)

$$\begin{aligned} \mathcal {Q}(t)&=\dfrac{\varepsilon ^{+}}{\varepsilon ^{+}-\varepsilon ^{-}}e^{-i(\omega _{q}-\varepsilon ^{-})t}-\dfrac{\varepsilon ^{-}}{\varepsilon ^{+}-\varepsilon ^{-}}e^{-i(\omega _{q}-\varepsilon ^{+})t}, \end{aligned}$$

(A5b)

$$\begin{aligned} B_{\nu }(t)&=g\sqrt{\dfrac{\kappa }{2\pi }} \left( \dfrac{1}{(\varepsilon ^{+}-\varepsilon ^{-})(\omega _{q}-\nu -\varepsilon ^{-})} e^{-i(\omega _{q}-\varepsilon ^{-})t} \right. \nonumber \\&\quad \left. -\dfrac{1}{(\varepsilon ^{+}-\varepsilon ^{-})(\omega _{q}-\nu -\varepsilon ^{+})} e^{-i(\omega _{q}-\varepsilon ^{+})t}+\dfrac{\varepsilon ^{+}\varepsilon ^{-}}{(\omega _{q}-\nu -\varepsilon ^{-})(\omega _{q}-\nu -\varepsilon ^{+})}e^{-i\nu t} \right) . \end{aligned}$$

(A5c)

The following term

$$\begin{aligned} \varepsilon ^{\pm }= \dfrac{1}{2}\left( \Delta \pm \sqrt{4g^{2}+\Delta ^{2}}\right) , \end{aligned}$$

(A6)

where $\Delta =\omega _{q}-\left( \omega _{r}-i\kappa /2\right)$, corresponds to the complex single-excitation resonances of the qubit open-resonator system.

Appendix B Derivation of the Hamiltonian (12)

In this appendix, the effective Hamiltonian (12) is obtained by the Hadamard formula

$$\begin{aligned} e^{\lambda A}B e^{-\lambda A}=B+\lambda [A,B]+\dfrac{\lambda ^{2}}{2!}[A,[A,B]]+... \end{aligned}$$

(B7)

In terms of Eq. (10) and Eq. (11), this relation to the second order of $\lambda$ takes the form

$$\begin{aligned} \sum _{{j}=1,2}e^{\lambda _{{j}} \hat{X}}\hat{\mathcal {H}}e^{-\lambda _{{j}} \hat{X}}=\sum _{{j}=1,2}\left( \hat{\mathcal {H}}+\lambda _{{j}}[\hat{X},\hat{\mathcal {H}}]+\dfrac{\lambda _{{j}}^{2}}{2!}[\hat{X},[\hat{X},\hat{\mathcal {H}}]]\right) , \end{aligned}$$

(B8)

where $\hat{X}=\hat{a}^{\dag }_{{j}}\hat{\sigma }_{-}^{\text{c}}-\hat{a}_{{j}}\hat{\sigma }_{+}^{\text{c}}$.

After executing all commutators in Eq. (B8), one can reach

$$\begin{aligned} \begin{aligned} \hat{\mathcal {H}}_\text {eff}&= \hat{\mathcal {H}}_{0}+\hbar \sum _{{j}=1,2}\left( \omega _{{j}}^{r}+\lambda _{{j}}f_{{j}}\hat{\sigma }^{\text{c}}_{{z}} \right) \hat{a}^{\dag }_{{j}}\hat{a}_{{j}}+\hbar \sum _{{j}=1,2}J_{{j}}\left( \hat{a}^{\dag }_{{j}}\hat{c}_{{j}}+\hat{a}_{{j}}\hat{c}^{\dag }_{{j}}\right) +\hbar J'\left( \hat{a}^{\dag }_{2}\hat{a}_{1} \right. \\&\quad \left. + \hat{a}_{2}\hat{a}^{\dag }_{1}\right) + \hbar \sum _{{j}=1,2}\,\lambda _{{j}}\left[ g_{{j}}\left( \hat{\sigma }^{\text{c}}_{+}\hat{\sigma }_{-}^{\text{s}}+\hat{\sigma }^{\text{c}}_{-}\hat{\sigma }_{+}^{\text{s}}\right) +J_{{j}}\left( \hat{c}^{\dag }_{{j}}\hat{\sigma }^{\text{c}}_{-}+\hat{c}_{{j}}\hat{\sigma }^{\text{c}}_{+}\right) \right] +\mathcal {O}(\lambda _{{j}}^{2}), \end{aligned} \end{aligned}$$

(B9)

where $\hat{\mathcal {H}}_{0}=\hat{\mathcal {H}}_{\text{s}\text{q}}+\hat{\mathcal {H}}_{{f}}+\hat{\mathcal {H}}_{{w}}$.

The first term in the following expression

$$\begin{aligned} \hbar \sum _{{j}=1,2}\,\lambda _{{j}}\left[ g_{{j}}\left( \hat{\sigma }^{\text{c}}_{+}\hat{\sigma }_{-}^{\text{s}}+\hat{\sigma }^{\text{c}}_{-}\hat{\sigma }_{+}^{\text{s}}\right) +J_{{j}}\left( \hat{c}^{\dag }_{{j}}\hat{\sigma }^{\text{c}}_{-}+\hat{c}_{{j}}\hat{\sigma }^{\text{c}}_{+}\right) \right] \end{aligned}$$

(B10)

describes the coupling between the source qubit and the control qubit. The second term describes the coupling between the filters and the control qubit. Since $\lambda _{{j}}$ is a vanishing parameter (see Eq. (9)) and considering that inter-qubits detuning and control-qubit-filters detuning are large, we neglect these two terms. Consequently, the Hamiltonian $\hat{\mathcal {H}}_\text {eff}$ given by Eq. (B9) is reduced to the form of (12).

Appendix C System Dynamics

1.1 C.1 Heisenberg Equations

Using the Hamiltonian $\hat{\mathcal {H}}_\text {eff}$ given by Eq. (12), one obtains the Heisenberg equations for the source-qubit variable

$$\begin{aligned} \left( \dfrac{\partial }{\partial t}+i\omega _{\text{s}}\right) \hat{\sigma }_{-}^{\text{s}}=i\hat{\sigma }_{{z}}^{\text{s}}\sum _{{j}=1}^{2}g_{{j}}\hat{a}_{{j}}. \end{aligned}$$

(C11)

The equation of motion for the j-th resonator variable is read as

$$\begin{aligned} \left( \dfrac{\partial }{\partial t}+i\varpi _{{j}}^{r}\right) \hat{a}_{{j}}=-ig_{{j}}\hat{\sigma }_{-}^{\text{s}}-iJ^{\prime }\hat{a}_{{j}'}-iJ_{{j}}\hat{c}_{{j}}, \quad {j}'\ne {j}, \end{aligned}$$

(C12)

and for the j-th filter variable

$$\begin{aligned} \left( \dfrac{\partial }{\partial t}+i\omega _{{j}}^{{f}}\right) \hat{c}_{{j}}=-iJ_{{j}}\hat{a}_{{j}}-iU_{{j}}\int d\nu \hat{b}_{{j}\nu }, \end{aligned}$$

(C13)

where $\{{j},{j}'\}\in \{1,2\}$. Waveguides variable obeys the equation of motion as follows

$$\begin{aligned} \left( \dfrac{\partial }{\partial t}+i\nu \right) \hat{b}_{{j}\nu }=-iU_{{j}}\hat{c}_{{j}}, \end{aligned}$$

(C14)

with the formal solution written as

$$\begin{aligned} \hat{b}_{{j}\nu }(t)=\hat{b}_{{j}\nu }(0)e^{-i\nu t}-iU_{{j}}\int _{0}^{t}d\tau e^{-i\nu (t-\tau )}\hat{c}_{{j}}(\tau ). \end{aligned}$$

(C15)

Integration of both sides of the above relation over photon frequencies $\nu$ leads to

$$\begin{aligned} \int d\nu \hat{b}_{{j}\nu }=\hat{B}_{{j}}^{in}-i\sqrt{\dfrac{\pi \kappa _{{j}}}{2}}\hat{c}_{{j}}, \end{aligned}$$

(C16)

where operator $\hat{B}_{{j}}^{in}=\int d\nu \exp (-i\nu t)\hat{b}_{{j}\nu }(0)$ stands for the input operator of the field in the ${j}$-th waveguide [56]. Substituting Eq. (C16) into Eq. (C13), one obtains

$$\begin{aligned} \left( \dfrac{\partial }{\partial t}+i\tilde{\omega }_{{j}}^{{f}}\right) \hat{c}_{{j}}=-iJ_{{j}}\hat{a}_{{j}}-iU_{{j}}\hat{B}_{{j}}^{in}, \end{aligned}$$

(C17)

where we have introduced a notation $\tilde{\omega }_{{j}}^{{f}}=\omega _{{j}}^{{f}}-i\kappa _{{j}}/2$.

1.2 C.2 Wave Function of the System

Fig. 6

States of the subsystem $\mathcal {S}$ in the single-excitation sector and transition pathways between these states. Dashed lines indicate an irreversible leakage of the photon from the resonator to the waveguide. The initial state of the subsystem $\mathcal {S}$ is shown by the shaded bar

In the dispersive regime interaction between the control qubit and the drain resonators, the number of excitation in the subsystem $\mathcal {S}$ is conserved since $\left[ \hat{\mathcal {N}}_{ex}^{\mathcal {S}},\hat{\mathcal {H}}_\text {eff}\right] =0$, where $\hat{\mathcal {N}}_{ex}^{\mathcal {S}}$ stands for the operator of the excitation number in $\mathcal {S}$, given by

$$\begin{aligned} \hat{\mathcal {N}}_{ex}^{\mathcal {S}}=\sigma _{+}^{\text{s}}\sigma _{-}^{\text{s}}+\sum _{{j}=1}^{2}\left( \hat{a}^{\dag }_{{j}}\hat{a}_{{j}}+\hat{c}^{\dag }_{{j}}\hat{c}_{{j}}+\int d\omega \hat{b}^{\dag }_{{j}\omega }\hat{b}_{{j}\omega }\right) . \end{aligned}$$

(C18)

Thus, in the dispersive regime (9), the state of the system at the arbitrary moment t can be expressed as

$$\begin{aligned} |\Psi (t)\rangle =|\psi _{\mathcal {S}}(t)\rangle \otimes |\Phi _{C}\rangle , \end{aligned}$$

(C19)

where $|\psi _{\mathcal {S}}\rangle$ and $|\Phi _{C}\rangle$ denote the states of the subsystem $\mathcal {S}$ and the control qubit, respectively.

The subsystem $\mathcal {S}$ is expressed as

$$\begin{aligned} \begin{aligned} |\psi _{\mathcal {S}}(t)\rangle =&\sum _{{j}=1}^{2}\int d\nu \mathcal {B}_{{j}\nu }(t)\hat{b}^{\dag }_{{j}\nu }|\varnothing \rangle \\&+\sum _{{j}=1}^{2}\left[ \mathcal {A}_{{j}}(t)\hat{a}^{\dag }_{{j}} +\mathcal {C}_{{j}}(t)\hat{c}^{\dag }_{{j}}\right] |\varnothing \rangle +\mathcal {Q}(t)\hat{\sigma }_{+}^{\text{s}}|\varnothing \rangle , \end{aligned} \end{aligned}$$

(C20)

where $|\varnothing \rangle =|g\rangle |0;0\rangle _{\text{r}}|0;0\rangle _{{f}}|0;0\rangle _{{w}}$ is a vacuum state of the subsystem $\mathcal {S}$. The initial (at $t=0$) state of the system $|\Psi \rangle _{in}\equiv |\Psi (0)\rangle$ is given by

$$\begin{aligned} |\Psi \rangle _{in}=\hat{\sigma }_{+}^{\text{s}}|\varnothing \rangle . \end{aligned}$$

(C21)

Fig. 7

Excitation dynamics of subsystem $\mathcal {S}$. The density probabilities $|Q(t)|^2$ (blue), $|A_{{j}}(t)|^2$ (orange for ${j}=1$ and red for ${j}=2$) are depicted on (a); $|C_{{j}}(t)|^2$ (pink for ${j}=1$ and purple for ${j}=2$) are depicted on (b). The parameters are the same as in Fig. 5

The schematic illustration of the state of the system conversion is depicted on Fig. 6.

Here, we neglect the effect of thermal photons on the dynamics of the system. Circuit QED setups typically operate at temperatures $T_{s}\sim 10-20 mK$ that gives the average number of thermal photons in the system $n_{th}\sim 10^{-3}$ justifying our approximation.

The probability amplitudes entering the wave function (C20) are governed by the equations of motion as follows

$$\begin{aligned} {\textbf {A}}(t)\equiv \left( \begin{array}{c} \mathcal {Q}(t)\\ \mathcal {A}_{{j}}(t)\\ \mathcal {C}_{{j}}(t)\\ \mathcal {B}_{{j}\nu }(t) \end{array} \right) = \left( \begin{array}{c} \langle \varnothing |\hat{\sigma }_{-}^{\text{s}}(t)|\Psi _{in}\rangle \\ \langle \varnothing |\hat{a}_{{j}}(t)|\Psi _{in}\rangle \\ \langle \varnothing |\hat{c}_{{j}}(t)|\Psi _{in}\rangle \\ \langle \varnothing |\hat{b}_{{j}\nu }(t)|\Psi _{in}\rangle \end{array} \right) , \end{aligned}$$

(C22)

$$\begin{aligned} \left( {\textbf {I}}\dfrac{\partial }{\partial t}+{\textbf {X}}\right) {\textbf {A}}(t)=0, \end{aligned}$$

(C23)

where ${\textbf {I}}$ stands for the identity matrix and ${\textbf {X}}$ reads as

$$\begin{aligned} \left( \begin{array}{c c c c c c c} \omega _{s} &{} g_{1} &{} g_{2} &{} 0 &{} 0 &{} 0 &{} 0 \\ g_{1} &{} \varpi _{1}^{\text{r}} &{} J^{\prime } &{} J_{1} &{} 0 &{} 0 &{} 0\\ g_{2} &{} J^{\prime } &{} \varpi _{2}^{\text{r}} &{} 0 &{} J_{2} &{} 0 &{} 0\\ 0 &{} J_{1} &{} 0 &{} \tilde{\omega }_{1}^{{f}} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} J_{2} &{} 0 &{} \tilde{\omega }_{2}^{{f}} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} U_{1} &{} 0 &{} \nu &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} U_{2} &{} 0 &{} \nu \end{array} \right) . \end{aligned}$$

(C24)

The solution of Eq. C23 is used to study the dynamics of wave function in the system (see Figs. 5 and 7).