Pulse Shape Analysis in Low-temperature Calorimeters Read-Out by NTD Thermistors

Abstract

We present the application of a simplified thermal model for the description of the response function of low-temperature calorimeters consisting of $\hbox {TeO}_2$ crystals read-out by NTD thermistors operated at temperatures $T \sim 10$ mK. Relying on both the analysis of the NTD load curves (from which we measured the main thermal conductances of the system) (Biassoni et al. in J Low Temp Phys 206:80–96, 2022) and on the analysis of the shape of thermal pulses acquired at different temperatures, we identified and quantified the physical parameters that determine the characteristic time constants of the pulses. In particular, we identified three different contributions to the heat capacity of the detector: the crystal phonon system (scaling as $T^3$), the NTD electron system (scaling as T) and a term related to the metalization process of the NTD electrodes (scaling as $T^{-2}$).

1 Introduction to Low-temperature Detectors

In a low-temperature detector operating in quasi-equilibrium mode, the energy deposited by a particle is converted into phonons and measured as a temperature variation ( [2,3,4] and references therein). In a simplified model, the detector consists of three main components: an absorber, where the energy released by a particle causes an increase in its temperature, a temperature sensor, which converts the phonon excitation into a measurable electric signal, and a weak thermal link between the detector and a heat bath kept at constant temperature, which allows the system to return to the initial base temperature.

The detectors have to be operated at cryogenic temperatures ($10-100$ mK), otherwise the unavoidable thermal fluctuations would hide the signal generated by the energy deposition. The amplitude of thermal pulses is proportional to the deposited energy E and inversely proportional to the thermal capacity C(T) of the detector, which is a function of the temperature.

Neutron transmutation-doped germanium thermistors (NTDs) [5, 6] are widely used as temperature sensors. Below $\sim 10$ K, in the Variable Range Hopping (VRH) electrical conductivity regime [7], the relation between electrical resistivity $\rho$ and electrons temperature $T_e$ is described by the Efros–Shklovskii variant of the Mott law:

$$\begin{aligned} \rho (T_e) = \rho _0 \exp \left( \dfrac{T_0}{T_e} \right) ^{\frac{1}{2}} \end{aligned}$$

(1)

where $\rho _0$ and $T_0$ are two parameters related to the concentration of the dopants.

For low enough values of bias voltage, the NTD is in an ohmic regime, while for higher values it enters in a non-ohmic regime [8, 9].

2 Dynamic Electro-Thermal Model

When a particle interacts in the absorber of a cryogenic detector, the released energy flows towards the heat bath through the thermal conductances. A way to describe the dynamic response of a low-temperature calorimeter consists in the modelling of the detector as an electro-thermal circuit. The associated out-of-equilibrium differential equations have to be solved in order to determine the shape of the pulse and the values of the unknown parameters (namely electric and thermal capacities and thermal conductances). This system of differential equations can be solved using numerical methods. Alternatively, the complexity of the description of the system can be reduced, so that approximated solutions can be calculated analytically. In this paper, we will discuss the simplest model that can be formulated for a low-temperature calorimeter.

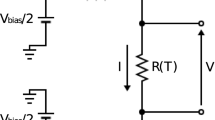
Figure 1a shows the general electro-thermal circuit of a calorimeter in which the thermal nodes of the absorber and of the NTD are linked, through different thermal conductances, among themselves and with the heat bath. In the minimal representation of the thermal model (single-stage thermal model, see Fig. 1b), the absorber and the temperature sensor can be considered as a single thermal body with a total thermal capacity C (that accounts for the thermal capacities of both the crystal absorber and of the NTD). The link to the thermal bath is described by a single effective conductance $G_{eff}$. In the small-signal limit, in which the temperature increase due to the energy deposition is much smaller than the base temperature $T_b$, thermal capacities and thermal conductances can be considered constant over time. The solution $\varDelta T(t) = T(t) - T_b$ of the simplified circuit, that describes the response function of the system, is:

$$\begin{aligned} \varDelta T(t) = \dfrac{\tau _D \quad \tau _R}{\tau _D - \tau _R} \, \left( e^{-\frac{t}{\tau _D}} - e^{-\frac{t}{\tau _R}} \right) \quad , \quad \tau _R = R_{dyn} C_p \quad , \quad \tau _D = \dfrac{C}{G_{eff}} \end{aligned}$$

(2)

where $R_{dyn}$ is the NTD dynamic impedance and $C_p$ is the parasitic capacitance of the NTD read-out wires. If $\tau _R < \tau _D$, the pulse shape is described as an exponential rising edge with characteristic time constant $\tau _R$ and an exponential decay tail with characteristic time constant $\tau _D$.

Fig. 1

a) Scheme of a general electro-thermal circuit for a system NTD-absorber-heat bath with the associated read-out circuit (from [10]). b) Single-stage approximation of the thermal circuit for a low-temperature calorimeter: a single thermal conductance couples the low-temperature calorimeter (considered as a whole) with the heat bath (color figure Online)

3 Experimental Set-up

We studied two low-temperature calorimeters consisting of tellurium dioxide ($\hbox {TeO}_2$) crystal absorbers read-out by Ge-NTDs, operated in an Oxford TLE-200 $^{3}\hbox {He}$ -$^{4}\hbox {He}$ dilution refrigerator [11] at the cryogenic facility of the University of Milano - Bicocca. The two crystals (labelled as A, B) have the same size and mass ($10 \times 10 \times 10 \,\mathrm {mm^3}$, 6.3 g), and each was equipped with two NTDs glued (through Araldite $\hbox {Rapid}^{\mathrm{TM}}$) on two opposite sides of the crystal itself. The NTDs belong to two different production sets: batch 33C and a test batch used for tests on gold deposition for the NTD electrodes. The 33C-NTDs have identical size and mass ($\simeq 3 \times 3 \times 1 \,\mathrm {mm^3}$, $\simeq 48$ mg), while the test-NTDs are bigger ($\simeq 3.3 \times 3 \times 1.4 \,\mathrm {mm^3}$, $\simeq 75$ mg). 33C-NTDs and test-NTDs were produced from two different germanium wafers that were irradiated with similar doses of neutrons in order to reach similar doping conditions. The electrodes of NTDs belonging to different batches are produced differently. In both cases the surface of the germanium wafers, from which the NTDs are produced, is ion-implanted with $^{11}\hbox {B}$ ions (the implantation thickness is 200 nm). The $^{11}\hbox {B}$ implantation flux was $\simeq 4.2 \cdot 10^{14}$ ions/cm$^2$ for 33C-NTDs and $\simeq 3.45 \cdot 10^{14}$ ions/cm$^2$ for test-NTDs. Then, a metal adhesion layer (20 nm thick) is evaporated: it consists in a palladium film for 33C-NTDs, while for test-NTDs it is made of chromium. Atop of it, the electric contact is provided by gold pads (400 nm thick in 33C-NTDs and 50 nm thick in test-NTDs), that are read-out by gold wires ($50 \, \mathrm {\mu m}$ diameter).

The experimental set-up is shown in Fig. 2. The two $\hbox {TeO}_2$ crystals were glued, through one spot of Araldite Rapid^TM, to a copper holder. The holder was screwed to a copper plate linked to the mixing chamber of the dilution refrigerator. The temperature of the copper plate was measured using a Noise Thermometer (NT) [12].

We acquired data over three different runs. After the first run, both crystal A and its test-NTD got unglued. The test-NTD was discarded, while crystal A, with only its 33C-NTD (labelled NTD-$\alpha$) still glued on it, was re-glued to the holder.

Fig. 2

Picture of the experimental set-up: acrylic and copper samples mounts are linked to the mixing chamber of the cryostat. The noise thermometer is attached to the top of the mixing chamber cold plate, as shown. This work focuses on the two $\hbox {TeO}_2$ calorimeters (labelled as A, B) attached to the copper mount. The acrylic holder was not considered for this study (color figure Online)

4 Pulse Shape Analysis

In order to study the dynamic thermal response of the NTDs in the copper holder, we acquired, at different temperatures (from $\simeq 10$ mK to $\simeq 20$ mK), thermal pulses generated by the energy deposition of real particles in the detector absorber. For this purpose, during the data acquisition, $^{60}\hbox {Co}$ and $^{232}\hbox {Th}$ radioactive $\gamma$-sources were deployed outside of the outer vacuum chamber (OVC) of the cryostat.

NTDs were operated in the ohmic regime, namely in a configuration of low bias current ($I_{bias} \sim$ pA). We studied three NTDs: NTD-3 (belonging to the test batch), NTD-$\alpha$ and NTD-$\beta$ (both belonging to batch 33C). NTD-3 and NTD-$\beta$ were glued to crystal B, while NTD-$\alpha$ to crystal A.

According to the single-stage dynamic thermal model, we performed the fit of single thermal pulses with Eq. 2. At each temperature, the best estimation of rise time and decay time was evaluated as the median of the values obtained from the fit of all the single pulses not suffering from pile-up. Moreover, an upper cut on the $\chi ^2$ of the fit of single pulses was applied in order to reject cases for which the fit does not converge due to deformed pulses or baseline instabilities. The number of events fulfilling these requirements that were used to evaluate the median of the pulses time constants of different detectors at different temperatures varies from $\gtrsim$ 100 to $\gtrsim$ 8000. Figure 3 shows examples of fit of single pulses acquired by NTD-$\beta$ at two different temperatures and the associated normalized residuals. The response function evaluated from the thermal model describes with good accuracy the shape of real pulses throughout the temperature range. By comparing Fig. 3a and 3b, we point out that pulses become much faster as the temperature increase, but they also became smaller in amplitude (compare the relative amplitudes between the normalized pulse and the baseline fluctuations).

Fig. 3

Example of the normalized fit of single pulses acquired by NTD-$\beta$ on detector B operated at: a) temperature $T=11$ mK and bias current $I_{bias} \simeq$ 7 pA; b) temperature $T=19.8$ mK and bias current $I_{bias} \simeq$ 7 pA. The normalized fit residuals are also shown for each case (color figure Online)

Fig. 4

Plot of the ratio between dynamic resistance $R_{dyn}$ and static resistance R as a function of the bias voltage for NTD-$\beta$ at different temperatures. The vertical line represents the value of $V_{bias}$ ($V_{bias} = 0.1$ V) at which pulses were acquired (color figure Online)

4.1 Pulse Rise Time

According to the single-stage thermal model, the rise time is linearly correlated with the NTD dynamic impedance $R_{dyn}=\frac{dV}{dI}$ (Eq. 2). The dynamic impedance can be evaluated from the NTD current–voltage (I–V) load curve [1]. Pulses were acquired with $V_{bias} = 0.1$ V and load resistance $R_{load} = 15$ G$\varOmega$, a working point for which NTDs are in the ohmic regime, and dynamic and static resistances are almost equal ($R_{dyn} \simeq R$) (Fig. 4). Figure 5a shows the relation between the pulse rise times and the NTD static resistance. By performing a linear fit with Eq. 2, we estimated the parasitic capacitance of read-out wires to be $C_p^{fit}=(423 \pm 25)$ pF, in agreement with the value obtained independently with a dedicated measurement,

$C_p^{meas}=(407 \pm 20)$ pF.

4.2 Pulse Decay Time

According to the single-stage thermal model, the decay time is correlated to a C/G pole (Eq. 2). The conductance that determines the link between each calorimeter and the heat bath was quantified (through the analysis of NTD load curves acquired at different temperatures) and identified to be the conductance of the glue between the $\hbox {TeO}_2$ crystal absorbers and the copper holder [1]:

$$\begin{aligned} G_{eff}(T) \equiv G_{glue}(T) = g_{glue} \quad T^{\alpha } \quad , \quad g_{glue} \sim 10^{-3} \quad \mathrm {W/K^{\alpha +1}} \quad , \quad \alpha = 3.0 \pm 0.1. \end{aligned}$$

(3)

The total thermal capacity C(T) of each calorimeter is given by the sum of the crystal contribution $C_{crystal}$ and of the NTD contribution $C_{NTD}$:

$$\begin{aligned} C(T) = C_{crystal}(T) + C_{NTD,tot}(T) \quad , \quad C_{NTD,tot}(T) = \sum _{i=1}^{n} \quad C_{NTD,i}(T) \end{aligned}$$

(4)

where n is the number of NTDs glued on each crystal. $\hbox {TeO}_2$ is a dielectric and diamagnetic crystal: at temperatures well below the Debye temperature $\varTheta _D ({\hbox {TeO}_2}) = 232$ K [13], the crystal thermal capacity is described by the Debye law . For our $1 \times 1 \times 1 \,\mathrm {cm^3}$ crystals:

$$\begin{aligned} C_{crystal}(T) = 2.76 \cdot 10^{-5} \quad T[K]^3 \quad \mathrm {J/K}. \end{aligned}$$

(5)

We model the thermal capacity of each NTD as the sum of two contributions:

$$\begin{aligned} C_{NTD}(T) = V \quad c_e(T) + C'(T) \end{aligned}$$

(6)

where V is the NTD volume and $c_e$ is the electron specific heat per unitary volume, scaling as:

$$\begin{aligned} c_e(T) = \gamma \quad T. \end{aligned}$$

(7)

$C'$ is an additional thermal capacity contribution, parametrized as:

$$\begin{aligned} C'(T) = S \quad c_S(T) \quad , \quad c_S(T) = A \quad T^{-2} \end{aligned}$$

(8)

where S is the electrode area and $c_S$ is an additional specific heat (per unitary area). A similar behaviour has been already reported in the literature ( [14]) for variable range hopping (VRH) semiconductors, claiming some Schottky anomaly related to the interaction of $\hbox {B}^+$ ions with the germanium substrate.

Figure 5b shows the plot of $C_{NTD,tot} \quad T_e^2$ vs $T_e^3$. $C_{NTD,tot}$ was experimentally evaluated knowing the pulse decay time constant, the effective thermal conductance and the crystal thermal capacity (Eqs. 2, 3, 4 and 5). In the plot, data associated with the configurations in which one or two NTDs were glued on the same crystal are well separated. In order to estimate $\gamma$ and A, we performed a simultaneous fit of all the data using:

$$\begin{aligned} C_{NTD}(T) = V \quad \gamma \quad T + S \quad A \quad T^{-2} \end{aligned}$$

(9)

where we considered the contribution from a 33C-NTD alone or from both a 33C-NTD and a test-NTD depending on the configuration. Since all the NTDs have shown experimentally similar doping properties ($\overline{T_0} = (4.76 \pm 0.04)$ K [1]), the parameter $\gamma$ associated to the electron specific heat is assumed to be the same for all of them (Table 1). Parameter A is assumed to be different for NTDs of the two batches because of the different electrode realization processes. The values of parameter A estimated from the fit (Table 1) for 33C-NTDs and for test-NTDs differ by roughly an order of magnitude. Given the associated uncertainties, parameter A is compatible with zero for the 33C-NTDs, while it is not for the test-NTDs. Therefore we can infer that the contribution of the Schottky anomaly term to the thermal capacity appears to be not negligible for the test-NTDs. We aim to perform further studies in the near future to better investigate the source of this additional specific heat contribution. In fact, the identification of the different physical parameters that determine the characteristic time constants of thermal pulses is of great importance in order to understand the behaviour of low-temperature calorimetric experiments and to optimize their performance. This is especially true regarding the determination of NTD specific heat contributions, since their detailed characterization can help in the optimization of calorimeters overall.

Fig. 5

a) Distribution of rise time as a function of NTDs resistance. b) Distribution of the total thermal capacity of the NTDs on each crystal as a function of the electron temperature (color figure Online)

Table 1 Estimation, from the analysis of the decay time of pulses acquired at different temperatures, of the parameters related to different contributions to the NTDs specific heat

5 Conclusions

We applied a simplified electro-thermal model to study the response function of low-temperature calorimeters consisting of two $\hbox {TeO}_2$ crystals read-out by NTDs. The pulse shape is described as an exponential rising edge and an exponential decay tail. The rise time is determined by the coupling of the NTD resistance with the parasitic capacitance of read-out wires, while the decay time by the coupling of the calorimeter thermal capacity with the thermal conductance between detector and heat bath. From the measured pulse decay times, and relying on the analysis of NTD load curves (that allowed us to measure the dominant thermal conductance), we identified two contributions to the NTD thermal capacity: one associated with the electron system of the NTD (scaling as T) and an additional one (scaling as $T^{-2}$) that appears to correlate with the process of realization of the NTD electrode.