Abstract
My contribution to this collection of articles in honor of David Lee and John Reppy on their 90th birthdays is a reflection on the remarkable phenomenology of the excitation spectra of superfluid \(^3\)He, in particular the B-phase which was identified by NMR and acoustic spectroscopy as the Balian–Werthamer state shown in 1963 to be the ground state of a spin-triplet, p-wave superconductor within weak-coupling BCS theory. The superfluid phases of \(^3\)He provide paradigms for electronic superconductors with broken space-time symmetries and non-trivial ground-state topology. Indeed, broken spin- and orbital rotation symmetries lead to a rich spectrum of collective modes of the order parameter that can be detected using NMR, acoustic and microwave spectroscopies. The topology of the BW state implies its low-temperature, low-energy transport properties are dominated by gapless Majorana modes confined on boundaries or interfaces. Given the central role the BW state played I discuss the acoustic and electromagnetic signatures of the BW state, the latter being relevant if an electronic analog of superfluid \(^3\)He-B is realized.




Similar content being viewed by others
Notes
Many features of the analysis to follow are semi-quantitatively correct for anisotropic unconventional superconductors.
I omitted contributions from off-resonant collective modes with \(J\ne 0\). This is justified in the London limit \(v_fq\ll \Delta\). Note that
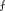 is principal part integration in the neighborhood of the integrable singularities at \(\pm \frac{1}{2}\eta\).
is principal part integration in the neighborhood of the integrable singularities at \(\pm \frac{1}{2}\eta\).Note that the discoveries of the \(J=0^{+}\) Higgs mode in NbSe\(_2\) and the \(J=2^{+}\) Higgs mode in \(^3\)He-B were all published in Physical Review Letters within a month of each other in the summer of 1980.
The BW state remains the ground state within weak-coupling theory even with an additional attractive, but subdominant, pairing channel, e.g., an attractive f-wave pairing interaction [86]. However, as is well known, strong-coupling corrections to the weak-coupling free energy functional stabilize anisotropic states. Indeed, the A phase is the realization of the anisotropic Anderson–Morel state.
References
R. Balian, N.R. Werthamer, Superconductivity with Pairs in a relative P-state. Phys. Rev. 131, 1553 (1963)
P.W. Anderson, P. Morel, Generalized Bardeen-Cooper-Schrieffer states and the proposed low-temperature phase of \(^3\)He. Phys. Rev. 123, 1911 (1961)
A.J. Leggett, Theoretical description of the new phases of liquid \(^3\)He. Rev. Mod. Phys. 47, 331 (1975)
P.W. Anderson, W.F. Brinkman, in The Physics of Liquid and Solid Helium. (J. ed. by K. Benneman, J. Ketterson (Wiley & Sons, New York, 1978), pp. 177–286
D.M. Lee, R.C. Richardson, in The Physics of Liquid and Solid Helium. ed. by K. Benneman, J. Ketterson (J. Wiley & Sons, New York, 1978), pp. 287–496
D. Vollhardt, P. Wölfle, The Superfluid Phases of\(^3\)He (Taylor & Francis, New York, 1990)
J. Bardeen, L. Cooper, J. Schrieffer, Theory of superconductivity. Phys. Rev. 108, 1175 (1957)
P.W. Anderson, coherent excited states in the theory of superconductivity: gauge invariance and the meissner effect. Phys. Rev. 110, 827 (1958)
Y. Nambu, Quasi-particles and gauge invariance in the theory of superconductivity. Phys. Rev. 117, 648 (1960)
P.W. Anderson, Random-phase approximation in the theory of superconductivity. Phys. Rev. 112, 1900 (1958)
N.N. Bogoliubov, V.V. Tolmachev, D.V. Shirkov, New Methods in the Theory of Superconductivity (Academy of Science, Moscow, 1958)
J.A. Sauls, Broken Symmetry and Non-Equilibrium Superfluid \(^3\)He, in Topological Defects and Non-Equilibrium Symmetry Breaking Phase Transitions—Lecture Notes for the 1999 Les Houches Winter School edited by H. Godfrin, Y. Bunkov. (Elsievier Science Publishers, Amsterdam, 2000), pp. 239–265, arXiv:9910260 [cond-mat]
A.I. Larkin, A.B. Migdal, Theory of a superfluid fermi liquid superconductor: application to the nucleus. Sov. Phys. JETP 17, 1146 (1963)
P.W. Anderson, Plasmons, gauge invariance, and mass. Phys. Rev. 130, 439 (1963)
P.W. Higgs, Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 13, 508 (1964)
T. Tsuneto, Transverse collective excitations in superconductors and electromagnetic absorption. Phys. Rev. 118, 1029 (1960)
V.G. Vaks, V.M. Galitskii, A.I. Larkin, Collective Excitations in a Superconductor. Zh. Eskp. Teor. Fiz. 41, 1655 (1961) [JETP, 14 , 1177 (1962)]
A. Bardasis, J.R. Schrieffer, Excitons and plasmons in superconductors. Phys. Rev. 121, 1050 (1961)
D.M. Ginsberg, M. Tinkham, Far infrared transmission through superconducting films. Phys. Rev. 118, 990 (1960)
P.L. Richards, M. Tinkham, Far-infrared energy gap measurements in bulk superconducting In, Sn, Hg, Ta, V, Pb, and Nb. Phys. Rev. 119, 575 (1960)
D. Hess, T.A. Tokuyasu, J.A. Sauls, Broken symmetry in an unconventional superconductor: a model for the double transition in UPt\(_3\). J. Phys. Cond. Matt. 1, 8135 (1989)
H.F. Hess, R.B. Robinson, R.C. Dynes, J.M. Valles, J.V. Waszczak, Scanning-tunneling-microscope observation of the abrikosov flux lattice and the density of states near and inside a fluxoid. Phys. Rev. Lett. 62, 214 (1989)
R. Parks (ed.), Superconductivity, vol. I (Marcel Dekker Inc., New York, 1969)
K. Maki, Propagation of zero sound in the Balian-Werthamer state. J. Low Temp. Phys. 16, 465 (1974)
J.W. Serene, Theory of Collisionless Sound in Superfluid 3He. Ph.D. thesis. (Cornell University, 1974)
P. Wölfle, in Progress in Low Temperature Physics, vol. VIIa, ed. by D.F. Brewer (North Holland, Amsterdam, 1978)
J.A. Sauls, J.W. Serene, Coupling of order-parameter modes with \(l > 1\) to zero sound in 3He-B. Phys. Rev. B 23, 4798 (1981)
P. Hirschfeld, P. Wölfle, J.A. Sauls, D. Einzel, W.O. Putikka, Electromagnetic absorption in anisotropic superconductors. Phys. Rev. B 40, 6695 (1989)
S.K. Yip, J.A. Sauls, Circular dichroism and birefringence in unconventional superconductors. J. Low Temp. Phys. 86, 257 (1992)
J.A. Sauls, H. Wu, S.B. Chung, Anisotropy and strong-coupling effects on the collective mode spectrum of chiral superconductors: application to Sr\(_2\)RuO\(_4\). Front. Phys. 3, 36 (2015)
H. Uematsu, T. Mizushima, A. Tsuruta, S. Fujimoto, J.A. Sauls, Chiral higgs mode in nematic superconductors. Phys. Rev. Lett. 123, 237001 (2019)
A.A. Abrikosov, L.P. Gorkov, Spin-orbit interaction and the knight shift in superconductors. Sov. Phys. JETP 15, 752 (1962)
A. Layzer, D. Fay, Spin-fluctuation exchange: mechanism for a superfluid transition in liquid \(^3\)He. Sol. State Comm. 15, 599 (1974)
E.V. Thuneberg, S.-K. Yip, M. Fogelström, J.A. Sauls, Scattering models for superfluid \(^3\)He in aerogel. Phys. Rev. Lett. 80, 2861 (1998)
W. Halperin, Superfluid \(^3\)He in aerogel. Ann. Rev. Condens. Matter Phys. 10, 155 (2019)
G.E. Volovik, The Universe in a Helium Droplet (Clarendon Press, Clarendon, UK, 2003)
G.E. Volovik, Fermion zero modes at the boundary of superfluid \(^3\)He-B. JETP Lett. 90, 398 (2009)
T. Mizushima, M. Sato, K. Machida, Symmetry protected topological order and spin susceptibility in superfluid \(^{3}He-B\). Phys. Rev. Lett. 109, 165301 (2012)
H. Wu, J.A. Sauls, Majorana excitations, spin and mass currents on the surface of topological superfluid \(^{3}\)He-B. Phys. Rev. B 88, 184506 (2013)
J.A. Sauls, T. Mizushima, On the Nambu Fermion-Boson relations for superfluid \(^3\)He. Phys. Rev. B 95, 094515 (2017)
J.W. Serene, Order Parameter Modes, Zero Sound and Symmetries in Superfluid 3He, in Quantum Fluids and Solids—1983, vol. 103 (A.I.P, New York, 1983), p. 305
J.A. Sauls, J.W. Serene, Superflow Coupling of Zero Sound and the Real Squashing Modes, in Proceedings of LT-17 edited by U. Eckern, A. Schmid, W. Weber, H. Wühl. (North Holland, New York, 1984), p. 776
R.S. Fishman, J.A. Sauls, Particle-hole symmetry violation in normal \(^3{H}e\). Phys. Rev. B 31, 251 (1985)
V.N. Popov, Functional Integrals and Collective Excitations, Cambridge Monographs on Mathematical, physics. (Cambridge University Press, Cambridge, UK, 1987)
A. Leggett, The spin dynamics of an anisotropic fermi superfluid \(^3\)He. Ann. Phys. 85, 11 (1974)
V.V. Zavjalov, S. Autti, V.B. Eltsov, P.J. Heikkinen, G.E. Volovik, Light Higgs channel of the resonant decay of magnon condensate in superfluid \(^3\)He-B. Nature Comm. 7, 10294 (2016)
R.W. Giannetta, A. Ahonen, E. Polturak, J. Saunders, E.K. Zeise, Observation of a new sound attenuation peak in superfluid \(^3\)He-B. Phys. Rev. Lett. 45, 262 (1980)
P. Wölfle, Collisionless collective modes in superfluid \(^3\)He. Phys. Lett. 47A, 224 (1974)
Y.A. Vdovin, in Methods of Quantum Field Theory to the Many Body Problem. Effects of P-state Pairing in Fermi Systems. (Gosatomizdat, Moscow, 1963), pp. 94–109
V.E. Koch, P. Wölfle, Coupling of new order parameter collective modes to sound waves in superfluid \(^3\)He. Phys. Rev. Lett. 46, 486 (1981)
J.A. Sauls, J.W. Serene, Interaction effects on the Zeeman splitting of collective modes in superfluid \(^3\)He-B. Phys. Rev. Lett. 49, 1183 (1982)
N. Schopohl, M. Warnke, L. Tewordt, Effect of gap distortion on the field splitting of the collective modes in superfluid \(^3\)He-B. Phys. Rev. Lett. 50, 1066 (1983)
D.B. Mast, B.K. Sarma, J.R. Owers-Bradley, I.D. Calder, J.B. Ketterson, W.P. Halperin, Measurements of high frequency sound propagation in \(^3\)He-B. Phys. Rev. Lett. 45, 266 (1980)
O. Avenel, E. Varoquaux, H. Ebisawa, Field splitting of the new sound attenuation peak in \(^3\)He-B. Phys. Rev. Lett. 45, 1952 (1980)
P.N. Fraenkel, R. Keolian, J.D. Reppy, Pressure dependence of the zero-temperature real squashing mode in 3B. Phys. Rev. Lett. 62, 1126 (1989)
R.S. Fishman, J.A. Sauls, Response functions and collective modes of superfluid \(^3\)He-B in strong magnetic fields. Phys. Rev. B 33, 6068 (1986)
R.S. Fishman, J.A. Sauls, Doublet splitting and low-field evolution of the real squashing modes in superfluid \(^3\)He-B. Phys. Rev. Lett. 61, 2871 (1988)
B.S. Shivaram, M.W. Meisel, B.K. Sarma, W.P. Halperin, J.B. Ketterson, Nonlinear Zeeman shifts in the collective mode spectrum of \(^3\)He-B. Phys. Rev. Lett. 50, 1070 (1983)
E. Polturak, P.G.N. de Vegvar, E.K. Zeise, D.M. Lee, Soliton-like propagation of zero sound in superfluid \(^3\)He. Phys. Rev. Lett. 46, 1588 (1981)
J.A. Sauls, Soliton propagation of zero sound in superfluid \(^3\)He-B. Phys. Rev. Lett. 47, 530 (1981)
R.H. McKenzie, J.A. Sauls, Acoustic-order-parameter three-wave resonance in superfluid \(^3{H}e\)-B. Euro. Phys. Lett. 9, 459 (1989)
R.H. McKenzie, J.A. Sauls, in Helium Three edited by W.P. Halperin and L.P. Pitaevskii. Collective Modes and Nonlinear Acoustics in Superfluid \(^3He\)-B. (Elsevier Science Publishers, Amsterdam, 1990), p. 255. arXiv:1309.6018
J.A. Sauls, R.H. McKenzie, Parametric excitation of the \(J=2^+\) modes by zero sound in superfluid \(^3\)He-B. Physica B 169, 170 (1991)
R.H. McKenzie, J. Sauls, Nonlinear acoustic effects in superfluid \(^3\)He-B, Physica B Condensed Matter 178, 219 (1992) (Proceedings of the Körber Symposium on Superfluid \(^3\)He in Rotation)
K. Torizuka, J.P. Pekola, A.J. Manninen, J.M. Kyynäräinen, R.H. McKenzie, Two-phonon absorption by the real squashing mode in superfluid \(^3\)He-B. Phys. Rev. Lett. 66, 3152 (1991)
A.J. Manninen, H. Alles, K. Torizuka, A.V. Babkin, J.P. Pekola, Experiments on nonlinear acoustics in \(^3\)He-B. J. Low Temp. Phys. 95, 579 (1994)
G.F. Moores, J.A. Sauls, Transverse waves in superfluid \(^3\)He-B. J. Low Temp. Phys. 91, 13 (1993)
J.A. Sauls, Y. Lee, T.M. Haard, W.P. Halperin, Magneto-acoustic rotation of transverse waves in \(^3\)He-B. Physica B 284, 267 (2000) (Proceedings of LT22)
Y. Lee, T. Haard, W. Halperin, J.A. Sauls, Discovery of an acoustic Faraday effect in superfluid \(^3\)He-B. Nature 400, 431 (1999)
C.A. Collett, J. Pollanen, J.I.A. Li, W.J. Gannon, W.P. Halperin, Nonlinear field dependence and \(f\)-wave interactions in superfluid \(^3\)He. Phys. Rev. B 87, 024502 (2013)
J.P. Davis, J. Pollanen, H. Choi, J.A. Sauls, W.P. Halperin, Discovery of an excited pair state in superfluid \(^3\)He-B. Nature Physics 4, 571 (2008)
W.P. Halperin, E. Varoquaux, Order Parameter Collective Modes in Superfluid \(^3He\), in Helium Three. ed. by W.P. Halperin, L.P. Pitaevskii (Elsevier Science Publishers, Amsterdam, 1990), p. 353
P.J.C. Signore, B. Andraka, M.W. Meisel, S.E. Brown, Z. Fisk, A.L. Giorgi, J.L. Smith, F. Gross-Alltag, E.A. Schuberth, A.A. Menovsky, Inductive measurements of UPt\(_3\) in the superconducting state. Phys. Rev. B 52, 4446 (1995)
A.P. Schnyder, S. Ryu, A. Furusaki, A.W.W. Ludwig, Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008)
Y. Hatsugai, Edge states in the integer quantum Hall effect and the Riemann surface of the Bloch function. Phys. Rev. B 48, 11851 (1993)
T.C. Wu, H.K. Pal, P. Hosur, M.S. Foster, Power-law temperature dependence of the penetration depth in a topological superconductor due to surface states. Phys. Rev. Lett. 124, 067001 (2020)
I.M. Lifshitz, L.P. Pitaevskii, in Landau and Lifshitz, Course in Theoretical Physics, vol. 10, 1st edn. Physical Kinetics. (Pergamon Press, New York, 1981)
J. Peters, G. Eska, Pair breaking by two phonons in \(^3\)He-B. Euro. Phys. Lett. 20, 137 (1992)
R. Sooryakumar, M.V. Klein, Raman scattering by superconducting-gap excitations and their coupling to charge-density waves. Phys. Rev. Lett. 45, 660 (1980)
M.-A. Méasson, Y. Gallais, M. Cazayous, B. Clair, P. Rodière, L. Cario, A. Sacuto, Amplitude Higgs mode in the 2H-NbSe\(_2\) superconductor. Phys. Rev. B 89, 060503 (2014)
P. Littlewood, C. Varma, Gauge-invariant theory of the dynamical interaction of charge density waves and superconductivity. Phys. Rev. Lett. 47, 811 (1981)
R. Matsunaga, Y.I. Hamada, K. Makise, Y. Uzawa, H. Terai, Z. Wang, R. Shimano, Higgs amplitude mode in the BCS superconductors \(Nb_{1-x}Ti_{x}N\) induced by Terahertz pulse excitation. Phys. Rev. Lett. 111, 057002 (2013)
C. Vaswani, J.H. Kang, M. Mootz, L. Luo, X. Yang, C. Sundahl, D. Cheng, C. Huang, R.H.J. Kim, Z. Liu, Y.G. Collantes, E.E. Hellstrom, I.E. Perakis, C.B. Eom, J. Wang, Light quantum control of persisting Higgs modes in iron-based superconductors. Nat. Comm. 12, 258 (2021)
L. Gorkov, V.M. Galitskii, Superfluidity in a fermi system in the presence of pairs with non-zero angular momentum. Sov. Phys. JETP 13, 792 (1961)
V.G. Vaks, V.M. Galitskii, A.I. Larkin, Collective excitations with non-zero angular momemtum pairing. Zh. Eskp. Teor. Fiz. 42, 1319 (1962) [JETP, 15, 5, 914 (1962)]
J.A. Sauls, F-wave correlations in superfluid \(^3\)He. Phys. Rev. B 34, 4861 (1986)
P. Nozieres, in Bose-Einstein Condensation, edited by A. Griffin, D. W. Snoke, and S. Stringari (Cambridge University Press, Cambridge, UK, 1995), pp. 15–30
Acknowledgements
This work was supported by National Science Foundation Grant DMR-150873. I thank Anton Vorontsov for his translation of the Vdovin paper to English, and for discussions on the analysis in Vdovin’s paper. I thank Bill Halperin for many discussions on the remarkable phenomena revealed by acoustic, NMR and thermodynamic studies in pursuit of understanding the BW state of \(^3\)He-B. I congratulate Dave Lee and John Reppy on the occasion of their 90th birthdays and especially thank them for all the beautiful physics they have revealed by pushing the frontiers of quantum fluids and solids at ultra-low temperatures.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Vdovin’s Contribution
In 1987 I gave an invited talk at the March meeting of the American Physical Society held in New York on the “Theory of Sound Propagation and Attenuation in Superfluid \(^3\)He” including the Zeeman and Paschen–Back effects of the \(J=2^{\pm }\) collective modes. This was the “Woodstock of Physics” meeting that highlighted the discovery of high-temperature superconductivity in the cuprates. Tony Leggett was the chair of my session, and after the talk, he told me that the collective mode spectrum had been obtained by Yu. Vdovin years before the discovery of \(^3\textrm{He-B}\) and the theoretical works of Wölfle, Serene and Maki on the collective modes and their acoustic signatures. Tony kindly sent me a copy of a collection of articles published in Moscow in 1963 on “Methods of Quantum Field Theory to the Many Body Problem,” which included the article by Vdovin titled “Effects of pairing in Fermi systems in a P-state” [49]. Tony also drew my attention to a sentence at the end of the abstract stating that the work had been completed in 1961! That was two years before the publication of the work by Balian and Werthamer, and the same year as the publication of the papers by Anderson and Morel [2], Gorkov and Galitskii [84], and Vaks Galitskii and Larkin [17]. As far as I know the first reference to Vdovin’s paper in the literature on \(^3\)He or collective modes in superconductors was my review of collective modes and nonlinear acoustics with R. McKenzie in 1990 [62]. About the same time Vollhardt and Wölfle cited Vdovin’s paper in their treatise, “The Superfluid Phases of Helium 3,” and pointed out that Vdovin’s work “fell into oblivion.” That appears to be true, as Vaks, Galitskii and Larkin, who published work on collective excitations in higher angular momentum states in 1962 [85], appear to have been unaware of Vdovin’s work. However, the connection between Vdovin’s paper and these four early papers on the theory of pairing in higher angular momentum states is I think worth clarifying in an article reflecting on the impact of the BW ground state on both the physics of superfluid \(^3\)He, as well as the theory of unconventional superconductors. The existence of Vdovin’s early work, and that it appears to have been done as early as 1961, has been interpreted to imply that Vdovin should be credited equally with Balian and Werthamer for the theoretical prediction for the ground state of a spin-triplet, p-wave superconductor, i.e., what I have referred to as the BW ground state, c.f. Ref. [35]. However, that is incorrect.
Balian and Werthamer proved that the \(^3\)P\(_0\) state with \(L=1\), \(S=1\) and \(J=0\) was the absolute minimum of the weak-coupling BCS free energy functional within the p-wave/spin-triplet manifold. See Sect. 3, p. 1556 of the BW paper [1]. The physical reason is that within the most attractive pairing channel, the lowest free energy state(s) is the linear superposition that maximizes the pairing gap over the Fermi surface, and for the spin-triplet, p-wave manifold this is the BW state.Footnote 5
Vdovin made no such analysis of the stability of phases within the p-wave, triplet manifold. Rather he assumed the ground state was the \(^3\)P\(_0\) state. From paragraph 3 on p. 95 of Ref. [49], “Both single-particle and collective excitations are considered in this system. Different branches of the collective excitation spectrum, corresponding to dynamics of bound pairs with different moments J, are obtained in the assumption that the condensate is made from pairs in \(^3\)P\(_0\) state.”
The basis for Vdovin’s assumption of a \(^3\)P\(_0\) ground state is the paper of Gorkov and Galitskii (GG) [84]. However, the paper by GG contains fundamental errors and is not a proof that the \(^3\)P\(_0\) state is the ground state. GG start from an ansatz for the two-particle density matrix, \(\rho _{\alpha \beta ;\gamma \rho } (p,-p;p',-p')\equiv \langle \psi _{\alpha }(p)\psi _{\beta }(-p) \psi ^{\dag }_{\gamma }(p') \psi ^{\dag }_{\delta }(-p')\rangle\), which is not a BCS condensate, but rather a fragmented condensate [87], i.e. \((2l+1)\) condensates with macroscopic eigenvalues of the form (1st equation on p. 793 of Ref. [84]),
GG posit an equation for each m of the form,
then assert that “since the angular momentum is zero,” the diagonal (quasiparticle) propagator is isotropic with
With this assumption, GG eliminate all pairing states that do not have an isotropic excitation gap. Specifically, GG argue that since the diagonal propagator is isotropic then \(\hat{F}_m(p)\propto Y_{lm}(\mathbf{p})\) as is \(\hat{\Delta }_m(p)\), and thus based on Eq. (2), each \(\hat{\Delta }_m(p)\) has the same amplitude, in which case the addition theorem for the spherical harmonics generates an isotropic excitation gap given by,
It is a circular argument disconnected from the BCS free energy functional and the BCS gap equation, which is the stationarity condition of the former [86].
By contrast BCS condensation corresponds to macroscopic occupation of a single two-particle state
where the spin- and orbital structure of the Cooper pair amplitude, \(F_{\alpha \beta }(p)=\langle \psi _{\alpha }(p)\psi _{\beta }(-p)\rangle\) is determined self-consistently by the BCS mean field gap equation,
The linearized form of the gap equation separates into a set of eigenvalue equations determined by pairing interactions, \(V_l\), for each of the irreducible representations of the symmetry group of the normal state, which in this case is \(\texttt {SO(3)}_{\mathrm{L}}\). The superconducting transition is then driven by the most attractive pairing interaction, e.g., \(V_1\), resulting in an anomalous self energy of the form
where \(\hat{S}_{1,m_s}\) are the \(2\times 2\) matrix representation of spin states \(\displaystyle \vert \,{1,m_s}\,\rangle\) and \(Y_{1,m_L}(\mathbf{p})\) are the p-wave orbital basis states, i.e., the \(L=1\) spherical harmonics. The amplitudes \(\Delta _{m_s,m_L}\) are determined by solutions to the full nonlinear BCS gap equation, which is the stationarity condition for the weak coupling BCS free energy functional. The lowest energy state among the solutions to the gap equation is the ground state, which for \(L=1\), \(S=1\), is the BW state.
To summarize, Vdovin’s contribution was the original prediction of the Bosonic collective modes based on the assumed BW ground state using the field theory method developed by Vaks, Galitskii and Larkin [17]. However, neither Vdovin, nor Gorkov and Galitskii proved that the ground state of a spin-triplet, p-wave superconductor is the \(^3\)P\(_0\) state. That was the work of Balian and Werthamer.
Appendix B: Evaluation of the Response Function
Equation 23 for the static condensate response is obtained by evaluating Eq. 8 with \(\omega =0\) and changing the integration variable to \(\xi =\mathrm{sgn}(\varepsilon )\sqrt{\varepsilon ^2-|\Delta |^2}\). The symbol  implies principal part integration in the neighborhood of the singularities on the real \(\xi\) axis at \(\pm \eta /2\). This integral is most easily evaluated by using the Matsubara representation for the hyperbolic tangent function,
implies principal part integration in the neighborhood of the singularities on the real \(\xi\) axis at \(\pm \eta /2\). This integral is most easily evaluated by using the Matsubara representation for the hyperbolic tangent function,
where \(\varepsilon _n=(2n+1)\pi T\) are the Fermion Matsubara frequencies with \(n\in {\mathbb {Z}}\). Thus, Eq. 23 becomes

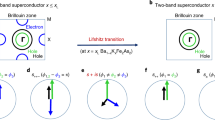
The principal part integral on the real axis is a component of the integral over the closed contour shown in Fig. 5, i.e.,  where
where  is the path of the principal part integral on the real \(\xi\)-axis, \({\mathscr {C}}_{\pm }\) is an infinitesimal half circle in the upper half \(\xi\)-plane of radius \(\delta \rightarrow 0^+\) centered at \(\xi _{\pm }=\pm \eta /2\), and \({\mathscr {C}}_{\infty }\) is a half circle in the upper half plane of radius \(R\rightarrow \infty\). The integrand
is the path of the principal part integral on the real \(\xi\)-axis, \({\mathscr {C}}_{\pm }\) is an infinitesimal half circle in the upper half \(\xi\)-plane of radius \(\delta \rightarrow 0^+\) centered at \(\xi _{\pm }=\pm \eta /2\), and \({\mathscr {C}}_{\infty }\) is a half circle in the upper half plane of radius \(R\rightarrow \infty\). The integrand
is analytic on contour \({\mathscr {C}}_{\infty }\), except at isolated points on the imaginary axis that can be avoided and vanishes faster than \(1/|\xi |\) for \(|\xi |\rightarrow \infty\) which implies that the corresponding integral of the integrand in Eq. 59 vanishes. For the small semi-circles \(\xi =\pm \eta /2+\delta e^{i\theta }\) for \(\theta \in \{0,\pi \}\). Integration around the small semi-circles yields,
Thus, \(\int _{{\mathcal {C}}_{+}+{\mathcal {C}}_{-}}d\xi \,I(\xi ) \equiv 0\), yielding a regular response function for \(\eta \rightarrow 0\) and  . Contour \({\mathcal {C}}\) encloses a meromorphic integrand with a simple pole at \(\xi =+i\sqrt{\varepsilon _n^2 + |\Delta |^2}\). Evaluating Eq. 59 with the residue of the integrand yields Eq. 24.
. Contour \({\mathcal {C}}\) encloses a meromorphic integrand with a simple pole at \(\xi =+i\sqrt{\varepsilon _n^2 + |\Delta |^2}\). Evaluating Eq. 59 with the residue of the integrand yields Eq. 24.
Integration contours for evaluating the principal part integral in Eq. 59 for the static condensate response function \(\lambda (\eta )\) (Color figure online)
Rights and permissions
About this article
Cite this article
Sauls, J.A. On the Excitations of a Balian–Werthamer Superconductor. J Low Temp Phys 208, 87–118 (2022). https://doi.org/10.1007/s10909-022-02748-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10909-022-02748-2




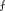 is principal part integration in the neighborhood of the integrable singularities at
is principal part integration in the neighborhood of the integrable singularities at 