Abstract
We study the logarithmic transition sensitivities to temperature and current, α and β, of bare Mo/Au TES sensors without any normal metal structure, with and without relevant weak link effects. Both parameters display a smooth dependence with bias. We analyze them as a function of bias, bath temperature and TES size. We observe relevant differences in the behavior of α and β as the aspect ratio increases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
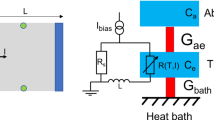
Performances of TES are intimately linked to the sensitivity of their electrical resistance to temperature and current, within the superconducting transition. Two parameters quantify this sensitivity: α and β, which are the logarithmic derivatives of the device resistance to temperature and current, respectively. The stability and noise (and therefore energy resolution) of a TES depend on α and β, as described by Irwin and Hilton [1].
The transition of TES, and thus α and β, can be dominated by the so-called weak link (WL) effects, that arise from the longitudinal proximity effect due to the superconducting contacts, with much higher Tc [2]. In this case, the transition can be described by the RSJ model [3]; for long enough TESs, with irrelevant WL effects, the two-fluid model [4] is expected to hold.
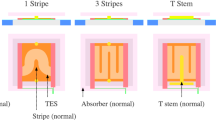
The relevance of a good understanding of the transition shape has been evidenced in several studies [5,6,7,8,9,10,11,12,13]. Most of them, however, analyze data of devices with absorber, normal metal structures or banks; all these features may alter the current distribution inside the TES, therefore modifying the response intended to explore.
In this paper we report on the α and β parameters of bare Mo/Au TES sensors without absorber, banks or normal metal structures and with different aspect ratio. A smooth, monotonous dependence on bias is observed for both parameters, which allows for comparison of their evolution with bias, TES size and bath temperature. Significant differences are observed for α and β with bath temperature and sizes, which can provide insights in view of optimizing the devices’ figure of merit. It is also shown that the temperature and current sensitivities not only depend on TES aspect ratio, and thus effects of both width and length should be rather analyzed separately.
2 Experimental
Mo/Au (45 nm/265 nm) TESs with normal state square resistance 24 mΩ and Nb/Mo contacts and leads were fabricated on Si3N4 membranes as reported elsewhere [13]. The five devices studied in this work correspond to a single batch (wafer), with Mo/Au intrinsic critical temperature Tci = 92 mK; five devices with sizes (width x length, w x L) 25 × 25, 25 × 50, 25 × 75, 25 × 100 and 120 × 120 μm2 were studied. Two of them display critical temperature Tc > Tci: the 25 × 25 (Tc = 112 mK) and the 25 × 50 (Tc = 96 mK), which is a first evidence of the existence of weak link (WL) effects, though somehow weaker than usually reported [2, 14]. The analysis of the field dependence of critical current, Ic(B), reveals indeed a well resolved Fraunhofer-like pattern for the 25 × 25 device (not shown); the 25 × 50 and 25 × 75 devices only show remnants of satellite peaks, indicating a very feeble WL effect, in accordance to the proximity of its Tc to Tci. The two larger TESs do not show evidences of Fraunhofer-like behavior.
Dark characterization of the devices was performed in a Kelvinox dilution refrigerator, under DC bias. All the data analyzed were recorded under zero magnetic field: the eventual remnant field was determined from the maximum of the critical current as a function of the magnetic field H, applied with a small Helmhotz coil placed in the vicinity of the TES. The determined Hrem was thus cancelled with the same coil, prior to measuring I-V curves and complex impedance Z(ω) at different bath temperatures Tbath. Hrem values are usually of 2–3 μT; the self-field Hself, estimated from the asymmetry of Ic(B) [5], is at least one order of magnitude lower, with dHself/dIc ~ 1 μT/mA for the 25 × 25 TES and ~ 2 μT/mA for the 25 × 100 one.
Extraction of TES parameters from I-V and Z(ω) data was done following standard procedures, and assuming a single thermal block. The uncertainty in the determination of α and β values is usually below 10% (see error bars in Fig.1). Two data sets taken at different times for the same TES were checked to provide nearly identical values, well within the confidence intervals.
Bias dependences of the logarithmic derivatives of the resistance as a function of temperature, α (Left) and current, β (Right) at 50 mK, for the different devices. Error bars are shown for all data points, but for most of them are not visible because they fall within the symbol size. Solid (dashed) lines are fits to the bias dependences expected from the RSJ [3] (two-fluid [4]) model. (Color figure online)
3 Results and Discussion
Figure 1 displays the logarithmic derivatives α and β as a function of bias, for all the characterized devices. Their behavior with bias is very smooth, likely because of the absence of normal metal features on their top [6], and the fact that data were obtained under zero field [5]. The values of both parameters as well as their ratio range within most of those reported for a variety of TESs [4,5,6,7,8,9,10,11].
The temperature sensitivity α for the three smaller TESs with w = 25 μm is nearly coincident at small biases. Yet, as L increases α smoothens its decay with bias, which results in an increase of α with L at higher biases. The two larger TESs, without traces of WL effects, 25 × 100 and 120 × 120, display higher α values. The highest temperature sensitivity corresponds indeed to the large square TES, thus indicating that the relevant parameter to maximize α may not be the aspect ratio but the length. We come back to this issue below.
The current sensitivity β displays a different behavior with size: its highest value is found for the smallest TES (25 × 25), decreases for devices showing some WL effect and increasing L, reaches a minimum for L = 75 μm and increases again for larger L (TESs without evident WL). This points to distinct dependences of α and β—and therefore the temperature and current dependences of TES resistance—on TES size.
Figure 1 also displays the fits to the two most used TES transition models: the RSJ and the two-fluid. The 25 × 25 is very well described by the RSJ model, as expected. The two-fluid model seems to work better at least for the TES with highest aspect ratio, while the situation is not clear for the rest; a study with more data points would be required to discern between models. Even more, it must be taken into account that the bias dependence of α can be masked by its strong temperature dependence. This is not the case for β, whose fits are therefore more reliable for this transition model comparison.
From Fig.1 it becomes evident that α and β are not directly related to Rn (or, equivalently, TES aspect ratio). This is more clearly appreciated in Fig. 2, displaying the figure of merit K, often used to evaluate the TES performances that can be expected from the transition sensitivity to current and temperature. K values fall within the ranges reported for a variety of other devices [7, 9]. The TES with strong WL effects (25 × 25) displays the lowest figure of merit. Notice that for constant width and increasing aspect ratio (and therefore progressively weaker weak link effect) K increases. Even so, the larger, square TES (120 × 120) displays the highest K values. Therefore, the relevant parameter to maximize K is not -or not only- the aspect ratio. A plausible reason might be related to the fact that the current density through the TES changes with TES width, so that for a given TES length L wider TESs would display lower values of the current density ratio J/Jc, where Jc is the critical current density. And it is well known that TES resistance is a strongly nonlinear function of J/Jc, especially at low biases. Thus, further studies on the effects of TES size, decoupling width and length effects, might be interesting.
As shown on Fig. 2, it is found that α and β are related through a power law α~βn, with the exponent n taking values between 0.6 and 0.9. This empirical law, with similar exponents, has also been reported recently for Ti/Au TESs displaying WL effects [11].
Finally, we turn to the dependence of the logarithmic derivatives on the bath temperature. Figure 3 displays α and β for a selection of representative devices at different Tbath. For all TESs, α displays a small—though clear—increase with increasing Tbath. β, however, shows differentiated behaviors depending on TES size: for TESs with L = 25, 50 and 75 μm it increases with Tbath; while the opposite dependence is observed for the two larger TESs. These differences, again, point to a distinct dependence of β on size with respect to α, for TESs with or without WL. It is significant that the change of tendency of β with Tbath occurs for the TES displaying the minimum of β with size, that is, the 25 × 75 one, which is the longest displaying any trace of WL effects.
4 Conclusions
We have determined the temperature and current sensitivities of several Mo/Au bare TES (without absorber, membranes or normal metal structures) with different sizes, displaying or not weak link effects, as a function of bias and for different bath temperatures. Both α and β decrease monotonously with bias (% R/Rn) and show a very weak dependence with Tbath. Size effects are different for α and β. Whereas α increases with TES size, especially for devices without WL effects, β is largest for the smallest TES (the one with very clear WL effects), displays a minimum at intermediate TES lengths (which roughly correspond to the lengths where WL effects become irrelevant) and increases again for longer and larger TESs. It is worth noting that, while α increases with Tbath for any TES size, β displays opposite dependences on Tbath, for TES sizes respectively below and above its minimum.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
References
K.D. Irwin, G.C.Hilton, in Enss C. (eds.) Cryogenic Particle Detection, Topics in Appl. Phys. 99, Springer, Berlin Heidelberg (2005) https://doi.org/10.1007/10933596_3
J.E. Sadleir et al., Phys. Rev. Lett. 104, 047003 (2010), https://doi.org/10.1103/PhysRevLett.104.047003
A.Kozorezov et al., Appl. Phys. Lett. 99, 063503 (2011) https://doi.org/10.1063/1.3621829
D.A. Bennett et al., J. Low Temp. Phys. 167, 102 (2012) https://doi.org/10.1007/s10909-011-0431-4
S.J.Smith et al., J.Appl. Phys. 114, 074513 (2013) https://doi.org/10.1063/1.4818917
N.A. Wakeham et al., J. Low Temp. Phys. 193, 231 (2018). https://doi.org/10.1007/s10909-018-1898-z
K.M. Morgan et al., Appl. Phys. Lett. 110, 212602 (2017) https://doi.org/10.1063/1.4984065
Y. Zhou et al., J. Low Temp. Phys. 193, 321 (2018) https://doi.org/10.1007/s10909-018-1970-8
S. Zhang et al., J.Appl. Phys. 121, 074503 (2017) https://doi.org/10.1063/1.4976562
Y. Zhou, J. Phys.: Conf. Ser. 1590, 012032 (2020). https://doi.org/10.1088/1742-6596/1590/1/012032
M.de Wit et al., J. Appl. Phys. 128, 223902 (2020) https://doi.org/10.1063/5.0033577
D.A. Bennett et al., Phys. Rev. 87, 020508 (2013) https://doi.org/10.1103/PhysRevB.87.020508
C. Pobes et al., IEEE Trans. Appl. Supercond. 27, 2101505 (2017) https://doi.org/10.1109/TASC.2016.2637337
M.L. Ridder et al., J. Low Temp. Phys. 199, 962 (2020) https://doi.org/10.1007/s10909-020-02401-w
L. Fàbrega et al., Supercond. Sci. Technol 32, 015006 (2019) https://doi.org/10.1088/1361-6668/aaebf4
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature. Financial support from the Spanish Ministerio de Ciencia e Innovación MICINN, through Project RTI2018-096686-B-C22 and FPI contract (MM), is acknowledged. Personnel from ICMAB acknowledge also MICINN for support through the Severo Ochoa Program for Centers of Excellence (Project FUNFUTURE, CEX2019-000917-S).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fàbrega, L., Camón, A., Strichovanec, P. et al. Temperature and Current Sensitivities of Bare Mo/Au Transition-Edge Sensors. J Low Temp Phys 209, 287–292 (2022). https://doi.org/10.1007/s10909-022-02712-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10909-022-02712-0