Small Size Transition-Edge Sensors for Future X-Ray Applications

Abstract

Large arrays of transition edge sensors (TESs) are the baseline for a number of future space observatories. For instance, the X-ray integral field unit (X-IFU) instrument on board the ATHENA space telescope will consist of $\sim$3000 TESs with high energy resolution ($2\,{\mathrm{eV}}$ at X-ray energies up to 7 keV). In this contribution we report on the development of an X-ray TES array as a backup detector technology for X-IFU. The baseline readout technology for this mission is time domain multiplexing where the detectors are DC biased. Specifically, we report on the characterization of four different Ti/Au TESs with the following dimensions ($\hbox {L}\times \hbox {W}$): $30\times 15$, $30\times 30$, $50\times 25$ and $50\times 50\,\mu \hbox {m}^2$, all of which are coupled to a $2.3\,\mu \hbox {m}$ thick Au absorber of area $240\times 240\,\mu \hbox {m}^2$. We have performed our characterization using our standard frequency domain multiplexing readout connecting only pixels at low frequencies, where nonlinear effects due to the AC biasing are negligible. Promising energy resolution has been obtained, for instance $1.78\pm 0.10\,\hbox {eV}$ and $1.75\pm 0.10\,\hbox {eV}$ at 5.9 keV for the $50\times 25$ and $50\times 50\,\mu \hbox {m}^2$ detectors respectively. Uniformity over a kilo-pixel array (of detectors with the same geometry) has been also studied, confirming the high quality of our fabrication process.

1 Introduction

In recent years, extensive work has been done to provide a Ti/Au transition-edge sensor (TES) array as a backup detector technology for the X-ray integral field unit (X-IFU) [1] instrument on board the ATHENA space telescope [2]. In particular, different detector designs have been successfully explored in order to match the requirements of the baseline readout technique of the project. During the initial phase, high aspect-ratio devices [3, 4] and uniform kilo-pixel arrays have shown promising performance [5] and subsequently, remarkable steps forward have been made in demonstrating a high multiplexing factor with our frequency domain multiplexing (FDM) readout technique [6, 7].

Recently, the baseline readout technology for X-IFU has been changed from FDM, where the devices are AC biased with bias frequencies ranging from 1 MHz up to 5 MHz, to time domain multiplexing (TDM) where the devices are DC biased. In order to optimise the detectors with the new readout system, aspects of the pixel design need to be reconsidered, e.g. the thickness of the bilayer, the normal resistance $R_{{\mathrm {N}}}$, and thus the aspect ratio of the device. In this work we present four different Ti/Au TES designs with aspect ratio intended to produce lower normal resistance than previous devices optimised for FDM readout. The designs have the following dimensions ($\hbox {L}\times \hbox {W}$): $30\times 15, 30\times 30$, $50\times 25$ and $50\times 50\,\mu \hbox {m}^2$, each coupled to a $2.3\,\mu \hbox {m}$ thick Au absorber of area $240\times 240\,\mu \hbox {m}^2$.

Since a DC setup able to readout and characterise a large number of pixels is currently under development, we have performed the present investigation using only the lower bias frequencies ($\le$ 2 MHz) of our standard FDM readout system. At low bias frequencies the nonlinear effects due to the AC bias are negligible, and the detector performance is in agreement with the results expected from an ideal DC bias setup [8]. Energy resolution (${\varDelta } E$) at 5.9 keV will be reported and the expected performance based on differences in the transition curve parameters ($\alpha =\frac{\partial {\mathrm {log}}R}{\partial {\mathrm {log}}T}$ and $\beta =\frac{\partial {\mathrm {log}}R}{\partial {\mathrm {log}}I}$) will be discussed. Moreover, a uniform kilo-pixel array hosting the $50\times 50\,\mu \hbox {m}^2$ TESs has been characterised in order to show the quality of our fabrication process.

It is worth noting, for future X-ray applications, that this kind of detector can also be compatible with a microwave readout technique [9], currently being developed at SRON as part of the AHEAD program in collaboration with Physikalisch-Technische Bundesanstalt (PTB).

2 Pixel Design and Arrays Under Test

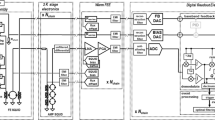
An $8 \times 8$ mixed array and a $32 \times 32$ kilo-pixel array (Fig.  1a, g) have been selected to pursue two different goals: (i) to find the best detector performance among four different pixel designs (Fig.  1c–f) and more important, to understand the features of each geometry in order to narrow down further the ideal pixel design under DC bias; (ii) to verify the uniformity of the performance over a large array and evaluate the quality of our fabrication process.

Our standard FDM readout technique has been used to characterise these arrays [7]. Figure 1b reports the mixed array under test, where the connected pixels are grouped by the bias frequency of the corresponding resonator (pink: low frequency, green: middle frequency, purple: high frequency). Although only the lower bias frequencies will be considered for a direct comparison with the results expected from an ideal DC setup, more pixels have been explored to improve the statistics and our understanding of the different geometries. Figure  1g shows all the 45 pixels, with geometry $50\times 50\,\mu \hbox {m}^2$ (Fig. 1c), which have been connected in the uniform kilo-pixel array and characterised during three different cooling runs. To avoid systematics from the calibration or non-repeatability of the measurement, three pixels have been measured both in run1 and in run2 .

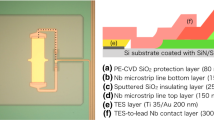
All the detectors under test consist of a bilayer of Ti(35 nm)/Au(200 nm) deposited on a 500 nm thick SiN membrane. The bilayer geometries include two square designs ($30\times 30$ and $50\times 50\,\mu \hbox {m}^2$) with a $R_{{\mathrm {N}}} = 26\,\hbox {m}{{{\Omega }}}$ and two moderately high aspect ratios ($30\times 15$ and $50\times 25\,\mu \hbox {m}^2$) with a normal resistance $R_{{\mathrm {N}}} = 52\,\hbox {m}{{{\Omega }}}$. The bilayer is coupled to a $240\times 240\,\mu \hbox {m}^2, 2.3\,\mu \hbox {m}$ thick Au absorber (heat capacity $C = 0.85\,\hbox {pJ/K}$ at 90 mK) via two central pillars, with four additional corner stems providing mechanical support as shown from Fig.  1c–f. All the details of the TES array fabrication are reported in another paper[10].

Fig. 1

a Top view of the $8\times 8$ mixed array; b Pixels under test are divided by bias frequency (pink: low frequency, green: middle frequency, purple: high frequency) and pair of columns hosts a different geometry (from left to right: c $50\times 50$, d $50\times 25$, e $30\times 30$ and f $30\times 15\,\mu \hbox {m}^2$); g top view of the uniform kilo-pixel array where 45 pixels $50\times 50\,\mu \hbox {m}^2$ are divided by measurement run (brown: run1, dark blue: run2 and purple: run3) (Color figure online)

3 Results

3.1 8$\times$8 Mixed Array Performance

In order to compare the four detector designs, we need to look for differences in the transition curve such as the logarithmic resistance sensitivity with respect to temperature ($\alpha$) and current ($\beta$). The most powerful method for performing such an investigation is the complex impedance measurement [11]. This technique, implemented to our FDM readout system [12], provides the ratio $\alpha$/$\beta$ for each geometry, as shown in Fig. 2(left). In particular, the length of the device has a substantial impact on this ratio, but the width could also play a role. The larger devices have $\alpha$/$\beta$ about 2–3 times higher than the smaller devices. The solid lines in the figure show a fit to an empirical model for the relation between $\alpha$ and $\beta$: $\alpha$=c$\beta ^{{\mathrm {n}}}$. The results for each fit are given in the legend for each geometry. This ratio plays a major role in the evaluation of the theoretical energy resolution (${\varDelta } E_{{\mathrm {the}}}$) we expect from each geometry under test, expressed by the following equation:

$$\begin{aligned} {\varDelta } E_{{\mathrm {the}}}=2\sqrt{2ln2}\sqrt{4k_{{\mathrm {B}}}T^2\frac{C}{\alpha }\sqrt{(1+\frac{5}{2}\beta +\frac{3}{2}\beta ^2)(1+M^2)}}, \end{aligned}$$

(1)

where $k_{{\mathrm {B}}}$ is Boltzmann’s constant and M is a factor that expresses the difference between the experimental and the theoretical noise when the TES Johnson noise is best explained by the Resistively-Shunted-Junction model [13]. The nature of the M factor is mainly internal thermal fluctuation noise as explained by Wakeham et al. [14] and further investigated by M. de Wit et al. [15] Fig. 2 (right) shows how we expect the larger devices, with their higher $\alpha$/$\beta$, to have a better energy resolution. Larger devices are less affected by the longitudinal proximity effect from the leads [16], resulting in steeper transition curves [17] with consequently higher $\alpha$/$\beta$ ratios [18].

This trend has been confirmed by measuring about 10000 X-ray photons at the best bias points ($\sim$15% of $R_{{\mathrm {N}}}$) in order to evaluate the energy resolution at 5.9 keV. Figure 3 (left) shows the best spectrum measured for each geometry (open symbols), where the solid lines are fit following the Holzer method to extract the energy resolution, indicated next to each spectrum. An overview of the X-ray resolutions, with the associated error bars, measured for all pixels is shown in Fig.  3 (right). This includes measurements for all bias frequencies up to 3.6 MHz, far outside of the optimal operating frequency for these TDM pixels. Still, very good energy resolutions are achieved, in particular by the $50\,\mu \hbox {m}$ length devices which achieve energy resolution around $1.8 \pm 0.1$ eV for bias points up to 2.4 MHz.

Fig. 2

(Left) $\alpha$ as a function of $\beta$ for the four geometries (open symbols) and corresponding best fit function (line); (Right) Theoretical energy resolution based on Eq. 1 (open symbols). Dashed lines serve no purpose other than guide the eye (Color figure online)

Fig. 3

(Left) The best response to 5.9 keV X-ray of the four geometries at $\sim$15% of $R_{{\mathrm {N}}}$ (open symbols) and corresponding best fit to data (solid line); (Right) Energy resolution measured for all the geometries connected to the bias frequencies available in the setup (open symbols) (Color figure online)

3.2 Kilo-Pixel Array Uniformity

In order to study the uniformity of our kilo-pixel array, we have evaluated the critical temperature $T_{{\mathrm {c}}}$ and the energy resolution ${\varDelta } E$ for 45 pixels divided in three measurement runs. Again, only pixels connected to resonators with bias frequencies lower than 2 MHz have been considered. These data (open circles) have been used to create a surface plot as shown in Fig.  4 (left) to highlight the uniformity over the array. Two peaks are visible in $T_{{\mathrm {c}}}$, corresponding to the northern (higher $T_{{\mathrm {c}}}$) and southern quadrant (lower $T_{{\mathrm {c}}}$), respectively. The averaged value of $T_{{\mathrm {c}}}$ and its variance ($T_{{\mathrm {c}}} = 80.77 \pm 0.70\,\hbox {mK}$) might be the consequence of non-uniformity in some of the critical aspects of the overall fabrication process [5]. Nevertheless, a scatter of about 2 mK at 80 mK corresponds to a scatter in the energy resolution of less then 4%, which is $< 0.1\,\hbox {eV}$ at 2.0 eV. As a matter of fact, ${\varDelta } E$ is uniform over the array between 2.1 and 2.3 eV, showing an average of $2.21\pm 0.14\,\hbox {eV}$. Data measured during run1 have not been considered because of the larger inductance (500 nH) in the bias circuit compared to that used during run2 and run3 (320 nH), but they help to evaluate the impact of the inductance on the energy resolution. Figure 4 (right) shows how ${\varDelta } E$ scales as a function of the inductance when we also include the data from the same geometry in the $8\times 8$ array. This is also the reason why we are currently not able to reach the theoretical energy resolution we have reported in Fig. 2 (right): a further decrease of the inductance could lead to an even better energy resolution.

Fig. 4

(Left) $T_{{\mathrm {c}}}$ and ${\varDelta } E$ measured over the kilo-pixel array (open symbols) used to create a smoothed surface plot to visualise the uniformity of the array, where the pixel density on the Z-axis identifies pixels with similar $T_{{\mathrm {c}}}$ and ${\varDelta } E$. To ensure a fair comparison, pixels measured in run1 are not included due to a larger inductance L; (Right) Impact of L on the energy resolution for the pixels measured during the three runs (closed symbols) and for the $50\times 50\,\mu \hbox {m}^2$ detectors measured in the mixed array (open symbols) (Color figure online)

4 Conclusion and Steps Forward

Meeting the performance requirements for specific instruments forces an optimization between the detector design and the readout technology. Because of the recent change from FDM to TDM in the baseline of the readout technology for the X-IFU instrument, we are currently pursuing the most promising Ti/Au TES design under DC bias after years of successfully optimizing the TES design under AC bias. In this paper we have presented the performance of four Ti/Au TESs with the following dimensions ($\hbox {L}\times \hbox {W}$): $30\times 15$, $30\times 30$, $50\times 25$, and $50\times 50\,\mu \hbox {m}^2$, respectively, as a backup option for the X-IFU detector technology. Our results have shown that longer devices with square or moderately high aspect ratio and low normal resistance are the way forward for further optimisation toward the ultimate design. Higher $\alpha /\beta$ gives a better energy resolution due to the lower longitudinal proximity effect from the bias leads in the longer devices. Taking these TES size effects into account, other specific designs will be tested in a dedicated setup, currently under assembly, where pixels will eventually be DC-biased. The outcome of the large array characterization has also shown that our current fabrication process guarantees a uniform $32\times 32$-pixel array.