1 Introduction

The first mineral perovskite CaTiO\(_3\) was found in the Akhmatov mine in Ural mountains of Russia by A. B. Kemmerer and studied by Rose [1]. In the ideal form the perovskite-type materials adopt a structure with the general stoichiometry ABX\(_3\), where A and B are cations at the center and at the corners of the unit cell, respectively, and X are anions (usually oxygens) situated at the face center of the edges of the unit cell [2]. Perovskites exhibit many interesting and intriguing properties from both the theoretical and the experimental point of view. Potential applications of these materials are associated with the unique features such as a near-zero temperature coefficient of resistivity [3], negative thermal expansion [4], high-temperature superconductivity [5], magnetostriction [6], and giant magnetoresistance [7]. The above properties result from a complex interplay between the crystal structure, electronic state of the transition metal and amount of defects [8].

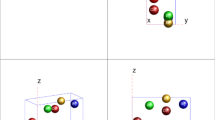
Another interesting group of materials having perovskite-type structure are antiperovskites. In inorganic antiperovskite compounds the oxygen atoms are replaced by transition metals and the positions of anions and cations are interchanged. For example, in well-studied MgCNi\(_3\), C atom is centered in the octahedron composed of six Ni atoms, and Ni has only two nearest-neighbor C atoms in contrast to the CaTiO\(_3\) in which a transition metal Ti has six nearest-neighbor oxygens [9]. Figure 1 presents an example of the simplest cubic antiperovskites structure, where atoms at corner and atom at body center are anions while face centered atoms are cations.

Fig. 1
figure 1

Unit cell of cubic antiperovskite. The green atoms at corner and blue atom at body center are anions while face centered red atoms are cations (Color figure online)

Full size image

Mentioned above antiperovskite MgCNi\(_3\) is characterized by a high content of Ni element which usually results in magnetism behavior. Surprisingly, in this case not the ferromagnetism but the superconductivity near 8 K was experimentally discovered by He et al. [10]. Several attempts have been made to investigate the structural, electronic, magnetic, elastic, vibrational, and thermodynamic properties of this novel superconductor [11–17]. However, the nature of superconductivity in this material is still not clear whether the mechanism for superconductivity is conventional or not [18, 19]. The evidence of phonon-mediated pairing mechanism of superconductivity was provided both by the experimental results [10, 20, 21] and theoretical estimations [22, 23]. Especially interesting is paper [23], where the strong electron–phonon coupling was derived from specific heat data in the normal and superconducting states independently. Moreover, the relevance of soft phonons and Van Hove-type singularity in the electronic density of states near the Fermi energy have also been suggested [23].

The existence of superconductivity in MgCNi\(_3\) has inspired the intensive research of other non-oxide perovskite-type materials [24–27] in particular the main attention was paid to nickel-based antiperovskite. Literature reveals that in CdCNi\(_3\), AlCNi\(_3\) and ZnNNi\(_3\) also exhibit superconductivity [28–32]. In particular, Uehara et al. observed in the experimental work that CdCNi\(_3\) is a superconductor with \(T_\mathrm{C}=\) 2.5–3.2 K and also does not show ferromagnetism [33]. The crystal synthesized using the high-pressure technique has the same structure as MgCNi\(_3\) but the lattice constant is \({\sim }1\,\%\) larger than that of MgCNi\(_3\). Uehara et al. concluded that the lower \(T_\mathrm{C}\) of CdCNi\(_3\), in comparison to MgCNi\(_3\), may be due to the reduced value of density of states at the Fermi energy (75 states/Ry for MgCNi\(_3\) and 59 states/Ry for CdCNi\(_3\)). However, it is also possible that the enhanced ferromagnetic correlation suppresses the critical temperature in CdCNi\(_3\) [33].

In connection to still ongoing research on the superconducting state of antiperovskite-type materials [34–36], in the presented paper we conducted the comprehensive theoretical analysis of all important thermodynamic properties of CdCNi\(_3\). Moreover, the obtained results were compared with that of previously computed for MgCNi\(_3\) compound [13]. We expect that the presented results will expand the currently existing knowledge on the superconducting state in antiperovskites and can stimulate further exploration and discovery of new antiperovskite-type materials.

This paper is organized as follows. Section 2 contains a short outline of the theoretical model and computational methods. In Sect. 3, we discuss and compare the thermodynamic properties of superconducting CdCNi\(_3\) and MgCNi\(_3\) systems. Section 4 summarizes the obtained results.

2 Methods of Research

2.1 Essentials of the Eliashberg Formalism

The precise prediction of superconducting properties such as the transition temperature, superconducting energy gap or specific heat is one of the most important challenges in condensed matter physics [37–42]. In conventional superconductors below the critical temperature electron pairing results from interplay between the electron–electron repulsive Coulomb effect and the attractive electron–phonon interaction [43]. Starting from the Bardeen, Cooper and Schrieffer (BCS) theory [44, 45] several approaches to the calculation of the superconducting properties have been proposed. A more sophisticated description of the superconductivity extending the original ideas of BCS theory is the Eliashberg theory of superconductivity [46] which allows to reproduce the superconducting properties of a conventional superconductors within an experimental accuracy. The advantage of the Eliashberg theory over the BCS theory is that the first one takes into account the strong-coupling effects and the fact that the interaction between electrons mediated by phonons is retarded in time.

Starting from the Fröhlich model of an electron–phonon interaction [47] and introducing the Nambu spinors [48] to provide a convenient matrix representation of the Fröhlich Hamiltonian, the Eliashberg equations for the order parameter function and for the wave function renormalization factor can be derived using Green’s functions theory [49–51]. The equations formulated on the imaginary frequency axis take the following form [46, 50]:

$$\begin{aligned} \phi _{n}=\frac{\pi }{\beta }\sum _{m=-M}^{M} \frac{\lambda \left( i\omega _{n}-i\omega _{m}\right) -\mu ^{\star }\theta \left( \omega _{\mathrm{c}}-|\omega _{m}|\right) }{\sqrt{\omega _m^2Z^{2}_{m}+\phi ^{2}_{m}}}\phi _{m} \end{aligned}$$
(1)

and

$$\begin{aligned} Z_{n}=1+\frac{1}{\omega _{n}}\frac{\pi }{\beta }\sum _{m=-M}^{M} \frac{\lambda \left( i\omega _{n}-i\omega _{m}\right) }{\sqrt{\omega _m^2Z^{2}_{m}+\phi ^{2}_{m}}} \omega _{m}Z_{m}, \end{aligned}$$
(2)

where \(\omega _{n}\equiv \left( \pi / \beta \right) \left( 2n-1\right) \) are the Matsubara frequencies with \(n=0,\pm 1,\pm 2,\dots ,\pm M\), and \(M=1100\). Symbol \(\beta \) denotes a inversion of temperature \(\beta \equiv \left( k_{\mathrm{B}}T\right) ^{-1}\). Moreover, \(\mu ^{\star }\) represents the Coulomb pseudopotential with a cut-off frequency \(\omega _{\mathrm{c}}\) equals three times the maximum phonon frequency (\(\omega _{\mathrm{c}}=3\Omega _\mathrm{{max}}\)), the quantity \(\theta \) denotes the Heaviside function, and \(\lambda \left( i\omega _{n}-i\omega _{m}\right) \) is a pairing kernel for the electron–phonon interaction:

$$\begin{aligned} \lambda \left( i\omega _{n}-i\omega _{m}\right) \equiv 2\int _0^{\Omega _\mathrm{{max}}}\mathrm{d}\Omega \frac{\Omega }{(\omega _{n}-\omega _{m})^{2}+\Omega ^2}\alpha ^{2}F\left( \Omega \right) . \end{aligned}$$
(3)

The value of the maximum phonon frequency (\(\Omega _\mathrm{max}\)) is equal to 77.8 meV [28].

At this point, it should be noted that the physical values of the order parameter functions \(\phi \) and the wave function renormalization factor Z can be determined using the Eliashberg equations formulated on the real frequency axis [52].

2.2 Computational Details

Within the framework of the Eliashberg formalism, the superconductivity arising from the electron–phonon coupling is characterized by the Eliashberg spectral function \(\alpha ^{2}F\left( \omega \right) \), which can be written as

$$\begin{aligned} \alpha ^2F(\omega )=\frac{1}{2\pi \rho \left( 0\right) }\sum _{\mathbf{q}j}\frac{\gamma _{\mathbf{q}j}}{\hbar \omega _{\mathbf{q}j}}\delta (\omega -\omega _{\mathbf{q}j}), \end{aligned}$$
(4)

where \(\rho \left( 0\right) \) is the value of the electron density of states at the Fermi level. The quantities \(\delta (x)\) represent the Dirac delta function, \(\omega _{\mathbf{q}j}\) is phonon frequency of the jth phonon mode at vector \(\mathbf{q}\), and symbol \(\gamma _{\mathbf{q}j}\) denotes the phonon linewidth [53]. The \(\alpha ^2F(\omega )\) function for CdCNi\(_3\) was determined in paper [28] using the first-principles pseudopotential method based on the density-functional theory. The phonon density of states and the Eliashberg function were calculated using \(28\times 28\times 28\) k mesh with the Gaussian width \(\sigma =0.02\) Ry [28]. All calculations were preformed for a cubic CdCNi\(_3\) with the space-group symmetry \(Pm\overline{3}m\) where the atomic positions are Cd at (0, 0, 0), C at (0.5, 0.5, 0.5) and Ni at (0.5, 0.5, 0), (0.5, 0, 0.5), (0, 0.5, 0.5). The unit cell looks the same, as that visualized using VESTA software [54] in Fig. 1.

Fig. 2
figure 2

Diagram of calculation procedure (Color figure online)

Full size image

In the present paper, to investigate the superconducting properties of antiperovskite CdCNi\(_3\) within the experimental accuracy, we adopted the numerical methods described in paper [55] and successfully used in our previous studies [56–59]. The scheme of conducted calculation was shown in Fig. 2. In particular, taking as a input parameters the Eliashberg spectral function and measured value of \(T_\mathrm{C}\) we can calculate the critical value of Coulomb pseudopotential. Then, we resolve Eqs. (1) and (2) for different temperatures. The solutions of the Eliashberg equations on the imaginary axis are use in the calculations of the free energy difference between the superconducting and the normal state [50]:

$$\begin{aligned} \frac{\Delta F}{\rho \left( 0\right) }= & {} -\frac{2\pi }{\beta }\sum _{n=1}^{M} \left( \sqrt{\omega ^{2}_{n}+\Delta ^{2}_{n}}- \left| \omega _{n}\right| \right) \\ \nonumber&\times \left( Z^{\mathrm{S}}_{n}-Z^{\mathrm{N}}_{n}\frac{\left| \omega _{n}\right| }{\sqrt{\omega ^{2}_{n}+\Delta ^{2}_{n}}}\right) , \end{aligned}$$
(5)

where symbols \(Z^{\mathrm{S}}_{n}\) and \(Z^{\mathrm{N}}_{n}\) denote the wave function renormalization factor for the superconducting state and for the normal state, respectively. In a similar way it is possible to calculate the London penetration depth (\(\lambda _{\mathrm{L}}\)):

$$\begin{aligned} \frac{1}{e^2v^2_\mathrm{F}\rho \left( 0\right) \lambda ^2_\mathrm{L}\left( T\right) }=\frac{4}{3}\frac{\pi }{\beta }\sum _{n=1}^{M} \frac{\Delta ^{2}_{n}}{Z^{\mathrm{S}}_{n}\left[ \omega ^{2}_{n}+\Delta ^{2}_{n}\right] ^{3/2}}, \end{aligned}$$
(6)

where symbols e and \(v^{}_\mathrm{F}\) denote the electron charge and the Fermi velocity, respectively.

In the next step, the thermodynamic critical field (\(H_\mathrm{C}\)) is calculated from the free energy difference:

$$\begin{aligned} \frac{H_{\mathrm{C}}}{\sqrt{\rho \left( 0\right) }}=\sqrt{-8\pi \left[ \Delta F/\rho \left( 0\right) \right] }. \end{aligned}$$
(7)

The entropy difference between the superconducting and normal state is determined by the first derivative of \(\Delta F\):

$$\begin{aligned} \frac{\Delta S}{k_{\mathrm{B}}\rho \left( 0\right) }=-\frac{d\left[ \Delta F/\rho \left( 0\right) \right] }{d\left( k_{\mathrm{B}}T\right) }, \end{aligned}$$
(8)

and the specific heat difference between the superconducting and normal state (\(\Delta C=C^\mathrm{S}-C^\mathrm{N}\)) follows from the second derivative of \(\Delta F\) through:

$$\begin{aligned} \frac{\Delta C}{k_{\mathrm{B}}\rho \left( 0\right) }=-\frac{1}{\beta }\frac{d^{2}\left[ \Delta F/\rho \left( 0\right) \right] }{d\left( k_{\mathrm{B}}T\right) ^{2}}. \end{aligned}$$
(9)

The specific heat in the normal state is defined as \(C^{\mathrm{N}}=\gamma /{\beta }\), where the Sommerfeld constant (\(\gamma \)) has the form: \(\gamma \equiv ({2}/{3})\pi ^{2}\left( 1+\lambda \right) k_{\mathrm{B}}\rho \left( 0\right) \).

The knowledge of the solutions of the Eliashberg equations on the imaginary frequencies axis allows also to obtain the solutions on the real frequencies axis. On the basis of these results, the exact value of the order parameter can be obtained in the following way:

$$\begin{aligned} \Delta \left( T\right) =\mathrm{Re}\left[ \Delta \left( \omega =\Delta \left( T\right) ,T\right) \right] , \end{aligned}$$
(10)

and the electron effective mass (\(m^{\star }_{\mathrm{e}}\)) can be determined from the relation: \(m^{\star }_{\mathrm{e}}/m_{\mathrm{e}}=\mathrm{Re}\left[ Z\left( 0\right) \right] \), where \(m_{\mathrm{e}}\) denotes the electron band mass.

On the basis of above thermodynamic functions we can estimate the dimensionless ratios: \(R_{\Delta }\equiv 2\Delta (0)/k_{\mathrm{B}}T_{\mathrm{C}}\), \(R_{\mathrm{C}}\equiv {\Delta C\left( T_{\mathrm{C}}\right) }/{C^{\mathrm{N}}\left( T_{\mathrm{C}}\right) }\) and \(R_{\mathrm{H}}\equiv {T_{\mathrm{C}}C^{\mathrm{N}}\left( T_{\mathrm{C}}\right) }/{H_{\mathrm{C}}^{2}\left( 0\right) }\). The above ratios (marked by blue fill on the diagram in Fig. 2) play a very important role in theory of superconductivity because they can be determined in experimental measurements and compared with theoretical predictions.

3 Results and Discussion

The critical temperature of CdCNi\(_3\) (\(T_\mathrm{C}=3.2\) K) has been determined from the magnetization measurement in paper [33]. On this basis, we are able to calculate the critical value of Coulomb pseudopotential \(\mu ^{\star }_\mathrm{C}\). In particular, in the Eliashberg equations we assumed that \(T=T_\mathrm{C}\) and then we have increased the value of the parameter \(\mu ^{\star }\) until we have reached the equality \(\Delta _\mathrm{m=1}(\mu ^{\star }_\mathrm{C})=0\), where the order parameter is defined as follows: \(\Delta _{n}\equiv \phi _{n}/Z_{n}\). The received results are shown in Fig. 3a, where the dependence of the order parameter on the Matsubara frequencies is plotted. The full dependence of \(\Delta _{m=1}\) on \(\mu ^{\star }\) we can trace in Fig. 3b.

Fig. 3
figure 3

a The order parameter on the imaginary axis for the selected values of the Coulomb pseudopotential. b The full dependency of the maximum value of the order parameter on the Coulomb pseudopotential at \(T_\mathrm{C}\) (Color figure online)

Full size image
Fig. 4
figure 4

a The energy dependencies of the order parameter functions on the real axis for selected values of temperature. b The normalized energy gap at the reduced temperature. The inset presents the total normalized density of states for selected temperatures (Color figure online)

Full size image

The high value of the Coulomb pseudopotential suggests that the critical temperature of CdCNi\(_3\) cannot be correctly evaluated by means of the analytical McMillan (McM) formula for \(T_\mathrm{C}\) [60]:

$$\begin{aligned} T_{\mathrm{C}}^\mathrm{(McM)}=\frac{\omega _\mathrm{ln}}{1.2}\exp \left[ \frac{-1.04\left( 1+\lambda \right) }{\lambda -\mu ^{\star }\left( 1+0.62\lambda \right) }\right] , \end{aligned}$$
(11)

where symbol \(\lambda \) denotes the electron–phonon coupling constant and \(\omega _{\mathrm{ln}}\) is the logarithmic average of the phonon frequencies:

$$\begin{aligned} \lambda =2\int _0^{\Omega _\mathrm{{max}}}\mathrm{d}\omega \frac{\alpha ^2F(\omega )}{\omega } \end{aligned}$$
(12)

and

$$\begin{aligned} \omega _{\mathrm{ln}}\equiv \exp \left[ \frac{2}{\lambda }\int ^{\Omega _\mathrm{{max}}}_{0}\mathrm{d}\omega \frac{\alpha ^{2}F\left( \omega \right) }{\omega }\ln \left( \omega \right) \right] . \end{aligned}$$
(13)

In particular, for CdCNi\(_3\) we achieved: \(\lambda =0.8\), \(\omega _{\mathrm{ln}}=101.6\) meV and finally \(T_{\mathrm{C}}^\mathrm{(McM)}=1.69\) K.

The temperature-dependent solutions of the Eliashberg equations on the imaginary frequency axis at \(\mu ^{\star }_\mathrm{C}\) were used as the input parameters to the real axis Eliashberg equations. The form of the order parameter on the real frequency axis for selected values of T is plotted in Fig. 4a. On this basis and from Eq. (10) we concluded that the maximum value of the energy gap at the Fermi surface (\(2\Delta (0)=2\Delta (T_0)\)) is equal to 1.03 meV, where \(T_0\) denotes a minimum value of temperature for which convergence of the solutions was obtained. In our case, solutions are stable from \(T_0=0.4\) K. The temperature dependency of the energy gap can be modeled by the simple analytical formula: \(2\Delta \left( T\right) =2\Delta \left( T_0\right) \sqrt{1-\left( {T}/{T_{\mathrm{C}}}\right) ^{\alpha }}\), where the parameter \(\alpha \) is equal to 3.3.

The energy gap decreases with temperature and vanishes at \(T_\mathrm{C}\) in a manner consistent with behavior of conventional superconductors. In Fig. 4b, the dependence of the normalized gap on the temperature is presented.

Fig. 5
figure 5

a The free energy difference, b entropy difference, and c the specific heat as a function of temperature for antiperovskite CdCNi\(_3\) (Color figure online)

Full size image
Fig. 6
figure 6

a The thermodynamic critical field, b deviation of the thermodynamic critical field, and c the normalized London penetration depth as a function of temperature (Color figure online)

Full size image

Moreover, the obtained results are compared with prediction of the BCS theory, where \(\alpha =3\). As we can see the differences are not as large as for example in the case of MgCNi\(_3\) where \(\alpha =3.6\) [13]. Knowledge of the gap function enables us to calculate the total normalized density of states, defined as [50]:

$$\begin{aligned} \mathrm{NDOS}(\omega )=\frac{\mathrm{DOS_{S}}(\omega )}{\mathrm{DOS_{N}}(\omega )}=\mathrm{Re}\left[ \frac{\left| \omega -i\Gamma \right| }{\sqrt{\left( \omega -i\Gamma \right) ^{2}-\Delta ^{2}\left( \omega \right) }}\right] , \end{aligned}$$
(14)

where the symbols \(\mathrm DOS_{S}\left( \omega \right) \) and \(\mathrm DOS_{N}\left( \omega \right) \) denote the density in the superconducting and normal state, respectively. The pair breaking parameter \(\Gamma \) is equal to 0.15 meV. The obtained results for selected temperatures are presented in the inset of Fig. 4b.

Also from the solution of the Eliashberg equations formulated on the real frequency axis we determined the value of the electron effective mass at \(T_\mathrm{C}\). In particular, for CdCNi\(_3\) we obtained \(m^{\star }_{\mathrm{e}}=1.81m_{\mathrm{e}}\), wherein the MgCNi\(_3\) is characterized by \(m^{\star }_{\mathrm{e}}=2.55m_{\mathrm{e}}\) [13]. At this point it should be emphasized that the value of \(m^{\star }_{\mathrm{e}}\) is directly related to the electron–phonon coupling constant and in a simple analytical way this fact can be written as \(m^{\star }_{\mathrm{e}}\simeq (1+\lambda )m_{\mathrm{e}}\).

In the next step, according to the scheme shown in Fig. 2 and using Eqs. (5)–(9), we calculated the free energy, the specific heat and the entropy difference between the superconducting and normal state, the thermodynamic critical field and the London penetration depth. Moreover, our calculations were supplemented by the thermodynamic critical field deviation:

$$\begin{aligned} D(T) = \frac{H_\mathrm{C}\left( T\right) }{H_\mathrm{C}\left( 0\right) }-\left[ 1-\left( \frac{T}{T_\mathrm{C}}\right) ^2\right] . \end{aligned}$$
(15)

The obtained results are presented in Figs. 5 and 6. Particularly interesting is to compare the obtained results with those predicted by the classical BCS theory. On the basis of Fig. 6b, c we can see that our calculations indicate that CdCNi\(_3\) is a BCS superconductor, which is in a general agreement with the experimental observation [33] and previous theoretical study [28].

The presented thermodynamic functions enabled us to estimate the dimensionless ratios \(R_{\Delta }\), \(R_{\mathrm{C}}\) and \(R_{\mathrm{H}}\). It should be mentioned that in the BCS theory, the above parameters take the well-known universal values: 3.53, 1.43, and 0.168, respectively [44, 45]. In the case of antiperovskite CdCNi\(_3\), the obtained results are presented in Table 1.

Table 1 The comparison of the most important superconducting ratios for CdCNi\(_3\) and related MgCNi\(_3\) [13] antiperovskites
Full size table

We can see that \(R_{\Delta }\) and \(R_{\mathrm{C}}\) are close to, although slightly higher than, the prediction of the BCS theory, while the value of \(R_{\mathrm{H}}\) is slightly lower. This is a typical behavior of medium-coupling superconductors.

From the physical point of view, there are two reasons causing the deviation from the BCS theory [43]. The first one is connected with the fact that the BCS model bases on the time-independent interaction. The second one arises from the failure of taking into account the strong-coupling effects. In the Eliashberg formalism the above effects are described by the ratio of \(k_{\mathrm{B}}T_{\mathrm{C}}\) to \(\omega _\mathrm{ln}\), in the weak-coupling limit we have: \(k_{\mathrm{B}}T_{\mathrm{C}}/\omega _\mathrm{ln}\rightarrow 0\). In Table 1 we can see the obtained values for Mg- and Cd-based carbides-nitrides antiperovskite.

During the comparison of the thermodynamic properties of sister antiperovskites CdCNi\(_3\) and MgCNi\(_3\) we can conclude that the larger mass of Cd-ion than Mg-ion is the cause of the deterioration of the superconducting properties of CdCNi\(_3\).

4 Conclusion

In this paper we investigated the thermodynamic properties of the superconducting state existing in CdCNi\(_3\) compound. In the framework of the Eliashberg formalism we had calculated all the most important parameters. Then, due to the fact that the crystal structures of CdCNi\(_3\) have the same antiperovskite-type such as MgCNi\(_3\), we compared the obtained parameters of CdCNi\(_3\) with that of earlier estimated for MgCNi\(_3\). The comparative studies indicate that the larger mass of Cd-ion than Mg-ion reduces the values of superconducting parameters of CdCNi\(_3\). In particular, it can be observed in the case of \(T_\mathrm{C}\) and the dimensionless parameters \(R_{\Delta }\), \(R_{\mathrm{C}}\) and \(R_{\mathrm{H}}\). For CdCNi\(_3\) we have \(T_\mathrm{C}=3.2\) K, \(R_{\Delta }=3.74\), \(R_{\mathrm{C}}=1.50\) and \(R_{\mathrm{H}}=0.162\), whereas for MgCNi\(_3\) we have \(T_\mathrm{C}=8\) K, \(R_{\Delta }=4.19\), \(R_{\mathrm{C}}=2.27\), and \(R_{\mathrm{H}}=0.141\). We strongly encourage all readers to quantitatively verify the presented thermodynamic parameters by means of the available experimental methods.