1 Introduction

Spintronics, starting in 1988, is still an active research field by now, which may fabricate electron devices with brand-new physical properties by using eletcron spin and even realize quantum memory and quantum computation, then improve greatly the efficiency of electron device. So it has a potential impact on information technology. Spin-splitting induced by the spin-orbit interaction is sometimes confused with Zeeman splitting originating from the magnetic field. The later requires the time-reversal symmetry broken. However, the former originating from the space inversion asymmetry, is known as the Rashba effect, which plays an important role in semiconductor spintronics . In recent years, the Rashba effect in low-dimensional systems has attracted more attention from experimental and theoretical physicists. Based on an analytical methodology, a three-electron-quantum dot (QD) in the presence of Rashba spin-orbit interaction under cylindrical symmetry is investigated by Hassanabadi et al. [1]. By means of the Keldysh Green’s function method, Zhang et al. [2] reported a theoretical study on producing an electrically spin-polarized current in the Rashba ring with parallel double dots embedded, which are subjected to two time-dependent microwave fields. Hassanabadi et al. [3] theoretically investigated a three-electron QD in the presence of Rashba spin-orbit interaction by an analytical methodology. Using nonequilibrium Green’s function technique, Li et al. [4] investigated the spin current through the three QD device. Manvir [5] proposed the theoretical investigation of the effect of the Rashba-type spin-orbit interaction on the Fock-Darwin energy spectrum in the parabolically confined QDs in the presence of a perpendicular magnetic field. A detailed investigation of the nonlinear optical properties such as optical absorption and refractive index change associated with intersubband transitions in a three-electron QD in two dimensions in the presence of the Rashba spin-orbit interaction has been carried out by Hassanabadi et al. [6]. Crisan et al. [7] studied the formation of local moments in quantum dots arising in quasi-one-dimensional electron wires due to localized spin-orbit interaction. Using an Anderson-type model to describe the occurrence of the magnetic moments in these Rashba dots, the local magnetization was calculated within the mean-field approximation. Chakraborty et al. [8] reported on a theoretical approach developed to investigate the influence of the Bychkov–Rashba interation on a few interacting electrons confined in a QD. Using the Hartree approximation, the \(8\times 8\) kane Hamiltonian, and the envelope-function scheme the electronic structure of electrons bound within an inversion layer on p-InAs in a Mosfet geometry is computed self-consistently and studied as a function of the two-dimensional electron density \(N_{s}\) and the doping concentration \(N_{A -} N_{D}\) by Lamari [9]. Kanobb et al. [10] investigated the electronic structure of Rashba spin-split quantum wires in a magnetic field. Reynoso et al. [11] studied the edge states in a two-dimensional electron gas with a transverse magnetic field and Rashba spin-orbit (SO) coupling. Matsuyama et al. [12] discussed the dependence of the spin-orbit interaction on electron density in inversion layers of metal-oxide-semiconductor field-effect transistors on p-type InAs by magnetotransport at liquid-helium temperatures. Considering the influence of the Rashba SO interaction on the condition of the electron–LO phonon strong coupling in a parabolic QD, Yin et al. [13] calculated the bound polaron ground state energy by the variational method of Pekar. The condition of electric–LO phonon strong coupling in a parabolic QD was studied in detail by Li et al. [14] and the polaron ground state energy was derived by the variational method of Pekar, considering the influence of the Rashba SO interaction. However, few people have investigated the Rashba effect on the ground state energy of the strong-coupling bound polaron in an asymmetric QD at present. Especially the electron with heavy hole characteristics in an asymmetric QD has never been studied by employing the LLP variational method yet.

In this paper, we investigate the Rashba effect on bound polaron in an asymmetric QD within the LLP variational method. The paper is arranged as follows. First, we derive the expression of the ground state energy of the polaron. Then, our numerical results are presented and discussed. Finally, a conclusion is drawn in our investigation.

2 Theory and Model

At zero magnetic field, we consider a polar crystal system in which an electron with heavy hole characteristics is moving and interacting with the bulk LO phonons. Due to the phonon field and the polar crystal boundary effect, the moving of the electron in every direction is quantized. On the basis of effective mass approximation, the Hamiltonian of the electron–phonon interaction system with a hydrogenic impurity at the center can be written as

$$\begin{aligned} H=H_e +H_{LO} +H_{e-LO} +H_{SO}.\end{aligned}$$
(1)
$$\begin{aligned} H_e =\frac{P_{//}^2 }{2m}+\frac{P_z^2 }{2m}+V_p ( r)+V_c ( r), \end{aligned}$$
(2)
$$\begin{aligned} V_P (r)=\frac{1}{2}m\omega _1^2 \rho ^2+\frac{1}{2}m\omega _2^2 z^2, \end{aligned}$$
(2a)
$$\begin{aligned} V_c ( r)=-\frac{e^2}{\varepsilon _0 r}. \end{aligned}$$
(2b)

Here \(V_{P} ( r)\) represents the three-dimensional anisotropic harmonic potential in the \(x-y\) plane and \(z\)-direction, \(V_c ( r)\) is the Coulomb bound potential, \(r=( {\rho ,z})\) refers to the position operator of an electron and \(\omega _1 ( {\omega _2 })\) is the measure of the transverse (longitudinal) confinement strength.

The second and the third terms in Eq. (1) describe the LO-phonon field and the interaction energy of the electron–LO phonon. They are given by

$$\begin{aligned} H_{LO}&= \sum \limits _{k} {\hbar \omega _{LO} b_\mathrm{k}^+ b_\mathrm{k}},\end{aligned}$$
(3)
$$\begin{aligned} H_{e-LO}&= \sum \limits _{k}{({V_\mathrm{k} b_\mathrm{k} e^{i\mathrm{k}\cdot \mathrm{r}}+h.c})} \end{aligned}$$
(4)
$$\begin{aligned} V_{k} = i\left( {\frac{{\hbar \omega _{{LO}} }}{k}} \right) {\left( {\frac{{\hbar }}{{2m\omega {L_o}}}} \right) }^{{1/4}} \left( {\frac{{4\pi \alpha }}{V}} \right) ^{{1/2}}, \end{aligned}$$
(4a)
$$\begin{aligned} \alpha =\left( {\frac{e^2}{2\hbar \omega _{LO} }}\right) \left( {\frac{2m\omega _{LO}}{\hbar }}\right) ^{{1}/{2}}\left( {\frac{1}{\varepsilon _\infty }-\frac{1}{\varepsilon _0}}\right) . \end{aligned}$$
(4b)

Where \(b_\mathrm{k}^+ ( {b_\mathrm{k}})\) is the creation (annihilation) operator of the LO phonons with the wave vector \(k\) and the frequency \(\omega _{LO} \), \(V\) is the volume of the crystal and the electron–LO phonon coupling strength is represented by \(\alpha \). \(\varepsilon _0 \) and \(\varepsilon _\infty \) are the static dielectric constant and high frequency adiabatic constant, respectively.

The last term in Eq. (1) is the contribution of the Rashba spin-orbit interaction. It can be expressed as [15]

$$\begin{aligned} H_{SO} =i\frac{a_R }{\hbar }\left( {P_-^3 {\hat{\sigma }}_+ -P_+^3 {\hat{\sigma }}_- }\right) . \end{aligned}$$
(5)

Using the notation \(P_\pm =P_x \pm iP_y ,{\hat{\sigma }}_\pm ={\hat{\sigma }}_x \pm i{\hat{\sigma }}_y \), where \({\hat{P}}\), \({\hat{\sigma }}\) denote the electron momentum operator and Pauli matrices, respectively. In a semiconductor structure, the Rashba parameter \(a_R \) is determined by many factors.

We expand the Coulomb bound potential with the Fourier expansion

$$\begin{aligned} -\frac{e^2}{\varepsilon _0 r}=-\frac{4\pi e^2}{\varepsilon _0 V}\sum \limits _\mathrm{{k}} {\frac{1}{k^2}\exp (-i\hbox {k}\cdot \hbox {r})}. \end{aligned}$$
(6)

Then, we carry out the Lee-Low-Pines transformation to Eq. (1)

$$\begin{aligned} U=\exp \left[ {\sum \limits _\mathrm{{k}} {b_\mathrm{k}^+\!f_{k}-b_\mathrm{k}f_k^*} } \right] . \end{aligned}$$
(7)

Where \(f_k ( {f_k^*})\) is the variational function to be determined by minimizing the energy. For the ground state of the system, we choose the following variational trial wave function

$$\begin{aligned} \left| \psi \right\rangle&= \left( {\lambda ^2/\pi }\right) ^{{1}{/}{2}}\exp \left( {-\lambda ^2\rho ^2/2}\right) \left( {\mu ^2/\pi }\right) ^{{1} {/}{4}} \nonumber \\&\quad \times \exp \left( {-\mu ^2z^2/2}\right) \left( {ax_{{1}/{2}}}+bx_{-{1}/{2}}\right) \left\langle {0_{ph} } \right\rangle . \end{aligned}$$
(8)

Where \(\chi _{{1}/{2}} =\left( \begin{array}{l} 1 \\ 0 \\ \end{array}\right) \) and \(\chi _{{-1}/{2}} =\left( \begin{array}{l} 0 \\ 1 \\ \end{array} \right) \) refer to the up and down states of the spin, \(a\)and \(b\) are coefficients and \(\left| 0 \right\rangle _{ph} \) is the unperturbed zero-phonon state which satisfies \(b_\mathrm{{k}} \left| 0 \right\rangle _{ph} =0\). \(\lambda \) and \(\mu \) are variational parameters which can be determined by minimizing the total energy of the system.

The total energy of the system can be obtained by computing the expectation value \(\left\langle \psi \right| U^{-1}HU\left| \psi \right\rangle \). We have

$$\begin{aligned} E_{\uparrow \downarrow }&= \frac{\hbar ^2k^2}{2m}+\frac{\hbar ^2}{2m\lambda ^2l_1^4 }+\frac{\hbar ^2}{4m\mu ^2l_2^4 }-\left( {\sqrt{2} \alpha \hbar \omega _{LO} \left( {\frac{\hbar }{2m\omega _{LO} }}\right) ^{{1} {/ }{2}} +\beta }\right) \nonumber \\&\frac{\mu }{\sqrt{\pi }} \left( {1-\frac{\mu ^2}{\lambda ^2}}\right) ^{-1/2}\arcsin \left( {1-\frac{\mu ^2}{\lambda ^2}}\right) ^{{1} {/} {2}} \pm a_R k^3. \end{aligned}$$
(9)

where \(E_\uparrow \), \(E_\downarrow \) are the ground state energy of the spin-up and spin-down components with the spin-splitting energy \(E_{SO} =a_R k^3\), \(\beta =\frac{e^2}{\varepsilon _0 }\sqrt{\frac{m}{\pi \hbar }}\) is the Coulomb bound potential and \(l_1 =\sqrt{\frac{\hbar }{m\omega _1 }}\) \(l_2 =\sqrt{\frac{\hbar }{m\omega _2 }} \) are the transverse and longitudinal effective confinement lengths, respectively.

From Eq. (9), we can see that the spin-splitting energy \(E_{SO} \) is proportional to \(k^3\)rather than \(k\). The result is consistent with [16]. The reason is that the electron in conduction band owns heavy hole characteristic. As a result of it, the spin-splitting energy \(E_{SO} \) is proportional to \(k^3\).

3 Numerical Results and Discussion

To show more obviously the influence of the Rashba effect on the properties of the bound polaron in an asymmetric QD, we perform a numerical calculation. For the sake of simplicity, the usual polaron units (\(\hbar =2m=\omega _{LO} =1)\) are adopted. The results are presented in Figs. 1, 2, 3, 4.

Fig. 1
figure 1

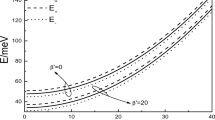
The relation between polaron ground state energy \(E_0 \), and spin-up(spin-down) splitting energy \(E_\uparrow ( {E_\downarrow })\) with electron–phonon coupling strength \(\alpha \) at different Coulomb bound potential \(\beta \). They are expressed by the full line, the dash dotted line and the dotted line, respectively

Full size image
Fig. 2
figure 2

The relation between polaron ground state energy \(E_0 \), and spin-up(spin-down) splitting energy \(E_\uparrow ( {E_\downarrow })\) with wave vector \(k\) at different Coulomb bound potential \(\beta \). They are expressed by the full line, the dash dotted line and the dotted line, respectively

Full size image
Fig. 3
figure 3

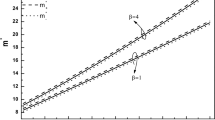
The relation between polaron ground state energy \(E_0 \), and spin-up(spin-down) splitting energy \(E_\uparrow ( {E_\downarrow })\) with the transverse effective confinement length \(l_1 \) at different Coulomb bound potential \(\beta \). They are expressed by the full line, the dash dotted line and the dotted line, respectively

Full size image
Fig. 4
figure 4

The relation between polaron ground state energy \(E_0 \), and spin-up(spin-down) splitting energy \(E_\uparrow ( {E_\downarrow })\) with the longitudinal effective confinement length \(l_2 \) at different coulomb bound potential \(\beta \). They are expressed by the full line, the dash dotted line and the dotted line, respectively

Full size image

Figure 1 shows the relationship between the ground state energy \(E_0 \), the spin-up splitting energy \(E_\uparrow \) and the spin-down splitting energy \(E_\downarrow \) varying with the electron–phonon coupling strength \(\alpha \) for fixed \(k=3\), \(l_1 =0.2\), \(l_2 =0.6\) and \(a_R =0.01\). From this figure, we can see that the ground state energy, the spin-up splitting energy and the spin-down splitting energy decrease rapidly with the increase of the electron–phonon coupling strength. With the increase of the coupling strength, the electron interacts with more phonons. But the contribution of the electron–phonon interaction to the polaron energies in Eq. (9) is a negative value. For this reason, the polaron energies will enhance with the decrease of the electron–phonon coupling strength. We also can see from the figure that the change of the energy spacing between spin-up and spin-down is zero with the increasing of electron–phonon coupling strength. So we can draw a conclusion that the influence of the interaction between the electron and LO–phonon on the Rashba effect can be neglected.

Figure 2 illustrates the ground state energy \(E_0 \), the spin-up splitting energy \(E_\uparrow \) and the spin-down splitting energy \(E_\downarrow \) as functions of the wave vector \(k\) with \(l_1 =0.2\), \(l_2 =0.4\), \(\alpha =6\) and \(a_R =0.01\). It can be seen that the polaron energies are all parabolic linearly increased with the increase of the wave vector. This is attributed to the first term in Eq. (9) that the square of the wave vector is a positive value to the energy. Therefore, the polaron energies will vary with the above changes. One can also see from the figure that the energy spacing between spin-up and spin-down becomes larger with the increase of the wave vector. From \(E_{SO} =a_R k^3\), we know that \(k^3\) is proportional to \(E_{SO} \). Hence, the energy spacing will enhance with increasing wave vector.

In Fig. 3, we plot the relational curves of the ground state energy \(E_0 \), the spin-up splitting energy \(E_\uparrow \) and the spin-down splitting energy \(E_\downarrow \) with the transverse effective confinement length \(l_1 \)for \(k=3\), \(l_2 =0.6\), \(\alpha =5\) and \(a_R =0.05\). Figure 4 presents the influence of the longitudinal effective confinement length \(l_2 \)on the ground state energy \(E_0 \), the spin-up splitting energy \(E_\uparrow \) and the spin-down splitting energy \(E_\downarrow \) for fixed \(k=3\), \(l_1 =0.2\), \(\alpha =5\) and \(a_R =0.05\), respectively. From the two figures, one can see that the polaron energies decrease when the transverse and longitudinal effective confinement lengths increase. These can be attributed to the quantum size effects. One can also see from them that the energy spacing between the spin-up and the spin-down becomes larger with increasing transverse and longitudinal effective confinement lengths. We can arrive at a conclusion that the influence of transverse and longitudinal effective confinement lengths on the Rashba effect should be considered. Comparing Fig.  3 with Fig. 4, we can see that the influence of the transverse effective confinement length on the ground state energy is smaller than the longitudinal effective confinement length.

In Fig. 1, 2, 3, 4, at the same position (same value of \(\alpha \), \(k\), \(l_1 \) and \(l_2 \), respectively), we find that the smaller the Coulomb bound potential is, the larger the polaron energy is. There is Coulomb bound potential between the electron and the hydrogen-like impurity because of the existence of a hydrogen-like impurity in the center of an asymmetric QD. Since the presence of the Coulomb potential is equivalent introducing another new confinement on the electron, which leads to greater electron wavefunction overlapping with each other, the electron–phonon interaction will be enhanced. In Eq. (9), we know that the contribution of the Coulomb bound potential to the polaron energy has a negative value. Hence, we can obtain the results mentioned above.

4 Conclusion

In conclusion, based on the LLP vibrational method, we investigate the influence of the Rashba effect on the properties of the polaron in an asymmetric QD. It is found that the ground state energy splits into two branches, that is, spin-up splitting energy and spin-down splitting energy. At different Coulomb bound potentials, we discuss the relations between the ground state energy with the electron–phonon coupling strength, the wave vector, the transverse effective confinement length and the longitudinal effective confinement length, respectively. The results show that the ground state energy is a decreasing function of the Coulomb bound potential, the electron–phonon coupling strength, the transverse effective confinement length and the longitudinal effective confinement length. However, it is an increasing function of the wave vector.