Response of a Mechanical Oscillator in Solid ⁴He

Abstract

We present the first measurements of the response of a mechanical oscillator in solid ⁴He. We use a lithium niobate tuning fork operating in its fundamental resonance mode at a frequency of around 30 kHz. Measurements in solid ⁴He were performed close to the melting pressure. The tuning fork resonance shows substantial frequency shifts on cooling from around 1.5 K to below 10 mK. The response shows an abrupt change at the bcc-hcp transition. At low temperatures, below around 100 mK, the resonance splits into several overlapping resonances.

Introduction

The mechanical properties of solid ⁴He have received considerable attention in recent years following claims of a possible ‘supersolid’ response in torsional oscillator experiments [1]. There is now growing evidence that supersolidity was not observed in these measurements, and that the effects observed are more likely to be associated with changes in the mechanical properties of the solid, possibly related to the dynamics of defects [2–4]. Here we present preliminary measurements of the response of a lithium niobate miniature tuning fork immersed in solid ⁴He. The device provides a simple technique to study the mechanical properties of solid helium over a very wide temperature range.

Miniature tuning forks have been used for many research applications, such as scanning probe microscopy [5] and high performance characterization of liquids [6]. In recent years they have been used in quantum fluids research to study many different properties such as viscosity [7, 8], turbulence [9, 10], cavitation [11], Andreev scattering [12, 13], and acoustic modes [14, 15].

The tuning forks are made from a piezoelectric material. The driving force is supplied by an alternating voltage V=V ₀ e ^−iωt applied to electrodes on the surfaces of the fork prongs. The driving force on each prong can be written as [16]

$$ F = a V /2 $$

(1)

where a is the fork constant. The fork motion produces a piezoelectric current I proportional to the tip velocity v of the prongs,

$$ I = a v $$

(2)

The fork constant can be estimated from [16]

$$ a = \sqrt{\frac{4 \pi m_{\rm eff}\, \varDelta f_2\, I_0}{V_0}} $$

(3)

where Δf ₂ is the width of the resonance, I ₀ is the current amplitude at the resonant frequency, V ₀ is the amplitude of the driving voltage, and the effective mass in vacuum is $m_{\rm eff}=\rho LTW/4$ where ρ is the density of the piezoelectric material [15]. Direct optical measurements [17] of prong velocities of quartz tuning forks in vacuum show that the above expression for the fork constant is correct to within about 10 %.

For many applications it is important to minimise intrinsic losses, so miniature tuning forks are often made from quartz. To study solid ⁴He it is more important to optimise the piezoelectric properties to allow large driving forces and large signal currents for small velocities. For this purpose we have made tuning forks with lithium niobate which has a much larger piezoelectric modulus [18].

Experimental Details

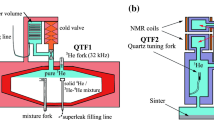
A schematic of the experimental cell, viewed from above, is given in Fig. 1a. The cell body is made from epoxy. This is potted in Stycast 1266 within a larger epoxy container (not shown) to give sufficient strength to withstand pressures in excess of 70 bar. The helium is cooled by a small pad of silver sinter in the center of the cell which connects to a larger pad of sinter in the mixing chamber of the dilution refrigerator [19] via a high purity annealed silver wire. The lithium niobate tuning fork is located along-side the sinter pad as indicated. The fork is held upright and fixed to the base of the cell with Stycast 1266. The cell contains 2 commercial pressure sensors [20], a ‘floppy’ wire and an array of quartz tuning forks (these devices were used for separate experiments to be discussed elsewhere). The temperature was measured with a calibrated resistance thermometer located in the mixing chamber of the refrigerator.

Fig. 1

(a) A schematic of the experimental cell as viewed from above, ‘P’ indicates the locations of two pressure sensors. The lithium niobate tuning fork is orientated with the prongs vertical. (b) Image of the lithium niobate tuning fork before (right) and after (left) coating with Cr/Au (Color figure online)

The lithium niobate tuning fork is shown in Fig. 1b. It has prongs of length L=6 mm, width W=1 mm, thickness T=1.1 mm and separation, D=0.6 mm. The tuning fork was produced in-house by mechanically cutting a LiNbO3 Y-cut wafer and using a parallel arrangement of electrodes [21] as shown in Fig. 1b (right). The fork was coated with Cr/Au using an RF sputtering system to increase the electromechanical coupling, shown in Fig. 1b (left).

Measurements in helium were made using isotopically pure ⁴He produced in Lancaster [22]. The solid samples were grown at various constant temperatures ranging from below 10 mK to around 1.6 K. The solid samples were grown by increasing the pressure until the fill-line located at the very top of the cell became blocked. It is inevitable that, after filling, small pockets of liquid will remain trapped, most likely in the top corners of the cell. The measurements described below were therefore taken at, or close to, the melting pressure. This was confirmed by measurements of the two pressure sensors.

Fork Operation and Characterisation

The tuning fork was driven by a function generator whose output was attenuated to give a sufficiently small drive voltage. The signal current was measured with a custom-made current-to-voltage converter [23] and a lock-in amplifier. Measurements in vacuum at 4 K found the fundamental resonance to have a frequency of 24.581 kHz and a width of Δf ₂=0.18 Hz. The fork constant, using Eq. (3) is found to be a=4.2×10⁻⁴ NV⁻¹.

A simple model gives the following theoretical expression for the fork constant $a_{\rm th}$ at the fundamental resonance mode [16]

$$ a_{\rm th} = 3 d E \frac{TW}{L} $$

(4)

where d is the appropriate piezoelectric modulus. For the lithium niobate tuning fork studied here, this gives $a_{\rm th}=2.3\times 10^{-3}$ NV⁻¹. This is roughly five times larger than the experimental value. We note that for quartz tuning forks, the theoretical expression often overestimates the fork constant by a factor of three or so [16, 17].

Measurements Around the bcc-hcp Phase Transition

Measurements were made by sweeping the frequency at a constant drive amplitude whilst measuring the signal current. We measure the components of the signal which are in-phase and out-of-phase with the driving voltage. After subtracting the background signals due to the measurement circuit, we obtain the signal due to the fork motion which gives the prong tip velocity using Eq. (2).

Figure 2 shows the amplitude of the in-phase prong tip velocity, v _x versus frequency and temperature. The driving force amplitude was F=1.78 mN. The corresponding stress, σ=F/LW=3 mbar, is well below the measured yield stress, ∼100 mbar, of solid ⁴He [24]. The mean power dissipated by the fork (both prongs) can be computed as the product $\dot{Q}=Fv_{x}$. The figure is constructed from a series of frequency sweeps made whilst warming through the hcp-bcc phase transition. The transition is seen at around 1.44 K, slightly lower than the expected transition temperature of 1.46 K [25]. The discrepancy is most likely due to a small temperature gradient between the cell and the thermometer on the mixing chamber of the refrigerator. The figure shows a single resonance in the hcp phase at a frequency of around 41 kHz. On warming, the response changes discontinuously on entering the bcc phase, showing two overlapping resonances at frequencies of around 37 kHz and 38 kHz. The response is reproducible on cooling but different samples show different behaviours. All samples show a discontinuous change at the bcc-hcp transition but the change in frequency at the transition varies from around −4 kHz to +5 kHz.

Fig. 2

The in-phase velocity amplitude versus frequency and temperature of the tuning fork around the hcp-bcc transition (Color figure online)

Measurements in the hcp Phase Down to Very Low Temperatures

Figure 3 shows the behavior of the tuning fork on cooling in the hcp phase to low temperatures. For this particular helium sample, the resonant frequency first increases from f ₀≈37 kHz to f ₀≈38.5 kHz on cooling to T≈1.2 K. On cooling further the frequency passes through a maximum and then falls to f ₀≈35 kHz. Below T≈0.15 K the response shifts discontinuously and an additional small resonance appears at f ₀≈36.5 kHz. At T≈80 mK there is another discontinuous change and further resonance peaks appear.

Fig. 3

The in-phase velocity amplitude versus frequency and temperature of the tuning fork in the hcp phase (Color figure online)

The behaviour is reproducible for a given cool-down, but differs between helium samples. The resonance always splits into several overlapping narrower resonances at low temperatures but the changes are not always discontinuous. Figure 4 shows an example of the amplitudes of the velocity components versus frequency at T=3 mK. The figure shows 20 or more overlapping resonances from around 39 kHz to 42 kHz. The individual resonances are much narrower than the resonances observed at higher temperatures.

Fig. 4

The amplitudes of the in-phase and out-of-phase velocity components of the tuning fork versus frequency in the hcp phase at T=3 mK (Color figure online)

Discussion

The resonance frequency in the solid is significantly higher than the vacuum frequency. The large frequency shift corresponds to the extra elastic restoring force provided by the solid. This will depend on both the shear modulus and bulk modulus of the solid helium surrounding the prongs. The elastic properties of solid helium are quite anisotropic particularly at low temperatures [26] so we expect the frequency to depend on the precise structure and orientation of each crystal which will vary for different samples. Indeed we find a significant variation in the resonant frequency in both phases for different samples. The resonance frequencies can vary by about 10 kHz under nominally identical conditions. We always observe a discontinuity in the response at the bcc-hcp phase transition although the precise behaviour varies for different samples.

The tuning fork motion in the solid is quite heavily damped as evident from the large frequency widths of the response. This indicates viscoelastic behavior. Damping may result from the motion of defects and/or vacancies in the solid. We have made further studies of the viscoelastic properties of solid ⁴He using the ‘floppy’ wire shown in Fig. 1. These measurements will be discussed in an accompanying paper.

The temperature at which the tuning fork resonance splits into multiple narrower resonances in the hcp phase is similar to the temperatures where changes in the mechanical properties have been observed by many groups [1–4]. It has been suggested that the elasticity of the solid may change at low temperatures due to pinning of defects by ³He impurities [26]. This may be responsible for the low temperature behaviour of the tuning fork. We believe that the multiple resonances correspond to resonances of the entire crystal, defined by the geometry of the cell. We note that the samples studied here were grown from isotopically pure ⁴He, but the gas handling system was previously used for ³He samples so there may be a small residue of ³He.

To conclude, we have presented the first measurements of the response of a lithium niobate tuning fork vibrating in solid ⁴He over a wide temperature range. The response of the tuning fork is sensitive to the viscoelastic properties of the solid and is dependent on the crystal structure and orientation. The device offers a very simple and versatile tool to complement other studies of solid helium.