Plastic Properties of Solid ⁴He Probed by a Moving Wire: Viscoelastic and Stochastic Behavior Under High Stress

Abstract

We present measurements of a thin wire moving through solid ⁴He. Measurements were made over a wide temperature range at pressures close to the melting curve. We describe the new experimental technique and present preliminary measurements at relatively high driving forces (stresses) and velocities (strain rates). The wire moves by plastic deformation of the surrounding solid facilitated by quantum tunneling of vacancies and the motion of defects. In the bcc phase we observe very pronounced viscoelastic effects with relaxation times spanning several orders of magnitude. In the hcp phase we observe stochastic step-like motion of the wire. During the step, the wire can move at extremely high velocities. On cooling, the wire ceases to move at a temperature of around 1 K. We are unable to detect any motion at lower temperatures, down to below 10 mK.

Introduction

The mechanical properties of solid ⁴He have been a topic of intense interest in recent years following speculations of ‘supersolid’ properties at low temperatures inferred from torsional oscillator experiments [1]. Later observations of changes in the elastic properties of the solid [2–5] suggest that the newly discovered properties may be caused by changes in plasticity [6, 7] rather than supersolidity.

Here we discuss direct measurements of plastic deformations made by observing the motion of a thin wire through the solid. We show preliminary results for the bcc and hcp phases for the case where a large driving force (stress) is applied to the wire.

Experimental Details

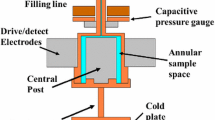
A schematic of the experimental cell, viewed from above, is shown in Fig. 1a. The epoxy cell wall is potted in Stycast 1266 inside a larger epoxy container (not shown) which provides sufficient strength to hold pressures in excess of 70 bar. The helium in the cell is cooled by a pad of silver sinter which connects, via a high purity annealed silver wire, to a larger pad of silver sinter in the mixing chamber of the dilution refrigerator [8]. The cell contains 2 commercial pressure sensors,¹ a lithium niobate tuning fork (to be discussed in an accompanying article) and several tuning forks which are not important for the present discussion.

Fig. 1

(a) A schematic of the experimental cell as viewed from above; ‘P’ indicates the locations of two pressure sensors; also indicated are the positions of various tuning forks (not used in the current experiment); the ‘floppy’ wire crossbar is located a few mm above the other devices and is free to move sideways. (b) Schematic of the wire loop viewed sideways, the other devices are omitted for clarity. The two pick-up coils are located outside of the helium volume and are potted in the surrounding stycast 1266 used to strengthen the cell, see text

The ‘floppy’ wire used for the measurements described below is shown schematically from a sideways perspective in Fig. 1b (other devices in the cell are not shown here for clarity). The wire loop is formed from an insulated CuNi clad filamentary NbTi wire. The formvar insulation gives a smooth surface of diameter 55 μm. The loop is 20 mm high with a crossbar D=10 mm long that is 1 mm above the other devices in the cell and 0.7 mm below the top of the cell. The loop is free to move horizontally perpendicular to the crossbar by applying a dc current I through the wire in a vertical magnetic field, B. This produces a Lorentz force, F=IBD. The position of the crossbar is measured using two pick-up coils located above the wire as indicated in Fig. 1b. A small high frequency (∼30 kHz) ac probe current is superimposed on the dc current through the wire. This induces voltages in the pick-up coils which depends on the position of the crossbar. The operational details of such a device are described more fully elsewhere [9].

Calibration of Position Measurements

We first calibrate the coil response to determine the position x of the crossbar. We assume that the displacement (in vacuum or in a fluid) varies linearly with the dc current (force), and use the known separation L=15 mm between the cell walls. A calibration in superfluid ⁴He at a temperature of T=1.5 K and a field B=132 mT is shown in Fig. 2. Here we plot the normalised coil response (signal voltage divided by the ac probe current) of the two coils as a function of the dc current, I. When the crossbar hits the walls of the cell the response becomes much flatter as shown in the figure. The very small variation in the response whilst the wire is in contact with the walls is probably due to a slight misalignment so the wire bends slightly until it is flat against the wall at higher currents. The absolute position of the crossbar is calculated as

$$ x = \frac{L}{\varDelta I} I $$

(1)

where ΔI is the difference between the currents required for the wire to touch the two walls. In practice there is a small (∼5 %) hysteresis in the wire displacement. The position of the wire with no dc current is dependent on the field but the coil calibration is otherwise independent of the magnetic field. We attribute these effects to flux line pinning in the NbTi filaments, as discussed in earlier work [10]. In principle we can use the response of either coil to determine the position, but in practice we use the ratio of the coil responses, also shown in Fig. 2. We fit this ratio versus the position. This provides the transfer function to determine the position of the crossbar from the measured coil responses.

Fig. 2

The calibration for position measurements. The black and red lines show the normalised response (left axis) for coil 1 and 2 respectively, versus the dc current, I. The blue line shows the ratio of the responses which is used to find the position of the wire crossbar (top axis), see text. The positions of the cell walls are shown by the dashed lines (Color figure online)

Measurements in Solid Helium

We have studied the motion of the wire in solid ⁴He over a wide range of temperatures and driving forces. We have studied several different solid samples. We grow the samples by varying the pressure at an approximately constant temperature. For the measurements presented below, the samples were grown at low temperatures, below 10 mK. Different samples show qualitatively similar behavior. At low driving forces (low stress), we observe slow motion of the wire in both the hcp and bcc phases above 1 K. This type of motion was studied previously in the vicinity of the bcc-hcp phase transition [11, 12] and is thought to be due to the diffusion of vacancies around the wire via quantum tunneling [13]. The first attempt at measuring the motion of an object through solid helium was made by Andreev et al. [14] in 1969. Later measurements were performed on dragging rods and spheres through the solid [15] and also on the plastic deformation of single crystals [16].

Below we present some preliminary measurements on the behaviour of the wire at high driving forces (high stress). All the measurements were taken at temperatures above 1 K and at pressures close to the melting curve. At lower temperatures we see no significant motion of the wire down to temperatures below 10 mK. Measurements made with lower driving forces will be discussed elsewhere.

Measurements in the hcp Phase

Figure 3 shows measurements for large driving forces in the hcp phase at a temperature of T=1.15 K and a magnetic field of B=1.99 T. At a time t=927 s the driving force is ramped linearly from F=−9.3 mN to F=+9.3 mN over a period of 105 s. At first, the wire remains stationary at a position x=0.08 mm. At t=1343 s, the wire suddenly moves to x=0.9 mm and then abruptly stops. It remains here until t=1921 s when the wire suddenly moves to x≈1.0 mm. After this there are a further five steps and the wire finally reaches x≈1.5 mm at t=6627 s, more than an hour after the force was changed. Then, at t=7033 s force is ramped back to F=−9.3 mN over a period of 105 s. Just before the end of the ramp, the wire suddenly moves to x=0.07 mm for a short period and then moves to x=−0.8 mm.

Fig. 3

Measurements of the wire position versus time in the hcp phase (right axis). The large driving force (left axis) is first negative, then ramped to a positive value for a period of approximately 6000 s, and is then ramped back to the starting value. In response, the wire shows several stochastic step-like changes in position, see text (Color figure online)

The behaviour is highly stochastic, the step distance and the time at which a step occurs vary randomly over a wide range. If the driving force is kept at a constant value, then the wire will continue to step in the direction of the force until it reaches the wall of the cell. (When it touches the wall it often becomes partially stuck and larger forces are needed to detach it.) During a step, the wire velocity is very large. For the data shown in Fig. 3, the time between the measurement points is approximately 60 ms. The larger steps are seen to occur over a time period of Δt≈300 ms and the velocity of the crossbar during the step often exceeds 1 mms⁻¹. Such velocities are enormous compared to typical velocities, v≈1 nms⁻¹, observed at low driving forces [11].

We further note that the steps are only observed in the hcp phase at temperatures above ∼1.1 K and we do not observe any changes in pressure during the steps.

Measurements in the bcc Phase

Figure 4 shows measurements in the bcc phase. We plot the position of the wire crossbar versus time, note that the time axis now spans more than 4×10⁵ s≈5 days. The driving force starts at a large positive value, F=3.1 mN. At time t=1602 s the force is ramped linearly to a large negative value F=−3.1 mN over a time period of 80 s. The wire responds immediately, moving in the direction of the force. The initial wire velocity, v∼−1 μms⁻¹, is much slower than that observed during the step-like motion in the hcp phase discussed above. However the wire velocity falls rapidly at first, reaching a near constant value of v∼−7 nms⁻¹ after ∼5000 s. The motion then remains quite uniform until the driving force is quickly ramped to zero at t=80937 s.

Fig. 4

Measurements of the wire position versus time in the bcc phase (left axis). The applied force (right axis) is first ramped from a large positive to a large negative value. Af t=80937 s the force is quickly ramped to zero. In response, the wire position changes smoothly and gradually in a non-linear fashion, indicative of viscoelastic behavior of the surrounding solid, see text. The measurements were taken whilst the cell was slowly warming from 1.48 K to 1.71 K (Color figure online)

Remarkably the wire is not stationary in the absence of an applied force. Instead, it relaxes very slowly towards some new position. The initial velocity after removing the driving force is comparable to the velocity before removing the force, but is in the opposite direction. The velocity then slows over the next couple of days, reaching a near constant value of v≈0.4 nms⁻¹, indicated by the dashed line in the Fig. 4. By comparing with our measurements at low driving forces, we conclude that the bare restoring force of the wire, which can be found from the data in Fig. 2, is roughly ten times too small to account for the late time behaviour. Presumably after waiting for a sufficient time, the wire will stop at some final resting place which will depend on its history. However, the time scales are very long, even after several days the wire shows no sign of slowing further.

Discussion

The step-like behaviour in the hcp phase shown in Fig. 3 was very unexpected. More work is needed to understand their origin but we may offer some speculations. The abrupt motion, separated by long intervals of time where the wire is static, is reminiscent of the ‘stick-slip’ mechanism of friction [17]. We speculate that the wire might ‘stick’ to complex networks of tangled dislocations in the solid. After some time, conditions prevail that allow the wire to cut through the tangle, triggered by some stochastic mechanism. The wire will then ‘slip’ until it encounters another obstacle. The extremely high velocities observed during each slip suggest that the solid in the immediate vicinity of the wire must become extremely mobile, possibly fluid-like. From the results of neutron scattering experiments on aerogel [18] we might anticipate a thin liquid layer at the wire surface. The presence of a large non-hydrostatic strain induced by the wire might then lead to an instability similar to that found in bulk liquid–solid interfaces [19] and a sudden growth of the liquid layer to generate a slip event.

In the bcc phase, the response gives a very clear demonstration of viscoelastic properties, see Fig. 4. When a large driving force is applied, the wire moves in the direction of the force, storing up elastic energy in the surrounding solid. When the force is removed, the elastic energy relaxes and the wire moves back towards where it came from. The very long time scales involved show that the motion is extremely dissipative and viscous-like. We note that viscoelastic effects have been considered recently on theoretical grounds in an attempt to explain the anomalous mechanical behavior observed at low temperatures [20, 21].

Motion of the wire requires mass transport in the surrounding solid. Atoms must move from the front to the rear of the wire, requiring flow through the crystal along many directions. For small driving forces this is realised by the diffusion of vacancies from the rear to the front of the wire as observed previously [11]. At higher driving forces, mass flow can also be generated by the motion of dislocations in the solid [15]. We speculate that the strikingly different behaviors observed in the two phases may be a consequence of different defect dynamics. In the bcc phase there are many ‘easy’ planes in which defects may glide quite freely. In the hcp phase however, defects can only move freely in the basal planes, as was demonstrated in recent experiments at lower temperatures [7].